問題3 の攻略
平成29年から令和4年までの6年間は、バーチャート工程表の出題で、工程表の読みと、出来高表の計算およびまとめの問題であるが、それ以前は、ネットワーク工程表が出題されつづけていた。
ネットワーク工程表の問題にもどることは、まず考えにくいが、簡単な解き方はおさえておきたい。
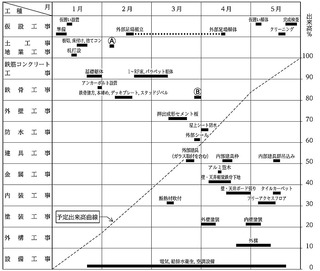
木造2階建て住宅の建設工事における右の工程表と出来高表に関し、次の 1.から 3.の問いに答えなさい。
なお、工程表は工事着手時点のものであり、予定出来高曲線を破線で表示している。
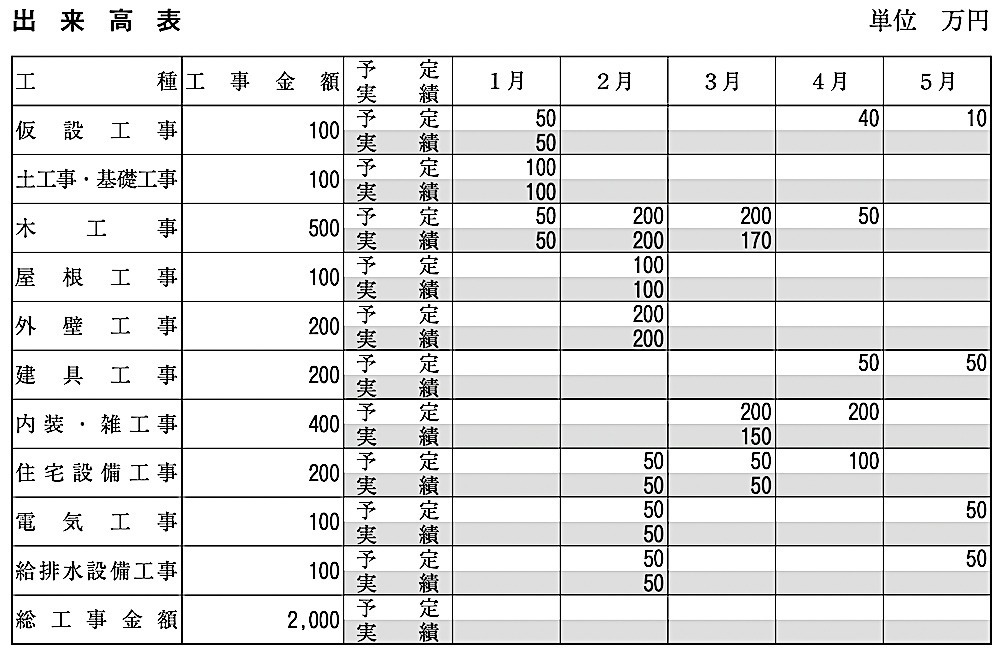
また、出来高表は3月末時点のものを示しているが、建具工事のうち外部アルミニウム製建具の出来高及び総工事金額の月別出来高は、記載していない。
用 途:住 宅
構造・規模:木造在来軸組工法 2階建て 延べ面積 100 m2
基 礎:ベタ基礎
仕 上 げ:屋根は、住宅屋根用化粧スレート張り
外壁は、塗装窯業系サイディングボード張り
内装は、壁天井ともせっこうボード下地クロス仕上げ
床はフローリング仕上げ
工 程 表
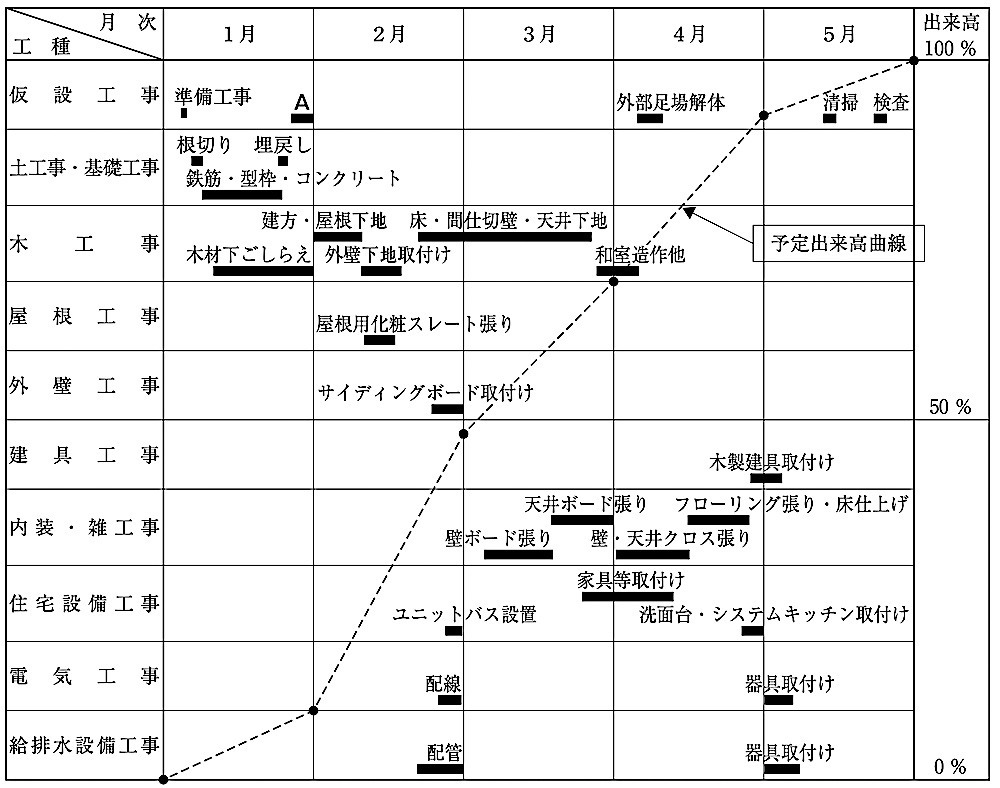
1.工程表の仮設工事のA に該当する作業名を記述しなさい。
解答
外部足場設置
[ 解説 ]
① Aは、工程表より仮設工事。
② 4月に外部足場解体がある。
③ 2月から建方が始まる。
以上のことから、Aは外部足場設置
と考えられる。
2.建具工事における外部アルミニウム建具の取付け作業の工程は、未記入となっている。適当な工程となるように、取付け作業の開始日を月次と旬日で定めて、記入しなさい。
ただし、解答の旬日は、上旬、中旬、下旬とする。
解答
2月中旬
[ 解説 ]
外部アルミニウム建具の取付けは、
①屋根葺き完成後
②外壁サイディング工事前
となるので、2月中旬の作業開始が妥当である。
3. 出来高表から、総工事金額に対する3月末までの完成出来高の累計をパーセントで記入しなさい。
解答
66%
[ 解説 ]
3月までの工事実績は、予定金額より△80万円(木工事△30、内装・雑工事△50)。全体工事2000万円において占める割合は、
80/2000 × 100 = 4%
3月末までの予定出来高は、予定出来高曲線により 70%であるので、4%遅れていることになる。
したがって出来高は、
70 – 4 = 66%
となる。
なお、外部アルミニウム建具は、出来高表100%の内訳には入っていない。
3月末までの出来高表は下記のようになる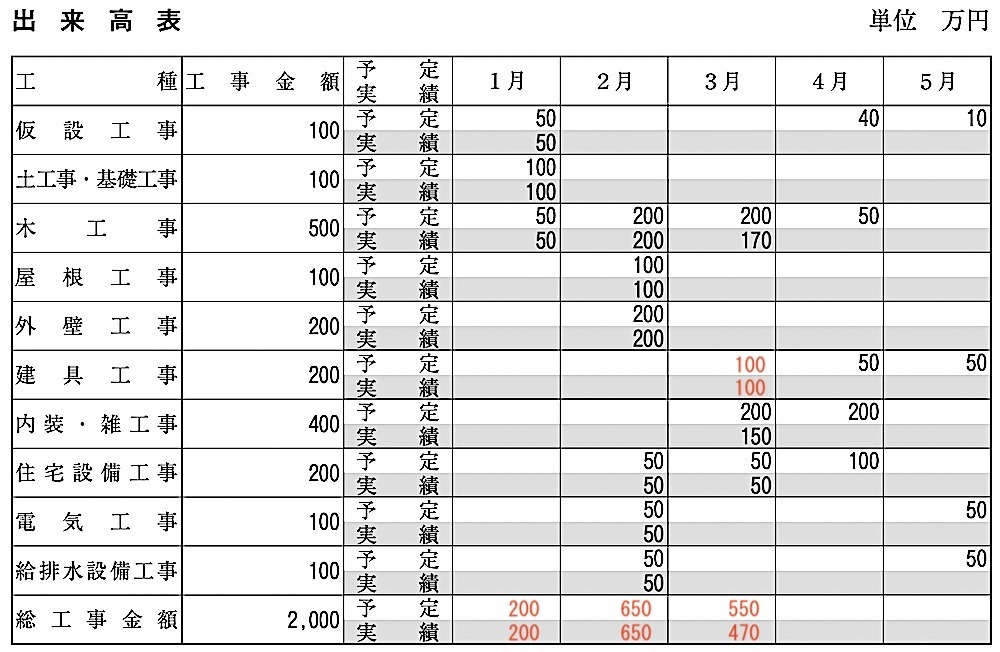
図に示すネットワーク工程表について、次の 1.から 3.の問いに答えなさい。
なお、 ◯内の数字はイベント番号を、実線の矢線は作業を、破線の矢線はダミーを示し、また、矢線の上段のアルファベットは作業名を、下段の数値は所要日数を示すものとする。
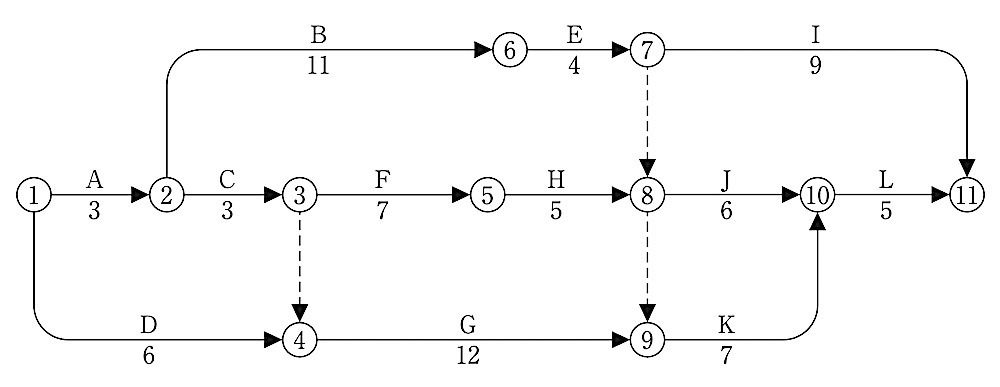
ネットワーク工程表
1. 工程表において、①から⑪までの総所要日数を答えなさい。
解答
30日
[ 解説 ]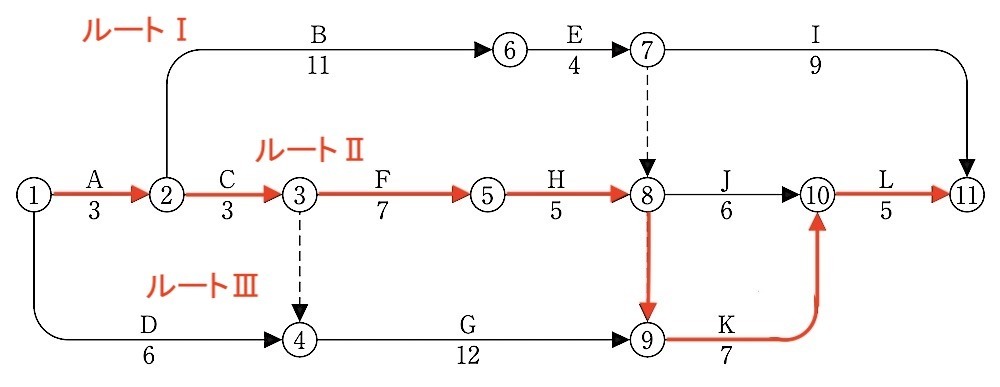
総所要日数
ルートⅠ:
① → ② → ⑥ → ⑦ → ⑪
ルートⅡ:
① → ② → ③ → ⑤ → ⑧(⑦終了まで待ち)→ ⑩ → ⑪
ルートⅢ:
① → ④(③終了まで待ち) → ⑨(⑧終了まで待ち)→ ⑩ → ⑪
ルートⅠの計算
= A + B + E + I
= 3 + 11 + 4 + 9 = 27日
ルートⅡの計算
= A + C + F + H + J + L
= 3 + 3 + 7 + 5 + 6 + 5 = 29日
( A + B + E = 3 + 11 + 4 =18日待ち)
ルートⅢの計算
= D + G + K + L
= 6 + 12 + 7 + 5 = 30日
(A + C + F + H = 18日待ち)
よって、ルートⅢの 30日が総所要日数となる。
2. 工程の再検討を行ったところ、作業Hの所要日数が1日、作業Jが2日増加することが分かった。このときのクリティカルパスを、作業名で工程順に並べて答えなさい。
解答
A → C → F → H → J → L
[ 解説 ]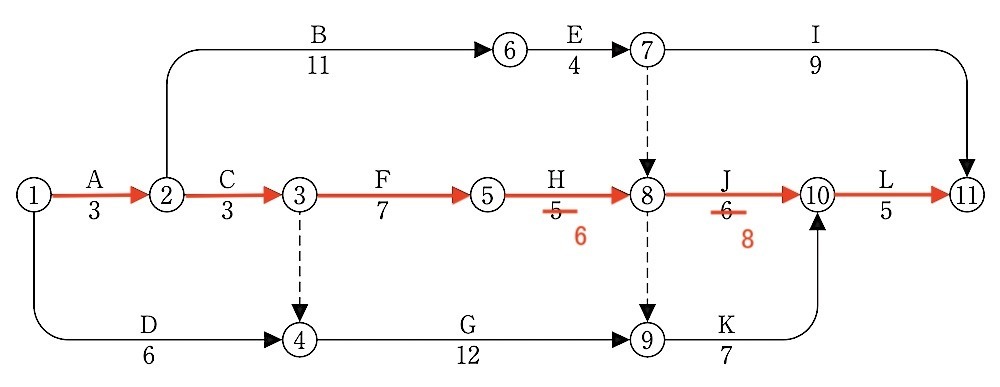
H が 6日、Jが 8日となる。
⑧までの所要日数は、
① → ② → ③ → ⑤ → ⑧
= A + C + F + H
= 3 + 3 + 7 + 6 = 19日
全体は、
⑧ → ⑩ → ⑪ = 8 + 5 = 13日
を加えて
計19 + 13 = 32日
となる。
⑨ → ⑩ の作業Kは、
⑧が終了しなければ行うことができない。
⑧まで19日なので、
⑨ → ⑩ → ⑪
= K + L
= 7 + 5 = 12日
とを加えて、
計19 + 12 = 31日
となる。
したがって、クリティカルパスは、
① → ② → ③ → ⑤ → ⑧ → ⑩ → ⑪
= A + C + F + H + J + L
である。
3. 作業Hの所要日数が1日、作業Jが2日増加するときの①から⑪までの総所要日数を当初と同じ日数とするために、作業Bと作業Fの日程短縮により調整する場合、作業Bと作業Fはそれぞれ最小限何日短縮すればよいか答えなさい。
解答
作業Bを1日短縮、作業Fを2日短縮する。
[ 解説 ]
上記 32日を作業B、作業Fを短縮して 30日とする。
クリティカルパス32日を2日短縮するためには、
まず作業Fを2日短縮する。すなわち、
F = 7- 2 = 5日
となる。
次に、
① → ② → ③ → ⑤ → ⑧
= A + C + F + H
= 3 + 3 + 5 + 6 =17日となり、
⑧までは 17日としなければならない。
よって、
① → ② → ⑥ → ⑦ = ⑧
= A + B + E = 17日としなければならない。
現在、18日間であるので、作業Bを1日短縮し、
11 – 1 = 10日とする。
図に示すネットワーク工程表について、次の 1.から 3.の問いに答えなさい。
なお、◯内の数字はイベント番号を、実線の矢線は作業を、破線の矢線はダミーを示し、矢線の上段のアルファベットは作業名を、下段の数値は所要日数を示すものとする。
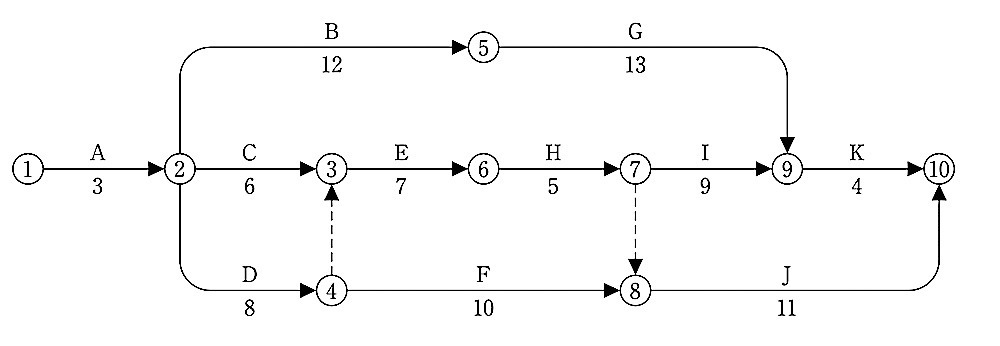
1. 工程表において、クリティカルパスを作業名で工程順に並べて答えなさい。
解答
クリティカルパス
A → D → E → H → I → K
[ 解説 ]
クリティカルパスとは、該当するネットワーク中で最も日数を要する経路のことをいい、その日数が総所要日数である。
作業の開始と終了のときに付ける◯印をイベントという。
→ をアロー(矢線)といい、矢線の上に作業名、下に所要日数が記載される。
このイベントと矢線と作業名、所要日数をまとめてアクティビティという。
アクティビティが連結されて、ネットワーク工程表が作成される。
①全イベントの右上に□を表示する。(形は□でなくてもよい)
②最初のイベント①の□に 0 を記入し、最初の作業Aの最早開始時刻とする。
③イベント番号の若い順に、□(最早開始時刻)と所要日数との和を記入する。
これが各作業の最早開始時刻となる。
④2本以上の矢線がイベントに流入するときは、そのうちの最大値を最早開始時刻とする。こうして計算した、最終イベントの最早開始時刻が工期(クリティカルパス)となる。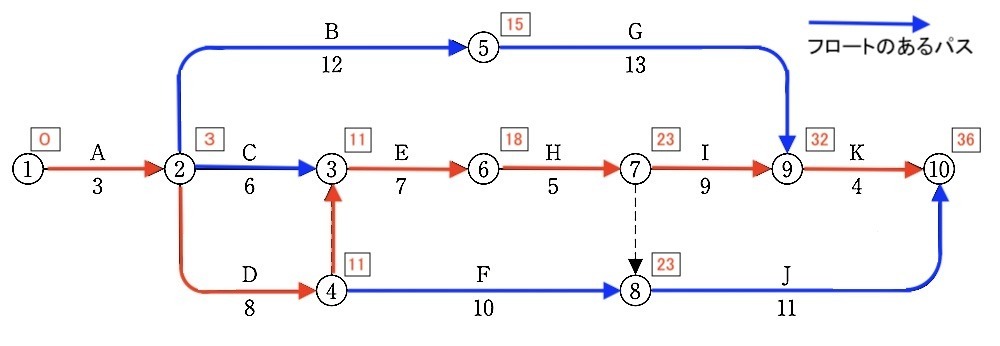
2. 工程の再検討を行ったところ、イベント番号⑥から⑤への所要日数2日の新たな作業Lが発生した。この時の①から⑩までの総所要日数を答えなさい。
解答
37日
[ 解説 ]
総所要日数(LST)の計算
① → ② → ④ → ③ → ⑥ → ⑤ → ⑨ → ⑩
= A → D → E → L → G → K
=3 + 8 + 7 + 2 + 13 + 4
=37 日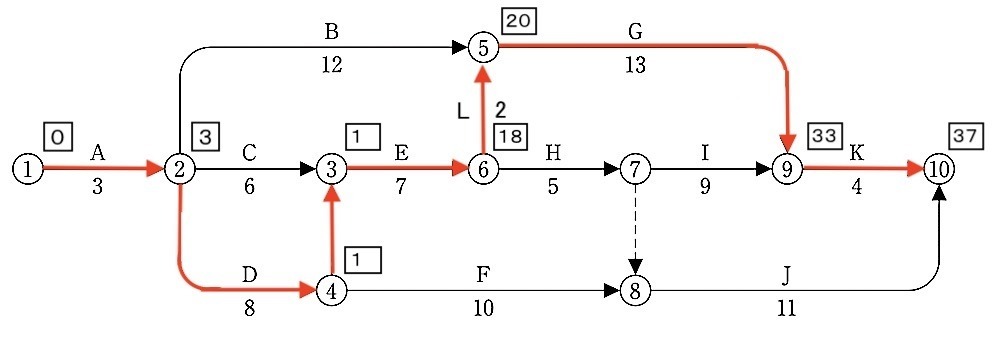
3. 新たな作業Lが発生する前と発生した後の作業Bのフリーフロートをそれぞれ日数で答えなさい。
解答
作業Lが発生する前の作業Bのフリーフロート(余裕時間)
= 0 日
作業Lが発生した後の作業Bのフリーフロート
= 5 日
[ 解説 ]
総所要日数(LST)の計算
作業 L が発生する前と発生した後の作業B のフリーフロート(余裕時間)の日数
作業 L が発生する前の作業Bのフリーフロート(余裕時間)=0
作業Bはイベント②~⑤間。①~⑤間で日数を比較考察する。
最速日数 = ① → ② → ⑤
= 3 + 12 = 15 日
最遅日数 = ① → ② → ⑤
= 3 + 12 = 15 日
フリーフロート = 最遅日数 - 最早日数
= 15日 – 15日 = 0日
作業Lが発生した後の作業Bのフリーフロート = 5日
イベント①~⑥間で日数を比較考察する。
最速日数 = ① → ② → ⑤
= 3 + 12 = 15 日
最遅日数 = ① → ② → ④ → ③ → ⑥
= 3 + 8 + 7 + 2 = 20 日
フリーフロート = 最遅日数 - 最早日数
= 20日 – 15日 = 5日
図に示すネットワーク工程表について、次の1.から3.の問いに答えなさい。
なお、内の数字はイベント番号、矢線の上段のアルファベットは作業名、下段の数値は所要日数を示す。
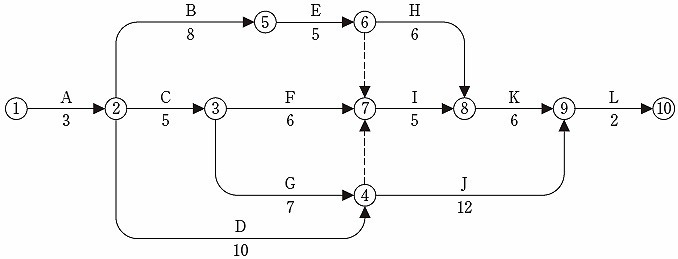
1.工程表において、①からまでの総所要日数を答えなさい。
解答
30日
[ 解説 ]
総所要日数の計算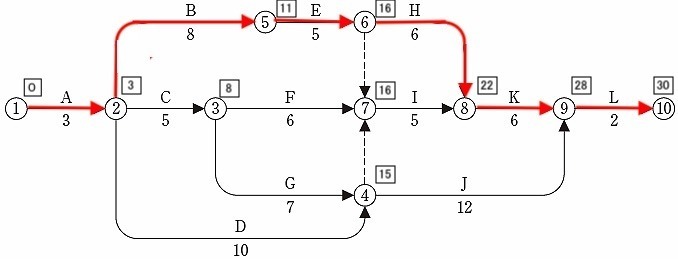
まず、最初のイベント①の右肩に [ 0 ] と記入する。
次に、イベント②の右肩に 作業Aの作業日数3を加えて [ 3 ]と記入する。
順次、その足し算を行うが、
イベントに対してアロー(矢印)が2本以上入ってる部分のイベントについては、最大の日数を記入して上記工程表のようにクリティカルパスを得る。総所要日数は 30日となる。
2.工程表において、作業Cと作業Dがそれぞれ3日間遅延したときのクリティカルパスを作業名で工程順に並べて答えなさい。
解答
A → C → G → J → L
[ 解説 ]
作業C、作業Dがそれぞれ3日間遅延したときのクリティカルパス
作業C(② → ③)が3日遅延、作業日数 5日 → 8日
作業D(② → ④)が3日遅延、作業日数10日 →13日
と変更し、問1と同じ操作を行い、下記のネットワーク工程表を得る。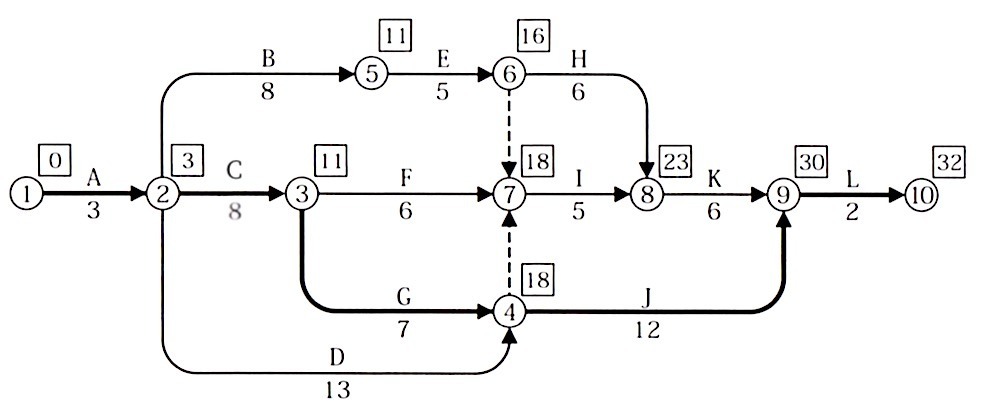
3.工程表において、作業Cと作業Dがそれぞれ3日間遅延したとき、①から⑩までの総所要日数を当初と同じ日数とするために、作業Iと作業Jの作業日数のみを短縮する場合、作業Iと作業Jは、それぞれ最小限何日間短縮すればよいか答えなさい。
解答
作業 Ⅰ を1日間短縮、作業Jを2日間短縮する。
[ 解説 ]
作業C、作業Dが3日間遅延したとき、当初総所要日数にするために作業 I、作業Jは最小限何日間短縮すればよいか?
作業C、作業Dが3日間遅延であるので、問題2のネットワーク工程表をベースに考察する。
当初の総所要日数にするので、イベント⑩の右肩の数字を [30] とする。
Lの作業日数を引くと、イベント⑨の右肩の数字は [28]となる。
同様に計算して、作業 I の作業終了時のイベント⑧の右肩の数字は [22]となり、
下記ネットワーク工程表を得る。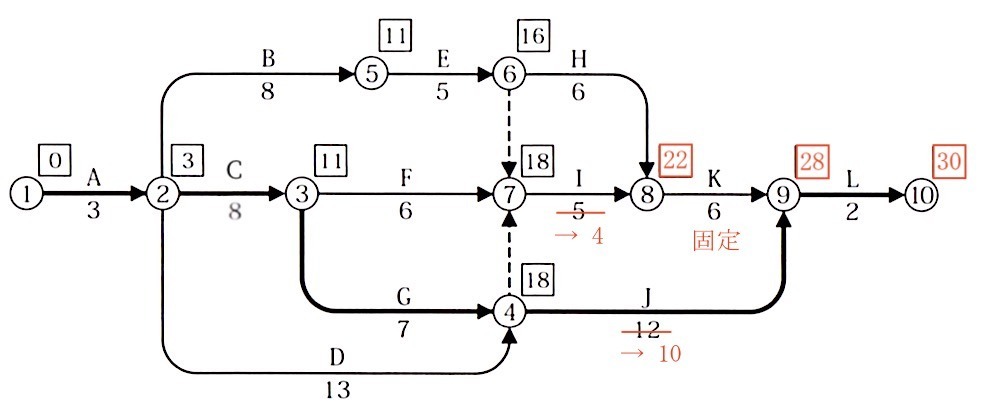
以上の結果より作業 I を1日間、作業J を2日間短縮する。
ちなみに、右肩の□マークの数字は、次の作業の最早開始時刻(EST)という。
図に示すネットワーク工程表について、次の 1.から 3.の問いに答えなさい。
なお、 ◯内の数字はイベント番号、矢線の上段のアルファベットは作業名、下段の数値は所要日数を示す。
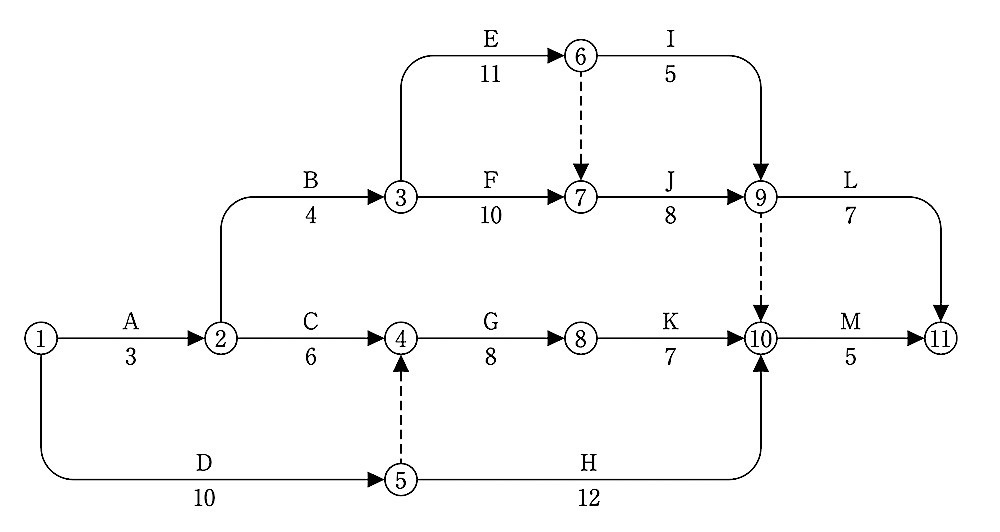
1. 工程表において、クリティカルパスを、作業名で工程順に並べて答えなさい。
解答
A → B → E → J → L
[ 解説 ]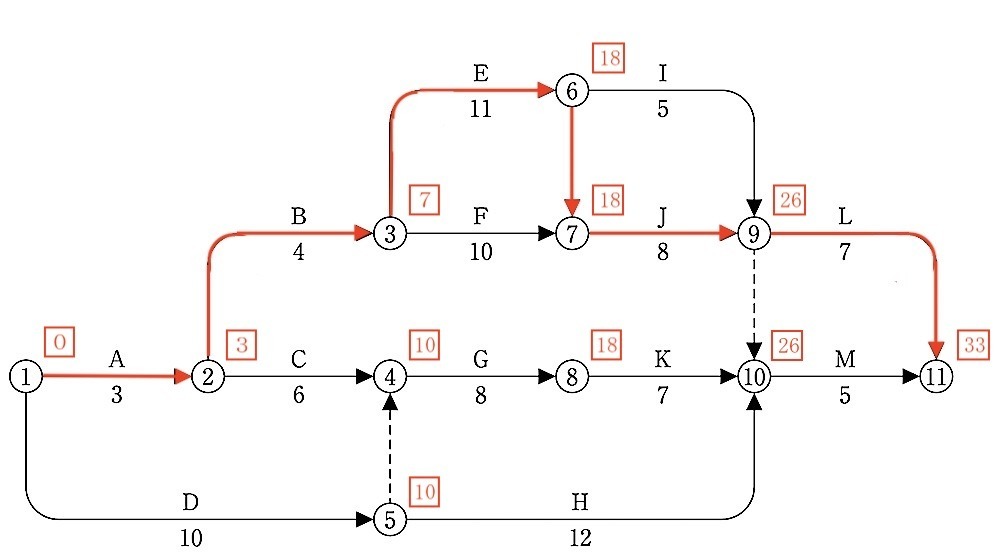
①全イベントの右上に□を表示する。(形は□でなくても、何でも良い)
②最初のイベントの右上の□に 0 を記入し、最初の作業Aの最早開始時刻(EST)とする。
③イベント番号の若い順に、□(最早開始時刻)と所要日数との和を記入する。
これが各作業の最早開始時刻となる。
④2本以上の矢線(アロー)がイベントに流入するときは、そのうち最大値(max)を最早開始時刻とする。こうして計算した、最終イベントの最早開始時刻が工期となり、その経路がクリティカルパスとなる。
A → B → E → J → L
= 3 + 4 + 11 + 8 + 7
= 33日
2. 工程表において、作業Hの EFT(最早終了時刻)とフリーフロートをそれぞれ日数で答えなさい。
解答
EFT(最早終了時刻):22日
フリーフロート :4日
[ 解説 ]
EFT(最早終了時刻)とは、その作業が最も早く終了できる時刻である。
その作業の最早開始時刻(EST) + 所要日数(D)
により求める。
つまり、その作業が開始できる時刻になって、直ちに開始し、予定の所要日数で終了する時刻をいう。
作業 H のEFTは、
最早開始時刻(10日) + 所要時間(12日)
= 22 日
フリーフロートとは、作業の中で自由に使っても、継続する作業に影響を及ぼさない余裕時間のことである。
作業 H のフリーフロートは、
イベント⑩の最早開始時刻(26日)- イベント⑤の最早開始時刻(10日)– 作業日数(12日)
= 4日
3. 工程表において、作業Dと作業Kがそれぞれ3日間遅延したときの①から⑪までの総所要日数を答えなさい。
解答
36日
[ 解説 ]
工程表において、作業Dと作業Kがそれぞれ3日間遅延したときのクリティカルパスは図による。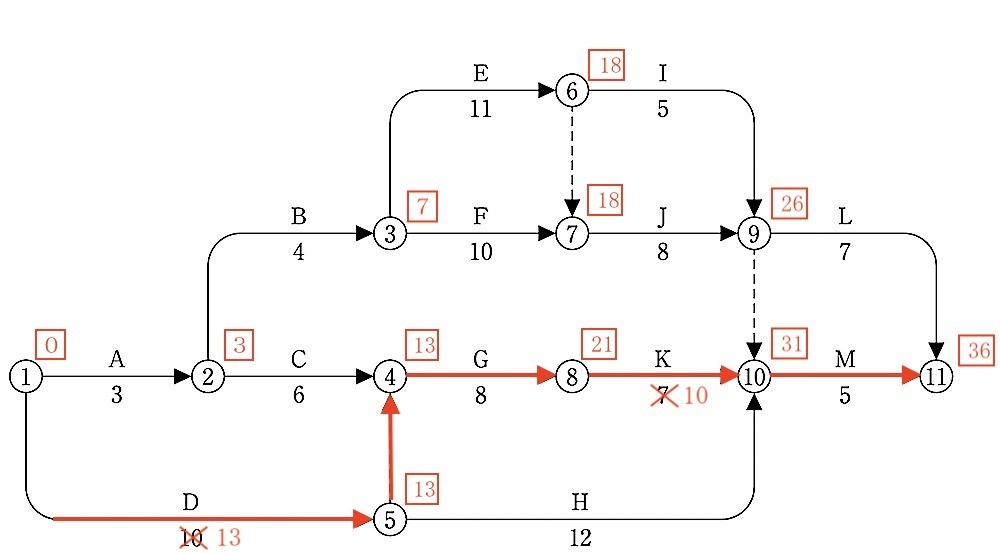
D + G + K + M
= 13日 + 8日 + 10日 + 5日
= 36日