【 構造力学 】
< 反力及び応力を求める問題 >
( 1 )
図に示す単純梁ABに集中荷重P1及びP2が作用するとき、CD間に作用するせん断力の値の大きさとして、正しいものはどれか。(令和4年前期_No.9)
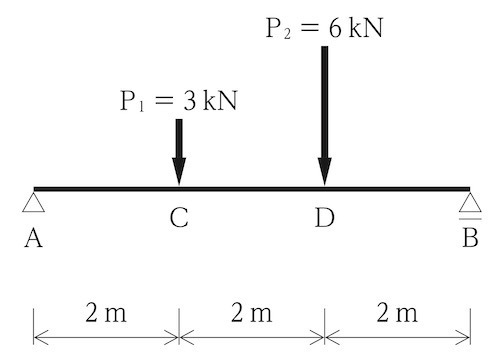
1.1 kN 2.3 kN 3.4 kN 4.5 kN
答え
1
[ 解答解説 ]
点AニおけるモーメントをMAとすると、
MA = 0より
MA = 3kN × 2m + 6kN × 4m - VB [ kN ] × 6m =0
よって、VB = 5kN ・・・①
鉛直方向の力のつり合いより
VA [ kN ] + VB [ kN ] - 3kN - 6kN = 0
VA + VB = 9kN
①を代入して、VAについて解くと
VA = 4kN
よって、せん断力図(Q図)は以下のようになる。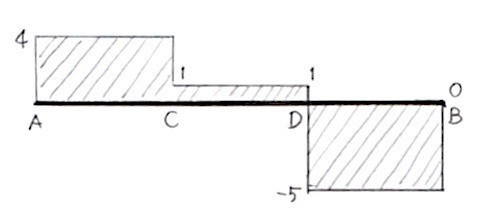
VA = 4kNより、A点はプラス方向に4とし、C点へせん断力が伝わる。
P1 = 3kNより、C点で 4 – 3 = 1kNとなり、D点まで伝わる。
よって、CD間に作用するせん断力は1kNとなる。
D点では、P2 = 6kNにより、1-6 =-5kNとなり、B点へ伝わる。
B点は、VB = -5kNより、-5 + 5 = 0kNとなり、
せん断力図が完成する。
ゆえに、CD間に作用するせん断力は、1kNなので、
正答肢は 1
( 2 )
図に示す単純梁ABに等変分布荷重が作用するとき、支点Aの垂直反力VA及び支点Bの垂直反力VBの大きさの比率として、正しいものはどれか。(令和3年後期_No.9)
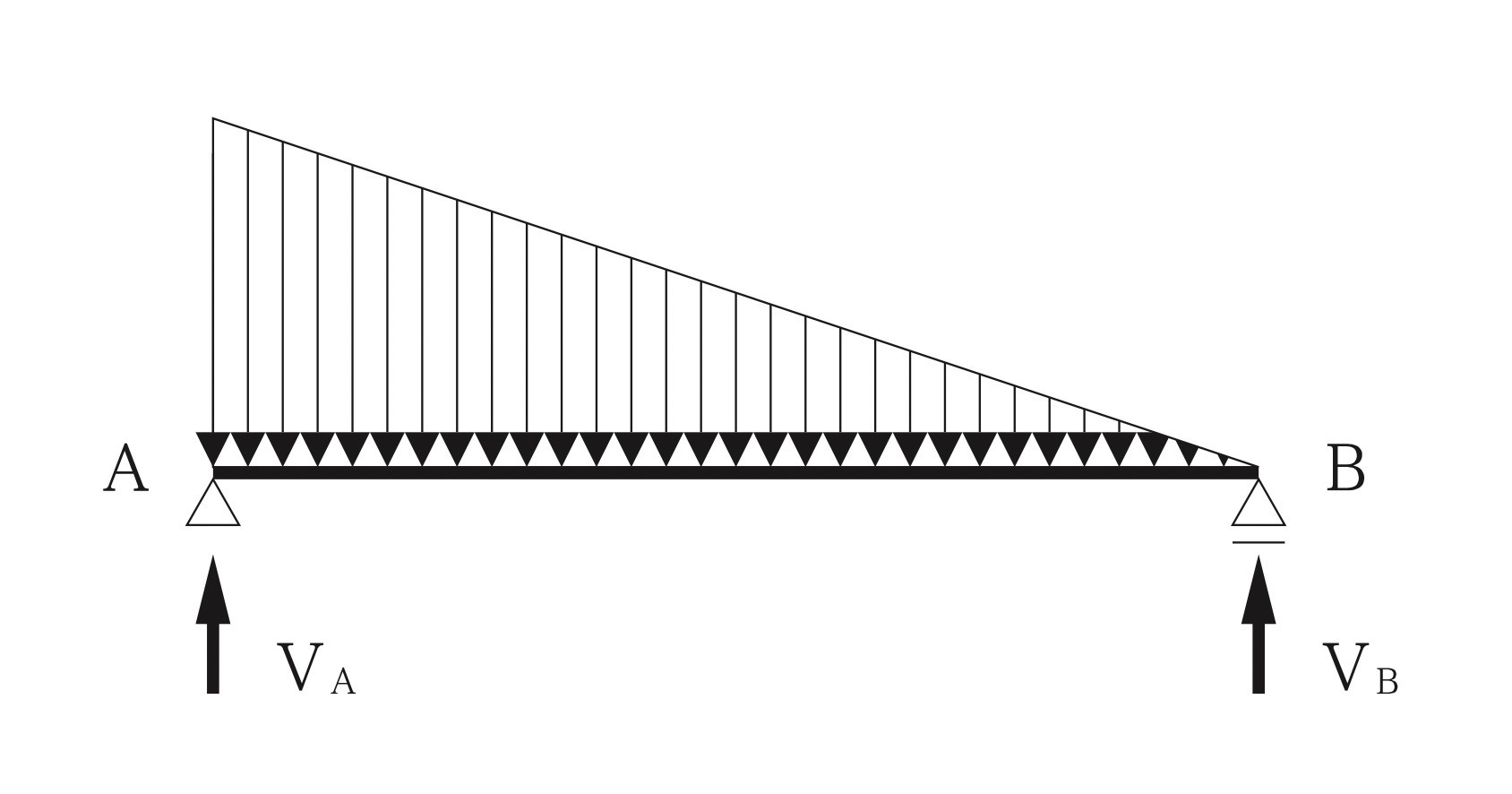
1.VA:VB=1:1
2.VA:VB=2:1
3.VA:VB=3:1
4.VA:VB=4:1
答え
2
[ 解答解説 ]
図-1のように、等変分布荷重、梁の長さを仮定する。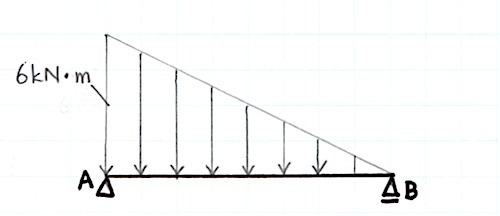
図-1
仮定した等変分布荷重を集中荷重に置き換えると図-2のようになる。
(三角形の重心の位置)
ΣV = 0 より、
VA – 9 + VB = 0
VA + VB = 9 ・・・①
支点Aは回転支点なので、モーメントMAは発生しない。
よって、
MA = 9 × 1 - VB × 3 = 0
3VB = 9
VB = 3 kN(上向き)
①に代入して、
VA + 3 = 9
VA = 6 kN(上向き)
∴ VA : VB = 6:3 = 2;1
( 3 )
図に示す単純梁ABにおいて、点Cにモーメント荷重Mが作用したとき、点Dに生じる応力の値の大きさとして、正しいものはどれか。(令和3年前期_No.9)
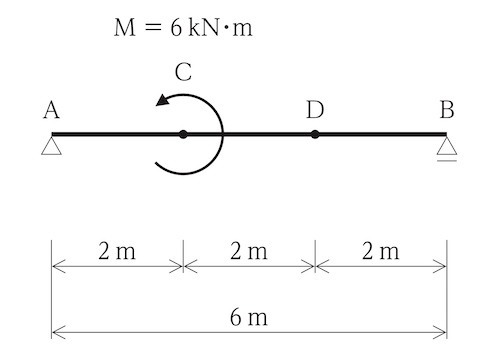
1.せん断力は、1kNである。
2.せん断力は、2kNである。
3.曲げモーメントは、3kN・mである。
4.曲げモーメントは、4kN・mである。
答え
1
[ 解答解説 ]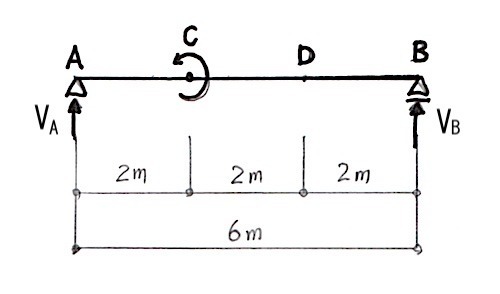
図-1
図-1のように、各支点の垂直反力とVA、VB と仮定し、支点Aは、回転支点なので、モーメントは発生しないことを利用する。
MA = Mc – VB × 6 = 0
MA = – 6 – VB × 6 = 0
– 6VB = 6
VB = – 1 [ kN ] (上向き)
答えがマイナスなので逆向きとなり、
VB = 1 [ kN ](下向き)
点Dの各応力を求めたいので、点Dより右半分 図-2で考える。
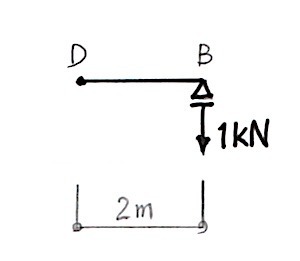
図-2
曲げモーメントは、
MD = 1 × 2 = 2 [ kN・m ]
せん断力は、
QD – 1 = 0
QD = 1 [ kN ]
∴ 正しいものは 1となる。
( 4 )
図に示す単純梁に集中荷重P1及びP2が作用したとき、支点Aの鉛直方向の反力の値の大きさとして、正しいものはどれか。(令和2年後期_No.9)
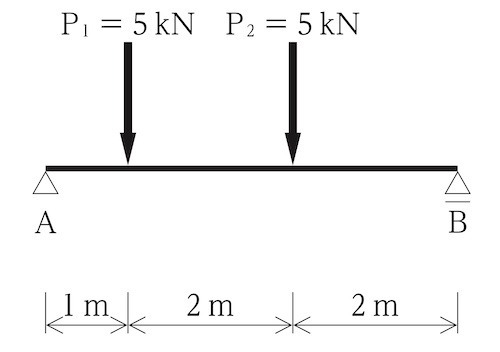
1.4kN
2.5kN
3.6kN
4.8kN
答え
3
[ 解答解説 ]
支点Aにおける反力をPAとすると、P1、P2の反力であるPAは上向きの力が生じる。支点BにおけるモーメントをMBとすると、モーメントのつり合いより
MB = 0
である。
モーメントの方向を、時計方向を正、反時計方向を負とすると、MBは次のようになる。
MB = +PA ×( 1 + 2 + 2 ) -P1 ×(2+2)–P2 × 2 = 0 [ kN・m ]
P1 = 5kN、P2 = 5kN より
+ 5PA ~ 5 × 4 - 5 × 2 = 0
PA – 4 - 2 = 0
PA = 6 [ kN ]
( 5 )
図に示す単純梁にモーメント荷重が作用したとき、支点Bに生じる鉛直反力の値の大きさとして、正しいものはどれか。(令和元年後期_No.9)
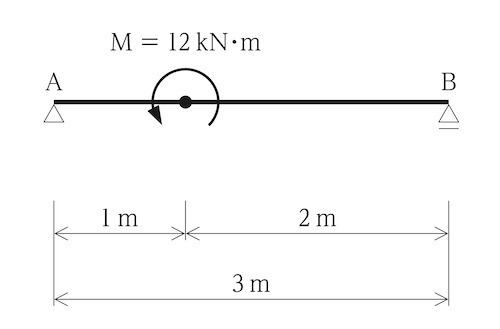
1.12kN
2.6kN
3.4kN
4.3kN
答え
3
[ 解答解説 ]
モーメント荷重に対するB点の反力をVBとすると、以下の図のようになる。
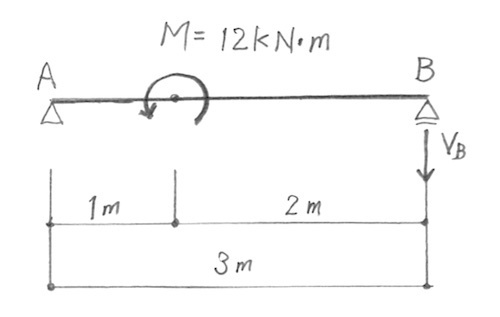
A点におけるモーメントのつりあいより
MA = VB × 3 =3VB ・・・・①
題意よりM = 12 [ kN・m ] を①式に代入して、
12 = 3VB
VB = 4 [ kN・m ] となる。
したがって、正答は、3となる。
( 6 )
図に示す張り出し梁の点C に集中荷重P が作用したとき、点D に生じる応力の値の大きさとして、正しいものはどれか。(令和元年前期_No.9)
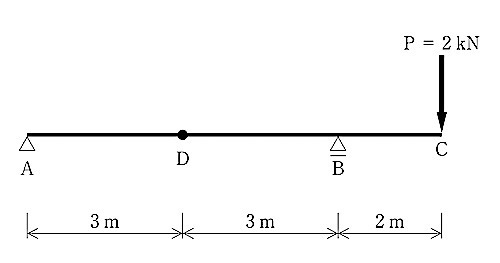
1. せん断力 Q= 1 kN
2. せん断力 Q= 2 kN
3. モーメントM= 2 kN・m
4. モーメントM= 3 kN・m
答え
3
[ 解答解説 ]
張り出し梁(キャンティレバー)の各応力を次のように定める。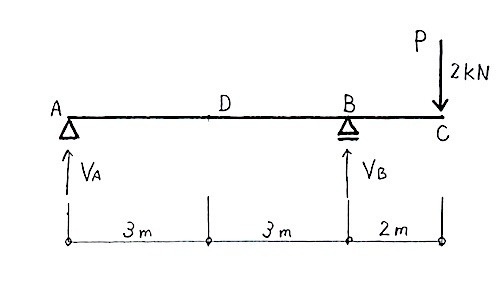
鉛直方向の力のつり合いより、
VA + VB - P = 0
VA + VB = 2kN ・・①
点Bでのモーメントは
MB = P・a = 2kN × 2m = 4 kN・m
点Aでのモーメントは
MA =( 3 + 3 + 2 )× 2kN +( 3 + 3 )× (–VB) = 0
16kN = 6VB
VB =8/3
∴ ①より
VA + 8/3 = 2kN
VA = -2/3(上向き)
よって、D点でのせん断力は 2/3 kN
D点のモーメントを求めると、D点から左側をみて、
MD = 3m × VA
= 3 ×(2/3)
= 2 kN・m
よって、正答は3となる。
尚、張り出し梁(キャンティレバー)のせん断力とモーメント図は次のとおりである。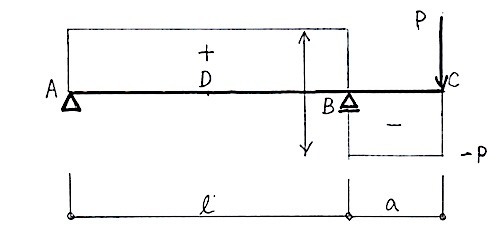
せん断力図(Q図)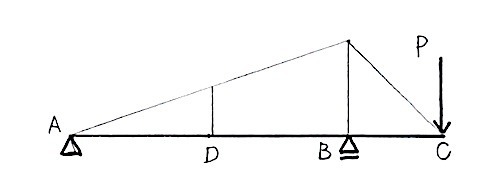
モーメント図(M図)
( 7 )
図に示す片持ち梁に等変分布荷重が作用したとき、C 点に生じる応力の値として正しいものはどれか。(平成30年後期_No.9)
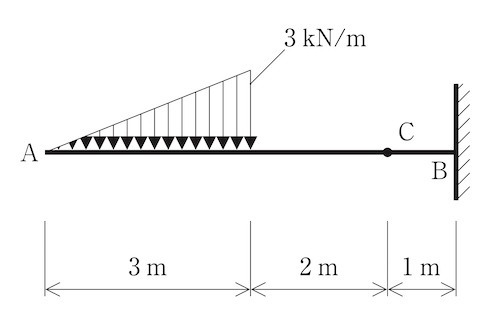
1. せん断力は、3 kN である。
2. せん断力は、9 kN である。
3. 曲げモーメントは、4.5 kN・m である。
4. 曲げモーメントは、13.5 kN・m である。
答え
4
[ 解答解説 ]
等分布荷重を集中荷重に置き換えると下記のようになる。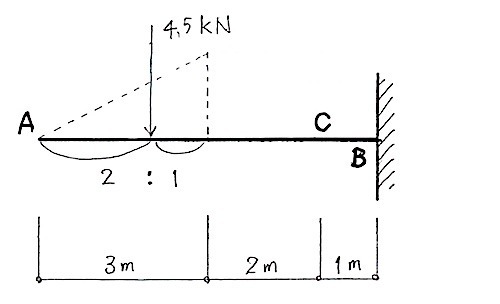
B点におけるモーメントMBを求める。
- 3 kN/m × 3m /2 × 4m =18 kN・m
これより、モーメント図は下記のようになり、C点におけるモーメントを求めると下記のようになる。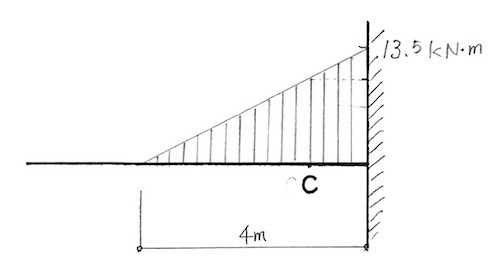
18 kN・m × 3/4 = 13.5 kN・mとなる。
ゆえに、正解は4となる。
( 8 )
図に示す単純梁に等分布荷重が作用したとき、支点に生じる鉛直反力VA及びVBの値の大きさの組合せとして、正しいものはどれか。(平成30年前期_No.9)
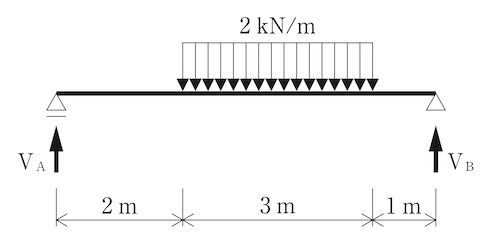
1. VA=2.0kN、VB=4.0kN
2. VA=2.5kN、VB=3.5kN
3. VA=3.0kN、VB=3.0kN
4. VA=3.5kN、VB=2.5kN
答え
2
[ 解答解説 ]
等分布荷重を集中荷重に置き換えて示すと下記のようになる。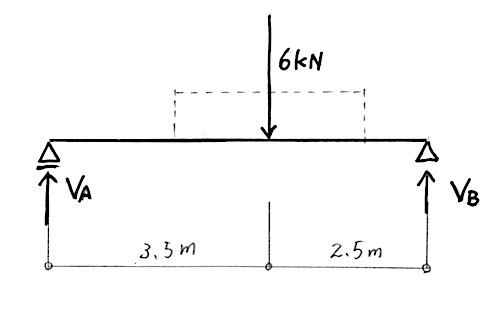
鉛直方向の力のつり合いより、
VA + VB = 6 kN ( = 2 kN/m × 3m )・・・①
B点におけるモーメントのつり合いより
MB = 6m × VA + 2.5m ×(–6kN )= 0
∴ VA = 2.5 kN
①に代入して、VB = 3.5 kN
よって、正解は 2となる。
< モーメントを求める問題 >
( 1 )
図に示す片持ち梁ABの点Cに曲げモーメントMが作用する場合の曲げモーメント図として、正しいものはどれか。ただし、曲げモーメントは、材の引張側に描くものとする。(令和4年前期_No.10)
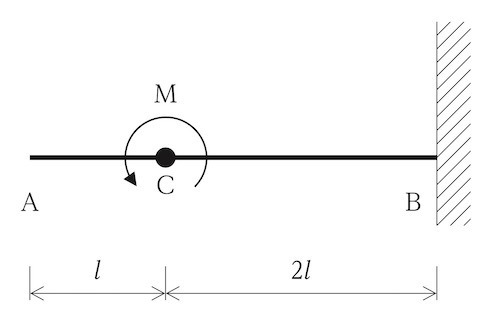
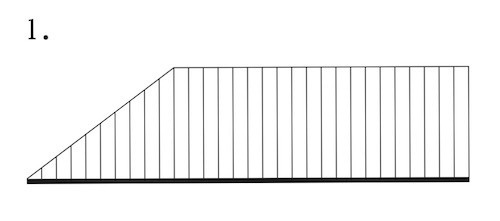
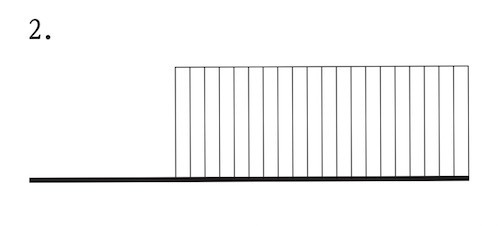
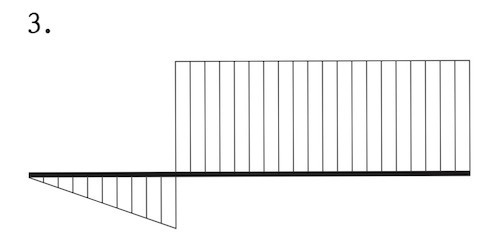
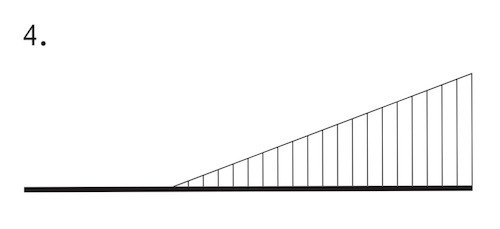
答え
2
[ 解答解説 ]
片持ち梁に集中モーメントが生じている場合のモーメント図は、下図のようになる。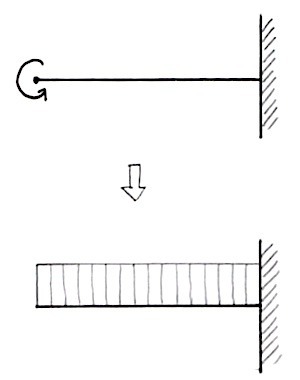
AC間はなんの荷重も作用していないフリーの状態である。
C点で曲げモーメントが生じているので、選択肢2 のようになる。
( 2 )
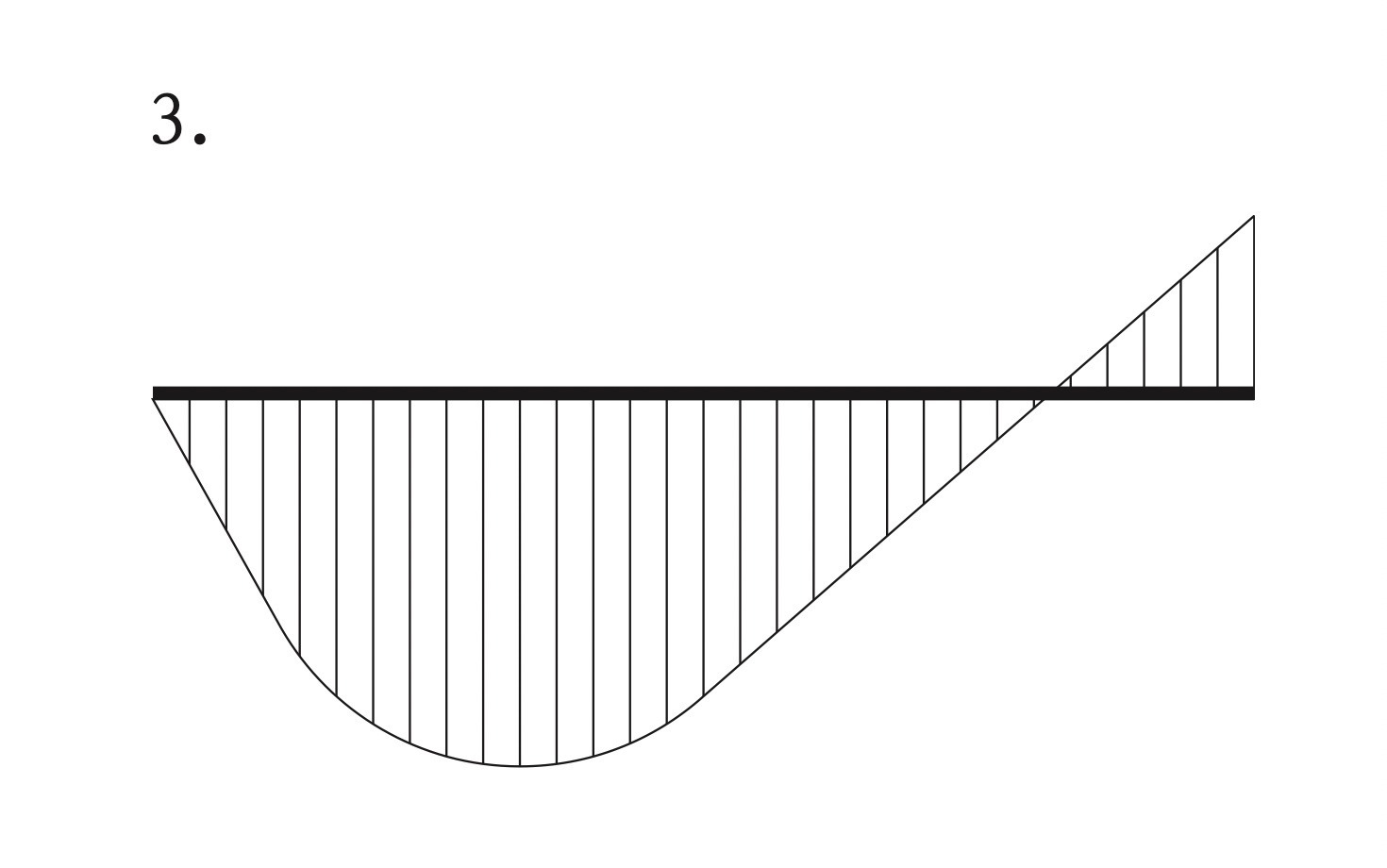
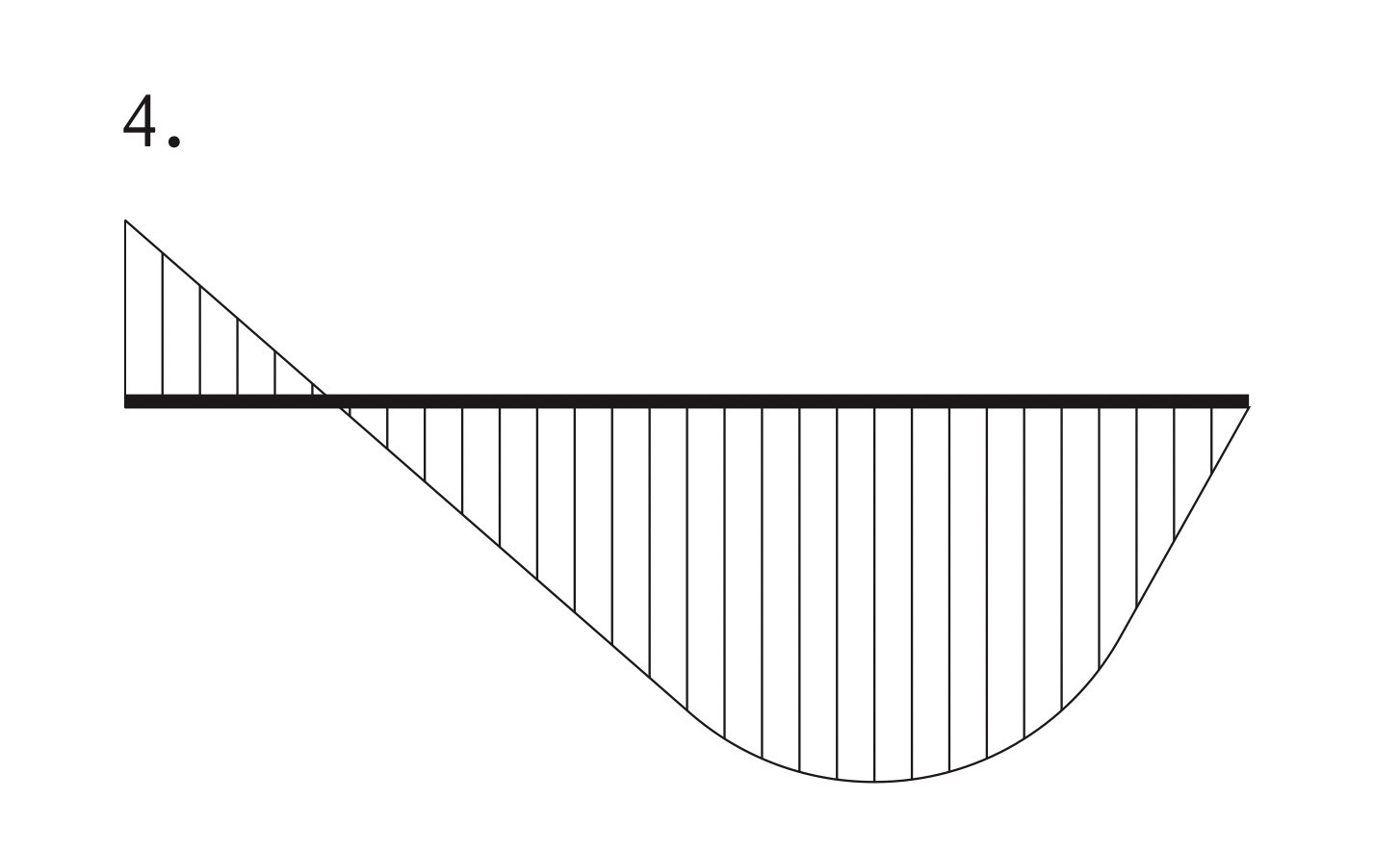
図に示す単純梁ABのBC間に等分布荷重wが作用したときの曲げモーメント図として、正しいものはどれか。ただし、曲げモーメントは、材の引張側に描くものとする。(令和3年後期_No.10)
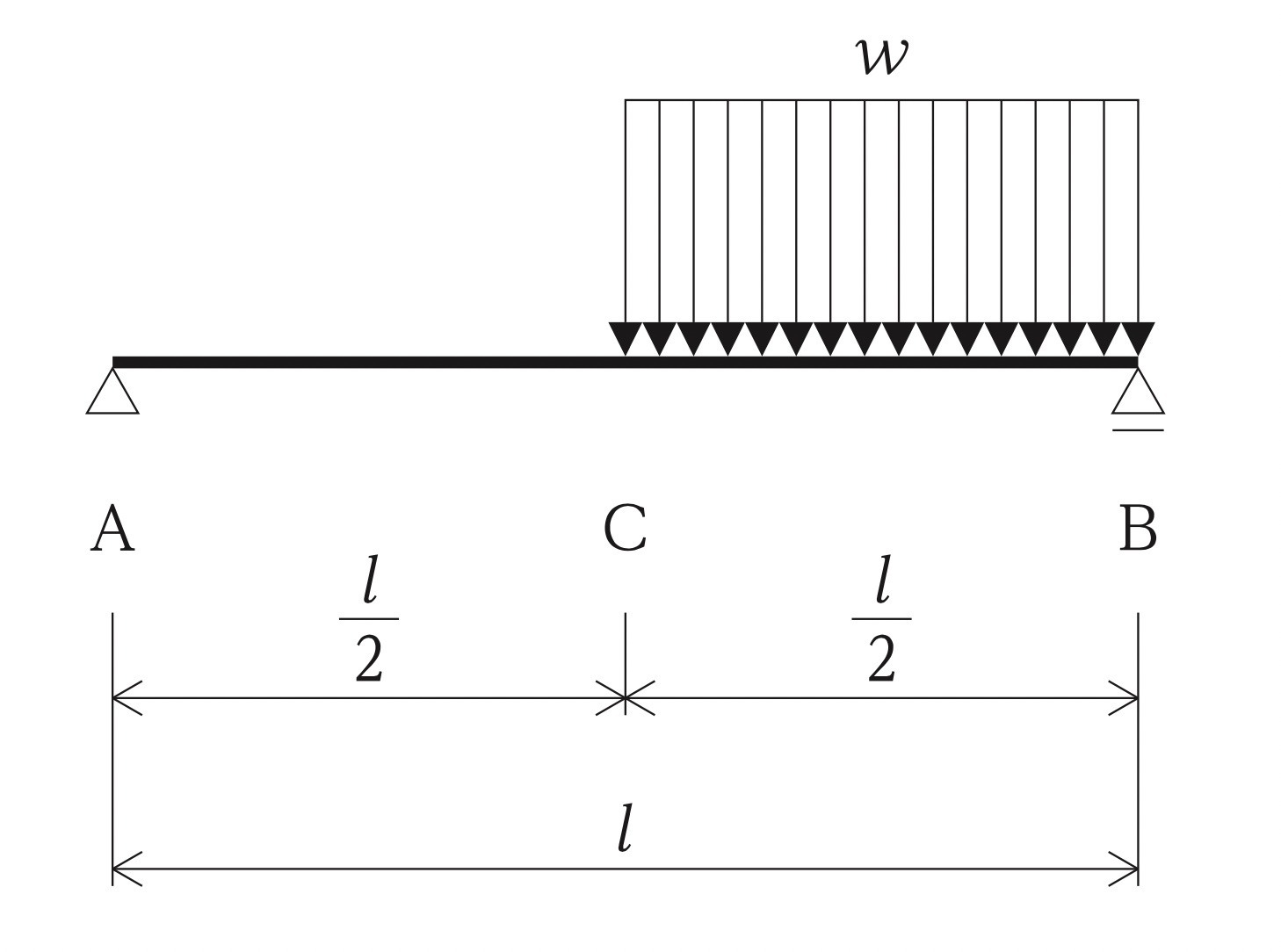
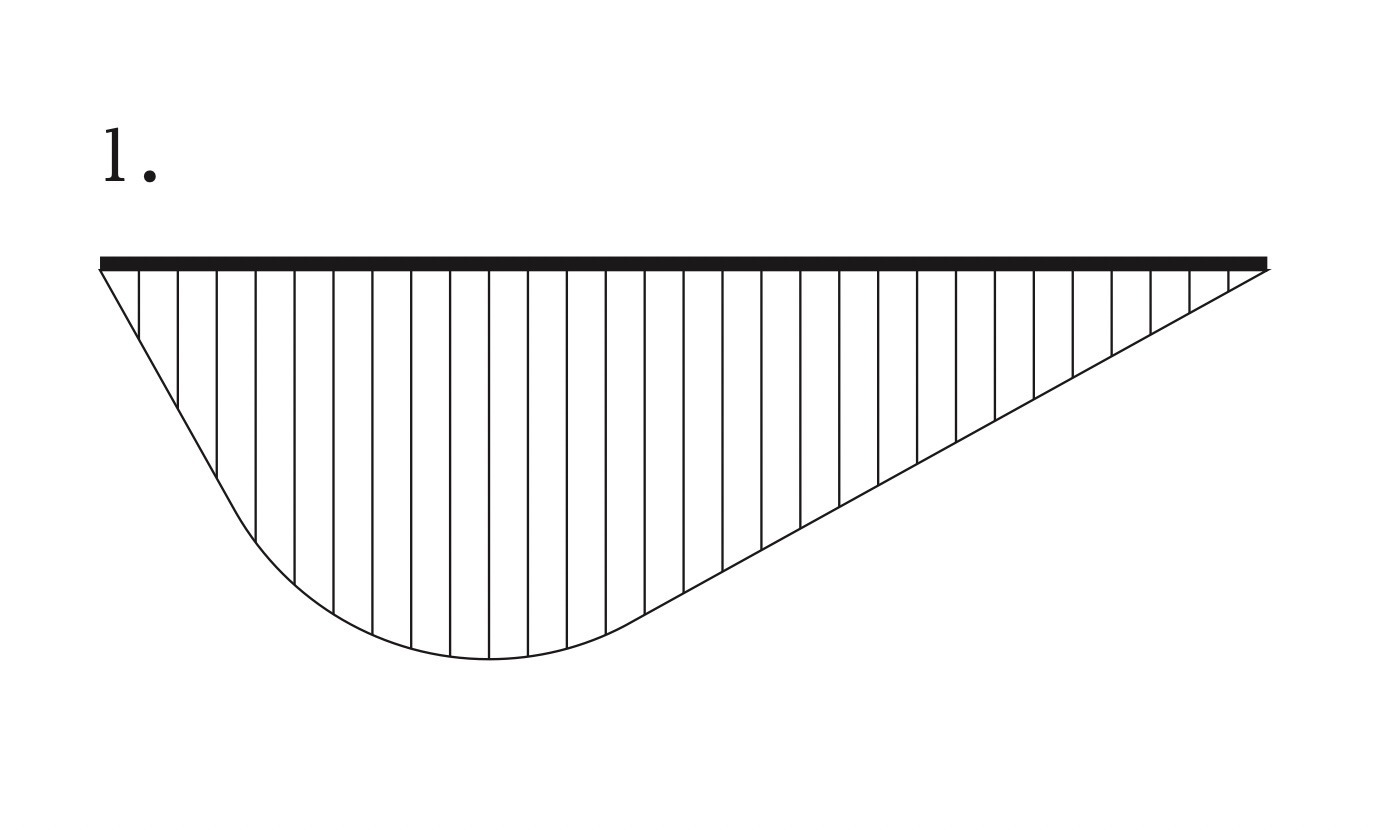
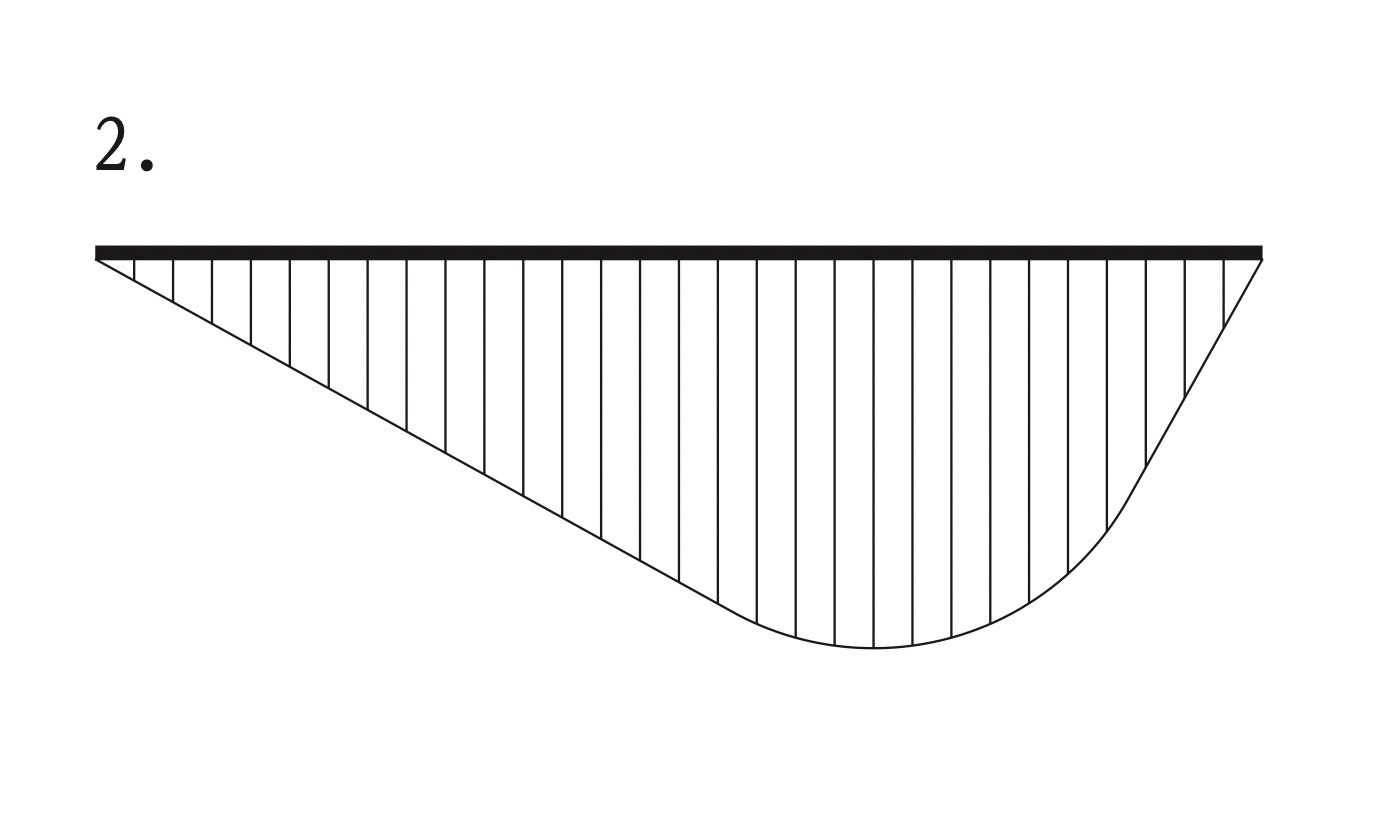
答え
2
[ 解答解説 ]
集中荷重での曲げモーメント図は「力×距離」より、比例(直線)となる。
等分布荷重での曲げモーメント図は、反力の「力 × 距離 」– 荷重の「力 × 距離」より、2次曲線となる。
よって、A~C区間は直線、C~B区間は曲線となり、肢2又は肢4になる。
また、支点Aは回転支点であるから、モーメントは発生しないため、肢4は不適切である。
∴、正解は 2となる。
( 3 )
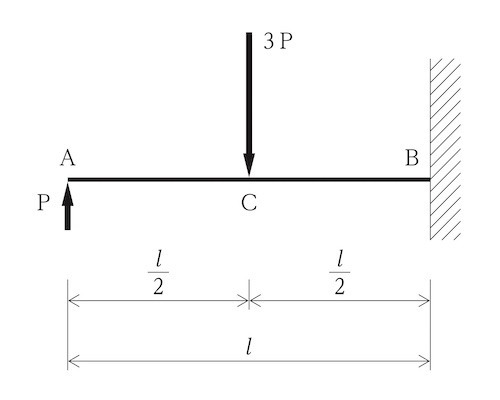
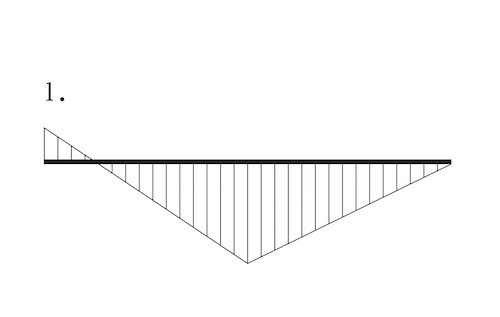
図に示す片持梁ABにおいて、点Aに集中荷重P及び点Cに集中荷重3Pが同時に作用したときの曲げモーメント図として、正しいものはどれか。ただし、曲げモーメントは、材の引張側に描くものとする。(令和3年前期_No.10)
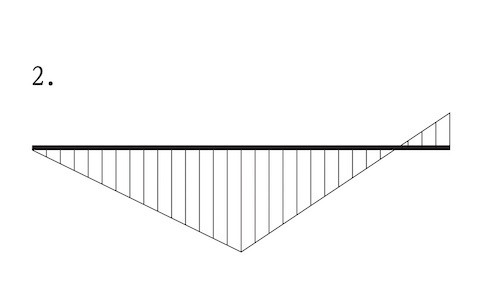
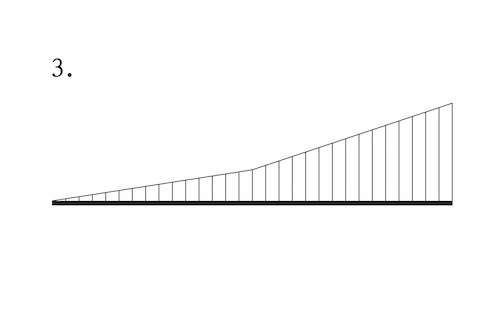
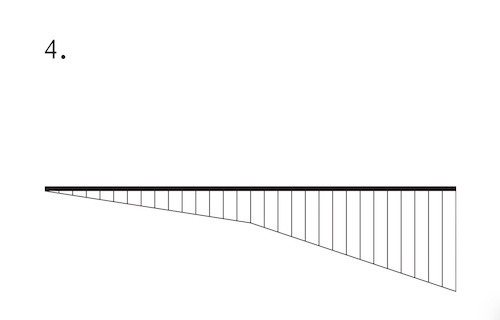
答え
2
[ 解答解説 ]
A点には、モーメントが発生しないので、1のM図は誤りである。
また、C点には上部から荷重がかかってるので、モーメントは下側に発生する。
ゆえに、3のM図は誤りである。
B点のモーメントMBは、
MB = P ×ℓ +(-3P)× ℓ/2
=-1P ℓ/2
よって、B点には反時計方向の曲げモーメントが生じる。(上側が引っ張り側になる)
∴ 正解は2となる。
※単純梁のこの荷重条件の時のモーメントのおおよその形状は覚えておく必要がある。
( 4 )
図に示す単純梁に等変分布荷重が作用したときの曲げモーメント図として、正しいものはどれか。ただし、曲げモーメントは、材の引張側に描くものとする。(令和2年後期_No.10)
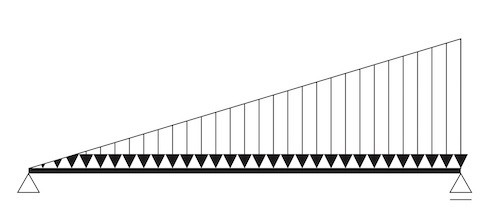
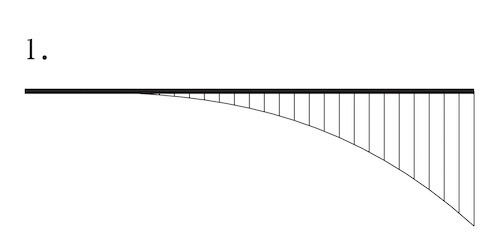
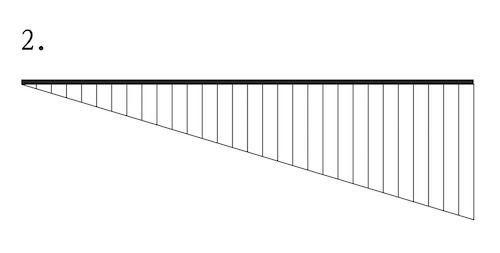
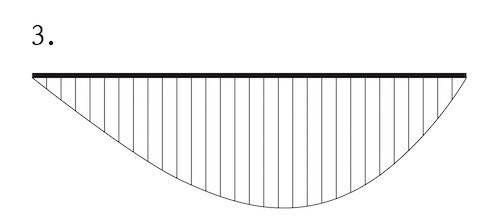
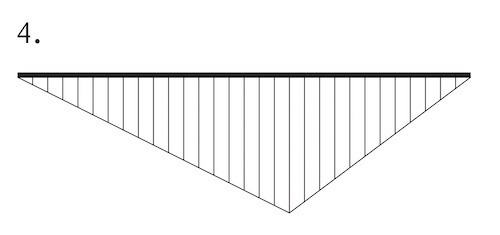
答え
3
[ 解答解説 ]
単純梁に等分布荷重が作用したときの曲げモーメントは次のようになる。
両端はピン構造なので、モーメントは 0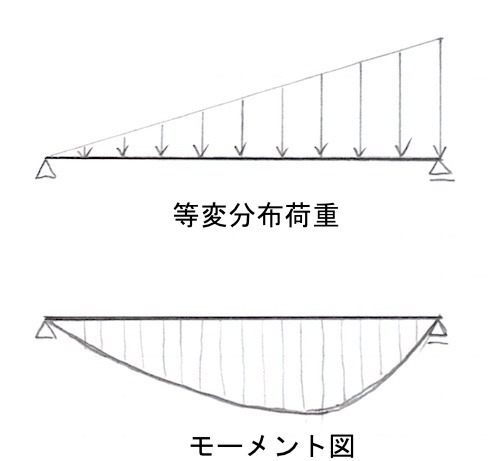
したがって、この単純梁への荷重(応力)が偏って、等変分布荷重になった場合はの曲げモーメントは次のようになる。
ゆえに、正解は3となる。
( 5 )
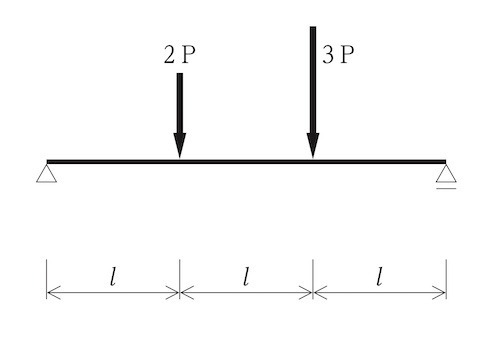
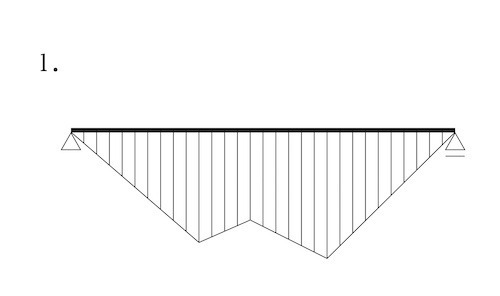
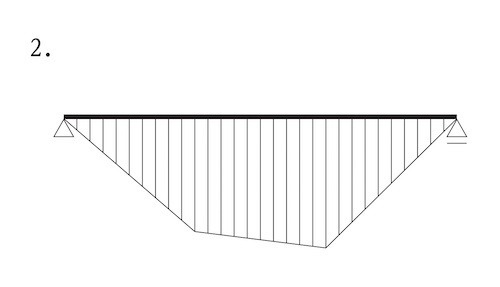
図に示す単純梁に集中荷重2P及び3Pが作用したときの曲げモーメント図として、正しいものはどれか。ただし、曲げモーメントは材の引張側に描くものとする。(令和元年後期_No.10)
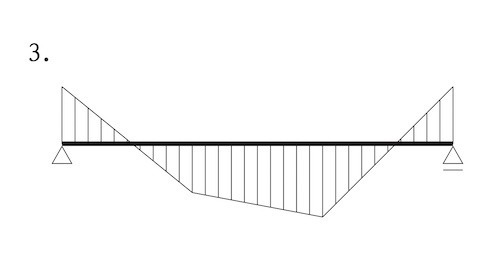
答え
2
[ 解答解説 ]
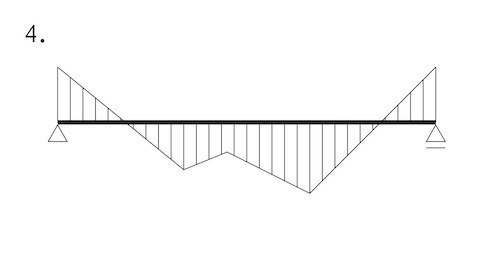
単純梁に集中荷重 2P及び3Pが作用したときの曲げモーメント図は、集中荷重2Pのみが作用したときの曲げモーメントと集中荷重3Pのみが作用したときの曲げモーメント図との足し合わせとなるので、図3のようになる。ゆえに、正解は2。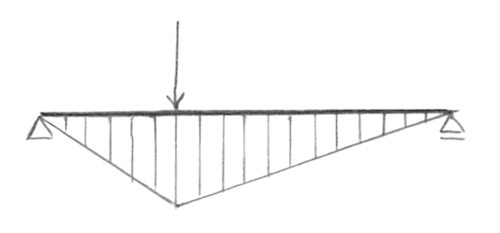
図1 集中荷重 2P のみが作用した問いの曲げモーメント図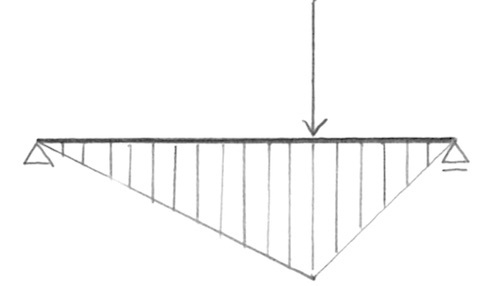
図2 集中荷重 3P のみが作用した問いの曲げモーメント図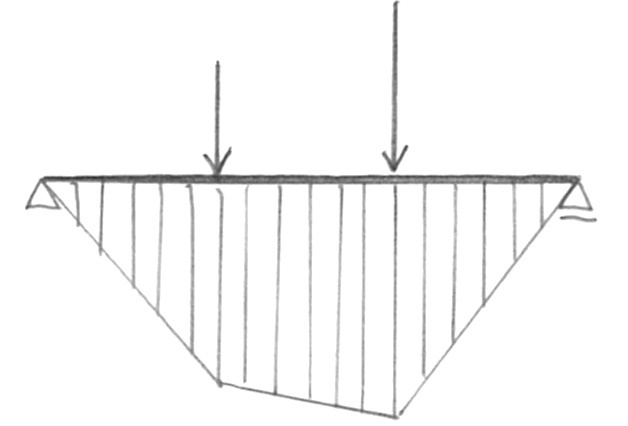
図3 図1と図2の曲げモーメント図を合成した曲げモーメント図
( 6 )
図に示すラーメンに集中荷重P が作用したときの曲げモーメント図として、正しいものはどれか。ただし、曲げモーメントは材の引張り側に描くものとする。(令和元年前期_No.10)
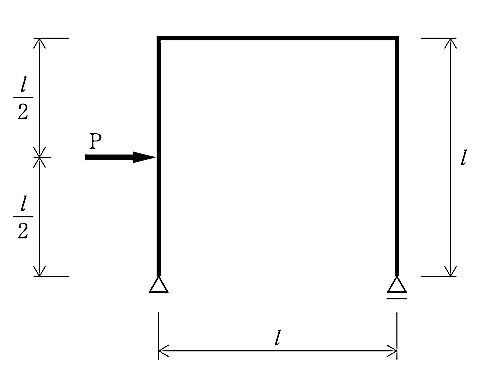
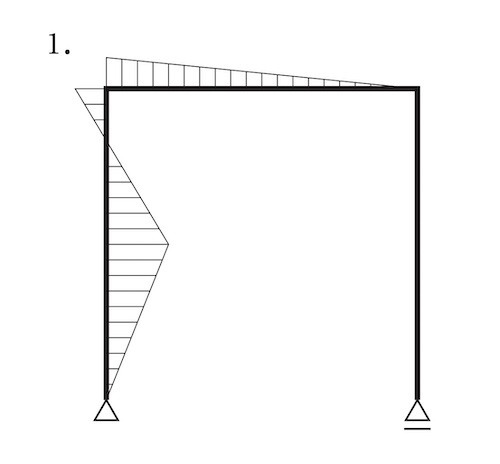
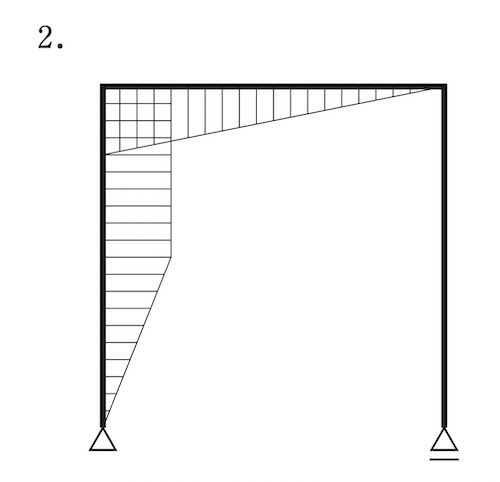
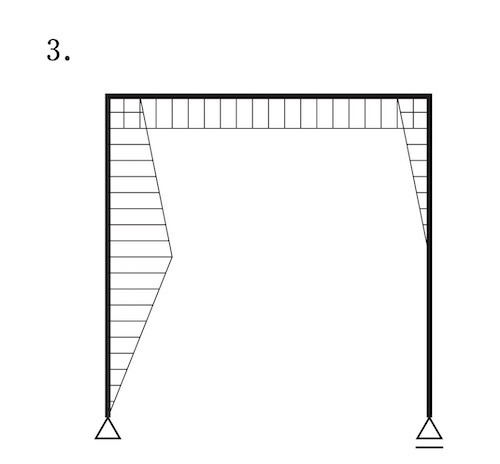
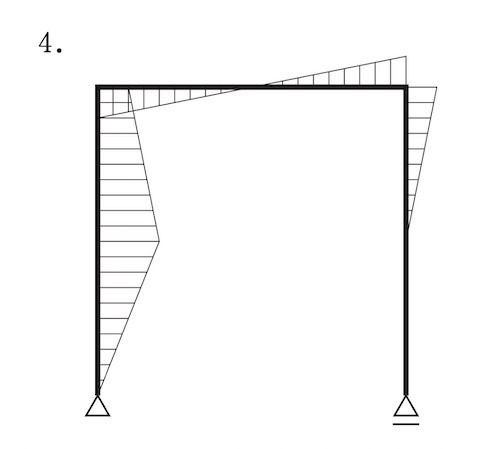
答え
2
[ 解答解説 ]
ラーメン静定構造図の各応力と次のように仮定する。
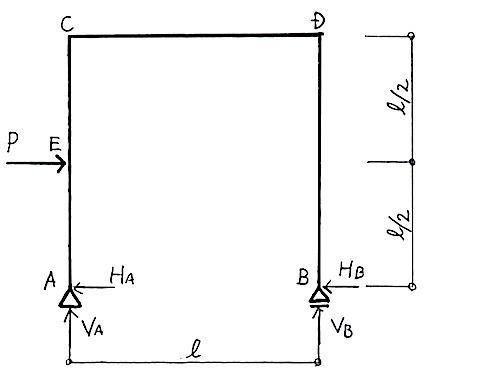
① X方向のつり合いより、ΣX = 0
HA = P
HB はすべり支承なのでゼロ
この時点で、D点にはモーメントが発生しないので、
正答は 1. 又は 2. に限定される。
② Y方向のつり合いより、ΣY = 0
VA + VB = 0
VA = – VB
③ A点でのモーメントのつり合いより、ΣMA = 0
MA = – P ×(ℓ/2) + VB × ℓ= 0
これを解くと
VB × ℓ= P ×(ℓ/2)
VB = P/2(上むき)
②より VA = – P/2(下むき)
④E点のモーメントを計算する。
ME = P ×(ℓ/2)
= Pℓ/2
⑤AC材のC点のモーメントを計算する。
MC = – P ×(ℓ/2) + P × ℓ
= Pℓ/2
ゆえに、正答は 2. となる。
( 7 )
図に示す片持ち梁に集中荷重P が作用したときの曲げモーメント図として、正しいものはどれか。ただし、曲げモーメントは材の引張側に描くものとする。(平成30年後期_No.10)
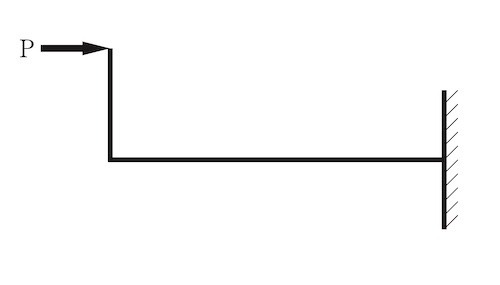
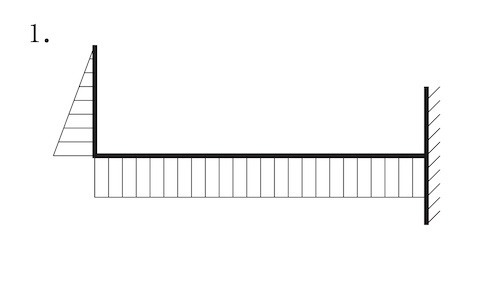
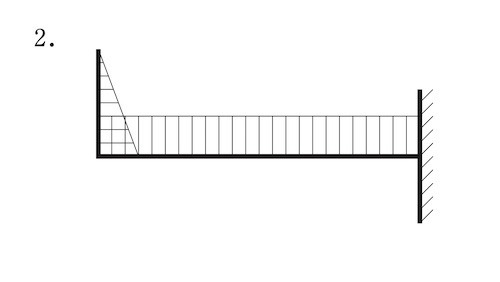
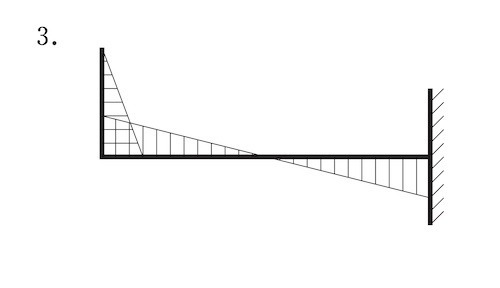
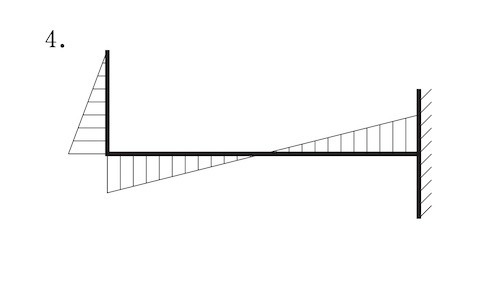
答え
1
[ 解答解説 ]
問題の片持ち梁の節点を下記のように設定する。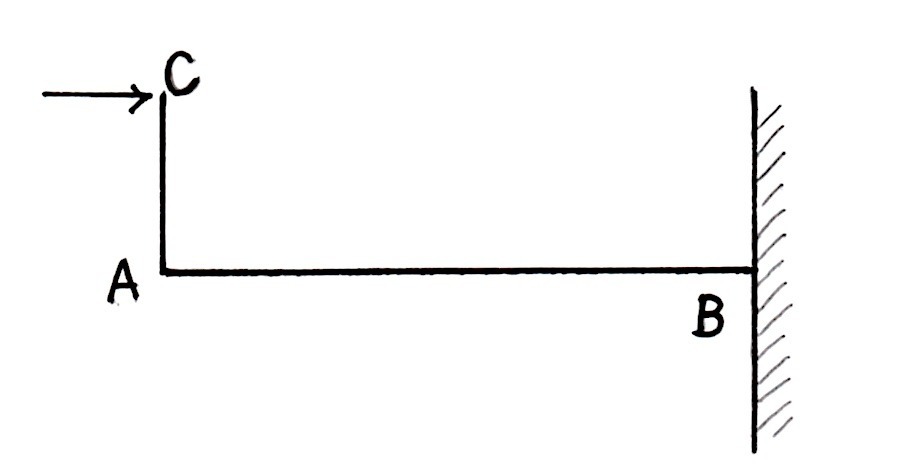
曲げモーメントは材の引張側に描くものとするとあるので、
AC間の部材は、下端部の引張側は左側に発生する。
ゆえに、1又は4に限定できる。
また、図の力が加わるとAB間の部材は下側が弓状になるこことが想像できる。よってAB材には下側の部分に引張力が発生する。同じモーメント力がそのまま伝わるので正答は1となる。
モーメントが途中で反転し、0になるようなことはない。4とはならない。
( 8 )
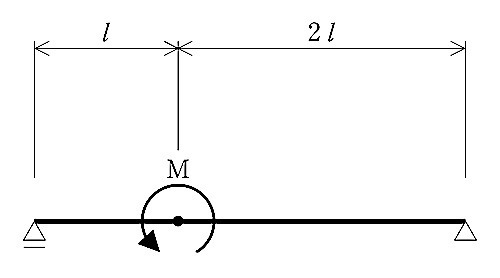
図に示す単純梁にモーメント荷重Mが作用したときの曲げモーメント図として、正しいものはどれか。ただし、曲げモーメントは材の引張側に描くものとする。(平成30年前期_No.10)
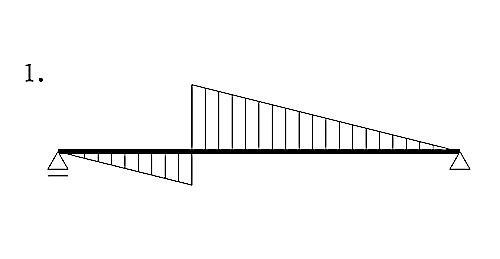
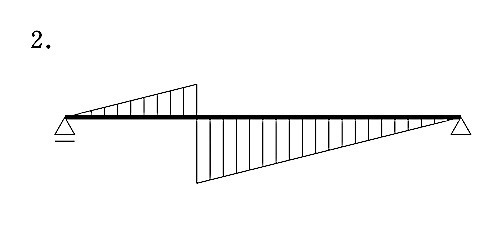
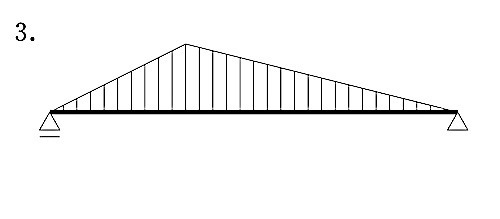
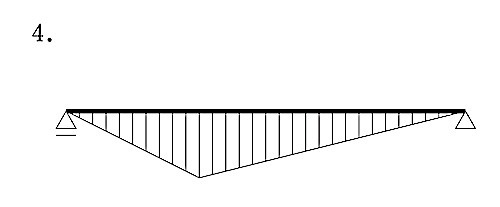
答え
1
[ 解答解説 ]
題意のモーメント荷重Mが作用する単純梁の変形を極端に作図すると下記のようになる。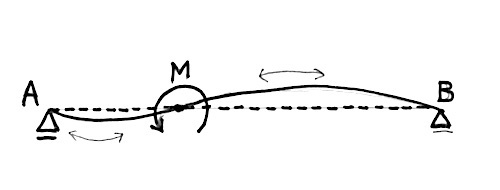
点Mより左側は梁の下端が引張となり、右側は梁の上側が引張となる。
従って、解答は 1となる。

