実地試験 解答・解説
問題3
図に示すネットワーク工程表について、次の 1.から 3.の問いに答えなさい。
なお、◯内の数字はイベント番号を、実線の矢線は作業を、破線の矢線はダミーを示し、矢線の上段のアルファベットは作業名を、下段の数値は所要日数を示すものとする。
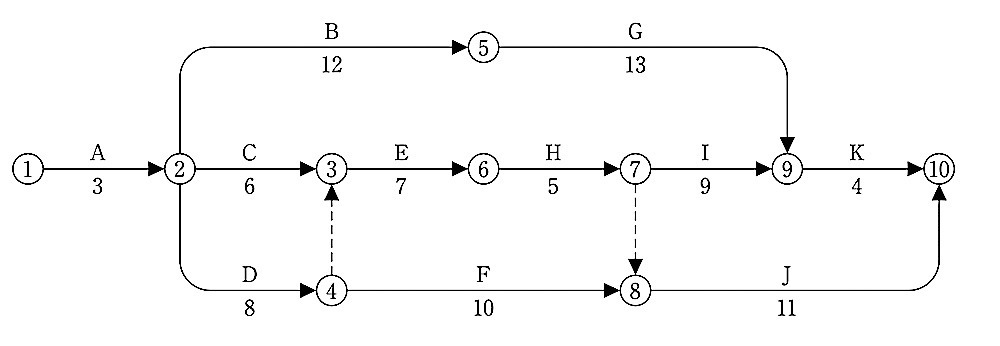
1. 工程表において、クリティカルパスを作業名で工程順に並べて答えなさい。
解答
クリティカルパス
A → D → E → H → I → K
[ 解説 ]
クリティカルパスとは、該当するネットワーク中で最も日数を要する経路のことをいい、その日数が総所要日数である。
作業の開始と終了のときに付ける◯印をイベントという。
→ をアロー(矢線)といい、矢線の上に作業名、下に所要日数が記載される。
このイベントと矢線と作業名、所要日数をまとめてアクティビティという。
アクティビティが連結されて、ネットワーク工程表が作成される。
①全イベントの右上に□を表示する。(形は□でなくてもよい)
②最初のイベント①の□に 0 を記入し、最初の作業Aの最早開始時刻とする。
③イベント番号の若い順に、□(最早開始時刻)と所要日数との和を記入する。
これが各作業の最早開始時刻となる。
④2本以上の矢線がイベントに流入するときは、そのうちの最大値を最早開始時刻とする。こうして計算した、最終イベントの最早開始時刻が工期(クリティカルパス)となる。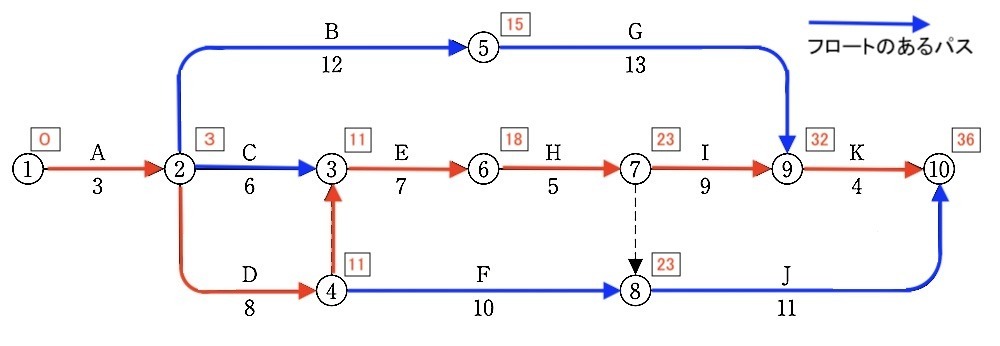
2. 工程の再検討を行ったところ、イベント番号⑥から⑤への所要日数2日の新たな作業Lが発生した。この時の①から⑩までの総所要日数を答えなさい。
解答
37日
[ 解説 ]
総所要日数(LST)の計算
① → ② → ④ → ③ → ⑥ → ⑤ → ⑨ → ⑩
= A → D → E → L → G → K
=3 + 8 + 7 + 2 + 13 + 4
=37 日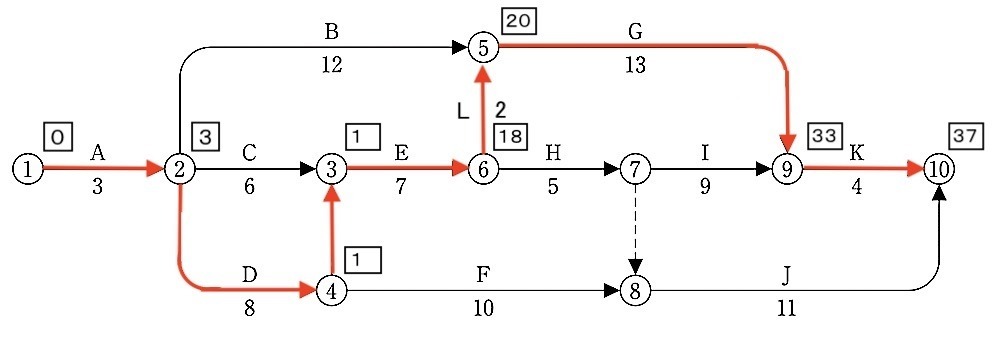
3. 新たな作業Lが発生する前と発生した後の作業Bのフリーフロートをそれぞれ日数で答えなさい。
解答
作業Lが発生する前の作業Bのフリーフロート(余裕時間)
= 0 日
作業Lが発生した後の作業Bのフリーフロート
= 5 日
[ 解説 ]
総所要日数(LST)の計算
作業 L が発生する前と発生した後の作業B のフリーフロート(余裕時間)の日数
作業 L が発生する前の作業Bのフリーフロート(余裕時間)=0
作業Bはイベント②~⑤間。①~⑤間で日数を比較考察する。
最速日数 = ① → ② → ⑤
= 3 + 12 = 15 日
最遅日数 = ① → ② → ⑤
= 3 + 12 = 15 日
フリーフロート = 最遅日数 - 最早日数
= 15日 – 15日 = 0日
作業Lが発生した後の作業Bのフリーフロート = 5日
イベント①~⑥間で日数を比較考察する。
最速日数 = ① → ② → ⑤
= 3 + 12 = 15 日
最遅日数 = ① → ② → ④ → ③ → ⑥
= 3 + 8 + 7 + 2 = 20 日
フリーフロート = 最遅日数 - 最早日数
= 20日 – 15日 = 5日
-
no image
-
no image
-
no image
-
no image
-
no image

