新規記事の投稿を行うことで、非表示にすることが可能です。
2018年04月30日
一生役に立つ暗算・掛け算(パートⅠ最終総合100題)
これまで12回に亘って「一生役立つ暗算掛け算問題」をご紹介してきましたが、
最後にこれまで総合問題として100題リストします。
通常目にしたり使用したりする頻度の高いと思われるもの(特に19x19の表の部分)を多くしています。
ブロック単位ですので、方法を思いだせばブロック内は直ぐ計算できますね。
数の組合せの特徴を見てすぐ方法が思い出せるまで練習してみて下さい。
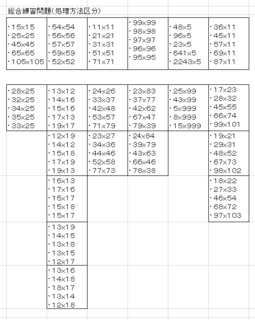
ブロック単位でスムースに出来るようになったら、
次のほぼランダムに並べた問題に進んでみて下さい。
コツはまず2乗(4通り)かどうか、次にどのパターン(方法)かを見抜くことでしょうか。
あなたの一番やりやすい方法の流れを探してみて下さい。
・48x5
・15x15
・36x11
・12x17
・68x72
・25x25
・57x11
・45x45
・45x55
・105x105
・54x54
・13x18
・56x56
・17x16
・57x57
・15x18
・59x59
・13x14
・52x52
・24x84
・11x11
・67x73
・13x19
・16x13
・21x21
・32x25
・14x18
・31x31
・33x25
・51x51
・27x33
・71x71
・99x99
・87x11
・97x97
・15x16
・96x96
・13x12
・95x95
・96x5
・23x5
・641x5
・2243x5
・45x11
・8x999
・69x11
・28x25
・65x65
・35x25
・14x16
・98x98
・17x13
・19x17
・24x26
・33x37
・42x48
・53x57
・71x79
・23x83
・34x25
・37x77
・15x18
・67x47
・78x38
・12x18
・79x39
・25x99
・13x15
・43x99
・5x999
・17x23
・28x32
・66x74
・99x101
・12x19
・14x12
・17x19
・15x999
・19x13
・19x21
・23x27
・34x36
・52x58
・77x73
・43x63
・15x17
・66x46
・29x31
・48x52
・98x102
・39x79
・18x22
・46x54
・97x103
・14x15
・44x46
・13x16
・42x62
・18x17
とにかく数の組み合わせの特徴をすばやく見抜いて下さい。
最後に
今では誰でも携帯やスマホに電卓アプリがあり、計算に困ることは有りません。
従って、「苦労してまでして一部の計算しか出来ない暗算方法を覚える必要なんて無い」とお考えの方もいらっしゃると思います。
しかし敢えて私が暗算掛け算を紹介してきたのは、私自身の目標でもあります。
この暗算計算を習得することは以下のメリットがあると思っています。
一定の条件にあう数の組み合わせについてだけの計算ではありますが、
・簡単な計算はわざわざ電卓を使う必要もない。
・電卓が無い、使えない、使いづらい場所いる、状況にある場合には有効
・電卓より速く出来る。
・シニアには脳トレになる
・幼年者が出来るようになれば計算が得意になり数的な興味をもち、自然科学系が好き、得意になる可能性。
・そして一生役に立つので、一生涯で考えると時間の大きな節約になる。
・要はサッと暗算でできたら気持ちがいい
ということでしょうか。
長い間お付き合い頂きありがとうございました。
ところで
先日スーパーのレジのところに面白そうな本があったので早速買ってみました。
色々な算数の問題が載っています。
小学校で習った算数パズルとはいえ結構難しい問題も沢山あります。
「解けますか?小学校で習った算数プラス」

◆スマイルゼミ◆中学生向け通信教育

◆スマイルゼミ◆タブレットで学ぶ通信教育 【幼児コース】

最後にこれまで総合問題として100題リストします。
通常目にしたり使用したりする頻度の高いと思われるもの(特に19x19の表の部分)を多くしています。
ブロック単位ですので、方法を思いだせばブロック内は直ぐ計算できますね。
数の組合せの特徴を見てすぐ方法が思い出せるまで練習してみて下さい。
ブロック単位でスムースに出来るようになったら、
次のほぼランダムに並べた問題に進んでみて下さい。
コツはまず2乗(4通り)かどうか、次にどのパターン(方法)かを見抜くことでしょうか。
あなたの一番やりやすい方法の流れを探してみて下さい。
・48x5
・15x15
・36x11
・12x17
・68x72
・25x25
・57x11
・45x45
・45x55
・105x105
・54x54
・13x18
・56x56
・17x16
・57x57
・15x18
・59x59
・13x14
・52x52
・24x84
・11x11
・67x73
・13x19
・16x13
・21x21
・32x25
・14x18
・31x31
・33x25
・51x51
・27x33
・71x71
・99x99
・87x11
・97x97
・15x16
・96x96
・13x12
・95x95
・96x5
・23x5
・641x5
・2243x5
・45x11
・8x999
・69x11
・28x25
・65x65
・35x25
・14x16
・98x98
・17x13
・19x17
・24x26
・33x37
・42x48
・53x57
・71x79
・23x83
・34x25
・37x77
・15x18
・67x47
・78x38
・12x18
・79x39
・25x99
・13x15
・43x99
・5x999
・17x23
・28x32
・66x74
・99x101
・12x19
・14x12
・17x19
・15x999
・19x13
・19x21
・23x27
・34x36
・52x58
・77x73
・43x63
・15x17
・66x46
・29x31
・48x52
・98x102
・39x79
・18x22
・46x54
・97x103
・14x15
・44x46
・13x16
・42x62
・18x17
とにかく数の組み合わせの特徴をすばやく見抜いて下さい。
最後に
今では誰でも携帯やスマホに電卓アプリがあり、計算に困ることは有りません。
従って、「苦労してまでして一部の計算しか出来ない暗算方法を覚える必要なんて無い」とお考えの方もいらっしゃると思います。
しかし敢えて私が暗算掛け算を紹介してきたのは、私自身の目標でもあります。
この暗算計算を習得することは以下のメリットがあると思っています。
一定の条件にあう数の組み合わせについてだけの計算ではありますが、
・簡単な計算はわざわざ電卓を使う必要もない。
・電卓が無い、使えない、使いづらい場所いる、状況にある場合には有効
・電卓より速く出来る。
・シニアには脳トレになる
・幼年者が出来るようになれば計算が得意になり数的な興味をもち、自然科学系が好き、得意になる可能性。
・そして一生役に立つので、一生涯で考えると時間の大きな節約になる。
・要はサッと暗算でできたら気持ちがいい
ということでしょうか。
長い間お付き合い頂きありがとうございました。
ところで
先日スーパーのレジのところに面白そうな本があったので早速買ってみました。
色々な算数の問題が載っています。
小学校で習った算数パズルとはいえ結構難しい問題も沢山あります。
「解けますか?小学校で習った算数プラス」
◆スマイルゼミ◆中学生向け通信教育
◆スマイルゼミ◆タブレットで学ぶ通信教育 【幼児コース】
【このカテゴリーの最新記事】
-
no image
-
no image
-
no image
-
no image
2018年04月25日
一生役に立つ暗算・掛け算(一旦終了、纏めと練習問題集)
前回の十の位の数字の和が10で一の位の数が同じの計算はいかがでしたでしょうか。
さて長きに亘ってご訪問いただきました暗算・掛け算シリーズですが、
とりあえず次回で一旦終了する事にしました。
暗算計算は他にもまだありますが、
それを覚えるよりも当面はこれまでご紹介して来た方法を使いこなす事の方が大事だと思います。
(後日パートⅡとしてご紹介すると共により広い計算への挑戦をしたいとおもます。)
そこで、下表にこれまでご紹介してきた暗算計算の例を纏めました。ご参考になればとおもいます。
そして再度、各5個の問題を計算して見て下さい。
またやり方を忘れたり、もう一度詳しく解説を見たいときには、過去のブログ(日付欄に記載)をもう一度ご参照下さい。
<暗算計算全体まとめと例題各5個>
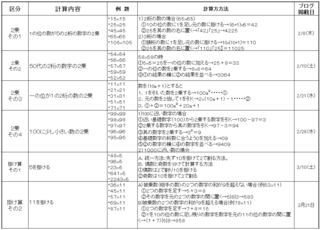

さて、次回は今シリーズ(パートⅠ)の最後として、今回のシリーズで計算出来る組み合わせを沢山集めて、ランダムに記載した問題集を考えています。
どうぞお楽しみに。
◆スマイルゼミ◆中学生向け通信教育

◆スマイルゼミ◆タブレットで学ぶ通信教育 【幼児コース】

さて長きに亘ってご訪問いただきました暗算・掛け算シリーズですが、
とりあえず次回で一旦終了する事にしました。
暗算計算は他にもまだありますが、
それを覚えるよりも当面はこれまでご紹介して来た方法を使いこなす事の方が大事だと思います。
(後日パートⅡとしてご紹介すると共により広い計算への挑戦をしたいとおもます。)
そこで、下表にこれまでご紹介してきた暗算計算の例を纏めました。ご参考になればとおもいます。
そして再度、各5個の問題を計算して見て下さい。
またやり方を忘れたり、もう一度詳しく解説を見たいときには、過去のブログ(日付欄に記載)をもう一度ご参照下さい。
<暗算計算全体まとめと例題各5個>
さて、次回は今シリーズ(パートⅠ)の最後として、今回のシリーズで計算出来る組み合わせを沢山集めて、ランダムに記載した問題集を考えています。
どうぞお楽しみに。
◆スマイルゼミ◆中学生向け通信教育
◆スマイルゼミ◆タブレットで学ぶ通信教育 【幼児コース】
2018年04月23日
一生役に立つ暗算・掛け算(十の位の和が10で、一の位が同じ数、abxcb,a+c=10)
おまたせしました。
今回事情があり間が空いてしましました。
とここで、前回の25の掛け算はいかがでしたか。
何はともあれ、
忘れても、直ぐ思い出せるようになるまで何度も練習してみてください。
さて
今回は一の位の数は同じで、十の位の数を足すと10になる組み合わせの掛け算です。
あれ以前と同じではと思われた方もあるかも知れませんが、前回の問題は、十の位が同じで、一の位を足したら10になる数の組み合わせでした。
今回は一の位と十の位の数の関係が逆ですので、お間違えのないように。
では
早速問題です。先ずはいつものようにビフォー値を測っておいて下さいね。
では/ヨーイ、スタート
・23x83
・37x77
・42x62
・67x47
・79x39
ビフォー値:
それでは
今回の掛け算の計算方法を説明します。
例として38x78とすると
①先ず十の位の数同士を掛けて一の位を足す→(3x7+8)=29
②1の位の数字を掛ける(今回は2乗になる)→8x8=64
③①の結果を左に②の結果を右に並べて4桁の数字とします。→29|64→2,964
(左右に並べるという意味を|で表すことにします)
これだけです。
簡単ですね。
では
頭初の問題を本法で計算します。
・24x84:(2x8+4)|(4x4)→20|16→2,016
・37x77:(3x7+7)|(7x7)→28|49→2,849
・42x62:(4x6+2)|(2x2)→26|04→2、604
(一桁の自乗が一桁となる時は0を付けて2桁とする)
・67x47:(6x4+7)|(7x7)→31|49→3,149
・79x39:(7x3+9)|(9x9)→30|81→3,081
簡単ですね。
慣れた後のアフター値: はいかがでしたか。
大部差がありましたか?
それでは
いつもの様に、練習問題。10題です。サクッと暗算して下さい。
・34x74=
・23x83=
・67x47=
・46x66=
・54x54=
・88x28=
・96x16=
・69x49=
・76x36=
・85x25=
慣れれば簡単にできますね。
速く出来るように練習してください。
とにかく
2つの数が「一の位が同数で十の位を足すと10になる数」(abxcb,a+c=10)の条件に合致しているかどうかを間違えないことですね。
それでは
次回もお楽しみに。
◆スマイルゼミ◆中学生向け通信教育

◆スマイルゼミ◆タブレットで学ぶ通信教育 【幼児コース】

今回事情があり間が空いてしましました。
とここで、前回の25の掛け算はいかがでしたか。
何はともあれ、
忘れても、直ぐ思い出せるようになるまで何度も練習してみてください。
さて
今回は一の位の数は同じで、十の位の数を足すと10になる組み合わせの掛け算です。
あれ以前と同じではと思われた方もあるかも知れませんが、前回の問題は、十の位が同じで、一の位を足したら10になる数の組み合わせでした。
今回は一の位と十の位の数の関係が逆ですので、お間違えのないように。
では
早速問題です。先ずはいつものようにビフォー値を測っておいて下さいね。
では/ヨーイ、スタート
・23x83
・37x77
・42x62
・67x47
・79x39
ビフォー値:
それでは
今回の掛け算の計算方法を説明します。
例として38x78とすると
①先ず十の位の数同士を掛けて一の位を足す→(3x7+8)=29
②1の位の数字を掛ける(今回は2乗になる)→8x8=64
③①の結果を左に②の結果を右に並べて4桁の数字とします。→29|64→2,964
(左右に並べるという意味を|で表すことにします)
これだけです。
簡単ですね。
では
頭初の問題を本法で計算します。
・24x84:(2x8+4)|(4x4)→20|16→2,016
・37x77:(3x7+7)|(7x7)→28|49→2,849
・42x62:(4x6+2)|(2x2)→26|04→2、604
(一桁の自乗が一桁となる時は0を付けて2桁とする)
・67x47:(6x4+7)|(7x7)→31|49→3,149
・79x39:(7x3+9)|(9x9)→30|81→3,081
簡単ですね。
慣れた後のアフター値: はいかがでしたか。
大部差がありましたか?
それでは
いつもの様に、練習問題。10題です。サクッと暗算して下さい。
・34x74=
・23x83=
・67x47=
・46x66=
・54x54=
・88x28=
・96x16=
・69x49=
・76x36=
・85x25=
慣れれば簡単にできますね。
速く出来るように練習してください。
とにかく
2つの数が「一の位が同数で十の位を足すと10になる数」(abxcb,a+c=10)の条件に合致しているかどうかを間違えないことですね。
それでは
次回もお楽しみに。
◆スマイルゼミ◆中学生向け通信教育
◆スマイルゼミ◆タブレットで学ぶ通信教育 【幼児コース】
2018年04月10日
一生役に立つ暗算・掛け算(x25)
前回の99や999の掛け算は実用的にはあまりないかも知れませんが、電卓を使えない場合はこの方法を思い出してください。
さて今回は25の掛け算です。
早速問題です。
いつもの様に
ヨーイ、スタート
・28x25=
・32x25=
・33x25=
・34x25=
・35x25=
ビフォー値:
今回は考え方が良く解るような数字にしました。
それでは説明します。
先ず25は100を4で割った数字つまり25=100/4ですから、
先ず100を掛けて次に4で割ればいいわけですね。
そうすると例題は
・28x25=28x100÷4=2800÷4=700
・32x25=32x100÷4=3200÷4=800
・33x25=33x100÷4=3300÷4=825
・34x25=34x100÷4=3400÷4=850
・35x25=35x100÷4=3500÷4=875
となります。
このやり方で全て出来るわけですが、
もっとわり切った考え方でする方法もあります。
それは先ず4で割って桁数を少なくするという考え方です。
全ての数字は4で割ると
割り切れるつまり余り0の場合と、余りがそれぞれ1、2、3の4通りになりますね。
そこで各余りを4で割るとそれぞれ、0.25、0.5、0.75となり、
これらに100を掛けるとそれぞれ25、50、75となります。
従ってある数に25を掛ける場合、
先ず4で割って、
1.割り切れる時はそのまま100倍する。
2.余りが1の時は、4で割った整数部分に100を掛けて25を足す。
3.余りが2の時は、同様にして50を足す。
4.余りが3の時も、同様にして75を足す。
ということになります。
上記の例で示せば、
・28x25=:28÷4=7余り0→7x100=700
・32x25=:32÷4=8余り0→8x100=800
・33x25=:33÷4=8余り1→8x100+25=825
・34x25=:34÷4=8余り2→8x100+50=850
・35x25=:35÷4=8余り3→8x100+75=875
という具合です。
いずれかお好きな方でやればいいと思いますが、
私はこの先ず4で割って桁数を少なくして、余りの数に応じて計算するほうが
暗記的に行えるのでやり易いのかなと思っています。
では
いつもの様に練習問題です。
・24x25=
・26x25=
・36x25=
・39x25=
・37x25=
・44x25=
・49x25=
・42x25=
・64x25=
・75x25=
上から順、下から順、ランダム等何度も練習して見て下さい。
すぐ出来るようになった人は、3桁の数字にも挑戦してみて下さい。
ところで
ランダムな数字の作り方は、考えて作ると意外と作りにくいので、以下の方法はいかがでしょう。
1。ビー玉10個に0から9の数字を字消しペンで書いておいて適当に3個(3桁)取り出す方法
2.エクセルのランダム関数(RND())と整数関数(INT())で作る
等の方法があります。
(もっといい方法があるのかもしれませんが・・・)
街中やどこかで、2桁や3桁の数字を見つけたら、すぐ上記方法で25を掛けて計算してみて下さい。
それでは次回をお楽しみに。
◆スマイルゼミ◆中学生向け通信教育

◆スマイルゼミ◆タブレットで学ぶ通信教育 【幼児コース】

さて今回は25の掛け算です。
早速問題です。
いつもの様に
ヨーイ、スタート
・28x25=
・32x25=
・33x25=
・34x25=
・35x25=
ビフォー値:
今回は考え方が良く解るような数字にしました。
それでは説明します。
先ず25は100を4で割った数字つまり25=100/4ですから、
先ず100を掛けて次に4で割ればいいわけですね。
そうすると例題は
・28x25=28x100÷4=2800÷4=700
・32x25=32x100÷4=3200÷4=800
・33x25=33x100÷4=3300÷4=825
・34x25=34x100÷4=3400÷4=850
・35x25=35x100÷4=3500÷4=875
となります。
このやり方で全て出来るわけですが、
もっとわり切った考え方でする方法もあります。
それは先ず4で割って桁数を少なくするという考え方です。
全ての数字は4で割ると
割り切れるつまり余り0の場合と、余りがそれぞれ1、2、3の4通りになりますね。
そこで各余りを4で割るとそれぞれ、0.25、0.5、0.75となり、
これらに100を掛けるとそれぞれ25、50、75となります。
従ってある数に25を掛ける場合、
先ず4で割って、
1.割り切れる時はそのまま100倍する。
2.余りが1の時は、4で割った整数部分に100を掛けて25を足す。
3.余りが2の時は、同様にして50を足す。
4.余りが3の時も、同様にして75を足す。
ということになります。
上記の例で示せば、
・28x25=:28÷4=7余り0→7x100=700
・32x25=:32÷4=8余り0→8x100=800
・33x25=:33÷4=8余り1→8x100+25=825
・34x25=:34÷4=8余り2→8x100+50=850
・35x25=:35÷4=8余り3→8x100+75=875
という具合です。
いずれかお好きな方でやればいいと思いますが、
私はこの先ず4で割って桁数を少なくして、余りの数に応じて計算するほうが
暗記的に行えるのでやり易いのかなと思っています。
では
いつもの様に練習問題です。
・24x25=
・26x25=
・36x25=
・39x25=
・37x25=
・44x25=
・49x25=
・42x25=
・64x25=
・75x25=
上から順、下から順、ランダム等何度も練習して見て下さい。
すぐ出来るようになった人は、3桁の数字にも挑戦してみて下さい。
ところで
ランダムな数字の作り方は、考えて作ると意外と作りにくいので、以下の方法はいかがでしょう。
1。ビー玉10個に0から9の数字を字消しペンで書いておいて適当に3個(3桁)取り出す方法
2.エクセルのランダム関数(RND())と整数関数(INT())で作る
等の方法があります。
(もっといい方法があるのかもしれませんが・・・)
街中やどこかで、2桁や3桁の数字を見つけたら、すぐ上記方法で25を掛けて計算してみて下さい。
それでは次回をお楽しみに。
◆スマイルゼミ◆中学生向け通信教育
◆スマイルゼミ◆タブレットで学ぶ通信教育 【幼児コース】
2018年04月03日
一生役に立つ暗算・掛け算(x99、x999)
前回の計算は「10の位が同数で1の位を足すと10になる数の掛け算」という、
全45通りの中の制限された数字の掛け算ではありますが、いかがでしたでしょうか。
さて今回はズバリ、x99とx999の掛け算についてです。
いつもの様に早速問題です。
・25x99=
・43x99=
・5x999=
・8x999=
・15x999=
ビフォー値:
今回はかなり時間が掛かったかも知れませんね。
普通にやればとても暗算ができそうに有りませんがこれも暗算で出来ます。
ではやり方の説明です。
被乗数をn(今回は1桁又は2桁に限定)とすると、
1.nx99の時は100を掛けてnを引く
2.nx999の時は1000を掛けてnを引く
これだけです。
「なーんだ」という声が聞こえて来そうですが、
しかしサッと答えを出すには、やはり少し慣れが必要です。
今回は、もはや計算方法を乗せる必要も無い位ですが、一応従来通り例示しておきますね。
・25x99=25x100-25=2500-25=2475
・43x99=43x100-43=4300-43=4257
・5x999=5x1000-5=5000-5=4995
・9x999=9x1000-9=9000-9=8991
・15x999=15x1000-15=15000-15=14985
何回か練習した後のアフター値:
後は慣れるため後の練習問題をどうぞ。
しかし、上記の方法(100倍又は1000倍した大きな数字から直接引くやり方)はやりにくいという方には次の方法もあります。
一見より複雑なようですが、大きな数字をまず計算し、その間に足す方の値を計算して加えるという方法です。とにかく先ず被乗数nから1を引くというのがミソです。
計算式は
1.nx99の時は →→ (n-1)x100+(100-n)
2.nx999の時は →→ (n-1)x1000+(1000-n)
です。
上の例題は、
・43x99=(43-1)x100+(100-43)=4200+57=4257
・15x999=(15-1)x1000+(1000-15)=14000+985=14985
ですね。
お好きな方法で、以下の練習問題をやってみて下さい。
・13x99=
・24x99=
・36x99=
・47x99=
・78x99=
・4x999=
・9x999=
・3x999=
・6x999=
・7x999=
・23x999=
・35x999=
・46x999=
・57x999=
・68x999=
何度かやって慣れて下さい。
今までの計算の全てにいえますが、
速くできなくても
暗算で計算出来るということだけでも大きな飛躍です。
後は
この計算方法に十分慣れたら電卓に挑戦してみて下さい。
それでは今回は此の辺で。次回をお楽しみに。
ご訪問ありがとうございました。
◆スマイルゼミ◆中学生向け通信教育

◆スマイルゼミ◆タブレットで学ぶ通信教育 【幼児コース】

全45通りの中の制限された数字の掛け算ではありますが、いかがでしたでしょうか。
さて今回はズバリ、x99とx999の掛け算についてです。
いつもの様に早速問題です。
・25x99=
・43x99=
・5x999=
・8x999=
・15x999=
ビフォー値:
今回はかなり時間が掛かったかも知れませんね。
普通にやればとても暗算ができそうに有りませんがこれも暗算で出来ます。
ではやり方の説明です。
被乗数をn(今回は1桁又は2桁に限定)とすると、
1.nx99の時は100を掛けてnを引く
2.nx999の時は1000を掛けてnを引く
これだけです。
「なーんだ」という声が聞こえて来そうですが、
しかしサッと答えを出すには、やはり少し慣れが必要です。
今回は、もはや計算方法を乗せる必要も無い位ですが、一応従来通り例示しておきますね。
・25x99=25x100-25=2500-25=2475
・43x99=43x100-43=4300-43=4257
・5x999=5x1000-5=5000-5=4995
・9x999=9x1000-9=9000-9=8991
・15x999=15x1000-15=15000-15=14985
何回か練習した後のアフター値:
後は慣れるため後の練習問題をどうぞ。
しかし、上記の方法(100倍又は1000倍した大きな数字から直接引くやり方)はやりにくいという方には次の方法もあります。
一見より複雑なようですが、大きな数字をまず計算し、その間に足す方の値を計算して加えるという方法です。とにかく先ず被乗数nから1を引くというのがミソです。
計算式は
1.nx99の時は →→ (n-1)x100+(100-n)
2.nx999の時は →→ (n-1)x1000+(1000-n)
です。
上の例題は、
・43x99=(43-1)x100+(100-43)=4200+57=4257
・15x999=(15-1)x1000+(1000-15)=14000+985=14985
ですね。
お好きな方法で、以下の練習問題をやってみて下さい。
・13x99=
・24x99=
・36x99=
・47x99=
・78x99=
・4x999=
・9x999=
・3x999=
・6x999=
・7x999=
・23x999=
・35x999=
・46x999=
・57x999=
・68x999=
何度かやって慣れて下さい。
今までの計算の全てにいえますが、
速くできなくても
暗算で計算出来るということだけでも大きな飛躍です。
後は
この計算方法に十分慣れたら電卓に挑戦してみて下さい。
それでは今回は此の辺で。次回をお楽しみに。
ご訪問ありがとうございました。
◆スマイルゼミ◆中学生向け通信教育
◆スマイルゼミ◆タブレットで学ぶ通信教育 【幼児コース】

