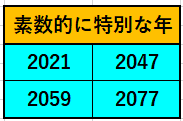
2021�N06��15��
2021�N�͑f�����猩��Ɣ��ɓ��ʂȔN�A����2047�N�B�@�@�֘A�Ƃ��ĈÎZ�|�Z�Ƒf���[�~���B
�Q�O�Q�O�N�ƂQ�O�Q�P�N�͌㐢���猩��Ƒ�ςȔN�����ƋL�^����Ă��邱�Ƃł��傤�B
���̗��R�͂������V�^�R���i�Ɉ˂�p���f�~�b�N��I�����s�b�N�֘A�ł����A
�f���Ō�����Q�O�Q�P�N�͓��ʂȔN�ł���(���N�ȍ~���������I�j�Ƃ�����̂ł��B
�Q�O�Q�O�N�͉[�N�ł͂���܂������A�f���I�ɂ͕��ʂ̔N�ł����B�Q�O�P�X�N�������ł����B
�܂��f�����������O�H�ɂ��u�f���[�~�v�Ƃ����̂�����܂��B
�Ƃ������
������Q�O�O�O�N�ȍ~�̐���̐����Ƒf���Ƃ̊֘A�������̒������������Љ�܂��B
�܂�
�P�B�f���Ƃ͉����B
�f�����u���ꎩ�g�ƂP�ȊO�̐����ł͊���Ȃ����v�ƒ�`����Ă��܂��B
���ӂ��Ȃ��Ă͂����Ȃ��̂́A�P���g�͑f���ł͂Ȃ��̂ł��B
�Q�B�P�O�O�ȉ��̑f���ɂ͂ǂ�Ȑ��������邩�B
�@�Q�A�R�C�T�A�V�A�P�P�C�P�R�E�E�E�E�E�ƂQ�T������܂��B
�@�ڂ����͈ȉ��̕\�����Ă��������B
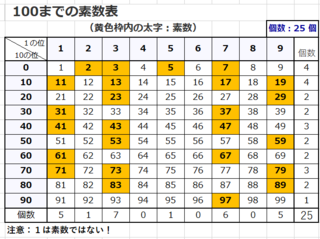
��N�Q�O�Q�O�N�͉[�N�A���N�Q�O�Q�P�N�͕��N�ŁA���N�Q�O�Q�Q�N�����N�ŁA���N�����ʓ���ȔN�ɂ͊����܂���B�������f���Ƃ̊W������ƈ�ڗđR�A��N�◈�N�Ƃ͑S���قȂ��Ă��邱�Ƃ�������܂��B
�ł͑������ׂĂ݂Ă݂܂��傤�B
�R�B�Q�O�Q�P�N�̂P�N�O��̐��������̂Q�T�̑f���Ŋ���Z���Ă݂܂��B
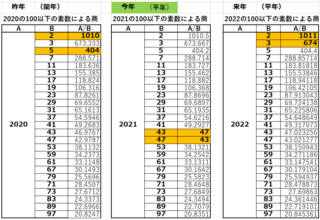
���̗l�ɁA���N�̂Q�O�Q�P�Ƃ��������������鐮���͂Ȃ���S�O��̗ד��m�̑f���Ȃ̂ł��B
���ꂪ�����ɓ���ł��邩�́A���N���܂ޑO���P�O�N�i�Q�O�O�O�`�Q�O�R�O�j�ɂ��Č���Ƃ킩��܂��B
�S�B�Q�O�O�O�N����̂Q�O�R�O�N�̐������Q�T�̑f���Ŋ��萮���ƂȂ���������
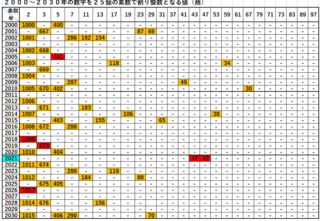
���̐����̓��A�X�ɑf����Ԙg�Ŏ����Ă��܂��B
������݂ė�R�Ƃ킩��悤�ɁA�f�����P����N�͂S����܂����A�Q����N�͂Q�O�Q�P�N��������܂���B�S�R�Ŋ���ƂS�V�ɁA�S�V�Ŋ���ƂS�R�ɂȂ�܂����A���̓�̐����ׂ͗荇���Ă��鐔���ł��B
�ׂ荇���Ă���Ƃ��������i���j�͑��ɂ�������܂����Ԙg���̑f���Ɋւ��Ă͂��̂Q�����ł��B
���̇@�f���̏����Q����Ƃ������ƁA�A���̂Q���ׂ荇���Ă���Ƃ����̂��u���ʁv�̈Ӗ���������ł��B
�ł͍X�ɂQ�O�R�P�N�ȍ~�ɂ��Ă͂ǂ��Ȃ̂��Ƃ����^�₪�����N���܂��ˁB
�Ƃ������Ƃő������ׂĂ݂܂����B
�T�B�Q�O�R�P�N����̂Q�O�T�O�N�̐������Q�T�̑f���Ŋ��萮���ƂȂ���������
���ʂ����\�Ɏ����܂��B
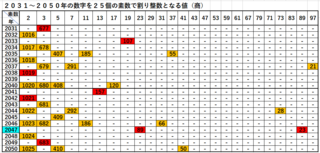
�������ڗđR�ł��ˁB
������Ɨ���Ă͂��邪�f�����Q����N���L��܂����I�I�I
�Q�R�ƂW�X�ł��B�Q�R���W�X���Q�O�S�V�@�ł��B
�܂�
�Q�O�R�O�N�ȍ~�ɂP�O�O�ȉ����Q�̑f���������̂͂Q�O�S�V�N�ł��B
�Q�O�T�P�N�ȍ~���Q�f���������N������Ǝv���܂��̂ŁA�����̂���l�̓g���C���Ă��������B
2�D�ÎZ�|���Z
�Ƃ���ŁA
����ɏ����܂����A�ÎZ�|���Z�ɂ��ď����lj����܂��B
����́A���u���O�ňȑO�ɁA�u�ꐶ�𗧂ÎZ�|���Z�v�Ƒ肵���V���[�Y�ŁA�Q���̐����̊|���Z�̂Ȃ���
�u�P�O�̈ʂ̐����������łP�̈ʂ̐����̘a���P�O�ɂȂ鎞�͈ÎZ�ŊȒP�Ɍv�Z�ł���v�Ƃ������̂ł��B
��ʎ��ŏ������i10a+b)�w(10a+c)�ƂȂ�A���̓����́�����100(a�w(a+1))+bc�ňÎZ�ł���
�ƌ������Ƃł��B
����̂Q�O�Q�P�͂S�R���S�V�ł��̂ŁA�P�O�O���i�S���T�j�{�Q�P�ƈÎZ�Ōv�Z�ł���ƌ������Ƃł��B
���̈ÎZ�|���Z�ɂ��ẮA�ڂ������O�̃u���O�����Q�Ƃ��������B��R�̗��K���Ǝ��̗U�����L�q���Ă��܂��B
3�D�f���[�~
�f���[�~�ɂ��ẮA�A�����J�ł͂P�R�N�ƂP�V�N�̑f���̔N�����Ŕ�������Z�~�����āA
���N�����́h��ʔ����̔N�h�ɂȂ��Ă��Ęb��ɂȂ��Ă��邻���ł��B
������
���̑f���[�~�̘b�͒P�ɃZ�~�̐��Ԃ��ʔ����̔�Q�̖�肾���ł͂Ȃ��A
�����Ƒ傫�ȃe�[�}�Ƃ��ẮA�n���̗��j����Z�~�̎�Ƃ��Ă̐������ё�A
�Ђ��Ă͐l�ނ̐��������A�ŖS��܂ōl����������قǂ̓��e���܂�ł��܂��B
�f���̓�̉𖾂ɍv���������{�l������Ƃ������͌ւ炵�����̂ł��B
�A��
���̑f���[�~�Ɋւ�����e�͐[���̂ŁA����̓j���[�X�Ɠ���Ɖ���T�C�g�̏Љ���ɂ��܂��̂�
�������������B
�P�j�j���[�X
�E�ē����ŃZ�~����ʔ����@17�N�ʼnH������u�����[�~�v
�Q�j����
�E�����C�̑唭�����H�A�����J�Łg17�N�����[�~�h�u�u���[�h�w�v�H���n�܂�
�R�j�����
�E���\���C����ʔ����I �č���17�N�Ԃ�Ɍ��ꂽ�u�����[�~�v�������҂Ƌ��ɒǂ��Č����Ă�������
�E2021�N�A�A�����J�Ő����C�́u�f���[�~�v����ʔ����c���́u�[���̗��R�v�Ƃ́H
�E�������2021�N�ɑ唭���B�X�͊������т��u�f���[�~�v�̋����̐����헪
�S�j�H����
�E17�N�����[�~�Ŋ��������͂������H �����\�ȐH���� �ăV�F�t
������f���Ɋւ���ʔ����b��E�𗧂��������Ύ��グ�Ă����Ǝv���Ă��܂��B
���̗��R�͂������V�^�R���i�Ɉ˂�p���f�~�b�N��I�����s�b�N�֘A�ł����A
�f���Ō�����Q�O�Q�P�N�͓��ʂȔN�ł���(���N�ȍ~���������I�j�Ƃ�����̂ł��B
�Q�O�Q�O�N�͉[�N�ł͂���܂������A�f���I�ɂ͕��ʂ̔N�ł����B�Q�O�P�X�N�������ł����B
�܂��f�����������O�H�ɂ��u�f���[�~�v�Ƃ����̂�����܂��B
�Ƃ������
������Q�O�O�O�N�ȍ~�̐���̐����Ƒf���Ƃ̊֘A�������̒������������Љ�܂��B
�܂�
�P�B�f���Ƃ͉����B
�f�����u���ꎩ�g�ƂP�ȊO�̐����ł͊���Ȃ����v�ƒ�`����Ă��܂��B
���ӂ��Ȃ��Ă͂����Ȃ��̂́A�P���g�͑f���ł͂Ȃ��̂ł��B
�Q�B�P�O�O�ȉ��̑f���ɂ͂ǂ�Ȑ��������邩�B
�@�Q�A�R�C�T�A�V�A�P�P�C�P�R�E�E�E�E�E�ƂQ�T������܂��B
�@�ڂ����͈ȉ��̕\�����Ă��������B

��N�Q�O�Q�O�N�͉[�N�A���N�Q�O�Q�P�N�͕��N�ŁA���N�Q�O�Q�Q�N�����N�ŁA���N�����ʓ���ȔN�ɂ͊����܂���B�������f���Ƃ̊W������ƈ�ڗđR�A��N�◈�N�Ƃ͑S���قȂ��Ă��邱�Ƃ�������܂��B
�ł͑������ׂĂ݂Ă݂܂��傤�B
�R�B�Q�O�Q�P�N�̂P�N�O��̐��������̂Q�T�̑f���Ŋ���Z���Ă݂܂��B

���̗l�ɁA���N�̂Q�O�Q�P�Ƃ��������������鐮���͂Ȃ���S�O��̗ד��m�̑f���Ȃ̂ł��B
���ꂪ�����ɓ���ł��邩�́A���N���܂ޑO���P�O�N�i�Q�O�O�O�`�Q�O�R�O�j�ɂ��Č���Ƃ킩��܂��B
�S�B�Q�O�O�O�N����̂Q�O�R�O�N�̐������Q�T�̑f���Ŋ��萮���ƂȂ���������

���̐����̓��A�X�ɑf����Ԙg�Ŏ����Ă��܂��B
������݂ė�R�Ƃ킩��悤�ɁA�f�����P����N�͂S����܂����A�Q����N�͂Q�O�Q�P�N��������܂���B�S�R�Ŋ���ƂS�V�ɁA�S�V�Ŋ���ƂS�R�ɂȂ�܂����A���̓�̐����ׂ͗荇���Ă��鐔���ł��B
�ׂ荇���Ă���Ƃ��������i���j�͑��ɂ�������܂����Ԙg���̑f���Ɋւ��Ă͂��̂Q�����ł��B
���̇@�f���̏����Q����Ƃ������ƁA�A���̂Q���ׂ荇���Ă���Ƃ����̂��u���ʁv�̈Ӗ���������ł��B
�ł͍X�ɂQ�O�R�P�N�ȍ~�ɂ��Ă͂ǂ��Ȃ̂��Ƃ����^�₪�����N���܂��ˁB
�Ƃ������Ƃő������ׂĂ݂܂����B
�T�B�Q�O�R�P�N����̂Q�O�T�O�N�̐������Q�T�̑f���Ŋ��萮���ƂȂ���������
���ʂ����\�Ɏ����܂��B

�������ڗđR�ł��ˁB
������Ɨ���Ă͂��邪�f�����Q����N���L��܂����I�I�I
�Q�R�ƂW�X�ł��B�Q�R���W�X���Q�O�S�V�@�ł��B
�܂�
�Q�O�R�O�N�ȍ~�ɂP�O�O�ȉ����Q�̑f���������̂͂Q�O�S�V�N�ł��B
�Q�O�T�P�N�ȍ~���Q�f���������N������Ǝv���܂��̂ŁA�����̂���l�̓g���C���Ă��������B
2�D�ÎZ�|���Z
�Ƃ���ŁA
����ɏ����܂����A�ÎZ�|���Z�ɂ��ď����lj����܂��B
����́A���u���O�ňȑO�ɁA�u�ꐶ�𗧂ÎZ�|���Z�v�Ƒ肵���V���[�Y�ŁA�Q���̐����̊|���Z�̂Ȃ���
�u�P�O�̈ʂ̐����������łP�̈ʂ̐����̘a���P�O�ɂȂ鎞�͈ÎZ�ŊȒP�Ɍv�Z�ł���v�Ƃ������̂ł��B
��ʎ��ŏ������i10a+b)�w(10a+c)�ƂȂ�A���̓����́�����100(a�w(a+1))+bc�ňÎZ�ł���
�ƌ������Ƃł��B
����̂Q�O�Q�P�͂S�R���S�V�ł��̂ŁA�P�O�O���i�S���T�j�{�Q�P�ƈÎZ�Ōv�Z�ł���ƌ������Ƃł��B
���̈ÎZ�|���Z�ɂ��ẮA�ڂ������O�̃u���O�����Q�Ƃ��������B��R�̗��K���Ǝ��̗U�����L�q���Ă��܂��B
3�D�f���[�~
�f���[�~�ɂ��ẮA�A�����J�ł͂P�R�N�ƂP�V�N�̑f���̔N�����Ŕ�������Z�~�����āA
���N�����́h��ʔ����̔N�h�ɂȂ��Ă��Ęb��ɂȂ��Ă��邻���ł��B
������
���̑f���[�~�̘b�͒P�ɃZ�~�̐��Ԃ��ʔ����̔�Q�̖�肾���ł͂Ȃ��A
�����Ƒ傫�ȃe�[�}�Ƃ��ẮA�n���̗��j����Z�~�̎�Ƃ��Ă̐������ё�A
�Ђ��Ă͐l�ނ̐��������A�ŖS��܂ōl����������قǂ̓��e���܂�ł��܂��B
�f���̓�̉𖾂ɍv���������{�l������Ƃ������͌ւ炵�����̂ł��B
�A��
���̑f���[�~�Ɋւ�����e�͐[���̂ŁA����̓j���[�X�Ɠ���Ɖ���T�C�g�̏Љ���ɂ��܂��̂�
�������������B
�P�j�j���[�X
�E�ē����ŃZ�~����ʔ����@17�N�ʼnH������u�����[�~�v
�Q�j����
�E�����C�̑唭�����H�A�����J�Łg17�N�����[�~�h�u�u���[�h�w�v�H���n�܂�
�R�j�����
�E���\���C����ʔ����I �č���17�N�Ԃ�Ɍ��ꂽ�u�����[�~�v�������҂Ƌ��ɒǂ��Č����Ă�������
�E2021�N�A�A�����J�Ő����C�́u�f���[�~�v����ʔ����c���́u�[���̗��R�v�Ƃ́H
�E�������2021�N�ɑ唭���B�X�͊������т��u�f���[�~�v�̋����̐����헪
�S�j�H����
�E17�N�����[�~�Ŋ��������͂������H �����\�ȐH���� �ăV�F�t
������f���Ɋւ���ʔ����b��E�𗧂��������Ύ��グ�Ă����Ǝv���Ă��܂��B
���̋L���ւ̃R�����g
�R�����g������
���̋L���ւ̃g���b�N�o�b�NURL
https://fanblogs.jp/tb/10798041
���u���O�I�[�i�[�����F�����g���b�N�o�b�N�̂ݕ\������܂��B
�����y�����N�̂Ȃ��g���b�N�o�b�N�͎�M����܂���B
���̋L���ւ̃g���b�N�o�b�N