2018�N01��28��
�ꐶ�𗧂ÎZ�|���Z�i���̂P�D�a�ƍ��̐ς͂Q��Q��̍��j
�����Ȃ�ł����A�v�Z���Ă݂ĉ������B
�ȉ��̂T�̌v�Z���A�d����g��Ȃ������Ɠd����g�����@�Ōv�Z���|���������Ԃ����ꂼ�ꃁ�����Ă����Ă��������B
�iBefore�l�Ƃ��āj
����ł͑������肢���܂��B
���[�C�A�X�^�[�g
17��23�C�@28��32�C�@45��55�C�@66��74�A�@99��101
�ǂ�ʊ|����܂����ł��傤���B
�d����g��Ȃ��ł�30�b�ȓ��ŏI������l�͂��̃u���O�̓X���[���ĉ������B
����ł��ÎZ�|���Z�ɂ��S�̂���l�͂ǂ����B
�܂�����
�̂́u�ǂݏ����Z�Ձi�����j�v����{�I�ȋZ�p�Ƃ��Ċo���Ȃ�������܂���ł����B
���݂Ȃ炳�����߁u�ǂݏ����p�\�R���v�ł��傤���B
���͗c�����낻���m�ɒʂ��܂������A3���܂łŒ��f���Ă��܂��܂����B
�����p�����ĂP��~���i���炢�܂ŏ����o���Ă�����ÎZ�����Ȃ蓾�ӂɂȂ��Ă�����������܂��E�E�E�B
��ʂɂ����Œi�ʂ������Ă���l�͈ÎZ�����ӂŁA���ɂ��������Z�\�͂͑A�܂�������ł��B
���̐l�B�̂����́A�u�����ɕ`���ċʂ����Ă����v�����ł��ˁB
�Ƃ����
����͖w�ǂ̐l���g�т��X�}�z�������Ă��܂���ˁB
�����Ă��̋@�\�̒��ɓd�삪���Ƃ��Ƃ��邩���̓A�v���ŃC���X�g�[������Ă���
�����ł��ǂ��ł��ȒP�֗��Ɍv�Z�o�����Ԃł��傤�B
�����Z�ł́A���ʂ������Ȃ�ƕ��ʓd��i�X�}�z�j�Ōv�Z���܂����A�ÎZ�����ӂȐl�ɂ͊����܂���B
�|���Z�ɂ��ẮA���͒N�ł������ł���ł��傤���A�������傫���Ȃ�Ƃ��͂�d��Ȃ��ł͍ς݂܂���B
�i�C���h�����͂P�X���P�X���Ƃ��j
����ł��ÎZ�ŏo����悤�ȊȒP�Ȋ|���Z�E����Z���d��Ōv�Z���Ă���l�������̂ł͎v���܂��B
�Ƃ��낪
����������������ꕔ�̐����̊|���Z�E����Z�ɂ��Ă͈ÎZ���\�ŁA�d�삪�����Ă��A�܂��d���葬���������o�����Ƃ��ł��܂��B
��������������������ꕔ�̐����̊|���Z�E����Z�ɂ��āA���ꂩ������ɕ����ďЉ����čs���܂��B
�Ƃ����킯�ŁA�O�u���������Ȃ�܂������A
����͎�����ԍD���Ȍv�Z�����ł����u�a�ƍ��̐ς͎��掩��̍��v�i2��Q��Ƃ������܂��j�̌������g�����������Љ�܂��B
�w�Z�ŏK���܂�����ˁB������Y�ꂽ�l�����邩������܂��A�v���o���ĉ������B
�L���ŏ����ƊȒP�ŁA
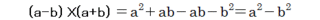
���̌������g���ĈÎZ�v�Z�o���鐔���̓����Ƃ́A
����i�Q��j���錳�̐������Ȍ��Ŏ戵�Ղ����ƂƁA���̐����ƂP~�X�̃v���X�A�}�C�i�X�̍��̂��鐔���Ƃ������Ƃł��B
��̓I�ɂ���̎���
a�ɂ��Ă�
�P�O�C�Q�O�C�R�O�C�E�E�E�E�E�E�P�O�O�C�Q�O�O�C�R�O�O�E�E�E�E�P�O�O�O�ł��B
���̑��ɓK���Ȑ������邩������܂��A�v�͎������ÎZ�o����͈͓��̈ÎZ�Ƃ������ƂɂȂ�܂��B
���ɂ��Ă��A�ÎZ���o����͈͂̐����Ƃ������Ƃ��P~�X�܂łƂ��܂��B
�]���ĈÎZ�ŏo����Q�̐����̑g�ݍ��킹�͂��Ȃ���肳��܂����A
���퐶���Ŏg����ʂ����X����Ǝv���܂��B
����͂��Ă����A
������L�������g���Ď��ۂɊ�b���K���Ă݂܂��傤�B
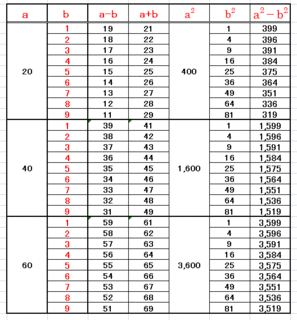
�ȉ��̕\��a-b ��a+b�̐����̌`�ia�{���Ca-b�j���o���Ă����A�@���ɑ������ۂ̌v�Z�̒����炱��ɊY�����邩�����邩�ł��B
�ȉ����Ꭶ���܂��̂ŁA�Ƃɂ����Q�̐������悭���Čv�Z�Ɋ���Ă��������B
�����Ă����v�Z�o����悤�ɂ��ĉ������B�i�N���b�N����Ƒ傫���Ȃ�܂��j
�@
���̑g�ݍ��킹�͉��\���Q�l�ɂ��ĉ������B�i�N���b�N����Ɗg�債�܂��j
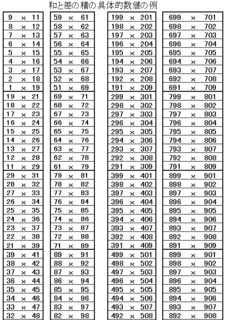
��
a=100�̏ꍇ�̑傫�ȕ\��\�t���܂��̂ŃG�N�Z���Ő������Ă݂ĉ������B
�����đ��̌v�Z�����S�ė��Č��ĉ������B
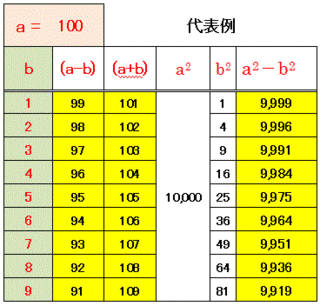
��ʂ茩�Ē����܂�����
�����̌v�Z����L�̕��@�ňÎZ�v�Z����Ă݂ĉ������B
�X�g�b�v�E�I�b�`��ݒ肵��
����ł̓��[�C�A�X�^�[�g
17��23 =�Q�O�̂Q��|9��
28��32���R�O�̂Q��|�S��
45��55���T�O�̂Q��|�Q�T��
66��74���V�O�̂Q��|�P6��
99��101���P�O�O�̂Q��|�P��
�ȒP�ɂł����Ǝv���܂��B
�������ł��������x�̎��Ԃ́A��v�Z�ł̃r�t�H�[�l��肩�Ȃ菬�����Ȃ������Ƃł��傤�B
�Ȃ��Ɠd��Ɠ����ȉ��i���ꂪ�ڕW�j�ɂȂ�܂��B
�i�ŏ��͓d����|�P�b�g�ɂ��ꂽ��ԂŃX�^�[�g�Ƃ���̂����������j
���Ō�Ɂ�
���̈ÎZ�͊w�Z�ł͐������Ȃ���������܂��A
���p�I�Ȏ��ƁA���������o����Ε\��Ƃ����悤�Ɉꐶ���ɗ��̂ŁA
����Љ����@���܂߂āA���q����ɂ��ł��邾�����������A
�ł���Ώ��w����w�N��������������������Ă����ꂽ�炢����
�v���܂��B
���z��V�[����
�i���ꂩ��Љ�镪���܂߂āA����������������g�ݍ��킹�̌v�Z�ɂ��Ắj
�P�D�d�삪�����Ă��A�d����g��Ȃ��Ă��v�Z�o����B
�Q�D���̐l���|�P�b�g��o�b�O����d������o�������ɂ�
�@�@�����v�Z�͏I����Ă���
���X�}�C���[�~�����w�������ʐM����

���X�}�C���[�~���^�u���b�g�Ŋw�ԒʐM���� �y�c���R�[�X�z

�ȉ��̂T�̌v�Z���A�d����g��Ȃ������Ɠd����g�����@�Ōv�Z���|���������Ԃ����ꂼ�ꃁ�����Ă����Ă��������B
�iBefore�l�Ƃ��āj
����ł͑������肢���܂��B
���[�C�A�X�^�[�g
17��23�C�@28��32�C�@45��55�C�@66��74�A�@99��101
�ǂ�ʊ|����܂����ł��傤���B
�d����g��Ȃ��ł�30�b�ȓ��ŏI������l�͂��̃u���O�̓X���[���ĉ������B
����ł��ÎZ�|���Z�ɂ��S�̂���l�͂ǂ����B
�܂�����
�̂́u�ǂݏ����Z�Ձi�����j�v����{�I�ȋZ�p�Ƃ��Ċo���Ȃ�������܂���ł����B
���݂Ȃ炳�����߁u�ǂݏ����p�\�R���v�ł��傤���B
���͗c�����낻���m�ɒʂ��܂������A3���܂łŒ��f���Ă��܂��܂����B
�����p�����ĂP��~���i���炢�܂ŏ����o���Ă�����ÎZ�����Ȃ蓾�ӂɂȂ��Ă�����������܂��E�E�E�B
��ʂɂ����Œi�ʂ������Ă���l�͈ÎZ�����ӂŁA���ɂ��������Z�\�͂͑A�܂�������ł��B
���̐l�B�̂����́A�u�����ɕ`���ċʂ����Ă����v�����ł��ˁB
�Ƃ����
����͖w�ǂ̐l���g�т��X�}�z�������Ă��܂���ˁB
�����Ă��̋@�\�̒��ɓd�삪���Ƃ��Ƃ��邩���̓A�v���ŃC���X�g�[������Ă���
�����ł��ǂ��ł��ȒP�֗��Ɍv�Z�o�����Ԃł��傤�B
�����Z�ł́A���ʂ������Ȃ�ƕ��ʓd��i�X�}�z�j�Ōv�Z���܂����A�ÎZ�����ӂȐl�ɂ͊����܂���B
�|���Z�ɂ��ẮA���͒N�ł������ł���ł��傤���A�������傫���Ȃ�Ƃ��͂�d��Ȃ��ł͍ς݂܂���B
�i�C���h�����͂P�X���P�X���Ƃ��j
����ł��ÎZ�ŏo����悤�ȊȒP�Ȋ|���Z�E����Z���d��Ōv�Z���Ă���l�������̂ł͎v���܂��B
�Ƃ��낪
����������������ꕔ�̐����̊|���Z�E����Z�ɂ��Ă͈ÎZ���\�ŁA�d�삪�����Ă��A�܂��d���葬���������o�����Ƃ��ł��܂��B
��������������������ꕔ�̐����̊|���Z�E����Z�ɂ��āA���ꂩ������ɕ����ďЉ����čs���܂��B
�Ƃ����킯�ŁA�O�u���������Ȃ�܂������A
����͎�����ԍD���Ȍv�Z�����ł����u�a�ƍ��̐ς͎��掩��̍��v�i2��Q��Ƃ������܂��j�̌������g�����������Љ�܂��B
�w�Z�ŏK���܂�����ˁB������Y�ꂽ�l�����邩������܂��A�v���o���ĉ������B
�L���ŏ����ƊȒP�ŁA
���̌������g���ĈÎZ�v�Z�o���鐔���̓����Ƃ́A
����i�Q��j���錳�̐������Ȍ��Ŏ戵�Ղ����ƂƁA���̐����ƂP~�X�̃v���X�A�}�C�i�X�̍��̂��鐔���Ƃ������Ƃł��B
��̓I�ɂ���̎���
a�ɂ��Ă�
�P�O�C�Q�O�C�R�O�C�E�E�E�E�E�E�P�O�O�C�Q�O�O�C�R�O�O�E�E�E�E�P�O�O�O�ł��B
���̑��ɓK���Ȑ������邩������܂��A�v�͎������ÎZ�o����͈͓��̈ÎZ�Ƃ������ƂɂȂ�܂��B
���ɂ��Ă��A�ÎZ���o����͈͂̐����Ƃ������Ƃ��P~�X�܂łƂ��܂��B
�]���ĈÎZ�ŏo����Q�̐����̑g�ݍ��킹�͂��Ȃ���肳��܂����A
���퐶���Ŏg����ʂ����X����Ǝv���܂��B
����͂��Ă����A
������L�������g���Ď��ۂɊ�b���K���Ă݂܂��傤�B
�ȉ��̕\��a-b ��a+b�̐����̌`�ia�{���Ca-b�j���o���Ă����A�@���ɑ������ۂ̌v�Z�̒����炱��ɊY�����邩�����邩�ł��B
�ȉ����Ꭶ���܂��̂ŁA�Ƃɂ����Q�̐������悭���Čv�Z�Ɋ���Ă��������B
�����Ă����v�Z�o����悤�ɂ��ĉ������B�i�N���b�N����Ƒ傫���Ȃ�܂��j
�@
���̑g�ݍ��킹�͉��\���Q�l�ɂ��ĉ������B�i�N���b�N����Ɗg�債�܂��j
��
a=100�̏ꍇ�̑傫�ȕ\��\�t���܂��̂ŃG�N�Z���Ő������Ă݂ĉ������B
�����đ��̌v�Z�����S�ė��Č��ĉ������B
��ʂ茩�Ē����܂�����
�����̌v�Z����L�̕��@�ňÎZ�v�Z����Ă݂ĉ������B
�X�g�b�v�E�I�b�`��ݒ肵��
����ł̓��[�C�A�X�^�[�g
17��23 =�Q�O�̂Q��|9��
28��32���R�O�̂Q��|�S��
45��55���T�O�̂Q��|�Q�T��
66��74���V�O�̂Q��|�P6��
99��101���P�O�O�̂Q��|�P��
�ȒP�ɂł����Ǝv���܂��B
�������ł��������x�̎��Ԃ́A��v�Z�ł̃r�t�H�[�l��肩�Ȃ菬�����Ȃ������Ƃł��傤�B
�Ȃ��Ɠd��Ɠ����ȉ��i���ꂪ�ڕW�j�ɂȂ�܂��B
�i�ŏ��͓d����|�P�b�g�ɂ��ꂽ��ԂŃX�^�[�g�Ƃ���̂����������j
���Ō�Ɂ�
���̈ÎZ�͊w�Z�ł͐������Ȃ���������܂��A
���p�I�Ȏ��ƁA���������o����Ε\��Ƃ����悤�Ɉꐶ���ɗ��̂ŁA
����Љ����@���܂߂āA���q����ɂ��ł��邾�����������A
�ł���Ώ��w����w�N��������������������Ă����ꂽ�炢����
�v���܂��B
���z��V�[����
�i���ꂩ��Љ�镪���܂߂āA����������������g�ݍ��킹�̌v�Z�ɂ��Ắj
�P�D�d�삪�����Ă��A�d����g��Ȃ��Ă��v�Z�o����B
�Q�D���̐l���|�P�b�g��o�b�O����d������o�������ɂ�
�@�@�����v�Z�͏I����Ă���
���X�}�C���[�~�����w�������ʐM����
���X�}�C���[�~���^�u���b�g�Ŋw�ԒʐM���� �y�c���R�[�X�z
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
-
no image
-
no image
���̋L���ւ̃R�����g
�R�����g������
���̋L���ւ̃g���b�N�o�b�NURL
https://fanblogs.jp/tb/7248807
���u���O�I�[�i�[�����F�����g���b�N�o�b�N�̂ݕ\������܂��B
�����y�����N�̂Ȃ��g���b�N�o�b�N�͎�M����܂���B
���̋L���ւ̃g���b�N�o�b�N

