�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2018�N05��14��
2B7007�@��l�̂��ї��Ƃ��@���p�̌���
�J�̓��́@�X���[���C�t�̕���
���p�̌���
�Q���́@���L�@�݂�����
������
�������̂́@��������Ȃ�
��肪�@����Ƃł���
�s���Ă݂܂��傤
�����́@����Ȋ�����
��
�������@�N�������
��悪�@���Ă邩��
���[�g���@�Ƃ��
�ł����̏ꍇ
������
cos�@�����@���߂��
�^���W�F���g�̓�����
�����̌�������
�ό`����
�R�T�C�����@�́@������
���[�@�����
�E���Ɂ@�@�Ȃ@�����Ă���܂���
�ꉞ
�O�̂���
�������ƌ�������
�v���X�}�C�i�X��
���[�g������������
���g���@���̖ł�
���g���@�}�C�i�X�ɂȂ��
�����͈̔͂��@�����Ă��܂�����
��i-1�j�@���@i
�Ƃ���
��́@�O�Ɂ@i
��i-3�j�@�ˁ@�i��R�j�@�E�@i
�b���@���ɖ߂���
�v���X�}�C�i�X
�����悪�@270�������R�U�O�@�Ȃ̂�
�R�T�C���́@�v���X�̕�
�R�T�C�����@���ł���
���p�ɑ������
�v���X�}�C�i�X�Ł@�o�ė���
������́@�����@���������
135������180�Ȃ̂�����
�v���X�̕�
3/5
�R�T�C���̕���
���p�̌����Ɂ@�������
������
��������@����������
�}�C�i�X�̕�
�܂Ƃ߂�Ɓ@����Ȋ�����
�������@���܂��܂���
�v�Z����
���W�A���ŗ��Ă邩��
�x�Ɂ@������
�����ɑ������
������
��������@����������
�v���X�Ȃ̂�
����Ȋ���
�����
��d������
�O���Ȃ��̂�
���̂܂܂Ȃ�ł���
�O�̂���
���Ԃ�@�o�ė����������炳
���Ȃ�����
���̂܂܁@��悵�ā@�O���Ƃ���
���g���@�W�J�������̂�
�C�R�[���Ł@�����
����������i�C�X�J
�b���@�߂���
���x�́@�R�T�C��
����ς�@�@��/8
�����Ɂ@�������
����Ȋ�����
�^���W�F���g��
�s���Ă݂܂��傤
���̂܂܂���
����Ȃ�
���������@�Ƃ��
��
������́@�^���W�F���g�́@�v���X�Ȃ̂�
����Ȃł���
��
�_��
���`��d�������@�O��邩��
�O�������
�L��������
����@���q�@������
���@����́@�L����������
���́@��̑O���@�Q�ɂȂ�l��
���ό`����
�S���@��́@���Ɂ@����������
�Q��ɂȂ�ł���
��
�����ā@�P�Q�@�����ā@�R�Q
�����Z�́@�`������
�傫���ق��@�[�@�������ق�
��
��������
��2-�P
����
�U�O�i�@
���p�̌�����
�m�F���邶��i�C�X�J
�P�P���P�T���@���@
�Q�{���ā@�Q�Ł@�����
���q��
�Q�Q���R�O��
�P�P���P�T���́@11.25�x��
�T�C���́@�v���X
��́@���g�̕���
�Q�Q���R�O�����@
�Q�{���ā@�Q�Ŋ����
���q��
�U�O�i�Ȃ̂�
�S�T��
�Q�Q���R�O���́@22.5���Ȃ̂�
�R�T�C���́@�v���X
���́@���Ɂ@����q������
�v�Z������
����Ȋ�����
����
���
���ꂱ��̂Ƃ�
�E�E
�^���W�F���g�́@������
�������@��
���ό`����
�����������
����������
��������@��������
�R�T�C���́@�v���X
�^���W�F���g�́@�������
��������
�v���X�̕�
�����@�������
�����P��
�^���W�F���g�̓������@������������
�R�T�C��
0�������P�W�O�@�́@�^���W�F���g��
�}�C�i�X��
90�������P�W�O
���͈̔͂́@�R�T�C���́@�}�C�i�X
���p�̌����Ɂ@������čs����
��������
��
�v���X�}�C�i�X
���x��
������
����Ɂ@�X�O�������P�W�O�́@�������
��/2
�Ł@����������
45�������X�O
���͈̔͂́@�R�T�C���́@�v���X
�L�������ā@
����Ȋ�����
�Ō��
�ؖ����
���p�́@�������@�g���悤�ł���
�ǂ�����ł���
�^�����@�W�J��������i�C�X�J��
��
�������́@����
�ӁX�@��������
���ό`���Ă��܂���
���ӂ́@����
�^���W�F���g�́@���p�̌�����
������������̂�
��
������@������
�����̂�
���Ӂ�
�E�Ӂ�
���Ӂ@���@�E�Ӂ@��
�����ł���Ƃ���
�V���@�V��
��l�@���ӂɁ@�W�߂�
���O�@�Ł@�@��������
���
���@���Ӂ@�E�Ӂ@�ɂ���̂ł���
��
����������́@���ό`���@�ł��Ă���
�����܂ł��@�������܂���
����������́@���ό`��
�^���́@�W�J��
�^���́@�W�J����
���������@����ł���l�@����
�ό`����
�������
�����ł���Ƃ���
�V���@�V��
���@�A�@���@�A���@
�܂܂Ȃ����ɂȂ����̂�
���@�A�@���@�A�Ɂ@���W�ł���
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 14:35| ��l�̂��ї��Ƃ��@
2018�N05��09��
????? ��l�̂��ї��Ƃ��@�Ɍ��̌v�Z�@0/0�`
�J�̓��́@�X���[���C�t�̕���
���̋Ɍ��̋��ߕ��̖���
�O��
�ڂ����@�v�Z������ĂȂ�����
�悤�Ɂ@�v������
���ނ���
����Ă݂����Ǝv���܂���
�S�@�T�@�U��
��
�p�^�[����������
��
�Ɍ���
�����@����Ȃ��@a�Ɂ@�߂Â��Ƃ���
���i���j���@���Ƃ����l��
����Ȃ��@�߂Â��Ă����Ȃ��
���̋Ɍ��́@�l��
����a�@�̎��@���i���j�@���@���@�Ƃ�
Lim
����a�@�@���i���j����

����́@�v�Z����
���Ă��܂���
���p�^�[��������̂ł���
�����
�O/�O�@�`

0/0�`�̎���
�������Ȃ�@��
�������Ȃ�@�����Ȑ����@������
����ōs���Ă݂܂��傤

����
�����@����Ȃ��@�P�Ɂ@�߂Â��Ƃ�
�ꉞ�@�ڕW�l�I�Ɂ@�����P���@������Ă݂��
������@���q���@�O�@�́@0/0�`

������
���������ł�����������

�����������Ă݂܂���
����́@���|���
���q��
�����藝��
x���P�̎��@�O�ɂȂ��Ă��܂�����
�������������
�g�����@�Ƃ��@�g���Ȃ���
�W����������
�i���|�P�j�@���@�����Ɂ@���̂�����
�i���|�P�j���O�ɂ���@x�̒l��
�����
�R�������@�P�����@�Ŋ���������
��ԏ�́@�Q���@�Ł@�P���@�Ł@�萔�Ł@�]��@�́@�O
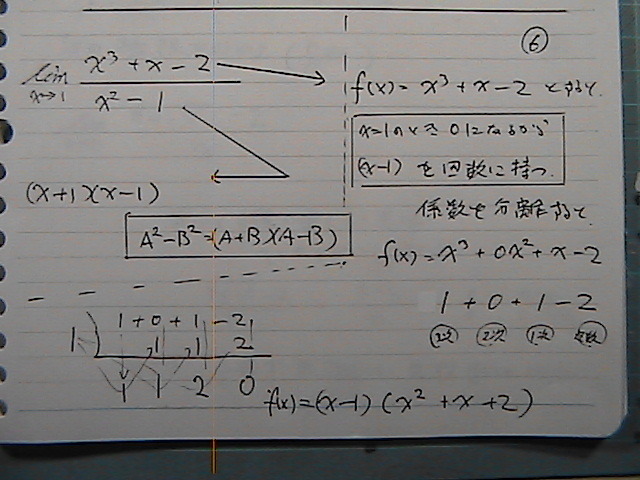
�ł���Ƃ���
�V���@�V��
������
0/0��Ԃ�E�����̂�
�����P���@�߂ł����@�������
�Ɍ��́@�Q

0/0�`�́@������́@�p�^�[����
���������@�����Ă�ꍇ
��͂�
x=�O�@���@�������
�ڕW�l�@�I�ȁ@�Ɍ����@0/0�@�`�Ł@�łȂ��̂�

���́@�l���@�ς����Ɂ@���ό`
×�@�P�{�Ȃ�@�l�́@�ς��Ȃ�����
�|����ׂ��@���𐔂��@���ꕪ�q�Ɂ@������

���[���́@��������
��������
����
������
0/0��Ԃ�E�o�����̂�
�����O���@��������
�Ɍ��l��
1/4

0/0�`��
�����@����Ȃ��P�ɋ߂Â��Ƃ��̖���
�P���@���������@����ł��@��������������ł�
�����P�Ɂ@�߂Â��Ă悭
�������@���@not= 1�@�Ȃ̂�����
�Ł@�i���|�P�j�@���@�Ă��܂���
�Ɍ��́@���̂��@�o����

0/0��Ԃ��@�E���Ă����
�����P���@�_�C���N�g�́@�������
�Ɍ����@���܂�B

�������@���܂��܂���
�ޑ�
�ڕW�l�ȁ@�Ɍ���
0/0�`��ԂȂ̂�
�������Ȃ��Ƃ����Ȃ���
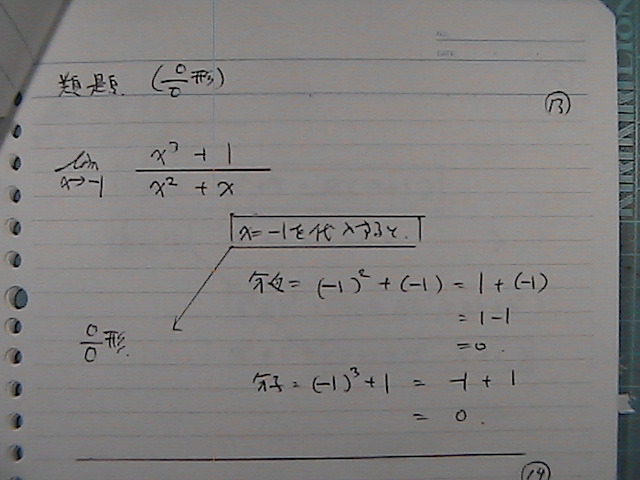
���������ł������Ȃ̂�

����́@x�Ł@��������
���q�́@�R��́@��������

�₭����Ƃ�
�V���@�V��
0/0��Ԃ�E��������
�����|�P���@�������
�Ɍ��́@-3

����
�܂��@�ʕ��@����i�C�X�J��
������@
�����́@�Ɍ��Ɂ@�Ȃ�Ȃ�
�O/�O�`

��������
�����@����
������
0/0��Ԃ��@�E�����̂�
�����O���@�������
�@
�Ɍ��l�́@-1

�C�}�n�@�p�^�[���@0/0�`�@�Ȃ̂�
������@0/0�`
�����
��������
����@���q�Ɂ@�Ⴄ���̂��@�����Ă�̂�
�Q��@
���ꂼ��́@���𐔂��@�����Ăł���

�܂�
����̕�
��������

���x�́@���q�̕�
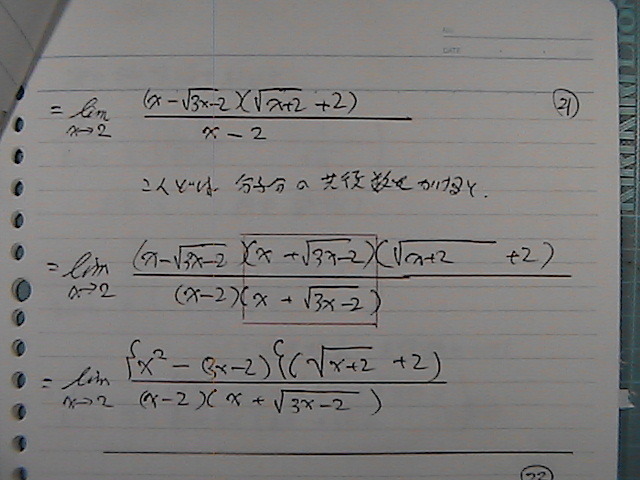
����Ɂ@���������@�������������
���ł���
0/0��Ԃ��@�E�����̂�
�����Q���@���
�Ɍ��l�́@1

����
�Ȃ�
���ϕω����̂Ƃ��́@�悤�ȁ@�`��
�����������@�ʕ�
���q�́@��������
���𐔂��@������

����
0/0��Ԃ��@�����Ł@�E��������
�����O���@�������

����Ȋ�����

����
�����u�Ԃ�
����@
�����
���O�@�́@�����@�́@�^�����O�@�Ȃ̂�����
��Βl�́@�Ƃ肠�����@�|���炸��
���̑O�ɂł���
���ό`��
���O�́@�v�Z�@�@���́@�Ɠ������炳
�v���o������������
�������Ɂ@�ό`����

��Βl�́@���́@�@�@0/0�`
������@���q���@���������ł������Ȃ̂�

���[���Ɓ@�R��́@�������@�g����
��������
��Ƃ��@�V���@�V��
������
0/0�`���@�E��������
�����Q���@�������

�������炳
1/3

�����Ł@
�����Ɂ@�������̂�����
����������Ɓ@�������
�������@����Ɂ@������
-log�R

���P�̎�
���O��
��蕶�Ɂ@�����ĂȂ��Ă�
�Öق́@�������@����̂ł���
����́@�g���܂���ł����ł���
�ꂪ�@�O<�ꁃ�P�̎��́@�P������
�ꂪ�@�P����̎��́@�P������
�^���́@�^�����O
��
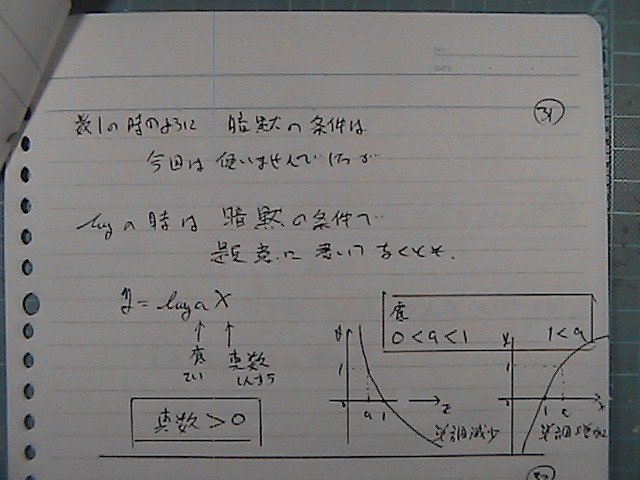
���X�g��
���������@������
0/0�`�ł���

�����
�����Ɓ@���ƈႢ�܂�
�Ȃ̂�
�R��̌������g����

�����@�����ā@�g����
�������́@�^���́@���Ɂ@�����ۂ��@�����
�R��́@�����Ɂ@�����
���������@�O���
�i�@���q�����@�j
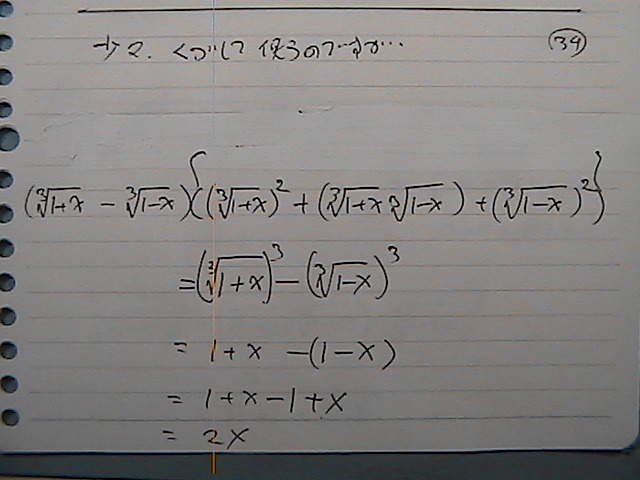
�Ȃ̂�
���ό`��
�l���@�ς��Ȃ��悤�Ɂ@�����ۂ��@
��������ł���
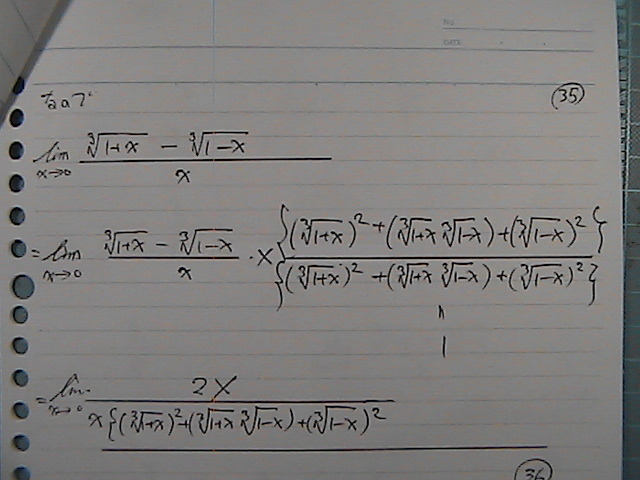
������
0/0�`���@�E�����̂�
�����O���@���������
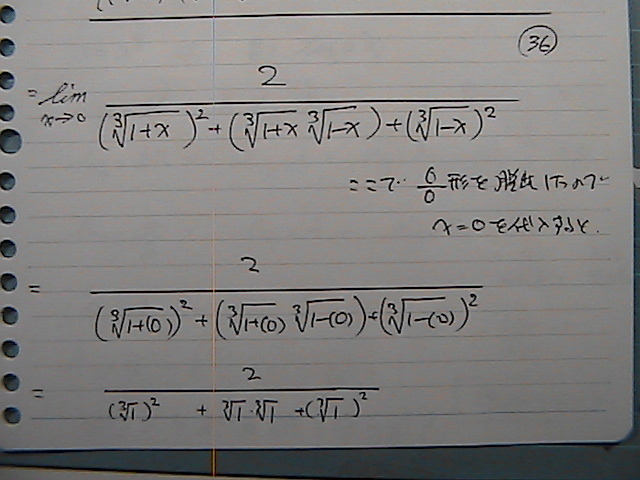
�o�܂�����

����́@�K�т₷����
���̕ӂ���
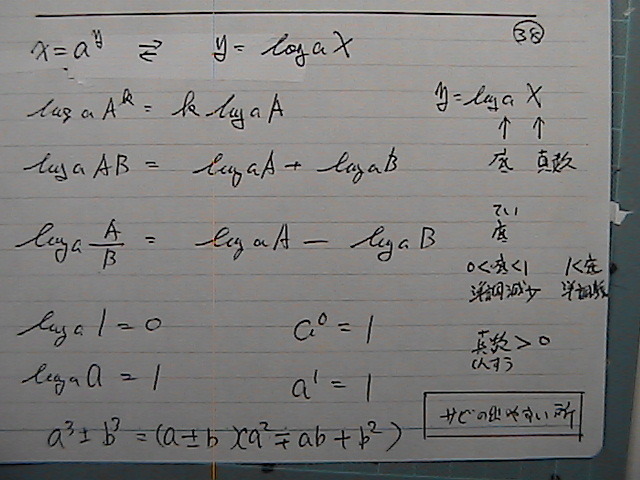
���Q�@���R�@�́@
�Öق̗�����
���P�́@�S�͈͂��@�����Ă���̂�
���c���������
����̂ł���
���[�@�b�́@�S�R�Ⴄ���ǂ�
�匟�@���ā@���邶��i�C�X�J
���w�Ł@�匟��̂́@
���Z���Ƃ�����@����ł�
�����Ă����ł���
���P����
���Ƃ��Ă�
��x�Ɂ@�S�͈͂��@
�P�w���@�Q�w���@�R�w���@�Ɂ@�������ق���
�ȒP�ł���
�匟�@�^���Ɂ@����Ă�l���@������
�n���ɂ��Ắ@�Ȃ�܂����B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���̋Ɍ��̋��ߕ��̖���
�O��
�ڂ����@�v�Z������ĂȂ�����
�悤�Ɂ@�v������
���ނ���
����Ă݂����Ǝv���܂���
�S�@�T�@�U��
��
�p�^�[����������
��
�Ɍ���
�����@����Ȃ��@a�Ɂ@�߂Â��Ƃ���
���i���j���@���Ƃ����l��
����Ȃ��@�߂Â��Ă����Ȃ��
���̋Ɍ��́@�l��
����a�@�̎��@���i���j�@���@���@�Ƃ�
Lim
����a�@�@���i���j����
����́@�v�Z����
���Ă��܂���
���p�^�[��������̂ł���
�����
�O/�O�@�`
0/0�`�̎���
�������Ȃ�@��
�������Ȃ�@�����Ȑ����@������
����ōs���Ă݂܂��傤
����
�����@����Ȃ��@�P�Ɂ@�߂Â��Ƃ�
�ꉞ�@�ڕW�l�I�Ɂ@�����P���@������Ă݂��
������@���q���@�O�@�́@0/0�`
������
���������ł�����������
�����������Ă݂܂���
����́@���|���
���q��
�����藝��
x���P�̎��@�O�ɂȂ��Ă��܂�����
�������������
�g�����@�Ƃ��@�g���Ȃ���
�W����������
�i���|�P�j�@���@�����Ɂ@���̂�����
�i���|�P�j���O�ɂ���@x�̒l��
�����
�R�������@�P�����@�Ŋ���������
��ԏ�́@�Q���@�Ł@�P���@�Ł@�萔�Ł@�]��@�́@�O
�ł���Ƃ���
�V���@�V��
������
0/0��Ԃ�E�����̂�
�����P���@�߂ł����@�������
�Ɍ��́@�Q
0/0�`�́@������́@�p�^�[����
���������@�����Ă�ꍇ
��͂�
x=�O�@���@�������
�ڕW�l�@�I�ȁ@�Ɍ����@0/0�@�`�Ł@�łȂ��̂�
���́@�l���@�ς����Ɂ@���ό`
×�@�P�{�Ȃ�@�l�́@�ς��Ȃ�����
�|����ׂ��@���𐔂��@���ꕪ�q�Ɂ@������
���[���́@��������
��������
����
������
0/0��Ԃ�E�o�����̂�
�����O���@��������
�Ɍ��l��
1/4
0/0�`��
�����@����Ȃ��P�ɋ߂Â��Ƃ��̖���
�P���@���������@����ł��@��������������ł�
�����P�Ɂ@�߂Â��Ă悭
�������@���@not= 1�@�Ȃ̂�����
�Ł@�i���|�P�j�@���@�Ă��܂���
�Ɍ��́@���̂��@�o����
0/0��Ԃ��@�E���Ă����
�����P���@�_�C���N�g�́@�������
�Ɍ����@���܂�B
�������@���܂��܂���
�ޑ�
�ڕW�l�ȁ@�Ɍ���
0/0�`��ԂȂ̂�
�������Ȃ��Ƃ����Ȃ���
���������ł������Ȃ̂�
����́@x�Ł@��������
���q�́@�R��́@��������
�₭����Ƃ�
�V���@�V��
0/0��Ԃ�E��������
�����|�P���@�������
�Ɍ��́@-3
����
�܂��@�ʕ��@����i�C�X�J��
������@
�����́@�Ɍ��Ɂ@�Ȃ�Ȃ�
�O/�O�`
��������
�����@����
������
0/0��Ԃ��@�E�����̂�
�����O���@�������
�@
�Ɍ��l�́@-1
�C�}�n�@�p�^�[���@0/0�`�@�Ȃ̂�
������@0/0�`
�����
��������
����@���q�Ɂ@�Ⴄ���̂��@�����Ă�̂�
�Q��@
���ꂼ��́@���𐔂��@�����Ăł���
�܂�
����̕�
��������
���x�́@���q�̕�
����Ɂ@���������@�������������
���ł���
0/0��Ԃ��@�E�����̂�
�����Q���@���
�Ɍ��l�́@1
����
�Ȃ�
���ϕω����̂Ƃ��́@�悤�ȁ@�`��
�����������@�ʕ�
���q�́@��������
���𐔂��@������
����
0/0��Ԃ��@�����Ł@�E��������
�����O���@�������
����Ȋ�����
����
�����u�Ԃ�
����@
�����
���O�@�́@�����@�́@�^�����O�@�Ȃ̂�����
��Βl�́@�Ƃ肠�����@�|���炸��
���̑O�ɂł���
���ό`��
���O�́@�v�Z�@�@���́@�Ɠ������炳
�v���o������������
�������Ɂ@�ό`����
��Βl�́@���́@�@�@0/0�`
������@���q���@���������ł������Ȃ̂�
���[���Ɓ@�R��́@�������@�g����
��������
��Ƃ��@�V���@�V��
������
0/0�`���@�E��������
�����Q���@�������
�������炳
1/3
�����Ł@
�����Ɂ@�������̂�����
����������Ɓ@�������
�������@����Ɂ@������
-log�R
���P�̎�
���O��
��蕶�Ɂ@�����ĂȂ��Ă�
�Öق́@�������@����̂ł���
����́@�g���܂���ł����ł���
�ꂪ�@�O<�ꁃ�P�̎��́@�P������
�ꂪ�@�P����̎��́@�P������
�^���́@�^�����O
��
���X�g��
���������@������
0/0�`�ł���
�����
�����Ɓ@���ƈႢ�܂�
�Ȃ̂�
�R��̌������g����
�����@�����ā@�g����
�������́@�^���́@���Ɂ@�����ۂ��@�����
�R��́@�����Ɂ@�����
���������@�O���
�i�@���q�����@�j
�Ȃ̂�
���ό`��
�l���@�ς��Ȃ��悤�Ɂ@�����ۂ��@
��������ł���
������
0/0�`���@�E�����̂�
�����O���@���������
�o�܂�����
����́@�K�т₷����
���̕ӂ���
���Q�@���R�@�́@
�Öق̗�����
���P�́@�S�͈͂��@�����Ă���̂�
���c���������
����̂ł���
���[�@�b�́@�S�R�Ⴄ���ǂ�
�匟�@���ā@���邶��i�C�X�J
���w�Ł@�匟��̂́@
���Z���Ƃ�����@����ł�
�����Ă����ł���
���P����
���Ƃ��Ă�
��x�Ɂ@�S�͈͂��@
�P�w���@�Q�w���@�R�w���@�Ɂ@�������ق���
�ȒP�ł���
�匟�@�^���Ɂ@����Ă�l���@������
�n���ɂ��Ắ@�Ȃ�܂����B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 20:46| ��l�̂��ї��Ƃ��@
2018�N04��21��
2B7006�@�@��l�̂��ї��Ƃ��@�{�p�́@�����@�i�R�j
�J�̓��́@�X���[���C�t�̕���
�{�p�̌����i�R�j�@
�����Ȃ��
�ǂ������̂�
���
�[�ċz���Ăł���
��
����͂��@�p�^�[���́@���
���̖�肪�@�o�Ă�����
�v���o���݂����Ȋ�����
�o���ł���
���̂Ƃ����
�����́@�ϊ��Ƃ���
�p��́@�X�y���݂����Ɂ@��{�ʂ�
�����
�����������Ǝv���܂���
�ƌ������
�Ȃˁ@�ł���C�����ɂȂ���
���ꂵ���Ȃ�ł���
�s���Ă݂܂��傤
tan���������@�^������
sin2�� cos2�� ���@���Ł@�\���ł�

�����̔{�p�́@�����Ł@�W�J
����Ɂ@�������@���X�ł���
×�P�{�́@�����Ȃ̂�
�R�T�C���@���@�́@�@�R�T�C��
�Ł@�\������
��������
�|�����킹���
�^���W�F���g�@�Ɓ@�R�T�C���Q��
��������
���������̒��́@�^���W�F���g�@�Z�J���g�@���@�g���Ăł���

�R�T�C�����@�Z�J���g�Ɓ@�t���Ȃ���
�Ł@�łĂ������̂�
���������
�^���W�F���g�̎��ɂȂ���
tan�������@�Ɂ@�u���������
����

�R�T�C����
�]���̔{�p�̌�����
�R�T�C��������
�\����
�������́@�R�T�C�������@
�^���W�F���g�Ɂ@����������̂�
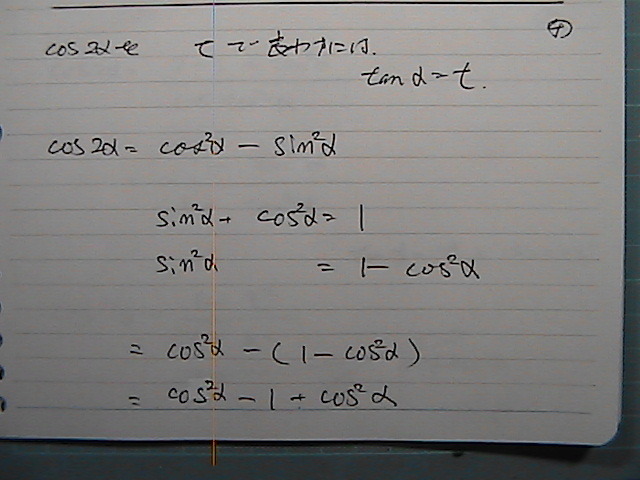
��������

����Ȋ�����

������@���܂��܂���
sin 2x + cos 2x�@���@���߂��ł���
tan�����@-2
��������Ƃ������炳
�����@�i�@sin )
�]���@�i�@cos )
�́@�{�p���@�^���W�F���g��
�\����̂�

�������݂�����
�����܂Ł@�����čs����
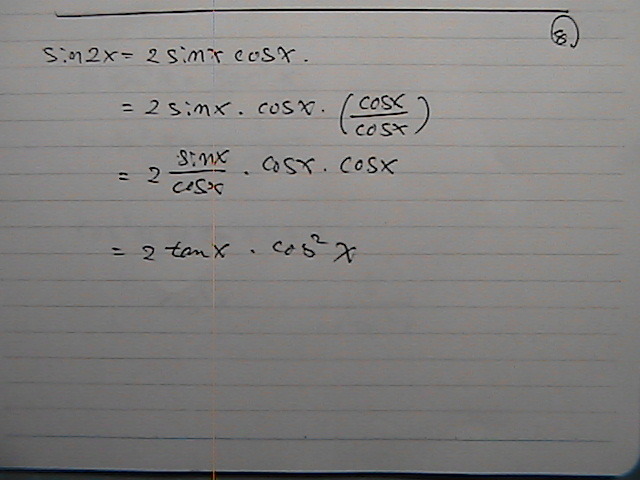
��
���̑O��
���������͂�
��l�@����Ȋ����ł���
���̂Ȃ�����
�^���W�F���g�́@�����̌�����
��������
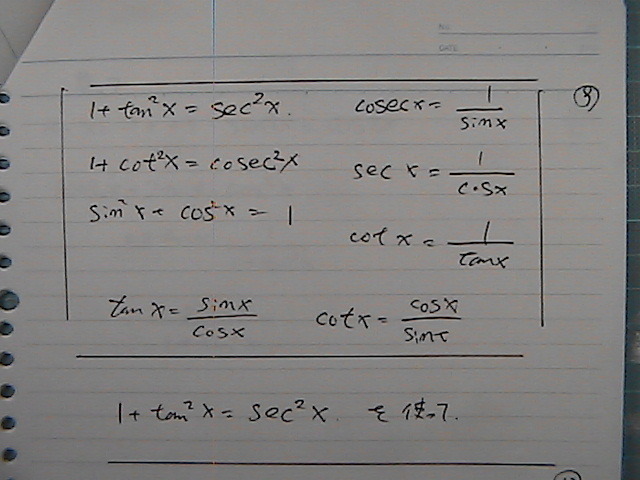
�R�T�C����悪
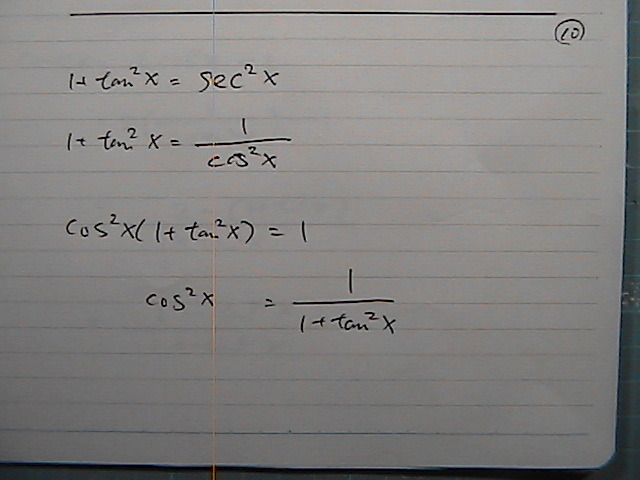
��
�������̂Ƃ��ց@�߂���
�R�T�C�������@�������
������
�������́@�J��Ԃ��ł���
sin�Q��

cos 2x�̕����ł���
�������݂�����
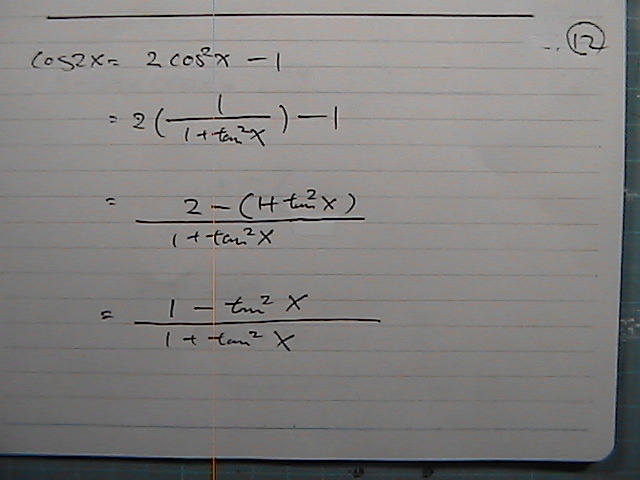
���
�������
�v�Z�ł���
����������������
�������肷���
�Z�����@��Ȃ�
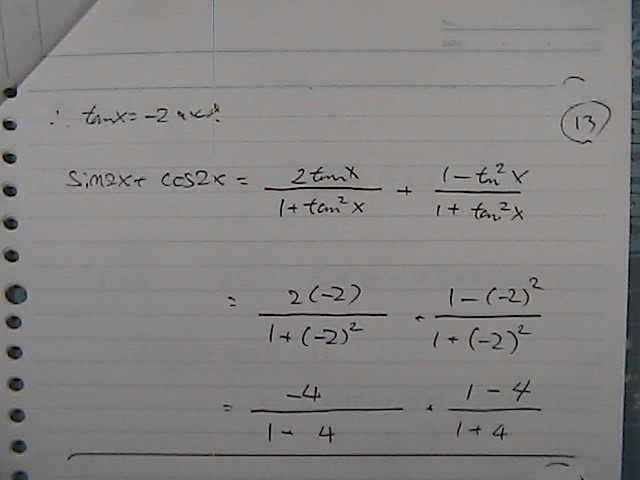
�������@����
����������@�m�F����

����
���Ȃ����ƂȂ�ł���
������Ɓ@�ѐF������Č����邯��
�W�J����ł���
sin cos�@�́@����������
�P�Ɂ@�ς���
�c���
�����̔{�p�́@�����́@���ʂł���
�܂��������݂�����
�R�T�C���@�R�T�C���@�Ł@
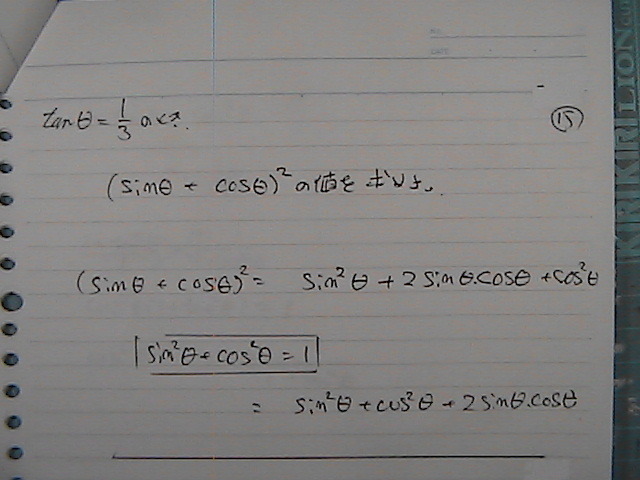
��������
�g�݂Ȃ�����
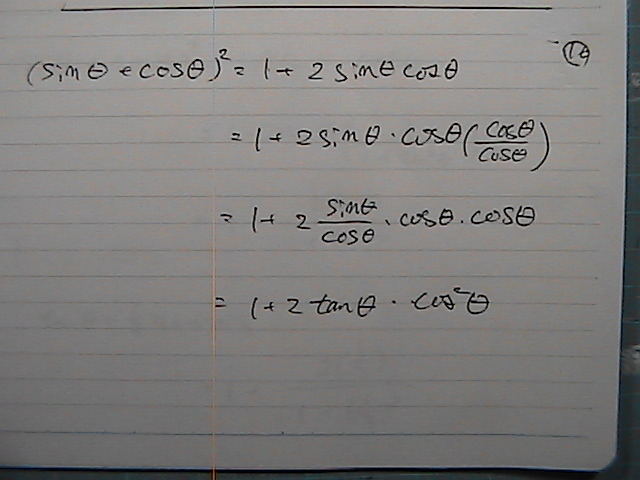
�������@�������Ɠ�����
�^���W�F���g�́@������������@�R�T�C���Q���
���o����

���
�^���W�F���g�́@����
���l���
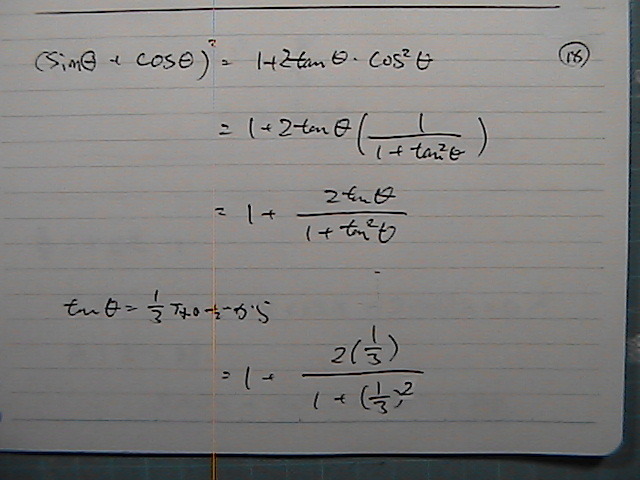
����Ȋ�����
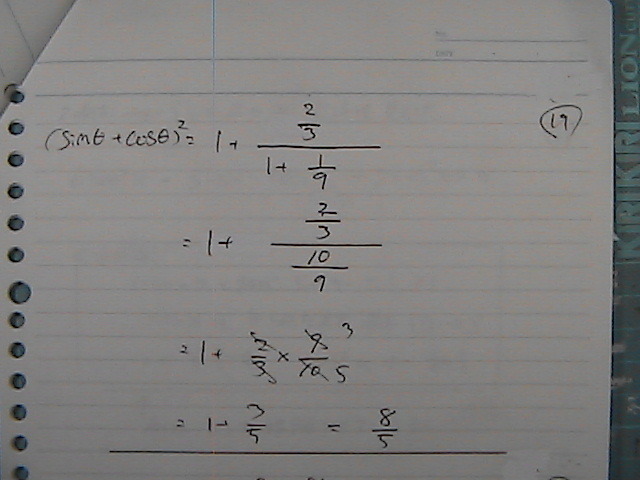
����Ȃ������̂��@�������̂�
�����@���Ɂ@�s���Ă݂܂���
���@��Ȃ�����@

��l�@�������@���邩�炳
��
���������@�����ւ��@�g����
���[���킯�Ȃ��ˁ[
���̂�
�킩��Ȃ��Ƃ��́@������Ȃ�����
������l���́@�y����
�����́@�q���g�́@�}�_�@�����ł��Ă܂���

�Ƃ肠����
�R�T�C���Q���
����Ƃł���
�^���W�F���g�́@�Q���������ɂȂĂł���
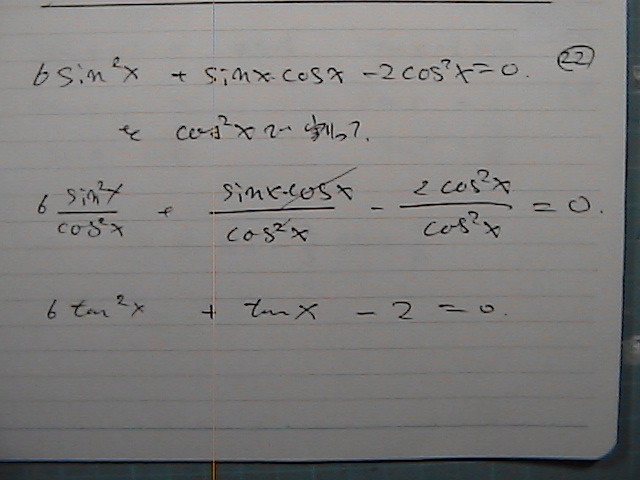
�������������肵��
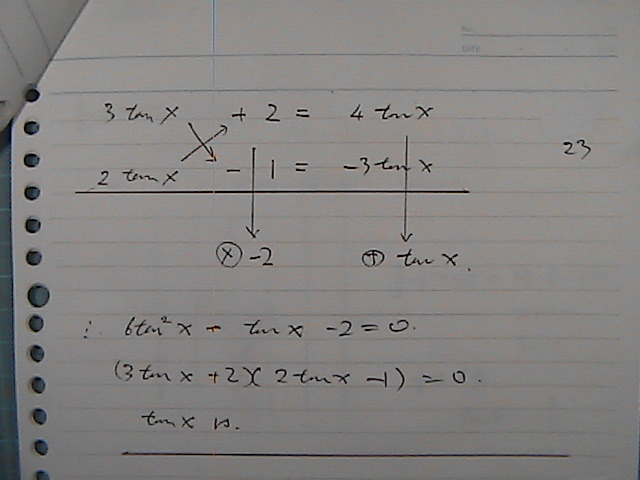
�^���W�F���g���@�Q��
��
�����悪�@���邩��
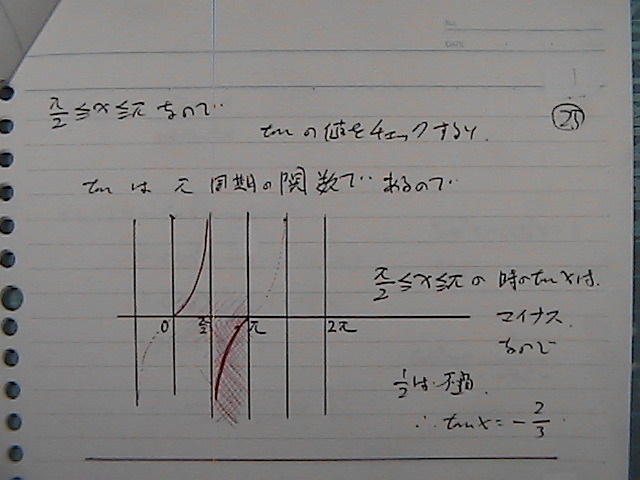
�^���W�F���g�́@�O���t���@�����Ă݂��
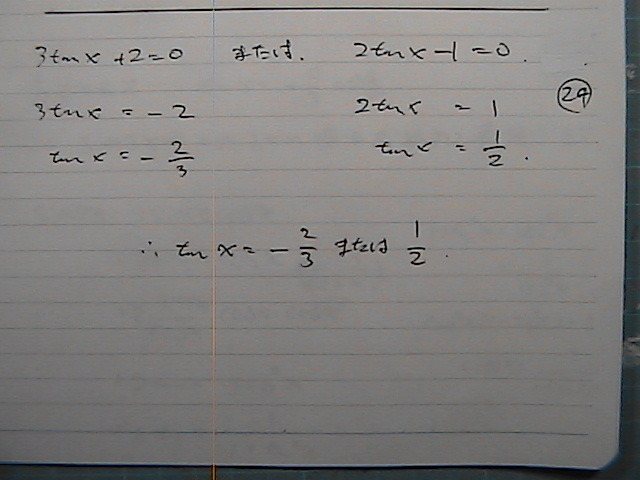
��/2�@�ȏ�@�Έȉ��́@�@�}�C�i�X�̈�
�i�^��
tan x = -2/3
����������
�����́@�܂����Ă�
����������
�X�y���́@���K���@���Ă���
���ό`��
���l���@���������i�C�X�J��

sin 2x

cos 2x

�v�Z����
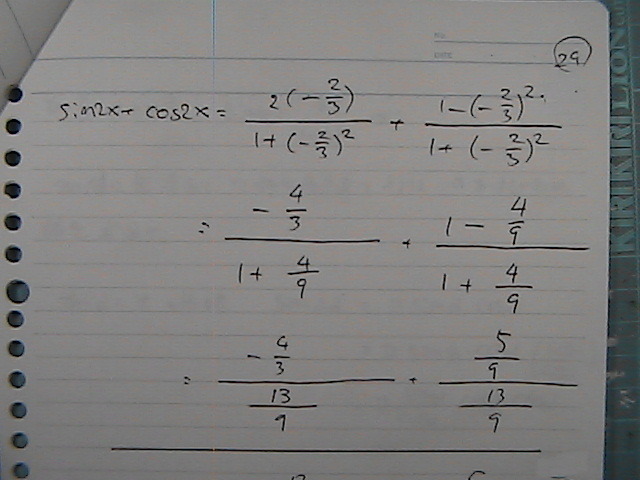
����Ȋ�����

�Ō��
����͂�
�������@����������
��������
���������ǂ�
�n�߂Ɂ@����Ă�����
����
�r���܂Ł@�g����

�r���܂ł�
�n�߂́@���
��
������
��ӂ̂悤��
��/2�@�́@tan�Ɂ@�����

sin�Q���́@sin x �Ə����邩��
��
���ʂ��@�m���Ă�����@�g�����݂����Ȋ�����
sin x �́@����Ȋ����Ȃ���

���́@�l�Ɓ@��ӂ��̒l��
�������킯�Ȃ���

�C�R�[����
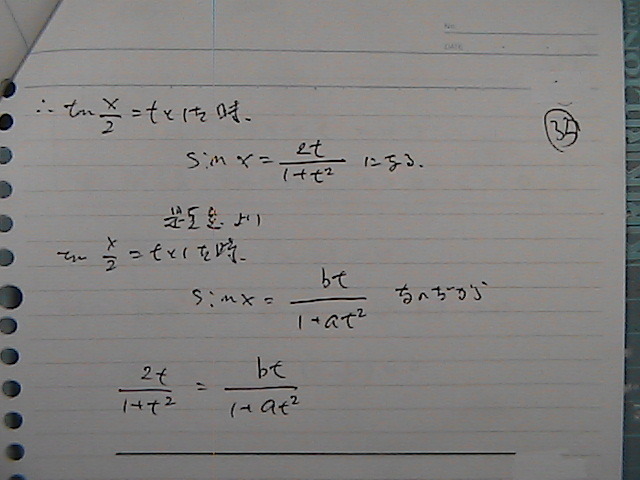
����ɂ���
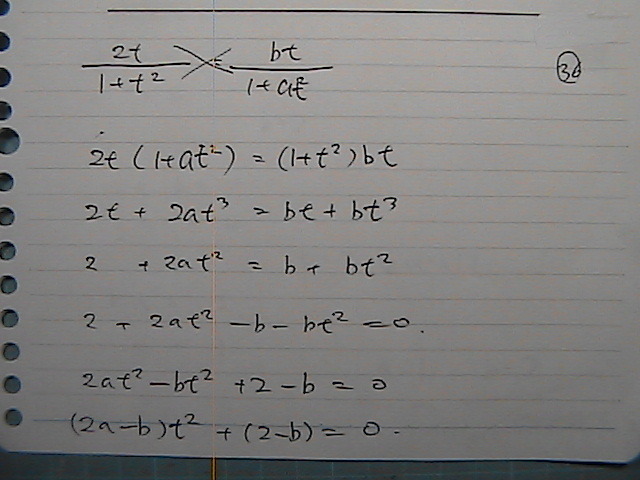
��������́@�P����
ax���@+�@�����@+�@�@���@��0�@���@
��ɐ��藧�Ȃ��
a=b=c=0
�����Ɂ@���������

����Ȋ�����

���w�́@���Q�̎��́@�Öق̗�����
���P�́@�S�͈͂��@���Ă��܂�����
�Y��Ă�Ƃ�
�����ւ�Ȃ�
�������@��l�ɂȂ��Ă킩��
�Y��₷���Ƃ���
�w���̌v�Z�Ƃ��@�R��̓W�J�@���������̌����Ƃ�
���ƌW���́@�W�Ƃ�
�e���p
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�{�p�̌����i�R�j�@
�����Ȃ��
�ǂ������̂�
���
�[�ċz���Ăł���
��
����͂��@�p�^�[���́@���
���̖�肪�@�o�Ă�����
�v���o���݂����Ȋ�����
�o���ł���
���̂Ƃ����
�����́@�ϊ��Ƃ���
�p��́@�X�y���݂����Ɂ@��{�ʂ�
�����
�����������Ǝv���܂���
�ƌ������
�Ȃˁ@�ł���C�����ɂȂ���
���ꂵ���Ȃ�ł���
�s���Ă݂܂��傤
tan���������@�^������
sin2�� cos2�� ���@���Ł@�\���ł�
�����̔{�p�́@�����Ł@�W�J
����Ɂ@�������@���X�ł���
×�P�{�́@�����Ȃ̂�
�R�T�C���@���@�́@�@�R�T�C��
�Ł@�\������
��������
�|�����킹���
�^���W�F���g�@�Ɓ@�R�T�C���Q��
��������
���������̒��́@�^���W�F���g�@�Z�J���g�@���@�g���Ăł���
�R�T�C�����@�Z�J���g�Ɓ@�t���Ȃ���
�Ł@�łĂ������̂�
���������
�^���W�F���g�̎��ɂȂ���
tan�������@�Ɂ@�u���������
����
�R�T�C����
�]���̔{�p�̌�����
�R�T�C��������
�\����
�������́@�R�T�C�������@
�^���W�F���g�Ɂ@����������̂�
��������
����Ȋ�����
������@���܂��܂���
sin 2x + cos 2x�@���@���߂��ł���
tan�����@-2
��������Ƃ������炳
�����@�i�@sin )
�]���@�i�@cos )
�́@�{�p���@�^���W�F���g��
�\����̂�
�������݂�����
�����܂Ł@�����čs����
��
���̑O��
���������͂�
��l�@����Ȋ����ł���
���̂Ȃ�����
�^���W�F���g�́@�����̌�����
��������
�R�T�C����悪
��
�������̂Ƃ��ց@�߂���
�R�T�C�������@�������
������
�������́@�J��Ԃ��ł���
sin�Q��
cos 2x�̕����ł���
�������݂�����
���
�������
�v�Z�ł���
����������������
�������肷���
�Z�����@��Ȃ�
�������@����
����������@�m�F����
����
���Ȃ����ƂȂ�ł���
������Ɓ@�ѐF������Č����邯��
�W�J����ł���
sin cos�@�́@����������
�P�Ɂ@�ς���
�c���
�����̔{�p�́@�����́@���ʂł���
�܂��������݂�����
�R�T�C���@�R�T�C���@�Ł@
��������
�g�݂Ȃ�����
�������@�������Ɠ�����
�^���W�F���g�́@������������@�R�T�C���Q���
���o����
���
�^���W�F���g�́@����
���l���
����Ȋ�����
����Ȃ������̂��@�������̂�
�����@���Ɂ@�s���Ă݂܂���
���@��Ȃ�����@
��l�@�������@���邩�炳
��
���������@�����ւ��@�g����
���[���킯�Ȃ��ˁ[
���̂�
�킩��Ȃ��Ƃ��́@������Ȃ�����
������l���́@�y����
�����́@�q���g�́@�}�_�@�����ł��Ă܂���
�Ƃ肠����
�R�T�C���Q���
����Ƃł���
�^���W�F���g�́@�Q���������ɂȂĂł���
�������������肵��
�^���W�F���g���@�Q��
��
�����悪�@���邩��
�^���W�F���g�́@�O���t���@�����Ă݂��
��/2�@�ȏ�@�Έȉ��́@�@�}�C�i�X�̈�
�i�^��
tan x = -2/3
����������
�����́@�܂����Ă�
����������
�X�y���́@���K���@���Ă���
���ό`��
���l���@���������i�C�X�J��
sin 2x
cos 2x
�v�Z����
����Ȋ�����
�Ō��
����͂�
�������@����������
��������
���������ǂ�
�n�߂Ɂ@����Ă�����
����
�r���܂Ł@�g����
�r���܂ł�
�n�߂́@���
��
������
��ӂ̂悤��
��/2�@�́@tan�Ɂ@�����
sin�Q���́@sin x �Ə����邩��
��
���ʂ��@�m���Ă�����@�g�����݂����Ȋ�����
sin x �́@����Ȋ����Ȃ���
���́@�l�Ɓ@��ӂ��̒l��
�������킯�Ȃ���
�C�R�[����
����ɂ���
��������́@�P����
ax���@+�@�����@+�@�@���@��0�@���@
��ɐ��藧�Ȃ��
a=b=c=0
�����Ɂ@���������
����Ȋ�����
���w�́@���Q�̎��́@�Öق̗�����
���P�́@�S�͈͂��@���Ă��܂�����
�Y��Ă�Ƃ�
�����ւ�Ȃ�
�������@��l�ɂȂ��Ă킩��
�Y��₷���Ƃ���
�w���̌v�Z�Ƃ��@�R��̓W�J�@���������̌����Ƃ�
���ƌW���́@�W�Ƃ�
�e���p
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 22:59| ��l�̂��ї��Ƃ��@
2018�N04��17��
2B07005 ��l�̂��ї��Ƃ��@�{�p�̌����@�i�Q�j
�J�̓��́@�X���[���C�t�̕���
�{�p�̌����i�Q�j�@�Ȃ̂ł���
sin���@+ cos���@���@a
�@
���^����ꂽ��
sin a cos a�@���@���
�������ł�
��肪�@�����Ăł���
���̒l�����߂Ȃ���

(�P)�́@sin�QA���@���߂�
�����̔{�p�̌������g������i�C�X�J
�������܁@sin a cos a
���@�����������@�o�ė���
sin�QA���Qsin a cos a
��ӂ���
sinA + cosA= 1/2
�Ȃ̂�
������@���������
sin���A �@�@�@cos���A�@�́@�ԂɁ@
�@�Qsin a cos a
���ꂪ�@�S�̂Ł@1/4�Ȃ̂�����
sin���A �@�@�@cos���A�@�́@�P�ɂȂ���
�Qsin a cos a���@-3/4

������
���߂�̂�
sin2A �Ȃ̂�����
sin2A�@���@�Qsin a cos a���@-3/4
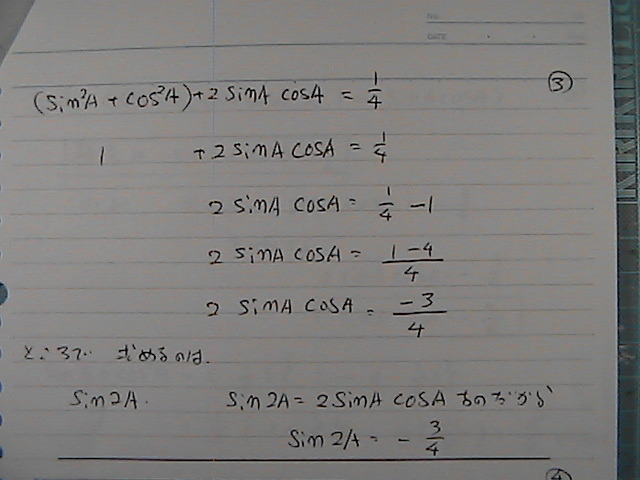
(�Q)��
�R��+�R��̂�����
���������́@���́@�������g����

���@���́@1��
�ւĂ���
��ӂ��
�l���������Ă�@�Ƃ���
�i�P�j�́@������
�Qsin a cos a���@-3/4�Ȃ̂�����
sin a cos a���@-3/8
�������@�������
11/16
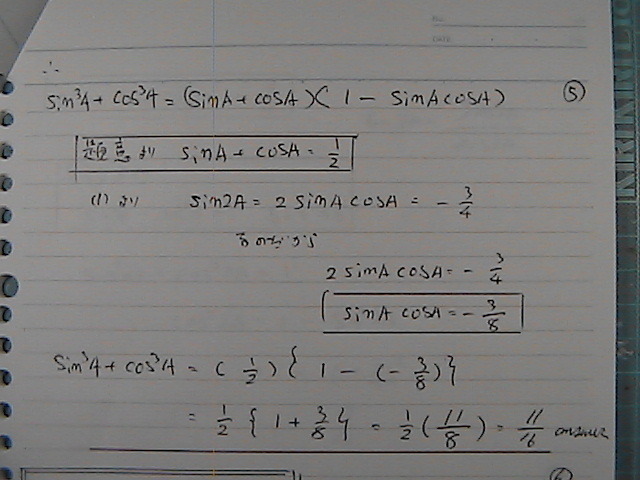
tan2A�@���@���߂�
����͂�
���������邯��
sin cos�@�Ł@�\�����@�̕���
�悳����������
����i�C�X�J

sin2A�@���@-3/4
���@�킩�Ă邩��
�����������g����

cos�QA=�@�}�@��7/4
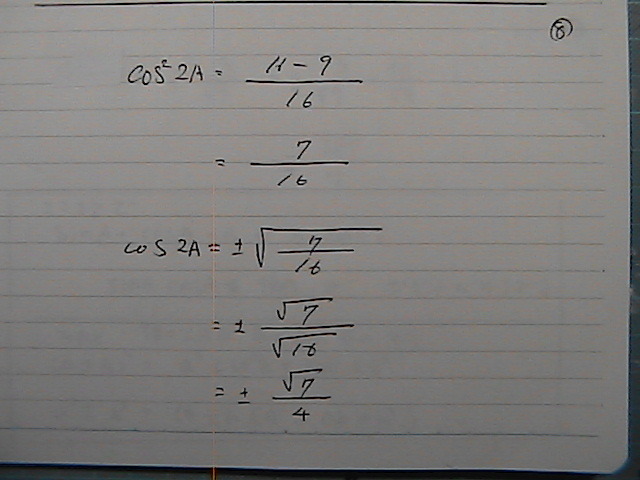
���q�́@�}�C�i�X���@�l�����
�}�C�i�X�v���X�@�ɂȂ���
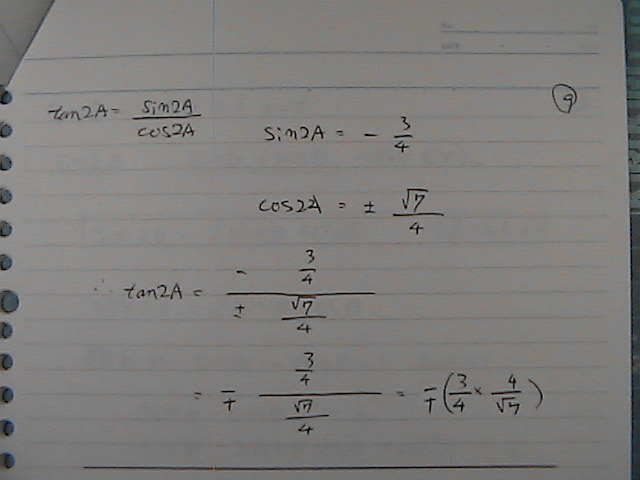
����́@���[�g���@�͂�����
���[�g���@���q�Ɂ@�����Ă���
�}�C�i�X�v���X�R��7/7

�ȏ���@���܂��܂���
�����@���ɍs���Ă݂܂��傤
�[���ł���
sin ���@-�@cos ���@���@1�@�̎�
sin 2���@�A�@sin ���@+�@cos�@���@�A
�̒l�����߂Ȃ���
�܂�
sin���@+ cos���@���@a
�@
���^����ꂽ��
sin a cos a�@���@���
��
sin2���@���@�Qsin��cos��
sin ���@-�@cos ���@���@1�@���@���������
sin��惦�@�@�@cos��惦�@�́@�ԂɁ@
�@-�Qsin ��cos��
���@�o�ė��ā@�����@�S�̂Ł@�P�Ȃ̂�

����������
0
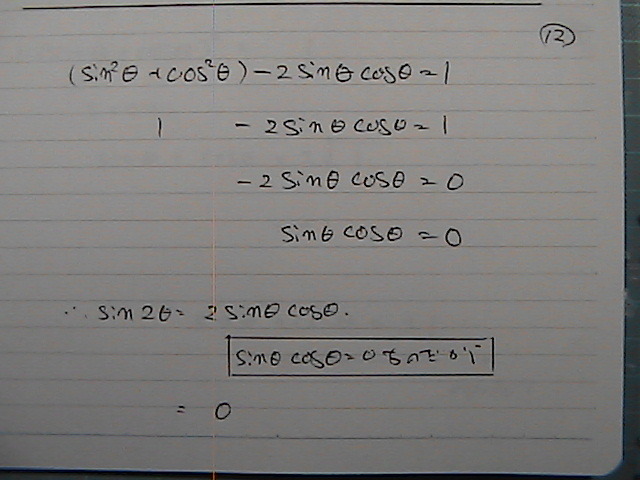
����
sin���@+�@cos��
��
���������
sin��惦�@+�@cos��惦�@+�@�Qsin ��cos����
�isin���@+�@cos���j�̓�悪
�P+�Qsin ��cos���@�Ȃ̂�����
�������@�Qsin ��cos�����@0�@�������̂�
�P
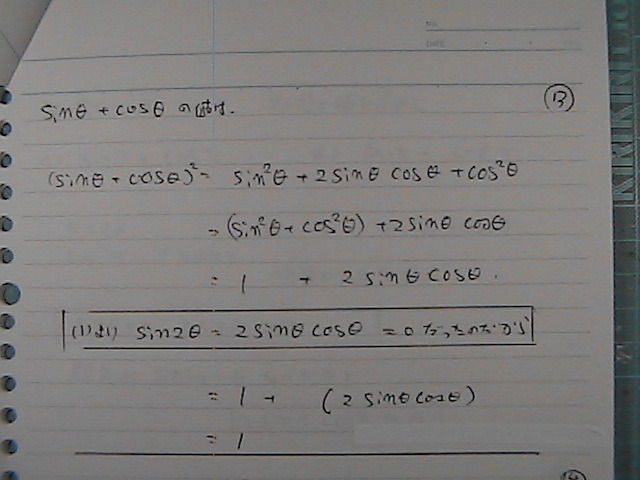
��
������
�����ł́@����܂����
���������@���߂Ăł���
�}1
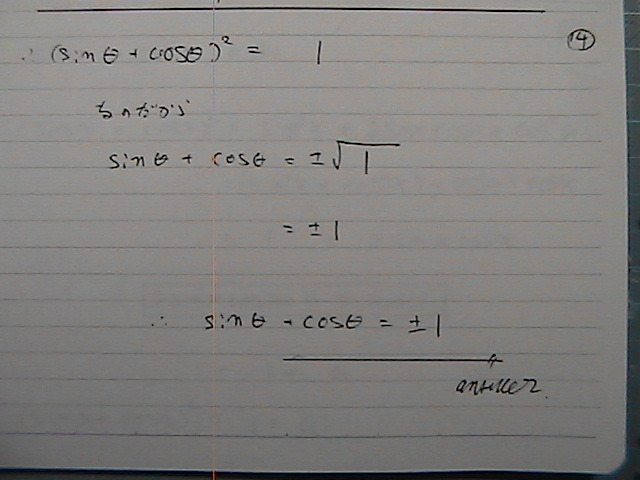
sin2x=a �̎��@���̒l��
���߂�
(1)sin x + cos x (2) tan x + cot x
�܂��ł���
�i�P�j
�Q���@�Ɓ@���@���@���݂��Ă�̂�
�����̔{�p�̌�����
sin2x=�Qsin �� cos ��
��ӂ��@���ꂪ�@��a�Ȃ̂�����
�Qsin �� cos ����a

(1)sin x + cos x
���@��������
�������������@�P+�@�Qsin �� cos ��
�ɂȂ�̂�
�isin x + cos x�j�̓�悪�@1+a

��������
�v���X�}�C�i�X�Ł�i1+a)
(2) tan x + cot x
�́@sin cos
�Ł@�l���ā@�ʕ�����

�Qsin �� cos ����a�Ȃ̂�����
sin �� cos ����a/2

���ʂ͂�����
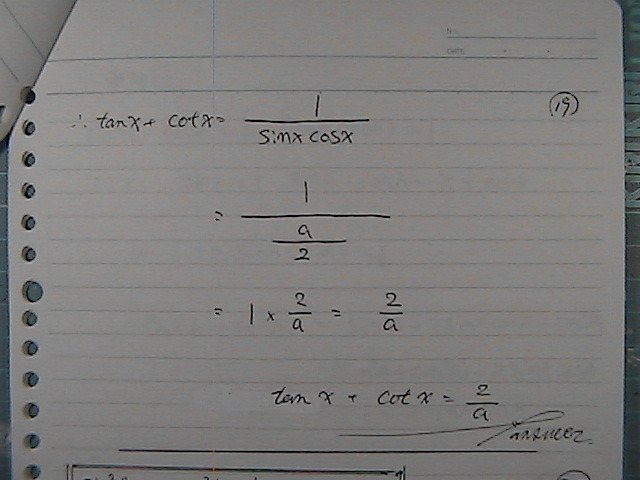
�R��\�R�恁�P���@�^�����Ă�
sinA�@-�@cosA���@���߂�
������
�[��������ł���
���Ȃ�@���ԂȂ����Ăł�
�������́@���������ł���
�����܂ł́@�ǂ�����

�����ł�
sinA�@-�@cosA���@���ƒu������
�����
sinA�@-�@cosA���������
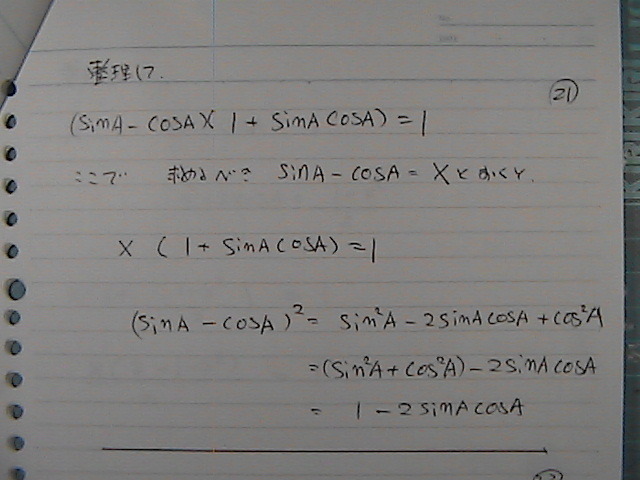
������
�������Ă��܂���
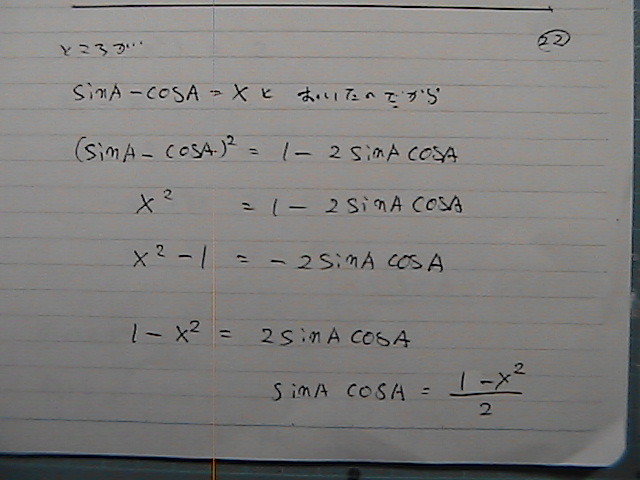
���̌`�́@�R��������
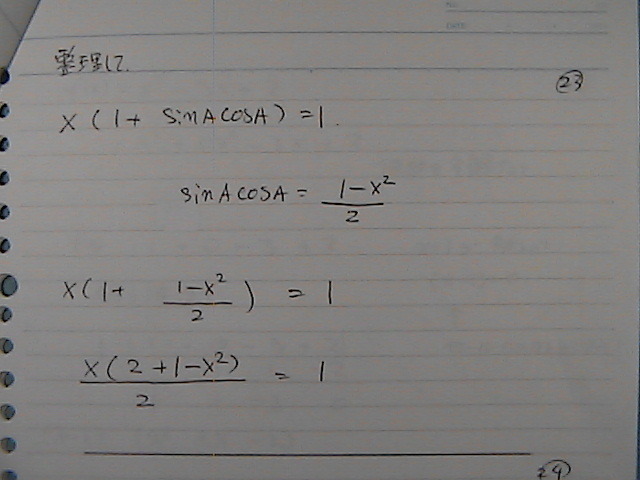
��������
�o�Ă��������@���i���j�@�Ƃł�������
���Q�́@�Öق̗�����
���P�̑S�͈͂��@�����Ă��܂��̂�
���c�����@����Ɓ@�i�߂Ȃ��@�ꍇ���@����܂���
�����́@�������傾��
�����藝���g����
��������
�����P�̎��@f(x)���O������
�i���|�P�j�@�Ł@�������
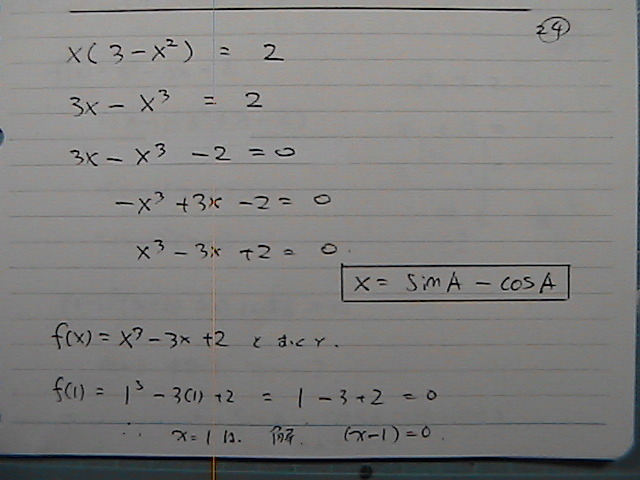
�W�����@��������
�Ȃ��Q��̍��́@�O�ɂ���
�g�����@��
�����藝�́@�����Ł@����
���i�P�j
�i���|�P�j���O
���������@�ς���Ɓ@�C�R�[���[���ɂȂ�@���Ł@�����

��
�����@���̂�������
���������ł�������
������
����1�@�܂��́@-2�@�Ȃ̂ł���
�������
�҂����ł�
��ȗ\����
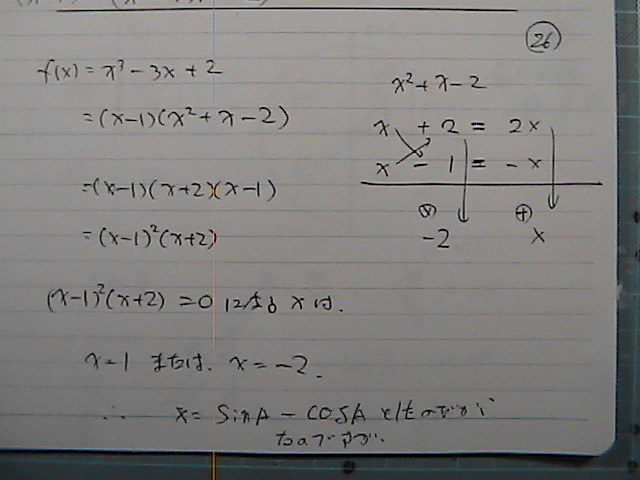
���̂ł���
���́@�����̂Ƃ����
����͂�
�����@�Ⴄ�`�ɂ��@��������������
���Ă���Ȃ��I�H�ɂȂ��ĂāH�H
���`�`�`�`
��������
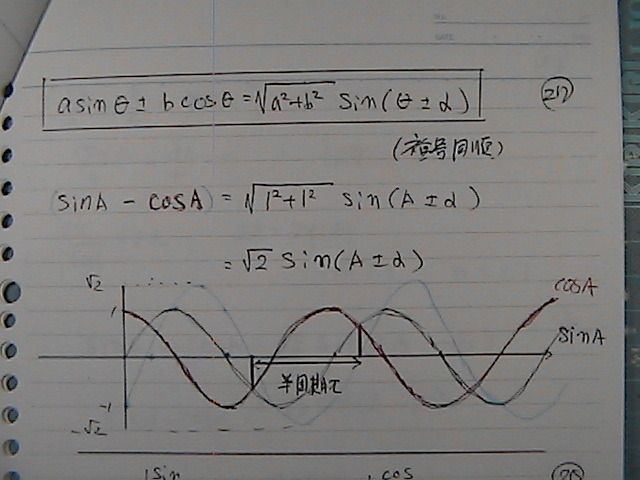
�ő�U����
�}��2
���`�`�`�`
����́@���́@�ǂ��Ȃ��������
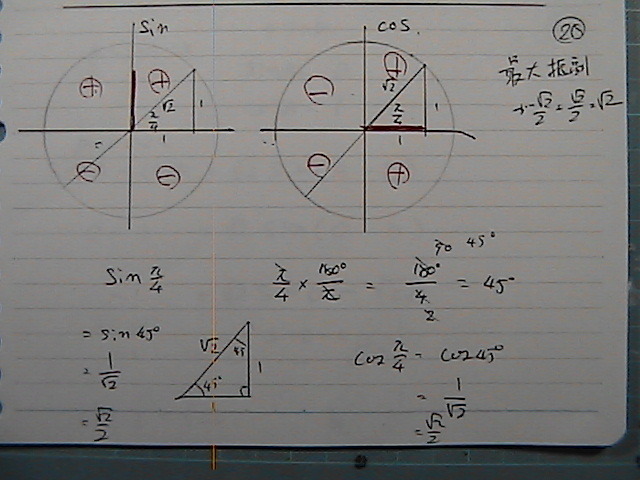
�O���t����
���������@������
���ʎ����́@sin�́@�Q�@�����炳
��Βla���P
a���}�P
�p�x��
��ʓI�Ȃ��̂��@���߂��`�Ɂ@�����

�O���t����@�O���t��̂P�_���@���
������@��
A=0�̎�
sinA=0 cosA=1
���@�������

sinA�@-�@cosA�@���@��2�@�Esin ( A - 45 )

�Ȃ̂ł���
�i�^��
�ő�U���́@��Βl���@��2�ȉ�
��2�́@�@1.1421356�@�Ƃ�������ł���
����1�@�܂��́@-2�@��
-�Q�́@�s�K
����������
�����P
x�́@sinA�@-�@cosA�@�����@�Ƃ��Ă܂��̂�
sinA�@-�@cosA�@��1

�����@�[����ł����
���ꂱ��́@�W������Ƃ�
cos2A+cos2B�@�̒l���@���߂�

����͂�
�p�Y���݂����Ȋ�����
cos�̂Q�{�p��
�����Ă��ł���
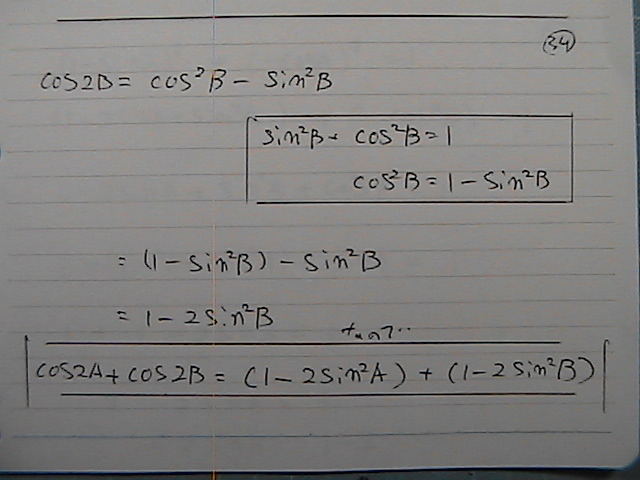
������
��������
��₱��������
���x��
sin�́@�l���o���ׂ�

����������
�{�p��sin
�ł͂Ȃ��Ă�
�Q�{��sin
������
sin�̒l���o�ė���

�Ȃ@���炩�肻��������
�������@�̂肱�����
���イ�Ɂ@�Ȃ���

��́@�������
�P����
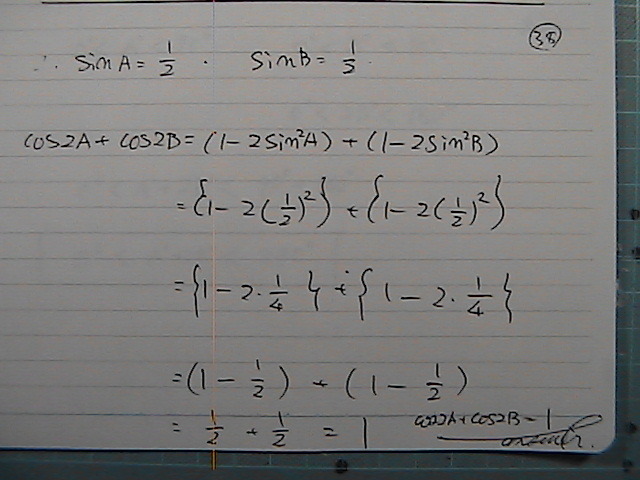
����@�[���Ƃ���
�|���v�����@�����̂�
���Ӑ[���@�i��ł��܂���

�܂��@�@�O����270�x�́@�Ԃł���
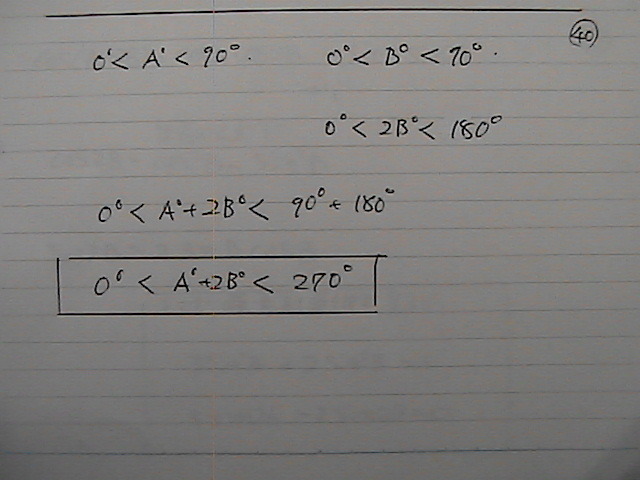
cos���@�g����
�p�x���@�\�������
���@�藝���@���������Ȃ̂�
������@�g����
���낻��
�[���Ȃ�̂Ɂ@�����Ȃ���

�������@���ā@�[�����@�\�����Ăł���

�ł��邾���@�}�Ɂ@�[���Ȃ�Ȃ����
�����@�ό`����
�܂�肪�@�����Ȃ��Ȃ�Ȃ��悤��
�ڈ�́@�Ȃ��J�i
�����͂ł���
���@�藝�́@�W�J���̒�
�́@�����I�ȂƂ���
���������@�����Ɂ@�g�����

��������
���@�藝�́@�W�J�����@�O�����@�ł܂�������
�㔼���@���Ă��ł���

�����I�Ɍ��ė���
�܂��g���ĂȂ���������
�ό`���Ă���
�S���@�g�݂��Ăā@����������
��0

�[���H
���[�@
cos�́@�l���@�[���@�Ȃ���
�s�������ł���
�p�x�𑫂����@���a���ł���
�����Ɂ@���e��

�X�O�x
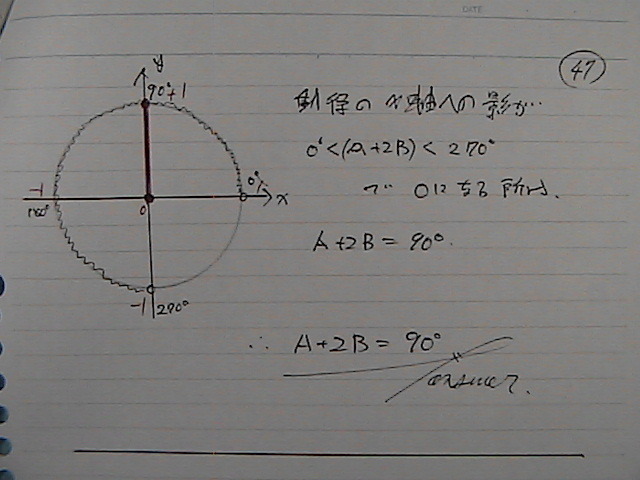
�ЂƂ����w�Ɓ@�e�w��
�`���L���@�����
���ꂩ
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�{�p�̌����i�Q�j�@�Ȃ̂ł���
sin���@+ cos���@���@a
�@
���^����ꂽ��
sin a cos a�@���@���
�������ł�
��肪�@�����Ăł���
���̒l�����߂Ȃ���
(�P)�́@sin�QA���@���߂�
�����̔{�p�̌������g������i�C�X�J
�������܁@sin a cos a
���@�����������@�o�ė���
sin�QA���Qsin a cos a
��ӂ���
sinA + cosA= 1/2
�Ȃ̂�
������@���������
sin���A �@�@�@cos���A�@�́@�ԂɁ@
�@�Qsin a cos a
���ꂪ�@�S�̂Ł@1/4�Ȃ̂�����
sin���A �@�@�@cos���A�@�́@�P�ɂȂ���
�Qsin a cos a���@-3/4
������
���߂�̂�
sin2A �Ȃ̂�����
sin2A�@���@�Qsin a cos a���@-3/4
(�Q)��
�R��+�R��̂�����
���������́@���́@�������g����
���@���́@1��
�ւĂ���
��ӂ��
�l���������Ă�@�Ƃ���
�i�P�j�́@������
�Qsin a cos a���@-3/4�Ȃ̂�����
sin a cos a���@-3/8
�������@�������
11/16
tan2A�@���@���߂�
����͂�
���������邯��
sin cos�@�Ł@�\�����@�̕���
�悳����������
����i�C�X�J
sin2A�@���@-3/4
���@�킩�Ă邩��
�����������g����
cos�QA=�@�}�@��7/4
���q�́@�}�C�i�X���@�l�����
�}�C�i�X�v���X�@�ɂȂ���
����́@���[�g���@�͂�����
���[�g���@���q�Ɂ@�����Ă���
�}�C�i�X�v���X�R��7/7
�ȏ���@���܂��܂���
�����@���ɍs���Ă݂܂��傤
�[���ł���
sin ���@-�@cos ���@���@1�@�̎�
sin 2���@�A�@sin ���@+�@cos�@���@�A
�̒l�����߂Ȃ���
�܂�
sin���@+ cos���@���@a
�@
���^����ꂽ��
sin a cos a�@���@���
��
sin2���@���@�Qsin��cos��
sin ���@-�@cos ���@���@1�@���@���������
sin��惦�@�@�@cos��惦�@�́@�ԂɁ@
�@-�Qsin ��cos��
���@�o�ė��ā@�����@�S�̂Ł@�P�Ȃ̂�
����������
0
����
sin���@+�@cos��
��
���������
sin��惦�@+�@cos��惦�@+�@�Qsin ��cos����
�isin���@+�@cos���j�̓�悪
�P+�Qsin ��cos���@�Ȃ̂�����
�������@�Qsin ��cos�����@0�@�������̂�
�P
��
������
�����ł́@����܂����
���������@���߂Ăł���
�}1
sin2x=a �̎��@���̒l��
���߂�
(1)sin x + cos x (2) tan x + cot x
�܂��ł���
�i�P�j
�Q���@�Ɓ@���@���@���݂��Ă�̂�
�����̔{�p�̌�����
sin2x=�Qsin �� cos ��
��ӂ��@���ꂪ�@��a�Ȃ̂�����
�Qsin �� cos ����a
(1)sin x + cos x
���@��������
�������������@�P+�@�Qsin �� cos ��
�ɂȂ�̂�
�isin x + cos x�j�̓�悪�@1+a
��������
�v���X�}�C�i�X�Ł�i1+a)
(2) tan x + cot x
�́@sin cos
�Ł@�l���ā@�ʕ�����
�Qsin �� cos ����a�Ȃ̂�����
sin �� cos ����a/2
���ʂ͂�����
�R��\�R�恁�P���@�^�����Ă�
sinA�@-�@cosA���@���߂�
������
�[��������ł���
���Ȃ�@���ԂȂ����Ăł�
�������́@���������ł���
�����܂ł́@�ǂ�����
�����ł�
sinA�@-�@cosA���@���ƒu������
�����
sinA�@-�@cosA���������
������
�������Ă��܂���
���̌`�́@�R��������
��������
�o�Ă��������@���i���j�@�Ƃł�������
���Q�́@�Öق̗�����
���P�̑S�͈͂��@�����Ă��܂��̂�
���c�����@����Ɓ@�i�߂Ȃ��@�ꍇ���@����܂���
�����́@�������傾��
�����藝���g����
��������
�����P�̎��@f(x)���O������
�i���|�P�j�@�Ł@�������
�W�����@��������
�Ȃ��Q��̍��́@�O�ɂ���
�g�����@��
�����藝�́@�����Ł@����
���i�P�j
�i���|�P�j���O
���������@�ς���Ɓ@�C�R�[���[���ɂȂ�@���Ł@�����
��
�����@���̂�������
���������ł�������
������
����1�@�܂��́@-2�@�Ȃ̂ł���
�������
�҂����ł�
��ȗ\����
���̂ł���
���́@�����̂Ƃ����
����͂�
�����@�Ⴄ�`�ɂ��@��������������
���Ă���Ȃ��I�H�ɂȂ��ĂāH�H
���`�`�`�`
��������
�ő�U����
�}��2
���`�`�`�`
����́@���́@�ǂ��Ȃ��������
�O���t����
���������@������
���ʎ����́@sin�́@�Q�@�����炳
��Βla���P
a���}�P
�p�x��
��ʓI�Ȃ��̂��@���߂��`�Ɂ@�����
�O���t����@�O���t��̂P�_���@���
������@��
A=0�̎�
sinA=0 cosA=1
���@�������
sinA�@-�@cosA�@���@��2�@�Esin ( A - 45 )
�Ȃ̂ł���
�i�^��
�ő�U���́@��Βl���@��2�ȉ�
��2�́@�@1.1421356�@�Ƃ�������ł���
����1�@�܂��́@-2�@��
-�Q�́@�s�K
����������
�����P
x�́@sinA�@-�@cosA�@�����@�Ƃ��Ă܂��̂�
sinA�@-�@cosA�@��1
�����@�[����ł����
���ꂱ��́@�W������Ƃ�
cos2A+cos2B�@�̒l���@���߂�
����͂�
�p�Y���݂����Ȋ�����
cos�̂Q�{�p��
�����Ă��ł���
������
��������
��₱��������
���x��
sin�́@�l���o���ׂ�
����������
�{�p��sin
�ł͂Ȃ��Ă�
�Q�{��sin
������
sin�̒l���o�ė���
�Ȃ@���炩�肻��������
�������@�̂肱�����
���イ�Ɂ@�Ȃ���
��́@�������
�P����
����@�[���Ƃ���
�|���v�����@�����̂�
���Ӑ[���@�i��ł��܂���
�܂��@�@�O����270�x�́@�Ԃł���
cos���@�g����
�p�x���@�\�������
���@�藝���@���������Ȃ̂�
������@�g����
���낻��
�[���Ȃ�̂Ɂ@�����Ȃ���
�������@���ā@�[�����@�\�����Ăł���
�ł��邾���@�}�Ɂ@�[���Ȃ�Ȃ����
�����@�ό`����
�܂�肪�@�����Ȃ��Ȃ�Ȃ��悤��
�ڈ�́@�Ȃ��J�i
�����͂ł���
���@�藝�́@�W�J���̒�
�́@�����I�ȂƂ���
���������@�����Ɂ@�g�����
��������
���@�藝�́@�W�J�����@�O�����@�ł܂�������
�㔼���@���Ă��ł���
�����I�Ɍ��ė���
�܂��g���ĂȂ���������
�ό`���Ă���
�S���@�g�݂��Ăā@����������
��0
�[���H
���[�@
cos�́@�l���@�[���@�Ȃ���
�s�������ł���
�p�x�𑫂����@���a���ł���
�����Ɂ@���e��
�X�O�x
�ЂƂ����w�Ɓ@�e�w��
�`���L���@�����
���ꂩ
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 19:58| ��l�̂��ї��Ƃ��@
2018�N04��14��
2B7004�@��l�̂��ї��Ƃ��@�{�p�̌���
�J�̓��́@�X���[���C�t�̕���
�{�p�̌����ł�
�O�p���̂ł���
��
�܂���
������������

�o����藧�Ă�
�T�����߂�
���^�����O����
�V���
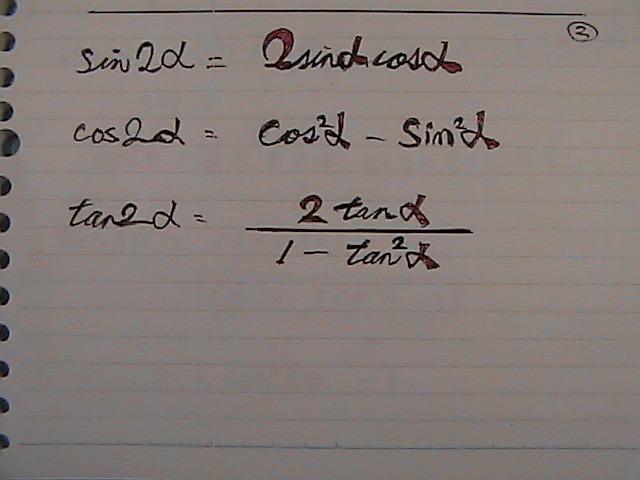
����Ȃ��
�o������
�ǂ�����
���
cos�S�����@1/4�̎�
cos�S�惦�@�|�@sin4�惦
cos�S�惦�@+�@sin4�惦
���@���߂Ȃ���
�{�p�̌����́@cos��
�܂��@���������Ł@�ό`�ł���̂�
����Ȋ����ł���
cos�Q�惦�����܂��
cos�S����o����Ǝv����̂�
cos�Q����@���߂�ׂ�
�i��ł�����

cos�́@�{�p�@�̌������@�g����
�R�T�C���S�Ƃ̒l���@�������Ă邯��
���߂�̂�
�S��́@�R�T�C���@�T�C��
��
�S�Ɓ@�ł́@�Ȃ��@��
������
�S�V�[�^���@�V�[�^�@�Ɂ@�ϊ����Ȃ��Ƃ����Ȃ�
�i�Q�{�́@�Q�Ɓj�ōl����ł���
�����ɑ������
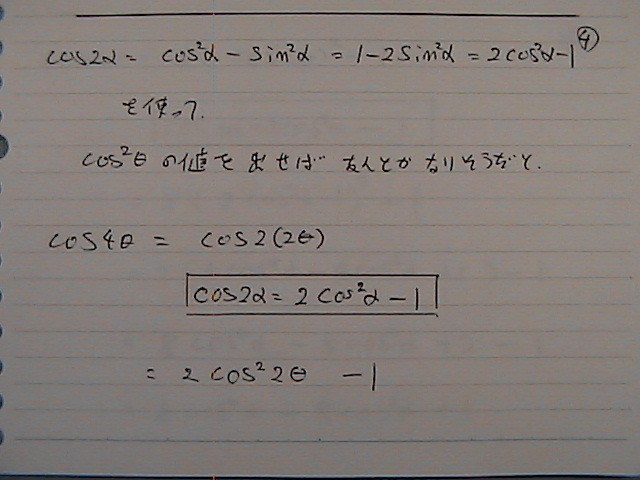
�����
�i�R�T�C���Q��Q�V�[�^�j�@�@��
�i�i�R�T�C���Q�Ɓj�̂Q��j�@�@�ɍl����
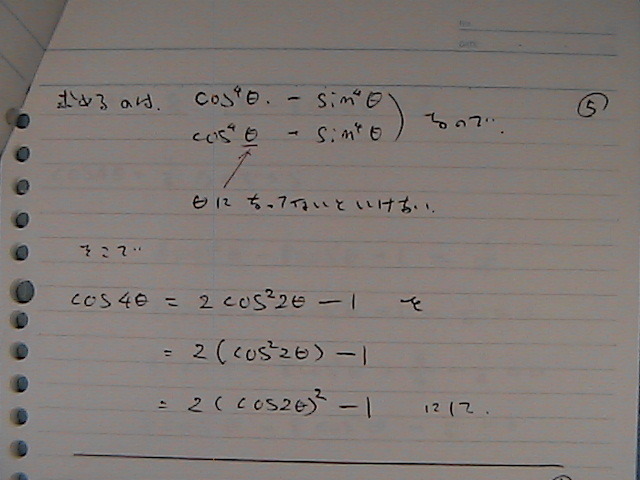
�^����ꂽ�@
�R�T�C���S�V�[�^�@���@�ό`������
�R�T�C���@�����́@�S���������ɂȂ���
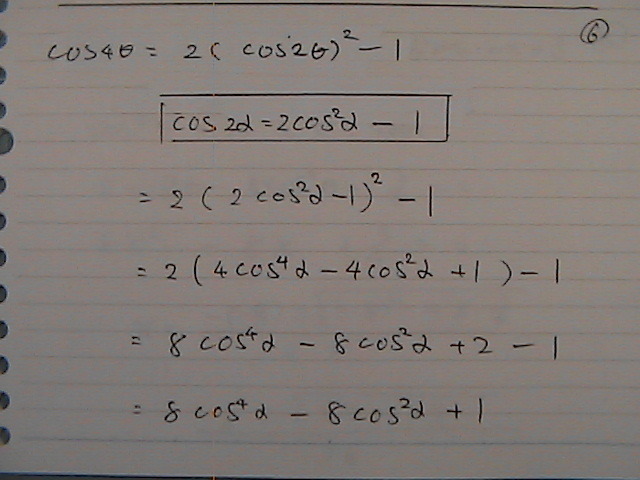
���̒l��
1/4
�f�V��
���[������
�R���Ɓ@�P���@���Ȃ�
�R�T�C���́@�S���������ɂȂ�������
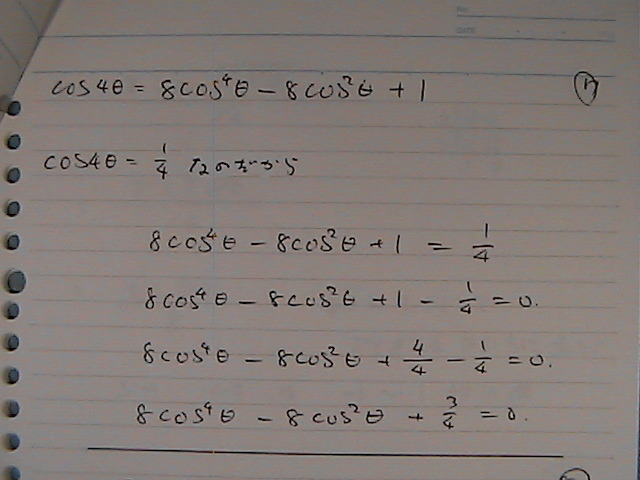
�R�T�C���Q��V�[�^�@���@���@X�Ƃ���
X�́@�Q����������
�R�T�C���Q�惦��
���߂��
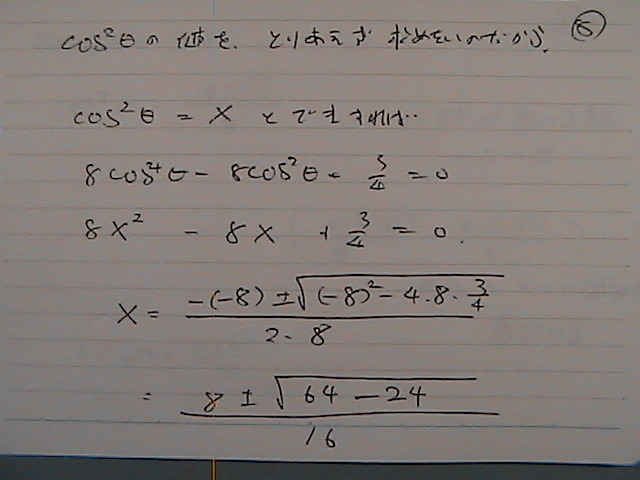
����Ȋ�����
��
�����Ƃ��ā@�g���邩�́@�`�F�b�N���K�v�łł���
�T�C���@�R�T�C���@�́@���a�́@�~�^����
Y���@X���@�Ɂ@���e�������̂�
��̒l�Ȃ̂�
-1�@�ȏ�@1�ȉ�
�͈̔�
�T�C���@�R�T�C���@�̑O�Ɂ@�t�@�N�^�[�@���@���Ȃ����
�傫���Ȃ�Ȃ�
�ЂƂ܂�́@�݂���ɂȂ�ԁ@��
�v�Z�����

����͂�
�R�T�C���́@��悾����
0�Ɓ@�P�́@�ԂɁ@����͂��Ȃ���
�ǂ�����@�������Ă�̂�
�R�T�C���Q�悪�@�ł܂���

��
���悢��
�R�T�C���S��V�[�^�@�@�|�@�T�C���S��V�[�^
��
�R�T�C���S��́@���̂܂�
���́@�T�C���S���
�i�i�T�C���Q��j�̓��j
�ɂ���
���g��
�P�܂��Ȃ��@�R�T�C���Q�惦
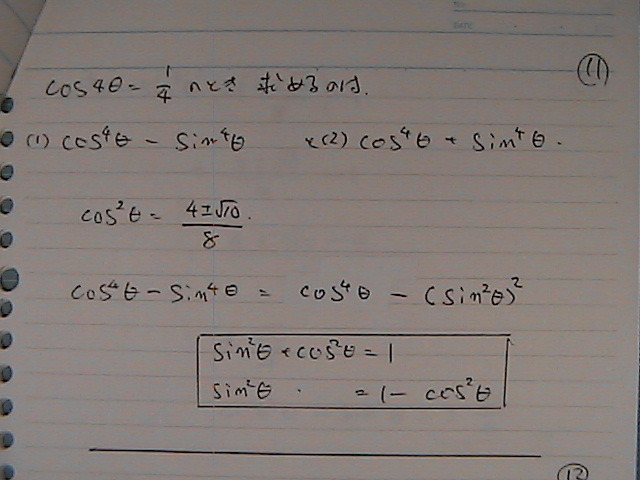
���������@�W�J������
�r����
���܂�����
�S��̍����@�����ł���
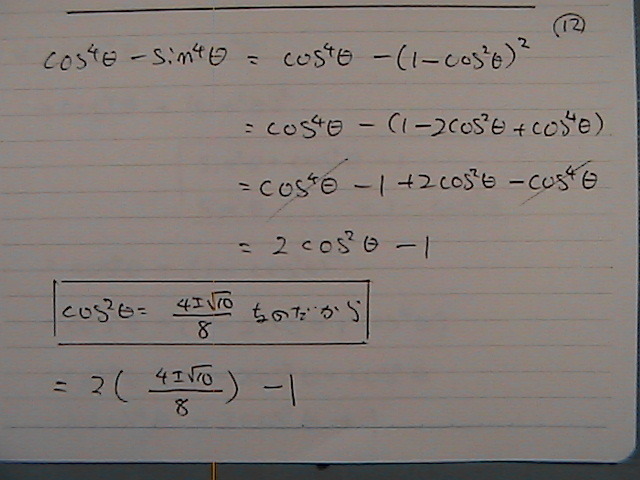
�v�Z�̌���
����ł�
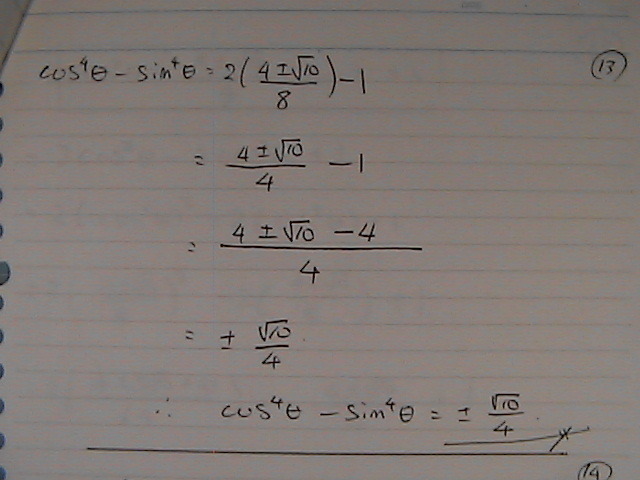
�������
�R�T�C���S�惦�@+�@�T�C���S�惦
����Ȃ�������
���̃T�C�����@�R�T�C����
�W�J����ł���
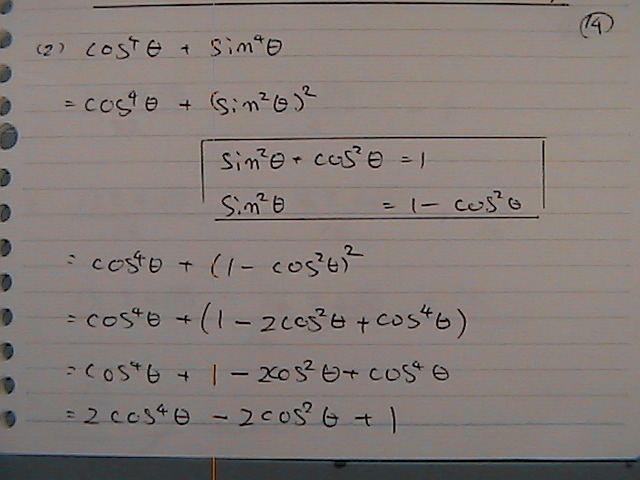
�W�J�̌�����
�W�J�����
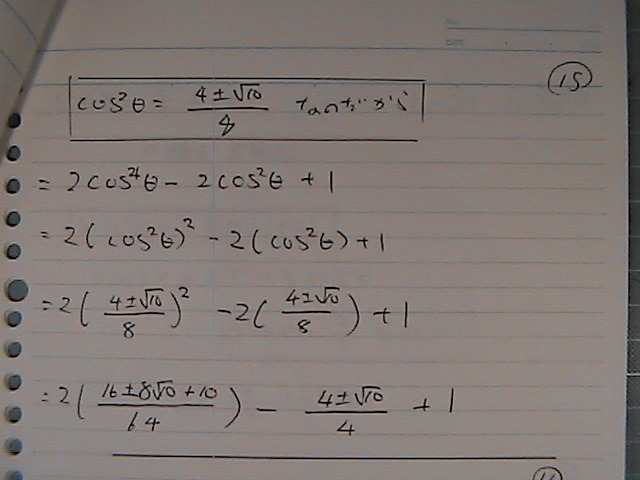
�Ł@�ʕ�������
�r����
�}�C�i�X���@��������
���̂S��P�O��
�}�C�i�X�v���X�@�ɂȂ���
����ł�

����
�T�C�������^�����Ă�Ƃ�
�Q�{�p�́@�T�C���@�R�T�C���@�^���W�F���g
���@���߂Ȃ���
����͂�
�����̎���
�v�Z����
�l���@�ς���ā@�o�Ă���@�p�^�[���ł����
�T�C���́@�{�p�̌�����
�T�C���Q�����@�ό`����

��́@�R�T�C��
������������
�R�T�C�������@�������@�݂����Ȋ����ł���

��
�T�C�����@���
����
�R�T�C�����@�ł��
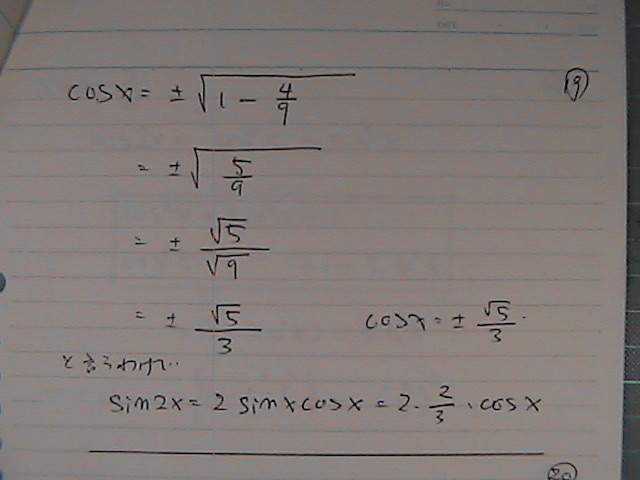
�������́@�����Ɂ@�������
����
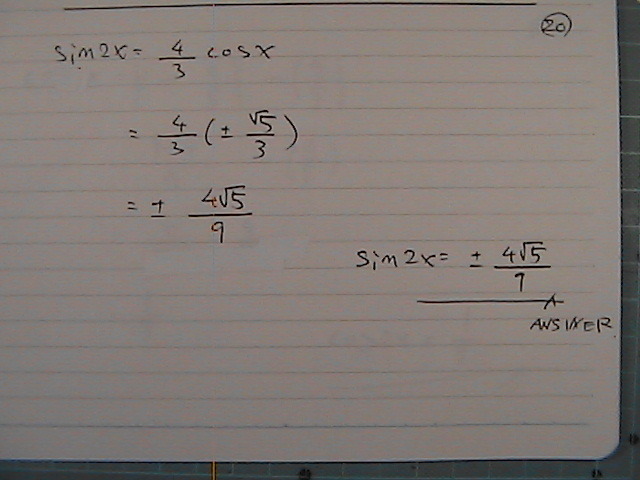
�R�T�C���̂Q����
�{�p�́@�������@������
�ό`����
������������
�T�C�������ɂ���
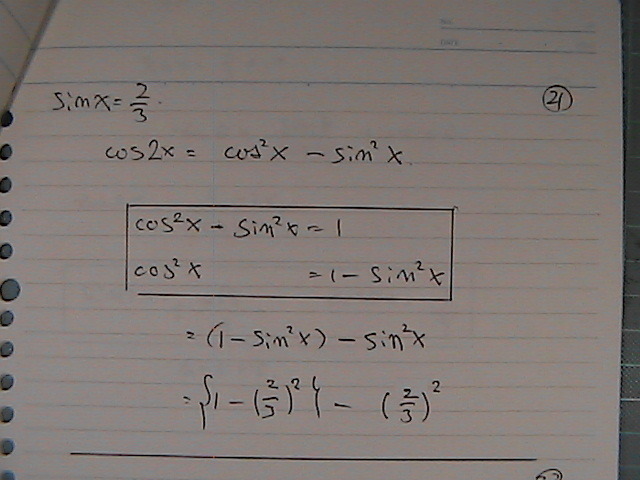
�R���_��
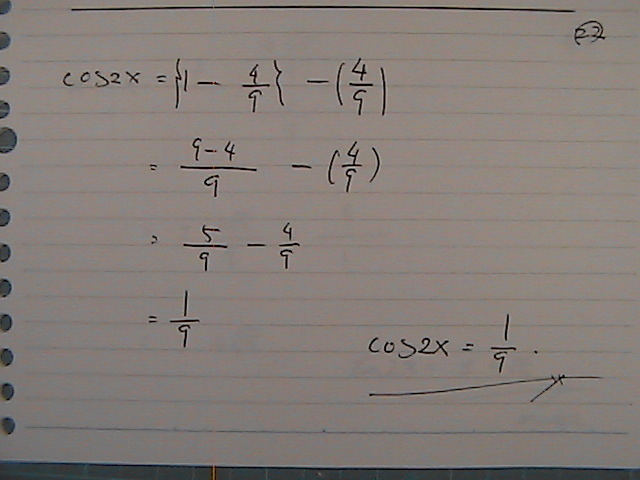
�^���W�F���g��
�T�C���@�R�T�C�����o�Ă邩��
�O�p���́@�v�Z��
�T�C���@�R�T�C���Ł@�@
��
������
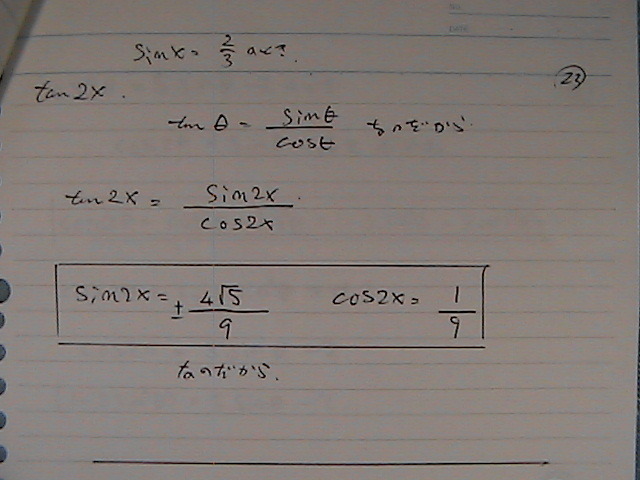
��

���x��
�R�T�C���Q����
���ꂱ��̎�
�R�T�C���Q�Ɓ@�{�T�C�������@���߂Ȃ���
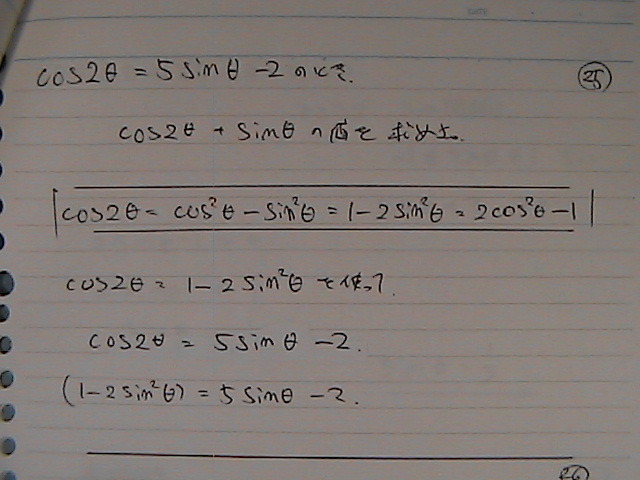
�R�T�C���́@�{�p�̌����̒���
�T�C���Ɂ@�Ȃ�@�̂��@���邶��@�i�C�X�J��
���ꂪ���@�@�Tsin���@+�@sin���@��������
�C�R�[����
�����
�������炳
�T�C���́@�Q�����Ɂ@

������������
�T�C�������@�ł�̂������
�T�C�����́@-1�@����@1�܂�
sin��+�R�́@���O�@�ɂȂ邩��
2sin���@-�@1�@�̕����@���O
��
�T�C���́@1/2
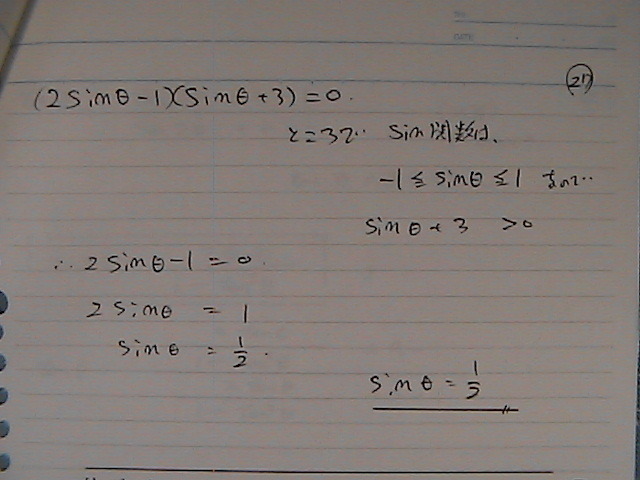
���߂�@cos2���{sin�Ƃ�
�R�T�C�����́@���p�̌�������
�ό`����
�i�P�|sin�Q�惦�@�j+�@�@�@�@�����Ɂ@sin��
�T�C�������@1/2�@��������
�������
�P

���x��
�^���W�F���g�Ȃ�ł���
����Ȃ̂�
�����ɂ́@�łȂ��Ǝv������
�Q�l���ɂ́@����Ȃ��[

�{�p�́@����������
�Q�V�[�^���@�@���@�Ɂ@
�^���W�F���g�����@�����@�Ƃ�����
007
�́H
�����Ɓ@�E�E�ς��[
�I�N�g�p�V�[�ł���
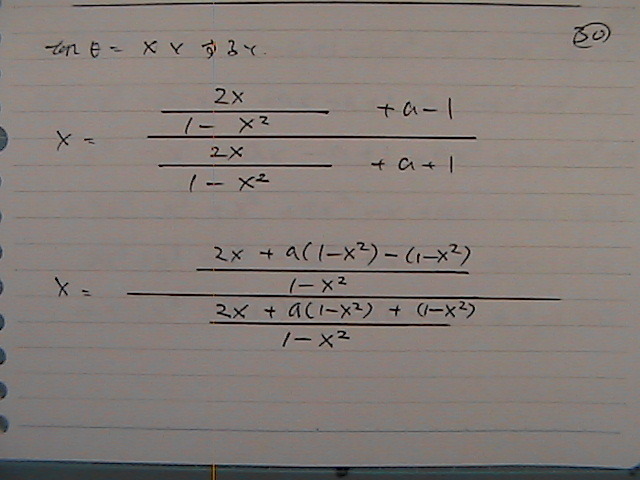
���`�@���
��������
�ʕ�����
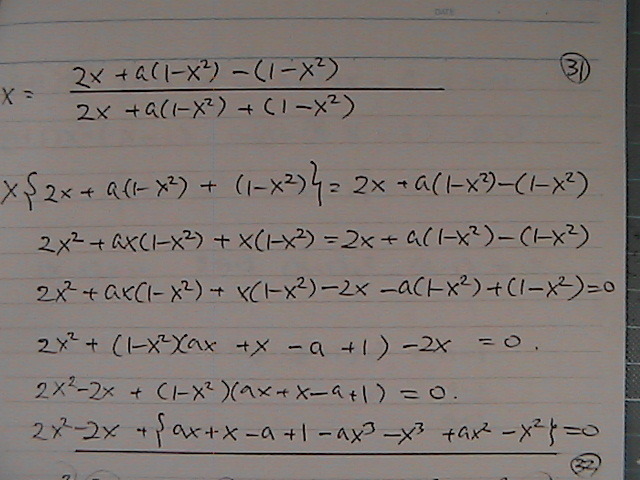
��������
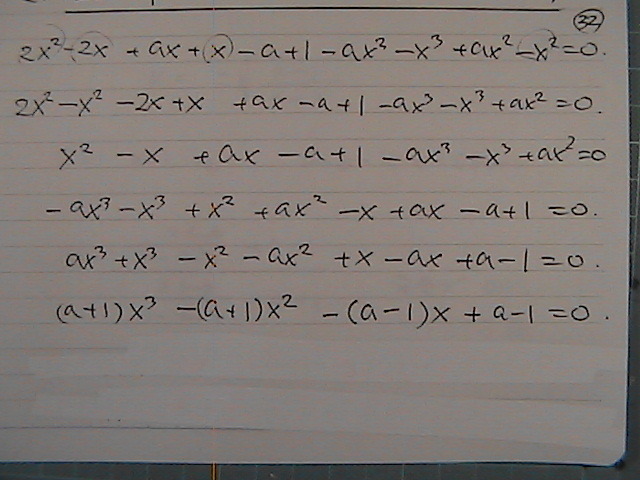
�����P�܂���
����Ȋ���������
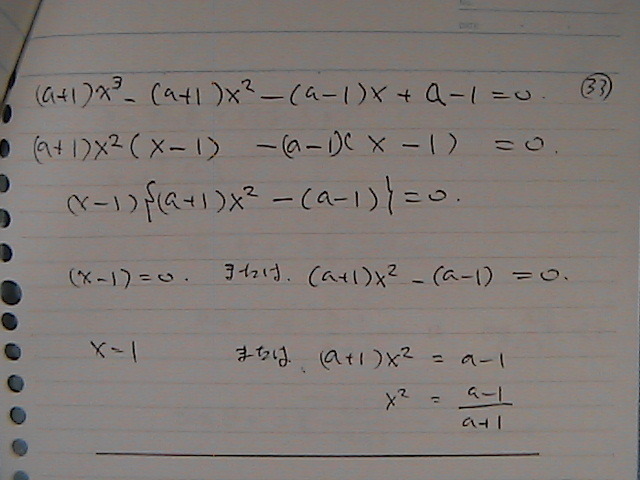
�Ƃ��낪��
���̎��́@�����́@���ꂪ
tan�����P�@���Ɓ@�O�@�ɂȂ��Ă��܂��̂�
�����P�́@�s�K
��

�����́@�܂����́@����Ȋ���
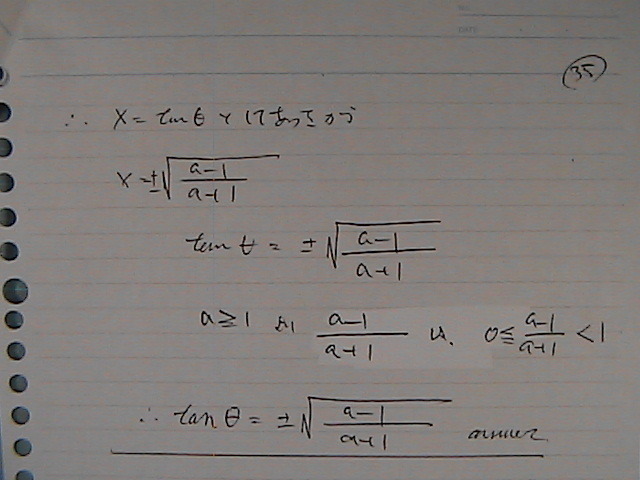
���́@������l������^��
������悤�Ɂ@�Ȃ��Ă܂�
���������ā@���������邱�Ƃ��@�m�F���Ăł���
������
���R�Ȋw�́@����ł�
�n����Ɓ@���ǂ��Ȃ�Ȃ���
�킩��Ȃ����Ƃ��炯�ł�
���Ȃ��́@�Ⴂ���Ɂ@����o����
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�{�p�̌����ł�
�O�p���̂ł���
��
�܂���
������������
�o����藧�Ă�
�T�����߂�
���^�����O����
�V���
����Ȃ��
�o������
�ǂ�����
���
cos�S�����@1/4�̎�
cos�S�惦�@�|�@sin4�惦
cos�S�惦�@+�@sin4�惦
���@���߂Ȃ���
�{�p�̌����́@cos��
�܂��@���������Ł@�ό`�ł���̂�
����Ȋ����ł���
cos�Q�惦�����܂��
cos�S����o����Ǝv����̂�
cos�Q����@���߂�ׂ�
�i��ł�����
cos�́@�{�p�@�̌������@�g����
�R�T�C���S�Ƃ̒l���@�������Ă邯��
���߂�̂�
�S��́@�R�T�C���@�T�C��
��
�S�Ɓ@�ł́@�Ȃ��@��
������
�S�V�[�^���@�V�[�^�@�Ɂ@�ϊ����Ȃ��Ƃ����Ȃ�
�i�Q�{�́@�Q�Ɓj�ōl����ł���
�����ɑ������
�����
�i�R�T�C���Q��Q�V�[�^�j�@�@��
�i�i�R�T�C���Q�Ɓj�̂Q��j�@�@�ɍl����
�^����ꂽ�@
�R�T�C���S�V�[�^�@���@�ό`������
�R�T�C���@�����́@�S���������ɂȂ���
���̒l��
1/4
�f�V��
���[������
�R���Ɓ@�P���@���Ȃ�
�R�T�C���́@�S���������ɂȂ�������
�R�T�C���Q��V�[�^�@���@���@X�Ƃ���
X�́@�Q����������
�R�T�C���Q�惦��
���߂��
����Ȋ�����
��
�����Ƃ��ā@�g���邩�́@�`�F�b�N���K�v�łł���
�T�C���@�R�T�C���@�́@���a�́@�~�^����
Y���@X���@�Ɂ@���e�������̂�
��̒l�Ȃ̂�
-1�@�ȏ�@1�ȉ�
�͈̔�
�T�C���@�R�T�C���@�̑O�Ɂ@�t�@�N�^�[�@���@���Ȃ����
�傫���Ȃ�Ȃ�
�ЂƂ܂�́@�݂���ɂȂ�ԁ@��
�v�Z�����
����͂�
�R�T�C���́@��悾����
0�Ɓ@�P�́@�ԂɁ@����͂��Ȃ���
�ǂ�����@�������Ă�̂�
�R�T�C���Q�悪�@�ł܂���
��
���悢��
�R�T�C���S��V�[�^�@�@�|�@�T�C���S��V�[�^
��
�R�T�C���S��́@���̂܂�
���́@�T�C���S���
�i�i�T�C���Q��j�̓��j
�ɂ���
���g��
�P�܂��Ȃ��@�R�T�C���Q�惦
���������@�W�J������
�r����
���܂�����
�S��̍����@�����ł���
�v�Z�̌���
����ł�
�������
�R�T�C���S�惦�@+�@�T�C���S�惦
����Ȃ�������
���̃T�C�����@�R�T�C����
�W�J����ł���
�W�J�̌�����
�W�J�����
�Ł@�ʕ�������
�r����
�}�C�i�X���@��������
���̂S��P�O��
�}�C�i�X�v���X�@�ɂȂ���
����ł�
����
�T�C�������^�����Ă�Ƃ�
�Q�{�p�́@�T�C���@�R�T�C���@�^���W�F���g
���@���߂Ȃ���
����͂�
�����̎���
�v�Z����
�l���@�ς���ā@�o�Ă���@�p�^�[���ł����
�T�C���́@�{�p�̌�����
�T�C���Q�����@�ό`����
��́@�R�T�C��
������������
�R�T�C�������@�������@�݂����Ȋ����ł���
��
�T�C�����@���
����
�R�T�C�����@�ł��
�������́@�����Ɂ@�������
����
�R�T�C���̂Q����
�{�p�́@�������@������
�ό`����
������������
�T�C�������ɂ���
�R���_��
�^���W�F���g��
�T�C���@�R�T�C�����o�Ă邩��
�O�p���́@�v�Z��
�T�C���@�R�T�C���Ł@�@
��
������
��
���x��
�R�T�C���Q����
���ꂱ��̎�
�R�T�C���Q�Ɓ@�{�T�C�������@���߂Ȃ���
�R�T�C���́@�{�p�̌����̒���
�T�C���Ɂ@�Ȃ�@�̂��@���邶��@�i�C�X�J��
���ꂪ���@�@�Tsin���@+�@sin���@��������
�C�R�[����
�����
�������炳
�T�C���́@�Q�����Ɂ@
������������
�T�C�������@�ł�̂������
�T�C�����́@-1�@����@1�܂�
sin��+�R�́@���O�@�ɂȂ邩��
2sin���@-�@1�@�̕����@���O
��
�T�C���́@1/2
���߂�@cos2���{sin�Ƃ�
�R�T�C�����́@���p�̌�������
�ό`����
�i�P�|sin�Q�惦�@�j+�@�@�@�@�����Ɂ@sin��
�T�C�������@1/2�@��������
�������
�P
���x��
�^���W�F���g�Ȃ�ł���
����Ȃ̂�
�����ɂ́@�łȂ��Ǝv������
�Q�l���ɂ́@����Ȃ��[
�{�p�́@����������
�Q�V�[�^���@�@���@�Ɂ@
�^���W�F���g�����@�����@�Ƃ�����
007
�́H
�����Ɓ@�E�E�ς��[
�I�N�g�p�V�[�ł���
���`�@���
��������
�ʕ�����
��������
�����P�܂���
����Ȋ���������
�Ƃ��낪��
���̎��́@�����́@���ꂪ
tan�����P�@���Ɓ@�O�@�ɂȂ��Ă��܂��̂�
�����P�́@�s�K
��
�����́@�܂����́@����Ȋ���
���́@������l������^��
������悤�Ɂ@�Ȃ��Ă܂�
���������ā@���������邱�Ƃ��@�m�F���Ăł���
������
���R�Ȋw�́@����ł�
�n����Ɓ@���ǂ��Ȃ�Ȃ���
�킩��Ȃ����Ƃ��炯�ł�
���Ȃ��́@�Ⴂ���Ɂ@����o����
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 09:26| ��l�̂��ї��Ƃ��@
2018�N03��31��
2B7003 �@�@�ؖ����
�J�̓��́@�X���[���C�t�̕���
��l�̂��ї��Ƃ���
����@����Ȃ�n��
���Ɂ@�����Ă��ł���
�g�����@������Ă��Ă�����Ă܂�
���x�������߂�������Ȃ�
��s���`�@�́@����̂��Ƃ��@�S�z����
���Ɂ@���ꂵ���v���Ă܂���
���ʔŁ@�i�^��
���������Ɂ@�A�j���Ɂ@������@�I�Ȃ��Ƃ��ł���
�������ł���
�ނ���
�`�����`�����@�{�[�O�@�m����H
���@�藝�Z�N�V�����i�^��
���̕ӂ��@������Ă��
�ł���@�ƌ����̂��@�Öق́@������
�s���Ă݂܂��傤�B

�E�ӂ��@�����
�i��+���j�@�Ƃ��@�i���|���j�@�Ƃ����Ȃ��ł���
������
���@�藝�Ł@�ό`���čs���Ɓ@�ł���
��
�����́@�G�Ł@�o���Ă邽��
���@���@�@�@�@���@���@�@�@�@
���@���E�Ɂ@�o�ė��ā@�@�T�C���@�R�T�C���@�^���W�F���g��
�Ȃ��@�������@�}�@∓�v���X
������@�R�T�C���́@���ƂȂ�
�����́@�f�U�C���Ł@�o���Ă���

�^���W�F���g���@���̑����@�݂����ł���

�T�C���́@���@�藝�́@�������@������
�^����
����Ȃ�
�������@���@���@�Ł@�����Ƃ���
�v���X���@�@�@�}�C�i�X��

�W�J���邶��i�C�X�J
�������@���ׂď����ł���
�����@�ł���Ƃ��������
��
�łĂ������̂��@➀�Ƃ��Ăł���

�E�ӂ��@�������
�T�C���o�[�W�����@�@�@�R�T�C���o�[�W����
�T�C���o�[�W�����@���@�s���Ă݂��
������������
�R�T�C�����@�T�C���Ɂ@����������
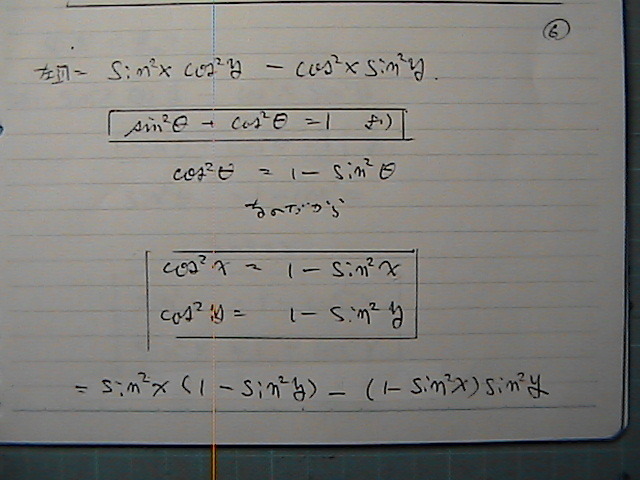
����������
�����ł���Ƃ��������
��
�߂ł����@�E�Ӂ@�i�@�T�C���o�[�W�����@�j
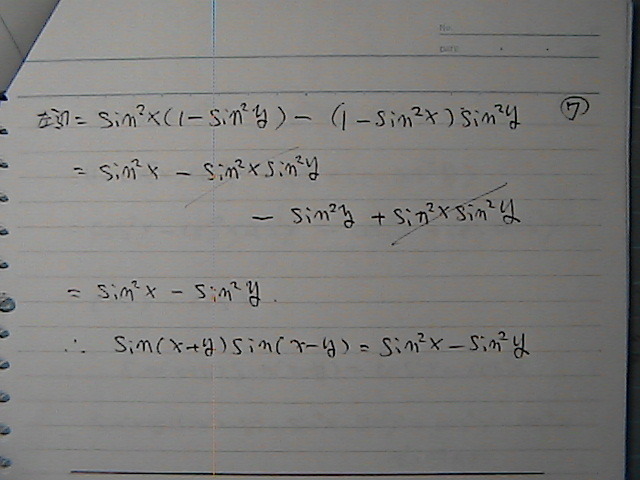
➀�܂Ł@�߂���
���@�E�Ӂ@�H�@�����J�i�H
���x��
�����̌�������
�R�T�C���o�[�W����
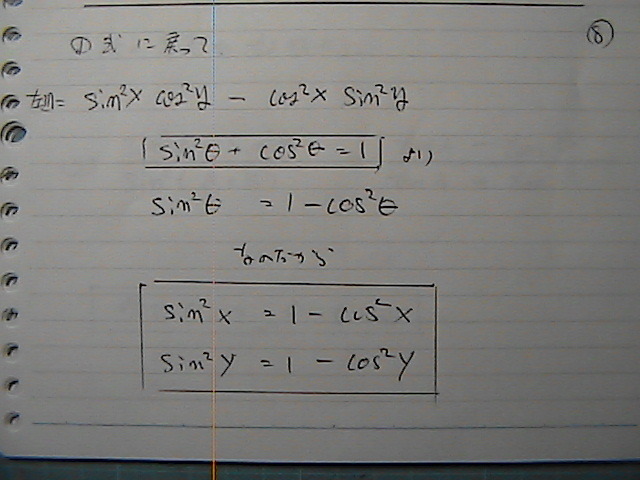
��������
�����ł���Ƃ����o�ė���
�߂ł����@���@�E�Ӂ@�i�R�T�C���o�[�W�����@�j
������@����ł����̂����@����
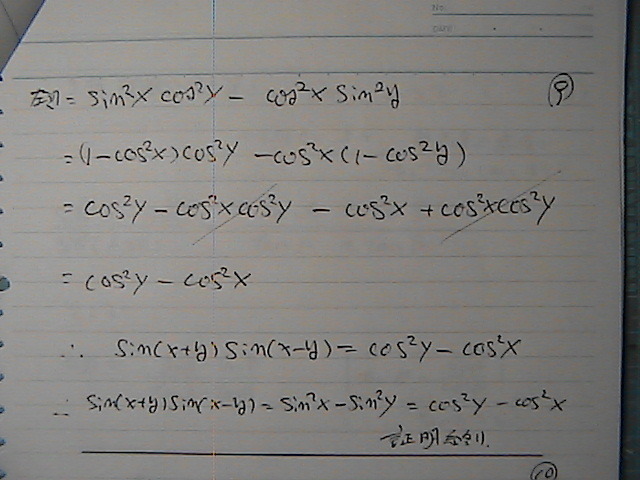
�������@�^���W�F���g���@����������

�O�p����
�T�C���@�R�T�C���@�Ł@�v�Z�@��������������
������
�����
�E�ӂ��@��������
���ӂɁ@�����čs������

�T�C����������
����ԂɁ@�������Ɂ@�������|��
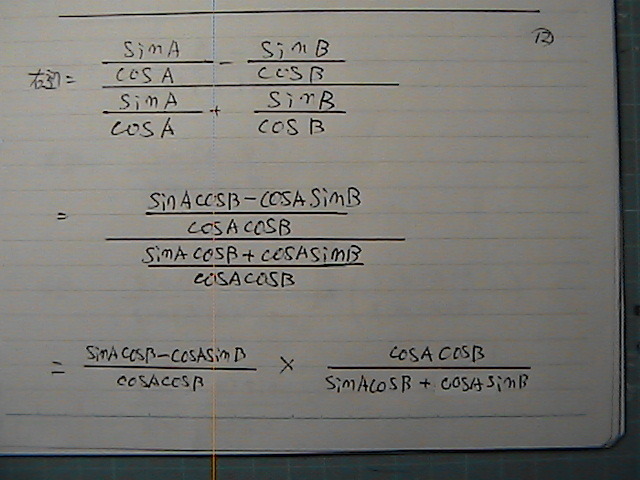
��
�łĂ�������
���ꂪ��
���@�藝�́@�W�J�����`�ɂȂ��Ă邩��
�t�@���@�藝�@�i�@�����J�i�j

��
���Ζʁ@���@������
�߂�
�ł���
������
�l���@�ς��Ȃ��悤��
�߂Â��Ă�����

���������Ɂ@�����̂����邯��
�O�p���Ɂ@���̂܂g�Ă������̂�
��[
����ȗ��\�ȁ@
��������
�������I
�������@�P���Ă��邶���
�i�P�j

�������P�́@�T�C���o�[�W������
X�@Y�@���@���ꂽ��
����Ł@�������

��Ȃ��Ƃ����
�������
�����@��蒼���ā@�Q��܂��傤
�������́@�������@�P�Ɓ@�Ȃ��Ă邩��
���ӂ�
���@�藝��
����������
�W�J����

����������
���Ԃ��@�����@�ł���ł���
�܂��@��ɂ����
��➀�ɂ���

�������ƈႤ�̂�
�T�C���o�[�W�����@�R�T�C���o�[�W�����łȂ���
�T�C���@�R�T�C���@X�@Y�@���@�g�ɂȂ��Ă�
��
�E�ӂ��@�\������
�R�T�C��X�@�@�T�C��Y�@���@�c���悤��
����������
�T�C���@�R�T�C���@�����g����
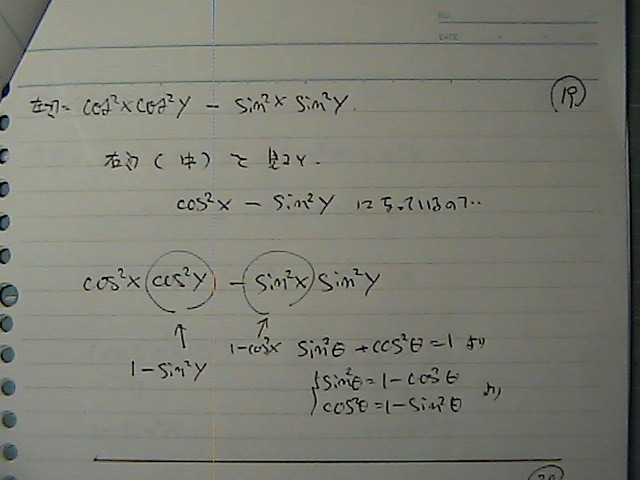
������ā@����������
�E�Ӂ@

���@➀���ɖ߂���
���x��
������g�́@�g�ݍ��킹��
�T�C���@�R�T�C��
���������@�g����
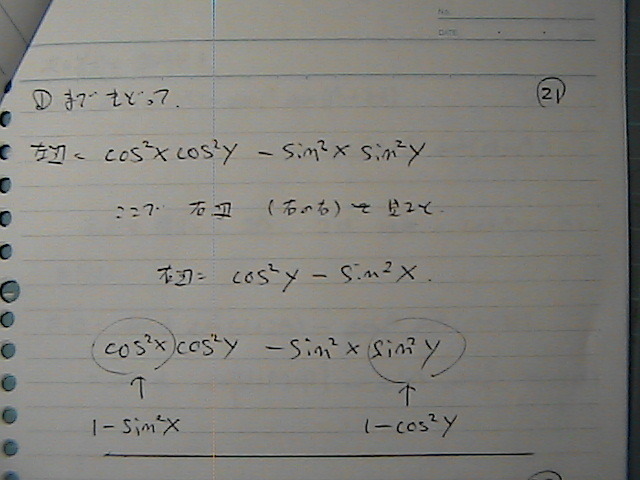
�������
��������
�܂���������
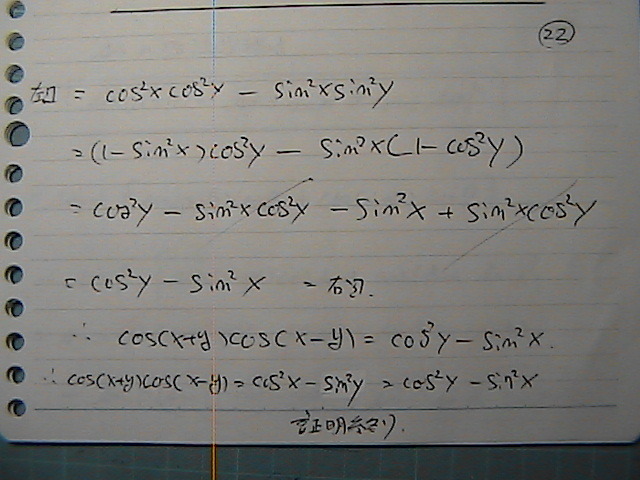
���͂�
������
�}�W���K�[Z�̂Ƃ��݂�����
�����Ȃ�@�ѐF�̈Ⴄ�̂�
�o�ė���
�܂��@��{�p�́@����ĂȂ����
�\�K����
���

��
�킩��Ȃ��������
��Ӂ@�Ђ��܂���
�o���Ȃ�������
�ǂ����悤��
�Ђ�����@�Y��ł���
���z���@����ė�����
��
��������
�e�Ɋp
�����Ɂ@�͂߂Ă��ł���

�d�����Ă܂���
�����ł���Ƃ����łĂ���
�������ā@����������

���������Ɂ@���Ă��������
�W�J�����@�`�́@���@�藝�ɂȂ��Ă邩��
�t�@���@�藝
�Ł@�E��

��
����
�T�C���́@���@�藝�Ł@�����̂�

�����@���@�藝�Ł@�W�J����
��������
����������
�Ԉ���Ă��@�e�X�g�̓��Ă�
����Ȃ��Ƃ��@�����Ȃ��悤��
�ł���
���́@���키
�{�́@�N�b�N�h�D�[�h�D���h�D�[
�N�W���́@�Q�[�@
�݂����ȁ@������
�����ł���
�ؖ��I���

���͂ł���
����͂�
�ǂ����́@�Z���Z��
�D��������
�e�X�g�Ɂ@�ł���Ƃ�

����ς�ł���
���w�ɂ�
�_���E�́@�֕���
�����Ăȁ@��]�Ł@�����@����Ắ@�܂���
�Ԏl�p�@����Ł@���߂����Ȃ�
�v�����Ƃ������ł���
�����́@�����܂����
�i�^��
�^���W�F���g�́@���@�藝��
�������@�ό`���邶��i�C�X�J
������Ȃ������̂�
�q���g���@�������茩�܂���
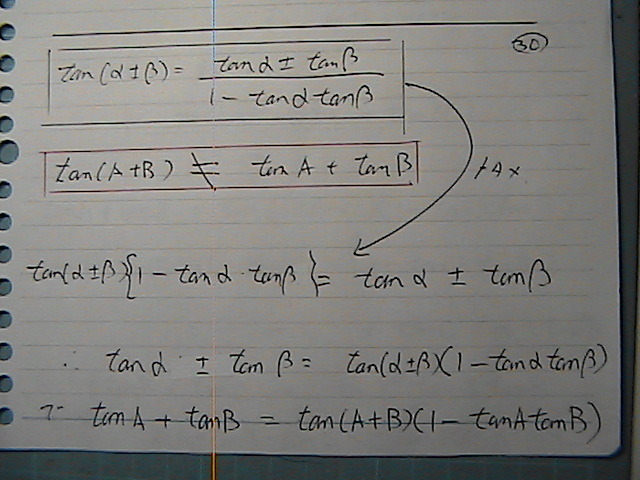
��
������
�ǂ��Ԃ₢�Ă�
��p�̒藝��
-�@Tan�@C�@���o�Ă����ł���

���
�����@�ό`���čs����
�߂ł����܂ł����B
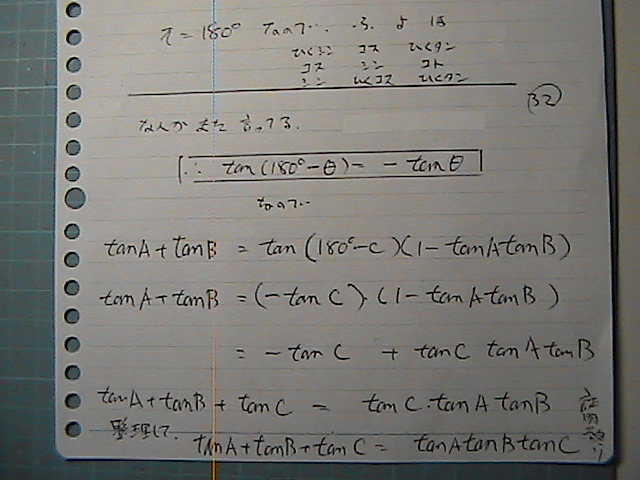
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��l�̂��ї��Ƃ���
����@����Ȃ�n��
���Ɂ@�����Ă��ł���
�g�����@������Ă��Ă�����Ă܂�
���x�������߂�������Ȃ�
��s���`�@�́@����̂��Ƃ��@�S�z����
���Ɂ@���ꂵ���v���Ă܂���
���ʔŁ@�i�^��
���������Ɂ@�A�j���Ɂ@������@�I�Ȃ��Ƃ��ł���
�������ł���
�ނ���
�`�����`�����@�{�[�O�@�m����H
���@�藝�Z�N�V�����i�^��
���̕ӂ��@������Ă��
�ł���@�ƌ����̂��@�Öق́@������
�s���Ă݂܂��傤�B
�E�ӂ��@�����
�i��+���j�@�Ƃ��@�i���|���j�@�Ƃ����Ȃ��ł���
������
���@�藝�Ł@�ό`���čs���Ɓ@�ł���
��
�����́@�G�Ł@�o���Ă邽��
���@���@�@�@�@���@���@�@�@�@
���@���E�Ɂ@�o�ė��ā@�@�T�C���@�R�T�C���@�^���W�F���g��
�Ȃ��@�������@�}�@∓�v���X
������@�R�T�C���́@���ƂȂ�
�����́@�f�U�C���Ł@�o���Ă���
�^���W�F���g���@���̑����@�݂����ł���
�T�C���́@���@�藝�́@�������@������
�^����
����Ȃ�
�������@���@���@�Ł@�����Ƃ���
�v���X���@�@�@�}�C�i�X��
�W�J���邶��i�C�X�J
�������@���ׂď����ł���
�����@�ł���Ƃ��������
��
�łĂ������̂��@➀�Ƃ��Ăł���
�E�ӂ��@�������
�T�C���o�[�W�����@�@�@�R�T�C���o�[�W����
�T�C���o�[�W�����@���@�s���Ă݂��
������������
�R�T�C�����@�T�C���Ɂ@����������
����������
�����ł���Ƃ��������
��
�߂ł����@�E�Ӂ@�i�@�T�C���o�[�W�����@�j
➀�܂Ł@�߂���
���@�E�Ӂ@�H�@�����J�i�H
���x��
�����̌�������
�R�T�C���o�[�W����
��������
�����ł���Ƃ����o�ė���
�߂ł����@���@�E�Ӂ@�i�R�T�C���o�[�W�����@�j
������@����ł����̂����@����
�������@�^���W�F���g���@����������
�O�p����
�T�C���@�R�T�C���@�Ł@�v�Z�@��������������
������
�����
�E�ӂ��@��������
���ӂɁ@�����čs������
�T�C����������
����ԂɁ@�������Ɂ@�������|��
��
�łĂ�������
���ꂪ��
���@�藝�́@�W�J�����`�ɂȂ��Ă邩��
�t�@���@�藝�@�i�@�����J�i�j
��
���Ζʁ@���@������
�߂�
�ł���
������
�l���@�ς��Ȃ��悤��
�߂Â��Ă�����
���������Ɂ@�����̂����邯��
�O�p���Ɂ@���̂܂g�Ă������̂�
��[
����ȗ��\�ȁ@
��������
�������I
�������@�P���Ă��邶���
�i�P�j
�������P�́@�T�C���o�[�W������
X�@Y�@���@���ꂽ��
����Ł@�������
��Ȃ��Ƃ����
�������
�����@��蒼���ā@�Q��܂��傤
�������́@�������@�P�Ɓ@�Ȃ��Ă邩��
���ӂ�
���@�藝��
����������
�W�J����
����������
���Ԃ��@�����@�ł���ł���
�܂��@��ɂ����
��➀�ɂ���
�������ƈႤ�̂�
�T�C���o�[�W�����@�R�T�C���o�[�W�����łȂ���
�T�C���@�R�T�C���@X�@Y�@���@�g�ɂȂ��Ă�
��
�E�ӂ��@�\������
�R�T�C��X�@�@�T�C��Y�@���@�c���悤��
����������
�T�C���@�R�T�C���@�����g����
������ā@����������
�E�Ӂ@
���@➀���ɖ߂���
���x��
������g�́@�g�ݍ��킹��
�T�C���@�R�T�C��
���������@�g����
�������
��������
�܂���������
���͂�
������
�}�W���K�[Z�̂Ƃ��݂�����
�����Ȃ�@�ѐF�̈Ⴄ�̂�
�o�ė���
�܂��@��{�p�́@����ĂȂ����
�\�K����
���
��
�킩��Ȃ��������
��Ӂ@�Ђ��܂���
�o���Ȃ�������
�ǂ����悤��
�Ђ�����@�Y��ł���
���z���@����ė�����
��
��������
�e�Ɋp
�����Ɂ@�͂߂Ă��ł���
�d�����Ă܂���
�����ł���Ƃ����łĂ���
�������ā@����������
���������Ɂ@���Ă��������
�W�J�����@�`�́@���@�藝�ɂȂ��Ă邩��
�t�@���@�藝
�Ł@�E��
��
����
�T�C���́@���@�藝�Ł@�����̂�
�����@���@�藝�Ł@�W�J����
��������
����������
�Ԉ���Ă��@�e�X�g�̓��Ă�
����Ȃ��Ƃ��@�����Ȃ��悤��
�ł���
���́@���키
�{�́@�N�b�N�h�D�[�h�D���h�D�[
�N�W���́@�Q�[�@
�݂����ȁ@������
�����ł���
�ؖ��I���
���͂ł���
����͂�
�ǂ����́@�Z���Z��
�D��������
�e�X�g�Ɂ@�ł���Ƃ�
����ς�ł���
���w�ɂ�
�_���E�́@�֕���
�����Ăȁ@��]�Ł@�����@����Ắ@�܂���
�Ԏl�p�@����Ł@���߂����Ȃ�
�v�����Ƃ������ł���
�����́@�����܂����
�i�^��
�^���W�F���g�́@���@�藝��
�������@�ό`���邶��i�C�X�J
������Ȃ������̂�
�q���g���@�������茩�܂���
��
������
�ǂ��Ԃ₢�Ă�
��p�̒藝��
-�@Tan�@C�@���o�Ă����ł���
���
�����@�ό`���čs����
�߂ł����܂ł����B
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 20:56| ��l�̂��ї��Ƃ��@
2018�N03��24��
2B7002 ��l�̂��ї��Ƃ��@�O�p���́@�l�B
�J�̓��́@�X���[���C�t�̕���
�O�p���̒l�Ɋւ��܂��Ăł���
���Z�@�́@�Q�N�̎�����������
�P�N����@������������@�Z���Z��
���P�������������̂�
��
�V�ے��Ƃ��@���낢��@���������Ă���
�Q�N�̓r���܂�
���������@�����Ă����������@���Ƃ�
�v���o���Ă��܂���
��������
�o�����������
�o�����Ȃ��Ƃ���
�E�E�E�E�E
�ǂ������
�R�R��@����
�����́@�X�y���́@���K���@�����
�H�H
�悭��������
����@�����@�o����

�n�C�@�^���W�F���g�@�R�^���W�F���g
���ꂪ�@�^�����Ă�Ƃ�
COS�iA-B)�@���@���߂Ȃ���
����Ȋ�������������
����Ɂ@���ǂ���
���@�藝�̌����ł�
COS�iA-B)�́@�l��
tan
cot
�@
����͒��ڂ́@�����Ȃ̂�

�pA�Ɂ@�ւ��Ắ@�@�^���W�F���g����
�pB�Ɂ@�ւ��Ắ@�@�R�^���W�F���g����
�\���]���@�T�C���@�R�T�C�����@���߂Ă��܂���

�܂��@A��
tan
����@sin cos���@���߂���
�^���W�F���g�́@����������
�Z�J���g�@��悪�@���Ă�̂�
�Z�J���g���@�R�T�C���@���g����

�R�T�C���@���́@�`�ɂ���
�������Ă�@�^���W�F���g���@�����ɂイ����
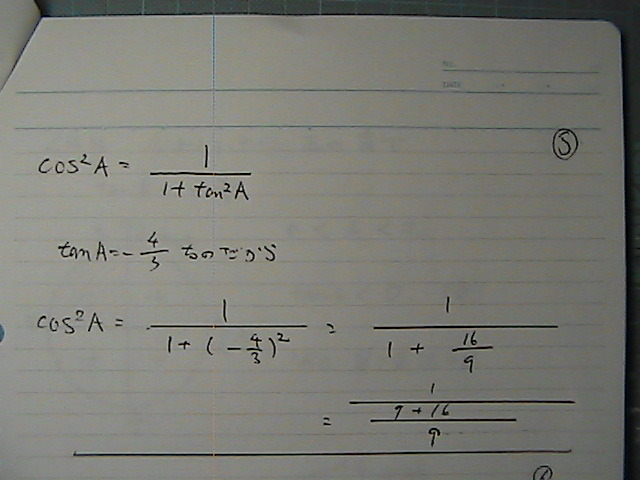
��
���ӂ́@���[�g�ɂ��Ă��܂���
�������ɂȂ��Ă��܂��̂�
������
�R�T�C���́@�����������@���߂�
�킴�Ɓ@�v���X�@�}�C�i�X�@�o�����Ă�����

�pA��
���Ł@���@������
�^���W�F���g�́@���̒l�Ɂ@�Ȃ��Ă�
�^���W�F���g���@�O����@�́@�͈͂�
���ɂȂ�̂�
���ی�
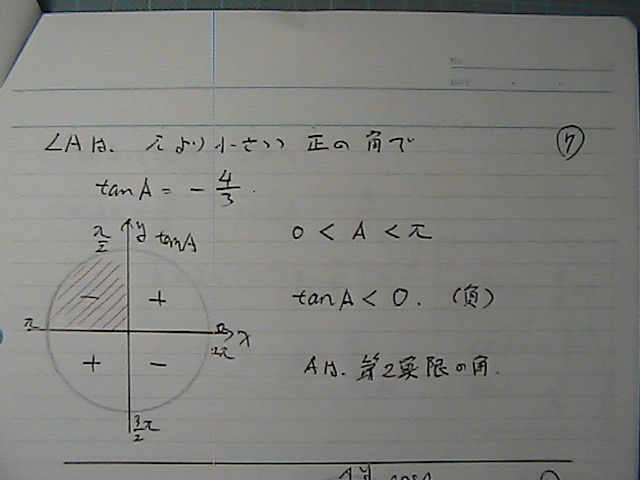
�Ƃ����킯��
���o���ė����@�R�T�C����
�����ׂ��
���ی��́@�}�C�i�X�́@��
�R�T�C�����@�ł��
�^���W�F���g��
�T�C���@�R�T�C���@�Ł@�\����
�����Ɂ@�R�T�C�����@�|�����
�T�C���ɂȂ�����
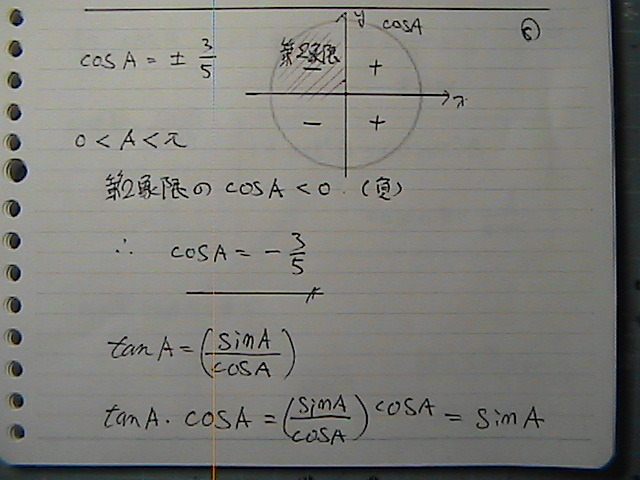
�����܂ł�
�^���W�F���g����
�R�T�C���@�Ɓ@�T�C���@�́@A���o�ė���

����
�R�^���W�F���g�@����
���x��
�R�^���W�F���g�́@���������́@�����ۂ�
�R�Z�J���g
�R�Z�J���g�́@�T�C���ɂ���������
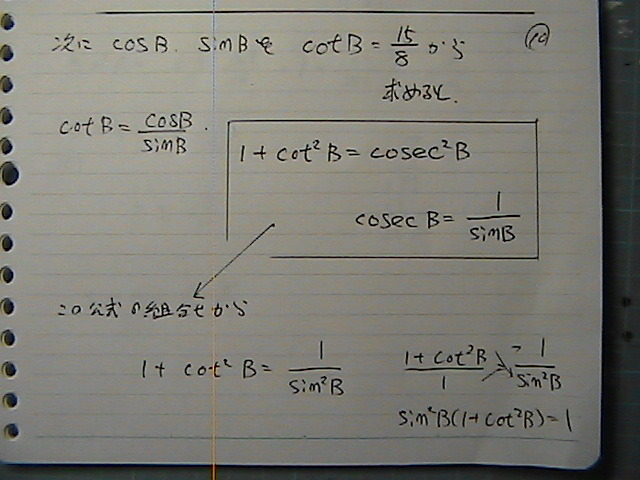
�T�C������
�܂����Ă�
�T�C���́@�������ŏo���Ă���

�킴�Ɓ@�}�ɂ��Ă�����
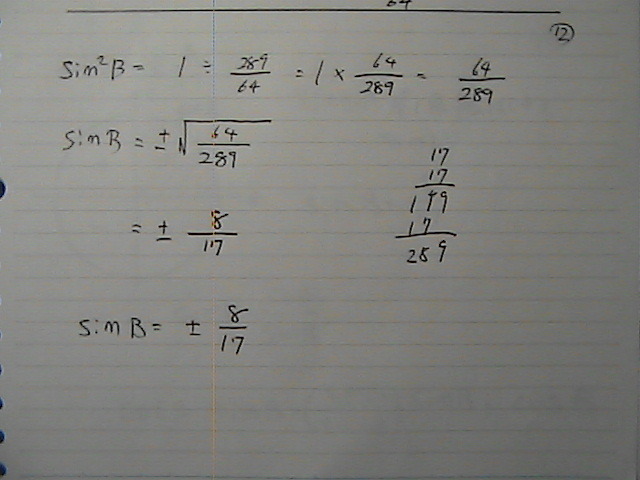
�pB��
�O�����
�R�^���W�F���g��
������
���ی���
�v���X�ɂȂ��Ă�̂�

�T�C���̑��ی��́@�v���X
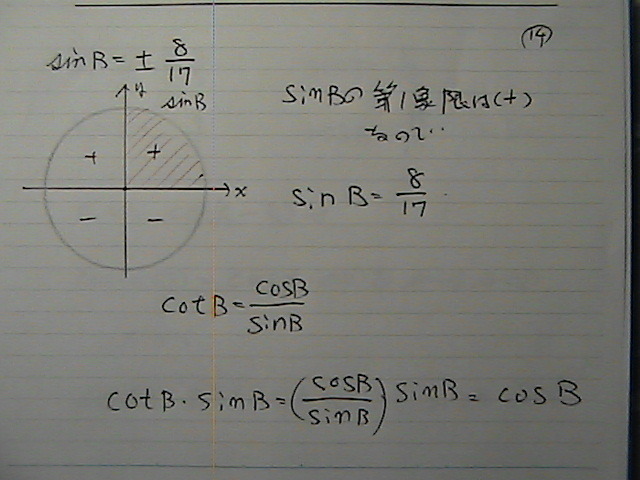
�R�T�C�����R�^���W�F���g����@�o������
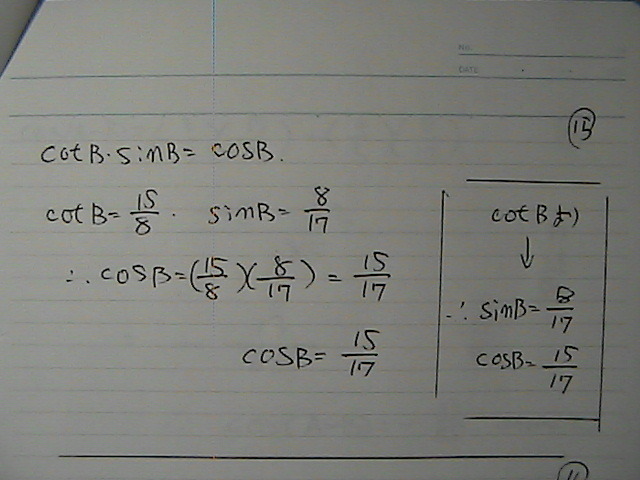
���@�藝�Ɂ@�������@���i���@�o��������̂�

����Ȋ�����
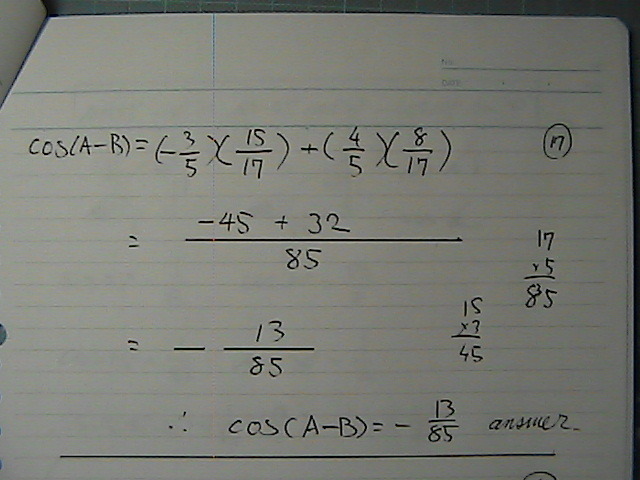
������@�g����
���i��
15�Ƃ��@�ł��Ȃ�������
���������킯�Ɂ@�����Ȃ�
�v�Z�ł���悤�Ɂ@�Ȃ��Ă��܂���

�킽������
�s��p�ł��̂�
���������@�����܂����Ă܂���

�ł��ł���
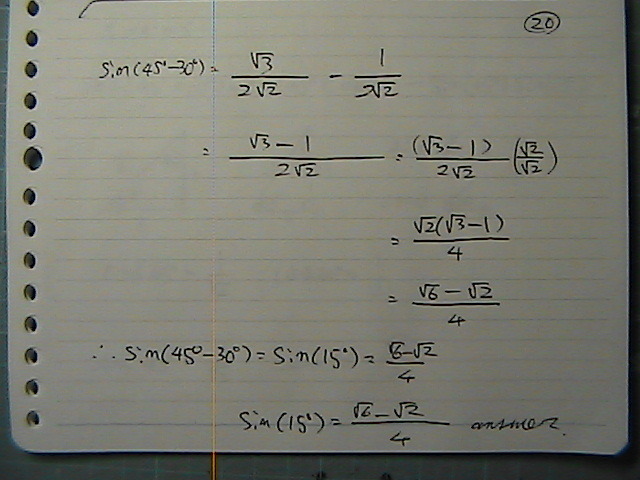
�����@����
�v�Z���

�Ԉ��Ȃ��悤��
����
�ł��邩�炳
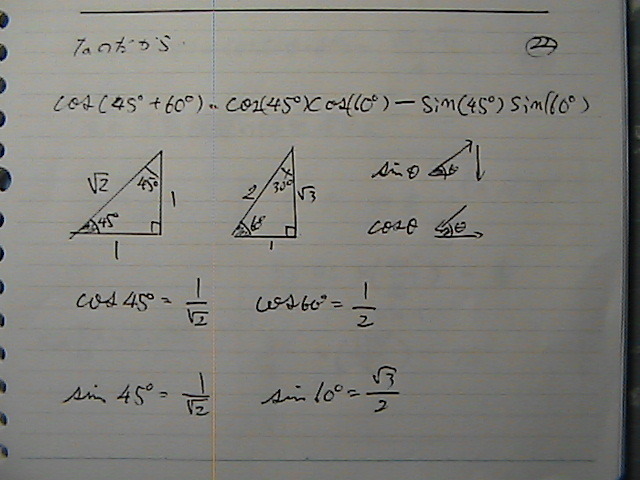
�ԈႤ�Ɓ@�Ԉ�����Ⴄ���炳
�܂�����Ȃ��悤�ɁE�E�E
�Ԉ���Ă�Ƃ���
�����������Ă�Ɓ@�܂�����

���W�A���Ł@�łĂ��Ă�Ƃ���
�Ε��̂P�W�O�{
�Ł@�x
�t�́@�P�W�O���̃p�C�Ł@���W�A��

�������@�R�R�炢������
�o����

�L�����̌v�Z��
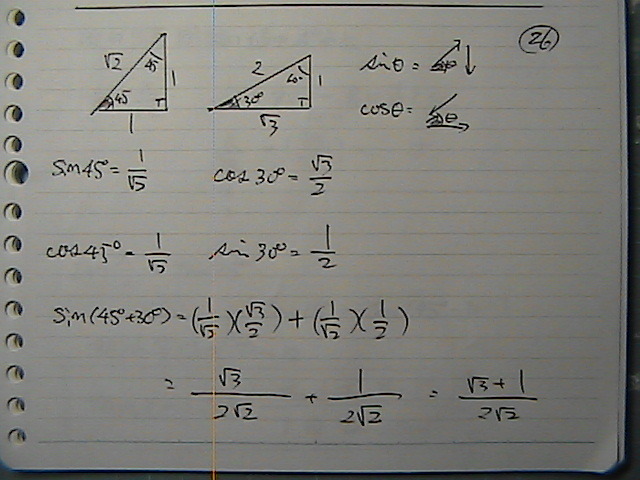
�Q�p�^�[���@���邯��

�^���W�F���g��
������������

���́@�s��p�Ȃ̂�
�}���@��������イ�����܂�
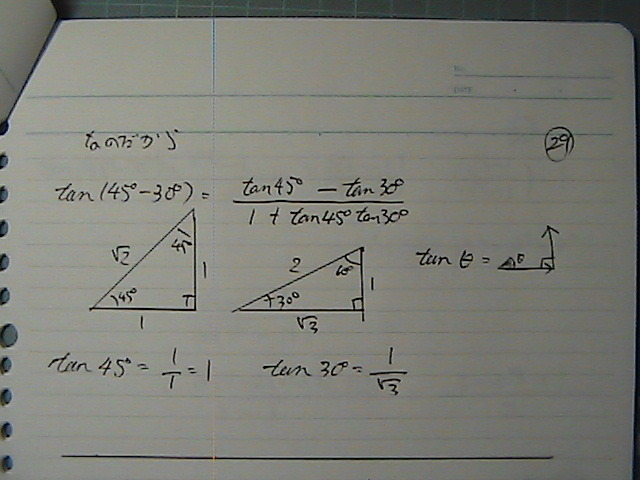
�L�����́@�Q�p�^�[���߁@��
�V�b�J���@�o�ė���
���K���ł��Ă��܂�
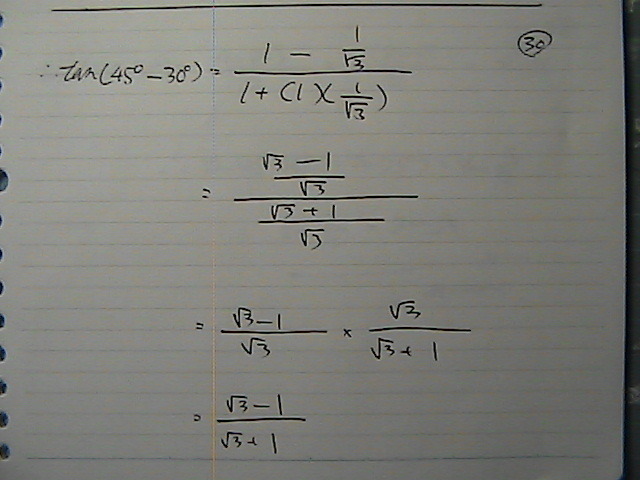
�v�Z�́@����Ȃ̂�
����@���Ɂ@�����@�ʂ�Ȃ���
�����܂���
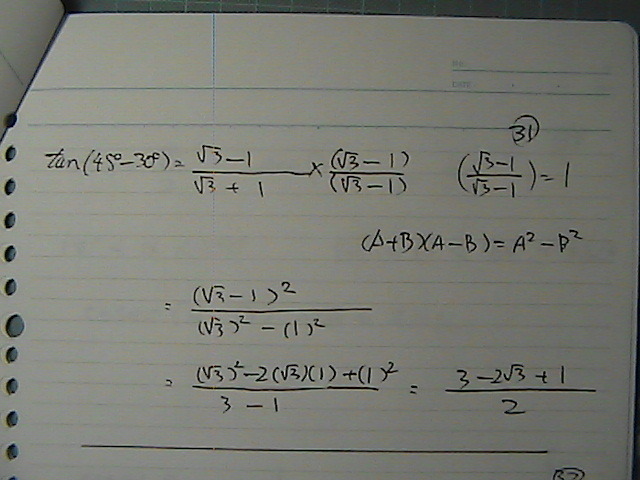
�����́@����Ȋ�����
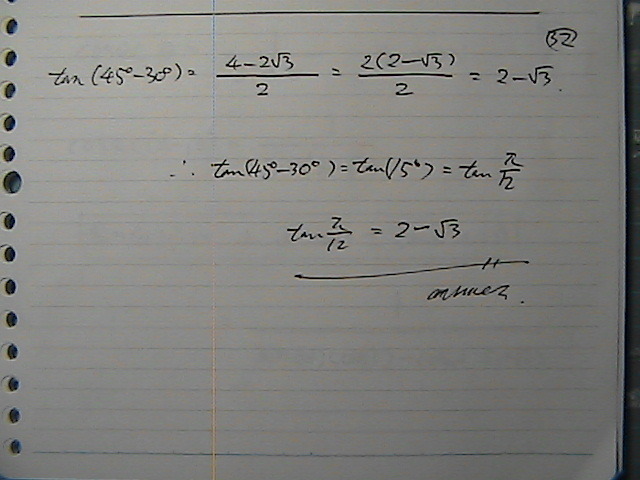
��
���x��
�������́@�n�߂Ɂ@������@�ޑ�
�R�Z�J���g��
���@�藝�́@������
�o�ė��ĂȂ��̂�
����Ȃ��Ƃ����܂��ʂ̂�

�H�삵��

������@�T�C����������
�R�^���W�F���g�Ł@���Ă邩��
���������Ɓ@�R�Z�J���g���@�g�ݍ��킹��

�T�C������
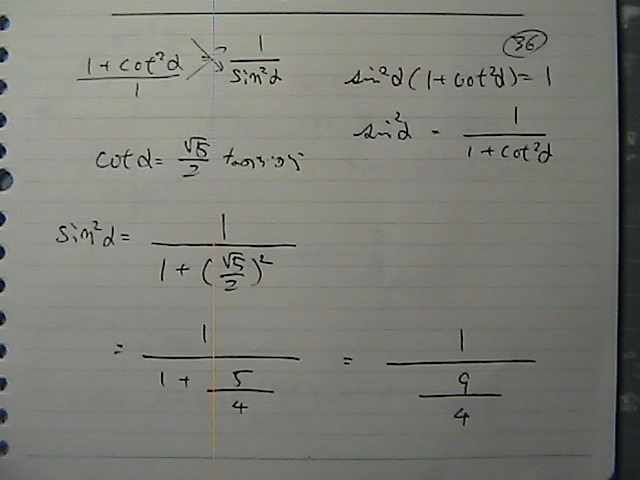
�O�p���́@�������@�ς�邱�Ƃ�����̂�
�v���X�}�C�i�X���@�c����悤��
�����������߂�

���́@��O�ی��̊p�x�Ȃ̂�
�T�C���̑�O�ی���
�}�C�i�X
�T�C�����@�ł��
�R�^���W�F���g�ɂ������킹��
�R�T�C��

�T�C���@�R�T�C���@�������@�o��

���x�́@���̕���
�Z�J���g��
�����
�R�T�C���́@�t��������

�Ђ�����Ԃ���
�T�C���̕���
������������
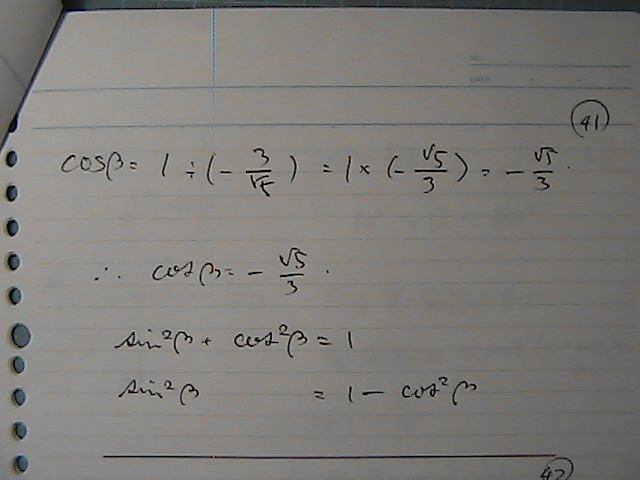
�܂����Ă�
�v���X�}�C�i�X���@�c���@�`��
�����������߂�
�x�[�^�p��
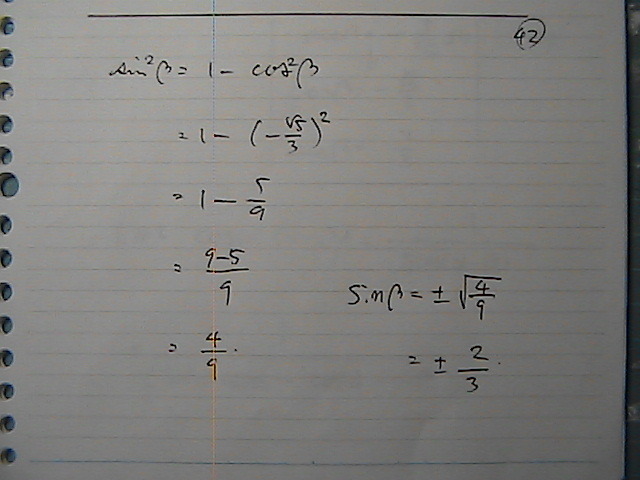
�x�[�^��
�@
���ی�������
�T�C���́@���ی��́@�v���X

�����̃T�C���@�R�T�C�����@�łĂ����̂�

�R�Z�J���g�́@���@�藝�Ɂ@�������
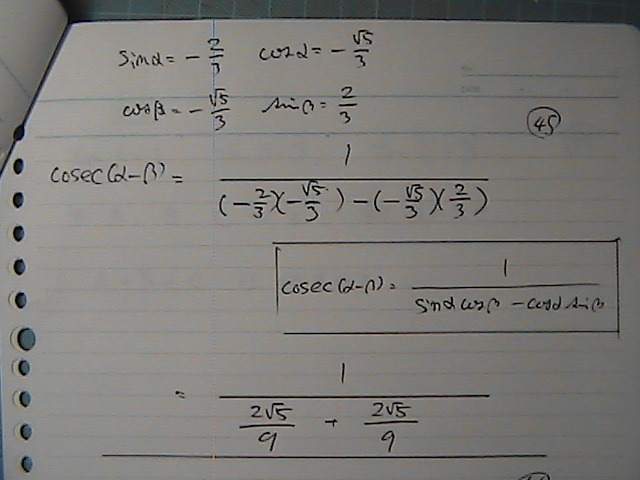
����Ȋ�����
���̂ł���
���t�́@�\�����Ă����̂�
�����Ɓ@���܂��Ȃ肽�����̍��ł�

�Ō��
�����@�ǂ�ł���������
�^���W�F���gA=1
�^���W�F���gB=2
�^���W�F���gC=3
A,B,C,���@���́@�s�p�̎�
A+B+C�́@���x��

�^���W�F���g��
���@�藝��
���������邩��
������
�Ղ炷�@�܂��Ȃ��@�@�@�܂��Ȃ��@�v���X��
�Ђ��������@�݂����Ɂ@�킴�Ƃ�����
�C���[�W�Ł@�������@�i�@�G�݂����Ɂ@�o���Ă��܂��@�j
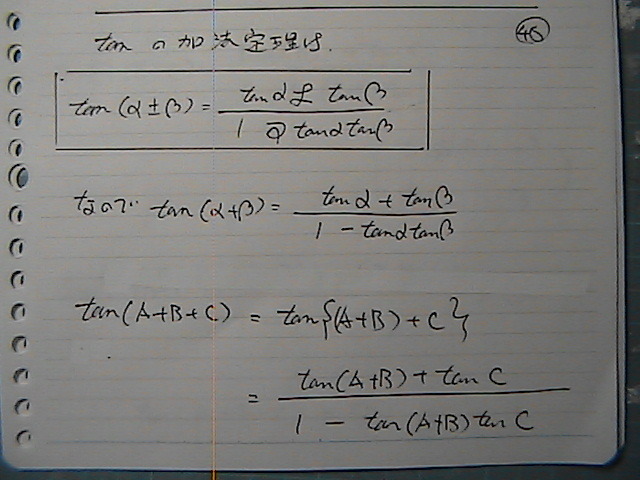
�s����
�������@����q�ɂ���
���@�g����
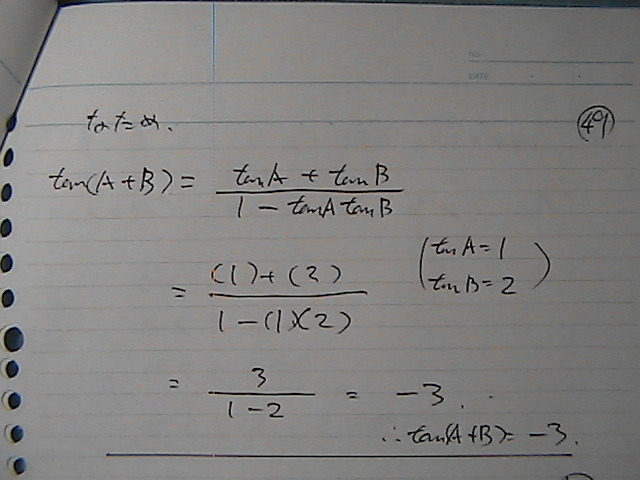
�����́@���O�Ȃ�
������ĂȂ�
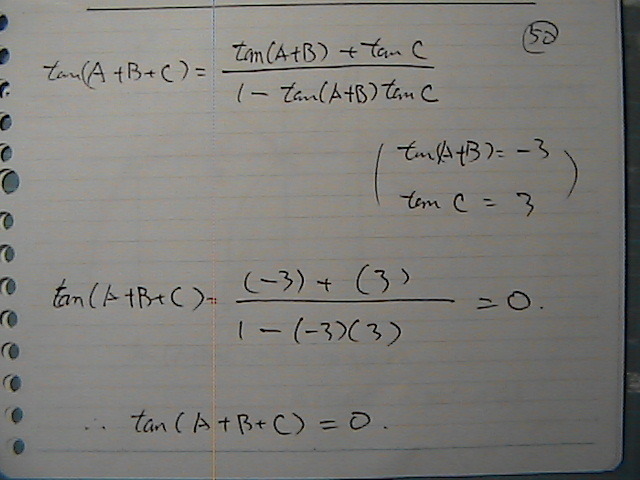
�p�x��
�������킹���
0�@���@A+B+C�@���@270

�^���W�F���g�́@�����́@������
�O���t���@������
���́@���������
�O�@�̂Ƃ����@������
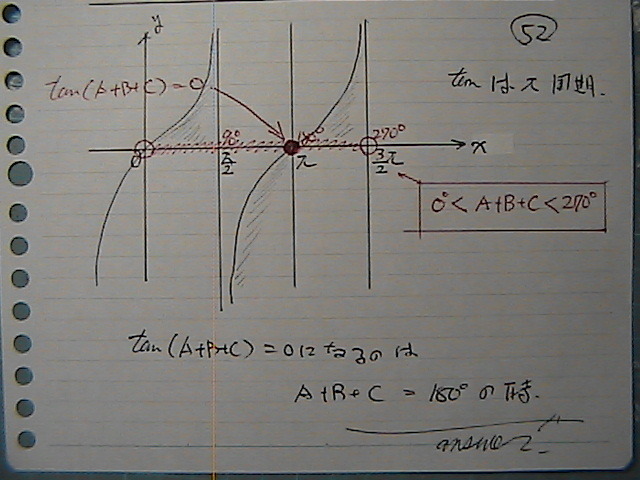
�P�W�O�x
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�O�p���̒l�Ɋւ��܂��Ăł���
���Z�@�́@�Q�N�̎�����������
�P�N����@������������@�Z���Z��
���P�������������̂�
��
�V�ے��Ƃ��@���낢��@���������Ă���
�Q�N�̓r���܂�
���������@�����Ă����������@���Ƃ�
�v���o���Ă��܂���
��������
�o�����������
�o�����Ȃ��Ƃ���
�E�E�E�E�E
�ǂ������
�R�R��@����
�����́@�X�y���́@���K���@�����
�H�H
�悭��������
����@�����@�o����
�n�C�@�^���W�F���g�@�R�^���W�F���g
���ꂪ�@�^�����Ă�Ƃ�
COS�iA-B)�@���@���߂Ȃ���
����Ȋ�������������
����Ɂ@���ǂ���
���@�藝�̌����ł�
COS�iA-B)�́@�l��
tan
cot
�@
����͒��ڂ́@�����Ȃ̂�
�pA�Ɂ@�ւ��Ắ@�@�^���W�F���g����
�pB�Ɂ@�ւ��Ắ@�@�R�^���W�F���g����
�\���]���@�T�C���@�R�T�C�����@���߂Ă��܂���
�܂��@A��
tan
����@sin cos���@���߂���
�^���W�F���g�́@����������
�Z�J���g�@��悪�@���Ă�̂�
�Z�J���g���@�R�T�C���@���g����
�R�T�C���@���́@�`�ɂ���
�������Ă�@�^���W�F���g���@�����ɂイ����
��
���ӂ́@���[�g�ɂ��Ă��܂���
�������ɂȂ��Ă��܂��̂�
������
�R�T�C���́@�����������@���߂�
�킴�Ɓ@�v���X�@�}�C�i�X�@�o�����Ă�����
�pA��
���Ł@���@������
�^���W�F���g�́@���̒l�Ɂ@�Ȃ��Ă�
�^���W�F���g���@�O����@�́@�͈͂�
���ɂȂ�̂�
���ی�
�Ƃ����킯��
���o���ė����@�R�T�C����
�����ׂ��
���ی��́@�}�C�i�X�́@��
�R�T�C�����@�ł��
�^���W�F���g��
�T�C���@�R�T�C���@�Ł@�\����
�����Ɂ@�R�T�C�����@�|�����
�T�C���ɂȂ�����
�����܂ł�
�^���W�F���g����
�R�T�C���@�Ɓ@�T�C���@�́@A���o�ė���
����
�R�^���W�F���g�@����
���x��
�R�^���W�F���g�́@���������́@�����ۂ�
�R�Z�J���g
�R�Z�J���g�́@�T�C���ɂ���������
�T�C������
�܂����Ă�
�T�C���́@�������ŏo���Ă���
�킴�Ɓ@�}�ɂ��Ă�����
�pB��
�O�����
�R�^���W�F���g��
������
���ی���
�v���X�ɂȂ��Ă�̂�
�T�C���̑��ی��́@�v���X
�R�T�C�����R�^���W�F���g����@�o������
���@�藝�Ɂ@�������@���i���@�o��������̂�
����Ȋ�����
������@�g����
���i��
15�Ƃ��@�ł��Ȃ�������
���������킯�Ɂ@�����Ȃ�
�v�Z�ł���悤�Ɂ@�Ȃ��Ă��܂���
�킽������
�s��p�ł��̂�
���������@�����܂����Ă܂���
�ł��ł���
�����@����
�v�Z���
�Ԉ��Ȃ��悤��
����
�ł��邩�炳
�ԈႤ�Ɓ@�Ԉ�����Ⴄ���炳
�܂�����Ȃ��悤�ɁE�E�E
�Ԉ���Ă�Ƃ���
�����������Ă�Ɓ@�܂�����
���W�A���Ł@�łĂ��Ă�Ƃ���
�Ε��̂P�W�O�{
�Ł@�x
�t�́@�P�W�O���̃p�C�Ł@���W�A��
�������@�R�R�炢������
�o����
�L�����̌v�Z��
�Q�p�^�[���@���邯��
�^���W�F���g��
������������
���́@�s��p�Ȃ̂�
�}���@��������イ�����܂�
�L�����́@�Q�p�^�[���߁@��
�V�b�J���@�o�ė���
���K���ł��Ă��܂�
�v�Z�́@����Ȃ̂�
����@���Ɂ@�����@�ʂ�Ȃ���
�����܂���
�����́@����Ȋ�����
��
���x��
�������́@�n�߂Ɂ@������@�ޑ�
�R�Z�J���g��
���@�藝�́@������
�o�ė��ĂȂ��̂�
����Ȃ��Ƃ����܂��ʂ̂�
�H�삵��
������@�T�C����������
�R�^���W�F���g�Ł@���Ă邩��
���������Ɓ@�R�Z�J���g���@�g�ݍ��킹��
�T�C������
�O�p���́@�������@�ς�邱�Ƃ�����̂�
�v���X�}�C�i�X���@�c����悤��
�����������߂�
���́@��O�ی��̊p�x�Ȃ̂�
�T�C���̑�O�ی���
�}�C�i�X
�T�C�����@�ł��
�R�^���W�F���g�ɂ������킹��
�R�T�C��
�T�C���@�R�T�C���@�������@�o��
���x�́@���̕���
�Z�J���g��
�����
�R�T�C���́@�t��������
�Ђ�����Ԃ���
�T�C���̕���
������������
�܂����Ă�
�v���X�}�C�i�X���@�c���@�`��
�����������߂�
�x�[�^�p��
�x�[�^��
�@
���ی�������
�T�C���́@���ی��́@�v���X
�����̃T�C���@�R�T�C�����@�łĂ����̂�
�R�Z�J���g�́@���@�藝�Ɂ@�������
����Ȋ�����
���̂ł���
���t�́@�\�����Ă����̂�
�����Ɓ@���܂��Ȃ肽�����̍��ł�
�Ō��
�����@�ǂ�ł���������
�^���W�F���gA=1
�^���W�F���gB=2
�^���W�F���gC=3
A,B,C,���@���́@�s�p�̎�
A+B+C�́@���x��
�^���W�F���g��
���@�藝��
���������邩��
������
�Ղ炷�@�܂��Ȃ��@�@�@�܂��Ȃ��@�v���X��
�Ђ��������@�݂����Ɂ@�킴�Ƃ�����
�C���[�W�Ł@�������@�i�@�G�݂����Ɂ@�o���Ă��܂��@�j
�s����
�������@����q�ɂ���
���@�g����
�����́@���O�Ȃ�
������ĂȂ�
�p�x��
�������킹���
0�@���@A+B+C�@���@270
�^���W�F���g�́@�����́@������
�O���t���@������
���́@���������
�O�@�̂Ƃ����@������
�P�W�O�x
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 23:41| ��l�̂��ї��Ƃ��@
2018�N03��23��
23023�@��l�̂��ї��Ƃ��@���x�@�����x
�J�̓��́@�X���[���C�t�̕���
���̂ł���
�ق�̏����@���͂��������Ă��܂��܂���
������Ƃ��@�ˁ@�Ƃ������
�����́@�Ƃ����@����
�O�p�����\�肾������ł���
�{����
�ˋ�̃L�����N�^�[
��̎В����@���}���������܂���
���[�@���C�Ł@����Ă邩
��������
���H��
��������Ă���Ă������炳
�T�C�{�[�O�@�O�O�X�@���������H
��[�@����Ȃ��Ƃ́@�Ȃ��Ǝv���܂���
���������Ƃ�
�����łƂ�
��
�n�܂�n�܂�
��������@�^������@�_�̍��W���ł���
�����́@���Ɂ@�Ȃ��Ă����
�������́@����
���i���[�g���@�j�@���@���́@�Ȃ�@��������
�����ځ@�g��Ȃ��Ł@�d��g�������Ă�
���ꂪ�ł���
���́@�����@���@���Ł@
�����́@���̂Ƃ����@���������
���x�́@�ω����ɂȂ����
�Ȃ@�����Ă��Ȃ������̂�
�łł���
���̓��_��
���X�@�������@�ς��邱�Ƃ��@����炵������
����Ȃ��ƒN���@���߂���
���̂ł���
������́@�����W������킷�@t�̎���
�R�����Ɂ@�Ȃ��Ă���
��肪������
�����W�́@t�Ɋւ���@�����������
��������
�i�P�j�@�o���@���Ă���@�O�D�T����́@���x
�i�Q�j�@�o�����Ă���@������Ɂ@�������ς�邩
�i�R�j�@�T���܂łɁ@�ǂꂭ�炢�@��������
�������E�E�E�E�̎���
���Ł@���������
���x�̕ω����ɂȂ����
����[�@
���̎��Ɂ@����0.5�@���@���ꂽ��
�������
�d��@������
����́@�����@�����Ă������肾����
���ꂪ�@�����Ă��炳
�ȂɁ@�E�E�E�E
4.5��
�P�ʂ́@���[�g��/��
�i�Q�j�@��
�Ł@�����ς��Ă���@���߂ā@�������@�ς���̂�
�����ォ�@
�������ā@���x�́@�����@�o�Ă邩��
���[
�ӂ�������������
�Ȃ�������
�����グ��Ɓ@���_�Ł@��������@���x���@�O�ɂȂ���
�݂����Ȃ��
��������
�����炳
�ӂ������������̎���
V���[V0��恁�@�Q�@���@S
�݂�����
���@��9.8��/���b���b
S�@�́@�ړ�����
�����x�@�����Ł@�����グ���
�����[�g��
�@
�オ�邩�@�݂�����
��
�Ȃ���
���̂�
V���̎����@�O�ɂȂ�Ƃ���
�v�Z������
�������@�Q�łĂ�������
�n�߂̕�
�P����
�i�R�j�@��
�T���܂łɁ@�������@����肾����
�s�����藈���肵�Ȃ���
�����ɂł��@����������ɂȂ���Ă̂�
�����܂ł́@�����Ȃ�����
�U�����炢����
�r����
�������@�ς���Ă����
�������̎���
�������ɂ�����@���́@����ꏊ
������
�܂�Ԃ��̕���
�B�ꂿ���Ȃ��悤��
�������@�ς��Ƃ���
�|�C���g��
�T���܂�
0,1,2,5�A
���܂�
���́@���W���@�v�Z����
0�A�@5�A�@4�A�@85�A�@�ɂȂ�������
�n�߂́@�O����T�@�́@�T
��������
���������
�������ʂ́@�T�|�S
���@
���������
�S����@�W�T�}�f�@������������
81
5+1+81�@���@87
���́@�d�Ԃ́@�^�]�肳��́@���
�ł���@�}�ɂ́@�~�܂�Ȃ�
�u���[�L��������
���b�@�������ā@�����[�g���@�i��Ł@�~�܂邩
��Ȃ��Ȃ���Ɂ@����
����������
�����@t�̎��ŁE�E�E�E�E
���́@����
��
���@��������Ɓ@���x�̕ω�������
���ꂪ��
�~�܂�@���@
���ꂾ
�����̂����
�����ł�
�[��������
����30
�Ł@��@��Ɂ@�߂���
����t�̎��Ɂ@�R�O���@�����
�d����@����������
405
��[�[
���̓d�Ԃ́@���H
��@���@���}�Z��
�����́@�����ٌ��w����Ȃ���
���[�@����������
���́@��ʔ�����
���������Ȃ����Ƃ����Ȃ��[
���x�͂�
���_���@������
���[�@������
���s���Ȃ���
�Ђ���[�@�������炪
�������炳
�Ȃ@�����l���Ă邩
����͂�
�ړ�����_�́@�������Ɋւ��鎮��
�Q�����
�߂�ǂ�����
����Ƃ��Ă���
���[�@��������
�ӂ�
����[�@���������Ⴈ
���́@�R��̂��@
�R���@�O�ɏo��
�R×�Q�Ɂ@
��낪�@���܁@���́@�R�肾�����̂��@
�Q��ɂȂ��ȁ@�ŁE�E�E�E�E�E�E
�Ȃ��炳�E�E�E�E�E
�E�E�E�E
��
���������ǁ@�����Ȃ��Ă����́H
��������@����
���́@�܂��@��ɂ����
�������ς��Ƃ�������
���O�ɂ����
����́@�R���ォ
�i�Q�j�@M�́@�����
�ʒu���@���߂�
����́@���̂����Ȃ�
����͂�
�̂ނ���
�k��
�k�C����w�́@�������ɏo�����Ƃ��������
�����炳
���݂�
���̂܂܁@��̎����@�����ā@�Q�Ŋ�����
���_�݂����ɂ����������
������@�������v��������
�ǂ�������
��
���́[
�����[�@�����₠��
��
�Ȃ�Ȃ�
�܂�
�������������@�U����
��������
��
����M�_���@�S�����U�������
�ǂꂭ�炢�@���������ƂɁ@�Ȃ邩
���́@M�̎���
M�̍��W�́@���̊���
���Ł@�����������
����́@�Q��@�������@�ς���
��������
����[�@�������݂�����
�|�C���g��
�}����
�d����@��������
���ׂ�
��́@�v�Z��
��������
���R���\����
���ȏ������̂܂܁@�d��@�ł���̂�����炵����
�����������@������
���[�[�[
���������ƂȂ�����Ȃ��[
���̔ԑg�́@�t�B�N�V�����ł���
�E�E�E�E�E�E�E�E�E
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 13:41| ��l�̂��ї��Ƃ��@
2018�N03��22��
2B7001�@��l�̂��ї��Ƃ��@�i�@���P����̑����@���Q�O�p���@�j
�O�p���̕��K�Ȃ�ł���
�~��`����
���a�@OP�@�̕\���p���@��
OP�@�́@�����@���@��
�_P�̍��W���@�i���A���j�@�Ƃ����
���ꂼ���
�O�p���́@���Ɓ@���@�@���@�Ɓ@���@�@���@�Ɓ@��
�Ł@�\���ŗ���
�����̎O�p����
�t���̌���
���݂̌���
�����̌���
��ʊp�̌���
�����@��������イ
�ςȂ��Ƃ��@�����Ă�
���p�@�]�p�@��p�@�̌���
����Ȃ̂��@
����������i�C�X�J
��
���Z�Q�N�Ɂ@�Ȃ�������
�L���ł���
�L���́@��������Ă��܂�
��
��N�Ɂ@�Ȃ�O��
�t�x�݁@�܂��́@���Ƃ���������
�H�H�H�H
�e���p
�����́@���K
�����@�Q��@�v�Z����
�o���Ƃ�����
���k������������
����Ă����悤��
�������킹�@�ł���悤�Ɂ@
�������@����������
�킩��Ȃ�������
��������
��������������
�������@������������@
���Ă邩��
�������@����悤��
����
���T
�ȒP���Ǝv������
�^�C��
�b�ƈႤ
��肩�����@�����킗
�킩��ˁ[
������@������
�W���[�N�Ł@�����悤�Ǝv���Ă��
�������́@�����̃��[�����@Y����
����
�i�Q�j�͂��@�ł���������
�ق�@�Ȃ�ł���
�E�E�E
�ł���ȁj���[
���������@�W�J����
�����̌������@����Ă���
�����@�ȒP�Ɂ@�Ȃ��Ă�����
����悠����
�ȒP�Ɂ@�Ȃ��Ă�����
����@�悪�@�����Ă���
���[�@�����@�ł������R
�\���ʂ�
�����́@�P
�i�P�j�@�́@�N���@�ł���
���ԏI��
������
���́@�T
�i�Q�j�́@�ł��邾��
�i�P�j�@�ł������̂�
�N�����Ȃ���
�\�K����������
���O�@�Q�l����������
�ł���Ƃ�������
�o���Ă�����̂�
�i�@���̎q�Ɂ@���Ă�@�`�����X���@������̂Ɂj
�V�ے��Ŕ��������������
�����ĂȂ�
�ȂɁ[�@�����ĂȂ��@�i�@���ĂȂ��Ȃ��[�j
�i���߂��Ȃ��[�j
�n�߂�
���q�́@����́@�ǂ�����
��p�̌�����
sin��
��ԉE�́@������@��p�łł��邩��
��������
�}�C�i�X�Ł@�����肾����
���p���@�������
��p�����
-cos��
��������
���@�}�C�i�X�@�Q�@
���@�}�C�i�X�@3/2�@�����
�ǂ�����
���������
���߂�
����͂�
�܂������ĂȂ���������
������
���[�[�[�[
��/2�@�@���@�@�}�@�@��
�ɂ���
�����@�����̎��́@���̂܂܁@��������
�����@��̎��́@���L�����@�]���Ɂ@�ς���
��
���@�ɂ������
�������@���ׂȂ��Ắ@�����Ȃ���
���̂܂܂̎��́@���̂܂�
���L�����@�ς����Ƃ���
���́@���L����
���a�̈ʒu���@�ǂ��Ɂ@���邩��
�v���X�@�}�C�i�X���@���肷��
���@-�@�Q�@�̕�����
������
��/2�@×�@���@�@�}�@�@���@�̌`��
���邾��
��������Ɓ@���̂Ƃ��낪�@�S�ɂȂ邩
����������
���L���́@���̂܂�
sin �ˁ@sin
���a�̈ʒu��
sin�́@���ی�������
�Ղ炷
��
sin��
��������
��
���[
��-3/2��
��/2�@×�@���@�@�}�@�@���@�̌`��
���邾��
�����R
�������
�]���Ɂ@�ς����
�����炳
������
�\��
�@
�o���ĂȂ��Ƃ����Ȃ�����
�ӂ�فE�E�E�E��
��������
���[�[�[���Ă������炳
�o��������������ǂ�
sin��cos�ɂȂ���
cos�@��
�����́@���a�̈ʒu
���̊���
sin������
sin�́@���ی��́@�v���X
��
��������
�v�Z������
����ȂɁ@�ȒP�ɂȂ��������
��
������
���i�@tan cot�@�́@���܂�o�ė��ĂȂ���
�v�Z�~�X�������Ȃ�����
�}���@�܂����Ă�������
���������
�]�p�Ɓ@��p��
-cos��
sin��
���@�}�C�i�X�@���Y���
�}�C�i�X
cos��
�}�C�i�X�@sin��
��@�@����������
�Ȃ�Ȃ���
������
�F�l�́@N����
�}�C�i�X�@���Ƃ��Ă܂���
���[
�悭�C���t������
��
�߂ł���
1
�L�����@�N�����Ƃ����
�ޑ�@�s���Ă݂܂��傤
�R�Z�J���g���@�T�C���ɂ���
�T�C���@�R�T�C���@�^���W�F���g
�]�p�̌���
�]�p�̌���
��p�̌���
��p�̌���
�[��
����
�x�ŏ����Ă��邩��
���W�A���Ɂ@������
��p�̌���
�]�p�̌���
��������
�v����������
��/2�@×�@���@�@�}�@�@���@�̌`��
�����@�����̎��́@���̂܂܁@��������
�����@��̎��́@���L�����@�]���Ɂ@�ς���
�����́@
���̂܂܂̎��́@���̂܂�
���L�����@�ς����Ƃ���
���́@���L����
���a�̈ʒu���@�ǂ��Ɂ@���邩��
�v���X�@�}�C�i�X���@���肷��
���̎O�p���́@cos������
cos�́@��l�ی��́@�v���X
�ς�����@���L���V�[�^�Ɂ@�v���X��
sin ��
3/2�|����
���x�́@sin
��/2�@×�@���@�@�}�@�@���@�̌`��
���̂Ƃ��́@�R
�������
���L����
sin��cos
���a�̈ʒu��
����sin���̕�����
�l����
��R�ی��́@�}�C�i�X
�}�C�i�Xcos ��
�^���W�F���g��
����������
�ǂ����́@�����Ł@�s������
�ʕ�����
���q��
�R�T�C���Q��V�[�^
��
�P
�����́@�ؖ�
����
���q���@��t�ۂЂ낱�@�́@�ؖ���
�f��قŁ@���f����Ă���
�����@�^�o�R����������
�F�l�́@�s�����@�������Ă��܂��Ă�������
�F�l��
�f����@�����������
�������炪�@������
����t����
���Ƃ����[�[�[��
�E�E�E�E
���Ƃ��Ȃ�E�E�E
�E�E�E
���E�E�E
�E�E�E
�b���@���ɖ߂���
��������
�E�ӂ̕��Ɂ@�b���@�ڂ��Ă���
�C�R�[���@����
�O�p����
�ꍇ
�W�J�����
���i�Ɓ@������@�`��
�����Ă��܂�
�Ȃ̂�
�t�Ɂ@������������Ƃ���
�C���t�����̂�
�Y��Ă���̂�����
������Ɓ@���ʓ����@�v�Z���Ă݂�
�^�̊|���Z��
���ԓ���ւ���
����Ȋ�����
���Z�̍�
�O�p����
�����́@�D���ł�����
���ї��Ƃ��́@����
���Q���ʂ�
���P�́@�܂��@����ĂȂ����ʂ�
�������Ă��܂�
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 11:50| ��l�̂��ї��Ƃ��@
2018�N01��02��
��l�̂��ї��Ƃ��@25007�@�P�ʍs��
�J�̓��́@�X���[���C�t�̕���
�P�ʍs��
�ƌ������̂������ł���
����s��@A�ɂł���
A�́@������@�|���Ă�
A�́@�E����@�|���Ă�
�������@�����ɂȂ�
�������@�����́@A�ł�
��ʂɁ@�s���
�|����@�������@����ւ���
�������@����Ă��܂�
���@�Ȏ����@������
��
�P�ʍs���
���ۂɁ@�|���Ă݂�ł���
A�́@�����炩�����Ƃ����@A
����
A�́@�E������@�|���Ă݂��i�C�X�J��
�P�O�����@����Ă���ȁ`
�������̘b�ł�
�łł���
����ς�
�����́@A
�����s���
���ォ��@�E����
�Ίp�������@�S�ĂP
���̑����@�S�ĂO�@��
�s���
�P�ʍs��ƌ�����
�C�ӂ̃x�N�g�����@�����
�@
�����@�x�N�g����
�ϊ����邱�Ƃ�
�P���ϊ��@�ƌ�������
���ۂ�
����Ă݂��
����Ȋ�����
������@���܂�
���
�ǂ�ł���������
�i�P�j�ł���
�܂�
���́@�v�Z�ł���
�Ł@�������@��������
�|�P�́@�����{�ɂȂ��Ă�Ɓ@�l����
�[�ł������
�[�iE)�@
�i�Q�j��
�܂��@���i���@���낦��
���ꂭ�炢�ł�������
E�Ƃ��@J�Ƃ��́@�O�́@�����́@�����{�Ɠ���������
�͂��Ă��钆��
��̓I��
����������ł���
�����{�Ȃ��
�W�����m�Ł@�v�Z����ł���
������@���i��
E�́@����
E�ɂȂ���@�m���߂Ă�����
E���́@E
J���́[E
���@���ꂼ��@������Ă���
�����ǂ����́@���Z�́@�����Ȃ̂�
������@
C�́@�v�f
����
�X��
���i���@�v�Z���邶��i�C�X�J��
�ق�ƂɁ@�Ȃ��Ȃ��[
���@�������̘b�����炳
��
������ė��܂���
�Ȃ�������i�C�X�J
����
�ǂ�ł��������Ăł���
�������@�P�C�Q�@���@����ł���
���ƌW���̊W
����́@���P�Ȃ���
�����������Ɂ@���[�[�[�Ɂ@�悭�o�ė��܂���
���炭����Ă܂����
�����ł������܂�
������
�������������܂���
����ȁ@���|�[�g���@���܂���
��G�c�Ɂ@�R�p�^�[��
���́@�R�Ԗځ@��������@�g���Ăł���
���̑O��
��ӂ��̎���
�W�J����
���ӂɏW�߂�
���Ɂ@���ā@�܂Ƃ߂��
���́@�Q����
���ƌW���̊W����
���������@�N�������
���������i�C�X�J
���P��
����Ɓ@������@���Ɂ@����
��������
�����
����������i�C�X�J
�����Ɂ@�ς���������ł���
�W�J����
���ɂ��Ă܂Ƃ߂�
�������́@�������Ɓ@���l������
�W�����@�Ђ����ł���
�œ����́@�ؖ�������
���Ӂ\�E�ӂŁ@�s���Ă݂�ł���
���{��
�����@���@�łĂ�������
������
�������@�W����r�@�Ł@�o���ė����̂�
����ł����
��
�s��́@�|���Z�́@������×�c����
�s��́@�����{�́@�e�����́@�����{
�s��́@�����Z�@�����Z��
�e�����́@�����@����
��
�����܂�����
�O
���ėp���ɂ�
����ȏ��������Ă�
�܂����̂�
�����@���������@����������
���������ā@�Ƃ�
��
���͂�
������Ȃ������̂�
���@���ƂɁ@�������Ă܂���܂���
�K�b�R��@�m�́@�Z���Z��
�l�m�ꂸ�@�ҕ��@���Ƃ�Ƃł���
���́@���k�@�Ȃ�����
�Y�݂Ȃ���
�O�i���Ă��܂�
��@���i�́@�ؖ��������Ƃ���
�łł���
�������@���X�Ȃ���
�J�j�@�H�ׂĂ�H
�������̘b�����炳
��
P�̂�
�����Ɂ@���ڂ��Ăł�
�コ
�ق��́@A�A�@B�A�@E�A�ɂ��@���ڂ��Ă݂��
C�x�N�g���ƌ����̂�
�l����
P=A-C
�����
�����̏ؖ��Ƃ�����
��������
�́@
���Ӂ\�E�ӂ�
�s����̂�
�܂Ƃ߂�
���́@C+B�@�@CB
�̂Ƃ���
���i���@���Ƃ�
CB�Ɂ@�X�e�[�Ƃ�����
�����肽����
�������̘b������
��
�����
��������
������������
CB��
����Ɂ@��������
������������
��
CB=BC�@�ɂ��@�Ȃ����
�����Ă݂��
➀�Ɂ@�߂���
����ł���
C+B�@�@CB�@�@�Ɂ@�������
�����{������
�����@�`���@��������
������
��������������
�Ł@��������@�ǁ[����
�Ȃ�ł���
�i�P�j��
���́@���������́@���ʂ��@���O�@�ɂȂ�
�ؖ������Ă��邽��
�g���܂��̂�
���l��
�������
���Ӂ\�E�ӂ���
��������
�������
������������
�i�P�j�̏ؖ����ʂ��@�g����
���Ӂ\�E�Ӂ��O�Ȃ̂�
���Ӂ��E�Ӂ@
�ؖ��I���
�@
�����ꂳ�܁`
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 16:14| ��l�̂��ї��Ƃ��@