2018�N05��09��
????? ��l�̂��ї��Ƃ��@�Ɍ��̌v�Z�@0/0�`
�J�̓��́@�X���[���C�t�̕���
���̋Ɍ��̋��ߕ��̖���
�O��
�ڂ����@�v�Z������ĂȂ�����
�悤�Ɂ@�v������
���ނ���
����Ă݂����Ǝv���܂���
�S�@�T�@�U��
��
�p�^�[����������
��
�Ɍ���
�����@����Ȃ��@a�Ɂ@�߂Â��Ƃ���
���i���j���@���Ƃ����l��
����Ȃ��@�߂Â��Ă����Ȃ��
���̋Ɍ��́@�l��
����a�@�̎��@���i���j�@���@���@�Ƃ�
Lim
����a�@�@���i���j����

����́@�v�Z����
���Ă��܂���
���p�^�[��������̂ł���
�����
�O/�O�@�`

0/0�`�̎���
�������Ȃ�@��
�������Ȃ�@�����Ȑ����@������
����ōs���Ă݂܂��傤

����
�����@����Ȃ��@�P�Ɂ@�߂Â��Ƃ�
�ꉞ�@�ڕW�l�I�Ɂ@�����P���@������Ă݂��
������@���q���@�O�@�́@0/0�`

������
���������ł�����������

�����������Ă݂܂���
����́@���|���
���q��
�����藝��
x���P�̎��@�O�ɂȂ��Ă��܂�����
�������������
�g�����@�Ƃ��@�g���Ȃ���
�W����������
�i���|�P�j�@���@�����Ɂ@���̂�����
�i���|�P�j���O�ɂ���@x�̒l��
�����
�R�������@�P�����@�Ŋ���������
��ԏ�́@�Q���@�Ł@�P���@�Ł@�萔�Ł@�]��@�́@�O
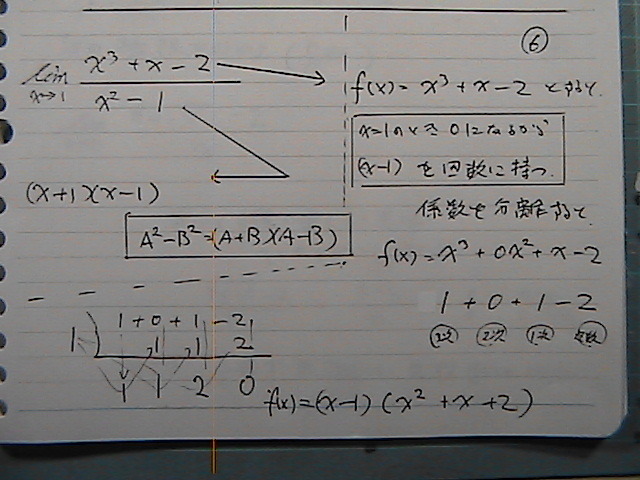
�ł���Ƃ���
�V���@�V��
������
0/0��Ԃ�E�����̂�
�����P���@�߂ł����@�������
�Ɍ��́@�Q

0/0�`�́@������́@�p�^�[����
���������@�����Ă�ꍇ
��͂�
x=�O�@���@�������
�ڕW�l�@�I�ȁ@�Ɍ����@0/0�@�`�Ł@�łȂ��̂�

���́@�l���@�ς����Ɂ@���ό`
×�@�P�{�Ȃ�@�l�́@�ς��Ȃ�����
�|����ׂ��@���𐔂��@���ꕪ�q�Ɂ@������

���[���́@��������
��������
����
������
0/0��Ԃ�E�o�����̂�
�����O���@��������
�Ɍ��l��
1/4

0/0�`��
�����@����Ȃ��P�ɋ߂Â��Ƃ��̖���
�P���@���������@����ł��@��������������ł�
�����P�Ɂ@�߂Â��Ă悭
�������@���@not= 1�@�Ȃ̂�����
�Ł@�i���|�P�j�@���@�Ă��܂���
�Ɍ��́@���̂��@�o����

0/0��Ԃ��@�E���Ă����
�����P���@�_�C���N�g�́@�������
�Ɍ����@���܂�B

�������@���܂��܂���
�ޑ�
�ڕW�l�ȁ@�Ɍ���
0/0�`��ԂȂ̂�
�������Ȃ��Ƃ����Ȃ���
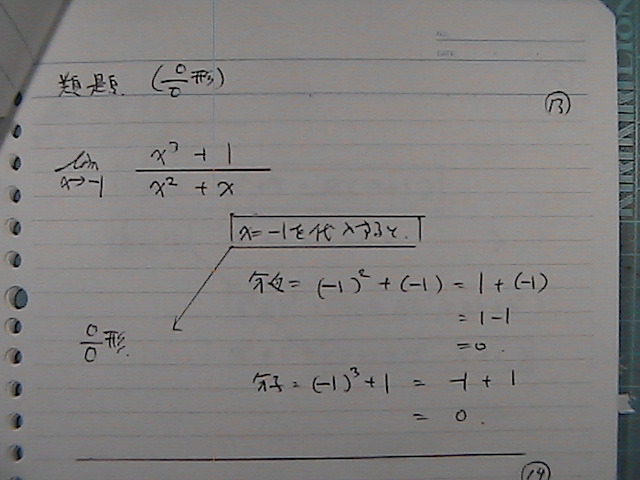
���������ł������Ȃ̂�

����́@x�Ł@��������
���q�́@�R��́@��������

�₭����Ƃ�
�V���@�V��
0/0��Ԃ�E��������
�����|�P���@�������
�Ɍ��́@-3

����
�܂��@�ʕ��@����i�C�X�J��
������@
�����́@�Ɍ��Ɂ@�Ȃ�Ȃ�
�O/�O�`

��������
�����@����
������
0/0��Ԃ��@�E�����̂�
�����O���@�������
�@
�Ɍ��l�́@-1

�C�}�n�@�p�^�[���@0/0�`�@�Ȃ̂�
������@0/0�`
�����
��������
����@���q�Ɂ@�Ⴄ���̂��@�����Ă�̂�
�Q��@
���ꂼ��́@���𐔂��@�����Ăł���

�܂�
����̕�
��������

���x�́@���q�̕�
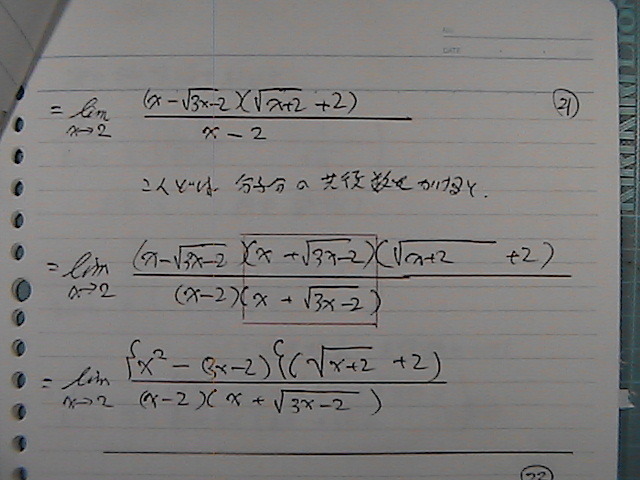
����Ɂ@���������@�������������
���ł���
0/0��Ԃ��@�E�����̂�
�����Q���@���
�Ɍ��l�́@1

����
�Ȃ�
���ϕω����̂Ƃ��́@�悤�ȁ@�`��
�����������@�ʕ�
���q�́@��������
���𐔂��@������

����
0/0��Ԃ��@�����Ł@�E��������
�����O���@�������

����Ȋ�����

����
�����u�Ԃ�
����@
�����
���O�@�́@�����@�́@�^�����O�@�Ȃ̂�����
��Βl�́@�Ƃ肠�����@�|���炸��
���̑O�ɂł���
���ό`��
���O�́@�v�Z�@�@���́@�Ɠ������炳
�v���o������������
�������Ɂ@�ό`����

��Βl�́@���́@�@�@0/0�`
������@���q���@���������ł������Ȃ̂�

���[���Ɓ@�R��́@�������@�g����
��������
��Ƃ��@�V���@�V��
������
0/0�`���@�E��������
�����Q���@�������

�������炳
1/3

�����Ł@
�����Ɂ@�������̂�����
����������Ɓ@�������
�������@����Ɂ@������
-log�R

���P�̎�
���O��
��蕶�Ɂ@�����ĂȂ��Ă�
�Öق́@�������@����̂ł���
����́@�g���܂���ł����ł���
�ꂪ�@�O<�ꁃ�P�̎��́@�P������
�ꂪ�@�P����̎��́@�P������
�^���́@�^�����O
��
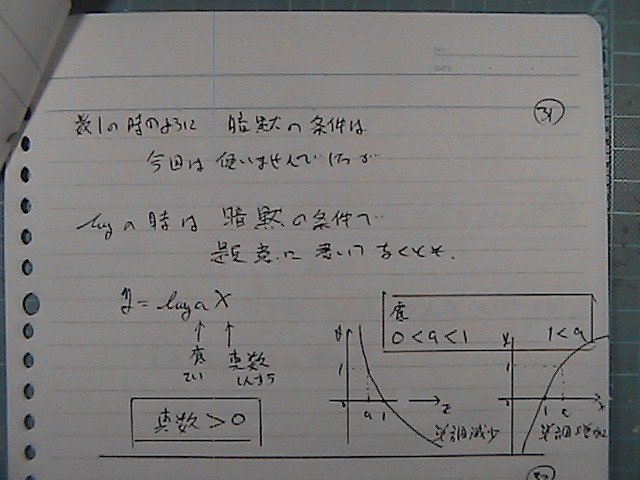
���X�g��
���������@������
0/0�`�ł���

�����
�����Ɓ@���ƈႢ�܂�
�Ȃ̂�
�R��̌������g����

�����@�����ā@�g����
�������́@�^���́@���Ɂ@�����ۂ��@�����
�R��́@�����Ɂ@�����
���������@�O���
�i�@���q�����@�j
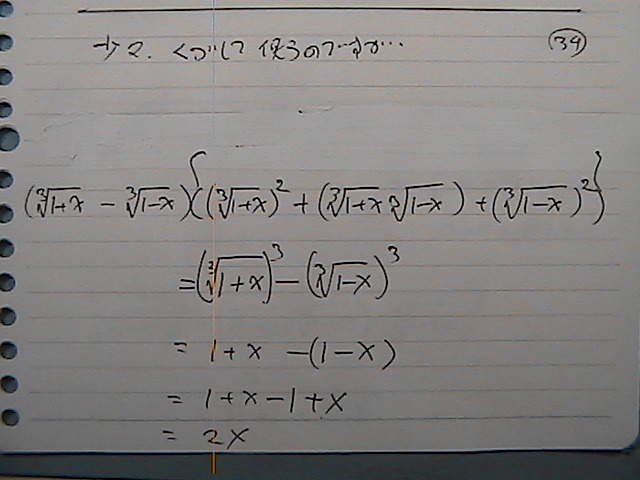
�Ȃ̂�
���ό`��
�l���@�ς��Ȃ��悤�Ɂ@�����ۂ��@
��������ł���
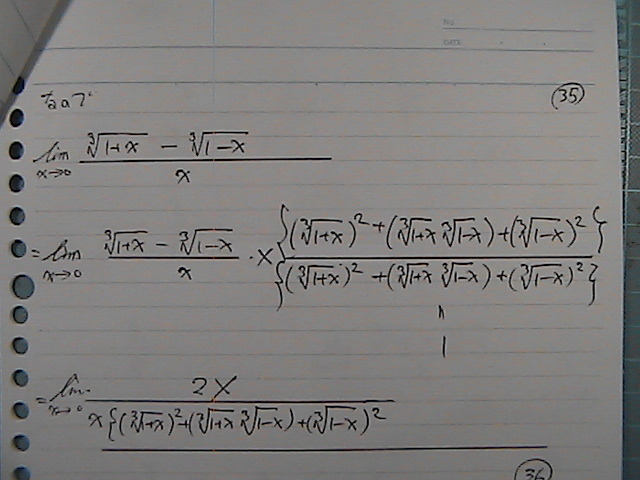
������
0/0�`���@�E�����̂�
�����O���@���������
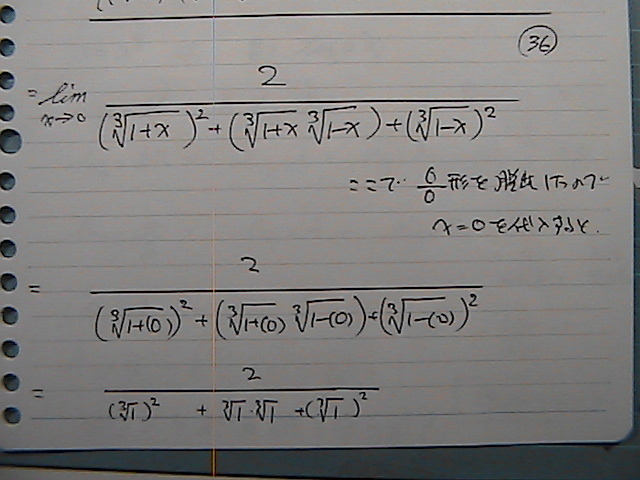
�o�܂�����

����́@�K�т₷����
���̕ӂ���
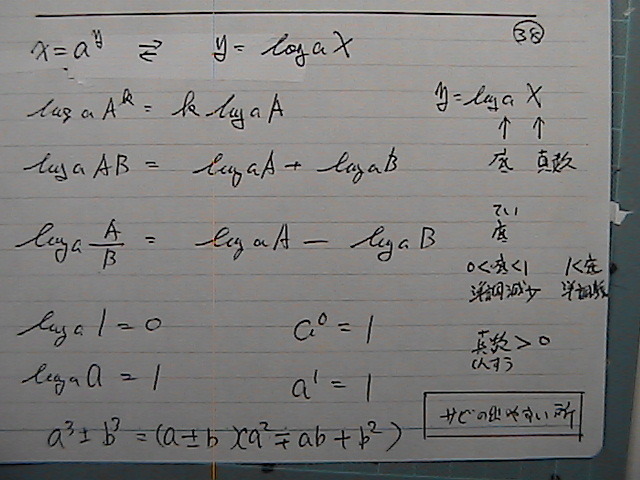
���Q�@���R�@�́@
�Öق̗�����
���P�́@�S�͈͂��@�����Ă���̂�
���c���������
����̂ł���
���[�@�b�́@�S�R�Ⴄ���ǂ�
�匟�@���ā@���邶��i�C�X�J
���w�Ł@�匟��̂́@
���Z���Ƃ�����@����ł�
�����Ă����ł���
���P����
���Ƃ��Ă�
��x�Ɂ@�S�͈͂��@
�P�w���@�Q�w���@�R�w���@�Ɂ@�������ق���
�ȒP�ł���
�匟�@�^���Ɂ@����Ă�l���@������
�n���ɂ��Ắ@�Ȃ�܂����B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���̋Ɍ��̋��ߕ��̖���
�O��
�ڂ����@�v�Z������ĂȂ�����
�悤�Ɂ@�v������
���ނ���
����Ă݂����Ǝv���܂���
�S�@�T�@�U��
��
�p�^�[����������
��
�Ɍ���
�����@����Ȃ��@a�Ɂ@�߂Â��Ƃ���
���i���j���@���Ƃ����l��
����Ȃ��@�߂Â��Ă����Ȃ��
���̋Ɍ��́@�l��
����a�@�̎��@���i���j�@���@���@�Ƃ�
Lim
����a�@�@���i���j����
����́@�v�Z����
���Ă��܂���
���p�^�[��������̂ł���
�����
�O/�O�@�`
0/0�`�̎���
�������Ȃ�@��
�������Ȃ�@�����Ȑ����@������
����ōs���Ă݂܂��傤
����
�����@����Ȃ��@�P�Ɂ@�߂Â��Ƃ�
�ꉞ�@�ڕW�l�I�Ɂ@�����P���@������Ă݂��
������@���q���@�O�@�́@0/0�`
������
���������ł�����������
�����������Ă݂܂���
����́@���|���
���q��
�����藝��
x���P�̎��@�O�ɂȂ��Ă��܂�����
�������������
�g�����@�Ƃ��@�g���Ȃ���
�W����������
�i���|�P�j�@���@�����Ɂ@���̂�����
�i���|�P�j���O�ɂ���@x�̒l��
�����
�R�������@�P�����@�Ŋ���������
��ԏ�́@�Q���@�Ł@�P���@�Ł@�萔�Ł@�]��@�́@�O
�ł���Ƃ���
�V���@�V��
������
0/0��Ԃ�E�����̂�
�����P���@�߂ł����@�������
�Ɍ��́@�Q
0/0�`�́@������́@�p�^�[����
���������@�����Ă�ꍇ
��͂�
x=�O�@���@�������
�ڕW�l�@�I�ȁ@�Ɍ����@0/0�@�`�Ł@�łȂ��̂�
���́@�l���@�ς����Ɂ@���ό`
×�@�P�{�Ȃ�@�l�́@�ς��Ȃ�����
�|����ׂ��@���𐔂��@���ꕪ�q�Ɂ@������
���[���́@��������
��������
����
������
0/0��Ԃ�E�o�����̂�
�����O���@��������
�Ɍ��l��
1/4
0/0�`��
�����@����Ȃ��P�ɋ߂Â��Ƃ��̖���
�P���@���������@����ł��@��������������ł�
�����P�Ɂ@�߂Â��Ă悭
�������@���@not= 1�@�Ȃ̂�����
�Ł@�i���|�P�j�@���@�Ă��܂���
�Ɍ��́@���̂��@�o����
0/0��Ԃ��@�E���Ă����
�����P���@�_�C���N�g�́@�������
�Ɍ����@���܂�B
�������@���܂��܂���
�ޑ�
�ڕW�l�ȁ@�Ɍ���
0/0�`��ԂȂ̂�
�������Ȃ��Ƃ����Ȃ���
���������ł������Ȃ̂�
����́@x�Ł@��������
���q�́@�R��́@��������
�₭����Ƃ�
�V���@�V��
0/0��Ԃ�E��������
�����|�P���@�������
�Ɍ��́@-3
����
�܂��@�ʕ��@����i�C�X�J��
������@
�����́@�Ɍ��Ɂ@�Ȃ�Ȃ�
�O/�O�`
��������
�����@����
������
0/0��Ԃ��@�E�����̂�
�����O���@�������
�@
�Ɍ��l�́@-1
�C�}�n�@�p�^�[���@0/0�`�@�Ȃ̂�
������@0/0�`
�����
��������
����@���q�Ɂ@�Ⴄ���̂��@�����Ă�̂�
�Q��@
���ꂼ��́@���𐔂��@�����Ăł���
�܂�
����̕�
��������
���x�́@���q�̕�
����Ɂ@���������@�������������
���ł���
0/0��Ԃ��@�E�����̂�
�����Q���@���
�Ɍ��l�́@1
����
�Ȃ�
���ϕω����̂Ƃ��́@�悤�ȁ@�`��
�����������@�ʕ�
���q�́@��������
���𐔂��@������
����
0/0��Ԃ��@�����Ł@�E��������
�����O���@�������
����Ȋ�����
����
�����u�Ԃ�
����@
�����
���O�@�́@�����@�́@�^�����O�@�Ȃ̂�����
��Βl�́@�Ƃ肠�����@�|���炸��
���̑O�ɂł���
���ό`��
���O�́@�v�Z�@�@���́@�Ɠ������炳
�v���o������������
�������Ɂ@�ό`����
��Βl�́@���́@�@�@0/0�`
������@���q���@���������ł������Ȃ̂�
���[���Ɓ@�R��́@�������@�g����
��������
��Ƃ��@�V���@�V��
������
0/0�`���@�E��������
�����Q���@�������
�������炳
1/3
�����Ł@
�����Ɂ@�������̂�����
����������Ɓ@�������
�������@����Ɂ@������
-log�R
���P�̎�
���O��
��蕶�Ɂ@�����ĂȂ��Ă�
�Öق́@�������@����̂ł���
����́@�g���܂���ł����ł���
�ꂪ�@�O<�ꁃ�P�̎��́@�P������
�ꂪ�@�P����̎��́@�P������
�^���́@�^�����O
��
���X�g��
���������@������
0/0�`�ł���
�����
�����Ɓ@���ƈႢ�܂�
�Ȃ̂�
�R��̌������g����
�����@�����ā@�g����
�������́@�^���́@���Ɂ@�����ۂ��@�����
�R��́@�����Ɂ@�����
���������@�O���
�i�@���q�����@�j
�Ȃ̂�
���ό`��
�l���@�ς��Ȃ��悤�Ɂ@�����ۂ��@
��������ł���
������
0/0�`���@�E�����̂�
�����O���@���������
�o�܂�����
����́@�K�т₷����
���̕ӂ���
���Q�@���R�@�́@
�Öق̗�����
���P�́@�S�͈͂��@�����Ă���̂�
���c���������
����̂ł���
���[�@�b�́@�S�R�Ⴄ���ǂ�
�匟�@���ā@���邶��i�C�X�J
���w�Ł@�匟��̂́@
���Z���Ƃ�����@����ł�
�����Ă����ł���
���P����
���Ƃ��Ă�
��x�Ɂ@�S�͈͂��@
�P�w���@�Q�w���@�R�w���@�Ɂ@�������ق���
�ȒP�ł���
�匟�@�^���Ɂ@����Ă�l���@������
�n���ɂ��Ắ@�Ȃ�܂����B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 20:46| ��l�̂��ї��Ƃ��@