�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2017�N09��13��
21011�@��l�̂��ї��Ƃ��@���䐔��̘a�@
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���䐔��Ƃ����̂������Ăł���
�����̎���
�����@���ƍ��̊Ԃ��@���́@����������ł���
����́@
���鐔a�@�������ā@�����Ɂ@���X�Ɂ@���́@����(r)�����Ăł��鐔��ł�
��
���
���̐���́@���߂́@�����́@�a�����߂�

�X�̖��́@��琔��Ȃ�^^�ǂ�
�����Ł@���́@����̂��ė�����
���ׂ˂�
�܁[�@���݂Ɂ@�}�@���@�t���Ă邠�邩��
�ς��ȂƎv������
�����ł́@�Ȃ�

���䐔��ōl����
��ʍ��̌����Ɂ@�͂ߍ����
������ӂł�
��Ɂ@���[�������@�����
�������Ƃ��́@
�����Ɂ@�@����Ăł���
����ł���
������
���{�̂ǂ�����
�͂߂�@�b�e�����@���������邻����
�e���p

�Q���߁@�R���߂���
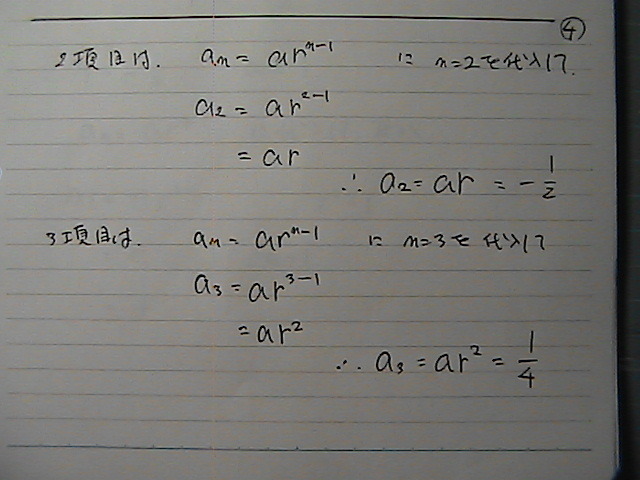
������@���߂�Ƃł���
�t���ŗ��Ă܂��̂�
��ד�@�Ђ�����Ԃ�
�����@�m��Ȃ��H
�W���@������
��

���䂪�������
������
���߂���@�o�Ă邯�ǂ�
���܂Ɂ@�Ⴄ�̂��@������Ă������炳
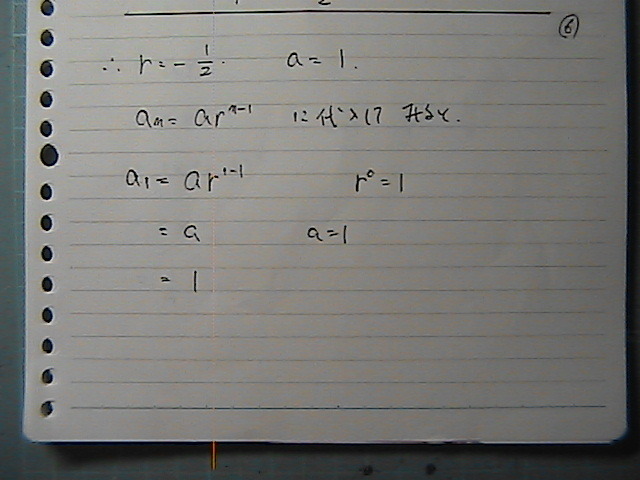
��l�@��ʍ����@�����Ă邩
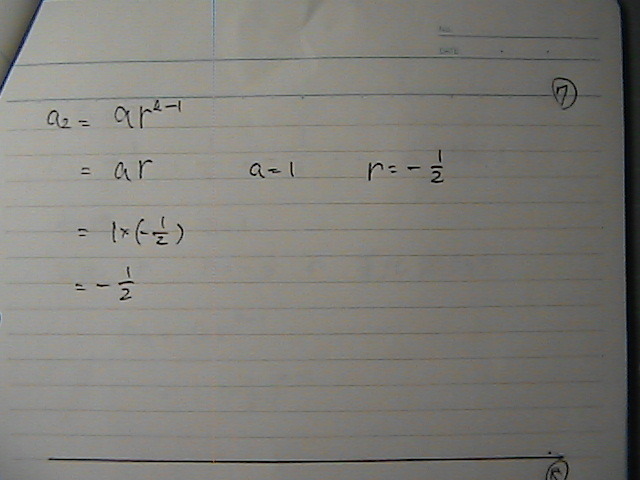
������Ɓ@�`�F�b�N���Ăł���
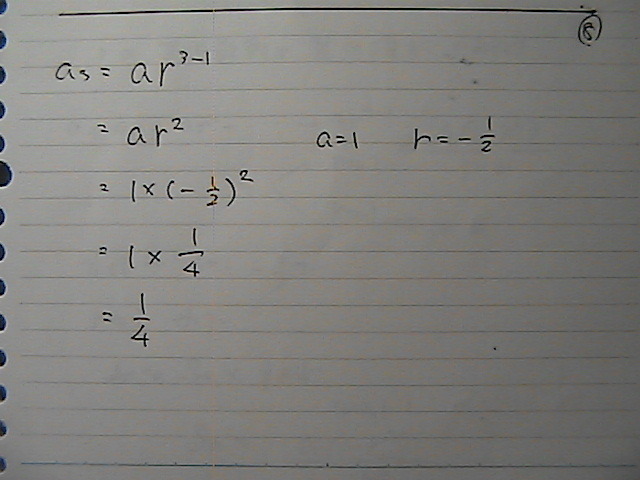
�Ȃ̂�
����Ȋ����ł���

������
���߂�̂́@����́@���߂́@�����̘a�Ȃ�
�����@�Ɓ@����@���@�������
��
���䂪�@�����ŗ��ă��Ƃ���
�ꍇ����
����́@�P�̎��@�P�łȂ��Ƃ���
�a�̌������@�ς���Ă��܂�����
�����̎���
���䂪�@���@�����̂Ƃ��@�v�Z�����
���䂪�@�P�ɂȂ��Ă��܂��@�����́@�l���@���邶��i�C�X�J
������Ƃ���
�`�F�b�N����

��
����́@�V�b�J���@�l���@�łĂ�
����́@�P�ł́@�Ȃ�����
�������́@�����ɓ����
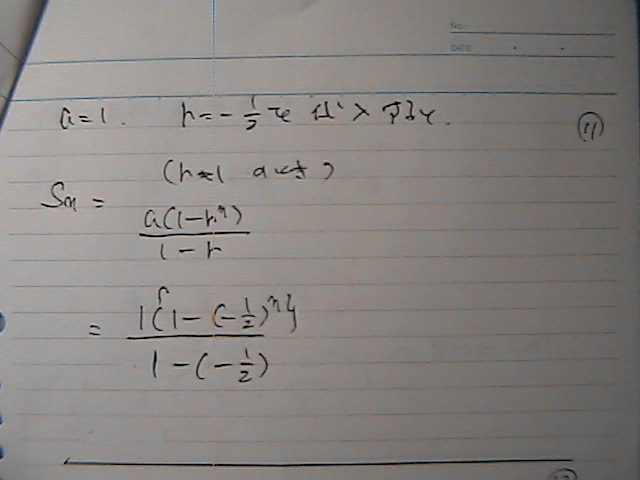
���ό`��
�����́@����
�v�Z�́@���i����
����ĂȂ���
�Ă��߂�Ɂ@�P�A���X�~�X���@������̂�
�ނ����͂�
�G�A���X�~�X�Ƃ������Ă�
�܂��@�P�A���X�~�X��
�����@�G�A���X�~�X�ł�
��k�́@�Ƃ�����
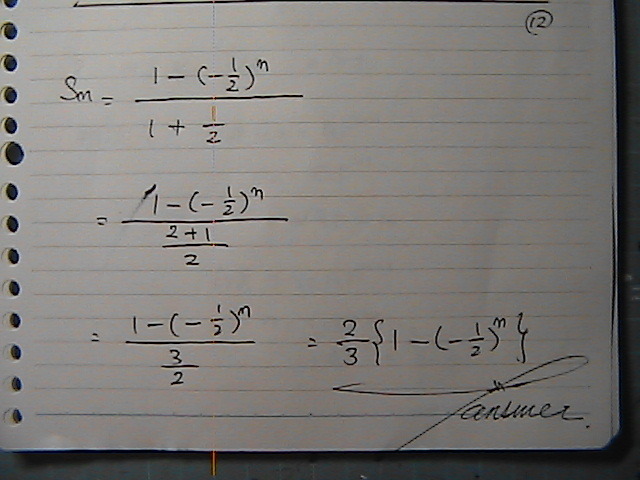
�����������傢���[
���L�\�o���������Ȃ��[
����Ł@�s�[���Ɨ��邨������
�o�C�N�́@���̍��@�w�A�X�^�C����
������@�C�ɂ��Ă܂�����
����
����ĂȂ�����
���s���܂���
���

������ł���
�������ā@�l����
�a���@���߂����̂��@�������킹���
�y�Ȏ����A���g
��ʍ��́@�����Ɂ@�Q���߁@�R���߁@���@
�����
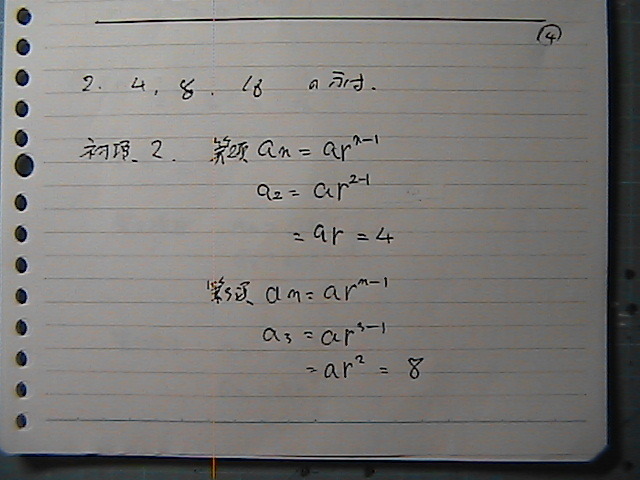
������@�����ɂ���
�₭���ā@���߂��

�㔼��
������
�Q���߁@�R���߂��@�g����

������@���߂�

��ʍ��Ł@�����Ƃ���
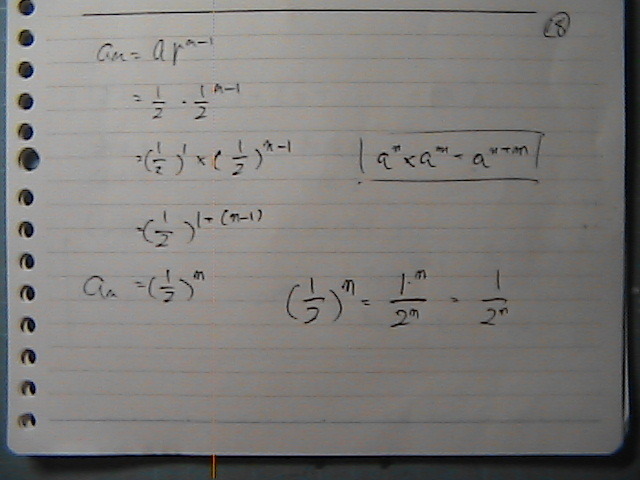
��
�����܂ł́@
���̐����
�Q�����@������ł����
�O�����@��딼��

��ʍ��Ł@
�O�����@�㔼��
��
���߂�̂́@���߂́@���@���܂ł́@�a�ł��̂�

�_�b�V���@�Ȃ��@�@�@�@��������@�t��
�������@�i�a�̌������@�j�@�O���@�㔼
�����ł���
�������

�v�Z���Ă��܂���
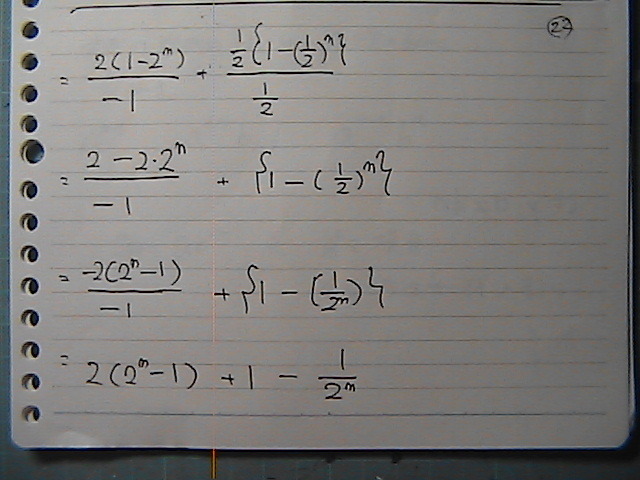
����Ȃ��
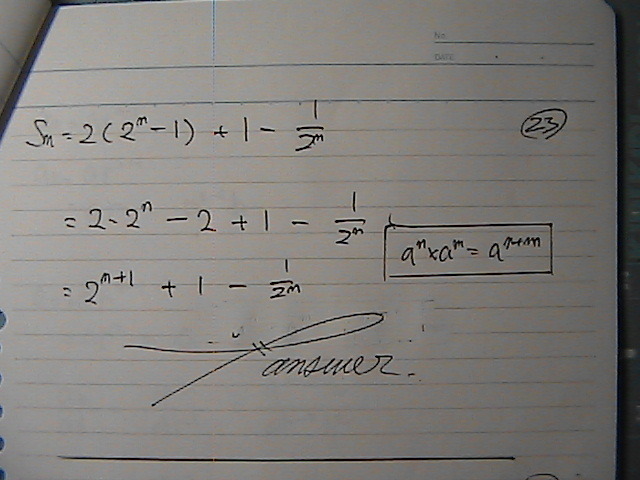
���͂ł���
�����ŗ��Ă܂���

������@��ʍ��Ɂ@�������
���߂��肩����
�Q���߁@�R���߁@���@�����ɂ���
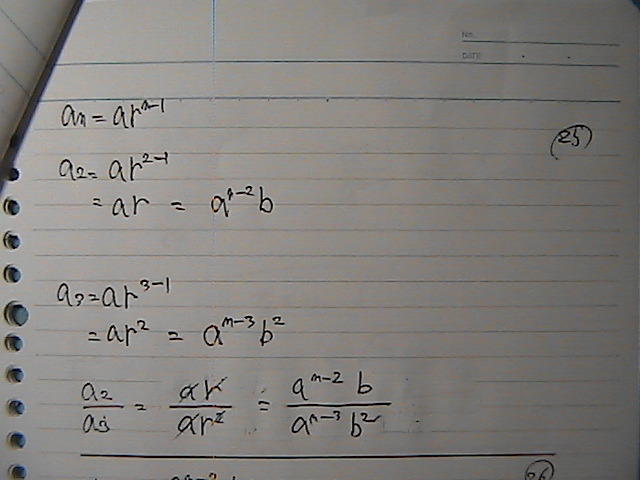
�w���̌v�Z
�����Ł@�����Ă����
�����V���V���@�Ł@�ł����Ⴄ����
��������
�H��
�������傩��
���s����

���͂����ł�
�����́@���@���ʂ�
���́@��Ɖ�
�ǂ����H

�����炳
������
�������Ɓ@����ĂȂ������ꍇ
���s�ł���
�����Ɓ@���䂪�o���̂�

�����́@�Ƃ��́@�����
���䂪�@�P�ɂȂ�Ƃ��́@�����́@�l��
�ꍇ�������Ăł���
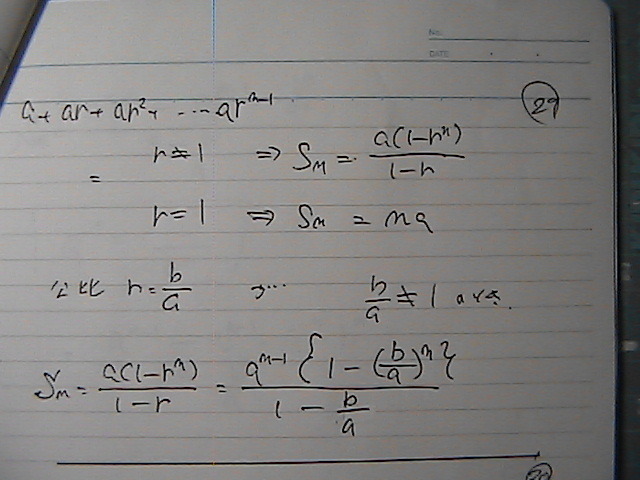
���䂪�@�P�Ł@�Ȃ��Ƃ�����
����Ȋ�����

�w���̌v�Z��
���܂Ɍ��Ă�����
���w�́@���o���@�K�т��炢

�_�C�W���u�ł��傤��
����
���E
����������
�E�E�E�E�E

�E�E�E�E
���o�[�X
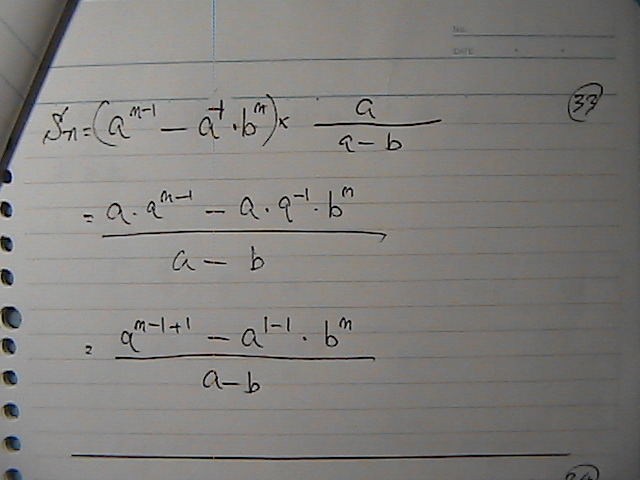
���ꂪ�@���䂪�@�P�łȂ��Ƃ�
�Ɓ@���䂪�@�P�̎���
����

�����l�ł�
���ɂ���́@�������ł���
����
�ޑ�
����͂�
���߂́@���@���̘a

��ʍ��Ɂ@�Q���߁@�R����
���@�������

����́@-1
�����́@1

���䂪�@�P�łȂ�����
������Ƃ����@�m�F����
�a�̌����Ɂ@����Ă��܂���
����

�����@�@���߂́@�����́@�a�����߂���
��ʍ��̌�����

�͂ߍ���ł��Ă���i�C�X�J
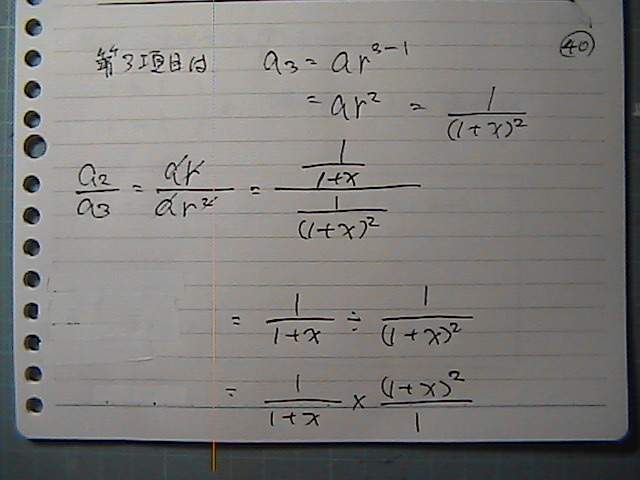
���o�[�X����

����Ɂ@�����������Ă�Ƃ���
�����́@�l�ɂ���Ă�
���䂪�@1�ɂȂ�Ƃ�������̂�
�V�b�J���@�`�F�b�N�@�ꍇ���������Ăł���

���䂪�@�P�ɂȂ�@x��
�[��
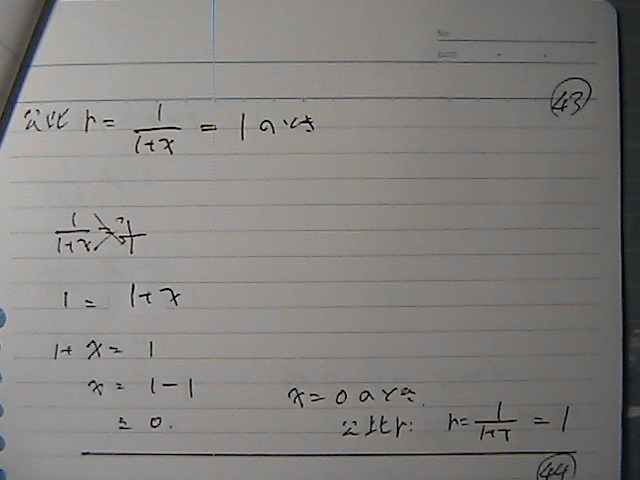
��
�a�́@��

���䂪�@1�łȂ��Ƃ���
�[������A
�Ȃ��ł�����

�������傩��
�Ђ�Ђ₵�Ȃ���
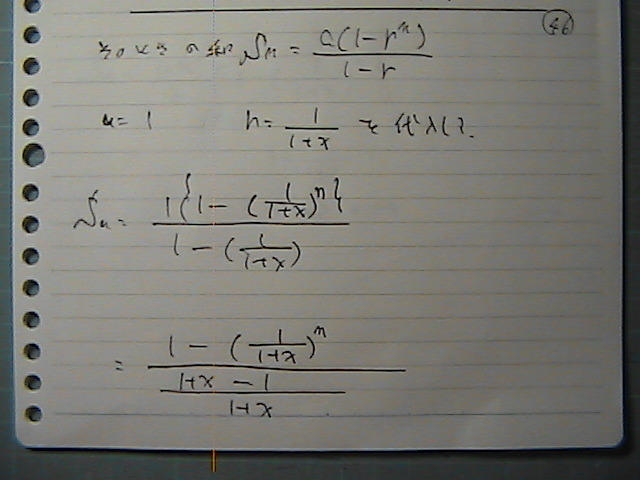
���Ƃ�
����Ă܂���
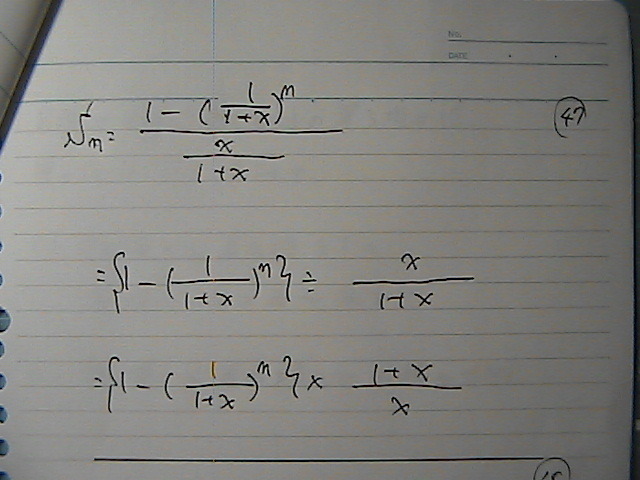
����
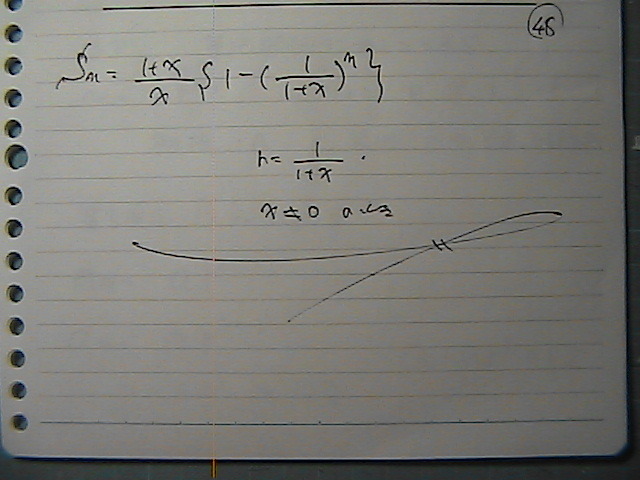
�{���́@���C���C�x���g��
����
���x�́@��������Ȃ��Ă�
������
���Ă܂��̂�
�V�b�J���@�v�Z�ł���

�e�����@���߂�
�e���́@�Q�悵�����̂�
���߂́@���@���̘a
������
���́@������@���߂�
��ʍ����@�o���ł���
������@��悵���Ⴆ��
�\���]���@�Q��ɂȂ�@��ʍ��ɂȂ���炳

�R���߁@�Ɓ@�U���߂���

������@������
�₭���ā@���߂��
��������

�łĂ����@������@��ʍ��Ɂ@�R���߂�
�������
�������o�ė���

���ꂪ�@���́@����
���́@���ꂼ��́@���́@���̘a������
���̈�ʍ����@�Q�悵�Ă�����
����
1.2.3....
�Ƃ���ā@��悷���

9,36,144�A�E�E�E
�ł���
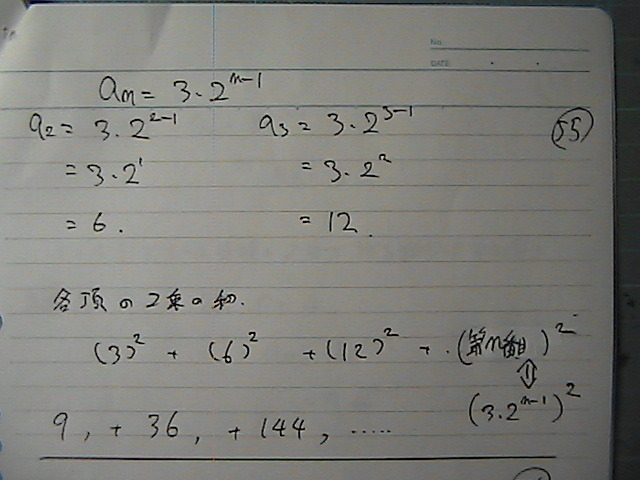
������@����́@��ʍ��Ɂ@�����
������@���߂��
4

�V�����ł�������́@��ʍ��́@���ꂾ����

�a�̌����Ɂ@�������
����ł����̂�
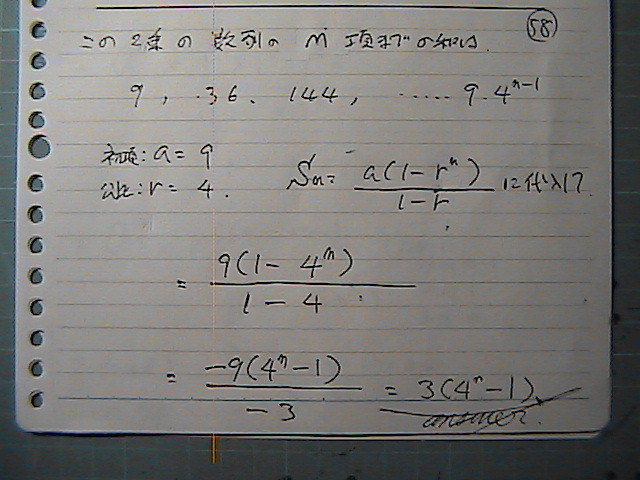
���X�g��
�������Q�͂ł���
���́@����
�͂��߂́@����̂��Ƃ���
�e���́@���߂̂��@���܂ł́@�ς����߂��
������₷����Ɂ@���������čl�����
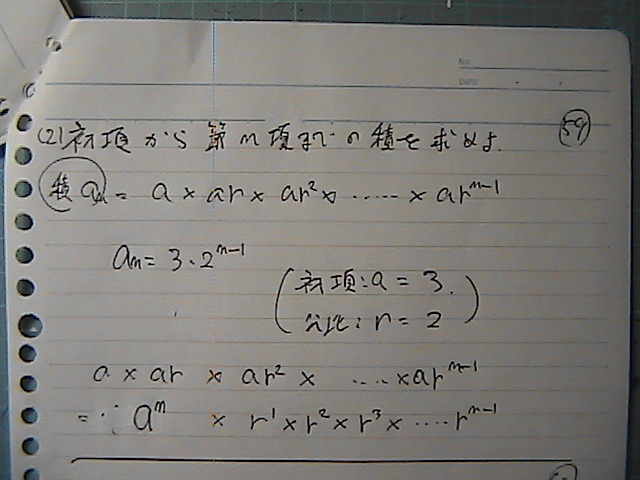
a�́@����
a�́@����@�@�|���Z������
����@���̕���
���̎w���v�Z��
�����@�����́@�w���̊|���Z��
���̎w���́@�����Z������
�������邩
�Ԉ��Ȃ��悤��
������
1����@��-1�@�܂�
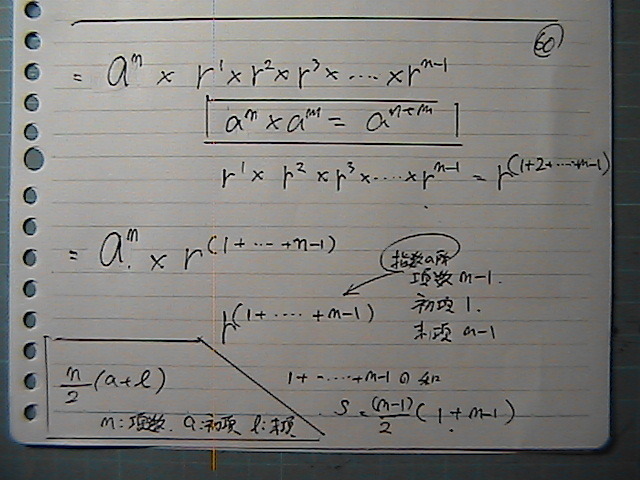
�����́@���䂒�́@�w���v�Z��
��������̘a���@�g����
����Ȋ�����
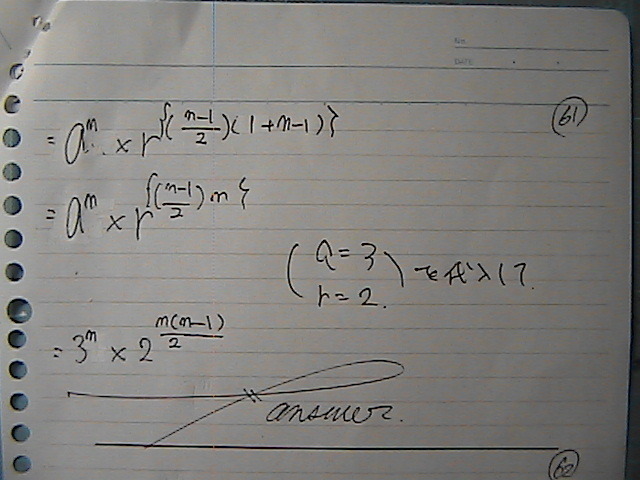
�����ꂳ�܁[�[�[
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���䐔��Ƃ����̂������Ăł���
�����̎���
�����@���ƍ��̊Ԃ��@���́@����������ł���
����́@
���鐔a�@�������ā@�����Ɂ@���X�Ɂ@���́@����(r)�����Ăł��鐔��ł�
��
���
���̐���́@���߂́@�����́@�a�����߂�
�X�̖��́@��琔��Ȃ�^^�ǂ�
�����Ł@���́@����̂��ė�����
���ׂ˂�
�܁[�@���݂Ɂ@�}�@���@�t���Ă邠�邩��
�ς��ȂƎv������
�����ł́@�Ȃ�
���䐔��ōl����
��ʍ��̌����Ɂ@�͂ߍ����
������ӂł�
��Ɂ@���[�������@�����
�������Ƃ��́@
�����Ɂ@�@����Ăł���
����ł���
������
���{�̂ǂ�����
�͂߂�@�b�e�����@���������邻����
�e���p
�Q���߁@�R���߂���
������@���߂�Ƃł���
�t���ŗ��Ă܂��̂�
��ד�@�Ђ�����Ԃ�
�����@�m��Ȃ��H
�W���@������
��
���䂪�������
������
���߂���@�o�Ă邯�ǂ�
���܂Ɂ@�Ⴄ�̂��@������Ă������炳
��l�@��ʍ����@�����Ă邩
������Ɓ@�`�F�b�N���Ăł���
�Ȃ̂�
����Ȋ����ł���
������
���߂�̂́@����́@���߂́@�����̘a�Ȃ�
�����@�Ɓ@����@���@�������
��
���䂪�@�����ŗ��ă��Ƃ���
�ꍇ����
����́@�P�̎��@�P�łȂ��Ƃ���
�a�̌������@�ς���Ă��܂�����
�����̎���
���䂪�@���@�����̂Ƃ��@�v�Z�����
���䂪�@�P�ɂȂ��Ă��܂��@�����́@�l���@���邶��i�C�X�J
������Ƃ���
�`�F�b�N����
��
����́@�V�b�J���@�l���@�łĂ�
����́@�P�ł́@�Ȃ�����
�������́@�����ɓ����
���ό`��
�����́@����
�v�Z�́@���i����
����ĂȂ���
�Ă��߂�Ɂ@�P�A���X�~�X���@������̂�
�ނ����͂�
�G�A���X�~�X�Ƃ������Ă�
�܂��@�P�A���X�~�X��
�����@�G�A���X�~�X�ł�
��k�́@�Ƃ�����
�����������傢���[
���L�\�o���������Ȃ��[
����Ł@�s�[���Ɨ��邨������
�o�C�N�́@���̍��@�w�A�X�^�C����
������@�C�ɂ��Ă܂�����
����
����ĂȂ�����
���s���܂���
���
������ł���
�������ā@�l����
�a���@���߂����̂��@�������킹���
�y�Ȏ����A���g
��ʍ��́@�����Ɂ@�Q���߁@�R���߁@���@
�����
������@�����ɂ���
�₭���ā@���߂��
�㔼��
������
�Q���߁@�R���߂��@�g����
������@���߂�
��ʍ��Ł@�����Ƃ���
��
�����܂ł́@
���̐����
�Q�����@������ł����
�O�����@��딼��
��ʍ��Ł@
�O�����@�㔼��
��
���߂�̂́@���߂́@���@���܂ł́@�a�ł��̂�
�_�b�V���@�Ȃ��@�@�@�@��������@�t��
�������@�i�a�̌������@�j�@�O���@�㔼
�����ł���
�������
�v�Z���Ă��܂���
����Ȃ��
���͂ł���
�����ŗ��Ă܂���
������@��ʍ��Ɂ@�������
���߂��肩����
�Q���߁@�R���߁@���@�����ɂ���
�w���̌v�Z
�����Ł@�����Ă����
�����V���V���@�Ł@�ł����Ⴄ����
��������
�H��
�������傩��
���s����
���͂����ł�
�����́@���@���ʂ�
���́@��Ɖ�
�ǂ����H
�����炳
������
�������Ɓ@����ĂȂ������ꍇ
���s�ł���
�����Ɓ@���䂪�o���̂�
�����́@�Ƃ��́@�����
���䂪�@�P�ɂȂ�Ƃ��́@�����́@�l��
�ꍇ�������Ăł���
���䂪�@�P�Ł@�Ȃ��Ƃ�����
����Ȋ�����
�w���̌v�Z��
���܂Ɍ��Ă�����
���w�́@���o���@�K�т��炢
�_�C�W���u�ł��傤��
����
���E
����������
�E�E�E�E�E
�E�E�E�E
���o�[�X
���ꂪ�@���䂪�@�P�łȂ��Ƃ�
�Ɓ@���䂪�@�P�̎���
����
�����l�ł�
���ɂ���́@�������ł���
����
�ޑ�
����͂�
���߂́@���@���̘a
��ʍ��Ɂ@�Q���߁@�R����
���@�������
����́@-1
�����́@1
���䂪�@�P�łȂ�����
������Ƃ����@�m�F����
�a�̌����Ɂ@����Ă��܂���
����
�����@�@���߂́@�����́@�a�����߂���
��ʍ��̌�����
�͂ߍ���ł��Ă���i�C�X�J
���o�[�X����
����Ɂ@�����������Ă�Ƃ���
�����́@�l�ɂ���Ă�
���䂪�@1�ɂȂ�Ƃ�������̂�
�V�b�J���@�`�F�b�N�@�ꍇ���������Ăł���
���䂪�@�P�ɂȂ�@x��
�[��
��
�a�́@��
���䂪�@1�łȂ��Ƃ���
�[������A
�Ȃ��ł�����
�������傩��
�Ђ�Ђ₵�Ȃ���
���Ƃ�
����Ă܂���
����
�{���́@���C���C�x���g��
����
���x�́@��������Ȃ��Ă�
������
���Ă܂��̂�
�V�b�J���@�v�Z�ł���
�e�����@���߂�
�e���́@�Q�悵�����̂�
���߂́@���@���̘a
������
���́@������@���߂�
��ʍ����@�o���ł���
������@��悵���Ⴆ��
�\���]���@�Q��ɂȂ�@��ʍ��ɂȂ���炳
�R���߁@�Ɓ@�U���߂���
������@������
�₭���ā@���߂��
��������
�łĂ����@������@��ʍ��Ɂ@�R���߂�
�������
�������o�ė���
���ꂪ�@���́@����
���́@���ꂼ��́@���́@���̘a������
���̈�ʍ����@�Q�悵�Ă�����
����
1.2.3....
�Ƃ���ā@��悷���
9,36,144�A�E�E�E
�ł���
������@����́@��ʍ��Ɂ@�����
������@���߂��
4
�V�����ł�������́@��ʍ��́@���ꂾ����
�a�̌����Ɂ@�������
����ł����̂�
���X�g��
�������Q�͂ł���
���́@����
�͂��߂́@����̂��Ƃ���
�e���́@���߂̂��@���܂ł́@�ς����߂��
������₷����Ɂ@���������čl�����
a�́@����
a�́@����@�@�|���Z������
����@���̕���
���̎w���v�Z��
�����@�����́@�w���̊|���Z��
���̎w���́@�����Z������
�������邩
�Ԉ��Ȃ��悤��
������
1����@��-1�@�܂�
�����́@���䂒�́@�w���v�Z��
��������̘a���@�g����
����Ȋ�����
�����ꂳ�܁[�[�[
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 09:34| ��l�̂��ї��Ƃ��@
2017�N09��07��
21010 ��l�̂��ї��Ƃ��@���䐔��
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���
���䐔�������
������@���߂�

���䐔����Ăǂ�Ȃ���������
�����Ɂ@�ł���
���鐔����������
�����Ɂ@���@���@�Ɂ@
���́@�������@�|���ā@�ł��鐔��
���@�F�@����

�Ł@���䐔��̎���
��ʍ���
������������

��蕶��
��
��+1
��+2
���@��ʍ��́@�����Ł@�o���ł�����
�Ł@��蕶�́@���Ɂ@�������

a , r , �O�łȂ��Ƃ���
���̓�����
�ӁX�@a���́@���|�P��Ł@�����
����Ȋ�����

����Ɂ@�����̂Ƃ���
�w���v�Z�́@������
�ȒP�ɂ��Ă��܂��Ƃł���

�����̂Ƃ���
�w���́@�|���Z�ɕς����
��������
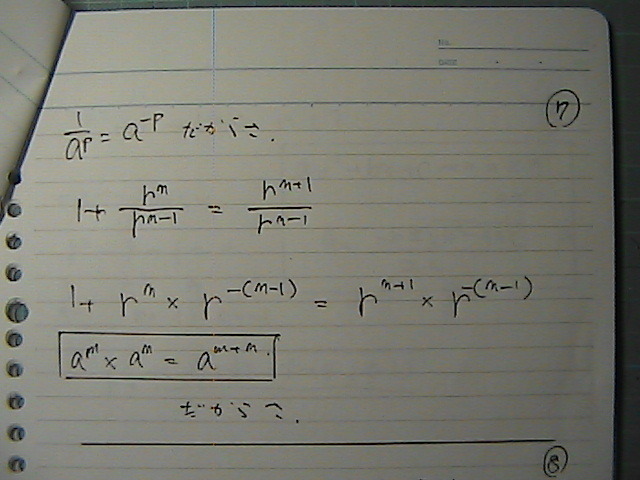
�������肵�Ă����ł���
�����
���́@�Q���������炳
���̌�����
�������Ⴄ��
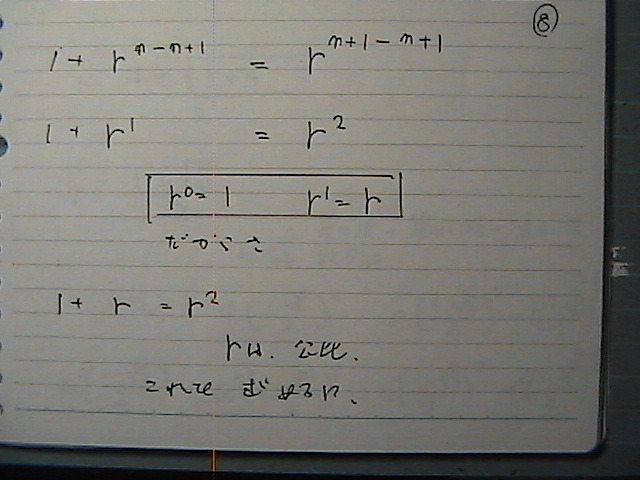
���̌����́@����Ȃ��������炳
�W���̂Ƃ���
���Ă͂߂�

���I�@������
�ł�����Ȃ����炳
��
����ȓ�����

����
�����
������
���ʂ炵����
�t�B�{�i�b�`����Ƃ����炵��
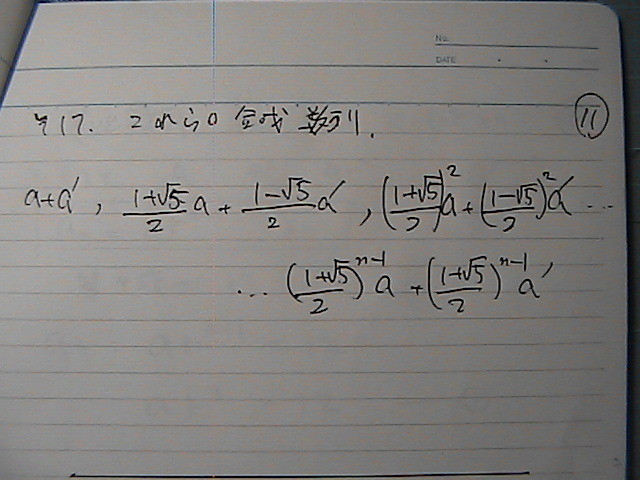
���x��
����������
������
�v�Z���ł�
��X���߂��@���߂�

��ʍ��́@����
���䐔��̂��@����������i�C�X�J
�S����

�U����
�������
���Ł@����ł��邩��
�����ɂ���
�ȒP�ɂ����
���́@�}4
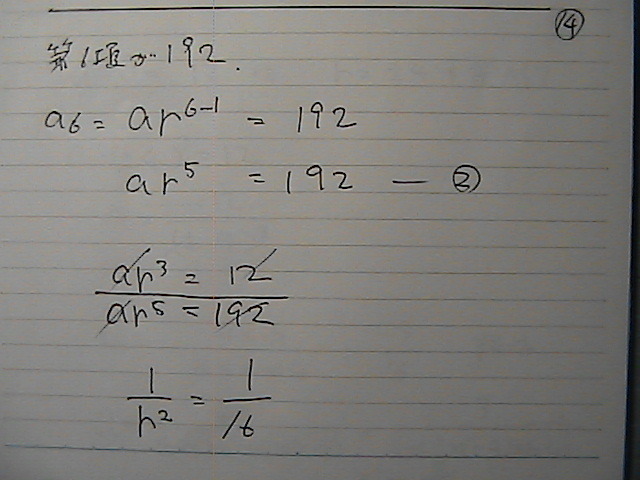
�l�p�̒��́@���P�́@�\���m���ł�
�������ƌ�������
�}�������
���[�g�Ł@�o�Ă�����
��̒��́@���Ƃ����@�Ȃ̂�
�v���X�̕�����
�}�C�i�X���@����Ƃ���
��-1�@���@i

���䂪�o���̂�
a���F�@���������߂��
-3/16
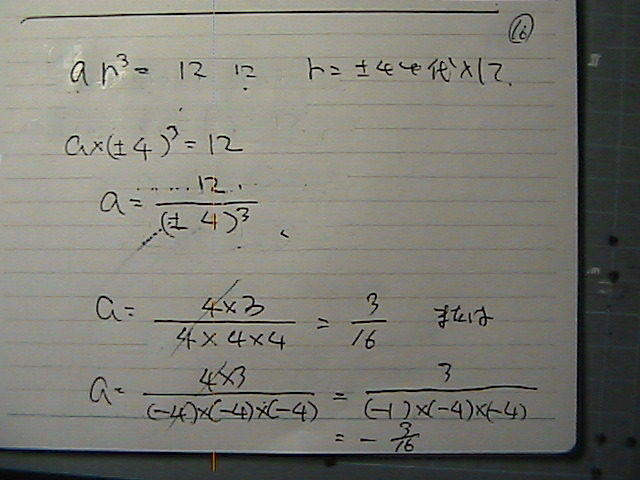
�Ȃ̂�
��X���߂�
�����ɂ��Ă͂߂ā@����i�C�X�J
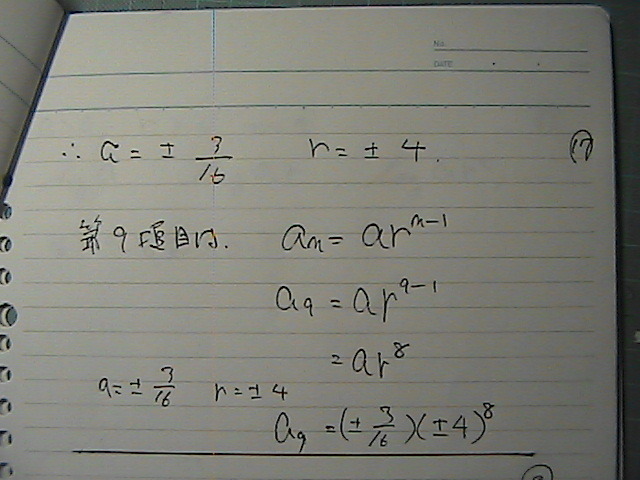
�v���X�}�C�i�X��
�łĂ��܂�����

�ꌩ�@���䐔��݂�����
��
����́@�ȁ@���@�����ł���
�ǂ�ȁ@����H

���K���Y���́@����@�ȗ����Ă���̂�
�ꂪ�P�O�́@��p�ΐ��Ƃ������Ƃ�

�R�����@���ꂼ��
�ו������Ă���

�ǂ����
����́@���䐔��ł͂Ȃ�
��������ɂȂ��Ă���

����
�Ȋw�̎����Ɂ@�o�ė�������
��ł���
���w�́@���ӎ����@�����Ăł���
�Ȃ̂�
�������s���܂���
��������
�N�����̒���
�r�[�J�[�Ł@���[�������@�H�ׂ�҂�
����炵����
���[�@������
�H�ׂ���@�����Ɓ@����Ƃ��悤�ɁI�I�I
����������������

�A���R�[�����@A
����W�Ƃ��Ăł�
���߂́@�S���@�A���R�[���łP�O�j��

��������
�Q�j���@�Ƃ��Ă��Ă�
�����@�Q�j���@�߂���
�A���R�[���́@�d�ʁ����@���Ȃ����Ă�����ł���
������@���@��@�s���Ɓ@��%�ɂȂ邩
���߂���@��߂���Ƃ���
���X�V�����_�[��
����������ǂ�
�����Ɂ@�Z�x�������@���邩��
��������
���������@�����
�Ƃ�
����H�H

���߂�
�A���R�[���P�O�j������
�Q�����@�Ƃ���
�����Q�����@�߂�����
�A���R�[���̏d�ʁ���80��

��������
�܂��@�Q�����@���o����
���o�����Ȃ��́@�A���R�[���d�ʂ́@1.6����

�c��́@�W�O���A���R�[���@�W�����̒��ɂ�
�A���R�[�����@6.4����
���@1.6����

�����ց@�Q�����̐����@�߂���
�A���R�[���́@�d�ʂ́@�U.4����
�S�̂Ł@�P�O����

���́@�U�S%�A���R�[������
�܂��@�Q�����@���o����
�Q�����@���́@�A���R�[������
1.28����

�U�S%�A���R�[���@�W�����̒��ɂ́@�A���R�[��5.12�����@

������
���Q�������@�߂���
�T�P�D�Q%�A���R�[��

������@���@��J��Ԃ���ł���
������
���䐔��́@�������g���Ăł���
a1,a2,a3������ł���
a2/a3�ŊȒP�ɂ����

����0.8
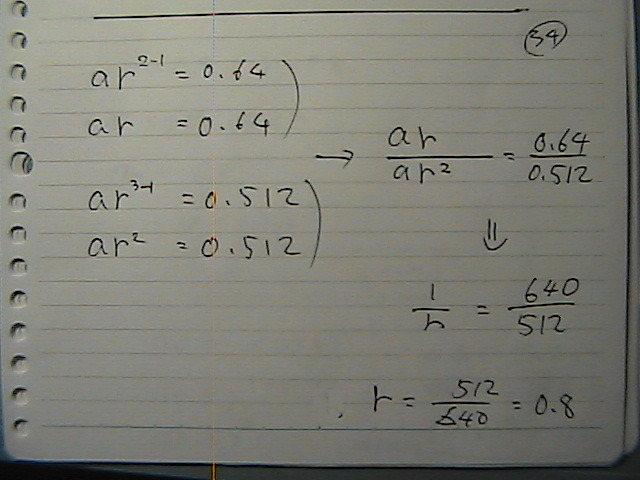
�����́@�����ɂȂ邩��
a��0.8

����Ł@�@�����ɓ����
�|�����킹���
��
�w���́@������
�ȒP�ɂ����
����ł�

�R�p�`��������
�R�ӂ��@���䐔����Ȃ��悤��
����͈̔͂����߂Ȃ�

�O�p�`�̏�����
�R�ӂ��@a,b,c,�Ƃ����
�Q�ӂ̘a�́@���̂P�ӂ��@�����̂��@�O�p�`�ł��̂�
����Ȋ�����
�����
�܂Ƃ߂��
���̂Q����
���`���Ł@������̂�
�l�p�̒��g�̗l�ɂȂ���

a,b,c,���@���ꂼ��
���䐔��́@���ɂ��Ă͂߂Ă�����
���������

➀�A�B

��������
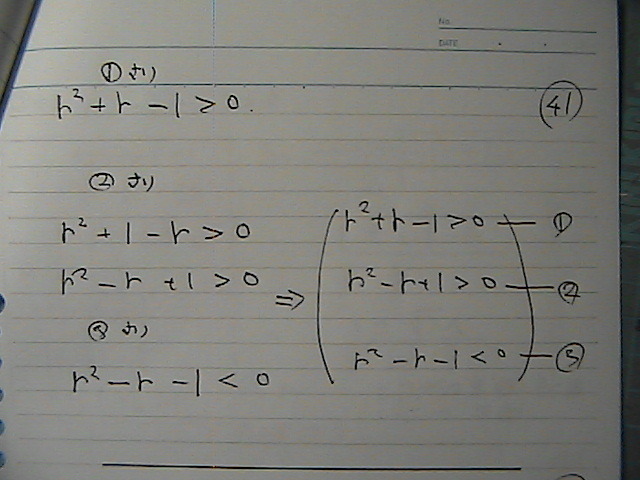
���̌�����
�s�������@➀���猩�Ă���
➀�͈̔�
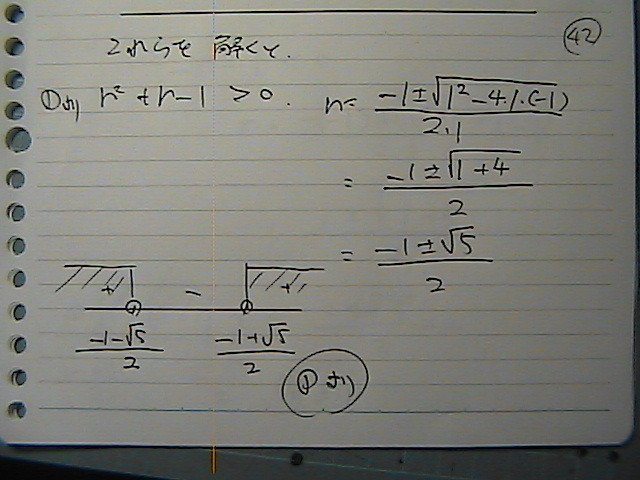
�A�͈̔͂�
����́@�������o�Ă��Ă��܂�������
�������������
�˂Ɂ@���Ȃ̂�
���́@�g�ݍ��킹�̎���
a,r,���@���Ɂ@�O�Ł@�Ȃ��̂�
�˂ɐ��藧��
�i�����j�̂Q��́@�O�ȏ�

�B�͈̔͂�
�s������
���̌����ʼn�����
�B�́@�͈͂��o�ė���
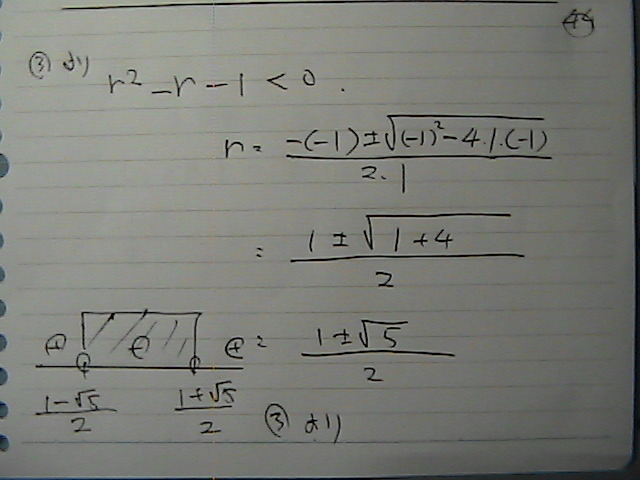
�d�˂��
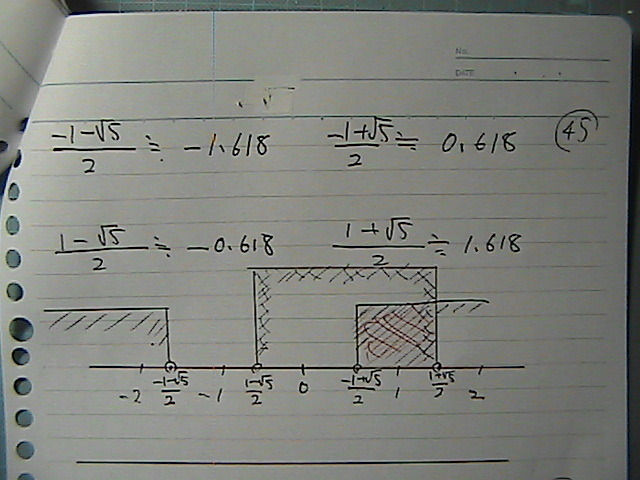
����ł�������

�����
�����@���Ă܂�����

���́@�t���ς��@�����Ăł���
���[���c�ȁ@��Q���܂���
���[�[�[�[
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���
���䐔�������
������@���߂�
���䐔����Ăǂ�Ȃ���������
�����Ɂ@�ł���
���鐔����������
�����Ɂ@���@���@�Ɂ@
���́@�������@�|���ā@�ł��鐔��
���@�F�@����
�Ł@���䐔��̎���
��ʍ���
������������
��蕶��
��
��+1
��+2
���@��ʍ��́@�����Ł@�o���ł�����
�Ł@��蕶�́@���Ɂ@�������
a , r , �O�łȂ��Ƃ���
���̓�����
�ӁX�@a���́@���|�P��Ł@�����
����Ȋ�����
����Ɂ@�����̂Ƃ���
�w���v�Z�́@������
�ȒP�ɂ��Ă��܂��Ƃł���
�����̂Ƃ���
�w���́@�|���Z�ɕς����
��������
�������肵�Ă����ł���
�����
���́@�Q���������炳
���̌�����
�������Ⴄ��
���̌����́@����Ȃ��������炳
�W���̂Ƃ���
���Ă͂߂�
���I�@������
�ł�����Ȃ����炳
��
����ȓ�����
����
�����
������
���ʂ炵����
�t�B�{�i�b�`����Ƃ����炵��
���x��
����������
������
�v�Z���ł�
��X���߂��@���߂�
��ʍ��́@����
���䐔��̂��@����������i�C�X�J
�S����
�U����
�������
���Ł@����ł��邩��
�����ɂ���
�ȒP�ɂ����
���́@�}4
�l�p�̒��́@���P�́@�\���m���ł�
�������ƌ�������
�}�������
���[�g�Ł@�o�Ă�����
��̒��́@���Ƃ����@�Ȃ̂�
�v���X�̕�����
�}�C�i�X���@����Ƃ���
��-1�@���@i
���䂪�o���̂�
a���F�@���������߂��
-3/16
�Ȃ̂�
��X���߂�
�����ɂ��Ă͂߂ā@����i�C�X�J
�v���X�}�C�i�X��
�łĂ��܂�����
�ꌩ�@���䐔��݂�����
��
����́@�ȁ@���@�����ł���
�ǂ�ȁ@����H
���K���Y���́@����@�ȗ����Ă���̂�
�ꂪ�P�O�́@��p�ΐ��Ƃ������Ƃ�
�R�����@���ꂼ��
�ו������Ă���
�ǂ����
����́@���䐔��ł͂Ȃ�
��������ɂȂ��Ă���
����
�Ȋw�̎����Ɂ@�o�ė�������
��ł���
���w�́@���ӎ����@�����Ăł���
�Ȃ̂�
�������s���܂���
��������
�N�����̒���
�r�[�J�[�Ł@���[�������@�H�ׂ�҂�
����炵����
���[�@������
�H�ׂ���@�����Ɓ@����Ƃ��悤�ɁI�I�I
����������������
�A���R�[�����@A
����W�Ƃ��Ăł�
���߂́@�S���@�A���R�[���łP�O�j��
��������
�Q�j���@�Ƃ��Ă��Ă�
�����@�Q�j���@�߂���
�A���R�[���́@�d�ʁ����@���Ȃ����Ă�����ł���
������@���@��@�s���Ɓ@��%�ɂȂ邩
���߂���@��߂���Ƃ���
���X�V�����_�[��
����������ǂ�
�����Ɂ@�Z�x�������@���邩��
��������
���������@�����
�Ƃ�
����H�H
���߂�
�A���R�[���P�O�j������
�Q�����@�Ƃ���
�����Q�����@�߂�����
�A���R�[���̏d�ʁ���80��
��������
�܂��@�Q�����@���o����
���o�����Ȃ��́@�A���R�[���d�ʂ́@1.6����
�c��́@�W�O���A���R�[���@�W�����̒��ɂ�
�A���R�[�����@6.4����
���@1.6����
�����ց@�Q�����̐����@�߂���
�A���R�[���́@�d�ʂ́@�U.4����
�S�̂Ł@�P�O����
���́@�U�S%�A���R�[������
�܂��@�Q�����@���o����
�Q�����@���́@�A���R�[������
1.28����
�U�S%�A���R�[���@�W�����̒��ɂ́@�A���R�[��5.12�����@
������
���Q�������@�߂���
�T�P�D�Q%�A���R�[��
������@���@��J��Ԃ���ł���
������
���䐔��́@�������g���Ăł���
a1,a2,a3������ł���
a2/a3�ŊȒP�ɂ����
����0.8
�����́@�����ɂȂ邩��
a��0.8
����Ł@�@�����ɓ����
�|�����킹���
��
�w���́@������
�ȒP�ɂ����
����ł�
�R�p�`��������
�R�ӂ��@���䐔����Ȃ��悤��
����͈̔͂����߂Ȃ�
�O�p�`�̏�����
�R�ӂ��@a,b,c,�Ƃ����
�Q�ӂ̘a�́@���̂P�ӂ��@�����̂��@�O�p�`�ł��̂�
����Ȋ�����
�����
�܂Ƃ߂��
���̂Q����
���`���Ł@������̂�
�l�p�̒��g�̗l�ɂȂ���
a,b,c,���@���ꂼ��
���䐔��́@���ɂ��Ă͂߂Ă�����
���������
➀�A�B
��������
���̌�����
�s�������@➀���猩�Ă���
➀�͈̔�
�A�͈̔͂�
����́@�������o�Ă��Ă��܂�������
�������������
�˂Ɂ@���Ȃ̂�
���́@�g�ݍ��킹�̎���
a,r,���@���Ɂ@�O�Ł@�Ȃ��̂�
�˂ɐ��藧��
�i�����j�̂Q��́@�O�ȏ�
�B�͈̔͂�
�s������
���̌����ʼn�����
�B�́@�͈͂��o�ė���
�d�˂��
����ł�������
�����
�����@���Ă܂�����
���́@�t���ς��@�����Ăł���
���[���c�ȁ@��Q���܂���
���[�[�[�[
posted by moriamelihu at 09:53| ��l�̂��ї��Ƃ��@
2017�N09��04��
21009 ��l�̂��ї��Ƃ��@���a����
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���a����@�Ƃ����̂�
����U���X�ł���
�ǂ�Ȃ��̂��Ƃ�����
�t������ł��Ă鐔���
�����@���a�����
�t���́@����������@�Ȃ��Ă���Ƃ�����ł���
�����ŏ����Ă���̂�
�����
���̂܂܁@���a�����
�v����������
���̂܂܂���
���ł���
����́@�t�����@�Ƃ��
��������ɂ��Ȃ�܂�
��������Ł@��������
���ʂ��@�Ђ�����Ԃ��ā@�߂�

�����肸�炢��������Ȃ�����
�t�����@�Ƃ��
��������
����́@����Ɂ@�t���́@���́@���a����
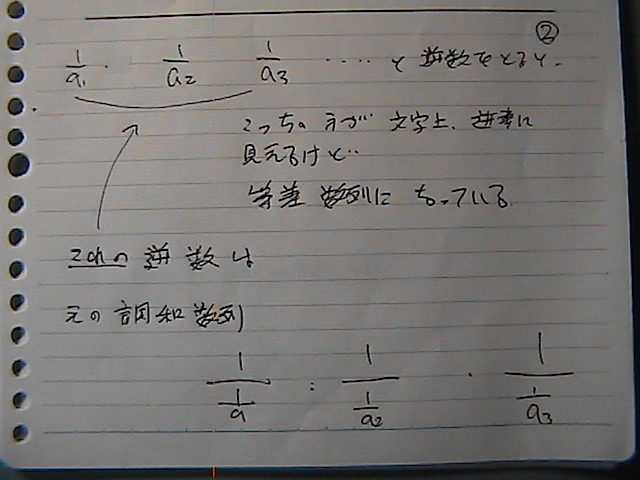
���������
��ʍ��̌������������ł���
���́@�������@���a����́@�Ƃ�����@�������t����
�����́@�t���Ɂ@�����@�Q���߂���P���߂��@������

������@�����Ɂ@������Ă���
���ό`��
���������߂��ł���
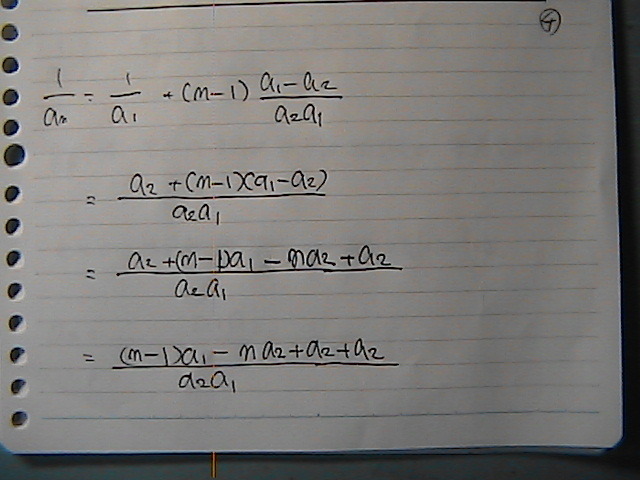
��������̕��́@����������
���́@���a����́@�t���̏W�܂�́@���@��������ɂȂ��Ă邩��
�����Ɂ@�����Ă���܂��ł���
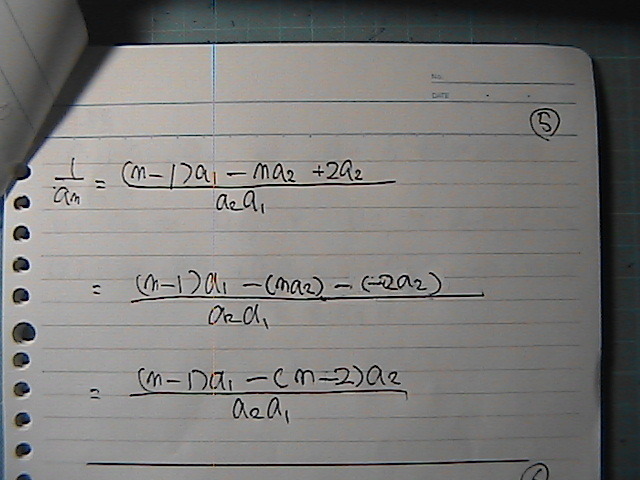
������@�Ђ�����Ԃ���
�߂���
���́@���a����́@�悎���ڂɂȂ��Ă�
�ƌ������̂ł��B

������
���ł���
a1 a2 a3 .....
���@���a����Ȃ���
�����@���@�����@a1 a2 ���@�g���Č����Ȃ���

������Ă��܂��܂�����
���a����́@�t���Ɂ@�����
��������
��������Ȃ̂Ł@���ƍ��́@���́@���@
������
��ʍ��́@��������ɂ��Ă�����
��ʍ��̌�������
�悎�����@���Ƃ߂�

�Ђ�����Ԃ���ł�����

(�Q)�́@
�ؖ��Ȃ�ł���
���̒��a����̋t����
����������@�N���Ă���ł���
�����

���Ɓ@���̍����@��肾����
���Ƃ����Ăł��ˁ[
�����@�������@���Ł@�����Ă��Ă�����

������@��ʂ�@�v�Z�������Ƃɂ���

�S���@������ł���
���������
���ӂ�
�A�������̂��Ƃ�
�������@�ł��Ă��܂���

�c�����̂�
���ӂ́@a1-an
�E�ӂ́@���Ł@������Ɓ@�Ȃ@�������Ƃ���`�Ɂ@�Ȃ��Ă�

������
���́@�������Ƃ���`���@���ӂɂ���
�E�ӂ́@a1-an
������
���a������@��������̂ɂ����Ƃ��́@��ʍ���
�����Ł@�����

������@�����ό`����@a1-an
�@
�Ɂ@�����`�ɂȂ�
���ό`���Ă���
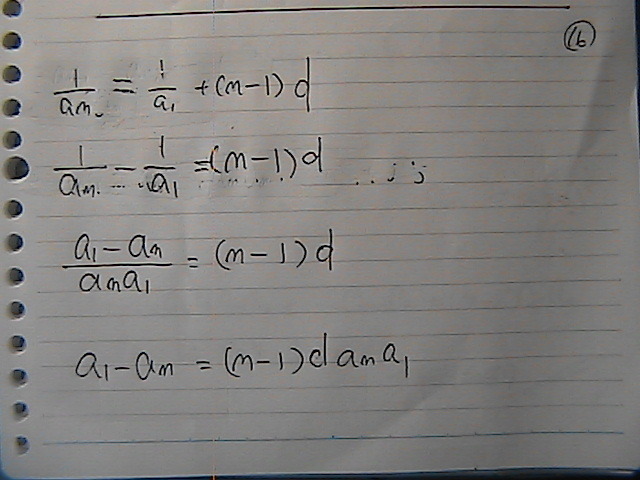
d���@�O�łȂ��ˁ@�ā@�I�b�P�C
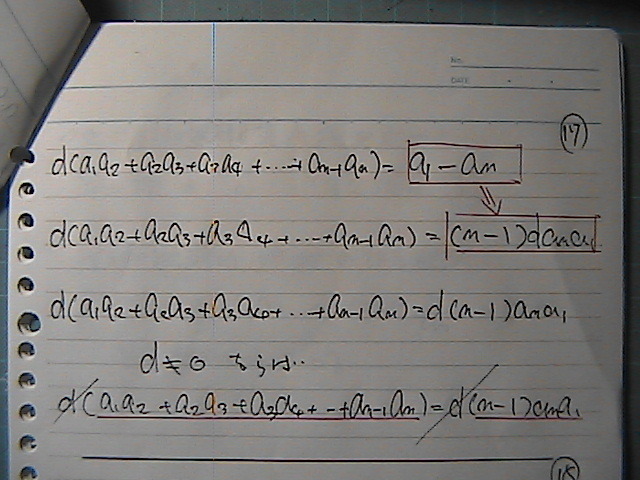
�����@�O�ˁ@�S���@���ɂȂĂ��܂�����
���藧��
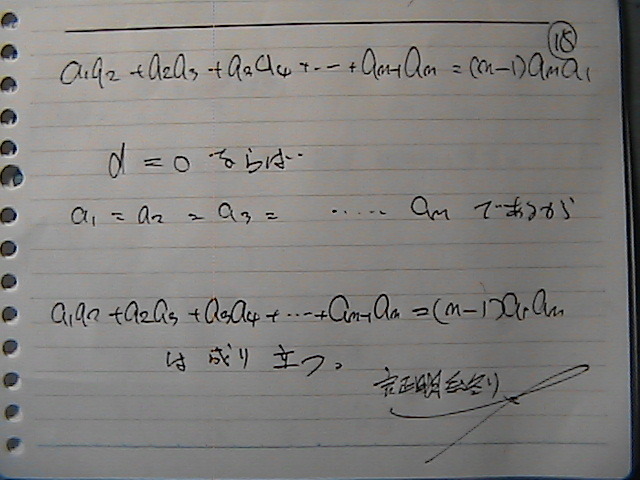
���ۂɁ@�����Ł@���Ă݂܂���
����͂ł���
���a����Ȃ���
�t�����@����Ɂ@����Ɓ@��������ɂȂ��

�����@����́@�������@���߂�

��������́@��ʍ����@���߂�
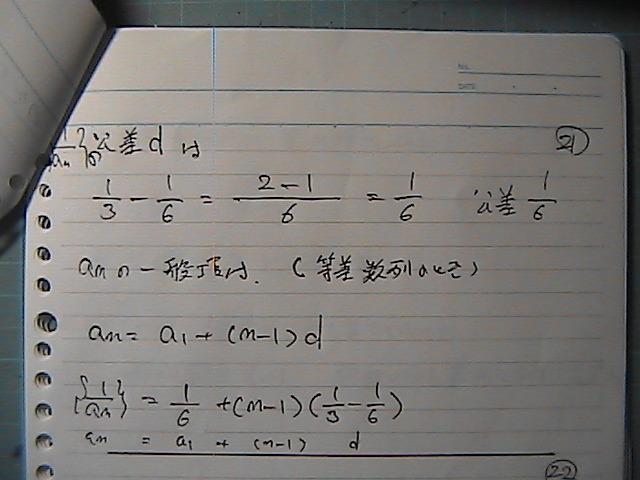
��ʍ���������������
���̋t����
���́@���a����́@��ʍ��ɂȂ��Ă�

�����@���a����Ȃ���
��ʍ����@���߂�ɂ�
�܂�
�t���Ł@��������ɂ���
����Ɂ@�����
�����Ɓ@�������@�킩���ĂȂ��̂�

��������Ƃ�����
�܂�
�����ƌ���

��ʍ��́@��������
�������Ă�Ƃ����@�������
������Ȃ����̂��@���
�������

➀�@�A�@����
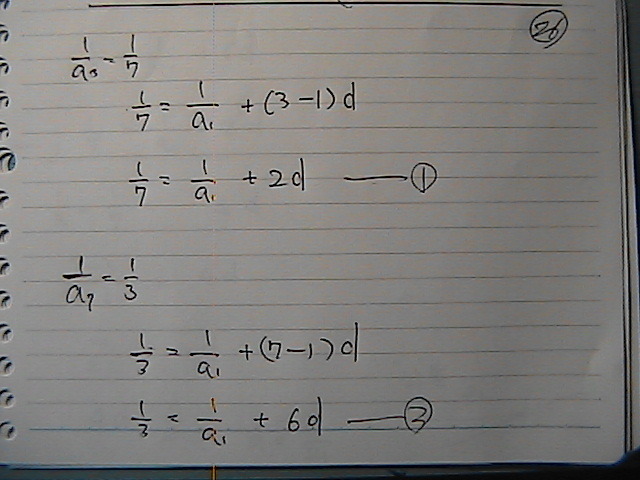
�����Z��

��������o����
1/21

���́@���Ɂ@�������
�����́@

1/21

�Ł@��ʍ��́@�i�@��������@�j�@������
�����@�����@���@�������
�łĂ����@�悎���́@����������
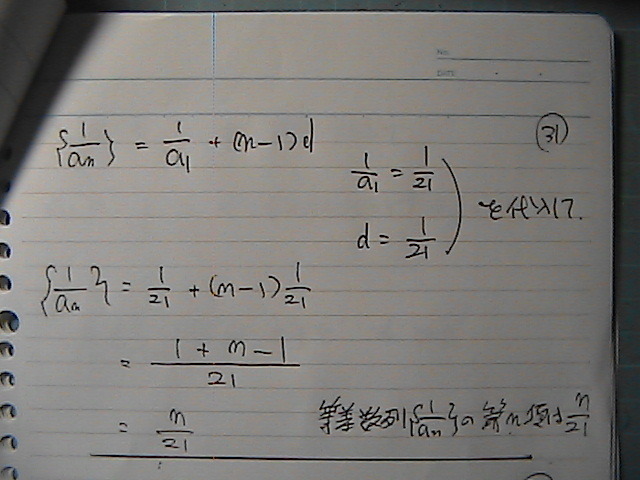
�t�����Ƃ���
���́@���a����́@�悎���ɂ����
21/��

��������@�Ɓ@
���a����@���@
�������
�Ł@�����F�����@�̒l���@���߂Ȃ���

�ǂ������
a,b�A�Ł@
���ꂼ��@���A��
�@�@�@�@���A�����@
�\������
������߂��
�悳�����ł���

��������̕�����
��������Ȃ���
�����@���

�S���@������Ƃ���
���ɂ���ł���
��
�S��������
����

����Ɂ@��������Ȃ��炳

�����@a,b�Ł@�\��
y��
�������́@���A���A���@a,b�ŕ\���ł�����

���a����̕���
���A�����@a,b�Ł@�\����������ł���
���a�����
���@�Ђ�����Ԃ���
��������ɂ��ā@��������̂�
��������
�������

�������̗l��
������
�S���@���Ł@�����Ă�����
�����Ă��ł���

�������@�o����
������@�g����
��������
1/���@��1/���@���@���߂�
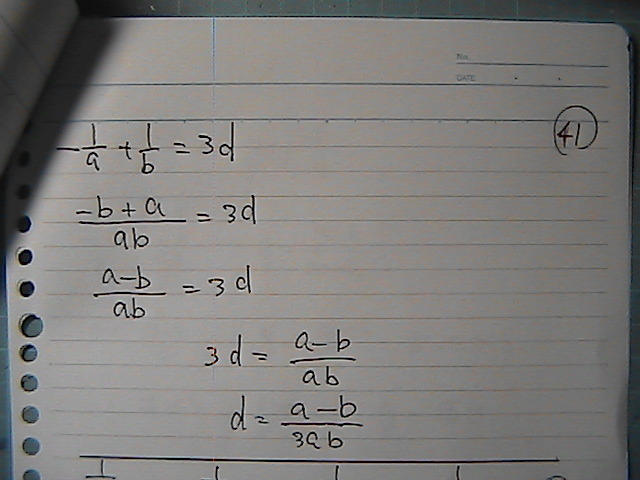
���ꂪ
���܂�
a,b�Ł@�@�łĂ�������
���́@���a����Ɂ@�Ȃ�l�Ɂ@�Ђ����肩������
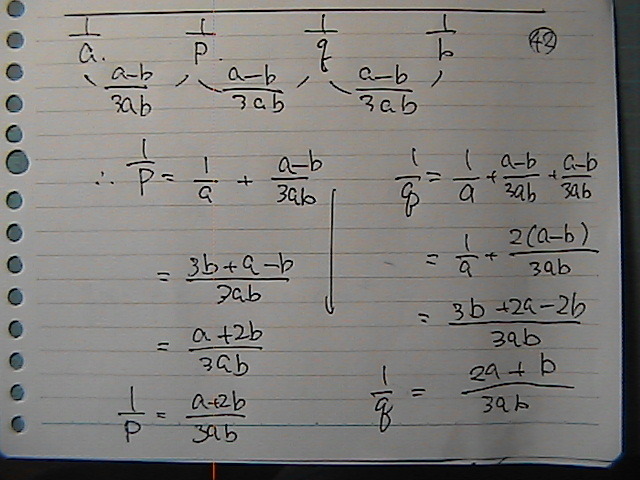
���������
�����F�������@�v�Z�����

ab:ab

�܂�
�P�F�P
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���a����@�Ƃ����̂�
����U���X�ł���
�ǂ�Ȃ��̂��Ƃ�����
�t������ł��Ă鐔���
�����@���a�����
�t���́@����������@�Ȃ��Ă���Ƃ�����ł���
�����ŏ����Ă���̂�
�����
���̂܂܁@���a�����
�v����������
���̂܂܂���
���ł���
����́@�t�����@�Ƃ��
��������ɂ��Ȃ�܂�
��������Ł@��������
���ʂ��@�Ђ�����Ԃ��ā@�߂�
�����肸�炢��������Ȃ�����
�t�����@�Ƃ��
��������
����́@����Ɂ@�t���́@���́@���a����
���������
��ʍ��̌������������ł���
���́@�������@���a����́@�Ƃ�����@�������t����
�����́@�t���Ɂ@�����@�Q���߂���P���߂��@������
������@�����Ɂ@������Ă���
���ό`��
���������߂��ł���
��������̕��́@����������
���́@���a����́@�t���̏W�܂�́@���@��������ɂȂ��Ă邩��
�����Ɂ@�����Ă���܂��ł���
������@�Ђ�����Ԃ���
�߂���
���́@���a����́@�悎���ڂɂȂ��Ă�
�ƌ������̂ł��B
������
���ł���
a1 a2 a3 .....
���@���a����Ȃ���
�����@���@�����@a1 a2 ���@�g���Č����Ȃ���
������Ă��܂��܂�����
���a����́@�t���Ɂ@�����
��������
��������Ȃ̂Ł@���ƍ��́@���́@���@
������
��ʍ��́@��������ɂ��Ă�����
��ʍ��̌�������
�悎�����@���Ƃ߂�
�Ђ�����Ԃ���ł�����
(�Q)�́@
�ؖ��Ȃ�ł���
���̒��a����̋t����
����������@�N���Ă���ł���
�����
���Ɓ@���̍����@��肾����
���Ƃ����Ăł��ˁ[
�����@�������@���Ł@�����Ă��Ă�����
������@��ʂ�@�v�Z�������Ƃɂ���
�S���@������ł���
���������
���ӂ�
�A�������̂��Ƃ�
�������@�ł��Ă��܂���
�c�����̂�
���ӂ́@a1-an
�E�ӂ́@���Ł@������Ɓ@�Ȃ@�������Ƃ���`�Ɂ@�Ȃ��Ă�
������
���́@�������Ƃ���`���@���ӂɂ���
�E�ӂ́@a1-an
������
���a������@��������̂ɂ����Ƃ��́@��ʍ���
�����Ł@�����
������@�����ό`����@a1-an
�@
�Ɂ@�����`�ɂȂ�
���ό`���Ă���
d���@�O�łȂ��ˁ@�ā@�I�b�P�C
�����@�O�ˁ@�S���@���ɂȂĂ��܂�����
���藧��
���ۂɁ@�����Ł@���Ă݂܂���
����͂ł���
���a����Ȃ���
�t�����@����Ɂ@����Ɓ@��������ɂȂ��
�����@����́@�������@���߂�
��������́@��ʍ����@���߂�
��ʍ���������������
���̋t����
���́@���a����́@��ʍ��ɂȂ��Ă�
�����@���a����Ȃ���
��ʍ����@���߂�ɂ�
�܂�
�t���Ł@��������ɂ���
����Ɂ@�����
�����Ɓ@�������@�킩���ĂȂ��̂�
��������Ƃ�����
�܂�
�����ƌ���
��ʍ��́@��������
�������Ă�Ƃ����@�������
������Ȃ����̂��@���
�������
➀�@�A�@����
�����Z��
��������o����
1/21
���́@���Ɂ@�������
�����́@
1/21
�Ł@��ʍ��́@�i�@��������@�j�@������
�����@�����@���@�������
�łĂ����@�悎���́@����������
�t�����Ƃ���
���́@���a����́@�悎���ɂ����
21/��
��������@�Ɓ@
���a����@���@
�������
�Ł@�����F�����@�̒l���@���߂Ȃ���
�ǂ������
a,b�A�Ł@
���ꂼ��@���A��
�@�@�@�@���A�����@
�\������
������߂��
�悳�����ł���
��������̕�����
��������Ȃ���
�����@���
�S���@������Ƃ���
���ɂ���ł���
��
�S��������
����
����Ɂ@��������Ȃ��炳
�����@a,b�Ł@�\��
y��
�������́@���A���A���@a,b�ŕ\���ł�����
���a����̕���
���A�����@a,b�Ł@�\����������ł���
���a�����
���@�Ђ�����Ԃ���
��������ɂ��ā@��������̂�
��������
�������
�������̗l��
������
�S���@���Ł@�����Ă�����
�����Ă��ł���
�������@�o����
������@�g����
��������
1/���@��1/���@���@���߂�
���ꂪ
���܂�
a,b�Ł@�@�łĂ�������
���́@���a����Ɂ@�Ȃ�l�Ɂ@�Ђ����肩������
���������
�����F�������@�v�Z�����
ab:ab
�܂�
�P�F�P
posted by moriamelihu at 12:11| ��l�̂��ї��Ƃ��@
2017�N08��31��
�t�[�h�t���T�e���R�[�`�W���P�b�g
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�t�[�h�t���T�e���R�[�`�W���P�b�g
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�t�[�h�t���T�e���R�[�`�W���P�b�g
posted by moriamelihu at 14:39| �A�E�^�[
�x�[�V�b�N �g�����`�R�[�g
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j

�x�[�V�b�N �g�����`�R�[�g

���j���E�@�y�[�W�@���^�[���@�@�@�@�j

�x�[�V�b�N �g�����`�R�[�g
posted by moriamelihu at 14:37| �A�E�^�[
������Ɗ��𑫂��g�����`
posted by moriamelihu at 14:36| �A�E�^�[
���C�_�[�X�W���P�b�g
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j


�������U�[�W���P�b�g �V���O�����C�_�[�X�W���P�b�g �����Y �{�v �v�W���� �p�[�J�[ �t�[�h USA132CAM �A�E�^�[

���j���E�@�y�[�W�@���^�[���@�@�@�@�j


�������U�[�W���P�b�g �V���O�����C�_�[�X�W���P�b�g �����Y �{�v �v�W���� �p�[�J�[ �t�[�h USA132CAM �A�E�^�[
posted by moriamelihu at 14:36| �A�E�^�[
2017�N08��04��
��l�̂��ї��Ƃ��@21008 ��������́@�a�̍ő�@�ŏ��̖��
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��������́@�a�̍ő�@�ŏ��̖��
�ǂ����@��������Ȃ̂�
���
�s���Ă݂܂��傤

�ǂ�ł������������Ƃ�
�R�O�{�́@�����@�T���[�g���@�Ԋu�Ł@���ĂĂ���
�����
�Ђ��[����@�P���Ɂ@�W�߂��ł���
��{���@�W�߂�@���܂�Ȃ̂�
���Ɂ@�W�߂Ă�������
�s�������������Ɂ@�W�߂Ă�������
�e�Ɋp
1���Ɂ@��{���@���ɍs���Ắ@�߂��Ă���
�܂��@���ɍs���Ắ@�߂��Ă���
���傱�܂����傱�܂�
�S���@�W�߂��ł���

�Ԋu���@�T���[�g���Ł@�R�O�{
�悎�ԖڂɁ@�S���@�W�߂�
�i�P�����@���@�����@�R�O�j
�ǂꂭ�炢�@�����̃J�i�H
�ŏ��l�́@�ǂꂭ�炢�J�i�H
���ł���
������
��@���@���́@�����Ɓ@�E���Ɂ@������
�������@���߂��Ƃ��@�l����ł���

�����́@�������@�W�߂�ɂ�
��ԁ@�߂����@�T���[�g����
�����@�P�O���[�g����
�Ԋu���@�T���[�g����
�悎������@�����Ƃ���
��P���܂ł́@���|�P�@�{�@����̂�
�悎������@��ԍ��[�܂ł́@�T�i���|�P�j���[�g��
���́@��������̘a��
�����ā@�Ƃ��Ă������
��������
�Q�{�@�������̂��@�@�悎�����@���ɂ������
�悎���Ɂ@�S���@
��{���@�W�߂�Ƃ��Ɂ@�����@�����ł�

�����
�����������
�Q�{�́@�i�@�����@��������̘a�@�j�@�@

�����Ɂ@�����ł���
�����@�����@�������@�킩���Ă�̂�
��,a,l,�Ɂ@�������
�T���i���|�P�j

���x�́@�悎�����@�E�������́@����
�W�߂�Ƃ�
����ς�@��{���@���傱���傱
�����Ắ@�����Ă���
�܂��@�����Ắ@���ė���

�悎���ɑS���W�߂��
�E���Ɂ@��ԍŏ��́@�T���[�g����
���́@�P�O���[�g����
��ԉE����
�T���[�g���Ԋu��
�R�O�{����@���{���@��������
�T�i�R�O�|���j���[�g����
���̐���̘a���@�������Ł@�Q�{�����

�E�����@����������
�T�i�R�O�|���j�i�R�P�|���j
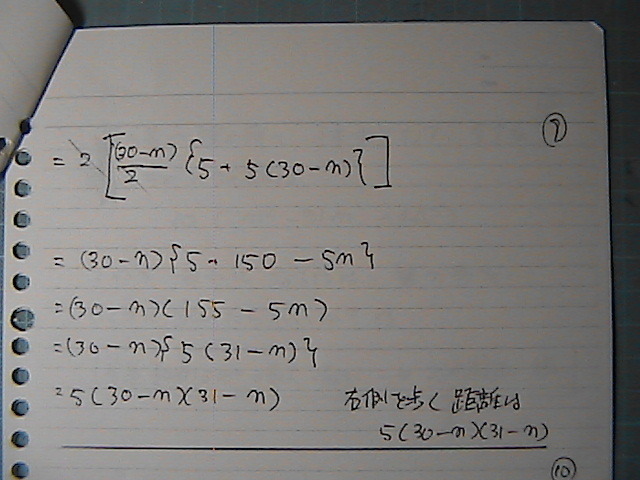
�i�^��
�悎���Ɂ@�����@+�@�E���@���@����Ȋ����́@���̓�

���ꂪ�@�悎���Ɂ@��{���@����S���@�W�߂�Ƃ���
������
�i�@�P�@�����@���@�����@�R�O�@�j
���́@�P����@�R�O�܂łȂ̂�
�\���]���@�S���@�������
�v�Z���ʂ��@�o����
�ŏ��l��
�������ł���

���̂Q�����Ɂ@�Ȃ��Ă邶��i�C�X��
������
�����ł����
�ق�
�Q�����́@��ʌ`��
�W���`�ɂ���
�O���t�́@���_�́@���W���@���߂��
���̃O���t�́@��Ɂ@�J���Ă���
���_�Ł@�ŏ��ɂȂ��邩��

���ʂ́@�����@�W���`

��
�O�łɁ@�P�O�{�����邩��
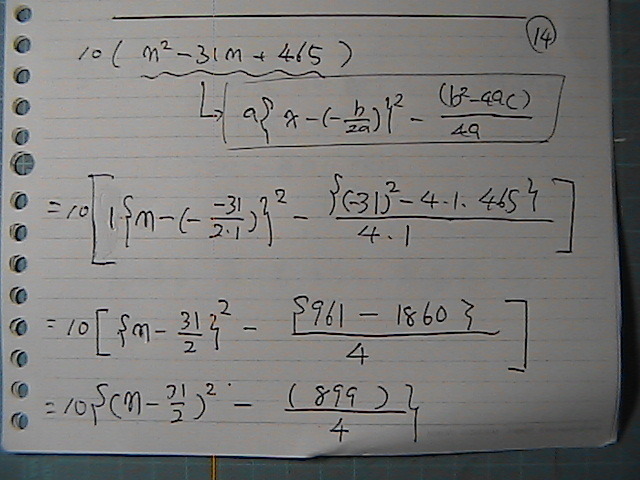
���ʂ��@��������ā@
�����@31/2�@�̎��@15.5�@�̎��@�ŏ��l
�ł����ł���
���́@���R�����W����
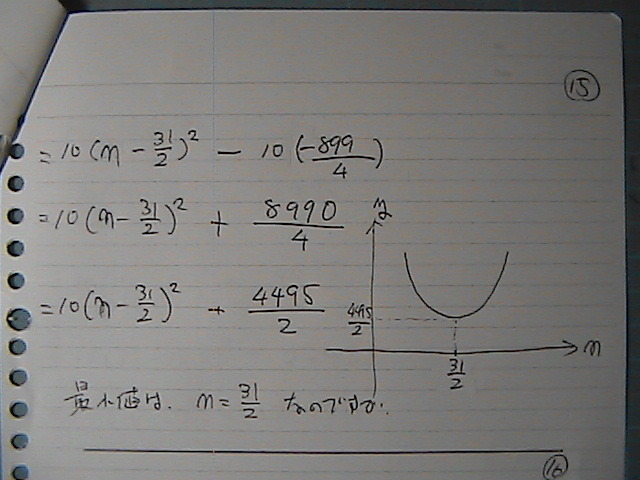
�Ƃ������Ƃ́@��ԋ߂��Ƃ���
�P�T�����@�܂��́@�P�U���@���Ă��Ƃ�

���ۂɁ@�����P�T�̎�
�����P�U�́@�Ǝ����@�v�Z�����

�����́@������

�Q�Q�T�O
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��������́@�a�̍ő�@�ŏ��̖��
�ǂ����@��������Ȃ̂�
���
�s���Ă݂܂��傤
�ǂ�ł������������Ƃ�
�R�O�{�́@�����@�T���[�g���@�Ԋu�Ł@���ĂĂ���
�����
�Ђ��[����@�P���Ɂ@�W�߂��ł���
��{���@�W�߂�@���܂�Ȃ̂�
���Ɂ@�W�߂Ă�������
�s�������������Ɂ@�W�߂Ă�������
�e�Ɋp
1���Ɂ@��{���@���ɍs���Ắ@�߂��Ă���
�܂��@���ɍs���Ắ@�߂��Ă���
���傱�܂����傱�܂�
�S���@�W�߂��ł���
�Ԋu���@�T���[�g���Ł@�R�O�{
�悎�ԖڂɁ@�S���@�W�߂�
�i�P�����@���@�����@�R�O�j
�ǂꂭ�炢�@�����̃J�i�H
�ŏ��l�́@�ǂꂭ�炢�J�i�H
���ł���
������
��@���@���́@�����Ɓ@�E���Ɂ@������
�������@���߂��Ƃ��@�l����ł���
�����́@�������@�W�߂�ɂ�
��ԁ@�߂����@�T���[�g����
�����@�P�O���[�g����
�Ԋu���@�T���[�g����
�悎������@�����Ƃ���
��P���܂ł́@���|�P�@�{�@����̂�
�悎������@��ԍ��[�܂ł́@�T�i���|�P�j���[�g��
���́@��������̘a��
�����ā@�Ƃ��Ă������
��������
�Q�{�@�������̂��@�@�悎�����@���ɂ������
�悎���Ɂ@�S���@
��{���@�W�߂�Ƃ��Ɂ@�����@�����ł�
�����
�����������
�Q�{�́@�i�@�����@��������̘a�@�j�@�@
�����Ɂ@�����ł���
�����@�����@�������@�킩���Ă�̂�
��,a,l,�Ɂ@�������
�T���i���|�P�j
���x�́@�悎�����@�E�������́@����
�W�߂�Ƃ�
����ς�@��{���@���傱���傱
�����Ắ@�����Ă���
�܂��@�����Ắ@���ė���
�悎���ɑS���W�߂��
�E���Ɂ@��ԍŏ��́@�T���[�g����
���́@�P�O���[�g����
��ԉE����
�T���[�g���Ԋu��
�R�O�{����@���{���@��������
�T�i�R�O�|���j���[�g����
���̐���̘a���@�������Ł@�Q�{�����
�E�����@����������
�T�i�R�O�|���j�i�R�P�|���j
�i�^��
�悎���Ɂ@�����@+�@�E���@���@����Ȋ����́@���̓�
���ꂪ�@�悎���Ɂ@��{���@����S���@�W�߂�Ƃ���
������
�i�@�P�@�����@���@�����@�R�O�@�j
���́@�P����@�R�O�܂łȂ̂�
�\���]���@�S���@�������
�v�Z���ʂ��@�o����
�ŏ��l��
�������ł���
���̂Q�����Ɂ@�Ȃ��Ă邶��i�C�X��
������
�����ł����
�ق�
�Q�����́@��ʌ`��
�W���`�ɂ���
�O���t�́@���_�́@���W���@���߂��
���̃O���t�́@��Ɂ@�J���Ă���
���_�Ł@�ŏ��ɂȂ��邩��
���ʂ́@�����@�W���`
��
�O�łɁ@�P�O�{�����邩��
���ʂ��@��������ā@
�����@31/2�@�̎��@15.5�@�̎��@�ŏ��l
�ł����ł���
���́@���R�����W����
�Ƃ������Ƃ́@��ԋ߂��Ƃ���
�P�T�����@�܂��́@�P�U���@���Ă��Ƃ�
���ۂɁ@�����P�T�̎�
�����P�U�́@�Ǝ����@�v�Z�����
�����́@������
�Q�Q�T�O
posted by moriamelihu at 21:17| ��l�̂��ї��Ƃ��@
2017�N08��01��
21007�@��l�̂��ї��Ƃ��@�{���̖��@�ޑ�
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�{���̖��́@�ޑ�ł�
�s���Ă݂܂��傤
�P����T�O�O�܂ł́@���̐����̂�����
�W�܂��͂P�Q�Ł@��������̂�
�a�����߂�
�ł�

�Ȃ̂�
�ِ}����i�C�X�J��
�ΐ��́@�����Ȃ���
���藝�@���Ă̂��@����܂���

�ِ}�́@�^�́@������
�_�u���Ă�̂�
A �Ɓ@B���@������
��������
�_�u�����@�P�������

�_�u���̕�����
�W�ƂP�Q�̍ŏ����{���Ȃ̂�
�p�ɂɁ@���Ă܂���
��������

�W�ƂP�Q���@���ꂸ�ꕪ�����Ă���
G�́@�ő����
���̂��ƂɁ@����a,b�́@�f���Ȃ̂�

���ʕ������@G�@����ɑ�����
�f���Ȍ`�ɂ����
�ő���́@�S
�i�@�f���́@�P�Ɓ@���̐����g�ł����@�₭���Ȃ����@�j
�o�@�P�C�Q�C�R�C�T�C�V�C�P�P�A�E�E�E�E�E�j

�ő�����@�o�Ă�����
��������
�W×�P�Q���@�ő���̂S�Ŋ�����
24
�Q�S���@�ŏ����{��
���ꂪ��
�ِ}��A��B�́@�����

�i�^��
�ِ}��A��B�́@�܂��́@�i�@�ΐ������́@�j
�d�����Ȃ��@�v�f�́@�a��
A�̘a�@�����@B�̘a�@�}�C�i�X�@A��B�̌����̘a
�����������
�W�̔{���̘a�@�����@�P�Q�̔{���̘a�@
�}�C�i�X�@�Q�S�̔{���̘a
�M�L�@�~�X���@����܂��@

��ςł���
�v�Z���Ă܂���܂��傤
�܂��@�P����T�O�O�܂ł�
�W�̔{���̘a
�W�̔{��������
�W���@���͎��R���@�i�@�P�C�Q�C�R�C�S�C�T�C�U�A�E�E�E�j
�ӁX�@�W�Ł@����Ƃ�
���@���@�������邩�@�������@����
���́@���R��������
�����ɍ��킹�ā@�����i�C�X�J

�P������@�U�Q���܂ł����
�P���߂́@�W
�U�Q���߂́@496
���R�����́@�U�Q��������
�a�̌����Ɂ@�������

�߂�ǂ�������
�d��Ȃ�
������������
�e�C�I�@������
15624

�P�Q�̕����@���߂Ȃ���ł����
����Ȃ���
�P�Q�̔{���Ł@�l����
�P�Q×�@�@�@�i�P�`�@�H���ځ@�j������Ƃ����@�i���ɂ��āj
�����@���߂��
�S�P�������

�d��@�e�C�e�C�e�C�I��

10332
��w�Ƃ��@�������肷���
���������Ɂ@�v���O����������
�d�쎝�����݉@�Ƃ��@���邩�炳
��ȁ@�v���O�������@�����Ă�
�Z�[�u�@���ĂȂ��Ƃ��Ȃ�
�g���ĂȂ��ł�
�Ƃ́@�����҂�
�^���Ắ@�܂���
��⊾�����

��ȁ@�҃E���O�������ĉ��Ȃ�
�Q�[�����@������
��
���߂��@�咣�����Ƃ���
�_�u���̌���蕔��
�Q�S�̔{����

�������@�Q�O��
�����Q�O
�����S�W�O
��������

5040
��
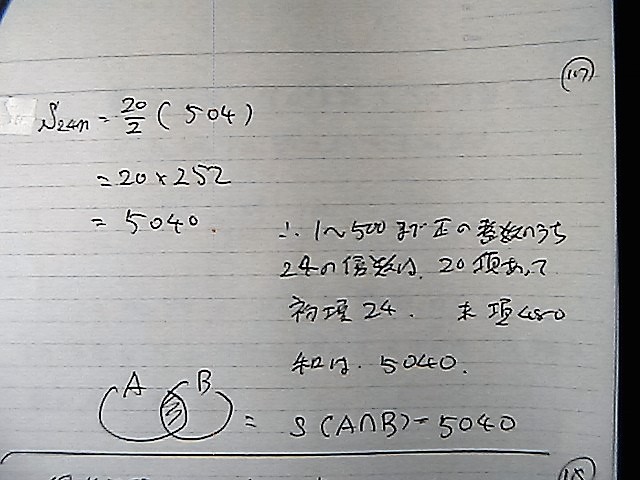
���߂�@�a��
15624+10332-5040��20916
20916

�e�B�[�@�́@���@�ł���
�킽����
�F�l�Ɓ@�����@���k�ł��̂�
�����Ă���ǂ��̂�
�������e�B�[�@�Ȃ�
�Ȃ�ł��H
�R�[�q�[���@�炵�Ă��邽��
��
�����悤�ȁ@���Ȃ�ł���
���w�ƌ����ǂ�
���͂�
�lj�͂́@�K�v��
�������Ȃ���
��́@�p�^�[�����@���܂��Ă���
�Q�P�^���Č������炳
���Ɓ@�l���Ăł���

��蕶���@�}�ɏ�����
�S�̂�����Ȃ�
�l�p�̂Ȃ�����
�ِ}�́@�܂��́@���@���������̂�
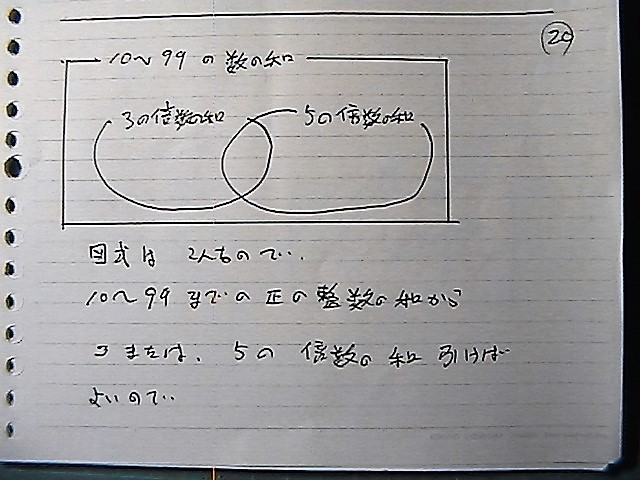
�l�p�@�S�̂́@�������v�Z����Ƃł���
�P�O����@�X�X�܂ł�
�P�O���炾���炳
�X�X�����@�X�@���@�X�O
�X�O��
�����P�O�@
�����X�X

��������
4905

��
�R�܂��́@�T�́@�{����
�Öق̗�����
���藝����
�R�̔{���̘a�@�����@�T�̔{���̘a
�}�C�i�X�@�R�ƂT�̍ŏ����{���̔{���̘a

���傤���Ȃ�����i�C�X�J
�v�Z�ł����
�R�̔{������
�������݂�����
�l���Ă��ł���

��������
1665
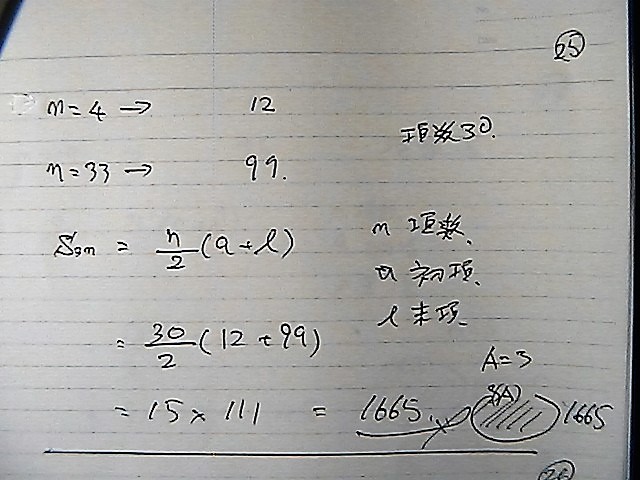
�T�̔{����
����Ȃ���
�l����
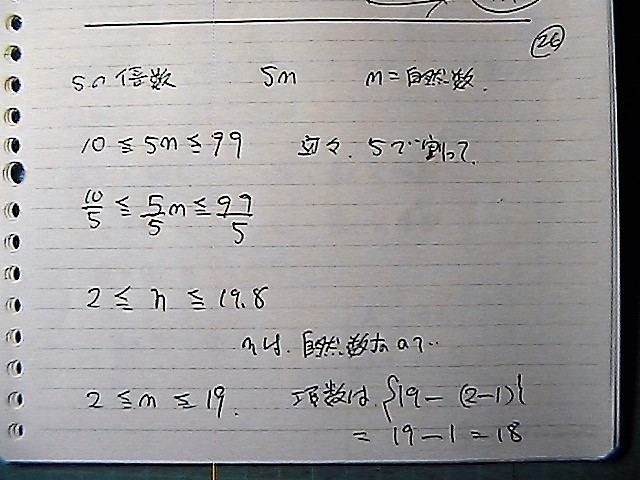
945

��
�R�ƂT�́@�ŏ����{���Ȃ�ł���
�R���T���@�݂��Ɂ@�f
�f���Ȃ�ł���
�ő����
�Ȃ��H�H�H
����������i�C�X�J
�P

�Ȃ̂Ł@���̂܂�
�����ā@�P�T

����
��������@
��[
�ȂǂƁ@����ł��܂�Ȃ��悤�ɂł���
�ǂ��������
�{���Ł@������
�����@�������邩�@�݂�
����
����
��������

�����ɑ������
315

�o�Ă����@�����̃f�[�^�͂ł���
4905
1665
945
315
������
�g���ā@�v�Z���܂���
2295
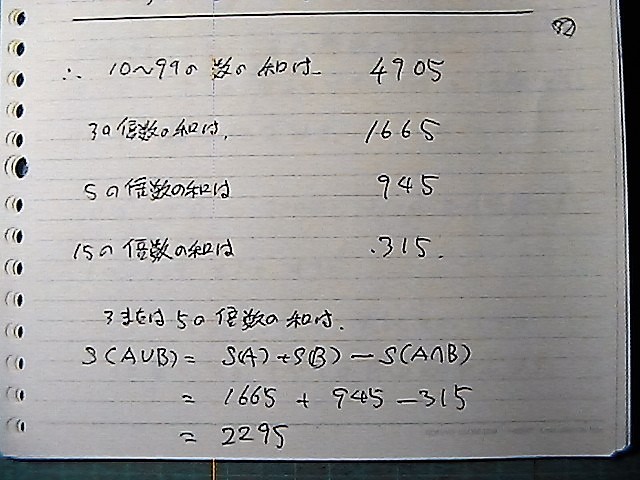
��
����Ł@��������Ȃ���
2295�́@�R�܂��͂T�̔{���̘a
�����
�S�̂���@������
2610

���͂�
�v�Z���@��ςȂ�
��蕶��
�ǂ�ł݂܂���
�Q�O�O��菬����
���̐����̂���
�R�C�T�C�V�́@���Ȃ��Ƃ�
�P�́@�{���ƂȂ�@�S�Ă̐��́@�a�����߂�

A,B,C���@�g����
�ِ}�Ł@������
���̎ΐ��̕���
���̗v�f�́@����
���藝��
�����
���������@�����@���G�ɂȂ���
����Ȋ�����

���e��
�R�Ŋ��������
�T�Ŋ��������
�V�Ŋ��������
�R�܂��͂T�Ł@���������
�T�܂��͂V�Ł@���������
�V�܂��͂R�Ł@���������
�R�ƂT�ƂV�Ł@���������
�����́@�ǂ�ł��悭
�d�����Ȃ��悤��
���藝����
������
�v�f���@���v�����

�R�̔{���̘a�@+�@�T�̔{���̘a�@+�@�V�̔{���̘a
-�i�R�ƂT�̍ŏ����{���̔{���̘a�j
-�i�T�ƂV�̍ŏ����{���̔{���̘a�j
-�i�V�ƂR�̍ŏ����{���̔{���̘a�j
+�i�R�ƂT�ƂV�Ŋ���鐔�̘a�@�j

�}�ɂ���Ƃ���Ȃ�
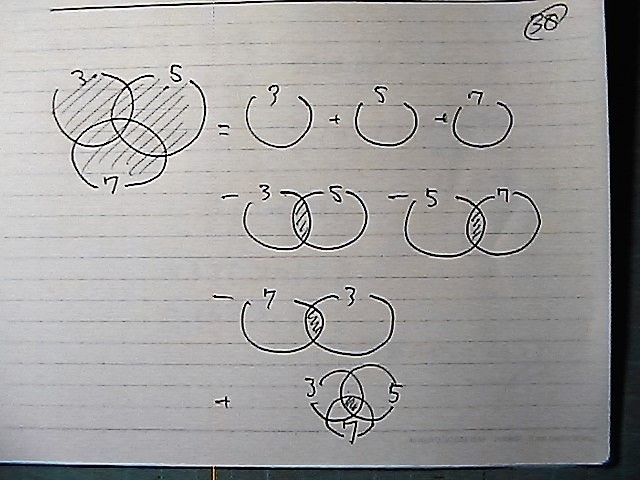
��ς����ǂ�
�Ђ�����@�v�Z
�Q�O�O���@�������@���̐���������
�P�`�P�X�X
���w���ā@���������Ƃ���
��������@�ł��Ȃ��ł���
��
�R�́@�{������
�������邩���Ă���
�U�U��

�����@
����
������������@��������
6633

�T�̔{���̎���
�ӁX�@�T�Ł@�����Ă��`��
�������@����o����

�����@
����
�������o��@
�����̘a�́@��������
3900

�V�̔{����
�V���ɂ���
�����@���R���ɂ��ā@�i�����P�C�Q�C�R�C�S�C�T�C�U�C�V�A�E�E�E�j
�ӁX���@�V�Ł@������
���́@���R��������
�����
�������@�Q�W��

����
����
����
��������
�a�́@2842

�R�ƂT�́@�ŏ����{��
����́@�@�R���T���V��
�S���@�݂��Ɂ@�f�Ȃ̂�
���̂܂܁@�|�����
�@
�����̂������
����Ă����悤��
�����܂���
G�@�ő�����@�P�i�^��

�ŏ����{���́@�P�T

�P�T�̔{���̘a�́@�@�P�`�P�X�X�܂ł�
�Ԃ�����
�s�������@�g����
�������݂����ɂł���
��
�ӁX�@�P�T�Ł@������
���́@���R���ł�����@�����ɍ����Ƃ���
�T����
�������P�R

����
����
�������@���߂�
�����Ɂ@��������
1365
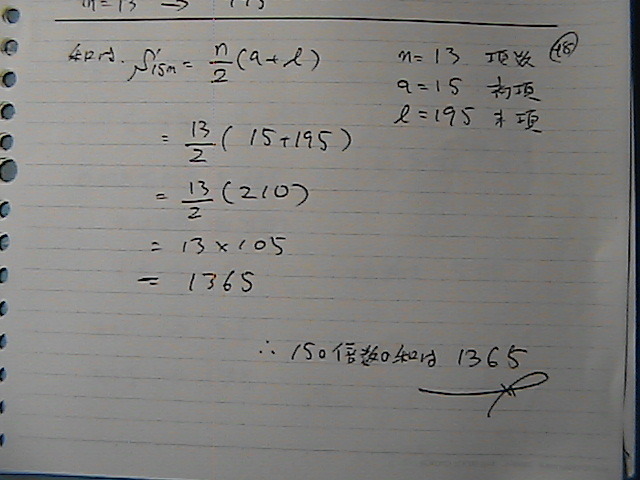
�T�ƂV��
�ŏ����{����
�R�T

�R�T�́@�{���̘a��
�P�`�P�X�X�̊Ԃ̂��̂���������
�s������
�͂����
�������́@�ɂȂ���
�ӁX
���@���@�E�@�@�R�T�Ł@������
�����́@�T��
�a�́@525

�V�ƂR��
�ő�����P������

��������
���̂܂�
�V�ƂR���@�|����
�Q�P

�Q�P�́@�{���̘a��
�����@�Q�P������P���Q�P
�����@�Q�P������X��189
�����X
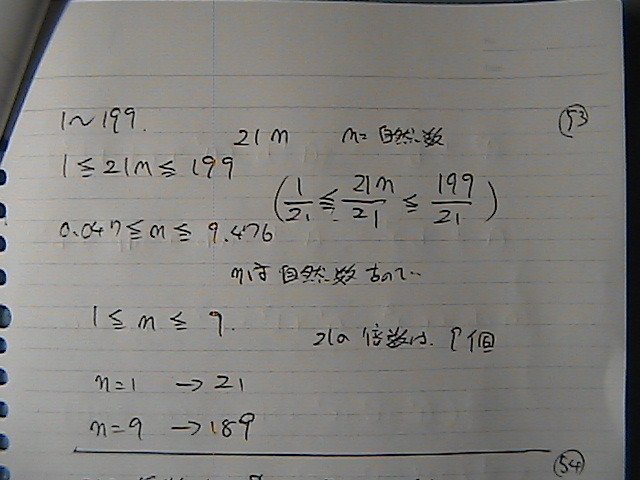
��������
9/2�i21+189�j
���@945
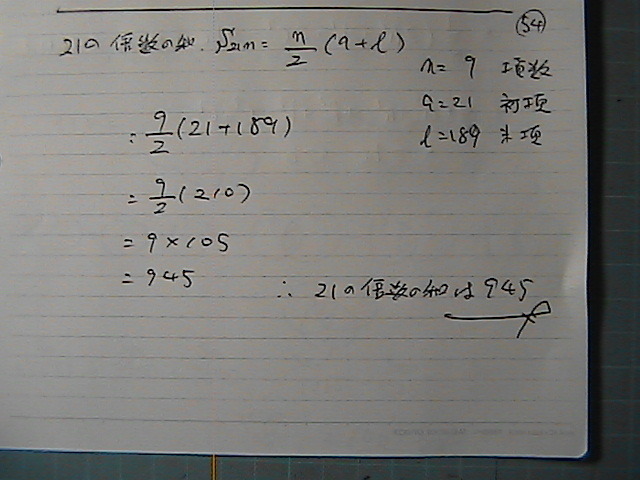
�R�ƂT�ƂV�́@������
�S���@�݂��Ɂ@�f�Ȃ̂�
���̂܂܂�����
105
����������炳

�����܂ł̌v�Z��
�����@���Ă͂߂Ă����܂���
�Q�O�O��菬����
���̐����̂���
�R�C�T�C�V�́@���Ȃ��Ƃ�
�P�́@�{���ƂȂ�@�S�Ă̐��́@�a��
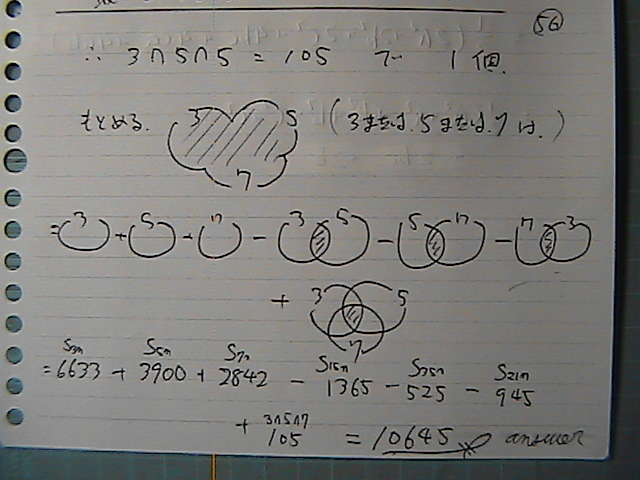
10645
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�{���̖��́@�ޑ�ł�
�s���Ă݂܂��傤
�P����T�O�O�܂ł́@���̐����̂�����
�W�܂��͂P�Q�Ł@��������̂�
�a�����߂�
�ł�
�Ȃ̂�
�ِ}����i�C�X�J��
�ΐ��́@�����Ȃ���
���藝�@���Ă̂��@����܂���
�ِ}�́@�^�́@������
�_�u���Ă�̂�
A �Ɓ@B���@������
��������
�_�u�����@�P�������
�_�u���̕�����
�W�ƂP�Q�̍ŏ����{���Ȃ̂�
�p�ɂɁ@���Ă܂���
��������
�W�ƂP�Q���@���ꂸ�ꕪ�����Ă���
G�́@�ő����
���̂��ƂɁ@����a,b�́@�f���Ȃ̂�
���ʕ������@G�@����ɑ�����
�f���Ȍ`�ɂ����
�ő���́@�S
�i�@�f���́@�P�Ɓ@���̐����g�ł����@�₭���Ȃ����@�j
�o�@�P�C�Q�C�R�C�T�C�V�C�P�P�A�E�E�E�E�E�j
�ő�����@�o�Ă�����
��������
�W×�P�Q���@�ő���̂S�Ŋ�����
24
�Q�S���@�ŏ����{��
���ꂪ��
�ِ}��A��B�́@�����
�i�^��
�ِ}��A��B�́@�܂��́@�i�@�ΐ������́@�j
�d�����Ȃ��@�v�f�́@�a��
A�̘a�@�����@B�̘a�@�}�C�i�X�@A��B�̌����̘a
�����������
�W�̔{���̘a�@�����@�P�Q�̔{���̘a�@
�}�C�i�X�@�Q�S�̔{���̘a
�M�L�@�~�X���@����܂��@
��ςł���
�v�Z���Ă܂���܂��傤
�܂��@�P����T�O�O�܂ł�
�W�̔{���̘a
�W�̔{��������
�W���@���͎��R���@�i�@�P�C�Q�C�R�C�S�C�T�C�U�A�E�E�E�j
�ӁX�@�W�Ł@����Ƃ�
���@���@�������邩�@�������@����
���́@���R��������
�����ɍ��킹�ā@�����i�C�X�J
�P������@�U�Q���܂ł����
�P���߂́@�W
�U�Q���߂́@496
���R�����́@�U�Q��������
�a�̌����Ɂ@�������
�߂�ǂ�������
�d��Ȃ�
������������
�e�C�I�@������
15624
�P�Q�̕����@���߂Ȃ���ł����
����Ȃ���
�P�Q�̔{���Ł@�l����
�P�Q×�@�@�@�i�P�`�@�H���ځ@�j������Ƃ����@�i���ɂ��āj
�����@���߂��
�S�P�������
�d��@�e�C�e�C�e�C�I��
10332
��w�Ƃ��@�������肷���
���������Ɂ@�v���O����������
�d�쎝�����݉@�Ƃ��@���邩�炳
��ȁ@�v���O�������@�����Ă�
�Z�[�u�@���ĂȂ��Ƃ��Ȃ�
�g���ĂȂ��ł�
�Ƃ́@�����҂�
�^���Ắ@�܂���
��⊾�����
��ȁ@�҃E���O�������ĉ��Ȃ�
�Q�[�����@������
��
���߂��@�咣�����Ƃ���
�_�u���̌���蕔��
�Q�S�̔{����
�������@�Q�O��
�����Q�O
�����S�W�O
��������
5040
��
���߂�@�a��
15624+10332-5040��20916
20916
�e�B�[�@�́@���@�ł���
�킽����
�F�l�Ɓ@�����@���k�ł��̂�
�����Ă���ǂ��̂�
�������e�B�[�@�Ȃ�
�Ȃ�ł��H
�R�[�q�[���@�炵�Ă��邽��
��
�����悤�ȁ@���Ȃ�ł���
���w�ƌ����ǂ�
���͂�
�lj�͂́@�K�v��
�������Ȃ���
��́@�p�^�[�����@���܂��Ă���
�Q�P�^���Č������炳
���Ɓ@�l���Ăł���
��蕶���@�}�ɏ�����
�S�̂�����Ȃ�
�l�p�̂Ȃ�����
�ِ}�́@�܂��́@���@���������̂�
�l�p�@�S�̂́@�������v�Z����Ƃł���
�P�O����@�X�X�܂ł�
�P�O���炾���炳
�X�X�����@�X�@���@�X�O
�X�O��
�����P�O�@
�����X�X
��������
4905
��
�R�܂��́@�T�́@�{����
�Öق̗�����
���藝����
�R�̔{���̘a�@�����@�T�̔{���̘a
�}�C�i�X�@�R�ƂT�̍ŏ����{���̔{���̘a
���傤���Ȃ�����i�C�X�J
�v�Z�ł����
�R�̔{������
�������݂�����
�l���Ă��ł���
��������
1665
�T�̔{����
����Ȃ���
�l����
945
��
�R�ƂT�́@�ŏ����{���Ȃ�ł���
�R���T���@�݂��Ɂ@�f
�f���Ȃ�ł���
�ő����
�Ȃ��H�H�H
����������i�C�X�J
�P
�Ȃ̂Ł@���̂܂�
�����ā@�P�T
����
��������@
��[
�ȂǂƁ@����ł��܂�Ȃ��悤�ɂł���
�ǂ��������
�{���Ł@������
�����@�������邩�@�݂�
����
����
��������
�����ɑ������
315
�o�Ă����@�����̃f�[�^�͂ł���
4905
1665
945
315
������
�g���ā@�v�Z���܂���
2295
��
����Ł@��������Ȃ���
2295�́@�R�܂��͂T�̔{���̘a
�����
�S�̂���@������
2610
���͂�
�v�Z���@��ςȂ�
��蕶��
�ǂ�ł݂܂���
�Q�O�O��菬����
���̐����̂���
�R�C�T�C�V�́@���Ȃ��Ƃ�
�P�́@�{���ƂȂ�@�S�Ă̐��́@�a�����߂�
A,B,C���@�g����
�ِ}�Ł@������
���̎ΐ��̕���
���̗v�f�́@����
���藝��
�����
���������@�����@���G�ɂȂ���
����Ȋ�����
���e��
�R�Ŋ��������
�T�Ŋ��������
�V�Ŋ��������
�R�܂��͂T�Ł@���������
�T�܂��͂V�Ł@���������
�V�܂��͂R�Ł@���������
�R�ƂT�ƂV�Ł@���������
�����́@�ǂ�ł��悭
�d�����Ȃ��悤��
���藝����
������
�v�f���@���v�����
�R�̔{���̘a�@+�@�T�̔{���̘a�@+�@�V�̔{���̘a
-�i�R�ƂT�̍ŏ����{���̔{���̘a�j
-�i�T�ƂV�̍ŏ����{���̔{���̘a�j
-�i�V�ƂR�̍ŏ����{���̔{���̘a�j
+�i�R�ƂT�ƂV�Ŋ���鐔�̘a�@�j
�}�ɂ���Ƃ���Ȃ�
��ς����ǂ�
�Ђ�����@�v�Z
�Q�O�O���@�������@���̐���������
�P�`�P�X�X
���w���ā@���������Ƃ���
��������@�ł��Ȃ��ł���
��
�R�́@�{������
�������邩���Ă���
�U�U��
�����@
����
������������@��������
6633
�T�̔{���̎���
�ӁX�@�T�Ł@�����Ă��`��
�������@����o����
�����@
����
�������o��@
�����̘a�́@��������
3900
�V�̔{����
�V���ɂ���
�����@���R���ɂ��ā@�i�����P�C�Q�C�R�C�S�C�T�C�U�C�V�A�E�E�E�j
�ӁX���@�V�Ł@������
���́@���R��������
�����
�������@�Q�W��
����
����
����
��������
�a�́@2842
�R�ƂT�́@�ŏ����{��
����́@�@�R���T���V��
�S���@�݂��Ɂ@�f�Ȃ̂�
���̂܂܁@�|�����
�@
�����̂������
����Ă����悤��
�����܂���
G�@�ő�����@�P�i�^��
�ŏ����{���́@�P�T
�P�T�̔{���̘a�́@�@�P�`�P�X�X�܂ł�
�Ԃ�����
�s�������@�g����
�������݂����ɂł���
��
�ӁX�@�P�T�Ł@������
���́@���R���ł�����@�����ɍ����Ƃ���
�T����
�������P�R
����
����
�������@���߂�
�����Ɂ@��������
1365
�T�ƂV��
�ŏ����{����
�R�T
�R�T�́@�{���̘a��
�P�`�P�X�X�̊Ԃ̂��̂���������
�s������
�͂����
�������́@�ɂȂ���
�ӁX
���@���@�E�@�@�R�T�Ł@������
�����́@�T��
�a�́@525
�V�ƂR��
�ő�����P������
��������
���̂܂�
�V�ƂR���@�|����
�Q�P
�Q�P�́@�{���̘a��
�����@�Q�P������P���Q�P
�����@�Q�P������X��189
�����X
��������
9/2�i21+189�j
���@945
�R�ƂT�ƂV�́@������
�S���@�݂��Ɂ@�f�Ȃ̂�
���̂܂܂�����
105
����������炳
�����܂ł̌v�Z��
�����@���Ă͂߂Ă����܂���
�Q�O�O��菬����
���̐����̂���
�R�C�T�C�V�́@���Ȃ��Ƃ�
�P�́@�{���ƂȂ�@�S�Ă̐��́@�a��
10645
posted by moriamelihu at 11:34| ��l�̂��ї��Ƃ��@
2017�N07��18��
��l�̂��ї��Ƃ��@21006�@�@�{���̖��
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�킽���́@���ꂮ����@���t�ł͂Ȃ�
����́@�Ⴆ��
�����@���k�̂���ł��̂�
�ݒ�Ƃ������܂��Ă�
����͂�
���ȏ��Ƃ��́@���Ƃ́@�Ⴄ���ǂ�
�u���O�Ł@�����@���Ă�����ĂĂł���
�������@�́@����Ȋ����ɂȂ������ǂ�
��
���肢�������܂�
���������ݒ��
�����Ƃ����ӌ����@����͂�����B
����̖��̑����ł���
�{���̖��
�{���Ȃ̂�
��������ɂȂ��Ă�킯��
�a���@���߂Ȃ����Ƃ��ł���
�����Ă݂܂�
�R���́@���R�����������
���̂�����
�S�ł��@�U�ł��@�����鐔�̘a
���̂�����
�S�܂��́@�U�Ł@�����鐔�̘a

�x���}�Ō����
����Ȋ�����
���́@�_�u��
�܂��́@�́@�S��
������
�v�f�̌��Ƃ��@�a�̎���
�C���t���˂�

��
�S�ł��@�U�ł��@���������
�ŏ����{�����@���Ƃ߂��
�����́@����������
�����
�P�Q���b�e�����邯��
���������@���G�Ȏ��́@�댯�Ȃ���
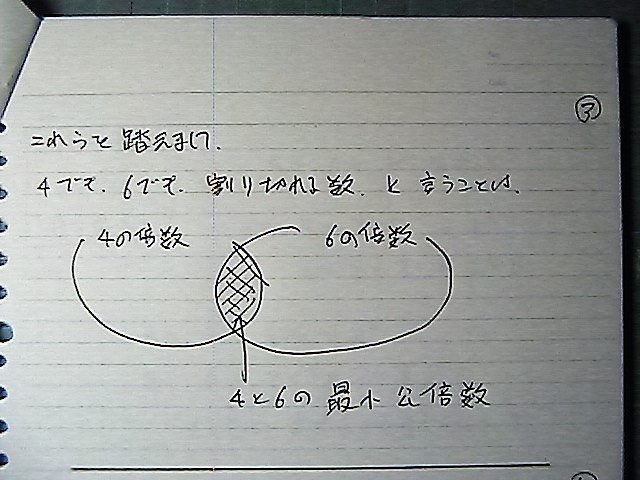
������Ƃ���Ă݂܂���
AB=GL
A��Ga
B=Gb
�Ȃ�@����������̂�
G�́@�ő����
L�́@�ŏ����{��
a,b�A�́@�f���ł�

�S�́@�Q������Q�@
�U�́@�Q������R
������ɂ���
�����́@���ʕ����́@�Q
���@�ő����
�R�Ɓ@�T�̏ꍇ��������
�ő���́@�Ȃ��H�H�H�H
�������@����ł���
�P�ł���
��

�ő�����@�Q�Ȃ̂�
A��Ga
B=Gb
�ɂ��Ă͂߂�Ƃł����
�S���Q������Q
�U���Q������R

�ŏ����{����
L������
���ό`�����
12

���́@�R���̎��R��������
�H�H�H
�X�X�́@�Q�P�^�@������
�P�O�O����
�P�O�O�O�͂S�P�^
������
�X�X�X�܂�
100�`999
���̊Ԃ́@�P�Q�̔{����
�������邩�Ȃ�

�P�Q�̔{��������@�P�Q����
���́@���R���@�i�@�����̂����@�[�����@�������@���́@�����@�j

�S���@�P�Q�Ŋ�����
����
��
���R���Ɂ@����Ƃ���

��
������
�Ԉ������������ǂ�
����́@�|�����ƂȂ�
���w�Z�Ł@�K�����ƂȂ�
�܂������Ɓ@���
������
����Ă��܂����B
��������ł����H

���̂�
���̍��ł���
�����ł���
�����
��
�������傾����

�i�^��
���̂P�Q�̔{���́@�W�܂��
����108�@����996�@����75
�����@�P�Q�́@��������@�����

�����炳
�a��
�������@���ꂾ���炳

�����������ق��ł���

����Ȃ�
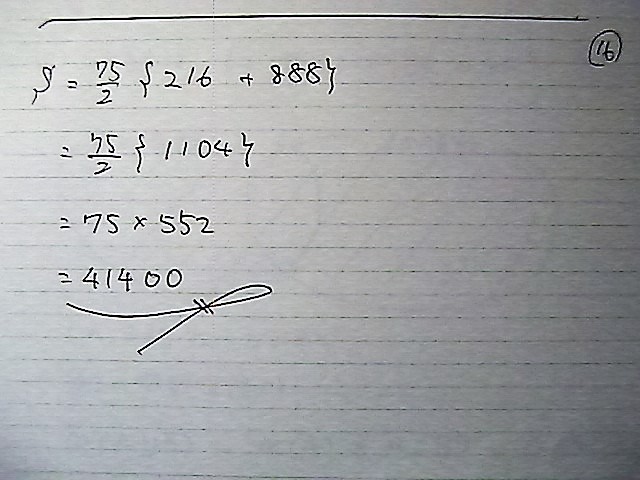
�ȒP�ȕ��Ł@����
����Ȃ�
������
�������Ⴄ��
�������
�������傾����
�i�P�j�́@�R���_

��
(�Q)�́@������肩�Ƃ�����
����S�̂�
���߂��
���P�́@���藝�@���Ă̂��@���������ǂ�
����g��Ȃ���
�����Ȃ��Ȃ��H
�Ł@�v���o���Ă݂��
����Ȃ���������

������Ȃ��Ă��@�a������
�����@S�Ɂ@�ς��Ă�
�_�u���
�O���\�}���@�����
�K�v�ȁ@���́@������

�i�P�j�@�Ł@�_�u���̌v�Z���@����ł邩��
�S�̔{���Ɓ@�U�̔{���́@�a���@���ꂼ��@
���߂ā@������
��������@�_�u�����@�����Ƃ����@�\�}�Ȃ̂�

�S�̔{������
�a�����߂��

�������݂����Ɂ@�@����Ă���
�����@�Q�Q�T��

�S�̔{��������
�����@�������߂�
�a�́@

123300

�U�̔{���̕���
����Ȃ����@�v�Z���Ă���

����Ȋ�����

82350

�������@�����Ƃ����@�\�}��
�������

���藝�@�W����
�˂˂�
����Ł@��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�킽���́@���ꂮ����@���t�ł͂Ȃ�
����́@�Ⴆ��
�����@���k�̂���ł��̂�
�ݒ�Ƃ������܂��Ă�
����͂�
���ȏ��Ƃ��́@���Ƃ́@�Ⴄ���ǂ�
�u���O�Ł@�����@���Ă�����ĂĂł���
�������@�́@����Ȋ����ɂȂ������ǂ�
��
���肢�������܂�
���������ݒ��
�����Ƃ����ӌ����@����͂�����B
����̖��̑����ł���
�{���̖��
�{���Ȃ̂�
��������ɂȂ��Ă�킯��
�a���@���߂Ȃ����Ƃ��ł���
�����Ă݂܂�
�R���́@���R�����������
���̂�����
�S�ł��@�U�ł��@�����鐔�̘a
���̂�����
�S�܂��́@�U�Ł@�����鐔�̘a
�x���}�Ō����
����Ȋ�����
���́@�_�u��
�܂��́@�́@�S��
������
�v�f�̌��Ƃ��@�a�̎���
�C���t���˂�
��
�S�ł��@�U�ł��@���������
�ŏ����{�����@���Ƃ߂��
�����́@����������
�����
�P�Q���b�e�����邯��
���������@���G�Ȏ��́@�댯�Ȃ���
������Ƃ���Ă݂܂���
AB=GL
A��Ga
B=Gb
�Ȃ�@����������̂�
G�́@�ő����
L�́@�ŏ����{��
a,b�A�́@�f���ł�
�S�́@�Q������Q�@
�U�́@�Q������R
������ɂ���
�����́@���ʕ����́@�Q
���@�ő����
�R�Ɓ@�T�̏ꍇ��������
�ő���́@�Ȃ��H�H�H�H
�������@����ł���
�P�ł���
��
�ő�����@�Q�Ȃ̂�
A��Ga
B=Gb
�ɂ��Ă͂߂�Ƃł����
�S���Q������Q
�U���Q������R
�ŏ����{����
L������
���ό`�����
12
���́@�R���̎��R��������
�H�H�H
�X�X�́@�Q�P�^�@������
�P�O�O����
�P�O�O�O�͂S�P�^
������
�X�X�X�܂�
100�`999
���̊Ԃ́@�P�Q�̔{����
�������邩�Ȃ�
�P�Q�̔{��������@�P�Q����
���́@���R���@�i�@�����̂����@�[�����@�������@���́@�����@�j
�S���@�P�Q�Ŋ�����
����
��
���R���Ɂ@����Ƃ���
��
������
�Ԉ������������ǂ�
����́@�|�����ƂȂ�
���w�Z�Ł@�K�����ƂȂ�
�܂������Ɓ@���
������
����Ă��܂����B
��������ł����H
���̂�
���̍��ł���
�����ł���
�����
��
�������傾����
�i�^��
���̂P�Q�̔{���́@�W�܂��
����108�@����996�@����75
�����@�P�Q�́@��������@�����
�����炳
�a��
�������@���ꂾ���炳
�����������ق��ł���
����Ȃ�
�ȒP�ȕ��Ł@����
����Ȃ�
������
�������Ⴄ��
�������
�������傾����
�i�P�j�́@�R���_
��
(�Q)�́@������肩�Ƃ�����
����S�̂�
���߂��
���P�́@���藝�@���Ă̂��@���������ǂ�
����g��Ȃ���
�����Ȃ��Ȃ��H
�Ł@�v���o���Ă݂��
����Ȃ���������
������Ȃ��Ă��@�a������
�����@S�Ɂ@�ς��Ă�
�_�u���
�O���\�}���@�����
�K�v�ȁ@���́@������
�i�P�j�@�Ł@�_�u���̌v�Z���@����ł邩��
�S�̔{���Ɓ@�U�̔{���́@�a���@���ꂼ��@
���߂ā@������
��������@�_�u�����@�����Ƃ����@�\�}�Ȃ̂�
�S�̔{������
�a�����߂��
�������݂����Ɂ@�@����Ă���
�����@�Q�Q�T��
�S�̔{��������
�����@�������߂�
�a�́@
123300
�U�̔{���̕���
����Ȃ����@�v�Z���Ă���
����Ȋ�����
82350
�������@�����Ƃ����@�\�}��
�������
���藝�@�W����
�˂˂�
����Ł@��������
posted by moriamelihu at 02:20| ��l�̂��ї��Ƃ��@


