2017�N09��13��
21011�@��l�̂��ї��Ƃ��@���䐔��̘a�@
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���䐔��Ƃ����̂������Ăł���
�����̎���
�����@���ƍ��̊Ԃ��@���́@����������ł���
����́@
���鐔a�@�������ā@�����Ɂ@���X�Ɂ@���́@����(r)�����Ăł��鐔��ł�
��
���
���̐���́@���߂́@�����́@�a�����߂�

�X�̖��́@��琔��Ȃ�^^�ǂ�
�����Ł@���́@����̂��ė�����
���ׂ˂�
�܁[�@���݂Ɂ@�}�@���@�t���Ă邠�邩��
�ς��ȂƎv������
�����ł́@�Ȃ�

���䐔��ōl����
��ʍ��̌����Ɂ@�͂ߍ����
������ӂł�
��Ɂ@���[�������@�����
�������Ƃ��́@
�����Ɂ@�@����Ăł���
����ł���
������
���{�̂ǂ�����
�͂߂�@�b�e�����@���������邻����
�e���p

�Q���߁@�R���߂���
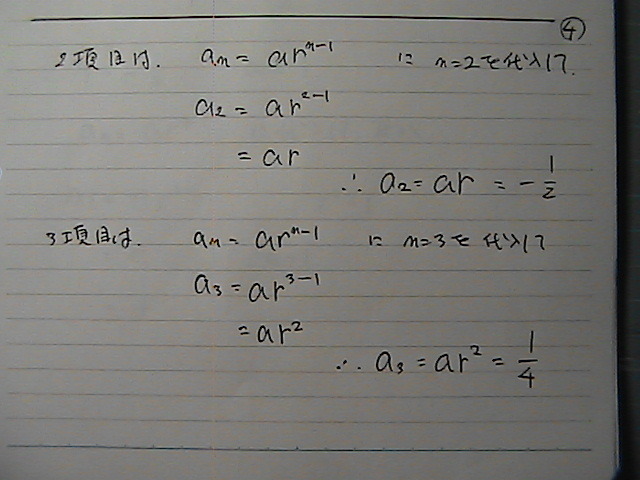
������@���߂�Ƃł���
�t���ŗ��Ă܂��̂�
��ד�@�Ђ�����Ԃ�
�����@�m��Ȃ��H
�W���@������
��

���䂪�������
������
���߂���@�o�Ă邯�ǂ�
���܂Ɂ@�Ⴄ�̂��@������Ă������炳
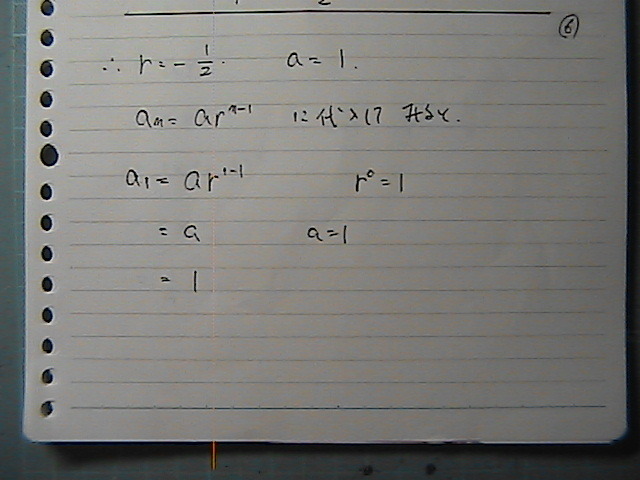
��l�@��ʍ����@�����Ă邩
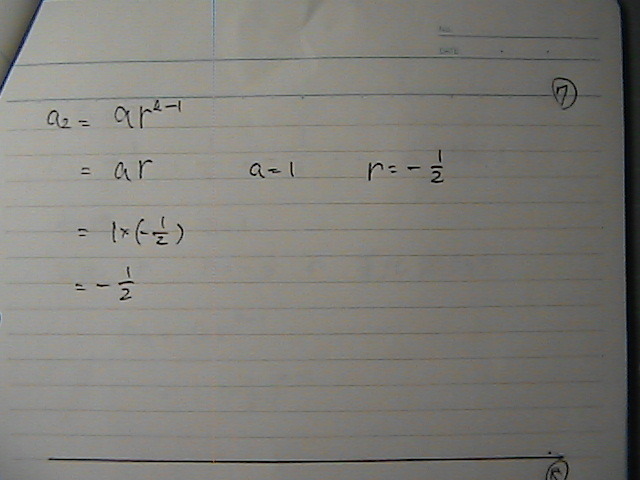
������Ɓ@�`�F�b�N���Ăł���
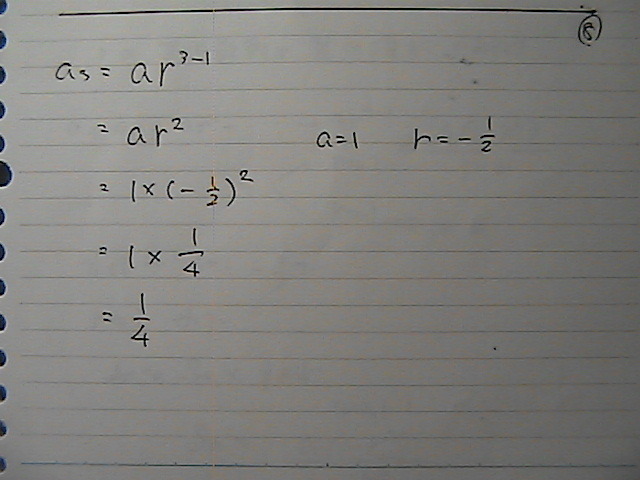
�Ȃ̂�
����Ȋ����ł���

������
���߂�̂́@����́@���߂́@�����̘a�Ȃ�
�����@�Ɓ@����@���@�������
��
���䂪�@�����ŗ��ă��Ƃ���
�ꍇ����
����́@�P�̎��@�P�łȂ��Ƃ���
�a�̌������@�ς���Ă��܂�����
�����̎���
���䂪�@���@�����̂Ƃ��@�v�Z�����
���䂪�@�P�ɂȂ��Ă��܂��@�����́@�l���@���邶��i�C�X�J
������Ƃ���
�`�F�b�N����

��
����́@�V�b�J���@�l���@�łĂ�
����́@�P�ł́@�Ȃ�����
�������́@�����ɓ����
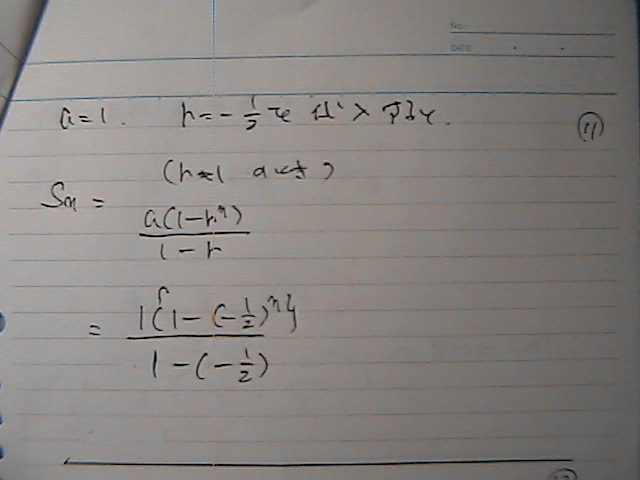
���ό`��
�����́@����
�v�Z�́@���i����
����ĂȂ���
�Ă��߂�Ɂ@�P�A���X�~�X���@������̂�
�ނ����͂�
�G�A���X�~�X�Ƃ������Ă�
�܂��@�P�A���X�~�X��
�����@�G�A���X�~�X�ł�
��k�́@�Ƃ�����
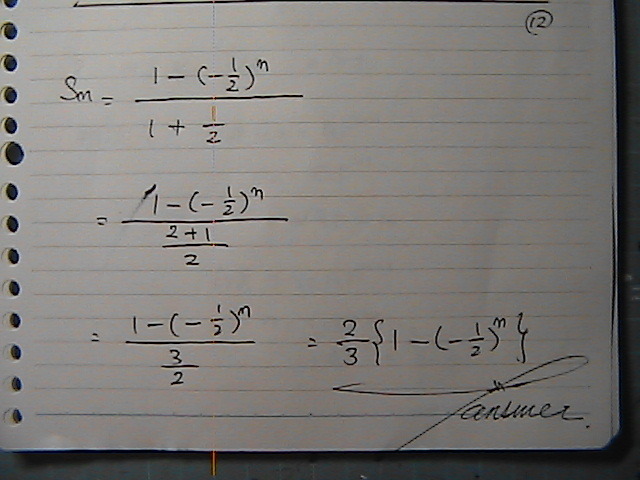
�����������傢���[
���L�\�o���������Ȃ��[
����Ł@�s�[���Ɨ��邨������
�o�C�N�́@���̍��@�w�A�X�^�C����
������@�C�ɂ��Ă܂�����
����
����ĂȂ�����
���s���܂���
���

������ł���
�������ā@�l����
�a���@���߂����̂��@�������킹���
�y�Ȏ����A���g
��ʍ��́@�����Ɂ@�Q���߁@�R���߁@���@
�����
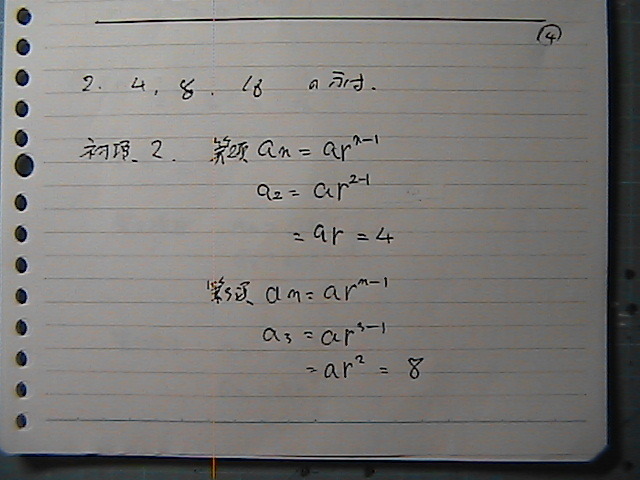
������@�����ɂ���
�₭���ā@���߂��

�㔼��
������
�Q���߁@�R���߂��@�g����

������@���߂�

��ʍ��Ł@�����Ƃ���
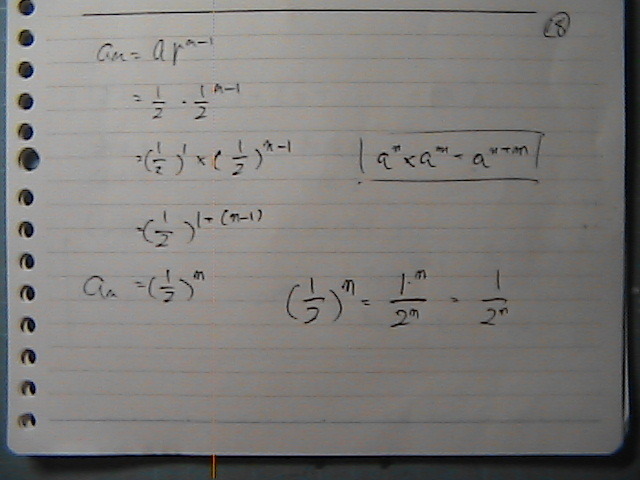
��
�����܂ł́@
���̐����
�Q�����@������ł����
�O�����@��딼��

��ʍ��Ł@
�O�����@�㔼��
��
���߂�̂́@���߂́@���@���܂ł́@�a�ł��̂�

�_�b�V���@�Ȃ��@�@�@�@��������@�t��
�������@�i�a�̌������@�j�@�O���@�㔼
�����ł���
�������

�v�Z���Ă��܂���
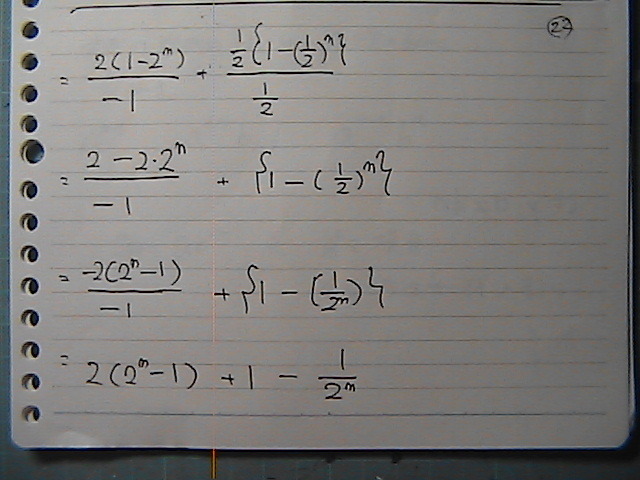
����Ȃ��
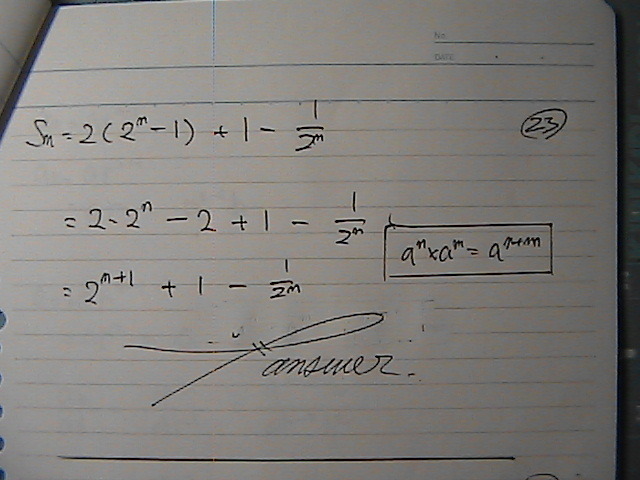
���͂ł���
�����ŗ��Ă܂���

������@��ʍ��Ɂ@�������
���߂��肩����
�Q���߁@�R���߁@���@�����ɂ���
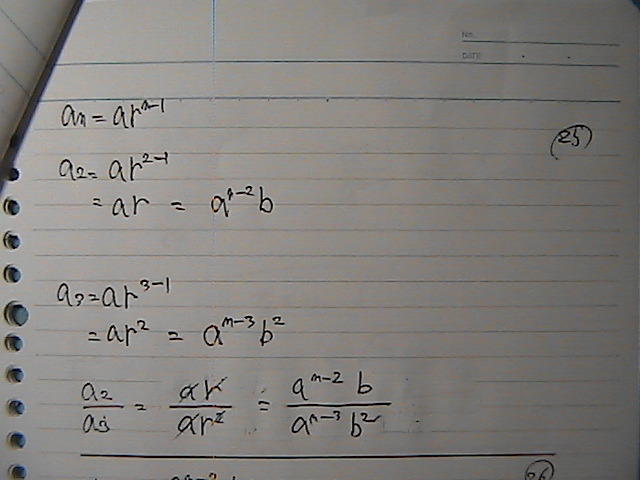
�w���̌v�Z
�����Ł@�����Ă����
�����V���V���@�Ł@�ł����Ⴄ����
��������
�H��
�������傩��
���s����

���͂����ł�
�����́@���@���ʂ�
���́@��Ɖ�
�ǂ����H

�����炳
������
�������Ɓ@����ĂȂ������ꍇ
���s�ł���
�����Ɓ@���䂪�o���̂�

�����́@�Ƃ��́@�����
���䂪�@�P�ɂȂ�Ƃ��́@�����́@�l��
�ꍇ�������Ăł���
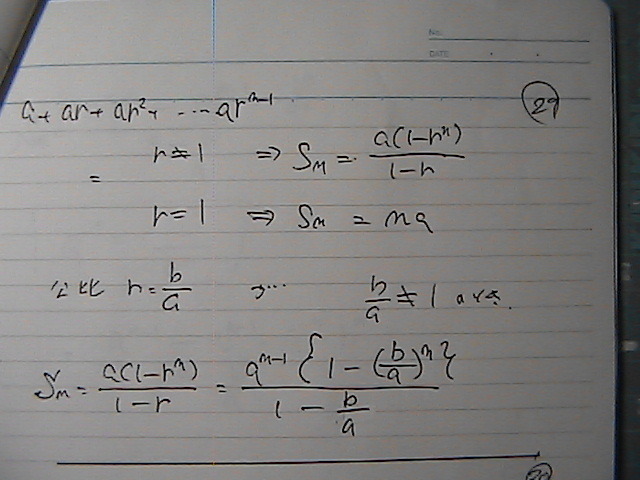
���䂪�@�P�Ł@�Ȃ��Ƃ�����
����Ȋ�����

�w���̌v�Z��
���܂Ɍ��Ă�����
���w�́@���o���@�K�т��炢

�_�C�W���u�ł��傤��
����
���E
����������
�E�E�E�E�E

�E�E�E�E
���o�[�X
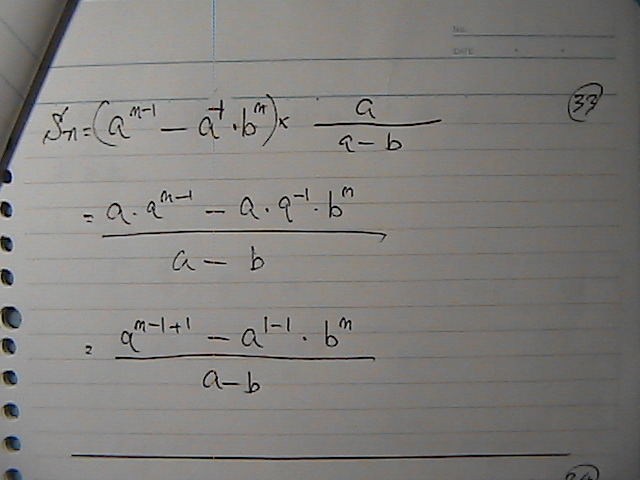
���ꂪ�@���䂪�@�P�łȂ��Ƃ�
�Ɓ@���䂪�@�P�̎���
����

�����l�ł�
���ɂ���́@�������ł���
����
�ޑ�
����͂�
���߂́@���@���̘a

��ʍ��Ɂ@�Q���߁@�R����
���@�������

����́@-1
�����́@1

���䂪�@�P�łȂ�����
������Ƃ����@�m�F����
�a�̌����Ɂ@����Ă��܂���
����

�����@�@���߂́@�����́@�a�����߂���
��ʍ��̌�����

�͂ߍ���ł��Ă���i�C�X�J
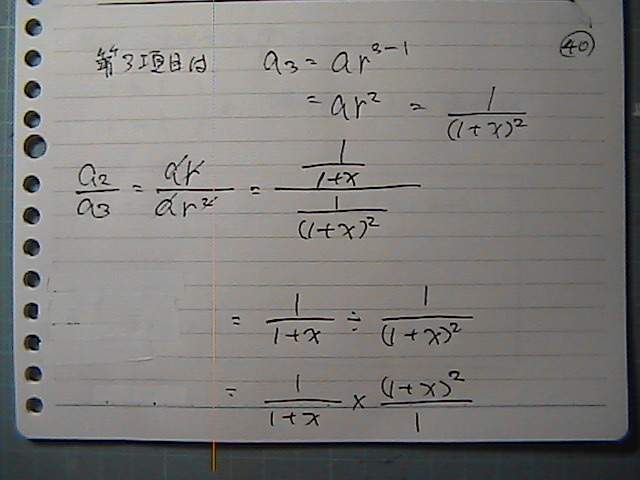
���o�[�X����

����Ɂ@�����������Ă�Ƃ���
�����́@�l�ɂ���Ă�
���䂪�@1�ɂȂ�Ƃ�������̂�
�V�b�J���@�`�F�b�N�@�ꍇ���������Ăł���

���䂪�@�P�ɂȂ�@x��
�[��
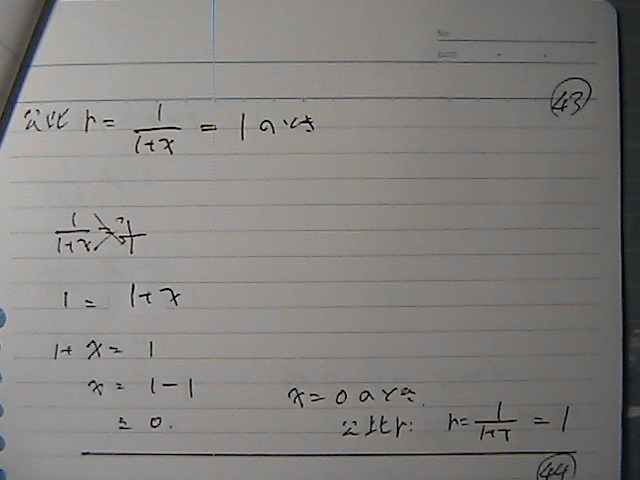
��
�a�́@��

���䂪�@1�łȂ��Ƃ���
�[������A
�Ȃ��ł�����

�������傩��
�Ђ�Ђ₵�Ȃ���
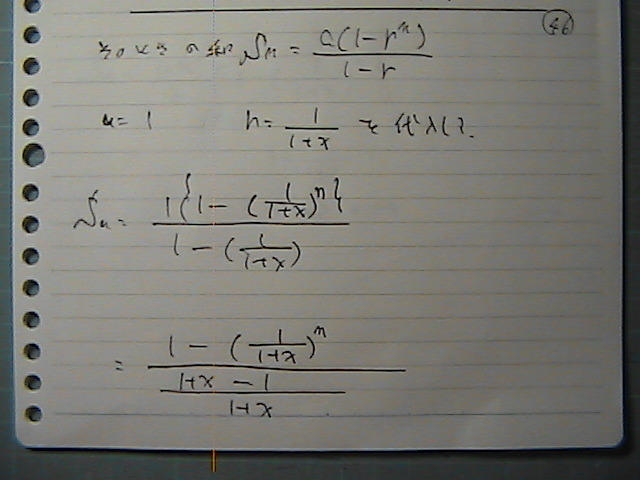
���Ƃ�
����Ă܂���
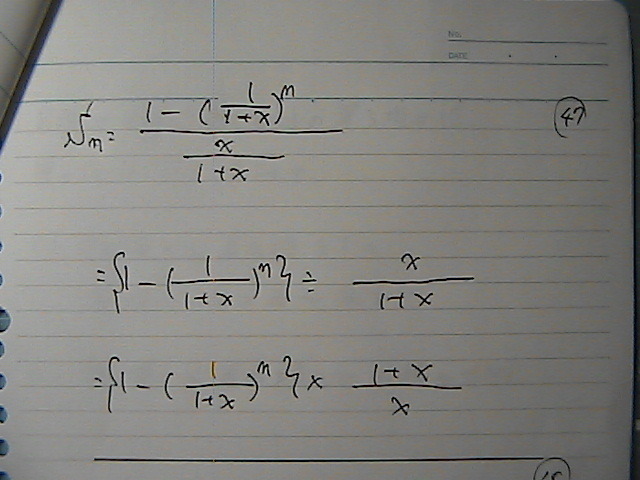
����
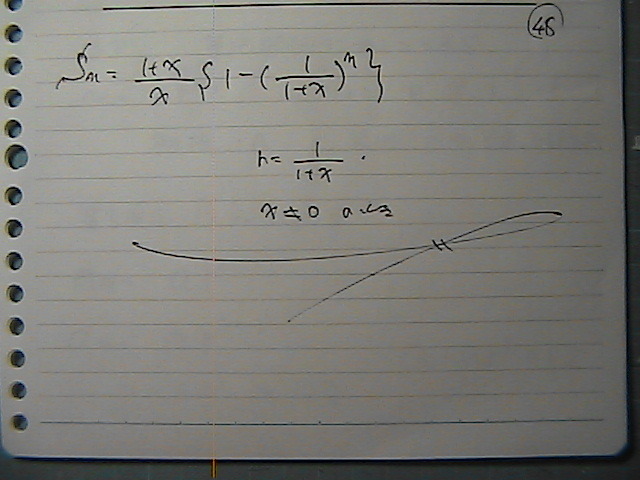
�{���́@���C���C�x���g��
����
���x�́@��������Ȃ��Ă�
������
���Ă܂��̂�
�V�b�J���@�v�Z�ł���

�e�����@���߂�
�e���́@�Q�悵�����̂�
���߂́@���@���̘a
������
���́@������@���߂�
��ʍ����@�o���ł���
������@��悵���Ⴆ��
�\���]���@�Q��ɂȂ�@��ʍ��ɂȂ���炳

�R���߁@�Ɓ@�U���߂���

������@������
�₭���ā@���߂��
��������

�łĂ����@������@��ʍ��Ɂ@�R���߂�
�������
�������o�ė���

���ꂪ�@���́@����
���́@���ꂼ��́@���́@���̘a������
���̈�ʍ����@�Q�悵�Ă�����
����
1.2.3....
�Ƃ���ā@��悷���

9,36,144�A�E�E�E
�ł���
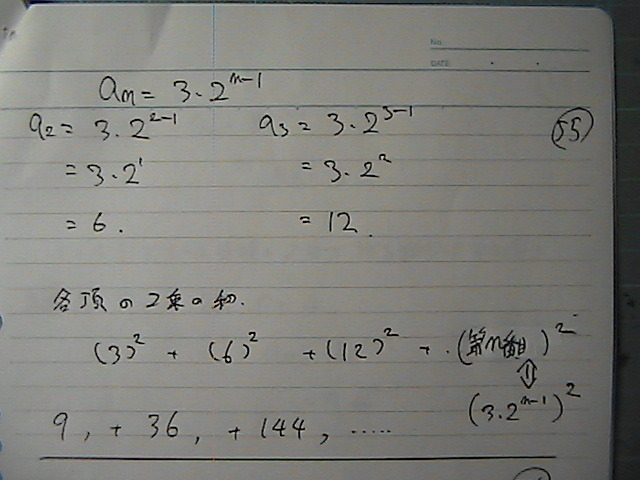
������@����́@��ʍ��Ɂ@�����
������@���߂��
4

�V�����ł�������́@��ʍ��́@���ꂾ����

�a�̌����Ɂ@�������
����ł����̂�
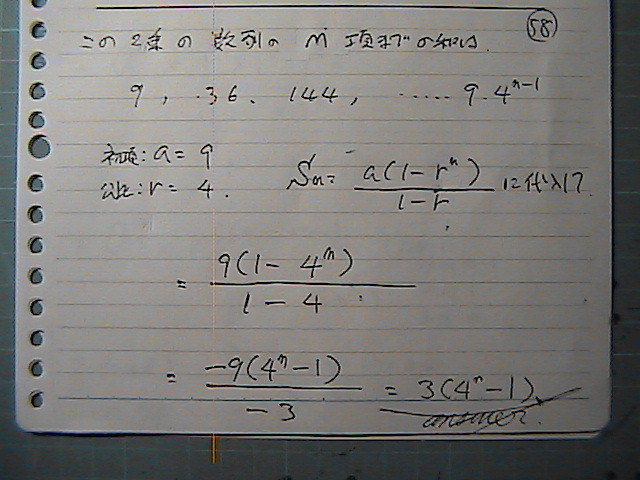
���X�g��
�������Q�͂ł���
���́@����
�͂��߂́@����̂��Ƃ���
�e���́@���߂̂��@���܂ł́@�ς����߂��
������₷����Ɂ@���������čl�����
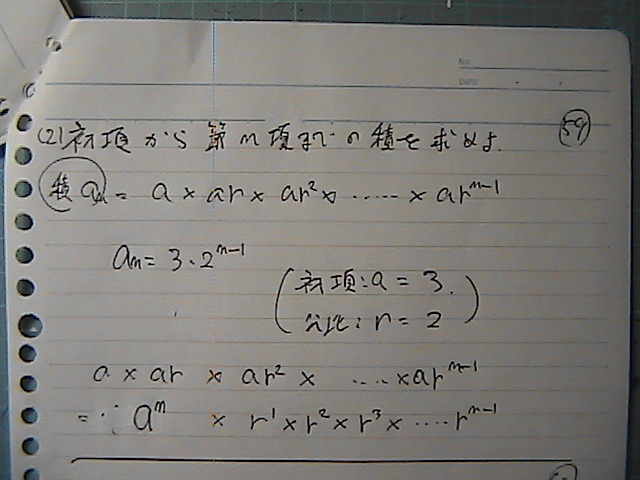
a�́@����
a�́@����@�@�|���Z������
����@���̕���
���̎w���v�Z��
�����@�����́@�w���̊|���Z��
���̎w���́@�����Z������
�������邩
�Ԉ��Ȃ��悤��
������
1����@��-1�@�܂�
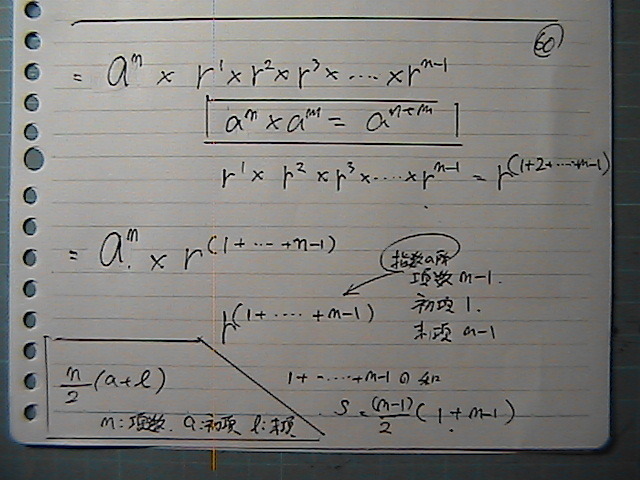
�����́@���䂒�́@�w���v�Z��
��������̘a���@�g����
����Ȋ�����
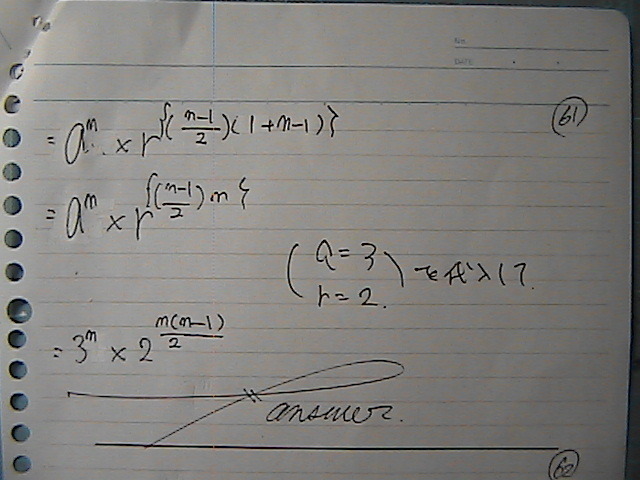
�����ꂳ�܁[�[�[
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���䐔��Ƃ����̂������Ăł���
�����̎���
�����@���ƍ��̊Ԃ��@���́@����������ł���
����́@
���鐔a�@�������ā@�����Ɂ@���X�Ɂ@���́@����(r)�����Ăł��鐔��ł�
��
���
���̐���́@���߂́@�����́@�a�����߂�
�X�̖��́@��琔��Ȃ�^^�ǂ�
�����Ł@���́@����̂��ė�����
���ׂ˂�
�܁[�@���݂Ɂ@�}�@���@�t���Ă邠�邩��
�ς��ȂƎv������
�����ł́@�Ȃ�
���䐔��ōl����
��ʍ��̌����Ɂ@�͂ߍ����
������ӂł�
��Ɂ@���[�������@�����
�������Ƃ��́@
�����Ɂ@�@����Ăł���
����ł���
������
���{�̂ǂ�����
�͂߂�@�b�e�����@���������邻����
�e���p
�Q���߁@�R���߂���
������@���߂�Ƃł���
�t���ŗ��Ă܂��̂�
��ד�@�Ђ�����Ԃ�
�����@�m��Ȃ��H
�W���@������
��
���䂪�������
������
���߂���@�o�Ă邯�ǂ�
���܂Ɂ@�Ⴄ�̂��@������Ă������炳
��l�@��ʍ����@�����Ă邩
������Ɓ@�`�F�b�N���Ăł���
�Ȃ̂�
����Ȋ����ł���
������
���߂�̂́@����́@���߂́@�����̘a�Ȃ�
�����@�Ɓ@����@���@�������
��
���䂪�@�����ŗ��ă��Ƃ���
�ꍇ����
����́@�P�̎��@�P�łȂ��Ƃ���
�a�̌������@�ς���Ă��܂�����
�����̎���
���䂪�@���@�����̂Ƃ��@�v�Z�����
���䂪�@�P�ɂȂ��Ă��܂��@�����́@�l���@���邶��i�C�X�J
������Ƃ���
�`�F�b�N����
��
����́@�V�b�J���@�l���@�łĂ�
����́@�P�ł́@�Ȃ�����
�������́@�����ɓ����
���ό`��
�����́@����
�v�Z�́@���i����
����ĂȂ���
�Ă��߂�Ɂ@�P�A���X�~�X���@������̂�
�ނ����͂�
�G�A���X�~�X�Ƃ������Ă�
�܂��@�P�A���X�~�X��
�����@�G�A���X�~�X�ł�
��k�́@�Ƃ�����
�����������傢���[
���L�\�o���������Ȃ��[
����Ł@�s�[���Ɨ��邨������
�o�C�N�́@���̍��@�w�A�X�^�C����
������@�C�ɂ��Ă܂�����
����
����ĂȂ�����
���s���܂���
���
������ł���
�������ā@�l����
�a���@���߂����̂��@�������킹���
�y�Ȏ����A���g
��ʍ��́@�����Ɂ@�Q���߁@�R���߁@���@
�����
������@�����ɂ���
�₭���ā@���߂��
�㔼��
������
�Q���߁@�R���߂��@�g����
������@���߂�
��ʍ��Ł@�����Ƃ���
��
�����܂ł́@
���̐����
�Q�����@������ł����
�O�����@��딼��
��ʍ��Ł@
�O�����@�㔼��
��
���߂�̂́@���߂́@���@���܂ł́@�a�ł��̂�
�_�b�V���@�Ȃ��@�@�@�@��������@�t��
�������@�i�a�̌������@�j�@�O���@�㔼
�����ł���
�������
�v�Z���Ă��܂���
����Ȃ��
���͂ł���
�����ŗ��Ă܂���
������@��ʍ��Ɂ@�������
���߂��肩����
�Q���߁@�R���߁@���@�����ɂ���
�w���̌v�Z
�����Ł@�����Ă����
�����V���V���@�Ł@�ł����Ⴄ����
��������
�H��
�������傩��
���s����
���͂����ł�
�����́@���@���ʂ�
���́@��Ɖ�
�ǂ����H
�����炳
������
�������Ɓ@����ĂȂ������ꍇ
���s�ł���
�����Ɓ@���䂪�o���̂�
�����́@�Ƃ��́@�����
���䂪�@�P�ɂȂ�Ƃ��́@�����́@�l��
�ꍇ�������Ăł���
���䂪�@�P�Ł@�Ȃ��Ƃ�����
����Ȋ�����
�w���̌v�Z��
���܂Ɍ��Ă�����
���w�́@���o���@�K�т��炢
�_�C�W���u�ł��傤��
����
���E
����������
�E�E�E�E�E
�E�E�E�E
���o�[�X
���ꂪ�@���䂪�@�P�łȂ��Ƃ�
�Ɓ@���䂪�@�P�̎���
����
�����l�ł�
���ɂ���́@�������ł���
����
�ޑ�
����͂�
���߂́@���@���̘a
��ʍ��Ɂ@�Q���߁@�R����
���@�������
����́@-1
�����́@1
���䂪�@�P�łȂ�����
������Ƃ����@�m�F����
�a�̌����Ɂ@����Ă��܂���
����
�����@�@���߂́@�����́@�a�����߂���
��ʍ��̌�����
�͂ߍ���ł��Ă���i�C�X�J
���o�[�X����
����Ɂ@�����������Ă�Ƃ���
�����́@�l�ɂ���Ă�
���䂪�@1�ɂȂ�Ƃ�������̂�
�V�b�J���@�`�F�b�N�@�ꍇ���������Ăł���
���䂪�@�P�ɂȂ�@x��
�[��
��
�a�́@��
���䂪�@1�łȂ��Ƃ���
�[������A
�Ȃ��ł�����
�������傩��
�Ђ�Ђ₵�Ȃ���
���Ƃ�
����Ă܂���
����
�{���́@���C���C�x���g��
����
���x�́@��������Ȃ��Ă�
������
���Ă܂��̂�
�V�b�J���@�v�Z�ł���
�e�����@���߂�
�e���́@�Q�悵�����̂�
���߂́@���@���̘a
������
���́@������@���߂�
��ʍ����@�o���ł���
������@��悵���Ⴆ��
�\���]���@�Q��ɂȂ�@��ʍ��ɂȂ���炳
�R���߁@�Ɓ@�U���߂���
������@������
�₭���ā@���߂��
��������
�łĂ����@������@��ʍ��Ɂ@�R���߂�
�������
�������o�ė���
���ꂪ�@���́@����
���́@���ꂼ��́@���́@���̘a������
���̈�ʍ����@�Q�悵�Ă�����
����
1.2.3....
�Ƃ���ā@��悷���
9,36,144�A�E�E�E
�ł���
������@����́@��ʍ��Ɂ@�����
������@���߂��
4
�V�����ł�������́@��ʍ��́@���ꂾ����
�a�̌����Ɂ@�������
����ł����̂�
���X�g��
�������Q�͂ł���
���́@����
�͂��߂́@����̂��Ƃ���
�e���́@���߂̂��@���܂ł́@�ς����߂��
������₷����Ɂ@���������čl�����
a�́@����
a�́@����@�@�|���Z������
����@���̕���
���̎w���v�Z��
�����@�����́@�w���̊|���Z��
���̎w���́@�����Z������
�������邩
�Ԉ��Ȃ��悤��
������
1����@��-1�@�܂�
�����́@���䂒�́@�w���v�Z��
��������̘a���@�g����
����Ȋ�����
�����ꂳ�܁[�[�[
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 09:34| ��l�̂��ї��Ƃ��@