2017”N09Œژ21“ْ
21012 ‘هگl‚ج‚³‚ر—ژ‚ئ‚µپ@“ٌ‚آ‚جگ”—ٌ
پiپ@گ°‚ê•”‰®‚ضپ@‰ئ’ëچط‰€‚ئ‚T‚eپ@‚S‚eپ@‚R‚eپ@‚Q‚eپ@1 F‚´‚ء‚©‚â
ƒپƒjƒ…ƒEپ@ƒyپ[ƒWپ@ƒٹƒ^پ[ƒ“پ@پ@پ@پ@پj
“ٌ‚آ‚جگ”—ٌپ@‚ئ‚¢‚¤‚±‚ئ‚إ
“™”نگ”—ٌ‚ئ
“™چ·گ”—ٌ‚ھ‚ ‚é‚ٌ‚إ‚·‚و
‚إ
‚«‚ه‚¤‚ح‚ث
“™”نگ”—ٌ‚جپ@ڈ‰‚ك‚جپ@‚ژپ@چ€‚جکa‚ھ
“™چ·گ”—ٌ‚جپ@ڈ‰‚ك‚جپ@‰½چ€پ@‚©‚جپ@کa‚ةپ@“™‚µ‚¢‚±‚ئ‚ً
ڈط–¾‚¹‚و‚إ‚·
چs‚ء‚ؤ‚ف‚ـ‚µ‚ه‚¤

“™”نگ”—ٌ‚ج•û‚©‚ç
ڈ‰‚ك‚جپ@‚ژپ@چ€‚جکa‚جŒِژ®‚ح
Œِ”نپ@‚’پ@‚ھپ@‚P‚إ‚ب‚¯‚ê‚خ
ڈc‚ةپ@•ہ‚ٌ‚إ‚é
ڈم‚جŒِژ®

—^‚¦‚ç‚ê‚ؤ‚é
“™”نگ”—ٌپ@‚حپ@1.9.81.729.پEپEپEپEپE
ڈ‰چ€‚حپ@‚±‚ꂾ‚ئپ@‚P‚¾‚©‚ç
ˆê”تچ€‚جپ@Œِژ®‚ةپ@“ü‚ê‚ؤ‚¢‚ء‚ؤ
‚Qچ€–ع

‚Rچ€–ع
‚Qچ€ٹش‚ج”ن‚ًپ@•ھگ”‚ة‚µ‚ؤ
‹پ‚ك‚ؤ‚‚ئ
ڈ‰چ€‚جپ@a‚حپ@–ٌ‚·‚ئ
ڈء‹ژ‚إ‚«‚é‚©‚ç
‚±‚ٌ‚بٹ´‚¶‚إ
ƒٹƒoپ[ƒX‚µ‚ؤ
9

Œِ”ن‚X‚جپ@“™”نگ”—ٌ
ڈ‰چ€‚ح‚P
ˆê‰
ŒںژZ‚إ
‚ژپپپ@‚P
‚ژپپپ@‚Q

‚ژپپپ@‚R
‚ژپپپ@‚S
‚ب‚é‚ث

‘و‚ژچ€‚ـ‚إ‚جپ@کa‚ًپ@‹پ‚ك‚é‚ئ
ˆê”تچ€‚جپ@Œِژ®‚ح
ژg‚ي‚ب‚¢‚¯پ[‚ا‚³
Œِ”ن‚ئ‚©پ@ڈ‰چ€‚ئ‚©
‚µ‚ç‚ׂ½‚©‚ء‚½‚©‚炳
‚إ
Œِژ®‚ة“ü‚ê‚ؤ

‚±‚ê‚ھپ@“™”نگ”—ٌ‚ج
ڈ‰‚ك‚جپ@‚ژپ@چ€‚جکa
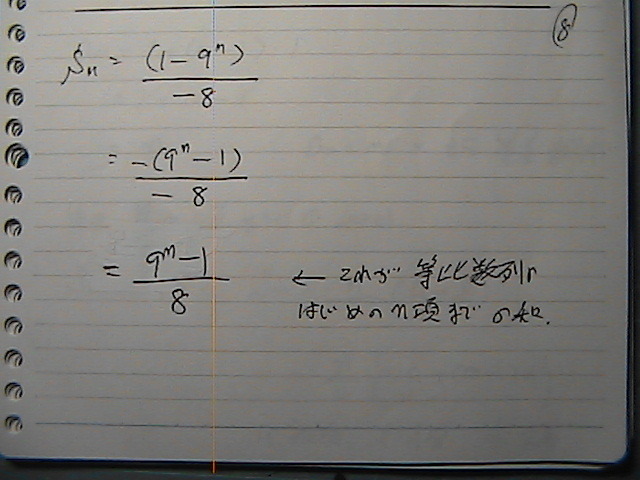
‚©‚½‚â
“™چ·گ”—ٌ‚ج•û‚ح
1.2.3.4.پEپEپEپE
‚ب‚ج‚إ
Œِچ·پ@‚P
ڈ‰چ€‚P
ˆê‰
ˆê”تچ€‚ح

Œِژ®‚©‚ç
‚ژ
‚±‚جگ”—ٌ‚ج
‘وپ@‚ژپ@چ€‚ـ‚إ‚جکa‚ح
Œِژ®‚©‚ç

‚¾‚©‚ç‚ة‚µ‚ؤ
‘م“ü‚µ‚ؤ
گ®—‚·‚ê‚خ
‚±‚ê
‚إ
–â‘è‚ح

“™”نگ”—ٌ‚جپ@‘وپ@‚ژپ@چ€‚ـ‚إ‚جکa‚ھ
“™چ·گ”—ٌ‚جپ@‘وپ@‰½چ€–عپ@‚©‚ـ‚إ‚جپ@کa‚ة
“™‚µ‚¢‚±‚ئ‚جپ@ڈط–¾
‚¾‚©‚ç
‚±‚ج‚³
Œ©‚½–ع‚جپ@–â‘肾‚¯‚ا
‘و‚ژپ@چ€‚ًپ@
‘و‚چپ@چ€‚ة‚µ‚ؤ
‚à‚¤پ@•¶ژڑ‚ھپ@ˆل‚¤‚©‚ç
–w‚ا‚جڈêچ‡پ@’l‚ھپ@ˆل‚¢‚ـ‚·

“™”نگ”—ٌ‚جپ@‚ژچ€‚ـ‚إ‚جکaپ@پپS
“™چ·گ”—ٌ‚جپ@‚چچ€‚ـ‚إ‚جکaپ@پپT
‚ئ‚·‚ê‚خ

S=T‚ة‚ب‚é‚ئ‚«‚ج
‚چ‚ًپ@‹پ‚ك‚ؤ
پiپ@‚ژ‚جژ®‚إپ@پj
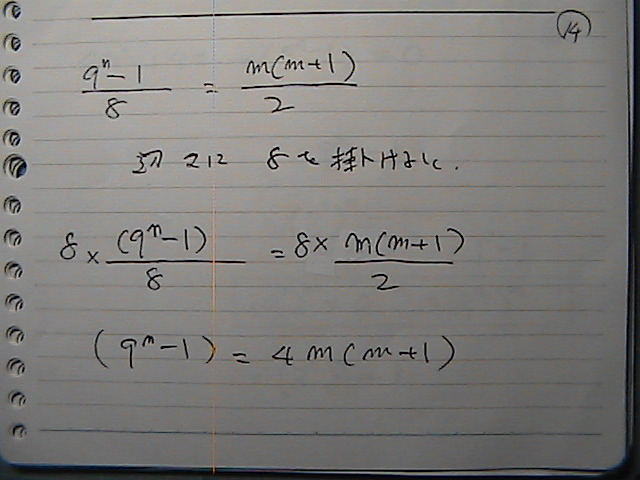
‚چ‚جپ@“ٌژںژ®‚ة‚ب‚ء‚½‚إ‚µ‚ه

ژwگ”‚ج
ˆِگ”•ھ‰ً‚ب‚ا
ڈ€”ُ‚µ‚ؤ
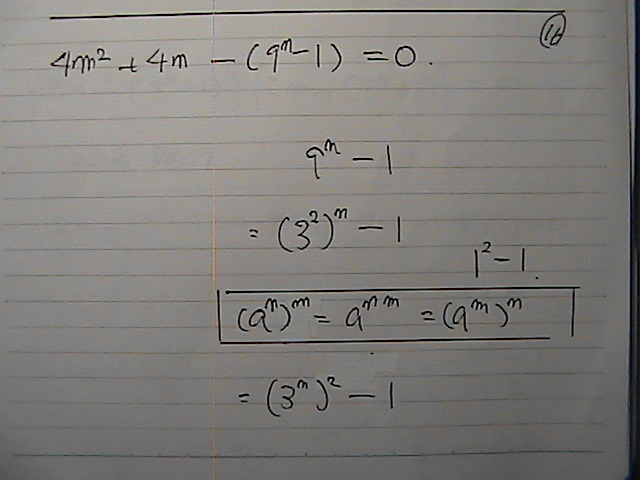
‚چ‚ج‚Qژںژ®‚ًپ@ˆِگ”•ھ‰ً‚µ‚ؤ
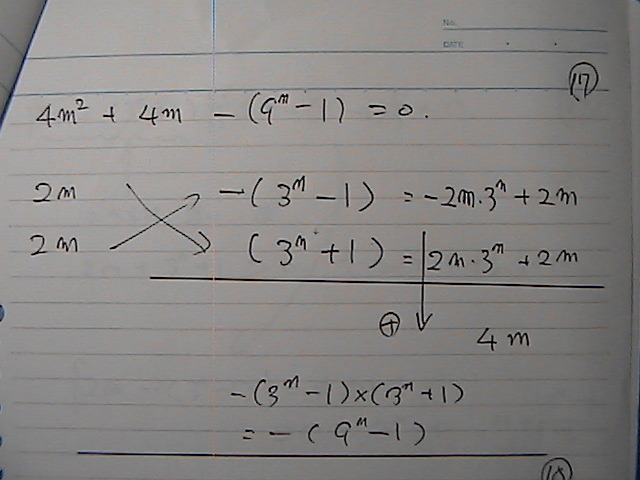
پپ‚O‚ًپ@‰ً‚¢‚ؤ
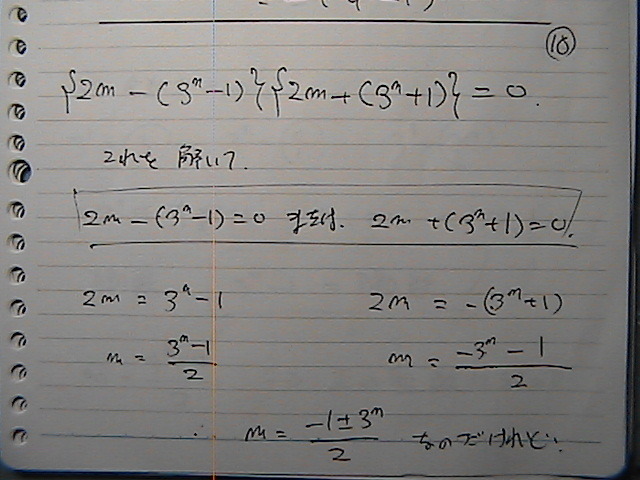
‚إپ@ڈ‰‚ك‚جٹ‡Œت‚ج’†‚ح
‚±‚ê‚ح‚³
‚O‚ئ‚©‚ةپ@‚ب‚炸
‚آ‚ث‚ةپ@گ³‚¾‚©‚ç
•s“K
Œم‚ë‚جٹ‡Œت‚ج’†‚ح
پپ‚O‚ة‚ب‚é‚ئ‚±‚ًپ@Œ©‚ؤ

•ھژq‚ح
‚¢‚آ‚àپ@ŒvژZ‚·‚é‚ئپ@‹ôگ”‚ة‚ب‚ء‚ؤ‚é‚ج‚إ
پiپ@‚R‚ج”{گ”پ@پ|پ@‚Pپ@‚إپ@‹ôگ”پ@پj
‚»‚ê‚ًپ@‚Q‚إٹ„‚ê‚خ
گ®گ”
گ³‚جگ®گ”
‚چ‚حپ@‚±‚ê‚إ‚·

‚ب‚ٌ‚©‚·‚ء‚«‚肵‚ب‚¢‚©‚炳
‚±‚ج‚ب‚ٌ‚¾
‚ژپپ‚Sپ@‚¾‚ء‚½‚ç
‚چ‚حپ@‚¢‚‚آ‚©Œ©‚é‚إ‚µ‚ه
‚S‚Oپ@‚¾‚ء‚ؤ
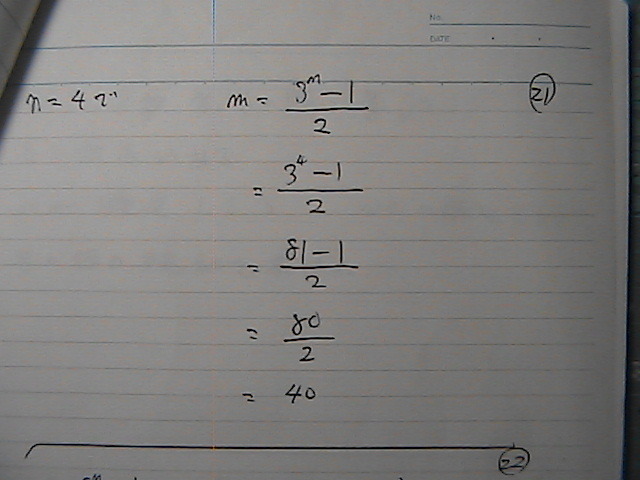
‚±‚ê‚ً
ƒ\ƒŒƒ]ƒŒپ@گ”—ٌ‚جکa‚جŒِژ®‚ة‘م“ü‚µ‚ؤ
“™”نگ”—ٌ‚جپ@ڈ‰‚ك‚ج‚Sچ€‚جکa‚ھ
“™چ·گ”—ٌ‚جپ@ڈ‰‚ك‚ج‚S‚Oچ€‚جکa‚ة‚ب‚ء‚½‚ئ
‚¾‚©‚ç
‚±‚جپ@‚چ‚جژ®‚حپ@‚ ‚ء‚ؤ‚é‚ئ
‚±‚ê‚ًپ@–‚½‚·پ@گ³‚جگ®گ”
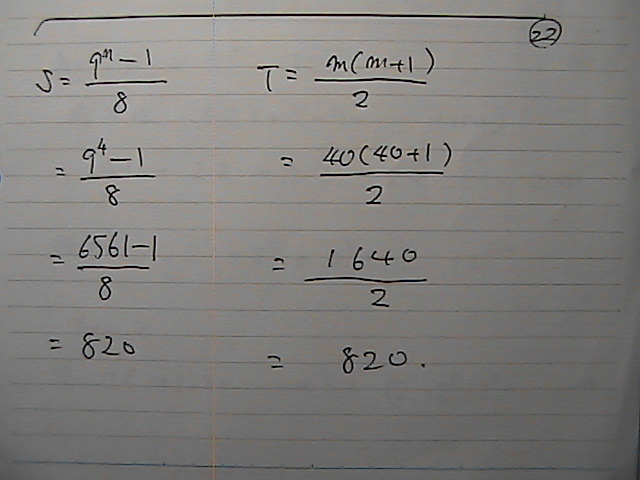
“ٌ‚آ‚ج•دگ”پ@‚کپA‚™پ@‚ھ‚ ‚ء‚ؤ
ٹضŒWژ®‚ھپ@‚±‚ê‚إ‚·
‚ک‚ًپ@‚P‚©‚çپ@‚P‚O‚O‚ـ‚إ
ڈ‡ژںپ@‘م“ü‚µ‚ؤ
‚™‚ج’l‚جپ@‘چکa‚ً‹پ‚ك‚ب‚³‚¢

‚·‚®‚ة
Œِژ®‚ةپ@“ü‚ê‚ç‚ê‚ê‚خپ@ٹy‚ب‚ٌ‚¾‚¯‚ا

‚ـ‚ئ‚à‚ةپ@‚â‚炸‚ة‚إ‚·‚ث
ڈ‚µپ@•ھ‰ً‚µ‚ؤ
ˆê‚آ‚أ‚آپ@•ھ‰ً‚µ‚ؤپ@•ہ‚ׂ½‚ç
‘O”¼‚حپ@“™چ·گ”—ٌ
•ھ‰ً‚µ‚½پ@Œم”¼‚حپ@“™”نگ”—ٌ‚ةپ@‚ب‚ء‚ؤ‚邶‚لƒiƒCƒXƒJ
‚»‚±‚إ
‚»‚ꂼ‚ê‚ج
کa‚جŒِژ®‚إ

ŒvژZ‚µ‚ؤ‚«‚ـ‚·‚ئ
“d‘ىپ@‚ا‚±چs‚ء‚½‚©‚ب
‚ٌ
‚ـپ[پ@‚±‚ٌ‚ب‚جپ@“d‘ى‚إ
گ”ژڑپ@ڈo‚µ‚½‚ئ‚ؤ
‚³
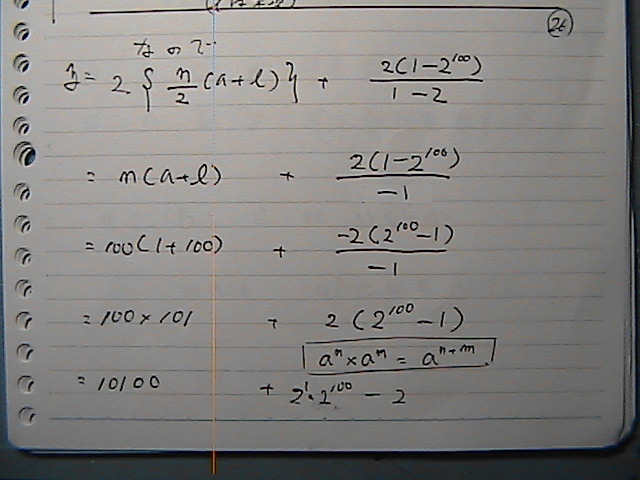
ژwگ”‚حپ@‚»‚ج‚ـ‚ـ‚إ‚¢‚¢‚ئ‚¢‚¤‚±‚ئ‚إ
‚±‚ê
•|‚¢‚ج‚ح
‚¤‚ء‚©‚肵‚ؤ‚é‚ئ
“d‘ى‚ةپ@—ٹ‚ء‚ؤ‚é‚©‚ç
ˆّ‚«ژZ‚ھپ@‰ِ‚µ‚¢
‚ف‚ب—l‚حپ@ŒvژZ—حپ@ژK‚ر‚ؤ‚ـ‚¹‚ٌ‚©پH

ژں‚ح‚ث
‚±‚ê‚ح
گ”ٹw‚جپ@ƒZƒ“ƒZ‚ئ‚©پ@چD‚«‚»‚¤‚ب–â‘è‚إ‚·‚و‚ث
‚¸‚¢‚ش‚ٌگج‚ٌ‚¾‚©‚ç
ڈo‚é‰آ”\گ«‚حپ@چ‚‚¢
“™چ·گ”—ٌ
“™”نگ”—ٌ
‚ھ‚ ‚é‚ٌ‚¾‚¯‚ا
کA‘±‚·‚éپ@‚Rگ”‚ھپ@‚»‚¤‚ب‚ٌ‚¾‚ء‚ؤ
‚±‚ê‚ح‚³
‚ب‚ٌ‚©پ@Œˆ‚ـ‚è‚ھ‚ ‚é‚ٌ‚¾‚¯‚ا
ˆê‰ٌپ@‚â‚ء‚ؤ‚¨‚¯‚خ
‚±‚ê‚حپ@‚»‚ٌ‚ب‚ةپ@‚¢‚¶‚ê‚ب‚¢‚©‚ç
ƒeƒXƒg‚ةپ@ڈo‚é‰آ”\گ«‚حپ@چ‚‚¢‚ئژv‚¤‚¯‚ا
‚إ

“™چ·گ”—ٌ‚¾‚©‚ç
Œِچ·ˆê’è
Œِچ·‚ًپ@‚„‚ئ’u‚¢‚ؤ‚إ‚·‚ث
‚إپ@ژlٹp‚إˆح‚ٌ‚¾ژ®

“™”نگ”—ٌ‚¾‚©‚ç
Œِ”ن‚ھپ@ˆê’è
Œِ”ن‚ً‚’‚ئ‚µ‚ؤ‚إ‚·‚ث

ژlٹp‚إپ@ˆح‚ٌ‚¾پ@ژ®
‚±‚جپ@“ٌ‚آ‚ًپ@کA—§‚µ‚ؤ
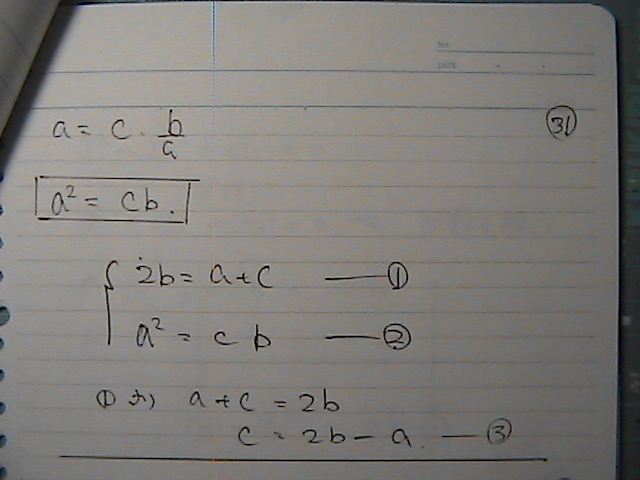
ˆê•¶ژڑپ@ڈء‹ژ‚·‚é‚ئ

“ٌژںٹضگ”‚ًپ@ˆِگ”•ھ‰ً‚إ‚µ‚ه
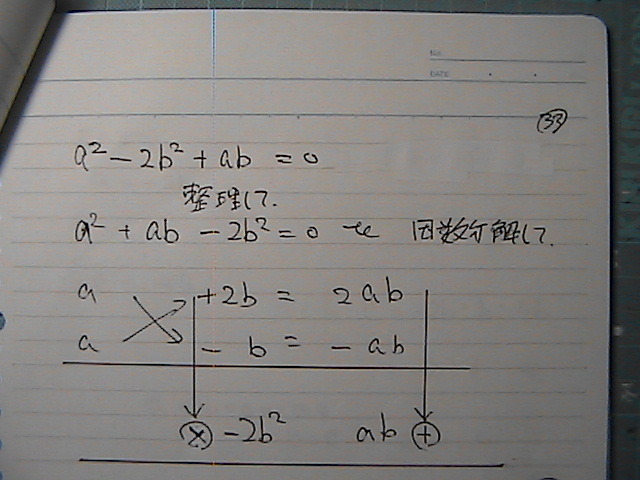
a‚ئپ@b‚جپ@ٹضŒW‚ھپ@‚ـ‚½‚ح‚إ
‚Q’ت‚è
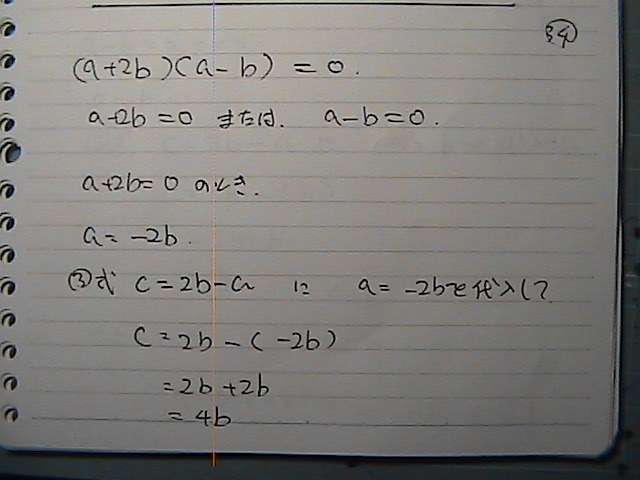
aپپپ|‚Q‚‚پ@‚جژ‚حپ@‚ƒپپپ@‚S‚‚
a:b:c = -2:1:4
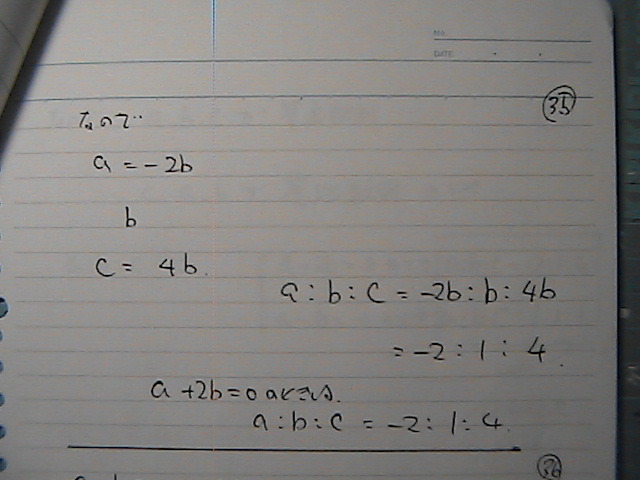
a=b‚جژ‚ح
‚ƒپپ‚‚‚إ
a=b=c
a:b:c پپپ@‚PپF‚PپF‚P

‚ب‚ج‚إ
“ڑ‚¦‚حپ@‚Q’ت‚è

ژں‚ح‚إ‚·‚ث
“ٌ‚آ‚جپ@گ”—ٌ‚ھپ@‚ ‚é‚ٌ‚إ‚·‚ھ
‚±‚جگ”—ٌ‚ج
‚Q‚ژ”ش–ع‚ئپ@پ@‚ژ”ش–عپ@‚ئپ@‚P‚ًپ@‚½‚µ‚½پ@پم‚ھ
ˆ½‚éگ®گ”‚ةپ@‚ب‚邱‚ئ‚ًپ@ڈط–¾‚¹‚و

a‚جگ”—ٌ‚ح
‚Q‚ژ”ش–ع‚حپ@‚P‚ھپ@‚Q‚ژŒآ•ہ‚ٌ‚¾Œ`‚¾‚©‚ç
“™”نگ”—ٌ‚جپ@کa‚جŒ`‚إ
‚ ‚ç‚ي‚¹‚ؤ
‚±‚ٌ‚ب‚إ

Œِژ®‚ةپ@“ü‚ê‚ؤŒvژZ‚·‚ê‚خپ@‚±‚¤
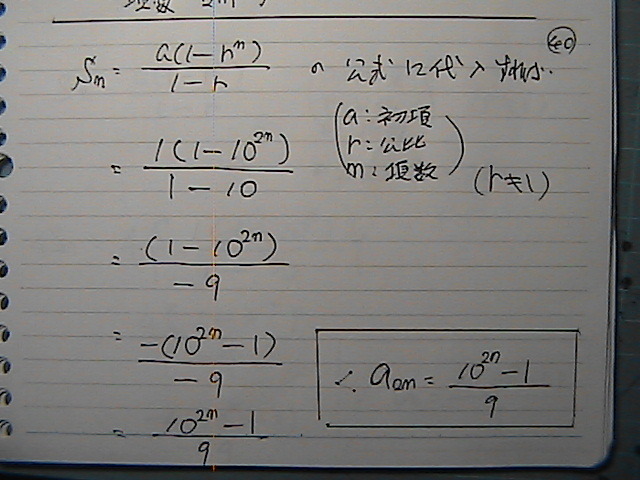
‚‚‚ج•û‚à
‚ژ”ش–ع‚حپ@
‚S‚ھپ@‚ژŒآ•ہ‚ٌ‚¾Œ`‚¾‚©‚ç
ژ®•دŒ`‚·‚ê‚خ
‚ ‚éپ@“™”نگ”—ٌ‚ج‚ژچ€‚ـ‚إ‚جکa‚جپ@‚S”{

Œِژ®‚ةپ@“ü‚ê‚ê‚خ
‚±

پمپ@‚جپ@ژ®‚ةپ@‘م“ü‚¶‚لƒiƒCƒXƒJ

‚إ
•ھ•ê‚ح
‚R‚ة‚ب‚ء‚ؤ
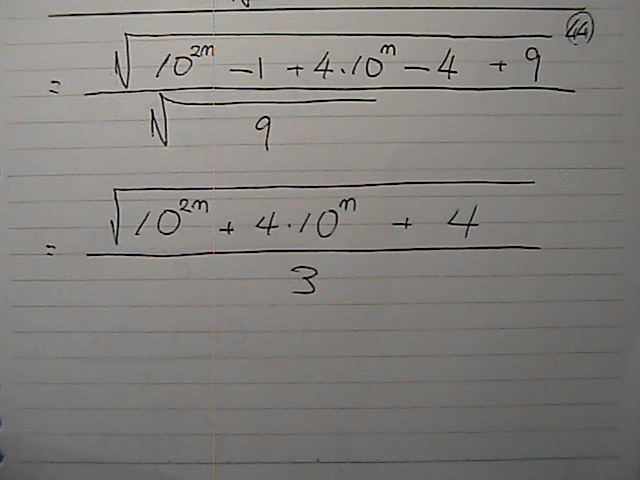
•ھژq‚حپ@‰½‚ئپ@ˆِگ”•ھ‰ً‚إ—ˆ‚ؤ
ٹ‡Œت‚جپ@‚Qڈو‚¾‚©‚ç
پم‚ھپ@ٹO‚ê‚ؤ
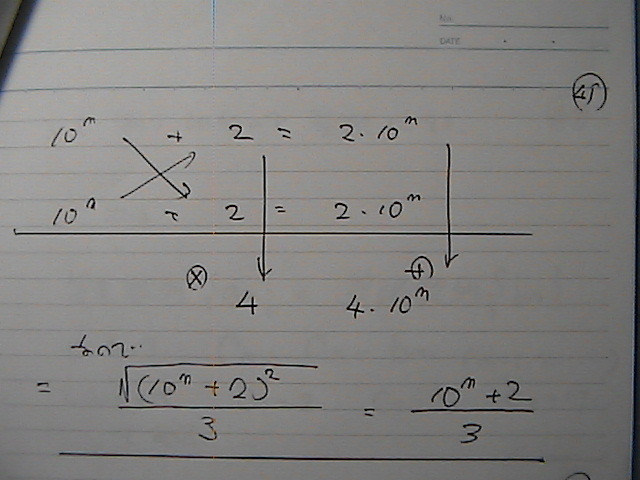
‚إ
ژ®•دŒ`‚·‚é‚ئ
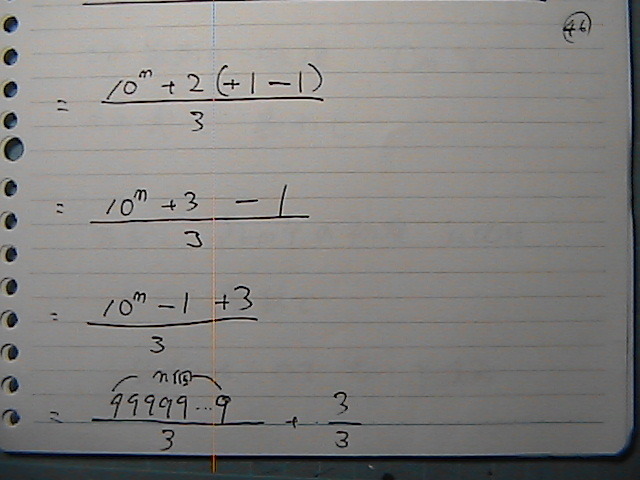
‚R‚إپ@ٹ„‚èگط‚ê‚ؤپ@گ®گ”‚ةپ@‚ب‚é‚à‚ج‚ةپ@‚P‚ً‘«‚·Œ`‚ب‚ج‚إ
گ®گ”‚ة‚ب‚é
‚±‚ê‚إ‚¢‚¢‚ئ‚µ‚ؤ‚‚¾‚³‚¢
‚إپ@ژں‚ح‚³

“™چ·گ”—ٌan
“™”نگ”—ٌbn
‚ھ‚ ‚ء‚ؤ
‚ƒ‚ژپ@‚ئ‚¢‚¤گ”—ٌ‚ح
‚ƒ‚ژپ@پپپ@an + bn
‚إ
‚ƒ‚Pپپپ@‚Qپ@پAپ@پ@‚ƒ‚Qپپپ@‚TپAپ@‚ƒ‚Rپپ‚P‚Vپ@پA‰½‚¾‚ء‚ؤ
‚ƒ‚ژپ@‚¤‚ًپ@‚ژپ@‚جژ®‚إ
•\‚¹
‚½‚¾‚µپ@bn‚جپ@ڈ‰چ€پ@Œِ”ن‚ح
‹¤‚ةگ®گ”‚إ
Œِ”ن‚حپ@‚O‚إ‚ح‚ب‚¢

‚»‚ٌ‚ب‚ةپ@“‚چl‚¦‚ب‚‚ؤ‚à
‚و‚³‚»‚¤‚¾‚ئ
‚½‚ش‚ٌپ@Œِژ®‚ًپ@‚¢‚¶‚ء‚ؤ‚¯‚خ
‚ئ
‚½‚©‚ً‚‚‚ء‚ؤ‚¢‚«‚ـ‚·‚ئ

‚ث
‚»‚ٌ‚ب‚ةپ@“‚پ@‚ب‚³‚»‚¤
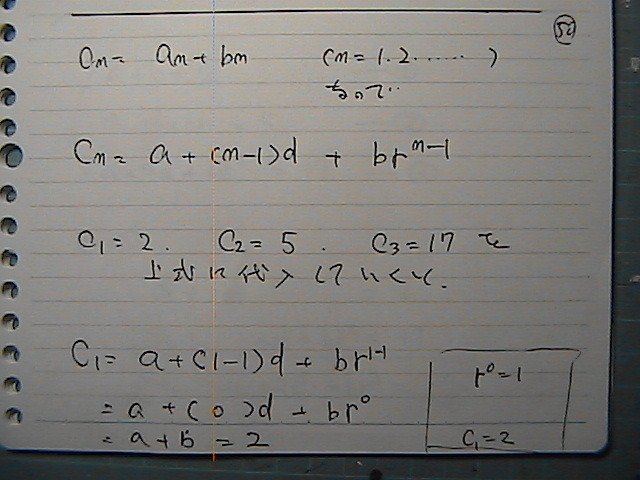
ڈ‡ژںپ@ژ®‚ةپ@’l‚ً‘م“ü‚µ‚ؤ‚‚ئ
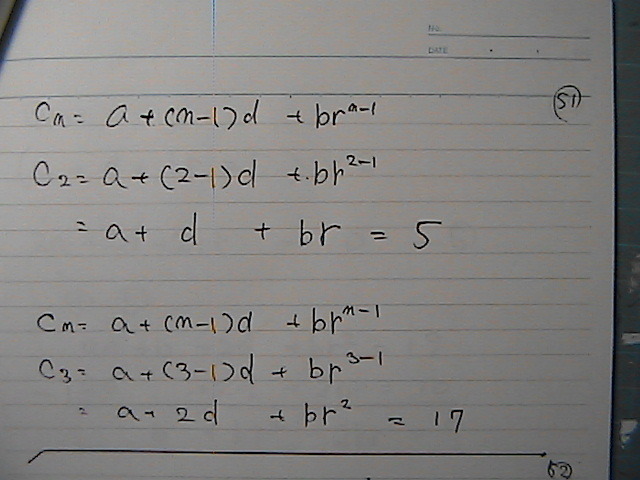
کA—§‚بپ@ژ®‚ھڈo‚ؤ—ˆ‚ؤ
‚إ‚à‚³
‚ب‚ٌ‚©پ@چ¢‚ء‚½‚±‚ئ‚ھ‚ ‚é
•¶ژڑ‚جگ”‚و‚è
کA—§‚جژ®‚جگ”‚ھ
ˆê‚آڈ‚ب‚¢
پH
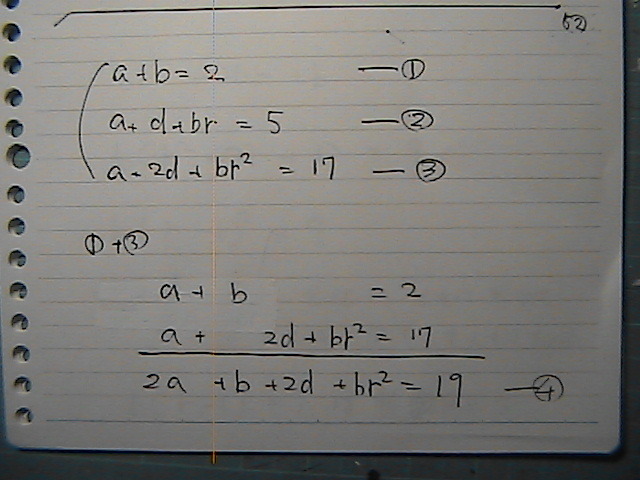
‚±‚±‚©‚çپ@‚اپ[‚·‚é‚©‚ب
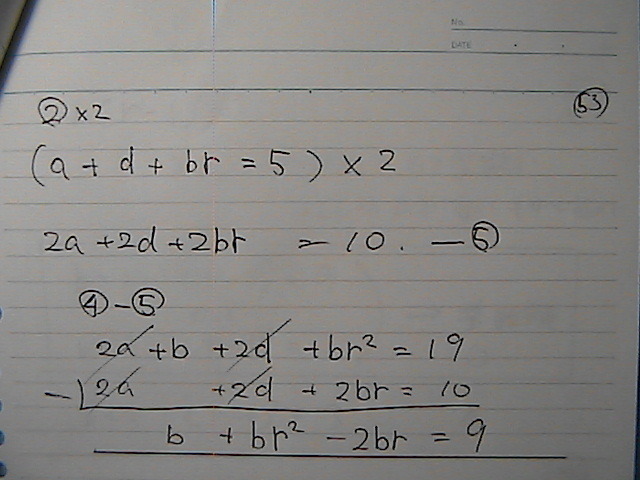
–â‘蕶‚ةپ@Œِ”نپ@ڈ‰چ€‚حپ@گ®گ”‚إ
پibn‚جپ@ڈ‰چ€پ@Œِ”ن‚حپ@گ®گ”‚إ
Œِ”ن‚حپ@‚O‚إ‚ح‚ب‚¢پj
‚à‚µ‚©‚µ‚ؤ‚إ‚·‚ھ
‚±‚ê‚ي‚³
گ³گ”‰ً
‚ج‚à‚ٌ‚¾‚¢

“ٌ‚آ‚جگ®گ”‚ًپ@ٹ|‚¯‚ؤپ@‚X‚ة‚ب‚é‚à‚ج‚إ
ڈًŒڈ‚ًپ@–‚½‚·‚à‚ج‚ًپ@’T‚·‚ئ

‚‚ڈ‰چ€پ@‚’Œِ”ن
‚‚‚ژ‚جپ@ڈ‰چ€پ@Œِ”ن‚حپ@گ®گ”‚إ
r‚حپ@‚O‚إ‚حپ@‚ب‚¢
‚ب‚½‚ك
‚ب‚ٌ‚©پ@“ٌ‚آ‚©پ@‚R‚ء‚آپ@ڈo‚ؤ—ˆ‚»‚¤‚إ
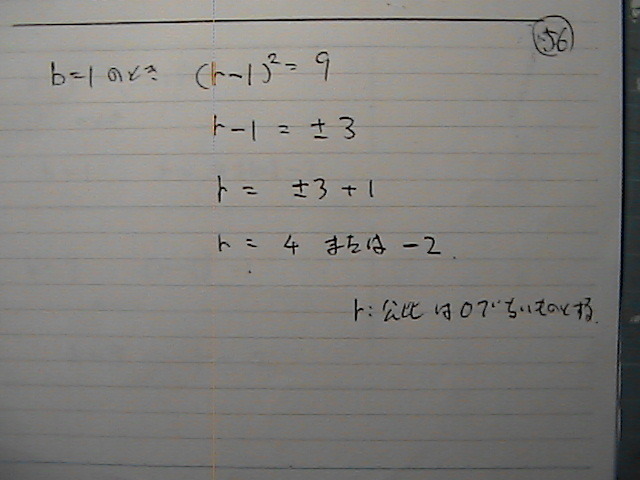
ژl‚آ‚إ‚ؤ‚«‚½‚¯‚ا
ڈًŒڈ‚ةپ@“K‚³‚ب‚¢‚à‚ج‚ً
Œ©‚ؤ

‚R’ت‚è
‚ٌپ[پ@ƒTƒ“ƒgƒٹپ[
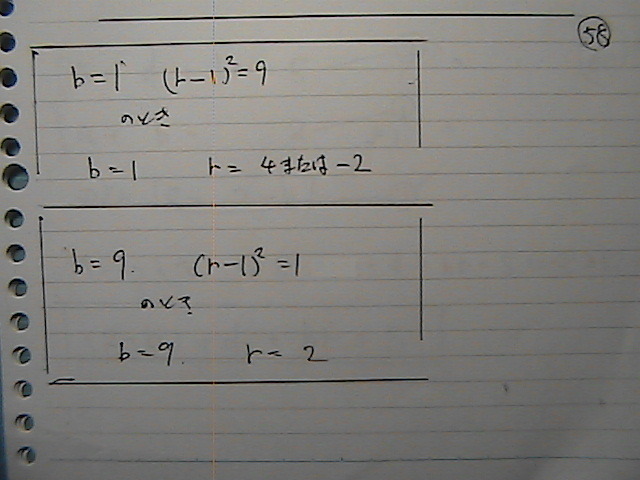
‚±‚±‚ـ‚إ‚جپ@•ْ‘—‚ح
ƒtƒ@ƒ“ƒuƒچƒOپ@
A‚Wƒlƒbƒg
ٹy“Vپ@
پEپEپE

‚؟‚ه‚ء‚ئ‚³
‰„’·‚إ‚·‚©
ڈo‚ؤ—ˆ‚ؤ‚½پ@کA—§‚جژ®‚ة
ڈ‡ژںپ@‚‚پ@پAپ@‚’پ@‚ًپ@‘م“ü‚µ‚ؤ
a,dپ@‚ًپ@‚ًپ@‹پ‚ك‚ؤ
an bn ‚جپ@ˆê”تچ€‚ًپ@ٹ®گ¬‚µ
‚ƒ‚ژپ@پپپ@an + bn
‚إ
‚R‚ئ‚¤‚èپ@ڈ‘‚¯‚خپ@“ڑ‚¦‚إ‚·

⓵پf‚ًپ@‡Aژ®‚ةپ@‘م“ü‚µ‚ؤ
‚‚پ@‚’پ@‚ةپ@‚»‚ꂼ‚ê
’l‚ًپ@‚R’ت‚è‘م“ü‚µ‚ؤ‚¯‚خ

‚P’ت‚è–ع
a=1
‚„پپ‚O
‚„‚ح
‚O‚إ‚àپ@ƒIƒbƒPƒC
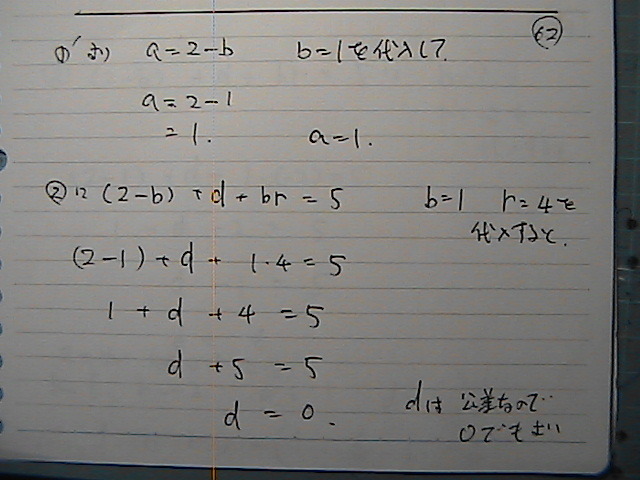
ˆê‘g–ع
ژں‚ة
‚‚پپ‚Pپ@‚’پپ-2‚جژ
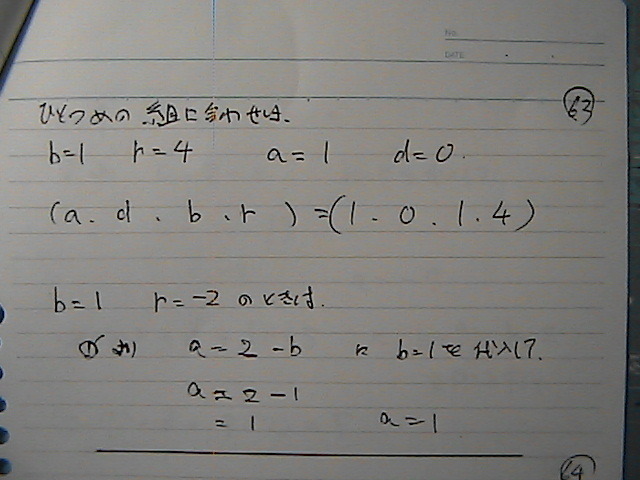
aپپ‚P
‚„پپپ@‚U
“ٌ‘g–ع‚حپ@‚±‚ê
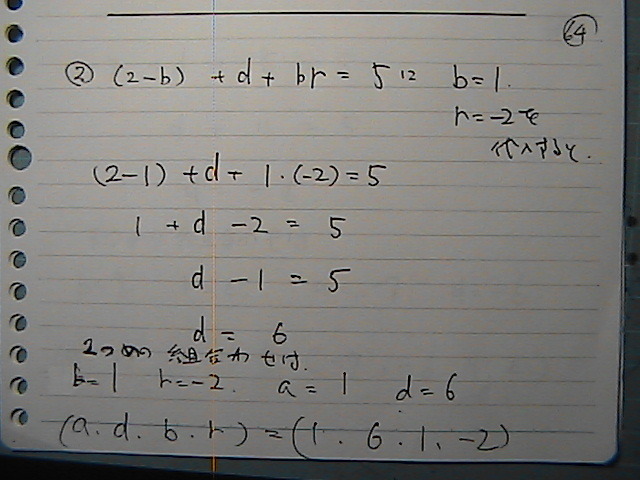
‚R‘g–ع
‚‚پپ‚Xپ@‚’پپ‚Q‚جژ
aپپ-7
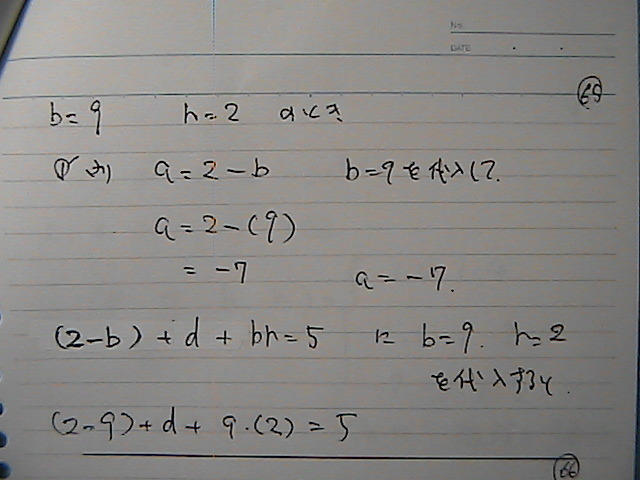
‚„پپ-6
‚R‘g–ع‚ح‚±‚ê

‘S•”پ@ڈo‚»‚ë‚ء‚½‚ئ‚±‚إ

‚ƒ‚ژپ@‚جپ@ژ®‚ةپ@‘م“ü‚µ‚ؤ‚‚ئ
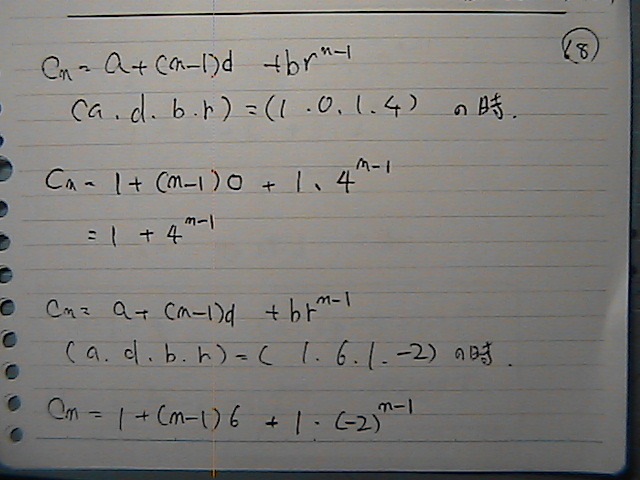
‚³‚ٌ‚ئ‚¤‚èپ[
‚¾‚©‚炳
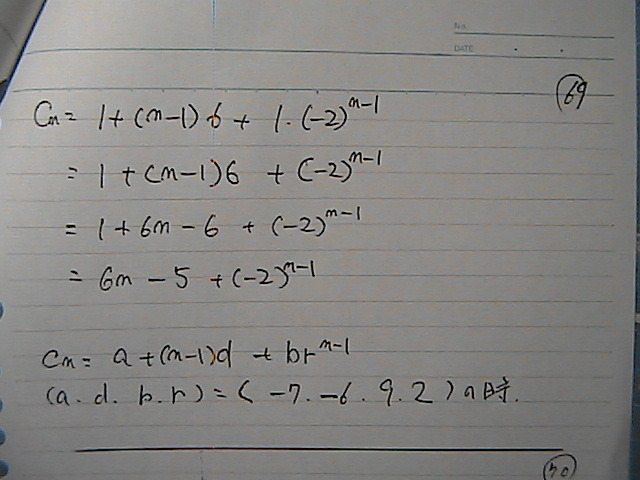
ڈ‚µپ@چإ‹كپ@ƒTƒ~پ[‚ة‚ب‚ء‚ؤ‚«‚ؤ‚邯‚ا
‚·‚ف‚ـ‚¹‚ٌ
ژv‚¢ڈo‚µ‚ؤ
ƒZƒ“ƒ`‚ةپ@‚ب‚ء‚ؤ‚ؤ‚ث
گي‘ˆ‚ئپ@گي‘ˆ‚ج‚¢‰\‚ھپ@•·‚±‚¦‚ؤ‚«‚ـ‚µ‚½
ژه‚ةپ@گM—ٹ‚·‚é‚à‚ج‚ح
چK‚¢‚إ‚·
‚ ‚ب‚½•û‚ةپ@‚ي‚½‚µ‚ج•½ˆہ‚ً
ژc‚µ‚ؤ‚¢‚
‚ي‚½‚µ‚ھپ@—^‚¦‚é‚à‚ج‚ح
گ¢‚ھپ@—^‚¦‚é‚à‚ج‚ئ‚حپ@ˆل‚¤
‚ ‚ب‚½•û‚ح
گS‚ًپ@‘›‚ھ‚¹‚ؤ‚حپ@‚ب‚ç‚ب‚¢
—ژ‚؟’…‚«‚ًپ@‚ب‚‚³‚ب‚¢‚و‚¤‚ة
ƒپƒjƒ…ƒEپ@ƒyپ[ƒWپ@ƒٹƒ^پ[ƒ“پ@پ@پ@پ@پj
“ٌ‚آ‚جگ”—ٌپ@‚ئ‚¢‚¤‚±‚ئ‚إ
“™”نگ”—ٌ‚ئ
“™چ·گ”—ٌ‚ھ‚ ‚é‚ٌ‚إ‚·‚و
‚إ
‚«‚ه‚¤‚ح‚ث
“™”نگ”—ٌ‚جپ@ڈ‰‚ك‚جپ@‚ژپ@چ€‚جکa‚ھ
“™چ·گ”—ٌ‚جپ@ڈ‰‚ك‚جپ@‰½چ€پ@‚©‚جپ@کa‚ةپ@“™‚µ‚¢‚±‚ئ‚ً
ڈط–¾‚¹‚و‚إ‚·
چs‚ء‚ؤ‚ف‚ـ‚µ‚ه‚¤
“™”نگ”—ٌ‚ج•û‚©‚ç
ڈ‰‚ك‚جپ@‚ژپ@چ€‚جکa‚جŒِژ®‚ح
Œِ”نپ@‚’پ@‚ھپ@‚P‚إ‚ب‚¯‚ê‚خ
ڈc‚ةپ@•ہ‚ٌ‚إ‚é
ڈم‚جŒِژ®
—^‚¦‚ç‚ê‚ؤ‚é
“™”نگ”—ٌپ@‚حپ@1.9.81.729.پEپEپEپEپE
ڈ‰چ€‚حپ@‚±‚ꂾ‚ئپ@‚P‚¾‚©‚ç
ˆê”تچ€‚جپ@Œِژ®‚ةپ@“ü‚ê‚ؤ‚¢‚ء‚ؤ
‚Qچ€–ع
‚Rچ€–ع
‚Qچ€ٹش‚ج”ن‚ًپ@•ھگ”‚ة‚µ‚ؤ
‹پ‚ك‚ؤ‚‚ئ
ڈ‰چ€‚جپ@a‚حپ@–ٌ‚·‚ئ
ڈء‹ژ‚إ‚«‚é‚©‚ç
‚±‚ٌ‚بٹ´‚¶‚إ
ƒٹƒoپ[ƒX‚µ‚ؤ
9
Œِ”ن‚X‚جپ@“™”نگ”—ٌ
ڈ‰چ€‚ح‚P
ˆê‰
ŒںژZ‚إ
‚ژپپپ@‚P
‚ژپپپ@‚Q
‚ژپپپ@‚R
‚ژپپپ@‚S
‚ب‚é‚ث
‘و‚ژچ€‚ـ‚إ‚جپ@کa‚ًپ@‹پ‚ك‚é‚ئ
ˆê”تچ€‚جپ@Œِژ®‚ح
ژg‚ي‚ب‚¢‚¯پ[‚ا‚³
Œِ”ن‚ئ‚©پ@ڈ‰چ€‚ئ‚©
‚µ‚ç‚ׂ½‚©‚ء‚½‚©‚炳
‚إ
Œِژ®‚ة“ü‚ê‚ؤ
‚±‚ê‚ھپ@“™”نگ”—ٌ‚ج
ڈ‰‚ك‚جپ@‚ژپ@چ€‚جکa
‚©‚½‚â
“™چ·گ”—ٌ‚ج•û‚ح
1.2.3.4.پEپEپEپE
‚ب‚ج‚إ
Œِچ·پ@‚P
ڈ‰چ€‚P
ˆê‰
ˆê”تچ€‚ح
Œِژ®‚©‚ç
‚ژ
‚±‚جگ”—ٌ‚ج
‘وپ@‚ژپ@چ€‚ـ‚إ‚جکa‚ح
Œِژ®‚©‚ç
‚¾‚©‚ç‚ة‚µ‚ؤ
‘م“ü‚µ‚ؤ
گ®—‚·‚ê‚خ
‚±‚ê
‚إ
–â‘è‚ح
“™”نگ”—ٌ‚جپ@‘وپ@‚ژپ@چ€‚ـ‚إ‚جکa‚ھ
“™چ·گ”—ٌ‚جپ@‘وپ@‰½چ€–عپ@‚©‚ـ‚إ‚جپ@کa‚ة
“™‚µ‚¢‚±‚ئ‚جپ@ڈط–¾
‚¾‚©‚ç
‚±‚ج‚³
Œ©‚½–ع‚جپ@–â‘肾‚¯‚ا
‘و‚ژپ@چ€‚ًپ@
‘و‚چپ@چ€‚ة‚µ‚ؤ
‚à‚¤پ@•¶ژڑ‚ھپ@ˆل‚¤‚©‚ç
–w‚ا‚جڈêچ‡پ@’l‚ھپ@ˆل‚¢‚ـ‚·
“™”نگ”—ٌ‚جپ@‚ژچ€‚ـ‚إ‚جکaپ@پپS
“™چ·گ”—ٌ‚جپ@‚چچ€‚ـ‚إ‚جکaپ@پپT
‚ئ‚·‚ê‚خ
S=T‚ة‚ب‚é‚ئ‚«‚ج
‚چ‚ًپ@‹پ‚ك‚ؤ
پiپ@‚ژ‚جژ®‚إپ@پj
‚چ‚جپ@“ٌژںژ®‚ة‚ب‚ء‚½‚إ‚µ‚ه
ژwگ”‚ج
ˆِگ”•ھ‰ً‚ب‚ا
ڈ€”ُ‚µ‚ؤ
‚چ‚ج‚Qژںژ®‚ًپ@ˆِگ”•ھ‰ً‚µ‚ؤ
پپ‚O‚ًپ@‰ً‚¢‚ؤ
‚إپ@ڈ‰‚ك‚جٹ‡Œت‚ج’†‚ح
‚±‚ê‚ح‚³
‚O‚ئ‚©‚ةپ@‚ب‚炸
‚آ‚ث‚ةپ@گ³‚¾‚©‚ç
•s“K
Œم‚ë‚جٹ‡Œت‚ج’†‚ح
پپ‚O‚ة‚ب‚é‚ئ‚±‚ًپ@Œ©‚ؤ
•ھژq‚ح
‚¢‚آ‚àپ@ŒvژZ‚·‚é‚ئپ@‹ôگ”‚ة‚ب‚ء‚ؤ‚é‚ج‚إ
پiپ@‚R‚ج”{گ”پ@پ|پ@‚Pپ@‚إپ@‹ôگ”پ@پj
‚»‚ê‚ًپ@‚Q‚إٹ„‚ê‚خ
گ®گ”
گ³‚جگ®گ”
‚چ‚حپ@‚±‚ê‚إ‚·
‚ب‚ٌ‚©‚·‚ء‚«‚肵‚ب‚¢‚©‚炳
‚±‚ج‚ب‚ٌ‚¾
‚ژپپ‚Sپ@‚¾‚ء‚½‚ç
‚چ‚حپ@‚¢‚‚آ‚©Œ©‚é‚إ‚µ‚ه
‚S‚Oپ@‚¾‚ء‚ؤ
‚±‚ê‚ً
ƒ\ƒŒƒ]ƒŒپ@گ”—ٌ‚جکa‚جŒِژ®‚ة‘م“ü‚µ‚ؤ
“™”نگ”—ٌ‚جپ@ڈ‰‚ك‚ج‚Sچ€‚جکa‚ھ
“™چ·گ”—ٌ‚جپ@ڈ‰‚ك‚ج‚S‚Oچ€‚جکa‚ة‚ب‚ء‚½‚ئ
‚¾‚©‚ç
‚±‚جپ@‚چ‚جژ®‚حپ@‚ ‚ء‚ؤ‚é‚ئ
‚±‚ê‚ًپ@–‚½‚·پ@گ³‚جگ®گ”
“ٌ‚آ‚ج•دگ”پ@‚کپA‚™پ@‚ھ‚ ‚ء‚ؤ
ٹضŒWژ®‚ھپ@‚±‚ê‚إ‚·
‚ک‚ًپ@‚P‚©‚çپ@‚P‚O‚O‚ـ‚إ
ڈ‡ژںپ@‘م“ü‚µ‚ؤ
‚™‚ج’l‚جپ@‘چکa‚ً‹پ‚ك‚ب‚³‚¢
‚·‚®‚ة
Œِژ®‚ةپ@“ü‚ê‚ç‚ê‚ê‚خپ@ٹy‚ب‚ٌ‚¾‚¯‚ا
‚ـ‚ئ‚à‚ةپ@‚â‚炸‚ة‚إ‚·‚ث
ڈ‚µپ@•ھ‰ً‚µ‚ؤ
ˆê‚آ‚أ‚آپ@•ھ‰ً‚µ‚ؤپ@•ہ‚ׂ½‚ç
‘O”¼‚حپ@“™چ·گ”—ٌ
•ھ‰ً‚µ‚½پ@Œم”¼‚حپ@“™”نگ”—ٌ‚ةپ@‚ب‚ء‚ؤ‚邶‚لƒiƒCƒXƒJ
‚»‚±‚إ
‚»‚ꂼ‚ê‚ج
کa‚جŒِژ®‚إ
ŒvژZ‚µ‚ؤ‚«‚ـ‚·‚ئ
“d‘ىپ@‚ا‚±چs‚ء‚½‚©‚ب
‚ٌ
‚ـپ[پ@‚±‚ٌ‚ب‚جپ@“d‘ى‚إ
گ”ژڑپ@ڈo‚µ‚½‚ئ‚ؤ
‚³
ژwگ”‚حپ@‚»‚ج‚ـ‚ـ‚إ‚¢‚¢‚ئ‚¢‚¤‚±‚ئ‚إ
‚±‚ê
•|‚¢‚ج‚ح
‚¤‚ء‚©‚肵‚ؤ‚é‚ئ
“d‘ى‚ةپ@—ٹ‚ء‚ؤ‚é‚©‚ç
ˆّ‚«ژZ‚ھپ@‰ِ‚µ‚¢
‚ف‚ب—l‚حپ@ŒvژZ—حپ@ژK‚ر‚ؤ‚ـ‚¹‚ٌ‚©پH
ژں‚ح‚ث
‚±‚ê‚ح
گ”ٹw‚جپ@ƒZƒ“ƒZ‚ئ‚©پ@چD‚«‚»‚¤‚ب–â‘è‚إ‚·‚و‚ث
‚¸‚¢‚ش‚ٌگج‚ٌ‚¾‚©‚ç
ڈo‚é‰آ”\گ«‚حپ@چ‚‚¢
“™چ·گ”—ٌ
“™”نگ”—ٌ
‚ھ‚ ‚é‚ٌ‚¾‚¯‚ا
کA‘±‚·‚éپ@‚Rگ”‚ھپ@‚»‚¤‚ب‚ٌ‚¾‚ء‚ؤ
‚±‚ê‚ح‚³
‚ب‚ٌ‚©پ@Œˆ‚ـ‚è‚ھ‚ ‚é‚ٌ‚¾‚¯‚ا
ˆê‰ٌپ@‚â‚ء‚ؤ‚¨‚¯‚خ
‚±‚ê‚حپ@‚»‚ٌ‚ب‚ةپ@‚¢‚¶‚ê‚ب‚¢‚©‚ç
ƒeƒXƒg‚ةپ@ڈo‚é‰آ”\گ«‚حپ@چ‚‚¢‚ئژv‚¤‚¯‚ا
‚إ
“™چ·گ”—ٌ‚¾‚©‚ç
Œِچ·ˆê’è
Œِچ·‚ًپ@‚„‚ئ’u‚¢‚ؤ‚إ‚·‚ث
‚إپ@ژlٹp‚إˆح‚ٌ‚¾ژ®
“™”نگ”—ٌ‚¾‚©‚ç
Œِ”ن‚ھپ@ˆê’è
Œِ”ن‚ً‚’‚ئ‚µ‚ؤ‚إ‚·‚ث
ژlٹp‚إپ@ˆح‚ٌ‚¾پ@ژ®
‚±‚جپ@“ٌ‚آ‚ًپ@کA—§‚µ‚ؤ
ˆê•¶ژڑپ@ڈء‹ژ‚·‚é‚ئ
“ٌژںٹضگ”‚ًپ@ˆِگ”•ھ‰ً‚إ‚µ‚ه
a‚ئپ@b‚جپ@ٹضŒW‚ھپ@‚ـ‚½‚ح‚إ
‚Q’ت‚è
aپپپ|‚Q‚‚پ@‚جژ‚حپ@‚ƒپپپ@‚S‚‚
a:b:c = -2:1:4
a=b‚جژ‚ح
‚ƒپپ‚‚‚إ
a=b=c
a:b:c پپپ@‚PپF‚PپF‚P
‚ب‚ج‚إ
“ڑ‚¦‚حپ@‚Q’ت‚è
ژں‚ح‚إ‚·‚ث
“ٌ‚آ‚جپ@گ”—ٌ‚ھپ@‚ ‚é‚ٌ‚إ‚·‚ھ
‚±‚جگ”—ٌ‚ج
‚Q‚ژ”ش–ع‚ئپ@پ@‚ژ”ش–عپ@‚ئپ@‚P‚ًپ@‚½‚µ‚½پ@پم‚ھ
ˆ½‚éگ®گ”‚ةپ@‚ب‚邱‚ئ‚ًپ@ڈط–¾‚¹‚و
a‚جگ”—ٌ‚ح
‚Q‚ژ”ش–ع‚حپ@‚P‚ھپ@‚Q‚ژŒآ•ہ‚ٌ‚¾Œ`‚¾‚©‚ç
“™”نگ”—ٌ‚جپ@کa‚جŒ`‚إ
‚ ‚ç‚ي‚¹‚ؤ
‚±‚ٌ‚ب‚إ
Œِژ®‚ةپ@“ü‚ê‚ؤŒvژZ‚·‚ê‚خپ@‚±‚¤
‚‚‚ج•û‚à
‚ژ”ش–ع‚حپ@
‚S‚ھپ@‚ژŒآ•ہ‚ٌ‚¾Œ`‚¾‚©‚ç
ژ®•دŒ`‚·‚ê‚خ
‚ ‚éپ@“™”نگ”—ٌ‚ج‚ژچ€‚ـ‚إ‚جکa‚جپ@‚S”{
Œِژ®‚ةپ@“ü‚ê‚ê‚خ
‚±
پمپ@‚جپ@ژ®‚ةپ@‘م“ü‚¶‚لƒiƒCƒXƒJ
‚إ
•ھ•ê‚ح
‚R‚ة‚ب‚ء‚ؤ
•ھژq‚حپ@‰½‚ئپ@ˆِگ”•ھ‰ً‚إ—ˆ‚ؤ
ٹ‡Œت‚جپ@‚Qڈو‚¾‚©‚ç
پم‚ھپ@ٹO‚ê‚ؤ
‚إ
ژ®•دŒ`‚·‚é‚ئ
‚R‚إپ@ٹ„‚èگط‚ê‚ؤپ@گ®گ”‚ةپ@‚ب‚é‚à‚ج‚ةپ@‚P‚ً‘«‚·Œ`‚ب‚ج‚إ
گ®گ”‚ة‚ب‚é
‚±‚ê‚إ‚¢‚¢‚ئ‚µ‚ؤ‚‚¾‚³‚¢
‚إپ@ژں‚ح‚³
“™چ·گ”—ٌan
“™”نگ”—ٌbn
‚ھ‚ ‚ء‚ؤ
‚ƒ‚ژپ@‚ئ‚¢‚¤گ”—ٌ‚ح
‚ƒ‚ژپ@پپپ@an + bn
‚إ
‚ƒ‚Pپپپ@‚Qپ@پAپ@پ@‚ƒ‚Qپپپ@‚TپAپ@‚ƒ‚Rپپ‚P‚Vپ@پA‰½‚¾‚ء‚ؤ
‚ƒ‚ژپ@‚¤‚ًپ@‚ژپ@‚جژ®‚إ
•\‚¹
‚½‚¾‚µپ@bn‚جپ@ڈ‰چ€پ@Œِ”ن‚ح
‹¤‚ةگ®گ”‚إ
Œِ”ن‚حپ@‚O‚إ‚ح‚ب‚¢
‚»‚ٌ‚ب‚ةپ@“‚چl‚¦‚ب‚‚ؤ‚à
‚و‚³‚»‚¤‚¾‚ئ
‚½‚ش‚ٌپ@Œِژ®‚ًپ@‚¢‚¶‚ء‚ؤ‚¯‚خ
‚ئ
‚½‚©‚ً‚‚‚ء‚ؤ‚¢‚«‚ـ‚·‚ئ
‚ث
‚»‚ٌ‚ب‚ةپ@“‚پ@‚ب‚³‚»‚¤
ڈ‡ژںپ@ژ®‚ةپ@’l‚ً‘م“ü‚µ‚ؤ‚‚ئ
کA—§‚بپ@ژ®‚ھڈo‚ؤ—ˆ‚ؤ
‚إ‚à‚³
‚ب‚ٌ‚©پ@چ¢‚ء‚½‚±‚ئ‚ھ‚ ‚é
•¶ژڑ‚جگ”‚و‚è
کA—§‚جژ®‚جگ”‚ھ
ˆê‚آڈ‚ب‚¢
پH
‚±‚±‚©‚çپ@‚اپ[‚·‚é‚©‚ب
–â‘蕶‚ةپ@Œِ”نپ@ڈ‰چ€‚حپ@گ®گ”‚إ
پibn‚جپ@ڈ‰چ€پ@Œِ”ن‚حپ@گ®گ”‚إ
Œِ”ن‚حپ@‚O‚إ‚ح‚ب‚¢پj
‚à‚µ‚©‚µ‚ؤ‚إ‚·‚ھ
‚±‚ê‚ي‚³
گ³گ”‰ً
‚ج‚à‚ٌ‚¾‚¢
“ٌ‚آ‚جگ®گ”‚ًپ@ٹ|‚¯‚ؤپ@‚X‚ة‚ب‚é‚à‚ج‚إ
ڈًŒڈ‚ًپ@–‚½‚·‚à‚ج‚ًپ@’T‚·‚ئ
‚‚ڈ‰چ€پ@‚’Œِ”ن
‚‚‚ژ‚جپ@ڈ‰چ€پ@Œِ”ن‚حپ@گ®گ”‚إ
r‚حپ@‚O‚إ‚حپ@‚ب‚¢
‚ب‚½‚ك
‚ب‚ٌ‚©پ@“ٌ‚آ‚©پ@‚R‚ء‚آپ@ڈo‚ؤ—ˆ‚»‚¤‚إ
ژl‚آ‚إ‚ؤ‚«‚½‚¯‚ا
ڈًŒڈ‚ةپ@“K‚³‚ب‚¢‚à‚ج‚ً
Œ©‚ؤ
‚R’ت‚è
‚ٌپ[پ@ƒTƒ“ƒgƒٹپ[
‚±‚±‚ـ‚إ‚جپ@•ْ‘—‚ح
ƒtƒ@ƒ“ƒuƒچƒOپ@
A‚Wƒlƒbƒg
ٹy“Vپ@
پEپEپE
‚؟‚ه‚ء‚ئ‚³
‰„’·‚إ‚·‚©
ڈo‚ؤ—ˆ‚ؤ‚½پ@کA—§‚جژ®‚ة
ڈ‡ژںپ@‚‚پ@پAپ@‚’پ@‚ًپ@‘م“ü‚µ‚ؤ
a,dپ@‚ًپ@‚ًپ@‹پ‚ك‚ؤ
an bn ‚جپ@ˆê”تچ€‚ًپ@ٹ®گ¬‚µ
‚ƒ‚ژپ@پپپ@an + bn
‚إ
‚R‚ئ‚¤‚èپ@ڈ‘‚¯‚خپ@“ڑ‚¦‚إ‚·
⓵پf‚ًپ@‡Aژ®‚ةپ@‘م“ü‚µ‚ؤ
‚‚پ@‚’پ@‚ةپ@‚»‚ꂼ‚ê
’l‚ًپ@‚R’ت‚è‘م“ü‚µ‚ؤ‚¯‚خ
‚P’ت‚è–ع
a=1
‚„پپ‚O
‚„‚ح
‚O‚إ‚àپ@ƒIƒbƒPƒC
ˆê‘g–ع
ژں‚ة
‚‚پپ‚Pپ@‚’پپ-2‚جژ
aپپ‚P
‚„پپپ@‚U
“ٌ‘g–ع‚حپ@‚±‚ê
‚R‘g–ع
‚‚پپ‚Xپ@‚’پپ‚Q‚جژ
aپپ-7
‚„پپ-6
‚R‘g–ع‚ح‚±‚ê
‘S•”پ@ڈo‚»‚ë‚ء‚½‚ئ‚±‚إ
‚ƒ‚ژپ@‚جپ@ژ®‚ةپ@‘م“ü‚µ‚ؤ‚‚ئ
‚³‚ٌ‚ئ‚¤‚èپ[
‚¾‚©‚炳
ڈ‚µپ@چإ‹كپ@ƒTƒ~پ[‚ة‚ب‚ء‚ؤ‚«‚ؤ‚邯‚ا
‚·‚ف‚ـ‚¹‚ٌ
ژv‚¢ڈo‚µ‚ؤ
ƒZƒ“ƒ`‚ةپ@‚ب‚ء‚ؤ‚ؤ‚ث
گي‘ˆ‚ئپ@گي‘ˆ‚ج‚¢‰\‚ھپ@•·‚±‚¦‚ؤ‚«‚ـ‚µ‚½
ژه‚ةپ@گM—ٹ‚·‚é‚à‚ج‚ح
چK‚¢‚إ‚·
‚ ‚ب‚½•û‚ةپ@‚ي‚½‚µ‚ج•½ˆہ‚ً
ژc‚µ‚ؤ‚¢‚
‚ي‚½‚µ‚ھپ@—^‚¦‚é‚à‚ج‚ح
گ¢‚ھپ@—^‚¦‚é‚à‚ج‚ئ‚حپ@ˆل‚¤
‚ ‚ب‚½•û‚ح
گS‚ًپ@‘›‚ھ‚¹‚ؤ‚حپ@‚ب‚ç‚ب‚¢
—ژ‚؟’…‚«‚ًپ@‚ب‚‚³‚ب‚¢‚و‚¤‚ة
پy‚±‚جƒJƒeƒSƒٹپ[‚جچإگV‹Lژ–پz
-
no image
posted by moriamelihu at 19:50| ‘هگl‚ج‚³‚ر—ژ‚ئ‚µپ@