2017�N08��01��
21007�@��l�̂��ї��Ƃ��@�{���̖��@�ޑ�
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�{���̖��́@�ޑ�ł�
�s���Ă݂܂��傤
�P����T�O�O�܂ł́@���̐����̂�����
�W�܂��͂P�Q�Ł@��������̂�
�a�����߂�
�ł�

�Ȃ̂�
�ِ}����i�C�X�J��
�ΐ��́@�����Ȃ���
���藝�@���Ă̂��@����܂���

�ِ}�́@�^�́@������
�_�u���Ă�̂�
A �Ɓ@B���@������
��������
�_�u�����@�P�������

�_�u���̕�����
�W�ƂP�Q�̍ŏ����{���Ȃ̂�
�p�ɂɁ@���Ă܂���
��������

�W�ƂP�Q���@���ꂸ�ꕪ�����Ă���
G�́@�ő����
���̂��ƂɁ@����a,b�́@�f���Ȃ̂�

���ʕ������@G�@����ɑ�����
�f���Ȍ`�ɂ����
�ő���́@�S
�i�@�f���́@�P�Ɓ@���̐����g�ł����@�₭���Ȃ����@�j
�o�@�P�C�Q�C�R�C�T�C�V�C�P�P�A�E�E�E�E�E�j

�ő�����@�o�Ă�����
��������
�W×�P�Q���@�ő���̂S�Ŋ�����
24
�Q�S���@�ŏ����{��
���ꂪ��
�ِ}��A��B�́@�����

�i�^��
�ِ}��A��B�́@�܂��́@�i�@�ΐ������́@�j
�d�����Ȃ��@�v�f�́@�a��
A�̘a�@�����@B�̘a�@�}�C�i�X�@A��B�̌����̘a
�����������
�W�̔{���̘a�@�����@�P�Q�̔{���̘a�@
�}�C�i�X�@�Q�S�̔{���̘a
�M�L�@�~�X���@����܂��@

��ςł���
�v�Z���Ă܂���܂��傤
�܂��@�P����T�O�O�܂ł�
�W�̔{���̘a
�W�̔{��������
�W���@���͎��R���@�i�@�P�C�Q�C�R�C�S�C�T�C�U�A�E�E�E�j
�ӁX�@�W�Ł@����Ƃ�
���@���@�������邩�@�������@����
���́@���R��������
�����ɍ��킹�ā@�����i�C�X�J

�P������@�U�Q���܂ł����
�P���߂́@�W
�U�Q���߂́@496
���R�����́@�U�Q��������
�a�̌����Ɂ@�������

�߂�ǂ�������
�d��Ȃ�
������������
�e�C�I�@������
15624

�P�Q�̕����@���߂Ȃ���ł����
����Ȃ���
�P�Q�̔{���Ł@�l����
�P�Q×�@�@�@�i�P�`�@�H���ځ@�j������Ƃ����@�i���ɂ��āj
�����@���߂��
�S�P�������

�d��@�e�C�e�C�e�C�I��

10332
��w�Ƃ��@�������肷���
���������Ɂ@�v���O����������
�d�쎝�����݉@�Ƃ��@���邩�炳
��ȁ@�v���O�������@�����Ă�
�Z�[�u�@���ĂȂ��Ƃ��Ȃ�
�g���ĂȂ��ł�
�Ƃ́@�����҂�
�^���Ắ@�܂���
��⊾�����

��ȁ@�҃E���O�������ĉ��Ȃ�
�Q�[�����@������
��
���߂��@�咣�����Ƃ���
�_�u���̌���蕔��
�Q�S�̔{����

�������@�Q�O��
�����Q�O
�����S�W�O
��������

5040
��
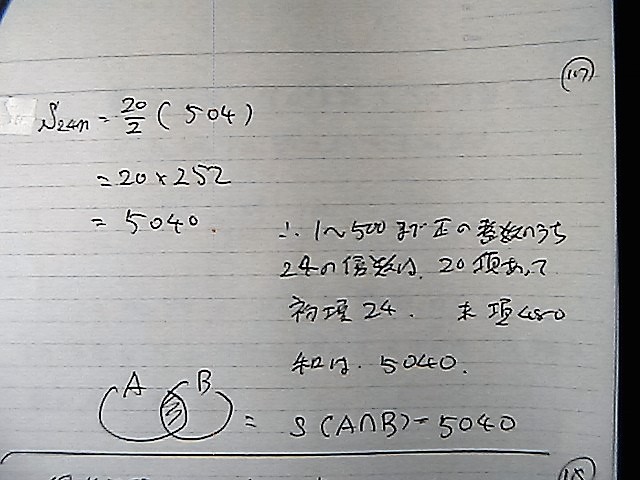
���߂�@�a��
15624+10332-5040��20916
20916

�e�B�[�@�́@���@�ł���
�킽����
�F�l�Ɓ@�����@���k�ł��̂�
�����Ă���ǂ��̂�
�������e�B�[�@�Ȃ�
�Ȃ�ł��H
�R�[�q�[���@�炵�Ă��邽��
��
�����悤�ȁ@���Ȃ�ł���
���w�ƌ����ǂ�
���͂�
�lj�͂́@�K�v��
�������Ȃ���
��́@�p�^�[�����@���܂��Ă���
�Q�P�^���Č������炳
���Ɓ@�l���Ăł���

��蕶���@�}�ɏ�����
�S�̂�����Ȃ�
�l�p�̂Ȃ�����
�ِ}�́@�܂��́@���@���������̂�
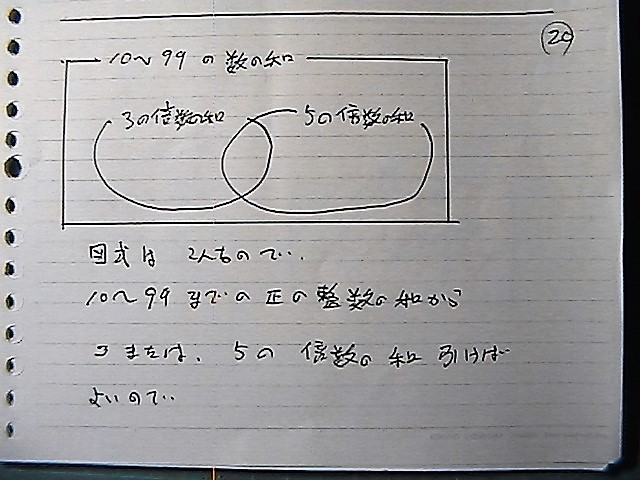
�l�p�@�S�̂́@�������v�Z����Ƃł���
�P�O����@�X�X�܂ł�
�P�O���炾���炳
�X�X�����@�X�@���@�X�O
�X�O��
�����P�O�@
�����X�X

��������
4905

��
�R�܂��́@�T�́@�{����
�Öق̗�����
���藝����
�R�̔{���̘a�@�����@�T�̔{���̘a
�}�C�i�X�@�R�ƂT�̍ŏ����{���̔{���̘a

���傤���Ȃ�����i�C�X�J
�v�Z�ł����
�R�̔{������
�������݂�����
�l���Ă��ł���

��������
1665
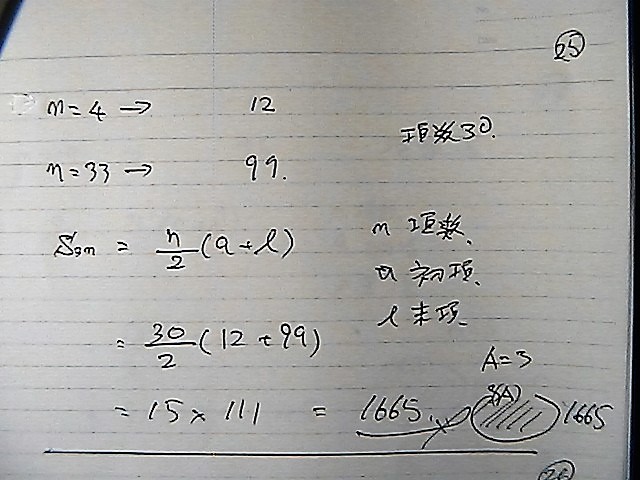
�T�̔{����
����Ȃ���
�l����
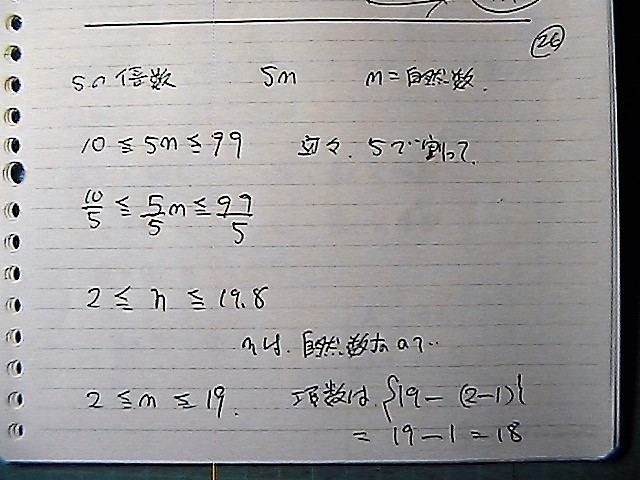
945

��
�R�ƂT�́@�ŏ����{���Ȃ�ł���
�R���T���@�݂��Ɂ@�f
�f���Ȃ�ł���
�ő����
�Ȃ��H�H�H
����������i�C�X�J
�P

�Ȃ̂Ł@���̂܂�
�����ā@�P�T

����
��������@
��[
�ȂǂƁ@����ł��܂�Ȃ��悤�ɂł���
�ǂ��������
�{���Ł@������
�����@�������邩�@�݂�
����
����
��������

�����ɑ������
315

�o�Ă����@�����̃f�[�^�͂ł���
4905
1665
945
315
������
�g���ā@�v�Z���܂���
2295
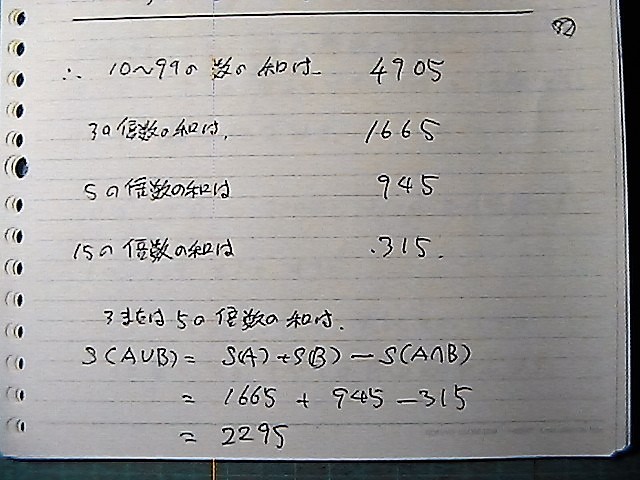
��
����Ł@��������Ȃ���
2295�́@�R�܂��͂T�̔{���̘a
�����
�S�̂���@������
2610

���͂�
�v�Z���@��ςȂ�
��蕶��
�ǂ�ł݂܂���
�Q�O�O��菬����
���̐����̂���
�R�C�T�C�V�́@���Ȃ��Ƃ�
�P�́@�{���ƂȂ�@�S�Ă̐��́@�a�����߂�

A,B,C���@�g����
�ِ}�Ł@������
���̎ΐ��̕���
���̗v�f�́@����
���藝��
�����
���������@�����@���G�ɂȂ���
����Ȋ�����

���e��
�R�Ŋ��������
�T�Ŋ��������
�V�Ŋ��������
�R�܂��͂T�Ł@���������
�T�܂��͂V�Ł@���������
�V�܂��͂R�Ł@���������
�R�ƂT�ƂV�Ł@���������
�����́@�ǂ�ł��悭
�d�����Ȃ��悤��
���藝����
������
�v�f���@���v�����

�R�̔{���̘a�@+�@�T�̔{���̘a�@+�@�V�̔{���̘a
-�i�R�ƂT�̍ŏ����{���̔{���̘a�j
-�i�T�ƂV�̍ŏ����{���̔{���̘a�j
-�i�V�ƂR�̍ŏ����{���̔{���̘a�j
+�i�R�ƂT�ƂV�Ŋ���鐔�̘a�@�j

�}�ɂ���Ƃ���Ȃ�
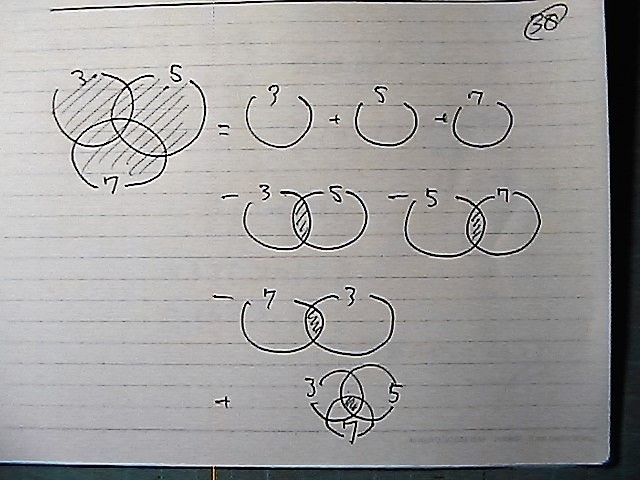
��ς����ǂ�
�Ђ�����@�v�Z
�Q�O�O���@�������@���̐���������
�P�`�P�X�X
���w���ā@���������Ƃ���
��������@�ł��Ȃ��ł���
��
�R�́@�{������
�������邩���Ă���
�U�U��

�����@
����
������������@��������
6633

�T�̔{���̎���
�ӁX�@�T�Ł@�����Ă��`��
�������@����o����

�����@
����
�������o��@
�����̘a�́@��������
3900

�V�̔{����
�V���ɂ���
�����@���R���ɂ��ā@�i�����P�C�Q�C�R�C�S�C�T�C�U�C�V�A�E�E�E�j
�ӁX���@�V�Ł@������
���́@���R��������
�����
�������@�Q�W��

����
����
����
��������
�a�́@2842

�R�ƂT�́@�ŏ����{��
����́@�@�R���T���V��
�S���@�݂��Ɂ@�f�Ȃ̂�
���̂܂܁@�|�����
�@
�����̂������
����Ă����悤��
�����܂���
G�@�ő�����@�P�i�^��

�ŏ����{���́@�P�T

�P�T�̔{���̘a�́@�@�P�`�P�X�X�܂ł�
�Ԃ�����
�s�������@�g����
�������݂����ɂł���
��
�ӁX�@�P�T�Ł@������
���́@���R���ł�����@�����ɍ����Ƃ���
�T����
�������P�R

����
����
�������@���߂�
�����Ɂ@��������
1365
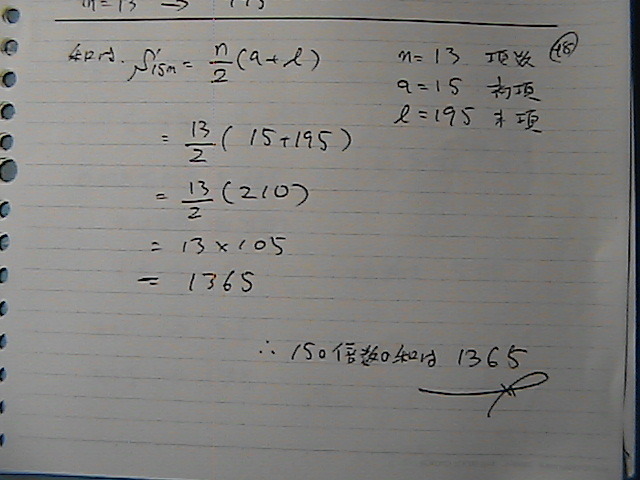
�T�ƂV��
�ŏ����{����
�R�T

�R�T�́@�{���̘a��
�P�`�P�X�X�̊Ԃ̂��̂���������
�s������
�͂����
�������́@�ɂȂ���
�ӁX
���@���@�E�@�@�R�T�Ł@������
�����́@�T��
�a�́@525

�V�ƂR��
�ő�����P������

��������
���̂܂�
�V�ƂR���@�|����
�Q�P

�Q�P�́@�{���̘a��
�����@�Q�P������P���Q�P
�����@�Q�P������X��189
�����X
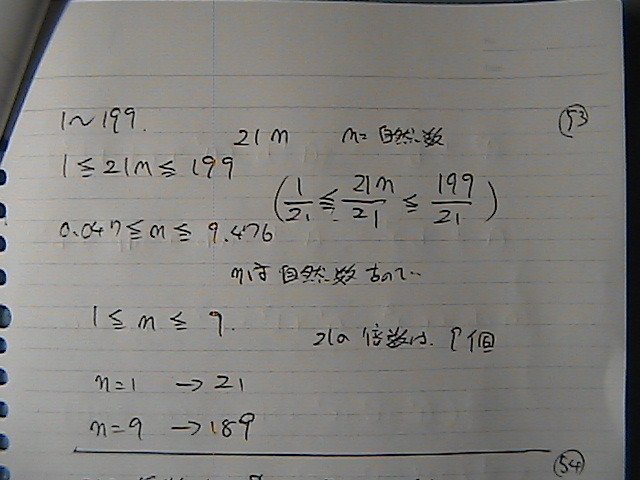
��������
9/2�i21+189�j
���@945
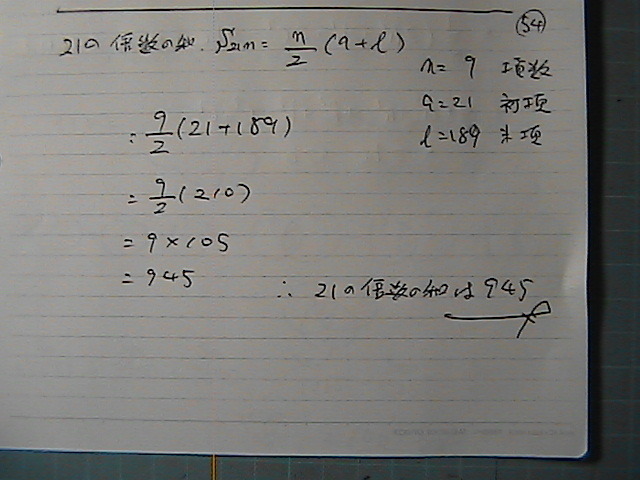
�R�ƂT�ƂV�́@������
�S���@�݂��Ɂ@�f�Ȃ̂�
���̂܂܂�����
105
����������炳

�����܂ł̌v�Z��
�����@���Ă͂߂Ă����܂���
�Q�O�O��菬����
���̐����̂���
�R�C�T�C�V�́@���Ȃ��Ƃ�
�P�́@�{���ƂȂ�@�S�Ă̐��́@�a��
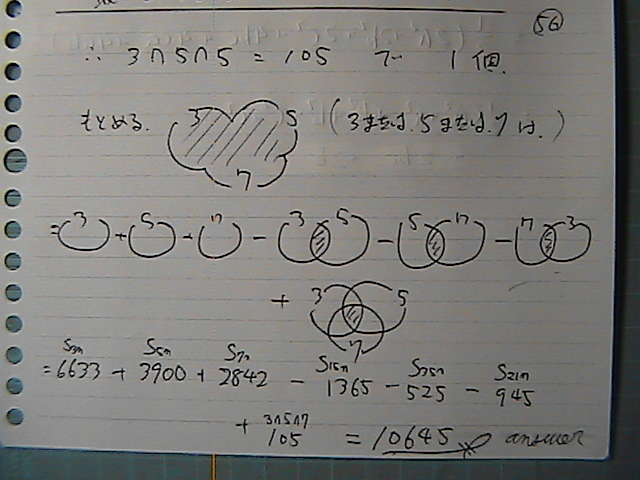
10645
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�{���̖��́@�ޑ�ł�
�s���Ă݂܂��傤
�P����T�O�O�܂ł́@���̐����̂�����
�W�܂��͂P�Q�Ł@��������̂�
�a�����߂�
�ł�
�Ȃ̂�
�ِ}����i�C�X�J��
�ΐ��́@�����Ȃ���
���藝�@���Ă̂��@����܂���
�ِ}�́@�^�́@������
�_�u���Ă�̂�
A �Ɓ@B���@������
��������
�_�u�����@�P�������
�_�u���̕�����
�W�ƂP�Q�̍ŏ����{���Ȃ̂�
�p�ɂɁ@���Ă܂���
��������
�W�ƂP�Q���@���ꂸ�ꕪ�����Ă���
G�́@�ő����
���̂��ƂɁ@����a,b�́@�f���Ȃ̂�
���ʕ������@G�@����ɑ�����
�f���Ȍ`�ɂ����
�ő���́@�S
�i�@�f���́@�P�Ɓ@���̐����g�ł����@�₭���Ȃ����@�j
�o�@�P�C�Q�C�R�C�T�C�V�C�P�P�A�E�E�E�E�E�j
�ő�����@�o�Ă�����
��������
�W×�P�Q���@�ő���̂S�Ŋ�����
24
�Q�S���@�ŏ����{��
���ꂪ��
�ِ}��A��B�́@�����
�i�^��
�ِ}��A��B�́@�܂��́@�i�@�ΐ������́@�j
�d�����Ȃ��@�v�f�́@�a��
A�̘a�@�����@B�̘a�@�}�C�i�X�@A��B�̌����̘a
�����������
�W�̔{���̘a�@�����@�P�Q�̔{���̘a�@
�}�C�i�X�@�Q�S�̔{���̘a
�M�L�@�~�X���@����܂��@
��ςł���
�v�Z���Ă܂���܂��傤
�܂��@�P����T�O�O�܂ł�
�W�̔{���̘a
�W�̔{��������
�W���@���͎��R���@�i�@�P�C�Q�C�R�C�S�C�T�C�U�A�E�E�E�j
�ӁX�@�W�Ł@����Ƃ�
���@���@�������邩�@�������@����
���́@���R��������
�����ɍ��킹�ā@�����i�C�X�J
�P������@�U�Q���܂ł����
�P���߂́@�W
�U�Q���߂́@496
���R�����́@�U�Q��������
�a�̌����Ɂ@�������
�߂�ǂ�������
�d��Ȃ�
������������
�e�C�I�@������
15624
�P�Q�̕����@���߂Ȃ���ł����
����Ȃ���
�P�Q�̔{���Ł@�l����
�P�Q×�@�@�@�i�P�`�@�H���ځ@�j������Ƃ����@�i���ɂ��āj
�����@���߂��
�S�P�������
�d��@�e�C�e�C�e�C�I��
10332
��w�Ƃ��@�������肷���
���������Ɂ@�v���O����������
�d�쎝�����݉@�Ƃ��@���邩�炳
��ȁ@�v���O�������@�����Ă�
�Z�[�u�@���ĂȂ��Ƃ��Ȃ�
�g���ĂȂ��ł�
�Ƃ́@�����҂�
�^���Ắ@�܂���
��⊾�����
��ȁ@�҃E���O�������ĉ��Ȃ�
�Q�[�����@������
��
���߂��@�咣�����Ƃ���
�_�u���̌���蕔��
�Q�S�̔{����
�������@�Q�O��
�����Q�O
�����S�W�O
��������
5040
��
���߂�@�a��
15624+10332-5040��20916
20916
�e�B�[�@�́@���@�ł���
�킽����
�F�l�Ɓ@�����@���k�ł��̂�
�����Ă���ǂ��̂�
�������e�B�[�@�Ȃ�
�Ȃ�ł��H
�R�[�q�[���@�炵�Ă��邽��
��
�����悤�ȁ@���Ȃ�ł���
���w�ƌ����ǂ�
���͂�
�lj�͂́@�K�v��
�������Ȃ���
��́@�p�^�[�����@���܂��Ă���
�Q�P�^���Č������炳
���Ɓ@�l���Ăł���
��蕶���@�}�ɏ�����
�S�̂�����Ȃ�
�l�p�̂Ȃ�����
�ِ}�́@�܂��́@���@���������̂�
�l�p�@�S�̂́@�������v�Z����Ƃł���
�P�O����@�X�X�܂ł�
�P�O���炾���炳
�X�X�����@�X�@���@�X�O
�X�O��
�����P�O�@
�����X�X
��������
4905
��
�R�܂��́@�T�́@�{����
�Öق̗�����
���藝����
�R�̔{���̘a�@�����@�T�̔{���̘a
�}�C�i�X�@�R�ƂT�̍ŏ����{���̔{���̘a
���傤���Ȃ�����i�C�X�J
�v�Z�ł����
�R�̔{������
�������݂�����
�l���Ă��ł���
��������
1665
�T�̔{����
����Ȃ���
�l����
945
��
�R�ƂT�́@�ŏ����{���Ȃ�ł���
�R���T���@�݂��Ɂ@�f
�f���Ȃ�ł���
�ő����
�Ȃ��H�H�H
����������i�C�X�J
�P
�Ȃ̂Ł@���̂܂�
�����ā@�P�T
����
��������@
��[
�ȂǂƁ@����ł��܂�Ȃ��悤�ɂł���
�ǂ��������
�{���Ł@������
�����@�������邩�@�݂�
����
����
��������
�����ɑ������
315
�o�Ă����@�����̃f�[�^�͂ł���
4905
1665
945
315
������
�g���ā@�v�Z���܂���
2295
��
����Ł@��������Ȃ���
2295�́@�R�܂��͂T�̔{���̘a
�����
�S�̂���@������
2610
���͂�
�v�Z���@��ςȂ�
��蕶��
�ǂ�ł݂܂���
�Q�O�O��菬����
���̐����̂���
�R�C�T�C�V�́@���Ȃ��Ƃ�
�P�́@�{���ƂȂ�@�S�Ă̐��́@�a�����߂�
A,B,C���@�g����
�ِ}�Ł@������
���̎ΐ��̕���
���̗v�f�́@����
���藝��
�����
���������@�����@���G�ɂȂ���
����Ȋ�����
���e��
�R�Ŋ��������
�T�Ŋ��������
�V�Ŋ��������
�R�܂��͂T�Ł@���������
�T�܂��͂V�Ł@���������
�V�܂��͂R�Ł@���������
�R�ƂT�ƂV�Ł@���������
�����́@�ǂ�ł��悭
�d�����Ȃ��悤��
���藝����
������
�v�f���@���v�����
�R�̔{���̘a�@+�@�T�̔{���̘a�@+�@�V�̔{���̘a
-�i�R�ƂT�̍ŏ����{���̔{���̘a�j
-�i�T�ƂV�̍ŏ����{���̔{���̘a�j
-�i�V�ƂR�̍ŏ����{���̔{���̘a�j
+�i�R�ƂT�ƂV�Ŋ���鐔�̘a�@�j
�}�ɂ���Ƃ���Ȃ�
��ς����ǂ�
�Ђ�����@�v�Z
�Q�O�O���@�������@���̐���������
�P�`�P�X�X
���w���ā@���������Ƃ���
��������@�ł��Ȃ��ł���
��
�R�́@�{������
�������邩���Ă���
�U�U��
�����@
����
������������@��������
6633
�T�̔{���̎���
�ӁX�@�T�Ł@�����Ă��`��
�������@����o����
�����@
����
�������o��@
�����̘a�́@��������
3900
�V�̔{����
�V���ɂ���
�����@���R���ɂ��ā@�i�����P�C�Q�C�R�C�S�C�T�C�U�C�V�A�E�E�E�j
�ӁX���@�V�Ł@������
���́@���R��������
�����
�������@�Q�W��
����
����
����
��������
�a�́@2842
�R�ƂT�́@�ŏ����{��
����́@�@�R���T���V��
�S���@�݂��Ɂ@�f�Ȃ̂�
���̂܂܁@�|�����
�@
�����̂������
����Ă����悤��
�����܂���
G�@�ő�����@�P�i�^��
�ŏ����{���́@�P�T
�P�T�̔{���̘a�́@�@�P�`�P�X�X�܂ł�
�Ԃ�����
�s�������@�g����
�������݂����ɂł���
��
�ӁX�@�P�T�Ł@������
���́@���R���ł�����@�����ɍ����Ƃ���
�T����
�������P�R
����
����
�������@���߂�
�����Ɂ@��������
1365
�T�ƂV��
�ŏ����{����
�R�T
�R�T�́@�{���̘a��
�P�`�P�X�X�̊Ԃ̂��̂���������
�s������
�͂����
�������́@�ɂȂ���
�ӁX
���@���@�E�@�@�R�T�Ł@������
�����́@�T��
�a�́@525
�V�ƂR��
�ő�����P������
��������
���̂܂�
�V�ƂR���@�|����
�Q�P
�Q�P�́@�{���̘a��
�����@�Q�P������P���Q�P
�����@�Q�P������X��189
�����X
��������
9/2�i21+189�j
���@945
�R�ƂT�ƂV�́@������
�S���@�݂��Ɂ@�f�Ȃ̂�
���̂܂܂�����
105
����������炳
�����܂ł̌v�Z��
�����@���Ă͂߂Ă����܂���
�Q�O�O��菬����
���̐����̂���
�R�C�T�C�V�́@���Ȃ��Ƃ�
�P�́@�{���ƂȂ�@�S�Ă̐��́@�a��
10645
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 11:34| ��l�̂��ї��Ƃ��@