2017�N08��04��
��l�̂��ї��Ƃ��@21008 ��������́@�a�̍ő�@�ŏ��̖��
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��������́@�a�̍ő�@�ŏ��̖��
�ǂ����@��������Ȃ̂�
���
�s���Ă݂܂��傤

�ǂ�ł������������Ƃ�
�R�O�{�́@�����@�T���[�g���@�Ԋu�Ł@���ĂĂ���
�����
�Ђ��[����@�P���Ɂ@�W�߂��ł���
��{���@�W�߂�@���܂�Ȃ̂�
���Ɂ@�W�߂Ă�������
�s�������������Ɂ@�W�߂Ă�������
�e�Ɋp
1���Ɂ@��{���@���ɍs���Ắ@�߂��Ă���
�܂��@���ɍs���Ắ@�߂��Ă���
���傱�܂����傱�܂�
�S���@�W�߂��ł���

�Ԋu���@�T���[�g���Ł@�R�O�{
�悎�ԖڂɁ@�S���@�W�߂�
�i�P�����@���@�����@�R�O�j
�ǂꂭ�炢�@�����̃J�i�H
�ŏ��l�́@�ǂꂭ�炢�J�i�H
���ł���
������
��@���@���́@�����Ɓ@�E���Ɂ@������
�������@���߂��Ƃ��@�l����ł���

�����́@�������@�W�߂�ɂ�
��ԁ@�߂����@�T���[�g����
�����@�P�O���[�g����
�Ԋu���@�T���[�g����
�悎������@�����Ƃ���
��P���܂ł́@���|�P�@�{�@����̂�
�悎������@��ԍ��[�܂ł́@�T�i���|�P�j���[�g��
���́@��������̘a��
�����ā@�Ƃ��Ă������
��������
�Q�{�@�������̂��@�@�悎�����@���ɂ������
�悎���Ɂ@�S���@
��{���@�W�߂�Ƃ��Ɂ@�����@�����ł�

�����
�����������
�Q�{�́@�i�@�����@��������̘a�@�j�@�@

�����Ɂ@�����ł���
�����@�����@�������@�킩���Ă�̂�
��,a,l,�Ɂ@�������
�T���i���|�P�j

���x�́@�悎�����@�E�������́@����
�W�߂�Ƃ�
����ς�@��{���@���傱���傱
�����Ắ@�����Ă���
�܂��@�����Ắ@���ė���

�悎���ɑS���W�߂��
�E���Ɂ@��ԍŏ��́@�T���[�g����
���́@�P�O���[�g����
��ԉE����
�T���[�g���Ԋu��
�R�O�{����@���{���@��������
�T�i�R�O�|���j���[�g����
���̐���̘a���@�������Ł@�Q�{�����

�E�����@����������
�T�i�R�O�|���j�i�R�P�|���j
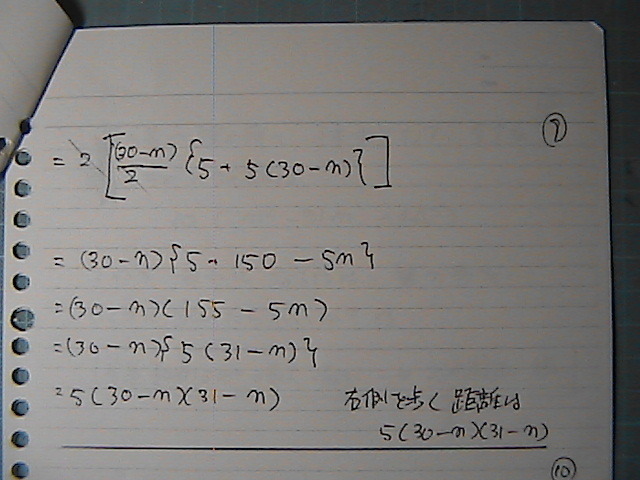
�i�^��
�悎���Ɂ@�����@+�@�E���@���@����Ȋ����́@���̓�

���ꂪ�@�悎���Ɂ@��{���@����S���@�W�߂�Ƃ���
������
�i�@�P�@�����@���@�����@�R�O�@�j
���́@�P����@�R�O�܂łȂ̂�
�\���]���@�S���@�������
�v�Z���ʂ��@�o����
�ŏ��l��
�������ł���

���̂Q�����Ɂ@�Ȃ��Ă邶��i�C�X��
������
�����ł����
�ق�
�Q�����́@��ʌ`��
�W���`�ɂ���
�O���t�́@���_�́@���W���@���߂��
���̃O���t�́@��Ɂ@�J���Ă���
���_�Ł@�ŏ��ɂȂ��邩��

���ʂ́@�����@�W���`

��
�O�łɁ@�P�O�{�����邩��
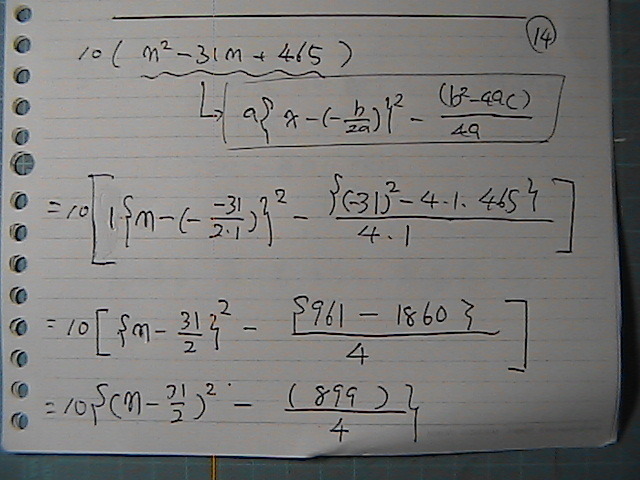
���ʂ��@��������ā@
�����@31/2�@�̎��@15.5�@�̎��@�ŏ��l
�ł����ł���
���́@���R�����W����
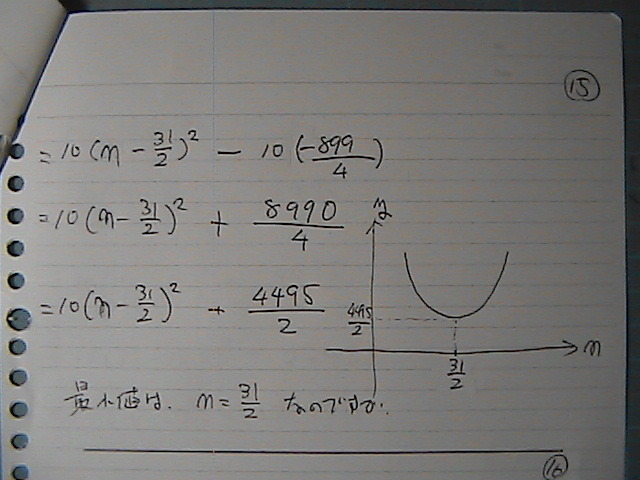
�Ƃ������Ƃ́@��ԋ߂��Ƃ���
�P�T�����@�܂��́@�P�U���@���Ă��Ƃ�

���ۂɁ@�����P�T�̎�
�����P�U�́@�Ǝ����@�v�Z�����

�����́@������

�Q�Q�T�O
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��������́@�a�̍ő�@�ŏ��̖��
�ǂ����@��������Ȃ̂�
���
�s���Ă݂܂��傤
�ǂ�ł������������Ƃ�
�R�O�{�́@�����@�T���[�g���@�Ԋu�Ł@���ĂĂ���
�����
�Ђ��[����@�P���Ɂ@�W�߂��ł���
��{���@�W�߂�@���܂�Ȃ̂�
���Ɂ@�W�߂Ă�������
�s�������������Ɂ@�W�߂Ă�������
�e�Ɋp
1���Ɂ@��{���@���ɍs���Ắ@�߂��Ă���
�܂��@���ɍs���Ắ@�߂��Ă���
���傱�܂����傱�܂�
�S���@�W�߂��ł���
�Ԋu���@�T���[�g���Ł@�R�O�{
�悎�ԖڂɁ@�S���@�W�߂�
�i�P�����@���@�����@�R�O�j
�ǂꂭ�炢�@�����̃J�i�H
�ŏ��l�́@�ǂꂭ�炢�J�i�H
���ł���
������
��@���@���́@�����Ɓ@�E���Ɂ@������
�������@���߂��Ƃ��@�l����ł���
�����́@�������@�W�߂�ɂ�
��ԁ@�߂����@�T���[�g����
�����@�P�O���[�g����
�Ԋu���@�T���[�g����
�悎������@�����Ƃ���
��P���܂ł́@���|�P�@�{�@����̂�
�悎������@��ԍ��[�܂ł́@�T�i���|�P�j���[�g��
���́@��������̘a��
�����ā@�Ƃ��Ă������
��������
�Q�{�@�������̂��@�@�悎�����@���ɂ������
�悎���Ɂ@�S���@
��{���@�W�߂�Ƃ��Ɂ@�����@�����ł�
�����
�����������
�Q�{�́@�i�@�����@��������̘a�@�j�@�@
�����Ɂ@�����ł���
�����@�����@�������@�킩���Ă�̂�
��,a,l,�Ɂ@�������
�T���i���|�P�j
���x�́@�悎�����@�E�������́@����
�W�߂�Ƃ�
����ς�@��{���@���傱���傱
�����Ắ@�����Ă���
�܂��@�����Ắ@���ė���
�悎���ɑS���W�߂��
�E���Ɂ@��ԍŏ��́@�T���[�g����
���́@�P�O���[�g����
��ԉE����
�T���[�g���Ԋu��
�R�O�{����@���{���@��������
�T�i�R�O�|���j���[�g����
���̐���̘a���@�������Ł@�Q�{�����
�E�����@����������
�T�i�R�O�|���j�i�R�P�|���j
�i�^��
�悎���Ɂ@�����@+�@�E���@���@����Ȋ����́@���̓�
���ꂪ�@�悎���Ɂ@��{���@����S���@�W�߂�Ƃ���
������
�i�@�P�@�����@���@�����@�R�O�@�j
���́@�P����@�R�O�܂łȂ̂�
�\���]���@�S���@�������
�v�Z���ʂ��@�o����
�ŏ��l��
�������ł���
���̂Q�����Ɂ@�Ȃ��Ă邶��i�C�X��
������
�����ł����
�ق�
�Q�����́@��ʌ`��
�W���`�ɂ���
�O���t�́@���_�́@���W���@���߂��
���̃O���t�́@��Ɂ@�J���Ă���
���_�Ł@�ŏ��ɂȂ��邩��
���ʂ́@�����@�W���`
��
�O�łɁ@�P�O�{�����邩��
���ʂ��@��������ā@
�����@31/2�@�̎��@15.5�@�̎��@�ŏ��l
�ł����ł���
���́@���R�����W����
�Ƃ������Ƃ́@��ԋ߂��Ƃ���
�P�T�����@�܂��́@�P�U���@���Ă��Ƃ�
���ۂɁ@�����P�T�̎�
�����P�U�́@�Ǝ����@�v�Z�����
�����́@������
�Q�Q�T�O
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 21:17| ��l�̂��ї��Ƃ��@