2017”N07Œژ18“ْ
‘هگl‚ج‚³‚ر—ژ‚ئ‚µپ@21006پ@پ@”{گ”‚ج–â‘è
پiپ@گ°‚ê•”‰®‚ضپ@‰ئ’ëچط‰€‚ئ‚T‚eپ@‚S‚eپ@‚R‚eپ@‚Q‚eپ@1 F‚´‚ء‚©‚â
ƒپƒjƒ…ƒEپ@ƒyپ[ƒWپ@ƒٹƒ^پ[ƒ“پ@پ@پ@پ@پj
‚ي‚½‚µ‚حپ@‚‚ê‚®‚ê‚àپ@‹³ژt‚إ‚ح‚ب‚
—§ڈê‚حپ@ˆل‚¦‚ا
“¯‚¶پ@گ¶“k‚ج‚آ‚à‚è‚إ‚·‚ج‚إ
گف’è‚ئ‚¢‚½‚µ‚ـ‚µ‚ؤ‚ح
‚±‚ê‚ح‚³
‹³‰بڈ‘‚ئ‚©‚جپ@–â‘è‚ئ‚حپ@ˆل‚¤‚¯‚ا‚³
ƒuƒچƒO‚إپ@–â‘è‚ًپ@Œ©‚ؤ‚à‚ç‚ء‚ؤ‚ؤ‚إ‚·‚ث
‰´‚ء‚؟پ@‚حپ@‚±‚ٌ‚بٹ´‚¶‚ة‚ب‚ء‚½‚¯‚ا‚³
‚إ
‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·
‚»‚¤‚¢‚¤گف’è‚إ
‚à‚ء‚ئ‚¢‚¢ˆسŒ©‚ھپ@‚ ‚é‚ح‚¸‚¾‚وپB
گ”—ٌ‚ج–â‘è‚ج‘±‚«‚إ‚·‚ھ
”{گ”‚ج–â‘è
”{گ”‚ب‚ج‚إ
“™چ·گ”—ٌ‚ة‚ب‚ء‚ؤ‚é‚ي‚¯‚إ
کa‚ًپ@‹پ‚ك‚ب‚³‚¢‚ئ‚©‚إ‚·‚ث
‚¢‚ء‚ؤ‚ف‚ـ‚·
‚RŒ…‚جپ@ژ©‘Rگ”‚ھ‚ ‚é‚ٌ‚¾‚ء‚ؤ
‚»‚ج‚¤‚؟‚إ
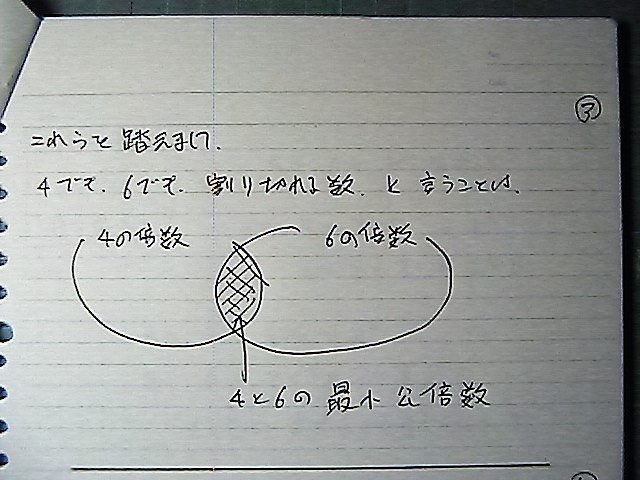
‚S‚إ‚àپ@‚U‚إ‚àپ@ٹ„‚èگط‚ê‚éگ”‚جکa
‚»‚ج‚¤‚؟‚إ
‚S‚ـ‚½‚حپ@‚U‚إپ@ٹ„‚èگط‚ê‚éگ”‚جکa

ƒxƒ“گ}‚إŒ©‚ê‚خ
‚±‚ٌ‚بٹ´‚¶‚إ
‚©‚آ‚حپ@ƒ_ƒu‚è
‚ـ‚½‚حپ@‚حپ@‘S‘ج
‚µ‚©‚µ
—v‘f‚جŒآگ”‚ئ‚©پ@کa‚جژ‚ح
‹C‚¨•t‚¯‚ث‚خ

‚إ
‚S‚إ‚àپ@‚U‚إ‚àپ@ٹ„‚èگط‚ê‚é‚ٌ‚¾‚©‚ç
چإڈ¬Œِ”{گ”‚ًپ@‚à‚ئ‚ك‚ê‚خ‚³
‚±‚±‚حپ@Œ©‚½‚¾‚¯‚إ
‚©‚ٌ‚إ
‚P‚Q‚¾ƒbƒe‚¢‚¦‚邯‚ا
‚à‚¤ڈ‚µپ@•،ژG‚بژ‚حپ@ٹ댯‚ب‚½‚ك
‚؟‚ه‚ء‚ئ‚â‚ء‚ؤ‚ف‚ـ‚·‚ئ
AB=GL
AپپGa
B=Gb
‚ب‚éپ@Œِژ®‚ھ‚ ‚é‚ج‚إ
G‚حپ@چإ‘هŒِ–ٌگ”
L‚حپ@چإڈ¬Œِ”{گ”
a,bپA‚حپ@‘fگ”‚إ‚·

‚S‚حپ@‚Q‚©‚¯‚é‚Qپ@
‚U‚حپ@‚Q‚©‚¯‚é‚R
‚¾‚©‚ç‚ة‚µ‚ؤ
‚±‚ê‚ç‚جپ@‹¤’ت•”•ھ‚حپ@‚Q
‚ھپ@چإ‘هŒِ–ٌگ”
‚R‚ئپ@‚T‚جڈêچ‡‚¾‚ء‚½‚ç
چإ‘هŒِ–ٌگ”‚حپ@‚ب‚¢پHپHپHپH
‚¢‚¢‚¦پ@‚ ‚é‚إ‚µ‚ه
‚P‚إ‚·‚و
‚إ

چإ‘هŒِ–ٌگ”‚ھپ@‚Q‚ب‚ج‚إ
AپپGa
B=Gb
‚ة‚ ‚ؤ‚ح‚ك‚é‚ئ‚إ‚·‚و‚ث
‚Sپپ‚Q‚©‚¯‚é‚Q
‚Uپپ‚Q‚©‚¯‚é‚R

چإڈ¬Œِ”{گ”‚ح
L‚¾‚©‚ç
ژ®•دŒ`‚·‚é‚ئ
12

–â‘è‚حپ@‚RŒ…‚جژ©‘Rگ”‚¾‚©‚ç
پHپHپH
‚X‚X‚حپ@‚QƒPƒ^پ@‚¾‚©‚ç
‚P‚O‚O‚©‚ç
‚P‚O‚O‚O‚ح‚SƒPƒ^
‚¾‚©‚ç
‚X‚X‚X‚ـ‚إ
100پ`999
‚±‚جٹش‚جپ@‚P‚Q‚ج”{گ”‚ح
‚¢‚‚آ‚ ‚é‚©‚ب‚ئ

‚P‚Q‚ج”{گ”‚¾‚©‚çپ@‚P‚Q‚ژ‚إ
‚ژ‚حپ@ژ©‘Rگ”پ@پiپ@گ®گ”‚ج‚¤‚؟پ@ƒ[ƒچ‚ًپ@ڈœ‚¢‚½پ@گ³‚جپ@گ®گ”پ@پj

‘S•”پ@‚P‚Q‚إٹ„‚ء‚ؤ
‚¾‚و
‚إ
ژ©‘Rگ”‚ةپ@‚·‚é‚ئ‚¾‚ب

‚إ
‚±‚±‚إ
ٹشˆل‚ء‚؟‚ل‚ء‚½‚ٌ‚¾‚¯‚ا‚³
‚±‚ê‚حپ@•|‚¢‚±‚ئ‚ب‚ٌ‚¾‚ث
ڈ¬ٹwچZ‚إپ@ڈK‚¤‚±‚ئ‚ب‚ٌ‚¾‚و
‚ـ‚؟‚ھ‚¤‚ئپ@‚â‚خ‚¢
‚µ‚©‚µ
‚â‚ء‚ؤ‚µ‚ـ‚ء‚½پB
‚¾‚¢‚¶‚ه‚إ‚·‚©پH

‚±‚ج‚³
‚±‚جچ·‚إ‚·‚و
‚¢‚¢‚إ‚µ‚ه
‚±‚ê‚إ
‚ث
‚¾‚¢‚¶‚ه‚¾‚ء‚½

ƒiƒ^ƒپ
‚±‚ج‚P‚Q‚ج”{گ”‚جپ@ڈW‚ـ‚è‚ح
ڈ‰چ€108پ@––چ€996پ@چ€گ”75
Œِچ·پ@‚P‚Q‚جپ@“™چ·گ”—ٌپ@‚¾‚ٌ‚×

‚¾‚©‚炳
کa‚ح
Œِژ®‚ھپ@‚±‚ꂾ‚©‚炳

‚â‚â‚ء‚±‚µ‚¢‚ظ‚¤‚إ‚â‚ê‚خ

‚±‚ٌ‚ب‚إ
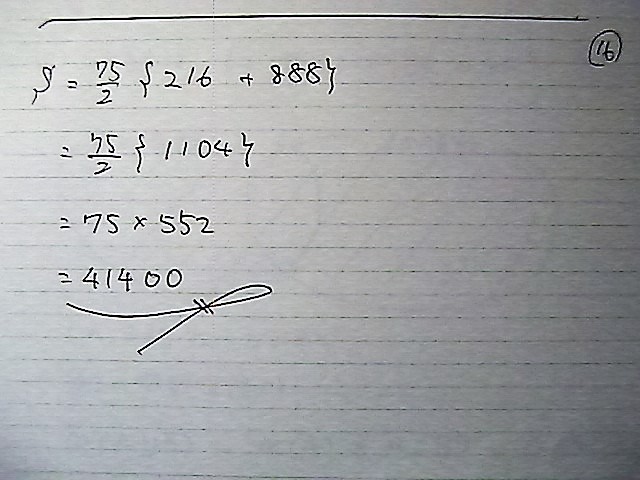
ٹب’P‚ب•û‚إپ@‚â‚ê‚خ
‚±‚ٌ‚ب‚إ
‚±‚±‚إ
“ڑ‚¦‚ھˆل‚¤‚ئ
‚â‚خ‚¢‚ٌ‚¾‚¯‚ا
‚¾‚¢‚¶‚ه‚¾‚©‚ç
پi‚Pپj‚حپ@ƒRƒŒƒ_

‚إ
(‚Q)‚حپ@‰½‚ھ–â‘è‚©‚ئ‚¢‚¤‚ئ
‚±‚ê‘S‘ج‚ً
‹پ‚ك‚é‚ة
گ”‚P‚جپ@Œآگ”’è—پ@‚ء‚ؤ‚ج‚ھپ@‚ ‚ء‚½‚¯‚ا‚³
‚»‚êژg‚ي‚ب‚¢‚ئ
‚¢‚¯‚ب‚‚ب‚¢پH
‚إپ@ژv‚¢ڈo‚µ‚ؤ‚ف‚é‚ئ
‚±‚ٌ‚ب‚¾‚ء‚½‚©‚ç

Œآگ”‚¶‚ل‚ب‚‚ؤ‚³پ@کa‚¾‚©‚ç
‚ژ‚ًپ@S‚ةپ@•د‚¦‚ؤ‚³
ƒ_ƒu‚è‚ً
ٹO‚·چ\گ}‚ًپ@چى‚ء‚ؤ
•K—v‚بپ@•¨‚حپ@‰½‚©‚ئ

پi‚Pپjپ@‚إپ@ƒ_ƒuƒٹ‚جŒvژZ‚ھپ@‚·‚ٌ‚إ‚é‚©‚ç
‚S‚ج”{گ”‚ئپ@‚U‚ج”{گ”‚جپ@کa‚ًپ@‚»‚ꂼ‚êپ@
‹پ‚ك‚ؤپ@‘«‚µ‚ؤ
‚»‚±‚©‚çپ@ƒ_ƒuƒٹ‚ًپ@ˆّ‚‚ئ‚¢‚¤پ@چ\گ}‚ب‚ج‚إ

‚S‚ج”{گ”‚©‚ç
کa‚ً‹پ‚ك‚é‚ئ

‚³‚ء‚«‚ف‚½‚¢‚ةپ@پ@‚â‚ء‚ؤ‚ء‚ؤ
Œآگ”‚ھپ@‚Q‚Q‚TŒآ

‚S‚ج”{گ”‚¾‚©‚ç
ڈ‰چ€پ@––چ€‹پ‚ك‚ؤ
کa‚حپ@

123300

‚U‚ج”{گ”‚ج•û‚à
‚¨‚ٌ‚ب‚¶‚پ@ŒvژZ‚µ‚ؤ‚‚ئ

‚±‚ٌ‚بٹ´‚¶‚إ

82350

‚³‚ء‚«پ@‚¾‚µ‚ئ‚¢‚½پ@چ\گ}‚ة
“ü‚ê‚ؤ‚‚ئ

Œآگ”’è—پ@ڈWچ‡‚ج
‚ث‚ث‚ث
‚±‚ê‚إپ@‚¢‚¢‚©‚ب
ƒپƒjƒ…ƒEپ@ƒyپ[ƒWپ@ƒٹƒ^پ[ƒ“پ@پ@پ@پ@پj
‚ي‚½‚µ‚حپ@‚‚ê‚®‚ê‚àپ@‹³ژt‚إ‚ح‚ب‚
—§ڈê‚حپ@ˆل‚¦‚ا
“¯‚¶پ@گ¶“k‚ج‚آ‚à‚è‚إ‚·‚ج‚إ
گف’è‚ئ‚¢‚½‚µ‚ـ‚µ‚ؤ‚ح
‚±‚ê‚ح‚³
‹³‰بڈ‘‚ئ‚©‚جپ@–â‘è‚ئ‚حپ@ˆل‚¤‚¯‚ا‚³
ƒuƒچƒO‚إپ@–â‘è‚ًپ@Œ©‚ؤ‚à‚ç‚ء‚ؤ‚ؤ‚إ‚·‚ث
‰´‚ء‚؟پ@‚حپ@‚±‚ٌ‚بٹ´‚¶‚ة‚ب‚ء‚½‚¯‚ا‚³
‚إ
‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·
‚»‚¤‚¢‚¤گف’è‚إ
‚à‚ء‚ئ‚¢‚¢ˆسŒ©‚ھپ@‚ ‚é‚ح‚¸‚¾‚وپB
گ”—ٌ‚ج–â‘è‚ج‘±‚«‚إ‚·‚ھ
”{گ”‚ج–â‘è
”{گ”‚ب‚ج‚إ
“™چ·گ”—ٌ‚ة‚ب‚ء‚ؤ‚é‚ي‚¯‚إ
کa‚ًپ@‹پ‚ك‚ب‚³‚¢‚ئ‚©‚إ‚·‚ث
‚¢‚ء‚ؤ‚ف‚ـ‚·
‚RŒ…‚جپ@ژ©‘Rگ”‚ھ‚ ‚é‚ٌ‚¾‚ء‚ؤ
‚»‚ج‚¤‚؟‚إ
‚S‚إ‚àپ@‚U‚إ‚àپ@ٹ„‚èگط‚ê‚éگ”‚جکa
‚»‚ج‚¤‚؟‚إ
‚S‚ـ‚½‚حپ@‚U‚إپ@ٹ„‚èگط‚ê‚éگ”‚جکa
ƒxƒ“گ}‚إŒ©‚ê‚خ
‚±‚ٌ‚بٹ´‚¶‚إ
‚©‚آ‚حپ@ƒ_ƒu‚è
‚ـ‚½‚حپ@‚حپ@‘S‘ج
‚µ‚©‚µ
—v‘f‚جŒآگ”‚ئ‚©پ@کa‚جژ‚ح
‹C‚¨•t‚¯‚ث‚خ
‚إ
‚S‚إ‚àپ@‚U‚إ‚àپ@ٹ„‚èگط‚ê‚é‚ٌ‚¾‚©‚ç
چإڈ¬Œِ”{گ”‚ًپ@‚à‚ئ‚ك‚ê‚خ‚³
‚±‚±‚حپ@Œ©‚½‚¾‚¯‚إ
‚©‚ٌ‚إ
‚P‚Q‚¾ƒbƒe‚¢‚¦‚邯‚ا
‚à‚¤ڈ‚µپ@•،ژG‚بژ‚حپ@ٹ댯‚ب‚½‚ك
‚؟‚ه‚ء‚ئ‚â‚ء‚ؤ‚ف‚ـ‚·‚ئ
AB=GL
AپپGa
B=Gb
‚ب‚éپ@Œِژ®‚ھ‚ ‚é‚ج‚إ
G‚حپ@چإ‘هŒِ–ٌگ”
L‚حپ@چإڈ¬Œِ”{گ”
a,bپA‚حپ@‘fگ”‚إ‚·
‚S‚حپ@‚Q‚©‚¯‚é‚Qپ@
‚U‚حپ@‚Q‚©‚¯‚é‚R
‚¾‚©‚ç‚ة‚µ‚ؤ
‚±‚ê‚ç‚جپ@‹¤’ت•”•ھ‚حپ@‚Q
‚ھپ@چإ‘هŒِ–ٌگ”
‚R‚ئپ@‚T‚جڈêچ‡‚¾‚ء‚½‚ç
چإ‘هŒِ–ٌگ”‚حپ@‚ب‚¢پHپHپHپH
‚¢‚¢‚¦پ@‚ ‚é‚إ‚µ‚ه
‚P‚إ‚·‚و
‚إ
چإ‘هŒِ–ٌگ”‚ھپ@‚Q‚ب‚ج‚إ
AپپGa
B=Gb
‚ة‚ ‚ؤ‚ح‚ك‚é‚ئ‚إ‚·‚و‚ث
‚Sپپ‚Q‚©‚¯‚é‚Q
‚Uپپ‚Q‚©‚¯‚é‚R
چإڈ¬Œِ”{گ”‚ح
L‚¾‚©‚ç
ژ®•دŒ`‚·‚é‚ئ
12
–â‘è‚حپ@‚RŒ…‚جژ©‘Rگ”‚¾‚©‚ç
پHپHپH
‚X‚X‚حپ@‚QƒPƒ^پ@‚¾‚©‚ç
‚P‚O‚O‚©‚ç
‚P‚O‚O‚O‚ح‚SƒPƒ^
‚¾‚©‚ç
‚X‚X‚X‚ـ‚إ
100پ`999
‚±‚جٹش‚جپ@‚P‚Q‚ج”{گ”‚ح
‚¢‚‚آ‚ ‚é‚©‚ب‚ئ
‚P‚Q‚ج”{گ”‚¾‚©‚çپ@‚P‚Q‚ژ‚إ
‚ژ‚حپ@ژ©‘Rگ”پ@پiپ@گ®گ”‚ج‚¤‚؟پ@ƒ[ƒچ‚ًپ@ڈœ‚¢‚½پ@گ³‚جپ@گ®گ”پ@پj
‘S•”پ@‚P‚Q‚إٹ„‚ء‚ؤ
‚¾‚و
‚إ
ژ©‘Rگ”‚ةپ@‚·‚é‚ئ‚¾‚ب
‚إ
‚±‚±‚إ
ٹشˆل‚ء‚؟‚ل‚ء‚½‚ٌ‚¾‚¯‚ا‚³
‚±‚ê‚حپ@•|‚¢‚±‚ئ‚ب‚ٌ‚¾‚ث
ڈ¬ٹwچZ‚إپ@ڈK‚¤‚±‚ئ‚ب‚ٌ‚¾‚و
‚ـ‚؟‚ھ‚¤‚ئپ@‚â‚خ‚¢
‚µ‚©‚µ
‚â‚ء‚ؤ‚µ‚ـ‚ء‚½پB
‚¾‚¢‚¶‚ه‚إ‚·‚©پH
‚±‚ج‚³
‚±‚جچ·‚إ‚·‚و
‚¢‚¢‚إ‚µ‚ه
‚±‚ê‚إ
‚ث
‚¾‚¢‚¶‚ه‚¾‚ء‚½
ƒiƒ^ƒپ
‚±‚ج‚P‚Q‚ج”{گ”‚جپ@ڈW‚ـ‚è‚ح
ڈ‰چ€108پ@––چ€996پ@چ€گ”75
Œِچ·پ@‚P‚Q‚جپ@“™چ·گ”—ٌپ@‚¾‚ٌ‚×
‚¾‚©‚炳
کa‚ح
Œِژ®‚ھپ@‚±‚ꂾ‚©‚炳
‚â‚â‚ء‚±‚µ‚¢‚ظ‚¤‚إ‚â‚ê‚خ
‚±‚ٌ‚ب‚إ
ٹب’P‚ب•û‚إپ@‚â‚ê‚خ
‚±‚ٌ‚ب‚إ
‚±‚±‚إ
“ڑ‚¦‚ھˆل‚¤‚ئ
‚â‚خ‚¢‚ٌ‚¾‚¯‚ا
‚¾‚¢‚¶‚ه‚¾‚©‚ç
پi‚Pپj‚حپ@ƒRƒŒƒ_
‚إ
(‚Q)‚حپ@‰½‚ھ–â‘è‚©‚ئ‚¢‚¤‚ئ
‚±‚ê‘S‘ج‚ً
‹پ‚ك‚é‚ة
گ”‚P‚جپ@Œآگ”’è—پ@‚ء‚ؤ‚ج‚ھپ@‚ ‚ء‚½‚¯‚ا‚³
‚»‚êژg‚ي‚ب‚¢‚ئ
‚¢‚¯‚ب‚‚ب‚¢پH
‚إپ@ژv‚¢ڈo‚µ‚ؤ‚ف‚é‚ئ
‚±‚ٌ‚ب‚¾‚ء‚½‚©‚ç
Œآگ”‚¶‚ل‚ب‚‚ؤ‚³پ@کa‚¾‚©‚ç
‚ژ‚ًپ@S‚ةپ@•د‚¦‚ؤ‚³
ƒ_ƒu‚è‚ً
ٹO‚·چ\گ}‚ًپ@چى‚ء‚ؤ
•K—v‚بپ@•¨‚حپ@‰½‚©‚ئ
پi‚Pپjپ@‚إپ@ƒ_ƒuƒٹ‚جŒvژZ‚ھپ@‚·‚ٌ‚إ‚é‚©‚ç
‚S‚ج”{گ”‚ئپ@‚U‚ج”{گ”‚جپ@کa‚ًپ@‚»‚ꂼ‚êپ@
‹پ‚ك‚ؤپ@‘«‚µ‚ؤ
‚»‚±‚©‚çپ@ƒ_ƒuƒٹ‚ًپ@ˆّ‚‚ئ‚¢‚¤پ@چ\گ}‚ب‚ج‚إ
‚S‚ج”{گ”‚©‚ç
کa‚ً‹پ‚ك‚é‚ئ
‚³‚ء‚«‚ف‚½‚¢‚ةپ@پ@‚â‚ء‚ؤ‚ء‚ؤ
Œآگ”‚ھپ@‚Q‚Q‚TŒآ
‚S‚ج”{گ”‚¾‚©‚ç
ڈ‰چ€پ@––چ€‹پ‚ك‚ؤ
کa‚حپ@
123300
‚U‚ج”{گ”‚ج•û‚à
‚¨‚ٌ‚ب‚¶‚پ@ŒvژZ‚µ‚ؤ‚‚ئ
‚±‚ٌ‚بٹ´‚¶‚إ
82350
‚³‚ء‚«پ@‚¾‚µ‚ئ‚¢‚½پ@چ\گ}‚ة
“ü‚ê‚ؤ‚‚ئ
Œآگ”’è—پ@ڈWچ‡‚ج
‚ث‚ث‚ث
‚±‚ê‚إپ@‚¢‚¢‚©‚ب
پy‚±‚جƒJƒeƒSƒٹپ[‚جچإگV‹Lژ–پz
-
no image
posted by moriamelihu at 02:20| ‘هگl‚ج‚³‚ر—ژ‚ئ‚µپ@