2017�N09��04��
21009 ��l�̂��ї��Ƃ��@���a����
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���a����@�Ƃ����̂�
����U���X�ł���
�ǂ�Ȃ��̂��Ƃ�����
�t������ł��Ă鐔���
�����@���a�����
�t���́@����������@�Ȃ��Ă���Ƃ�����ł���
�����ŏ����Ă���̂�
�����
���̂܂܁@���a�����
�v����������
���̂܂܂���
���ł���
����́@�t�����@�Ƃ��
��������ɂ��Ȃ�܂�
��������Ł@��������
���ʂ��@�Ђ�����Ԃ��ā@�߂�

�����肸�炢��������Ȃ�����
�t�����@�Ƃ��
��������
����́@����Ɂ@�t���́@���́@���a����
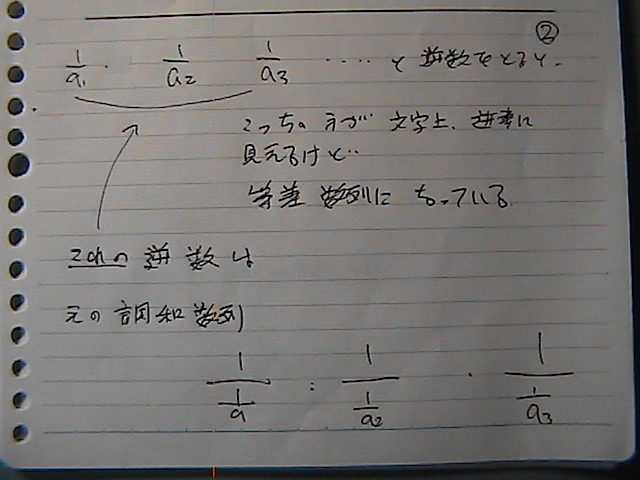
���������
��ʍ��̌������������ł���
���́@�������@���a����́@�Ƃ�����@�������t����
�����́@�t���Ɂ@�����@�Q���߂���P���߂��@������

������@�����Ɂ@������Ă���
���ό`��
���������߂��ł���
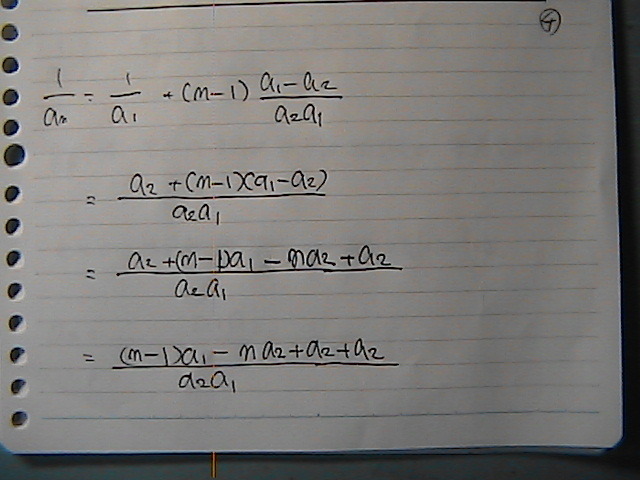
��������̕��́@����������
���́@���a����́@�t���̏W�܂�́@���@��������ɂȂ��Ă邩��
�����Ɂ@�����Ă���܂��ł���
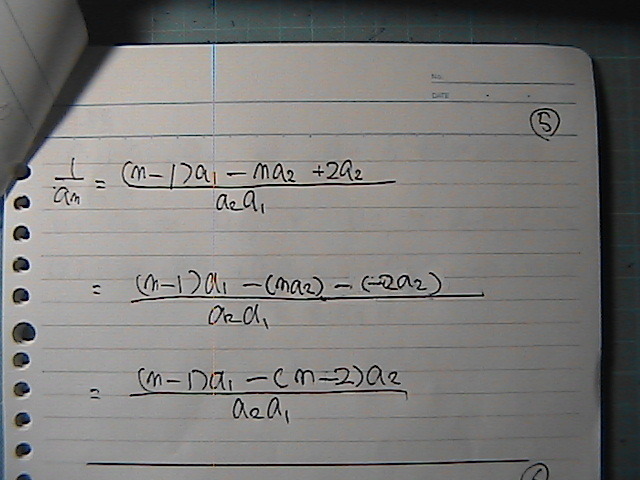
������@�Ђ�����Ԃ���
�߂���
���́@���a����́@�悎���ڂɂȂ��Ă�
�ƌ������̂ł��B

������
���ł���
a1 a2 a3 .....
���@���a����Ȃ���
�����@���@�����@a1 a2 ���@�g���Č����Ȃ���

������Ă��܂��܂�����
���a����́@�t���Ɂ@�����
��������
��������Ȃ̂Ł@���ƍ��́@���́@���@
������
��ʍ��́@��������ɂ��Ă�����
��ʍ��̌�������
�悎�����@���Ƃ߂�

�Ђ�����Ԃ���ł�����

(�Q)�́@
�ؖ��Ȃ�ł���
���̒��a����̋t����
����������@�N���Ă���ł���
�����

���Ɓ@���̍����@��肾����
���Ƃ����Ăł��ˁ[
�����@�������@���Ł@�����Ă��Ă�����

������@��ʂ�@�v�Z�������Ƃɂ���

�S���@������ł���
���������
���ӂ�
�A�������̂��Ƃ�
�������@�ł��Ă��܂���

�c�����̂�
���ӂ́@a1-an
�E�ӂ́@���Ł@������Ɓ@�Ȃ@�������Ƃ���`�Ɂ@�Ȃ��Ă�

������
���́@�������Ƃ���`���@���ӂɂ���
�E�ӂ́@a1-an
������
���a������@��������̂ɂ����Ƃ��́@��ʍ���
�����Ł@�����

������@�����ό`����@a1-an
�@
�Ɂ@�����`�ɂȂ�
���ό`���Ă���
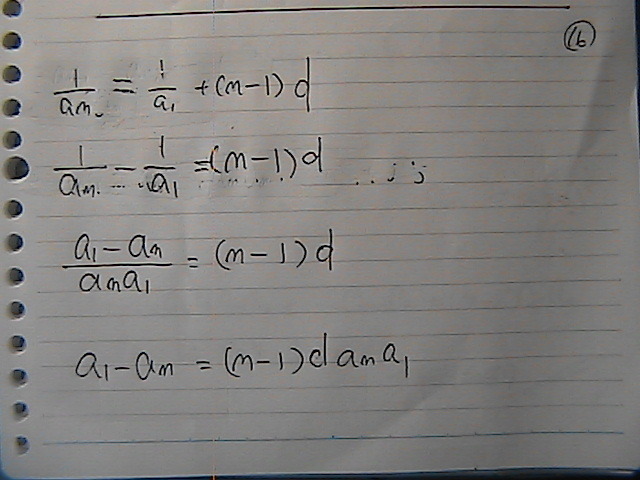
d���@�O�łȂ��ˁ@�ā@�I�b�P�C
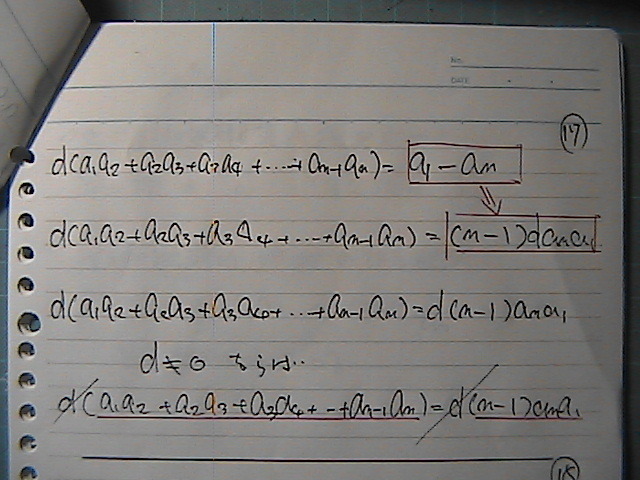
�����@�O�ˁ@�S���@���ɂȂĂ��܂�����
���藧��
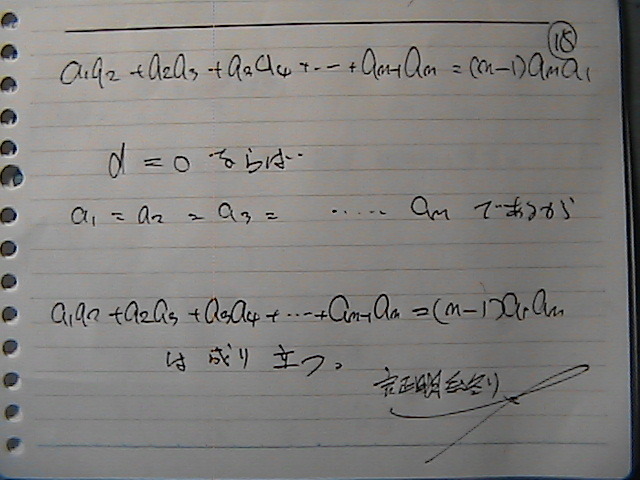
���ۂɁ@�����Ł@���Ă݂܂���
����͂ł���
���a����Ȃ���
�t�����@����Ɂ@����Ɓ@��������ɂȂ��

�����@����́@�������@���߂�

��������́@��ʍ����@���߂�
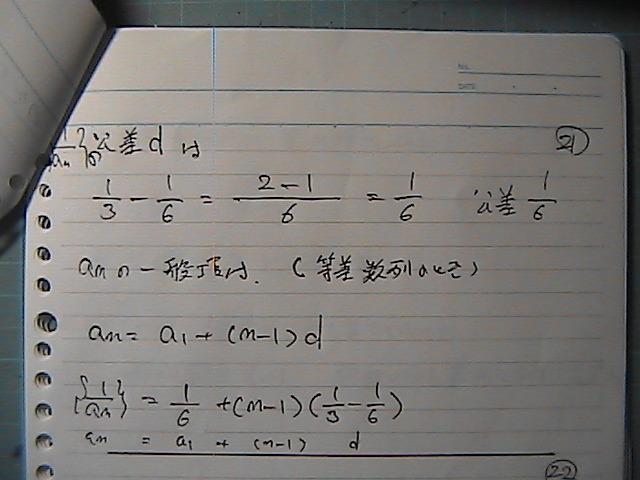
��ʍ���������������
���̋t����
���́@���a����́@��ʍ��ɂȂ��Ă�

�����@���a����Ȃ���
��ʍ����@���߂�ɂ�
�܂�
�t���Ł@��������ɂ���
����Ɂ@�����
�����Ɓ@�������@�킩���ĂȂ��̂�

��������Ƃ�����
�܂�
�����ƌ���

��ʍ��́@��������
�������Ă�Ƃ����@�������
������Ȃ����̂��@���
�������

➀�@�A�@����
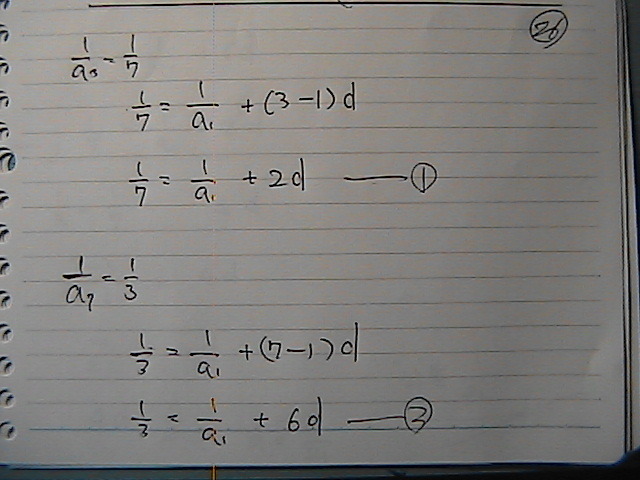
�����Z��

��������o����
1/21

���́@���Ɂ@�������
�����́@

1/21

�Ł@��ʍ��́@�i�@��������@�j�@������
�����@�����@���@�������
�łĂ����@�悎���́@����������
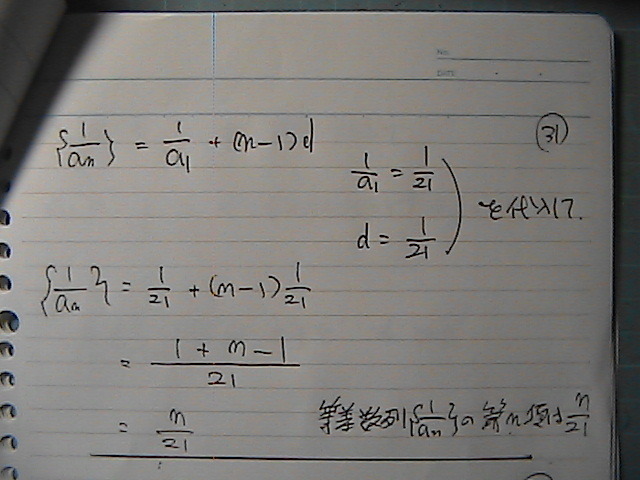
�t�����Ƃ���
���́@���a����́@�悎���ɂ����
21/��

��������@�Ɓ@
���a����@���@
�������
�Ł@�����F�����@�̒l���@���߂Ȃ���

�ǂ������
a,b�A�Ł@
���ꂼ��@���A��
�@�@�@�@���A�����@
�\������
������߂��
�悳�����ł���

��������̕�����
��������Ȃ���
�����@���

�S���@������Ƃ���
���ɂ���ł���
��
�S��������
����

����Ɂ@��������Ȃ��炳

�����@a,b�Ł@�\��
y��
�������́@���A���A���@a,b�ŕ\���ł�����

���a����̕���
���A�����@a,b�Ł@�\����������ł���
���a�����
���@�Ђ�����Ԃ���
��������ɂ��ā@��������̂�
��������
�������

�������̗l��
������
�S���@���Ł@�����Ă�����
�����Ă��ł���

�������@�o����
������@�g����
��������
1/���@��1/���@���@���߂�
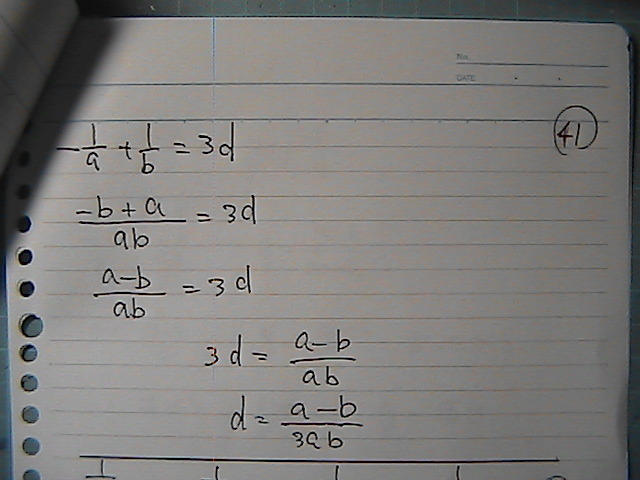
���ꂪ
���܂�
a,b�Ł@�@�łĂ�������
���́@���a����Ɂ@�Ȃ�l�Ɂ@�Ђ����肩������
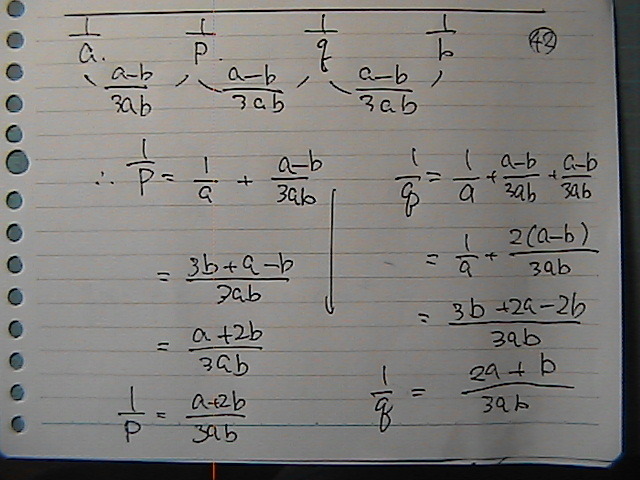
���������
�����F�������@�v�Z�����

ab:ab

�܂�
�P�F�P
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���a����@�Ƃ����̂�
����U���X�ł���
�ǂ�Ȃ��̂��Ƃ�����
�t������ł��Ă鐔���
�����@���a�����
�t���́@����������@�Ȃ��Ă���Ƃ�����ł���
�����ŏ����Ă���̂�
�����
���̂܂܁@���a�����
�v����������
���̂܂܂���
���ł���
����́@�t�����@�Ƃ��
��������ɂ��Ȃ�܂�
��������Ł@��������
���ʂ��@�Ђ�����Ԃ��ā@�߂�
�����肸�炢��������Ȃ�����
�t�����@�Ƃ��
��������
����́@����Ɂ@�t���́@���́@���a����
���������
��ʍ��̌������������ł���
���́@�������@���a����́@�Ƃ�����@�������t����
�����́@�t���Ɂ@�����@�Q���߂���P���߂��@������
������@�����Ɂ@������Ă���
���ό`��
���������߂��ł���
��������̕��́@����������
���́@���a����́@�t���̏W�܂�́@���@��������ɂȂ��Ă邩��
�����Ɂ@�����Ă���܂��ł���
������@�Ђ�����Ԃ���
�߂���
���́@���a����́@�悎���ڂɂȂ��Ă�
�ƌ������̂ł��B
������
���ł���
a1 a2 a3 .....
���@���a����Ȃ���
�����@���@�����@a1 a2 ���@�g���Č����Ȃ���
������Ă��܂��܂�����
���a����́@�t���Ɂ@�����
��������
��������Ȃ̂Ł@���ƍ��́@���́@���@
������
��ʍ��́@��������ɂ��Ă�����
��ʍ��̌�������
�悎�����@���Ƃ߂�
�Ђ�����Ԃ���ł�����
(�Q)�́@
�ؖ��Ȃ�ł���
���̒��a����̋t����
����������@�N���Ă���ł���
�����
���Ɓ@���̍����@��肾����
���Ƃ����Ăł��ˁ[
�����@�������@���Ł@�����Ă��Ă�����
������@��ʂ�@�v�Z�������Ƃɂ���
�S���@������ł���
���������
���ӂ�
�A�������̂��Ƃ�
�������@�ł��Ă��܂���
�c�����̂�
���ӂ́@a1-an
�E�ӂ́@���Ł@������Ɓ@�Ȃ@�������Ƃ���`�Ɂ@�Ȃ��Ă�
������
���́@�������Ƃ���`���@���ӂɂ���
�E�ӂ́@a1-an
������
���a������@��������̂ɂ����Ƃ��́@��ʍ���
�����Ł@�����
������@�����ό`����@a1-an
�@
�Ɂ@�����`�ɂȂ�
���ό`���Ă���
d���@�O�łȂ��ˁ@�ā@�I�b�P�C
�����@�O�ˁ@�S���@���ɂȂĂ��܂�����
���藧��
���ۂɁ@�����Ł@���Ă݂܂���
����͂ł���
���a����Ȃ���
�t�����@����Ɂ@����Ɓ@��������ɂȂ��
�����@����́@�������@���߂�
��������́@��ʍ����@���߂�
��ʍ���������������
���̋t����
���́@���a����́@��ʍ��ɂȂ��Ă�
�����@���a����Ȃ���
��ʍ����@���߂�ɂ�
�܂�
�t���Ł@��������ɂ���
����Ɂ@�����
�����Ɓ@�������@�킩���ĂȂ��̂�
��������Ƃ�����
�܂�
�����ƌ���
��ʍ��́@��������
�������Ă�Ƃ����@�������
������Ȃ����̂��@���
�������
➀�@�A�@����
�����Z��
��������o����
1/21
���́@���Ɂ@�������
�����́@
1/21
�Ł@��ʍ��́@�i�@��������@�j�@������
�����@�����@���@�������
�łĂ����@�悎���́@����������
�t�����Ƃ���
���́@���a����́@�悎���ɂ����
21/��
��������@�Ɓ@
���a����@���@
�������
�Ł@�����F�����@�̒l���@���߂Ȃ���
�ǂ������
a,b�A�Ł@
���ꂼ��@���A��
�@�@�@�@���A�����@
�\������
������߂��
�悳�����ł���
��������̕�����
��������Ȃ���
�����@���
�S���@������Ƃ���
���ɂ���ł���
��
�S��������
����
����Ɂ@��������Ȃ��炳
�����@a,b�Ł@�\��
y��
�������́@���A���A���@a,b�ŕ\���ł�����
���a����̕���
���A�����@a,b�Ł@�\����������ł���
���a�����
���@�Ђ�����Ԃ���
��������ɂ��ā@��������̂�
��������
�������
�������̗l��
������
�S���@���Ł@�����Ă�����
�����Ă��ł���
�������@�o����
������@�g����
��������
1/���@��1/���@���@���߂�
���ꂪ
���܂�
a,b�Ł@�@�łĂ�������
���́@���a����Ɂ@�Ȃ�l�Ɂ@�Ђ����肩������
���������
�����F�������@�v�Z�����
ab:ab
�܂�
�P�F�P
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 12:11| ��l�̂��ї��Ƃ��@