�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2017�N07��01��
���Ƃ��́@
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���Ƃ��́@�~�J�����@�������ł���

�ЊQ���@�N�������Ȃ��炢
�~���Ă�Ƃ������邯��
��Ȃ��Ƃ�����

���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���Ƃ��́@�~�J�����@�������ł���

�ЊQ���@�N�������Ȃ��炢
�~���Ă�Ƃ������邯��
��Ȃ��Ƃ�����
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
-
no image
posted by moriamelihu at 12:54| ���ƍ؉�
2017�N06��19��
����
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�����@���ʂ́@�_���Ɂ@�Ȃ肽�`��
�����@�W���[�N�ł���
���ƍ؉�
�悤�₭�@�R�c���@�����B��
�_�Ɓ@
�v���قǁ@�ȒP�ł́@����܂���
��
���낢��ȕ�����@�����Â�
�m�b���@��������
���c�����炵�Ȃ���
�������@���ނׂ�
�����@�O�i���Ă���܂�
�i�H�ύX�Ɂ@��N�@�������ł���

�����́@����
���Ɓ@�������@
����
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�����@���ʂ́@�_���Ɂ@�Ȃ肽�`��
�����@�W���[�N�ł���
���ƍ؉�
�悤�₭�@�R�c���@�����B��
�_�Ɓ@
�v���قǁ@�ȒP�ł́@����܂���
��
���낢��ȕ�����@�����Â�
�m�b���@��������
���c�����炵�Ȃ���
�������@���ނׂ�
�����@�O�i���Ă���܂�
�i�H�ύX�Ɂ@��N�@�������ł���

�����́@����
���Ɓ@�������@
����
posted by moriamelihu at 08:35| �͂ȂƖ��
2017�N06��18��
�W���K�C���Ȃ�
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�W���K�C���Ȃ�
�����Ɓ@�ʐ^���@�Ƃ�Ȃ���������
�@���ā@�k�������������
�Ȃ��݂���
���N���݂ł���
���N�́@�����Ɗ撣��ł���
�T�c�}�C���@���B���̂���
���߂́@���n�����܂���
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�W���K�C���Ȃ�
�����Ɓ@�ʐ^���@�Ƃ�Ȃ���������
�@���ā@�k�������������
�Ȃ��݂���
���N���݂ł���
���N�́@�����Ɗ撣��ł���
�T�c�}�C���@���B���̂���
���߂́@���n�����܂���
posted by moriamelihu at 20:18| ���ƍ؉�
2017�N06��12��
�ʂ˂��Ȃǁ@���n���Ă܂���
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�ʂ˂��Ȃǁ@���n���Ă܂���
����������Ɓ@���点���������̂ł���
������
���₢��@���Ă��܂���
���n�ɂȂ�܂���

�傫�����̂���
�����Ȃ��̂܂�
���ƍ؉������炳
���ꂭ�炢����B
�}�O�J�b�v�́@��������
������ĉ��H
���܂������H
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�ʂ˂��Ȃǁ@���n���Ă܂���
����������Ɓ@���点���������̂ł���
������
���₢��@���Ă��܂���
���n�ɂȂ�܂���

�傫�����̂���
�����Ȃ��̂܂�
���ƍ؉������炳
���ꂭ�炢����B
�}�O�J�b�v�́@��������
������ĉ��H
���܂������H
posted by moriamelihu at 13:25| ���ƍ؉�
2017�N05��24��
21005�@��l�̂��ї��Ƃ��@�@��������ł�������B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��������@�Ł@���邱�Ƃ�
�ؖ�������ł�
�s���Ă݂܂��傤
�悎�����@�^�����Ă�Ƃ�
�i�@����́@��������@�Ȃ��ā@�ؖ����Ă��������@�ƌ������́@�j
��
���߂́@�����́@�a���@����Ƃ�
�i�@���ꂪ���@�@����ς�@���̂́@��������Ȃ���
�@�@�ǂ�����@�ؖ��ł���H�@�ƌ������́j

���������
�Ȃ��
���Ɓ@���̊Ԃ��@�@���@�i�@�����@�j
a���@���@���ŗ^�����Ă�̂�
�����́@�ł���
���̂Ƃ����
���|�P�@�ɂ���
����ł�������

�������i�C�X�J
�W�J����

������@�ł��@�ˁ[�@
an�@�[�@a(n-1)
���@�v�Z�����ł���
P�Ɂ@�Ȃ����ł���
��ӂ��@P�́@���
������
��肾����
�@
��������
���[�@�����ł�
n�|�P�@�b�e�����@�ԍ����@�g���Ƃ���
���|�P�@���@�����Ɓ@�ԍ��Ƃ��ā@����悤��
�@���|�P�@�����@�P
�Ȃ̂Ł@�ڍs�����
���@�����@�Q

���́@�a�̒l���@�^�����Ă���
�}�Ō����
�͂��߁@����@an�܂ł̘a���@Sn
������
����́@S���́@��������̂�
������
n�|�P���@�������

�W�J����
Sn�@�|�@S(n�|�P�j�@�������
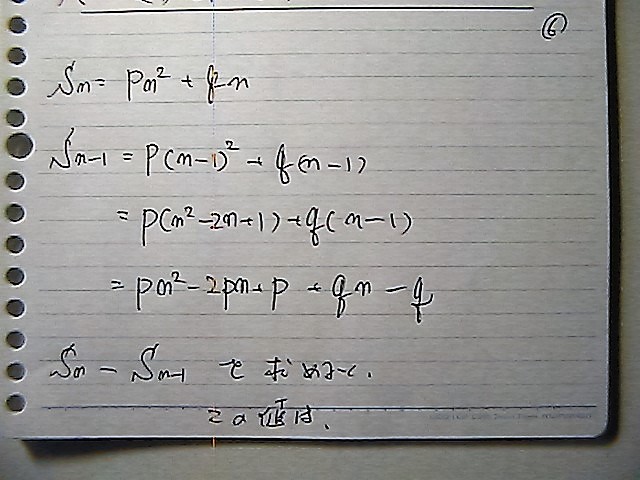
���̍����@a���@�ɂȂ�

�v�Z����ł���
��
��������
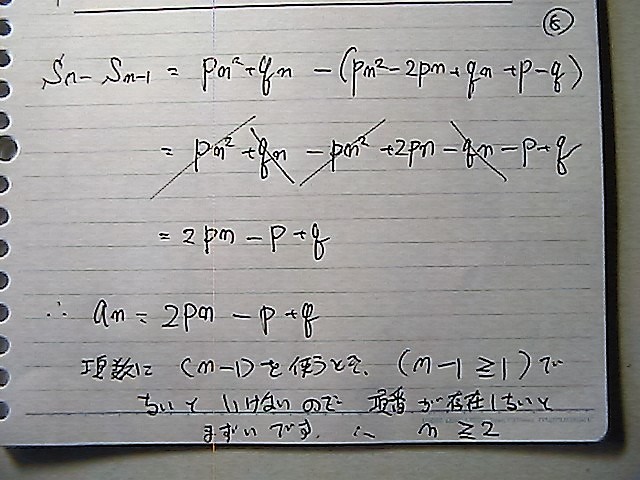
���|�P���@�ԍ��Ŏg���Ƃ���
���|�P�@���@�����Ɓ@�ԍ��Ƃ��ā@����悤��
�@���|�P�@�����@�P
�Ȃ̂Ł@�ڍs�����
���@�����@�Q

���[������
�������Q�ł���Ă�����ł���
an = �́@�Q���߂�����Ă��Ƃ�
�Ȃ̂�
�����́@Sn����@�����P���@�����
a�P

�ꉞ
a���̕��ɂ��@�����P�@���@����Č�����
��v������ł���

����́@�����
��������@��������̂悤�ł�

������������
�Q���߂���@��������ɂȂ��Ă�ꍇ

����Ȋ�����
�Ȃ�炵��
�����
��������ł�

����
�����@�悭�ǂނ�
����́@��ʍ����@���߂�ł�
��������@�s����
(�P)�́@���߂���@���������
�i�Q�j�́@�Q���߂���@���������
�i�P�j�@�́@��������
�i�Q�j�́@�����������@��������
��������@���߂Ă��܂���

n�|�P�Ԃ��@�g����

Sn�@�̎�����@a�P���@���߂�
�����ł�
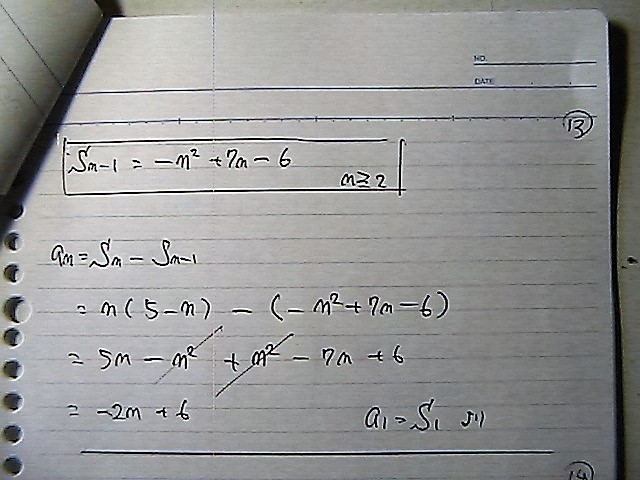
an ����́@a�P���@��v����̂�
���߂���@��������
��
��ʍ�

���|�P�Ԃ��@�g����

a���@����́@�P�ԖڂƁ@Sn �����
�P�Ԗڂ��@�����̂�

�������ł�

�������ł�

�����������@��������ȁ@��ʍ�

����
�������@�ǂ����H

�����Ɂ@���|�P�Ԃ��g��
�v�Z���Ă��ł���

��ʍ����o��

�Q���߁@����́@����ł����̂�
������
Sn����@���߂�Ƃ���i�C�X�J

����Ȋ����Ȃ�ł�

���ׂĂ݂�

c���@�O�ˁ@���߂���@��������
�����@�O�łȂ��ˁ@��������ł͂Ȃ�

���߂́@�����́@�a��
�^��������
��ʍ������߂�
���̐����
���̍��̘a���@���߂�

��ʍ���
���|�P�Ԃ��@�g����
Sn�@����@���߂邶��i�C�X�J

�������

��ʍ����o�ė���

�a�̌`�Ł@���Ă�̂�
�����́@Sn�@�Ɂ@�����P���@�����
S1=a�P
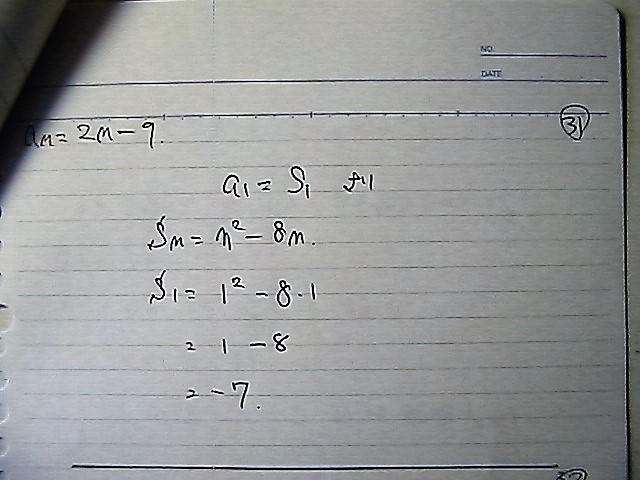
���߂��@�}�C�i�X��
����@�v���X�K���Ɂ@�ς���Ă��Ă��

�������@���Ȃ��Ƃ��́@���ł�������
�����Ȃ�����@�������
��ʍ���@�s������
���́@����
���߂���@�S�����@���̍�

�a�̌����ɑ������
�Q���́@�����@×�@�i�@�����@�{�@�����i�S���߁j�j

-16
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��������@�Ł@���邱�Ƃ�
�ؖ�������ł�
�s���Ă݂܂��傤
�悎�����@�^�����Ă�Ƃ�
�i�@����́@��������@�Ȃ��ā@�ؖ����Ă��������@�ƌ������́@�j
��
���߂́@�����́@�a���@����Ƃ�
�i�@���ꂪ���@�@����ς�@���̂́@��������Ȃ���
�@�@�ǂ�����@�ؖ��ł���H�@�ƌ������́j
���������
�Ȃ��
���Ɓ@���̊Ԃ��@�@���@�i�@�����@�j
a���@���@���ŗ^�����Ă�̂�
�����́@�ł���
���̂Ƃ����
���|�P�@�ɂ���
����ł�������
�������i�C�X�J
�W�J����
������@�ł��@�ˁ[�@
an�@�[�@a(n-1)
���@�v�Z�����ł���
P�Ɂ@�Ȃ����ł���
��ӂ��@P�́@���
������
��肾����
�@
��������
���[�@�����ł�
n�|�P�@�b�e�����@�ԍ����@�g���Ƃ���
���|�P�@���@�����Ɓ@�ԍ��Ƃ��ā@����悤��
�@���|�P�@�����@�P
�Ȃ̂Ł@�ڍs�����
���@�����@�Q
���́@�a�̒l���@�^�����Ă���
�}�Ō����
�͂��߁@����@an�܂ł̘a���@Sn
������
����́@S���́@��������̂�
������
n�|�P���@�������
�W�J����
Sn�@�|�@S(n�|�P�j�@�������
���̍����@a���@�ɂȂ�
�v�Z����ł���
��
��������
���|�P���@�ԍ��Ŏg���Ƃ���
���|�P�@���@�����Ɓ@�ԍ��Ƃ��ā@����悤��
�@���|�P�@�����@�P
�Ȃ̂Ł@�ڍs�����
���@�����@�Q
���[������
�������Q�ł���Ă�����ł���
an = �́@�Q���߂�����Ă��Ƃ�
�Ȃ̂�
�����́@Sn����@�����P���@�����
a�P
�ꉞ
a���̕��ɂ��@�����P�@���@����Č�����
��v������ł���
����́@�����
��������@��������̂悤�ł�
������������
�Q���߂���@��������ɂȂ��Ă�ꍇ
����Ȋ�����
�Ȃ�炵��
�����
��������ł�
����
�����@�悭�ǂނ�
����́@��ʍ����@���߂�ł�
��������@�s����
(�P)�́@���߂���@���������
�i�Q�j�́@�Q���߂���@���������
�i�P�j�@�́@��������
�i�Q�j�́@�����������@��������
��������@���߂Ă��܂���
n�|�P�Ԃ��@�g����
Sn�@�̎�����@a�P���@���߂�
�����ł�
an ����́@a�P���@��v����̂�
���߂���@��������
��
��ʍ�
���|�P�Ԃ��@�g����
a���@����́@�P�ԖڂƁ@Sn �����
�P�Ԗڂ��@�����̂�
�������ł�
�������ł�
�����������@��������ȁ@��ʍ�
����
�������@�ǂ����H
�����Ɂ@���|�P�Ԃ��g��
�v�Z���Ă��ł���
��ʍ����o��
�Q���߁@����́@����ł����̂�
������
Sn����@���߂�Ƃ���i�C�X�J
����Ȋ����Ȃ�ł�
���ׂĂ݂�
c���@�O�ˁ@���߂���@��������
�����@�O�łȂ��ˁ@��������ł͂Ȃ�
���߂́@�����́@�a��
�^��������
��ʍ������߂�
���̐����
���̍��̘a���@���߂�
��ʍ���
���|�P�Ԃ��@�g����
Sn�@����@���߂邶��i�C�X�J
�������
��ʍ����o�ė���
�a�̌`�Ł@���Ă�̂�
�����́@Sn�@�Ɂ@�����P���@�����
S1=a�P
���߂��@�}�C�i�X��
����@�v���X�K���Ɂ@�ς���Ă��Ă��
�������@���Ȃ��Ƃ��́@���ł�������
�����Ȃ�����@�������
��ʍ���@�s������
���́@����
���߂���@�S�����@���̍�
�a�̌����ɑ������
�Q���́@�����@×�@�i�@�����@�{�@�����i�S���߁j�j
-16
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 09:19| ��l�̂��ї��Ƃ��@
2017�N05��17��
21004�@����@�ޑ�@��l�̂��ї��Ƃ�
�v�X�́@�X�V�ł���
�ɔ�C��������������
�ق�Ƃ́@����@�ɔ�ł͂Ȃ��̂ł���
�H�ނƂ��ł���
�ŋ�
�ȂǂȂ�
�x���Ȃ��Ă��܂��܂���
�\���ʂ�
���Ȃ����́@�ޑ肩��ł���
��́@��������
�͂��߂ďo��@���ʍ���
���̋��ʍ��@�Ł@�ł��Ă鐔��̏��߂́@�P�O���̘a��
�ƌ������̂ł�
�܂�
����́@��ʍ��̌`��
�o���Ă��Ƃł���
�����@��������
������
���߂̕���
�Tm-4
�������
�����R�@�����@�V�Ȃ̂�
�V���|�S
���̓�����
���o�����
���ʂ̐����
�C�R�[���Ł@�����
���[
���@�Ԗځ@���@�����Ƃ́@����Ȃ��̂�
���@�Ɓ@���@�Ł@�\���Ă���܂�
���A���A�@�́@����
���ꂪ�@�V��������̌`�Ȃ���
���ꂶ��
�悭�킩��Ȃ��̂�
��������
��ʍ���
��@���@�Ԗڂɂ���
���o�������
�����@���@�Ł@�\����
�T���̂V��
���A���@����
�����́@�W���Ȃ̂�
�����ł́@�܂����ł�
���x�@�����Ɂ@�Ȃ�W��
���ʍ�
�����@�T�́@�{���Ȃ�@�����Ɂ@�Ȃ�̂�
�V�C�P�S�C�Q�P�A�E�E�E�E
�����T���@���@�iK=1,2,3,4,5,�E�E�E�E�E�j
�C�R�[���Ł@���@���Ɂ@��������
�V���|�S�@�̂Ƃ���Ɂ@����邶��i�C�X�J
�R�T���|�S
���ꂪ�@��ʍ�
������
�ŏ��́@�P����
�͂��߂ďo��@���ʍ���
31
�Ȃ̂�
������
�V�X�e�����@��������
�C�R�[���@�Ō����́@�Е���
���x�@�����ɂȂ�@�����T�@��
���x���o���@���@�́@��ʍ��ɂ��ׂ�
�����T���@�Ł@�������
Ck���R�T���|�S�Ȋ�����
�Ȃ̂�
�V�����ł����@�����
����
�����@�R�P
�����́@�R�T
���߂̂P�O���̘a��
��������
��ʂ�
���
�Q���́@����×�@�i�@�����@�{�@�����j
�R���_�Ɓ@��ʍ��́@������
��@�P�O�@���߂��@���߂Ă���łȂ��Ƃ��߂���
�P�O���ڂ́@346
�����P�O�@�����R�P�@����346
�����Ɂ@������
1885
�������
����
�����Ɓ@�����Ɓ@����
���@������Ώo��̂�
����������܂���
����ł�
��������Ȃ��Ɓ@�����
�ق��ƈꑧ�@��`�ł�
����
����Ƌ���
����Ă܂�
���Ȃ�
�傪���Ȃ���@���݁@�݂����Ȃ���ł�
���͂ł���
��̐������Ăł���
�Ȃ@����ׂ肪
��́@���Ԃ݂����Ɂ@�Ȃ�����@�^�J�i
���߂́@�Q���|�P���́@�a�́@�䂪
�悎���߁@�́@��Ɓ@�����ł��邱�Ƃ�
�ؖ����Ă��������@�ƌ������̂ł�
��ʍ���
��@�������@���߂�Ƃł���
���������ꂾ����
A,B�Ɓ@����ł���
�����
A�́@�������@a �����@��
B�́@�������@a' �������@d'
�Ȃ̂�
��ʍ��@�悎�@�Ԗځ@�̔�́@����Ȋ���
���ꂼ���
�Q���|�P�@���́@�a��
�����ɑ������
����Ȃ�����
��ɂ����
�����ɂȂ��Ă��ˁ[
������łȂ�����
�ւĂ���
��̐�������
B�́@���߂́@��̘a��
A�́@����@�A�������@��������@�́@�a�ɂȂ邱�Ƃ�
�����Ȃ�����
�����łł���
�܂��@����@�����ŕ\����
���ʂɁ@�S���@���ׂ��
�P�C�Q�C�R�C�S�C�T�E�E�E
��A�����@�܂����Ă邩��
�Q�{����
��������
�S���@�����ɂȂ���
�Q�C�S�C�U�C�W�A�E�E�E�E
��������@�P���@������
��Ɂ@�Ȃ邩��
�Q���|�P�@�Ł@����@�\������
B�́@���߂���@�Q���|�P���̘a��
�����ɂ��Ă͂߂�
����Ȋ����Ɂ@���Ă͂߂邶��i�C�X�J
�v�Z������
�܂Ƃ߂�Ɓ@
����Ȃł���
���Ɂ@���ꂪ�@�@�@A�́@����A������
������́@�a�Ɂ@�������̂�
���鐔����́@���鐔���@���@�Ƃł������
A�́@���Ԗڂ́@��
���Ԗڂ���@�����@��́@�A���́@�a��
�����Ɂ@����Ȋ�����
������邶��i�C�X�J
����ȁ@�����ɂȂ�܂�����
��
���ꂪ��
�������Ȃ�ɂ�
�C�R�[���ɂ���
�Q���|�P�́@�O�łȂ�����
�₭����
���������
������������
�Ȃ̂�
��ӂɉ�����
A�́@���@�Ԗڂ���
�n�܂�@�Q���|�P�@���̘a��
k���@�R�ōl���Ă݂��
��̐��́@�T
�����Ɂ@�v�Z����ł���
�Ȃ̂�
B�́@���߂���@��̘a��
A�́@���鐔����́@�����A����@�́@�a��
�������Ȃ�@�@���R�����@���݂���B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 16:04| ��l�̂��ї��Ƃ��@
2017�N05��14��
�^�C���@���ł�
�^�C���@���ł�

�����ł���
���Q�@�Ɋւ��܂��Ă�
�����@��@�Q�l�@�̎���
�������@�Q�l���@�g���Ă܂�������
���Ƃ��Ă��܂���
���\�N�@�o�߂����@��
���߂ā@���Ă܂��̂�
�g����@���Ȃ���
�{�����Ă��܂�
�Ȃ��߁@
���Ɂ@�����Ă܂���
����
�{���@��������@�Ă܂���܂���
���݂��@�W���[�N�f�X����
�l���́@�y�����ł���
�Ƃ�����
�^�C���@���@�o���܂܂ł�
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j

�����ł���
���Q�@�Ɋւ��܂��Ă�
�����@��@�Q�l�@�̎���
�������@�Q�l���@�g���Ă܂�������
���Ƃ��Ă��܂���
���\�N�@�o�߂����@��
���߂ā@���Ă܂��̂�
�g����@���Ȃ���
�{�����Ă��܂�
�Ȃ��߁@
���Ɂ@�����Ă܂���
����
�{���@��������@�Ă܂���܂���
���݂��@�W���[�N�f�X����
�l���́@�y�����ł���
�Ƃ�����
�^�C���@���@�o���܂܂ł�
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 17:18| �x�e��
2017�N05��05��
�Ȃ��Ȃ��E�E�E�E
���ƍ؉�
�Ȃ��Ȃ�
�v���悤�ɂ́@�ł�����
����̂ł���
����ł�
�悤�₭
�������@�l������悤��
�Ȃ�n�߂��J�i
��������
�^����@��������ł���
�����
���������@����������
�Ȃ��Ă��܂���
�܂��@���s���@�����̂ł���
�Ƃ����
���̃S�[���f���E�B�[�N��
�J���@�~��Ȃ��ā@�����Ă���܂�
����ς肳
�J�́@���
�Ȃ����
���@����Ă܂���
����
���Ȃ����́@�ޑ���@�����肾����
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�Ȃ��Ȃ�
�v���悤�ɂ́@�ł�����
����̂ł���
����ł�
�悤�₭
�������@�l������悤��
�Ȃ�n�߂��J�i
��������
�^����@��������ł���
�����
���������@����������
�Ȃ��Ă��܂���
�܂��@���s���@�����̂ł���
�Ƃ����
���̃S�[���f���E�B�[�N��
�J���@�~��Ȃ��ā@�����Ă���܂�
����ς肳
�J�́@���
�Ȃ����
���@����Ă܂���
����
���Ȃ����́@�ޑ���@�����肾����
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 20:30| ���ƍ؉�
2017�N04��26��
21003�@�@�@�@��l�̂��ї��Ƃ��@��̐���
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�ނ���������ˁ[
���ƌܕ��@�Q������
���@������ł���
�ł�
�@�@�@�@�k�l�̌��@�ԁ[
�Ђ�
���ꂶ��@�Ӗ��s����
���܂ʁ[
���ʂɁ@�܂܂�Ă�@����
�ǂ�ȁ@������@��邩
�܂�
���́@����́@�a�����߂Ȃ�����
����ƌ�����
��������̏ꍇ��
�����Ɓ@����
�Ł@��ʍ����@�\���ā@������
���[
�����
�ӂ��́@����́@���Ԗځ@���@��v�Ƃ�
����Ȃ��̂�
�Ⴄ�������@�킴�Ɓ@�g����
A
B
�́@��ʍ����@�o������i�C�X�J
A�́@����Ȋ�������������
�����́@�P�@
�����́@�R
��ʍ��@�悍�Ԗځ@�́@�@�R���|�Q
B�́@����Ȋ�������������
�����́@11�@
�����́@�P�O
��ʍ��@�悎�Ԗڂ́@�P�O��+1
A��B�Ɂ@���ʂɁ@�܂܂�Ă鐔��
�ǂ�ȁ@������@��邩�Ƃ������Ƃ�
am = bn
��
�@�C�R�[���Ō����
���ꂪ�@���藧�Ƃ��낪
�V�����@����
A�́@���ԖڂƁ@B�́@���Ԗڂ�
��������
�����@�Ł@�\����
���ꂪ�@�����Ɂ@�Ȃ�Ȃ��Ɓ@�����Ȃ��̂�
�����Ɂ@�Ȃ��Ă�Ƃ����@�@������`��
�Ȃ�ɂ�
���́@�R�̔{��
�Ȃ̂�
�V��������́@�悋�Ԗڂ�
������Ƃ���
�����@�R�̔{���̎��Ɂ@���藧�̂�����
�P�O��+1�Ɂ@�����R����
�������
�R�O��+1
�V�����@�ł����@������b�Ƃł�����
�悋�Ԗڂ�
�R�O��+1
���̐����
�L�������
�������k�Ƃł������
�����@���@�P�O�O�O�ȉ��łȂ��Ƃ����Ȃ��̂�
�k����33.3
����������@33
�Ɓ[�������Ƃ�
�V���������
�������@�S���Ł@33
�����́@31
�����́@30
������
�R�R�Ԗڂ�
991
�Ȃ̂�
�����@31�@����30�@�����@33�@����991
�ȁ@�����
��ʂ�́@���@��
�a���@�v�Z���܂���
����Ȋ�����
�������
�S�[���f���@�E�B�[�N�@�^�C���B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 20:43| ��l�̂��ї��Ƃ��@
2017�N04��19��
�V�C�悩������
�V�C�悩������
������Ă܂���
�ł���
���ꂵ������i�C�X�J
����@�ɂȂ��Ă���

�Ԃ�
���肩�Ԃ�
�A���Ă݂�����
�������傾��

�f����
�A�W�T�C�@�́@�c���@�����Ă��Ă����
���̂��݂��Ȃ��[

��������@
��Ɂ@
�������x�ɂȂ�

�ł܂�����

���ꂩ��
������@�A���Ƃ���
�u���b�R���[
�J���t����
�P�[��

�ǂꂪ�@�ǂꂾ��������
�킩��Ȃ��Ȃ��Ă��܂���

�I�[�g�L�����p�[��
�V�����̂���
�����ɂ́@�s���܂���
���[�@�Ԃ��炢�Ă�

�s���Ă݂Ă���
�Ɓ[
�����킯��

���[�v���܂���

���傤�ǁ@���J�ł����B
���쌧��
�ǂ����ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j


������Ă܂���
�ł���
���ꂵ������i�C�X�J
����@�ɂȂ��Ă���
�Ԃ�
���肩�Ԃ�
�A���Ă݂�����
�������傾��
�f����
�A�W�T�C�@�́@�c���@�����Ă��Ă����
���̂��݂��Ȃ��[
��������@
��Ɂ@
�������x�ɂȂ�
�ł܂�����
���ꂩ��
������@�A���Ƃ���
�u���b�R���[
�J���t����
�P�[��
�ǂꂪ�@�ǂꂾ��������
�킩��Ȃ��Ȃ��Ă��܂���
�I�[�g�L�����p�[��
�V�����̂���
�����ɂ́@�s���܂���
���[�@�Ԃ��炢�Ă�
�s���Ă݂Ă���
�Ɓ[
�����킯��
���[�v���܂���
���傤�ǁ@���J�ł����B
���쌧��
�ǂ����ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 22:24| �͂ȂƖ��