2017�N05��24��
21005�@��l�̂��ї��Ƃ��@�@��������ł�������B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��������@�Ł@���邱�Ƃ�
�ؖ�������ł�
�s���Ă݂܂��傤
�悎�����@�^�����Ă�Ƃ�
�i�@����́@��������@�Ȃ��ā@�ؖ����Ă��������@�ƌ������́@�j
��
���߂́@�����́@�a���@����Ƃ�
�i�@���ꂪ���@�@����ς�@���̂́@��������Ȃ���
�@�@�ǂ�����@�ؖ��ł���H�@�ƌ������́j

���������
�Ȃ��
���Ɓ@���̊Ԃ��@�@���@�i�@�����@�j
a���@���@���ŗ^�����Ă�̂�
�����́@�ł���
���̂Ƃ����
���|�P�@�ɂ���
����ł�������

�������i�C�X�J
�W�J����

������@�ł��@�ˁ[�@
an�@�[�@a(n-1)
���@�v�Z�����ł���
P�Ɂ@�Ȃ����ł���
��ӂ��@P�́@���
������
��肾����
�@
��������
���[�@�����ł�
n�|�P�@�b�e�����@�ԍ����@�g���Ƃ���
���|�P�@���@�����Ɓ@�ԍ��Ƃ��ā@����悤��
�@���|�P�@�����@�P
�Ȃ̂Ł@�ڍs�����
���@�����@�Q

���́@�a�̒l���@�^�����Ă���
�}�Ō����
�͂��߁@����@an�܂ł̘a���@Sn
������
����́@S���́@��������̂�
������
n�|�P���@�������

�W�J����
Sn�@�|�@S(n�|�P�j�@�������
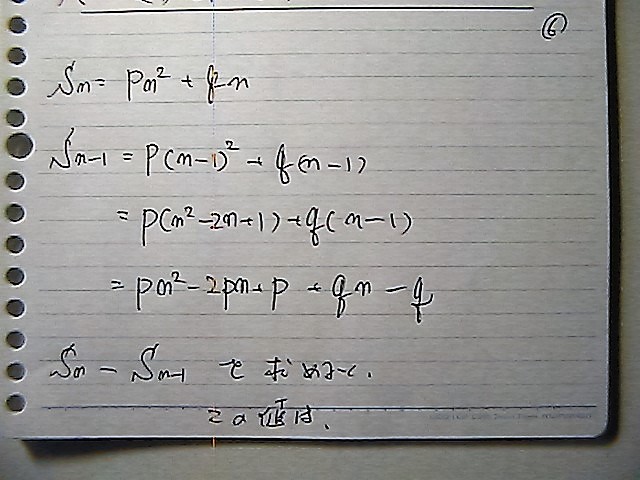
���̍����@a���@�ɂȂ�

�v�Z����ł���
��
��������
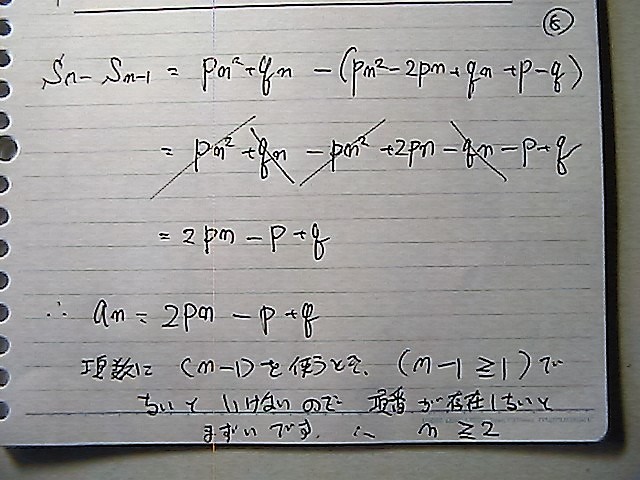
���|�P���@�ԍ��Ŏg���Ƃ���
���|�P�@���@�����Ɓ@�ԍ��Ƃ��ā@����悤��
�@���|�P�@�����@�P
�Ȃ̂Ł@�ڍs�����
���@�����@�Q

���[������
�������Q�ł���Ă�����ł���
an = �́@�Q���߂�����Ă��Ƃ�
�Ȃ̂�
�����́@Sn����@�����P���@�����
a�P

�ꉞ
a���̕��ɂ��@�����P�@���@����Č�����
��v������ł���

����́@�����
��������@��������̂悤�ł�

������������
�Q���߂���@��������ɂȂ��Ă�ꍇ

����Ȋ�����
�Ȃ�炵��
�����
��������ł�

����
�����@�悭�ǂނ�
����́@��ʍ����@���߂�ł�
��������@�s����
(�P)�́@���߂���@���������
�i�Q�j�́@�Q���߂���@���������
�i�P�j�@�́@��������
�i�Q�j�́@�����������@��������
��������@���߂Ă��܂���

n�|�P�Ԃ��@�g����

Sn�@�̎�����@a�P���@���߂�
�����ł�
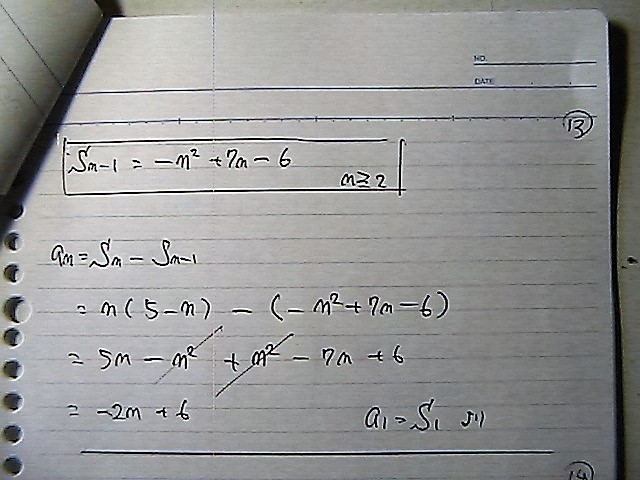
an ����́@a�P���@��v����̂�
���߂���@��������
��
��ʍ�

���|�P�Ԃ��@�g����

a���@����́@�P�ԖڂƁ@Sn �����
�P�Ԗڂ��@�����̂�

�������ł�

�������ł�

�����������@��������ȁ@��ʍ�

����
�������@�ǂ����H

�����Ɂ@���|�P�Ԃ��g��
�v�Z���Ă��ł���

��ʍ����o��

�Q���߁@����́@����ł����̂�
������
Sn����@���߂�Ƃ���i�C�X�J

����Ȋ����Ȃ�ł�

���ׂĂ݂�

c���@�O�ˁ@���߂���@��������
�����@�O�łȂ��ˁ@��������ł͂Ȃ�

���߂́@�����́@�a��
�^��������
��ʍ������߂�
���̐����
���̍��̘a���@���߂�

��ʍ���
���|�P�Ԃ��@�g����
Sn�@����@���߂邶��i�C�X�J

�������

��ʍ����o�ė���

�a�̌`�Ł@���Ă�̂�
�����́@Sn�@�Ɂ@�����P���@�����
S1=a�P
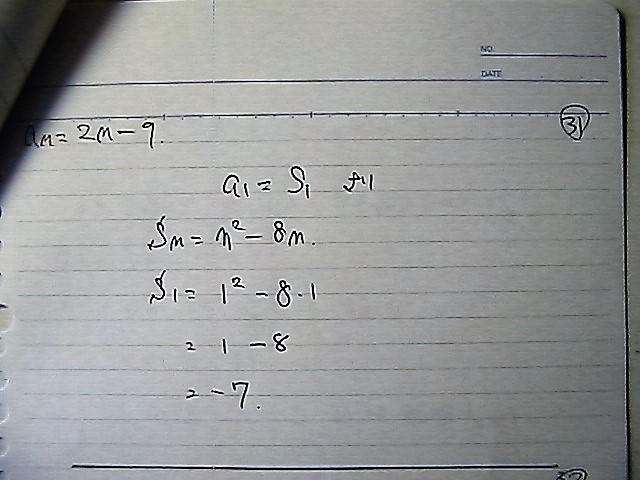
���߂��@�}�C�i�X��
����@�v���X�K���Ɂ@�ς���Ă��Ă��

�������@���Ȃ��Ƃ��́@���ł�������
�����Ȃ�����@�������
��ʍ���@�s������
���́@����
���߂���@�S�����@���̍�

�a�̌����ɑ������
�Q���́@�����@×�@�i�@�����@�{�@�����i�S���߁j�j

-16
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��������@�Ł@���邱�Ƃ�
�ؖ�������ł�
�s���Ă݂܂��傤
�悎�����@�^�����Ă�Ƃ�
�i�@����́@��������@�Ȃ��ā@�ؖ����Ă��������@�ƌ������́@�j
��
���߂́@�����́@�a���@����Ƃ�
�i�@���ꂪ���@�@����ς�@���̂́@��������Ȃ���
�@�@�ǂ�����@�ؖ��ł���H�@�ƌ������́j
���������
�Ȃ��
���Ɓ@���̊Ԃ��@�@���@�i�@�����@�j
a���@���@���ŗ^�����Ă�̂�
�����́@�ł���
���̂Ƃ����
���|�P�@�ɂ���
����ł�������
�������i�C�X�J
�W�J����
������@�ł��@�ˁ[�@
an�@�[�@a(n-1)
���@�v�Z�����ł���
P�Ɂ@�Ȃ����ł���
��ӂ��@P�́@���
������
��肾����
�@
��������
���[�@�����ł�
n�|�P�@�b�e�����@�ԍ����@�g���Ƃ���
���|�P�@���@�����Ɓ@�ԍ��Ƃ��ā@����悤��
�@���|�P�@�����@�P
�Ȃ̂Ł@�ڍs�����
���@�����@�Q
���́@�a�̒l���@�^�����Ă���
�}�Ō����
�͂��߁@����@an�܂ł̘a���@Sn
������
����́@S���́@��������̂�
������
n�|�P���@�������
�W�J����
Sn�@�|�@S(n�|�P�j�@�������
���̍����@a���@�ɂȂ�
�v�Z����ł���
��
��������
���|�P���@�ԍ��Ŏg���Ƃ���
���|�P�@���@�����Ɓ@�ԍ��Ƃ��ā@����悤��
�@���|�P�@�����@�P
�Ȃ̂Ł@�ڍs�����
���@�����@�Q
���[������
�������Q�ł���Ă�����ł���
an = �́@�Q���߂�����Ă��Ƃ�
�Ȃ̂�
�����́@Sn����@�����P���@�����
a�P
�ꉞ
a���̕��ɂ��@�����P�@���@����Č�����
��v������ł���
����́@�����
��������@��������̂悤�ł�
������������
�Q���߂���@��������ɂȂ��Ă�ꍇ
����Ȋ�����
�Ȃ�炵��
�����
��������ł�
����
�����@�悭�ǂނ�
����́@��ʍ����@���߂�ł�
��������@�s����
(�P)�́@���߂���@���������
�i�Q�j�́@�Q���߂���@���������
�i�P�j�@�́@��������
�i�Q�j�́@�����������@��������
��������@���߂Ă��܂���
n�|�P�Ԃ��@�g����
Sn�@�̎�����@a�P���@���߂�
�����ł�
an ����́@a�P���@��v����̂�
���߂���@��������
��
��ʍ�
���|�P�Ԃ��@�g����
a���@����́@�P�ԖڂƁ@Sn �����
�P�Ԗڂ��@�����̂�
�������ł�
�������ł�
�����������@��������ȁ@��ʍ�
����
�������@�ǂ����H
�����Ɂ@���|�P�Ԃ��g��
�v�Z���Ă��ł���
��ʍ����o��
�Q���߁@����́@����ł����̂�
������
Sn����@���߂�Ƃ���i�C�X�J
����Ȋ����Ȃ�ł�
���ׂĂ݂�
c���@�O�ˁ@���߂���@��������
�����@�O�łȂ��ˁ@��������ł͂Ȃ�
���߂́@�����́@�a��
�^��������
��ʍ������߂�
���̐����
���̍��̘a���@���߂�
��ʍ���
���|�P�Ԃ��@�g����
Sn�@����@���߂邶��i�C�X�J
�������
��ʍ����o�ė���
�a�̌`�Ł@���Ă�̂�
�����́@Sn�@�Ɂ@�����P���@�����
S1=a�P
���߂��@�}�C�i�X��
����@�v���X�K���Ɂ@�ς���Ă��Ă��
�������@���Ȃ��Ƃ��́@���ł�������
�����Ȃ�����@�������
��ʍ���@�s������
���́@����
���߂���@�S�����@���̍�
�a�̌����ɑ������
�Q���́@�����@×�@�i�@�����@�{�@�����i�S���߁j�j
-16
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 09:19| ��l�̂��ї��Ƃ��@