�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2017�N12��23��
25006�@�@��l�̂��ї��Ƃ��@�s��̐ρi�Q�j
�J�̓��́@�X���[���C�t�̕���
�����̏ؖ��Ȃ̂ł���
�����b��
�v�Z���ł���
�i�P�j�A�i�Q�j���@�ؖ�����̂�
�|���Z�Ɋւ��Ắ@������@×�@�c����
���i���@��Ɂ@�g�݂��ĂĂł���
���ӂ́@���i
AB
�E�ӂ́@�ԂЂ�BC
���ӂ���@�v�Z���Ă���
���Ɂ@�E�ӂ��v�Z����
���Ȃ��ł����
(�Q)���@���i���܂��@�g�ݗ��Ă�
�����Z��
���^���m�łȂ��Ƃ��߂ł���
���Ȃ��@�������m�́@�����Z��
�X���[�Ł@�s���܂���
�P�s�P��
�|���ā@�����ā@�����ɂ���
�Q�s�P��@
�|���ā@�����ā@�����ɂ���
�P�s�Q��
�|���ā@�����ā@�����ɂ���
�Q�s�Q��@
�|���ā@�����ā@�����ɂ���
����Ȃ�
�|���ā@�����ā@�����ɂ��Ă�
�܂����Ă��@�S��
�Ł@����Ȃ�
���i���@�ł��Ă����̂�
���ӂ���
���ӂ́@����
�E��
�E�ӂ́@����
�Ȃ̂�
������
���́@������
�����
�|���Z�����
��s��Ɂ@�Ȃ邱�Ƃ��@�����ł�
�ꌩ�@����[���Ɂ@�Ȃ�́H�Ȃ̂ł���
�����Z�@��@�����Z�ƈ����
�|���Z�́@����Ă݂Ȃ��Ɓ@
�����ɂ́@�����Ă��Ȃ�
�Ȃ̂�
�v�Z���Ă݂܂���
��s���
�|���ā@�����ā@�����ɂ���
�������@�v�Z����ł���
�O�@�ɂȂ����ł���
���́@���������藧�悤��
A���@���߂�ł���
�i�P�j�@�A�i�Q�j�A
��悪�@�O�s��
�Ƃ肠�����@�Q�悵�Ă݂Ăł���
���́@�������@�S���@�O�ɂȂ�̂�����
����ȁ@�����Ɂ@�A��������
���[
�A���@a�́[��
�����|a
�ł��邾��
�g���@�������@���Ȃ��܂Ƃ߂Ăł���
����Ȋ����Ł@��������
����
���Ȃ��@�v�̂�
�v�Z���Ă݂�
���ʂ��@�A���Ł@�o�Ă���
�����
�ł��邾���@�g���������@���Ȃ��܂Ƃ߂�
����ł�������
���ꂪ�ł���
�S�R
������Ȃ�����
�Q�Ă���ł���
�ؖ����
�Ƃ肠����
������Ƃ��܂Ł@�s���Ă݂��
�v�Z���Ă����Ƃł���
��Ɂ@a2 b2 c2 d2�@���@���߂Ă����Ăł���
��������@�ǂ�����낤��
���Ȃ�@�Y�̂ł���
�ӂƁ@�C���t������
��
������ā@����ł�����
����ł�
������@�͂����
����������@�s�����ł́@�Ȃ���
�ł��Ł@��������
�ǂ������
�Ȃ�������i�C�X�J
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 19:00| ��l�̂��ї��Ƃ��@
2017�N12��20��
25005�@��l�̂��ї��Ƃ��@�s��̐ρ@�i�P�j
�s��́@�ς��@�v�Z���Ȃ���
�Ƃ������ł�
�ӂ��́@���́@�|���Z�Ɓ@���傢�ƈႤ�炵���ł���
�|�����@�����̂����łȂ�
�s���Ă݂܂��傤
�܂��ł���
�|���Z���@�\���@�s�\��
�����̍s��́@��Ɓ@�E���̍s��́@�s�́@����
�������Ƃ��@�|���Z�@�\�ɂȂ�
����ւ��Ă݂��Ƃ���
������@��͂�@�����̍s��̗�Ɓ@�E���̍s��̍s��
�������̂Ł@�|���Z�@�\�ƂȂ�
�����@�C���t���܂�����
����
�Ȃɂ��@�C�ɂȂ�܂���ł�����
����
�������Ă邩�����@�@����������Ǝv���܂���
��Ɂ@�i��łł���
�|���Z�J�n
�����́@������Ɂ@�@�@�E���́@�c�����
��
�e�������@�|���ā@�����ā@�����ɂ���
�P�s�@�P��
�Q�s�@�P��
�P�s�@�Q��
�Q�s�@�Q��
�Ł@�������@�������Ă݂Ăł���
AB�Ł@�悶����@�����Ȃ�܂���
����
BA�Ł@�|������@�������
���ɗ���@�s��́@��Ɓ@�E�ɗ���s��́@�s��
�����@�������̂�
�@
�ς����݂�
���́@������
�E�́@�c����
��
�������m���@�|���ā@�����ā@�����ɂ�
����Ȃ�ł킩�邩��
�v�Z��������
�����Ł@�����@�����������ƌ�����
AB�@�@�Ɓ@�@BA�@�́@��ʓI�Ɂ@
�������Ȃ�Ȃ�
���ʂȏꍇ�̂ق��́@�s���
������@�������@�ς��Ɓ@�������@����Ă���
�s��́@A,B�@������Ƃ�
��AB�@�����݂��Ă��@BA���@���݂���Ƃ́@����Ȃ�
��AB�@�Ɓ@��BA�@���@���݂��Ă�
��ʓI�Ɂ@AB��BA�́@�������Ȃ�
AB=BA�̎��́@A��B�́@���@�ł���Ƃ���
�s��̌v�Z
�|���Z��
�ł��邩�i�@�\���@�j�@
�ł���Ȃ�@AB�ABA�����߂�
AB�́@�����̍s��́@��̐��Ɓ@
�E���̍s��́@�s�̐����@�������̂�
�|���Z�\
BA�̎���
���̍s��Ɓ@�E�̍s��́@��Ɓ@�s���@�������Ȃ��̂�
�|���Z�@�s�\
����Ȃ̂�
AB���@�v�Z����
����ȏ������Ł@�����邩��
�������@���傱���傱�@�v�Z�����ł���
����Ȋ�����
�����@�|���Z
����͂�
�Q���̐����s����
AB�@�@���@BA���@�|���Z�\
���Ԃ����@�Ⴄ���̂Ɂ@�Ȃ�Ǝv���܂���
AB����@�s���Ă݂܂���
����Ȋ�����
BA�Ł@A�ɑ��ā@B���@A�́@������@�|�����
�b�e�����Ƃ�
����
��ʂɁ@AB�@BA�@���@���݂���Ƃ�
AB��BA�́@�������Ȃ�
���Ⴂ�܂��˂�
�ˁ@�Ⴄ�ł���
������Ⴄ��ł���
����
�v�Z�ł���
���K���Ƃ��Ȃ���
����@�H�@���ꂪ�@�s��ł��B
�S�悾����
�����炳
�Q��ɂ�t
�Q��Ɂ@�������
�R��ɂ���
�R��Ɂ@�����������@�S�悾���炳
�ӂ݂ӂ�
�����́@��������
����������Ɓ@�炭���Ă悩��������
���������
���@�@���
�Ł@�S��
����Ȋ�����
�w���́@�v�Z�́@�����Ɂ@�o�Ă���̂�
��������イ�@�v�Z���Ă��
�K�тȂ�
����́@�ȂɂȂ́H
�Q�C�R�@���@�݂�
���������
����Ȋ���������
�������ƂɁ@�ω��������
���́@�P�s�Q��ڂ̐�����
���ꂾ���炳
�����Ȃ̂�
����́@�v�Z����
�m�F����������
�Ȃ̂�
�m�F������
���
���^�́@�s��́@�����Z�́@�������m�̑��Z
���ʂ̒����@������
��悵��
�s��̓�悾����
�����́@�łȂ�
����Ȃ���
����́@���ӂ�����
�E�ӂ�
�@
�����I�Ɂ@�v�Z���Ă���
�������킹����j��
A���
B���
�QAB�@�@�́@AB�̐ςɁ@�e�����Ɂ@�������@�Q�{
��������@�݂�ȑ�����
���[�[
��������������[
����Ȃ��Ă�
�������Ȃ����Ƃ́@�ؖ�
����ł����̂�
���̂́@�������Ȃ�
�ق��́@�ؖ�
���ӂ́@����̌v�Z���ʂ�
���Ɓ@�������Ă�Ƃ����@�����Ă���
�v�Z���ĂȂ��̂́@BA����������
�v�Z����
������@�������킹���
���x�́@�������Ȃ��Ɓ@�����
�������ł������`
�������傾����
���Ȃ݂�
�����Ȃǂ�
���ėp���ɂ�
���̗l�ȁ@���ƂŁ@��������
�������t���@�g����������
�䂦�Ɂ@���������ā@�@��ӂ��
�ȂǂȂ�
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 00:10| ��l�̂��ї��Ƃ��@
2017�N12��18��
25004 ��l�̂��ї��Ƃ��@�ꎟ�ϊ��̐���
�s��@�ꎟ�ϊ��́@�����ł�
�s���Ă݂܂��傤
�܂��@�����@�ǂނ���i�C�X�J��
�ϊ��������ʏ�̔C�ӂ̃x�N�g��
u,v, �ɑ���
�i�A)�@�i�C�j�@�̓�̐�����
�������Ă���Ƃ�
��{�x�N�g��
���@���ꂼ��@
e1' e2' �Ɂ@�ϊ������Ȃ��
u�ɂ�������
u'���Ȃ�́@�@���Ɂ@�Ȃ邱�Ƃ�
�ؖ�����
���̂ł���
�܂����Ă��Ȃ�ł���
����ĂȂ������Ƃ����@�o�Ă��܂��܂���
�x�N�g���@��ɂ��������
�Ȃ̂�
�����I�Ɂ@�@���Ă��܂���
�{���@���w�ł�
���@�K���Ă�@�������������Ƃ�
�O�i�ł��܂���
�����łȂ��ꍇ��
���Ƃ������@�ǂ��ɂ��邩������Ȃ��@��ԂȂ���
�i�߂Ȃ��@�Ȃ��Ă��܂��܂�
��
��{�x�N�g���ł���
x���@�����́@�������Ɂ@�����������@�P�́@�x�N�g��
e1 (1 ,0 )
e2�i�O�A1�j
�Ȃ̂�
�}�́@A�́@�x�N�g����
��{�x�N�g���Ł@�\����
���p�@�O�p�`�́@�ΕӂɂȂ�Ƃ���
��e1 + ye2
������@���܂��܂���
�ꎟ�ϊ���
u���@u'�� �Ȃ�@�́@���Ɂ@�Ȃ邱�Ƃ�
����̂ł���
�C�ӂ́@u�x�N�g���@���A���@�́@��x�N�g����
��{�x�N�g���Ł@����킵��
�����
�����@�i�A�j�i�C�j�@���@�g����
�ؖ����Ă�����
��{�x�N�g����
�\�������@�����@��̎l�p�̒��g���@�g����
�ό`���ā@�i�A�j
�����
�łĂ����@����
���̎l�p�̒��g�Ł@�ό`������
��
�s��́@�����{�́@�e�����́@�����{�ł���
�ւĂ���
�s��̑��Z��
���^�̎��Ɂ@�ł��ā@�e�������m�́@�����Z�ł���
�ꎟ�ϊ��́@��`��
�l�p�̒��g�@�Ȃ̂�
U'���@AU�@�Ɂ@�Ȃ�����
���[�@�x�N�g���́@�������ɐ����ĂȂ��ł�����
�{�[���y���́@���Ł@���Ă�������
�����ł́@�����@�����Ă邩�ƌ�����
�s��́@�a���@�ꎟ�ϊ��������̂�
�����Ɂ@�ꎟ�ϊ��������̂��@���������̂�
�������ʂɂȂ�Ƃ������Ƃł�
�ꎟ�ϊ��́@��`�͂���Ȃ̂�
�s���
�ꎟ�ϊ��́@��肪�@�o�Ă�����
�]���Ɂ@������@�������肵��
�v�Z�́@�⏕�ɂ��Ăł���
��
���܁@�����Ă����Ƃ�
���ۂɁ@�v�Z����
�ؖ�����Ƃł�
����Ȗ�肪�����Ăł���
��́@�x�N�g�����@�g���Ă�̂�
�\���]���@���P�A���P�@�@�@�@���Q�A���Q�@�Ƃł�����
�\���]��
�ꎟ�ϊ����邶��Ȃ��ł���
���́@���ꂼ��@�ꎟ�ϊ��������̂�
�����Z���Ă݂��
����Ȋ���
����
���x��
�\���]���@�ꎟ�ϊ�����O��
�s����@����������
������@�ꎟ�ϊ�����Ɓ[
����Ȋ�����
��
�������@���ꂼ��@�ꎟ�ϊ����ā@�������킹�����̂�
���������@�ȒP�Ɂ@�Ȃ�̂�
�����肾�����肷���
�����ɂȂ�������
���̎��́@�g�����
�����{�́@���̕���
�x�N�g���́@�����{��
���ꂼ��́@�����Ɂ@�����{����
���́@�ꎟ�ϊ����@���߂��
����Ȋ���
��Ɂ@�ꎟ�ϊ����Ă�����
������@�����{���Ă݂���
����Ȋ���
����Ȃ��@����i�C�X�J
������@�������@�@�ؖ��Ɂ@�g����
�@
��肪�@����Ƃł���
���܁@�ؖ������@�����@�g����
�ȒP�Ɂ@�ł��Ă��܂��܂�
������
����Ȃ̏o����
�ؖ��Ɂ@�g�������@�ؖ����ā@
�g����悤�ɂ��Ȃ��Ƃ����Ȃ�����
��ςȂ̂�
�@
���[�����̂́@�łȂ��@�Ɓ@������
��
�^���́@���ӂ��@�������ؖ�����
2�����@���X�Ɂ@�g���Ăł���
�ؖ��I���
���X�g�͂ł���
�_�C�W���J�i
�����P��
����͂�
�@
�������@�C���t��������
�������@�Ⴍ�Ȃ肽����
��蕶���@���Ă���������
�������܂�ł邯�ǂ�
���A���@���@���f�A���f�Ɂ@�ϊ������Ƃ���
�����́@�����́@�l�Ȃ���
���̐��E�́@�����܂Ł@����Ȃ��Ɓ@�S�̂ł́@�Ȃ��̂ł���
�w�҂���̂������ł́@������O�Ɂ@�o�Ă���
����
���ӎ��́@�@�����́@�������m
�����́@�����ǂ����Ł@�v�Z����
���
�_�C�W���J�i
��
�E�ӂ��@�W�J���Ă݂��
���ʂ́@�|���Z�́@�W�J�Ɓ@�������@�Ⴂ�܂���
�O���́@i��2�悪�@�|�P�ɂȂ�̂�
�����@�@�@�㔼�́@i�t�́@����
���A���p�[�g�@�Ɓ@�C�}�W�i���[�p�[�g�@���@�����Ăł���
i�Ł@���������@���ʂ̒��g�́@���f�ɂȂ邩��
����Ȋ����ł���
������@�ꎟ�ϊ��́@��`�Ɓ@����ׂ�
����Ƃ�
�Ȃ�����
�����ꂳ�܁`
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 20:36| ��l�̂��ї��Ƃ��@
2017�N12��17��
25003 �@��l�̂��ї��Ƃ��@�@�s��̈ꎟ�ϊ�
���̂ł���
�s��ł�
�����́@�ꎟ�ϊ�
���̕ӂ́@���ӏ�
����ׂ��Ă����Ȃ���
������܂��ʂ���
�Ƃ肠�����@������
������������������
���ꂩ��
��̓I�Ɂ@�����@�����Ȃ���
�������@�v���o�����������`��
�����ł��傤��
�s���Ă݂܂���
�s��@
�������@�s����
����ł��@�c���@��
�Ȃ̂�
�������Ɂ@�P�s�@������
�c�����Ɂ@�Q��@�����
����Ȋ�����
�i a b )
�������Ɂ@�s
�c�����Ɂ@��
�P�s×�Q��@�̍s���
�s�̐����@�P�s�����Ȃ��̂�
�s�x�N�g��
�@�P������
��x�N�g��
���W��́i���A���j�̏W������
���W��́@�i�@���f�A���f�j�@�̏W���ւ�
�ʑ���
�A���@�������ɂȂ��Ă܂���
�����
�s��́@�`�Ɂ@�����Ƃ�
�ꎟ�ϊ��ƌ�����
�ʒu�x�N�g����
U�@���g���ā@������
�l�p�Ɂ@�͂������Ɂ@�����Ă���
�`�Ɂ@�Ȃ�̂�
�������́@�A����������
���́@�ʒu�x�N�g���@u���@�g����
�ꎟ�ϊ��́@�s���
����Ȋ�����
��`�����
�d�����Ă܂���
����Ȋ�����
���̎���
A�Ł@�ꎟ�ϊ����@���܂�̂�
���́@A���@�ꎟ�ϊ���
�\���@�s��ƌ����܂�
�ꎟ�ϊ���
�s��Ł@�\����Ƃ킩�����̂�
��́@�ꎟ�ϊ�
A �Ɓ@�@B��
�g����
u�� u'�� u''
�Ɓ@���Ł@�ꎟ�ϊ�
���ā@����Ɂ@���Ł@�ꎟ�ϊ�
����Ȃ��
���ԂɁ@�ϊ����Ă���
�i�@�����́@�����Ȃ����Ă��������j
����
����
���̕ϊ���
AB�́@�ςɁ@�������Ȃ��ł���
�J��Ԃ������̂ł���
A�ŕϊ��������̂�
����Ɂ@B�Ł@�ϊ��������̂�
AB�̐ςɁ@������
�i�@����Ɂ@���������Ă��������@�j
������
���[
�����́@�X���[���[�V������
AB�́@�|���Z�̎d���ł���
���߂̍s����@�s�Ɂ@
���̍s����@���
�����ł���
��
�ԃy���@�́@�悤�ȁ@�|������
�P�s�P��
����
�Q�s�P��
�ւĂ���@�P�s�Q��
������
�Q�s�Q��
�����Ȃ�́@�悭�Ȃ��ł���
�������邭����
�s��Ɓ@��x�N�g�����@�|�����
���߂̍s����@�s�Ɍ���
���́@��Ɍ���
��
�s��́@�|���Z���@���藧�̂�
���߂̍s��́@��̐���
���̍s��́@�s�̐���
�������Ƃ�
�|���Z���ł��܂�
��
��̍s��̐ς�
���߂̍s����@�s�ŕ�����
���̍s����@��ŕ�����
�ł͂ł���
��̓I��
�����@���Ă݂邶��i�C�X�J��
��{�x�N�g�����@�Q�@������
�\���]��
�ꎟ�ϊ���
����@�x�N�g���Ɂ@�ϊ����ꂽ��
���̎��́@�ꎟ�ϊ����@���߂�
u�x�N�g�����@�ꎟ�ϊ�����ł�
�ꎟ�ϊ���
�Q�s�Q��́@�`�ƌ����@�^�ɂ���
�ϊ���́@u�f�́@�`×u
���Ł@����ĂȂ��ł���
���߂̍s����@�s�Ɍ���
��납��@����@�����ā@�����̂�
�X���[�Ł@�������Ƃ��́@�|������
�v�Z����
�ꎟ�ϊ��́@�������@�ł܂���
�Ȃ̂�
���́@A�s��Ɂ@u�x�N�g�����@
�|����ł���
���߂́i�@�����@�́@�s�Ō��āj
�E���́@��Ō���
�|�����
����
���́@�ꎟ�ϊ��ɂ��
�x�N�g���́@�������߂�
�����
�������Ɂ@�Ȃ�Ȃ�����������
���ł���
����ȏ�������
�ϊ����@�^�����Ă���
���A���Ɂ@�x�N�g�����@��������
�s�@�@���
����Ȋ���
����
�|�����́@���Ԃ��@�������
����ȂɁ@�|����Ȃ��Ă���
����
�ꎟ�ϊ���
���������@���G�ł���
�������̕���
�v�Z�����@�ǂ��₷�����
����Ȋ�����
�Ȃꂿ�Ⴆ��
����
�ǂ�ȁ@�ꎟ�ϊ���
����͂ł���
�ԃy���Ł@�������@���������
����܂���
����ȁ@������
�`��邩��
���
����������
���Ƃ�
�����邩��
�ꎟ�ϊ����@���߂�@���ł�����
��
�{���̃��X�g��
�����
�Q�_���@���ꂼ��
�@
�ꎟ�ϊ���
�ϊ����ꂽ�@���ʂ�����Ƃł�
���̈ꎟ�ϊ���
���߂Ȃ���
�ꎟ�ϊ���
A�Ƃ��ā@�������Ł@a�@b
�@�@�@�@�@�@�@�@�@�@c�@d�@�Ł@
�����Ă���܂���
�A����������
�Q�g
a
��
d
��
�Ƌ��߂�
�����́@����
�s��̊|���Z��
�s�@�@��@���@�s��
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 21:44| ��l�̂��ї��Ƃ��@
2017�N12��13��
25002 ��l�̂��ї��Ƃ��@�s��̉���
�s��̑��Z�@�����Z�́@����
�����Z�@�����Z��
���^�@�́@�s��̎��Ɂ@�\��
�������킹��Ƃ���
�������@����ւ���@�����@��
�������킹��Ƃ���
�����@���@�ς���@�����̖@����
�g�p�\��
�܂�
�����{�̎��́@�e�����Ɂ@�������@�����{
������@���܂��܂���
�v�Z���ł�
�����̂Ƃ���ł�
���ʂ́@�������̎��Ɠ�����
���ό`����
�ȒP�ɂ��Ă���
�s����@������Ă����Ƃł���
�^�����@���ό`����
�����@�̌`�ɂ���
�E�ӂ́@B�@�@A�@�Ɂ@�s���
�������
���
���������́@�ꏊ
���Ȃ��@�ʒu�ǂ����́@�����Z�����Z
�Ȃ̂�
�Q�s�@�Q��́@�s���
�����́@����
�\���]��
�����Z�ł����
���ꂩ��
�����{�̎���
���ꂼ��́@�������@�\���]���@�����������{
������
����Ȋ�����
�����Ă݂܂�����
�X�Ɂ@�v�Z�ł���
���x��
�������@������
���̒��́@X�s��@Y�s��@�̒l��
���߂��ł���
���̕ό`�Ɓ@�@������
��������@A�@B�@�s���
�\����
��́@�s����@���
���߂́@���ʂ̒����@�v�Z���Ă�����
���q�Ɂ@�Ȃ�Ȃ��悤��
��
���Ɂ@�߂��ā@�������
����ȓ����ł�
�����
�I���ł́@�Ȃ�
X�̕����@���߂Ȃ���Ȃ�Ȃ��̂�
X=�̎��́@A�Ɓ@Y�Ɂ@�������Ă�s����@�������
����Ȋ�����
�������@���
�ȒP�������ł�����
�v�����
�v�Z���Ȃ�ł���
���̕ӂ�
�Ԉ��Ȃ���@�I�b�P�C
��ςł���
�����Ɋ���Ă��
���������@�������
��������ƂɁ@����������
��
����@�������Ȃ�
���Ă邾��
������������
�v�Z�͂�
����@���ۂɁ@�������Ȃ���
�Ă��߂�Ɂ@�K�т邽��
����͂�
��l�́@���߂Ɂ@�����ł���
�]�g������i�C�X�J
�p�Y���݂����ȁ@�Z���Ȃ�ł�
���̕ӂ�
���܂ł́@�����̑����
�s����@�����
�e�������Ƃ�
�������Ɂ@��������݂�����
�v�Z�ӏ����@��������
������
��s�́@�ʒ�����Ȃ����ǂ�
�����߂��̎���
���́@��ςȂ�
�e�Ɋp��
�w���@���Ȃ���@�Ԉ��Ȃ����
���l���@�ʂ��Ăł����
�����Ł@�Ԉ������
���������Ȃ�����i�C�X�J�I
�C���ł��Ă��
�����M��
���݂܂���
����Ȋ�����
�v�Z������
����������̂Ƃ���
�|�������ł���
��
�������@�Ԉ��Ȃ��悤�ɂł���
�s���
�����́@�ǂꂩ���@������
�O�p�́@�Ȃ��ł�
�y�P�ł��̂�
�����́@��ł��@�Ⴄ��
�ʎ҃i�^��
������Ƃ����@��낵���@���肢�������܂�
�O�́@�ʐ^����
�s��Ԃ�
�������@�ς���Ă܂����
�v�Z�ԈႢ������
����������������
�����ԁ@�|�������ł���
���Ȃ݂�
���̍s��́@���s�@����@�ł���������
�����@�s�@
�c���@��
�Ȃ̂�
�Q×�R�́@�Q�s�R��@�́@�s��
����
X�����߂�ł���
�������̌v�Z��
�s���
��������`
�ȒP�ł���
�v�Z���ł���
�����́@���ό`
�������Ɠ������l���Ă���i�C�X�J��
X�@�Ɂ@�������Ă�@�s���������
�l�������������
�Z���ł�
�����炳
�ˁ[
��ςł���
�Ō�͂�
�������@���藧�悤�Ɂ@���A���A�����@���߂�ł�
�����܂ł����
�|�����@������
�������́@����ł�
���
�s�@�����@�܂�ł��Ă�
���^�́@�s�@�C�R�[���Ō���ă^��
�e�������@�������킯�ł�����
�A���������ɂ��ā@���o���Ă���
➀����@���ł���
�A����@���ł���
�C����@���f�V��
�Ł@�B�́@�����@���藧�Ă@�I�b�P�C�Ȃ̂�
�m�F����
����ł����̂�
����
�����@����������
����Ȃ�����Ȃ�
�Ђ�����
�v�Z
��ςȂ����ł���
�������̕����@�C���y�����
��
������܂ŗ�����
�e�������ƂɁ@�C�R�[���Ł@����Ł@���o����
�A�����������@�U��
�ȗ��ł���̂����邩��
�S��
��������
�������́@�v�Z��
���܂ł̂悤��
�˂˂�
���[�@������Ɓ\�����ł���
�^�_�@��ςȂ����́@�v�Z���K�Ȃ�ł���
���
���ʂ́@�v�Z�Ƃ́@�����Ⴄ���̂��@�o�ė��܂�
�P�ʍs��Ƃ��@�t�s��Ƃ��́@������
�����
�����@�ʓ|�Ɂ@��������̂��@�o�ė��܂���
�e�Ɋp
�����́@����@�������̂�
��ςȂƂ��ł�
�s�@���ӂȁ@�̂́@�N�H�H�H
�R���s���[�^�́@
�s�@���ӂł��B
AI�@���@����ׂ��
���[�@�s���D�����Ă����Ǝv���܂���
�|���Z�@����Z�@�̏ꍇ�́@�����Ȃ�́@�킯�킩��Ȃ����ǂ�
�����Z�@�����Z�@�̂�����Ȃ�
����Ł@�W������
�|��������
�@
�v���܂�
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 20:30| ��l�̂��ї��Ƃ��@
2017�N12��09��
25001�@�@��l�̂��ї��Ƃ��@�s��̈Ӗ��Ɓ@����
�s�����
�C�}�n�@�K����
�킽���́@�K��������
���̔N�́@�q�́@�K��Ȃ�
������
�܂��@���̎��̔N�́@�K�����Ƃ�
��́@�K�b�R�Ɂ@�s������
�u�`�̎�
���K���ĂȂ�
���ā@������������
�H�H�H���@�����Ȃ́H
�K�����l
�����ȉ�������
���̎��ł���
��
�l��������ł���
��Ђ́@���Y�\������Ƃ����ł���
������
�i�@�@�j�@�Ƃ��@[ ]
�Ł@��������
�s��@�Ƃ��@�}�g���b�N�X�@�b�e��������
�����炳
�����́@����l������
����Ȋ�����
�������肵�Ăł���
���炭���҂���������
�łł���
���x��
�������@���藧�ɂ�
�s��ł�
���Ȃ��@�^�̍s�@�����Ō���Ă��
�e�������@�i�@�v�f���@�j������
���̕��т��@�s
���Ă̕��т��@��
�Ȃ̂�
����́@�Q�s�Q��́@���^�̍s���
�������@�������Ȃ�l��
�Ȃ@�A���@��������
�S�{����݂����ȁ@�����J�i
➀�A���@�����Z����
�����@�������ā@x���o��
�����@�A�Ɂ@����Ł@��
�B�C�@�́@�����@�����Ɂ@
�������̂�
���藧��
����
�s��́@����
�܂�
�^���@�����ł��邱��
���Ɂ@�e�������@�����ł��邱��
���^���@3��
2�s2��̂��̂��@3����
�e�������@���Ă݂��
���Ȃ��@�ʒu�́@�l���@�����Ȃ炢���̂�
���Ɓ@�E�́@�������Ȃ�
�^�́@�v�Z���Ȃ��Ɓ@�������o�Ȃ�
�������@�o���Ă݂��
�ǂ�����
�E�Ɓ@������
���́@���͂��@�悭�ǂ�łł���
�������@ij�Ł@����킷��ł���
�s�Ɓ@��́@�����@���Ȃ����̂�
�����s��ƌ�����
3�s3������@3���́@�����s��
�e�������@�Y������
�\��������
�����ǂ����
�O�@���@1���@������
����Ȋ���
����
�������́@�ޑ�݂����ȁ@���ł���
�S�Ắ@�v�f�Ɂ@�ւ���
���藧���Ȃ���
�C�R�[���ł͂Ȃ�����
���܂�
���������
���Ł@�P�Ɂ@�Ȃ�̂́@�}�P
�P�Ƃ�
a���|�P���@����̂�
�����́@a�́[�P
���������Ă݂܂���
�v�Z�h�����݂����Ȃ���ł����
���Ȃ��@�����́@�g���Ă�Ƃ���
�ǂ������@���藧�悤��
������
��́@�v�Z���ł���
�S���@�������@���藧���Ă邩
�m�F����
��
�s��́@�����Z��
�����Z��
�e�������m��
�����Z�@�����Z
�Ȃ̂�
���^�łȂ��Ɓ@�s������
�����@�{�@�̎���
�e�����Ɂ@�������@�����{
�S�ā@�O�@�ŗ��Ă�@�s���
��s��@O
�s��́@���@�́@�����@�Ɓ@������
�ǂ������@�g����
�������@���������@�Ⴄ���̂�
�}�C�i�X��
�\�����
�����ꂳ�܁`
�i�@���ꕔ�����@�ƒ�؉�����������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 23:18| ��l�̂��ї��Ƃ��@
21014 �@��l�̂��ї��Ƃ��@���䐔��ł������ �@
�ޑ��
���邎���܂ł̘a��
�^��������
���̐���́@�ǂ�Ȑ��H
�a����@�悎�����@�o��������
���Ă͂߂ā@�l�����
�P����@�P�O�@�܂ő��������̂���
�P����@�@�X�܂ł��@���������̂�
������
�P�O�@�������@�c��킯��
������@�悎���ƍl�������
����i�C�X�J��
��
���̑���Ɂ@���|�P���@�����
���|�P�܂ł́@�a�����߂�ł���
�����ǂ����
Sn�|Sn-1��Xn�@�������Q
���Ă͂߂�
��́@�w���̌v�Z
��ʍ����o�ė���
�a�̌����̎���
���P�����P�Ȃ̂�
�������@���߂Ăł���
��ʍ��̎�����
�����Q�ȏ��
�@
�Q�C�R����
�����Ɓ@��ʍ�����̎���
�ǂ����
���̐����
������������
�Q���߂���́@���䐔��Ɂ@�Ȃ��Ă銴���ł���
������Ă݂��
�������݂�����
�a�̌�����
���Ă͂߂���悤��
���|�P���@������
��ʍ��@Xn���@���Ƃ߂��
�w���̌v�Z��
�����͂�
�����̗l��
�o����
���[�W����
����������
�Ȃ��
a�Ł@�����ɂ���
�w���́@��������
��ʍ�
���o����
��ʍ��́@�Q���߁@�ȉ���
�����́@S1��X1
����
S1�́@�|1/3
�Q���߁@�ȍ~�́@��ʍ��̎���
���߂�
�Q���߁@�R����
���ł�
�����P�́@�Ƃ����@���Ă݂��
����́@S1=X1�@����́@������
��ʍ�����́@�������@��v����̂�
���䐔��́@��ʍ��̎��Ɂ@���Ă͂߂�
����Ȋ����̐���
���x�͂�
���߂́@�����́@�a��
�����Ɂ@�B����Ă�
��������
�a�̌����@�́@Sn���@�@��o����
��������́@�������݂�����
���ł���
���O�@�o���Ă��܂���
�������������@��
���̌�낪�@�����@��
�^���́@���̐�
���Ɂ@�Ă��@���@�P�O�̂��̂��@��p�ΐ�
������
�v���o���Ă݂Ăł���
�S���́@�g��Ȃ�����
��������������
��
�{������
�܂���
�P�O�@�Ă��@�P�O�́@�P������
��×�P�Ƃ��Ă��@���ł���
�P���@log10 10
�ɂ���
�^���́@���Ɂ@�w���ɂ��ā@��荞���
���@���@������
�C�R�[���@������
�^���́@�C�R�[��
�Ƃ������Ƃ�
���O���@�O���Ă��܂���
�����܂ŗ�����
�����݂�����
Sn-1���@�����
��������
��ʍ�
�܂����Ă��@�w���̌v�Z��
S1���@���������Ƃ�
��ʍ�����
�Q���߁@�ȉ����@����
��ʍ�����
�������@���߂����̂�
S1����@���߂����̂Ɓ@��v�����̂�
�����
���䐔��́@��ʍ��̌����ǂ����
���x��
�a�̎����@���߂��ł���
���߂̂����܂ł́@�ρ@Pn�@�ƌ������̂�
�o�ė��܂���
Pn���@���͂��܂���
���߂́@�����́@�ς��@Pn
������
�����̂悤�Ȋ�����
Pn�|�P���@���߂�ł���
Pn�̎��́@�����@���|�P�ɂ��邶��i�C�X�J
��
����@���q��
Pn-1�@Pn�@�Ƃ����
�₭���ā@�o�����̂��@��ʍ��悎�Ԗ�
�@an
�l���@�������
a�����@���߂��
�w���̌v�Z��
�Q���߈ȍ~��
����
��
�|���Z�Ȃ̂�
a1��P1
�Q�C�R���߂Ă݂�
���䐔��́@�`���@�����Ă����̂�
�a�̌����Ɂ@�������
�v�Z��������i�C�X�J��
�Ȃ�
�}�C�i�X���@��u���ꂾ����
���q���@�}�C�i�X���@�o�Ă��邩��
����܂��ł�������
����
���́@��ʍ����@���߂�
����͂�
�Ȃ@�ʔ����`�Ȃ�ł���
a���|�P���@����Ă݂�ł���
�A���_�[���C���̂Ƃ���
a���|�P�̎��Ɂ@�u��������
��ʍ����@����Ȋ���
�ł��@�����ƈႤ�̂�
�������R
��������@������
�T�ł���
�Q���߁@a1=a2
�H�@�Ȃ̂Ł@�T
�R����
�T�Q
�S����
�T×�Q�̓��
�Ȃ̂�
��������Ɓ@����Ȋ�����
������Ɩʔ��������́@��ʍ��Ɂ@�Ȃ�܂����B
�@
�����ꂳ�܁`
�i�@���ꕔ�����@�ƒ�؉�����������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 21:58| ��l�̂��ї��Ƃ��@
2017�N12��01��
21013�@��l�̂��ї��Ƃ��@�@�@���䐔��ł���@����
��l�̂��ї��Ƃ�
�����́@�v�X�́@���Q
���䐔��ł���@����
�i�P�j�@�i�Q�j�@��
��肪����܂��ā@�ł���
�i�P�j����
�����߂����@
�萔×�@�����̎w���Ɂ@
�Ȃ��Ă�̂�
����́@
���䐔��炵����
��ʍ���
n ���ڂ����@�@�����@a×�@����́@n�|�P�@��ɂȂ�̂�
���̌`�Ɏ������݂����̂�����
�܂��@�Q�C�R�@���@���ׂĂ݂邶��i�C�X�J��
�P���߁@
�Q���߁@�R���߁@�f�V��
���ׂĂ݂�
�����@���@ab
�ȉ�
b���@����́@���䐔��
��
�����
��ʍ��̌`�Ɂ@�������݂����̂�
���߂Ɂ@�^����ꂽ����
���@�̂Ƃ�����@n�|�P�@�ɂ���ł���
��
a���@�́@�`�Ɂ@���ό`����
���߂Ɂ@�^����ꂽ�@���Ɂ@
�������
���|�P�@���@����
�ł�
���i�@����ĂȂ�����
�s�[���Ɓ@���Ȃ���ł���
�킽���́@���������܂��Ă�
������@�Ɓ[�@�����ł��@��
�E�Ɂ@��̓I�ȁ@�����Ł@����Ă݂邶��i�C�X�J
��
���́@�w���v�Z��
�ȒP�Ɂ@�Ȃ��Ă�
���́@���|�P�@���@�ł���
�����Q�ȏ�̎��́@��ʍ���
�����P�̎��́@����
�e���p
�����@ab�@����@���́@���䐔��
�i�Q�j�͂ł���
�a�̌�������
��ʍ����@���߂���̂�
������
�Q�C�R�@�������Ă݂��
�P�@�́@�a�́@����
�Q�̎�
�R�̎�
�����
����́@�a�́@������
���Ԗڂ܂Ł@���������̂���
����Ȃ�
���|�P�Ԗځ@�܂ő��������̂��@�����Ƃ�
��@���@�ԖڂɂȂ邶��i�C�X�J
�����Ł@�����@�Q�ȏ�łȂ���
S�@�́@n�|�P���@�O�@�ɂȂ��Ă܂��̂�
���@�́@�Q�ȏ���@������
�����Ɂ@�������
��ʍ��@���̂��Ԃ��@�T���
�܂����Ă��@�w���́@�v�Z����
���i����ĂȂ��̂�
�킽���́@�����Ă��܂��̂ł�
��
�@
�������݂����Ɂ@
����@�Ɓ[�@�����ł����@
�E�Ł@�������Ă݂Ă�
���S���@�m�F����
���[��
������ɂ���
�����@�Q�ȏ�̎���
��ʍ��́@����
��́@�����Z�̌����ł�
�����P�@�̎��́@���P�����P
�Ł@�����ł�
�����́@ab+c
������
���̐��@���䐔��Ɂ@�Ȃ邽�߂�
������
���P�����P
����o���@�����@ab+c ��
��ʍ��́@���́@�Q�ȏ�̂Ƃ���
���Q�@�ȉ����@����@���@������
�����P�Ł@�݂�
ab-a �@���@ab+c
�Ɓ@�������Ȃ�@��������
�����Ł@������
���Ă݂��
�����|a
�]�k�ł���
�����`�@���Ēm���Ă�H�@
�������ā@�����Ă�H�i�@SECA ���}�n�̃i�i�n��)
�r�K�X�K�����@�������
���肢��
�������@���m��
Z900RS�@���o�C�o���Ɂ@�R����
SECA�@������
��������
�������Ă܂���
�R�E���M�̂��Ƃ�
�i�@���ꕔ�����@�ƒ�؉�����������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 10:58| ��l�̂��ї��Ƃ��@
2017�N10��16��
�g������@���@�������
���߂͂�
���ʂ́@���C�_�[�@���Ǝv���Ă��̂�
�������l�@������
�����@���K��������
���`
�ߌ�����Ȃ��Ă������ǂ�

Gpz900R
����Ă݂�������
��́@������@�����Ă�l��
�J�X�^�����Ă��܂��X��������̂�
�����@�m�[�}����
�������낤��
�e���p
�X�^�C���́@�ǂ������Ȃ��[�E�E�E�E�E
 | �T�C�Y38�@TYPE G-1�@�v�W�����@�g���N���[�Y�@�g�b�v�K���@�R�b�N�s�b�gUSA COCKPIT USA �A�r���b�N�X ���i:103,680�~ |
�i�@���ꕔ�����@�ƒ�؉�����������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 09:17| �A�E�^�[
2017�N09��21��
21012 ��l�̂��ї��Ƃ��@��̐���
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��̐���@�Ƃ������Ƃ�
���䐔���
�����������ł���
��
���傤�͂�
���䐔��́@���߂́@���@���̘a��
��������́@���߂́@�����@���́@�a�Ɂ@���������Ƃ�
�ؖ�����ł�
�s���Ă݂܂��傤

���䐔��̕�����
���߂́@���@���̘a�̌�����
����@���@���@�P�łȂ����
�c�Ɂ@����ł�
��̌���

�^������
���䐔��@�́@1.9.81.729.�E�E�E�E�E
�����́@���ꂾ�Ɓ@�P������
��ʍ��́@�����Ɂ@����Ă�����
�Q����

�R����
�Q���Ԃ̔���@�����ɂ���
���߂Ă���
�����́@a�́@��
�����ł��邩��
����Ȋ�����
���o�[�X����
9

����X�́@���䐔��
�����͂P
�ꉞ
���Z��
�����@�P
�����@�Q

�����@�R
�����@�S
�Ȃ��

�悎���܂ł́@�a���@���߂��
��ʍ��́@������
�g��Ȃ����[�ǂ�
����Ƃ��@�����Ƃ�
����ׂ����������炳
��
�����ɓ����

���ꂪ�@���䐔���
���߂́@���@���̘a
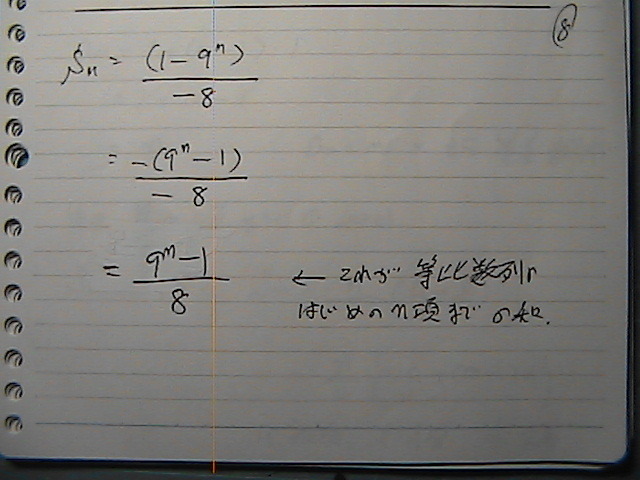
������
��������̕���
1.2.3.4.�E�E�E�E
�Ȃ̂�
�����@�P
�����P
�ꉞ
��ʍ���

��������
��
���̐����
��@���@���܂ł̘a��
��������

������ɂ���
�������
���������
����
��
����

���䐔��́@��@���@���܂ł̘a��
��������́@��@�����ځ@���܂ł́@�a��
���������Ƃ́@�ؖ�
������
���̂�
�����ڂ́@��肾����
�悎�@�����@
�悍�@���ɂ���
�����@�������@�Ⴄ����
�w�ǂ̏ꍇ�@�l���@�Ⴂ�܂�

���䐔��́@�����܂ł̘a�@��S
��������́@�����܂ł̘a�@��T
�Ƃ����

S=T�ɂȂ�Ƃ���
�����@���߂�
�i�@���̎��Ł@�j
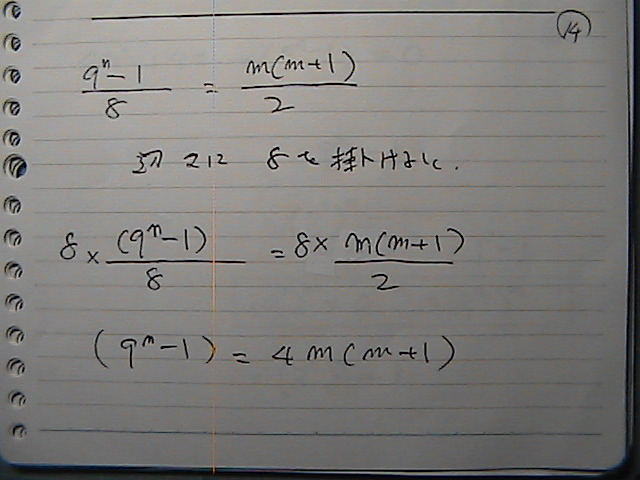
���́@���ɂȂ����ł���

�w����
���������Ȃ�
��������
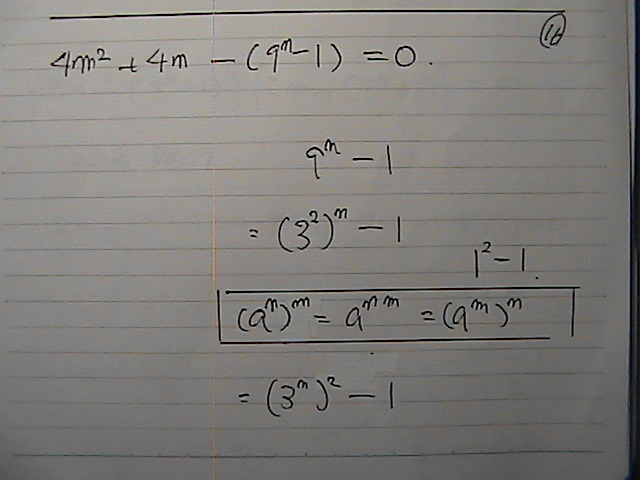
���̂Q�������@������������
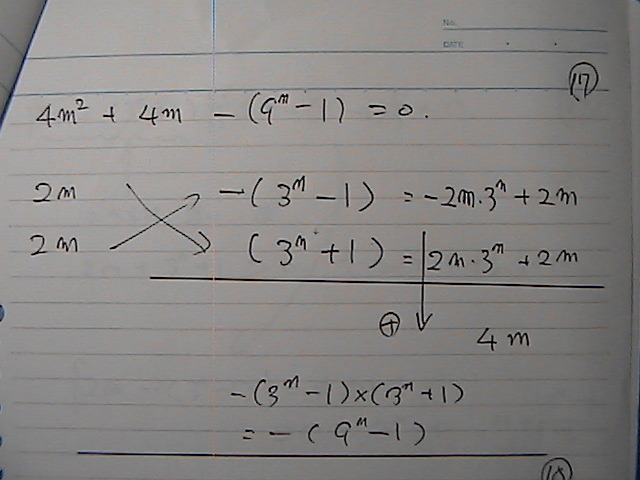
���O���@������
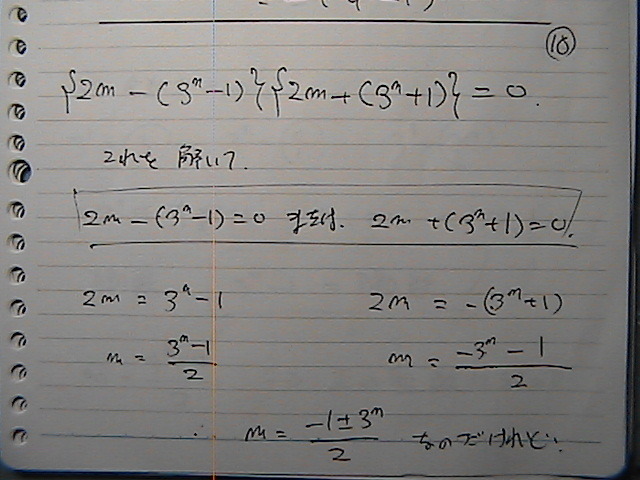
�Ł@���߂̊��ʂ̒���
����͂�
�O�Ƃ��Ɂ@�Ȃ炸
�˂Ɂ@��������
�s�K
���̊��ʂ̒���
���O�ɂȂ�Ƃ����@����

���q��
�����@�v�Z����Ɓ@�����ɂȂ��Ă�̂�
�i�@�R�̔{���@�|�@�P�@�Ł@�����@�j
������@�Q�Ŋ����
����
���̐���
���́@����ł�

�Ȃ������肵�Ȃ����炳
���̂Ȃ�
�����S�@��������
���́@����������ł���
�S�O�@������
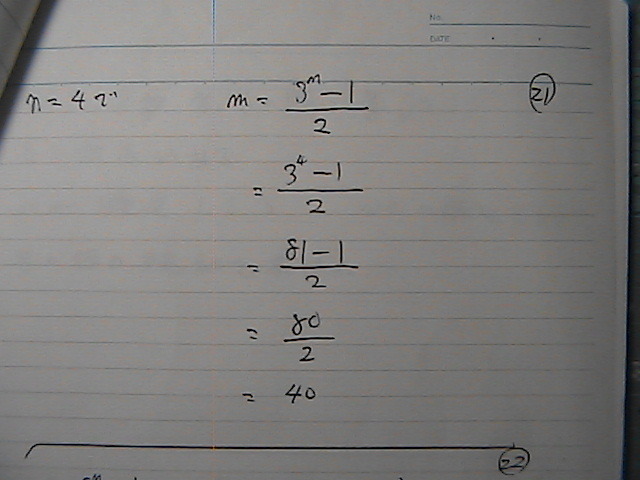
�����
�\���]���@����̘a�̌����ɑ������
���䐔��́@���߂̂S���̘a��
��������́@���߂̂S�O���̘a�ɂȂ�����
������
���́@���̎��́@�����Ă��
������@�������@���̐���
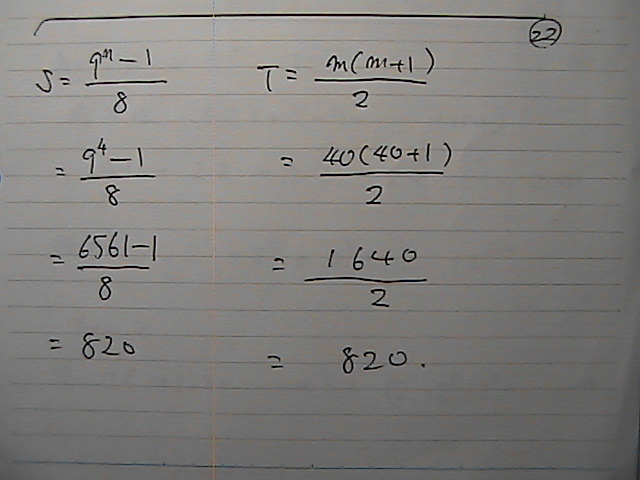
��̕ϐ��@���A���@��������
�W�����@����ł�
�����@�P����@�P�O�O�܂�
�����@�������
���̒l�́@���a�����߂Ȃ���

������
�����Ɂ@�������@�y�Ȃ���

�܂Ƃ��Ɂ@��炸�ɂł���
�����@��������
��Â@�������ā@���ׂ���
�O���́@��������
���������@�㔼�́@���䐔��Ɂ@�Ȃ��Ă邶��i�C�X�J
������
���ꂼ���
�a�̌�����

�v�Z���Ă��܂���
�d��@�ǂ��s��������
��
�܁[�@����Ȃ́@�d���
�����@�o�����Ƃ�
��
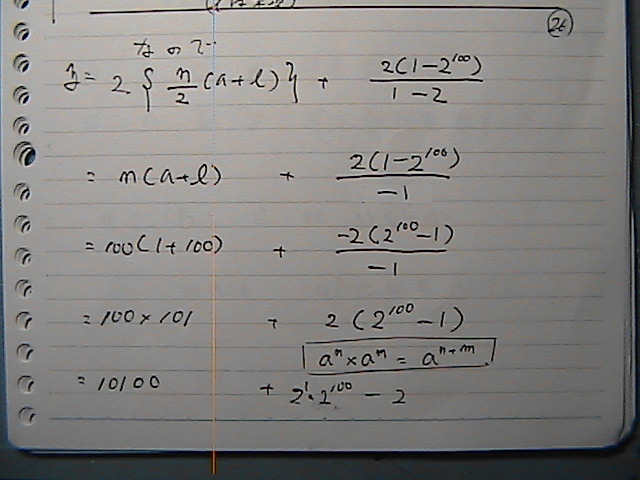
�w���́@���̂܂܂ł����Ƃ������Ƃ�
����
�|���̂�
�������肵�Ă��
�d��Ɂ@�����Ă邩��
�����Z���@������
�݂ȗl�́@�v�Z�́@�K�тĂ܂��H

���͂�
�����
���w�́@�Z���Z�Ƃ��@�D�������Ȗ��ł����
�����Ԃ�̂���
�o��\���́@����
��������
���䐔��
���������
�A������@�R�����@�����Ȃ���
����͂�
�Ȃ@���܂肪�������
���@���������
����́@����ȂɁ@������Ȃ�����
�e�X�g�Ɂ@�o��\���́@�����Ǝv������
��

����������
�������
�������@���ƒu���Ăł���
�Ł@�l�p�ň͂�

���䐔����
���䂪�@���
��������Ƃ��Ăł���

�l�p�Ł@�͂@��
���́@����@�A������
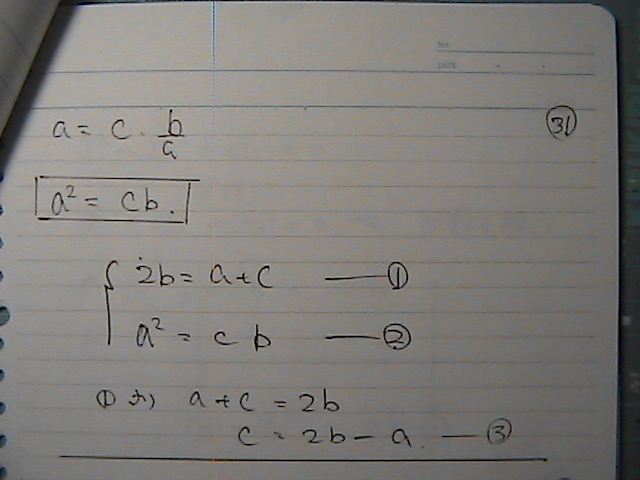
�ꕶ���@���������

�����@���������ł���
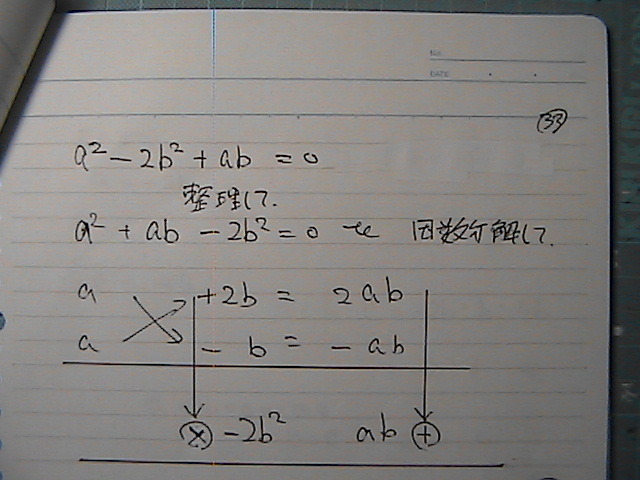
a�Ɓ@b�́@�W���@�܂��͂�
�Q�ʂ�
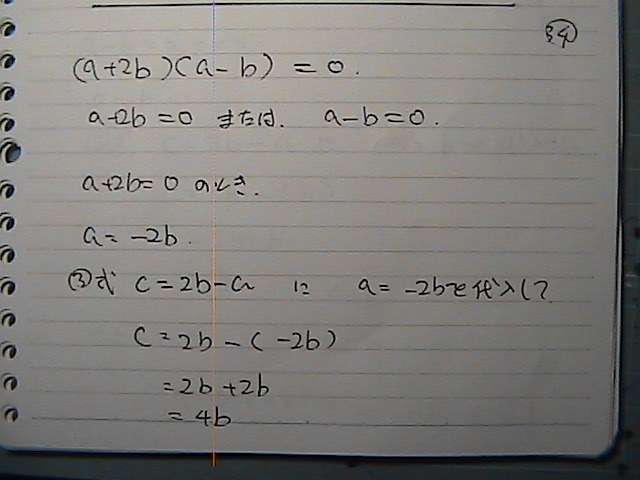
a���|�Q���@�̎��́@�����@�S��
a:b:c = -2:1:4
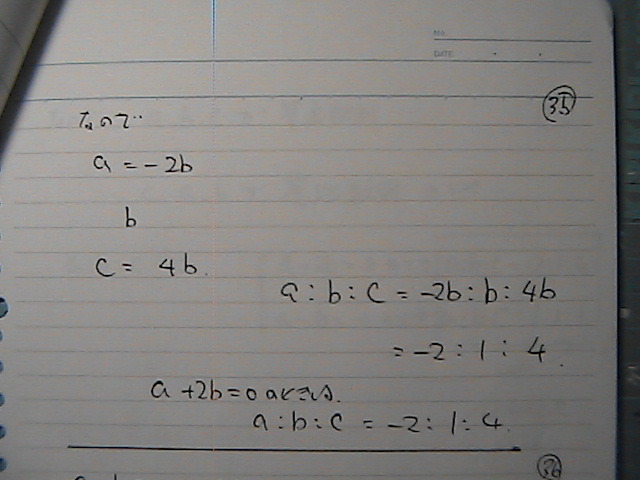
a=b�̎���
��������
a=b=c
a:b:c ���@�P�F�P�F�P

�Ȃ̂�
�����́@�Q�ʂ�

���͂ł���
��́@���@�����ł���
���̐����
�Q���ԖڂƁ@�@���Ԗځ@�Ɓ@�P���@�������@�オ
���鐮���Ɂ@�Ȃ邱�Ƃ��@�ؖ�����

a�̐����
�Q���Ԗڂ́@�P���@�Q�����`������
���䐔��́@�a�̌`��
����킹��
����Ȃ�

�����Ɂ@����Čv�Z����@����
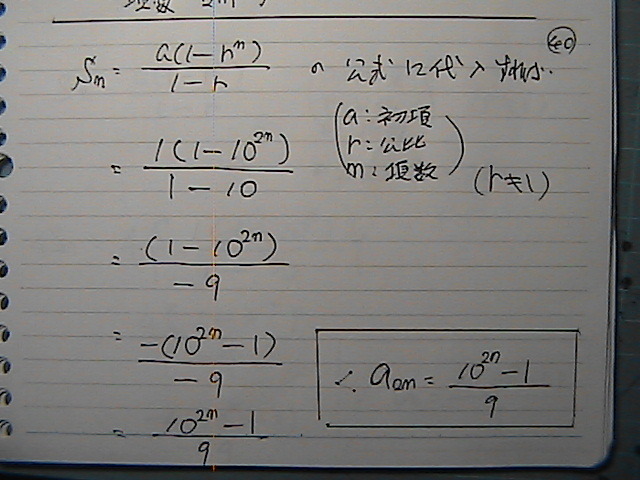
���̕���
���Ԗڂ́@
�S���@�����`������
���ό`�����
����@���䐔��̂����܂ł̘a�́@�S�{

�����Ɂ@������
��

��@�́@���Ɂ@�������i�C�X�J

��
�����
�R�ɂȂ���
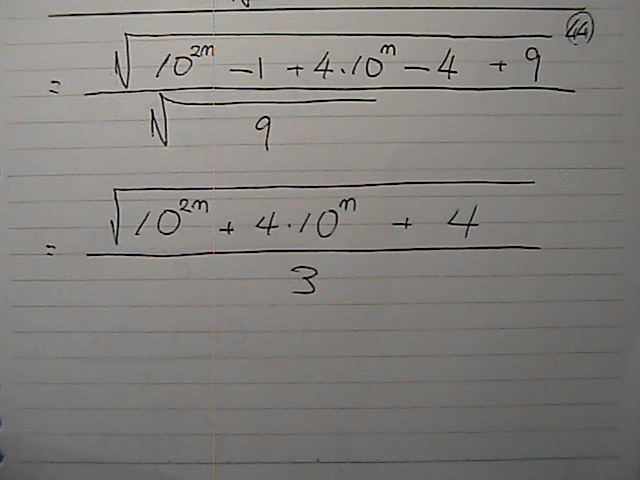
���q�́@���Ɓ@���������ŗ���
���ʂ́@�Q�悾����
�オ�@�O���
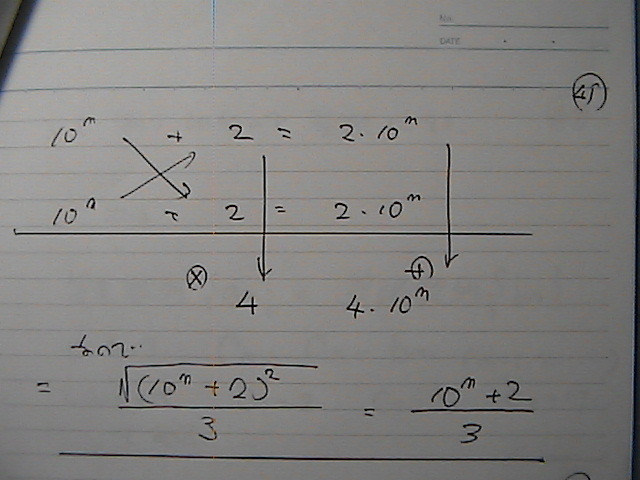
��
���ό`�����
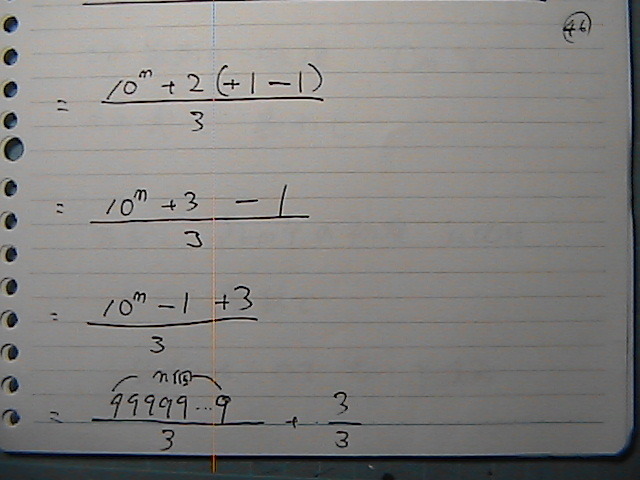
�R�Ł@�����ā@�����Ɂ@�Ȃ���̂Ɂ@�P�𑫂��`�Ȃ̂�
�����ɂȂ�
����ł����Ƃ��Ă�������
�Ł@���͂�

��������an
���䐔��bn
��������
�����@�Ƃ��������
�����@���@an + bn
��
���P���@�Q�@�A�@�@���Q���@�T�A�@���R���P�V�@�A��������
�����@�����@���@�̎���
�\��
�������@bn�́@�����@�����
���ɐ�����
����́@�O�ł͂Ȃ�

����ȂɁ@����l���Ȃ��Ă�
�悳��������
���Ԃ�@�������@�������Ă���
��
�������������Ă����܂���

��
����ȂɁ@����@�Ȃ�����
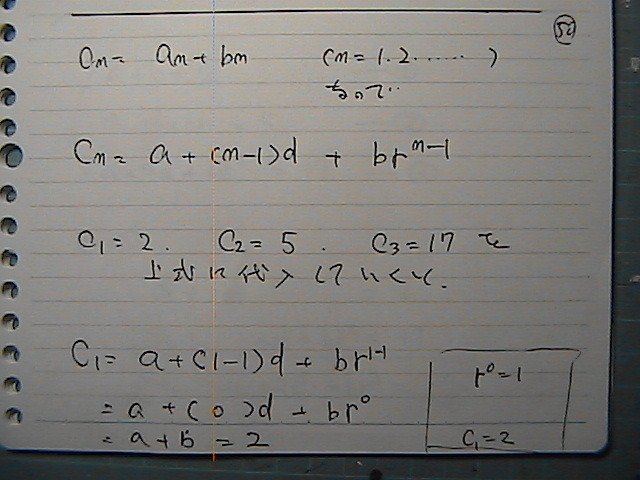
�����@���Ɂ@�l�������Ă���
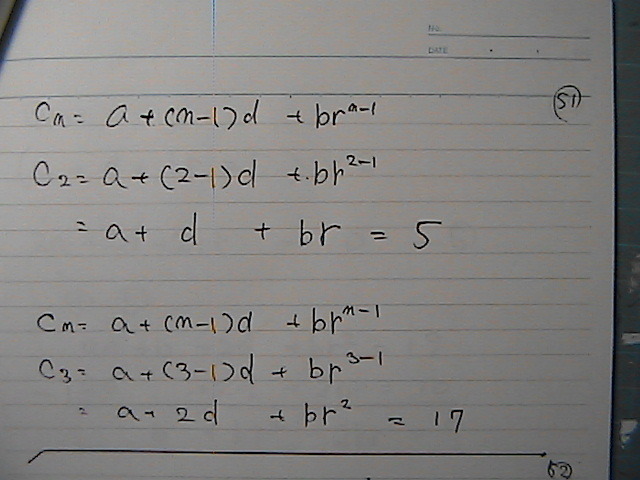
�A���ȁ@�����o�ė���
�ł���
�Ȃ@���������Ƃ�����
�����̐����
�A���̎��̐���
����Ȃ�
�H
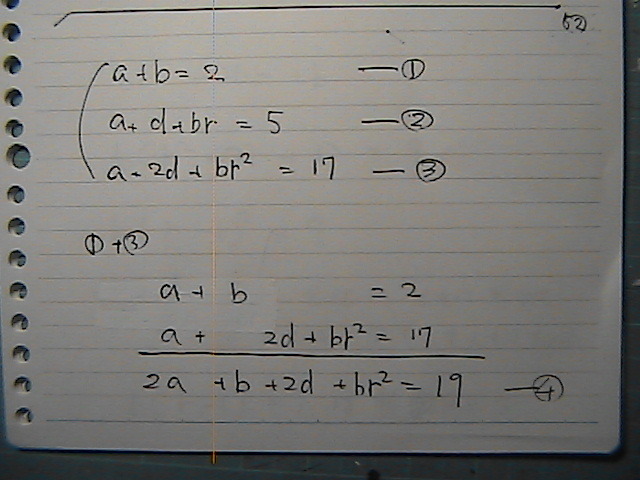
��������@�ǁ[���邩��
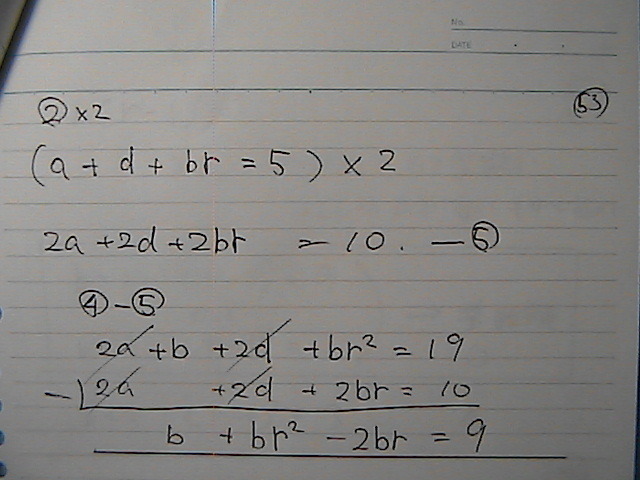
��蕶�Ɂ@����@�����́@������
�ibn�́@�����@����́@������
����́@�O�ł͂Ȃ��j
����������
����킳
������
�̂���

��̐������@�|���ā@�X�ɂȂ���̂�
�������@���������̂��@�T����

�������@������
�����́@�����@����́@������
r�́@�O�ł́@�Ȃ�
�Ȃ���
�Ȃ@����@�R���@�o�ė�������
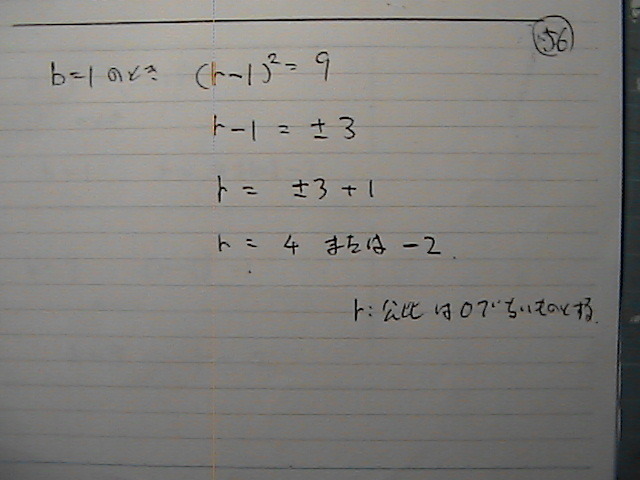
�l�łĂ�������
�����Ɂ@�K���Ȃ����̂�
����

�R�ʂ�
��[�@�T���g���[
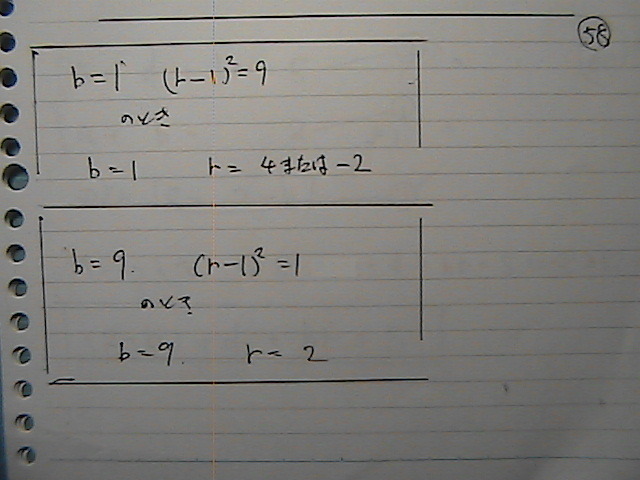
�����܂ł́@������
�t�@���u���O�@
A�W�l�b�g
�y�V�@
�E�E�E

������Ƃ�
�����ł���
�o�ė��Ă��@�A���̎���
�����@���@�A�@���@���@�������
a,d�@���@���@���߂�
an bn �́@��ʍ����@������
�����@���@an + bn
��
�R�Ƃ���@�����@�����ł�

⓵�f���@�A���Ɂ@�������
���@���@�Ɂ@���ꂼ��
�l���@�R�ʂ������Ă���

�P�ʂ��
a=1
�����O
����
�O�ł��@�I�b�P�C
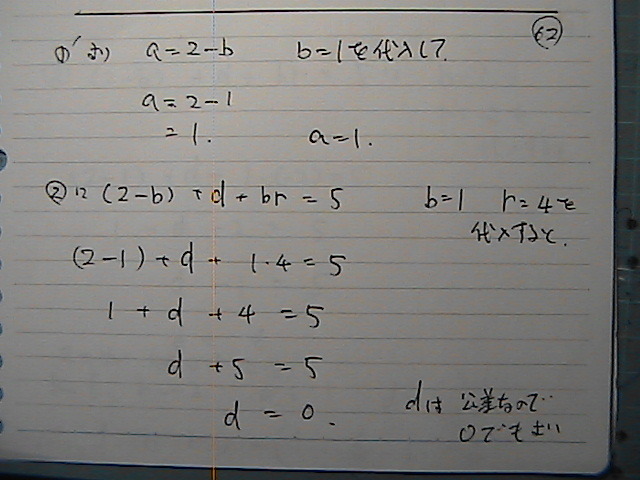
��g��
����
�����P�@����-2�̎�
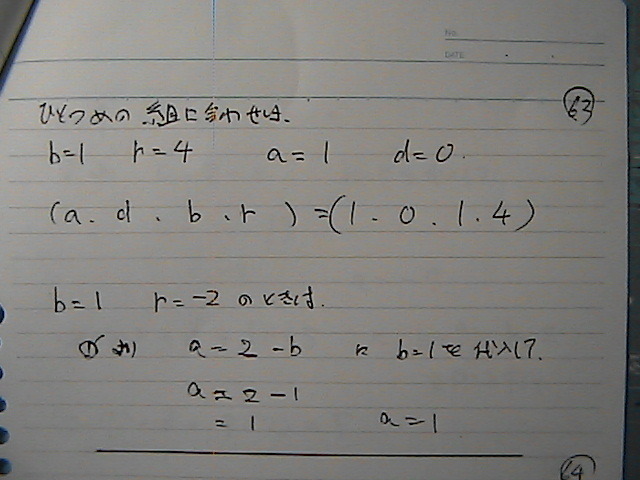
a���P
�����@�U
��g�ڂ́@����
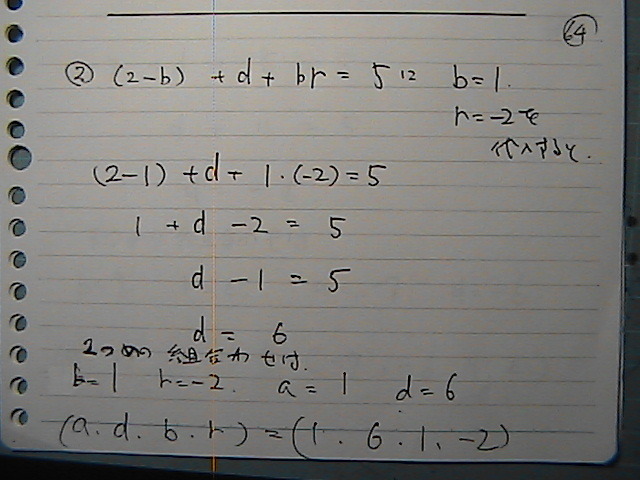
�R�g��
�����X�@�����Q�̎�
a��-7
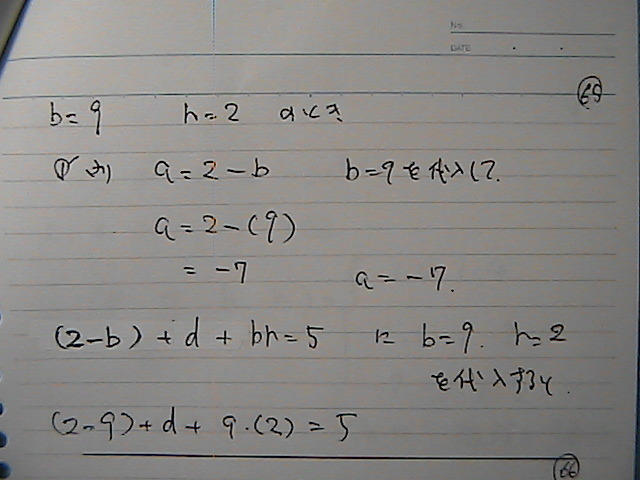
����-6
�R�g�ڂ͂���

�S���@�o��������Ƃ���

�����@�́@���Ɂ@������Ă���
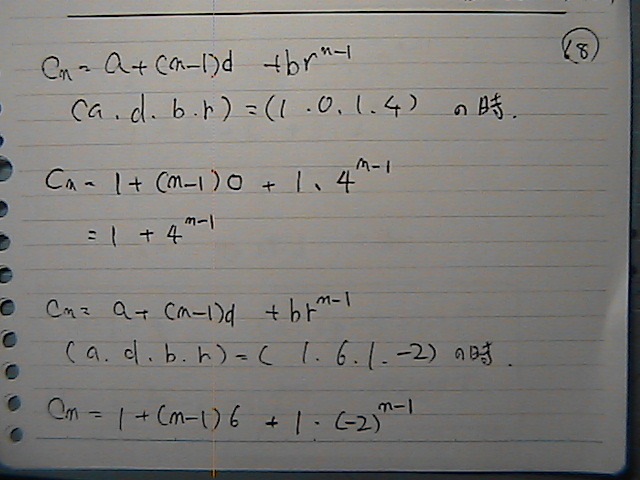
����Ƃ���[
�����炳
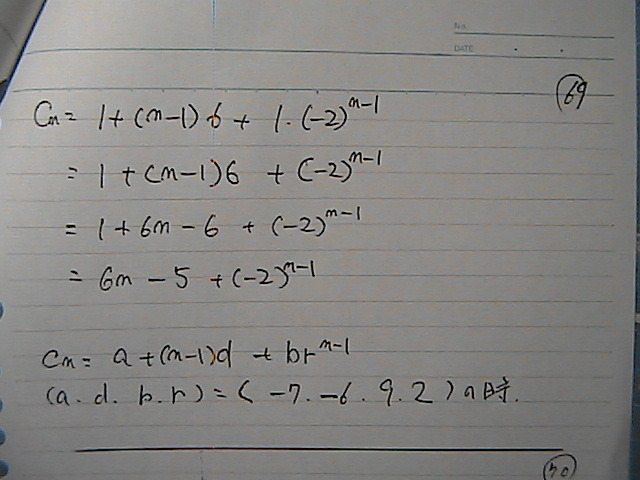
�����@�ŋ߁@�T�~�[�ɂȂ��Ă��Ă邯��
���݂܂���
�v���o����
�Z���`�Ɂ@�Ȃ��ĂĂ�
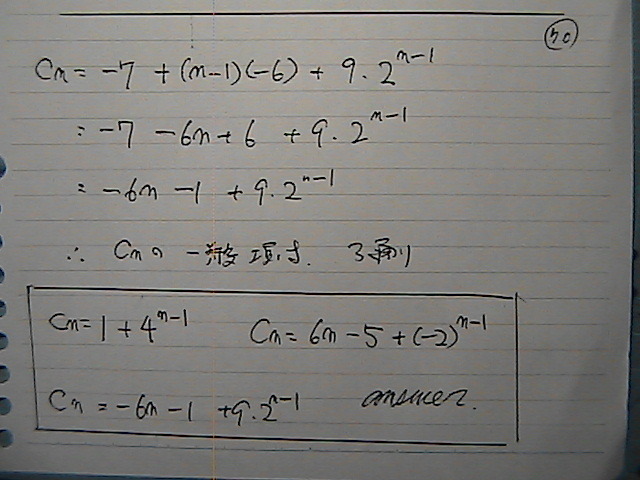
�푈�Ɓ@�푈�̂��\���@�������Ă��܂���
��Ɂ@�M��������̂�
�K���ł�
���Ȃ����Ɂ@�킽���̕�����
�c������
�킽�����@�^������̂�
�����@�^������̂Ƃ́@�Ⴄ
���Ȃ�����
�S���@�������Ắ@�Ȃ�Ȃ�
�����������@�Ȃ����Ȃ��悤��
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
��̐���@�Ƃ������Ƃ�
���䐔���
�����������ł���
��
���傤�͂�
���䐔��́@���߂́@���@���̘a��
��������́@���߂́@�����@���́@�a�Ɂ@���������Ƃ�
�ؖ�����ł�
�s���Ă݂܂��傤
���䐔��̕�����
���߂́@���@���̘a�̌�����
����@���@���@�P�łȂ����
�c�Ɂ@����ł�
��̌���
�^������
���䐔��@�́@1.9.81.729.�E�E�E�E�E
�����́@���ꂾ�Ɓ@�P������
��ʍ��́@�����Ɂ@����Ă�����
�Q����
�R����
�Q���Ԃ̔���@�����ɂ���
���߂Ă���
�����́@a�́@��
�����ł��邩��
����Ȋ�����
���o�[�X����
9
����X�́@���䐔��
�����͂P
�ꉞ
���Z��
�����@�P
�����@�Q
�����@�R
�����@�S
�Ȃ��
�悎���܂ł́@�a���@���߂��
��ʍ��́@������
�g��Ȃ����[�ǂ�
����Ƃ��@�����Ƃ�
����ׂ����������炳
��
�����ɓ����
���ꂪ�@���䐔���
���߂́@���@���̘a
������
��������̕���
1.2.3.4.�E�E�E�E
�Ȃ̂�
�����@�P
�����P
�ꉞ
��ʍ���
��������
��
���̐����
��@���@���܂ł̘a��
��������
������ɂ���
�������
���������
����
��
����
���䐔��́@��@���@���܂ł̘a��
��������́@��@�����ځ@���܂ł́@�a��
���������Ƃ́@�ؖ�
������
���̂�
�����ڂ́@��肾����
�悎�@�����@
�悍�@���ɂ���
�����@�������@�Ⴄ����
�w�ǂ̏ꍇ�@�l���@�Ⴂ�܂�
���䐔��́@�����܂ł̘a�@��S
��������́@�����܂ł̘a�@��T
�Ƃ����
S=T�ɂȂ�Ƃ���
�����@���߂�
�i�@���̎��Ł@�j
���́@���ɂȂ����ł���
�w����
���������Ȃ�
��������
���̂Q�������@������������
���O���@������
�Ł@���߂̊��ʂ̒���
����͂�
�O�Ƃ��Ɂ@�Ȃ炸
�˂Ɂ@��������
�s�K
���̊��ʂ̒���
���O�ɂȂ�Ƃ����@����
���q��
�����@�v�Z����Ɓ@�����ɂȂ��Ă�̂�
�i�@�R�̔{���@�|�@�P�@�Ł@�����@�j
������@�Q�Ŋ����
����
���̐���
���́@����ł�
�Ȃ������肵�Ȃ����炳
���̂Ȃ�
�����S�@��������
���́@����������ł���
�S�O�@������
�����
�\���]���@����̘a�̌����ɑ������
���䐔��́@���߂̂S���̘a��
��������́@���߂̂S�O���̘a�ɂȂ�����
������
���́@���̎��́@�����Ă��
������@�������@���̐���
��̕ϐ��@���A���@��������
�W�����@����ł�
�����@�P����@�P�O�O�܂�
�����@�������
���̒l�́@���a�����߂Ȃ���
������
�����Ɂ@�������@�y�Ȃ���
�܂Ƃ��Ɂ@��炸�ɂł���
�����@��������
��Â@�������ā@���ׂ���
�O���́@��������
���������@�㔼�́@���䐔��Ɂ@�Ȃ��Ă邶��i�C�X�J
������
���ꂼ���
�a�̌�����
�v�Z���Ă��܂���
�d��@�ǂ��s��������
��
�܁[�@����Ȃ́@�d���
�����@�o�����Ƃ�
��
�w���́@���̂܂܂ł����Ƃ������Ƃ�
����
�|���̂�
�������肵�Ă��
�d��Ɂ@�����Ă邩��
�����Z���@������
�݂ȗl�́@�v�Z�́@�K�тĂ܂��H
���͂�
�����
���w�́@�Z���Z�Ƃ��@�D�������Ȗ��ł����
�����Ԃ�̂���
�o��\���́@����
��������
���䐔��
���������
�A������@�R�����@�����Ȃ���
����͂�
�Ȃ@���܂肪�������
���@���������
����́@����ȂɁ@������Ȃ�����
�e�X�g�Ɂ@�o��\���́@�����Ǝv������
��
����������
�������
�������@���ƒu���Ăł���
�Ł@�l�p�ň͂�
���䐔����
���䂪�@���
��������Ƃ��Ăł���
�l�p�Ł@�͂@��
���́@����@�A������
�ꕶ���@���������
�����@���������ł���
a�Ɓ@b�́@�W���@�܂��͂�
�Q�ʂ�
a���|�Q���@�̎��́@�����@�S��
a:b:c = -2:1:4
a=b�̎���
��������
a=b=c
a:b:c ���@�P�F�P�F�P
�Ȃ̂�
�����́@�Q�ʂ�
���͂ł���
��́@���@�����ł���
���̐����
�Q���ԖڂƁ@�@���Ԗځ@�Ɓ@�P���@�������@�オ
���鐮���Ɂ@�Ȃ邱�Ƃ��@�ؖ�����
a�̐����
�Q���Ԗڂ́@�P���@�Q�����`������
���䐔��́@�a�̌`��
����킹��
����Ȃ�
�����Ɂ@����Čv�Z����@����
���̕���
���Ԗڂ́@
�S���@�����`������
���ό`�����
����@���䐔��̂����܂ł̘a�́@�S�{
�����Ɂ@������
��
��@�́@���Ɂ@�������i�C�X�J
��
�����
�R�ɂȂ���
���q�́@���Ɓ@���������ŗ���
���ʂ́@�Q�悾����
�オ�@�O���
��
���ό`�����
�R�Ł@�����ā@�����Ɂ@�Ȃ���̂Ɂ@�P�𑫂��`�Ȃ̂�
�����ɂȂ�
����ł����Ƃ��Ă�������
�Ł@���͂�
��������an
���䐔��bn
��������
�����@�Ƃ��������
�����@���@an + bn
��
���P���@�Q�@�A�@�@���Q���@�T�A�@���R���P�V�@�A��������
�����@�����@���@�̎���
�\��
�������@bn�́@�����@�����
���ɐ�����
����́@�O�ł͂Ȃ�
����ȂɁ@����l���Ȃ��Ă�
�悳��������
���Ԃ�@�������@�������Ă���
��
�������������Ă����܂���
��
����ȂɁ@����@�Ȃ�����
�����@���Ɂ@�l�������Ă���
�A���ȁ@�����o�ė���
�ł���
�Ȃ@���������Ƃ�����
�����̐����
�A���̎��̐���
����Ȃ�
�H
��������@�ǁ[���邩��
��蕶�Ɂ@����@�����́@������
�ibn�́@�����@����́@������
����́@�O�ł͂Ȃ��j
����������
����킳
������
�̂���
��̐������@�|���ā@�X�ɂȂ���̂�
�������@���������̂��@�T����
�������@������
�����́@�����@����́@������
r�́@�O�ł́@�Ȃ�
�Ȃ���
�Ȃ@����@�R���@�o�ė�������
�l�łĂ�������
�����Ɂ@�K���Ȃ����̂�
����
�R�ʂ�
��[�@�T���g���[
�����܂ł́@������
�t�@���u���O�@
A�W�l�b�g
�y�V�@
�E�E�E
������Ƃ�
�����ł���
�o�ė��Ă��@�A���̎���
�����@���@�A�@���@���@�������
a,d�@���@���@���߂�
an bn �́@��ʍ����@������
�����@���@an + bn
��
�R�Ƃ���@�����@�����ł�
⓵�f���@�A���Ɂ@�������
���@���@�Ɂ@���ꂼ��
�l���@�R�ʂ������Ă���
�P�ʂ��
a=1
�����O
����
�O�ł��@�I�b�P�C
��g��
����
�����P�@����-2�̎�
a���P
�����@�U
��g�ڂ́@����
�R�g��
�����X�@�����Q�̎�
a��-7
����-6
�R�g�ڂ͂���
�S���@�o��������Ƃ���
�����@�́@���Ɂ@������Ă���
����Ƃ���[
�����炳
�����@�ŋ߁@�T�~�[�ɂȂ��Ă��Ă邯��
���݂܂���
�v���o����
�Z���`�Ɂ@�Ȃ��ĂĂ�
�푈�Ɓ@�푈�̂��\���@�������Ă��܂���
��Ɂ@�M��������̂�
�K���ł�
���Ȃ����Ɂ@�킽���̕�����
�c������
�킽�����@�^������̂�
�����@�^������̂Ƃ́@�Ⴄ
���Ȃ�����
�S���@�������Ắ@�Ȃ�Ȃ�
�����������@�Ȃ����Ȃ��悤��
posted by moriamelihu at 19:50| ��l�̂��ї��Ƃ��@
�ŐV�L��
(11/04)233006�@��l�̂��ї��Ƃ��@���̋Ɍ��l�@�W���̌���
(11/01)233005�@��l�̂��ї��Ƃ��@f�ix�j�̓��������́@���̋Ɍ��l
(09/10)233004�@���̋Ɍ��l�@�C�@�Ɍ��l�Ȃ��@�́@�ꍇ
(09/03)233003 ��l�̂��ї��Ƃ��@���̋Ɍ��l3
(09/02)��l�̂��ї��Ƃ��@233002�@���̋Ɍ��l�@�A
(11/01)233005�@��l�̂��ї��Ƃ��@f�ix�j�̓��������́@���̋Ɍ��l
(09/10)233004�@���̋Ɍ��l�@�C�@�Ɍ��l�Ȃ��@�́@�ꍇ
(09/03)233003 ��l�̂��ї��Ƃ��@���̋Ɍ��l3
(09/02)��l�̂��ї��Ƃ��@233002�@���̋Ɍ��l�@�A
�^�O�N���E�h
�@�X���Ɓ@�ڐ� ��d�����Ɓ@�]�� �X���Ɓ@�ڐ��@�@�i�@�NjL����@�j �蒼���Ɂ@�ڂ�������@ �����̒�` ���ϕω��� �����W���@ �����W���@�Ɓ@�Ɍ��l �����W���̑��� �����@�@ �����@�@�@�@��d�����@�Ɓ@�]�� �ڐ��Ɋւ����� ���� �Ȑ���́@�ڐ��@�@�� �Ȑ��O�@�́@�_����@�������@�ڐ��@ �Ȑ��O�@�̓_����́@�ڐ��@�@���@�ޑ� �����Ɓ@�Ȑ��́@�ڂ���@�����@�i�@�J�R�����@�S�[�@�j �����Ɓ@�Ȑ��́@�ڂ�������@�ޑ�ł� �Q�Ȑ����@�ڂ�������@�ޑ� �Q�Ȑ����ڂ������
�J�e�S���[�A�[�J�C�u
�ʐ^�M�������[
����
���ʃA�[�J�C�u
2024�N11��(2)
2024�N09��(3)
2024�N08��(2)
2023�N10��(1)
2023�N09��(1)
2023�N08��(1)
2023�N07��(3)
2023�N06��(3)
2023�N05��(1)
2019�N08��(1)
2019�N07��(1)
2019�N05��(5)
2019�N01��(1)
2018�N12��(8)
2018�N10��(5)
2018�N09��(2)
2018�N08��(3)
2018�N07��(12)
2018�N06��(3)
2018�N05��(4)
2024�N09��(3)
2024�N08��(2)
2023�N10��(1)
2023�N09��(1)
2023�N08��(1)
2023�N07��(3)
2023�N06��(3)
2023�N05��(1)
2019�N08��(1)
2019�N07��(1)
2019�N05��(5)
2019�N01��(1)
2018�N12��(8)
2018�N10��(5)
2018�N09��(2)
2018�N08��(3)
2018�N07��(12)
2018�N06��(3)
2018�N05��(4)
���ʃA�[�J�C�u
�v���t�B�[��