2018�N04��17��
2B07005 ��l�̂��ї��Ƃ��@�{�p�̌����@�i�Q�j
�J�̓��́@�X���[���C�t�̕���
�{�p�̌����i�Q�j�@�Ȃ̂ł���
sin���@+ cos���@���@a
�@
���^����ꂽ��
sin a cos a�@���@���
�������ł�
��肪�@�����Ăł���
���̒l�����߂Ȃ���

(�P)�́@sin�QA���@���߂�
�����̔{�p�̌������g������i�C�X�J
�������܁@sin a cos a
���@�����������@�o�ė���
sin�QA���Qsin a cos a
��ӂ���
sinA + cosA= 1/2
�Ȃ̂�
������@���������
sin���A �@�@�@cos���A�@�́@�ԂɁ@
�@�Qsin a cos a
���ꂪ�@�S�̂Ł@1/4�Ȃ̂�����
sin���A �@�@�@cos���A�@�́@�P�ɂȂ���
�Qsin a cos a���@-3/4

������
���߂�̂�
sin2A �Ȃ̂�����
sin2A�@���@�Qsin a cos a���@-3/4
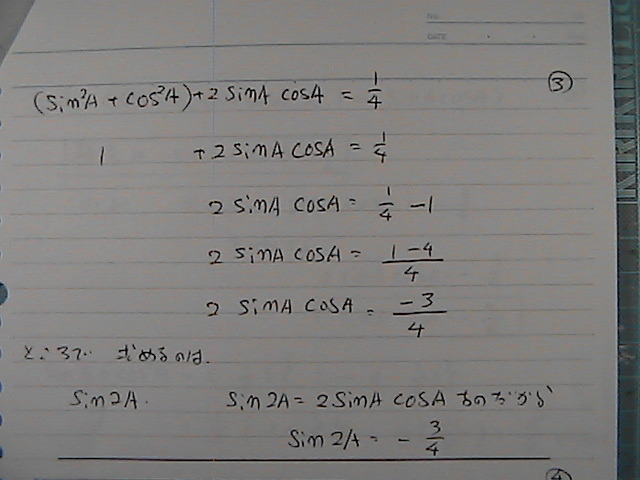
(�Q)��
�R��+�R��̂�����
���������́@���́@�������g����

���@���́@1��
�ւĂ���
��ӂ��
�l���������Ă�@�Ƃ���
�i�P�j�́@������
�Qsin a cos a���@-3/4�Ȃ̂�����
sin a cos a���@-3/8
�������@�������
11/16
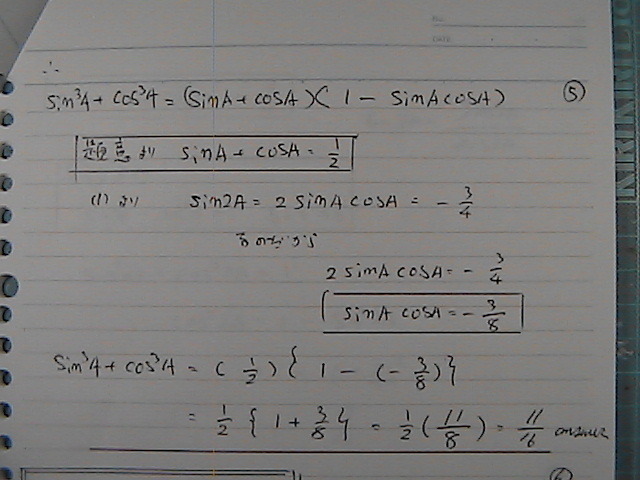
tan2A�@���@���߂�
����͂�
���������邯��
sin cos�@�Ł@�\�����@�̕���
�悳����������
����i�C�X�J

sin2A�@���@-3/4
���@�킩�Ă邩��
�����������g����

cos�QA=�@�}�@��7/4
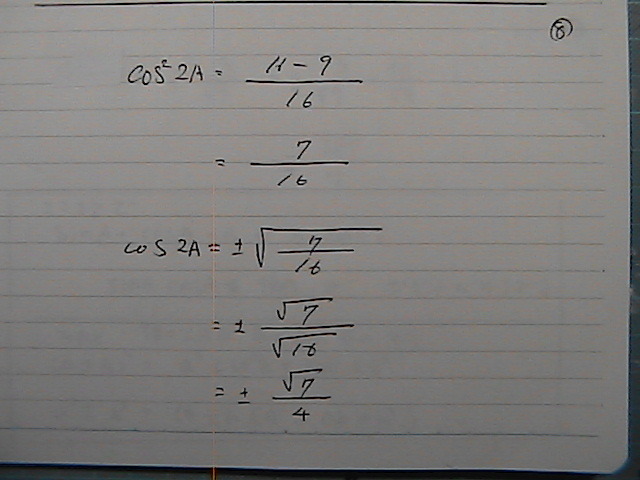
���q�́@�}�C�i�X���@�l�����
�}�C�i�X�v���X�@�ɂȂ���
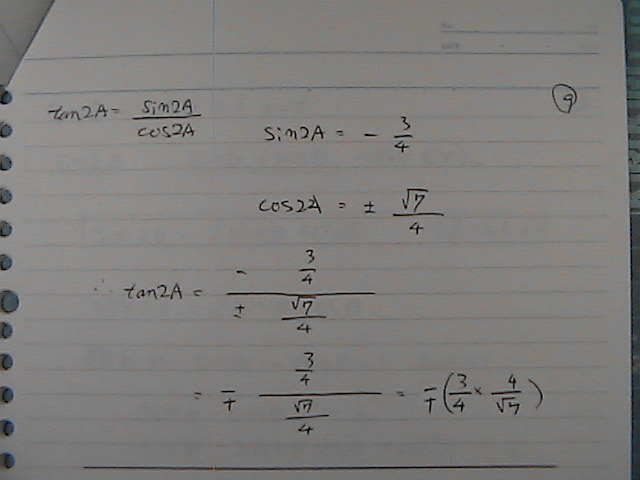
����́@���[�g���@�͂�����
���[�g���@���q�Ɂ@�����Ă���
�}�C�i�X�v���X�R��7/7

�ȏ���@���܂��܂���
�����@���ɍs���Ă݂܂��傤
�[���ł���
sin ���@-�@cos ���@���@1�@�̎�
sin 2���@�A�@sin ���@+�@cos�@���@�A
�̒l�����߂Ȃ���
�܂�
sin���@+ cos���@���@a
�@
���^����ꂽ��
sin a cos a�@���@���
��
sin2���@���@�Qsin��cos��
sin ���@-�@cos ���@���@1�@���@���������
sin��惦�@�@�@cos��惦�@�́@�ԂɁ@
�@-�Qsin ��cos��
���@�o�ė��ā@�����@�S�̂Ł@�P�Ȃ̂�

����������
0
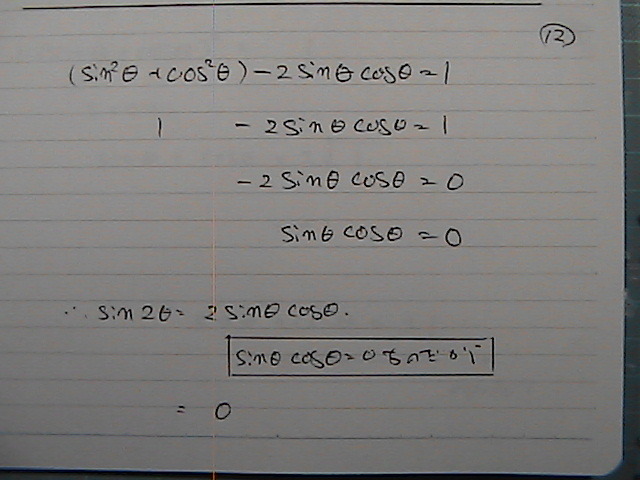
����
sin���@+�@cos��
��
���������
sin��惦�@+�@cos��惦�@+�@�Qsin ��cos����
�isin���@+�@cos���j�̓�悪
�P+�Qsin ��cos���@�Ȃ̂�����
�������@�Qsin ��cos�����@0�@�������̂�
�P
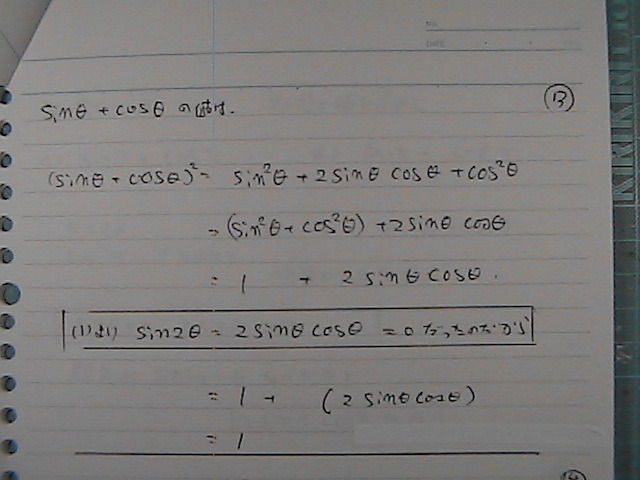
��
������
�����ł́@����܂����
���������@���߂Ăł���
�}1
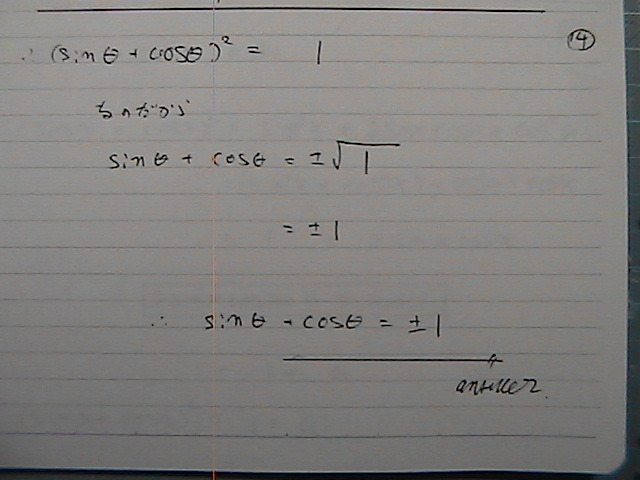
sin2x=a �̎��@���̒l��
���߂�
(1)sin x + cos x (2) tan x + cot x
�܂��ł���
�i�P�j
�Q���@�Ɓ@���@���@���݂��Ă�̂�
�����̔{�p�̌�����
sin2x=�Qsin �� cos ��
��ӂ��@���ꂪ�@��a�Ȃ̂�����
�Qsin �� cos ����a

(1)sin x + cos x
���@��������
�������������@�P+�@�Qsin �� cos ��
�ɂȂ�̂�
�isin x + cos x�j�̓�悪�@1+a

��������
�v���X�}�C�i�X�Ł�i1+a)
(2) tan x + cot x
�́@sin cos
�Ł@�l���ā@�ʕ�����

�Qsin �� cos ����a�Ȃ̂�����
sin �� cos ����a/2

���ʂ͂�����
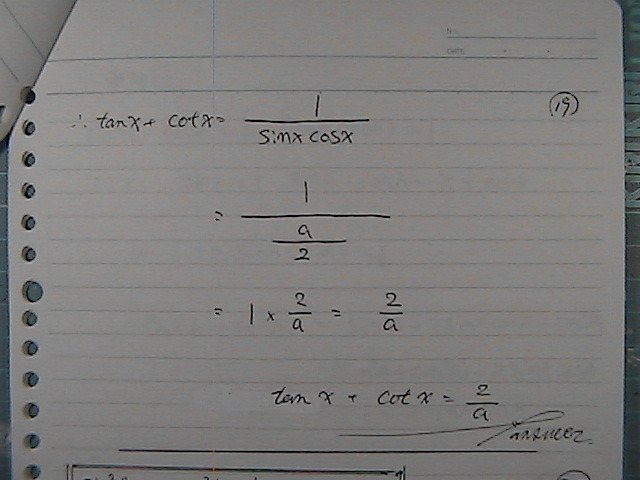
�R��\�R�恁�P���@�^�����Ă�
sinA�@-�@cosA���@���߂�
������
�[��������ł���
���Ȃ�@���ԂȂ����Ăł�
�������́@���������ł���
�����܂ł́@�ǂ�����

�����ł�
sinA�@-�@cosA���@���ƒu������
�����
sinA�@-�@cosA���������
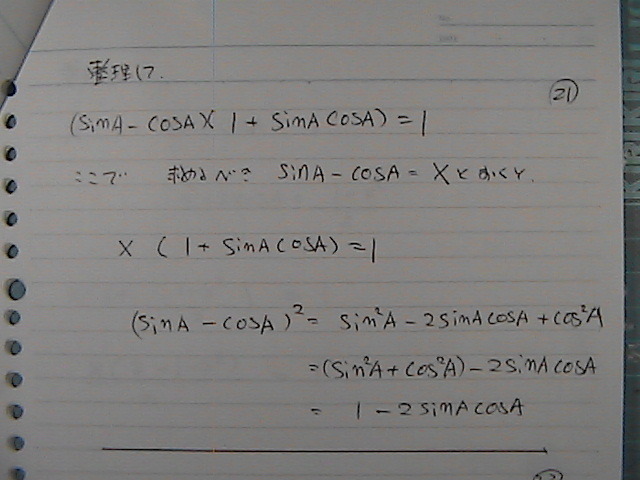
������
�������Ă��܂���
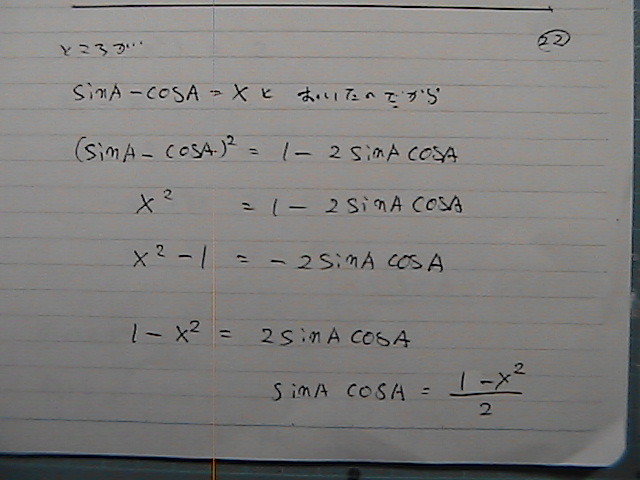
���̌`�́@�R��������
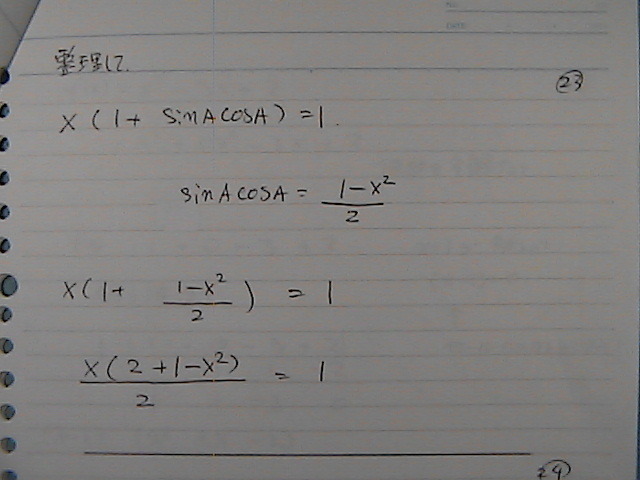
��������
�o�Ă��������@���i���j�@�Ƃł�������
���Q�́@�Öق̗�����
���P�̑S�͈͂��@�����Ă��܂��̂�
���c�����@����Ɓ@�i�߂Ȃ��@�ꍇ���@����܂���
�����́@�������傾��
�����藝���g����
��������
�����P�̎��@f(x)���O������
�i���|�P�j�@�Ł@�������
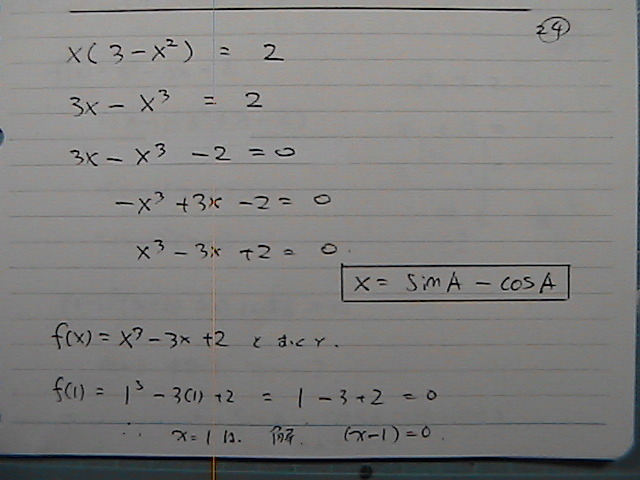
�W�����@��������
�Ȃ��Q��̍��́@�O�ɂ���
�g�����@��
�����藝�́@�����Ł@����
���i�P�j
�i���|�P�j���O
���������@�ς���Ɓ@�C�R�[���[���ɂȂ�@���Ł@�����

��
�����@���̂�������
���������ł�������
������
����1�@�܂��́@-2�@�Ȃ̂ł���
�������
�҂����ł�
��ȗ\����
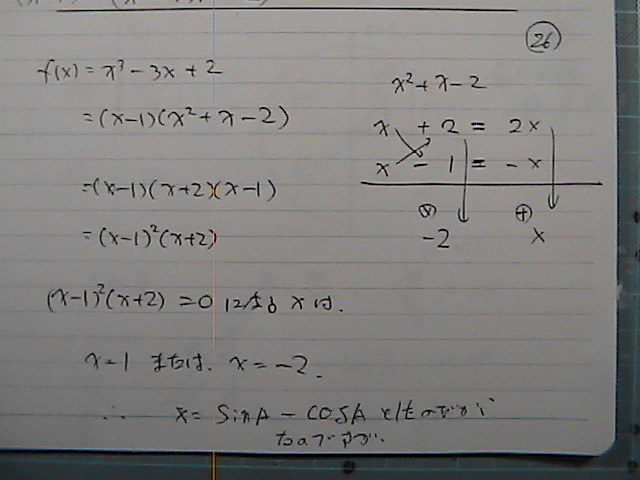
���̂ł���
���́@�����̂Ƃ����
����͂�
�����@�Ⴄ�`�ɂ��@��������������
���Ă���Ȃ��I�H�ɂȂ��ĂāH�H
���`�`�`�`
��������
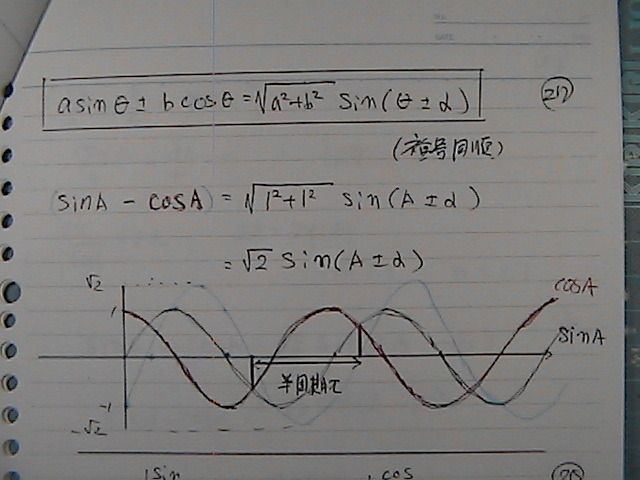
�ő�U����
�}��2
���`�`�`�`
����́@���́@�ǂ��Ȃ��������
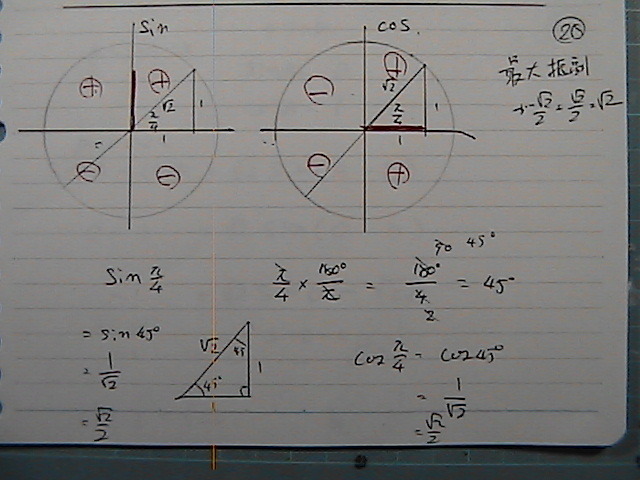
�O���t����
���������@������
���ʎ����́@sin�́@�Q�@�����炳
��Βla���P
a���}�P
�p�x��
��ʓI�Ȃ��̂��@���߂��`�Ɂ@�����

�O���t����@�O���t��̂P�_���@���
������@��
A=0�̎�
sinA=0 cosA=1
���@�������

sinA�@-�@cosA�@���@��2�@�Esin ( A - 45 )

�Ȃ̂ł���
�i�^��
�ő�U���́@��Βl���@��2�ȉ�
��2�́@�@1.1421356�@�Ƃ�������ł���
����1�@�܂��́@-2�@��
-�Q�́@�s�K
����������
�����P
x�́@sinA�@-�@cosA�@�����@�Ƃ��Ă܂��̂�
sinA�@-�@cosA�@��1

�����@�[����ł����
���ꂱ��́@�W������Ƃ�
cos2A+cos2B�@�̒l���@���߂�

����͂�
�p�Y���݂����Ȋ�����
cos�̂Q�{�p��
�����Ă��ł���
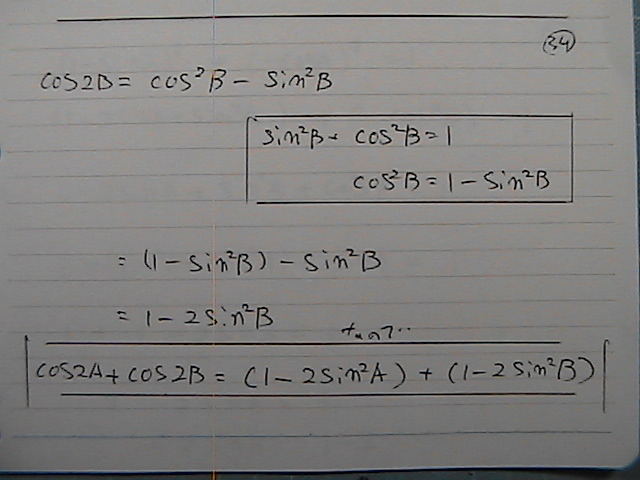
������
��������
��₱��������
���x��
sin�́@�l���o���ׂ�

����������
�{�p��sin
�ł͂Ȃ��Ă�
�Q�{��sin
������
sin�̒l���o�ė���

�Ȃ@���炩�肻��������
�������@�̂肱�����
���イ�Ɂ@�Ȃ���

��́@�������
�P����
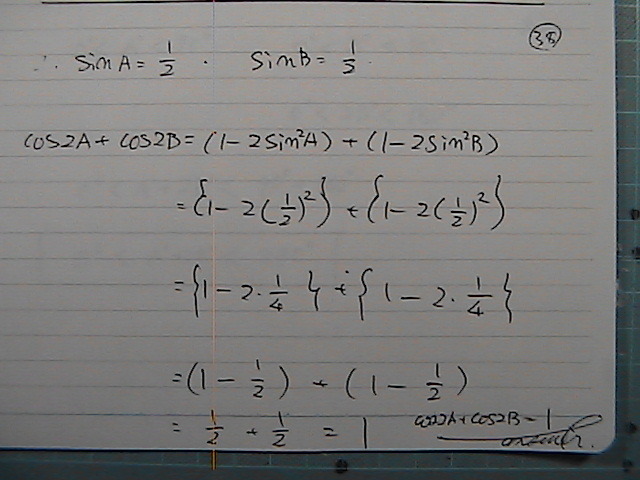
����@�[���Ƃ���
�|���v�����@�����̂�
���Ӑ[���@�i��ł��܂���

�܂��@�@�O����270�x�́@�Ԃł���
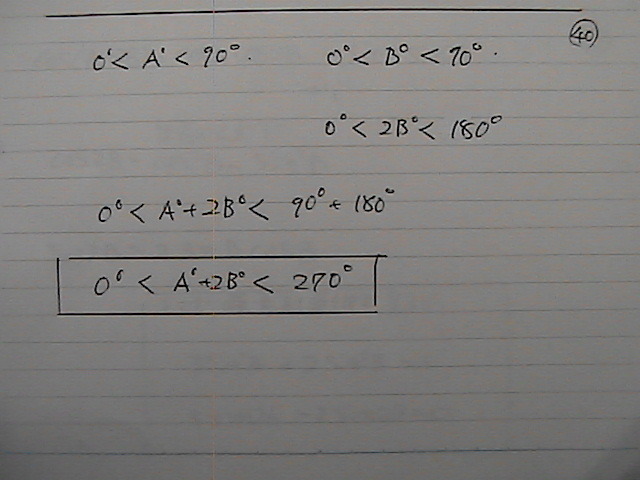
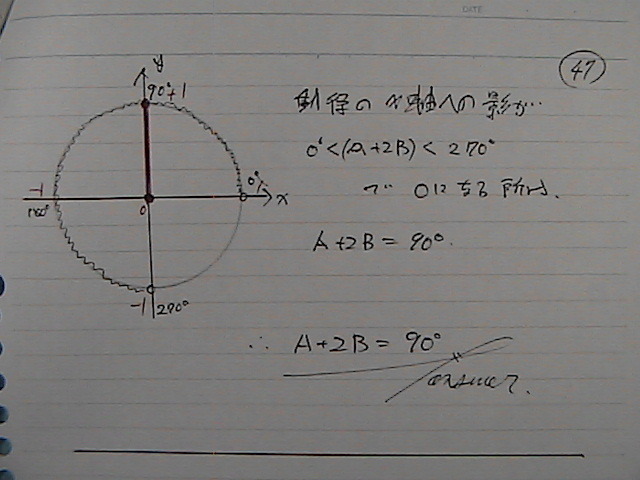
cos���@�g����
�p�x���@�\�������
���@�藝���@���������Ȃ̂�
������@�g����
���낻��
�[���Ȃ�̂Ɂ@�����Ȃ���

�������@���ā@�[�����@�\�����Ăł���

�ł��邾���@�}�Ɂ@�[���Ȃ�Ȃ����
�����@�ό`����
�܂�肪�@�����Ȃ��Ȃ�Ȃ��悤��
�ڈ�́@�Ȃ��J�i
�����͂ł���
���@�藝�́@�W�J���̒�
�́@�����I�ȂƂ���
���������@�����Ɂ@�g�����

��������
���@�藝�́@�W�J�����@�O�����@�ł܂�������
�㔼���@���Ă��ł���

�����I�Ɍ��ė���
�܂��g���ĂȂ���������
�ό`���Ă���
�S���@�g�݂��Ăā@����������
��0

�[���H
���[�@
cos�́@�l���@�[���@�Ȃ���
�s�������ł���
�p�x�𑫂����@���a���ł���
�����Ɂ@���e��

�X�O�x
�ЂƂ����w�Ɓ@�e�w��
�`���L���@�����
���ꂩ
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�{�p�̌����i�Q�j�@�Ȃ̂ł���
sin���@+ cos���@���@a
�@
���^����ꂽ��
sin a cos a�@���@���
�������ł�
��肪�@�����Ăł���
���̒l�����߂Ȃ���
(�P)�́@sin�QA���@���߂�
�����̔{�p�̌������g������i�C�X�J
�������܁@sin a cos a
���@�����������@�o�ė���
sin�QA���Qsin a cos a
��ӂ���
sinA + cosA= 1/2
�Ȃ̂�
������@���������
sin���A �@�@�@cos���A�@�́@�ԂɁ@
�@�Qsin a cos a
���ꂪ�@�S�̂Ł@1/4�Ȃ̂�����
sin���A �@�@�@cos���A�@�́@�P�ɂȂ���
�Qsin a cos a���@-3/4
������
���߂�̂�
sin2A �Ȃ̂�����
sin2A�@���@�Qsin a cos a���@-3/4
(�Q)��
�R��+�R��̂�����
���������́@���́@�������g����
���@���́@1��
�ւĂ���
��ӂ��
�l���������Ă�@�Ƃ���
�i�P�j�́@������
�Qsin a cos a���@-3/4�Ȃ̂�����
sin a cos a���@-3/8
�������@�������
11/16
tan2A�@���@���߂�
����͂�
���������邯��
sin cos�@�Ł@�\�����@�̕���
�悳����������
����i�C�X�J
sin2A�@���@-3/4
���@�킩�Ă邩��
�����������g����
cos�QA=�@�}�@��7/4
���q�́@�}�C�i�X���@�l�����
�}�C�i�X�v���X�@�ɂȂ���
����́@���[�g���@�͂�����
���[�g���@���q�Ɂ@�����Ă���
�}�C�i�X�v���X�R��7/7
�ȏ���@���܂��܂���
�����@���ɍs���Ă݂܂��傤
�[���ł���
sin ���@-�@cos ���@���@1�@�̎�
sin 2���@�A�@sin ���@+�@cos�@���@�A
�̒l�����߂Ȃ���
�܂�
sin���@+ cos���@���@a
�@
���^����ꂽ��
sin a cos a�@���@���
��
sin2���@���@�Qsin��cos��
sin ���@-�@cos ���@���@1�@���@���������
sin��惦�@�@�@cos��惦�@�́@�ԂɁ@
�@-�Qsin ��cos��
���@�o�ė��ā@�����@�S�̂Ł@�P�Ȃ̂�
����������
0
����
sin���@+�@cos��
��
���������
sin��惦�@+�@cos��惦�@+�@�Qsin ��cos����
�isin���@+�@cos���j�̓�悪
�P+�Qsin ��cos���@�Ȃ̂�����
�������@�Qsin ��cos�����@0�@�������̂�
�P
��
������
�����ł́@����܂����
���������@���߂Ăł���
�}1
sin2x=a �̎��@���̒l��
���߂�
(1)sin x + cos x (2) tan x + cot x
�܂��ł���
�i�P�j
�Q���@�Ɓ@���@���@���݂��Ă�̂�
�����̔{�p�̌�����
sin2x=�Qsin �� cos ��
��ӂ��@���ꂪ�@��a�Ȃ̂�����
�Qsin �� cos ����a
(1)sin x + cos x
���@��������
�������������@�P+�@�Qsin �� cos ��
�ɂȂ�̂�
�isin x + cos x�j�̓�悪�@1+a
��������
�v���X�}�C�i�X�Ł�i1+a)
(2) tan x + cot x
�́@sin cos
�Ł@�l���ā@�ʕ�����
�Qsin �� cos ����a�Ȃ̂�����
sin �� cos ����a/2
���ʂ͂�����
�R��\�R�恁�P���@�^�����Ă�
sinA�@-�@cosA���@���߂�
������
�[��������ł���
���Ȃ�@���ԂȂ����Ăł�
�������́@���������ł���
�����܂ł́@�ǂ�����
�����ł�
sinA�@-�@cosA���@���ƒu������
�����
sinA�@-�@cosA���������
������
�������Ă��܂���
���̌`�́@�R��������
��������
�o�Ă��������@���i���j�@�Ƃł�������
���Q�́@�Öق̗�����
���P�̑S�͈͂��@�����Ă��܂��̂�
���c�����@����Ɓ@�i�߂Ȃ��@�ꍇ���@����܂���
�����́@�������傾��
�����藝���g����
��������
�����P�̎��@f(x)���O������
�i���|�P�j�@�Ł@�������
�W�����@��������
�Ȃ��Q��̍��́@�O�ɂ���
�g�����@��
�����藝�́@�����Ł@����
���i�P�j
�i���|�P�j���O
���������@�ς���Ɓ@�C�R�[���[���ɂȂ�@���Ł@�����
��
�����@���̂�������
���������ł�������
������
����1�@�܂��́@-2�@�Ȃ̂ł���
�������
�҂����ł�
��ȗ\����
���̂ł���
���́@�����̂Ƃ����
����͂�
�����@�Ⴄ�`�ɂ��@��������������
���Ă���Ȃ��I�H�ɂȂ��ĂāH�H
���`�`�`�`
��������
�ő�U����
�}��2
���`�`�`�`
����́@���́@�ǂ��Ȃ��������
�O���t����
���������@������
���ʎ����́@sin�́@�Q�@�����炳
��Βla���P
a���}�P
�p�x��
��ʓI�Ȃ��̂��@���߂��`�Ɂ@�����
�O���t����@�O���t��̂P�_���@���
������@��
A=0�̎�
sinA=0 cosA=1
���@�������
sinA�@-�@cosA�@���@��2�@�Esin ( A - 45 )
�Ȃ̂ł���
�i�^��
�ő�U���́@��Βl���@��2�ȉ�
��2�́@�@1.1421356�@�Ƃ�������ł���
����1�@�܂��́@-2�@��
-�Q�́@�s�K
����������
�����P
x�́@sinA�@-�@cosA�@�����@�Ƃ��Ă܂��̂�
sinA�@-�@cosA�@��1
�����@�[����ł����
���ꂱ��́@�W������Ƃ�
cos2A+cos2B�@�̒l���@���߂�
����͂�
�p�Y���݂����Ȋ�����
cos�̂Q�{�p��
�����Ă��ł���
������
��������
��₱��������
���x��
sin�́@�l���o���ׂ�
����������
�{�p��sin
�ł͂Ȃ��Ă�
�Q�{��sin
������
sin�̒l���o�ė���
�Ȃ@���炩�肻��������
�������@�̂肱�����
���イ�Ɂ@�Ȃ���
��́@�������
�P����
����@�[���Ƃ���
�|���v�����@�����̂�
���Ӑ[���@�i��ł��܂���
�܂��@�@�O����270�x�́@�Ԃł���
cos���@�g����
�p�x���@�\�������
���@�藝���@���������Ȃ̂�
������@�g����
���낻��
�[���Ȃ�̂Ɂ@�����Ȃ���
�������@���ā@�[�����@�\�����Ăł���
�ł��邾���@�}�Ɂ@�[���Ȃ�Ȃ����
�����@�ό`����
�܂�肪�@�����Ȃ��Ȃ�Ȃ��悤��
�ڈ�́@�Ȃ��J�i
�����͂ł���
���@�藝�́@�W�J���̒�
�́@�����I�ȂƂ���
���������@�����Ɂ@�g�����
��������
���@�藝�́@�W�J�����@�O�����@�ł܂�������
�㔼���@���Ă��ł���
�����I�Ɍ��ė���
�܂��g���ĂȂ���������
�ό`���Ă���
�S���@�g�݂��Ăā@����������
��0
�[���H
���[�@
cos�́@�l���@�[���@�Ȃ���
�s�������ł���
�p�x�𑫂����@���a���ł���
�����Ɂ@���e��
�X�O�x
�ЂƂ����w�Ɓ@�e�w��
�`���L���@�����
���ꂩ
�����l�ł��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 19:58| ��l�̂��ї��Ƃ��@