�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2017�N01��13��
23016�@��l�̂��ї��Ƃ��@�@�蒼���ɐڂ�������@�ޑ�
�J�̓��́@�X���[���C�t�̕���
�R�������@������
�S���@�W�����@�����Ȃ�ł���
������
�Q�{�́@�ڐ��Ɓ@�Q�́@�ړ_���@�^�����Ă�̂�
�W���@a,b,c,d�@�A���@���߂�Ƃ������ƂȂ�ł���
�s���Ă݂܂��傤�B
�܂��@�_�i0,1�j�@�̂Ƃ����
������+1�@�ɐڂ���̂�
�ړ_���@�g����
�Ȑ���́@�_�ł����邶��i�C�X�J
�Ȑ����@f(x)�@�Ƃ���
���i�O�j���P�ɂȂ����ł���
������Ă��Ɓ@�����P
�܂�������
���f�i���j�@�́@�ړ_�Ɂ@������@�ڐ��́@�X���Ȃ���
�ڐ��́@�����ނ��@������+1�@�@�́@���́@�W���Ɠ���
�P�ł���
�ړ_�́@�i0,1�j
�Ȃ̂�
�@
���f(0) �́@�X�����@�P
���f�i�O�j���@�������
�v�Z���Ă��ā@���P������
�����P
��@�o��������
�����P�@�����P�@���@�Ȑ��Ɂ@������Ă��܂���
�����
�_�i�R�C�S�j�Ł@�����|2��+10�@�Ɛڂ��邩��
�ړ_���@�g����
�Ȑ���̓_�ł�����̂�
���i�R�j���S
������ā@���S
����Ȋ�����
���f�i�R�j�@�ړ_�@�����R�́@�X����
�ڐ��́@����-2���@+10�́@���́@�W���Ɓ@����������
-2
������ā@�v�Z���ā@��-2
�o����
��́@������
27a + 9b = 0
27a + 6b =�@-3
����
�����P
b���P���o���
a���@-1/3
������a=�@-1/3 , b=1, c=1, d=1,
���x�͂ł���
����́@������Ɓ@�Y�Ⴂ�܂�����
�Ȑ��Ɛړ_�Ɓ@�ڐ����@�^�����Ă銴���ł���
�ړ_�͓_�i-1�A�P�j�@�@�݂̂Ł@�����ɕ��s
�����Ɂ@���s���Ă��Ƃ́@����i�C�X�J
�O�ł�����
���i���j�@���@��������
���f�i���j�@�Ł@�X�����@�o����
���ꂪ�@���O�@����i�C�X�J
�����Ɂ@������������悤�ɂł���
�������傾�낤��
��������
2a - b = 3
�ւĂ���
�ړ_���@����̂�
�Ȑ���́@�_�ł��@���邶��i�C�X�J
������@���i-1�j��1
�������
�v�Z���ā@�@���P�@�Ȃ���
a- b + c = 2
2a - b = 3
a- b + c = 2
������@�Ȃ@�Ȃ����H��
���邶��i�C�X�J
�̂݁@�́@��肩
f�f(x)�́@�ڐ��́@�X����
���f�i���j�@���@�Q���������Ɂ@�Ȃ��Ă邯��
�ړ_�@�i�@���@�j�@���@�i�@-1,1�j�@�̂݁@���Ă��Ƃ�
�d���ł���@��
���ʎ����@�����Ă���
D=0
�����
�킩��Ȃ��������@�R���@�����@�R����
�@�@���@�R�{����
�B���@�����ā@a�̂Q��������
a���@�R
b���@�����R
���́@�Q
����
�Ȑ��s�ړ�������
�ڐ��Ɂ@�ڂ��܂����@�Ł@������
���ł�
�s���Ă݂܂��傤
�܂��@���s�@�ړ�����
�����́@���Ɂ@a����
�ړ������
���ꂼ��@�i���|a�j
����Ɂ@
�����́@���Ɂ@�������@
�ړ������
+��
������@���i���j�@�ƒu���Ăł���
���f�i���j�@��
�G�l���M�[�@��ł�
�����@���҂���������
���N�������������炳
�ꉞ�@�ڐ��́@�����ł���
���f�i���j�@���@�ڐ��́@�X���ɂȂ�̂�
���|�P
��������@
�ړ_���@����o���Ă�����i�C�X�J
�W�J����
��������
������������
���܂��@���������ł����
�C���������ł����
�d���Ɂ@�Ȃ��Ă���
�ړ_�́@��̂悤�ł���
������@���i���j�@�Ɂ@��������
�����@��
�ړ_�́@�ia+1,b)
�łł��ˁ@�ł���
�ڐ����@�킩���Ă����
��������
�܂��@�ڐ����@�N������i�C�X�J
�������̂Ȃ�ł�����@�ł����
�o���́@���@�́@�����@���Ł@�����
��������
��������
a+b=1
�����
�ړ�������
�ŏ��ɂȂ�Ƃ���
a�́@���ɂ���
���[�g�̒��g���@�Q�����Ȃ��
������������
�ŏ��l���@�@����͂�����i�C�X�J
���_���@�o���ł���
a���@1/2�́@�Ƃ��ŏ���
�i�@��̒��g�@�j
���̎��́@a�Ɓ@b��
a=b=1/2
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 06:52| ��l�̂��ї��Ƃ��@
2017�N01��11��
23015�@��l�̂��ї��Ƃ��@�蒼���Ɂ@�ڂ�������@
�J�̓��́@�X���[���C�t�̕���
�蒼���Ɂ@�ڂ������
�Ȑ��̎����@�������@�܂�Ł@�^�����Ă�
���̋Ȑ���
�蒼���Ɂ@�@�i-1�A-5�j�Ł@�ڂ���@�l�Ɂ@
�����́@�l���@��߂���
�s���Ă݂܂��傤
����́@�ړ_���@����Ɂ@�Ȃ�l��
�i-1�A-5�j�@�Ȃ���
�ړ_�́@�Ȑ���Ɂ@���邩��
���i-�P�j��-5
�ɂȂ�
��
�������́@���f�i���j�@�̕���
�������@�ڐ��ɂȂ�킯��
�X�����@�Q������
���f�i-1�j���Q
��������́@�@�A���@��������
a,b
a=5 b=9
���x��
�������Ɂ@�����邯��
�Ȑ��Ɂ@�ڐ����@�ڂ���l��
�ړ_�́@�^�����ĂȂ�
������@�@
�ړ_���@���肵�Ȃ��Ɓ@�����Ȃ���
�����̏�ɂ��@�ړ_�́@���݂���킯�Ȃ̂�
��������
�ړ_���@���肷���
�������@�́@���f�i���j���@�Q
����́@�ړ_�@���@�ɂ����ĂȂ���
����Ɂ@�����@�������
���f�i���j���@�Q
�ړ_���@�����́@������@���肵���ł���
�Ȑ���́@�_�ł�����킯��
�Ȑ��@���i���j�@�Ɂ@���@�A�Q���@���@��������
���i���j���Q��
���̇A�����@�������́@�@���Ɂ@�������
���@���P
a���P
���́@���́@�ޑ�ł�
�Ȑ��Ɓ@������������
�ڂ���悤��
a�́@�l���@��߂�
�ړ_���@�킩�ĂȂ��̂�
�Ȑ���ɂ��@������@�ɂ��@�ړ_�́@����̂�
��������@���肵��
�������́@���f�i���j�@�́@�ړ_���Ł@�X�����@�P������
f�f(���j���P
�ړ_�́@�Ȑ���ɂ�����킯������
�ړ_���@
��������
f(���j���@���[�P
�o�Ă����@��́@�W������
�A�Ɂ@�@���@�������
�W��a�́@
4/27
�S���@�Q�V���@����@�ȁ@������@��
���@�����傤�ԁ@���[��@��
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�^�O�F�蒼���Ɂ@�ڂ�������@
posted by moriamelihu at 07:30| ��l�̂��ї��Ƃ��@
2017�N01��10��
23014�@��l�̂��ї��Ƃ��@�X���Ɓ@�ڐ�
�J�̓��́@�X���[���C�t�̕���
�X���Ɛڐ�
�́@�ޑ�Ȃ�ł���
�Ȑ��́@���������@���@����������
���ꂼ��́@�Ȑ���́@�_�ɂ�����@�X���ɂȂ�܂�
��́@�_���@������邾��
�X�����X�Ȃ̂�
�t��
�����������̂��@�X�@�ɂȂ����悩��
���@���@����o����
������������
�R�܂��́@-1
�ڐ����@����Ă��ƂɂȂ邩��
���ꂼ��
�ڐ��́@��������
x���R�̂Ƃ�
x���|�P�̎�
�X���X�́@�ڐ��́@�Q�{
�ւĂ���
�����Ɂ@���s��������
�X�����@�O���Ă��ƂɁ@�Ȃ�̂�
��������
���O�ɂȂ�Ƃ�����
�ړ_�́@x���@�t�Ɂ@����o����
�O�܂���2
�ڐ��́@�������Ɂ@��������
x���ɕ��s�ȁ@�ڐ��Ȃ̂�
�����@����������
�ɂȂ�͂��ł���
�����Q��
�����|�Q
������
�����}2
11
���@����Ă��܂��܂�����
����
���Ȃ��Ȑ��Ȃ�ł���
�X�����@�ŏ��̎�
��������
���邶��i�C�X�J
�ǂ������
x���̑O�́@�W�����@���̐��ȁ@��
�O���t��
��ɊJ����������
�Ƃ������Ƃ�
�ŏ��l���@����@
�W���`��
���_���@���߂�ׂ��@
������������@�ό`���Ă��Ƃł���
�����Ȃ��Ă����Ȃ��ā@����
�W���`��
x���@�������@���ɂȂ��Ă��ł���
���_�́@�i1�A-3�j
���̂܂�
-3�@�ł��@������������Ȃ��ł���
�ꉞ�@���f�i���j�@�Ɂ@����Č��邶��i�C�X�J
�Ł@�ڐ��́@��������
��������
�������
����
���͂ł���
�������Ɂ@���s��
��̐ڐ��́@��������
���Ƃ�
�ڐ��@�ԁ@�́@�������@���߂��
��������̂�
�v�Z�ԈႢ����Ƃ�Ȃ̂�
�킴�Ɓ@�W�J����
��������
���ꂪ
�������Ɓ@���s������ɂ��Ăł���
�����������̂��@�X���Ł@�X���́@�P��
���������ł���
�ړ_���@��o�ė���
x���P�̎�
�����|1/3�̎�
��
�ڐ����@���
��
�������@�Ɂ@���s�Ȃ̂�
�X���P�́@�����Ɓ@�S�T�x���@�Ȃ��Ă邶��i�C�X�J
�Ɓ@�g��́@�����Ă܂�����
�T�C���S�T���@�g����
�ڐ��Ԃ́@�������@���߂��
�P�U��2/27
�Ō�͂ł���
�Ȃ@�������
�Ȑ���Ɂ@p�Ƃ����@�_�������ł���
���̂��ɂ�����@�ڐ���
�Ȑ����@�\���@���́@a�Ɂ@�e�����@�Ȃ�
p���@���߂Ăق����Ƃ������Ƃ̂悤�ł�
�e�Ɋp
�X���Ȃ̂�
��������
a�Ł@�������Ă݂�
p�_�́@�X���Ȃ̂�
p���@�������
a�Ɂ@���W�Ȃ���
a�i�@�j�@���O�@�Ȃ�
������
������������i�C�X�J
�������@�R���@�o��������
��ӂ���@p�́@�O�ł́@�Ȃ��Ƃ���̂�
1/2�@�Ɓ@1
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�^�O�F�@�X���Ɓ@�ڐ�
posted by moriamelihu at 08:53| ��l�̂��ї��Ƃ��@
2017�N01��07��
23013�@��l�̂��ї��Ƃ��@�X���Ɓ@�ڐ��@�@�i�@�NjL����@�j
�J�̓��́@�X���[���C�t�̕���
�X���Ɓ@�ڐ��Ɂ@�ւ��܂���
�������i���j�@���@�������́@�l�@�@���f�i���j��
x���@�������Ɓ@��������@���ɑ���@�ڐ��́@�X���ɂȂ�
��
�ڐ��́@�X���@�@
���f�i���j�@���@�@tan�@���@�ɓ�����
���@�����́@���́@�����Ƃ́@�Ȃ��p
������@���܂��@�s���Ă݂܂��傤
���s�ȁ@�ڐ��ƌ����Ă܂��̂�
�X���́@����
�Ȑ��O�@����Ƃ�
���s�Ł@�̎���
�ړ_�́@���W���@�킩���ĂȂ��̂�
���肵�Ă���i�C�X�J
���@�����Ɂ@
�ړ_�́@�����@��������̂��@
�Q�Ɓ@�������@
�i�����Q���j
��������@�ړ_�@�����@����o���Ă��܂��Ƃł���
��@�o�ė���
�ړ_���@���
�ڐ��́@�����Ɂ@������Ă���
�ڐ���
��o�ė��܂���
����
���ꂶ��
�ڐ����@������������邯��
�ڐ��́@�����ƂȂ��p�@�́@�V�[�^�@���@�O����@180��
0����@�p�C�@�܂ł́@�p�x�Ł@�l����Ƃ�
�ǂ�����@�ǂ��܂Ł@�́@�͈͂�
�����̂��ȁH
�b�e�������炵���ł�
�Ȑ��́@�����W���Ɂ@�ړ_�́@���W���@������
�X�����o��
���ꂪ�@���̂܂�
�^���W�F���g�@���@�i�@�V�[�^�@�j�@�ɂȂ��Ă邩��
�܂�����
��
�����́@���́@0�ȏ�
�|�P�@�@�́@�|�P
�Ƃ������Ƃ�
���̒l��
�|1�ȏ���Ă��ƂɁ@�Ȃ�ł���
������
�|�P�@�ȏ���ā@������
���ꂪ�@�^���W�F���g�@�V�[�^�@�Ɂ@������
�����łł���
�������肵�Ă���
�����Y�݂܂�����
3���@�ʁ@�Ȃ�������Ȃ��[
�b�e�@�߂����C���Ł@�W���[�N���@�l���Ă��
�_�l���@����Ł@���܂��B
���@�^���W�F���g����
�|1�@�@����@1�@�W���@�Ȃ������
�O���t�O���t
�V�[�^���@0����@�p�C
���@�i�@�l��@�j�@���@-1�@�ȏ�@
����ł����̂�
���a���P��
�P�ʉ~�Ł@������
�T�C���@�R�T�C���@�́@
���a���́@��
���a���́@���@
�@
�^���W�F���g�́@x���́@��
�NjL
�O�p���́@���[��
���T�@�͈̔͂̕�����
�������[�@������Ƃ���
������@��������@�^���W�F���g��
�P�ʉ~�Ł@���Ă���
�v���X�@�̂Ƃ��Ɓ@�}�C�i�X�̂Ƃ��@������ł���
�Ł@�T�C���R�T�C���^���W�F���g�@��
����Ȋ�����
�V�[�^�@���@�v�Z����i�C�X�J
�T�C���@�R�T�C���@�̃O���t�́@
�����@�l�悪�@-1�@����@1
�T�C���@�R�T�C���@�̑O�Ɂ@�t�@�N�^�[�@���@(�@���{�@�Ƃ�����@�傫���Ȃ邯�ǁ@�j
�Ȃ���@-1�@����@1
�Ƃ��낪��
�^���W�F���g�́@�@�}�C�i�X������@����@�Ղ炷������
�^���W�F���g�̎���
����́@�͈͂��@�O�ȏ�@�ȁ@�V�[�^�@�@�p�C�@����
���ی��́@�Ղ炷
���ی��́@�}�C�i�X
�@
�^���W�F���g�@�V�[�^�@���@�}�C�i�X�P�ȏゾ����
�}�C�i�X�P�̂Ƃ����@���ׂ��
��/���@������
�S�T�x
�P�ʉ~�́@���a���@�P������
��̒l����
���A���́@��2/2
�Ȃ���
����
�|�P�Ɂ@�Œ肵��
�@
�Ȃ��p���@���a���@�L�����Ƃ��Ă�
��̎O�p�`�́@�����`�Ȃ̂�
�p�x���@����
�Ȃ���
�P�C�S�@�ی��́@�����@�P�ɂ��Ă�
�Q�C�R�@�ی��́@�����@-�P�ɌŒ肵�Ă��܂���
�ȒP�ł���
�����@���̂܂�
��
���p�Q���ӎO�p�`�́@�䂩��@�P�F�P�F��Q
����i�C�X�J
�|�P�́@�S�T�x�@�A�@�O�x����@������Ɓ@�P�R�T�x
�@�@
������
x���̂��Ł@�@x��-1�@����1�@�|�P
�p�x���@���p���Ɂ@�s���ɂ��������ā@�}�C�i�X�Ɂ@������
�p�x���@�p�C���Ɂ@�s���ɂ��������ā@�O
�[�P�ȏ�́@�P�R�T�ǁ@����@180�@�܂�
�����̂Ƃ��́@
�O�����/2�@�@�@�Ɓ@�R��/4�@����@��
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 18:01| ��l�̂��ї��Ƃ��@
2017�N01��05��
23012�@��l�̂��ї��Ƃ��@�Ȑ��O�@�̓_����́@�ڐ��@�@���@�ޑ�
�J�̓��́@�X���[���C�t�̕���
�Ȑ��O�@�̓_����
�������Ɂ@�������@�ڐ�,�@���́@�ޑ�
�s���Ă݂܂��傤�B
�R���Ȑ��������ā@���_����@������
�ڐ����@���߂�
��������́@�ړ_�̍��W��
������Ȃ��ł���
x��a�Ƃł�����
�Ȑ���́@�_�Ł@���肵��
�ڐ��́@���������@�����
�ʉߓ_�@���_���@��������
���A���Aa�́@����
�����O�@�����O�@���@���ꂽ��ł�����
�ړ_�́@���W�@a���@�o��ł����
�����藝��
����������i�C�X�J
�K���Ɂ@�����@����Č��ā@���O�ɂȂ�Ȃ��
���̐��́@�����Ɂ@�܂܂�Ă���
a���P�̎���
���ia�j���O�@�Ȃ̂�
�g�����@��
���߂́@�Q���@���̂܂܉���
���́@�P�Ɓ@�Q���@�|���ā@���̈ʂ́@�\�R�̉��ց@�Q
�\�R��2���@�����ā@���Ɂ@-1
���́@�P�Ɓ@�|�P���@�|���ā@���́@�ʂ̉��ց@-1
0�Ɓ@-1���@�����ā@���Ɂ@-1
���́@�P�Ɓ@�|�P���@�|���ā@���́@�ʂ́@+1�̉��Ɂ@-1
�{�P�Ɓ@-1���@�����ā@���Ɂ@0
�R�����@�P���Ł@����������
�o�Ă����@�W���́@�擪�͂Q��
�Q���@�P���@�萔�@�]��
����Ɂ@�����@����������������i�C�X�J
a�́@�P�܂��́@-1/2
���ꂼ��
�ړ_�́@���W���@���߂�ł���
���_���@�ʂ����
����a���@�̃O���t
�X�������߂�
�ڐ��́@�Q�{
���́@�@���ł��̂�
�ڐ��ɐ����Ɂ@��������Ⴄ��ł���
�ڐ��Ɓ@�@���́@�X���́@�ς́@-1
�_P�́@�Ȑ���̓_�Ȃ̂�
�i���A�@p���j
�Ƃł������Ăł����
�Ȑ��́@�����Ɂ@p���@������ďo��̂�
�ڐ��̌X���Ȃ̂�
�@���́@�@���́@�X���́@-�@�t��
�X�����@�o���̂�
�����@ax + b
�̌`�ɂ���
�ʉߓ_
�i-1,2�j
�@
����-1�@�@����2�@���@�������@
�����ł��
�Ł@�ł����
�o�Ă����@�@���́@����
������́@�ʉߓ_
���@���@��������
�������@����p���
p�����́@���ɂȂ邩��
�o��͂�����i�C�X�J
x���W�����ł�������
�R�����̂悤�ł���
�����藝��
���i���j���@�ɂ��Ă�����
���i�P�j�@�̎��@�O�@�ɂȂ邩��
p���P�́@�����̈��
�g�����@��
���̌�����
x���W�����Ȃ̂�
����Ȋ�����
������́@�@�����@���ł�
����́@�Ȑ��O�́@�_���@��������Ɓ@���ɕ\���Ȃ��̂�
�������@�c��܂��B
�Ȑ��O�@�̓_����@�Q�{�́@�ڐ����@�������ł���
���ꂪ�@�������邱�Ƃ�
�ؖ�����
�����@������@�X���́@�ς��@-1�@
�ڐ����@�ł�@�ȒP�ɂȂ͂��Ȃ�ł���
���܂Œʂ�@��肭����i�C�X�J
�ړ_�́@���W���@�Ȑ���Ɂ@����ł����
�ڐ��́@���������@���߂�
������
�Ȑ������̓_
x���`�����`�����@�A�����@�قɂ��
���@��������
���肵���@�ړ_�@�����@�o���
�Ƃ��낪
�H�H�H
�Ȑ��O�̓_�́@����-1
��̓_��
x���W�́@���肳��Ȃ�
������
�ia�A-1�j�@�Ƃ��܂�������
�������@�c�����Ⴄ
�Y�o���o�Ă��Ȃ�
���̂܂܂ł́@�����Ȃ̂�
������
�����@���Ȃ��Ƃ����Ȃ���
�Ȑ������́@�_�Ɂ@�i�@�܂��́@�Ȑ����@�j�������@�܂�ł�Ƃ���
���ƌW����@�W���@�g����
�e�Ɋp�@�@�Q�_�Ł@�ڂ��Ă邩��
���P�@�@�A�@�@���Q�@�ƒu����
���������
�X����
1/2�@���P
��
1/2�@���Q
�ڐ��́@�X���̐ς�
�i���P���Q�j/4
�ڐ��̕������Ɂ@�Ȑ��O�̓_���@�������
�����@�Q�����@�ł����
�ړ_���@��������ā@���ł���
���́@
���P�A�@�@���Q�A���@
��́@�ړ_�ɂ����̂�
�@
���ƌW���̊W����
�����������@�W�J������
���P+���Q��2a
���P���Q��-4
�ڐ��́@�X���̐ς�
�i���P���Q�j/4
��
���P���Q��-4
���@��������
�X���̐ς́@�@-1
����ā@��������B
����
�Ȑ��O�́@�_�́@�͂�����Ɓ@�킩���Ă��ł���
�Ȑ��́@���Ɂ@����ȁ@�W�����@�܂܂�Ă�Ƃ�
�Ȑ��O�́@�_����@�Q�{�̐ڐ���������Ƃ���
�ړ_���@���Ԓ�����
��_��ʂ�@�����@�ؖ�����ł��B
�����̂悤��
�Ȑ��O�́@�_����́@�ڐ�������
�Ȑ���Ɂ@�ړ_���@���݂���
�ڐ��́@��������
�ڐ��́@������
���ꂪ
�Ȑ��O�@�̓_�@�i�P�C�O�j�@���@�ʂ��ł�����
��������
���A���A���@�̎��Ɂ@�@����1�@����0��
��������̂�
���@���@�o���ł���
�ǂ������
����ȌW���@a���@x�Ɂ@�������Ă�̂�
�������@�c���Ă��܂�
������
�ڐ��̕������Ɂ@�ʉߓ_���@�������
�ڐ����@�Q�{�����@�ȁ@
�Q�������@����������
���������
�ړ_��
���P�A���Q�@�Ɓ@�u����
x�P�Ax�Q���@���ԁ@�����́@�X����
�v�Z�ŗ��Ă��܂��̂�
�������@�܂܂�
�����ł���
�����́@�������Ȃ̂�
���@���@ax�@+�@���@�Ȍ`������
�ʉߓ_�́@�Е��@���P���@�������
���́@���������
�������u���Ƃ���
�ړ_���@������@�̎��́@����
���P�@�Ɓ@���Q�@���@�g����
�\�������
��́@�����@
���l������
���P+���Q��2
���P���Q��-1/a
���������
�����́@���ꎮ���o�ė���
�X���́@�ω����邯��
���@�ؕЂ́@�ς�炸
�Ȃ̂�
�i0�A�P�j�@���@��Ɂ@�ʂ�B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 04:15| ��l�̂��ї��Ƃ��@
2017�N01��04��
23011�@��l�̂��ї��Ƃ��@�Ȑ��O�@�́@�_����@�������@�ڐ��@
�J�̓��́@�X���[���C�t�̕���
�ڐ����@���������Ȃ�ł���
����́@�������@�O�́@�_����@�ڐ��������ꍇ
�s���Ă݂܂��傤�B
�ꉞ�ł���
�ʉ߁@�_���@��������Ɂ@�Ȃ����Ƃ�
�m�F����i�C�X�J
�i0�A-3�j
�����O���@�Ȑ��̎��Ɂ@�������Ɓ@�����O�@�̎��́@�Ȑ���́@���W�́@�P�Ȃ�ł���
�_�́@�ق��́@0�́@�Ƃ��@-3
�Ȑ��O�ł�
�Ȃ̂�
�ڐ��̎���
�ړ_�́@�X�����o�����߁@���������@����
�ړ_�́@x���W���������ł���
�ړ_���@���m�łȂ��̂�
����
�ړ_�́@����ł��@���@���Ă�����
�ړ_�́@�Ȑ���Ȃ̂�
���P�@�Ƃł��u���Ăł���
���P�A�@���P�̓��+1
�����
�ڐ��́@�������Ɂ@�������
���A���A���P�@�łł����@����
���Ɓ@�����@��������
x�P���@���܂�̂�
���������
x�P�́@�}2
�ڐ��́@�Q�{����炵���B
���ꂼ��@���P���Q
���P��-2
���@�v�Z�����
�ڐ��́@�Q�{
����
�Ȑ��O�́@�_����@�Q�{�ڐ����@������
���́@�ړ_���@Q,R�A�Ƃ���Ƃ���
����QR�́@����
�����Q����+2�@�ɂȂ邱�Ƃ��@�����ł��B
�������݂�����
�r���܂ōs���Ă݂܂���
�ڐ��́@���������@�o�Ă邩��
�������Ɠ�����
�Ȑ��O�̓_��
�ڐ��́@�ʉߓ_���@�������i�C�X�J
��������
�_�̍��W���@�i0�A-3�j�@����������
x�P���@�o�Ă�����ł���
����́@�i���A�O�j���[�[�[�[
�������@�c���Ă��܂���
�������Ȃ���
�l���邶��i�C�X�J
��
����́@�킩��Ȃ�������ł���
�ȂɂȂ�
��́@�ړ_���@���@�A�@���@�ƒu��
������
�K���Ȃ��Ƃ�
�X����
���́@�ω��ʂԂ�́@�@���̕ω���
�X���́@���{��
�Ƃ����
���@�A���@�́@�ڐ��@�́@���ł��@����
������
������
���P����@���ƌW���̊W��
����Ȃł�����
��̉����@�����ā@���������̌`���ł���
�W�J�����
���@�A�����@�Q�����́@�W���Ɂ@�Ȃ��Ă�B
�Ȃ̂�
��������
���{���@�@�@�����@���@�W���ɂȂ��Ă�Ƃ�����
���{�����@���o�������
���P�́@�Q�����Ɂ@���������Ăł���
���{���@���@�W������@���������
�Q��
�����́@��������
����ax+��
�X���@a�́@�Q��
�����Q�����@+��
�����@���߂�ׂ�
�@
����QR�́@��������́@���@�A�@�����@�ʉ߂���̂�
���̕����@�������ł���
�����o�ė���
�����
���[�[�[
��������Ȃ�
�����O��
�ڐ��́@���������@�������ł���
�����߂Ă�̂�
����QR�̎��Ȃ�ł���
�ڐ����@���A�����@�ʉ߂���̂�
���́@���̂Ƃ����@������Ă݂��
�˂˂�
�Ȃ�������i�C�X�J�B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 04:13| ��l�̂��ї��Ƃ��@
2017�N01��02��
���m�点
�J�̓��́@�X���[���C�t�̕���
�ǂȂ��l�ł��@���}�������܂���
�����́@�B�ꕔ����
�L�������@���₵�Ă����܂��B
����
��Ł@�n�߂��@���w�ł���
�����ɂ��@���������Ȃ����̂�
�����������܂�����
���Q�@�Ƃ��Ȃ��Ă����
���T�́@�ł��ĂȂ��Ɓ@�����܂���
�ȒP�ɂ́@�O�i�ł��܂���
������
�@
������@����Ɂ@�����Ł@�Y�Ȃ��[
���@�����l�^�Ɂ@�O�i�@���悤��
�l���Ƃ�܂��B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 06:50| ��l�̂��ї��Ƃ��@
2016�N12��29��
23010 ��l�̂��ї��Ƃ��@�Ȑ���́@�ڐ��@�@��
�J�̓��́@�X���[���C�t�̕���
�Ȑ���Ɂ@������@�ڐ��A�@���́@���ł�
�ڐ��Ɂ@�����Ȃ̂��@�@��
�ڐ��Ɩ@���́@�X���̐ς́@-1�@�ɂȂ�
�s���Ă݂܂��傤

�O���t�@��́@�_��
���ی��Ȃ̂�
���ی��̒��Ł@���@���R��@
�O���t�@�ゾ����@�������@�Ȃ�@�������R�悾���
�ڐ��́@�������@�����Ă���
�@���́@�������@�����Ă���

���i���j
���f�i���j�@���@�g���̂�
�����@��������
�����
�O���t��́@�_�@���@�ɂ�����
�ڐ���

��
�@���̕���
�X�����@�}�C�i�X�@�t��������

����Ȋ�����
�������
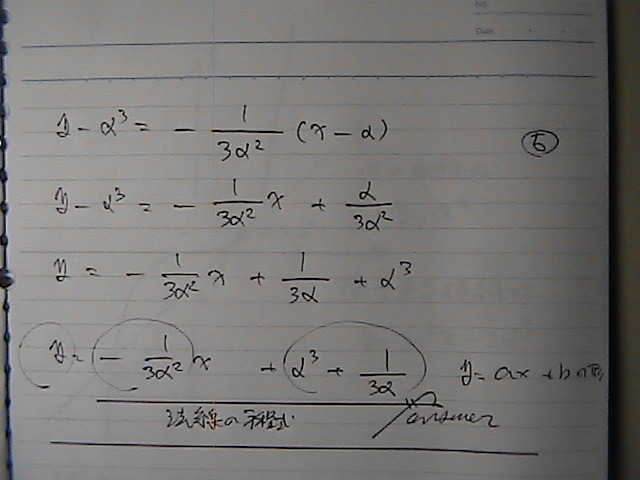
�ւĂ���
�i�Q�j�@��
�_P�ɂ�����@�ڐ���
x���@ý���@�Ɓ@���́@�Ȑ���
�����Ƃ����
���ꂼ��@
Q,R,S
�Ƃ����
PQ:QR:RS�͈��@�ł��邱�Ƃ��@����

�}���@�����Ă݂邶��i�C�X�J
P�́@���ی�
���̐ڐ���
�����Ɓ@�����@Q
����r\�ƌ����@R
����Ɂ@���̋Ȑ��Ɓ@������ā@S
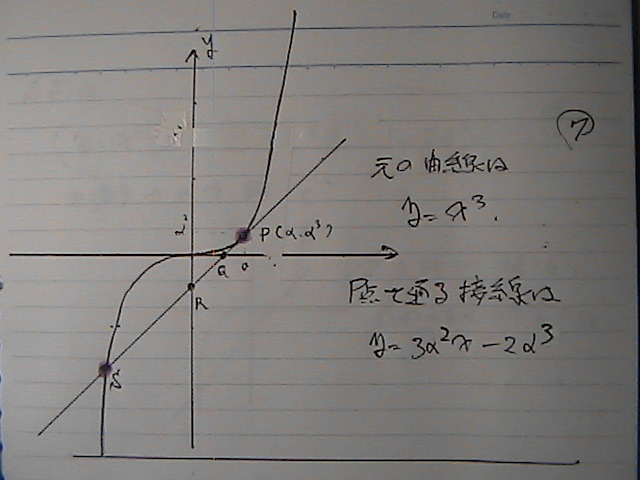
�܂�
Q�́@x���ゾ����@�����O�@��
�ڐ��ɑ�������
�����Q��/3

R�@�́@������Ɓ@�u���Ƃ���
�ڐ����@���̋Ȑ��ƌ����_S��
�Ȑ��̃O���t�Ɓ@�ڐ��́@�O���t��
����肾����
���@�Ɂ@�Ȃ�Ƃ��낾���炳
�A���ɂ���ł���

���@�Ł@�ނ����
��������
������@���������ł����
�������o��
�����v�����Ȃ���ł���

�ڐ��́@�ڂ��Ă���b�e�����܂���
���̐ړ_�́@�Ȑ���̓_�ł��̂�
�i�@�_�@���݂��邯�ǁ@�ʐς��Ȃ�����
�@�@�����������Ɂ@����ł���
�@�@���~���Ɓ@��K�Ł@��_������
�@�@�@��_�́@���邯��
�@�@�@�ʐς́@�Ȃ���ˁ@�j
�ړ_�́@���́@���̕������́@���ɂ���
x����
x�[�����O
(x�|���j
����Z����i�C�X�J
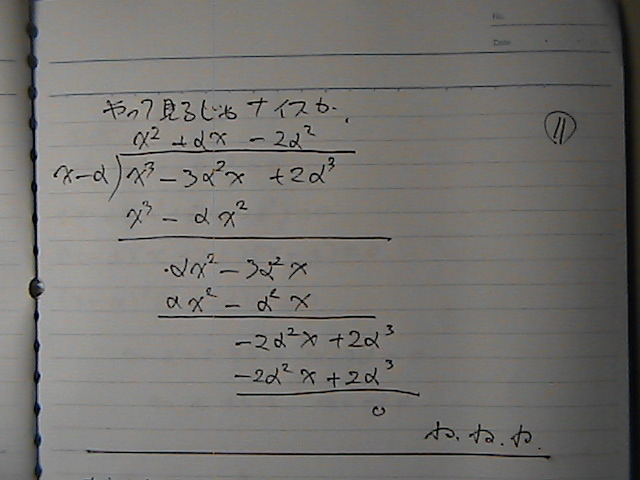
����ꂽ�ł���
�����
������������
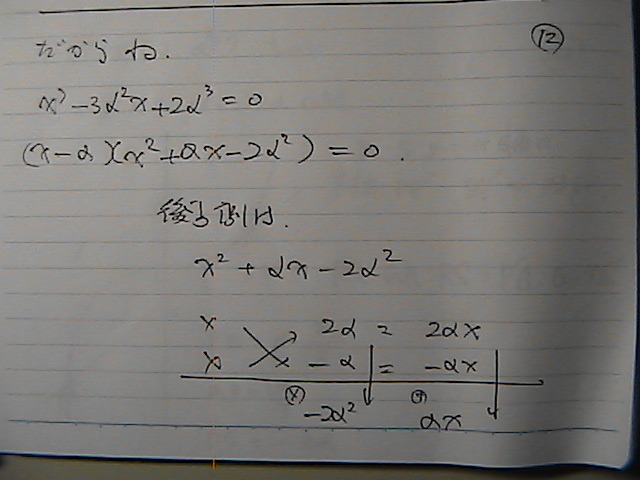
���@�������́@�|�Q��
�Ȃ���
���������ɂȂ��Ă�@(x�|���j�̕��́@�ړ_�Ȃ̂�
S�́@���@���W�́@�|�Q��
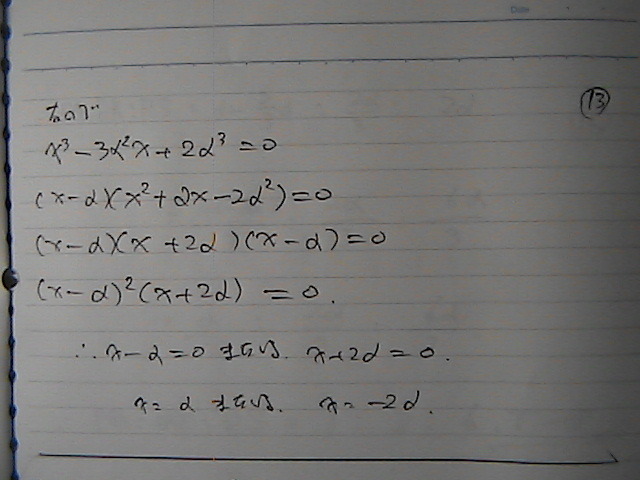
P�Ɓ@S����@x���Ɍ������ā@�������@���낵
���ꂼ��@P'�@�@S'�@�Ƃ���
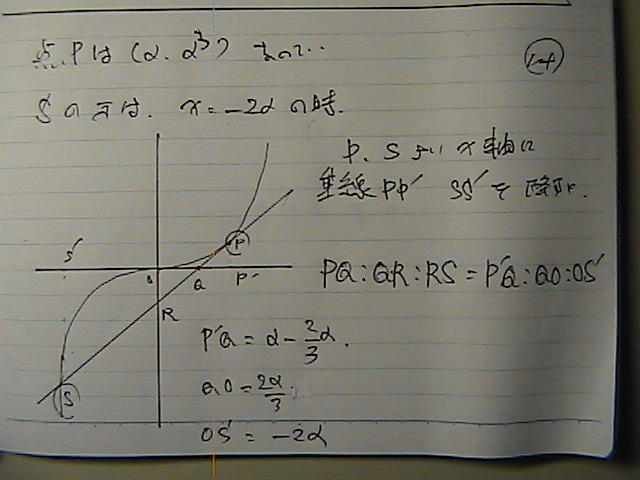
���ꂼ��́@x���W��
��̒l��
�v�Z�����
�������@������
1�F2�F6
���ł���

���炭���҂���������

�ޑ�
�ڐ��Ɓ@�@�����@���߂�

�ڐ��̌�����
���������ó�
���������@�K�v�Ȃ̂�
����Ƃ��Ăł���
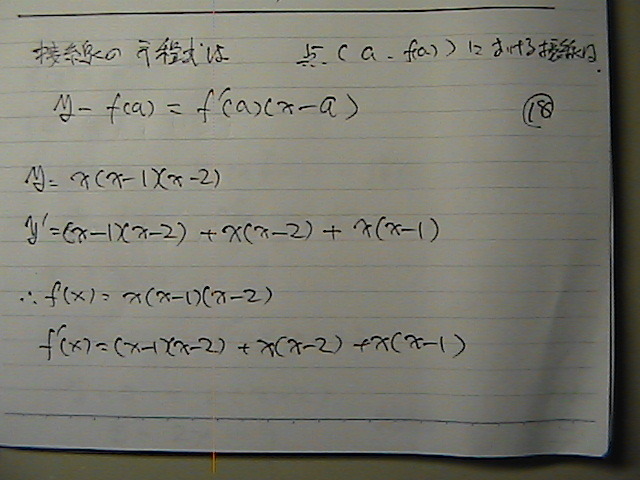
x���Q�̎��́@�ڐ���
���i�Q�j���O
���f�i�Q�j���Q
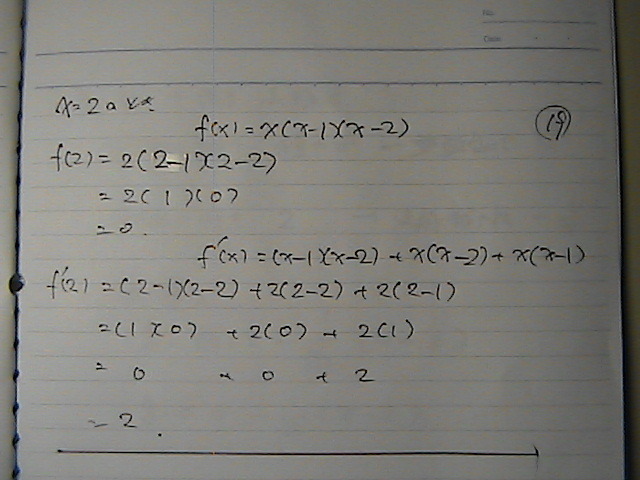
�����ɑ������
����Ȋ���

�@����
�X�����@�|�t��������ɂ��Ăł���
������

������Ɓ@�ڂ����Ƃ��Ăł���
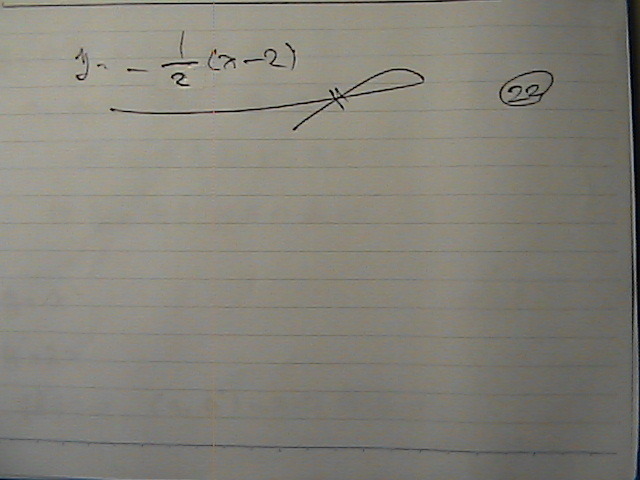
���Ȃ�
�����@X���@�́@���_�ȊO�̓_��
�ڐ��@�@�����@
�����Ɓ@�����_��
���ꂼ��@T�AN�@�Ƃ����
����TN�́@�����́@�@�ǂ�ȁ@�͈͂ɂȂ邩

�܂���
�ڐ��@�Ɓ@�@�����@���߂˂�
a�́@�O�łȂ��_��
�O���t��̓_��
�ia�Ca���j
���́@�������@�v�Z����

�ڐ��́@��������
�����Ȃ��Ă����Ȃ��Ă���

�@����
��������
������@�����Ȃ��ā@�����Ȃ��Ă���

�ڐ�
�@
�@��
���o���Ƃ���

���ꂼ��́@�����Ƃ́@��_��
�����O�@���@
���ꂼ��Ɂ@�������
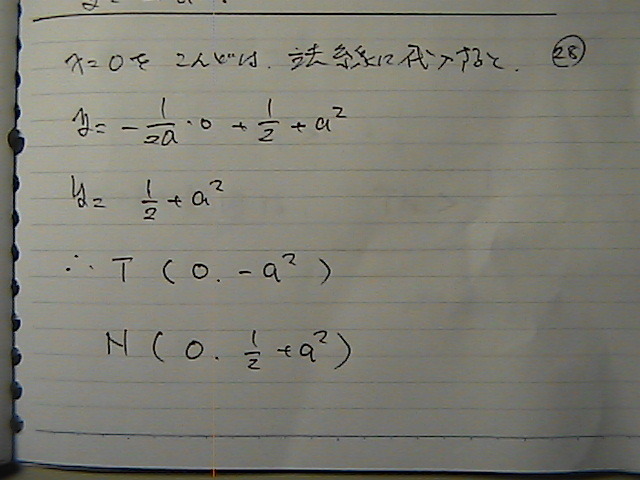
�v���X�@�}�C�i�X
�������Ƃ��Ă��ł���
�����́@�����Ȃ̂�
��Βl���@����

a�́��O�ł́@�Ȃ��̂�
2a���́��O�@�@�Ɓ@1/2
TN�@�@�@>�@�@1/2

���������ā@�ł���
���̃O���t��́@�_
�i�R�@���i�R�j�j�@�ɂ�����@�ڐ���
���́@�O���t�Ɓ@�o��_��
A,B�Ƃ���Ƃ�
AB�@�́@������
���Ƃ߂Ȃ���
�Ȃ�ł���

�܂Á@�ڐ����@���߂�ׂ�
���i���j�@���@��������
���f�i���j�Ɂ@�����R���@�������
�ڐ��́@�X�����@�o����
-4
�i�@�@�Z���Ԉ���Ă��܂��ā@�ʓ|������@�d�������������j
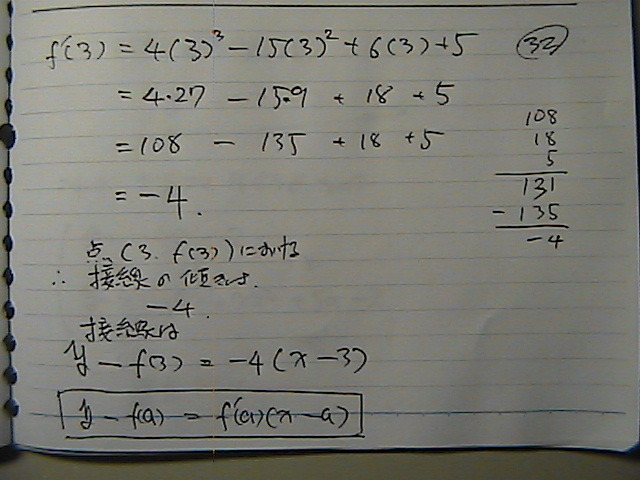
�ڐ��́@�����Ɂ@������ā@���������
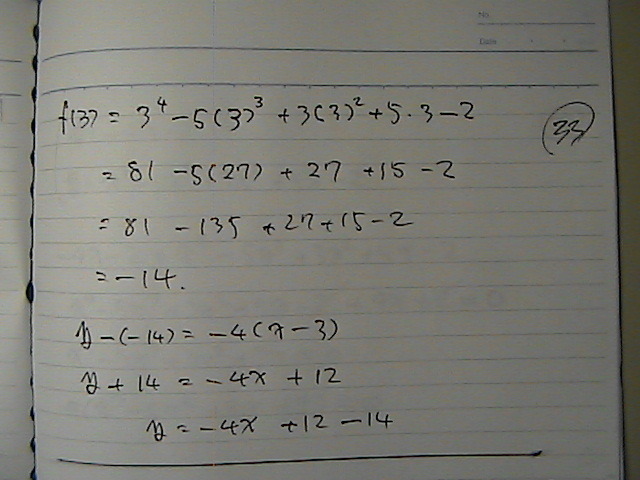
�ڐ��́@���ꂾ���
��
�ڐ���
�O���t�Ɓ@�o�����
�A���@����������i�C�X�J

���@�Ł@�����
�������ā@���O�@�ɂ���
���Ł@�����肾����
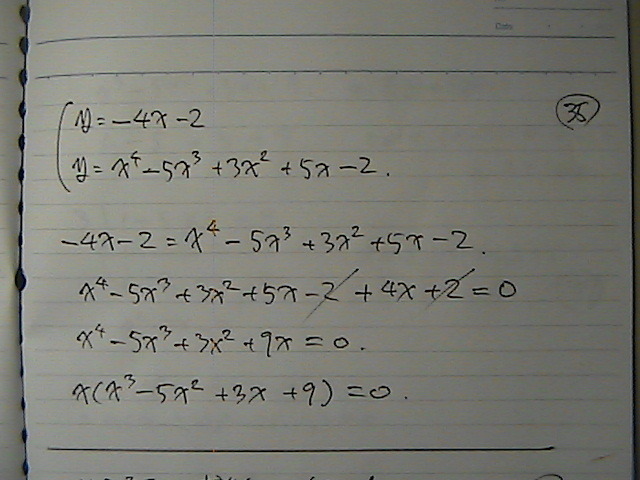
�Ƃ����
�ڐ��Ɓ@�Ȑ��́@�A����������
�ڐ��́@�ړ_�́@���́@�Ȑ���Ɂ@����̂�����
�ړ_�́@�����R�@��
���̘A���������́@���@�́@�����i�C�X�J

�����R�@
���|�R���O
�i���|�R�j�@�Ł@���́@3���́@�����@����Z�����
������͂��ł��̂�
����Ă݂��

�����
���������@���Ă݂��
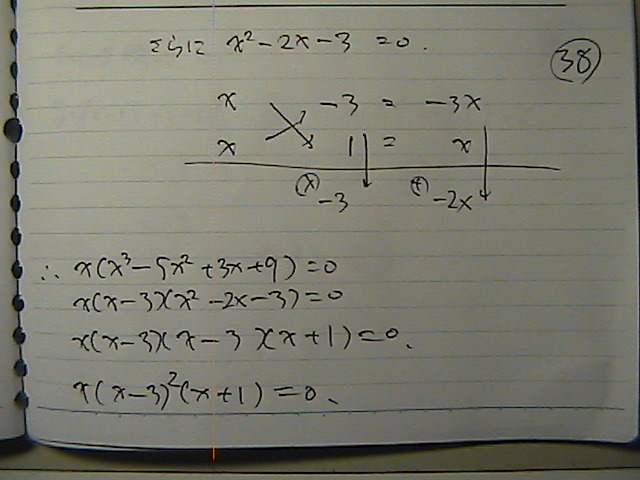
�����@3�̂Ƃ���́@�ړ_�Ȃ̂�
����ȊO�̂Ƃ���
�O�@�̂Ƃ��Ɓ@�|1�̂Ƃ���
�Ăс@�O���t�Ɓ@�o��Ƃ��ł���

A�AB�A
���ꂼ��@�_�̍��W��
�����O�@�����|�P��
���́@�Ȑ��Ɂ@�������ł���
�i�@�ڐ��Ɂ@������������@���������ł����j
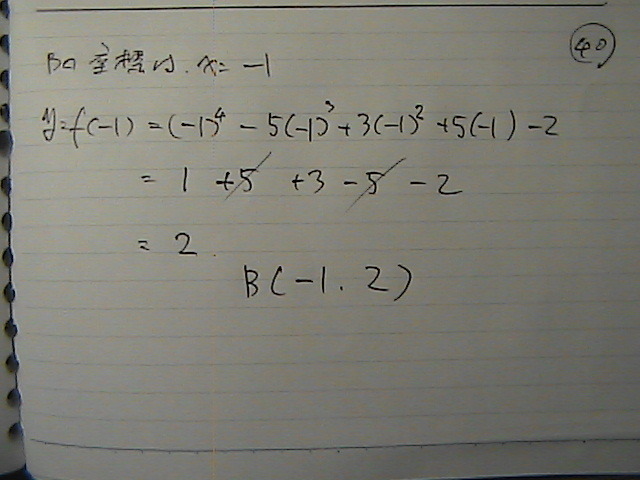
��
��������́@���P��
2�_�Ԃ́@�����́@����ȁ@����������̂�

AB�́@��17
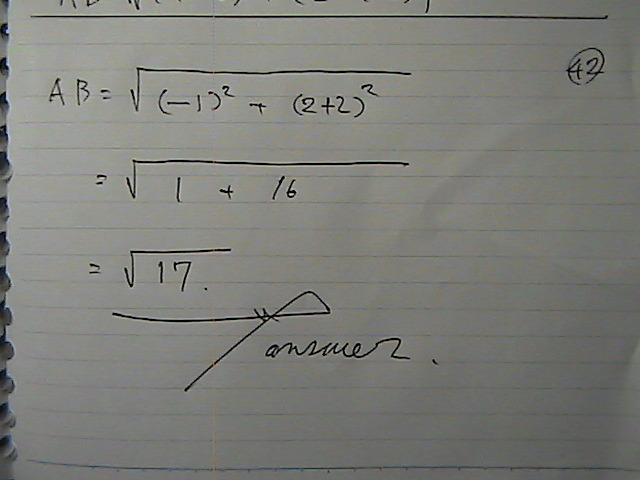
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�Ȑ���Ɂ@������@�ڐ��A�@���́@���ł�
�ڐ��Ɂ@�����Ȃ̂��@�@��
�ڐ��Ɩ@���́@�X���̐ς́@-1�@�ɂȂ�
�s���Ă݂܂��傤
�O���t�@��́@�_��
���ی��Ȃ̂�
���ی��̒��Ł@���@���R��@
�O���t�@�ゾ����@�������@�Ȃ�@�������R�悾���
�ڐ��́@�������@�����Ă���
�@���́@�������@�����Ă���
���i���j
���f�i���j�@���@�g���̂�
�����@��������
�����
�O���t��́@�_�@���@�ɂ�����
�ڐ���
��
�@���̕���
�X�����@�}�C�i�X�@�t��������
����Ȋ�����
�������
�ւĂ���
�i�Q�j�@��
�_P�ɂ�����@�ڐ���
x���@ý���@�Ɓ@���́@�Ȑ���
�����Ƃ����
���ꂼ��@
Q,R,S
�Ƃ����
PQ:QR:RS�͈��@�ł��邱�Ƃ��@����
�}���@�����Ă݂邶��i�C�X�J
P�́@���ی�
���̐ڐ���
�����Ɓ@�����@Q
����r\�ƌ����@R
����Ɂ@���̋Ȑ��Ɓ@������ā@S
�܂�
Q�́@x���ゾ����@�����O�@��
�ڐ��ɑ�������
�����Q��/3
R�@�́@������Ɓ@�u���Ƃ���
�ڐ����@���̋Ȑ��ƌ����_S��
�Ȑ��̃O���t�Ɓ@�ڐ��́@�O���t��
����肾����
���@�Ɂ@�Ȃ�Ƃ��낾���炳
�A���ɂ���ł���
���@�Ł@�ނ����
��������
������@���������ł����
�������o��
�����v�����Ȃ���ł���
�ڐ��́@�ڂ��Ă���b�e�����܂���
���̐ړ_�́@�Ȑ���̓_�ł��̂�
�i�@�_�@���݂��邯�ǁ@�ʐς��Ȃ�����
�@�@�����������Ɂ@����ł���
�@�@���~���Ɓ@��K�Ł@��_������
�@�@�@��_�́@���邯��
�@�@�@�ʐς́@�Ȃ���ˁ@�j
�ړ_�́@���́@���̕������́@���ɂ���
x����
x�[�����O
(x�|���j
����Z����i�C�X�J
����ꂽ�ł���
�����
������������
���@�������́@�|�Q��
�Ȃ���
���������ɂȂ��Ă�@(x�|���j�̕��́@�ړ_�Ȃ̂�
S�́@���@���W�́@�|�Q��
P�Ɓ@S����@x���Ɍ������ā@�������@���낵
���ꂼ��@P'�@�@S'�@�Ƃ���
���ꂼ��́@x���W��
��̒l��
�v�Z�����
�������@������
1�F2�F6
���ł���
���炭���҂���������
�ޑ�
�ڐ��Ɓ@�@�����@���߂�
�ڐ��̌�����
���������ó�
���������@�K�v�Ȃ̂�
����Ƃ��Ăł���
x���Q�̎��́@�ڐ���
���i�Q�j���O
���f�i�Q�j���Q
�����ɑ������
����Ȋ���
�@����
�X�����@�|�t��������ɂ��Ăł���
������
������Ɓ@�ڂ����Ƃ��Ăł���
���Ȃ�
�����@X���@�́@���_�ȊO�̓_��
�ڐ��@�@�����@
�����Ɓ@�����_��
���ꂼ��@T�AN�@�Ƃ����
����TN�́@�����́@�@�ǂ�ȁ@�͈͂ɂȂ邩
�܂���
�ڐ��@�Ɓ@�@�����@���߂˂�
a�́@�O�łȂ��_��
�O���t��̓_��
�ia�Ca���j
���́@�������@�v�Z����
�ڐ��́@��������
�����Ȃ��Ă����Ȃ��Ă���
�@����
��������
������@�����Ȃ��ā@�����Ȃ��Ă���
�ڐ�
�@
�@��
���o���Ƃ���
���ꂼ��́@�����Ƃ́@��_��
�����O�@���@
���ꂼ��Ɂ@�������
�v���X�@�}�C�i�X
�������Ƃ��Ă��ł���
�����́@�����Ȃ̂�
��Βl���@����
a�́��O�ł́@�Ȃ��̂�
2a���́��O�@�@�Ɓ@1/2
TN�@�@�@>�@�@1/2
���������ā@�ł���
���̃O���t��́@�_
�i�R�@���i�R�j�j�@�ɂ�����@�ڐ���
���́@�O���t�Ɓ@�o��_��
A,B�Ƃ���Ƃ�
AB�@�́@������
���Ƃ߂Ȃ���
�Ȃ�ł���
�܂Á@�ڐ����@���߂�ׂ�
���i���j�@���@��������
���f�i���j�Ɂ@�����R���@�������
�ڐ��́@�X�����@�o����
-4
�i�@�@�Z���Ԉ���Ă��܂��ā@�ʓ|������@�d�������������j
�ڐ��́@�����Ɂ@������ā@���������
�ڐ��́@���ꂾ���
��
�ڐ���
�O���t�Ɓ@�o�����
�A���@����������i�C�X�J
���@�Ł@�����
�������ā@���O�@�ɂ���
���Ł@�����肾����
�Ƃ����
�ڐ��Ɓ@�Ȑ��́@�A����������
�ڐ��́@�ړ_�́@���́@�Ȑ���Ɂ@����̂�����
�ړ_�́@�����R�@��
���̘A���������́@���@�́@�����i�C�X�J
�����R�@
���|�R���O
�i���|�R�j�@�Ł@���́@3���́@�����@����Z�����
������͂��ł��̂�
����Ă݂��
�����
���������@���Ă݂��
�����@3�̂Ƃ���́@�ړ_�Ȃ̂�
����ȊO�̂Ƃ���
�O�@�̂Ƃ��Ɓ@�|1�̂Ƃ���
�Ăс@�O���t�Ɓ@�o��Ƃ��ł���
A�AB�A
���ꂼ��@�_�̍��W��
�����O�@�����|�P��
���́@�Ȑ��Ɂ@�������ł���
�i�@�ڐ��Ɂ@������������@���������ł����j
��
��������́@���P��
2�_�Ԃ́@�����́@����ȁ@����������̂�
AB�́@��17
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�^�O�F�Ȑ���́@�ڐ��@�@��
posted by moriamelihu at 09:16| ��l�̂��ї��Ƃ��@
2016�N12��27��
23009 ��l�̂��ї��Ƃ��@��d�����Ɓ@�]��
�J�̓��́@�X���[���C�t�̕���
�Q�d�����Ɓ@�]��
�������@�Q�d�����Ł@���������́@�]�肪
���̂悤�Ɂ@�Ȃ邱�Ƃ��@�ؖ���
������g���ā@���ۂɁ@�]����@���߂���ł��B
�������@�Q�d�����Ł@���������́@�����@Q(x)�@�Ƃ��ā@
���܂�́@�Q�����Ł@����������@�P�����ȉ�
ax + b
���̕\������@����Ɂ@���f�i���j�@���@���߂��
�����́@����ȂȂ��
���̌�����
�����I�Ɂ@���̏�́@������
�g�ݍ��킹��
�o���������@
���
��d�����Ł@���������́@�]��Ȃ̂�
�����́@x�|���@���O�@�ɂȂ�@��
�����@���@���@
�������Ƃł���
����Ȋ����Ȃ̂�
a�����f�i���j�@���@�@�ɑ�������
�C���g�D�[�@�ł���
a ,b ���o�Ă����̂�
���߂�@�]��Ɂ@���Ă͂߂邶��i�C�X�J
��
������@�����ā@���ۂ�
����Ă݂܂���
a���@+�@�@���@�@��a�@�@���Ɂ@������Ƃ���
����Ȃł��̂�
���f�i���j�@����������
��d�����́@�����P�@���@��������
a=5
����
b�͂ˁ@�@-2
����Ȋ�����
����
������@��d������
�������]�肪�@�����Ȃ���
a,b���@���߂�
���Ł@�\�����ā@�ł���
�ւĂ���@�ӁX�����ł���
��������
�����@�Q�{�o�ė��܂���
��d�����@�����|�P�̎��́@�b�ł��̂�
x���|�P���@��������
a+b=-12
�����|�P�T
�����Ȃ��Ă����Ȃ��Ă���
���́@�킩��Ȃ������ł���
�ǂ����킩��Ȃ�������
���̖��ł�
�������ł���
�����@�����Ɓ@������@�`�Ɂ@�ݒ肵�܂��B
���������ā@�����Ă��邩�炳
��
���f�i���j�@�����߂�
��������
���̕\����
������@���@�����Ɓ@�Ⴄ�\���������̂�
�W�J��������
��́@�����Ȃ��ł���
�s�������Ȃ��@����ȓ����@����܂�
�₾�˂��[
����Ă��ł���
��
������
�W�����@��r�������
������
�����@a,b,c,d
�@
�̌`�ɂ����Ƃ���
a�̕�����@���Ԃ�
�����������i�C�X�J
��������
����Ȋ����Ɂ@�@�Ȃ�����
�����
��O�́@���Ɂ@�������ł���
a�@�Ł@��������
�W�J�̌�������
�t�Ɂ@������������
��ӂ��
���i�P�j��8/3
���i-1�j��0
���@�v�Z����
�����P
k���ł�@a���@1/3
�ł��Ă��܂��܂�����
�ޑ肪�@�ł���@�{���ł��B
�R�����̎���
�Ȃ�Ł@1/3�Łi��+���j�@�ɂ����낤��
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�^�O�F��d�����Ɓ@�]��
posted by moriamelihu at 13:40| ��l�̂��ї��Ƃ��@
2016�N12��26��
23008�@��l�̂��ї��Ƃ��@�����@�@�@�@��d�����@�Ɓ@�]��
�J�̓��́@�X���[���C�t�̕���
�������Ɂ@���Q�Ƃ��Ȃ��Ă����
�����ȒP�ɂ́@�s���܂��ʂ���
��������@�l����
�{�C�Ł@�����@�ƍl���Ƃ�܂�
�C���ςɁ@�Ȃ�Ȃ��悤��
�v�����f���ł�
���Ă邩�ȂƁ@�v������
�s���߂��ā@�����Ă��܂�
�E�E��k�́@�Ƃ�����
�����́@�����@�ł���
������@�܂Ƃ��Ɂ@���Ɓ@�v�Z�ԈႢ����
�Ȃ̂�
��������O��
�ł��邾���@���₷���@�ό`�����ł���
�w���́@�����Ɓ@���������̌���
�Ł@�ό`�������̂�
�����́@������
�������Ă�܂�
������
�Ȃ��Ă��܂��܂�����
�T�������炢�@�ԈႦ������
���e�́@��u�ł����B
��d�����@�Ɓ@�]��
����
�������@���̂悤�ȁ@�@���ʂ́@����
������Ȃ�@�@�A���t�@�@��
���i���j���O�@���f�i���j���O�@
�́u���ʉ��v�@���@��������
������@�g����
�����@�L�����ł��邱�Ƃ��@�ؖ�������ł�
�������@�P����ł�����
���ʉ��ł��邱�Ƃ�
�����̂�
��������Ⴄ�@�@x�����@���@�����ɂイ�����
���ꂪ�@�ˁ@���@�O�@�ɂȂ�͂��Ȃ�ł�
������́@�\�����@���w�ł����
������@���́@�@���鐔�@×�@��
�f�V��
�����
�������邶��i�C�X�J
���́@���Ɓ@
�������������@�o�ė���
����Ɂ@���ꂼ��@���@���@�������Ɓ@�ł�
f�f(���j���O
�Ȃ�������i�C�X�J
�Ł@
�������@�Q��
�ǂȂ�����˂�
���́@�Ȋw�҂́@�����ƈ����
������l���@���邽��
������悤�Ɂ@�Ȃ��Ă܂�
�Ȋw�����̏ꍇ�́@�n����Ɂ@�M�Ł@�߂Â��Ă�������
���Ԃ�@(�P)�̌��ʂ��@�g����ł���
��
���ʂP�ł́@
���i���j���O�A�@���f�i���j���O�@�@���@
�����@���ʉ��Ɂ@�����Ƃ�
�ؖ������̂�
������@�g����悤��
���f�i���j�@���@���߂ā@�ł�����i�C�X�J
���i���j���O�A�@���f�i���j���O�@�@�Ɂ@x�����@���@��������
�@�@�A�@���Ƃ��Ăł���
��������@���@���@���߁@�E�E
���O�@�O
�L�����́@
���P���@���邶��i�C�X�J
�����Ł@�\����@�����ł���
��
�L�������m�́@���Z�́@�������@�L����
�e���p
���@�́@�w���������@�����������̂�
�@�@��
�A�@��
�w���́@�v�Z���@�m�F�����肵�Ăł���
��@�����o�Ă����ł���
�����Z����
�}�C�i�X��
�����肾����
������
�n���C�~�o�G�@�Ⴂ�܂�
�c�G�c�G�o�G�@�@�ꖡ�́@����
��ȁ@�W���[�N�ł���
�~�o�G�@���@�悭����
�����@�o����
�L�������m�́@���Z�Ȃ̂�
�����@�L����
�Ƃ����
���́@�ł���
������Ƃ��@�b�e�����̂́@�藝�Ȃ���
�ؖ������
�����Ȃ������Ƃ���
�]�肪����@�@�]��́@�P���ȉ��Ȃ̂�
ax�@+�@���@�Ƃ���
���̗]����@���߂��
f(���j���O
f�f(���j���O
�Ȃ̂�
f(���j��a��+�����O
f�f(���j���O
�Ȃ̂�
�������Ƃ��Ăł���
f�f(���j��a���O
���������ā@a=b=0
��
���܂肪�@�O�@�ɂȂ��Ă��܂����̂�
����ꂽ�B
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
posted by moriamelihu at 22:13| ��l�̂��ї��Ƃ��@