2016�N12��29��
23010 ��l�̂��ї��Ƃ��@�Ȑ���́@�ڐ��@�@��
�J�̓��́@�X���[���C�t�̕���
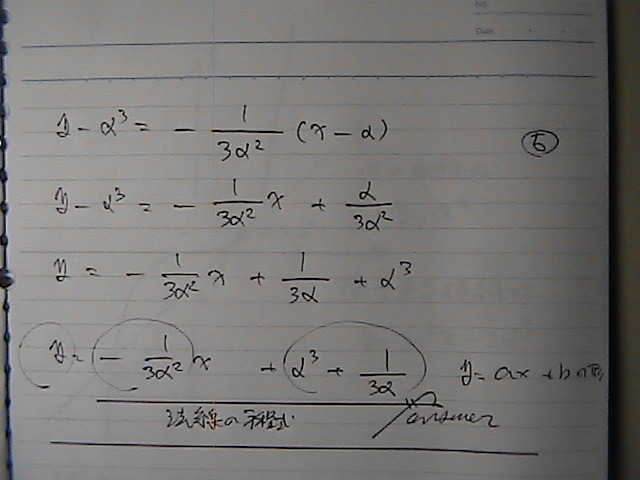
�Ȑ���Ɂ@������@�ڐ��A�@���́@���ł�
�ڐ��Ɂ@�����Ȃ̂��@�@��
�ڐ��Ɩ@���́@�X���̐ς́@-1�@�ɂȂ�
�s���Ă݂܂��傤

�O���t�@��́@�_��
���ی��Ȃ̂�
���ی��̒��Ł@���@���R��@
�O���t�@�ゾ����@�������@�Ȃ�@�������R�悾���
�ڐ��́@�������@�����Ă���
�@���́@�������@�����Ă���

���i���j
���f�i���j�@���@�g���̂�
�����@��������
�����
�O���t��́@�_�@���@�ɂ�����
�ڐ���

��
�@���̕���
�X�����@�}�C�i�X�@�t��������

����Ȋ�����
�������
�ւĂ���
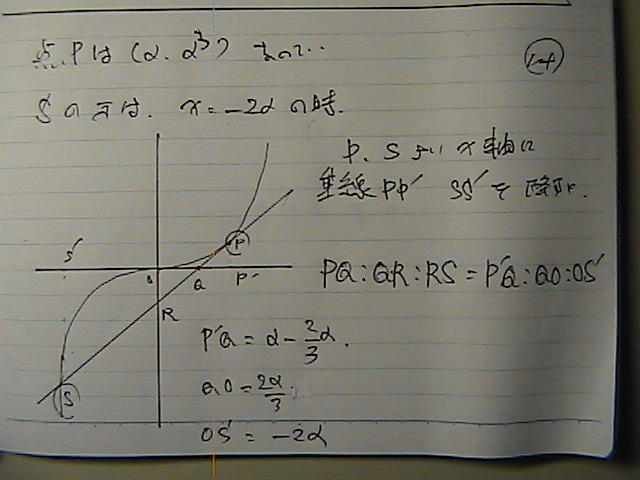
�i�Q�j�@��
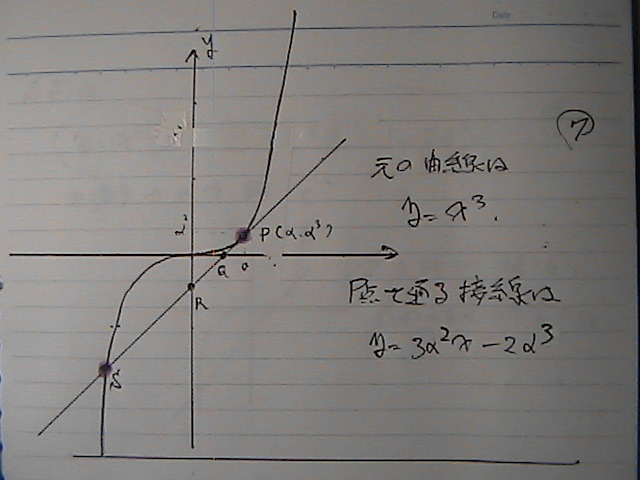
�_P�ɂ�����@�ڐ���
x���@ý���@�Ɓ@���́@�Ȑ���
�����Ƃ����
���ꂼ��@
Q,R,S
�Ƃ����
PQ:QR:RS�͈��@�ł��邱�Ƃ��@����

�}���@�����Ă݂邶��i�C�X�J
P�́@���ی�
���̐ڐ���
�����Ɓ@�����@Q
����r\�ƌ����@R
����Ɂ@���̋Ȑ��Ɓ@������ā@S
�܂�
Q�́@x���ゾ����@�����O�@��
�ڐ��ɑ�������
�����Q��/3

R�@�́@������Ɓ@�u���Ƃ���
�ڐ����@���̋Ȑ��ƌ����_S��
�Ȑ��̃O���t�Ɓ@�ڐ��́@�O���t��
����肾����
���@�Ɂ@�Ȃ�Ƃ��낾���炳
�A���ɂ���ł���

���@�Ł@�ނ����
��������
������@���������ł����
�������o��
�����v�����Ȃ���ł���

�ڐ��́@�ڂ��Ă���b�e�����܂���
���̐ړ_�́@�Ȑ���̓_�ł��̂�
�i�@�_�@���݂��邯�ǁ@�ʐς��Ȃ�����
�@�@�����������Ɂ@����ł���
�@�@���~���Ɓ@��K�Ł@��_������
�@�@�@��_�́@���邯��
�@�@�@�ʐς́@�Ȃ���ˁ@�j
�ړ_�́@���́@���̕������́@���ɂ���
x����
x�[�����O
(x�|���j
����Z����i�C�X�J
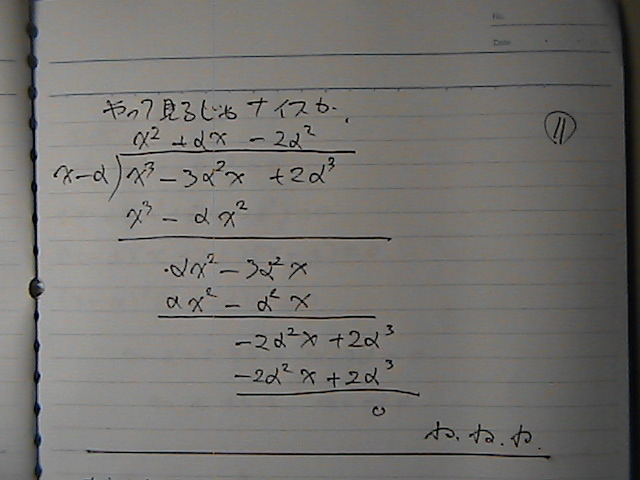
����ꂽ�ł���
�����
������������
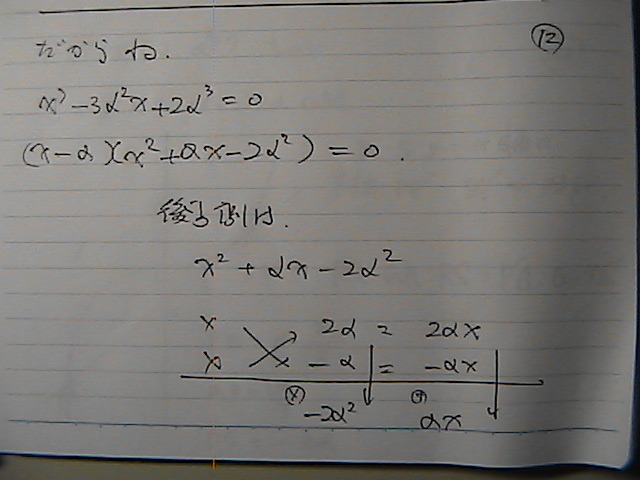
���@�������́@�|�Q��
�Ȃ���
���������ɂȂ��Ă�@(x�|���j�̕��́@�ړ_�Ȃ̂�
S�́@���@���W�́@�|�Q��
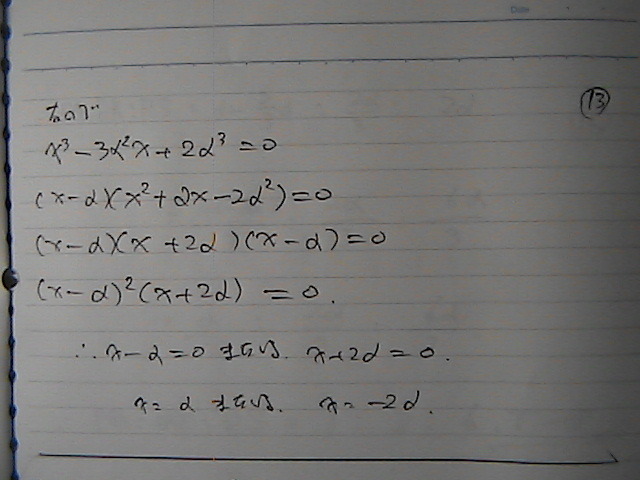
P�Ɓ@S����@x���Ɍ������ā@�������@���낵
���ꂼ��@P'�@�@S'�@�Ƃ���
���ꂼ��́@x���W��
��̒l��
�v�Z�����
�������@������
1�F2�F6
���ł���

���炭���҂���������

�ޑ�
�ڐ��Ɓ@�@�����@���߂�

�ڐ��̌�����
���������ó�
���������@�K�v�Ȃ̂�
����Ƃ��Ăł���
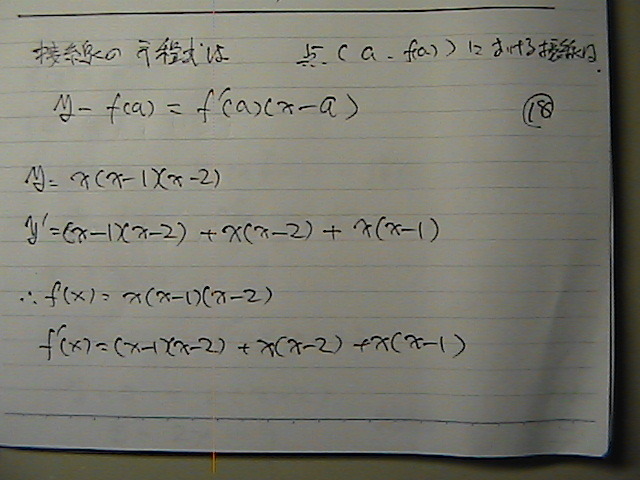
x���Q�̎��́@�ڐ���
���i�Q�j���O
���f�i�Q�j���Q
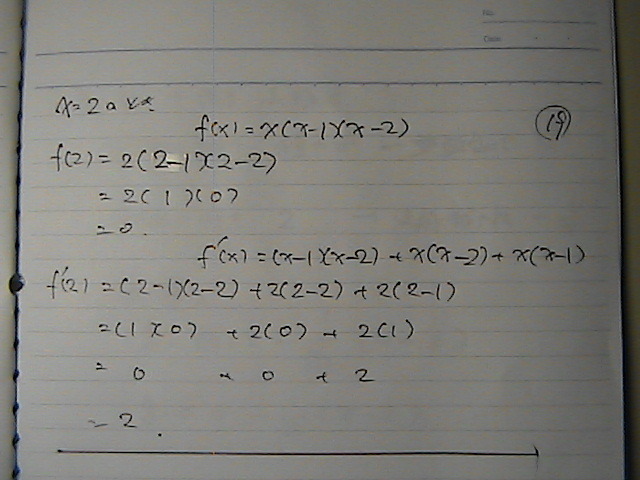
�����ɑ������
����Ȋ���

�@����
�X�����@�|�t��������ɂ��Ăł���
������

������Ɓ@�ڂ����Ƃ��Ăł���
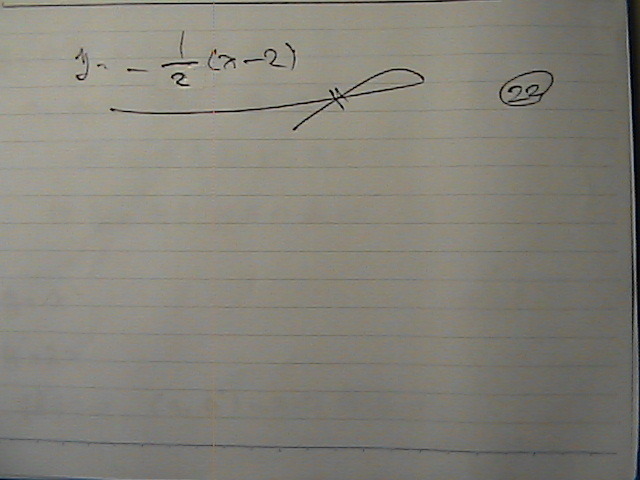
���Ȃ�
�����@X���@�́@���_�ȊO�̓_��
�ڐ��@�@�����@
�����Ɓ@�����_��
���ꂼ��@T�AN�@�Ƃ����
����TN�́@�����́@�@�ǂ�ȁ@�͈͂ɂȂ邩

�܂���
�ڐ��@�Ɓ@�@�����@���߂˂�
a�́@�O�łȂ��_��
�O���t��̓_��
�ia�Ca���j
���́@�������@�v�Z����

�ڐ��́@��������
�����Ȃ��Ă����Ȃ��Ă���

�@����
��������
������@�����Ȃ��ā@�����Ȃ��Ă���

�ڐ�
�@
�@��
���o���Ƃ���

���ꂼ��́@�����Ƃ́@��_��
�����O�@���@
���ꂼ��Ɂ@�������
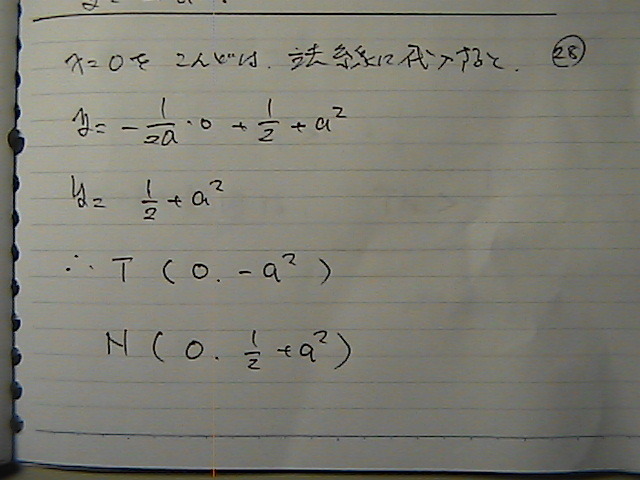
�v���X�@�}�C�i�X
�������Ƃ��Ă��ł���
�����́@�����Ȃ̂�
��Βl���@����

a�́��O�ł́@�Ȃ��̂�
2a���́��O�@�@�Ɓ@1/2
TN�@�@�@>�@�@1/2

���������ā@�ł���
���̃O���t��́@�_
�i�R�@���i�R�j�j�@�ɂ�����@�ڐ���
���́@�O���t�Ɓ@�o��_��
A,B�Ƃ���Ƃ�
AB�@�́@������
���Ƃ߂Ȃ���
�Ȃ�ł���

�܂Á@�ڐ����@���߂�ׂ�
���i���j�@���@��������
���f�i���j�Ɂ@�����R���@�������
�ڐ��́@�X�����@�o����
-4
�i�@�@�Z���Ԉ���Ă��܂��ā@�ʓ|������@�d�������������j
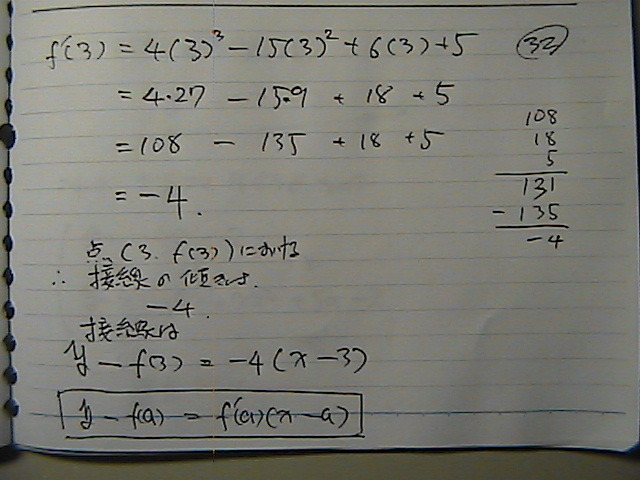
�ڐ��́@�����Ɂ@������ā@���������
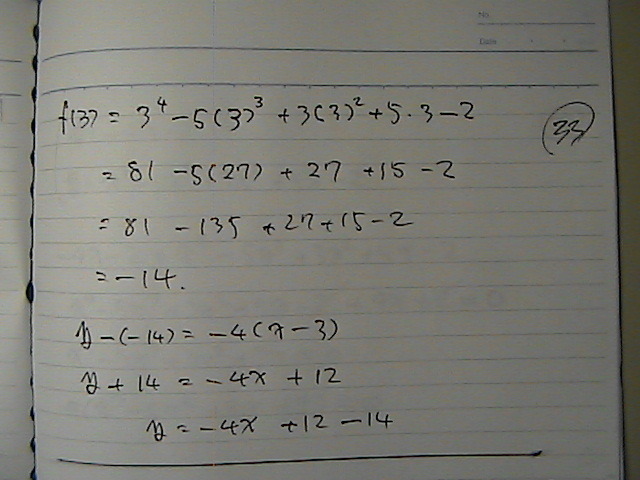
�ڐ��́@���ꂾ���
��
�ڐ���
�O���t�Ɓ@�o�����
�A���@����������i�C�X�J

���@�Ł@�����
�������ā@���O�@�ɂ���
���Ł@�����肾����
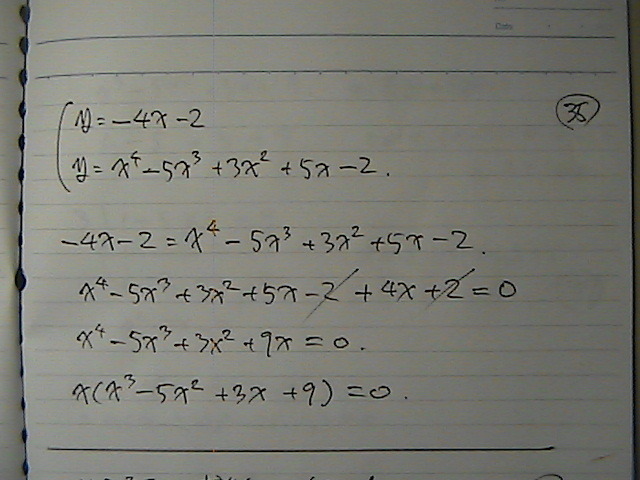
�Ƃ����
�ڐ��Ɓ@�Ȑ��́@�A����������
�ڐ��́@�ړ_�́@���́@�Ȑ���Ɂ@����̂�����
�ړ_�́@�����R�@��
���̘A���������́@���@�́@�����i�C�X�J

�����R�@
���|�R���O
�i���|�R�j�@�Ł@���́@3���́@�����@����Z�����
������͂��ł��̂�
����Ă݂��

�����
���������@���Ă݂��
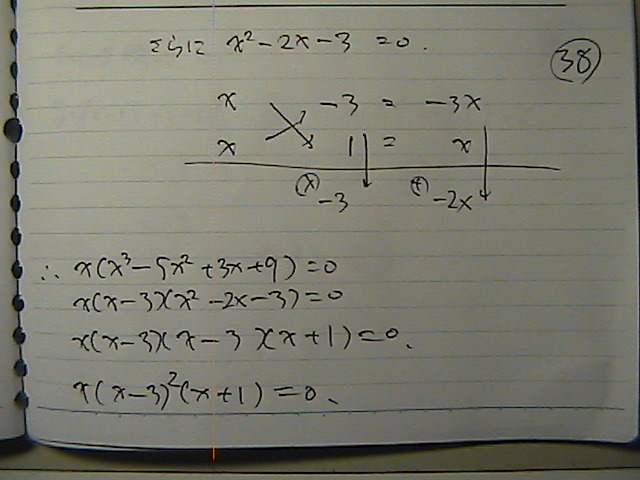
�����@3�̂Ƃ���́@�ړ_�Ȃ̂�
����ȊO�̂Ƃ���
�O�@�̂Ƃ��Ɓ@�|1�̂Ƃ���
�Ăс@�O���t�Ɓ@�o��Ƃ��ł���

A�AB�A
���ꂼ��@�_�̍��W��
�����O�@�����|�P��
���́@�Ȑ��Ɂ@�������ł���
�i�@�ڐ��Ɂ@������������@���������ł����j
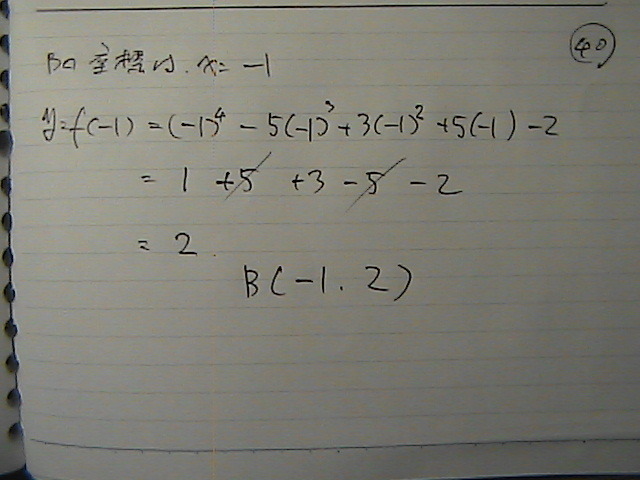
��
��������́@���P��
2�_�Ԃ́@�����́@����ȁ@����������̂�

AB�́@��17
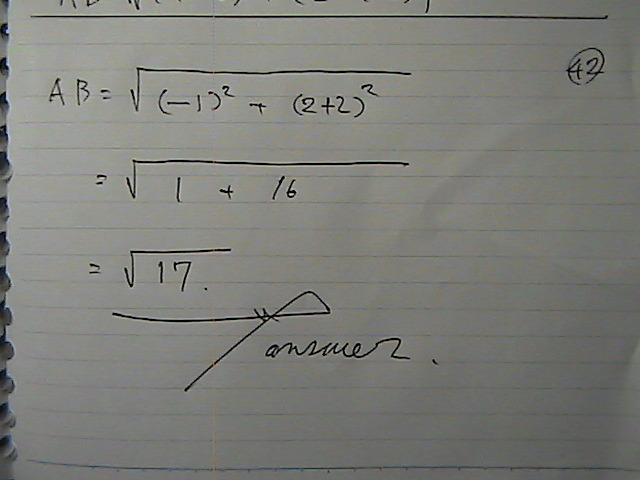
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�Ȑ���Ɂ@������@�ڐ��A�@���́@���ł�
�ڐ��Ɂ@�����Ȃ̂��@�@��
�ڐ��Ɩ@���́@�X���̐ς́@-1�@�ɂȂ�
�s���Ă݂܂��傤
�O���t�@��́@�_��
���ی��Ȃ̂�
���ی��̒��Ł@���@���R��@
�O���t�@�ゾ����@�������@�Ȃ�@�������R�悾���
�ڐ��́@�������@�����Ă���
�@���́@�������@�����Ă���
���i���j
���f�i���j�@���@�g���̂�
�����@��������
�����
�O���t��́@�_�@���@�ɂ�����
�ڐ���
��
�@���̕���
�X�����@�}�C�i�X�@�t��������
����Ȋ�����
�������
�ւĂ���
�i�Q�j�@��
�_P�ɂ�����@�ڐ���
x���@ý���@�Ɓ@���́@�Ȑ���
�����Ƃ����
���ꂼ��@
Q,R,S
�Ƃ����
PQ:QR:RS�͈��@�ł��邱�Ƃ��@����
�}���@�����Ă݂邶��i�C�X�J
P�́@���ی�
���̐ڐ���
�����Ɓ@�����@Q
����r\�ƌ����@R
����Ɂ@���̋Ȑ��Ɓ@������ā@S
�܂�
Q�́@x���ゾ����@�����O�@��
�ڐ��ɑ�������
�����Q��/3
R�@�́@������Ɓ@�u���Ƃ���
�ڐ����@���̋Ȑ��ƌ����_S��
�Ȑ��̃O���t�Ɓ@�ڐ��́@�O���t��
����肾����
���@�Ɂ@�Ȃ�Ƃ��낾���炳
�A���ɂ���ł���
���@�Ł@�ނ����
��������
������@���������ł����
�������o��
�����v�����Ȃ���ł���
�ڐ��́@�ڂ��Ă���b�e�����܂���
���̐ړ_�́@�Ȑ���̓_�ł��̂�
�i�@�_�@���݂��邯�ǁ@�ʐς��Ȃ�����
�@�@�����������Ɂ@����ł���
�@�@���~���Ɓ@��K�Ł@��_������
�@�@�@��_�́@���邯��
�@�@�@�ʐς́@�Ȃ���ˁ@�j
�ړ_�́@���́@���̕������́@���ɂ���
x����
x�[�����O
(x�|���j
����Z����i�C�X�J
����ꂽ�ł���
�����
������������
���@�������́@�|�Q��
�Ȃ���
���������ɂȂ��Ă�@(x�|���j�̕��́@�ړ_�Ȃ̂�
S�́@���@���W�́@�|�Q��
P�Ɓ@S����@x���Ɍ������ā@�������@���낵
���ꂼ��@P'�@�@S'�@�Ƃ���
���ꂼ��́@x���W��
��̒l��
�v�Z�����
�������@������
1�F2�F6
���ł���
���炭���҂���������
�ޑ�
�ڐ��Ɓ@�@�����@���߂�
�ڐ��̌�����
���������ó�
���������@�K�v�Ȃ̂�
����Ƃ��Ăł���
x���Q�̎��́@�ڐ���
���i�Q�j���O
���f�i�Q�j���Q
�����ɑ������
����Ȋ���
�@����
�X�����@�|�t��������ɂ��Ăł���
������
������Ɓ@�ڂ����Ƃ��Ăł���
���Ȃ�
�����@X���@�́@���_�ȊO�̓_��
�ڐ��@�@�����@
�����Ɓ@�����_��
���ꂼ��@T�AN�@�Ƃ����
����TN�́@�����́@�@�ǂ�ȁ@�͈͂ɂȂ邩
�܂���
�ڐ��@�Ɓ@�@�����@���߂˂�
a�́@�O�łȂ��_��
�O���t��̓_��
�ia�Ca���j
���́@�������@�v�Z����
�ڐ��́@��������
�����Ȃ��Ă����Ȃ��Ă���
�@����
��������
������@�����Ȃ��ā@�����Ȃ��Ă���
�ڐ�
�@
�@��
���o���Ƃ���
���ꂼ��́@�����Ƃ́@��_��
�����O�@���@
���ꂼ��Ɂ@�������
�v���X�@�}�C�i�X
�������Ƃ��Ă��ł���
�����́@�����Ȃ̂�
��Βl���@����
a�́��O�ł́@�Ȃ��̂�
2a���́��O�@�@�Ɓ@1/2
TN�@�@�@>�@�@1/2
���������ā@�ł���
���̃O���t��́@�_
�i�R�@���i�R�j�j�@�ɂ�����@�ڐ���
���́@�O���t�Ɓ@�o��_��
A,B�Ƃ���Ƃ�
AB�@�́@������
���Ƃ߂Ȃ���
�Ȃ�ł���
�܂Á@�ڐ����@���߂�ׂ�
���i���j�@���@��������
���f�i���j�Ɂ@�����R���@�������
�ڐ��́@�X�����@�o����
-4
�i�@�@�Z���Ԉ���Ă��܂��ā@�ʓ|������@�d�������������j
�ڐ��́@�����Ɂ@������ā@���������
�ڐ��́@���ꂾ���
��
�ڐ���
�O���t�Ɓ@�o�����
�A���@����������i�C�X�J
���@�Ł@�����
�������ā@���O�@�ɂ���
���Ł@�����肾����
�Ƃ����
�ڐ��Ɓ@�Ȑ��́@�A����������
�ڐ��́@�ړ_�́@���́@�Ȑ���Ɂ@����̂�����
�ړ_�́@�����R�@��
���̘A���������́@���@�́@�����i�C�X�J
�����R�@
���|�R���O
�i���|�R�j�@�Ł@���́@3���́@�����@����Z�����
������͂��ł��̂�
����Ă݂��
�����
���������@���Ă݂��
�����@3�̂Ƃ���́@�ړ_�Ȃ̂�
����ȊO�̂Ƃ���
�O�@�̂Ƃ��Ɓ@�|1�̂Ƃ���
�Ăс@�O���t�Ɓ@�o��Ƃ��ł���
A�AB�A
���ꂼ��@�_�̍��W��
�����O�@�����|�P��
���́@�Ȑ��Ɂ@�������ł���
�i�@�ڐ��Ɂ@������������@���������ł����j
��
��������́@���P��
2�_�Ԃ́@�����́@����ȁ@����������̂�
AB�́@��17
�i�@���ꕔ�����@�ƒ�؉����T�e�@�S�e�@�R�e�@�Q�e�@1 F��������
���j���E�@�y�[�W�@���^�[���@�@�@�@�j
�^�O�F�Ȑ���́@�ڐ��@�@��
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by moriamelihu at 09:16| ��l�̂��ї��Ƃ��@