新規記事の投稿を行うことで、非表示にすることが可能です。
2022年09月28日
22008 大人のさび落とし 分点ベクトル
大人のさび落とし
今日は 分点ベクトルですが
その前に
01
必要な知識を
まず
位置ベクトルの考え方
02
今日の本題
分点ベクトル
2本の ベクトルで
それぞれ
遠い方を かけ合わせる感じに
C=の公式を
3列目に 変形するにあたり
全体を 1と考えて
m:n 何のだから
m/(m+n)=t とすれば
n/(m+n)=1-tであるので
ソレゾレ
nが(1-t) mがt
03
特に
分点ベクトルで
中点は
また
外分の時は
04
重心ベクトルは
05
一次独立な
ベクトルが あるとき
06
直線になるとき
平面になるとき
07
立体になるとき
08
では 位置ベクトルを 使って
分点ベクトルの問題
09
ここで
表現の仕方ですが
ADは 辺
AB 上にある
つまり A,D,Bは
一直線上にあるのだから
AD=k AB
10
ODは OAに AD を足したものだ
ADは K倍のAB だから
そこんとこの k 倍は
m/(m+n)
OAは そのまま aベクトル
AB は OB-OA
だから b-a
ナタメ
11
こんな感じに なるですが
展開して
整理したらば
公式通りに
12
重心を Gとして
OGを 求めよ
ですが
三角形の
重心の特徴があったデショ
ABの中点をMとしたらば
OMは こんなデショ
OGは
OCとOMを 2:1に 内分するから
それが重心
だから
13
問題
14
作図してじゃナイスカ
AB CD の中点が
ソレゾレ
M,N
なので
OM ONは それぞれ
中点の 公式で
求めるのは
MNの 中点 OP
であるので
この答えは
四面体の 重心だね
15
四面体の中で
三角形 BCDの重心を G1
とすれば
四面体の三角形 BCDの 外にある
Aから G1への 線分を
3:1に内分する点を Q
として
OQ ベクトルは
重心の ベクトルを
計算して
Aと G1を 3:1に内分であるから
16
計算したら
これは
四面体の重心だね
17
問題
18
数学では
答を 予測すること大事で
一見違うものを
きっとこれに なるだろうと
近づけていくとかね
( 宇宙際 対比
ミューラー理論は
わかりませんが )
望月博士に
人の心に
思い浮かびもしなかったことが
供えられていたとしたら
いいなぁ
ホントにね
寅さんじゃないけど
上を向いたら
きりがなく
下を向いたら
後がない
やばいじゃんか なぁーな
さび落としが
お届けしています
2022年09月14日
22007 大人のさび落とし 空間座標とベクトル ベクトルの大きさ
大人のさび落とし
22007
ベクトルの大きさ
01
問題を 読んでね
この 条件式を 良く見ると

02
AB だけ 異物感があるでしょ
そこで
右辺の AB を 左辺の ベクトルで
表現したらば
これは
決まって使う手段ですが
AB= PB-PA

03
左辺に 集めて 整理すると

04
PC=2AP
ベクトルの 実数倍
方向が同じ
点Pを 共有している
つまり
A,P,Cは 一直線上にある
それで
AP:PC= 1:2
であるので

05
三角形ABCの 辺ACを 1:2に
内分する点が P
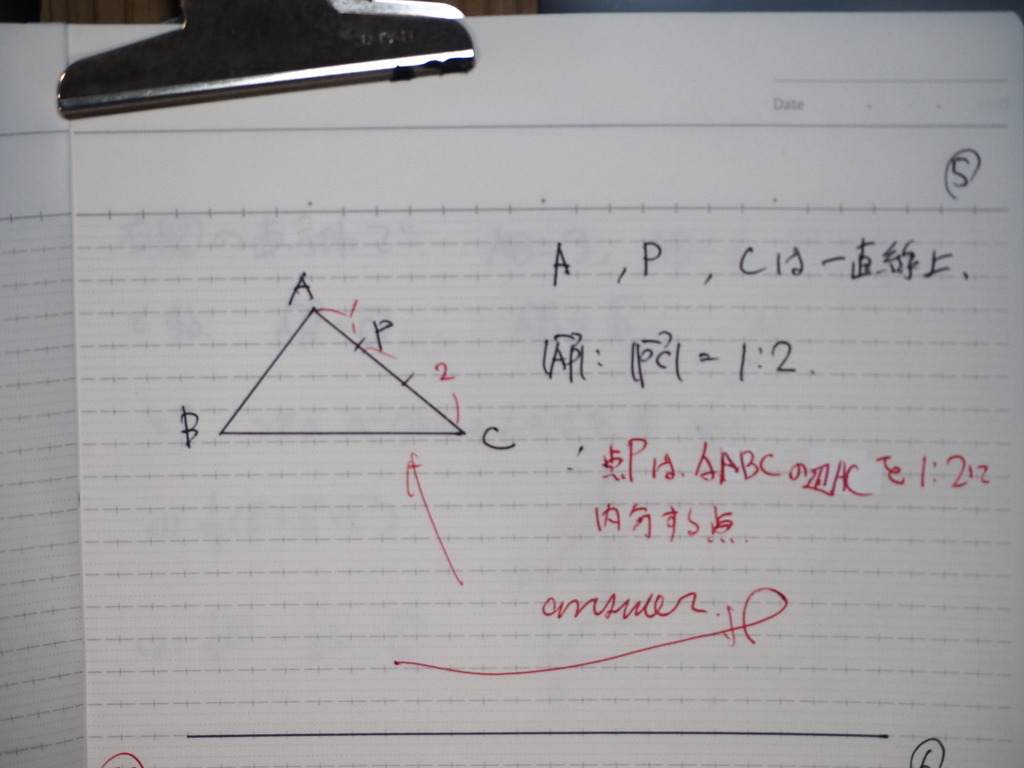
06
ここで
入れ知恵タイム
ベクトルの 大きさを 比較するとき
こんなカンじに 成るけど
右の 等号は a と bが 同じ向きの時
左の 等号は a と bが 反対向きの時

07
問題
右の図で
これこれの時
次の 値を 計算しなさい
良く見ると
a,b,c,は 互いに 垂直方向
そのまんま 足すわけには 行きません
立体的に
足し終えた後の
ベクトルの 大きさを 調べないと

08
こういう問題なんだね

09
AGが こんなだから

10
対角線AGの大きさを 調べて

11
(2)は
こんな感じに 成るから
この座表成分から
Aとの距離を 計算して

12
こんなですか

13
証明問題
まず
MN に関しては
こないだ も 同じものが出てたので
(22006の 1問目)

14
こんな感じで
ここまでは
出て来ますよ
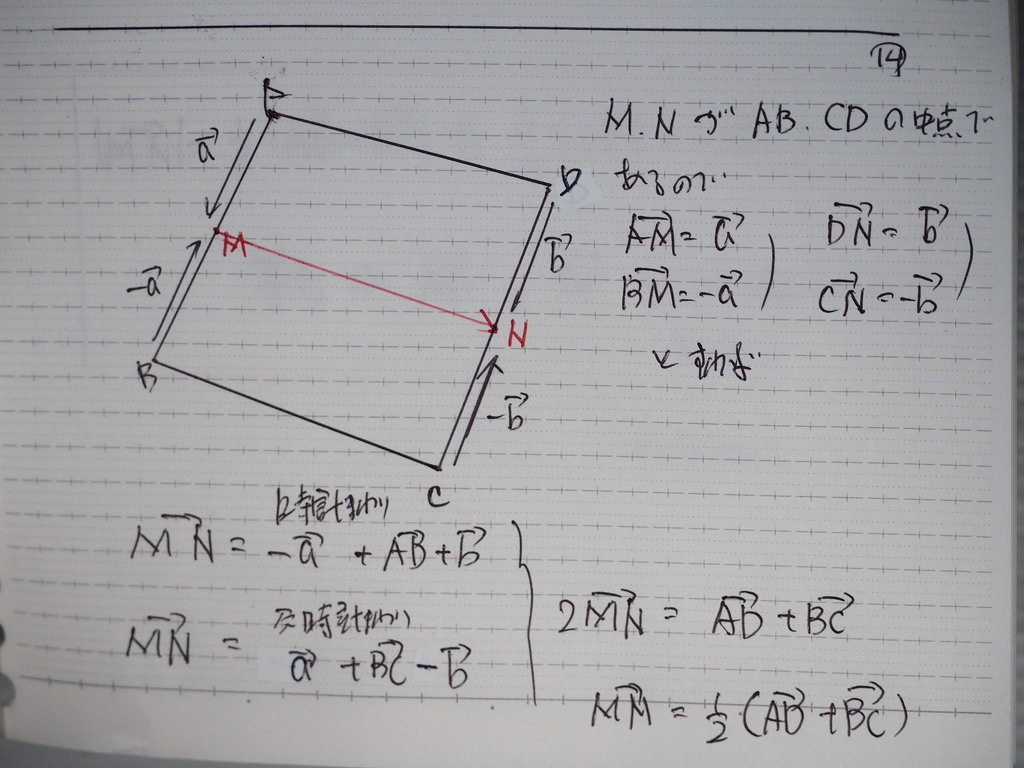
15
それで
これは 空間の ベクトルだから

16
左辺は 中辺に等しくて 右辺とは
こんな感じに 成る

17
問題
読んでいただいて
途中までは
一番 初めの問題と
ほぼ そっくり そのまま

18
こんな感じに

19
どがんな 位置に Pが あるか
見ると

20
こだからんな

21
題意より
求めるものは
三角形 ACP と BCP の
面積比
であるので
高さが おなじとかんがえて
底辺× 高さ 割る 2
違うとこは
底辺の 比だけ
なので
1:2
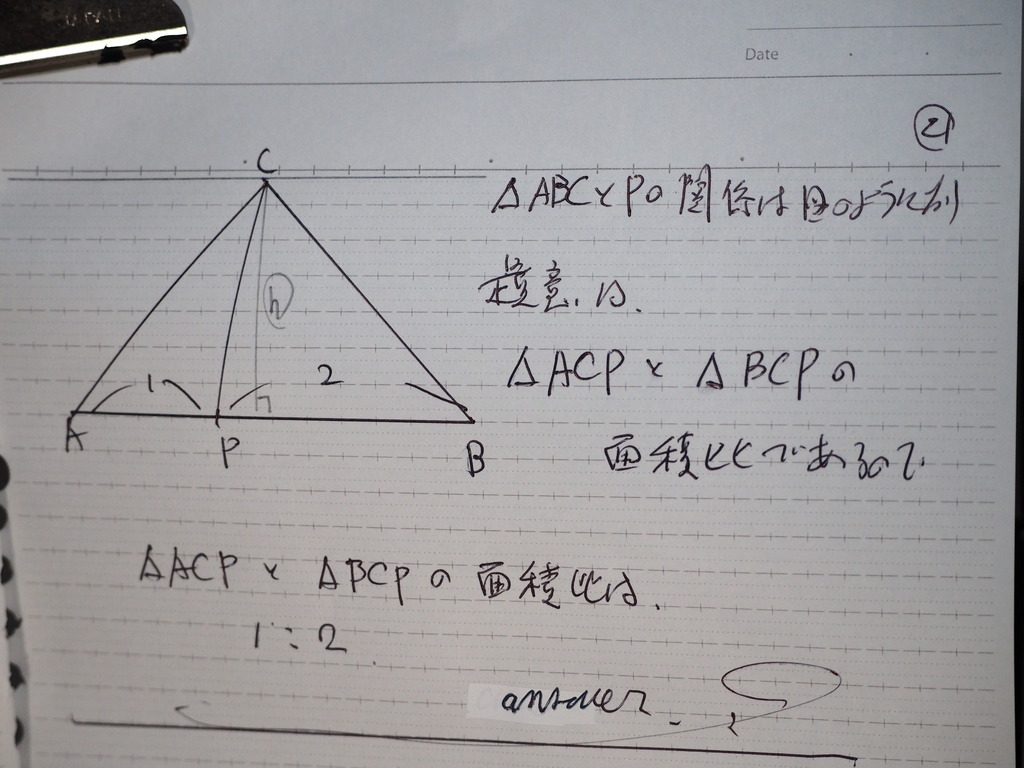
お疲れ様です。
メニュウ
22007
ベクトルの大きさ
01
問題を 読んでね
この 条件式を 良く見ると
02
AB だけ 異物感があるでしょ
そこで
右辺の AB を 左辺の ベクトルで
表現したらば
これは
決まって使う手段ですが
AB= PB-PA
03
左辺に 集めて 整理すると
04
PC=2AP
ベクトルの 実数倍
方向が同じ
点Pを 共有している
つまり
A,P,Cは 一直線上にある
それで
AP:PC= 1:2
であるので
05
三角形ABCの 辺ACを 1:2に
内分する点が P
06
ここで
入れ知恵タイム
ベクトルの 大きさを 比較するとき
こんなカンじに 成るけど
右の 等号は a と bが 同じ向きの時
左の 等号は a と bが 反対向きの時
07
問題
右の図で
これこれの時
次の 値を 計算しなさい
良く見ると
a,b,c,は 互いに 垂直方向
そのまんま 足すわけには 行きません
立体的に
足し終えた後の
ベクトルの 大きさを 調べないと
08
こういう問題なんだね
09
AGが こんなだから
10
対角線AGの大きさを 調べて
11
(2)は
こんな感じに 成るから
この座表成分から
Aとの距離を 計算して
12
こんなですか
13
証明問題
まず
MN に関しては
こないだ も 同じものが出てたので
(22006の 1問目)
14
こんな感じで
ここまでは
出て来ますよ
15
それで
これは 空間の ベクトルだから
16
左辺は 中辺に等しくて 右辺とは
こんな感じに 成る
17
問題
読んでいただいて
途中までは
一番 初めの問題と
ほぼ そっくり そのまま
18
こんな感じに
19
どがんな 位置に Pが あるか
見ると
20
こだからんな
21
題意より
求めるものは
三角形 ACP と BCP の
面積比
であるので
高さが おなじとかんがえて
底辺× 高さ 割る 2
違うとこは
底辺の 比だけ
なので
1:2
お疲れ様です。
メニュウ
2022年09月13日
22006 大人のさび落とし 空間ベクトル ベクトルの実数倍
大人のさび落とし
ベクトルの実数倍
01
問題を よんでいただいて
図を 書かないと
よくわかんないですが
02
その前に
中点の 使い方は
中点を はさんで
同じベクトルにするか
反対向きに大きさの等しいものにするか
または
全体を 中点までの 2倍にするか
03
それを 踏まえまして
問題のを作図すると こんな感じ
中点を はさんで
大きさの等しい
反対向きベクトルを
使いました
04
それで
中点を むすんだ 線分のベクトル
MN を
右回り 左回りで
計算して
ちゃんと 中点を 表現した
ベクトルを
式に 取り込むでしょ
そして
➀②を 足して
2で割れば
05
同じ問題の
別解
三角形に 考えて
ACの中L点をLとすれば
M,Lは
中点であるから
ML=1/2(BC)
06
お隣の三角形は
同様に
LN=1/2(AD)
MN=ML+LNであるから
MN=1/2(BC+AD)
07
問題を 読んでいただいて
08
作図するとじゃナイスカ
1:2に 内分を
c と d を 使って
09
こんな感じに
時計回り 反時計回りで
1:2 になってますよを
式に 取り込んで
➀②式
10
題意では PQを
aと bで 表せなので
c と dを 消去すべく
➀×2 + ②
で行ってみますと
11
こんな感じですか
12
直方体で
次の式を 証明せよ
13
AB= a
AD= b
AC= c
とすれば
各4ほんづつ
同じベクトルが出て来て
AG=AE+EF+EG とすれば
右辺は 2(a+b+c)
14
左辺は 計算してくと
なったですね
15
問題を 読んでいただいて
16
作図は こんな感じ
題意は M1 M2 M3が
一直線上に あることを言う
一直線上 ならば
M2M3= 実数倍の M1M2
そこで
17
4面体の 対辺同士の中点を
結んだ線分は
対辺の和の半分 ッテいうのを
思い出し
やったじゃナイスカ
今日の 一番初めの問題
四角形A1A2B2B1
と 四角形A2A3B3B2
に分けて
M1M2
M2M3 を 計算してみるとじゃナイスカ
まずは
四角形A1A2B2B1
時計回り➀しき
反時計回り②式
➀+②から
M1M2=1/2(a+b)
18
次に
四角形A2A3B3B2で
M2M3 時計回り③しき
反時計回り④式
③+④
M2M3=1/2k(a+b)
19
M1M2 と M2M3
の関係は 実数倍になっているので
ベクトルの 実数倍が等しい 方向が 同じ
M2M3 と M1M2は M2を
共有していて
方向が 同じ ということは
一直線上に ある
お疲れ様です。
2022年09月09日
22005 大人のさび落とし 空間ベクトル 和と差
空間ベクトル
和と差
01
まずは
復習から
空間の ベクトルも
平面のときと まったく同じですが
ベクトルは 大きさと 方向を
同時に持っているもの
大きさは 絶対値を 付けて
02
ベクトルの 相等は
大きさ 方向が 同じ
ことを言います
ベクトルは 自由に 平行移動して
考えてよいので
始点は
どこでもいいのですが
始点を定点にするという
考え方 位置ベクトル
これは
便利な考え方です
03
逆ベクトル
零ベクトル
>
04
ベクトルの
和は 差は
こんな感じでした
実数倍
05
演算の仕方は
こんなイメージで
06
分配の法則
ゼロについて
交換の法則
結合の法則
07
では
四辺形ABCD において
次の等式を
証明せよ
08
平行四辺形 BCDE を
CD=BE
AB+CD=AB+BE
=AE
AD+CB=AD+DE
=AE
09
左辺と 右辺の 橋渡しで
AとCを 結ぶと
ACを イコールで
結んで
式を 移行すると
10
なったでしょ
別のやり方で
始点の同じものに
着目して
式を作り
イコールでつなげて
11
整理して
題意の式に
ちかづけて
移行したら
12
また別の方法では
異と周り法
これは
面白いでしょ
始点から 始点に 向かって
ぐるっと足して
=0
ここから
左右に 分けていくと
13
平行6面体
平行四辺形になってるので
14
ベクトルの 足し算に
値を 代入して
15
こんな感じで
16
難しくはないけどさ
17
で 今の 同じ図形で
次の式の表すベクトルは?
可能性で
同じ 値になるベクトルを
つらつらと
書いて
しっぽと 頭が つながるように
18
可能性に かけてみましょう
さいごまで
たどり着いたのは
一つだったじゃナイスカ
19
面白いでしょ
20
問題
次の関係が 成り立つか?
って書いてある
21
左辺は
こんな感じ
22
中辺は
こんな感じ
23
右辺は こんな感じ
あれ?
右辺は イコールに 成んないな
まちがったかな?
解答には
あ~~~
題意にあったデショ
関係は
成り立つか?
いつもは 成り立つことを
証明しなさいが多い為
うっかりしてると
ねー
だからさ
これでいいんだ
左辺=中辺は成り立つ
中辺=右辺は不成立
24
お疲れ様です
また来週
2022年09月07日
22004 大人のさび落とし 空間座標とベクトル 球の方程式
空間座標とベクトル
球の方程式
01
空間に 直径の両端にあたる
2点の 座標が 示されている
この 球の方程式は?
また
この球が xy 交わる図形の
方程式 および
その 図形で囲まれた
面積は?
02
球の 方程式の
標準形は こんなでしたから
これは 中心の座標と
半径の大きさが
わかれば 出る
03
直径の両端が
分かってるので
中点の座標を 求めて
球の中心
直径の片方側
原点と中心の距離は
半径になるから
04
半径は 13
球の中心も分かってるので
球の方程式は
こんなです
05
これが
xy 平面と交わるには
z座標が ゼロ
z=0を 代入したらば
円の方程式
06
半径が 5だから
パイ アール 二乗
で
25π
07
球の中心座標と
半径が わかる様に
一般形を 標準形に
する問題
08
平方完成してくと
09
なので
中心の座標 と半径が
出て来て
10
球の方程式を
求める問題
球が xy平面と交わるとき
の xy平面にできる円の
中心と半径
球が xz平面と交わるときの
中心が わかってる時
球の方程式を 求め
この球と
x軸との交点を
求めなさい
という問題
11
求める 球の方程式を
こんな感じにして
xy 平面の切り口は
z=0
であるから
いくつかは
わからないけど
z1 の 二乗を r二乗から
引いたものが
半径になる形で
x1 と y1は
そのまま
12
であるから
これらから
13
x1=1 y1=2
r二乗ー z1二乗 =20
と
xz平面
との交わりが
14
だから
z1 は このまま z1=4
15
そうしたらば
元の球の半径は
プラスマイナス6 だけど
半径なので
正の数でないと いけないから
r=6
16
なので
球の方程式
半径
は こんなです
x軸との交点は
17
5 と まいなす3
であるから
座標で
こんな感じに
18
二点 O と Aに関して
PO:PA=2:1
になる Pに軌跡は?
19
内項の積 = 外項の積
二点間の 距離の 公式で
20
PA
PO
がこんなデショ
21
条件式を 辺々二乗して
代入したらば
22
展開して
左に 集めて整理して
今度は
円の式の標準形に持ってくと
23
平方完成して
24
こんな感じ
25
この軌跡は
球になり
球の中心 と 半径は
こんなです
26
四面体があって
こんな感じに
角度の 条件がついていて
この
各頂点を 通る
球の半径を
求めなさいと
27
図にすると
直交座標系に
成ってるじゃナイスカ
そこで
28
x、y、z軸に
重ねる形にしておいて
O,A,B,Cの 座標と
球の一般形を
こんな形にすれば
この 4点を
通るのであるから
29
代入してくと
Oを
代入したら
K=0
30
K=0が出たので
Aを 代入してくと
L=-a
31
Bを
代入したらば
m=-b
32
Cを 代入したらば
n=-c
33
であるから
球の方程式は
34
一般形を
展開して
標準形に
整理してきますと
35
こんなですよ
題意は
球の半径を 求めよ
であるから
こんな感じで
お疲れ様です。
2022年09月02日
22003 空間座標とベクトル 分点 重心
大人のさび落とし
分点 重心
01
四面体は辺が 6っ本あるので
立っている部分
底面の部分
ソレゾレ
辺の中点を L,M,N,P,Q,R
とすれば
LP,MQ.NRは
一点で 交わり
さらに 互いに他を 2等分する
これを 証明するのに
02
座標を 使わないとき
今回 平行四辺形を
使って
その性質から
対角線は 互いに 他を
2等分するを使って
証明してきますと
(LP,MQ.NR)
LP,.NR を 対角線にもつ
平行四辺形
LNPR
どうして
平行四辺形か と言えば
LNとRPに関しては
三角形ABC 訂正
三角形ABD
と
三角形CDBは
平面が交わっているので
BDが 共有直線
三角形 ABD において
L,Nは AB 、ADの中点であるので
LN 平行 BD
03
三角形 CDBにおいて
R、Pは
BC,CDの中点であるから
RP平行BD
LN 平行 BD
RP 平行 BD
から
LN平行RP
・・・・・・・
平行四辺形
LNPR
LN平行RPが言えたから
今度は
三角形ACD と 三角形ACBで
ACは共有直線
04
三角形ACDで N、Pは それぞれ
DA、DCの中点であるから
NP 平行 AC
三角形ACBで L,Rは それぞれ
AB、CBの中点であるから
比の値より
LR 平行 AC
NP 平行 AC
LR 平行 AC
より
NP 平行 LR
05
あるから 四辺形LNPRは
対辺が 互いに 平行で
LN 平行 RP NP 平行 LR
になっているので
平行四辺形であり
平行四辺形であるから
対角線は 互いに
他を 2等分する
より
(LP,MQ.NR)
LP,と NR は 互いに
他を 2等分する
06
同様に
視点を変えて
四辺形MNQRが
平行四辺形になることを
一組筒
対辺が 平行になってることを
示すため
MN 平行 CD
07
RQ 平行 CD
MN 平行 CD
RQ 平行 CD
MN 平行 RQ
08
平行四辺形の
もう一方の対辺も
同様にして
ふたつの 三角形と
交わっている 共有直線
二つの三角形の 共有直線以外の
それぞれの 2辺の 中点から
比の値により
平行である に持ち込み
09
四辺形MNQRの
もう一組の
対辺が QN 平行 RM
より
四辺形 MNQRは 平行四辺形であるから
10
同様に 四辺形LMQP にかんして
三角形ABC と 三角形DBC
は
BCを 共有直線とし
三角形ABCの側は
LM 平行 BC
11
三角形DBC の側は
QP 平行 BC
であるから
LM 平行 BC
QP 平行 BC
LM 平行 QP
12
また 四辺形LMQP にかんして
三角形CAD と 三角形BDAより
三角形CADの側は
MP 平行 AD
三角形BADの側は
LQ 平行 AD
MP 平行 AD
LQ 平行 AD
より
MP 平行 LQ
13
したがって
四辺形LMQP は 二組の
対辺が 互いに平行であるから
平行四辺形であり
平行四辺形であるから
対角線は 互いに 他を2等分する
ので
LP,MQ.は 互いに 他を2等分する
・・・・・・・・・・・・・・
➀
平行四辺形LNPRから
LP,と NR は 互いに
他を 2等分する
・・・・・・・・・・・・・・・・
②
MNQRが
平行四辺形になることから
対角線は
互いに 他を 2等分する
(LP,MQ.NR)
MQ.NRは 互いに 他を2等分する
・・・・・・・・・・・・・・・・・
③
四辺形LMQP は平行四辺形であるから
対角線は 互いに 他を2等分する
ので
LP,MQ.は 互いに 他を2等分する
・・・・・・・・・・・・・・・・
14
➀②③
より
LP,MQ.NR は
一点で交わり 互いに他を2等分する
証明終わり
15
この同じ問題を
16
座標を 使って
説明すると
LM,MQ,NRが 一点で
交わり
互いに 他を2等分する
というのは
それぞれの 中点を計算して
中点が
3っつとも 一致すればいいので
計算してみると
17
LPから
L 、Pは それぞれ
AB 、 CD の中点
18
この 中点を 結んだ 線分の中点を
G1とすれば
G1は
19
同様に
MQの 中点
M 、 Qは それぞれ
AC,BD の中点
MQの中点を G2とすれば
G2は
20
同様にして
NRも
Nは ADの中点
Rは BCの中点
NRの中点をG3とすれば
21
G3は
ナタメ
LP,MQ、NR
の中点 G1、G2、G3が
ことごとく 一致するので
22
先ほどの 証明と 同じことが言えた
23
問題を 読んでいただいて
24
座標を こんな感じに 設定して
25
内分点
P 、Q を
26
計算すると
27
ソレゾレ
出てきたところで
28
ソレゾレ 三角形の重心に
重なるか 計算来ますとして
三角形BDEの重心は
29
三角形CFHの重心は
であるので
オッケイ
30
問題
フィル インザ ブランクス
31
それぞれ
中線の足を
P,Q,R と置いて
AP、BQ、CR
二点間の距離を
計算して
一番長いものをじゃナイスカ
32
ここで
二点間の 距離は √の形で
出てくるので
√の値が 違ってくると
近似値を 使わないといけない
そこで
そんなことを しないように
二乗の形で 計算すれば
33
まず それぞれの 中点
P
34
APの 二乗は
35
中点Q
36
BQの二乗は
37
中点R
38
CRの二乗は
39
一番長いのは
AP
だね
だから 頂点A
からのものが 一番長い
40
問題を読んでいただいて
41
座標を使って
42
証明方法として
実際に 計算してみて
確かに そうであったと
実証する形でじゃナイスカ
頂点Aに対する
対面の重心は
三角形BCDの重心
空間の三角形の重心G1を
計算すると
43
次に 頂点Aと G1を
3対1に 内分する点を
計算すると
44
こんな値になったよ
45
頂点Bと対面する面の重心をG2
とすると
G2は 三角形ACDの重心
46
BとG2を
3対1に 内分する点を
計算すると
47
頂点Cと対面する面の重心を
G3として
G3は三角形ABCの重心であるから
48
C と G3を
3対1に 内分する点を
計算すると
49
こんな値
50
最後に 頂点についても
対面の 重心をG4 とすれば
G4は 三角形ABCの重心であるから
51
こんな値
52
ことごとく 一致するので
53
実証できたと
お疲れ様です。
2022年08月10日
22002大人のさび落とし 空間座標とベクトルより 2点間の距離
大人のさび落とし
空間座標とベクトルから
二点間の距離
01
問題
正三角形であることの
証明と
この正三角形を
一つの面とする
正四面体の他の頂点をを求めなさい

02
三辺の 長さが 等しい
を 使ってみますと

03
個々に 計算して
成ってるよね
だからさ
正三角形
整理すれば 同じ だからさ
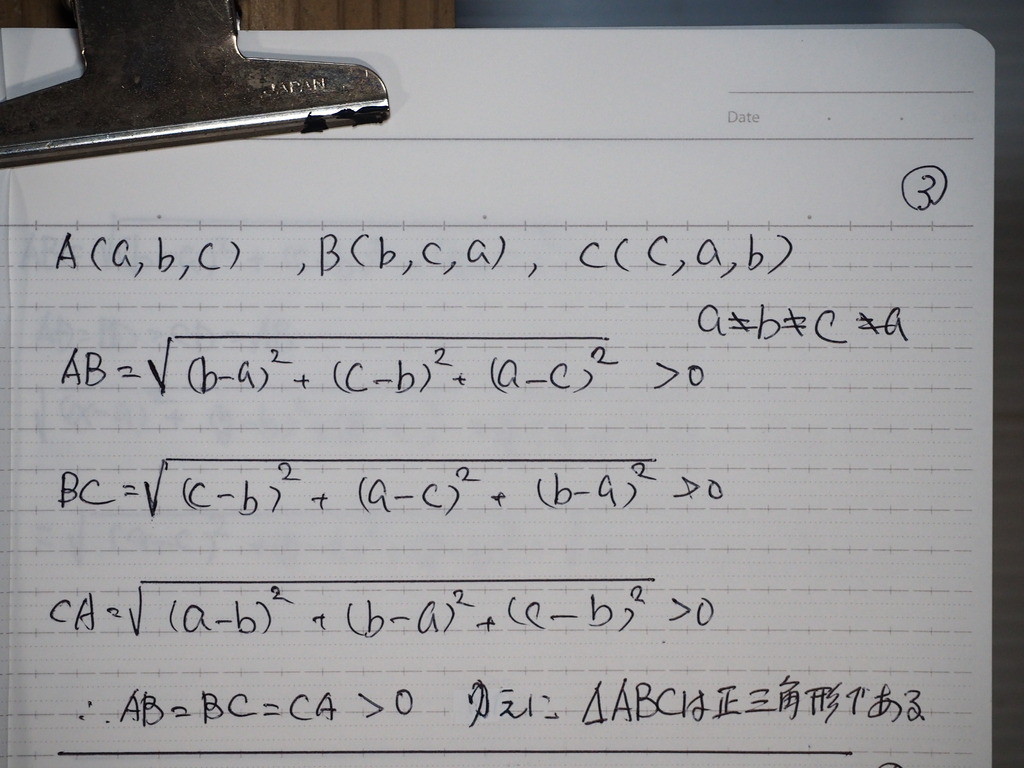
04
問題は
次だな
正四面体の 他の頂点
Dとすればさ
全て 正三角形の 面だから
AD=BD=CD=AB

05
これを 連立にしてくと
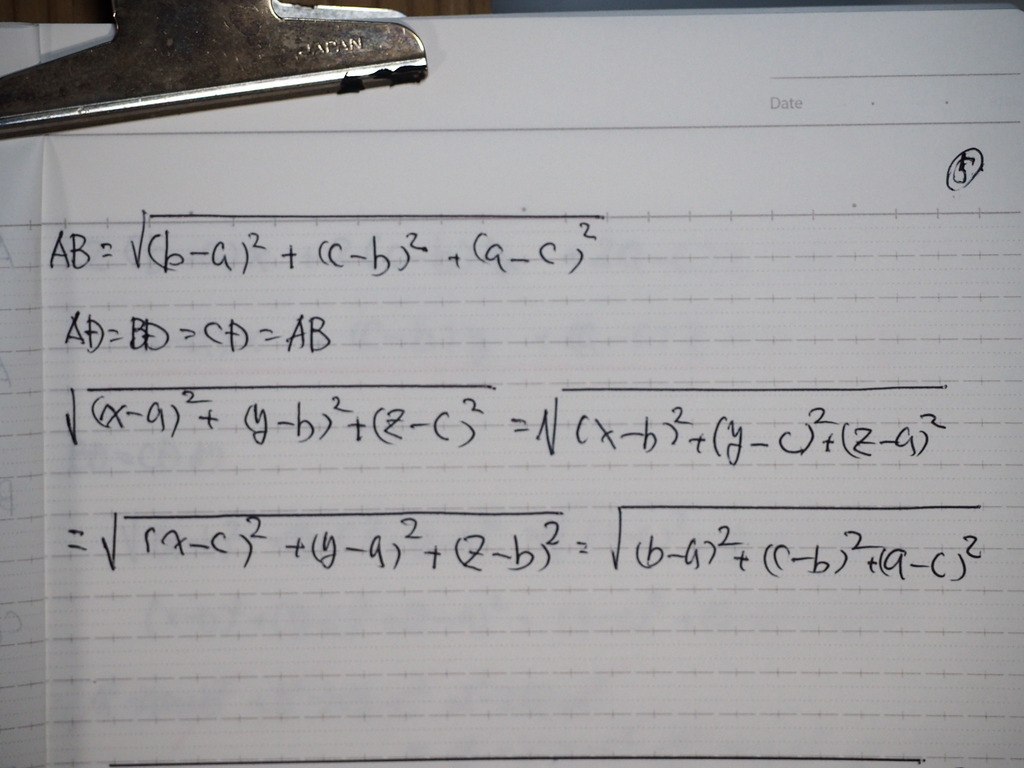
06
AD=BD より
計算してくと
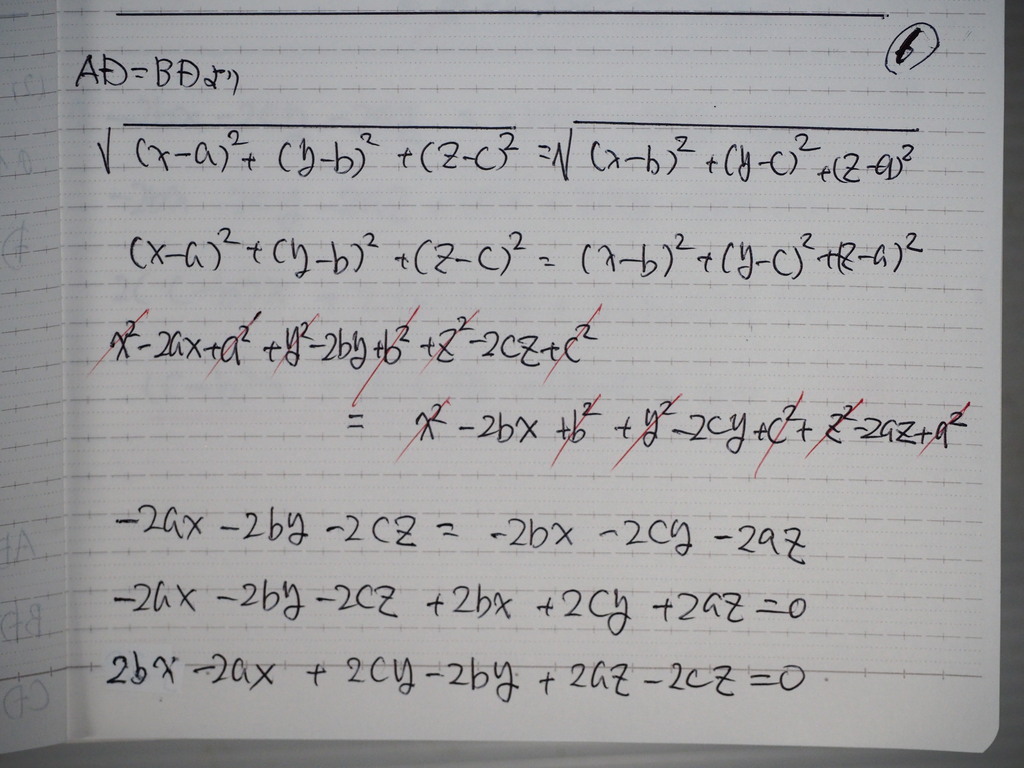
07
➀式
BD=CD より
計算してくと
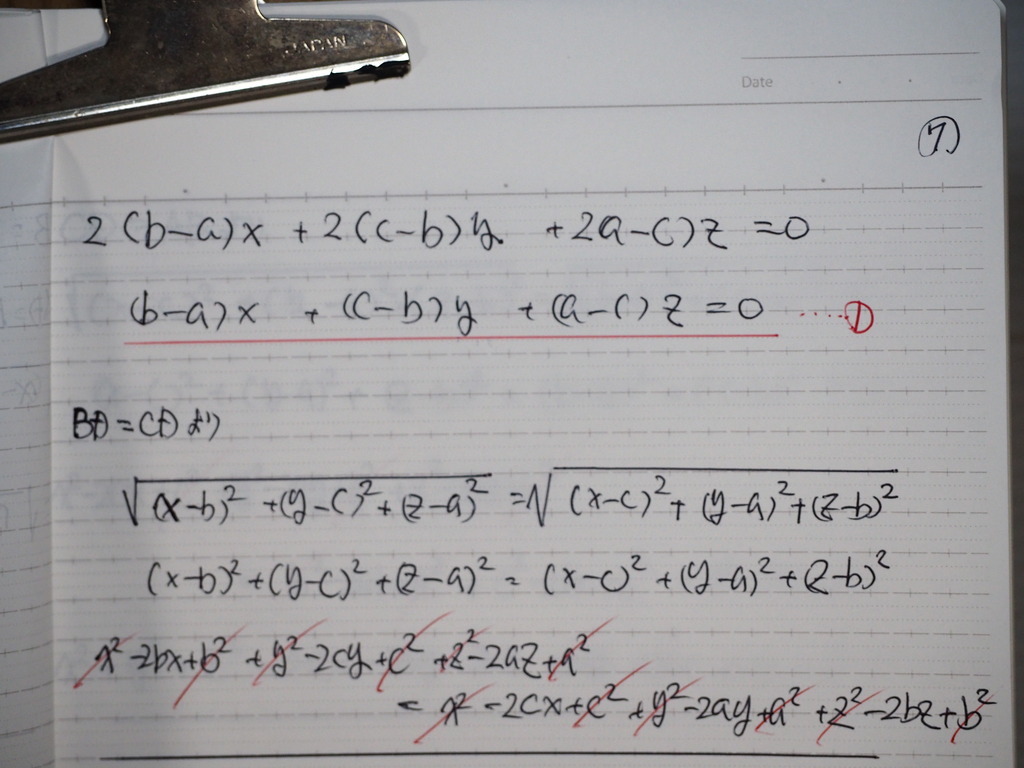
08
②式
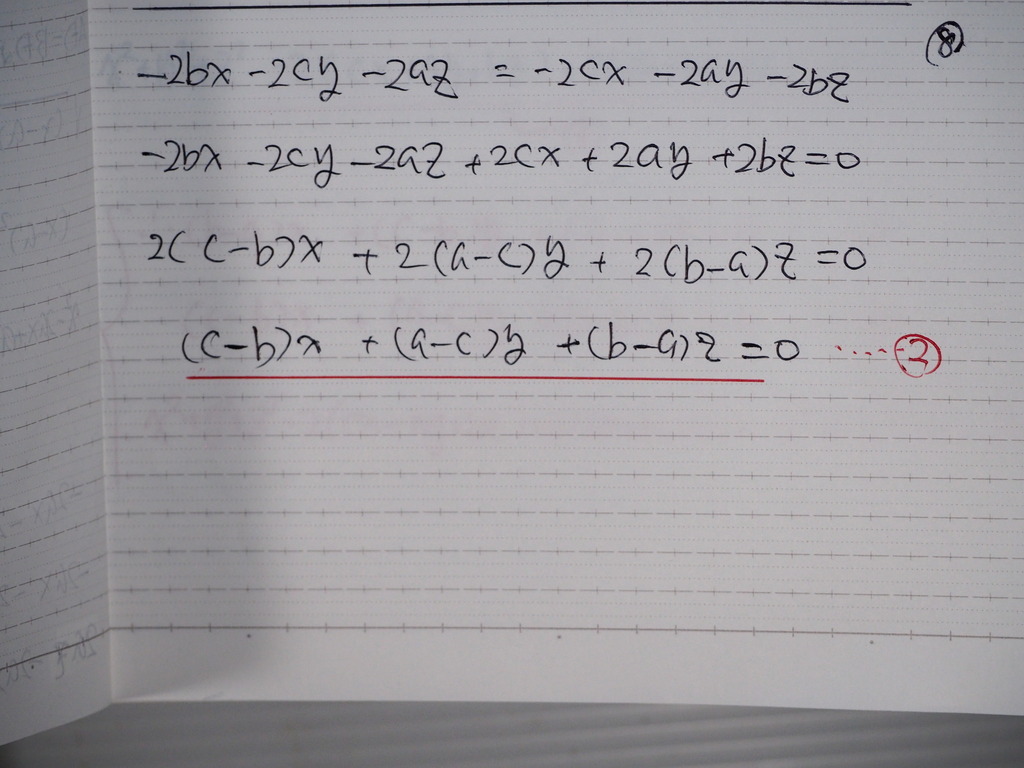
09
これも
コレは 種類が 違って見えるね
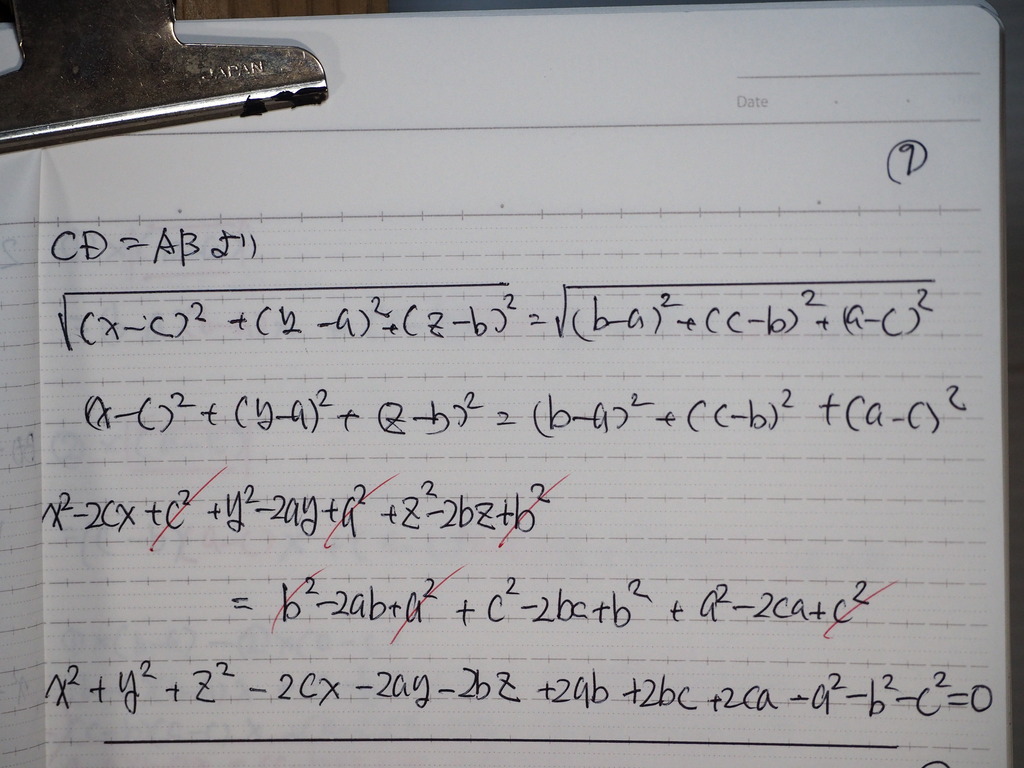
10
➀②③しきから
➀②をつかって
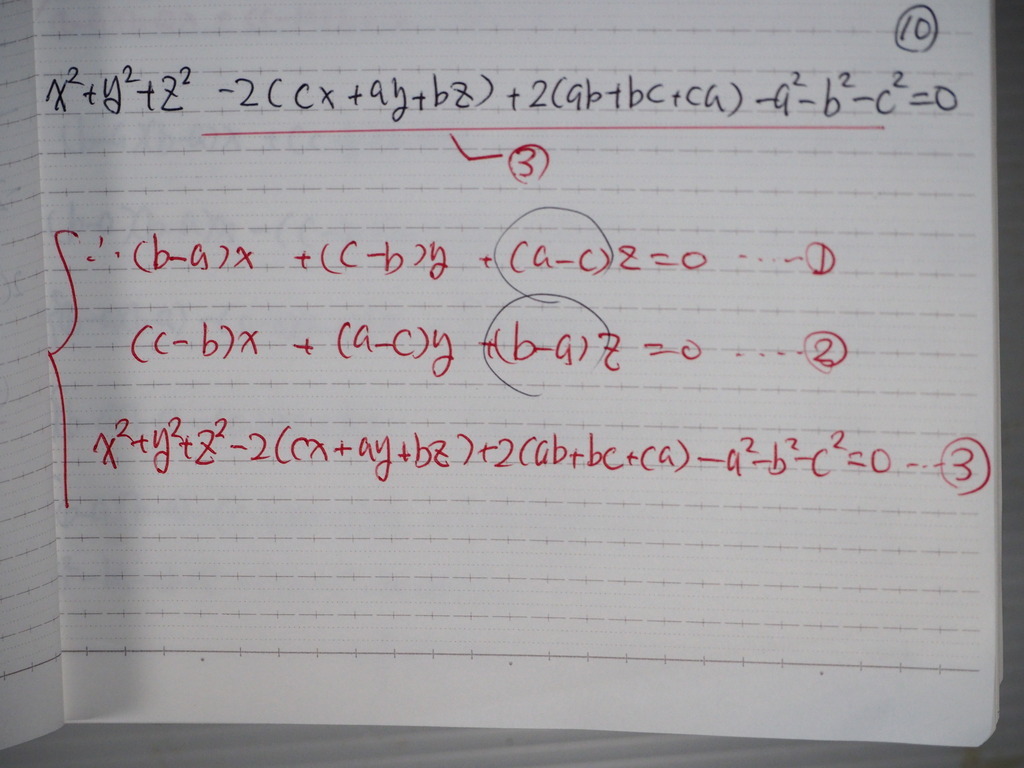
11
Zを 消去して
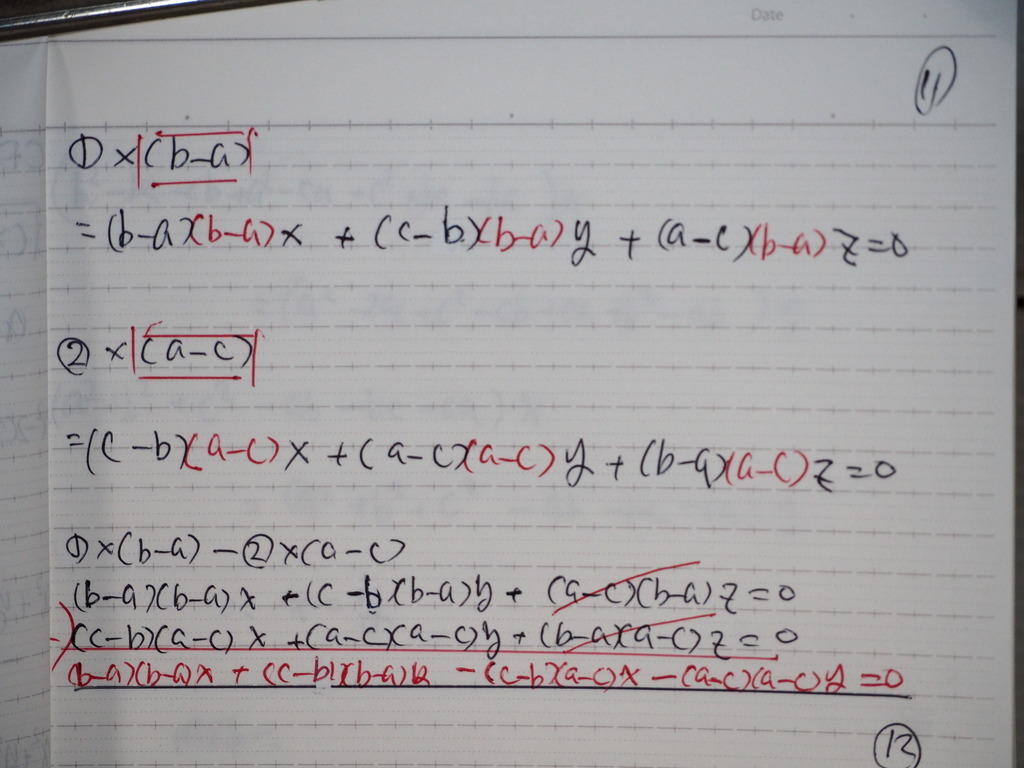
12
計算して
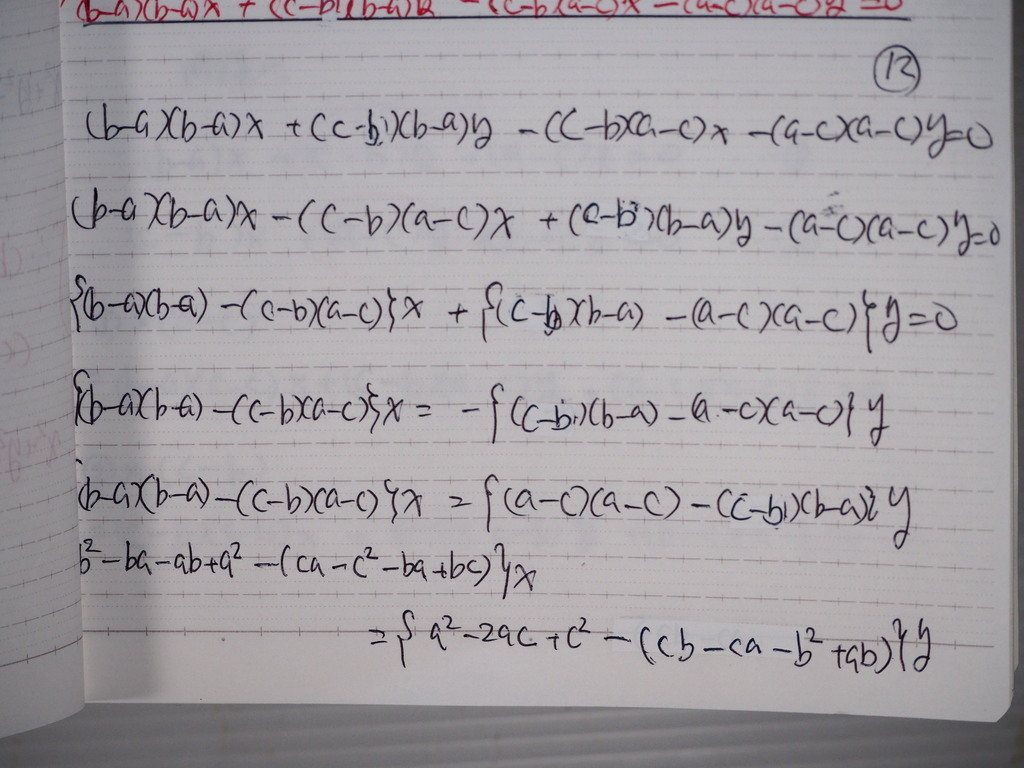
13
整理してくと
X=Y
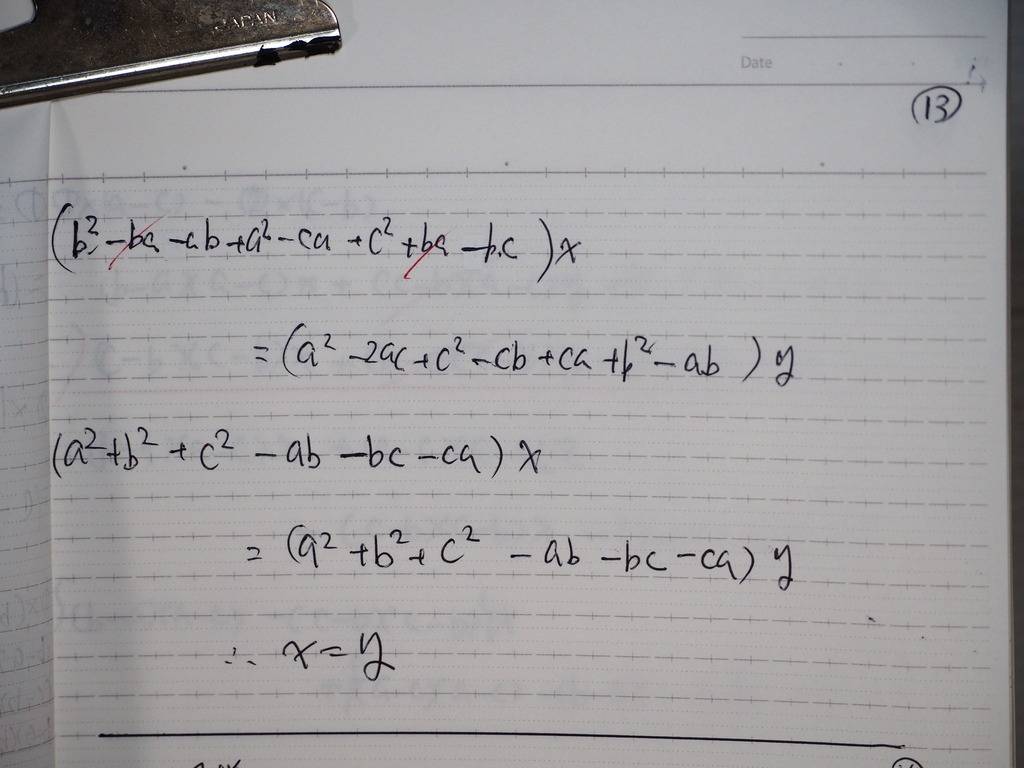
14
同様に
➀②を また少し変えて
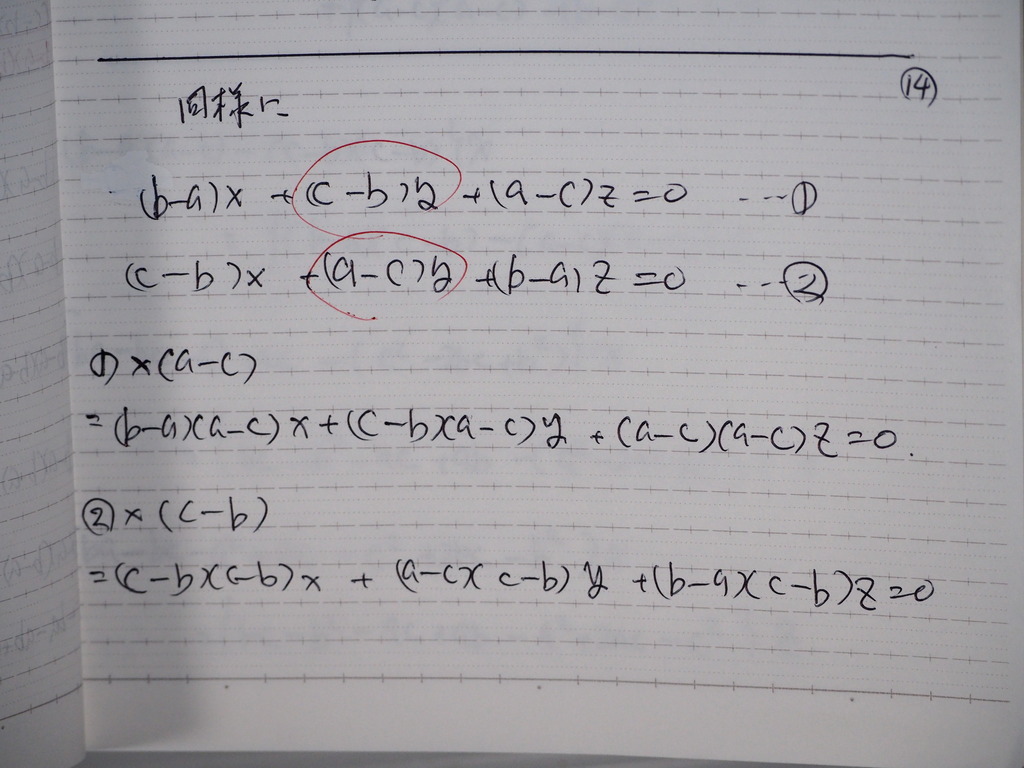
15
計算してくと
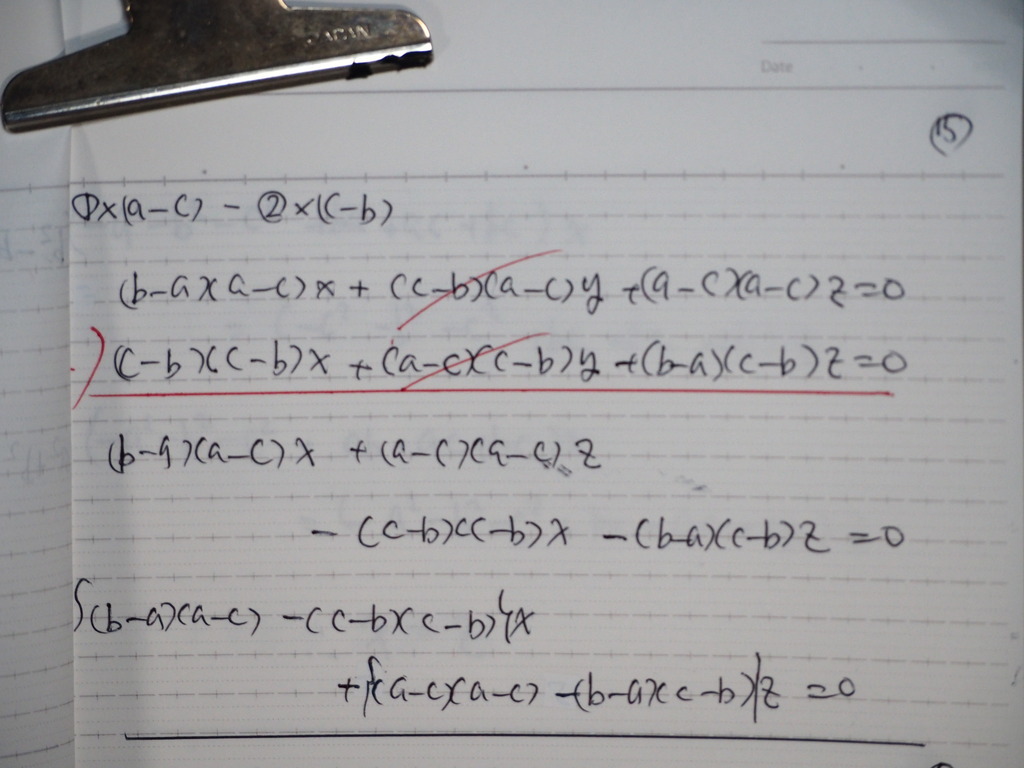
16
整理してくと
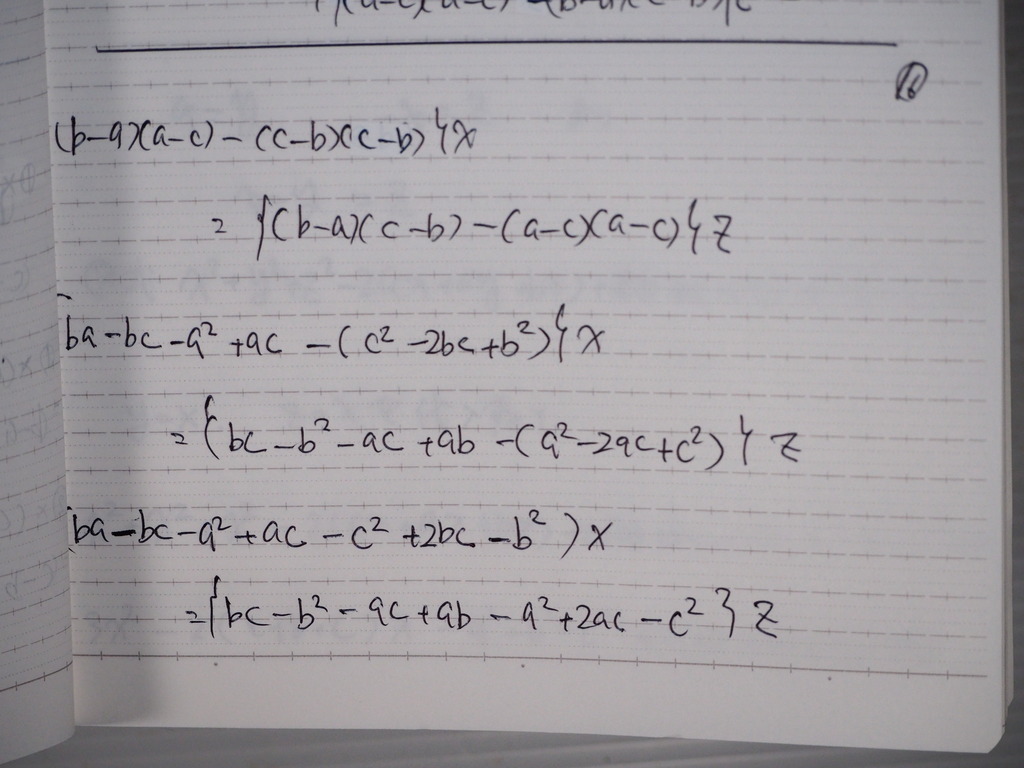
17
X=Z
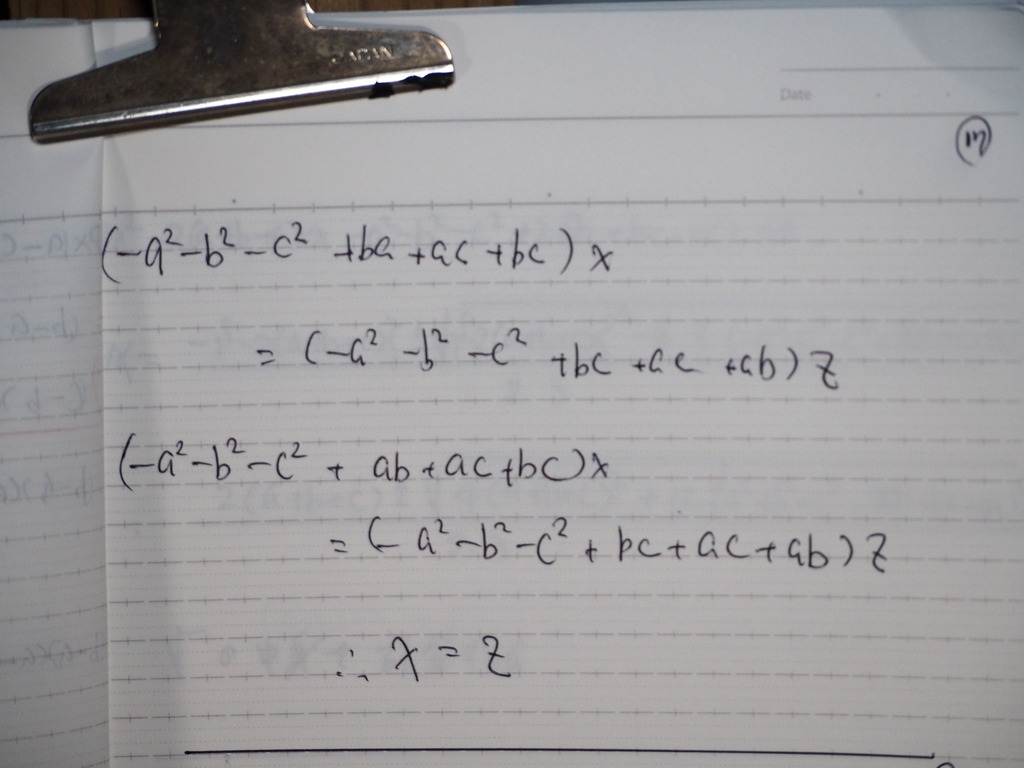
18
ナタメ X=Y=Z
これを ③式に
Y=X Z=X で
代入したらば

19
ここで
Xを 解の公式で 求めれば
X,Y,Z みんな 等しい値の
座標になるので
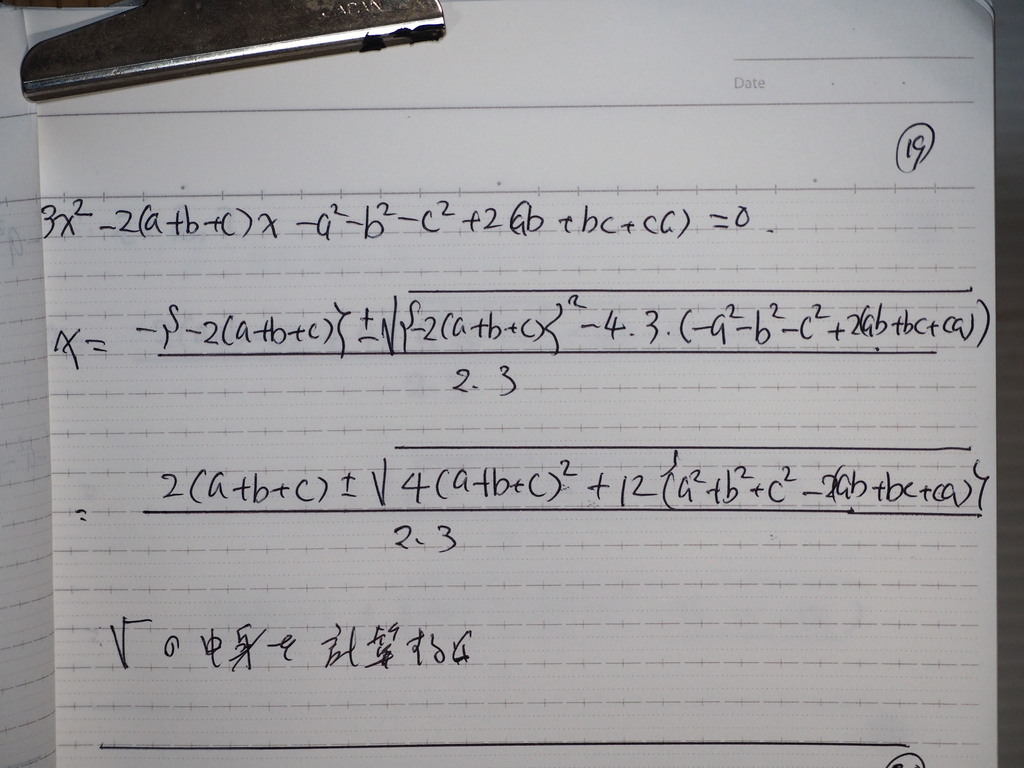
20
ルートの中身が出たから

21
整理してくと
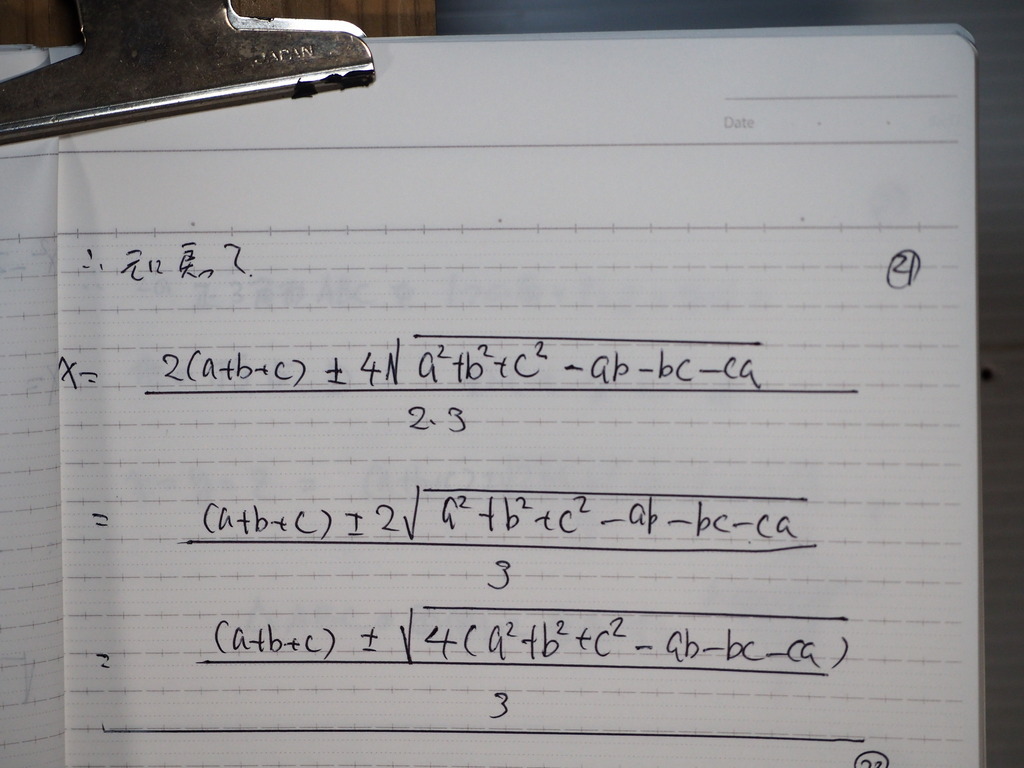
22
こんなカンじに
成ってじゃナイスカ
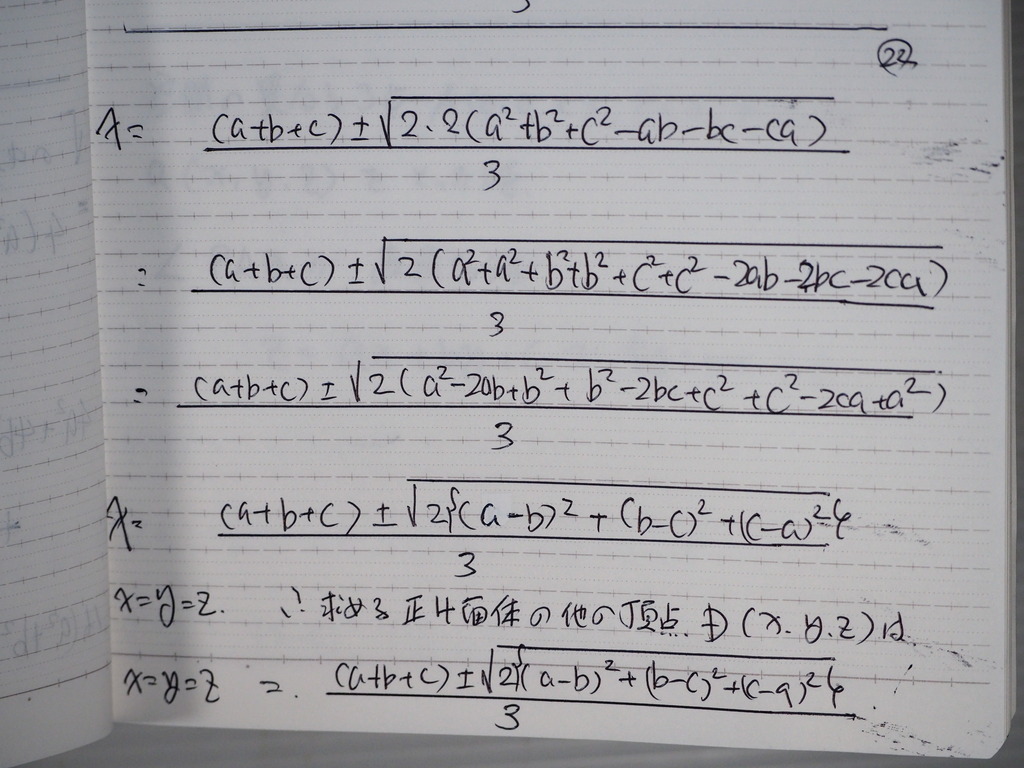
23
Dは 正三角形ABCの
両方の側に あるんだね

24
今度は なんか難しそうだけど
そんなことないですよ
行ってみましょう

25
この条件で 計算したらば
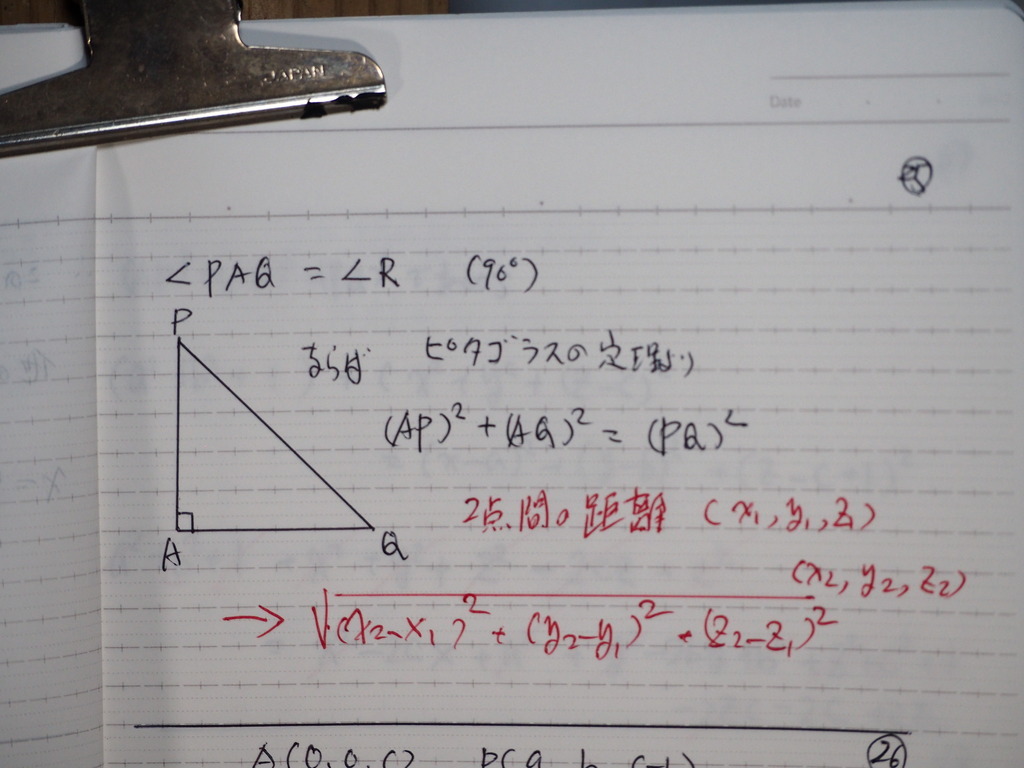
26
これを
ピタゴラスに入れて
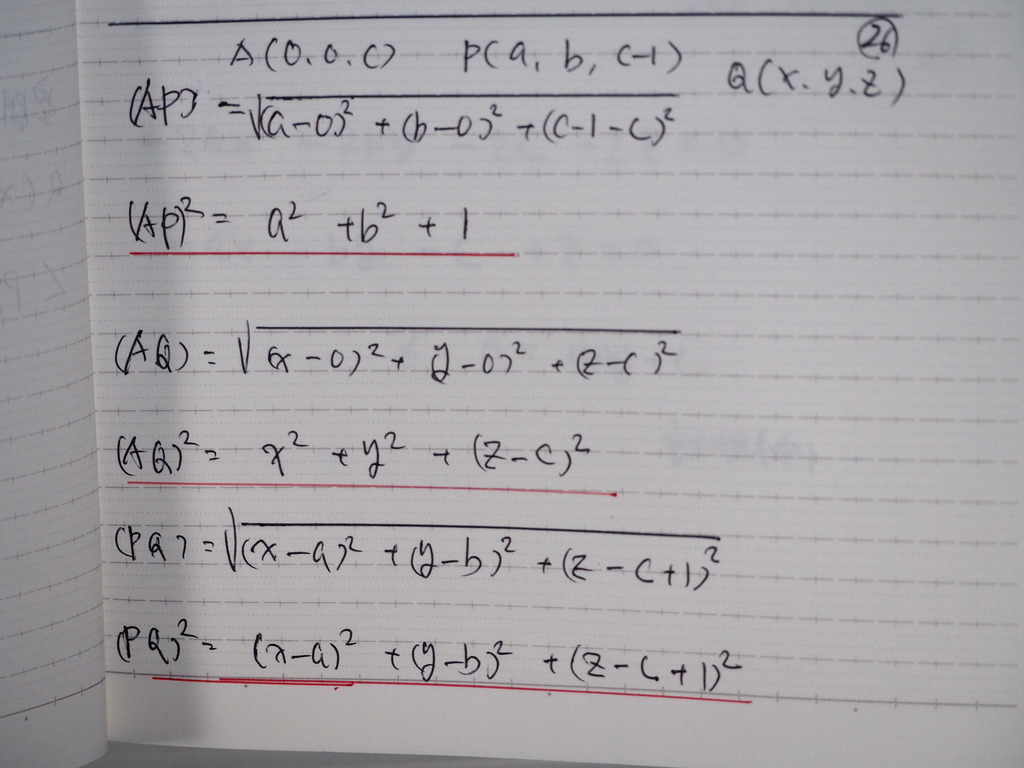
27
整理してくとだ
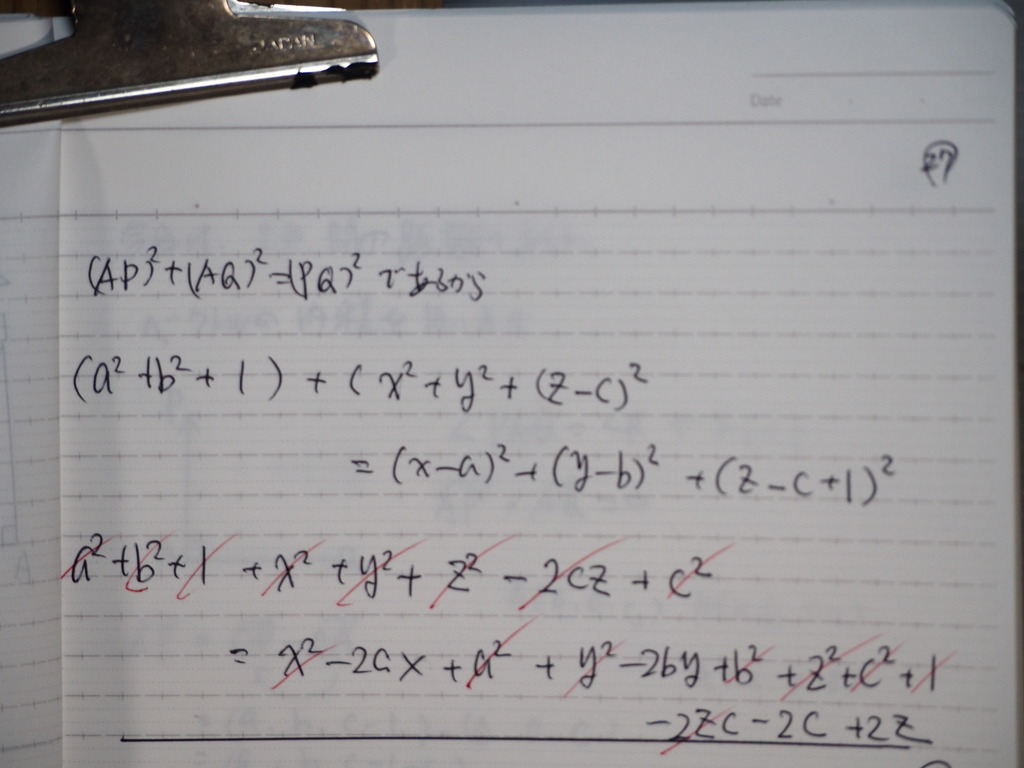
28
なったじゃナイスカ
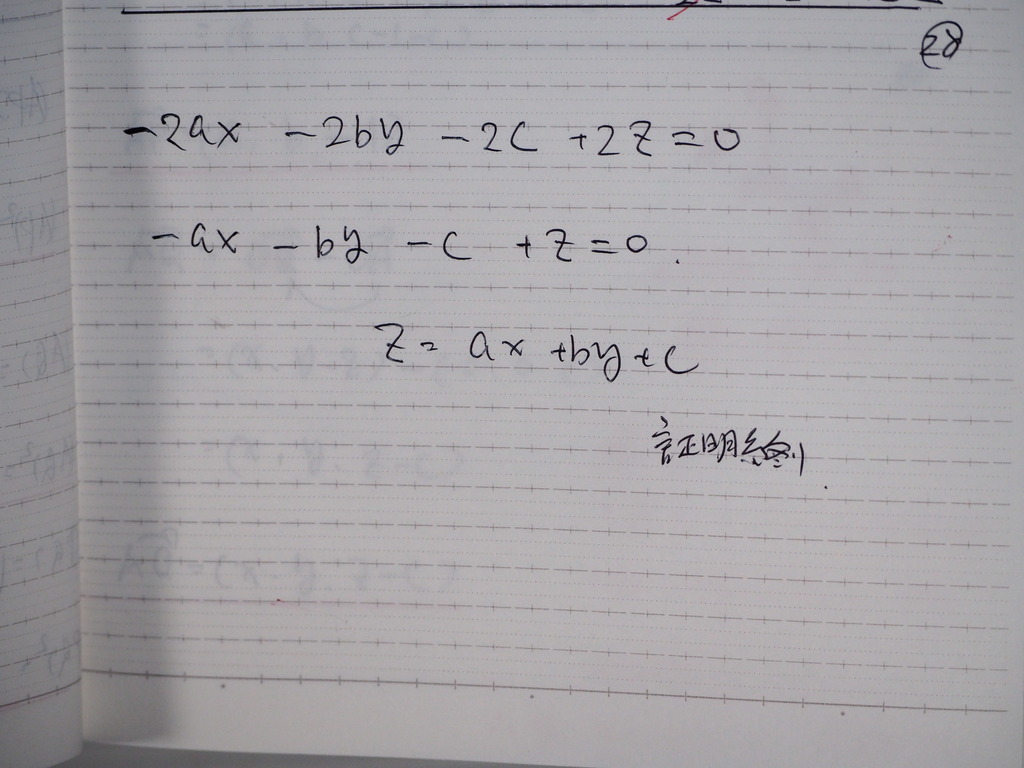
29
内積でも 解けるので
見ておくと

30
こっちの方が 早いね

31
今度 空間にある
正方形

32
条件を 見つけて

33
条件を 関係式に
してくと
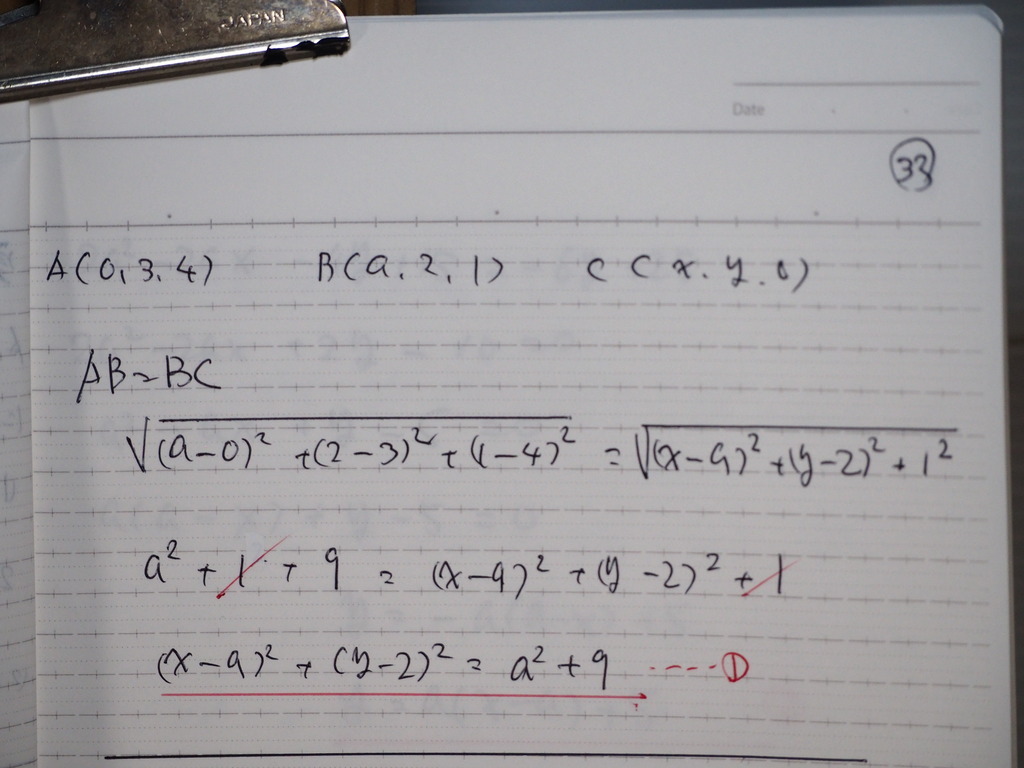
34
計算して
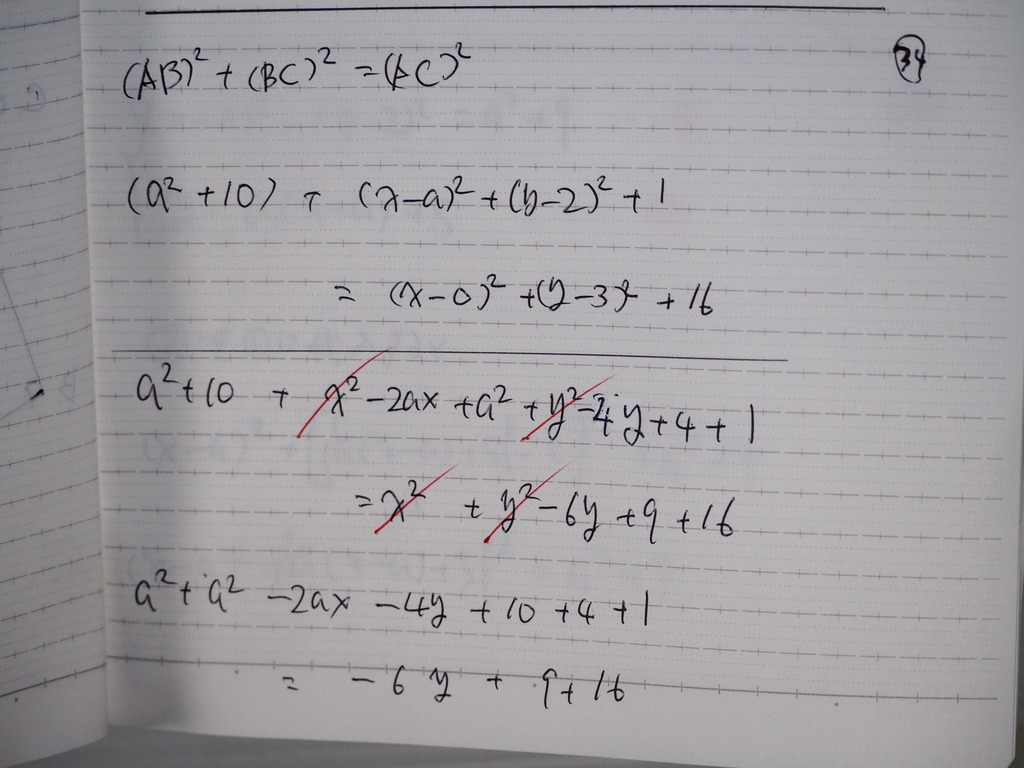
35
関係式 2本目
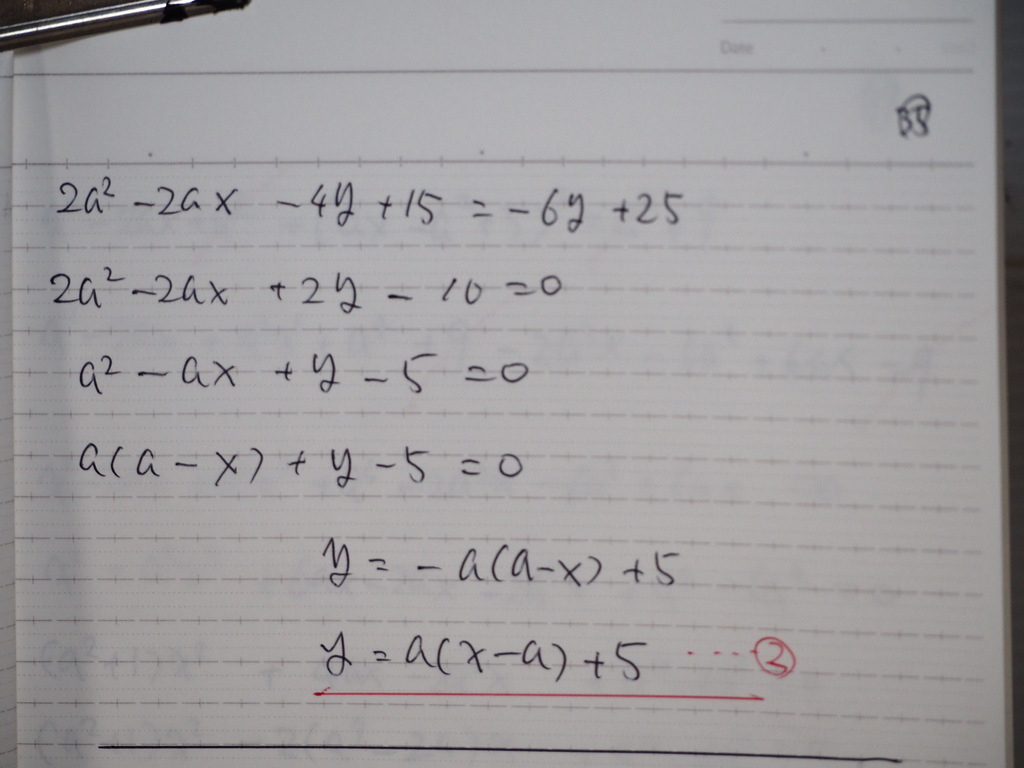
36
連立から
Xを解くと
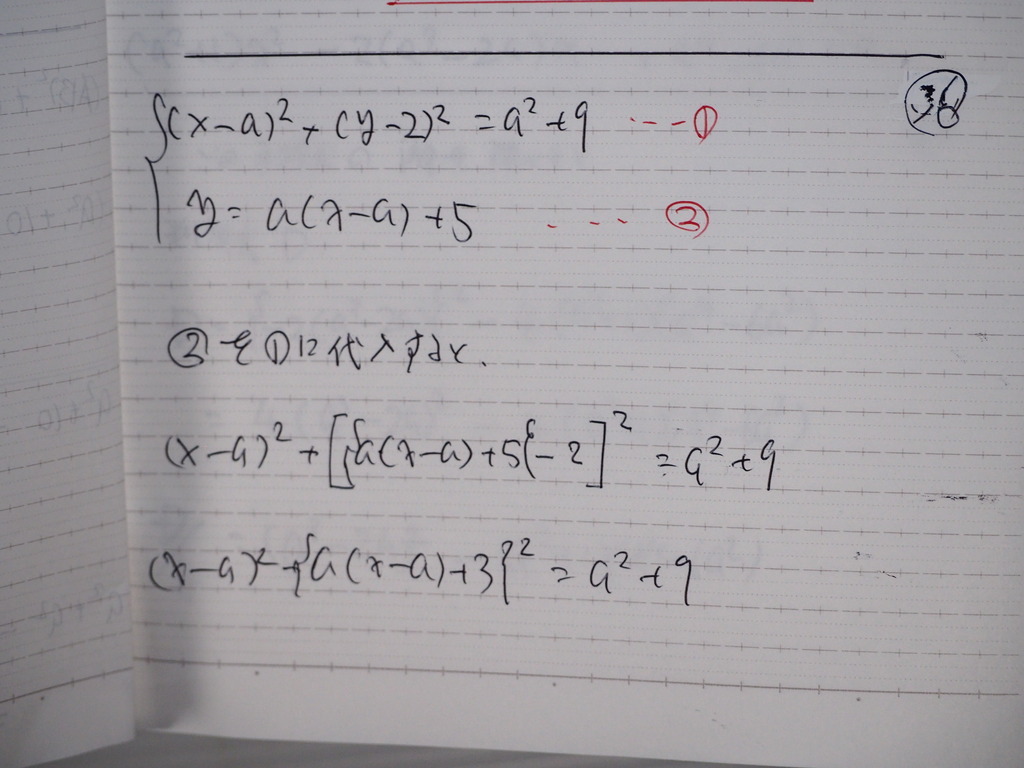
37
このXについての方程式は
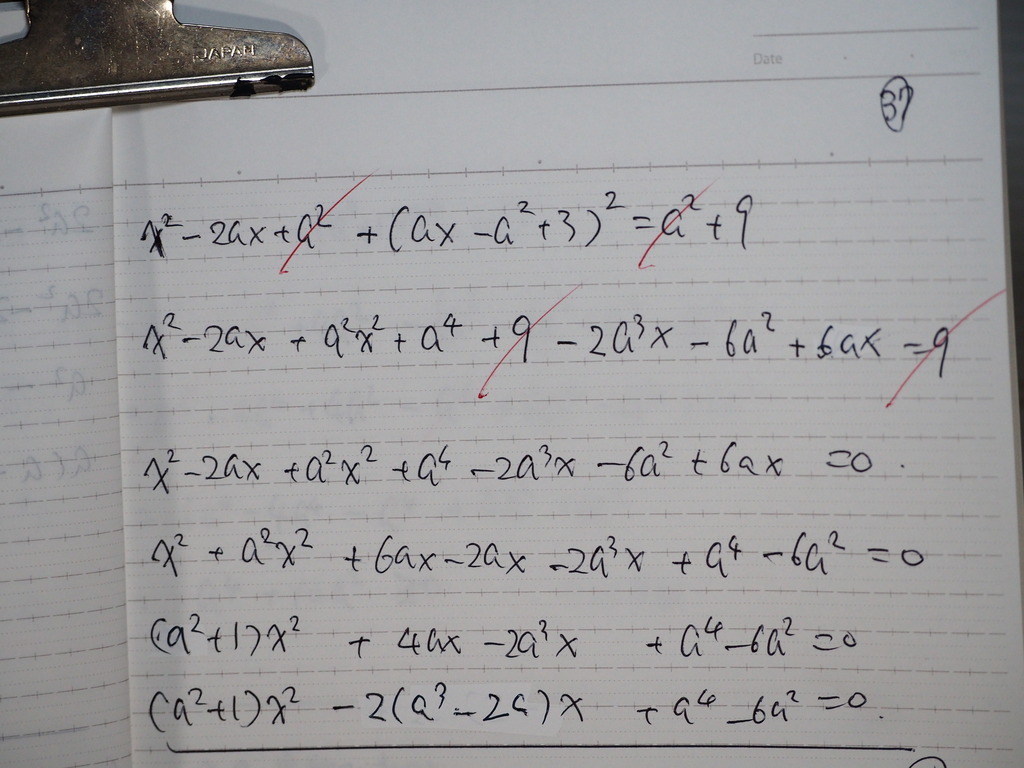
38
解を調べると
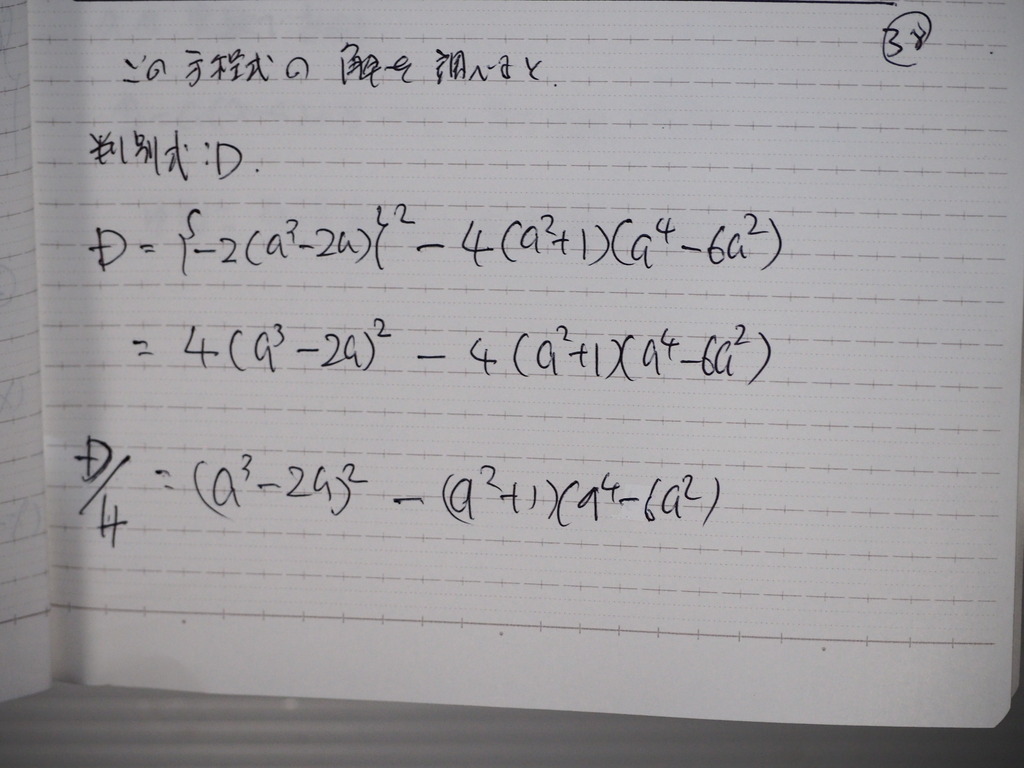
39
実数解を持つ
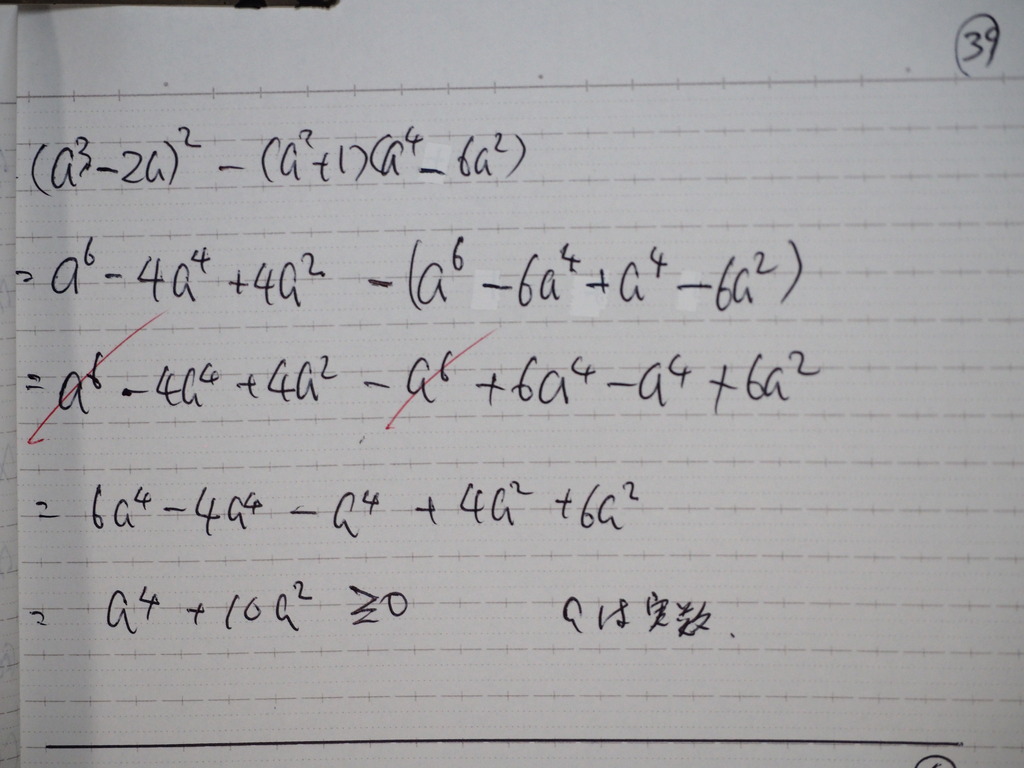
40
ナタメ
じゃナイスカ

おつかれさまです。
空間座標とベクトルから
二点間の距離
01
問題
正三角形であることの
証明と
この正三角形を
一つの面とする
正四面体の他の頂点をを求めなさい
02
三辺の 長さが 等しい
を 使ってみますと
03
個々に 計算して
成ってるよね
だからさ
正三角形
整理すれば 同じ だからさ
04
問題は
次だな
正四面体の 他の頂点
Dとすればさ
全て 正三角形の 面だから
AD=BD=CD=AB
05
これを 連立にしてくと
06
AD=BD より
計算してくと
07
➀式
BD=CD より
計算してくと
08
②式
09
これも
コレは 種類が 違って見えるね
10
➀②③しきから
➀②をつかって
11
Zを 消去して
12
計算して
13
整理してくと
X=Y
14
同様に
➀②を また少し変えて
15
計算してくと
16
整理してくと
17
X=Z
18
ナタメ X=Y=Z
これを ③式に
Y=X Z=X で
代入したらば
19
ここで
Xを 解の公式で 求めれば
X,Y,Z みんな 等しい値の
座標になるので
20
ルートの中身が出たから
21
整理してくと
22
こんなカンじに
成ってじゃナイスカ
23
Dは 正三角形ABCの
両方の側に あるんだね
24
今度は なんか難しそうだけど
そんなことないですよ
行ってみましょう
25
この条件で 計算したらば
26
これを
ピタゴラスに入れて
27
整理してくとだ
28
なったじゃナイスカ
29
内積でも 解けるので
見ておくと
30
こっちの方が 早いね
31
今度 空間にある
正方形
32
条件を 見つけて
33
条件を 関係式に
してくと
34
計算して
35
関係式 2本目
36
連立から
Xを解くと
37
このXについての方程式は
38
解を調べると
39
実数解を持つ
40
ナタメ
じゃナイスカ
おつかれさまです。
2022年08月05日
大人のさび落とし22001 空間の図形と座標
01
空間図形と座標
空間における
平面と言うものは
平行な時 交わるとき
さらに 平行な 2平面に
もう1平面が 交わるときなど
こんな感じになりますです
02
空間における
直線の場合は
平行な時と 交わるときは
同一平面
ねじれの位置の時は
同一平面にない
03
直線と平面の垂直
平面に 垂直な直線は
その平面上にある 全ての直線と
垂直
04
3垂線の定理
こうなるんだって
05
空間座標の表示の仕方は
こんな感じ
ここは 怖がらなくてもいいので
06
ここは ちょっと 苦手な人もいるのかな
点と直線の距離
分点座標
この分点座標で
外分ていうのが あるですが
外分を マイナスを 付けて
内分の公式に 入れればいいので
07
実際にやってみると
08
こんなカンじで
09
マイナスを 付ける方を入れ替えても
10
同じだね
11
球の方程式
12
もんだいは
こんな感じのものが出るらしい
いきなり
3垂線の証明問題
13
三角形を 作って
合同を利用して
垂直を 導いてくんですが
14
三角形OQM と 三角形OQN
二辺夾角相当により
合同
ここから
OM=ON
15
三角形POMと 三角形PON
ちょっと 図がですよ
まわして
何やってるんだ
まわして
で
二辺夾角相当により
合同
であるから
PM=PN
16
したらば
三角形PQM と 三角形PQNで
三辺等しいので
合同
すると
∠PQM = ∠PQN = ∠R
であるから
PQ ⊥ L である
17
次はですね
直線a,bの なす角を求めよ
18
(1)は
上から 見ると
対角線
正方形の 対角線になるわけで
90°
19
正四面体
これはね
MN PQが
ソレゾレ
三角形ABC と 三角形ACD
という 平面の中に ある
空間において
直線が 平行な時は
同じ 平面上にある
20
空間に 戻すと
正四面体の AC と DC の なす角に等しいから
60°
21
これも 少し
移動すれば
22
ここに 補助線を入れれば
三角形が できてきて
三辺の長さが 等しいわけだから
なす角は 60°
23
正四面体の問題
図の MN のながさを 求めなさい
24
MN を 求める為
三角形ANC と 三角形AND
で
三辺が等しく 合同であるから
ピタゴラスの定理で
ANの長さ
25
同様に
26
BNの長さ
が出て来て
そこから
三角形NMA と 三角形NMB
が 合同であるから
27
ピタゴラスで
こうです
28
空間座標は x、y、zの
ここでは
a、b、cの 互いに 直交座標
次のものを
求めるのですが
29
三角形ABCの面積
面積の 公式は
こんなだから
ここで
部品を 作ると
30
三角形 OABの面積を
利用して
31
また 分かってる
直交座標から
ABを求めて
32
であるからに
ODの長さは
しかるに
CDの長さは
33
で
出てきた ③と➀を
使って
34
三角形ABCの面積は
35
体積を だしておいて
さっき
求めた 三角形 ABCを底面にした
四面体の 高さが
ちょうど OH であるから
36
ここに
当てはめて
37
整理したらば
これでいいのだ
お疲れ様です。
2022年07月14日
28040 大人のさび落とし 平面のベクトル方程式
平面のベクトル方程式
01
平面は どうやって
表現すればいいの
ということの問題です
02
題意に出てくるのは
X0 a ベクトルですが
X0を 通って aベクトルに
垂直な 平面のベクトル方程式
平面上の 点を Xとすれば
X0 X ベクトルと
aベクトルは 垂直
これを 内積で 表せば じゃナイスカ
03
これが
平面の ベクトル方程式
04
さらに
具体的に値を
文字を 使って
当てはめて
内積の 成分で 展開すれば
05
イメージ的には
こんな感じで
ナタメ
これで十分
06
もう一度
まとめて 整理しますと
こんな感じで
07
一定のベクトル OHに対して
次のような 等式があるとき
ベクトル OP の 終点は
どんな 図形上にあるか
平面と 空間で 場合をわけて
答えなさい
08
内積の 中の式に
変形式を 代入するんですが
PHを考えて
そこから
移行して
OPは
こんなだから
09
内積を 成分で
展開して
題意より
その値が 絶対値OH二乗
整理したらば
この式の 意味するものは
10
平面だ考えると
まず OHベクトルありき
そこへ
PHベクトル が OHに 垂直になる
と言う意味だから
題意は
OPの終点は
であるから
点Hを 通り OHベクトルに
垂直な直線
11
空間の時も
式変形は
基本的に ほとんど
同じ
少し 変えてあるけど
12
一定の ベクトルOHがありき
そこに
空間において
HP ベクトルが
OH ベクトルに 常に
垂直であるのだから
点Hを通り OH
ベクトルに 垂直な 平面を描く
紙面では 点Hを通り が
抜けてましたが
点Hを 通りと
ちゃんと書いてください
13
原点Oから
平面πに おろした垂線の
方向余弦が (L,m,n)
OPの長さが Pの時
平面πの方程式
方向余弦とは
ここでは
OPを x、y、z 成分に
分解した 単位ベクトル
14
OPベクトルの 長さは P
eは 単位ベクトルだから
多さが 1なのだから
P倍すれ
OP の成分
15
平面上の 任意の点を Xとすれば
PXベクトルは
xベクトル - OPベクトル
であるので
その べくとると eは
垂直を 内積で 表して
16
内積の 成分で
展開してくでしょ
半径 rの球の 方程式で
半径を 1にすれば
17
計算してくと
ここに 落ち着いて
18
成分を
代入して
内積を 展開すれば
なったじゃナイスカ
あ 証明の時
なったじゃナイスカ とか
答案に 書かないでね
わかてるとおもうけどさ
であるからとか
ゆえに とか
19
今度は
実際に 値があるですが
行ってみましょう
20
図にすれば こんなデショ
ここで
平面に 垂直なベクトルが
必要なので
点Aを 通るように
平面に垂直なベクトル
AQを作って
OQベクトル (位置ベクトル )
Q(a,b,c)
すると
21
まず平面上の ベクトルの成分を
計算するでしょ
AB、 AC
22
次に AQの 成分を
計算するでしょ
23
これらの
ABとAQ
ACとAQ
が 垂直 これで
条件式をつくって
24
ここから
a,bを cで表し
25
まず a
26
次に b
27
ここからなんだけど
ここからだからさ
平面上の 任意の点P
x、y、z
APを 成分計算して
28
平面の方程式は 平面上のベクトルと
平面に 垂直なベクトルが
垂直
内積=0
で
出るのだから
29
その前に
AQベクトルに
a=c+2
b=c+1
を 代入したらば
30
これでさ
Cがゼロでないから
で
やくして
条件
31
どうやって
cはゼロでないを 言うのか
32
c=0だったとして
cは OQの成分の一つだから
実際に
成分が どうなるか
代入してみたらば
c=0 で
計算すると
OA ベクトルと 一致してしまい
Aを通り
平面に垂直な AQを 作ったのだから
仮定に 反してしまう
ナタメ
cは ゼロでは ない
33
ナタメ
条件は これです
34
点と 直線の 距離の
公式を 証明する問題
35
題意に 平面の方程式があるのだけれど
aベクトルと xベクトルが
あるとき
この 内積は
こんなデショ
なので
平面の方程式は
こう書けるよね
36
点Pから
平面に おろした 垂線の足をH
とすれば
37
hはxと 同じ 平面上なので
38
また HPベクトルは
平面に垂直なaベクトルの 実数倍
39
平面の 方程式に 代入して
40
展開して
HPベクトルの大きさが
が点と平面の 距離
HP= 絶対値 Kaベクトル
K(aベクトル二乗)が出ているので
それを 絶対値aで
割れば
距離なので
マイナスじゃなくて
絶対値を付けて
41
こんな感じで
お疲れ様です。
2022年06月29日
大人のさび落とし 幾何への応用 28039
01
正三角形を 4枚 張り合わせると
正四面体
その 正四面体に ついての問題
02
図を 書いてみると
こんな感じ
今回は 点Dを 原点にすれば
楽なので
こんな感じで
位置ベクトルを 設定して
03
AB と CD の 垂直かどうかは
内積で けいさんするのですが
先ず AB CD を 位置ベクトルで
表現して
内積を 計算すると
04
こんな感じなのですが
これでは まだ =0 になってないので
題意より
正四面体なので
すべて 辺の長さが 等しい
鱗辺との なす角が 60度
05
ちゃんと マイナスが 片方に
付いてるじゃナイスカ
=0
06
こっちもですよ
Cベクトルの半分と
OA OB の中点
の 分点ベクトル
07
AB の方は
こんな感じで
内積の計算を
してきますと
08
やくせる とこ やくして
題意より
正四面体 であるのだから
一辺を が長さ Lにしてみると
09
=0
オッケイ
10
次は
この 四辺形 PQRS が
正方形であることを
いうんですが
こんな手順で
対辺が 等しい
ベクトルで 書いてあるから
同時に 平行も言ってる
鱗辺の 長さが 等しいか見る
そして
鱗辺のなす角が 垂直を 確認する
11
ベクトルを 位置ベクトルで
表すと
PQは
12
SRは
PQベクトルと SRベクトルは
ひとしい
平行 大きさが 同じ
13
QRは
大きさなので
マイナスは
方向の意味なので
絶対値で
対処して
14
題意より
全て 辺の 長さが ひとしい
=L とでもすれば
15
長さにおいては
対辺PQとSR
隣辺PQとQR
同じ
PQとQRが 垂直か 調べると
16
まず PQベクトル
17
ついで QRベクトル
18
内積を 計算すると
題意より
辺の 長さ
が 等しいから
=0で
垂直が言えた
19
なので
正方形
20
今度は
四面体
OA⊥BC OB⊥CA
⇒ OC⊥ABであることを
証明せよ
21
位置ベクトルを
こんな感じに
設定して
題意から
次の 2つの 内積が =0
22
OA BC を 位置ベクトルで
表現して
内積の計算を する
これが =0
23
もう一つ
OB CAを 位置ベクトルで
表現して
内積を 計算する
これが =0
24
それで
本題の
内積を計算していくと
OC AB を 位置ベクトルで
表現して
内積を 計算した結果
こんなだから
25
➀の条件式から
書き換え
26
②の条件式から
書き換え
それで
OCとABの内積は =0
したがって
OC ⊥ AB である
27
今度は 直方体
位置ベクトルを
こんな風に 設定して
直方体の断面でできる
三角形 DACの 重心を Kとすれば
重心は こんなで
OFは 重心Kを通る
これらを
証明せよ
28
図は こんな感じで
ACの中点をMとすれば
OMベクトルは
へてから
OMベクトルと ODベクトルの
分点ベクトル
DMを 2:1に 内分する点が
重心になるのだから
29
なったじゃナイスカ
30
今度は OFベクトルを 求めていけば
OF が kを 通過するならば
O.K.F が 始点が同じで
実数倍になるはずだから
成ってるよね
31
今度は
立方体
断面が 三角形ABCになるように
したときに
三角形ABCの平面は
ODに 垂直であることを言え
32
まず
ODを 位置ベクトルで表すと
ベクトルは
自由に 平行移動して
考えていいので
CDベクトルは
OAベクトル+OBベクトルと 同じこと
33
三角形ABCの 平面についてみるので
三角形の 鱗辺の なす角 がある
平面
の 一辺 AB と AC につて
位置ベクトルで 表現して
34
まず
ODとABの 内積
35
ODとACを 位置ベクトルで
表現して
36
ODとACの内積
37
ここで
題意より
立方体であるから
辺の長さが ひとしい
それと
OAとOB OAとOC OBとOC
の内積が =0
38
そうしたらば
三角形ABCの辺ABと辺ACのなす
平面に対して
AB AC の 連立 内積が =0なので
39
OD ⊥ 三角形ABC である
お疲れ様です。
( 晴れ部屋へ 家庭菜園と ざっかや
メニュウ ページ リターン )