2023年01月12日
22039 大人のさび落とし 空間座標とベクトル 平面図形(2)
大人のさび落とし
空間座標とベクトル
平面図形(2)
01
問題
・・・・・
外心って なんだけ
垂心って 何だっけ
重心って 何だっけ

02
外心ってのは
この場合
三角形ABCの外接円の
中心
垂心ってのは
各頂点から
対辺に 下した垂線の交点
重心てのは
そこに 糸を 付けたとしたら
つり合うところ
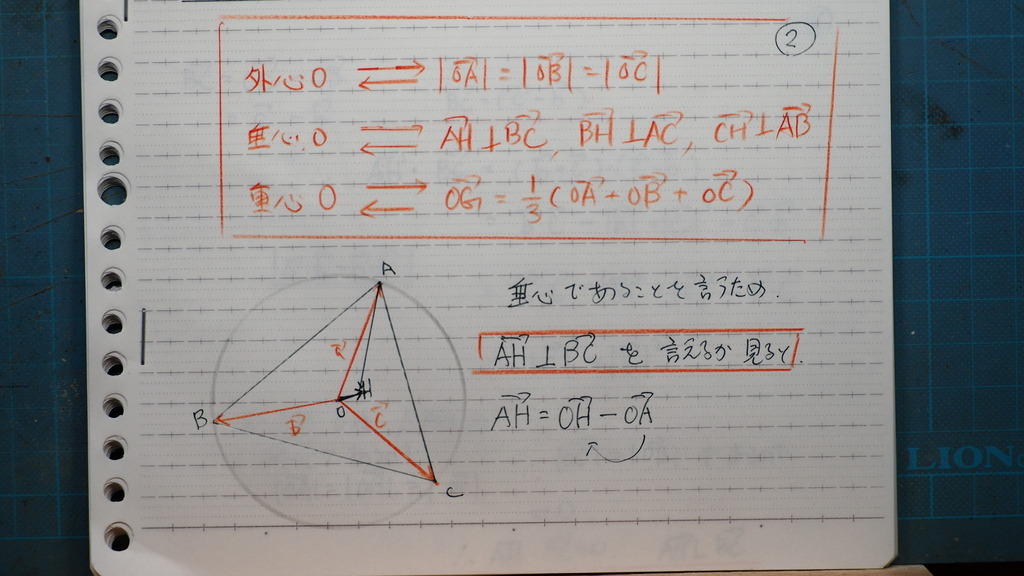
出ですよ
垂心であるから
例えば
AH が 対辺BCに 垂直か
調べれば
03
まず
題意よりの式
ベクトルを
設定して
AHは こうでしょ

04
BCは こうだよね
内積を
計算すると
ダメかなっと思ったとき
Oは 外心なので
OA OB OCは 等しい
なったじゃナイスカ

05
同様にですよ

06
なるでしょ

07
同様にですよ
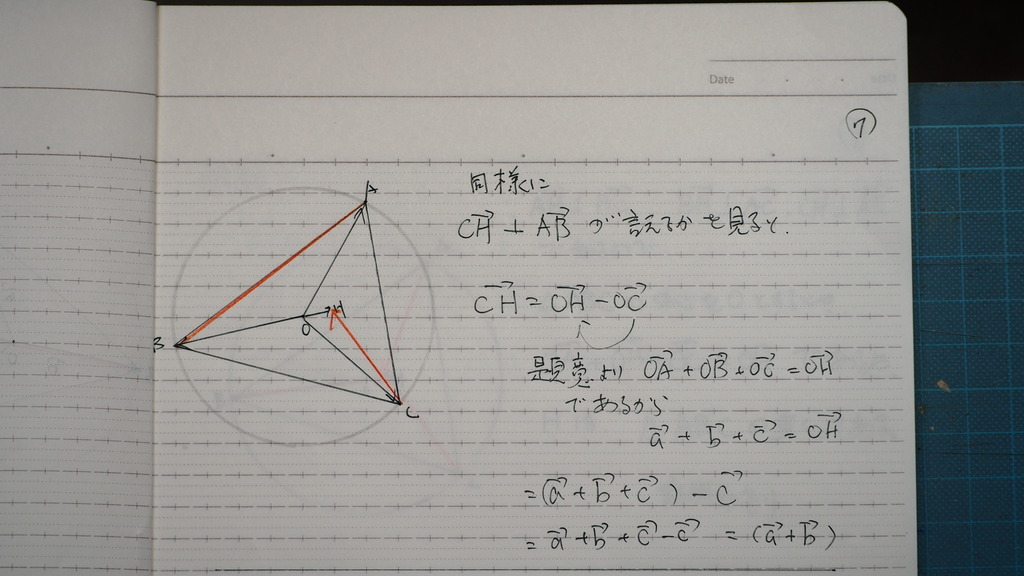
08
なりましたよ

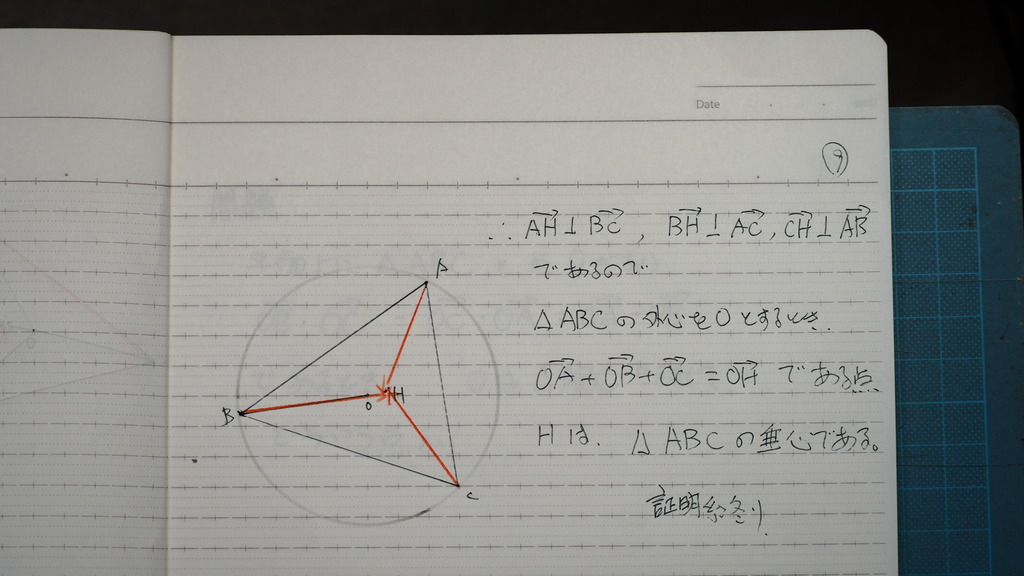
09
だからじゃナイスカ
10
今度は
一直線上に
三角形の
外心 重心 垂心が
あることを 言うんですが
重心を Gとしたら
OH は OGの 3倍
Oは 三角形の 外心
ハットトリックじゃナイスカ

11
問題

12
一見難しそう なんだけど
垂直が出てきたよ
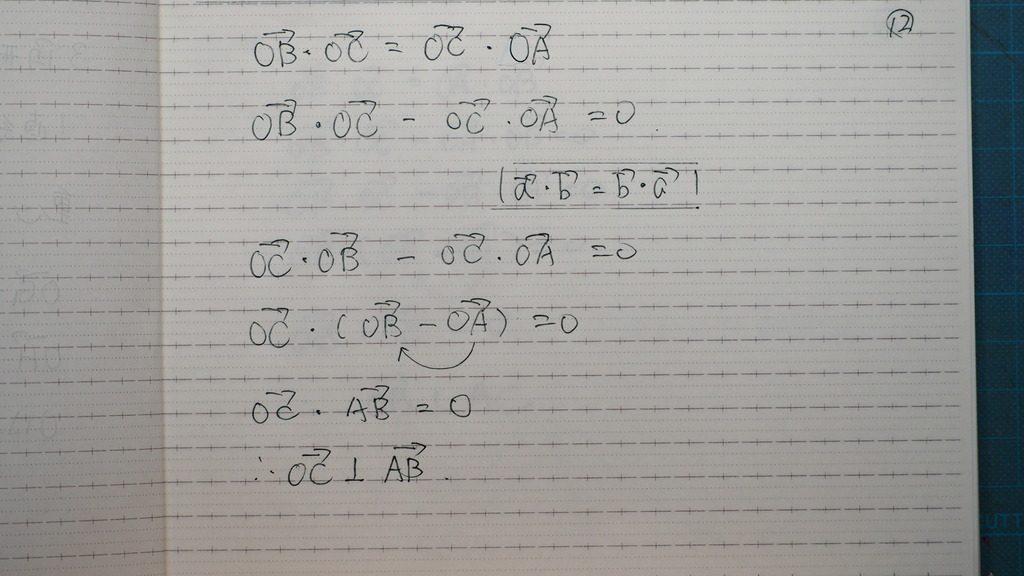
13
これも

14
これも

15
これは 垂心だよね
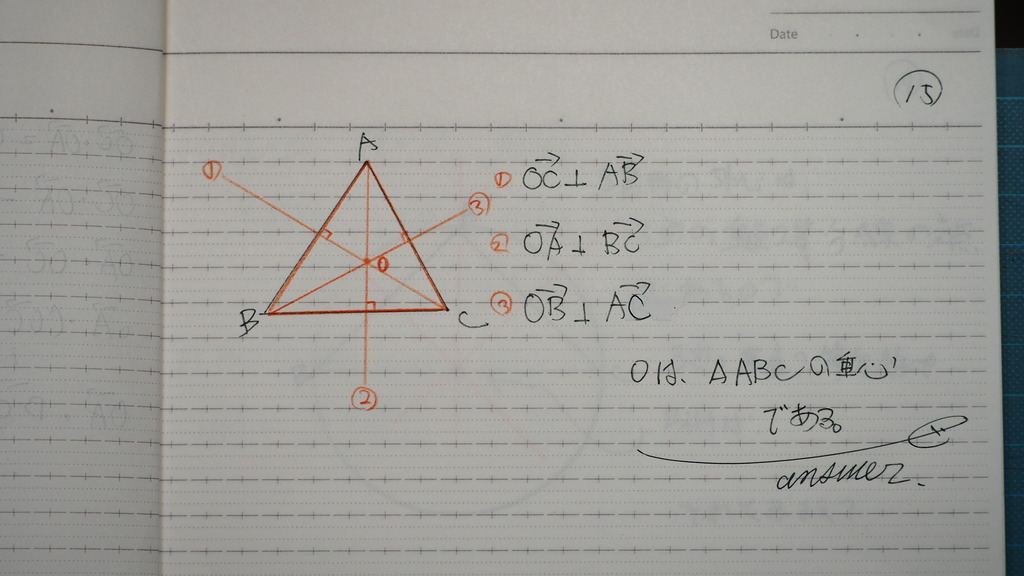
16
問題
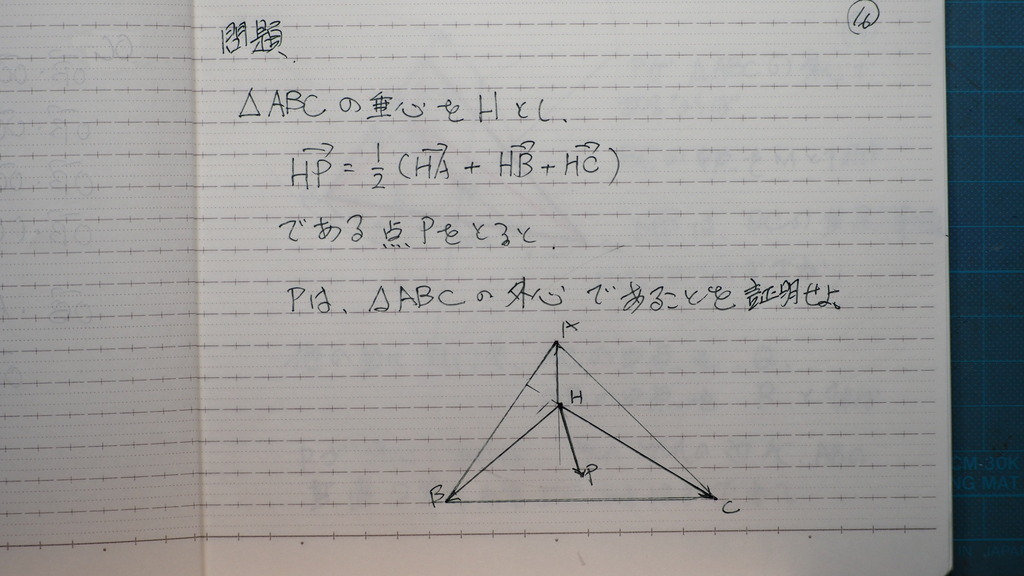
17
外心は
三辺の垂直2等分線
の 交点だから

18
P が 三角形ABCの
外心ならば
各辺の 垂直2等分線上に
Pがあるはずであるから
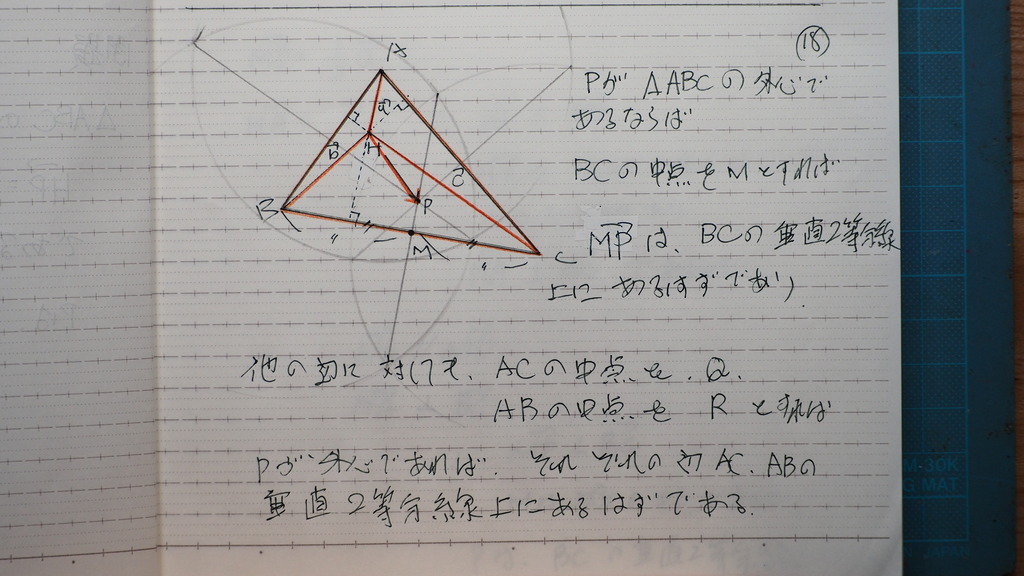
19
まず BC の 中点をMとすれば
HMは(b+c)/2
MPはHP-HM
これがさ

20
HA と 平行
Hは 垂心だから
HA と BC は 垂直
ということは
MPは HAと平行なんだから
MP垂直 BC
Mは BCの中点
なので
Pは BCの 垂直2等分線上にある

21
同様に
QPも

22
ACの 垂直2値応分線上に
Pがある

23
同様に

24
ABの垂直2等分線上にも
Pがあるので

25
Pは 外心である

26
問題

27
図にすれば
Pが 円周上を動くとき
波線を OK とおくと
Kは定点
定点と 動点の 引き算になる
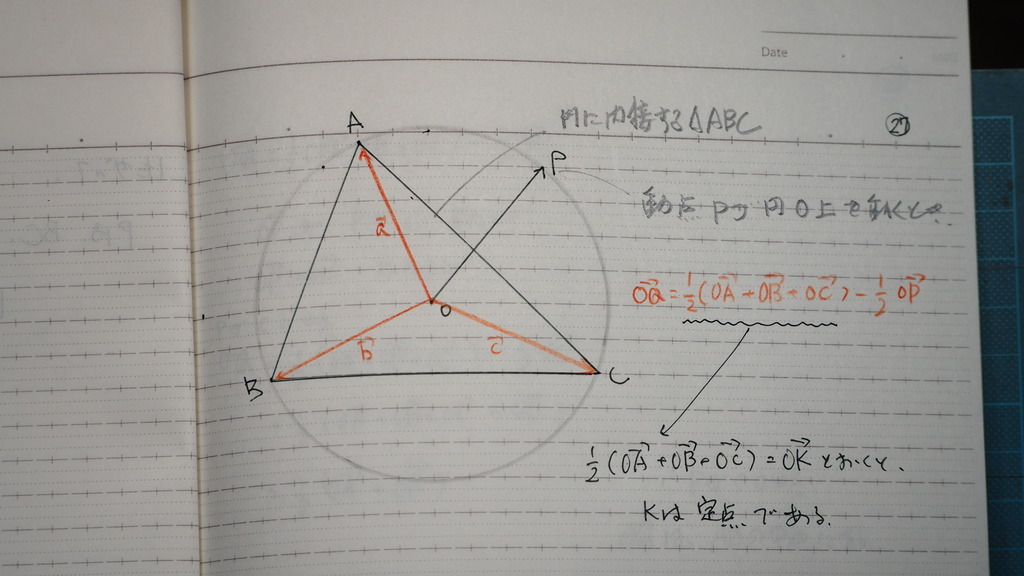
28
どうやら
Qは 円を 描くようで
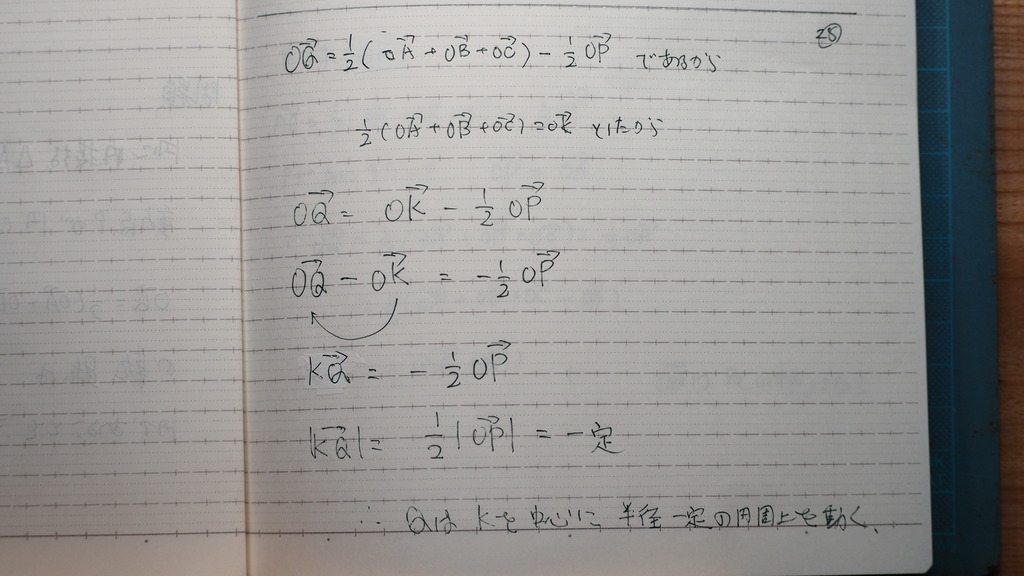
29
OPが 各頂点に来るとき
Oは 外心であるから
OPとOC
OPとOB
OPとOA
が それぞれ等しくなる
そうすると
中点を
通ってる

30
同様に
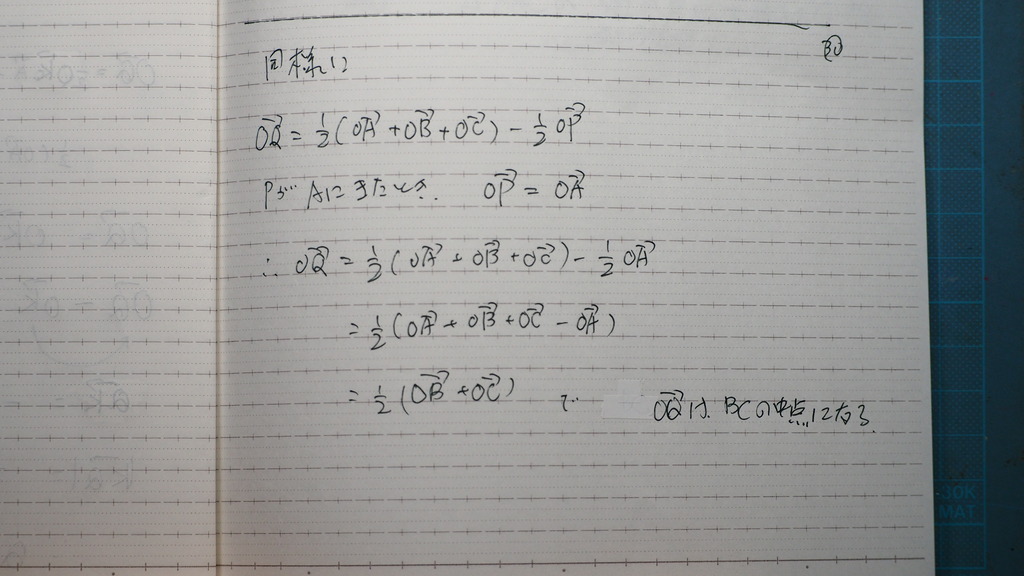
31
三角形 の 各辺の 中点を
通る円を 描く

お疲れ様です。
空間座標とベクトル
平面図形(2)
01
問題
・・・・・
外心って なんだけ
垂心って 何だっけ
重心って 何だっけ
02
外心ってのは
この場合
三角形ABCの外接円の
中心
垂心ってのは
各頂点から
対辺に 下した垂線の交点
重心てのは
そこに 糸を 付けたとしたら
つり合うところ
出ですよ
垂心であるから
例えば
AH が 対辺BCに 垂直か
調べれば
03
まず
題意よりの式
ベクトルを
設定して
AHは こうでしょ
04
BCは こうだよね
内積を
計算すると
ダメかなっと思ったとき
Oは 外心なので
OA OB OCは 等しい
なったじゃナイスカ
05
同様にですよ
06
なるでしょ
07
同様にですよ
08
なりましたよ
09
だからじゃナイスカ
10
今度は
一直線上に
三角形の
外心 重心 垂心が
あることを 言うんですが
重心を Gとしたら
OH は OGの 3倍
Oは 三角形の 外心
ハットトリックじゃナイスカ
11
問題
12
一見難しそう なんだけど
垂直が出てきたよ
13
これも
14
これも
15
これは 垂心だよね
16
問題
17
外心は
三辺の垂直2等分線
の 交点だから
18
P が 三角形ABCの
外心ならば
各辺の 垂直2等分線上に
Pがあるはずであるから
19
まず BC の 中点をMとすれば
HMは(b+c)/2
MPはHP-HM
これがさ
20
HA と 平行
Hは 垂心だから
HA と BC は 垂直
ということは
MPは HAと平行なんだから
MP垂直 BC
Mは BCの中点
なので
Pは BCの 垂直2等分線上にある
21
同様に
QPも
22
ACの 垂直2値応分線上に
Pがある
23
同様に
24
ABの垂直2等分線上にも
Pがあるので
25
Pは 外心である
26
問題
27
図にすれば
Pが 円周上を動くとき
波線を OK とおくと
Kは定点
定点と 動点の 引き算になる
28
どうやら
Qは 円を 描くようで
29
OPが 各頂点に来るとき
Oは 外心であるから
OPとOC
OPとOB
OPとOA
が それぞれ等しくなる
そうすると
中点を
通ってる
30
同様に
31
三角形 の 各辺の 中点を
通る円を 描く
お疲れ様です。