2023年04月14日
08033 大人のさび落とし 図形と方程式 図形の通る範囲
大人のさび落とし
図形の通る領域
01
yの2次関数があるんですが
変数aが 入っています
aが 実数の 値を とって
変化するとき
放物線の 通る範囲を
求めなさい

02
考え方なんですが
例えば (1,3) は通るかな
代入するでしょ
すると

03
aの値が 2つ 出て来て
-2 または 1 のとき
aが実数の値を とって
変わる とき
-2,1 になるときは
点(1,3)を 通るってことですよ
つまり
(1,3) は 通る範囲にある

04
(2,1) ならどうか
代入してみたらば
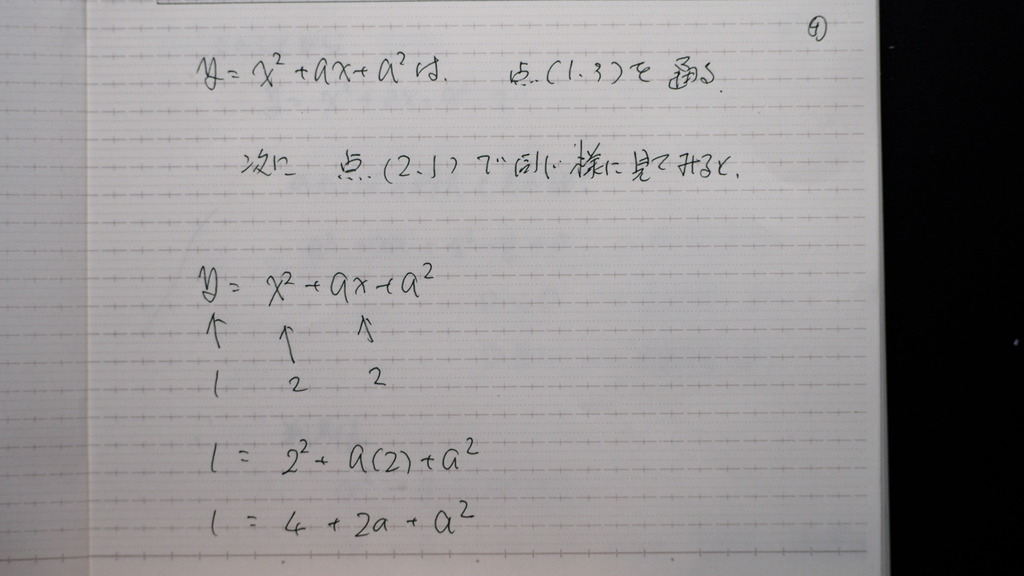
05
aの解が 虚数になった
実数でない
つまり
点(2,1) を 通るためには
aが 実数の範囲を
越えてしまうので
ダメ
通らない

06
このことから
(x、y) に 点の値を
代入して
つまり aの2次方程式にして
その解が
実数解を持つならば
通る
虚数解ならば
通らない
aの2次方程式に
整理して
判別式
Dは x、yの 関係式になっていて
Dが 0以上になれば 通る

07
こんな感じに
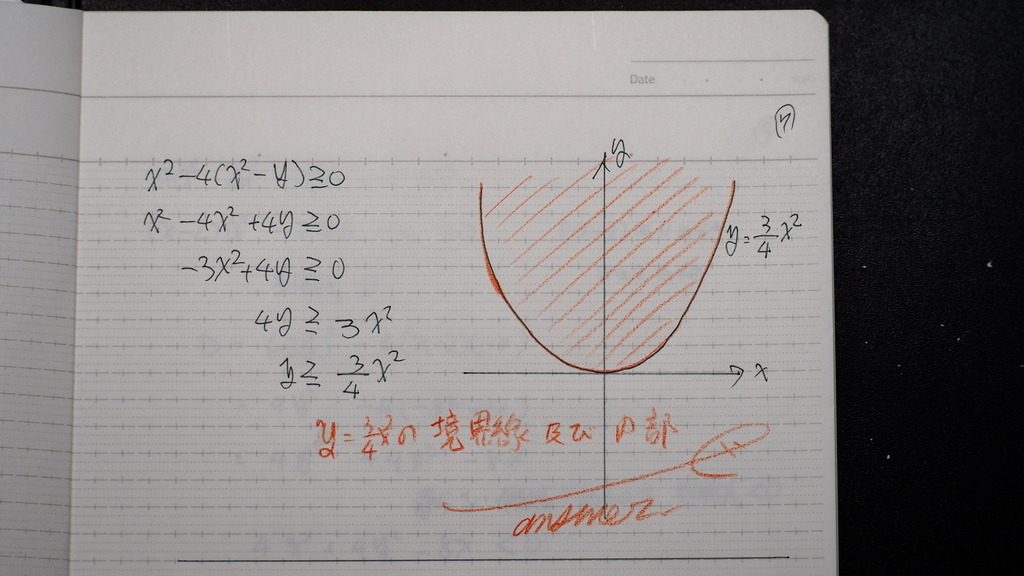
08
じゃあ 行きますよ
今度は
この直線が
通らない領域を
図示せよ
具体的に
(x、y) を 入れてくなんて
場合を 尽くすことは
出来ませんので
しかし
x、y が わかってるときは
この式は
aの 2次方程式になるよ
そこで
展開して
aの2次方程式に 整理して
判別式:D
D 0未満を求めると
x、yの 関係式で出て来て

09
円の 方程式になるかな

10
これで 終わりでは無くて
いま さっときてしまったけど
2次方程式でないと
判別式は 使えない
イマのは xが 2でない場合

11
xが 2の時は
2次方程式にならず
ya=-1
aは 変化する実数で
aの値が 変わっていく時に
この式が 成り立つものがあれば
通ることになる
通らない場合であるので
y=0

12
こんな感じで
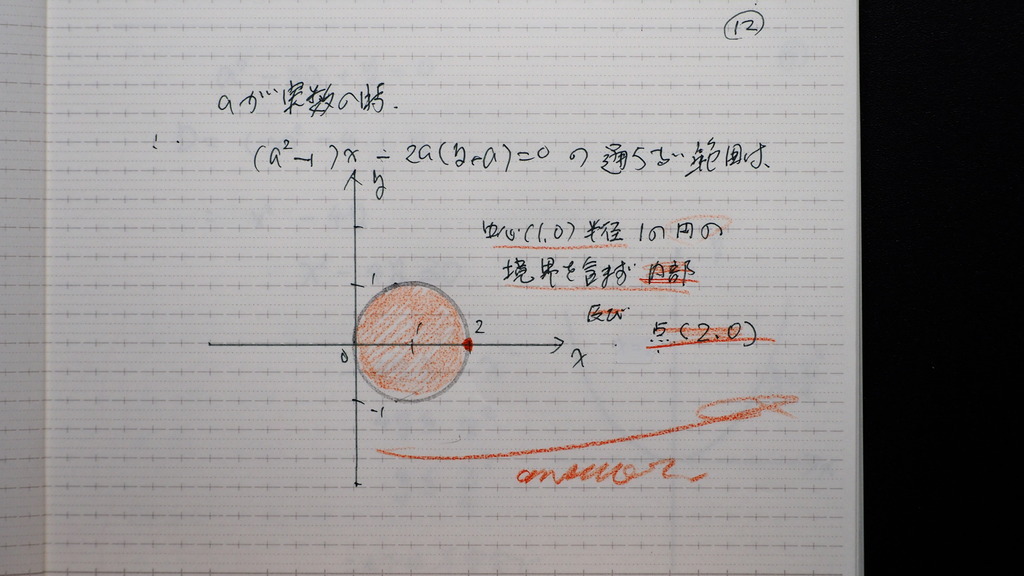
13
次は
直線が
通る領域を 図示せよ
aについての
2次方程式に整理して
判別式で

14
こんなグラフか
で グラフの 下側
って やりたいとこですが
これでは 不完全
aが 正の数の時
を どう表現するか?
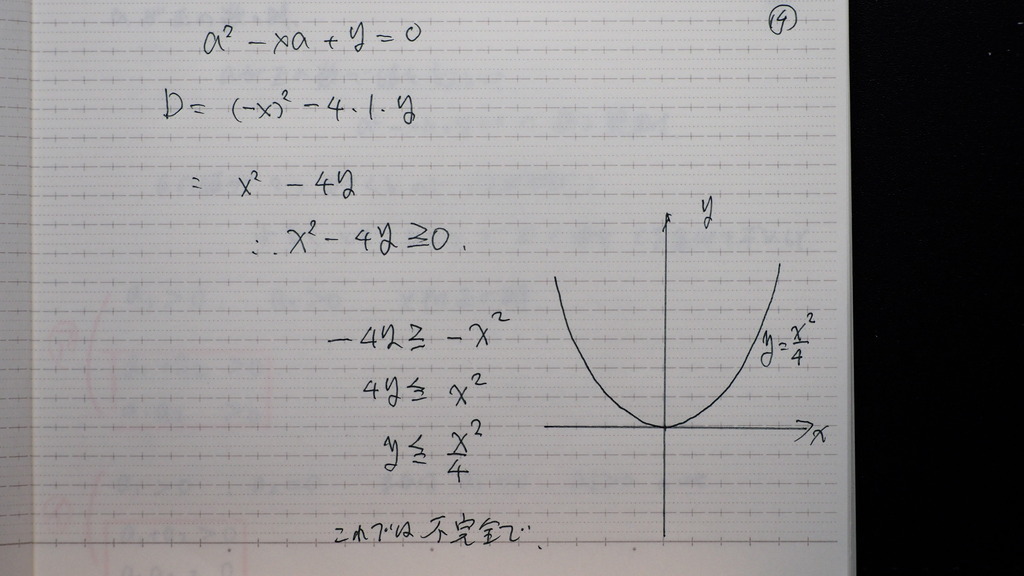
15
aについて 解くと
解が2つ 出てくるんだね
a1,a2
とするでしょ

16
aが 正の数で 値を 変える時
2次方程式なので
解が aの値が 2つある
少なくとも 1つが
正の数で あるためには
ア 2つとも正
イ どちらかが正で 他方が ゼロ

17
ウ 異符号の時
アから見てきますと
a1+a2 は 正
xは 正

18
a1a2 は 正
yは 正
であるから
赤枠
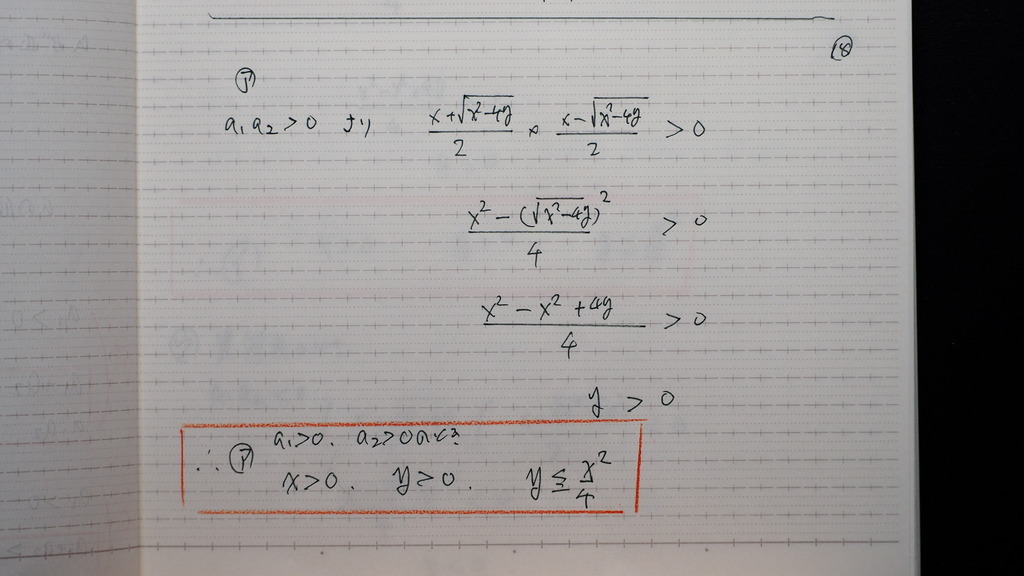
19
イ どちらかが 正で
他方が ゼロ
足せば 正
xは 正
かければ ゼロ

20
yは ゼロ
ウ のとき
掛ければ
yは 負
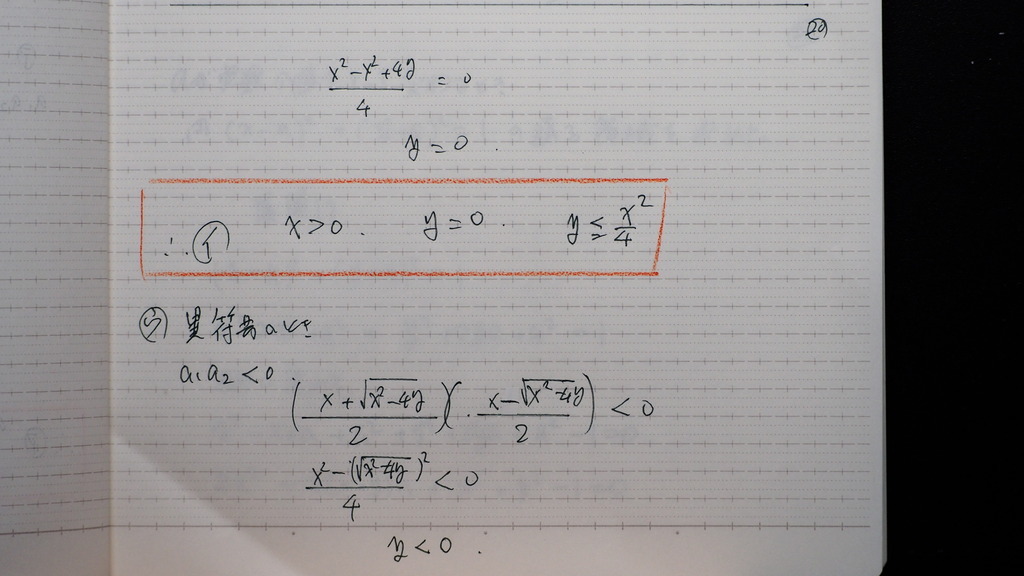
21
ア+イ+う は
こんな感じで
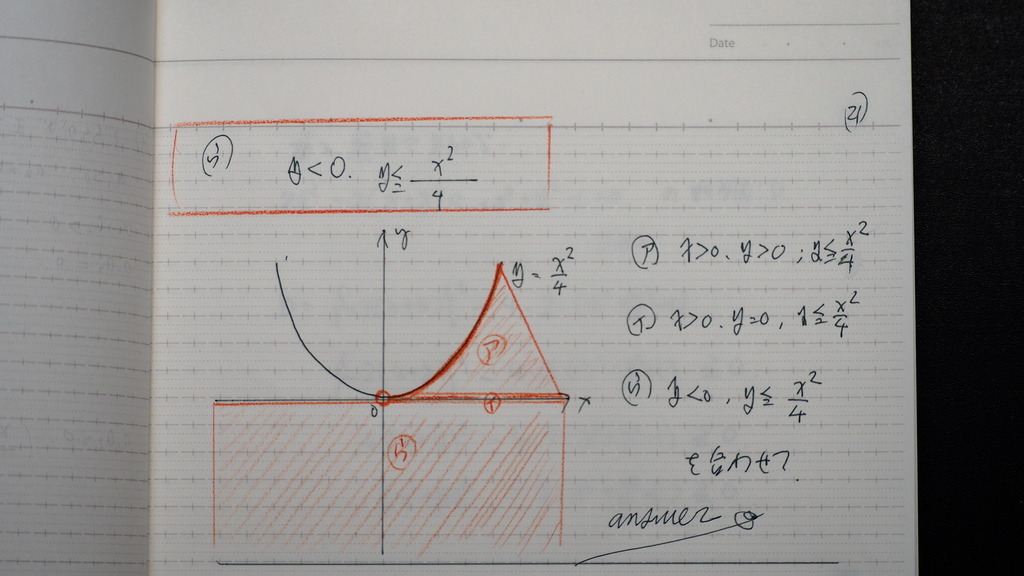
22
円があるんですが
aが 実数の値を
とってかわるとき
円の 通る 領域を求めよ
展開して
aで整理して

23
判別式が
ゼロ 以上のとこは
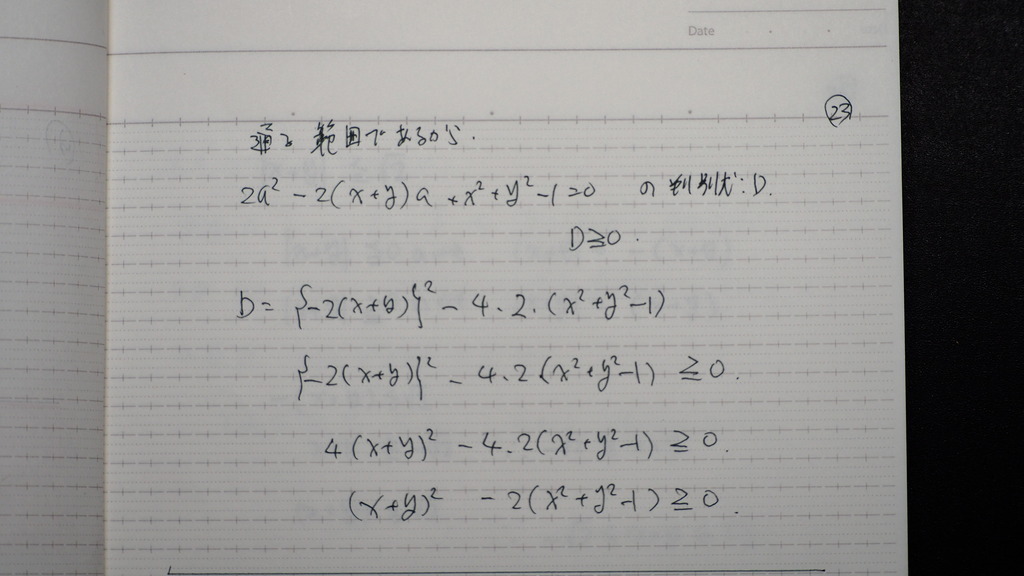
24
今回は
(x+y)の 二乗は
プラスだけど
(x+y)は マイナスの場合も
あるので
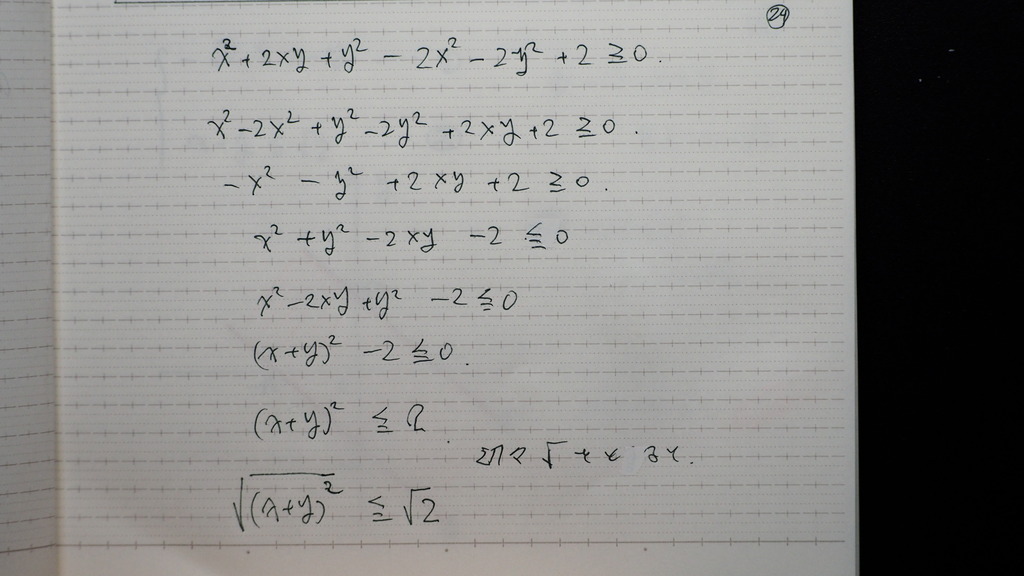
25
こうすればさ
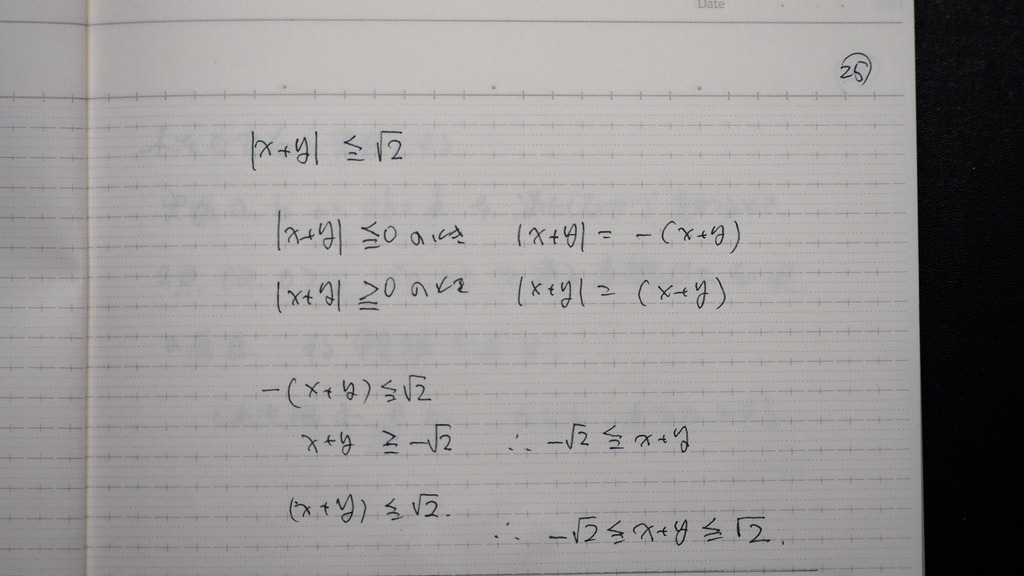
26
こんな感じで
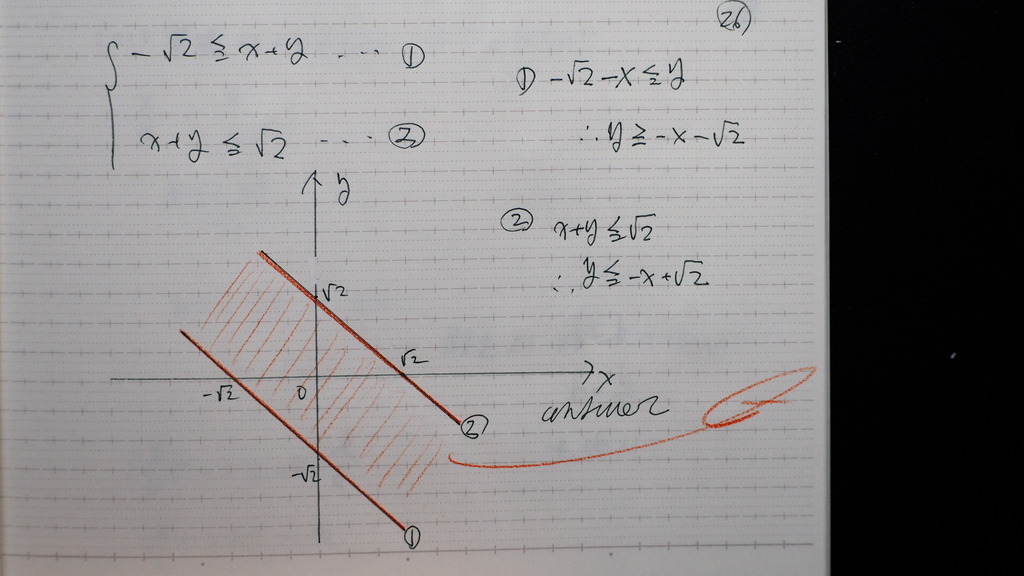
27
条件が いくつかあるんですが
2点を 通る直線上に 無い領域は?

28
今回の直線の 方程式は
両切片型なので
あったじゃナイスカ
こんな感じで
これを
平らにしてくと

29
実数変数のa,bを
aで表してるので
aの 2次方程式の 判別式にして
2次の項の係数yが
ゼロでないとき

30
方曲線の感じに
なってじゃナイスカ

31
2次の項の係数yが
ゼロの時
x=aで これは ゼロではない
逆に
このとき
y=0のとき X=0は 通らない

32
こんな感じですか
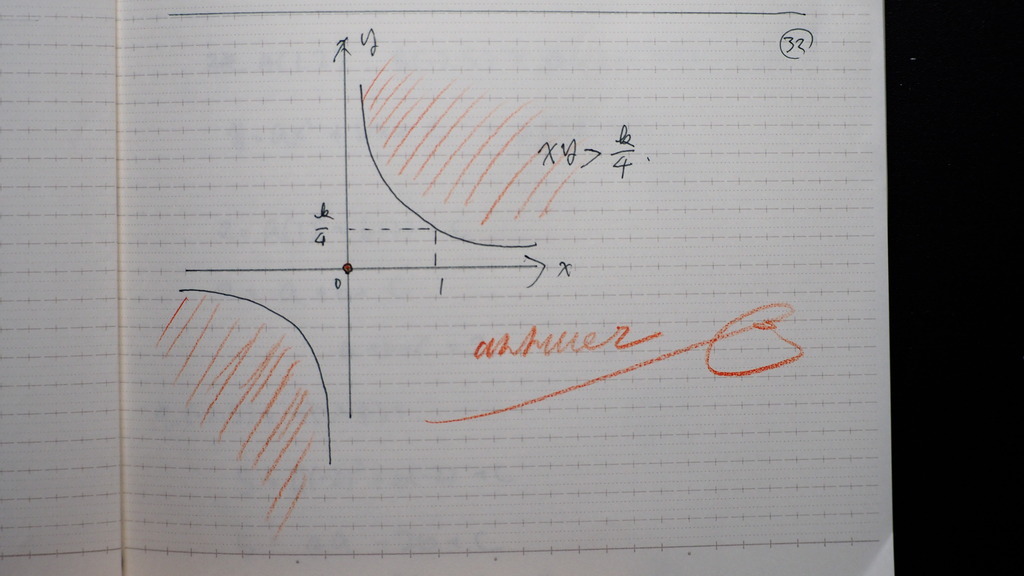
33
直交座標において
点A(1,2)、B(-2,5)を通る
どんな 2次曲線も
決して 通らない 点
を 求めよ

34
a,b,cを 全部 aで
表わせば
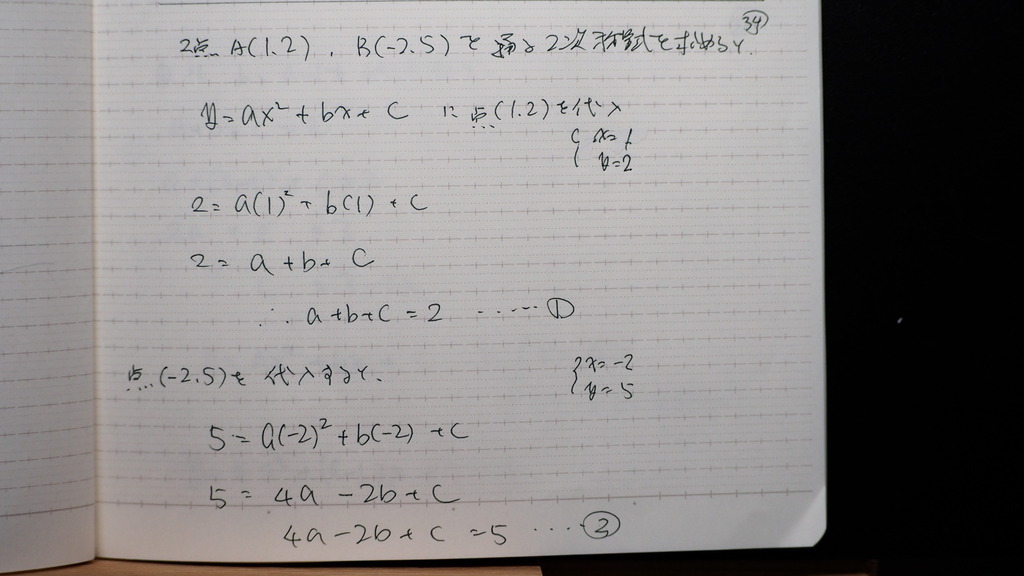
35
先ずb
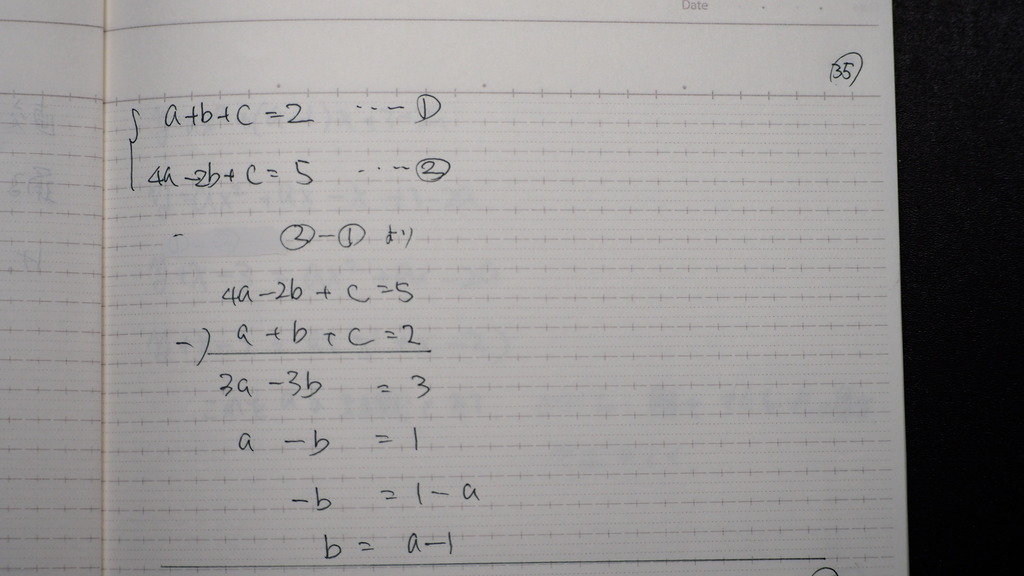
36
つぎにc
b、cを 代入して
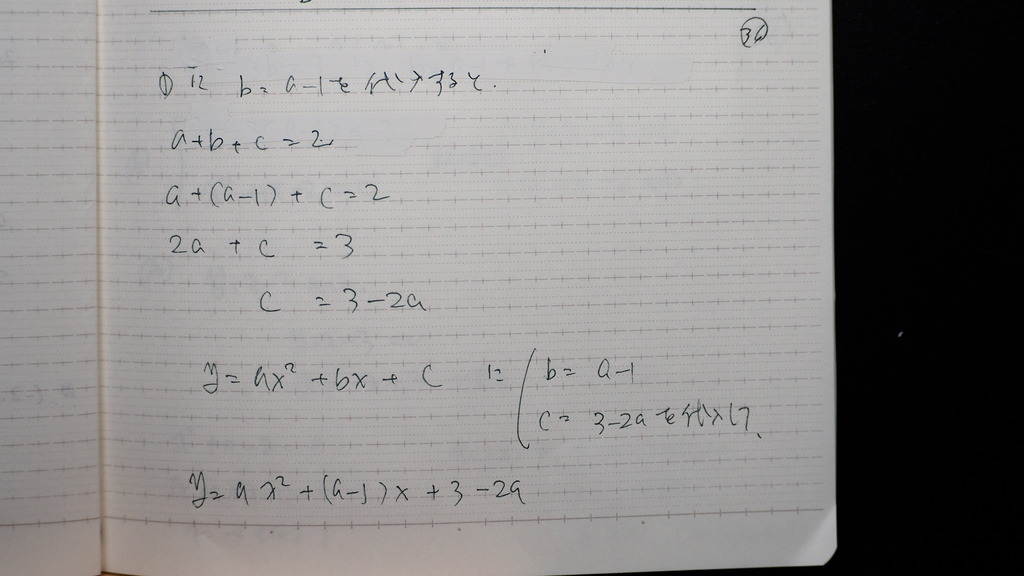
37
ここからなんですが
これを
aの方程式と考えて
ゼロでない
解を
持たない 点の集合を
求めると

38
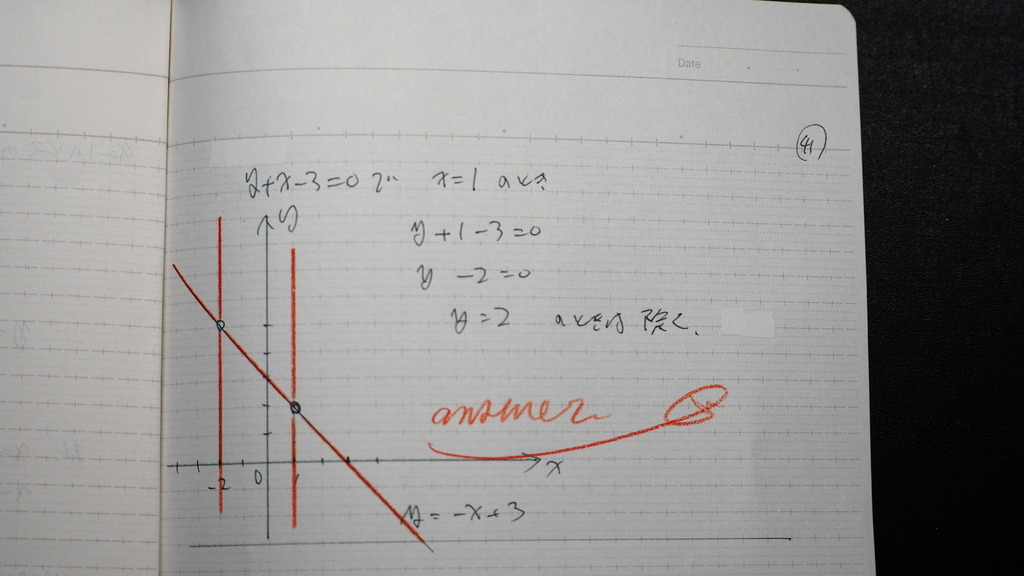
Ⓐ y=-x+3 ではない
もう一つの 式から
x=-2の時 y=5は
解になってしまうので
外す
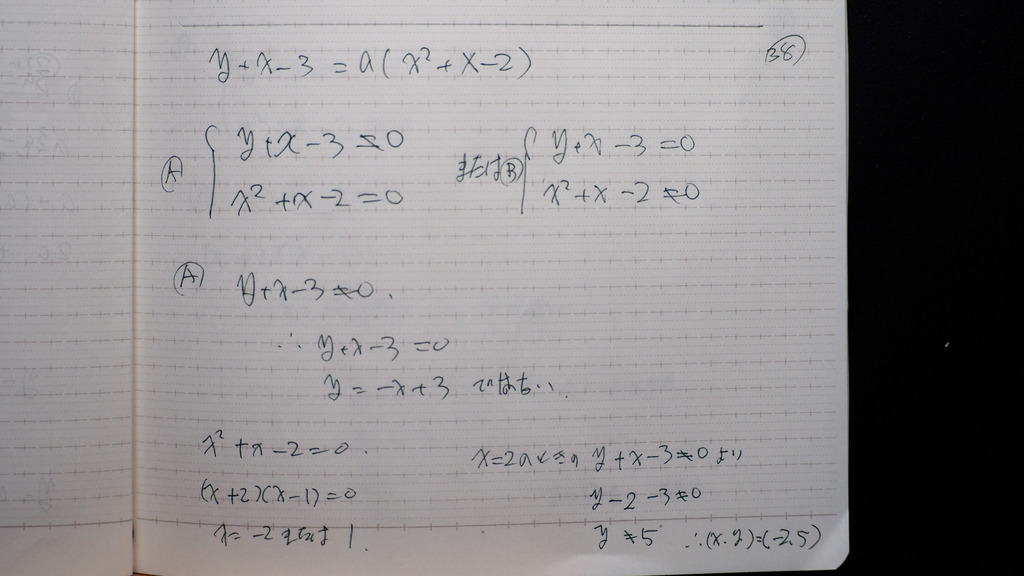
39
x=1の時
y=2は 解になってしまうので
外す

40
Ⓑも 見てみた結果

41
こんな感じで
赤い所
お疲れ様です。
図形の通る領域
01
yの2次関数があるんですが
変数aが 入っています
aが 実数の 値を とって
変化するとき
放物線の 通る範囲を
求めなさい
02
考え方なんですが
例えば (1,3) は通るかな
代入するでしょ
すると
03
aの値が 2つ 出て来て
-2 または 1 のとき
aが実数の値を とって
変わる とき
-2,1 になるときは
点(1,3)を 通るってことですよ
つまり
(1,3) は 通る範囲にある
04
(2,1) ならどうか
代入してみたらば
05
aの解が 虚数になった
実数でない
つまり
点(2,1) を 通るためには
aが 実数の範囲を
越えてしまうので
ダメ
通らない
06
このことから
(x、y) に 点の値を
代入して
つまり aの2次方程式にして
その解が
実数解を持つならば
通る
虚数解ならば
通らない
aの2次方程式に
整理して
判別式
Dは x、yの 関係式になっていて
Dが 0以上になれば 通る
07
こんな感じに
08
じゃあ 行きますよ
今度は
この直線が
通らない領域を
図示せよ
具体的に
(x、y) を 入れてくなんて
場合を 尽くすことは
出来ませんので
しかし
x、y が わかってるときは
この式は
aの 2次方程式になるよ
そこで
展開して
aの2次方程式に 整理して
判別式:D
D 0未満を求めると
x、yの 関係式で出て来て
09
円の 方程式になるかな
10
これで 終わりでは無くて
いま さっときてしまったけど
2次方程式でないと
判別式は 使えない
イマのは xが 2でない場合
11
xが 2の時は
2次方程式にならず
ya=-1
aは 変化する実数で
aの値が 変わっていく時に
この式が 成り立つものがあれば
通ることになる
通らない場合であるので
y=0
12
こんな感じで
13
次は
直線が
通る領域を 図示せよ
aについての
2次方程式に整理して
判別式で
14
こんなグラフか
で グラフの 下側
って やりたいとこですが
これでは 不完全
aが 正の数の時
を どう表現するか?
15
aについて 解くと
解が2つ 出てくるんだね
a1,a2
とするでしょ
16
aが 正の数で 値を 変える時
2次方程式なので
解が aの値が 2つある
少なくとも 1つが
正の数で あるためには
ア 2つとも正
イ どちらかが正で 他方が ゼロ
17
ウ 異符号の時
アから見てきますと
a1+a2 は 正
xは 正
18
a1a2 は 正
yは 正
であるから
赤枠
19
イ どちらかが 正で
他方が ゼロ
足せば 正
xは 正
かければ ゼロ
20
yは ゼロ
ウ のとき
掛ければ
yは 負
21
ア+イ+う は
こんな感じで
22
円があるんですが
aが 実数の値を
とってかわるとき
円の 通る 領域を求めよ
展開して
aで整理して
23
判別式が
ゼロ 以上のとこは
24
今回は
(x+y)の 二乗は
プラスだけど
(x+y)は マイナスの場合も
あるので
25
こうすればさ
26
こんな感じで
27
条件が いくつかあるんですが
2点を 通る直線上に 無い領域は?
28
今回の直線の 方程式は
両切片型なので
あったじゃナイスカ
こんな感じで
これを
平らにしてくと
29
実数変数のa,bを
aで表してるので
aの 2次方程式の 判別式にして
2次の項の係数yが
ゼロでないとき
30
方曲線の感じに
なってじゃナイスカ
31
2次の項の係数yが
ゼロの時
x=aで これは ゼロではない
逆に
このとき
y=0のとき X=0は 通らない
32
こんな感じですか
33
直交座標において
点A(1,2)、B(-2,5)を通る
どんな 2次曲線も
決して 通らない 点
を 求めよ
34
a,b,cを 全部 aで
表わせば
35
先ずb
36
つぎにc
b、cを 代入して
37
ここからなんですが
これを
aの方程式と考えて
ゼロでない
解を
持たない 点の集合を
求めると
38
Ⓐ y=-x+3 ではない
もう一つの 式から
x=-2の時 y=5は
解になってしまうので
外す
39
x=1の時
y=2は 解になってしまうので
外す
40
Ⓑも 見てみた結果
41
こんな感じで
赤い所
お疲れ様です。