2023年01月12日
22040 大人のさび落とし 空間座標とベクトル 空間図形(1)
大人のさび落とし
空間座標とベクトル
空間図形(1)
01
3垂線の定理と言うのがあるですが

02
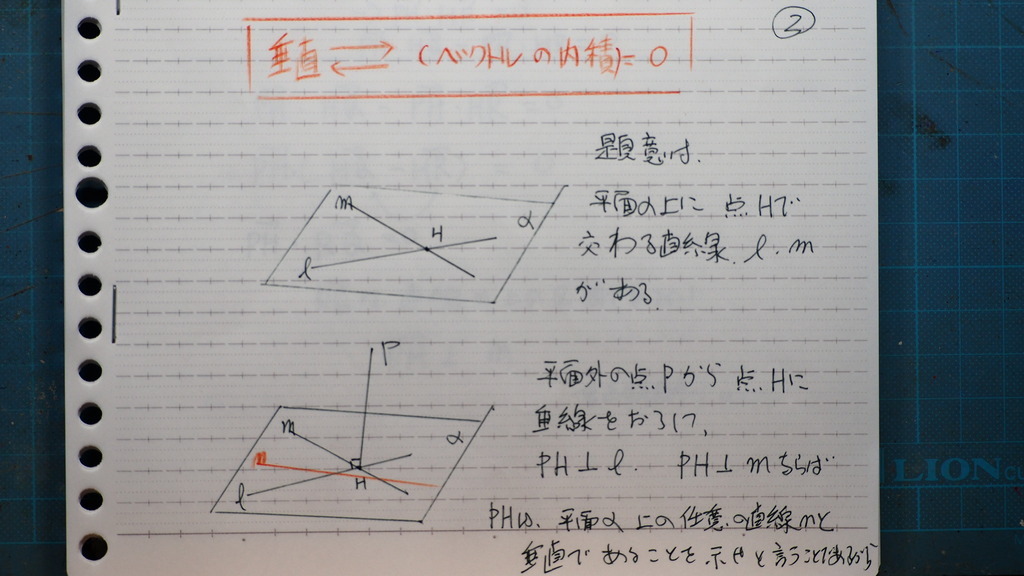
問題を
図にしてくと
平面上に
2本の直線があると
Hで 交わってる
そこへ
平面ほかのPから 垂線を
下したとき
2直線に
垂線が 垂直ならば
任意の 平面上の直線に対しても
垂直であることを
示せ
03
だから
平面上に
もう1本 n と言う
任意の直線を
引くじゃナイスカ
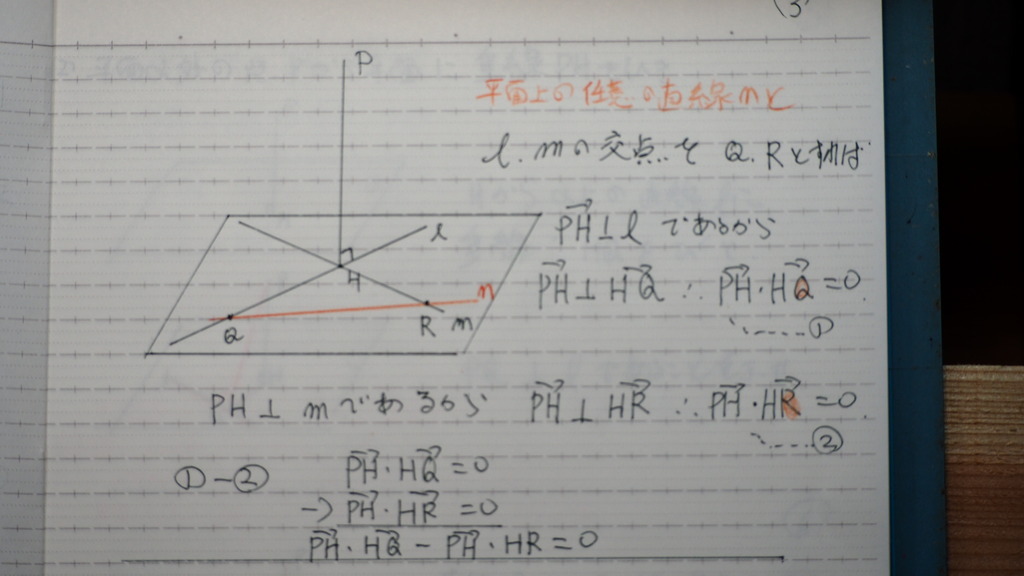
他の2直線との 交点を
Q,R とすれば
PH 垂直 L なので
L 上のベクトル HQとも
当然 垂直
PH 垂直 mであるから
m上のベクトル HR とも
当然垂直である
ここで
出てきた ➀②の式を
引算すると
PH で くくると
04
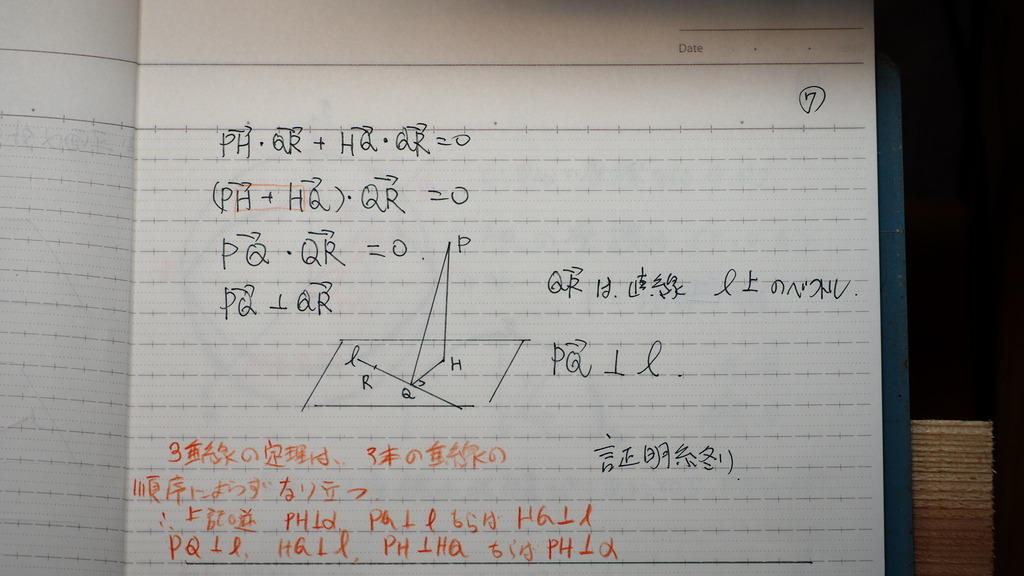
なんと
直線 n 上の ベクトル
RQ と 垂直になってる
だから
PH 垂直 n

05
今度は
Hから 平面上の 直線に
垂線を 引いたばあい
その交点を Qとすれが
PQ 垂直 L であるを
示せ

06
PH 垂直 Lであるから
とうぜん
L 上の ベクトル QRとも
垂直である
Hから Lに垂線を引いて
Qとしたのだから
当然
HQ 垂直 QRである
今度は
この ③④式を
足すと

07
なるんですよ
08
今度は
たまに 出て来そうな 問題です
地球は 丸かった
地球を 球と考えて
A地点を 北緯0度 東経0度
B地点を 北緯45度 統計35度
としたとき
地球の中心を 0として
角AOBは 何度か

09
空間座標を
考えるでしょ

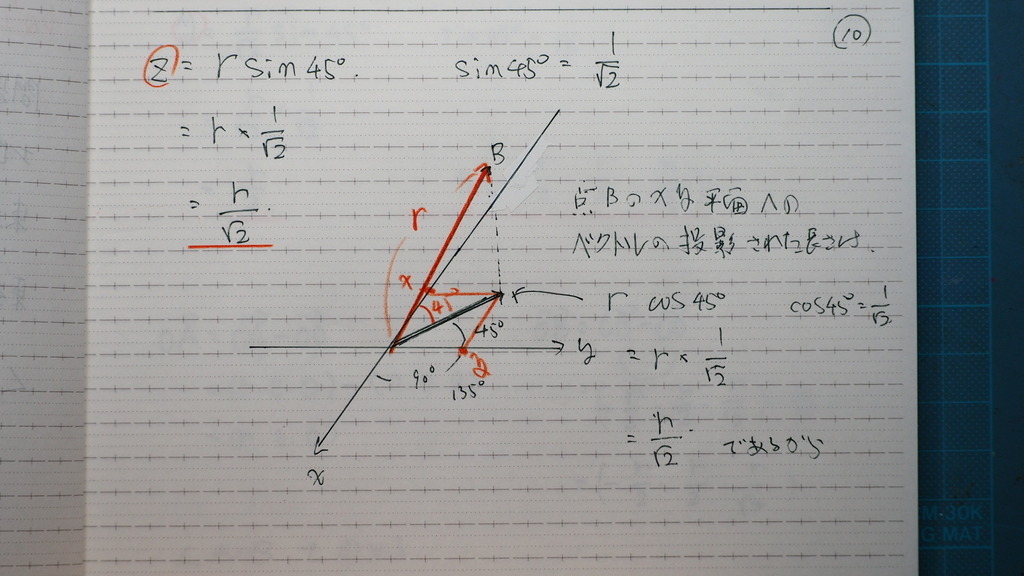
10
普段から
こういう 計算してないと
あれって思いませんか
11
だからね
コレ イメージわかるかな
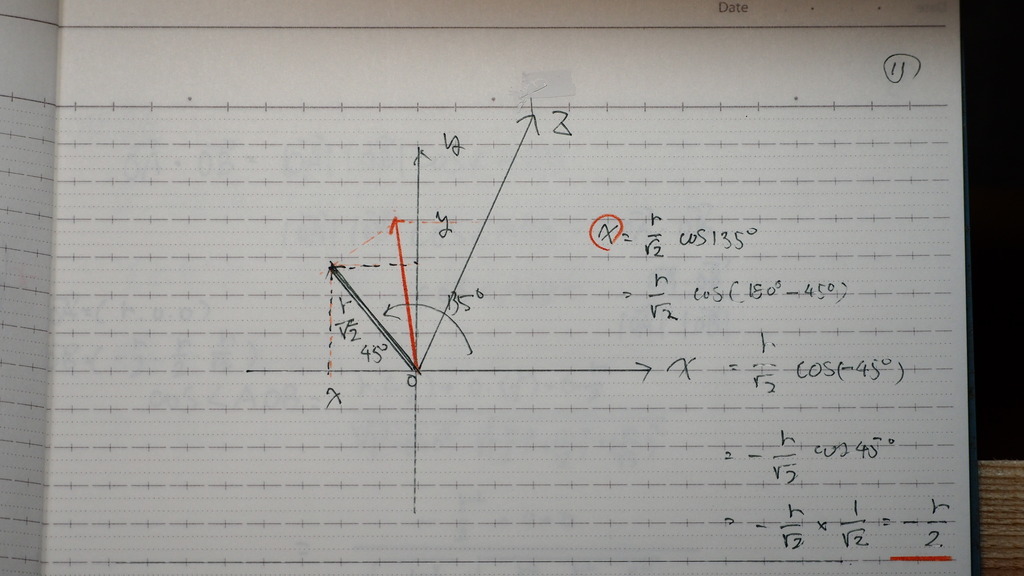
12
だからね
Bの座標は こうなんですよ
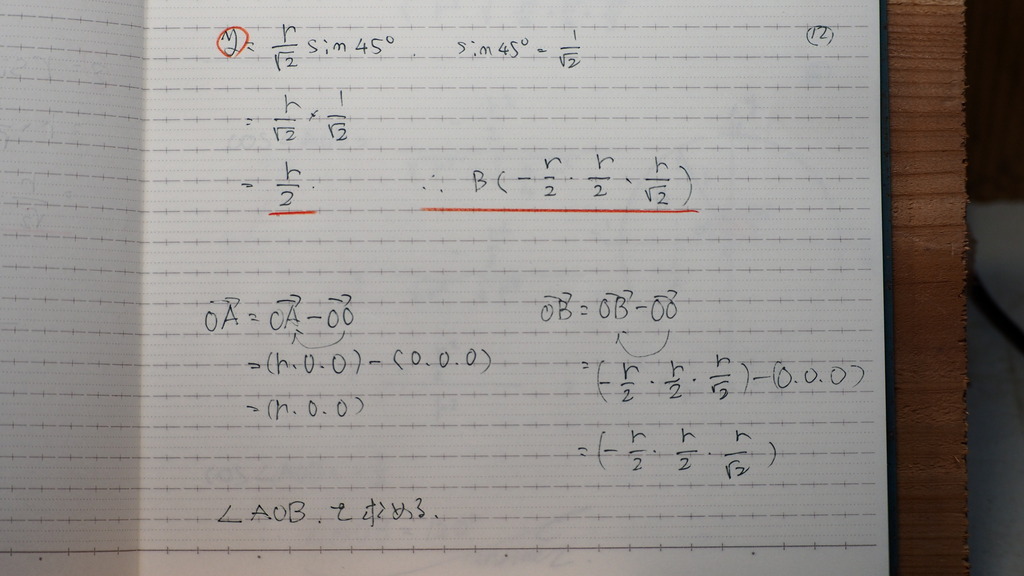
13
これで
空間座標の なす角を
求めると

14
120度
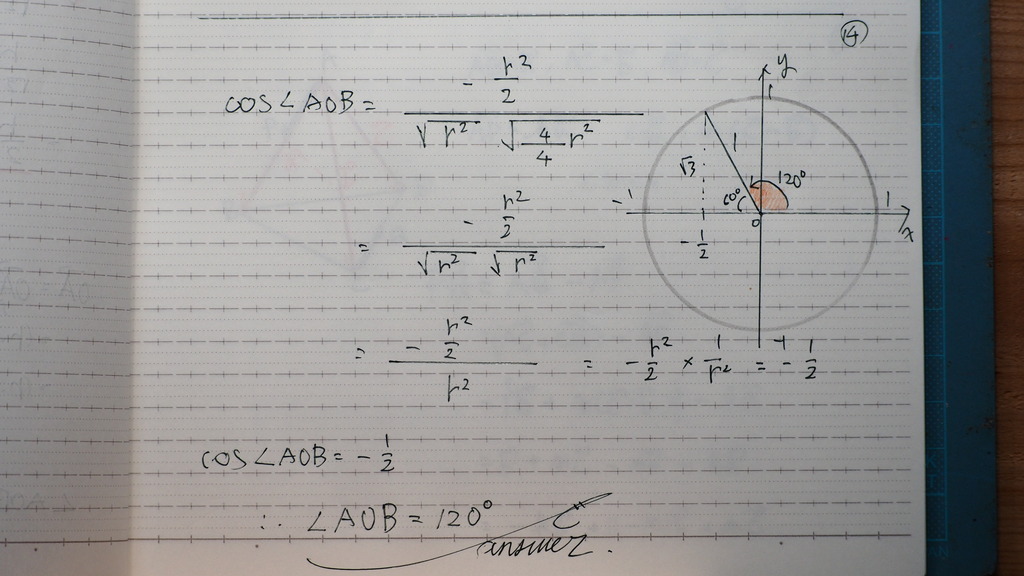
15
問題
これは
ベクトルの 設定が
出来れば
半分できた

16
まず 基本的な ベクトルは
こんな感じで
AP と CQ を
こんな感じにできれば

17
2乗で 内積を
展開してくと
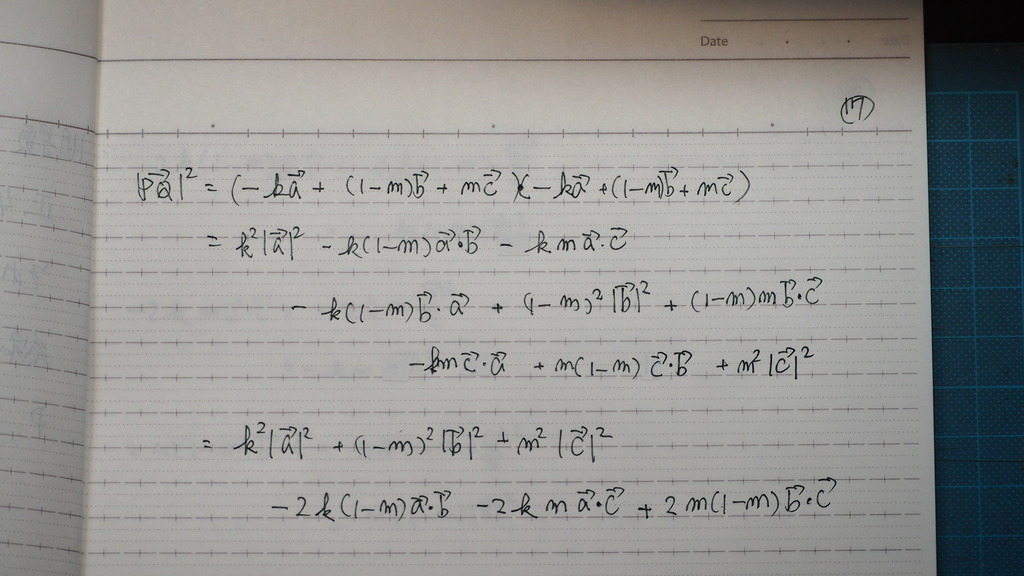
18
題意より
正四面体であるので
もうちょっと 簡単になる

19
こんな感じに
まとめて
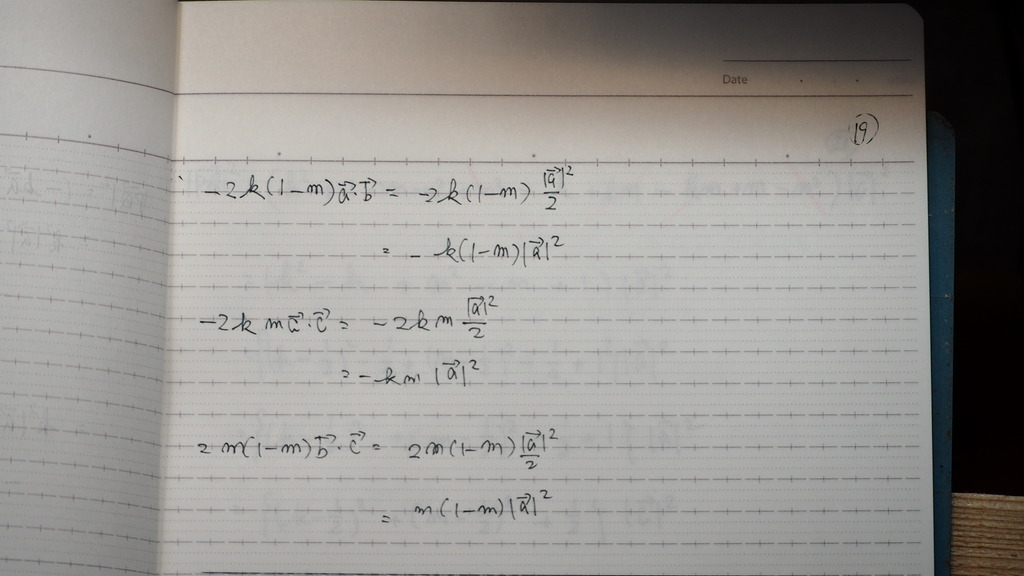
20
整理して
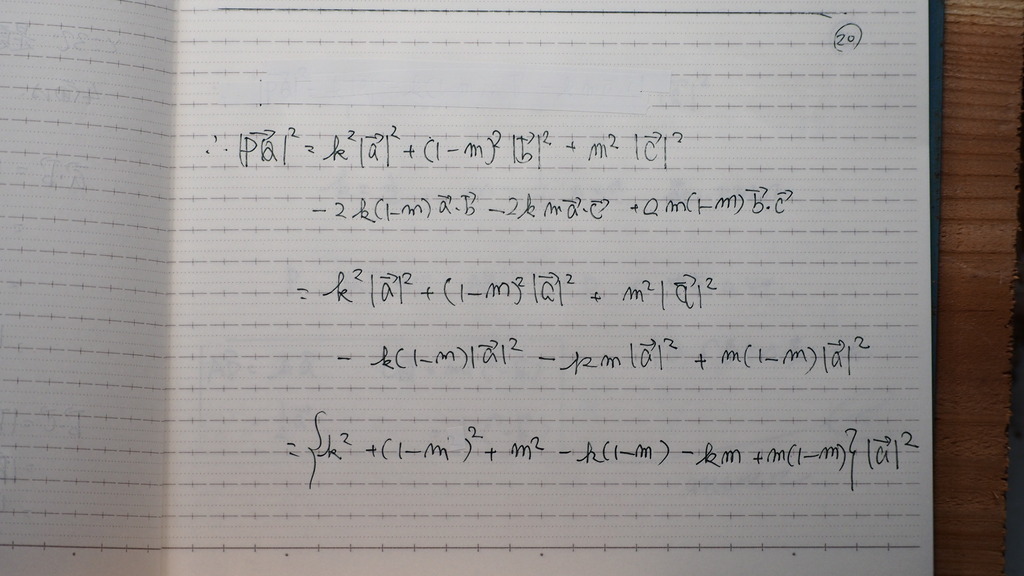
21
これをさ
平方を 作ると
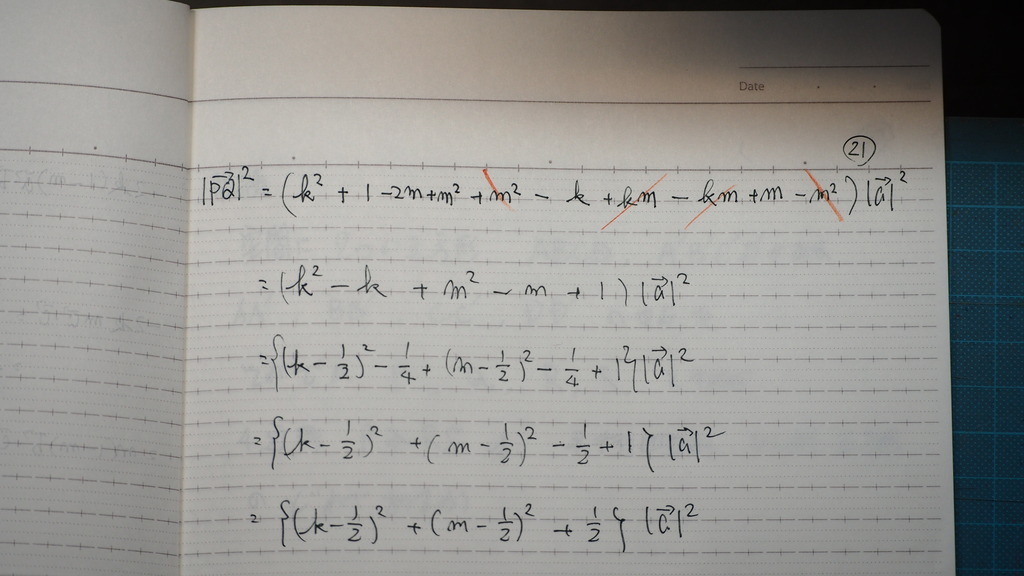
22
P,Qが それぞれ
中点の時
最初になる

23
問題

24
これはさ
中点の 連結定理で
計算したらば
PQは
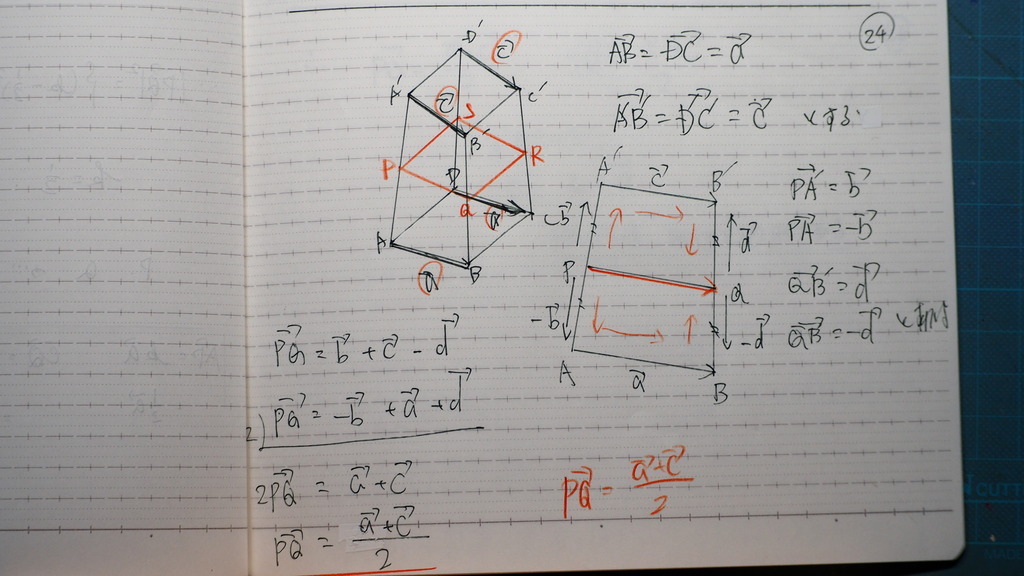
25
SRは
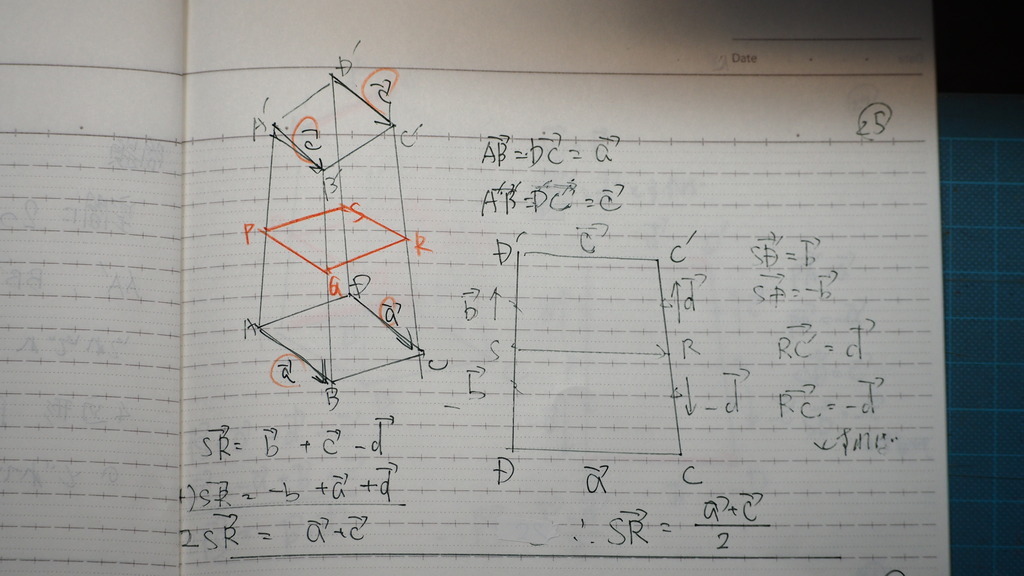
26
ここで
平行四辺形
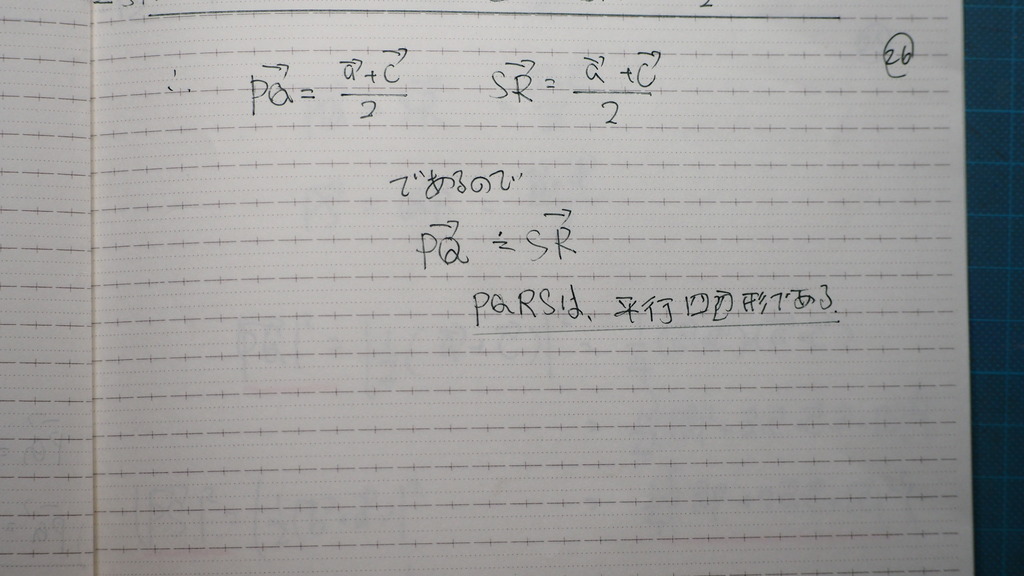
27
で
PSは
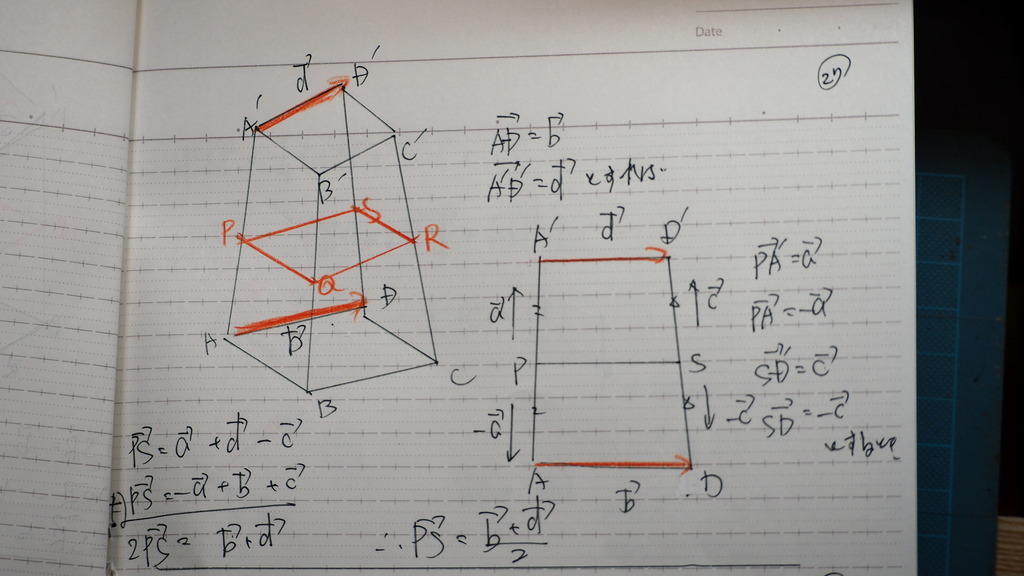
28
QRは

29
PQ と PSは
必ず 平行とは 限らない
であるから
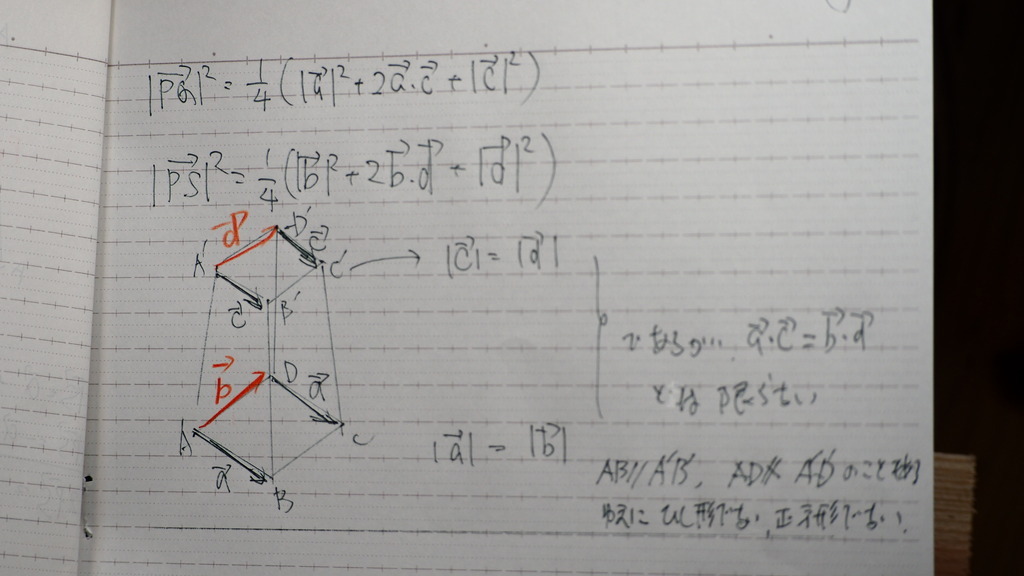
平行四辺形
お疲れ様です。
空間座標とベクトル
空間図形(1)
01
3垂線の定理と言うのがあるですが
02
問題を
図にしてくと
平面上に
2本の直線があると
Hで 交わってる
そこへ
平面ほかのPから 垂線を
下したとき
2直線に
垂線が 垂直ならば
任意の 平面上の直線に対しても
垂直であることを
示せ
03
だから
平面上に
もう1本 n と言う
任意の直線を
引くじゃナイスカ
他の2直線との 交点を
Q,R とすれば
PH 垂直 L なので
L 上のベクトル HQとも
当然 垂直
PH 垂直 mであるから
m上のベクトル HR とも
当然垂直である
ここで
出てきた ➀②の式を
引算すると
PH で くくると
04
なんと
直線 n 上の ベクトル
RQ と 垂直になってる
だから
PH 垂直 n
05
今度は
Hから 平面上の 直線に
垂線を 引いたばあい
その交点を Qとすれが
PQ 垂直 L であるを
示せ
06
PH 垂直 Lであるから
とうぜん
L 上の ベクトル QRとも
垂直である
Hから Lに垂線を引いて
Qとしたのだから
当然
HQ 垂直 QRである
今度は
この ③④式を
足すと
07
なるんですよ
08
今度は
たまに 出て来そうな 問題です
地球は 丸かった
地球を 球と考えて
A地点を 北緯0度 東経0度
B地点を 北緯45度 統計35度
としたとき
地球の中心を 0として
角AOBは 何度か
09
空間座標を
考えるでしょ
10
普段から
こういう 計算してないと
あれって思いませんか
11
だからね
コレ イメージわかるかな
12
だからね
Bの座標は こうなんですよ
13
これで
空間座標の なす角を
求めると
14
120度
15
問題
これは
ベクトルの 設定が
出来れば
半分できた
16
まず 基本的な ベクトルは
こんな感じで
AP と CQ を
こんな感じにできれば
17
2乗で 内積を
展開してくと
18
題意より
正四面体であるので
もうちょっと 簡単になる
19
こんな感じに
まとめて
20
整理して
21
これをさ
平方を 作ると
22
P,Qが それぞれ
中点の時
最初になる
23
問題
24
これはさ
中点の 連結定理で
計算したらば
PQは
25
SRは
26
ここで
平行四辺形
27
で
PSは
28
QRは
29
PQ と PSは
必ず 平行とは 限らない
であるから
平行四辺形
お疲れ様です。