2023年01月12日
22041 大人のさび落とし 空間座標とベクトル 最終ページ 空間図形(2)
大人のさび落とし
空間座標とベクトル
空間図形(2)
01
問題
こんな感じに
立方体から
中点を選んで
連結すると
正六角形になるんだって
証明して

02
であるから
座標を使ってじゃナイスカ
こんな感じで
2分の にするより
2倍しちゃえば
楽だから
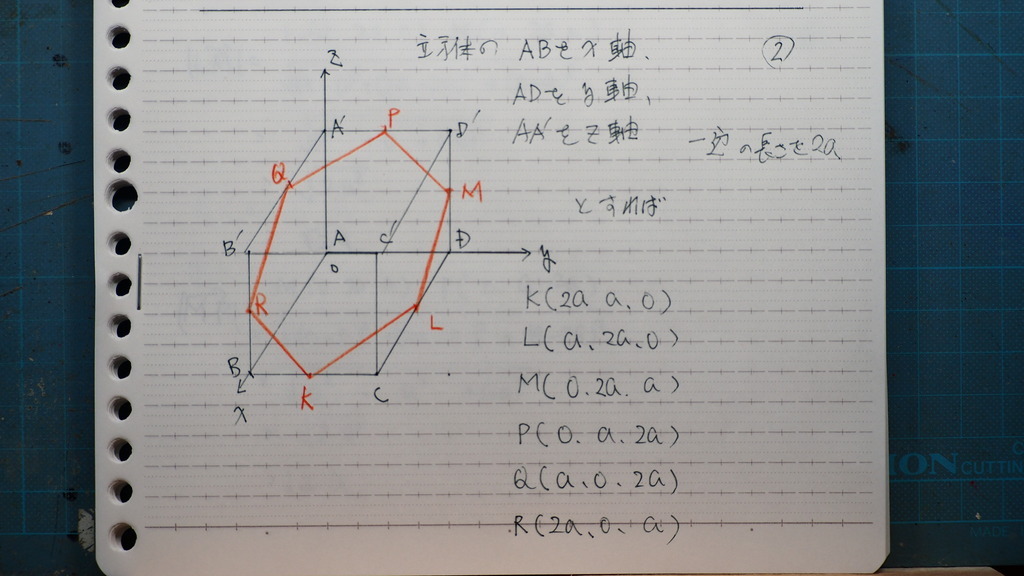
03
座標を
設定したところで
それぞれの
辺の長さが
等しいか
二点間の距離の計算が
6問

04
同だ
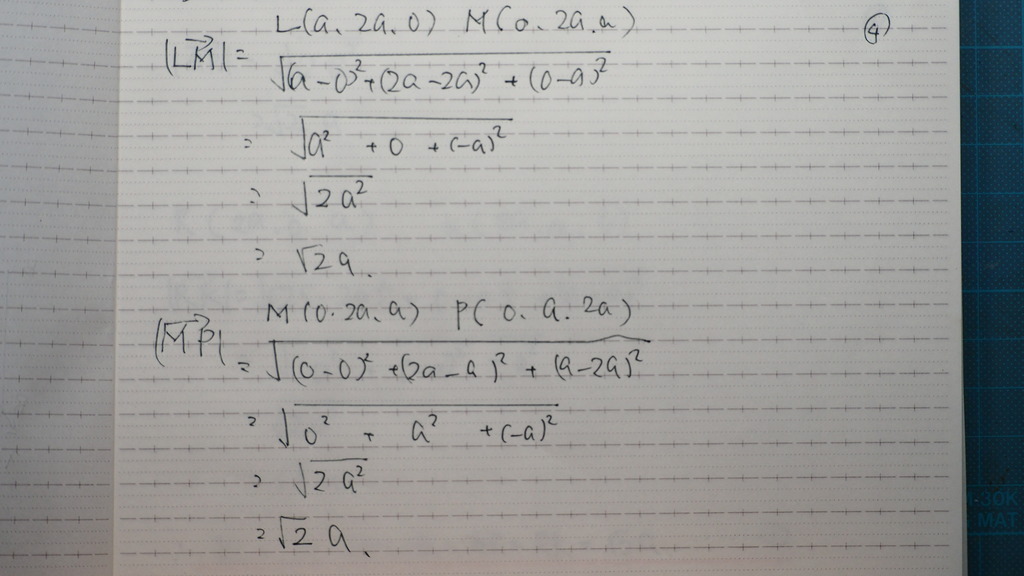
05
同だ
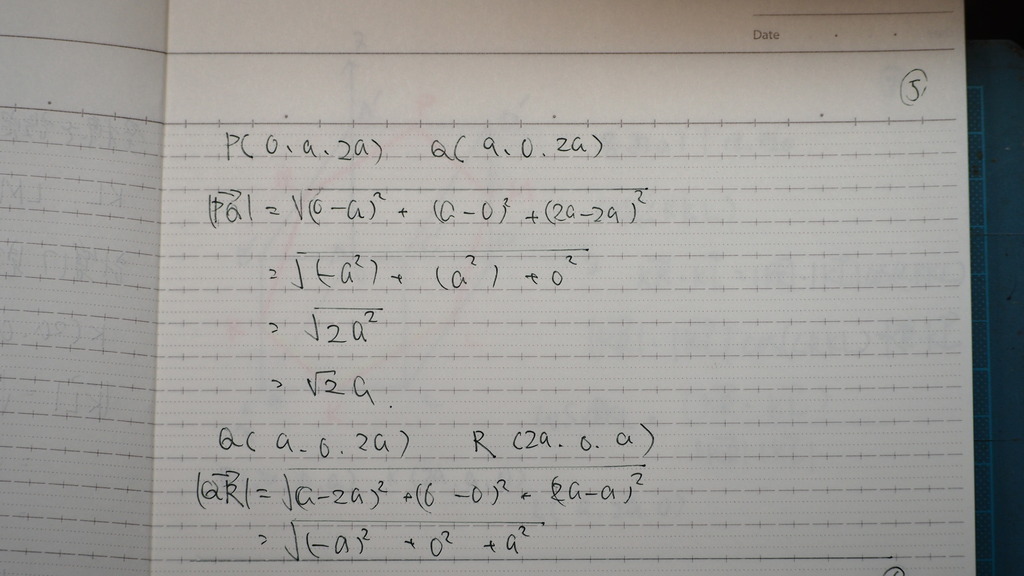
06
みんな 同じだった
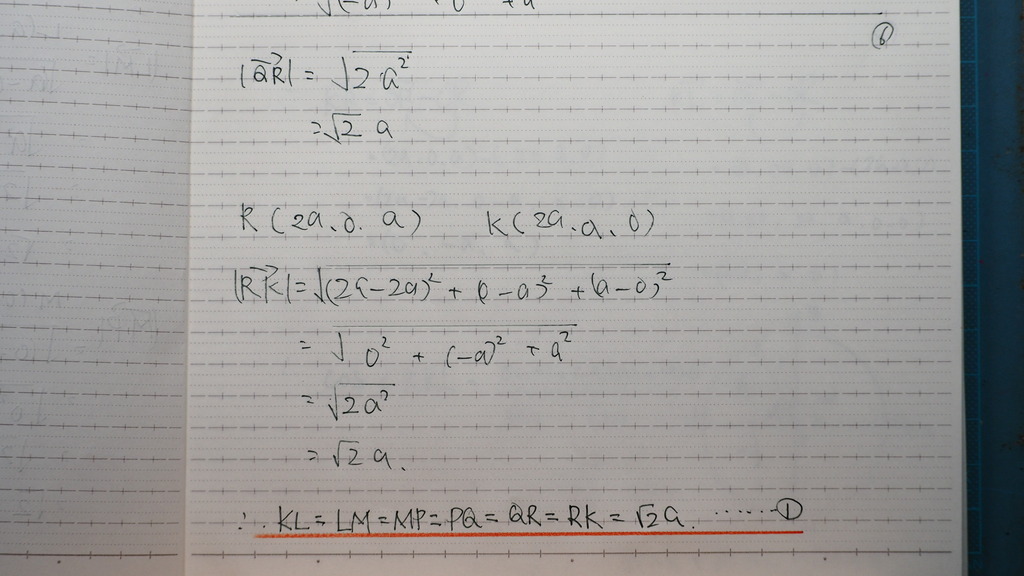
07
今度は
隣り合う辺の
なす角を
計算すると
計算問題 6問
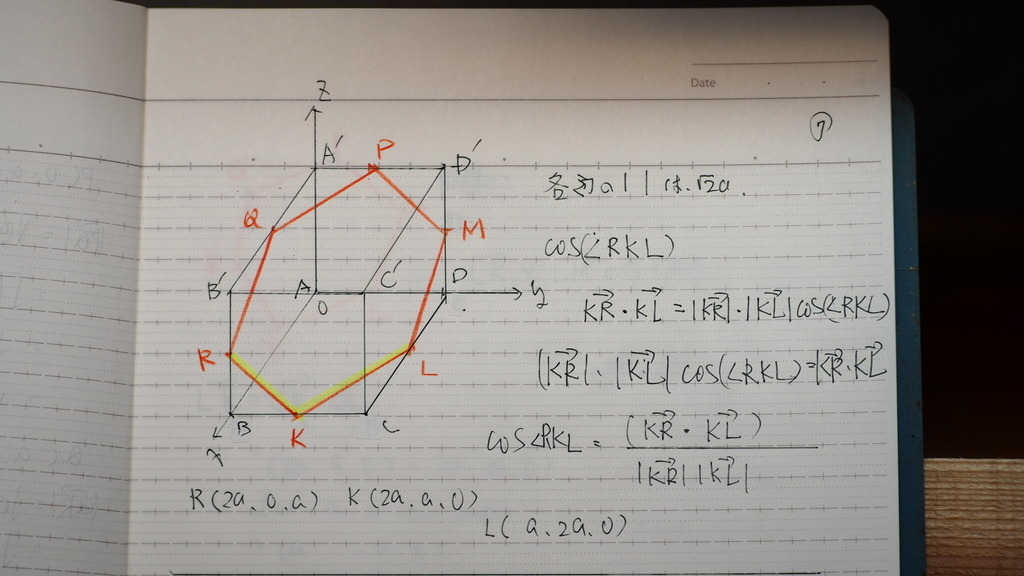
08
120ど

09
同様に
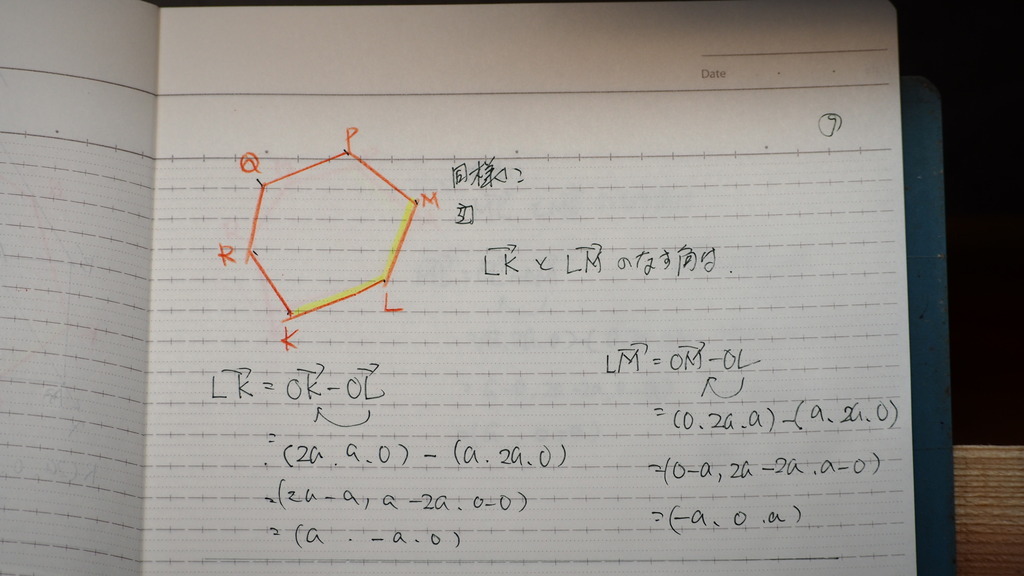
10
120度
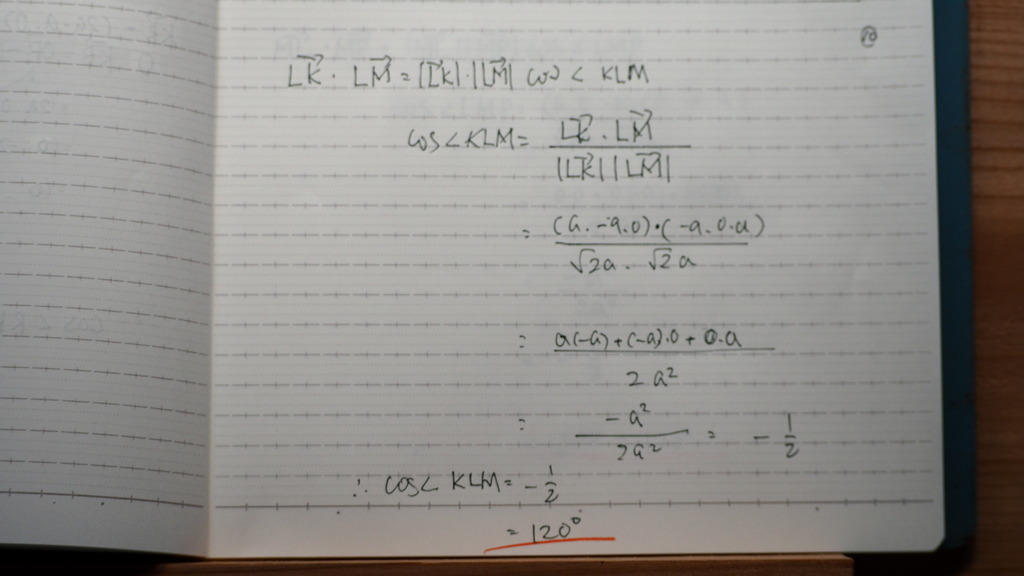
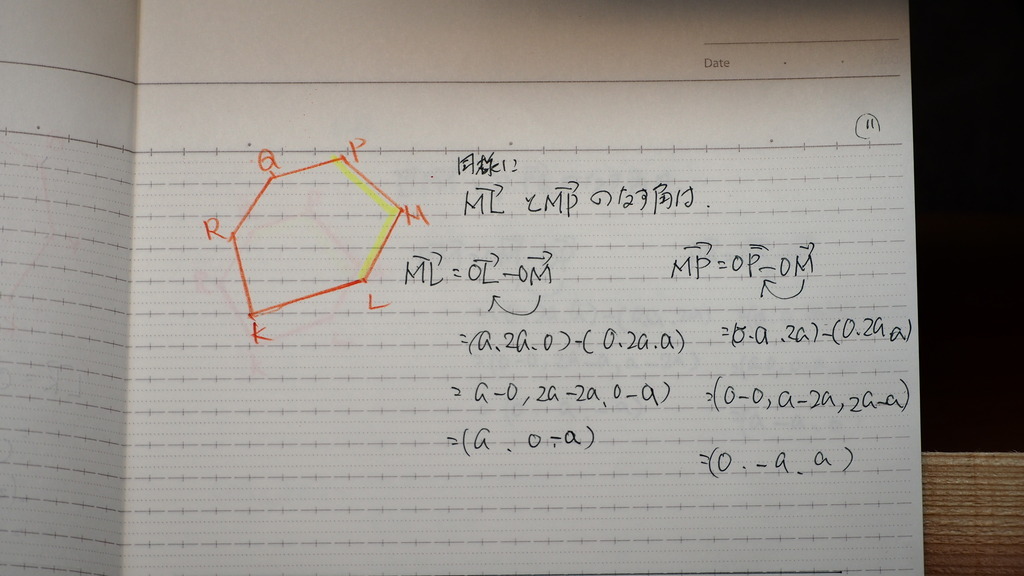
11
同様に
12
120ど
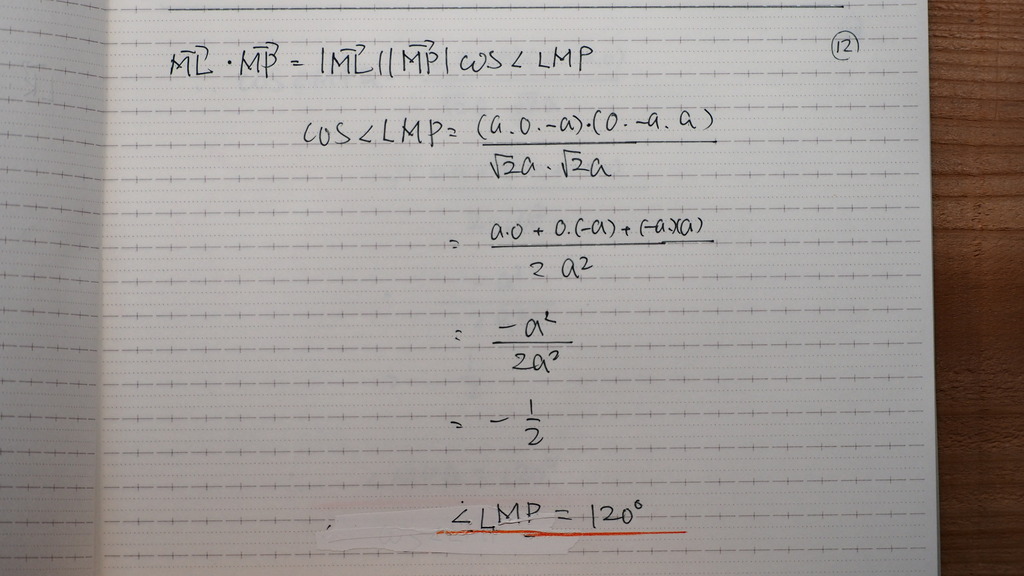
13
同様に
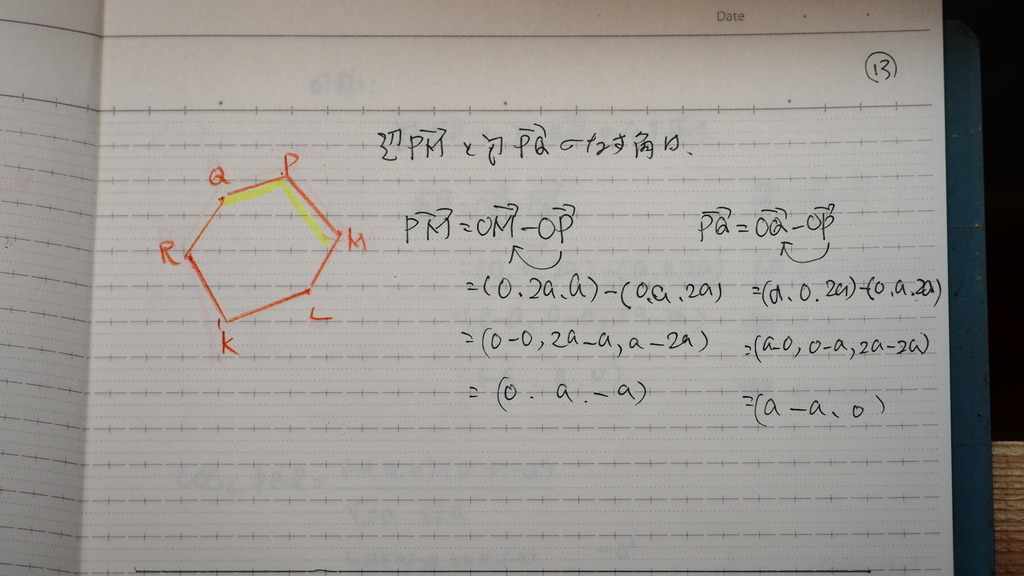
14
120度
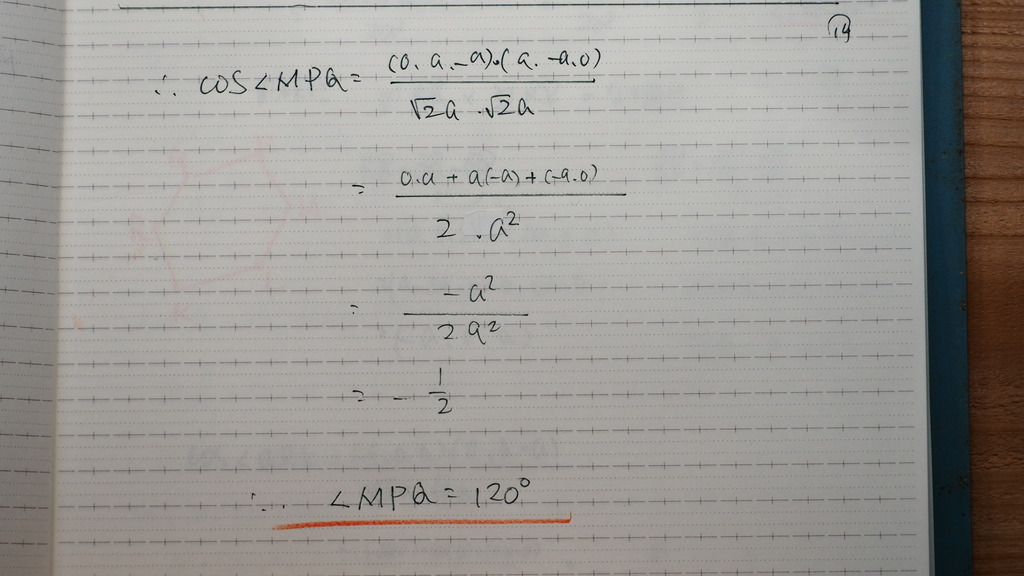
15
同様に
120度
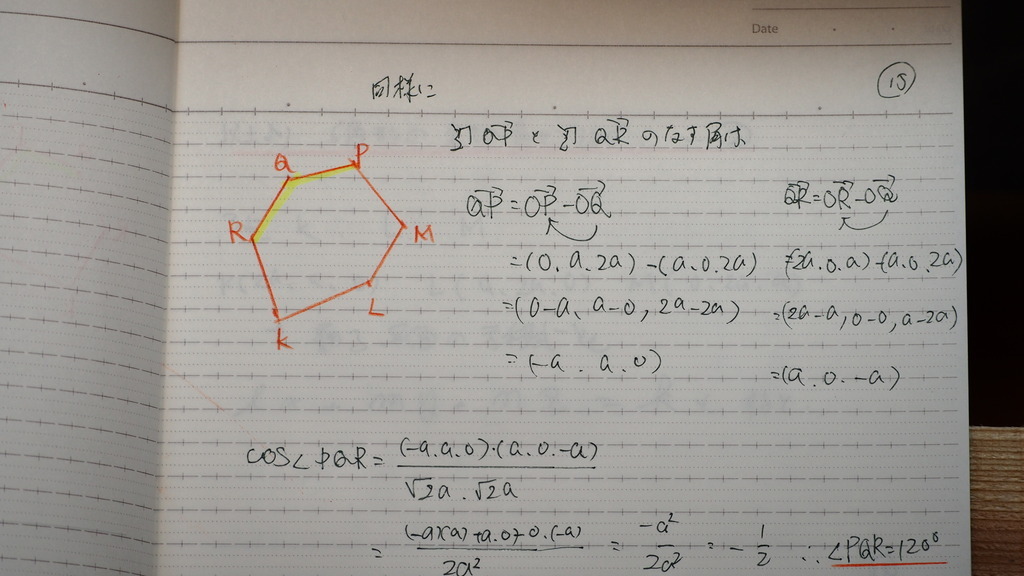
16
同様に
これはさ
実際に
過去に 某大学の入試に
出たんだそうだけど
やっぱり
全部 計算したのかな
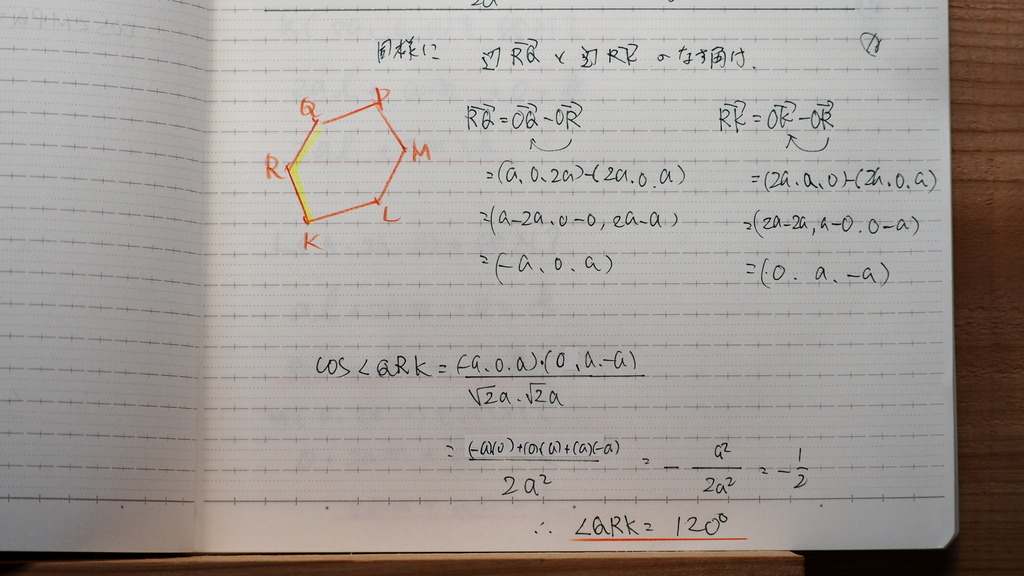
17
で さらに
3点を ひっぱり出してきて
平面の方程式を
求めると

18
媒介変数表示形から

19
3本式が出て来て

20
法線ベクトルが
みんな同じだから
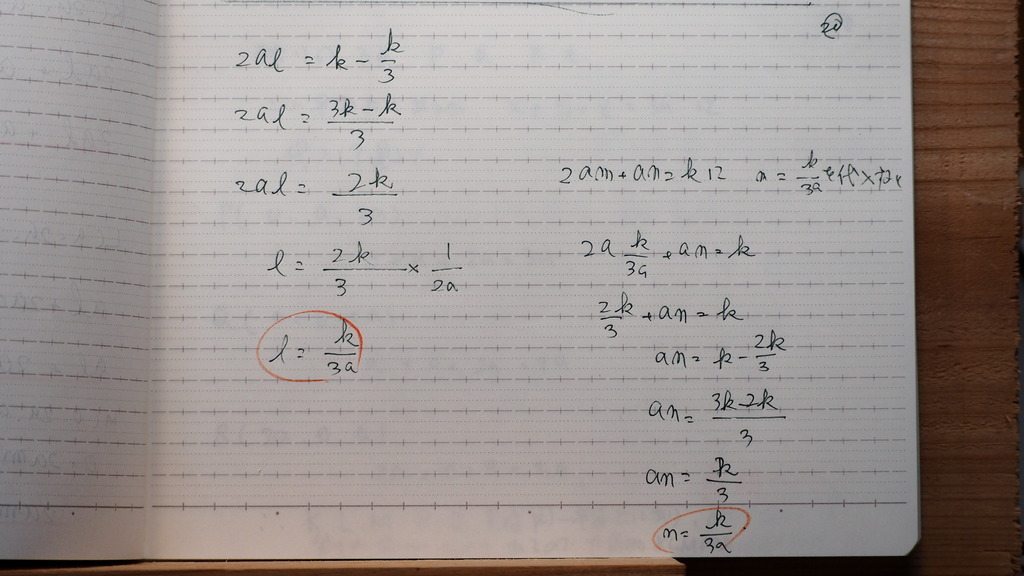
21
これが
平面の 方程式

22
残りの 3点を
ソレゾレ
代入したらば
全て
同一平面上にあるので
これはもう
正六角形だよ

23
問題

24
直線の 方程式は
こうだから

25
媒介変数表示形から
Z=0
を
代入して
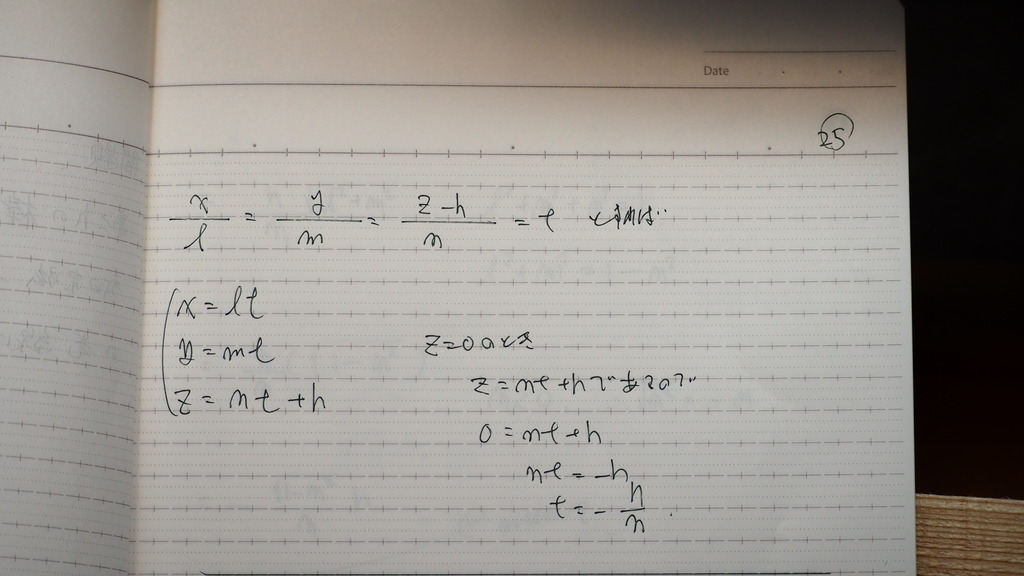
26
交点の 座標が出たので
影の 大きさは
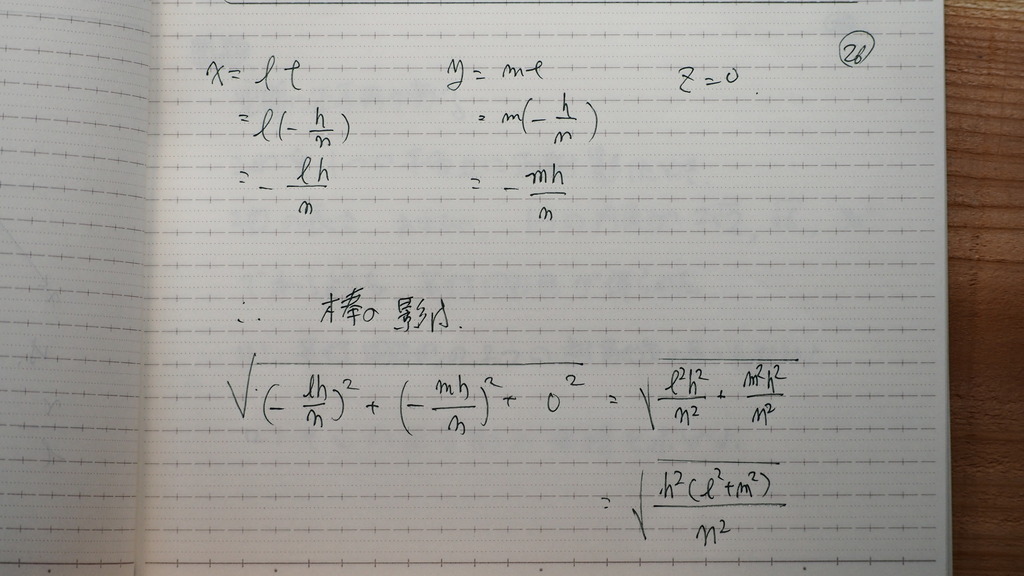
27
nは マイナスなんだね

28
問題
正方形を
平面に 正射影したんだって
そうしたら
影が
こんなで
平行四辺形になった
対角線のながさは
元の正方形の面積は

29
余弦定理を
使えば
早いよね
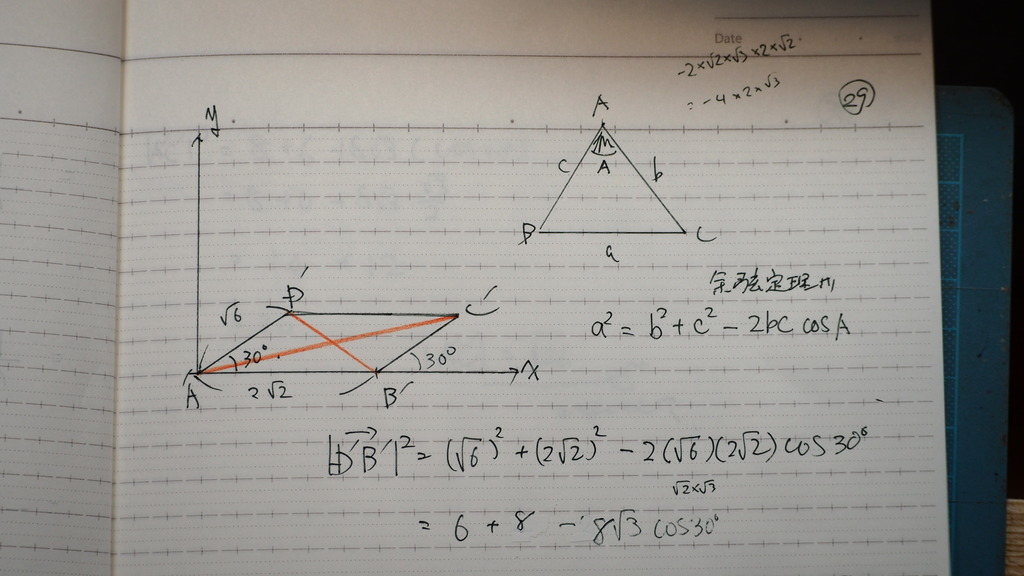
30
平行四辺形だからさ
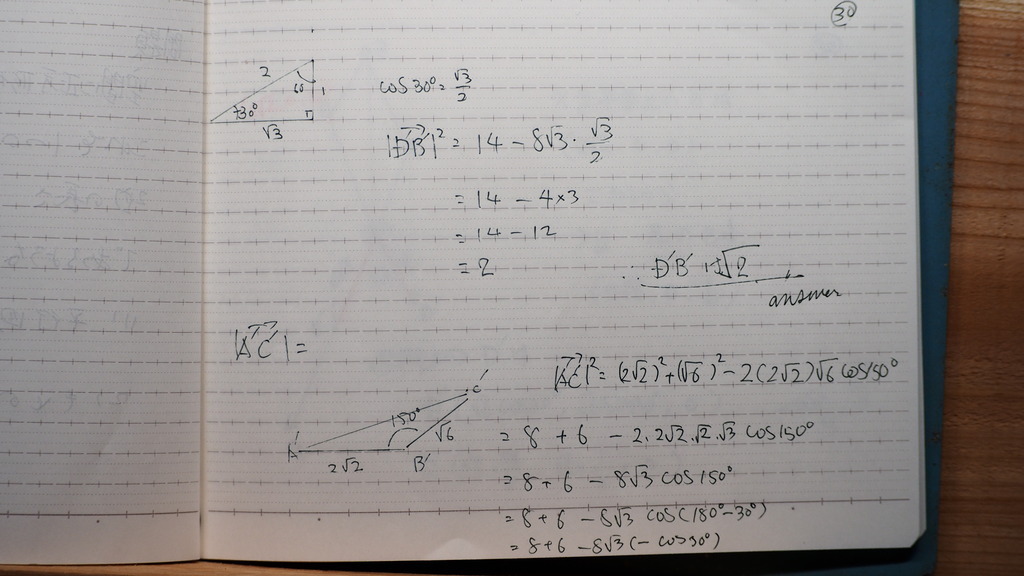
31
余弦定理は
2乗だからさ
ルートで
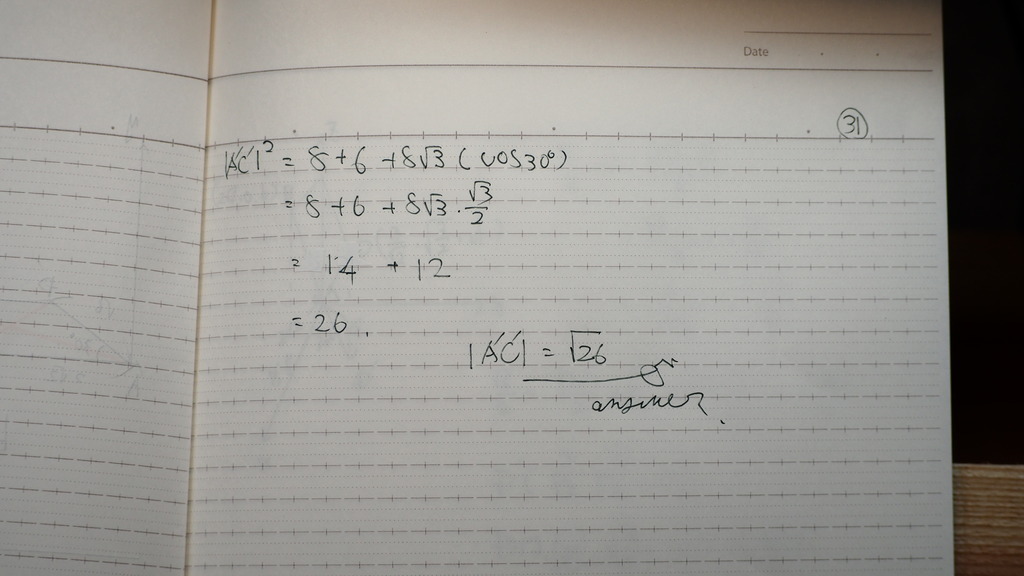
32
問題は
次なんだけどね
真上から
ななめに 成ってる
正方形を
投影してるでしょ
だから
座標は こんなんでさ
ただ
計算しやすいように
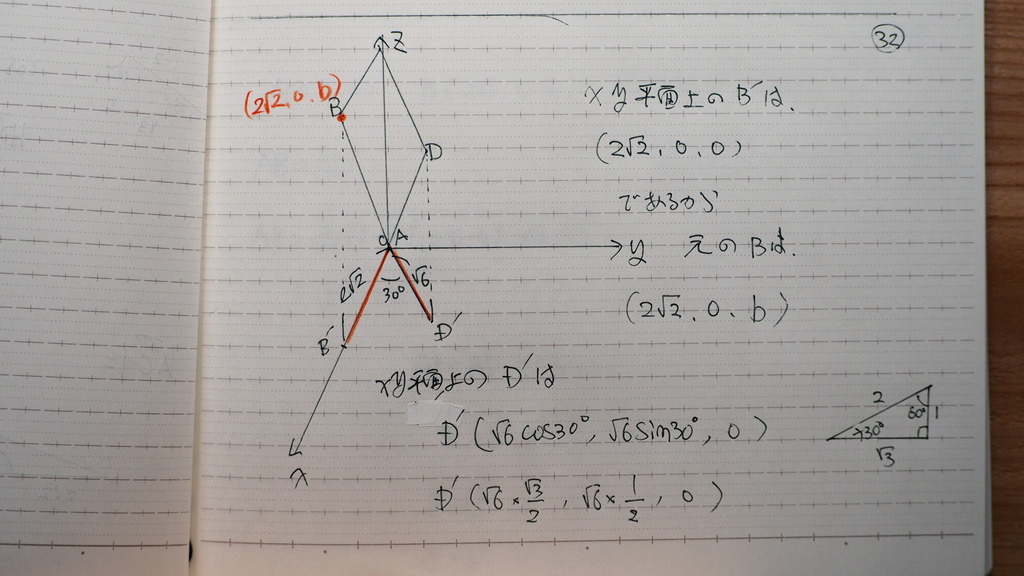
33
わざと
√2を 入れる形で
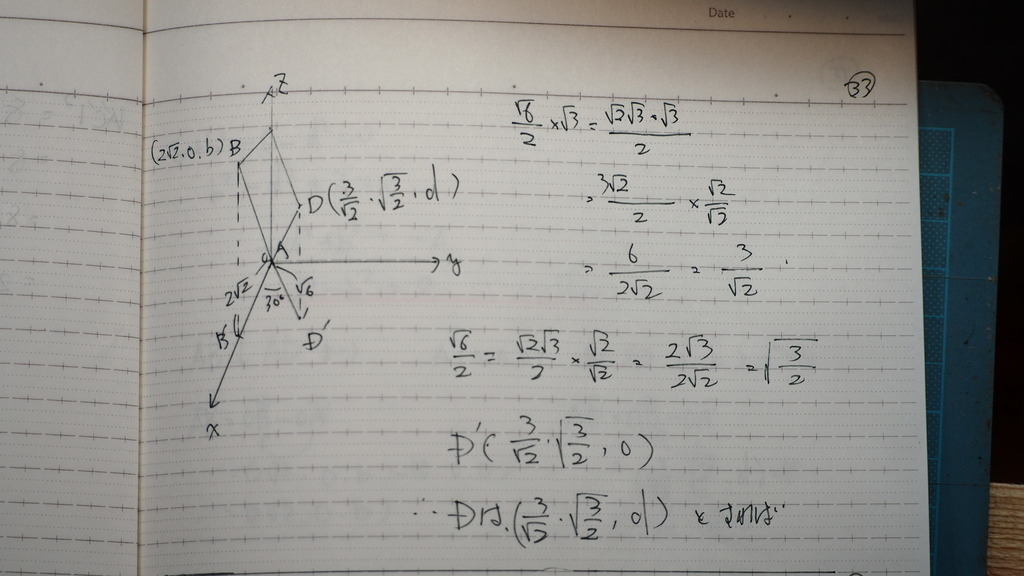
34
そうでもないか
で
なんか式が出て来て
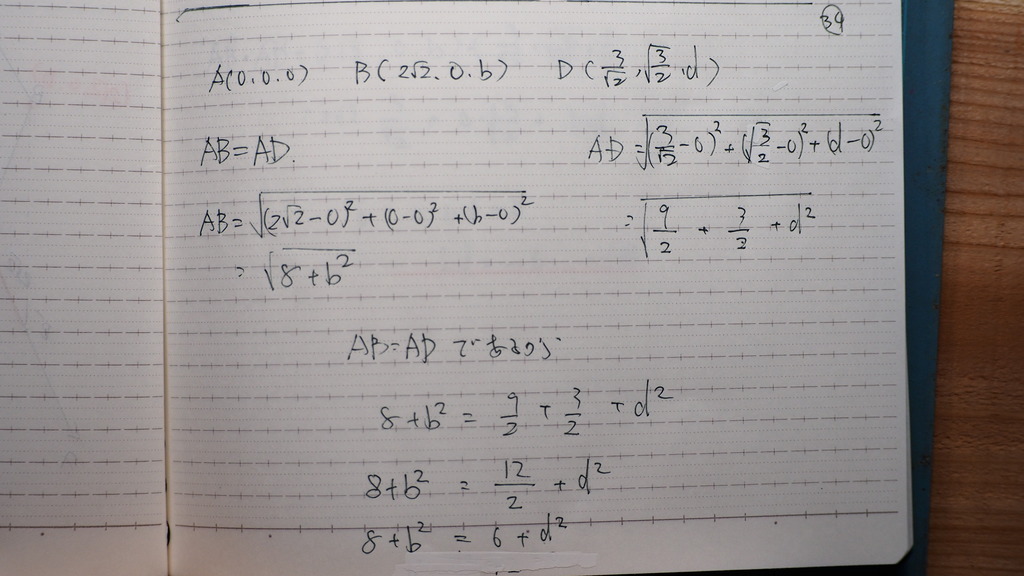
35
もう一本
内積の
成分の計算から
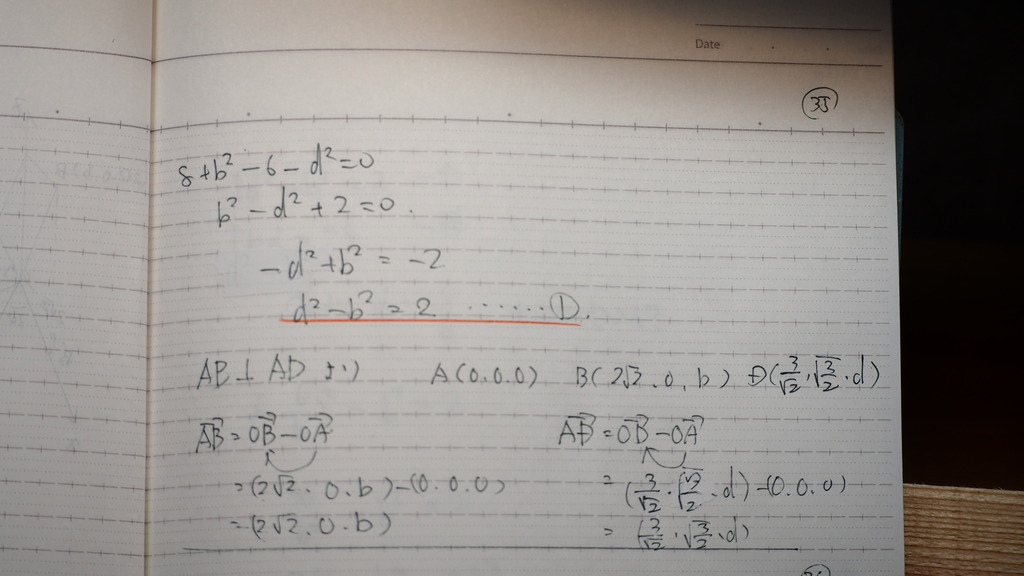
36
式が出て来て

37
これを
解くと
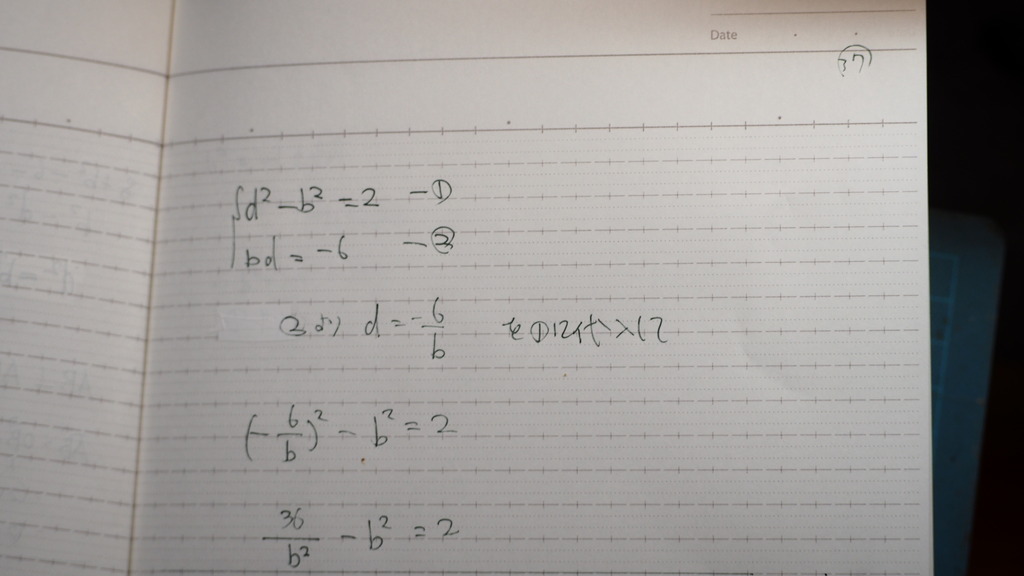
38
4乗だからさ
置き換えて
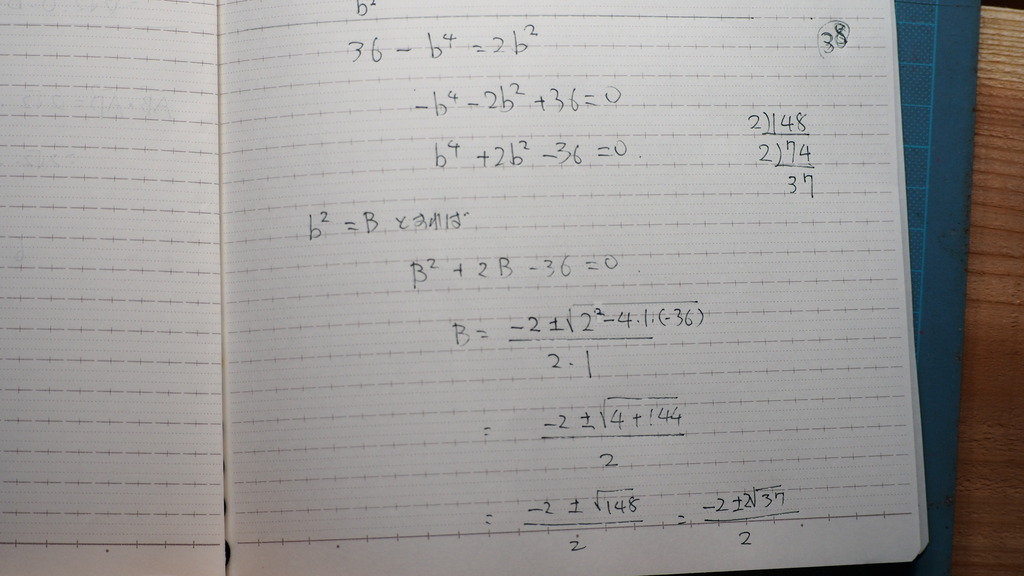
39
長さだから
マイナスは
まずいよな
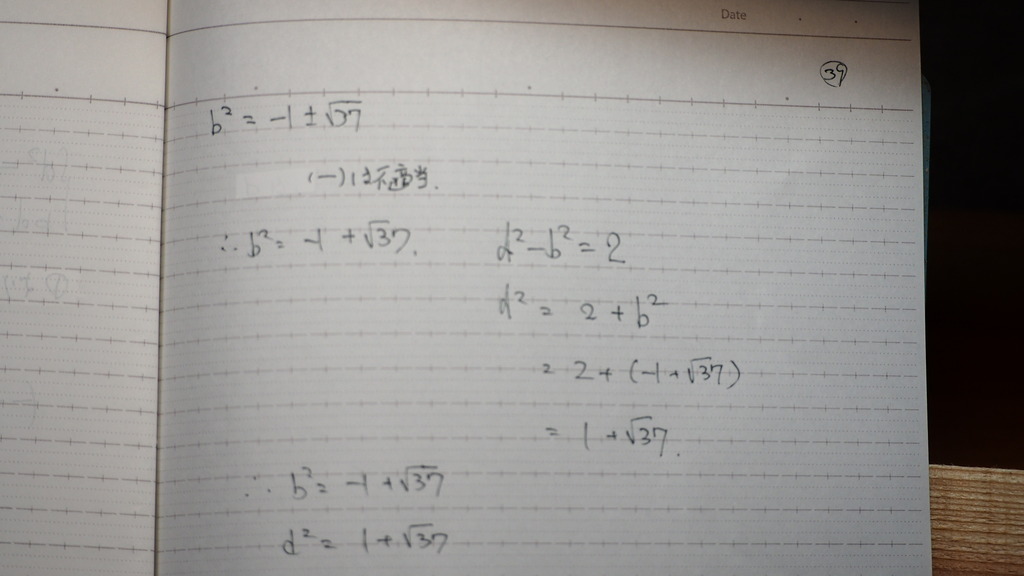
40
で
面積 ダメかな と思ったんだけど
正方形だから
ABの二乗で
行けるんだからさ
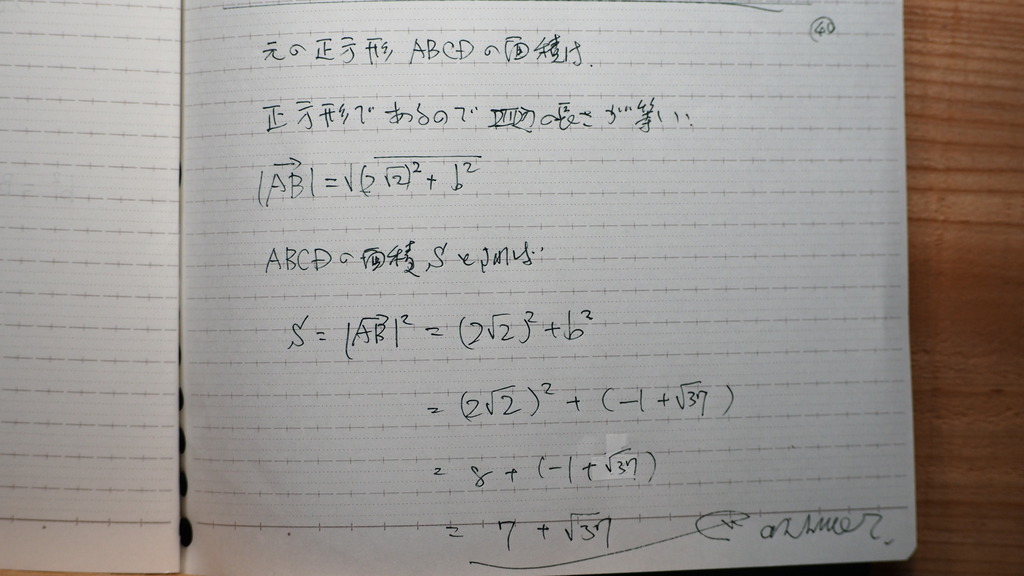
b2乗に -1+√37を 代入したら
7+√37
お疲れ様です。
空間座標とベクトル
空間図形(2)
01
問題
こんな感じに
立方体から
中点を選んで
連結すると
正六角形になるんだって
証明して
02
であるから
座標を使ってじゃナイスカ
こんな感じで
2分の にするより
2倍しちゃえば
楽だから
03
座標を
設定したところで
それぞれの
辺の長さが
等しいか
二点間の距離の計算が
6問
04
同だ
05
同だ
06
みんな 同じだった
07
今度は
隣り合う辺の
なす角を
計算すると
計算問題 6問
08
120ど
09
同様に
10
120度
11
同様に
12
120ど
13
同様に
14
120度
15
同様に
120度
16
同様に
これはさ
実際に
過去に 某大学の入試に
出たんだそうだけど
やっぱり
全部 計算したのかな
17
で さらに
3点を ひっぱり出してきて
平面の方程式を
求めると
18
媒介変数表示形から
19
3本式が出て来て
20
法線ベクトルが
みんな同じだから
21
これが
平面の 方程式
22
残りの 3点を
ソレゾレ
代入したらば
全て
同一平面上にあるので
これはもう
正六角形だよ
23
問題
24
直線の 方程式は
こうだから
25
媒介変数表示形から
Z=0
を
代入して
26
交点の 座標が出たので
影の 大きさは
27
nは マイナスなんだね
28
問題
正方形を
平面に 正射影したんだって
そうしたら
影が
こんなで
平行四辺形になった
対角線のながさは
元の正方形の面積は
29
余弦定理を
使えば
早いよね
30
平行四辺形だからさ
31
余弦定理は
2乗だからさ
ルートで
32
問題は
次なんだけどね
真上から
ななめに 成ってる
正方形を
投影してるでしょ
だから
座標は こんなんでさ
ただ
計算しやすいように
33
わざと
√2を 入れる形で
34
そうでもないか
で
なんか式が出て来て
35
もう一本
内積の
成分の計算から
36
式が出て来て
37
これを
解くと
38
4乗だからさ
置き換えて
39
長さだから
マイナスは
まずいよな
40
で
面積 ダメかな と思ったんだけど
正方形だから
ABの二乗で
行けるんだからさ
b2乗に -1+√37を 代入したら
7+√37
お疲れ様です。