2023年01月12日
22038 大人のさび落とし 平面図形(1)
大人のさび落とし
空間座標とベクトル
ベクトルの図形への応用
平面図形(1)
01
その前に
予備知識を
引算足し算
実数倍

02
同一 平面
垂直条件

03
分点 長さ なす角

04
三角形の面積
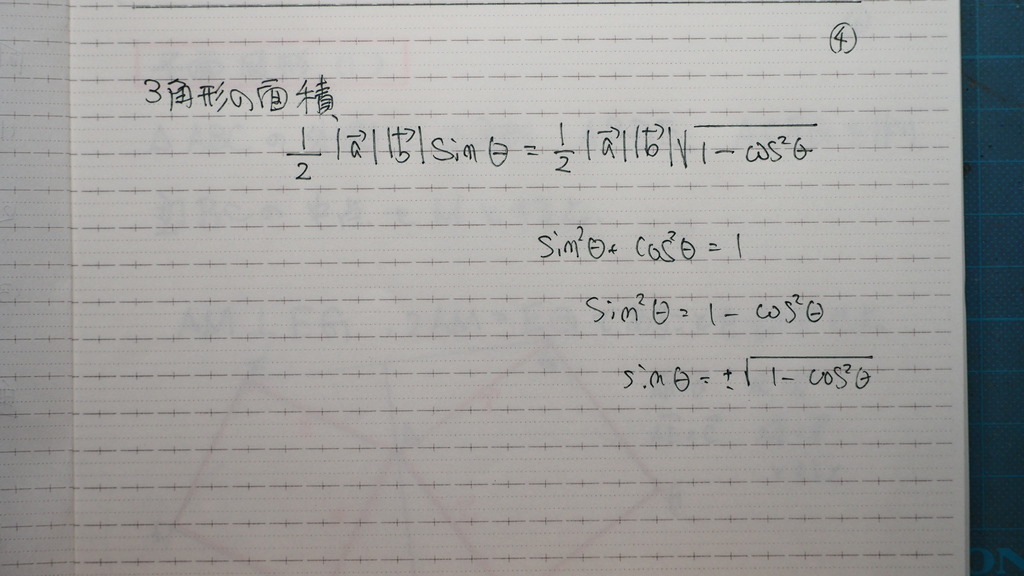
05
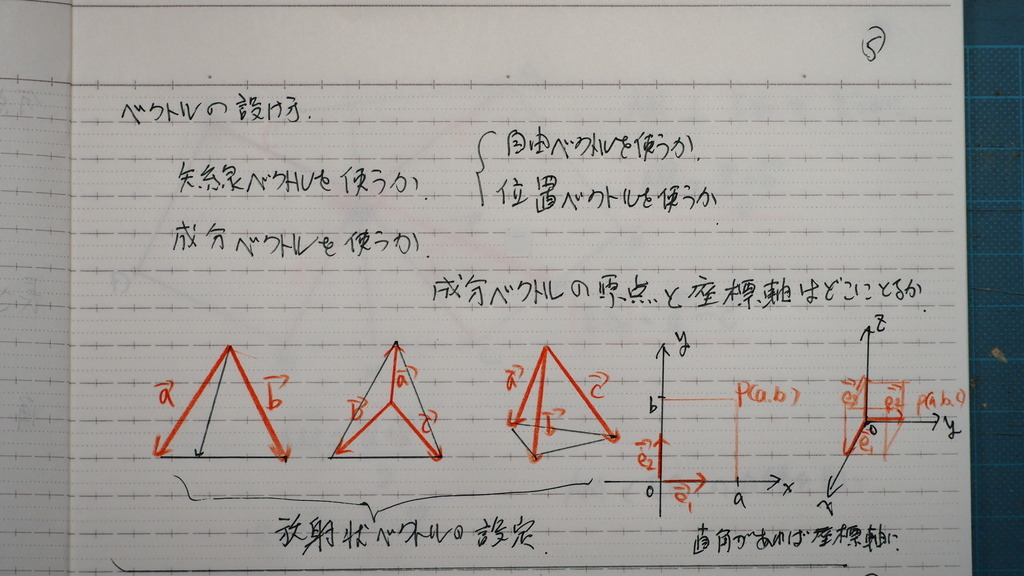
ベクトルの設け方た
これで
だいたい 決まってしまう
06
で
ここから 平面図形(1)
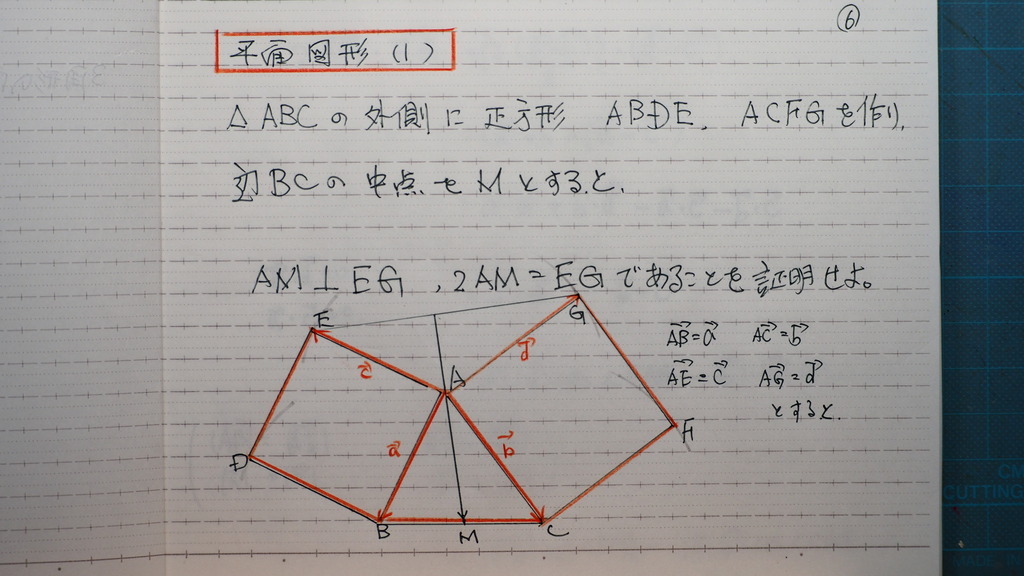
07
図のように
ベクトルを 設けて
AM と EG の 内積を
計算すればさ
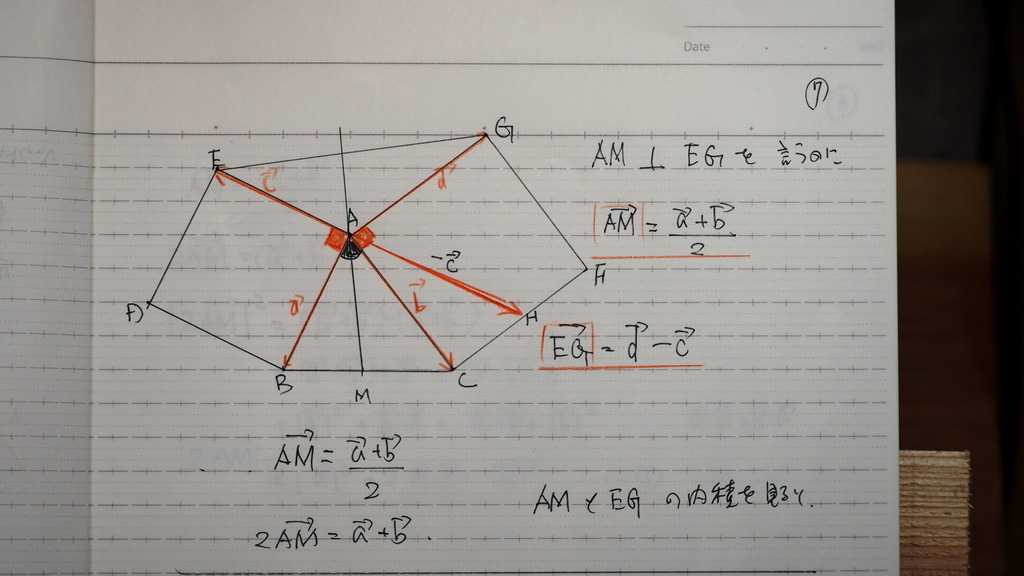
08
図形の 角度の問題で
=0になったので
AM 垂直 EG

09
(2)は 2AM = EGを
いうんですが
2乗して
内積で
展開してくと
➀

10
EGは ②

11
➀②は 絶対値2乗のとこは
等しいと
ドット のところ
内積のとこは
絶対値の
等しいとこを置き換えて
ーc・dは
180-EAG
この ∠GAHとすれば
⑦ページの 図を
良く見ていただくと
等しいのが 見えてくる

12
これはですよ
ベクトルの 設定で
決まってしまいます
これができれが
もう オッケイ
あとは
内積の計算をすれば
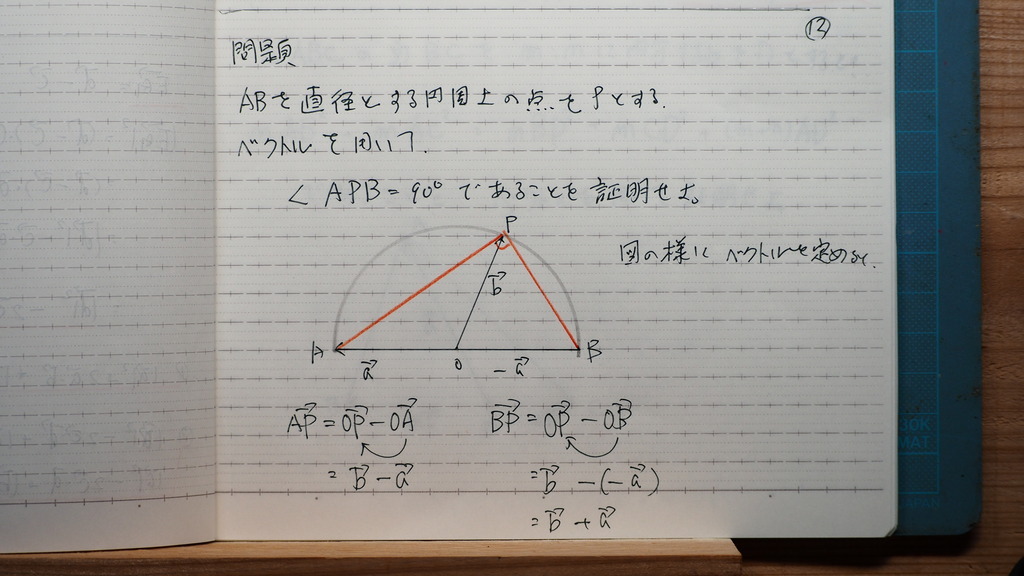
13
円周上なので
実は
a ベクトルも bベクトルも
半径で
長さが等しいので
=0
すなわち 垂直
∠APB=90度
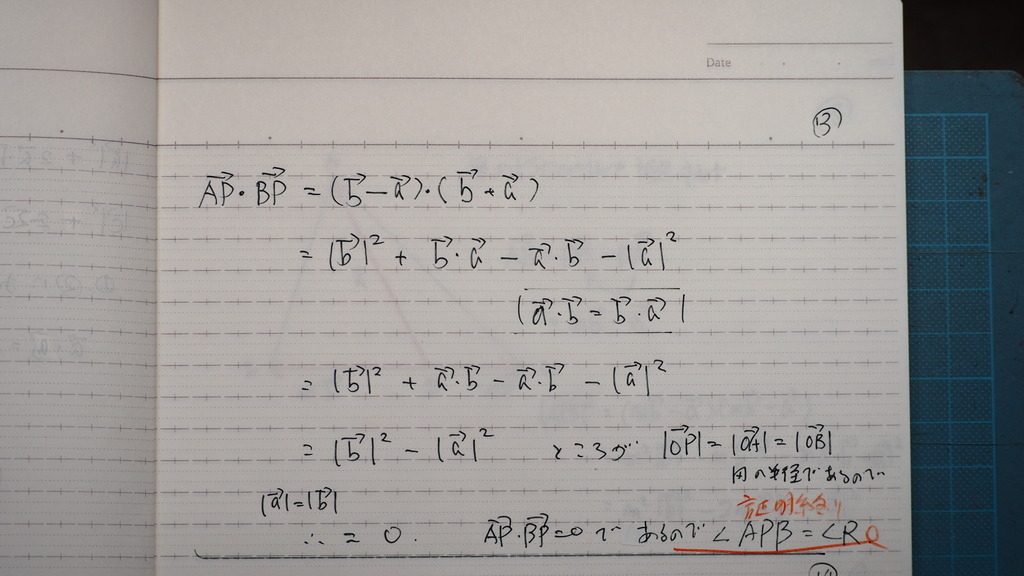
14
問題

15
図にように
ベクトルを
設定できさえすれば
もう
半分できた
あとは 計算あるのみ

16
計算は 自分の文字が
わかるように じゃナイスカ
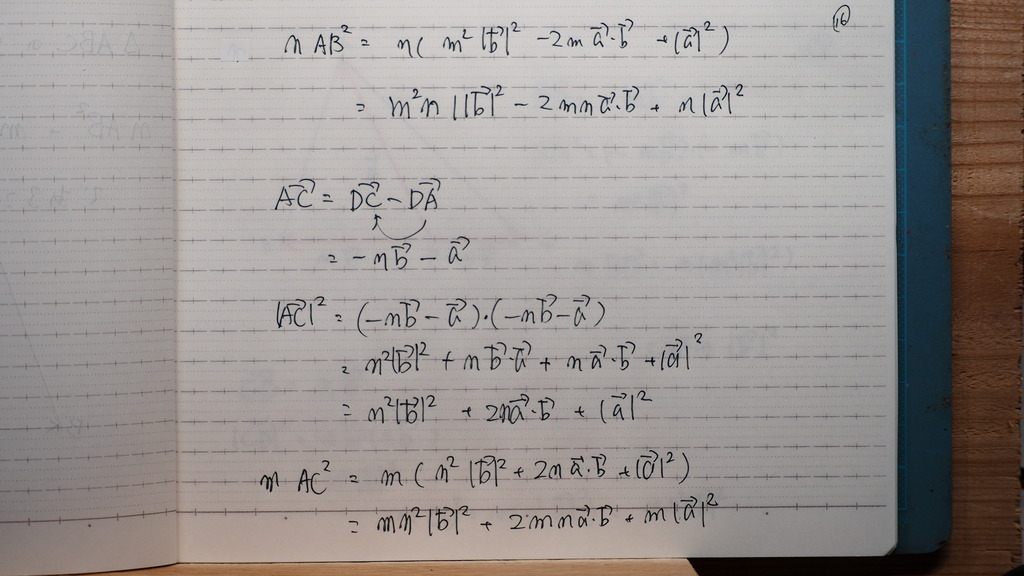
17
今日は 大丈夫だな
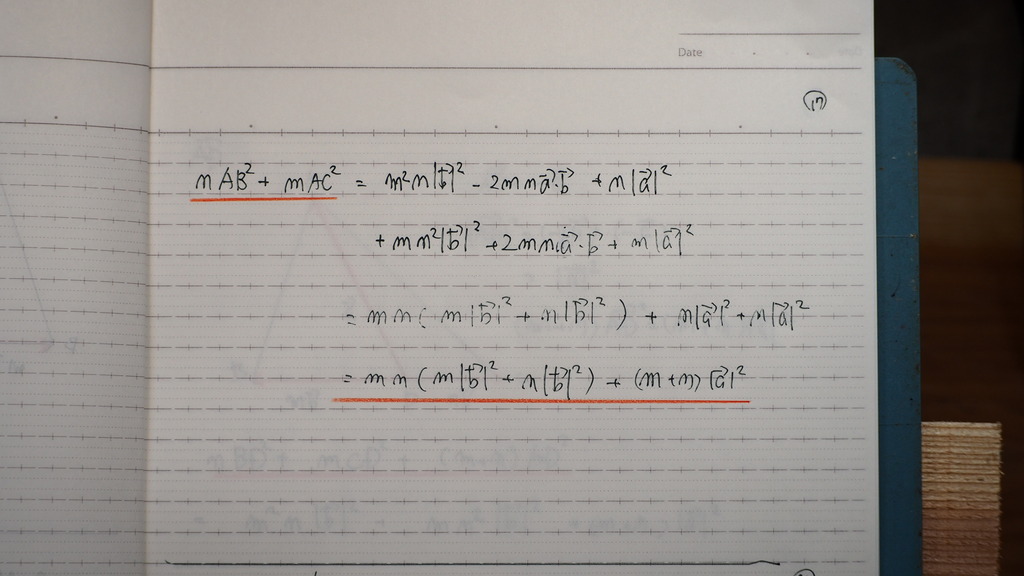
18
どこやってるか わかるかな
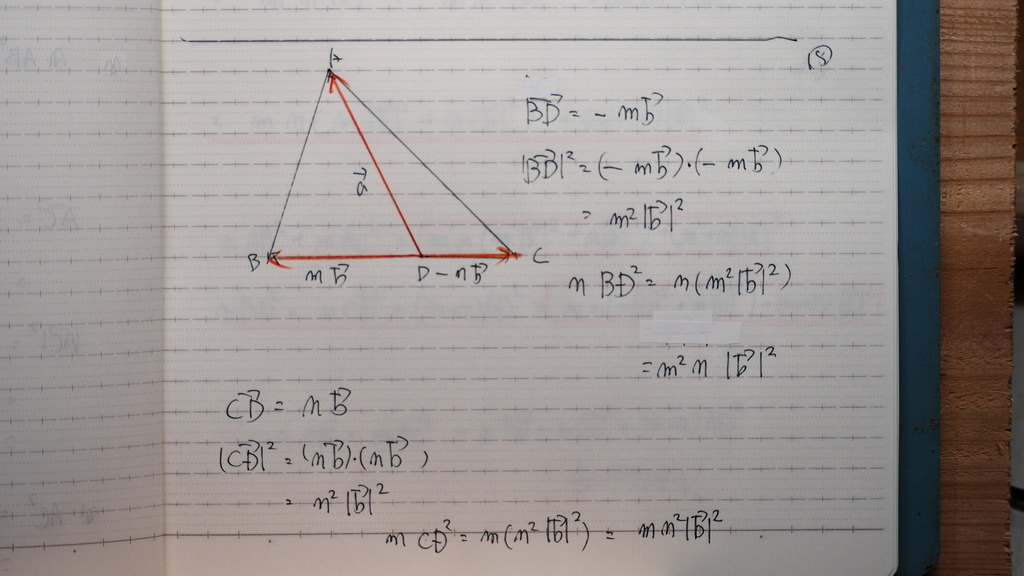
19
ソレゾレ
部品の 値を
計算してるんですが

20
で 全部 部品を 合計すると
左辺
右辺
おなじだったから
成り立つ

21
問題

22
図にすると
こんな感じで
ベクトルの設定を
こんな感じにしますと
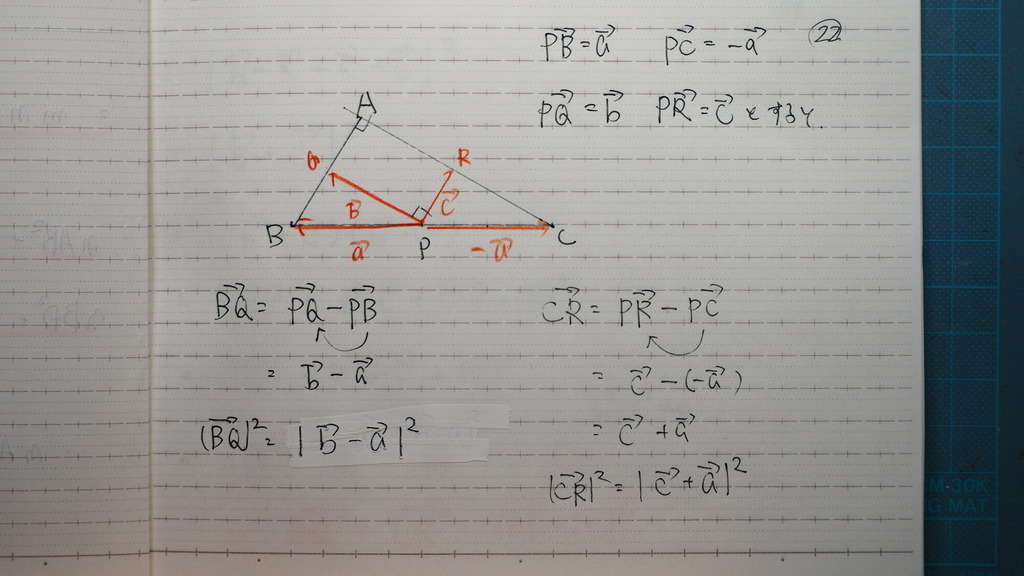
23
因数分解
みたいに 成ってるんですが
分かりますか
真ん中の項は =0

24
さらに 展開して
計算すると
こうでしょ
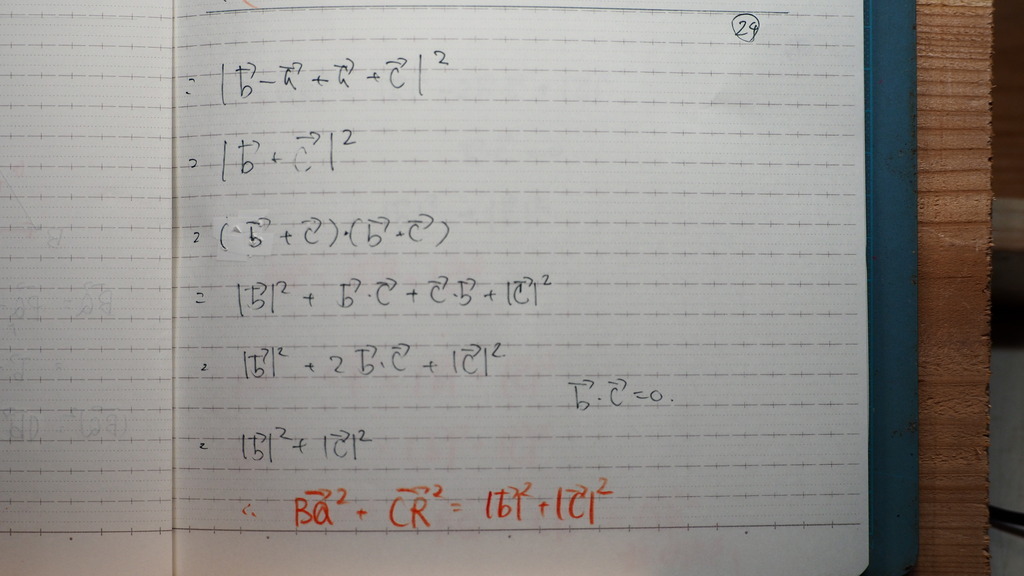
25
右辺は

26
で
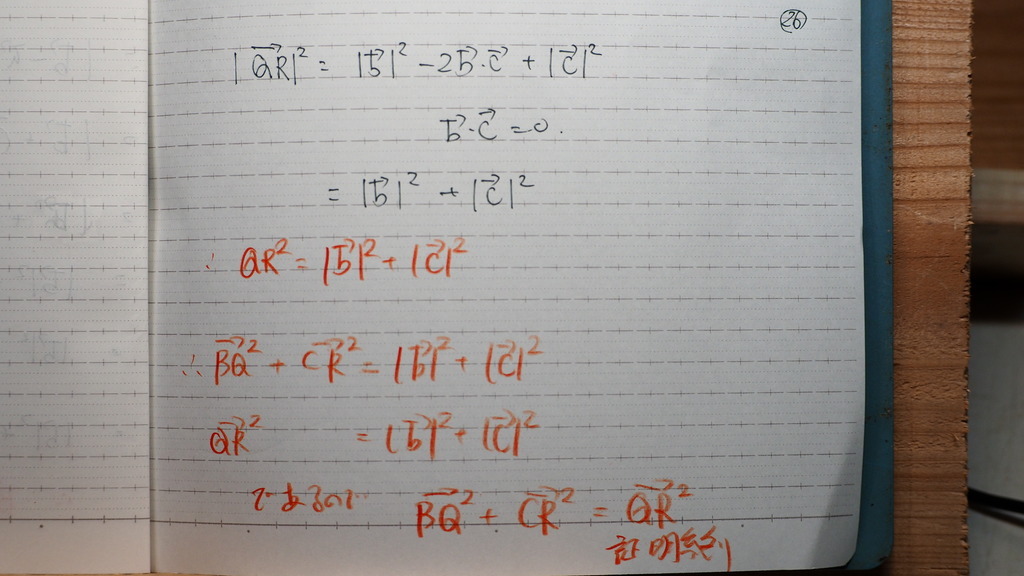
なったじゃナイスカ
お疲れ様です。
空間座標とベクトル
ベクトルの図形への応用
平面図形(1)
01
その前に
予備知識を
引算足し算
実数倍
02
同一 平面
垂直条件
03
分点 長さ なす角
04
三角形の面積
05
ベクトルの設け方た
これで
だいたい 決まってしまう
06
で
ここから 平面図形(1)
07
図のように
ベクトルを 設けて
AM と EG の 内積を
計算すればさ
08
図形の 角度の問題で
=0になったので
AM 垂直 EG
09
(2)は 2AM = EGを
いうんですが
2乗して
内積で
展開してくと
➀
10
EGは ②
11
➀②は 絶対値2乗のとこは
等しいと
ドット のところ
内積のとこは
絶対値の
等しいとこを置き換えて
ーc・dは
180-EAG
この ∠GAHとすれば
⑦ページの 図を
良く見ていただくと
等しいのが 見えてくる
12
これはですよ
ベクトルの 設定で
決まってしまいます
これができれが
もう オッケイ
あとは
内積の計算をすれば
13
円周上なので
実は
a ベクトルも bベクトルも
半径で
長さが等しいので
=0
すなわち 垂直
∠APB=90度
14
問題
15
図にように
ベクトルを
設定できさえすれば
もう
半分できた
あとは 計算あるのみ
16
計算は 自分の文字が
わかるように じゃナイスカ
17
今日は 大丈夫だな
18
どこやってるか わかるかな
19
ソレゾレ
部品の 値を
計算してるんですが
20
で 全部 部品を 合計すると
左辺
右辺
おなじだったから
成り立つ
21
問題
22
図にすると
こんな感じで
ベクトルの設定を
こんな感じにしますと
23
因数分解
みたいに 成ってるんですが
分かりますか
真ん中の項は =0
24
さらに 展開して
計算すると
こうでしょ
25
右辺は
26
で
なったじゃナイスカ
お疲れ様です。