2023年01月11日
22036 大人のさび落とし 空間座標とベクトル 回転体の方程式
空間座標と ベクトル
回転体の方程式
01
ななめの 空間直線を
z軸周りに
回転させてみたら
クビレ が できたよ
ッテいう
うれしい話ですが
この
方程式は
どんなモンジャラほいと

02
z軸周りに
回転させるので
断面は
xy平面に
原点中心の
半径が いくつかの円になる
しかしながら
zが したから 上に
上がっていくと
その断面の 半径が
k の関数で 変化していく
そこで
関数から
k を
消去して
z のかかわりを
出してくるんですが
やってみましょう
先ず 直線の
方程式を
求めてですよ

03
=k と置いて
媒介変数形表示

04
であるから
直線上の
任意の場所は
kを使って
こんな感じになるでしょ

05
Z軸上に
垂線を おろしてくると
半径
QPは
kの2次関数

06
Z=k の 交わり
は 円で
半径は kの関数

07
上から見たら
原点中心に
xy平面の 円
半径は
kの関数
Z=k を 代入して
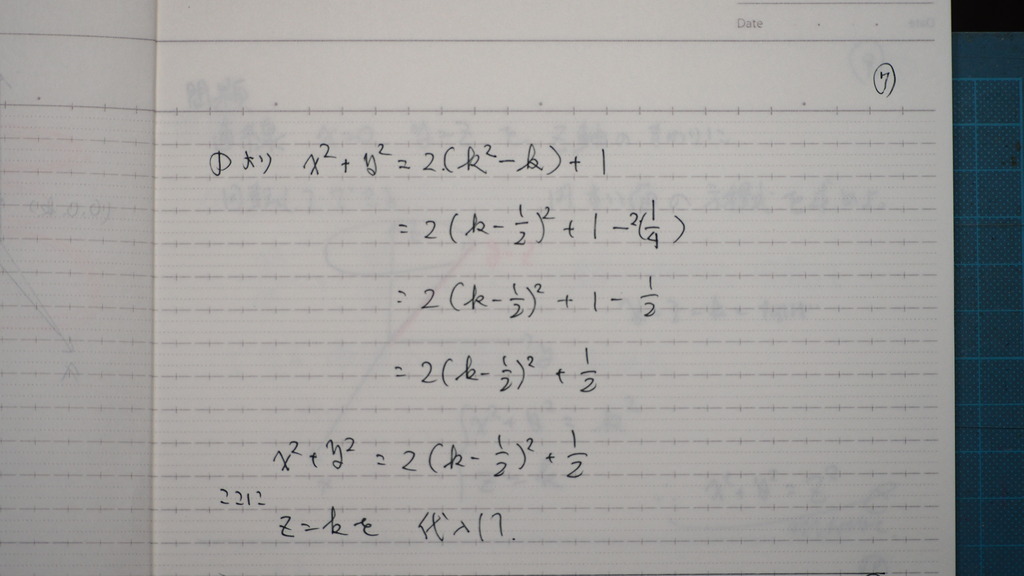
08
これが
今回の クビレ方程式
積分で
体積を だせば
こんな感じですが

09
問題
今度は
円すいの方程式
こんなんでいいカナ
簡単すぎる?

10
納得がいかない
じゃー
これは
難しいでしょ
説明が
しずらいですが
これです

11
今度はさ
いきなり
深いよ
今度は
xy 平面上の
楕円を
xじくまわりに
回すと
できる曲面の方程式は

12
楕円は
この 右辺が =1が
標準形で
a が b より大きいときは
aが 長軸の半径
bが 短軸の半径
b と aが
反対の時は
その逆
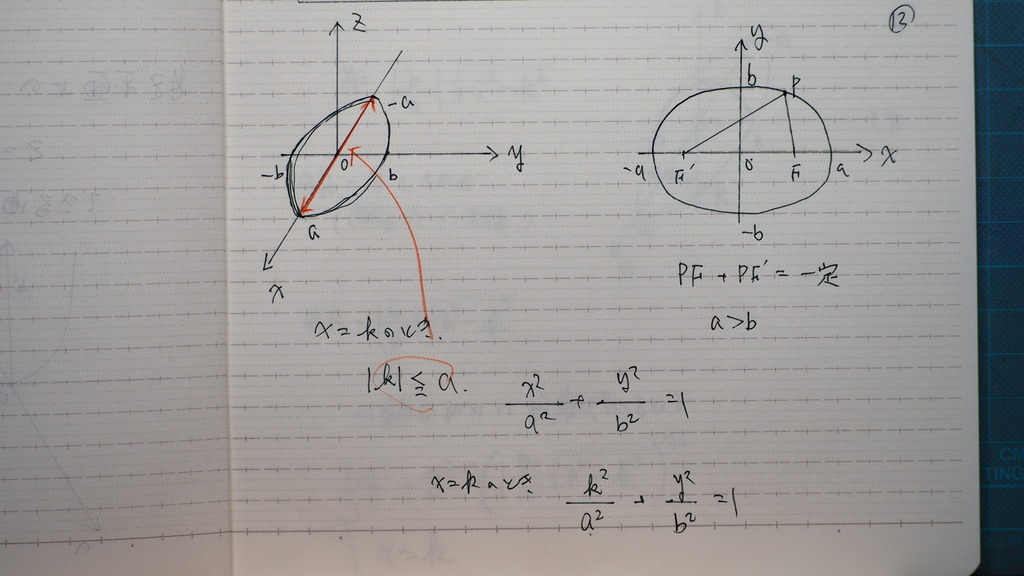
13
y=の式にするでしょ

14
図の QR が =y とすれば
断面の半径
x軸周りに
回転するので
xが 動くと
半径が 変わる
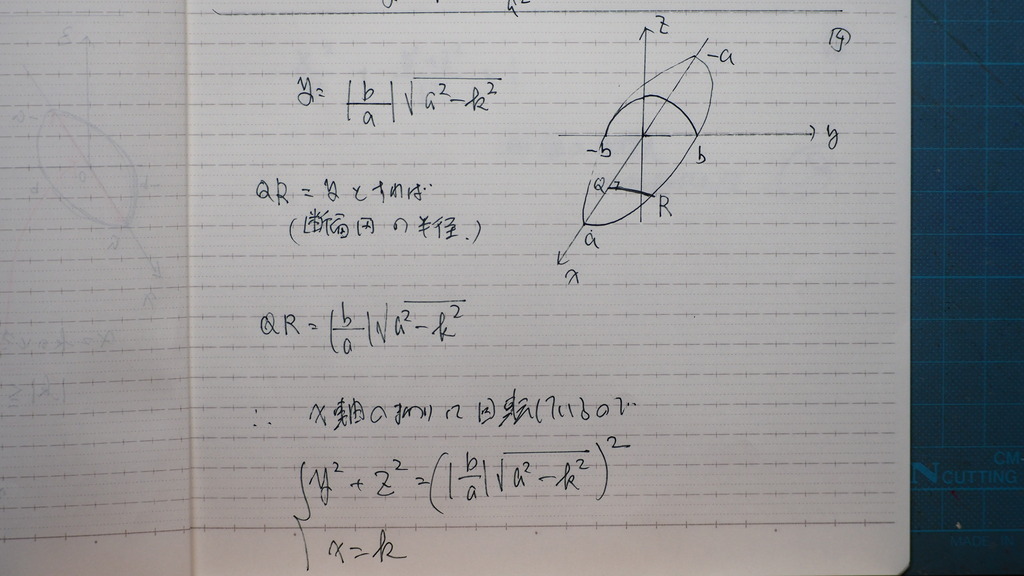
15
こんな感じになって

16
これが 曲面の方程式
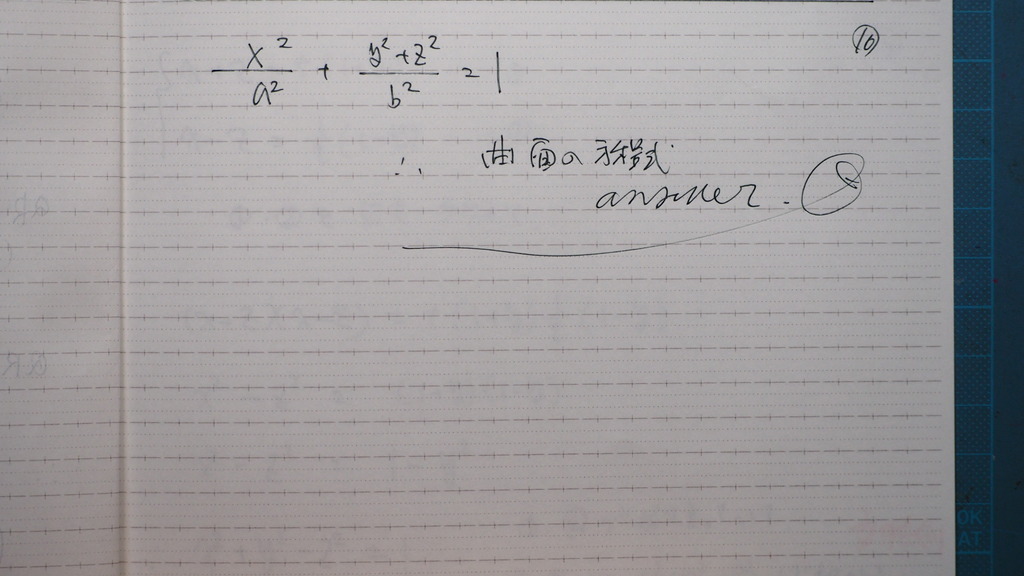
17
どうすりゃいいんだ

18
二つの 直線の
方程式を
掛け合わせるでしょ
そうしたら
題意の
曲面の方程式になったデショ
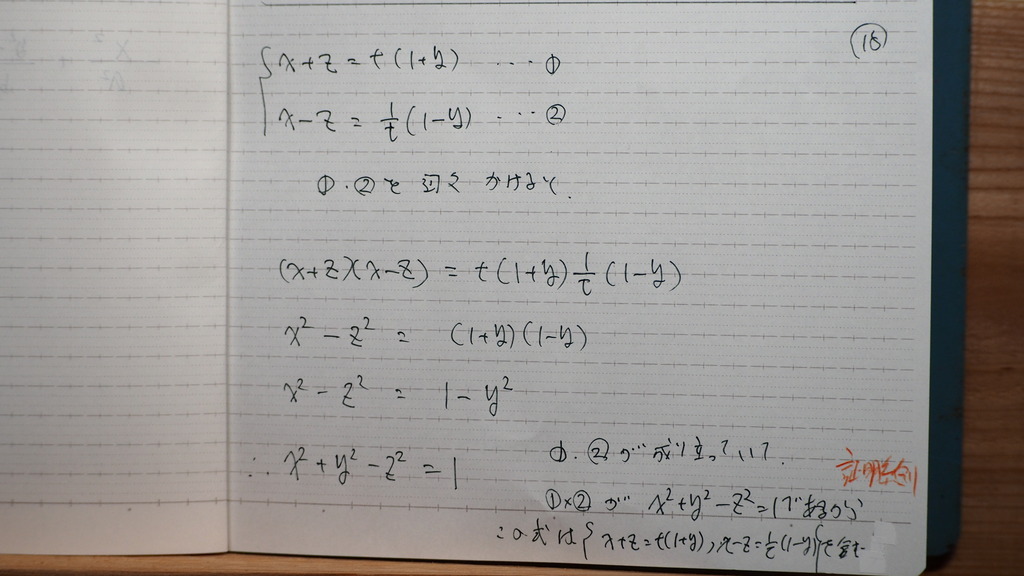
つまり
➀②が相方成り立っていて
掛け合わせたものが
曲面の式なので
曲面は 2直線を 含んでいる
お疲れ様です
回転体の方程式
01
ななめの 空間直線を
z軸周りに
回転させてみたら
クビレ が できたよ
ッテいう
うれしい話ですが
この
方程式は
どんなモンジャラほいと
02
z軸周りに
回転させるので
断面は
xy平面に
原点中心の
半径が いくつかの円になる
しかしながら
zが したから 上に
上がっていくと
その断面の 半径が
k の関数で 変化していく
そこで
関数から
k を
消去して
z のかかわりを
出してくるんですが
やってみましょう
先ず 直線の
方程式を
求めてですよ
03
=k と置いて
媒介変数形表示
04
であるから
直線上の
任意の場所は
kを使って
こんな感じになるでしょ
05
Z軸上に
垂線を おろしてくると
半径
QPは
kの2次関数
06
Z=k の 交わり
は 円で
半径は kの関数
07
上から見たら
原点中心に
xy平面の 円
半径は
kの関数
Z=k を 代入して
08
これが
今回の クビレ方程式
積分で
体積を だせば
こんな感じですが
09
問題
今度は
円すいの方程式
こんなんでいいカナ
簡単すぎる?
10
納得がいかない
じゃー
これは
難しいでしょ
説明が
しずらいですが
これです
11
今度はさ
いきなり
深いよ
今度は
xy 平面上の
楕円を
xじくまわりに
回すと
できる曲面の方程式は
12
楕円は
この 右辺が =1が
標準形で
a が b より大きいときは
aが 長軸の半径
bが 短軸の半径
b と aが
反対の時は
その逆
13
y=の式にするでしょ
14
図の QR が =y とすれば
断面の半径
x軸周りに
回転するので
xが 動くと
半径が 変わる
15
こんな感じになって
16
これが 曲面の方程式
17
どうすりゃいいんだ
18
二つの 直線の
方程式を
掛け合わせるでしょ
そうしたら
題意の
曲面の方程式になったデショ
つまり
➀②が相方成り立っていて
掛け合わせたものが
曲面の式なので
曲面は 2直線を 含んでいる
お疲れ様です