2023年01月09日
22035大人のさび落とし 空間座標とベクトル から 方べきの定理
大人のさび落とし
空間座標と ベクトル
方べきの定理
01
球に 点Aを通る 直線が
交わるとき
その 交点を P,Qとすれば
AP・AQは 常に 一定
であるということを
証明する問題

02
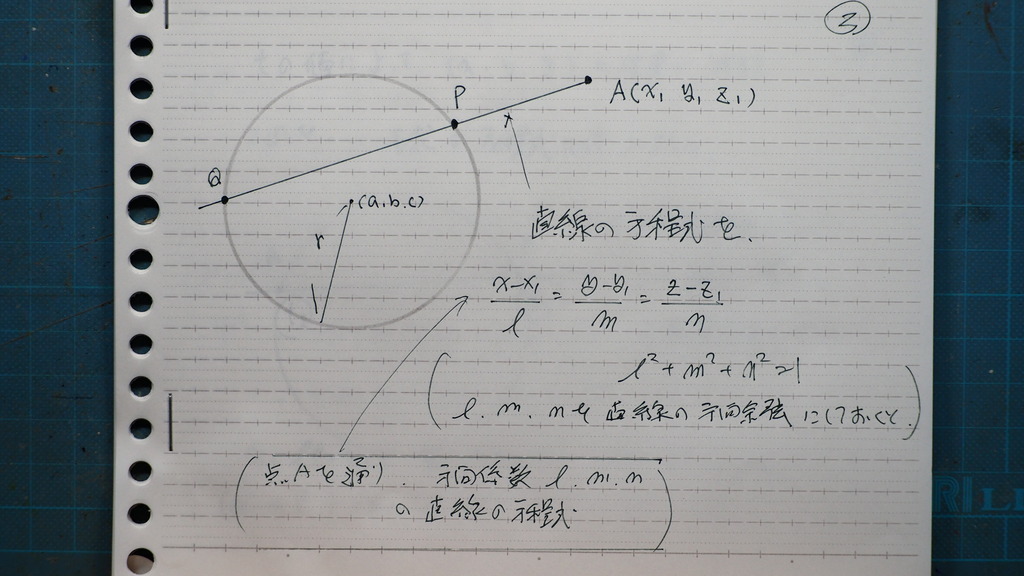
図に書くと こんなイメージで
直線の
方程式を
Aを 通る
方向係数
L,m,n の 直線
L,m,n は 方向余弦を 使うと
03
=t と置いて
直線の 媒介変数表示にして
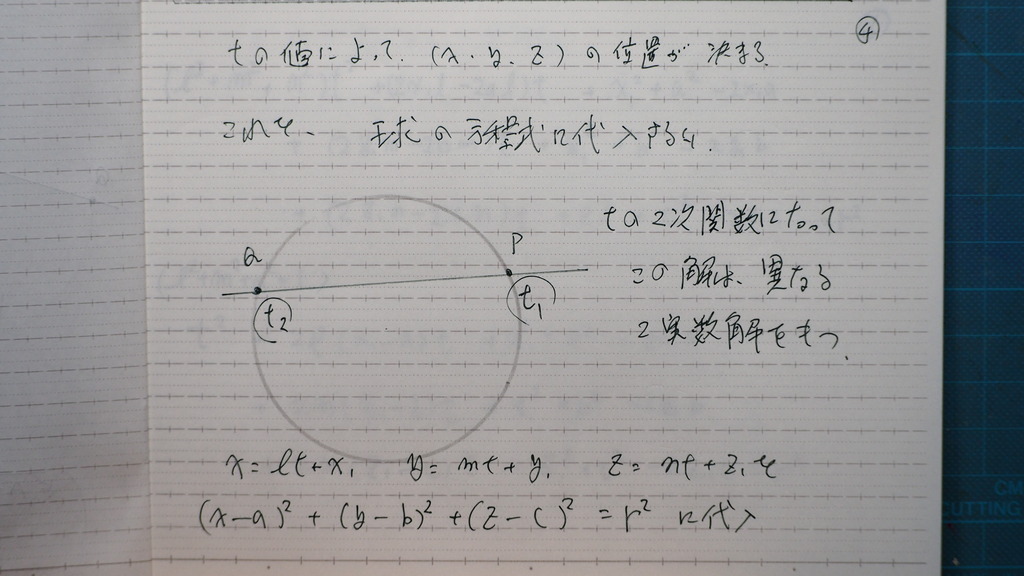
tの値で
直線上の 場所が 出るように

04
直線の 媒介変数表示形を
球の方程式に 代入すると
05
これを
tの2次関数に 整理して
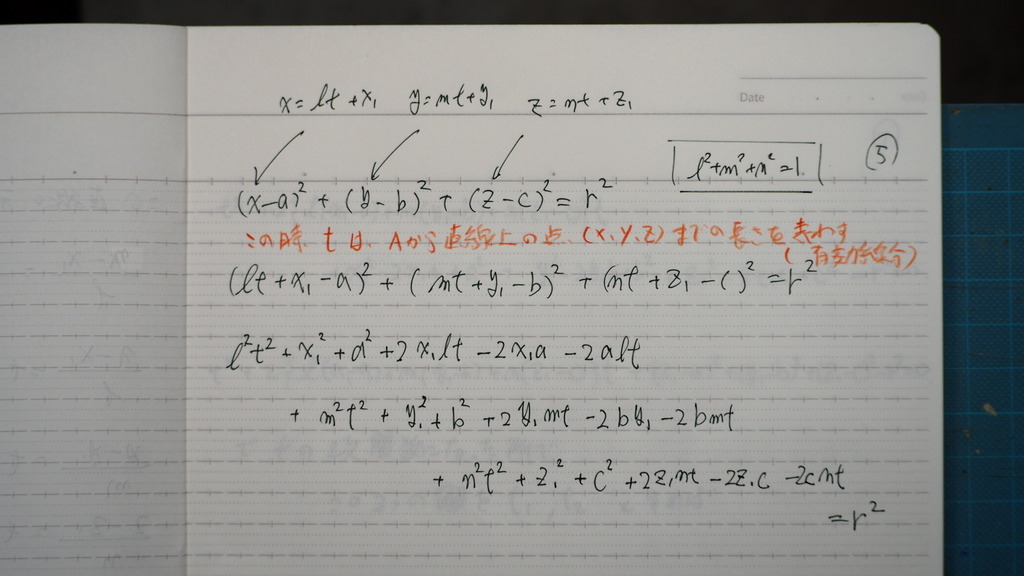
06
方向余弦を 使ってるので
=1を使って
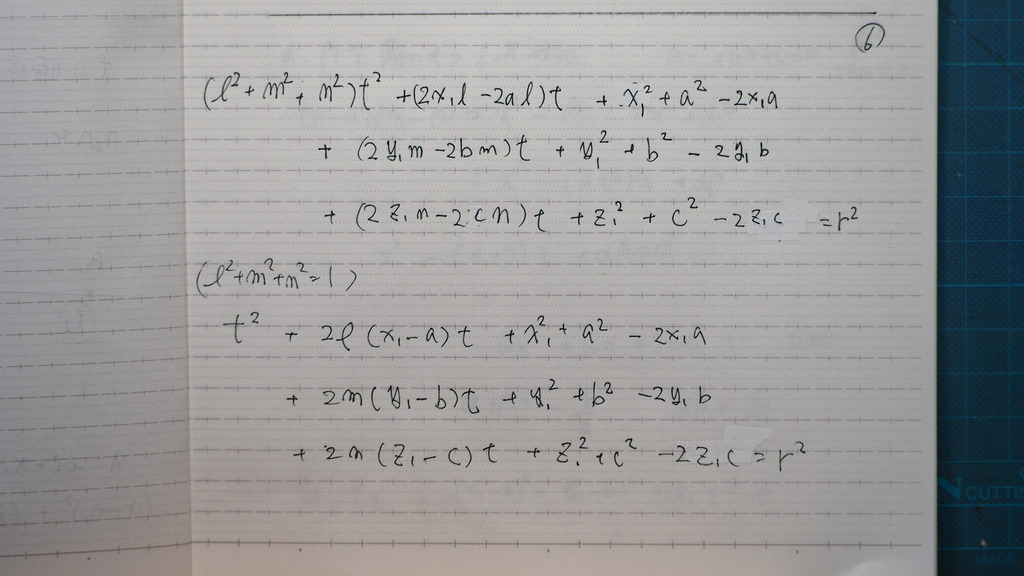
07
この2次関数の
2つの 解は
それぞれ
P 、Q を 表していて
今回は
点Aからの
線分とみなして

08
解と 係数の 関係から
α・β は t1・t2
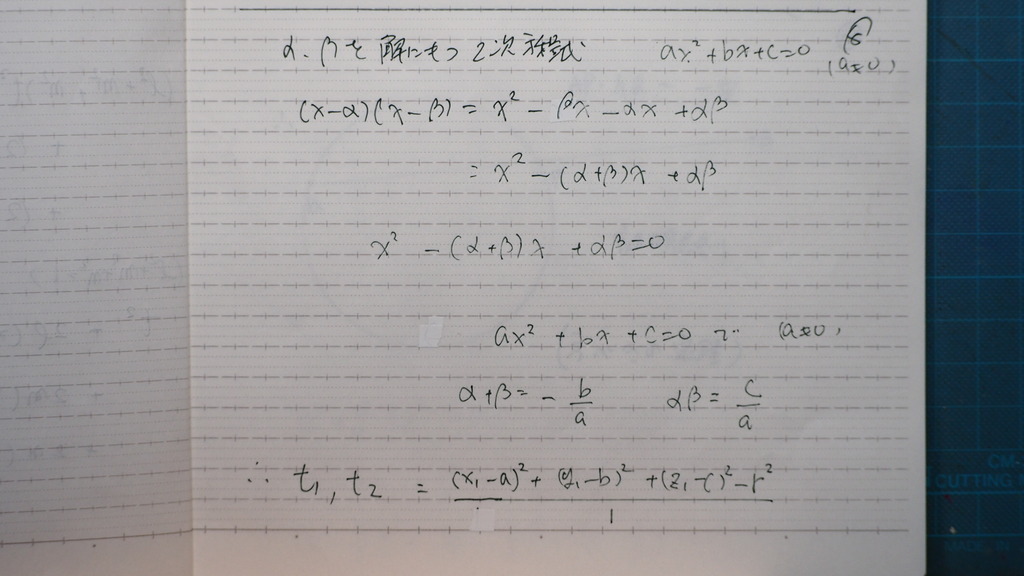
09
これが
AP・AQ の積と おなじであるから
一定である

10
方べきの定理
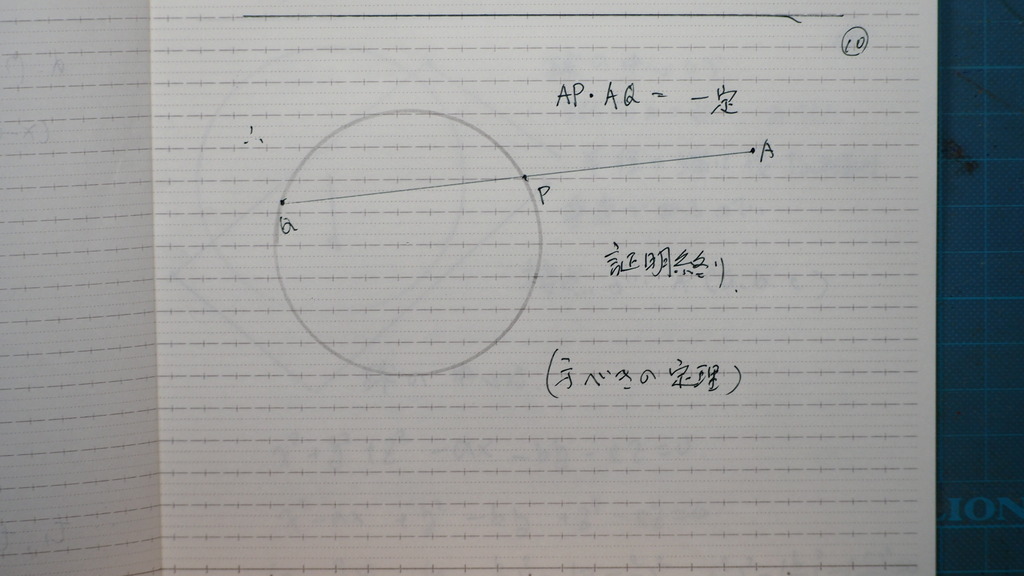
11
問題
先ず 球の接平面
次に
原点を 通る
直線と
球 、 接平面 の 交点を
P,Q
として
OP・OQ が 一定を
証明せよ

12
先ず 球の 接平面は
前回の とこでやってますが
球の 中心と そこからの
半径のはしに おける
平面との接点が 垂直であるから
まず
球の 中心を 知りたいから
変形して

13
球の 中心は これ
それと
接点Aとを 結ぶ
ベクトルが
平面の法線ベクトルだから
点A を 通り
法線ベクトルが分かれば

14
これを
展開した形に
しておくと
接平面の方程式
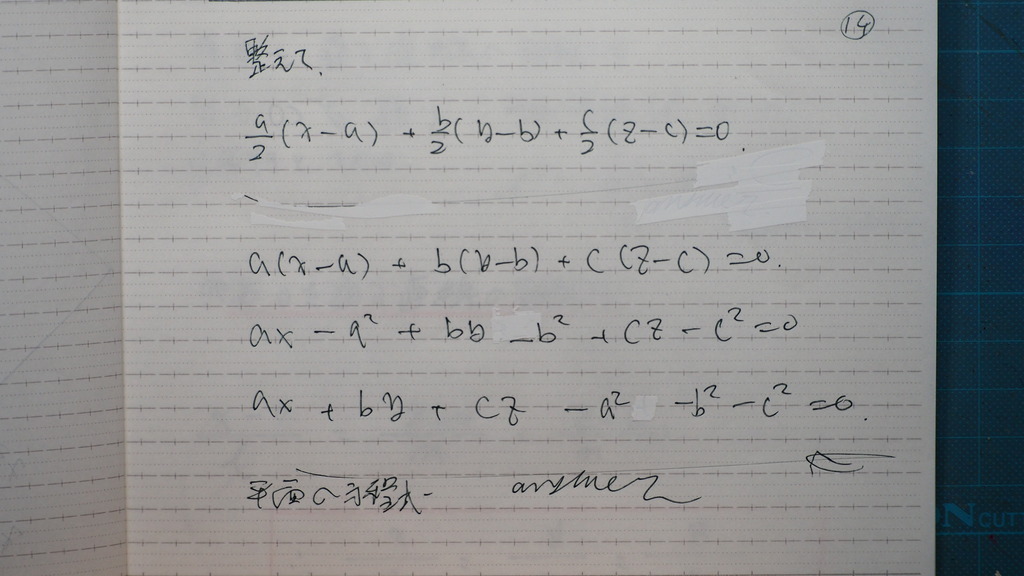
15
原点を
通る 直線が
球と この接平面に
交わるところを
P、Q としたとき
OP・OQの 積が
一定は

16
まず
原点(0,0,0)を 通る
直線であるので
方向係数を
L,m,n
方向余弦にして
それぞれの 2乗の 和が 1

17
使う方程式
3っ
直線の方程式
球の方程式
球の接平面の方程式

18
直線の 方程式を
媒介変数表示形にして
球の方程式に
代入していくと
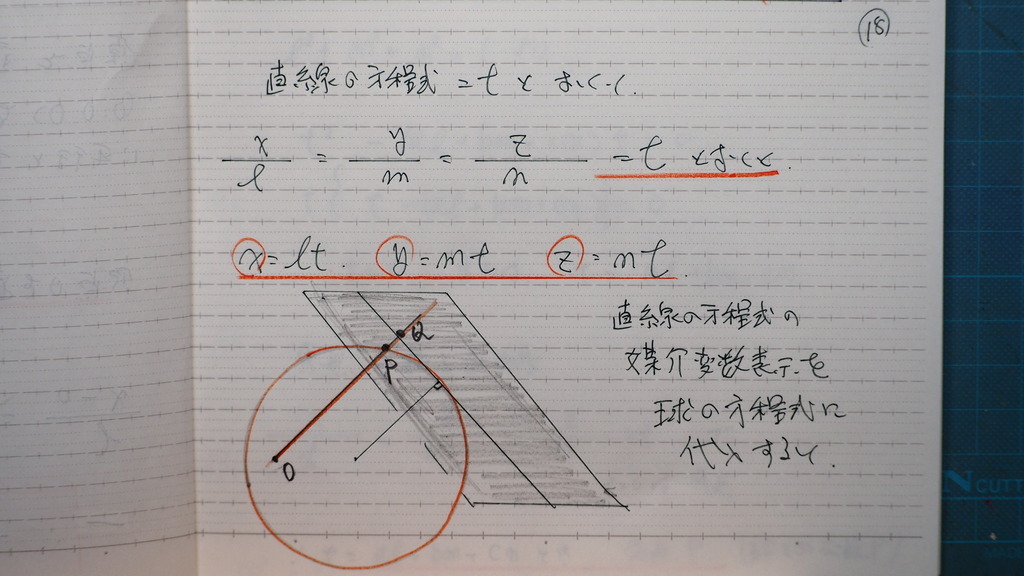
19
方向余弦を
使ってるので
=1になるを 使うんですよ
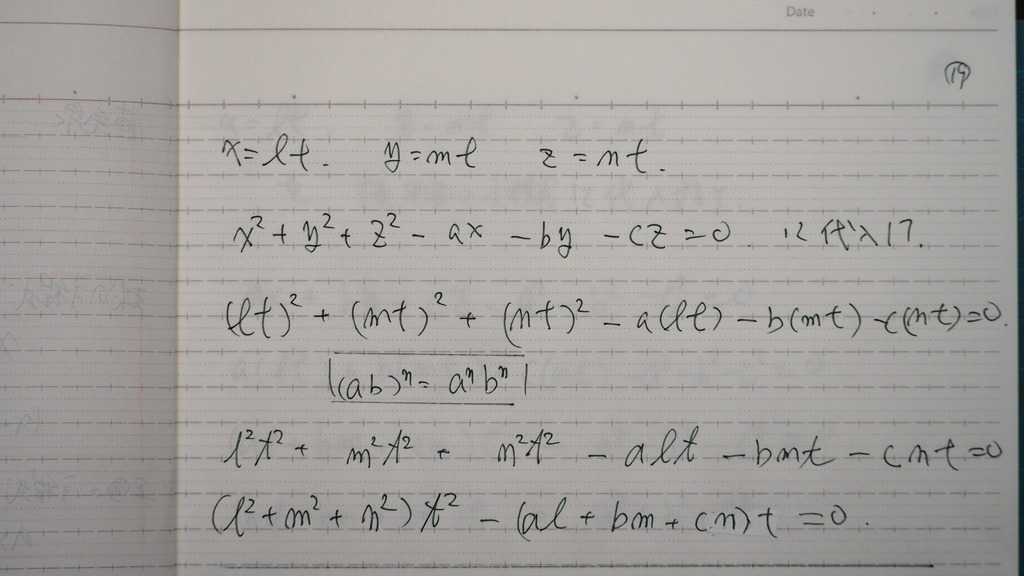
20
tは 0 または これこれ
t=0は
直線上で原点を 表してるので
もう一方が P
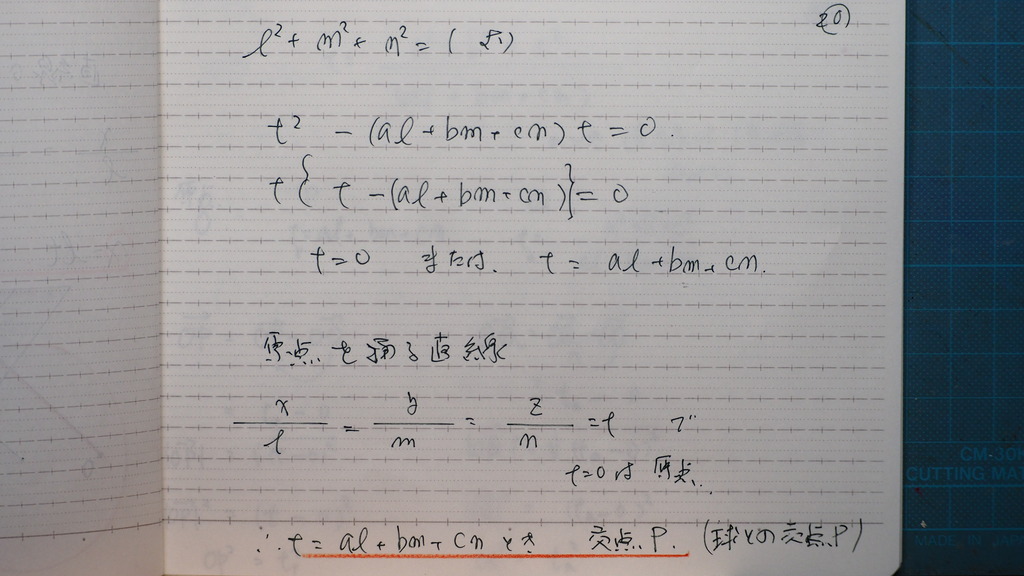
21
今度は
直線の媒介変数表示形を
球の接平面の方程式に
代入すると

22
tが
これは Qだから
OP OQ の二乗 を 計算して
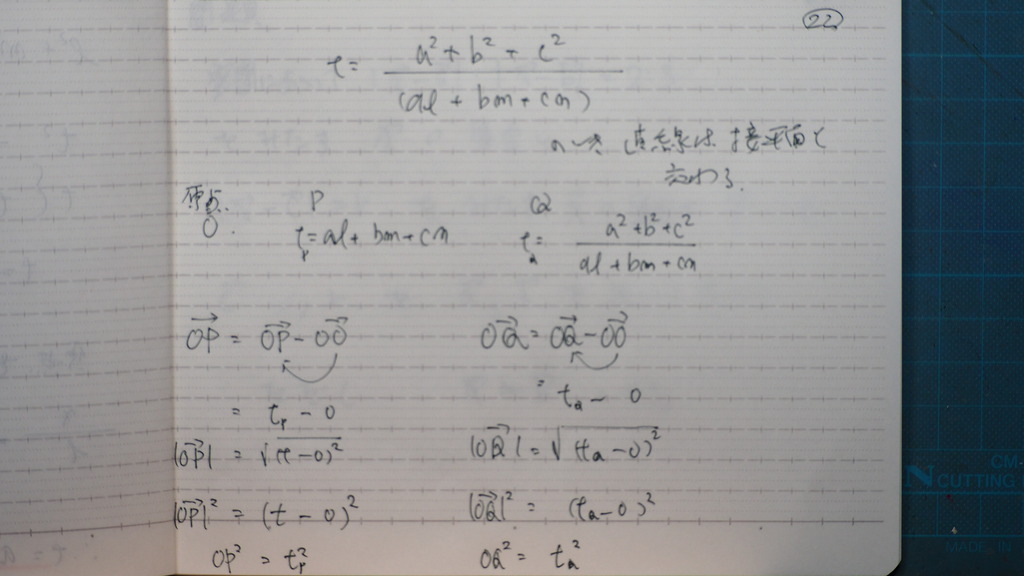
23
であるので
OP と OQの 積は
こんな感じで
これは
定点の値の 二乗の和の形
一定

24
問題
どういうことなのカナ

25
与式を
変形して
2乗して
展開して

26
ここから
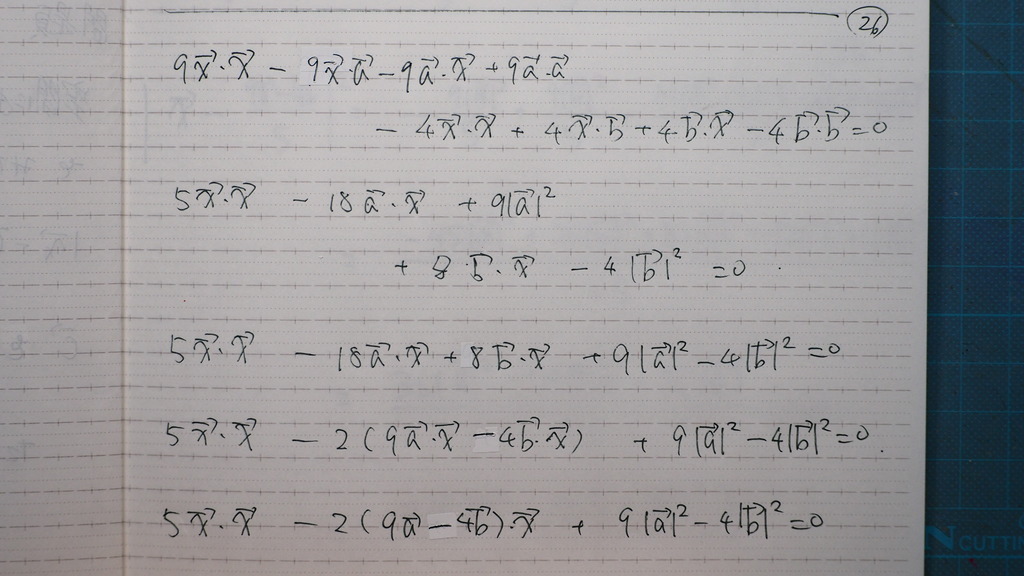
27
平方完成に 持ち込んで
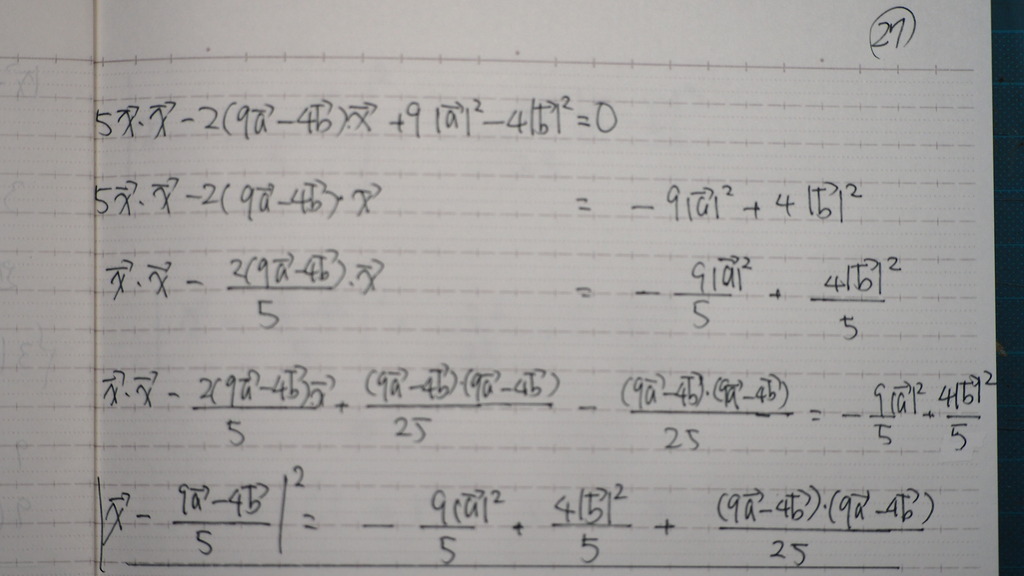
28
空気が 悪かったり
眠かったり
ブドウ糖が 減ってきたり
しますと
計算が
思うように 行きません
一回 寝て
起き
また ねて おき
3回目に
起きたときにですよ
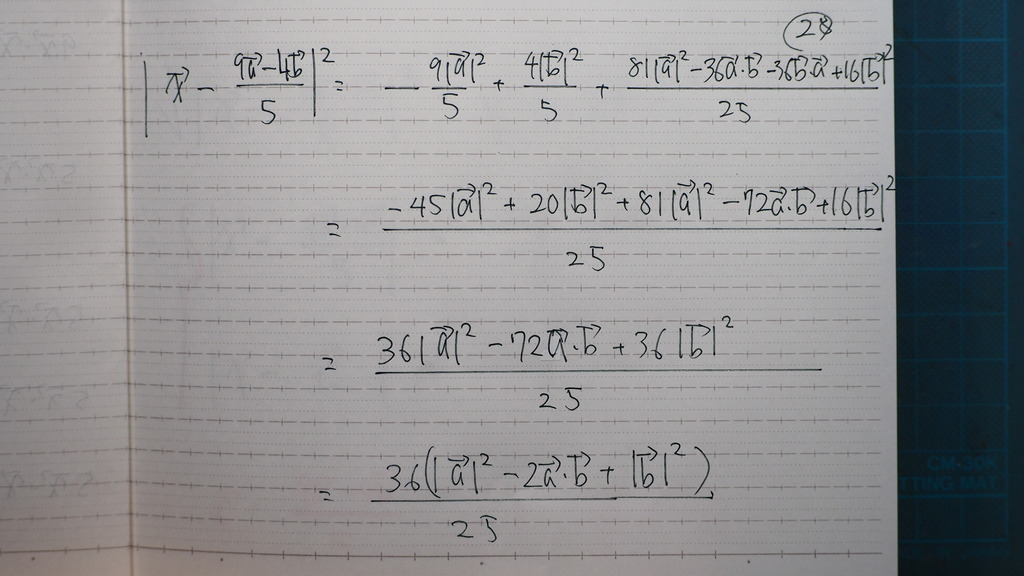
29
なんとか
たどり着きまして
出じゃナイスカ
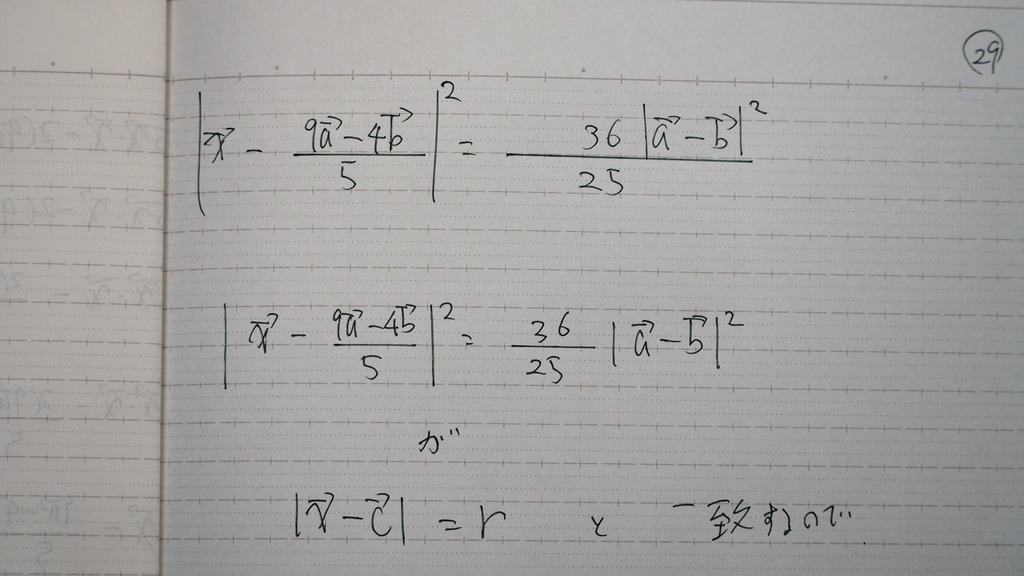
30
これがさ
なんだんだ
もう一つの 式に 等しいから
係数比較で
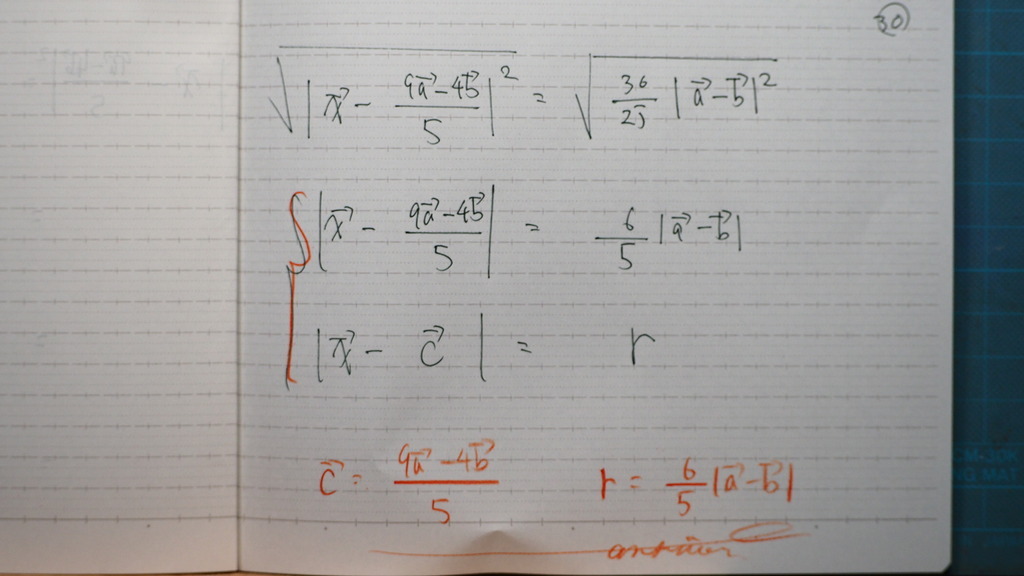
お疲れ様です。
空間座標と ベクトル
方べきの定理
01
球に 点Aを通る 直線が
交わるとき
その 交点を P,Qとすれば
AP・AQは 常に 一定
であるということを
証明する問題
02
図に書くと こんなイメージで
直線の
方程式を
Aを 通る
方向係数
L,m,n の 直線
L,m,n は 方向余弦を 使うと
03
=t と置いて
直線の 媒介変数表示にして
tの値で
直線上の 場所が 出るように
04
直線の 媒介変数表示形を
球の方程式に 代入すると
05
これを
tの2次関数に 整理して
06
方向余弦を 使ってるので
=1を使って
07
この2次関数の
2つの 解は
それぞれ
P 、Q を 表していて
今回は
点Aからの
線分とみなして
08
解と 係数の 関係から
α・β は t1・t2
09
これが
AP・AQ の積と おなじであるから
一定である
10
方べきの定理
11
問題
先ず 球の接平面
次に
原点を 通る
直線と
球 、 接平面 の 交点を
P,Q
として
OP・OQ が 一定を
証明せよ
12
先ず 球の 接平面は
前回の とこでやってますが
球の 中心と そこからの
半径のはしに おける
平面との接点が 垂直であるから
まず
球の 中心を 知りたいから
変形して
13
球の 中心は これ
それと
接点Aとを 結ぶ
ベクトルが
平面の法線ベクトルだから
点A を 通り
法線ベクトルが分かれば
14
これを
展開した形に
しておくと
接平面の方程式
15
原点を
通る 直線が
球と この接平面に
交わるところを
P、Q としたとき
OP・OQの 積が
一定は
16
まず
原点(0,0,0)を 通る
直線であるので
方向係数を
L,m,n
方向余弦にして
それぞれの 2乗の 和が 1
17
使う方程式
3っ
直線の方程式
球の方程式
球の接平面の方程式
18
直線の 方程式を
媒介変数表示形にして
球の方程式に
代入していくと
19
方向余弦を
使ってるので
=1になるを 使うんですよ
20
tは 0 または これこれ
t=0は
直線上で原点を 表してるので
もう一方が P
21
今度は
直線の媒介変数表示形を
球の接平面の方程式に
代入すると
22
tが
これは Qだから
OP OQ の二乗 を 計算して
23
であるので
OP と OQの 積は
こんな感じで
これは
定点の値の 二乗の和の形
一定
24
問題
どういうことなのカナ
25
与式を
変形して
2乗して
展開して
26
ここから
27
平方完成に 持ち込んで
28
空気が 悪かったり
眠かったり
ブドウ糖が 減ってきたり
しますと
計算が
思うように 行きません
一回 寝て
起き
また ねて おき
3回目に
起きたときにですよ
29
なんとか
たどり着きまして
出じゃナイスカ
30
これがさ
なんだんだ
もう一つの 式に 等しいから
係数比較で
お疲れ様です。