2023年01月07日
22034 大人のさび落とし 空間座標とベクトル 球と接平面
大人のさび落とし
球と 接平面
01
まず 問題
球の方程式を 導く

02
球面上の 一点での 接平面
と
2点を 通り
球接する平面

03
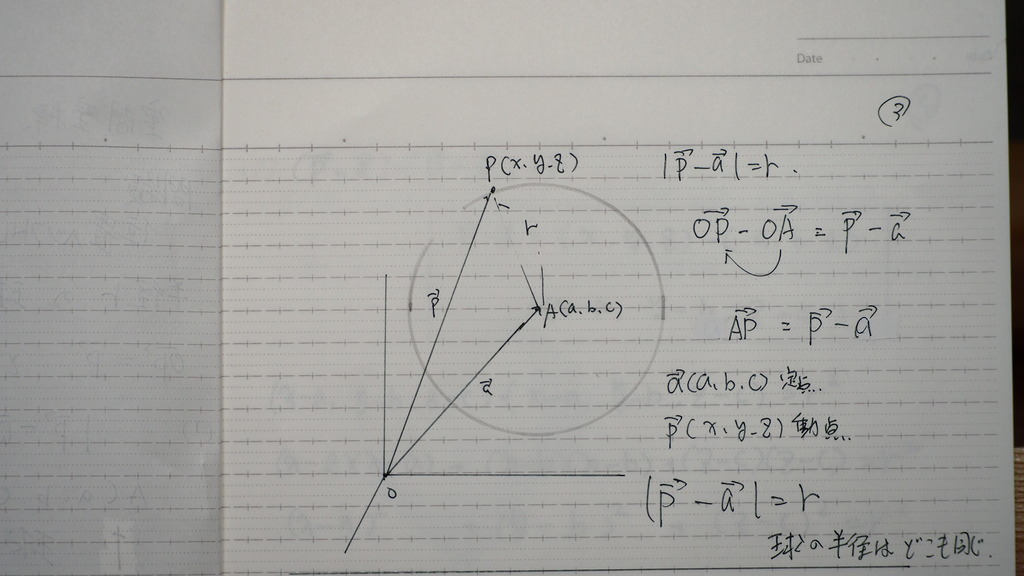
まず
ベクトルの 引き算で
出てきたものが
Pは 動点だから
動き回るんだけど
いも いつも 大きさが 同じ
ッテ式を
04
辺々2乗するでしょ
で
かっこの中身が
成分の引き算で

05
こんな感じに
成分の 引き算になるので
この 内積の 展開で
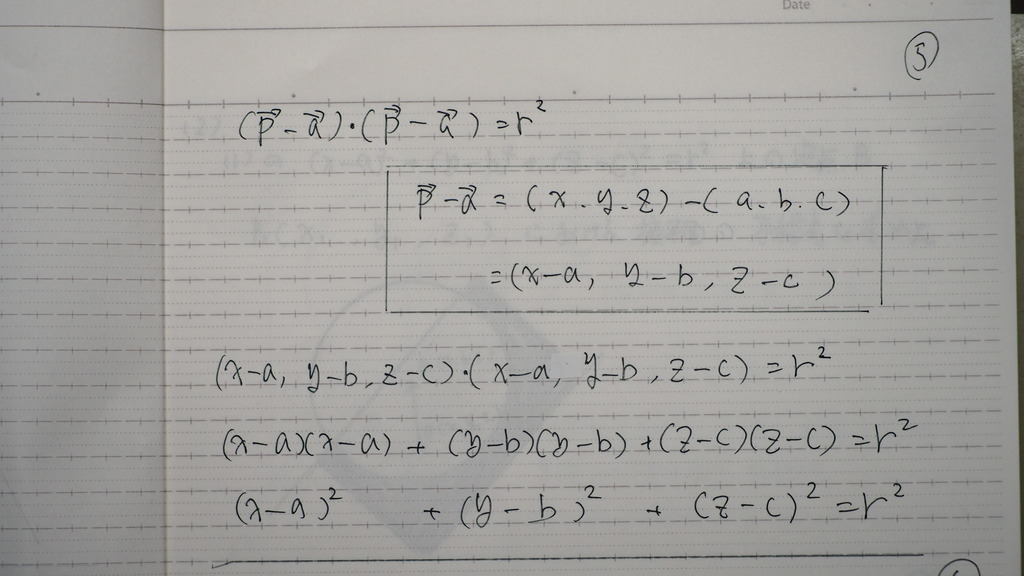
06
なりましたと
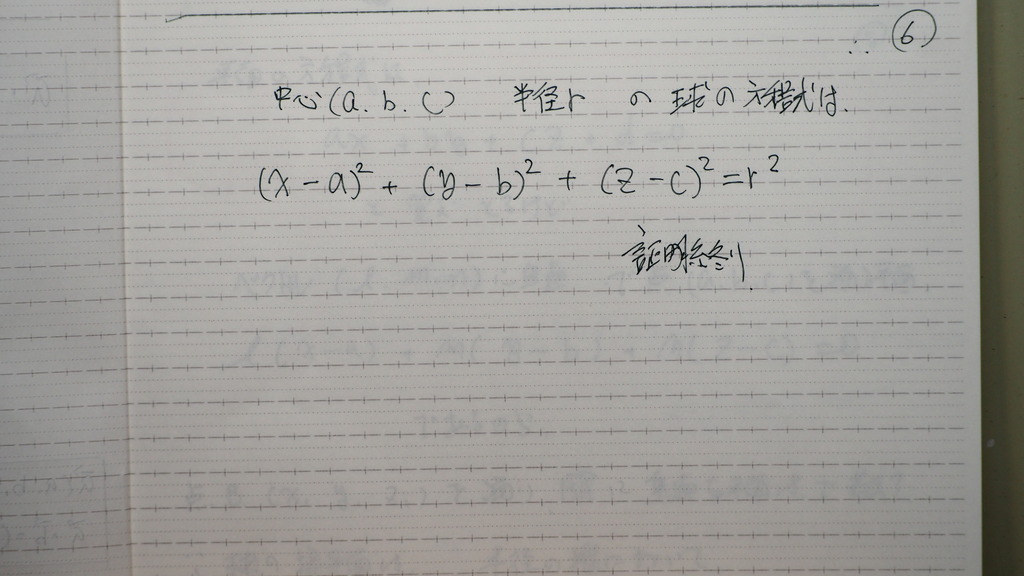
07
この 球面上の
点B における 接平面は
平面の 垂直成分は
球の中心から Bにおろした
垂線のベクトル
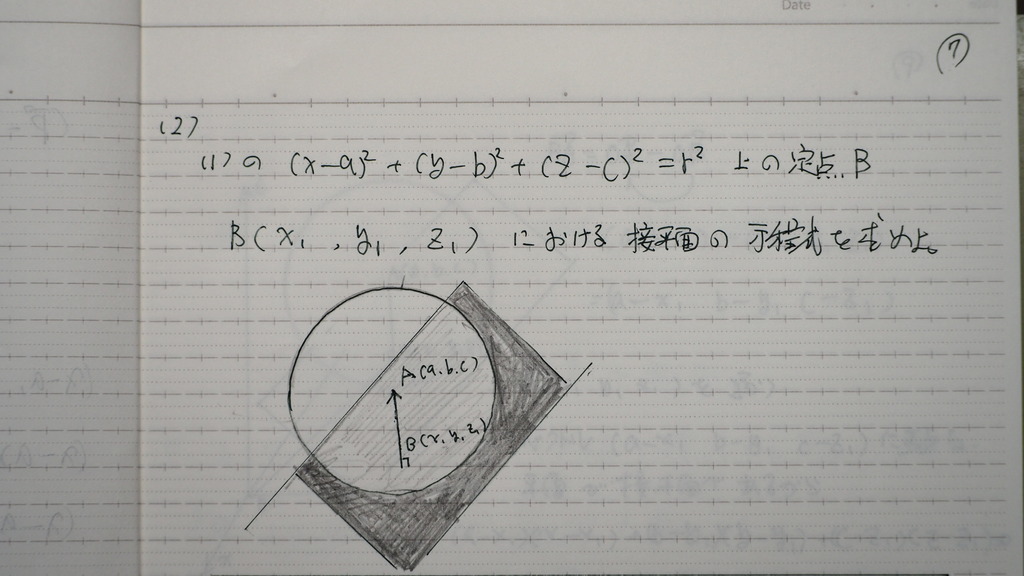
08
平面の 方程式は
垂直成分と
通過点がわかてるときの場合を
使って

09
BA ベクトル
平面に垂直な成分
と
通過点 B から
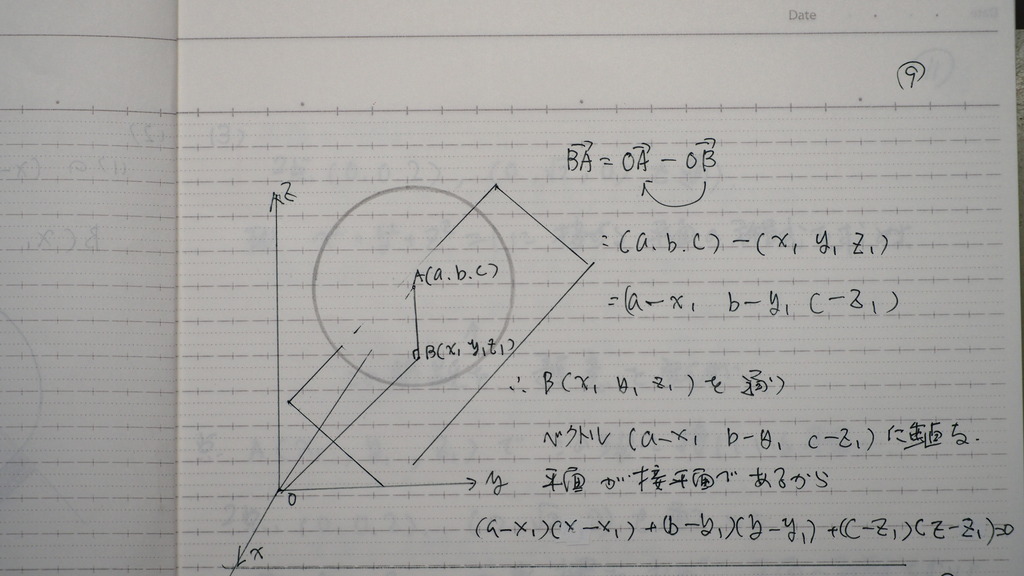
10
これに 代入してですよ

11
2点を 通り
球に接する平面は
今の (2) を
うまく使って
点B で
球に 接している
その平面が
2点も 通過するで
代入して
ここでは Aとすれば
Aの X1 Y1 Z1
を
特定すれば
平面の 方程式になるので

12
まず 球の方程式に
点Aで接する平面は

13
こんな形
それと
だいいから・・・

14
2点を
平面の 方程式に代入すると
②③
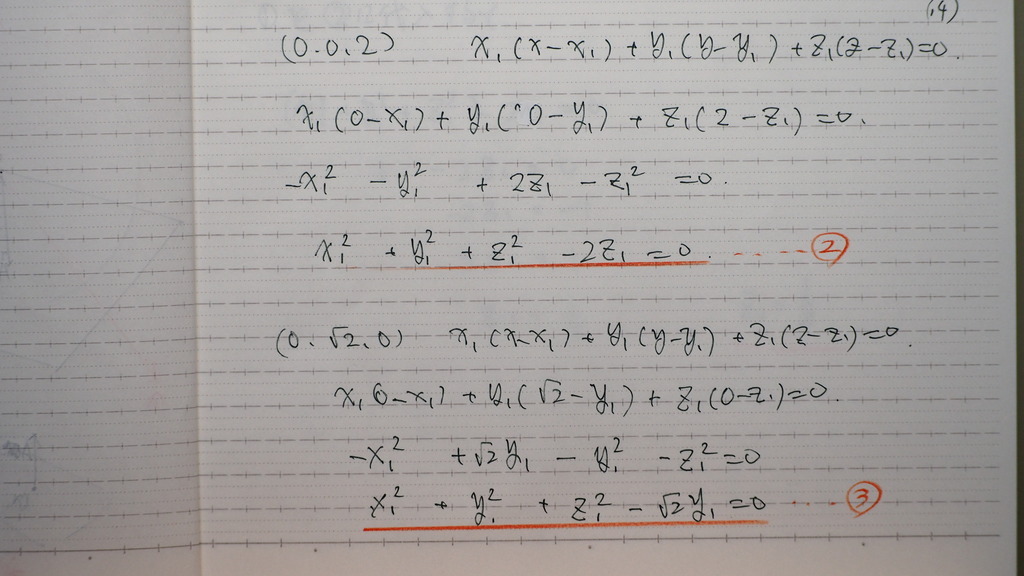
15
➀②③より
平面の方程式を
求めると

16
z1
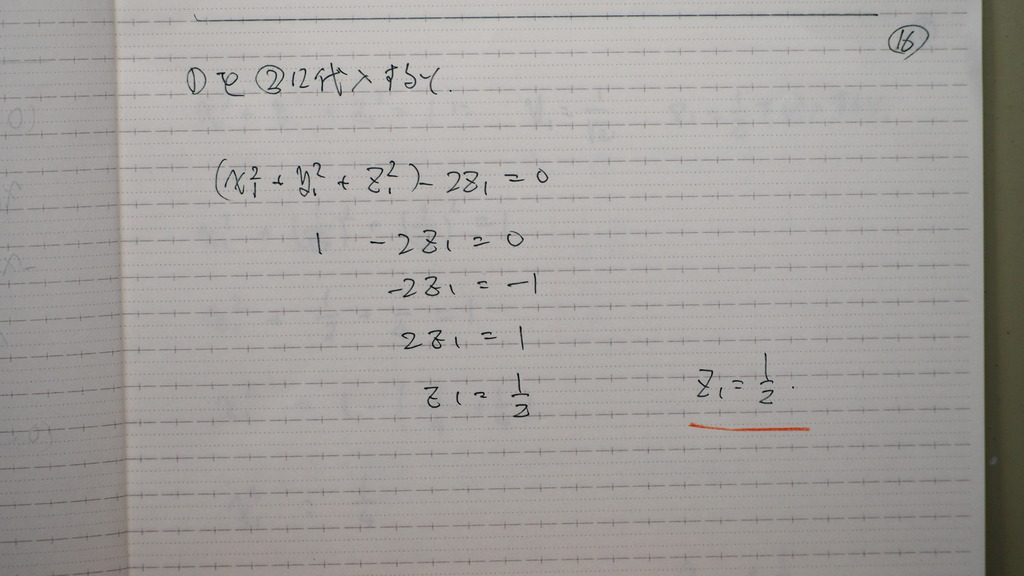
17
y1

18
x1
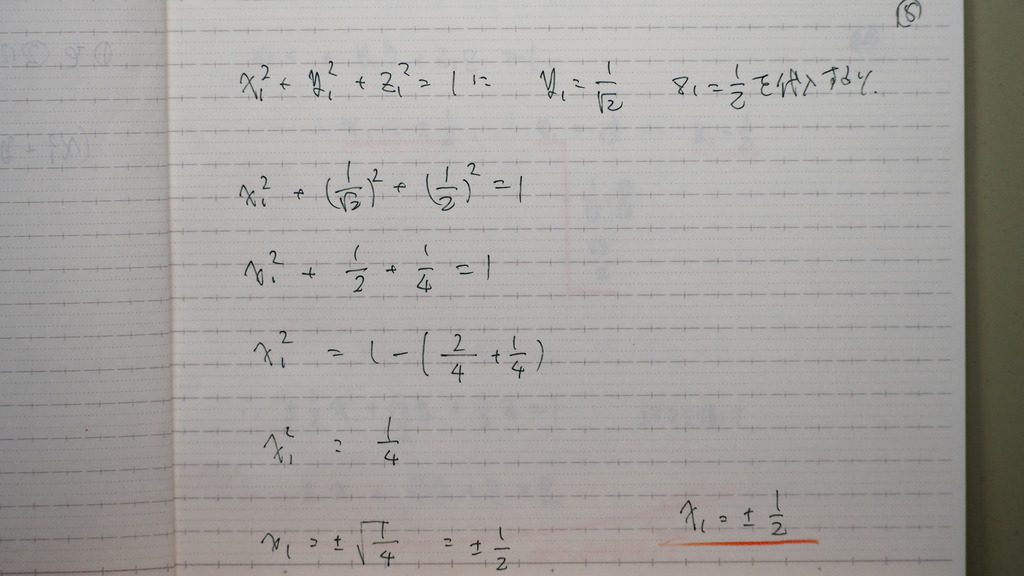
19
これを
整理した
平面の 方程式に 代入して
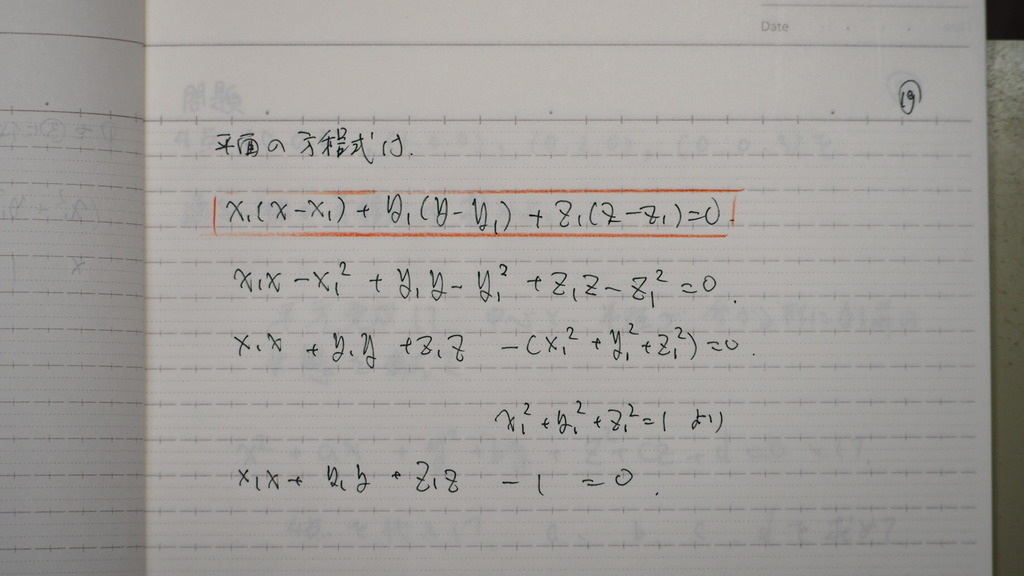
20
こんな感じに

21
4点を 通る
球の方程式
球の方程式の
平方完成する前の 形を
使って

22
4点を 逐次 代入してくと
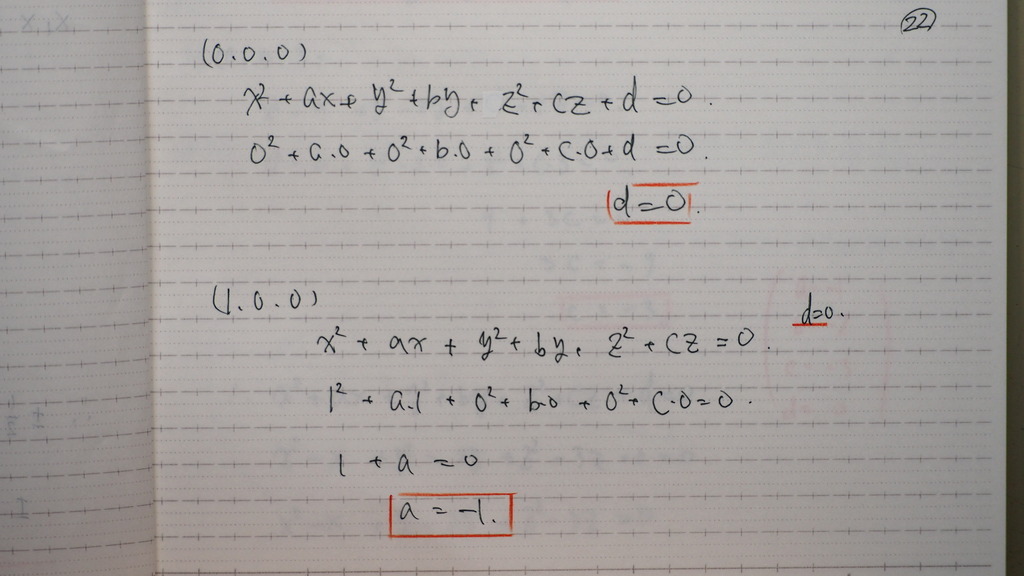
23
こんな感じに
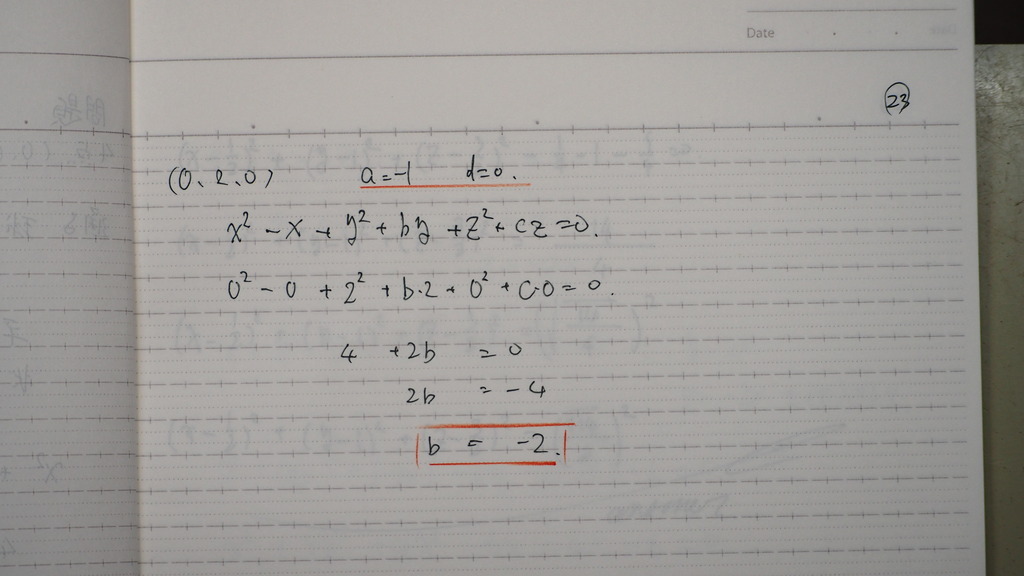
24
これらを
a,b,c,dに
代入したらば
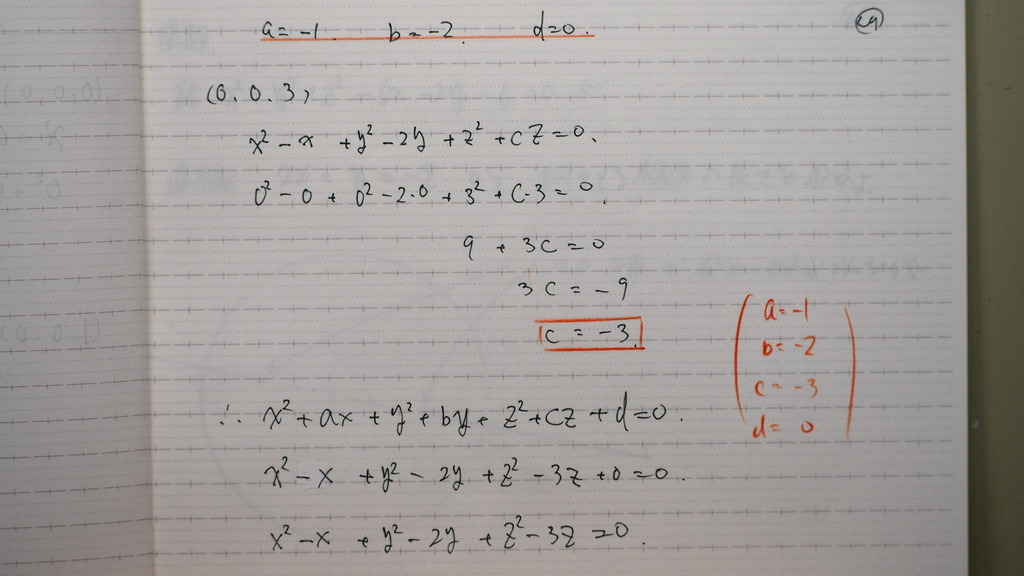
25
これです
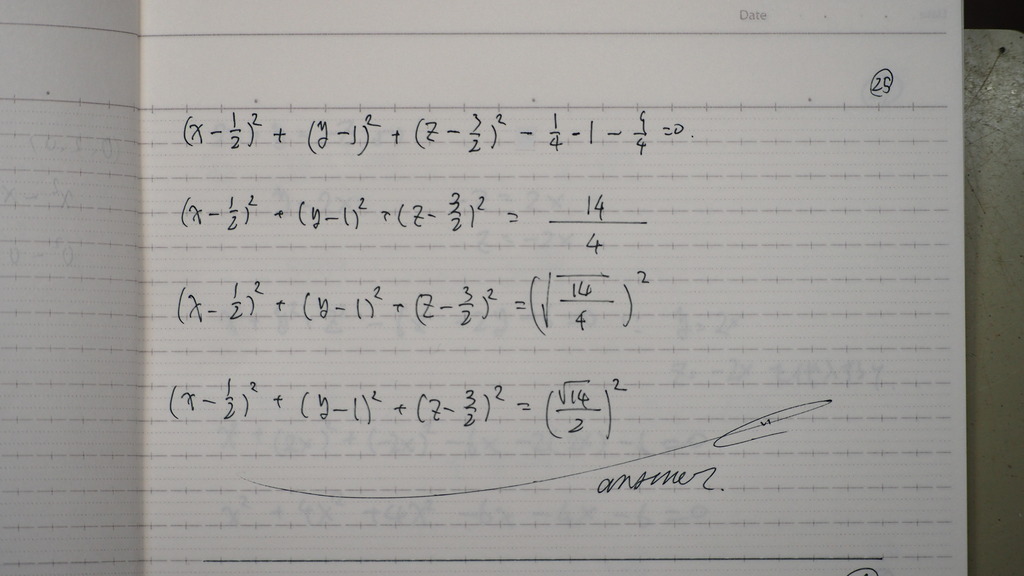
26
球の方程式が
切り取る
直線の 方程式の長さ

27
直線の 方程式の y、z を
xで 置き換えて
球の 方程式に
代入したらば
xの 2次方程式に
なるにおだけれど
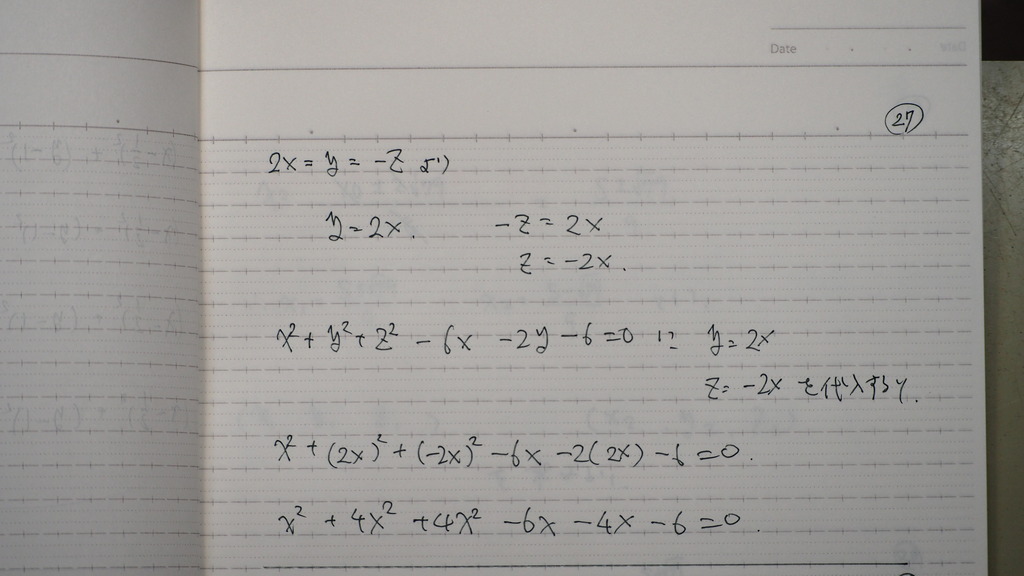
28
これは
異なる 2実数解を 持つので
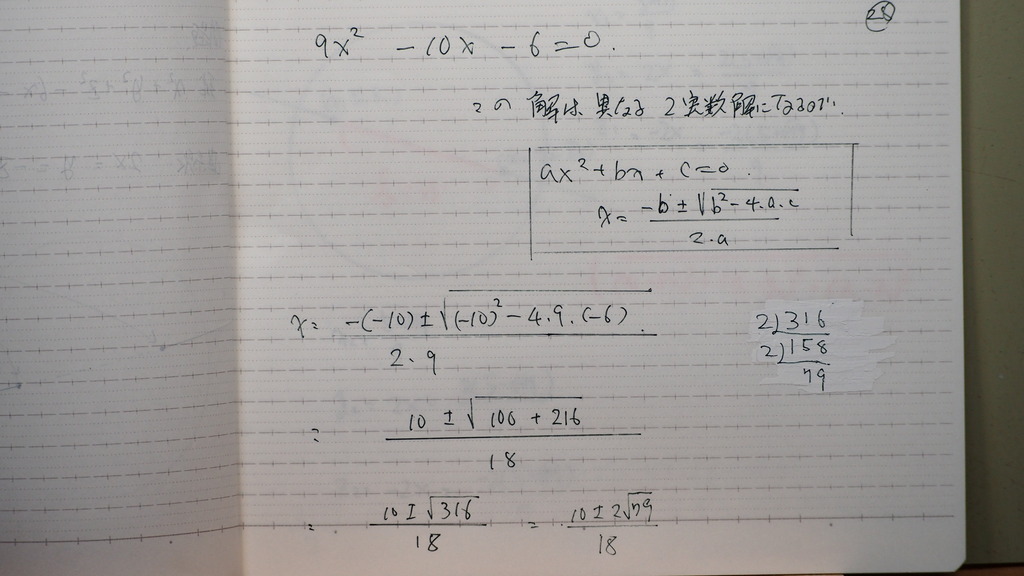
29
その一つを X1
もう一方を X2
として

30
2点間の 距離を
計算すると

31
こんなデショ
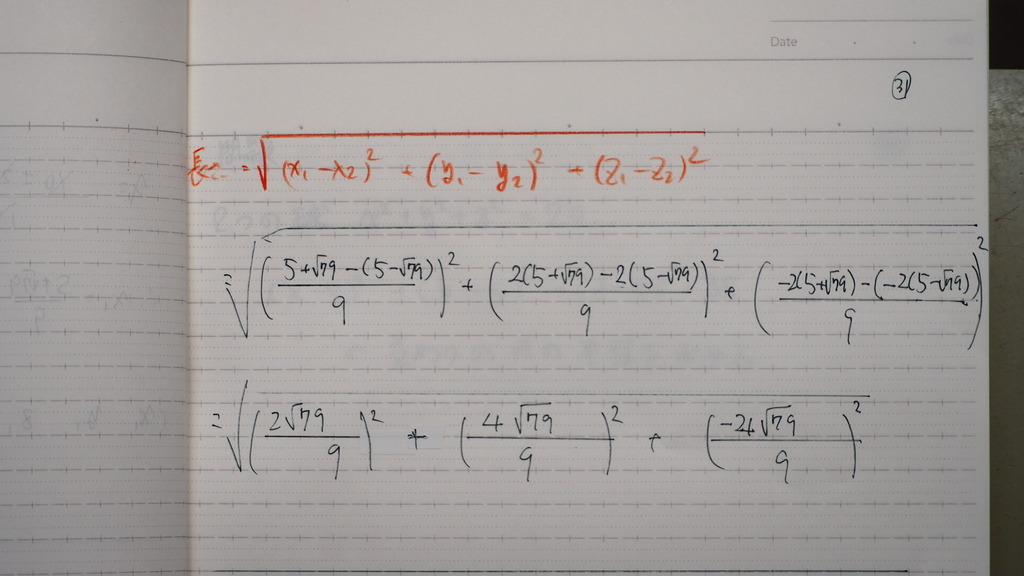
32
計算を
間違わないようにじゃナイスカ

33
2つの
球があってですよ
交わりの
円の 半径を 求めよ

34
平面のところで
こんなのを
やったんですが

35
球でも
おなじですよ

36
今回は
この式は
k=-1 とすれば
x2 y2 z2 が 消えて 平面を表す。
辺々引算して
出て来たのが
交円を含む 平面の方程式
のはずなので
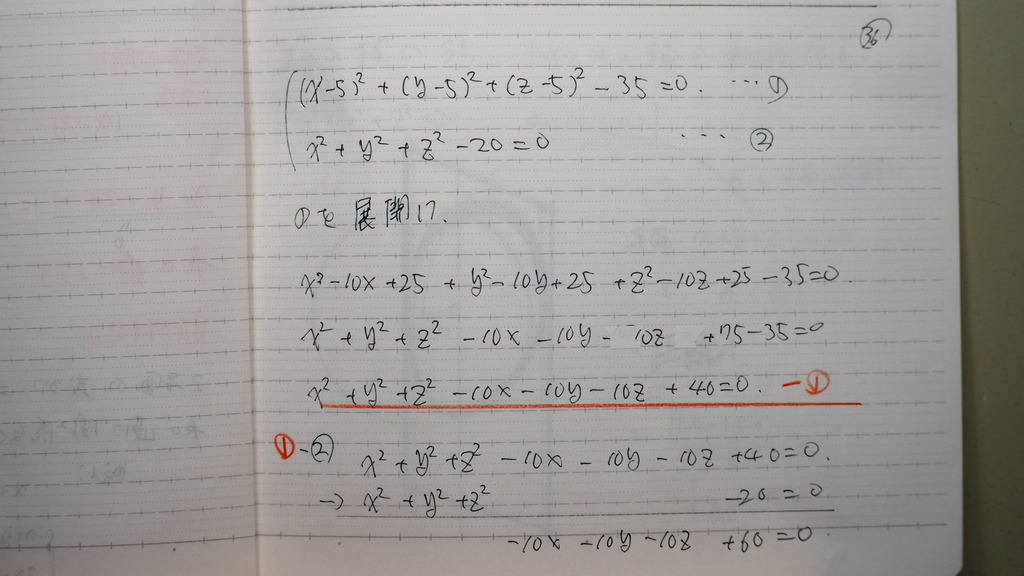
37
これを 使って

38
交円を 含む 平面までの
距離を 計算すると
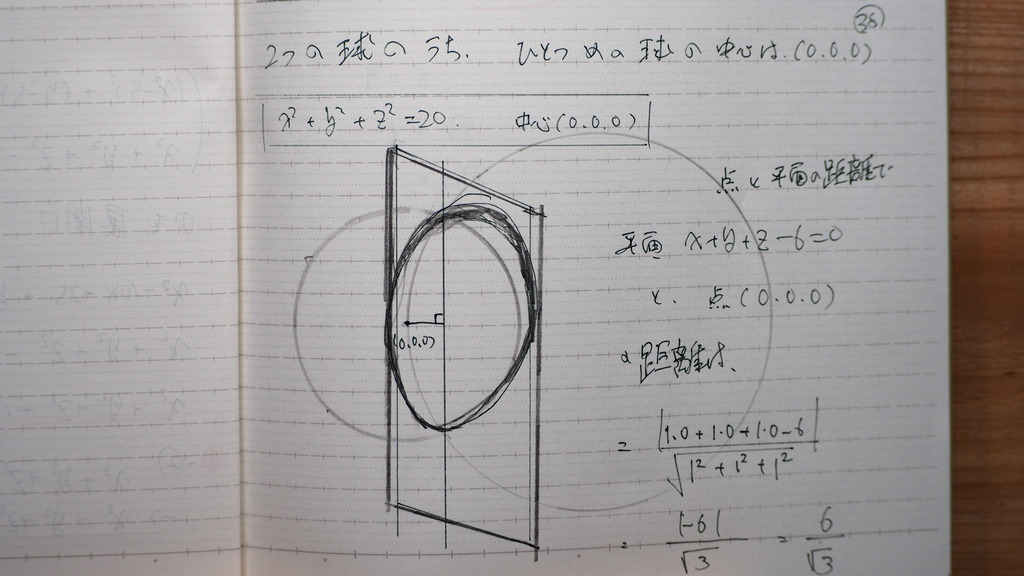
39
小さい球の
半径が分かってるので

お疲れ様です。
球と 接平面
01
まず 問題
球の方程式を 導く
02
球面上の 一点での 接平面
と
2点を 通り
球接する平面
03
まず
ベクトルの 引き算で
出てきたものが
Pは 動点だから
動き回るんだけど
ッテ式を
04
辺々2乗するでしょ
で
かっこの中身が
成分の引き算で
05
こんな感じに
成分の 引き算になるので
この 内積の 展開で
06
なりましたと
07
この 球面上の
点B における 接平面は
平面の 垂直成分は
球の中心から Bにおろした
垂線のベクトル
08
平面の 方程式は
垂直成分と
通過点がわかてるときの場合を
使って
09
BA ベクトル
平面に垂直な成分
と
通過点 B から
10
これに 代入してですよ
11
2点を 通り
球に接する平面は
今の (2) を
うまく使って
点B で
球に 接している
その平面が
2点も 通過するで
代入して
ここでは Aとすれば
Aの X1 Y1 Z1
を
特定すれば
平面の 方程式になるので
12
まず 球の方程式に
点Aで接する平面は
13
こんな形
それと
だいいから・・・
14
2点を
平面の 方程式に代入すると
②③
15
➀②③より
平面の方程式を
求めると
16
z1
17
y1
18
x1
19
これを
整理した
平面の 方程式に 代入して
20
こんな感じに
21
4点を 通る
球の方程式
球の方程式の
平方完成する前の 形を
使って
22
4点を 逐次 代入してくと
23
こんな感じに
24
これらを
a,b,c,dに
代入したらば
25
これです
26
球の方程式が
切り取る
直線の 方程式の長さ
27
直線の 方程式の y、z を
xで 置き換えて
球の 方程式に
代入したらば
xの 2次方程式に
なるにおだけれど
28
これは
異なる 2実数解を 持つので
29
その一つを X1
もう一方を X2
として
30
2点間の 距離を
計算すると
31
こんなデショ
32
計算を
間違わないようにじゃナイスカ
33
2つの
球があってですよ
交わりの
円の 半径を 求めよ
34
平面のところで
こんなのを
やったんですが
35
球でも
おなじですよ
36
今回は
この式は
k=-1 とすれば
x2 y2 z2 が 消えて 平面を表す。
辺々引算して
出て来たのが
交円を含む 平面の方程式
のはずなので
37
これを 使って
38
交円を 含む 平面までの
距離を 計算すると
39
小さい球の
半径が分かってるので
お疲れ様です。