2023年01月04日
22033大人のさび落とし 空缶座標とベクトル より 方向余弦
大人のさび落とし
空間座標 と ベクトル
より
方向余弦
01
空間直線が
x軸 y軸 z軸
と なす角を
ソレゾレ
α β γ とすれば
次の 等式が
成り立つことを 証明せよ

02
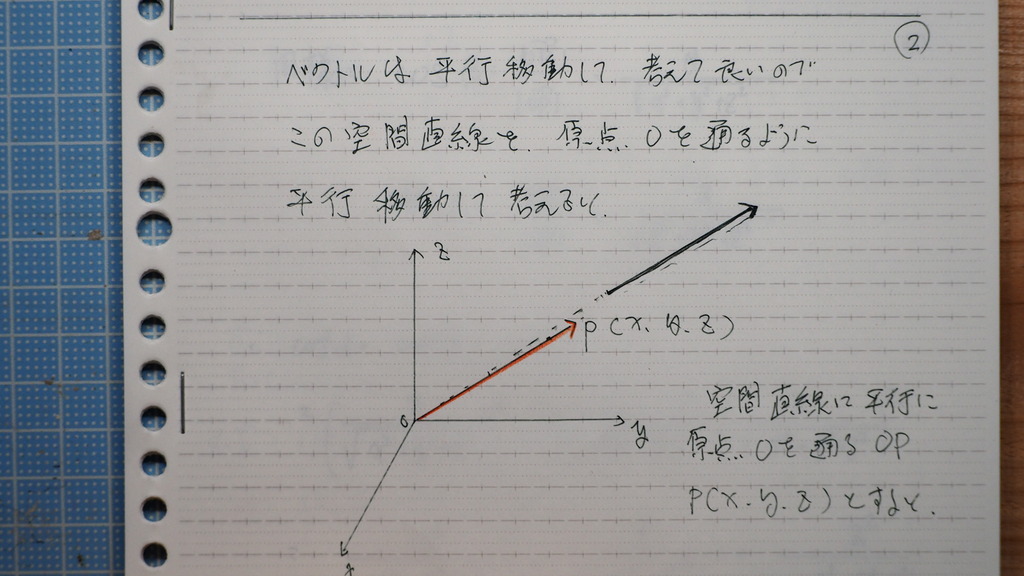
ベクトルは
平行移動していいので
原点まで
平行移動して
ソレゾレ
x軸 y軸 z軸
と なす角を
α β γ とすると
直線を P(x、y、z)
とする時
03
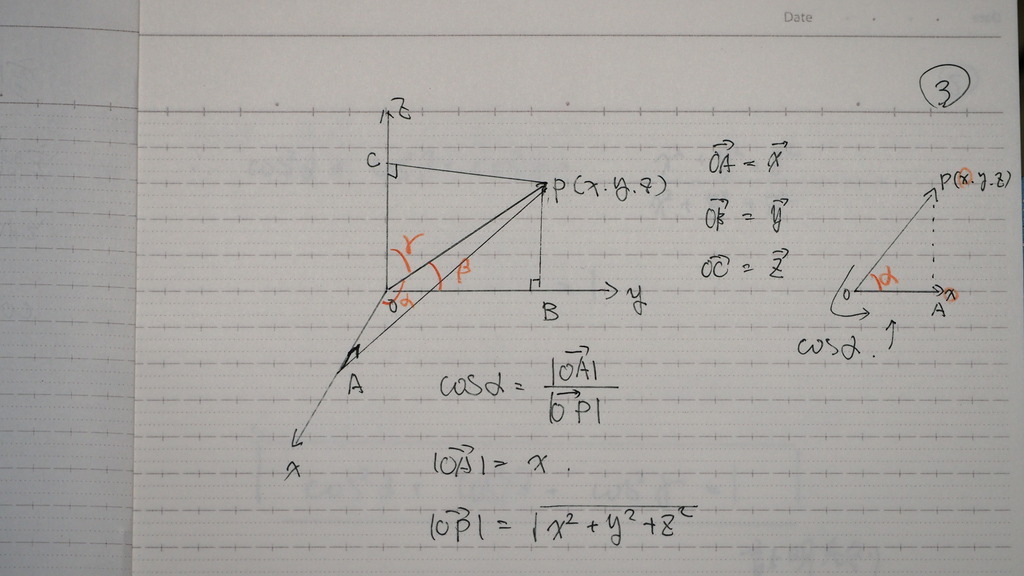
COSα
COSβ
COSγ
は
まず COSα から見てくと
OP 分の OA
04
COSβ
COSγ
も 同様にして
出そろった
COSα
COSβ
COSγ
を それぞれ 2乗して
足してみますと
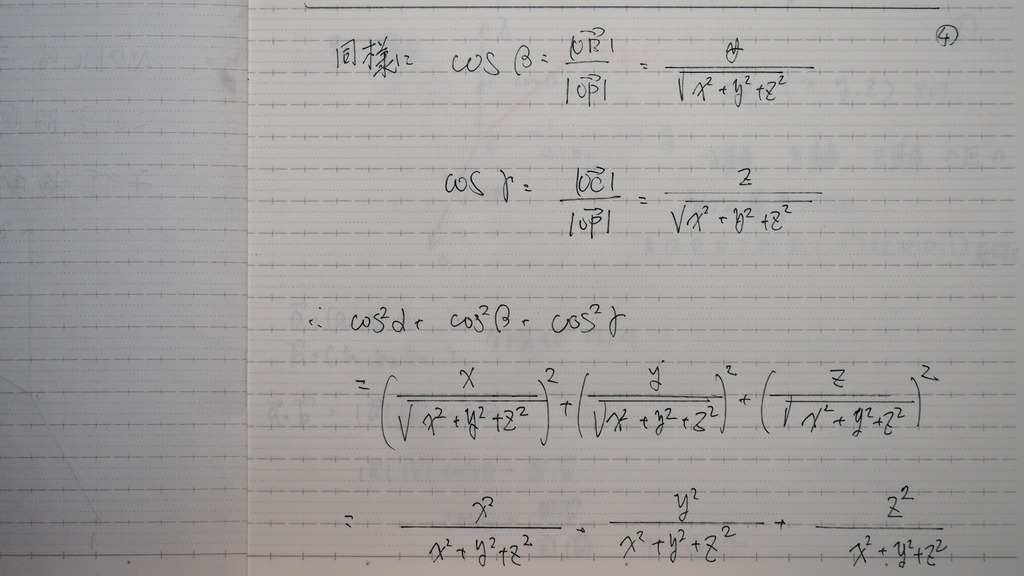
05
なったじゃナイスカ

06
ベクトルの
内積を 使った場合は
A,B,Cを
(1,0,0)(0,1,0)(0,0,1)
として
内積から
なす角 の COSを 求めると

07
こんな感じに

08
なるじゃ
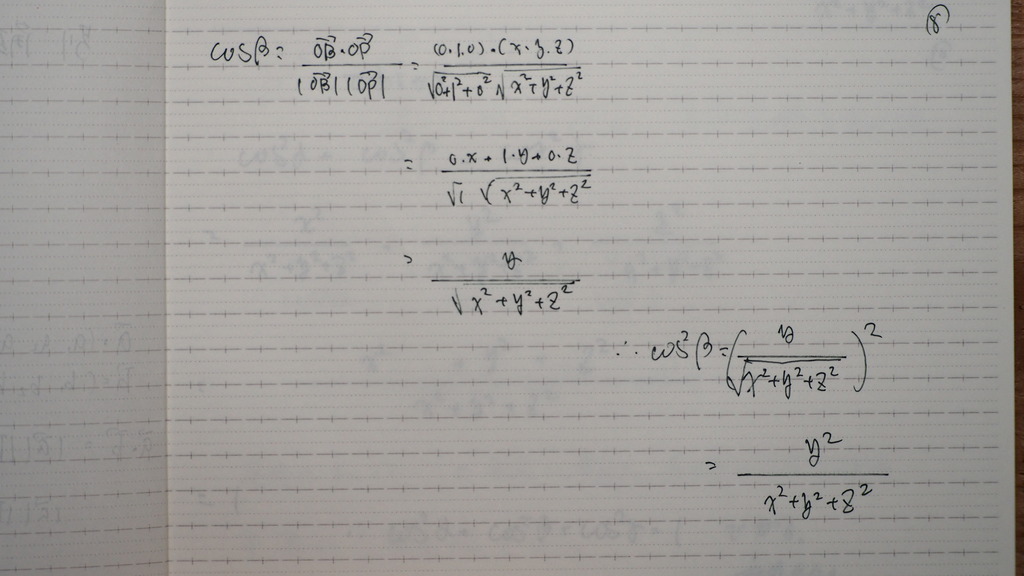
09
ナイスカ

10
であるから
ソレゾレ
2乗したものを
足すと
なったと
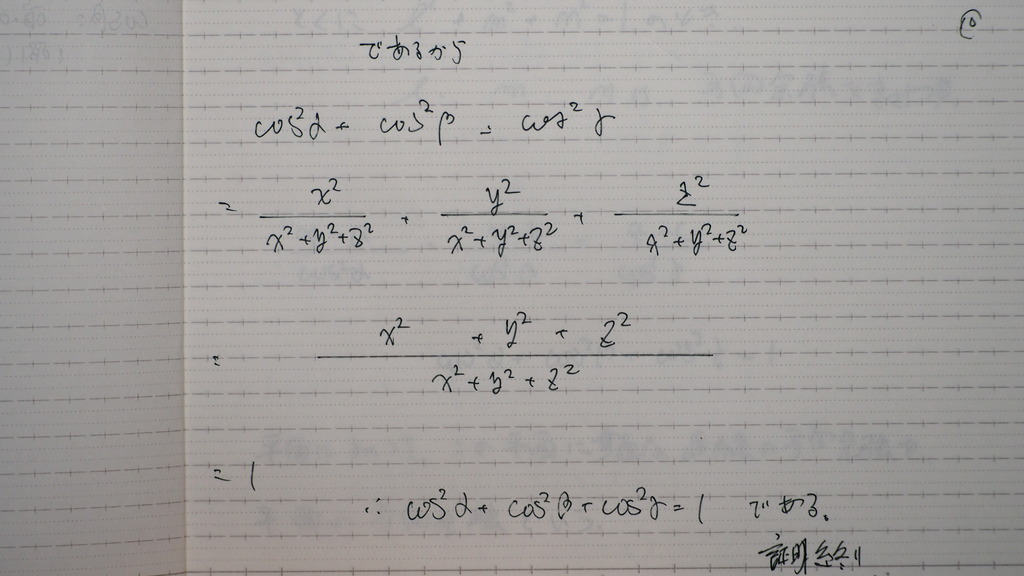
11
まとめ

12
こんな風にも
書けるてことカナ
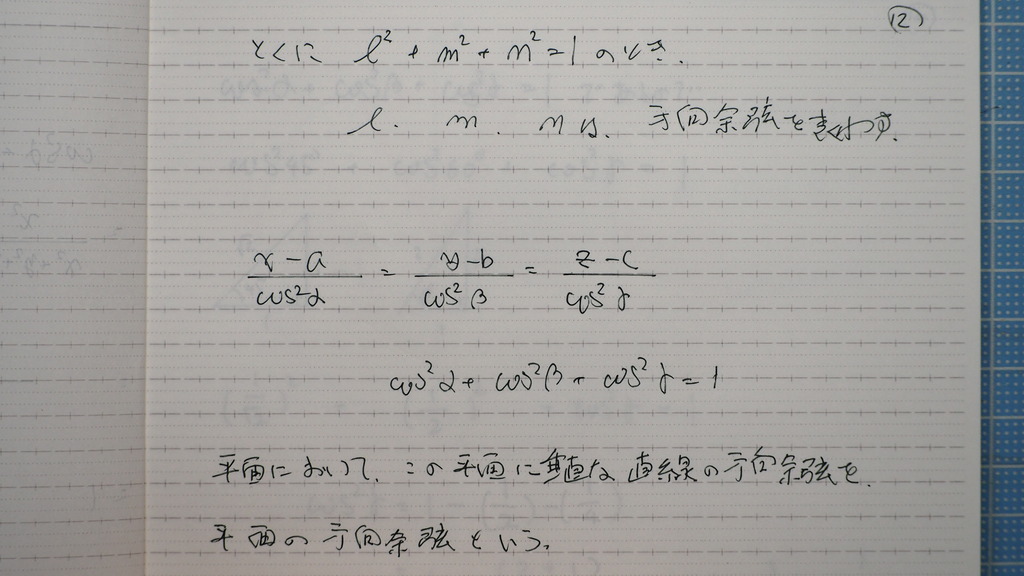
13
問題
空間直線が
x軸と 45度
y軸と 60度
の角度を
なすとき
z軸との なす角は
どれくらいか
群馬県では
懐かしい アニメを
夜中に
放送してましが
バルキリーが 放つ
ミサイルの横に
タコ酎ハイ に バドワイザー

14
で 今日は
z軸のなす角だから
さっき証明した式を
使って
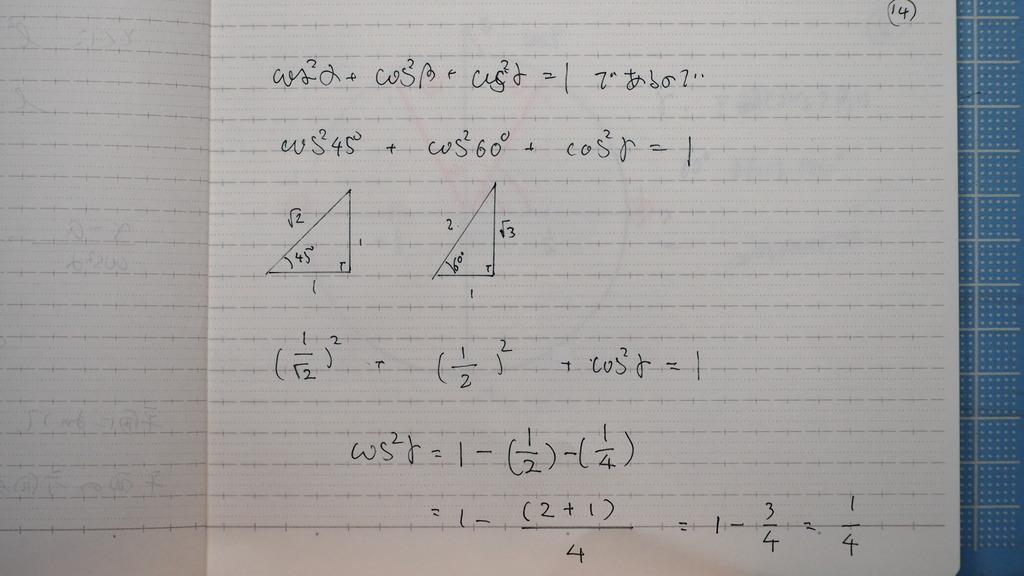
15
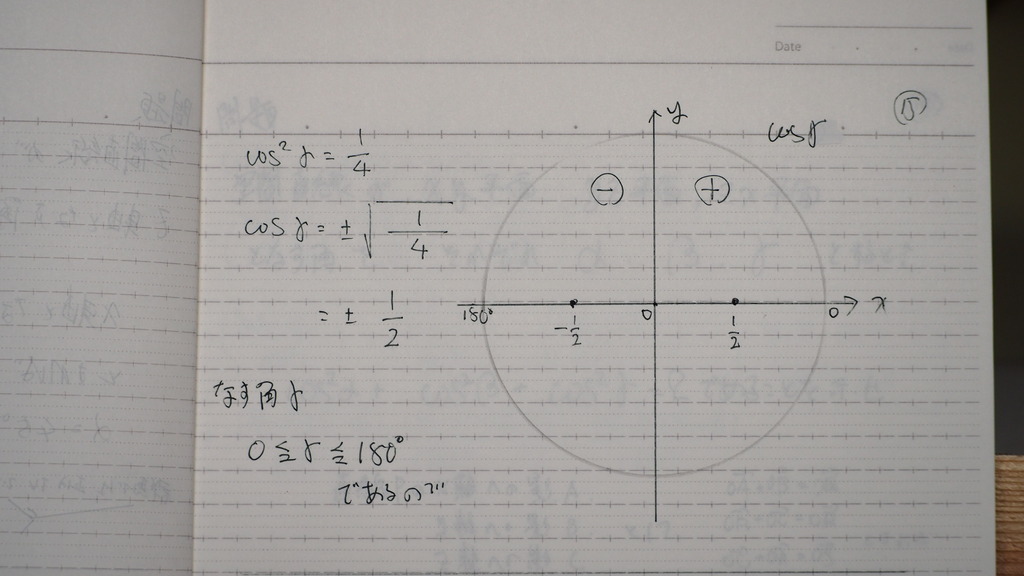
なす角は
0から180ど
その範囲で
プラスマイナスを
考えると
コサインなので
動径の x軸への影が
プラスマイナス 1/2
16
答は
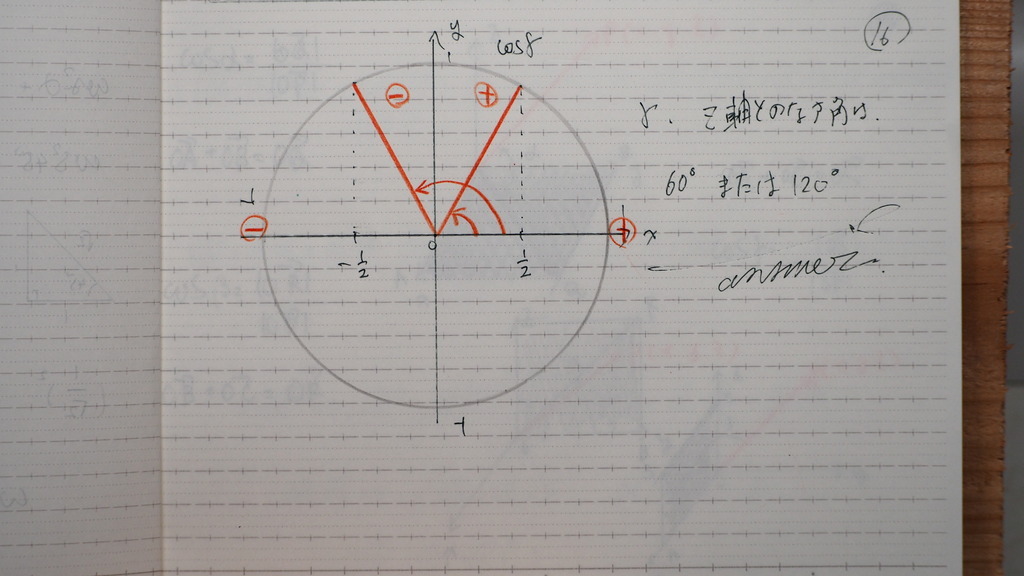
17
次は
ちょっと違うんですよ
直線が
平面と なす角
問題

18
xy yz zx
平面との
なす角であるから
こんな感じになるでよ
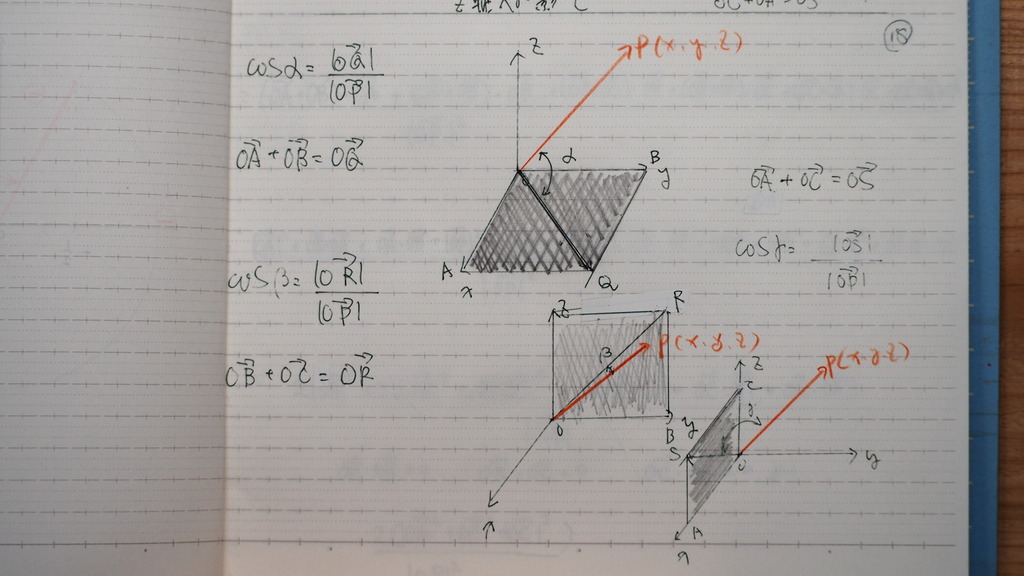
19
これを
計算してみると
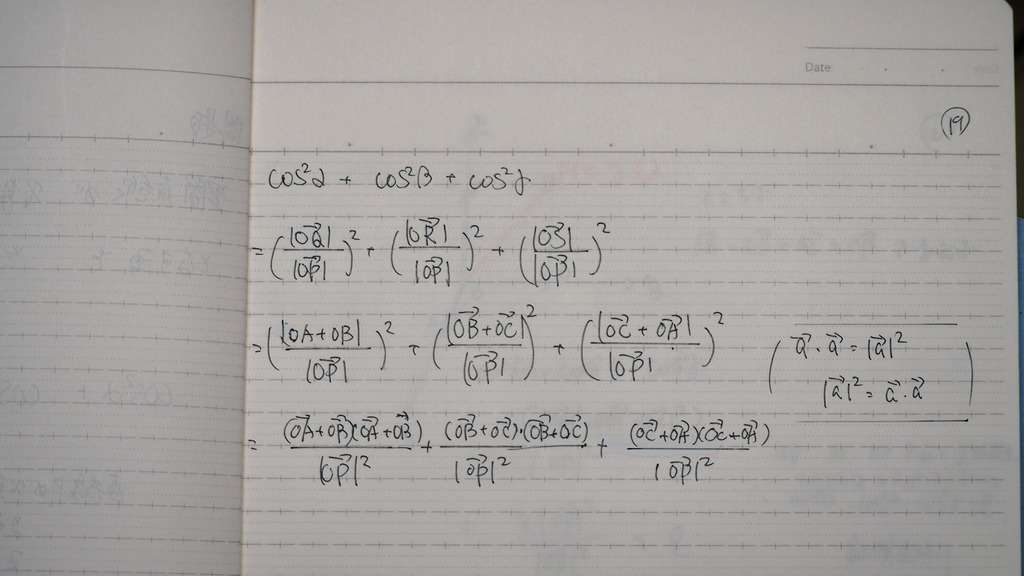
20
大丈夫かな
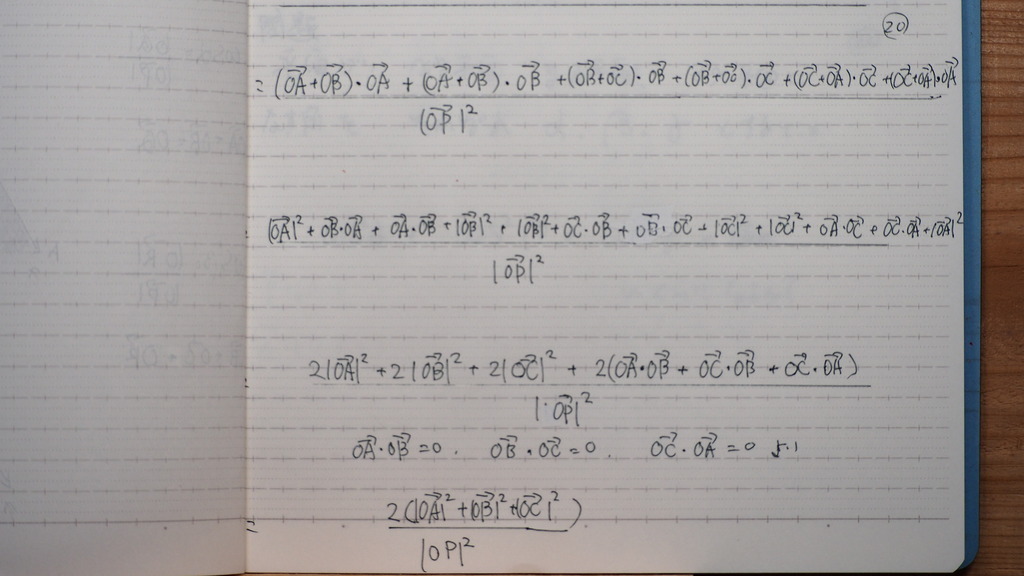
21
計算を
はぶいてますが
OA+OB+OC=OP
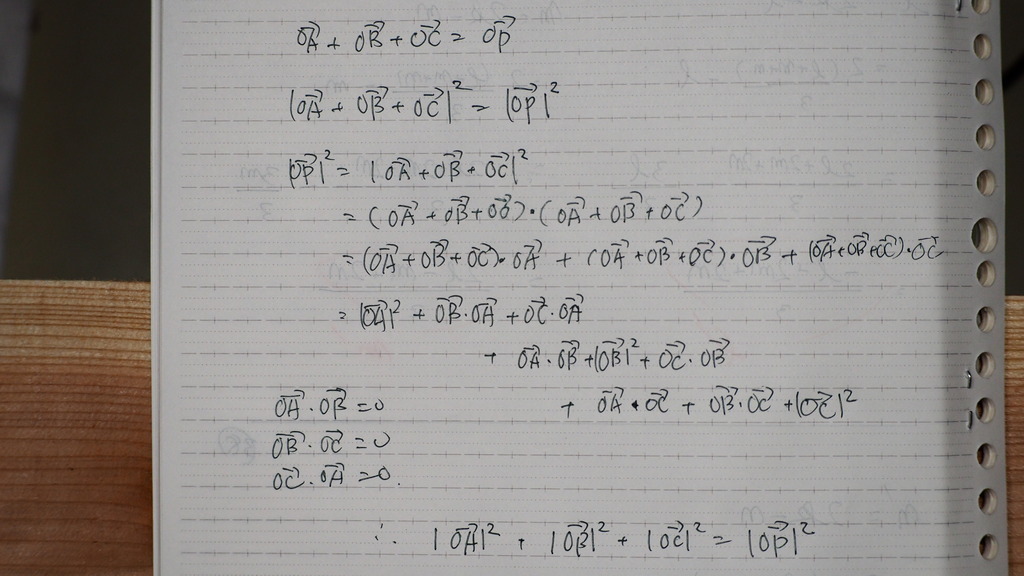
を
辺々 絶対値2乗すれば
直交座標系なので
OA OB OC の二乗以外の
項は =0 になってしまうので
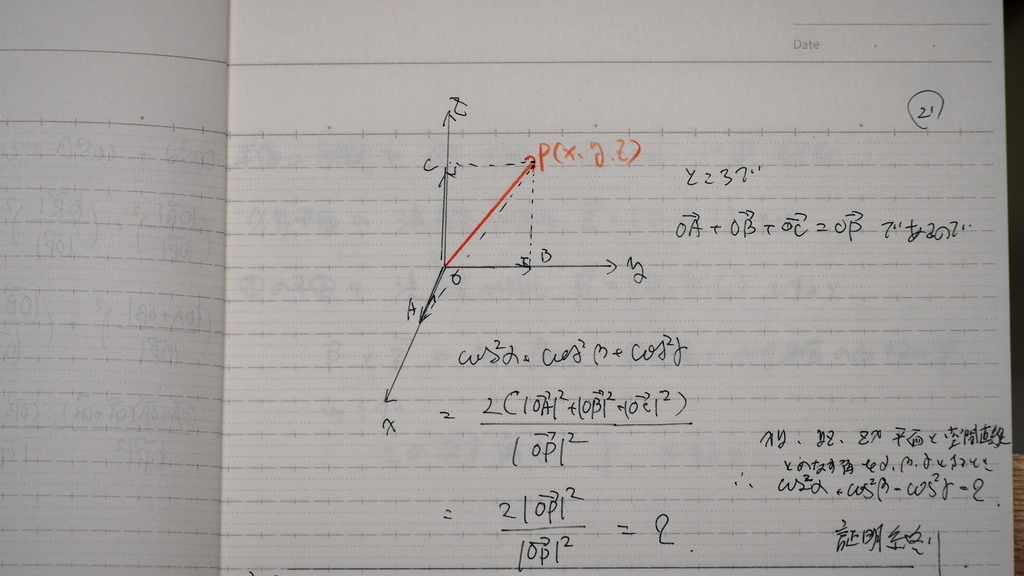
22
問題

23
平面の 方程式を ➀として
それぞれの 平面の法線ベクトル
と
平面の法線ベクトルで
なす角を 出してくると

24
xy平面は z方向が法線
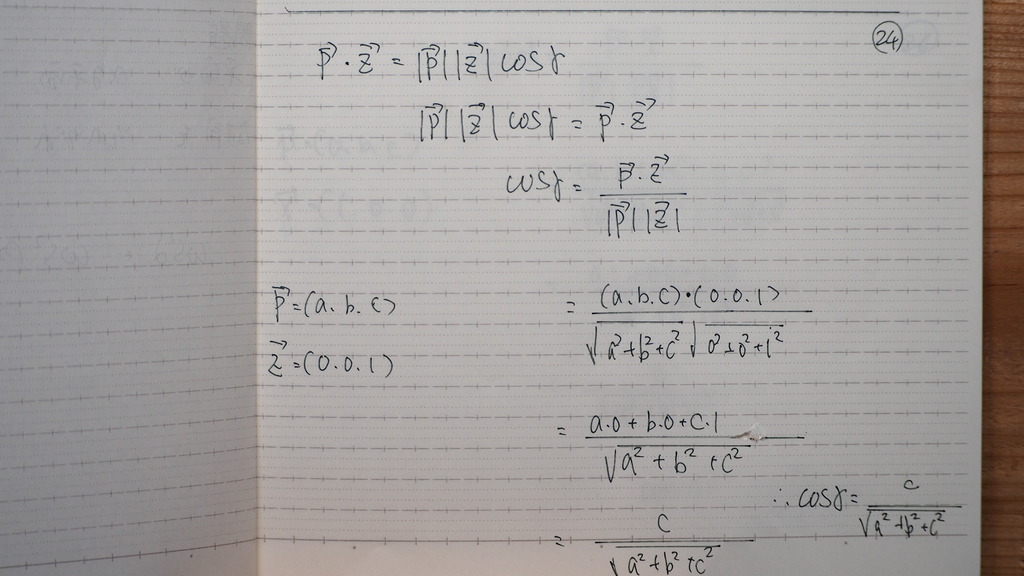
25
yz平面は x軸方向が 法線

26
こんな感じに
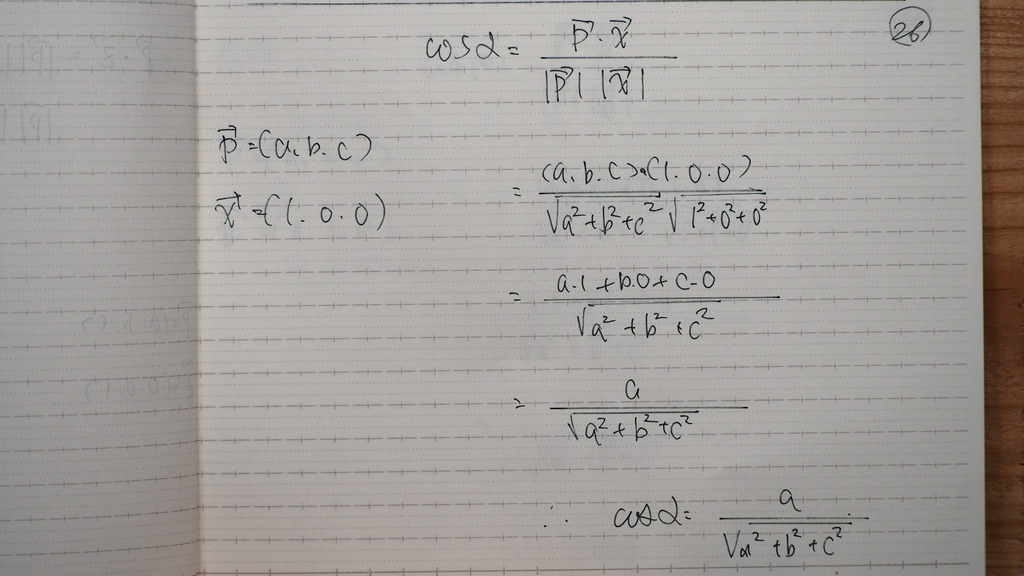
27
xz平面は y軸方向が 法線

28
出そろったので
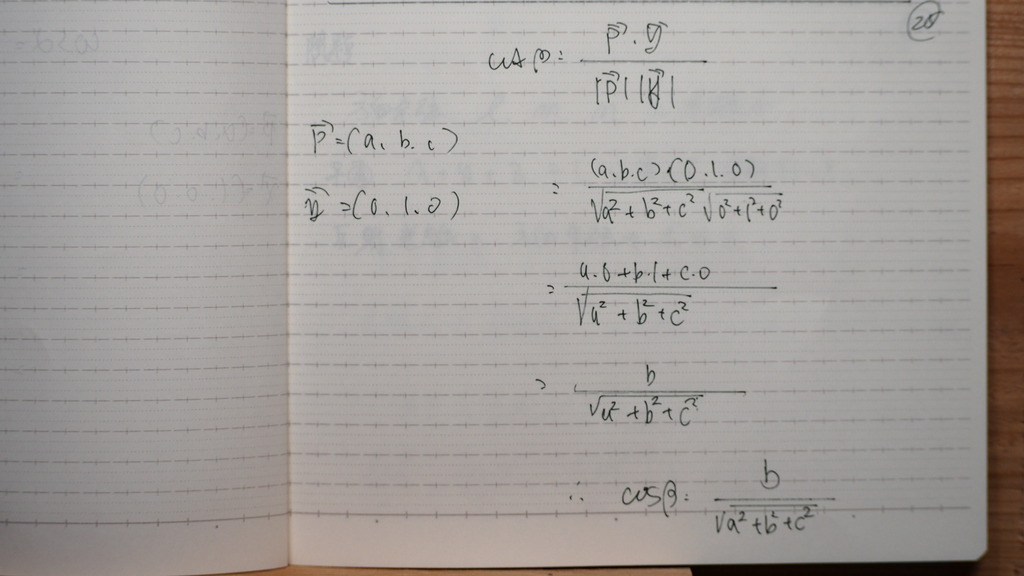
29
二乗して
計算してくと
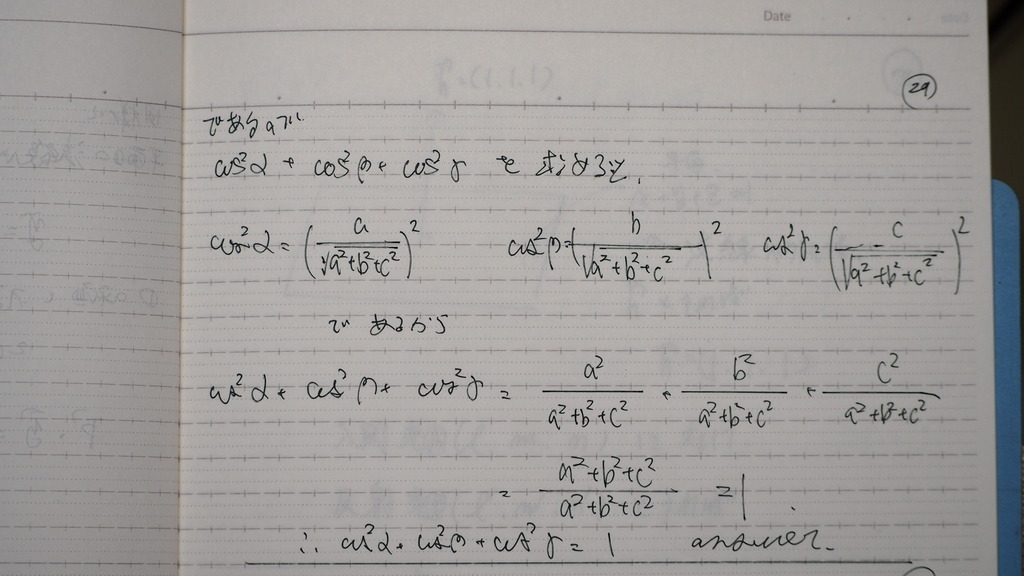
30
問題

31
こんな感じに
設定してですよ

32
入射光 反射光
対称になるから
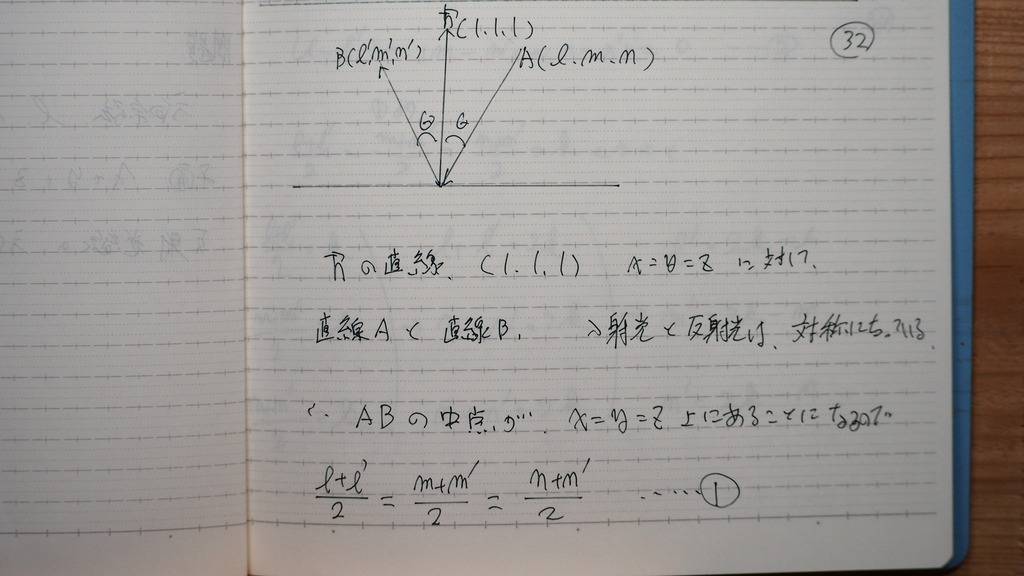
33
それと
AB と x=y=zは 垂直だから

34
中点が イコール を kと置いて
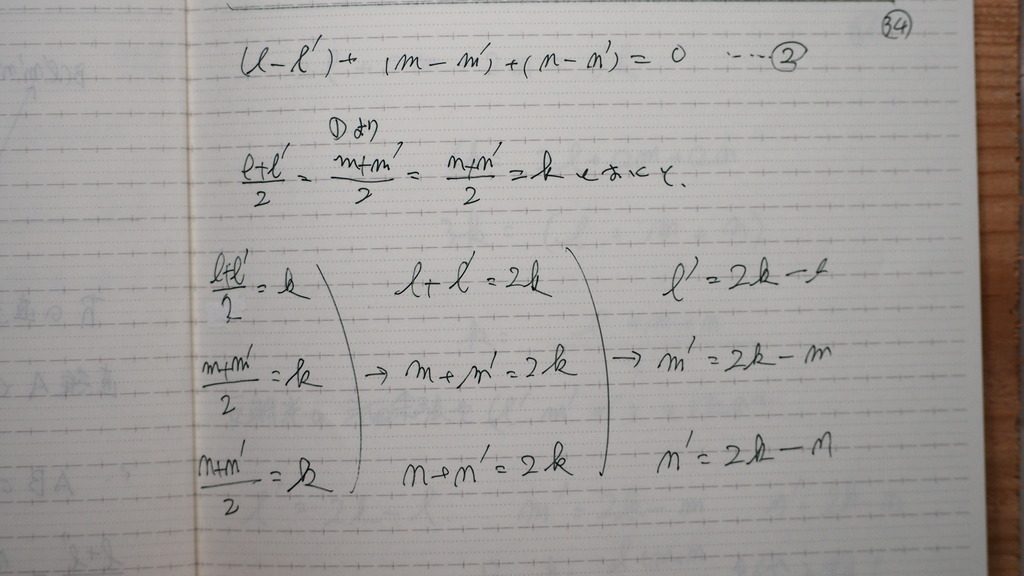
35
②式に 代入して
kを もとめて
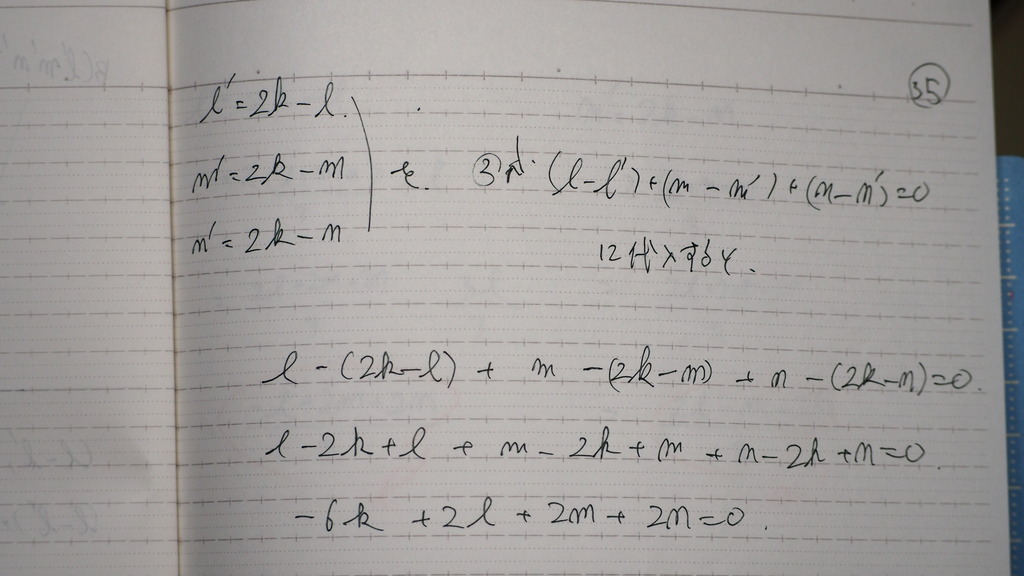
36
これで

37
反射光の 成分を
計算したらば
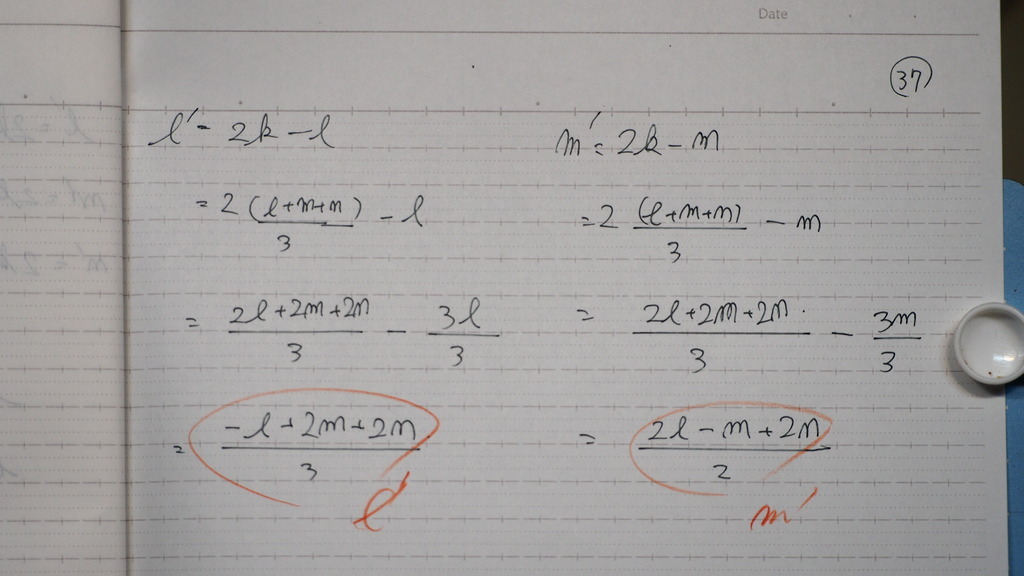
38
こんな感じ

空間座標 と ベクトル
より
方向余弦
01
空間直線が
x軸 y軸 z軸
と なす角を
ソレゾレ
α β γ とすれば
次の 等式が
成り立つことを 証明せよ
02
ベクトルは
平行移動していいので
原点まで
平行移動して
ソレゾレ
x軸 y軸 z軸
と なす角を
α β γ とすると
直線を P(x、y、z)
とする時
03
COSα
COSβ
COSγ
は
まず COSα から見てくと
OP 分の OA
04
COSβ
COSγ
も 同様にして
出そろった
COSα
COSβ
COSγ
を それぞれ 2乗して
足してみますと
05
なったじゃナイスカ
06
ベクトルの
内積を 使った場合は
A,B,Cを
(1,0,0)(0,1,0)(0,0,1)
として
内積から
なす角 の COSを 求めると
07
こんな感じに
08
なるじゃ
09
ナイスカ
10
であるから
ソレゾレ
2乗したものを
足すと
なったと
11
まとめ
12
こんな風にも
書けるてことカナ
13
問題
空間直線が
x軸と 45度
y軸と 60度
の角度を
なすとき
z軸との なす角は
どれくらいか
群馬県では
懐かしい アニメを
夜中に
放送してましが
バルキリーが 放つ
ミサイルの横に
タコ酎ハイ に バドワイザー
14
で 今日は
z軸のなす角だから
さっき証明した式を
使って
15
なす角は
0から180ど
その範囲で
プラスマイナスを
考えると
コサインなので
動径の x軸への影が
プラスマイナス 1/2
16
答は
17
次は
ちょっと違うんですよ
直線が
平面と なす角
問題
18
xy yz zx
平面との
なす角であるから
こんな感じになるでよ
19
これを
計算してみると
20
大丈夫かな
21
計算を
はぶいてますが
OA+OB+OC=OP
を
辺々 絶対値2乗すれば
直交座標系なので
OA OB OC の二乗以外の
項は =0 になってしまうので
22
問題
23
平面の 方程式を ➀として
それぞれの 平面の法線ベクトル
と
平面の法線ベクトルで
なす角を 出してくると
24
xy平面は z方向が法線
25
yz平面は x軸方向が 法線
26
こんな感じに
27
xz平面は y軸方向が 法線
28
出そろったので
29
二乗して
計算してくと
30
問題
31
こんな感じに
設定してですよ
32
入射光 反射光
対称になるから
33
それと
AB と x=y=zは 垂直だから
34
中点が イコール を kと置いて
35
②式に 代入して
kを もとめて
36
これで
37
反射光の 成分を
計算したらば
38
こんな感じ