2022年12月22日
22032大人のさび落とし 空間座標とベクトル 2平面のなす角
大人のさび落とし
空間座標とベクトル
2平面のなす角
A
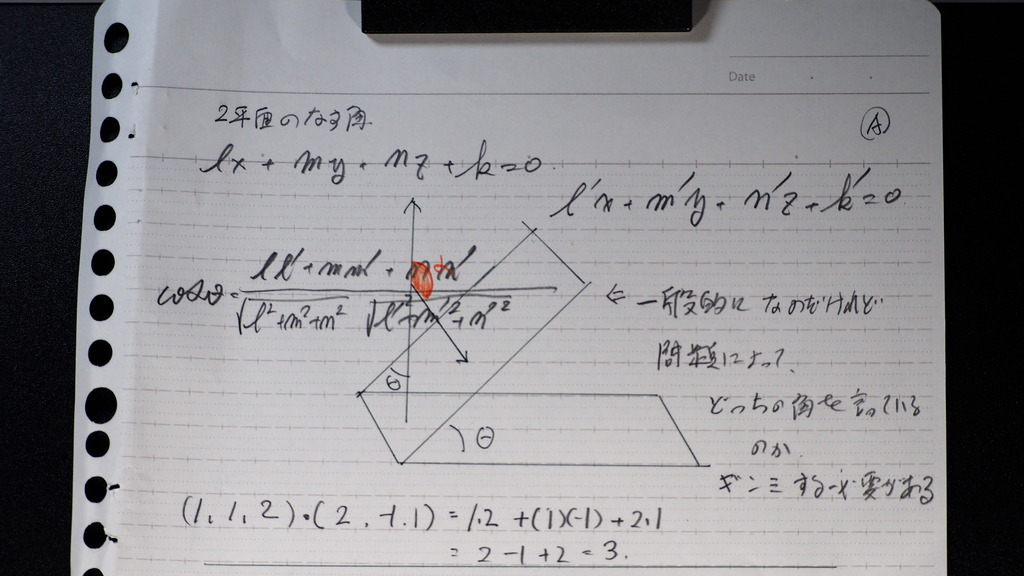
なす角の 計算は
平面同士の時は
法線ベクトル
の 内積で出るのだけれど
問題によって
どちらの 角度を
聞いているか
ぎんみ する必要がある
B
こちらの場合
隣接面の
側面の なす角
どっちかな
ッテ
吟味する必要がある
(机上の 数値計算の場合は)
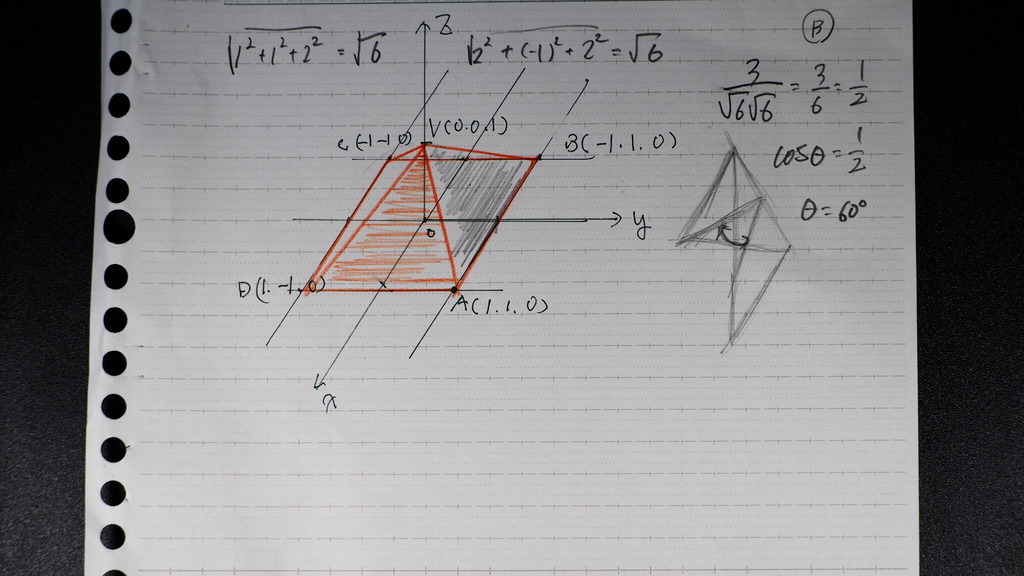
01
それらを
前置きしておいて
問題

02
xy 平面の
垂線ベクトルは
0,0,1
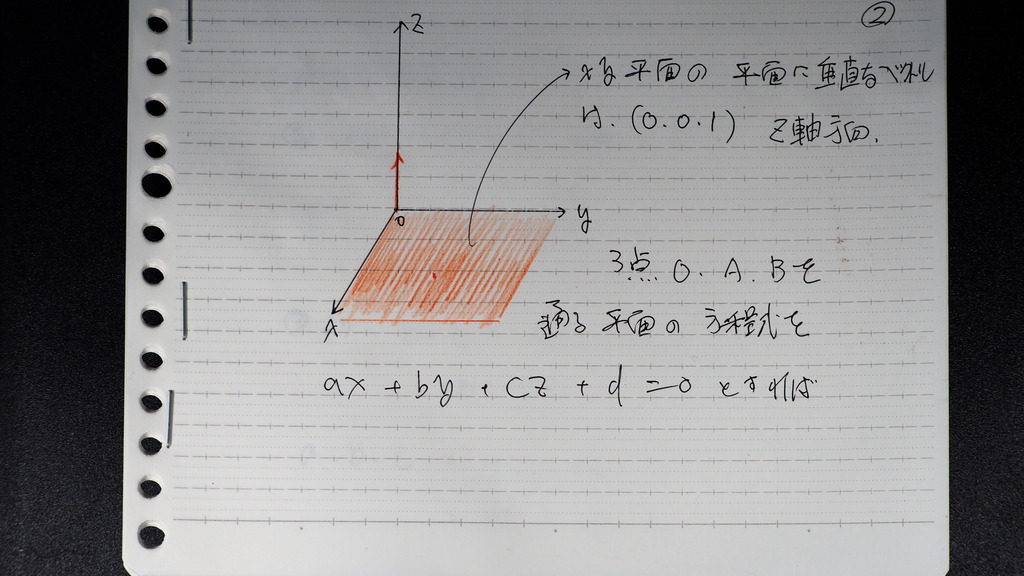
03
もう一つの 面は
計算しないと
わからないので
3点から
平面の式に
代入して
( 3点が わかるときは
ベクトルでも 出ますが )

04
全部 c で 表して
へてから -1、-1,1
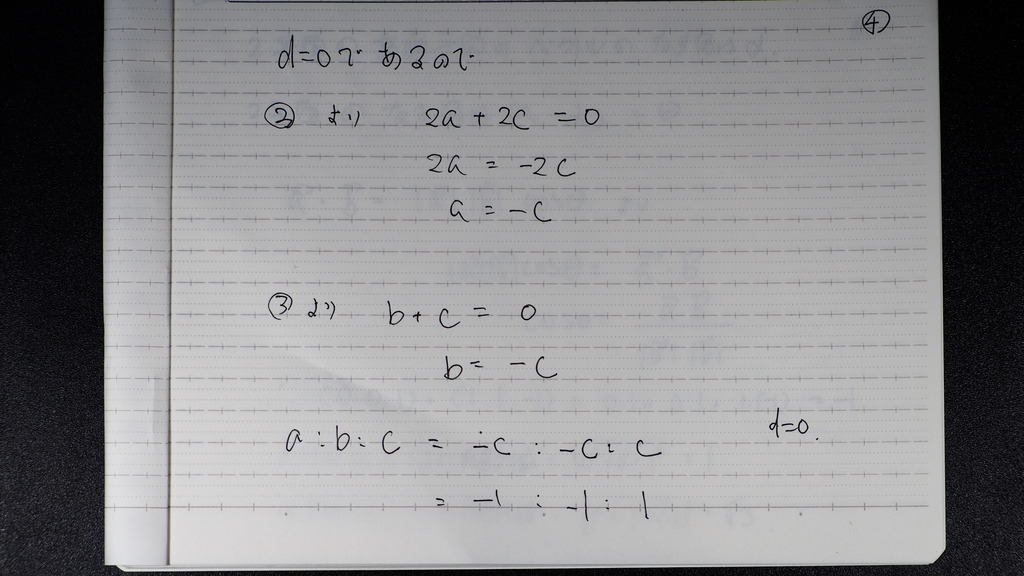
05
平面の式にして
符号を 整えて
1、1、-1
-1、-1,1 でもOK ですが
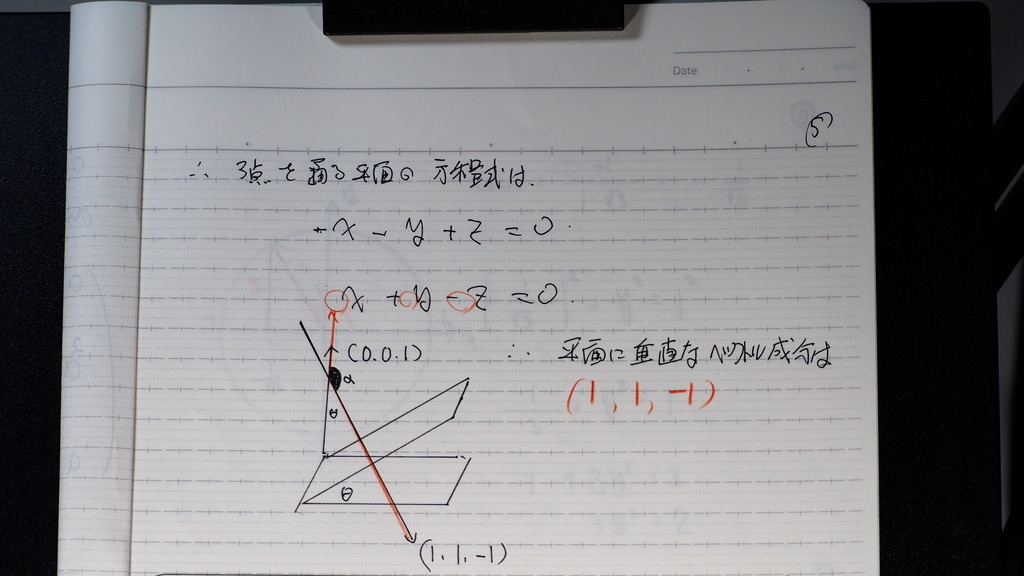
06
そうすれば
内積の計算から
コサインで
求めて

07
y を 求めると
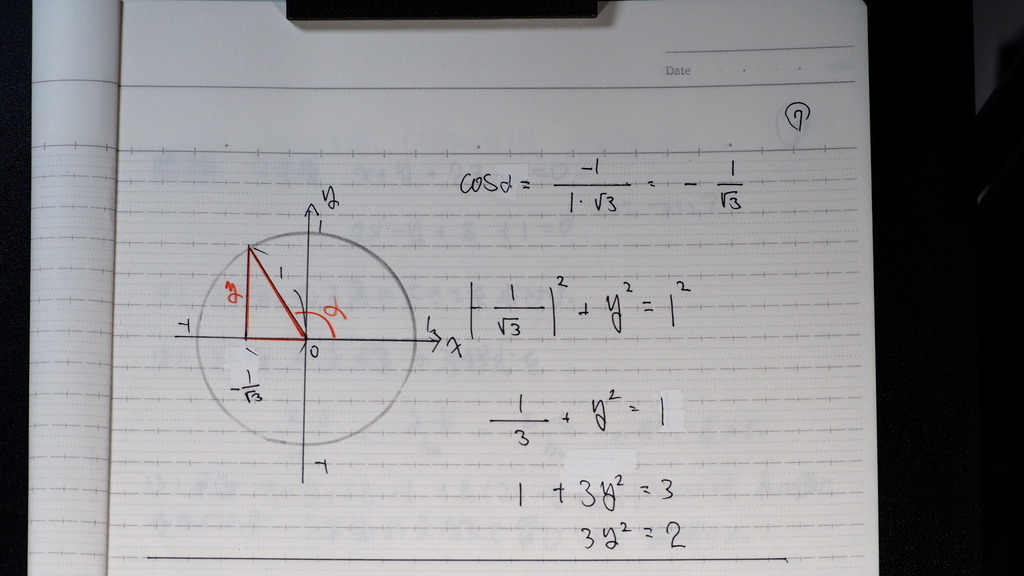
08
タンジェント αは -√2
図でいうところの
Θ が 今回 なす角 Θなので
補角を 使って
TanΘ は √2

09
今度は
そのまま 計算できるパターン
(1)なす角は
(2)2平面の 交線は
(3)この等式を 証明して
( 2平面の交線を 含む 平面の
方程式 )重要
(4)
を 落としてますが
原点と この2平面の 交線を
含む 平面の方程式を
求めよ
(3)の結果を 使うと早い

10
両平面の方程式から
垂線のベクトルを
内積で
計算して
なす角を 出すと

11
こんな感じに
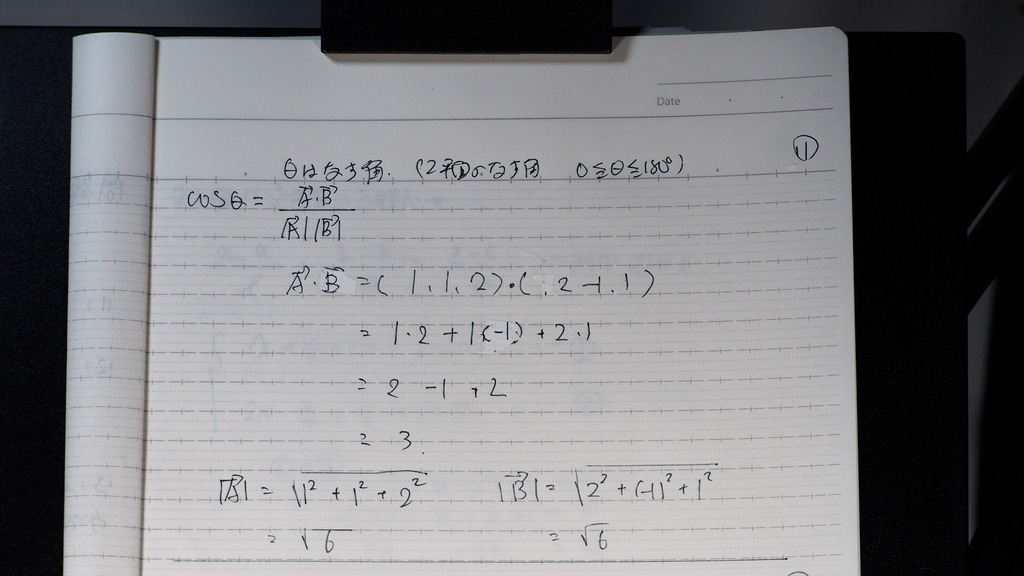
12
そのまま
60度
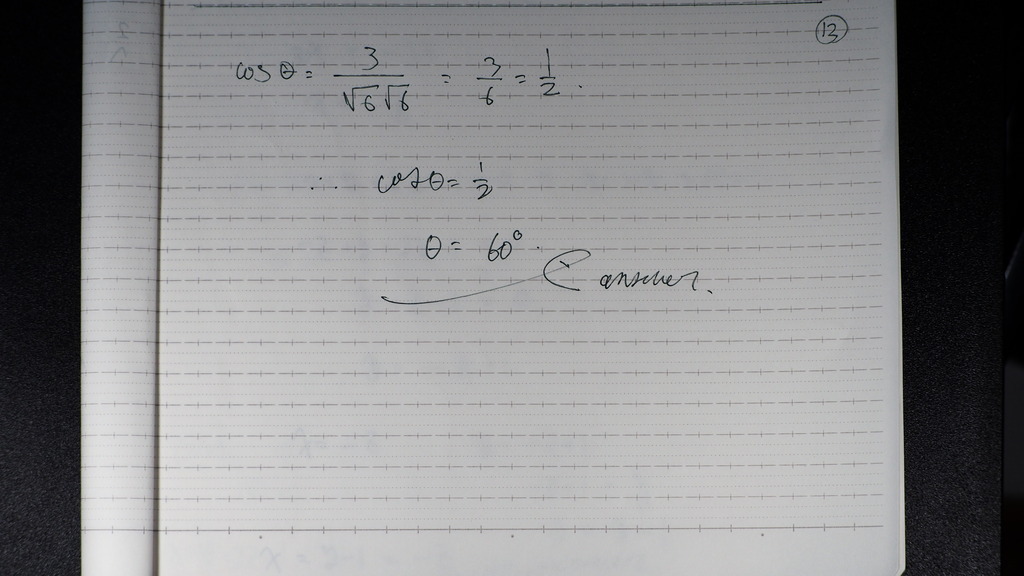
13
2平面の
交線は
そのまま 平面を
連立して解いて
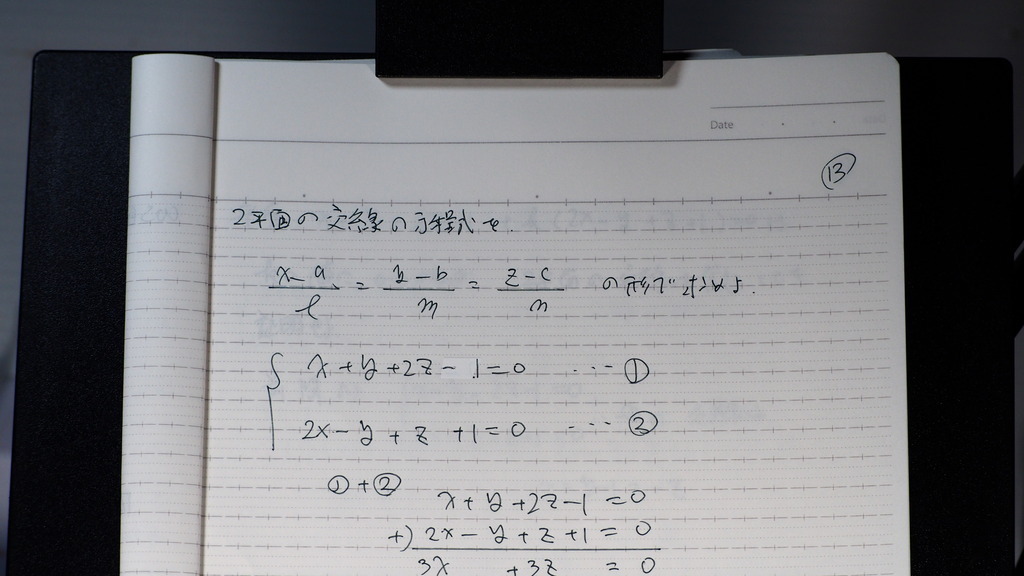
14
x=y-1=-z

15
この式を
証明して
まず
さっきの 2平面の連立
➀
これらの 二つの式は
すでに 成り立っている
しかも =0

16
0 + k(0) = 0
常に 成り立つデショ

17
今証明した
方程式を 使って
交線が 含まれているわけなんだから
さらに
指定された 点を 通るときの
kを 求めて
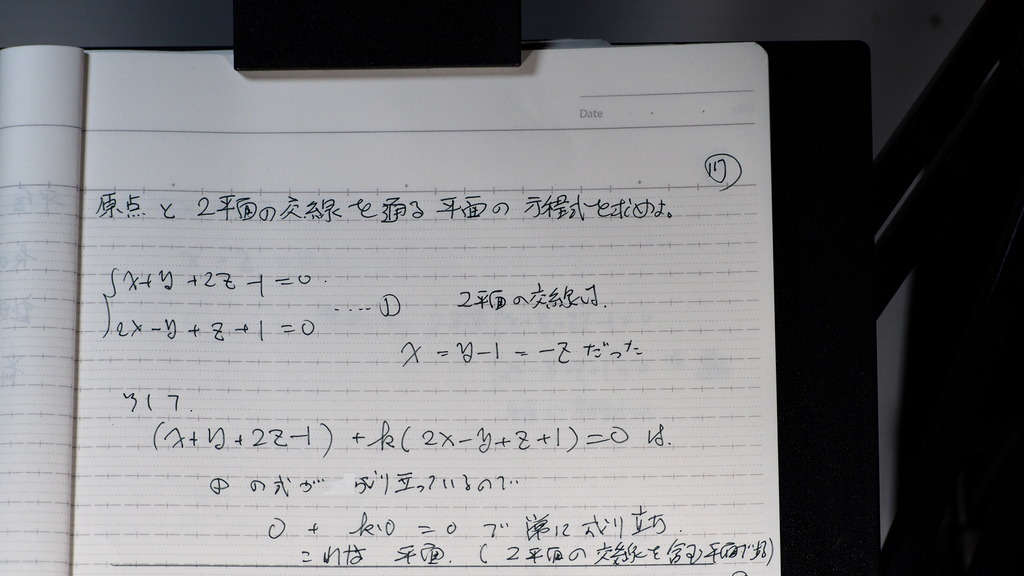
18
k=1
を 交線を 含む
平面の方程式の k に代入すれば
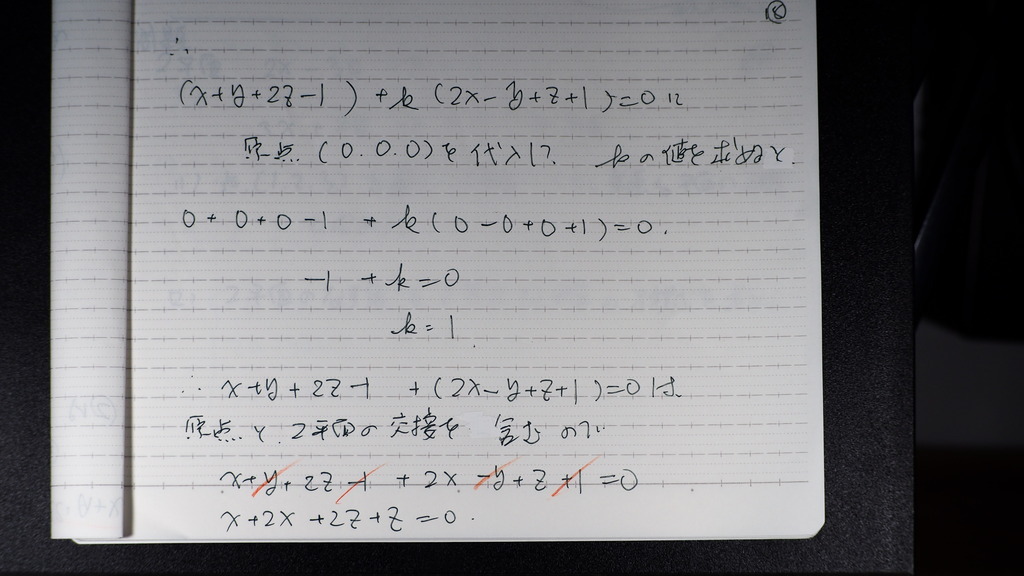
19
こんな感じに

20
問題

21
平面の 方程式を
ax + by + cz =d
と置いて
(1,2,3) を
代入
平面の方程式の 垂直成分
(a,b,c) と

22
それぞれの 平面の
垂直成分
(2、-3、4)
(3、 2、1)
の 内積が =0 を使って

23
計算してきますと
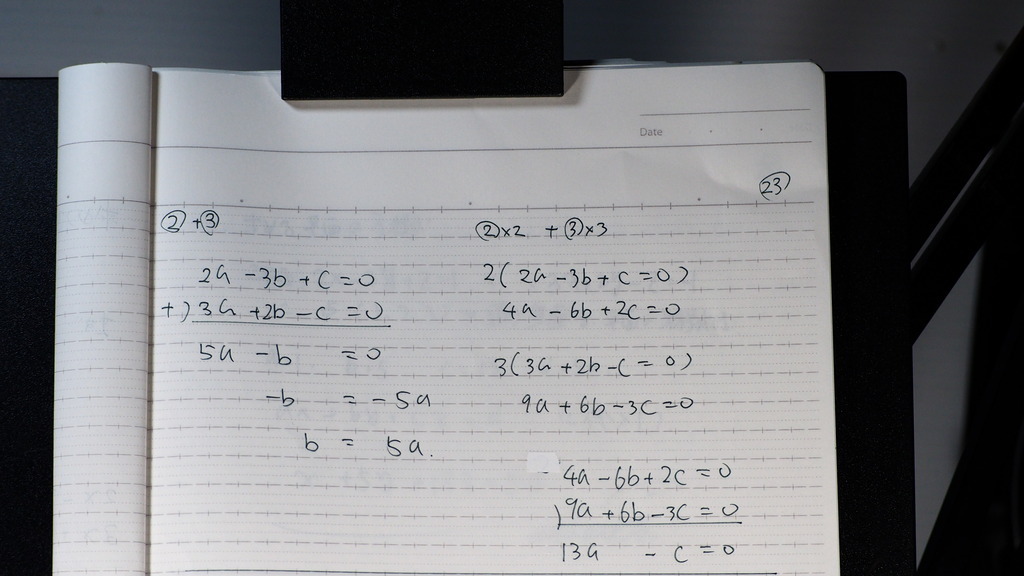
24
平面の方程式は
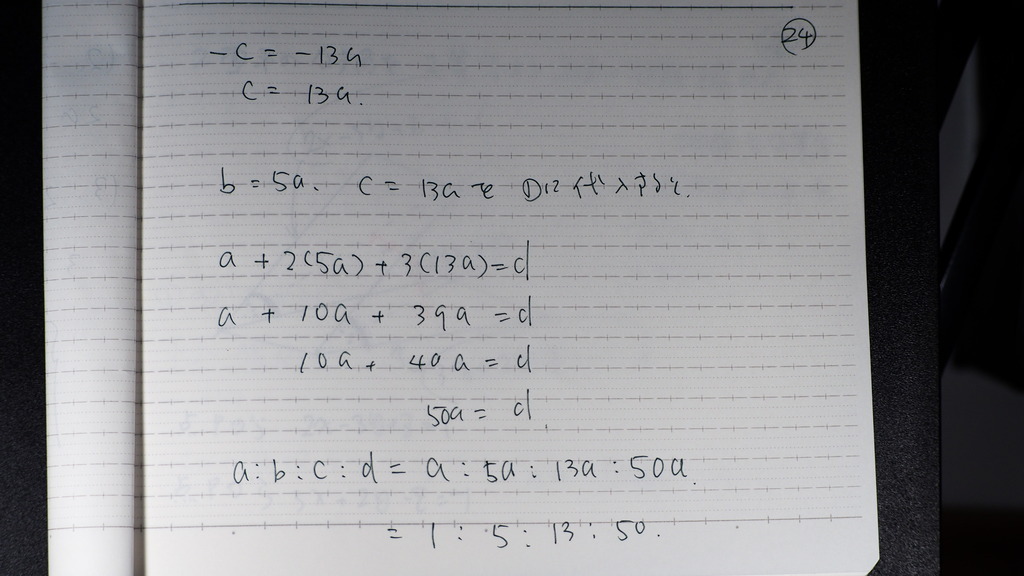
25
こんな感じで

26
2面の なす角を
2等分する
平面の 方程式は
なす角を
2等分する
平面上の 点をP (x、y、z)
とすれば
点と 平面との距離が
等しくなるよを
式で 表して

27
こんなかんじに 一つ目
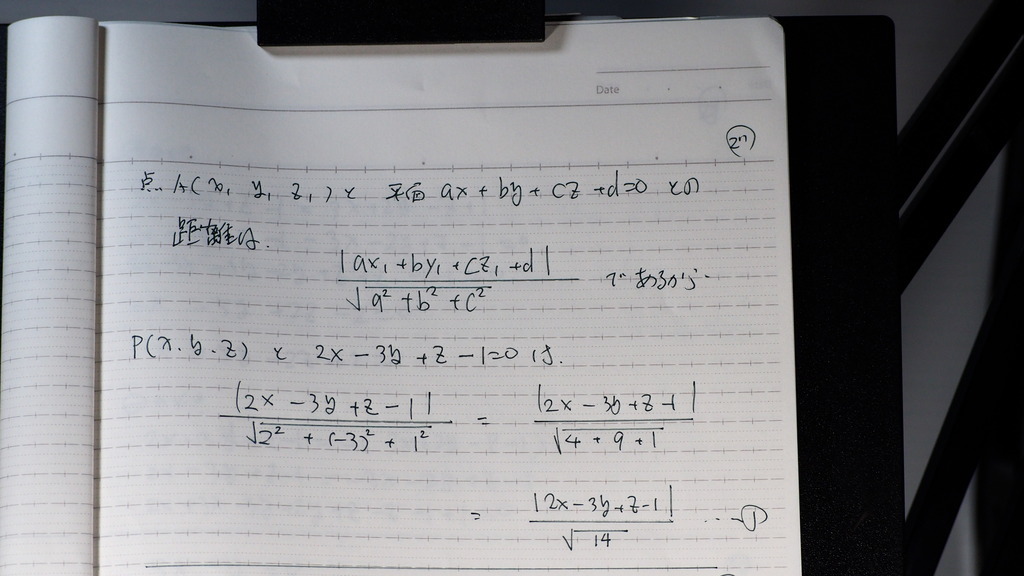
28
もう一方も
それを =で結んで
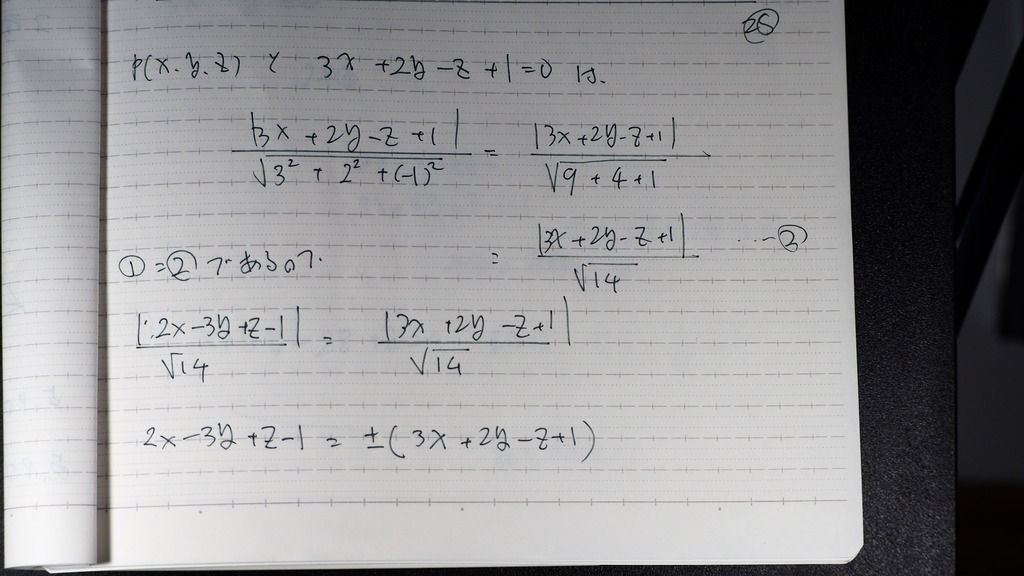
29
プラスの時
マイナスの時

30
であるので
こんな感じで

31
問題
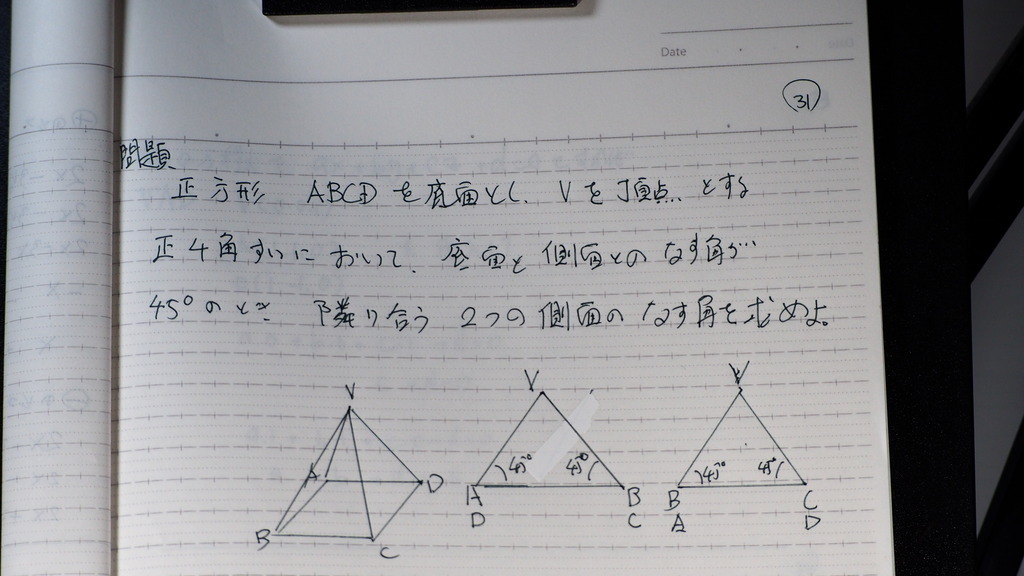
32
座標を 使ってみましょう
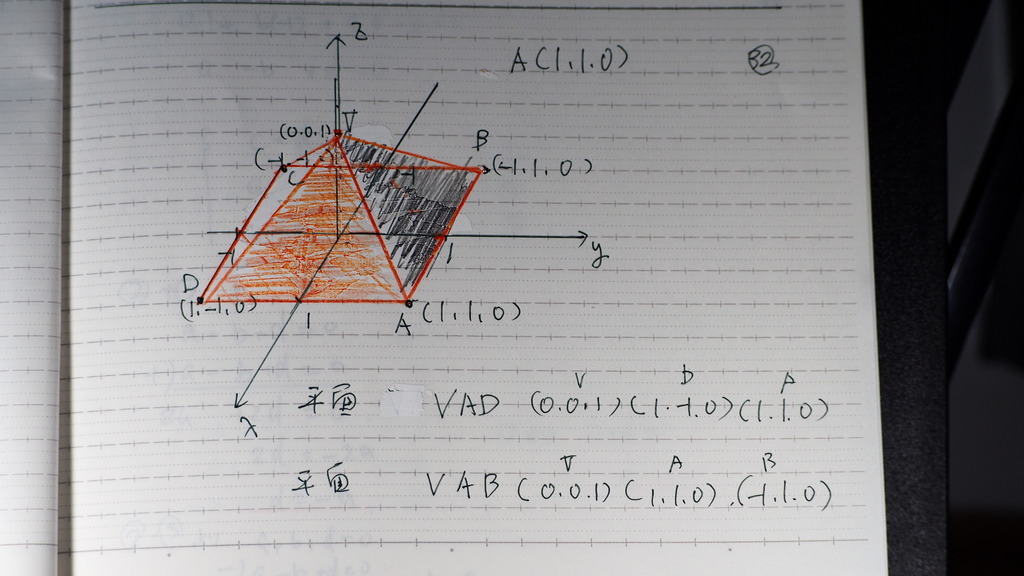
33
3点が わかれば
平面の 方程式が出るから
まず 平面VAD

34
計算ちゅうです

35
平面VADは x+z=1
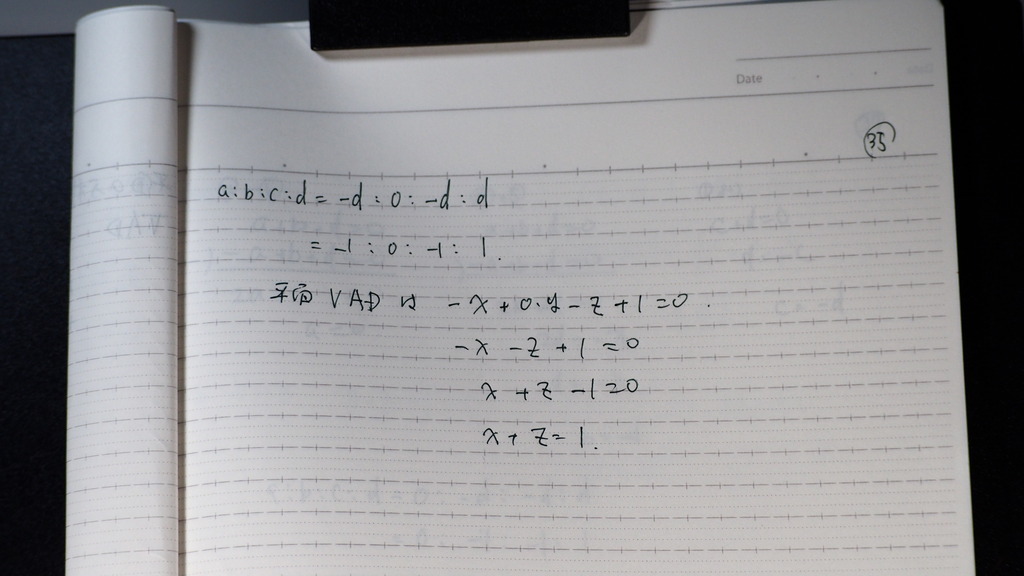
36
平面VABは

37
計算ちゅうです
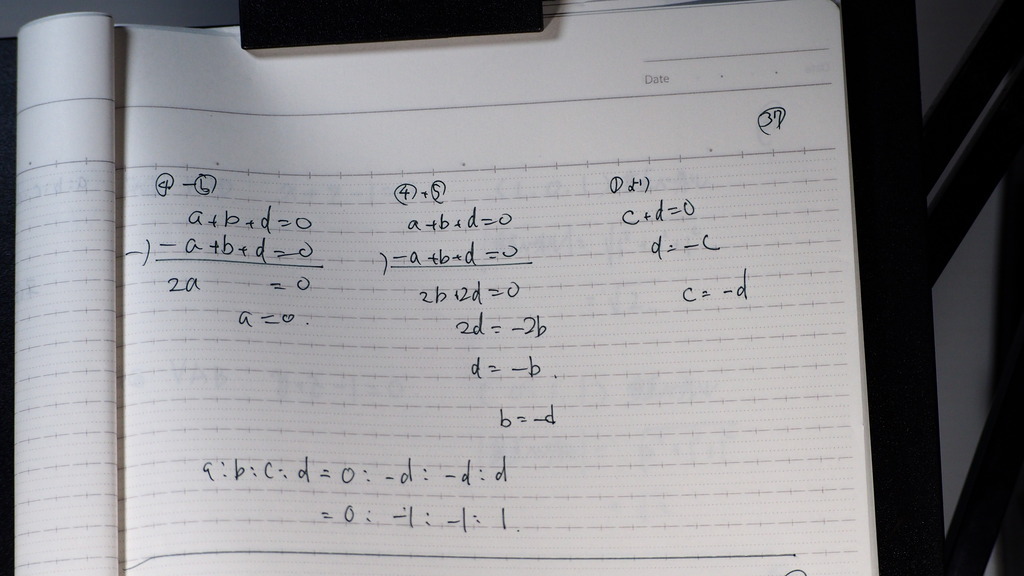
38
平面VABは y+z=1

39
で
なす角を 計算するんですが

40
側面のなす角は
120度
答は これです

考えてみましょう
お疲れ様です
空間座標とベクトル
2平面のなす角
A
なす角の 計算は
平面同士の時は
法線ベクトル
の 内積で出るのだけれど
問題によって
どちらの 角度を
聞いているか
ぎんみ する必要がある
B
こちらの場合
隣接面の
側面の なす角
どっちかな
ッテ
吟味する必要がある
(机上の 数値計算の場合は)
01
それらを
前置きしておいて
問題
02
xy 平面の
垂線ベクトルは
0,0,1
03
もう一つの 面は
計算しないと
わからないので
3点から
平面の式に
代入して
( 3点が わかるときは
ベクトルでも 出ますが )
04
全部 c で 表して
へてから -1、-1,1
05
平面の式にして
符号を 整えて
1、1、-1
-1、-1,1 でもOK ですが
06
そうすれば
内積の計算から
コサインで
求めて
07
y を 求めると
08
タンジェント αは -√2
図でいうところの
Θ が 今回 なす角 Θなので
補角を 使って
TanΘ は √2
09
今度は
そのまま 計算できるパターン
(1)なす角は
(2)2平面の 交線は
(3)この等式を 証明して
( 2平面の交線を 含む 平面の
方程式 )重要
(4)
を 落としてますが
原点と この2平面の 交線を
含む 平面の方程式を
求めよ
(3)の結果を 使うと早い
10
両平面の方程式から
垂線のベクトルを
内積で
計算して
なす角を 出すと
11
こんな感じに
12
そのまま
60度
13
2平面の
交線は
そのまま 平面を
連立して解いて
14
x=y-1=-z
15
この式を
証明して
まず
さっきの 2平面の連立
➀
これらの 二つの式は
すでに 成り立っている
しかも =0
16
0 + k(0) = 0
常に 成り立つデショ
17
今証明した
方程式を 使って
交線が 含まれているわけなんだから
さらに
指定された 点を 通るときの
kを 求めて
18
k=1
を 交線を 含む
平面の方程式の k に代入すれば
19
こんな感じに
20
問題
21
平面の 方程式を
ax + by + cz =d
と置いて
(1,2,3) を
代入
平面の方程式の 垂直成分
(a,b,c) と
22
それぞれの 平面の
垂直成分
(2、-3、4)
(3、 2、1)
の 内積が =0 を使って
23
計算してきますと
24
平面の方程式は
25
こんな感じで
26
2面の なす角を
2等分する
平面の 方程式は
なす角を
2等分する
平面上の 点をP (x、y、z)
とすれば
点と 平面との距離が
等しくなるよを
式で 表して
27
こんなかんじに 一つ目
28
もう一方も
それを =で結んで
29
プラスの時
マイナスの時
30
であるので
こんな感じで
31
問題
32
座標を 使ってみましょう
33
3点が わかれば
平面の 方程式が出るから
まず 平面VAD
34
計算ちゅうです
35
平面VADは x+z=1
36
平面VABは
37
計算ちゅうです
38
平面VABは y+z=1
39
で
なす角を 計算するんですが
40
側面のなす角は
120度
答は これです
考えてみましょう
お疲れ様です