2022年12月18日
22031 大人のさび落とし 空間座標とベクトル 直線と平面 ( 前置き 直線 平面 球)
大人のさび落とし
空間座標とベクトル
の 方程式
01
まず ざっと 方程式とか
理論とか
2直線の
平行

02
2直線の 垂直

03
2平面の 平行
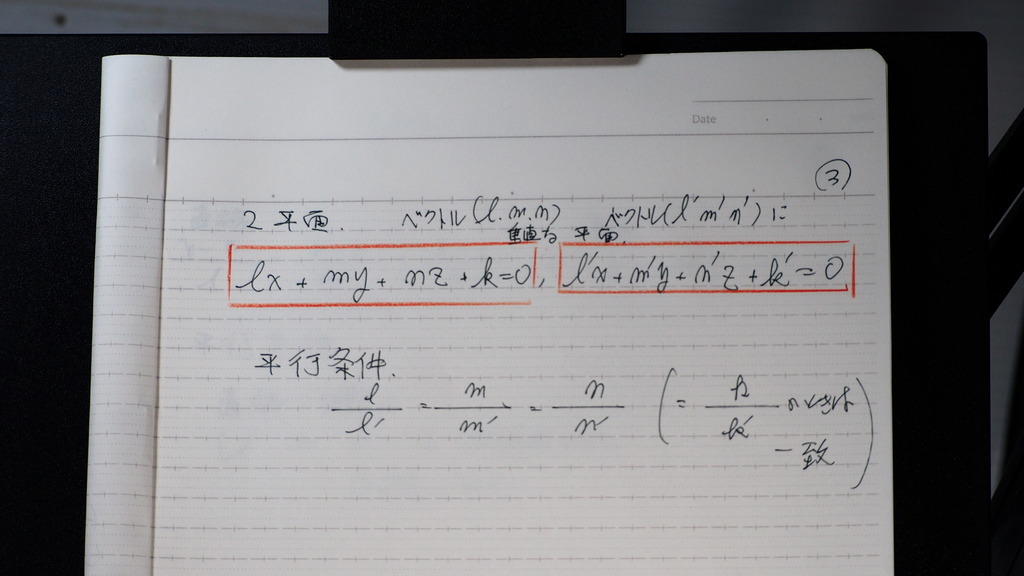
04
2平面の垂直

05
直線と 平面が 平行
直線の方向係数は
直線に平行

06
平面の方程式は
係数が 平面に垂直
であるので
内積が =0になる
逆に
直線が 平面に
垂直な時は
直線と 直線の 平行の時
のようになる

07
2平面のなす角
ここは 徐行して
確認してみてください
成ってるでしょ

08
であるから
2平面の垂直成分から
COSΘは こんな感じに

09
点と平面の距離は
こんな公式になるです

10
球の 方程式

11
A,Bが 直径の 両端に
あるときは

12
球面上の 接線の方程式は

13
以上踏まえまして
ここからは
問題を
今日は 平面と直線
空間の 点から
平面に おろした
垂線の長さ
つまり
点と平面の 距離
平面に 垂直な ベクトル
(a,b,c)
点Aを 通り
平面に 垂直な 直線と
平面の交点を
B とすれば

14
Bの 座標が分かっていれば
ABベクトルの 絶対値で
点A と 平面との
距離が出る

15
であるから
Bの座標を 求めたい
平面の 垂直成分が
そのまま
点Aを 通り
平面に 垂直な 直線の
方向係数ベクトル
であるので
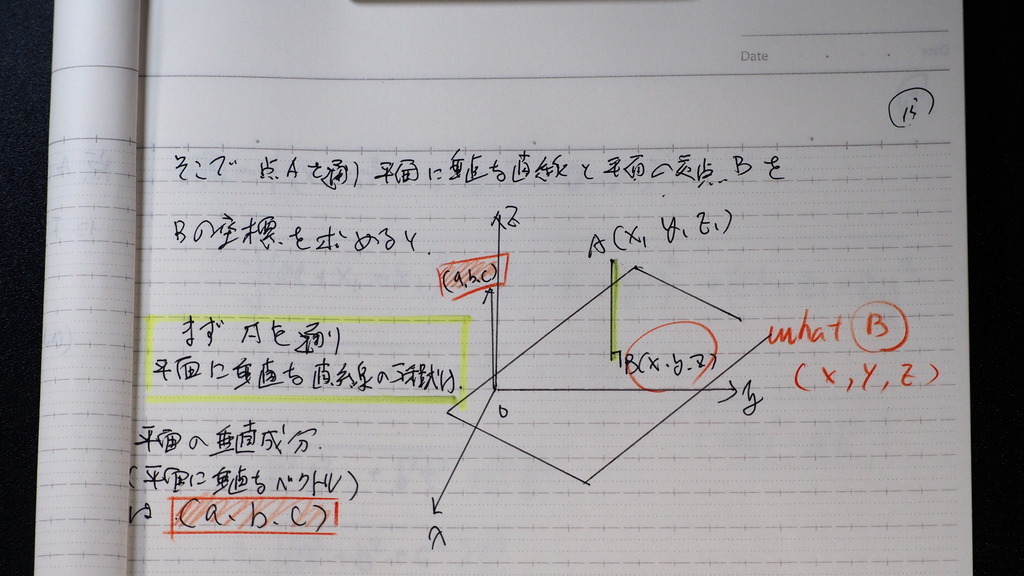
16
直線の 方程式は
こんな感じ
これに =t と置いて
媒介変数形にするでしょ
だから
Bの x、y、z に
これを 代入すればさ

17
これが
点Aを 通り
平面に 垂直な 直線
と
平面との
距離なんだけど
ここで
tが分かればいいのだから
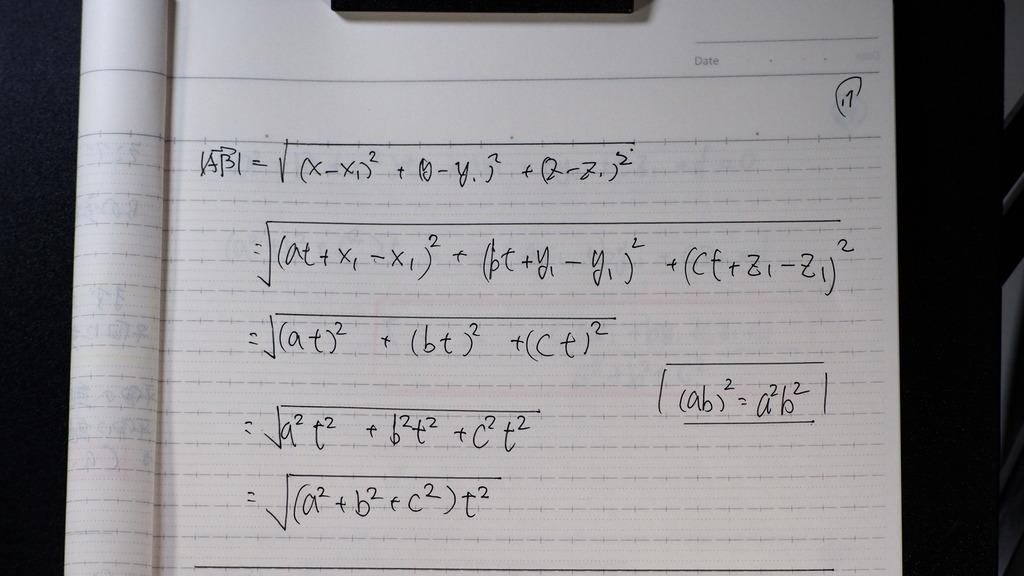
18
今度は
t を
求めるでしょ
X= Y= Z= の
媒介変数を
これは
直線上の点を
表してるので
平面の方程式に
代入すれば
共通なところ
交点になるので

19
すると
tは
こんなだから
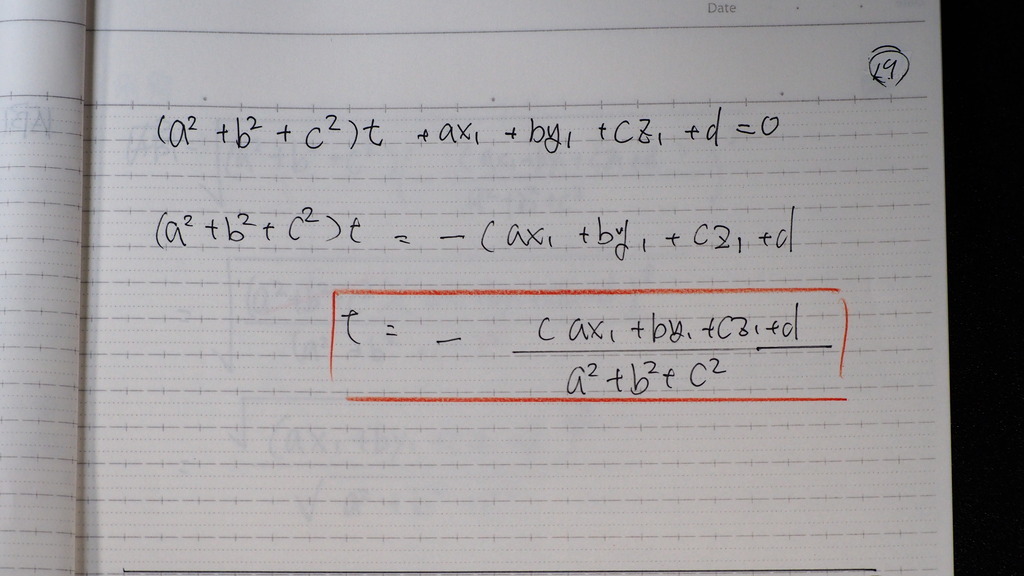
20
これを
さっきのに
代入したらば
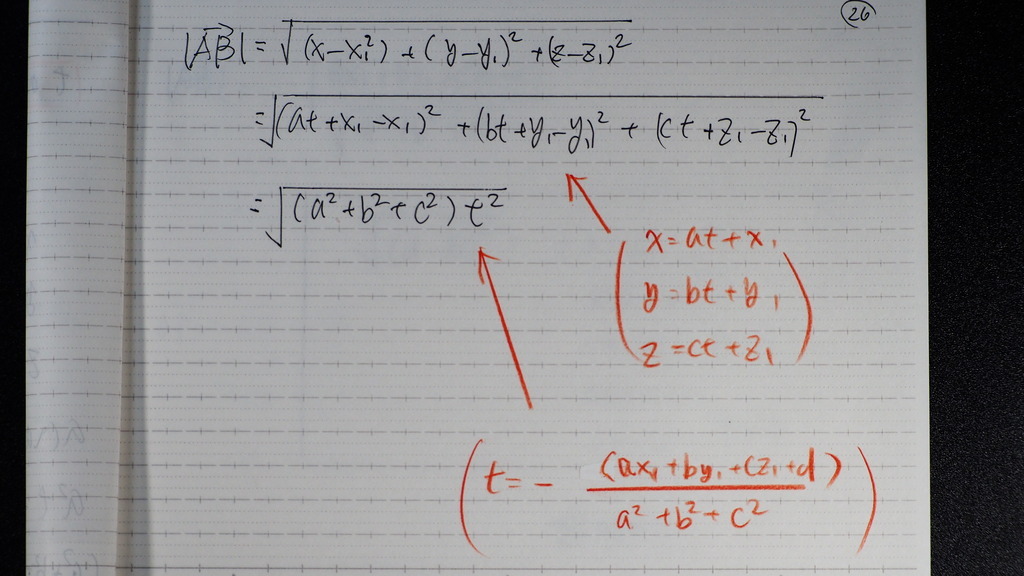
21
こんな感じで
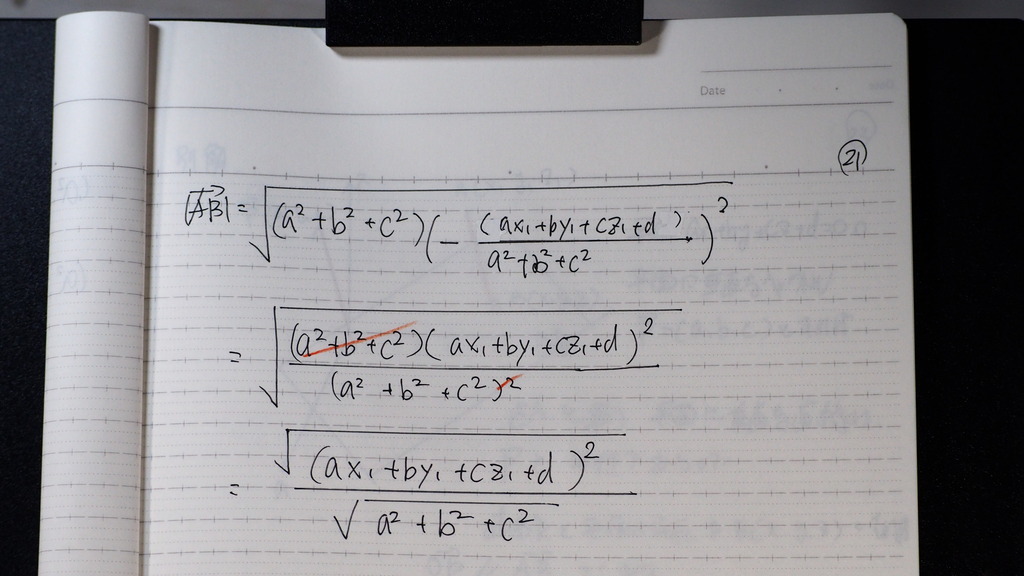
22
√を
外せば

23
別解は
平面の 垂直成分と
直線ABの方向係数が
等しいので
平行を使って
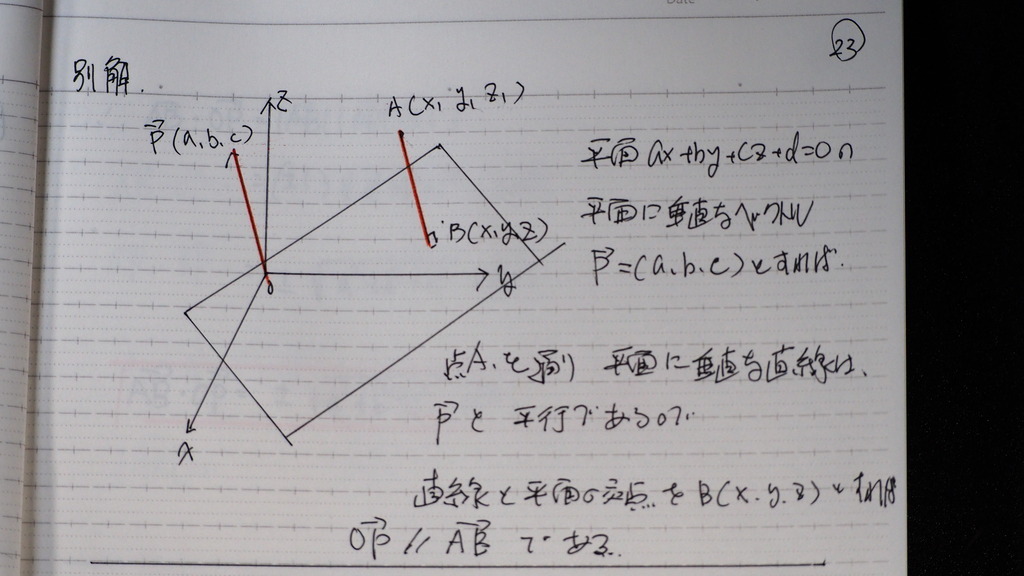
24
ABベクトル
OPベクトル
コサイン
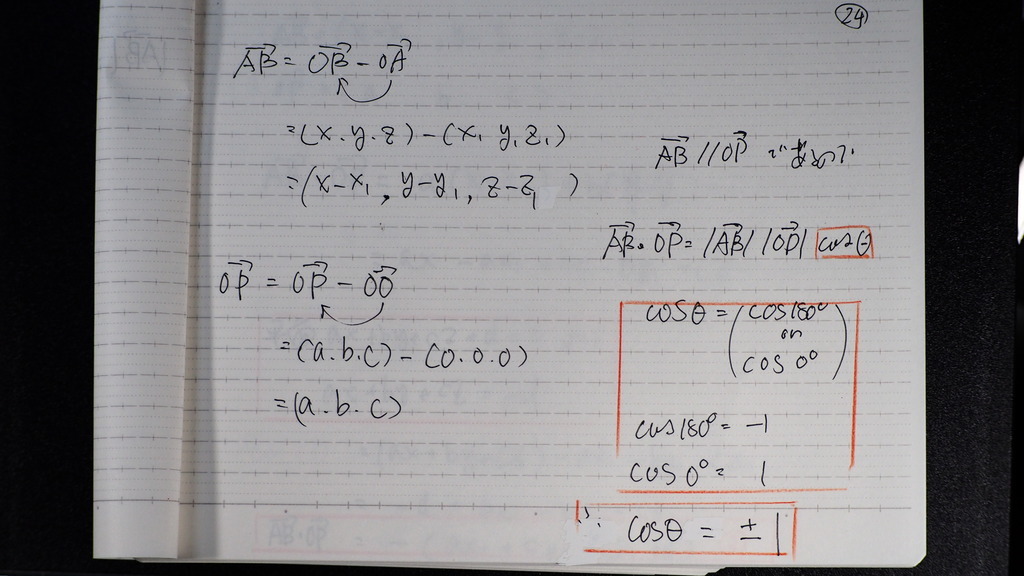
25
まず 矢線ベクトルから
➀

26
成分の内積から
②
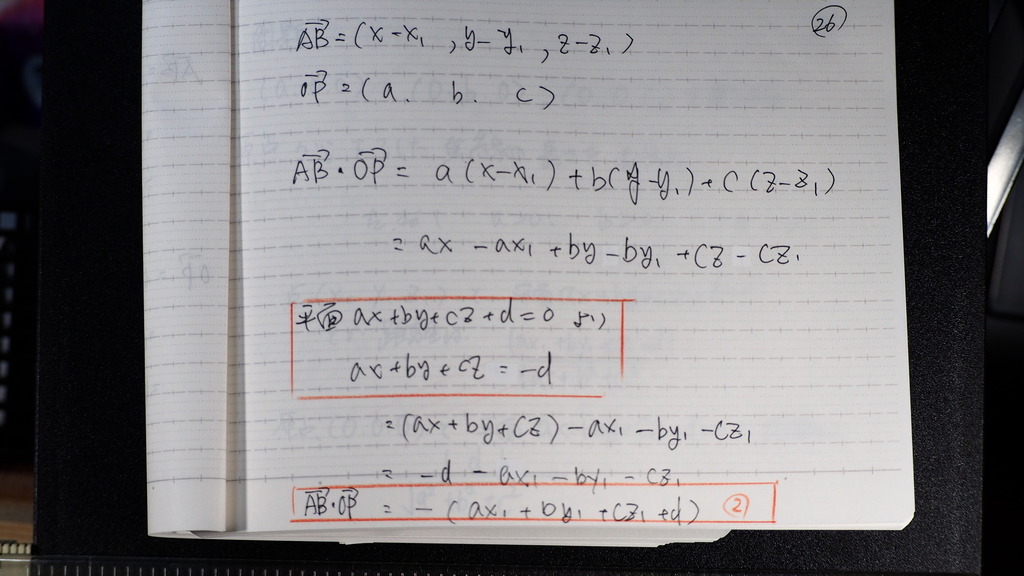
27
絶対値は
ゼロ以上だから

28
三点を 通る平面に
原点から
下した 垂線の長さ
原点と平面の距離だね

29
3点が
同一平面上にあれば
この式を
使って

30
平面の媒介変数形方程式
を 作っていくと

31
平面上の 全ての
ベクトルは
異なった 二つの
ベクトルの
和の形になる
じゃナイスカ
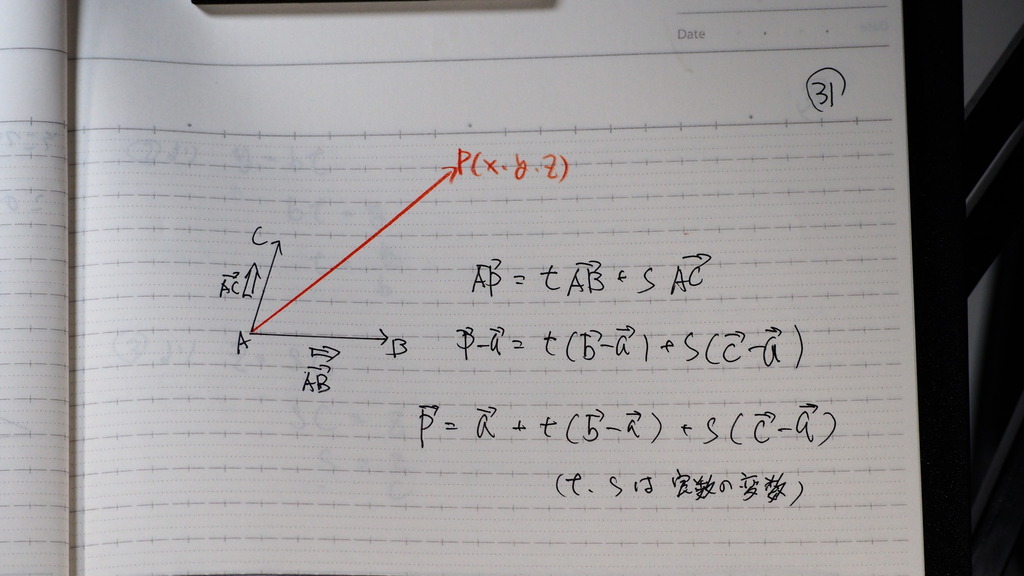
32
列で 書いた方が
分かりやすい
これを
連立に して
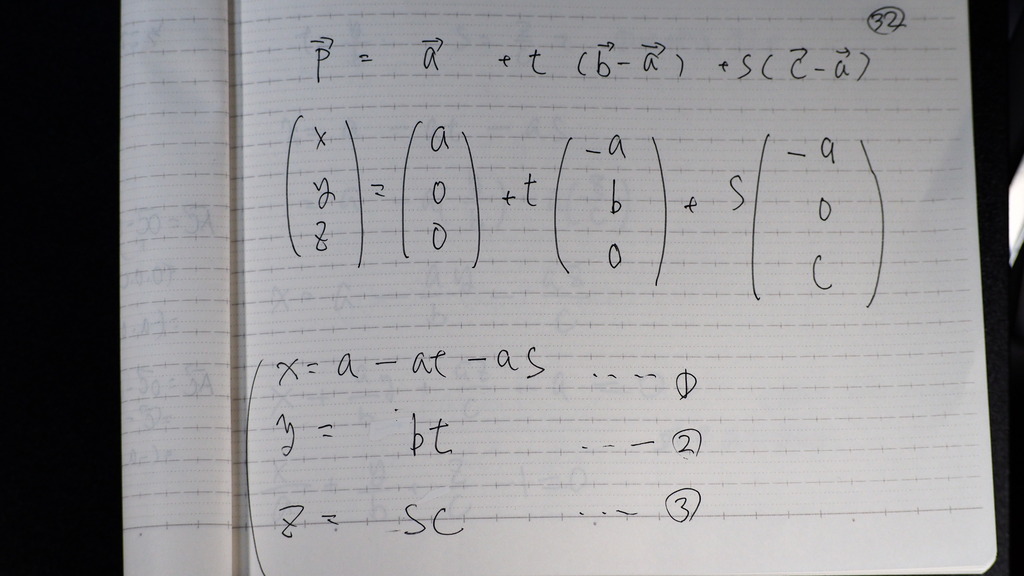
33
t は
s は
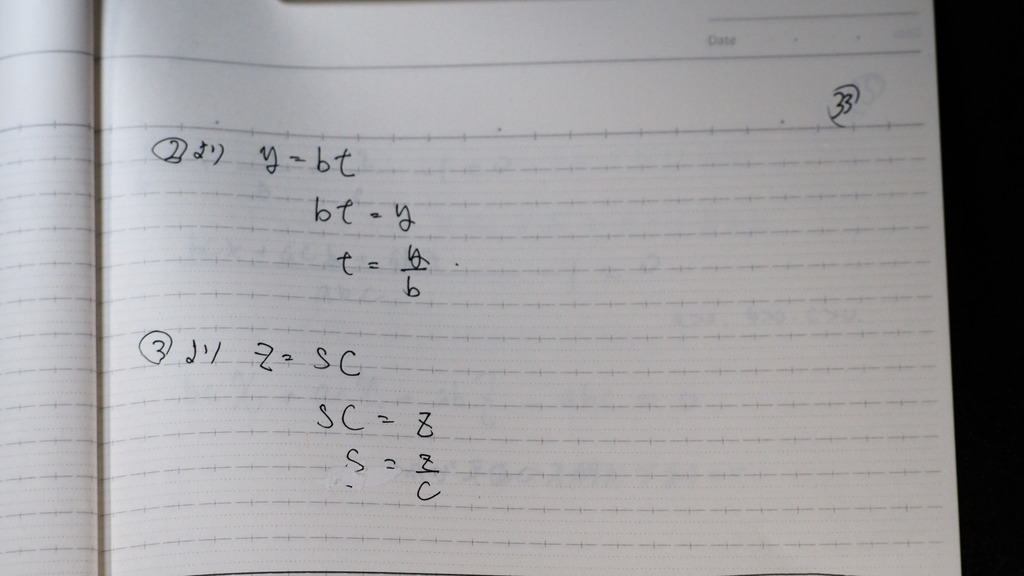
34
これを
➀に代入して
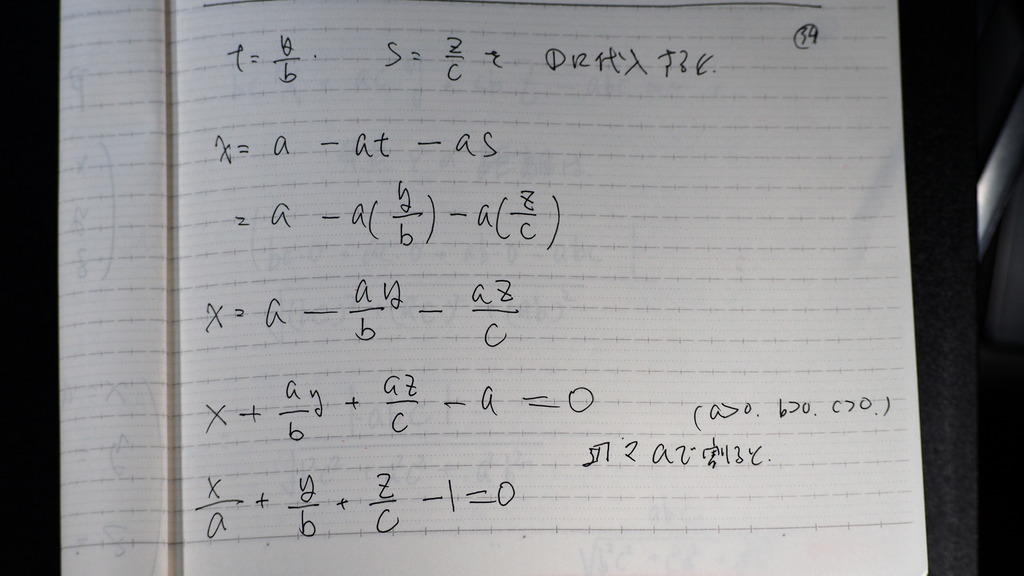
35
これが 平面の
方程式

36
原点との距離は
点と平面との
距離の公式を使って
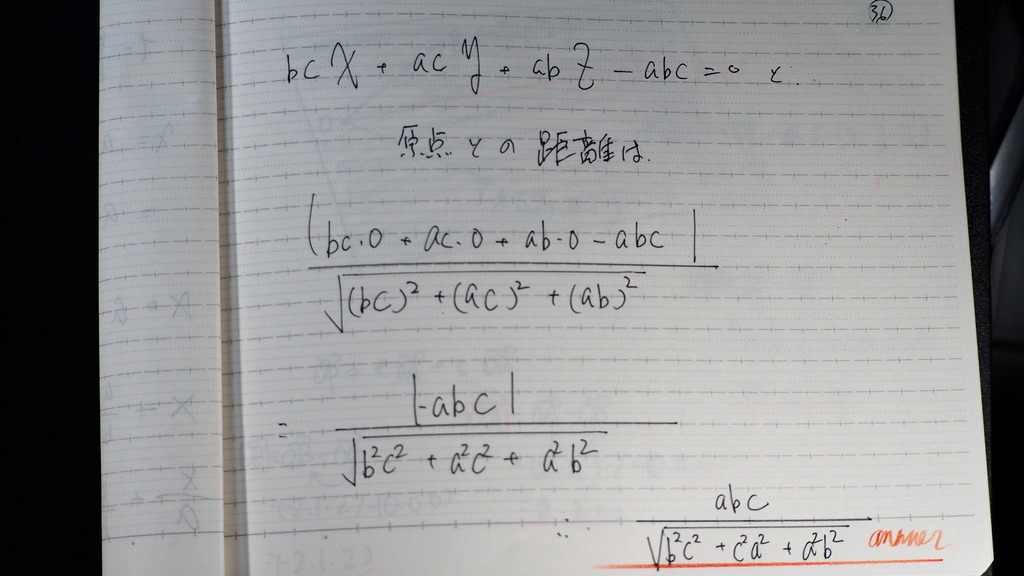
37
類題
今度は
原点でない 点と
平面との 距離
やり方は 同じ

38
AB ベクトル
と
ACベクトルの
和で
APベクトルを
出して

39
平面上に
原点が あるから
式が 少し簡単になる
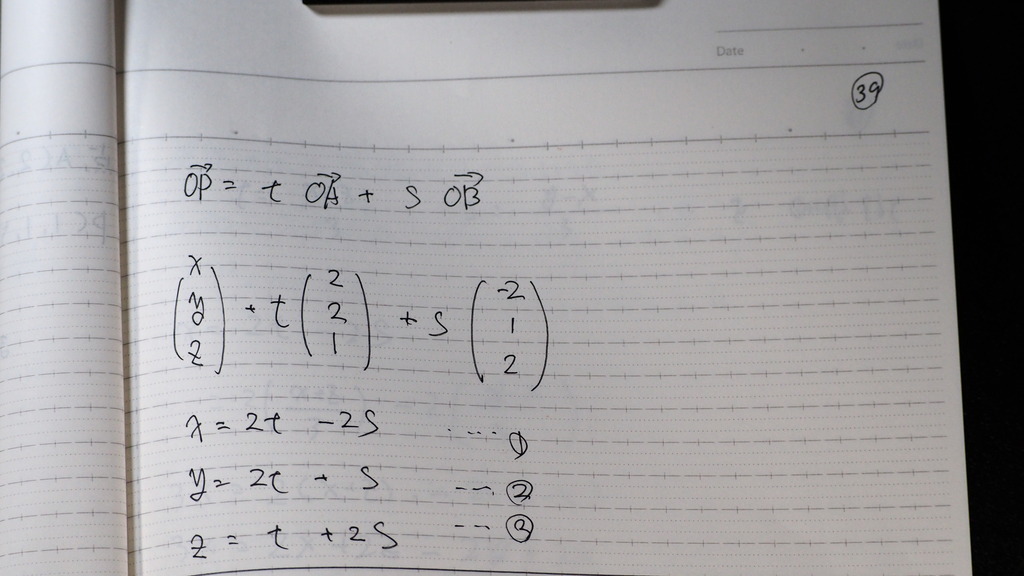
40
t s
を 求めて
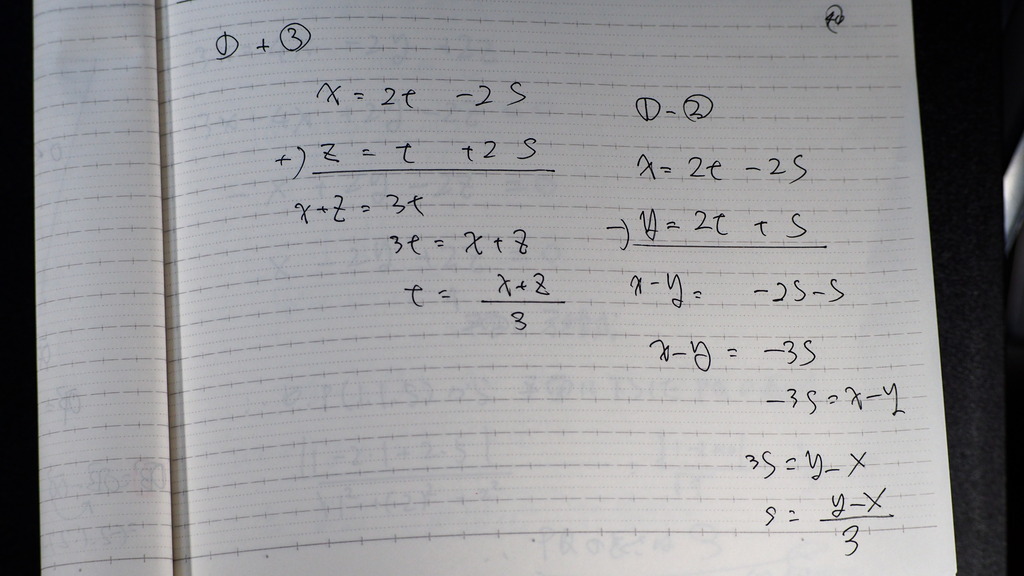
41
➀に 代入して
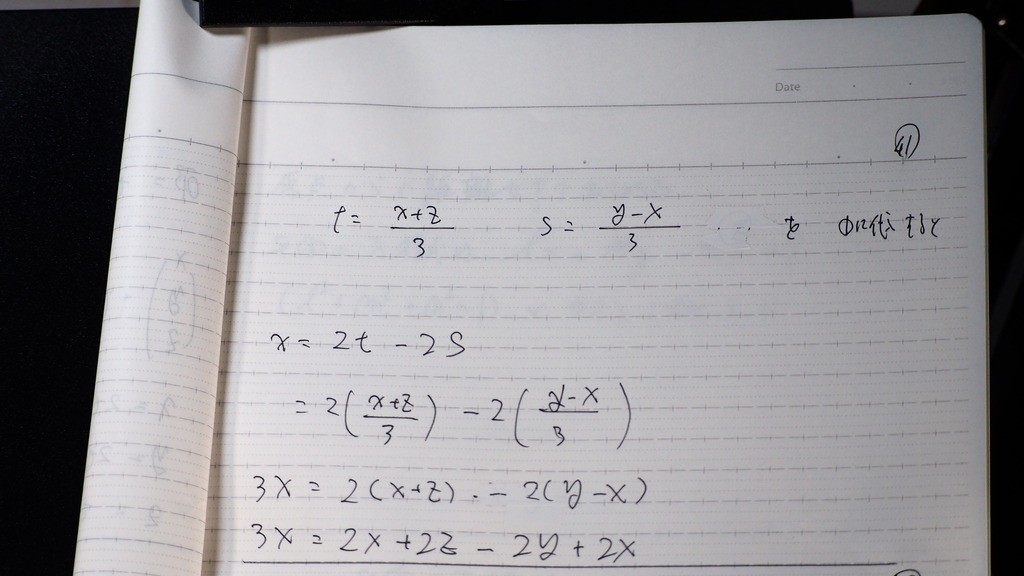
42
平面の
方程式が出たから
点と平面との距離
の公式で
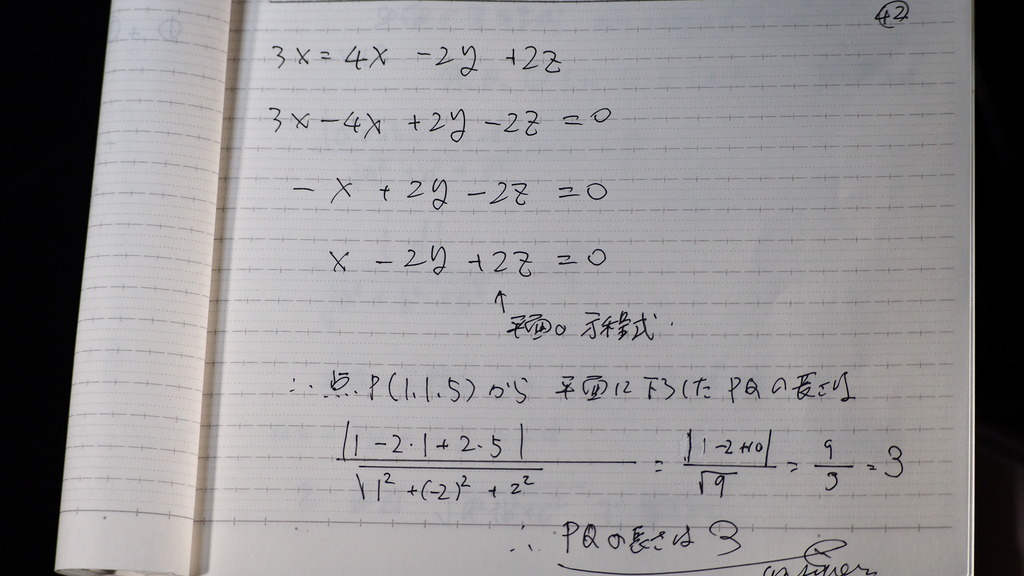
43
問題

44
まず 公式通りに
ここで
この 分母の
√を 使うんだって
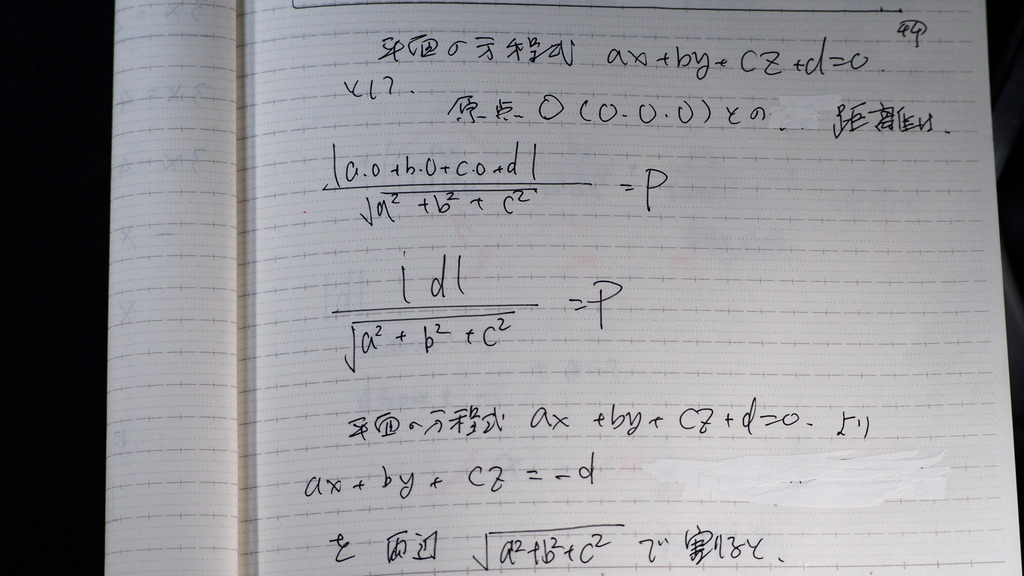
45
平面の式を
こんな感じに
考えれば

46
なるでしょ
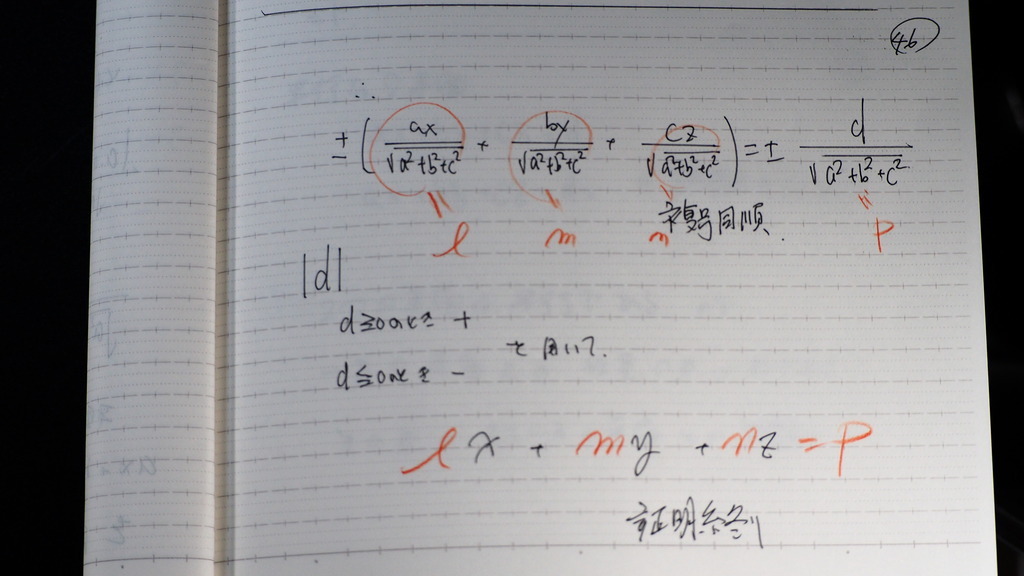
47
追記

48
平行な
2平面の距離は?

49
平面であれば
少なくとも
(a,b,c) の内
一つは ゼロではない
これを使って

50
こうなるんだって
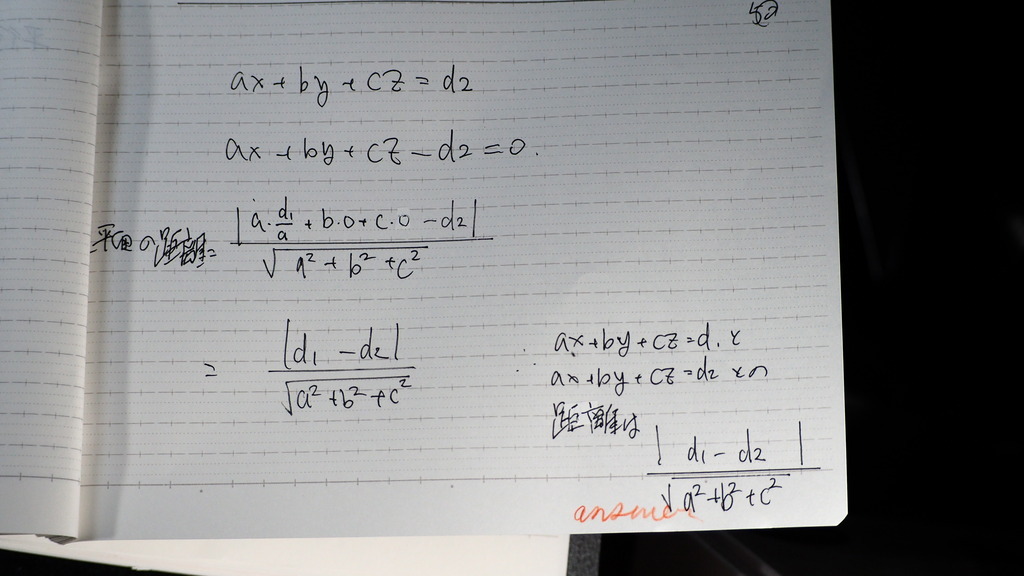
お疲れ様です。
空間座標とベクトル
の 方程式
01
まず ざっと 方程式とか
理論とか
2直線の
平行
02
2直線の 垂直
03
2平面の 平行
04
2平面の垂直
05
直線と 平面が 平行
直線の方向係数は
直線に平行
06
平面の方程式は
係数が 平面に垂直
であるので
内積が =0になる
逆に
直線が 平面に
垂直な時は
直線と 直線の 平行の時
のようになる
07
2平面のなす角
ここは 徐行して
確認してみてください
成ってるでしょ
08
であるから
2平面の垂直成分から
COSΘは こんな感じに
09
点と平面の距離は
こんな公式になるです
10
球の 方程式
11
A,Bが 直径の 両端に
あるときは
12
球面上の 接線の方程式は
13
以上踏まえまして
ここからは
問題を
今日は 平面と直線
空間の 点から
平面に おろした
垂線の長さ
つまり
点と平面の 距離
平面に 垂直な ベクトル
(a,b,c)
点Aを 通り
平面に 垂直な 直線と
平面の交点を
B とすれば
14
Bの 座標が分かっていれば
ABベクトルの 絶対値で
点A と 平面との
距離が出る
15
であるから
Bの座標を 求めたい
平面の 垂直成分が
そのまま
点Aを 通り
平面に 垂直な 直線の
方向係数ベクトル
であるので
16
直線の 方程式は
こんな感じ
これに =t と置いて
媒介変数形にするでしょ
だから
Bの x、y、z に
これを 代入すればさ
17
これが
点Aを 通り
平面に 垂直な 直線
と
平面との
距離なんだけど
ここで
tが分かればいいのだから
18
今度は
t を
求めるでしょ
X= Y= Z= の
媒介変数を
これは
直線上の点を
表してるので
平面の方程式に
代入すれば
共通なところ
交点になるので
19
すると
tは
こんなだから
20
これを
さっきのに
代入したらば
21
こんな感じで
22
√を
外せば
23
別解は
平面の 垂直成分と
直線ABの方向係数が
等しいので
平行を使って
24
ABベクトル
OPベクトル
コサイン
25
まず 矢線ベクトルから
➀
26
成分の内積から
②
27
絶対値は
ゼロ以上だから
28
三点を 通る平面に
原点から
下した 垂線の長さ
原点と平面の距離だね
29
3点が
同一平面上にあれば
この式を
使って
30
平面の媒介変数形方程式
を 作っていくと
31
平面上の 全ての
ベクトルは
異なった 二つの
ベクトルの
和の形になる
じゃナイスカ
32
列で 書いた方が
分かりやすい
これを
連立に して
33
t は
s は
34
これを
➀に代入して
35
これが 平面の
方程式
36
原点との距離は
点と平面との
距離の公式を使って
37
類題
今度は
原点でない 点と
平面との 距離
やり方は 同じ
38
AB ベクトル
と
ACベクトルの
和で
APベクトルを
出して
39
平面上に
原点が あるから
式が 少し簡単になる
40
t s
を 求めて
41
➀に 代入して
42
平面の
方程式が出たから
点と平面との距離
の公式で
43
問題
44
まず 公式通りに
ここで
この 分母の
√を 使うんだって
45
平面の式を
こんな感じに
考えれば
46
なるでしょ
47
追記
48
平行な
2平面の距離は?
49
平面であれば
少なくとも
(a,b,c) の内
一つは ゼロではない
これを使って
50
こうなるんだって
お疲れ様です。