2022年12月14日
22030 大人のさび落とし 空間座標とベクトル 平面の媒介変数形方程式
空間座標とベクトル
今日は
平面の方程式の
媒介変数形
01
問題

02
平面上の ベクトルは
異なる 二つのベクトルの
実数倍で
すべて 表せる

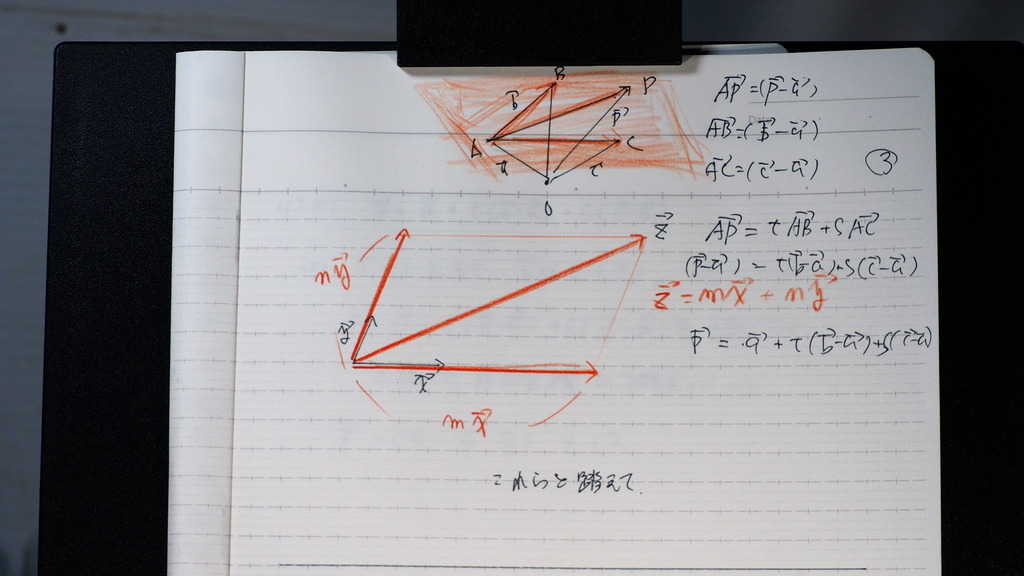
03
そこで
イメージとしては
対角線
APベクトルは
t倍のABベクトル
と
s倍のACベクトルの
和
(p-a)=t(b-a)+s(c-a)
この 左辺のaベクトルを
じゃナイスカ
04
なったデショ

05
実際に
ベクトル方程式に
数値を 入れると

06
列で書いた方が
見やすいと思ってさ
ね
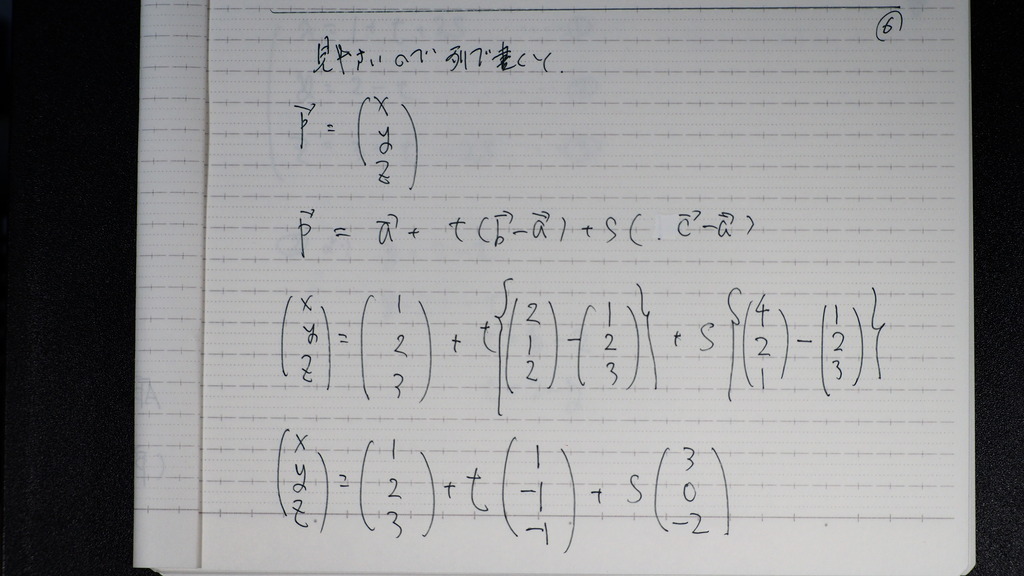
07
計算して
整理したらば

08
ここから
s、t を 消去して
x、y、z、定数の
式にすればいいので
まず t
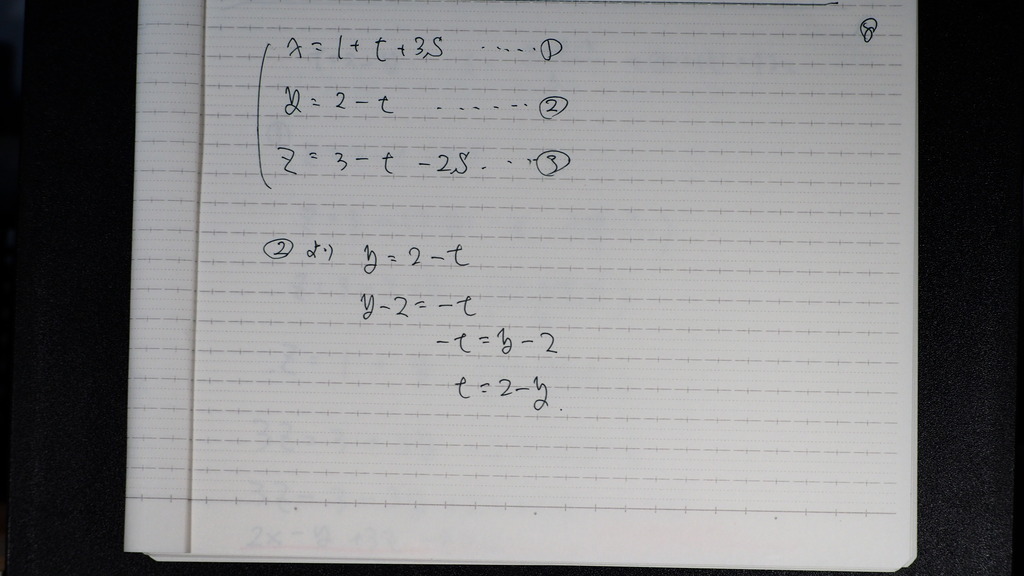
09
次に s

10
③式に t、sを 代入して
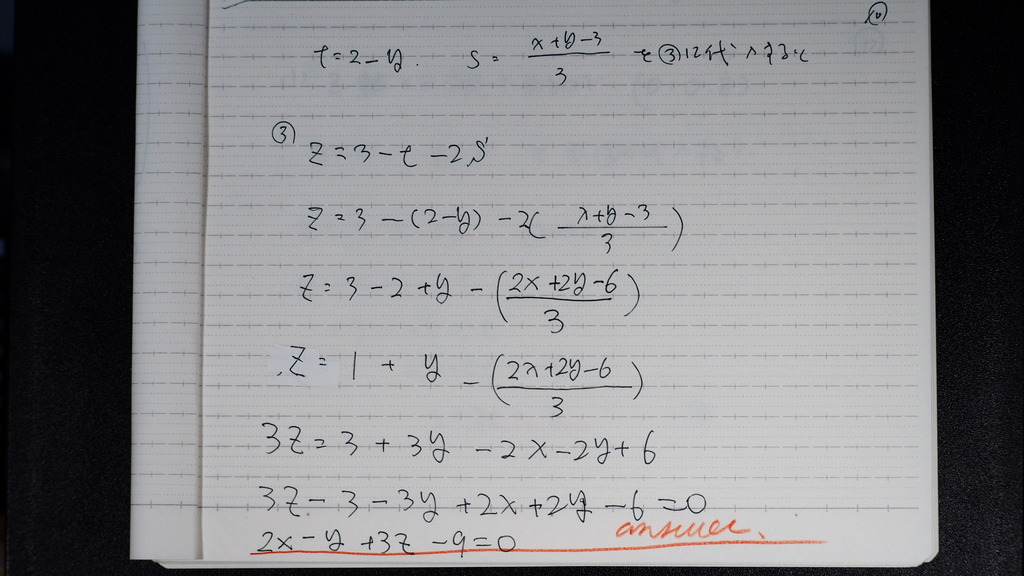
11
問題
まずですね
z軸との交点の座標は

12
x1=0、Y=0
を 代入したら
④

13
それと
⑤
④⑤より

14
tは 8/3

15
sは -7/3
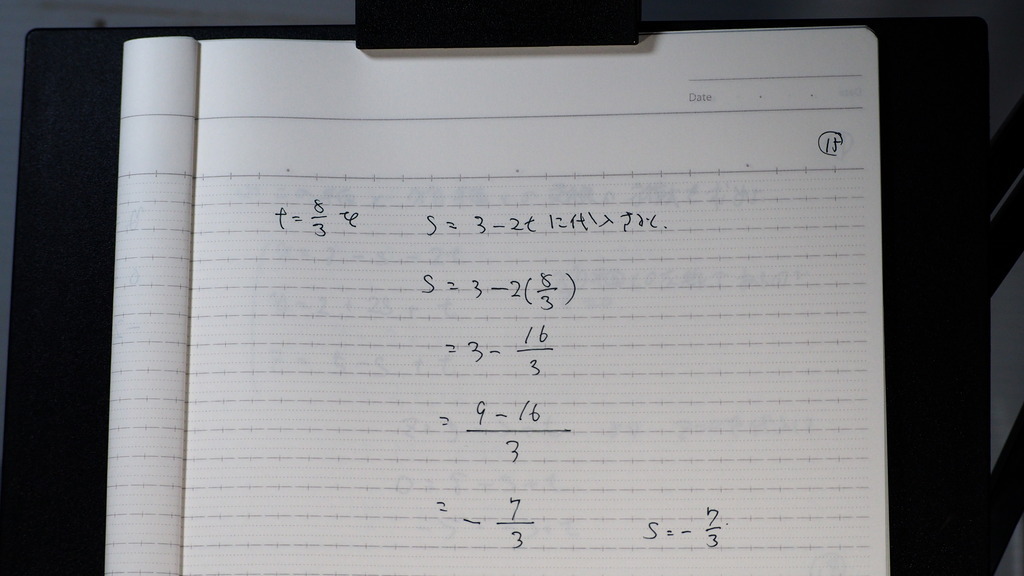
16
これら
t、sを
③式に 代入して
z=10
であるから
(0,0,10)

17
この平面と
xy平面の
交線は
Z=0を 代入して

18
xの式から
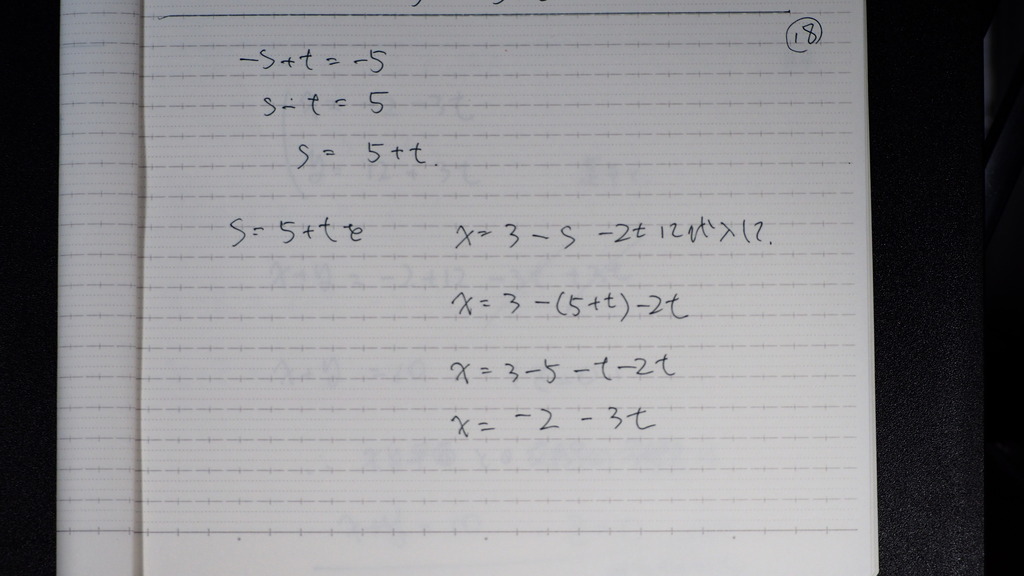
19
yの式から

20
これらを
足すでしょ
z=0の時に
x+y=10
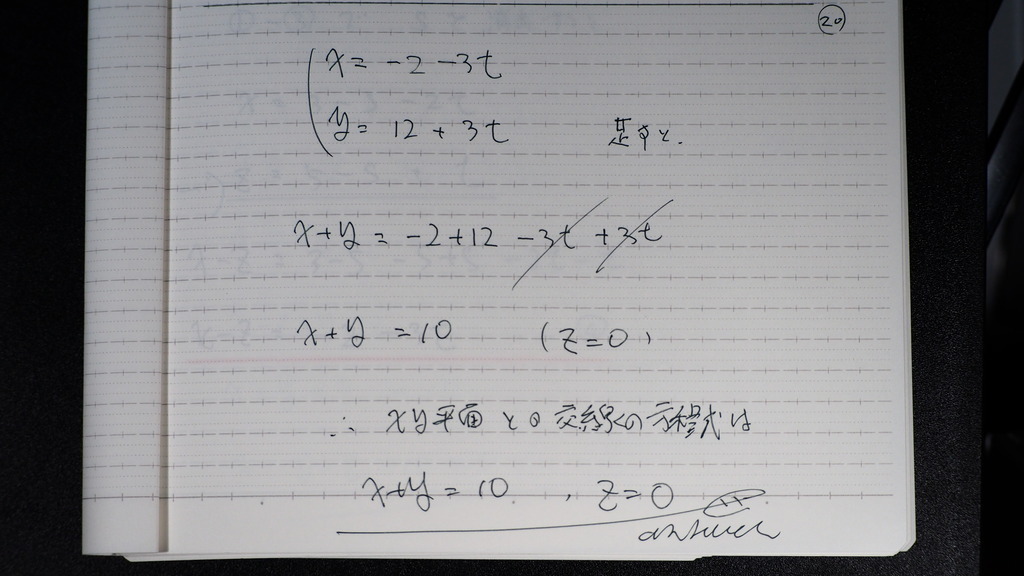
21
この さん式から
s、tを
消去すればいいのだから

22
色々やり方は
あるとおもいますが
➀-③から
④

23
②+③×2で
⑤

24
④⑤を 足すと
x+y+z-10=0
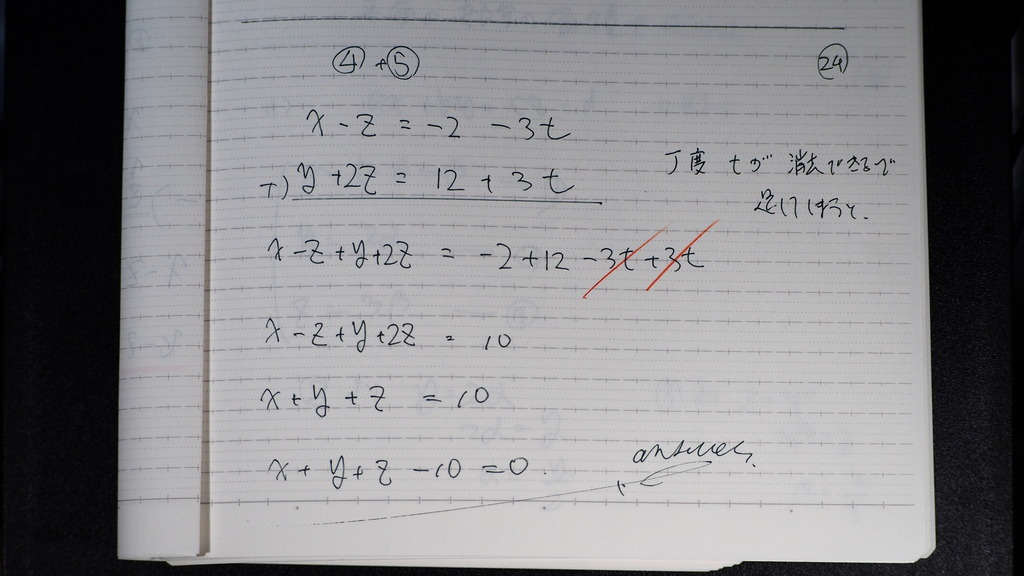
25
もんだい

26
(1)
y 、zから α 、β

27
平面の方程式は
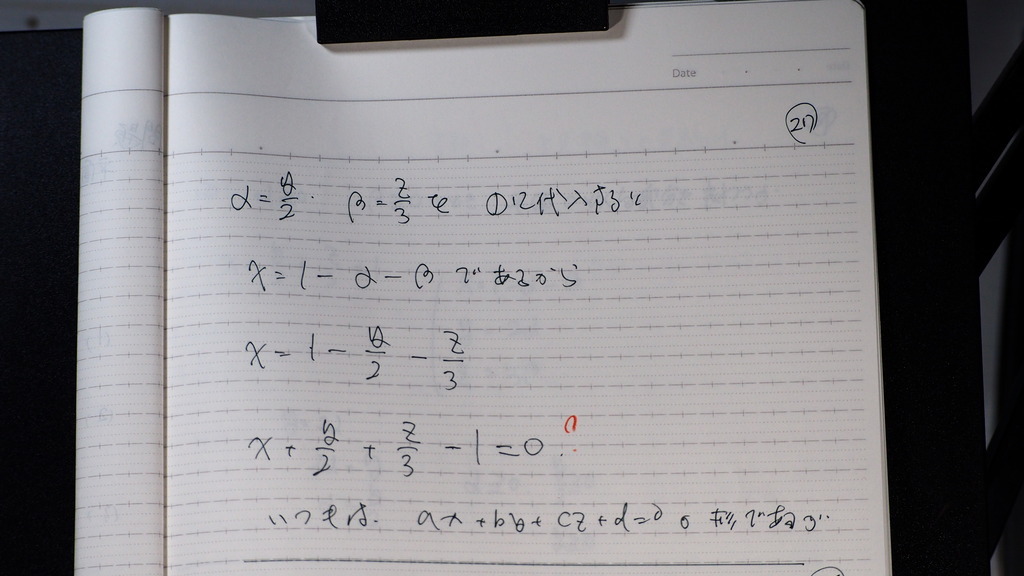
28
題意を 良く見ると
ax+by+cz+d=0
の形ではなく
ax+by+cz=d
であるので
ここで 指示違反で
原点は もったいない

29
(2)
α βの
範囲から
y、zは ゼロ以上

30
境界線を 求めると
y=-2x+2
xy平面は 平場ですが
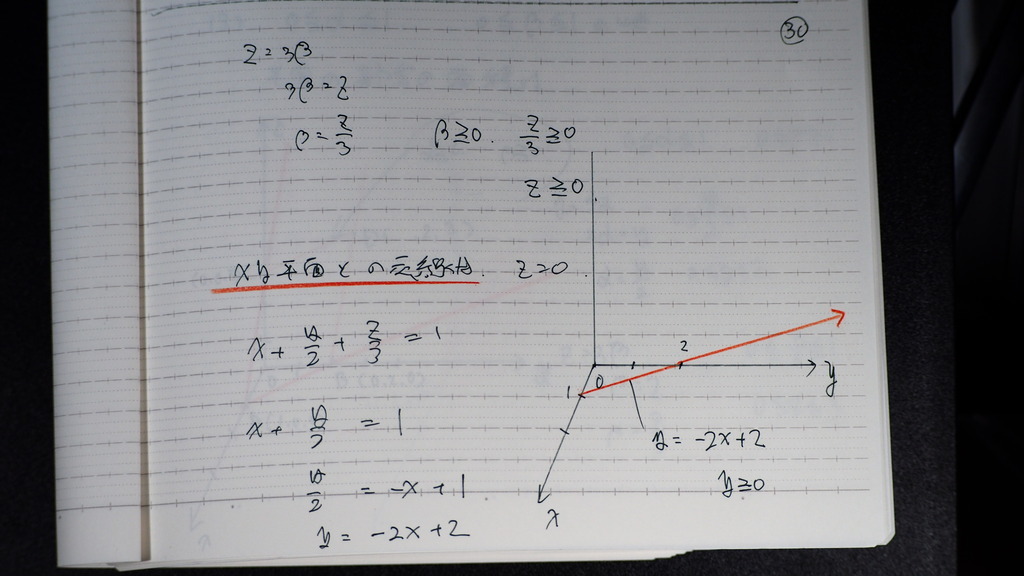
31
xz平面は
z=-3x+3
こんな感じで
赤斜線の部分
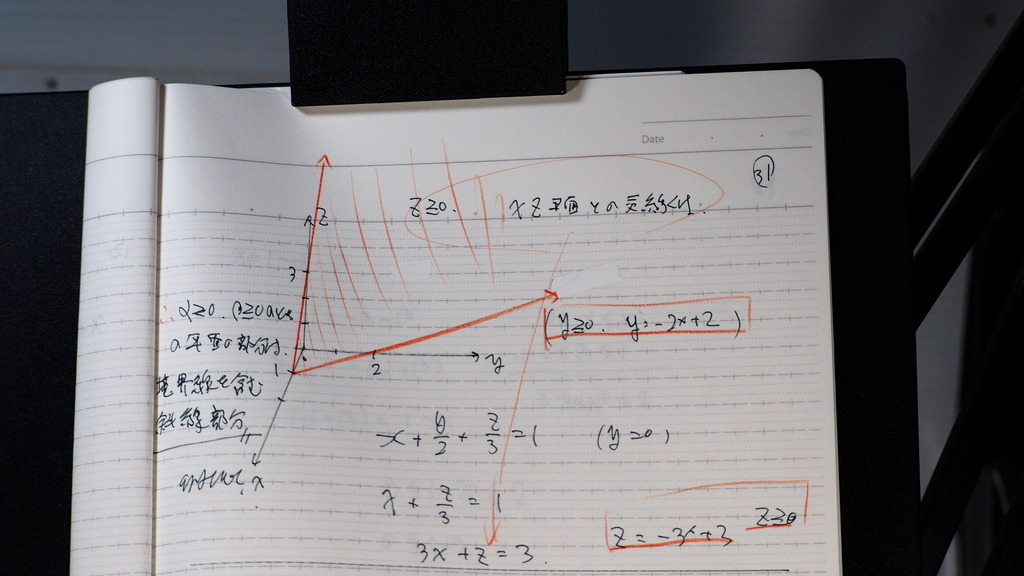
32
さらに
(3)
y z
の範囲が
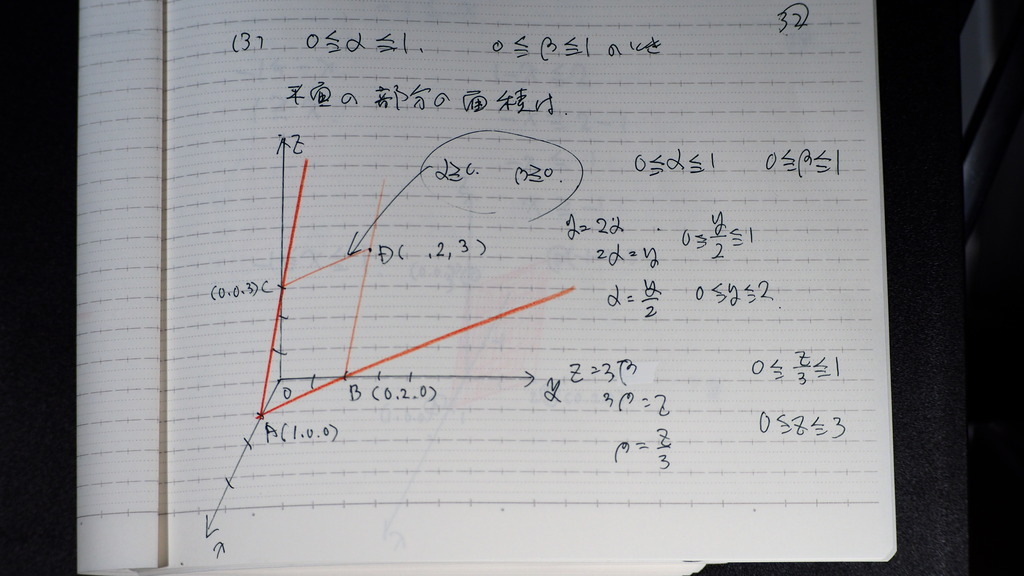
33
xの範囲は

34
座標にすれば
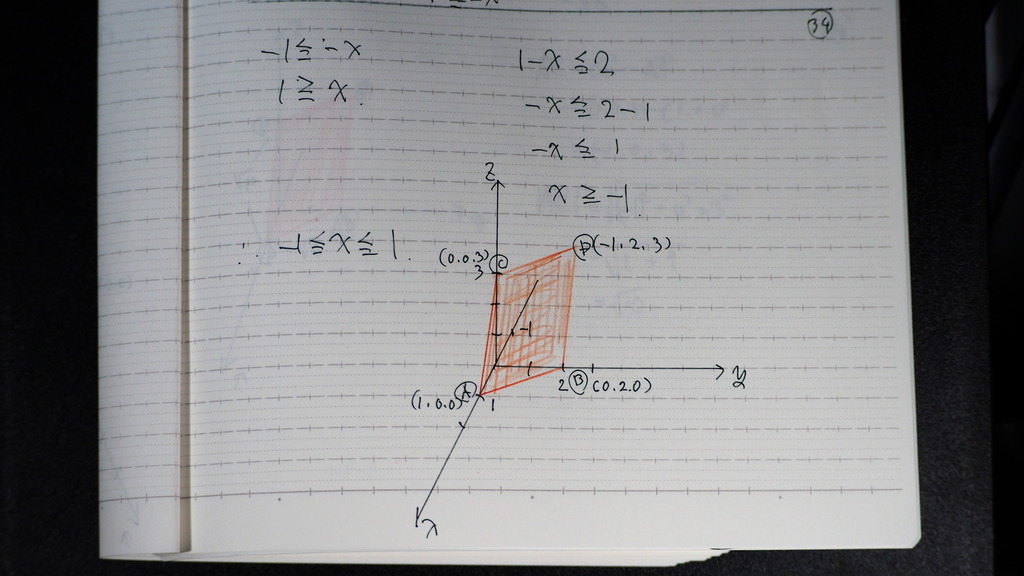
35
辺の長さは
ベクトルの
絶対値で求まるので

36
底辺√5
ななめが √10

37
角度を 求めて
sinを 使いたいので
内積を いじりながら

38
COSがでれば
sinが出るというわけで

39
ね
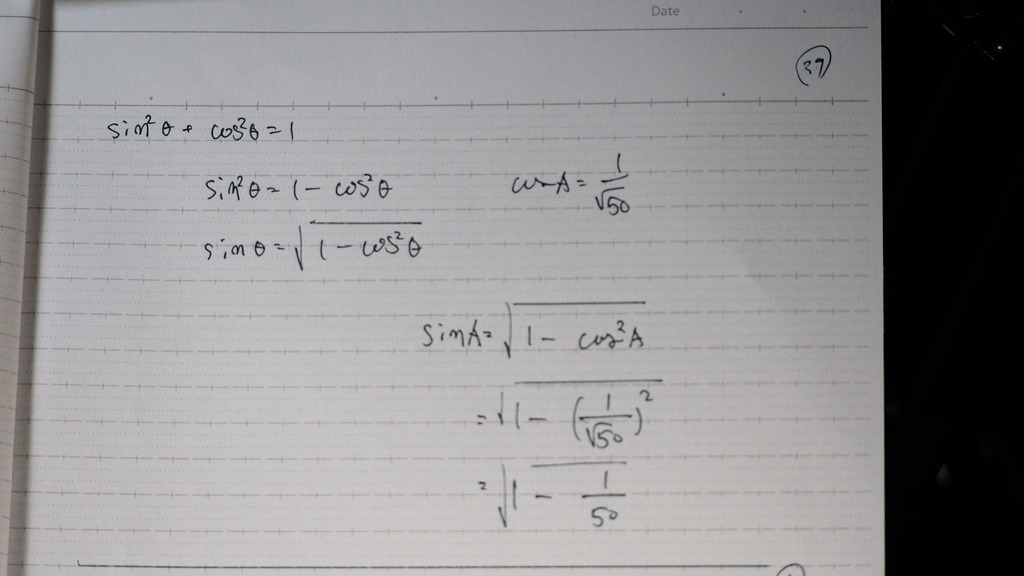
40
底辺 × 高さは
高さが 斜辺×sinA
であるので
7

お疲れ様です。
今日は
平面の方程式の
媒介変数形
01
問題
02
平面上の ベクトルは
異なる 二つのベクトルの
実数倍で
すべて 表せる
03
そこで
イメージとしては
対角線
APベクトルは
t倍のABベクトル
と
s倍のACベクトルの
和
(p-a)=t(b-a)+s(c-a)
この 左辺のaベクトルを
じゃナイスカ
04
なったデショ
05
実際に
ベクトル方程式に
数値を 入れると
06
列で書いた方が
見やすいと思ってさ
ね
07
計算して
整理したらば
08
ここから
s、t を 消去して
x、y、z、定数の
式にすればいいので
まず t
09
次に s
10
③式に t、sを 代入して
11
問題
まずですね
z軸との交点の座標は
12
x1=0、Y=0
を 代入したら
④
13
それと
⑤
④⑤より
14
tは 8/3
15
sは -7/3
16
これら
t、sを
③式に 代入して
z=10
であるから
(0,0,10)
17
この平面と
xy平面の
交線は
Z=0を 代入して
18
xの式から
19
yの式から
20
これらを
足すでしょ
z=0の時に
x+y=10
21
この さん式から
s、tを
消去すればいいのだから
22
色々やり方は
あるとおもいますが
➀-③から
④
23
②+③×2で
⑤
24
④⑤を 足すと
x+y+z-10=0
25
もんだい
26
(1)
y 、zから α 、β
27
平面の方程式は
28
題意を 良く見ると
ax+by+cz+d=0
の形ではなく
ax+by+cz=d
であるので
ここで 指示違反で
原点は もったいない
29
(2)
α βの
範囲から
y、zは ゼロ以上
30
境界線を 求めると
y=-2x+2
xy平面は 平場ですが
31
xz平面は
z=-3x+3
こんな感じで
赤斜線の部分
32
さらに
(3)
y z
の範囲が
33
xの範囲は
34
座標にすれば
35
辺の長さは
ベクトルの
絶対値で求まるので
36
底辺√5
ななめが √10
37
角度を 求めて
sinを 使いたいので
内積を いじりながら
38
COSがでれば
sinが出るというわけで
39
ね
40
底辺 × 高さは
高さが 斜辺×sinA
であるので
7
お疲れ様です。