2022年12月11日
22029 大人のさび落とし 空間座標とベクトル 平面の方程式
空間座標とベクトル 平面の方程式
01
平面の方程式
ある 空間ベクトルがあって
そのベクトルに 垂直な
平面
これが 平面の方程式なんですが
3次元空間で
ある方向に 矢印が向いてるでしょ
その
矢印に 垂直な
直線群を
考えると
無数にある 直線が
その
ベクトルに対して
平面を なしている

02
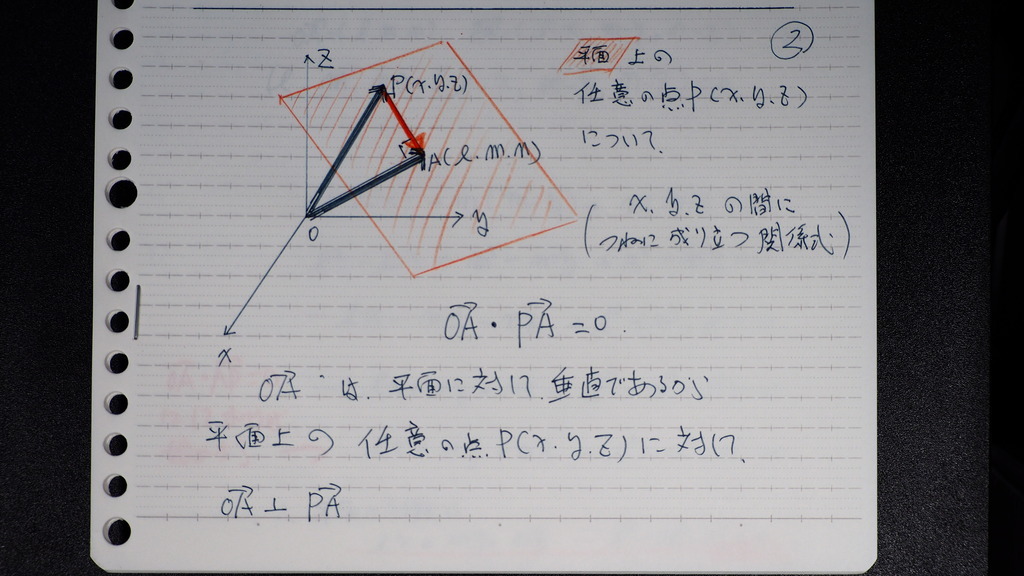
そこで
平面上の 任意の点を
どこにとっても
どんなにとっても
その 一つを P(x、y、z)
と しようか
PA ベクトルは
OA ベクトルに
垂直だよ
03
PA ベクトルを
けいさんして
成分でさ やったデショ
このベクトルと (l,m,n) が
垂直だから
内積=0

04
展開してくと
こんな感じで
途中で
マイナスを くくって
払ったんだけど
初めから
PA ベクトルじゃなくて
AP ベクトルで
計算すれば
同じこと
だから これが
平面の方程式

05
(a,b,c) は
平面に 垂直な ベクトルになるので
少なくとも
一つは 0 ではない
そうでないと
垂直な ベクトルにならず
点に なってしまう
(原点)
平面の
方程式に
平面上に ある 点を
代入して

06
➀②③④
として
➀-②
(②-➀) にした方がよかったかな
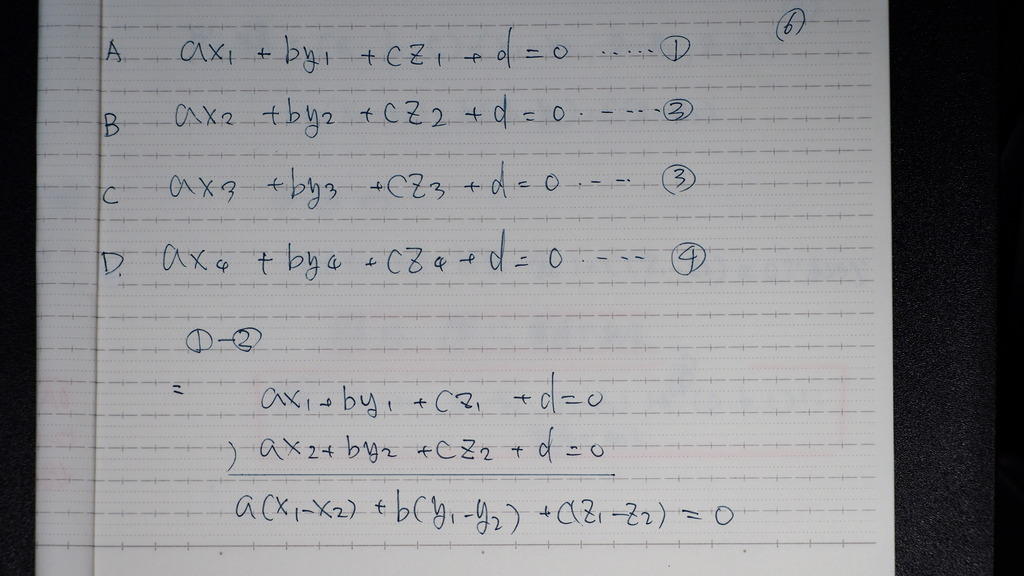
07
BA ベクトルと
P ベクトル と考えると
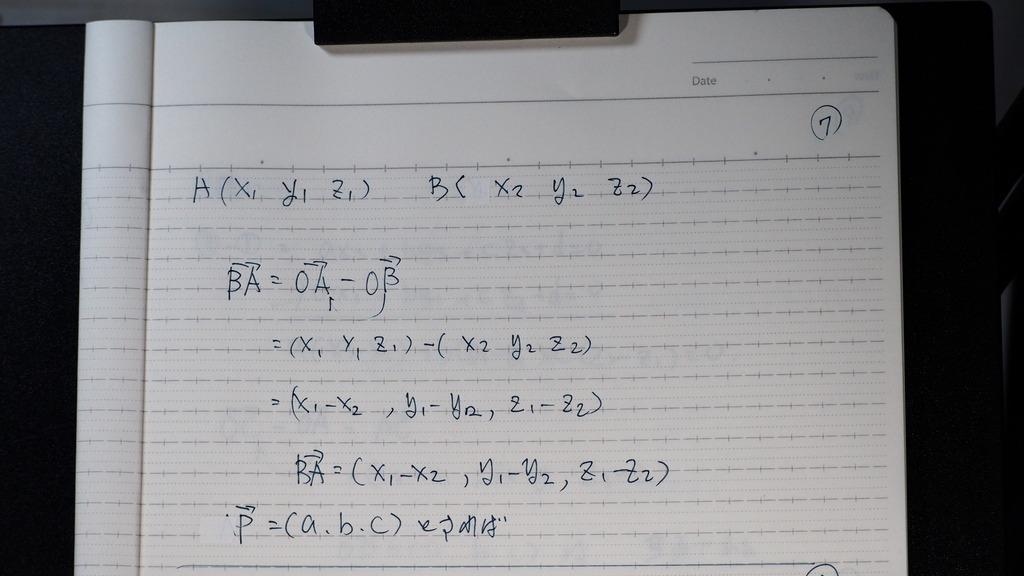
08
内積は こんな感じに 成るんだけど
このあたいは
➀-②より
=0
であるから
内積=0 で 垂直

09
同様に

10
同様に
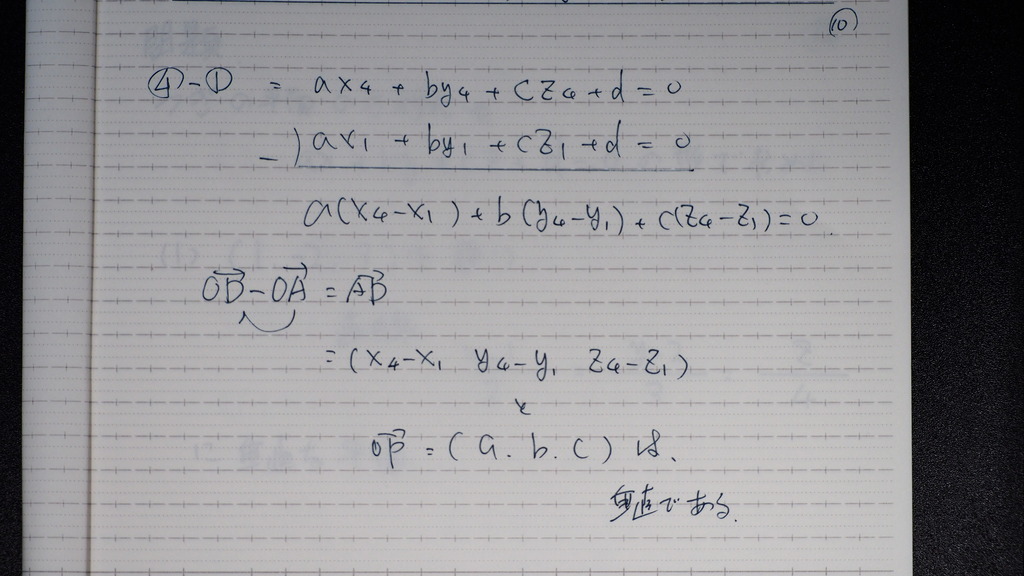
11
ゆえに

12
問題
これこれの点を とおり
これこれの 直線に 垂直な
平面の方程式
を
求めよ

13
平面の 方程式の 形は
こんなで
(a,b,c)は 平面に 垂直な
ベクトル
直線は こんな
で
直線の時の
分母は 方向係数
直線に平行な成分
題意では
直線に 垂直な平面とあるから
そのまま
直線の 方向係数が
今回は 平面の垂直方向を
向いている

14
であるので
平面の方程式に代入して
通過点を
(x,y,z)に 代入すれば
dは -8
求める
平面の方程式は
こんな

15
三点が
与えられてるときの
平面の
方程式

16
3点を 方程式に
代入して
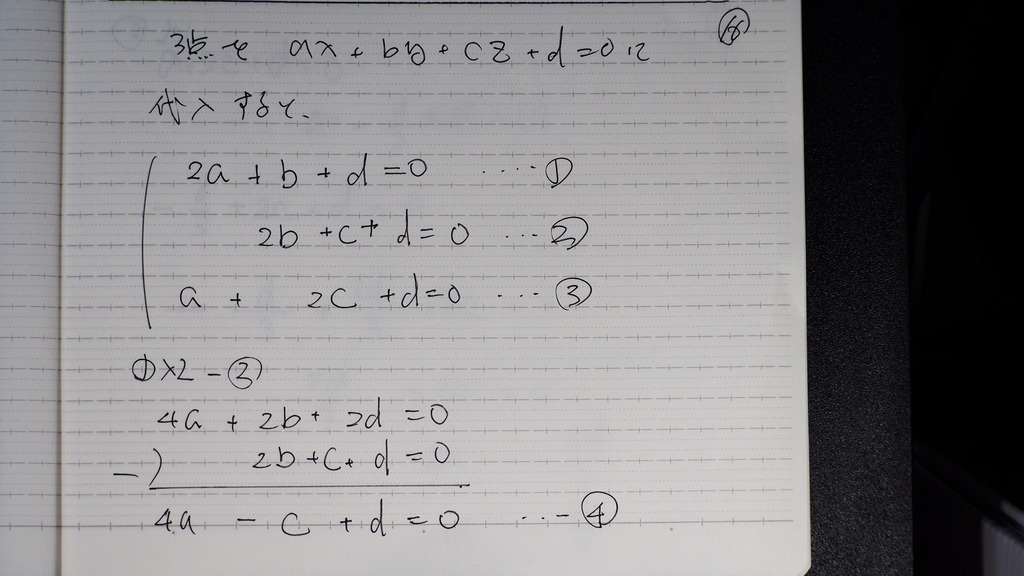
17
a=
-d/3
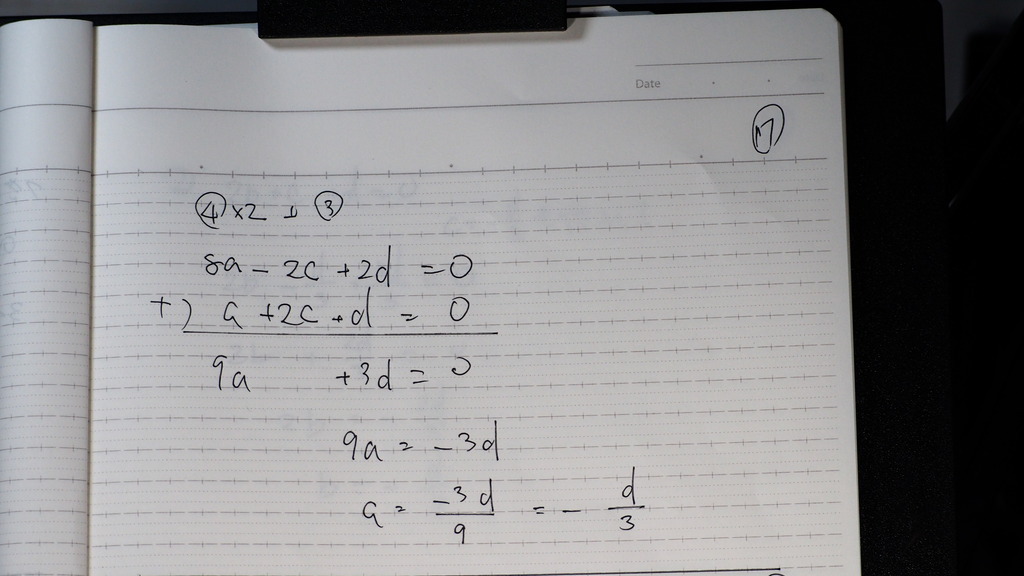
18
C=
-d/3
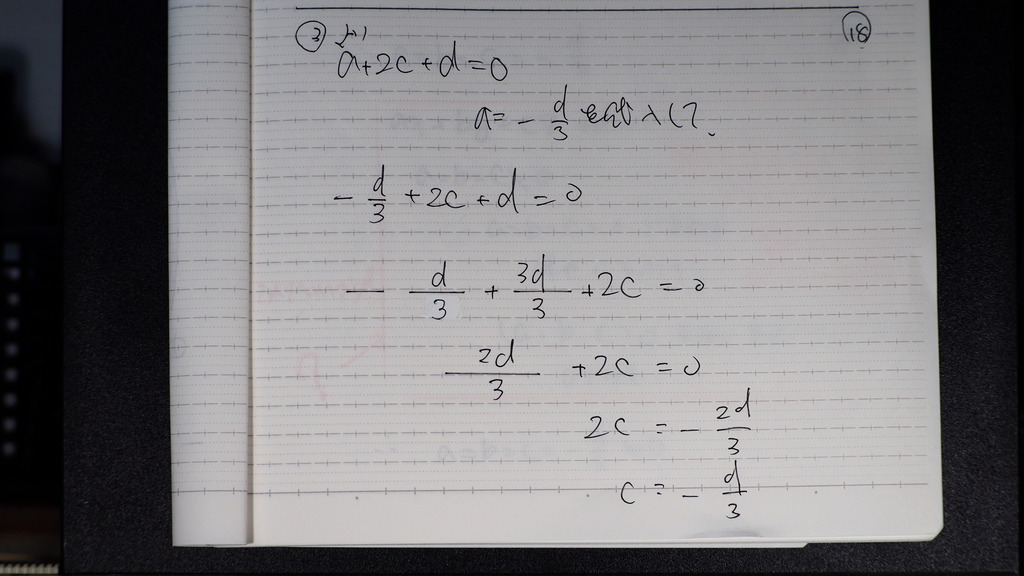
19
b=
-d/3
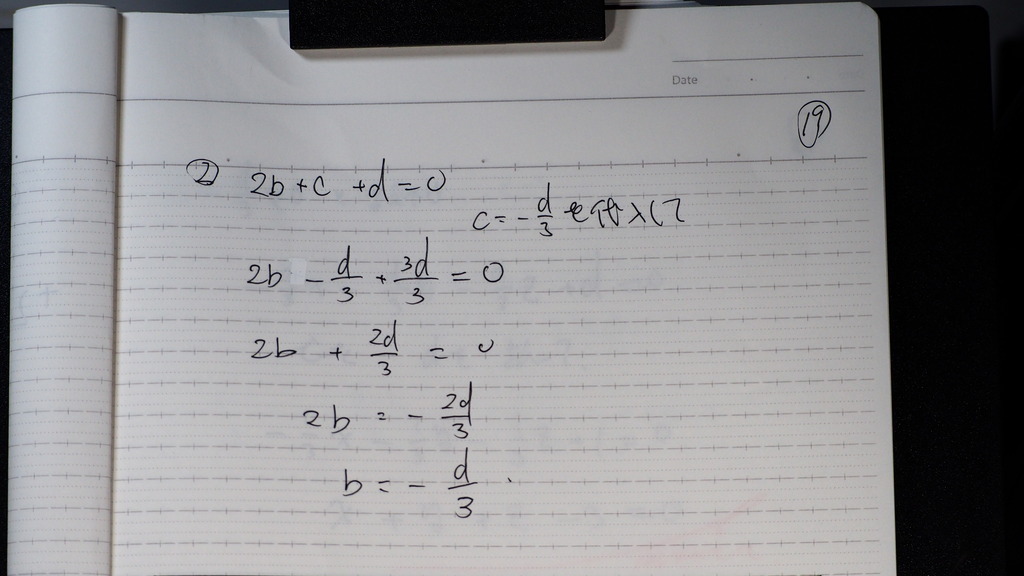
20
a=b=c=-d/3
a=b=cは 0ではないので
-d/3 も 0ではない
で
払って

21
整えると
平面の方程式は
こんな感じ
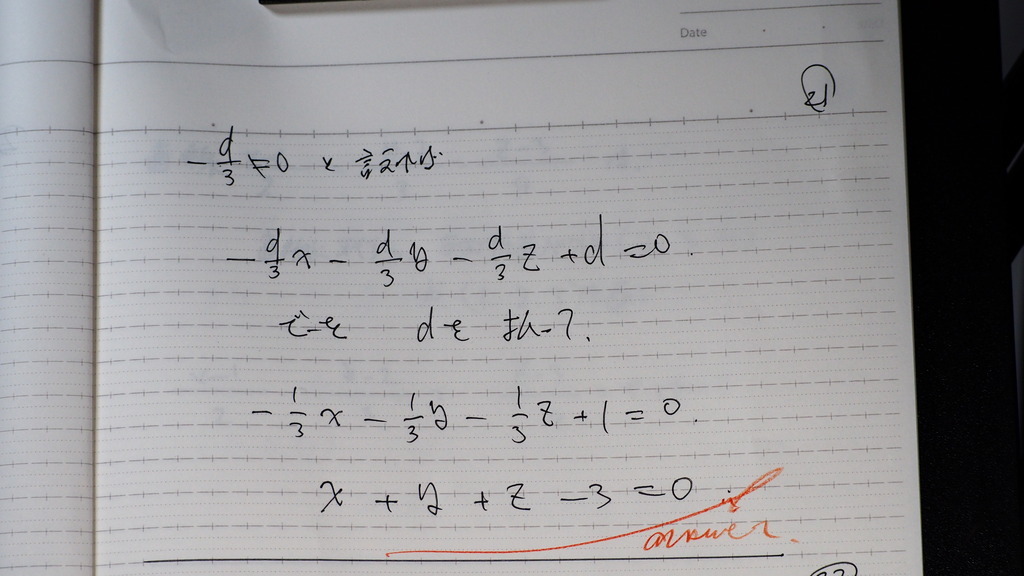
22
問題
平面の方程式を
求めよ

23
直線の
方程式から
これは (1,2,3)を 通る
方向ベクトルは
(2,3,4)

24
媒介変数表示にして
直線は
平面に 含まれてるから
tの値を
適当に 入れて
もう一点 求めて
t=1 とすれば

25
この 2点と
其の他 1点を
通るから

26
直線上の 2点と
(0,0,0) から
ベクトルを
2つ 出してベクトル
は 直線の方程式の
方向係数だから

27
直線の上の 2点の
ベクトルを
求めれば
一目瞭然

28
二点間の ベクトルは
直線の 方向係数に 成るでしょ
この3本と
平面に垂直なP(a,b,c)が 垂直だから

29
内積 =0 が3本
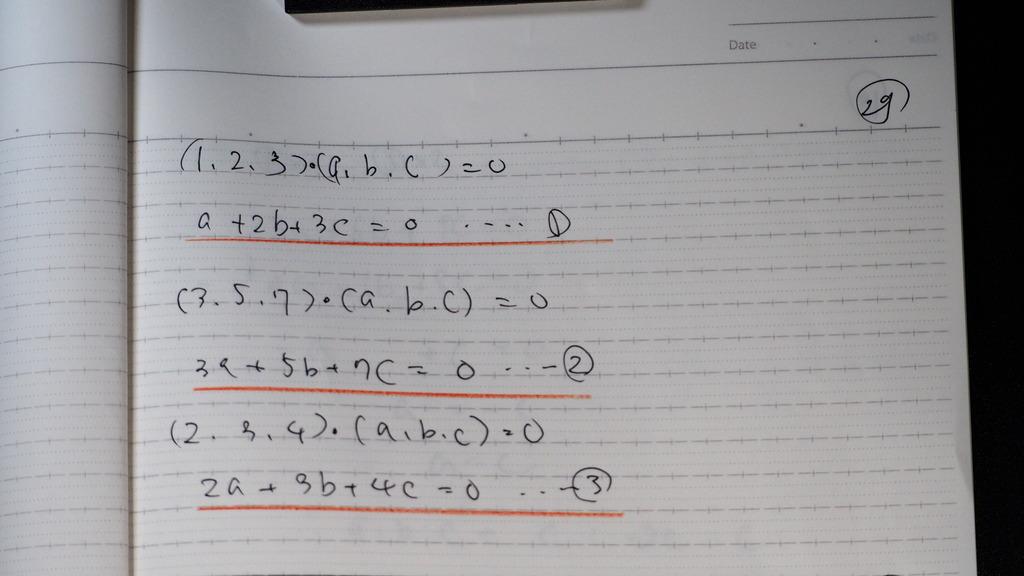
30
b=-2c
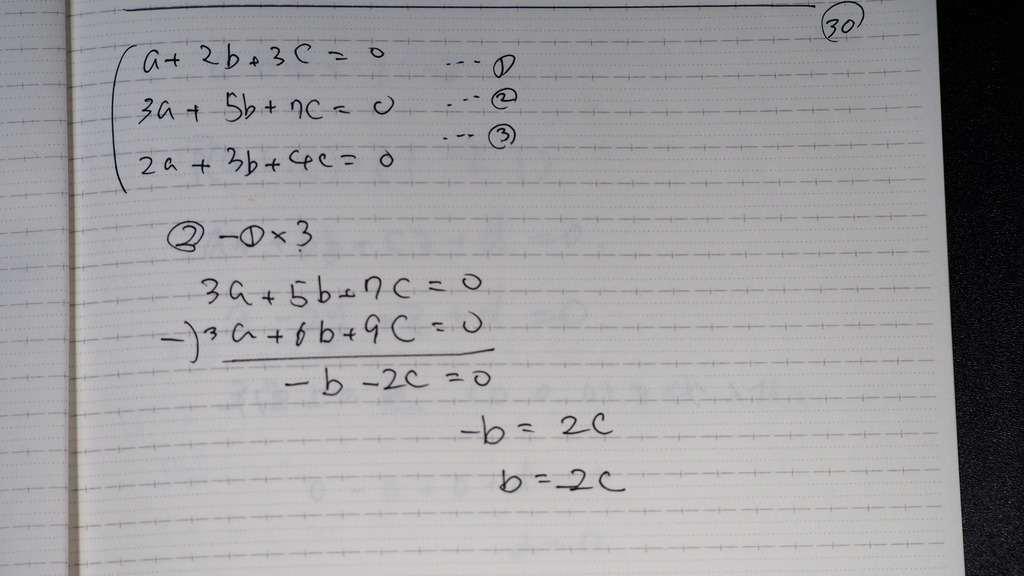
31
a=c
a:b:c=c:-2c:c
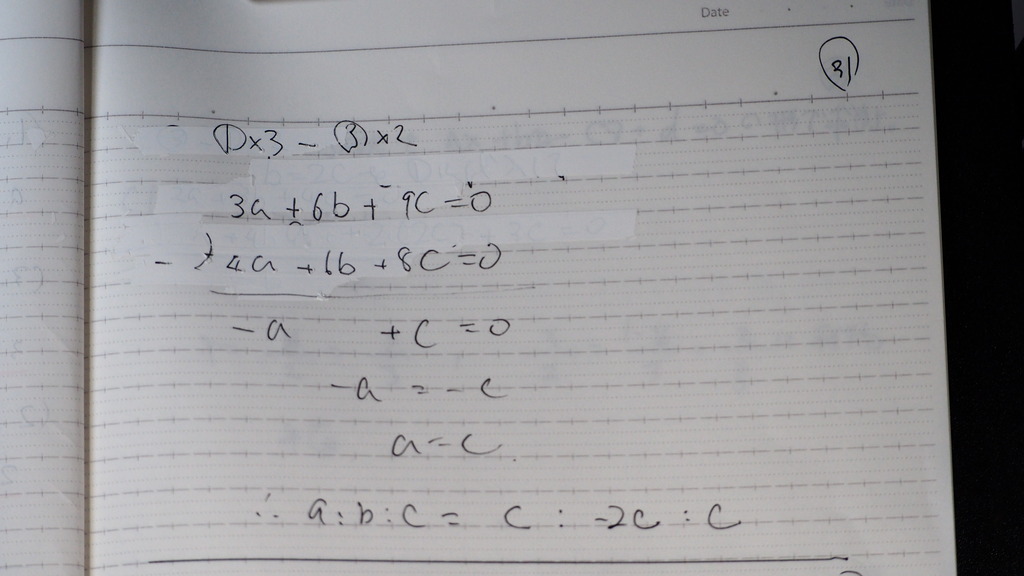
32
a:b:c= 1:-2:1
平面上の点と a,b,c
と 平面上の
点の座標から
d=0
であるので
平面の方程式は
こんな感じで

33
もんだい

34
2つの 直線の 方向係数ベクトル
と
平面の方程式の (a,b,c)は
垂直なので
内積の式が 2つ
文字が3つ

35
➀② と ③

36
➀②から
bは -c/7
aは -19c/7
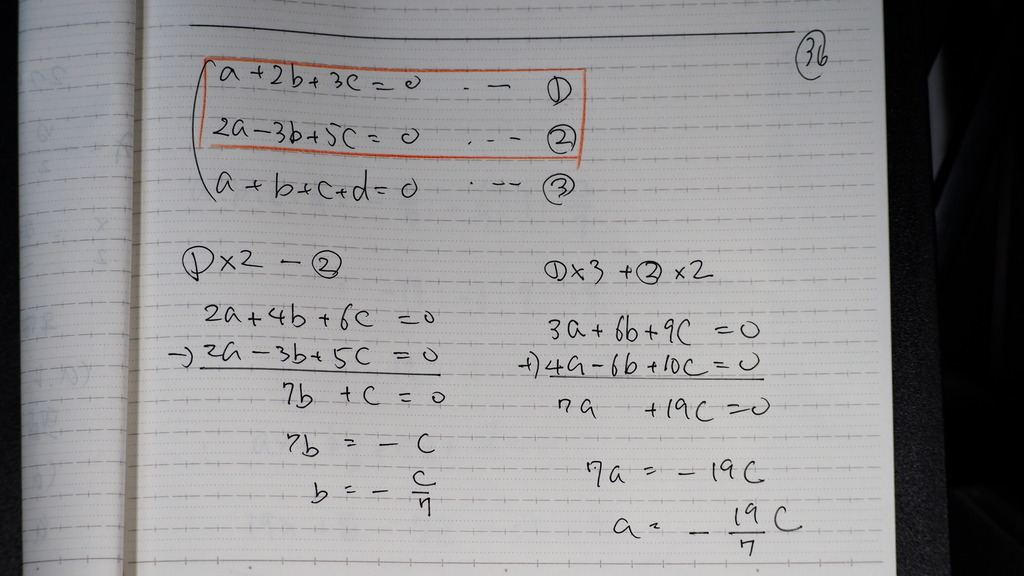
37
a:b:c は こんなデショ
で
③式より d=13c/7
でしょ
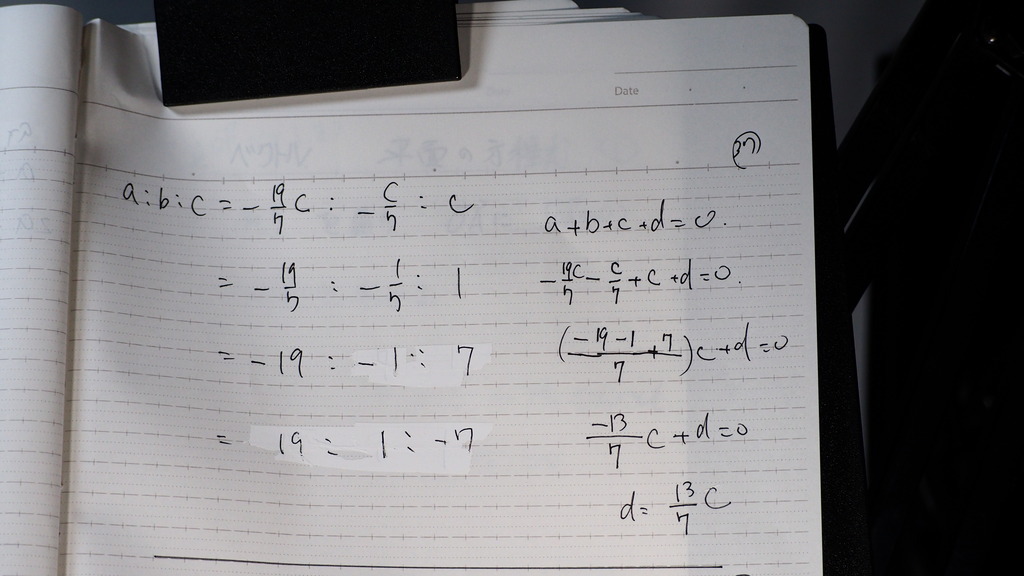
38
ナタメ
こうです

おつあれ様です。
01
平面の方程式
ある 空間ベクトルがあって
そのベクトルに 垂直な
平面
これが 平面の方程式なんですが
3次元空間で
ある方向に 矢印が向いてるでしょ
その
矢印に 垂直な
直線群を
考えると
無数にある 直線が
その
ベクトルに対して
平面を なしている
02
そこで
平面上の 任意の点を
どこにとっても
どんなにとっても
その 一つを P(x、y、z)
と しようか
PA ベクトルは
OA ベクトルに
垂直だよ
03
PA ベクトルを
けいさんして
成分でさ やったデショ
このベクトルと (l,m,n) が
垂直だから
内積=0
04
展開してくと
こんな感じで
途中で
マイナスを くくって
払ったんだけど
初めから
PA ベクトルじゃなくて
AP ベクトルで
計算すれば
同じこと
だから これが
平面の方程式
05
(a,b,c) は
平面に 垂直な ベクトルになるので
少なくとも
一つは 0 ではない
そうでないと
垂直な ベクトルにならず
点に なってしまう
(原点)
平面の
方程式に
平面上に ある 点を
代入して
06
➀②③④
として
➀-②
(②-➀) にした方がよかったかな
07
BA ベクトルと
P ベクトル と考えると
08
内積は こんな感じに 成るんだけど
このあたいは
➀-②より
=0
であるから
内積=0 で 垂直
09
同様に
10
同様に
11
ゆえに
12
問題
これこれの点を とおり
これこれの 直線に 垂直な
平面の方程式
を
求めよ
13
平面の 方程式の 形は
こんなで
(a,b,c)は 平面に 垂直な
ベクトル
直線は こんな
で
直線の時の
分母は 方向係数
直線に平行な成分
題意では
直線に 垂直な平面とあるから
そのまま
直線の 方向係数が
今回は 平面の垂直方向を
向いている
14
であるので
平面の方程式に代入して
通過点を
(x,y,z)に 代入すれば
dは -8
求める
平面の方程式は
こんな
15
三点が
与えられてるときの
平面の
方程式
16
3点を 方程式に
代入して
17
a=
-d/3
18
C=
-d/3
19
b=
-d/3
20
a=b=c=-d/3
a=b=cは 0ではないので
-d/3 も 0ではない
で
払って
21
整えると
平面の方程式は
こんな感じ
22
問題
平面の方程式を
求めよ
23
直線の
方程式から
これは (1,2,3)を 通る
方向ベクトルは
(2,3,4)
24
媒介変数表示にして
直線は
平面に 含まれてるから
tの値を
適当に 入れて
もう一点 求めて
t=1 とすれば
25
この 2点と
其の他 1点を
通るから
26
直線上の 2点と
(0,0,0) から
ベクトルを
2つ 出してベクトル
は 直線の方程式の
方向係数だから
27
直線の上の 2点の
ベクトルを
求めれば
一目瞭然
28
二点間の ベクトルは
直線の 方向係数に 成るでしょ
この3本と
平面に垂直なP(a,b,c)が 垂直だから
29
内積 =0 が3本
30
b=-2c
31
a=c
a:b:c=c:-2c:c
32
a:b:c= 1:-2:1
平面上の点と a,b,c
と 平面上の
点の座標から
d=0
であるので
平面の方程式は
こんな感じで
33
もんだい
34
2つの 直線の 方向係数ベクトル
と
平面の方程式の (a,b,c)は
垂直なので
内積の式が 2つ
文字が3つ
35
➀② と ③
36
➀②から
bは -c/7
aは -19c/7
37
a:b:c は こんなデショ
で
③式より d=13c/7
でしょ
38
ナタメ
こうです
おつあれ様です。