2022年12月09日
22028大人おさび落とし 空間座標とベクトル 2直線の垂直条件
心優しき圧力団体( PTA )の
方に捧ぐ大人のさび落とし
さいきんさ
色んな人が いろんなことを
見てるわけで
その中に 私もいたり
私もだったり
つまりね
世の中 不透明で
正直なことを いうと
ただでさえ 不安なのに
絶えられくなる
そんなわけで
余計なことを言わず
けっこう
みまもっててくださってまして
でもさ
お願いだ
受験生は もっと不安だし
親も同じだからさ
と
いうわけで
おもわず 頑張ってしまいました
16:39分
今日は仕上げるか
01
2直線の 垂直条件
まずさ
この辺を もう一回
おさえていただいて
こんな感じに 書けるときの
直線の方程式
分母は 方向係数
直線に 平行なベクトルになってる

02
Pの終点が
bの t倍で
動いていく

03
媒介変数を 使うと
直線上の 任意の点が
表現でき
t の 値によって
点の場所が決まる

04
で

05
問題

06
直線の 方程式を
辺々6で割って

07
こんな感じに
なったとこから
=t と置けば
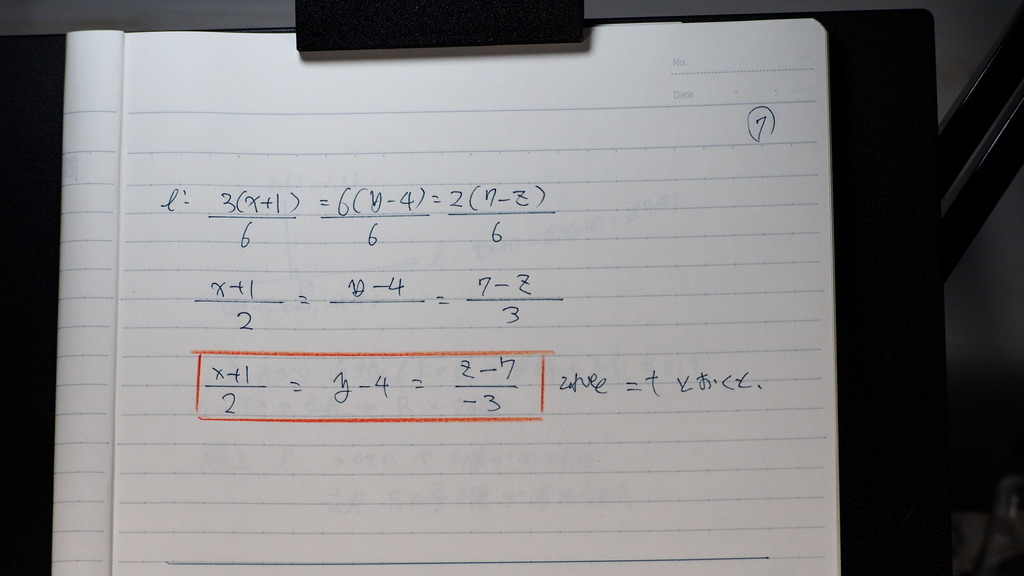
08
直線上の 任意の点は
媒介変数tを 使て
こうだから

09
Aから 直線上の 点に
おろした垂線の
交点を B とすれば
ベクトルの 内積を使って
ABベクトルと
直線の方向係数のベクトルが
垂直になるときの t を
求めればいいのだから

10
まず AB ベクトルは
で 直線の式から

11
方向係数のベクトル
直線に平行が (2,1、-3)である
ので
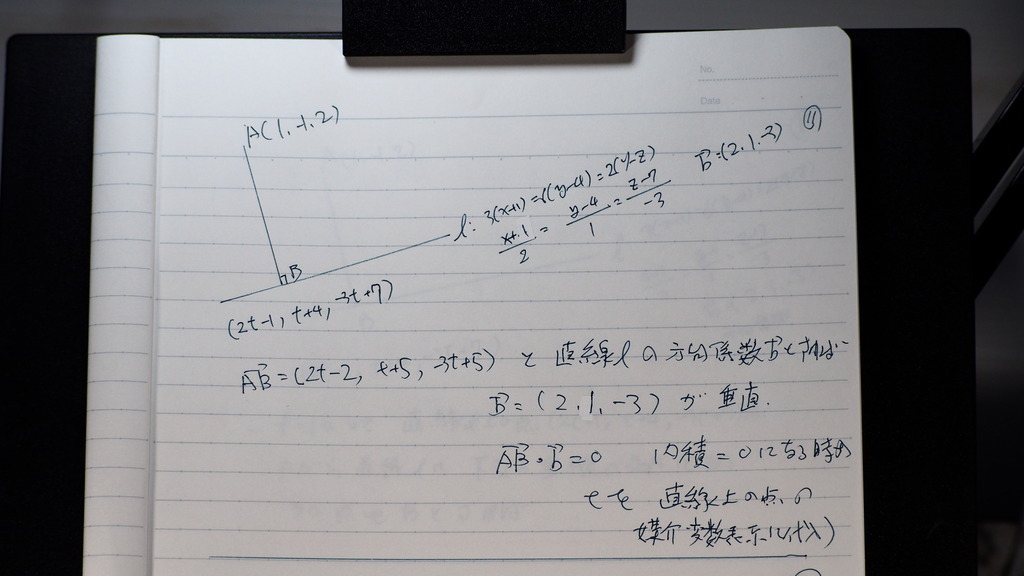
12
この 内積が =0になるとき
t=1

13
t=1を
直線上の
媒介変数表示に
代入すればさ
交点の 座標

14
こうだね

15
次に
この 直線の 方程式は
2点がわかるときの
公式から

16
答は これですが
たまたま
こんな感じのになってます
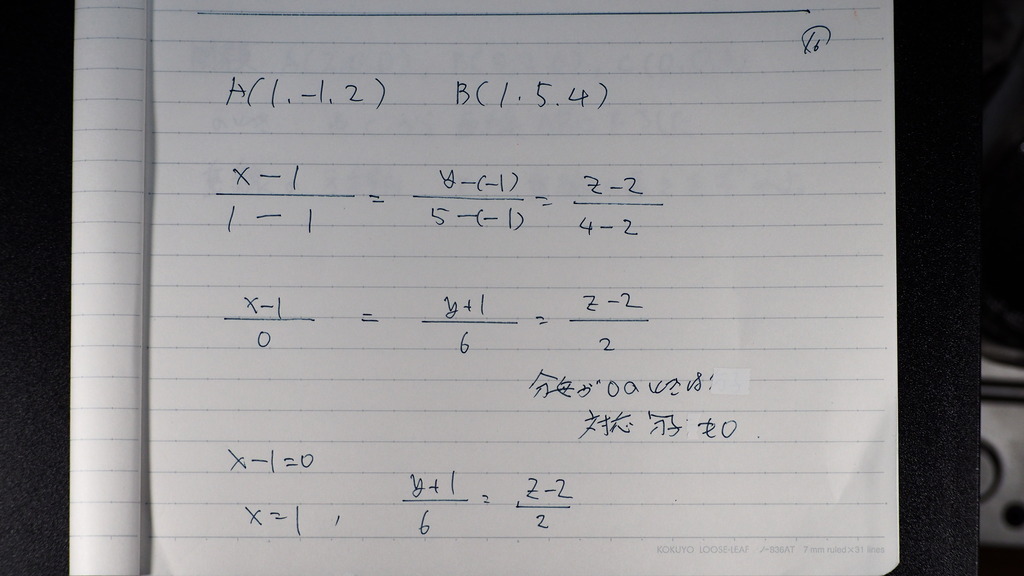
17
整理して
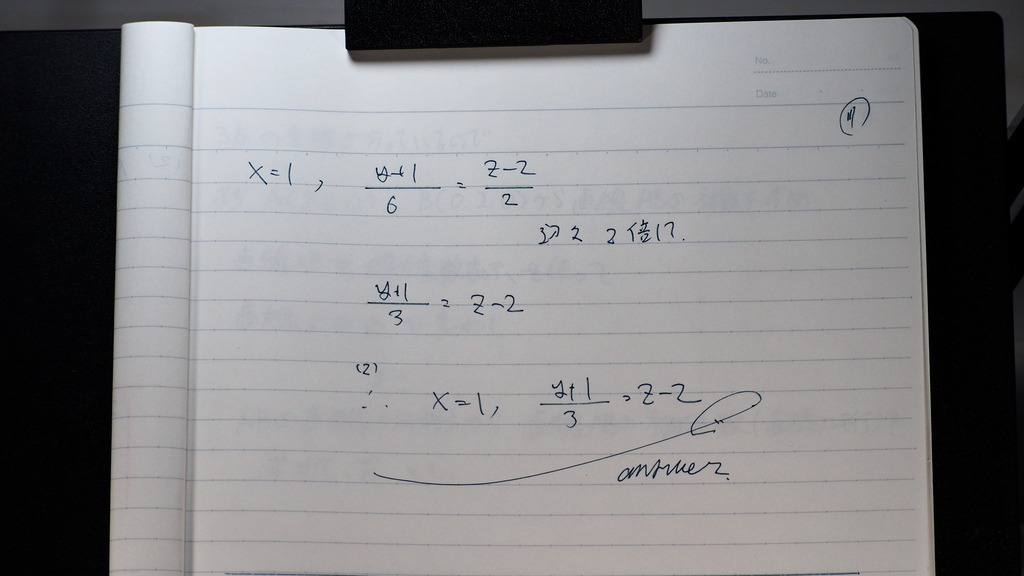
18
三点が 与えられていて
ややこしいんだけどさ

19
そこで
こんな手順で
行きたいと思います
ABの 方程式を求める
直線上の任意の点を
媒介表示にする
直線の方向係数を
方向ベクトル として
控えておく

20
直線上の 任意の点の中から
Cからの 垂線の交点のときを
Pとして
CP ベクトルをもとめ
CPベクトル と 方向ベクトル
の 内積から
t を 割り出し
P の 座標を決定して
C と P から
直線の方程式を
CPベクトルの 絶対値から
垂線の長さを

21
まず
直線の方てい式 AB

22
直線の方程式から
直線じょうの
任意の媒介変数表示
直線の 方向係数ベクトル

23
CP ベクトルは
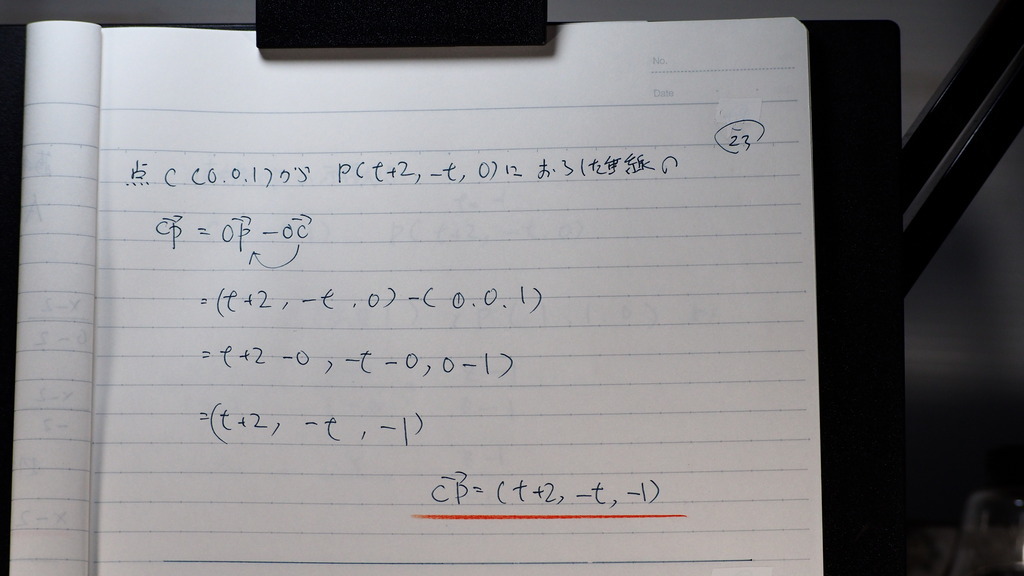
24
内積から tの値は
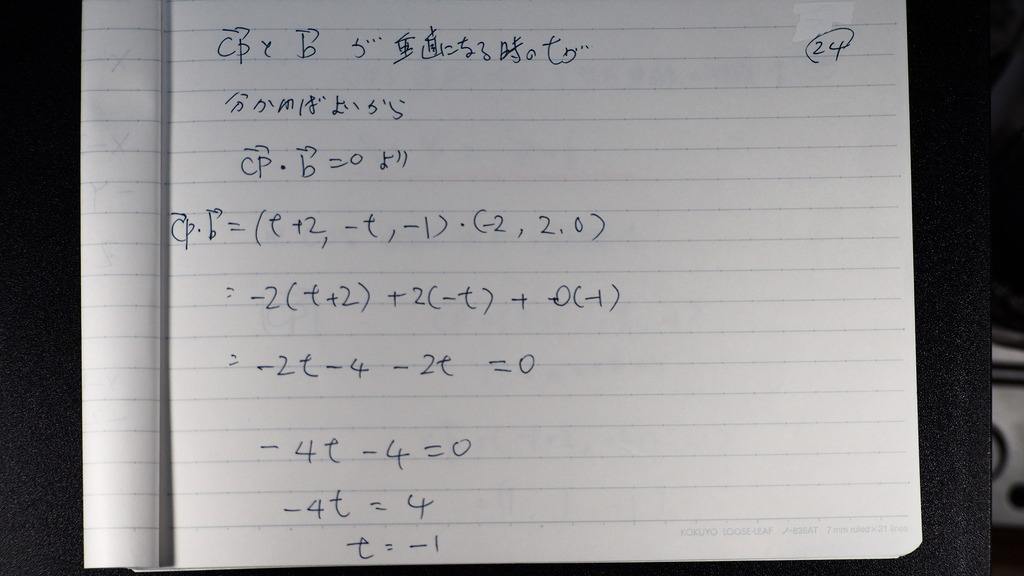
25
するって―ト
Pの座標は
コレダから
直線の方程式は こんなだね
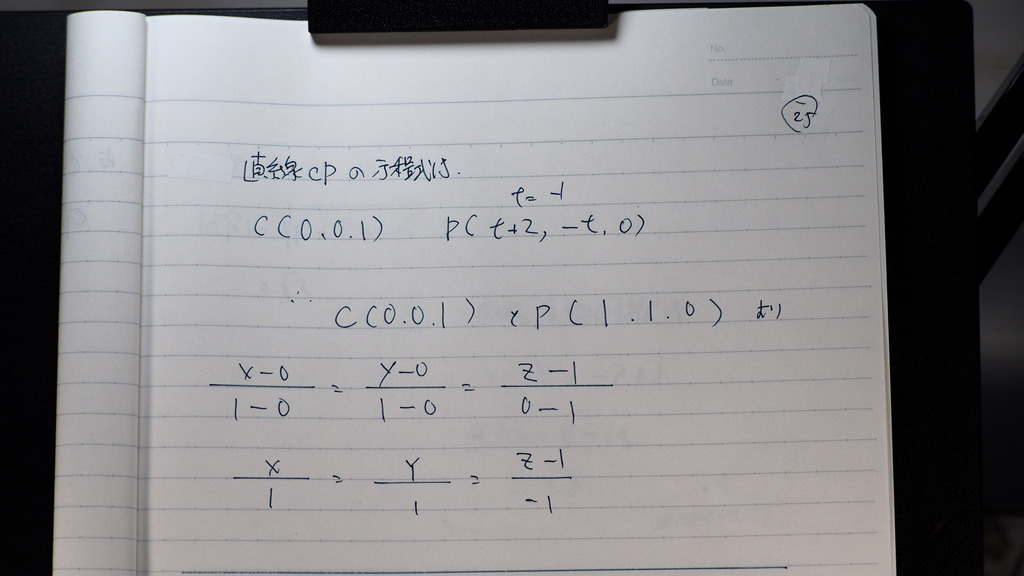
26
さっきの CPベクトルの
絶対値の値は
長さに 成るから

27
√3
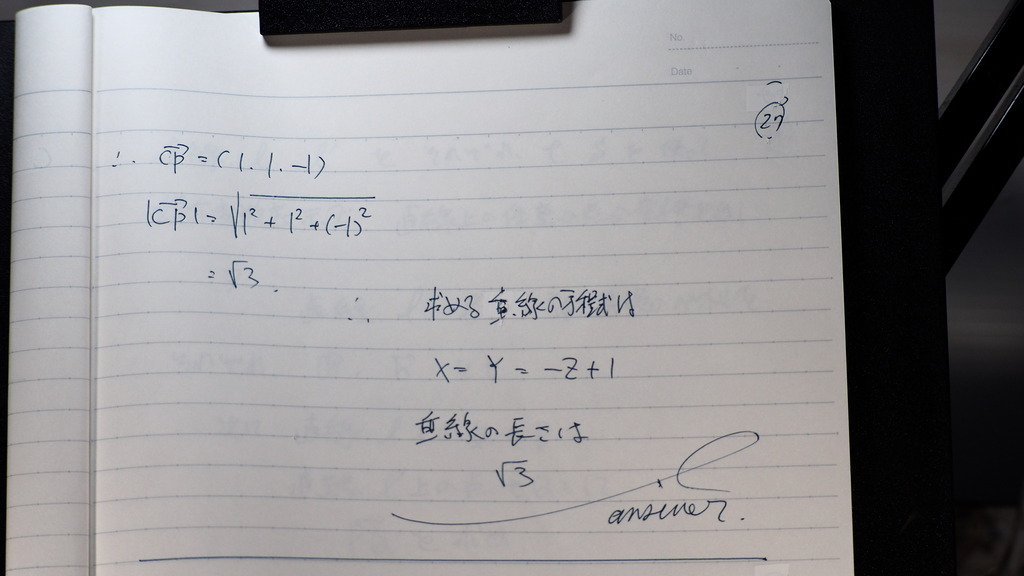
28
これはさ
ややっこしいんだ
問題

29
こんな手順で
ソレゾレ
2本の直線の方程式を
t、s と言う
媒介変数表示で
直線上の任意の点を
表し
また
それぞれの 方向係数を
a,b
で 表し
それぞれの 直線上の
点を P,Q とおいて
PQベクトルを 求めるでよ

30
両方の 直線の方向係数ベクトルに
PQベクトルが 垂直になるように
t s を 割り出すと
tから Pの座標
sから Qの座標
そうすれば 2点が出てるから
直線の方程式がわかると

31
直線L から
媒介変数表示
直線上の任意の点
と
方向係数ベクトル

32
直線L'も
媒介変数表示
直線上の任意の点の座標
と
方向係数ベクトル

33
PQ ベクトルは
こうでしょ
PQ・aは
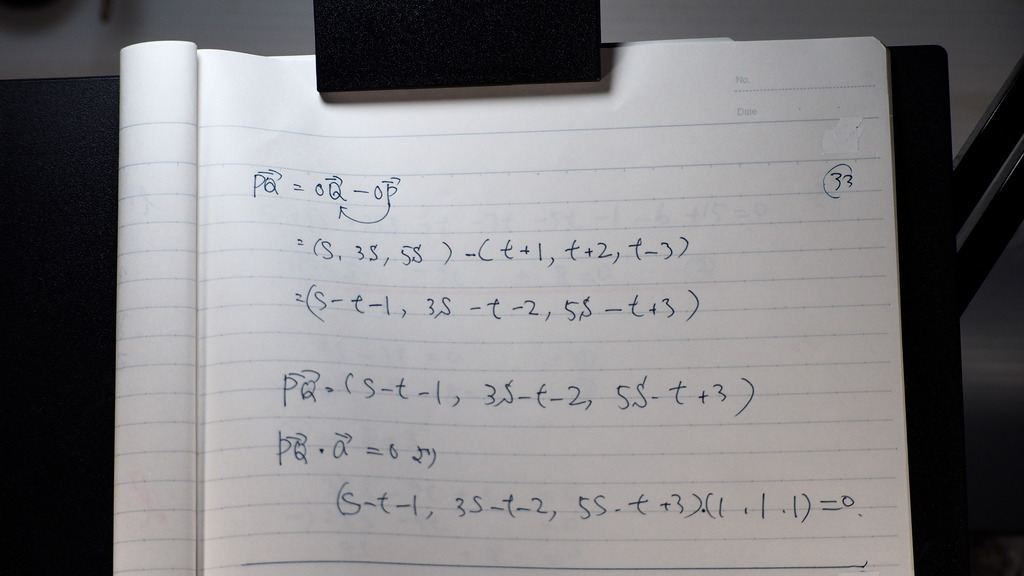
34
➀
PQ・bは
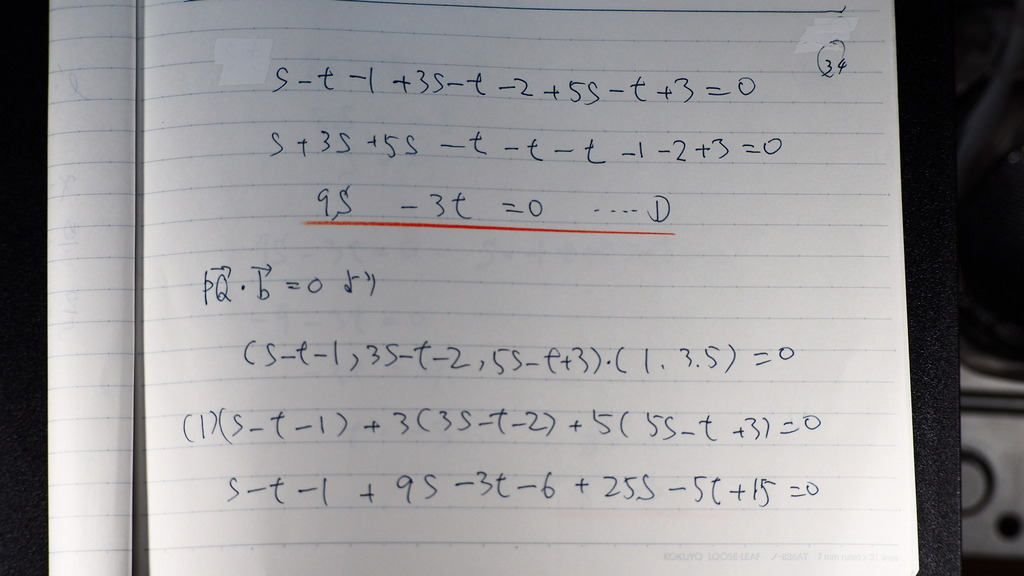
35
②
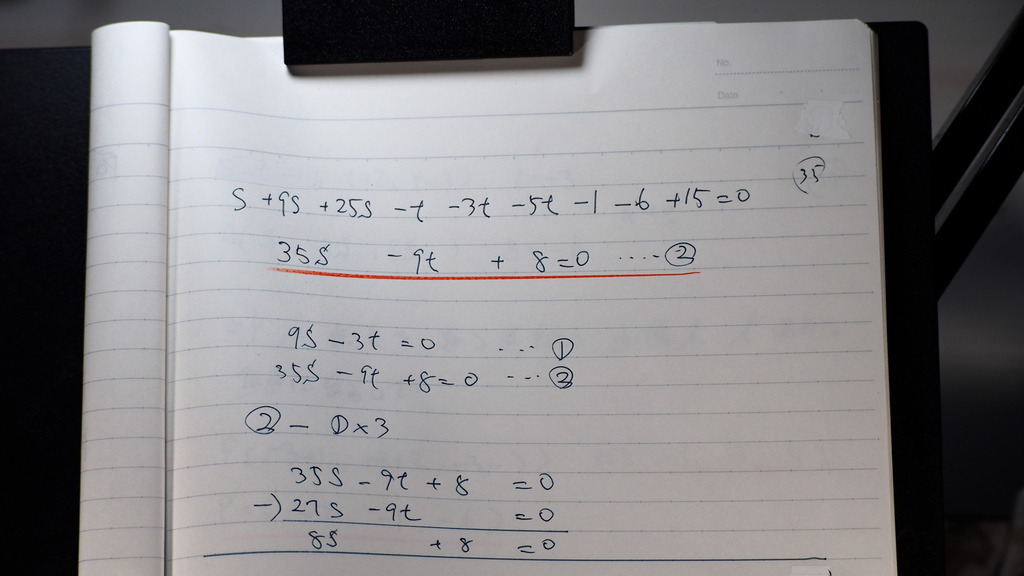
36
t、sが出てきたから
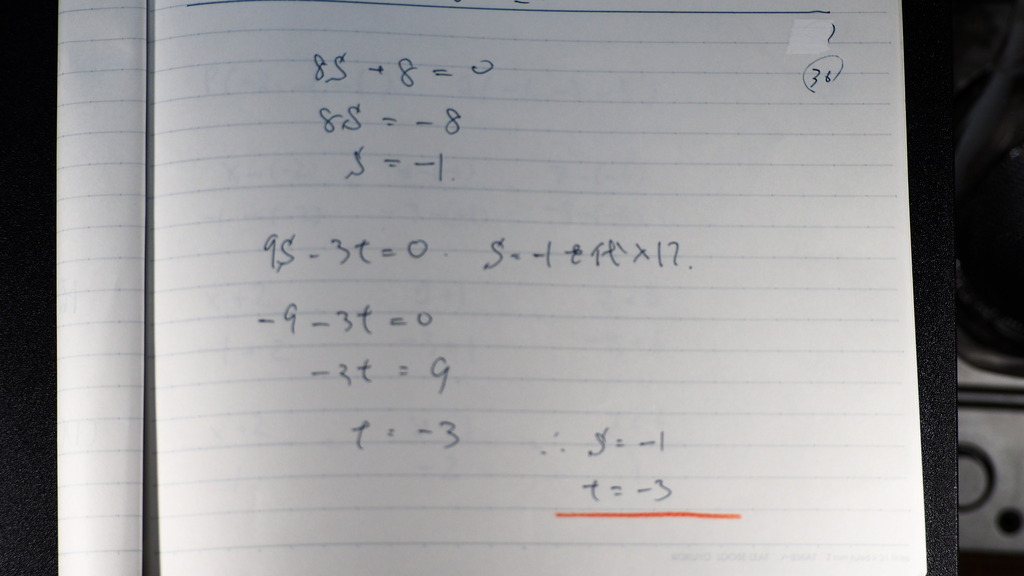
37
ソレゾレ
直線上の
垂直になるときの
座標
P と Q
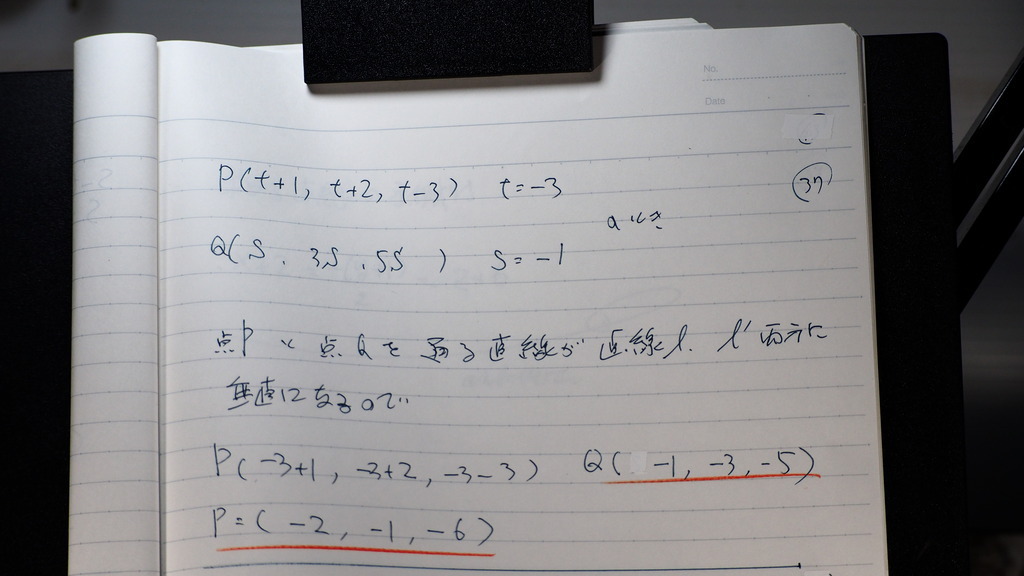
38
これがでれば
あとは 公式で
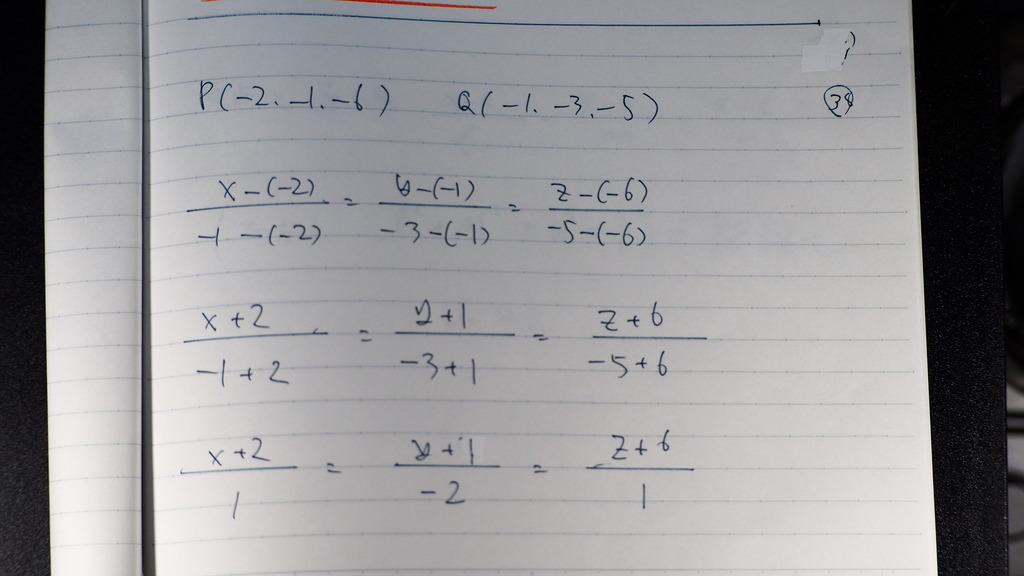
39
こんな感じですか
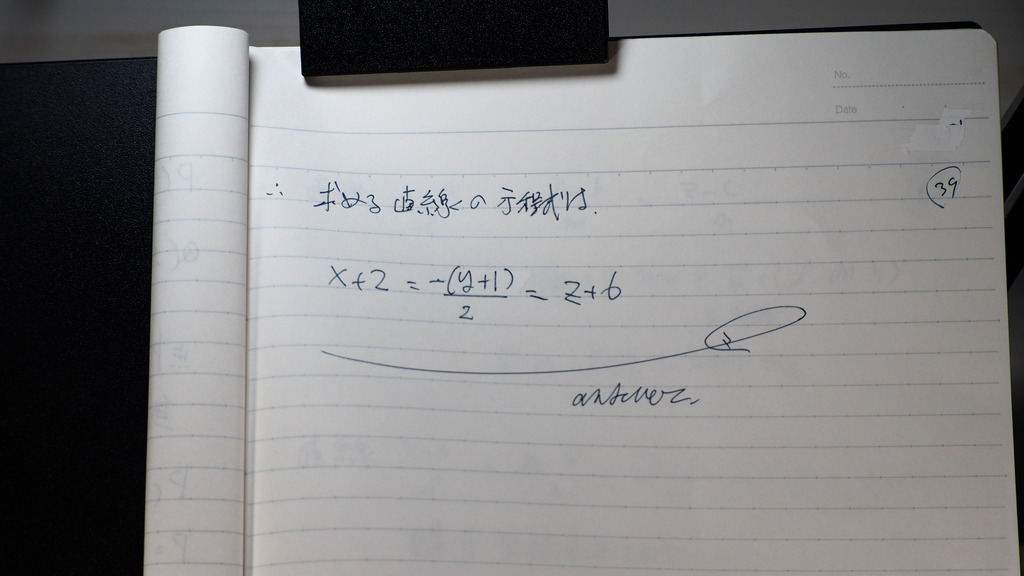
40
これはさ
計算がさ
対辺の様で そうでもなくて
どちなんだ
ま ともかく

41
直線の方向係数ベクトルは
分母から
つぎに
媒介変数表示にして
直線上の任意の点を
表現して

42
こんな感じに

43
原点と 直線上の点を
結ぶベクトルと
方向係数ベクトルが
垂直だから
この 内積の計算から
tの値を割り出し
OPベクトルの
絶対値で
距離を求めれば

44
ここがさ
文字の時は
全く同じだけれど
原点からのベクトルと
直線が 垂直になるとき
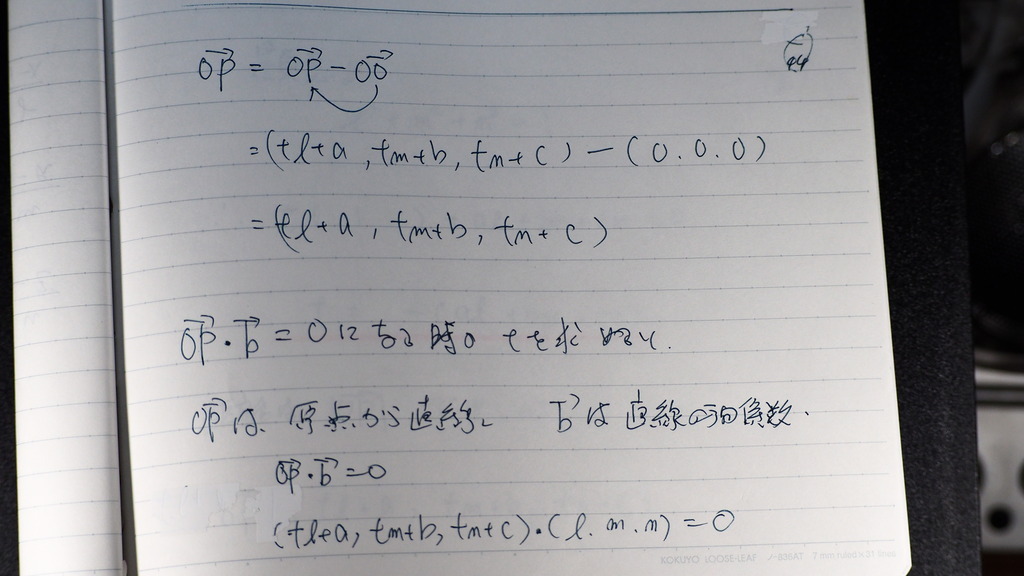
45
なんか 大変そうだな
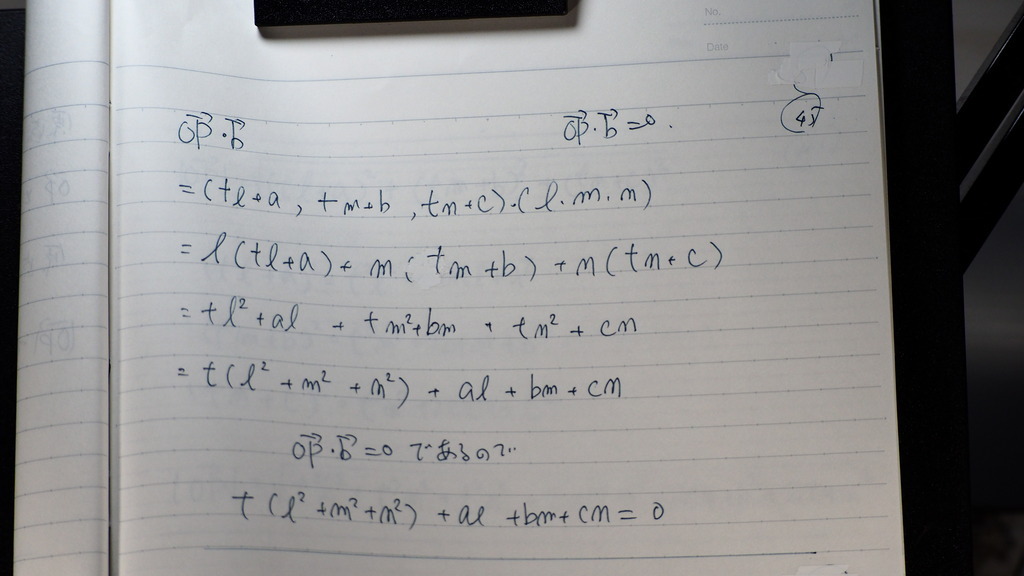
46
tはさ
こうだよ

47
で
いよいよ
距離を
ベクトルの おおきさから
求めると
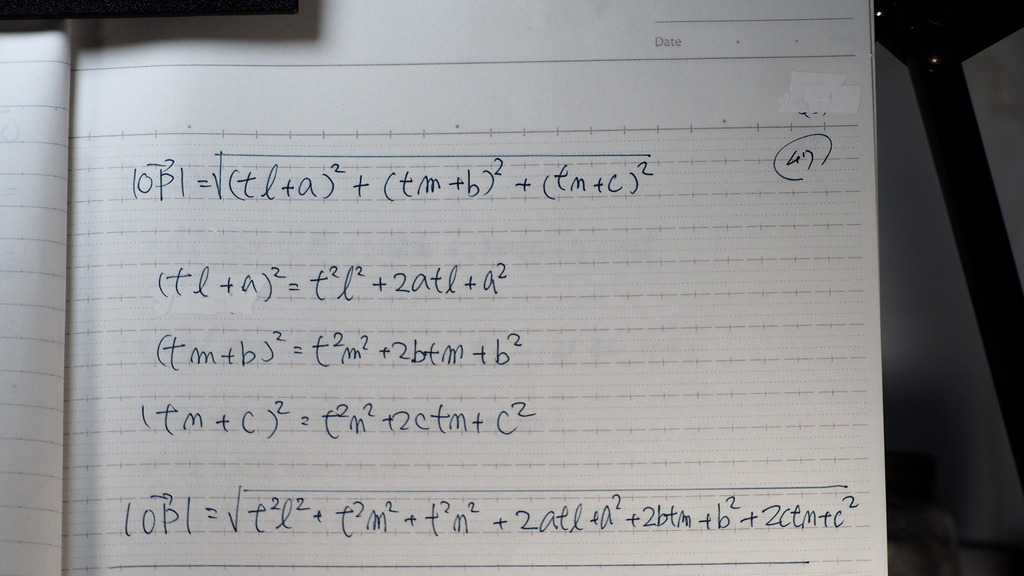
48
大丈夫そうな 感じで
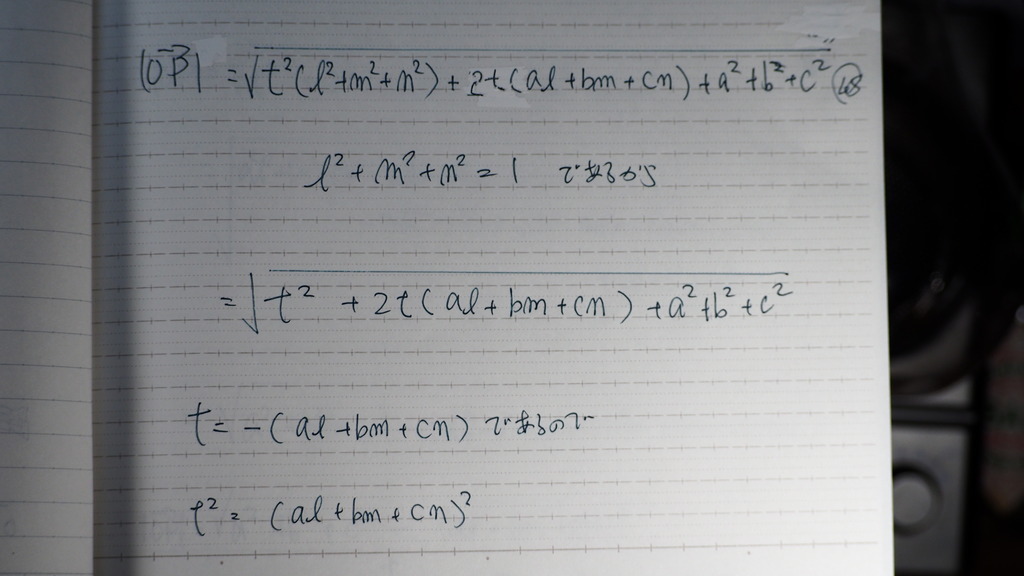
49
うまく できていて
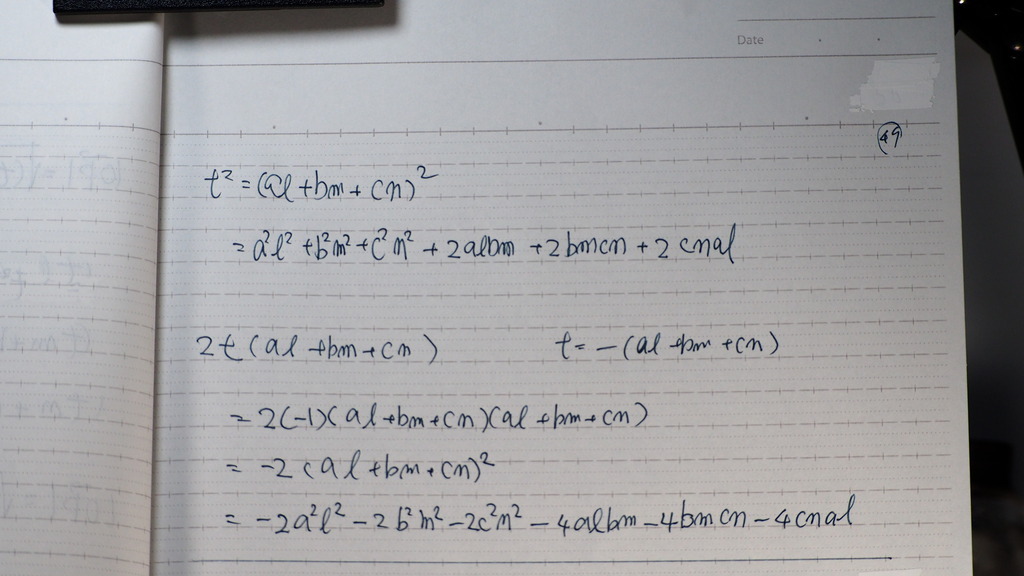
50
こんな感じです
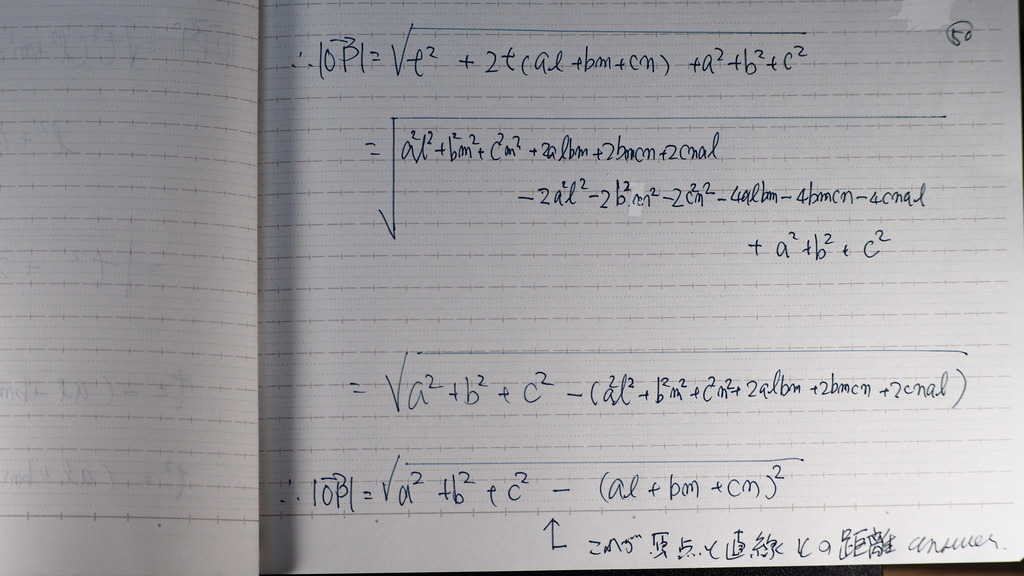
お疲れ様です。
方に捧ぐ大人のさび落とし
さいきんさ
色んな人が いろんなことを
見てるわけで
その中に 私もいたり
私もだったり
つまりね
世の中 不透明で
正直なことを いうと
ただでさえ 不安なのに
絶えられくなる
そんなわけで
余計なことを言わず
けっこう
みまもっててくださってまして
でもさ
お願いだ
受験生は もっと不安だし
親も同じだからさ
と
いうわけで
おもわず 頑張ってしまいました
16:39分
今日は仕上げるか
01
2直線の 垂直条件
まずさ
この辺を もう一回
おさえていただいて
こんな感じに 書けるときの
直線の方程式
分母は 方向係数
直線に 平行なベクトルになってる
02
Pの終点が
bの t倍で
動いていく
03
媒介変数を 使うと
直線上の 任意の点が
表現でき
t の 値によって
点の場所が決まる
04
で
05
問題
06
直線の 方程式を
辺々6で割って
07
こんな感じに
なったとこから
=t と置けば
08
直線上の 任意の点は
媒介変数tを 使て
こうだから
09
Aから 直線上の 点に
おろした垂線の
交点を B とすれば
ベクトルの 内積を使って
ABベクトルと
直線の方向係数のベクトルが
垂直になるときの t を
求めればいいのだから
10
まず AB ベクトルは
で 直線の式から
11
方向係数のベクトル
直線に平行が (2,1、-3)である
ので
12
この 内積が =0になるとき
t=1
13
t=1を
直線上の
媒介変数表示に
代入すればさ
交点の 座標
14
こうだね
15
次に
この 直線の 方程式は
2点がわかるときの
公式から
16
答は これですが
たまたま
こんな感じのになってます
17
整理して
18
三点が 与えられていて
ややこしいんだけどさ
19
そこで
こんな手順で
行きたいと思います
ABの 方程式を求める
直線上の任意の点を
媒介表示にする
直線の方向係数を
方向ベクトル として
控えておく
20
直線上の 任意の点の中から
Cからの 垂線の交点のときを
Pとして
CP ベクトルをもとめ
CPベクトル と 方向ベクトル
の 内積から
t を 割り出し
P の 座標を決定して
C と P から
直線の方程式を
CPベクトルの 絶対値から
垂線の長さを
21
まず
直線の方てい式 AB
22
直線の方程式から
直線じょうの
任意の媒介変数表示
直線の 方向係数ベクトル
23
CP ベクトルは
24
内積から tの値は
25
するって―ト
Pの座標は
コレダから
直線の方程式は こんなだね
26
さっきの CPベクトルの
絶対値の値は
長さに 成るから
27
√3
28
これはさ
ややっこしいんだ
問題
29
こんな手順で
ソレゾレ
2本の直線の方程式を
t、s と言う
媒介変数表示で
直線上の任意の点を
表し
また
それぞれの 方向係数を
a,b
で 表し
それぞれの 直線上の
点を P,Q とおいて
PQベクトルを 求めるでよ
30
両方の 直線の方向係数ベクトルに
PQベクトルが 垂直になるように
t s を 割り出すと
tから Pの座標
sから Qの座標
そうすれば 2点が出てるから
直線の方程式がわかると
31
直線L から
媒介変数表示
直線上の任意の点
と
方向係数ベクトル
32
直線L'も
媒介変数表示
直線上の任意の点の座標
と
方向係数ベクトル
33
PQ ベクトルは
こうでしょ
PQ・aは
34
➀
PQ・bは
35
②
36
t、sが出てきたから
37
ソレゾレ
直線上の
垂直になるときの
座標
P と Q
38
これがでれば
あとは 公式で
39
こんな感じですか
40
これはさ
計算がさ
対辺の様で そうでもなくて
どちなんだ
ま ともかく
41
直線の方向係数ベクトルは
分母から
つぎに
媒介変数表示にして
直線上の任意の点を
表現して
42
こんな感じに
43
原点と 直線上の点を
結ぶベクトルと
方向係数ベクトルが
垂直だから
この 内積の計算から
tの値を割り出し
OPベクトルの
絶対値で
距離を求めれば
44
ここがさ
文字の時は
全く同じだけれど
原点からのベクトルと
直線が 垂直になるとき
45
なんか 大変そうだな
46
tはさ
こうだよ
47
で
いよいよ
距離を
ベクトルの おおきさから
求めると
48
大丈夫そうな 感じで
49
うまく できていて
50
こんな感じです
お疲れ様です。