2022年12月07日
22027大人のさび落とし 空間座標とベクトル 空間の直線の方程式
大人のさび落とし
空間座標とベクトル 空間の直線の方程式
01
その前に
空間の 直線と 平面の
知識を 詰め込んで
行ってみましょう
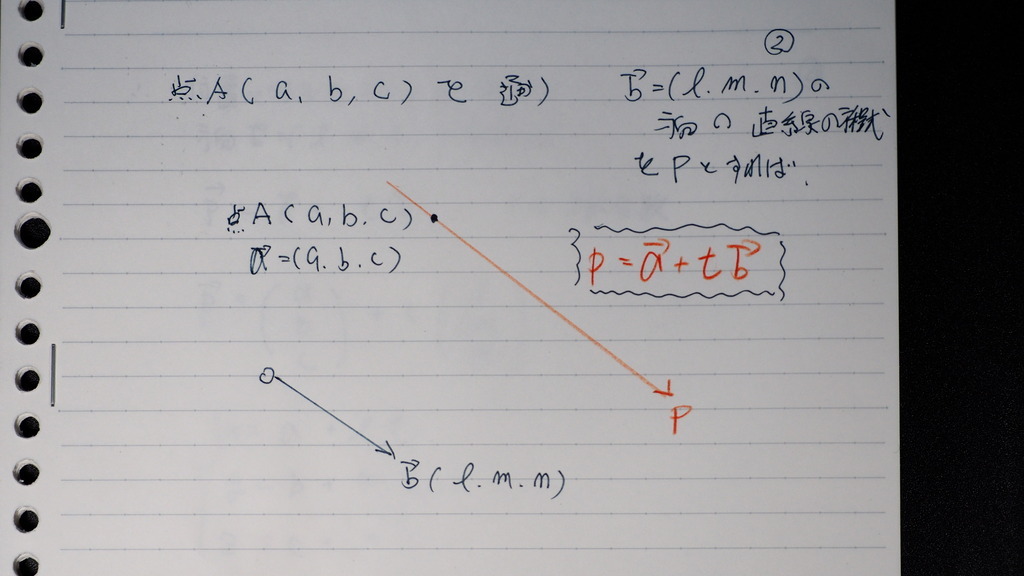
空間の直線の 方程式は
通過点 の 位置ベクトルと
方向係数が わかれば

02
これと これ
03
Pは aベクトルと
APベクトルの 和
APベクトルは
bベクトルの実数倍
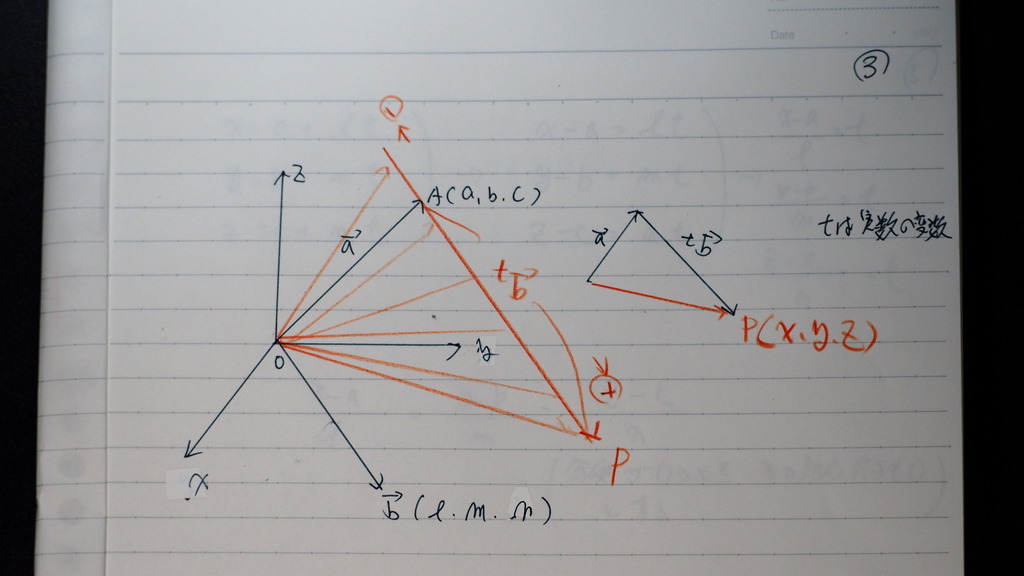
その結果
OPの 終点Pの 軌跡は
赤い直線になると
04
これを 媒介係数を使って
直交座標 (x、y、z)に分解すれば
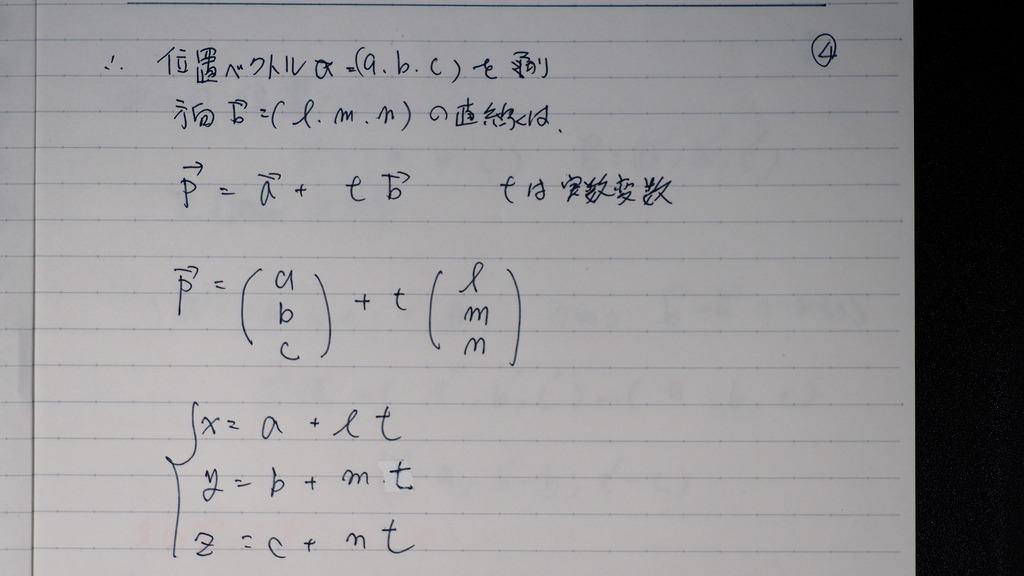
05
これらな
みな t=に形に
なるから
イコールで 結べて
こんな感じで 表せる
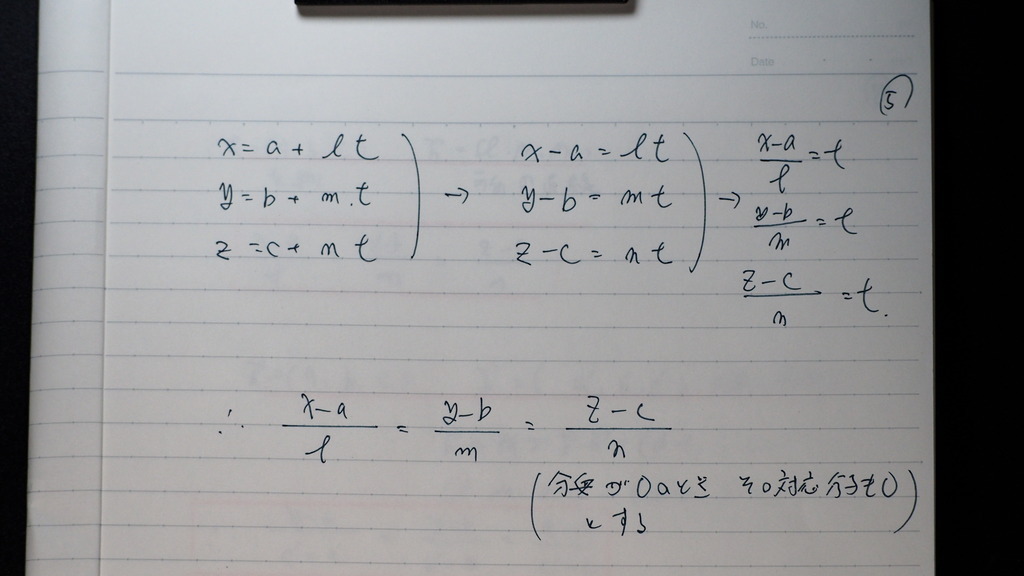
06
2点を 通るときは
一点は 通過点に考え
二点から
方向係数を 出せば
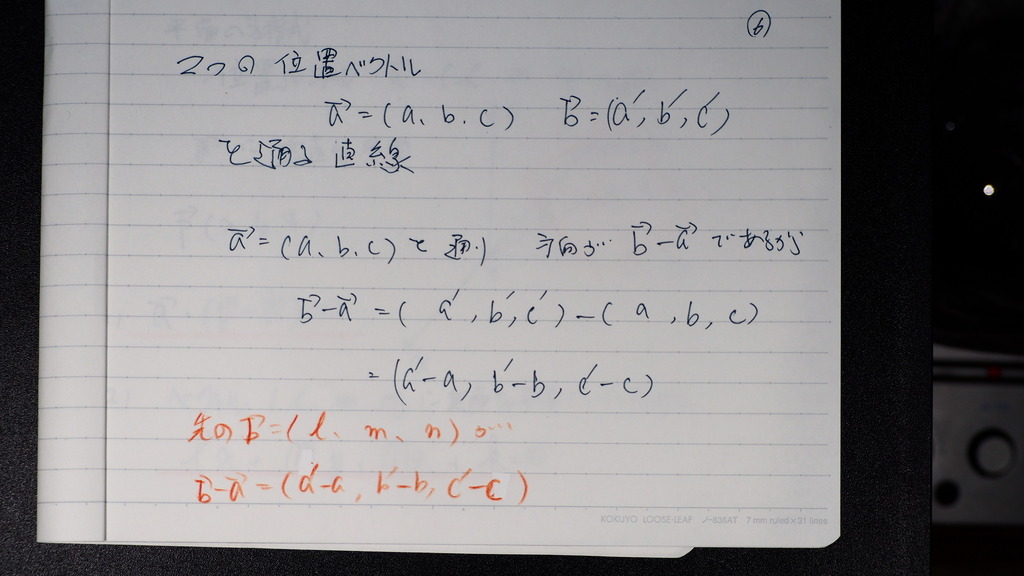
07
さっきと
おなじに
考えて
こんな感じでしょ
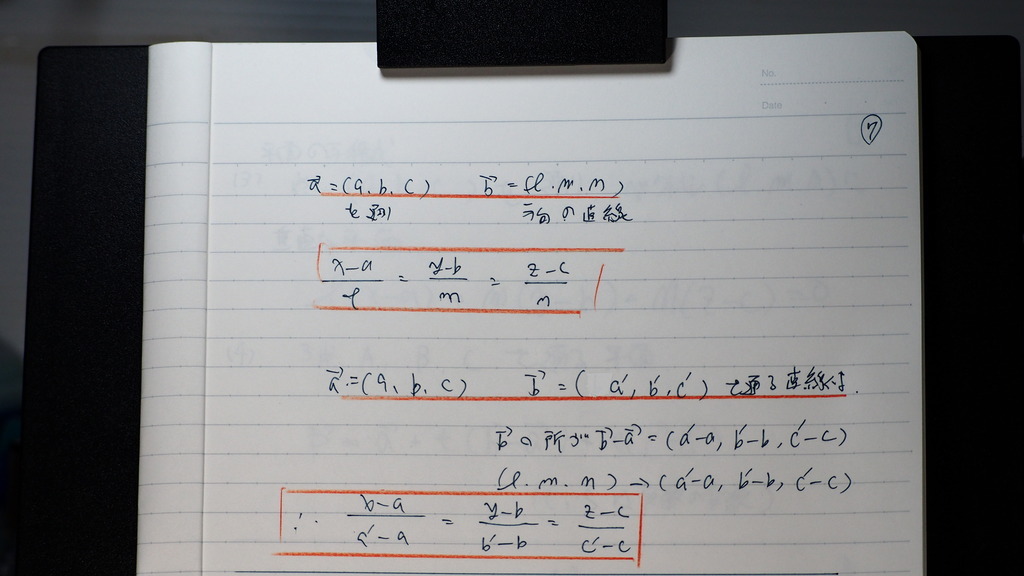
08
へてから
今度は
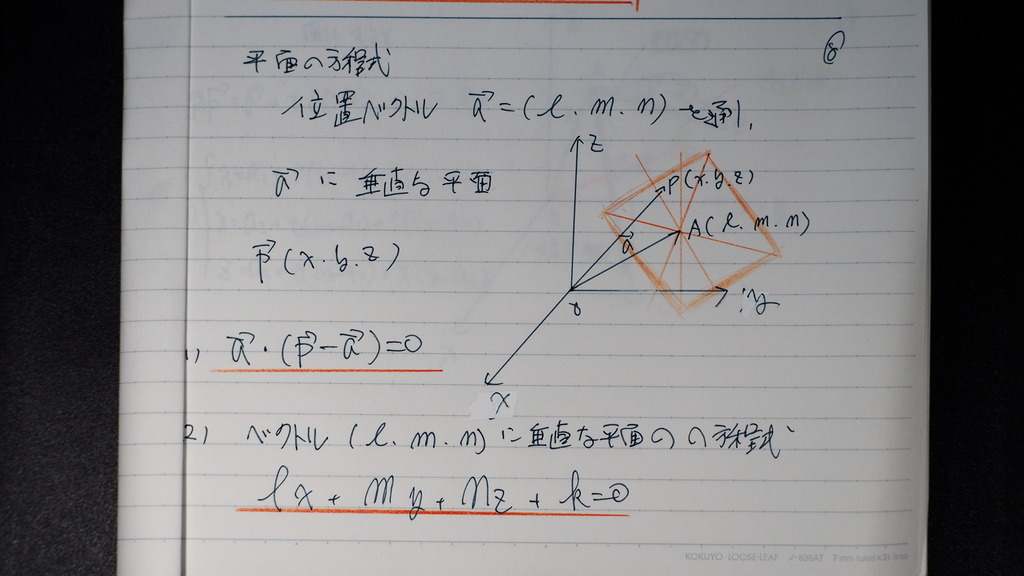
平面の方程式
パターン (1)
aベクトル を 通り
aベクトルに 垂直な平面
pベクトル マイナスbベクトルの
直線の中で
aベクトル 垂直なもの
の 集まり (平面)
(2)
ベクトル (L,M,N)に 垂直な
方程式
09
(3)
点Aを 通り
ベクトル(L,M,N)に垂直な 平面
(4)
3点 A,B,C を
通るときの 平面

10
図にすると
こんなだって
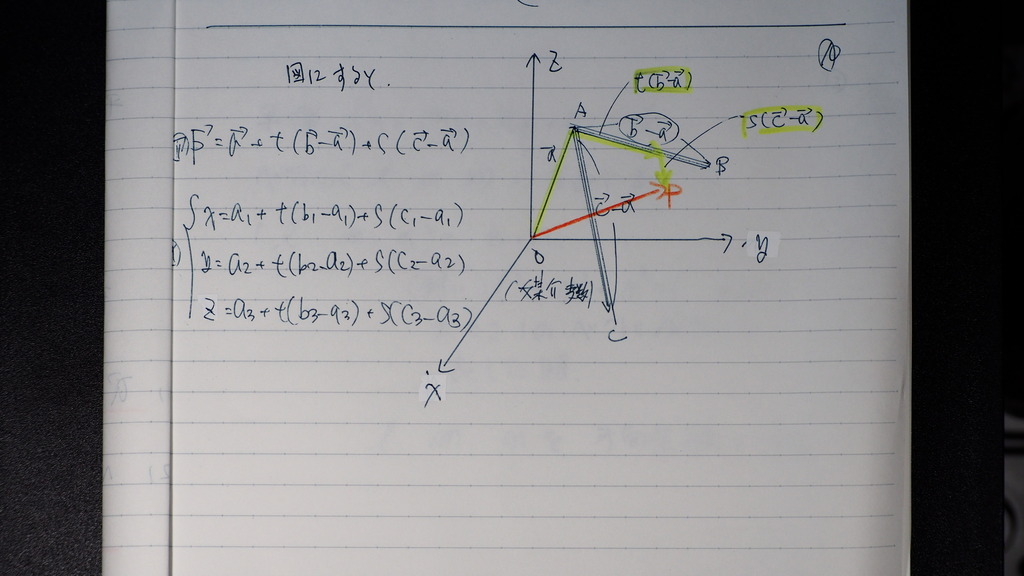
11
(5)
2平面が 交わるときは

12
捕捉

13
これらを 踏まえまして
今日は直線の方程式
問題行ってみましょう

14
(1)
ベクトルの 足し算で
OP 出てくるんですが
AP ベクトルのところは
bベクトルの実数倍
であるから

15
(2)
それぞれ
直交成分に すると
列で 書いた方が
分かりやすいカナと思って
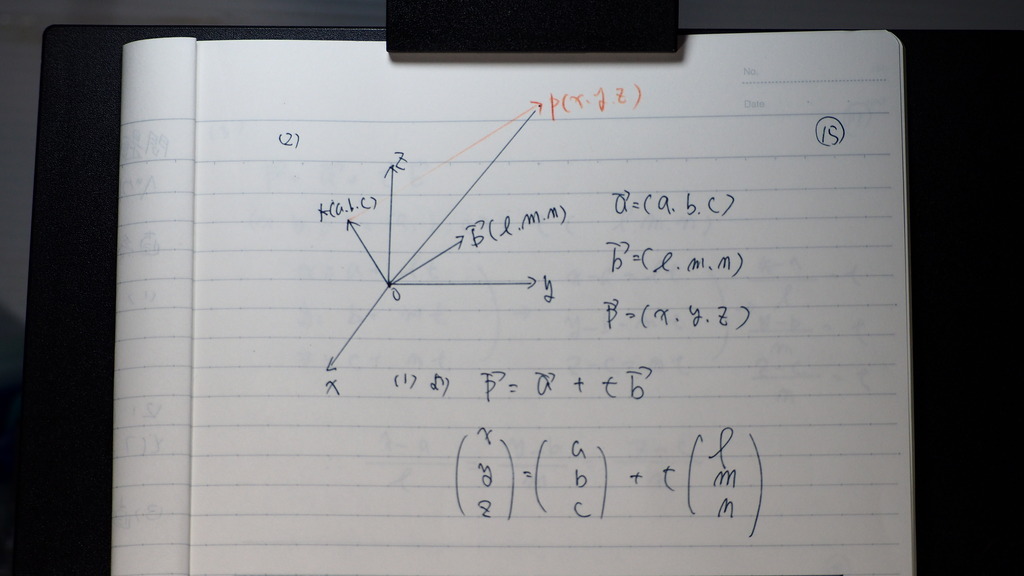
16
行で 書くと こんなだけど
同じことだからさ
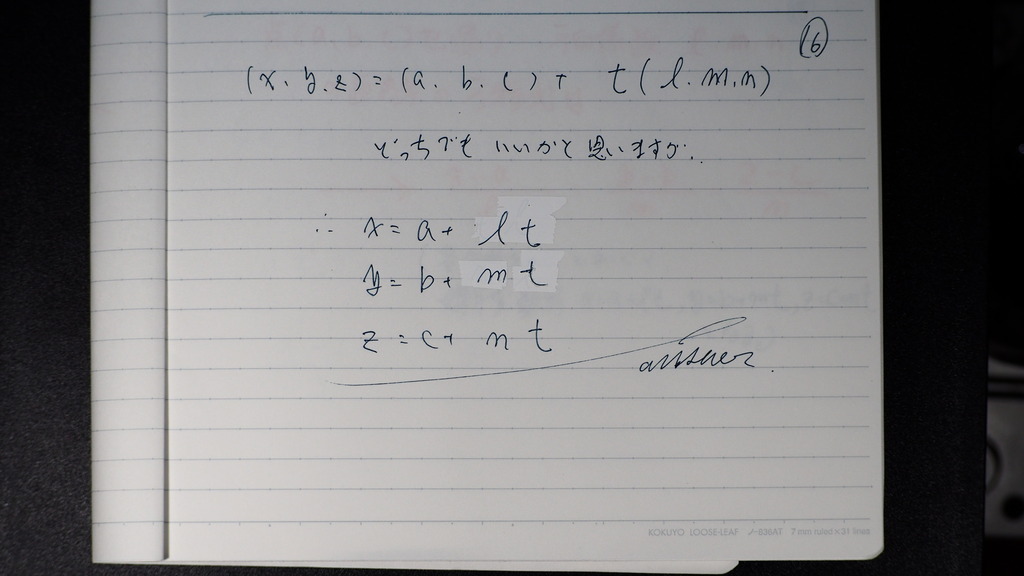
17
(3)
媒介変数付を
変形してくと
=t になるので
こんな 形に 書けますよ
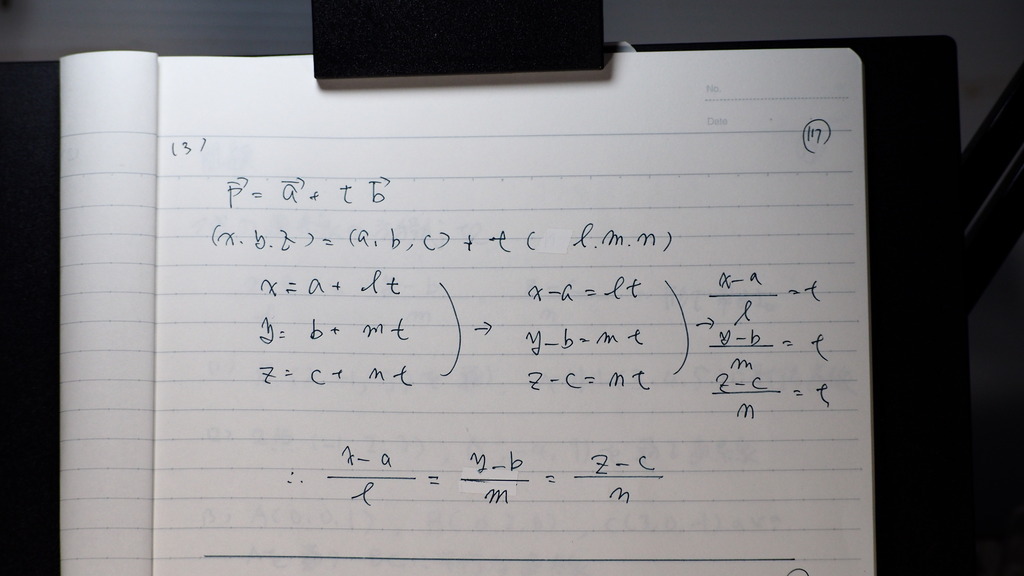
18
こんな 感じの 理論ですが

19
問題
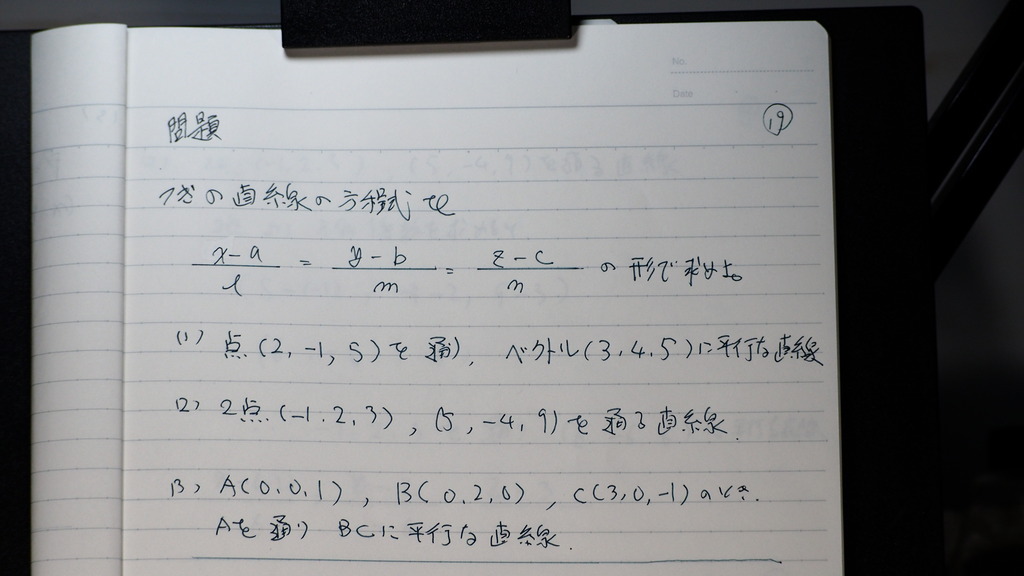
20
まず
(1) 理論に そのまま入れれば

21
片方を 通過点として
2点から 方向係数を 出せば
理論に入れて
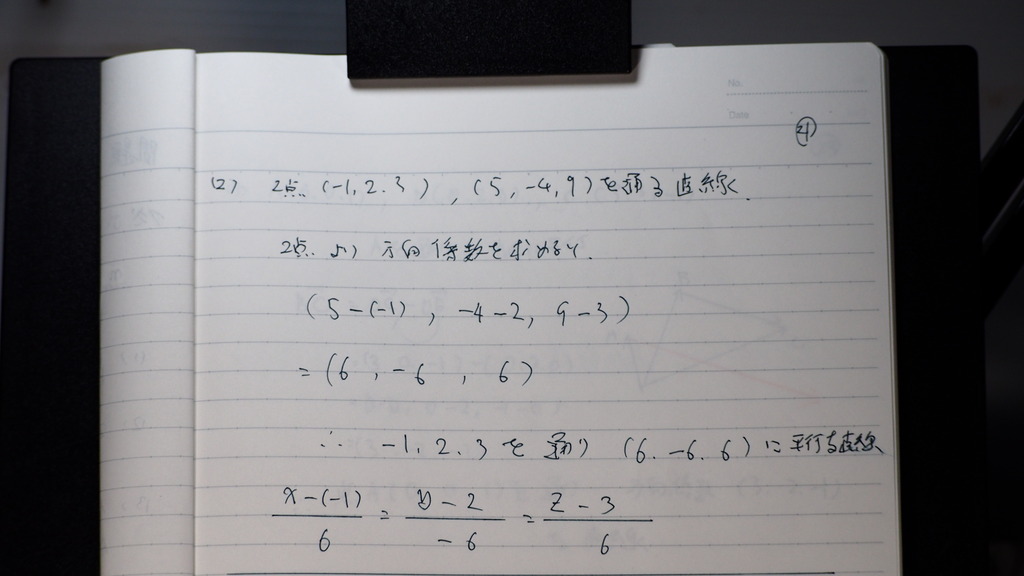
22
分母を はらうと
こんなですか
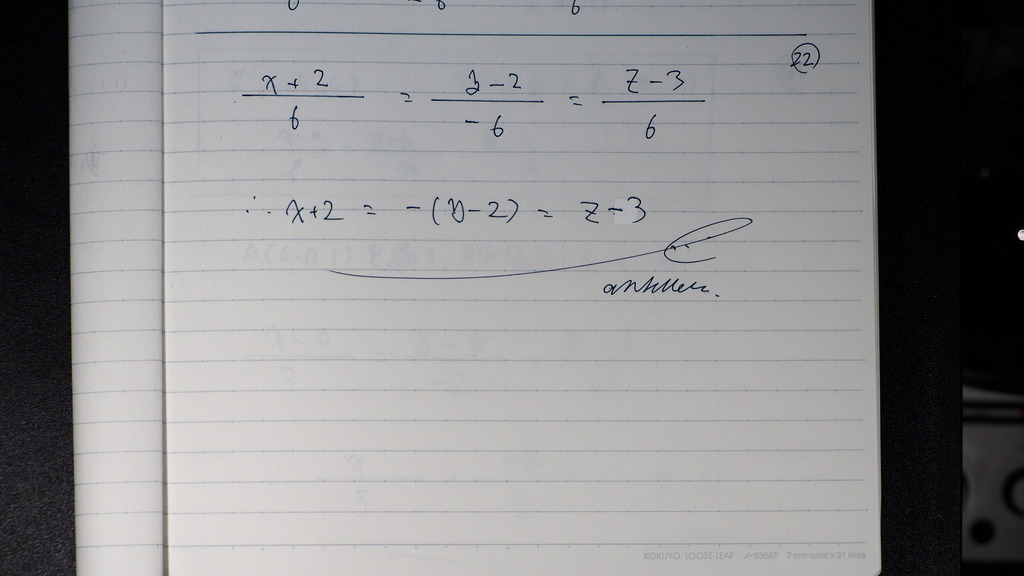
23
これもさ
似たようなもの
Aを とおって
方向係数は BC
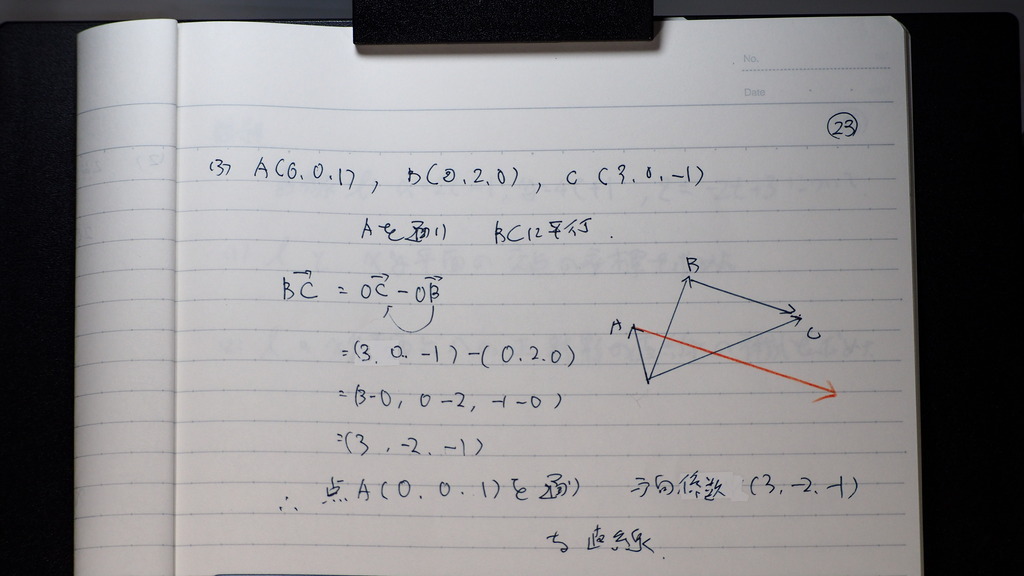
24
これを 理論に
入れれば

25
問題
今度は
媒介変数で
書いてあるけど

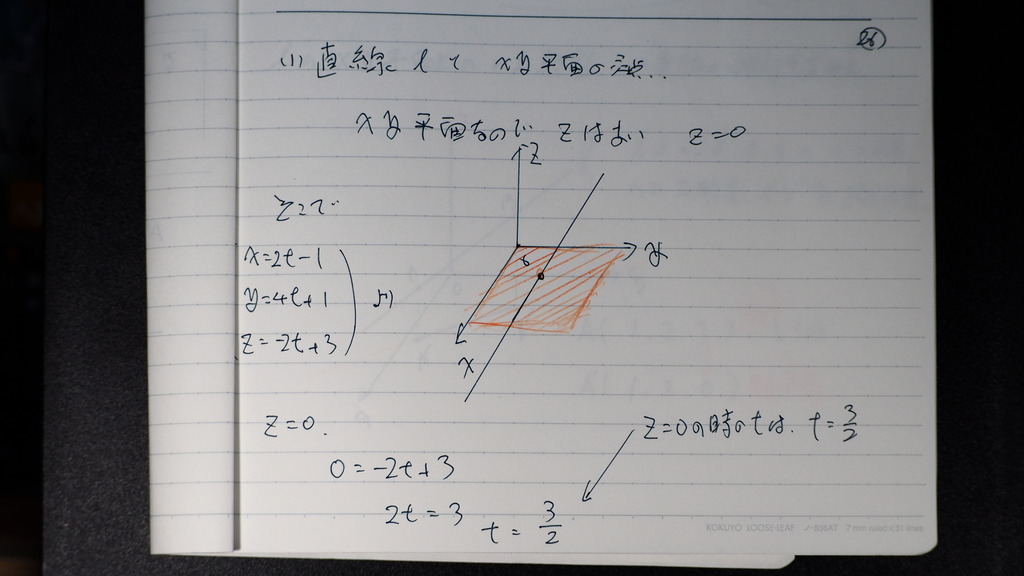
26
Z=0 ていうのが
XY 平面じゃナイスカ
だから
t を 先に 求めて
27
この時の 座標を
計算すると

28
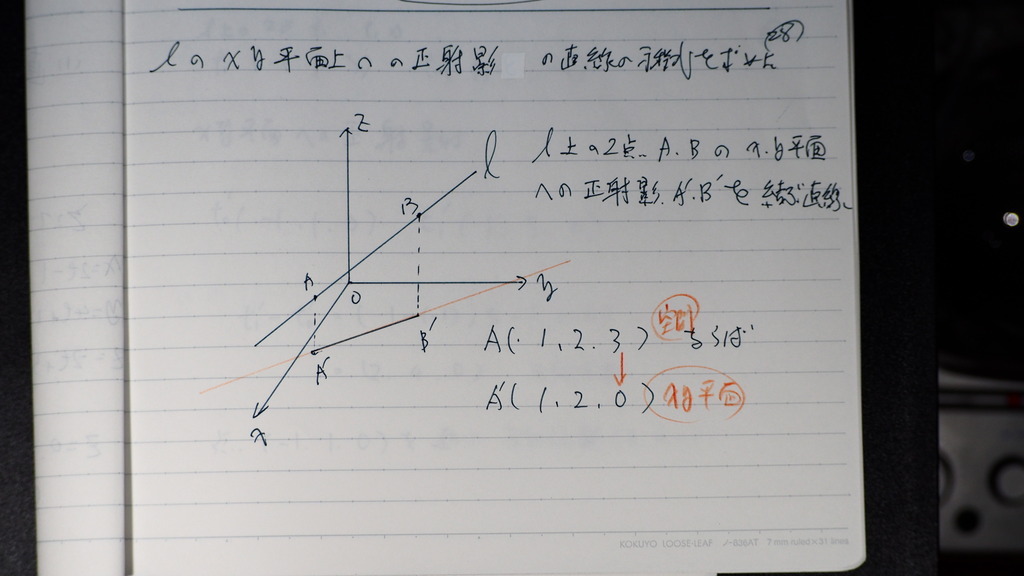
直線Lの XY平面への正射影
影は XY 平面上なので
Z成分が 0
A A'
みたいに
z成分が 0
29
そこで
この 直線Lで
tに 何か 値を 2つ
代入して
その時の 座標を 求め
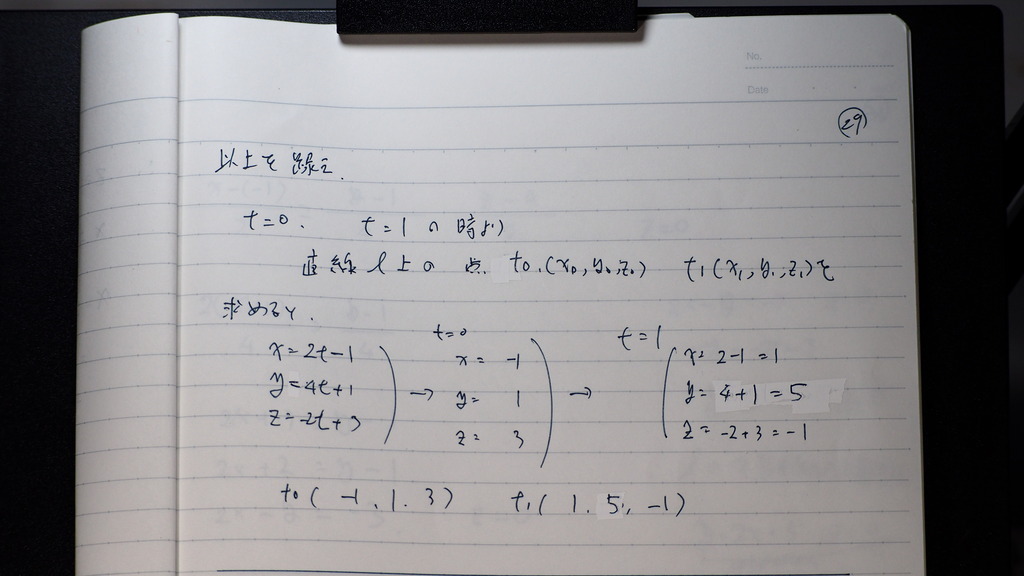
30
影は Z成分が 0であるので
あとは
方向係数 2,4,0
どちらか 点を 持ってきて
ここを 通るから

31
こんな感じで
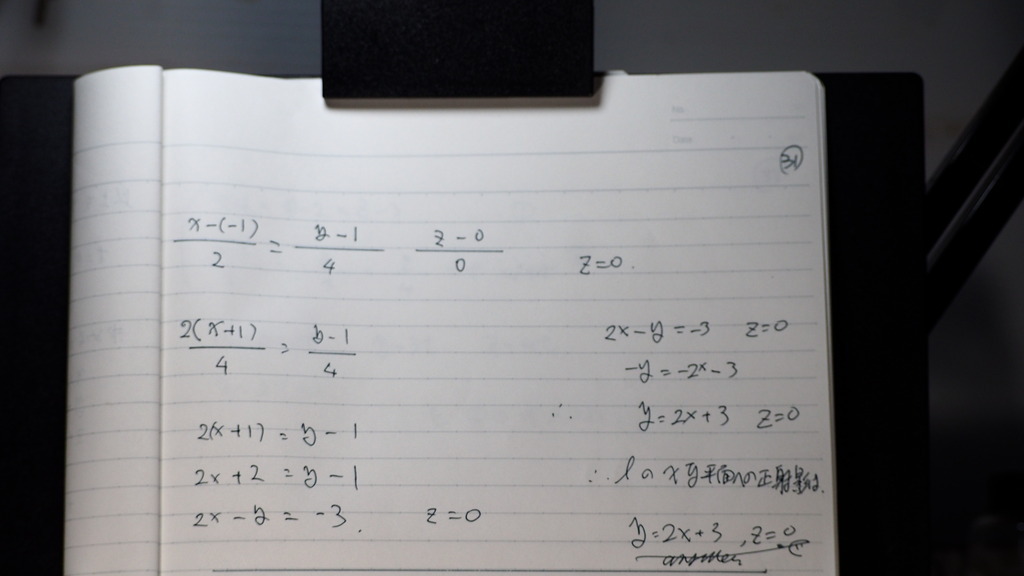
32
問題
2直線が 交わるとき
aの値と 交点の座標
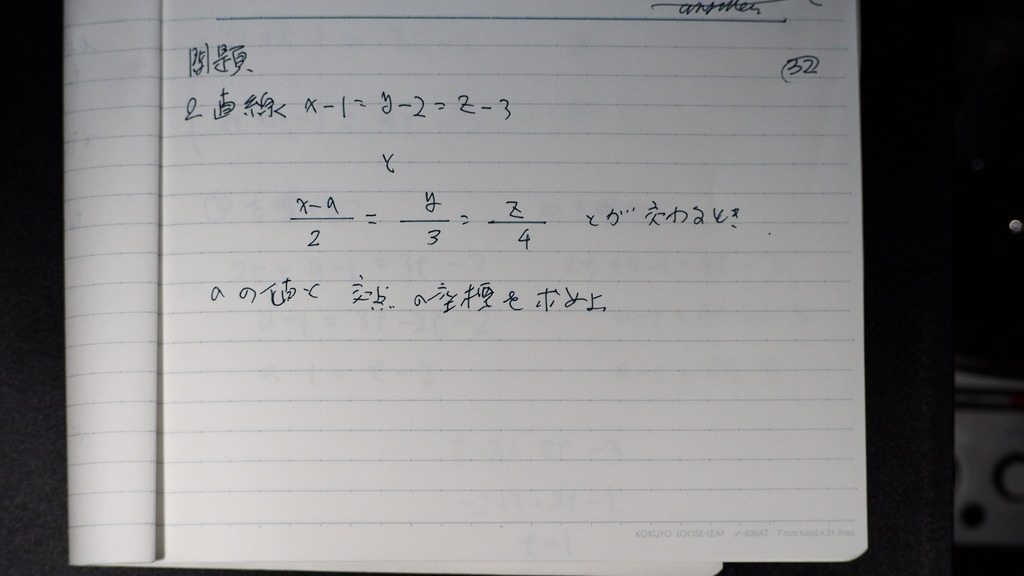
33
➀②から
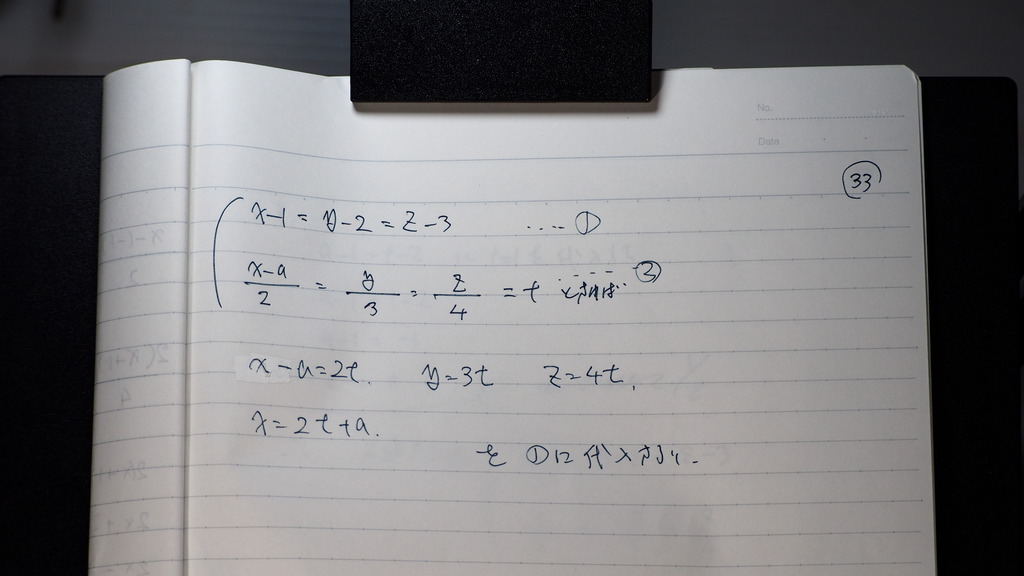
34
連立にして
2式 2変数であるから
出るわけで
tがでれば
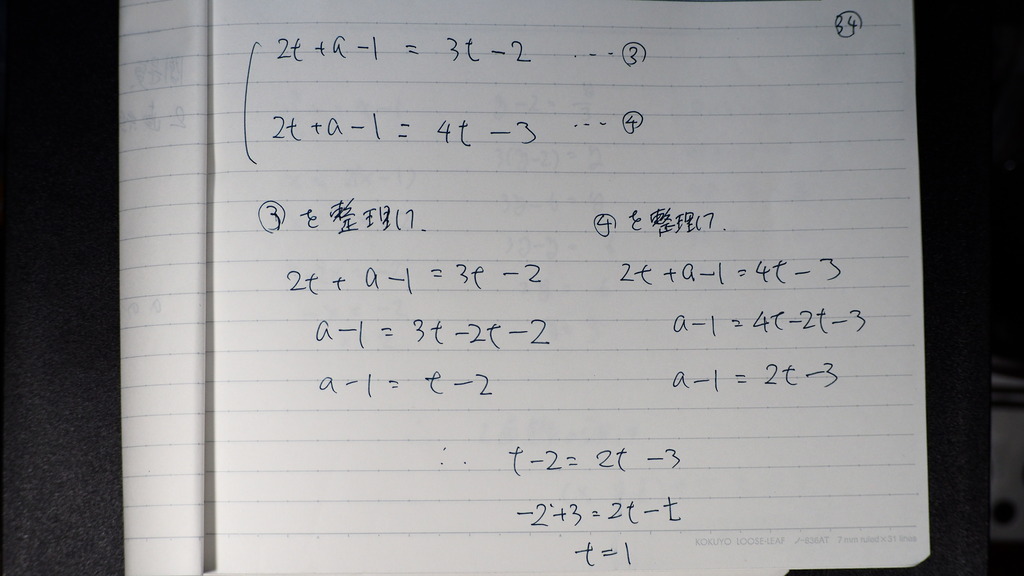
35
a=0
出てきた
二つの 直線の交点は
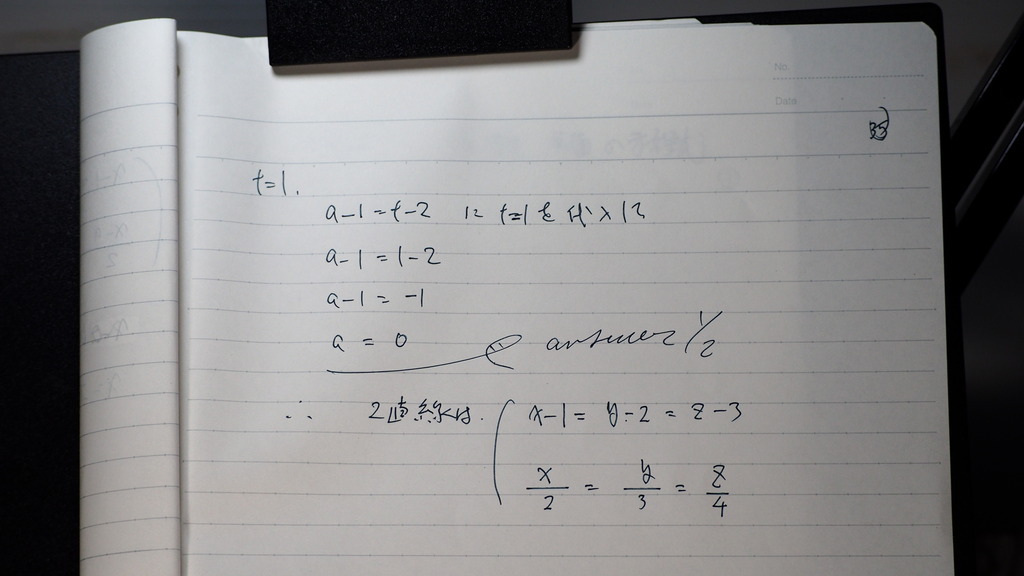
36
それぞれ x、y、z成分の
値が 同じくなるところなんだから
こんな感じで

おつかれさまです。
空間座標とベクトル 空間の直線の方程式
01
その前に
空間の 直線と 平面の
知識を 詰め込んで
行ってみましょう
空間の直線の 方程式は
通過点 の 位置ベクトルと
方向係数が わかれば
02
これと これ
03
Pは aベクトルと
APベクトルの 和
APベクトルは
bベクトルの実数倍
その結果
OPの 終点Pの 軌跡は
赤い直線になると
04
これを 媒介係数を使って
直交座標 (x、y、z)に分解すれば
05
これらな
みな t=に形に
なるから
イコールで 結べて
こんな感じで 表せる
06
2点を 通るときは
一点は 通過点に考え
二点から
方向係数を 出せば
07
さっきと
おなじに
考えて
こんな感じでしょ
08
へてから
今度は
平面の方程式
パターン (1)
aベクトル を 通り
aベクトルに 垂直な平面
pベクトル マイナスbベクトルの
直線の中で
aベクトル 垂直なもの
の 集まり (平面)
(2)
ベクトル (L,M,N)に 垂直な
方程式
09
(3)
点Aを 通り
ベクトル(L,M,N)に垂直な 平面
(4)
3点 A,B,C を
通るときの 平面
10
図にすると
こんなだって
11
(5)
2平面が 交わるときは
12
捕捉
13
これらを 踏まえまして
今日は直線の方程式
問題行ってみましょう
14
(1)
ベクトルの 足し算で
OP 出てくるんですが
AP ベクトルのところは
bベクトルの実数倍
であるから
15
(2)
それぞれ
直交成分に すると
列で 書いた方が
分かりやすいカナと思って
16
行で 書くと こんなだけど
同じことだからさ
17
(3)
媒介変数付を
変形してくと
=t になるので
こんな 形に 書けますよ
18
こんな 感じの 理論ですが
19
問題
20
まず
(1) 理論に そのまま入れれば
21
片方を 通過点として
2点から 方向係数を 出せば
理論に入れて
22
分母を はらうと
こんなですか
23
これもさ
似たようなもの
Aを とおって
方向係数は BC
24
これを 理論に
入れれば
25
問題
今度は
媒介変数で
書いてあるけど
26
Z=0 ていうのが
XY 平面じゃナイスカ
だから
t を 先に 求めて
27
この時の 座標を
計算すると
28
直線Lの XY平面への正射影
影は XY 平面上なので
Z成分が 0
A A'
みたいに
z成分が 0
29
そこで
この 直線Lで
tに 何か 値を 2つ
代入して
その時の 座標を 求め
30
影は Z成分が 0であるので
あとは
方向係数 2,4,0
どちらか 点を 持ってきて
ここを 通るから
31
こんな感じで
32
問題
2直線が 交わるとき
aの値と 交点の座標
33
➀②から
34
連立にして
2式 2変数であるから
出るわけで
tがでれば
35
a=0
出てきた
二つの 直線の交点は
36
それぞれ x、y、z成分の
値が 同じくなるところなんだから
こんな感じで
おつかれさまです。