2022年12月05日
22026 大人のさび落とし 空間座標とベクトル 三角関数の加法定理
大人のさび落とし
空間座標と
01
三角関数で
加法定理と言うのがあるですが
それを
内積を使って
証明して
という問題

02
こんな
感じに
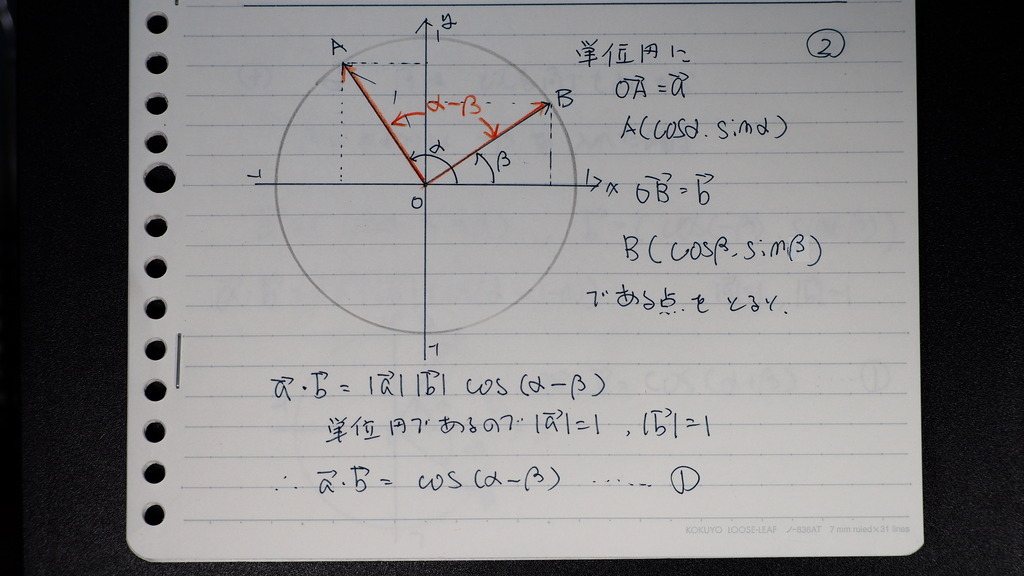
単位円を使って
Aベクトル Bベクトル
それぞれ
x軸となす角が
α 、 β
これを
座標を
使って 表せば
03
動径の 長さは 1だから
x成分は コサイン
y成分は サイン
矢線ベクトルの 内積の
定義式は
絶対値 A 、B は 共に1
コサインは Θがα-β...➀
成分の 内積は
コサインα コサインβ +
サインα サインβ.....②
➀②から
なったデショ
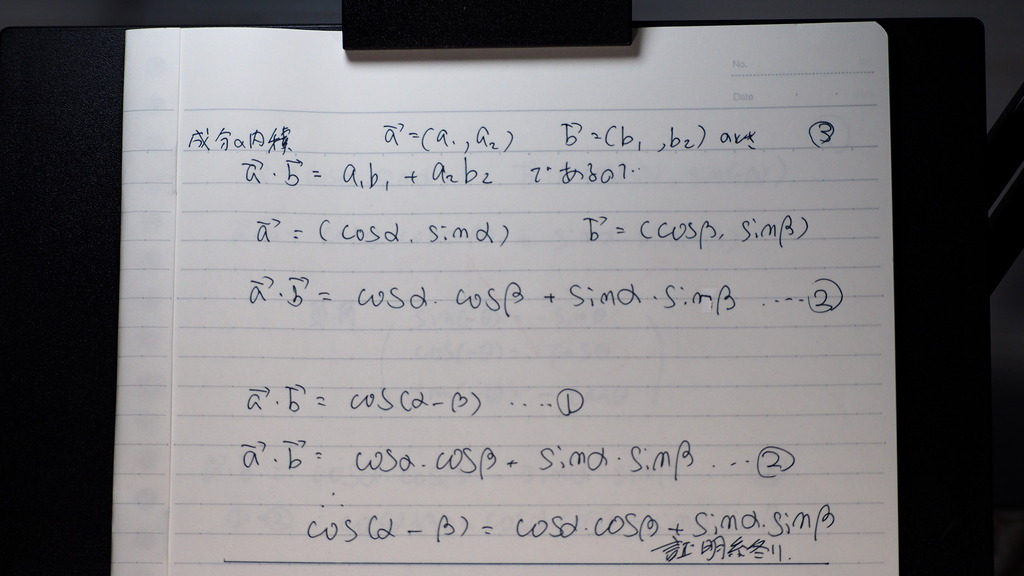
04
ここで
βを -βにすればさ
コサイン(α+β)

05
成分の方は
負角の公式から
書き換えられるので
なったデショ
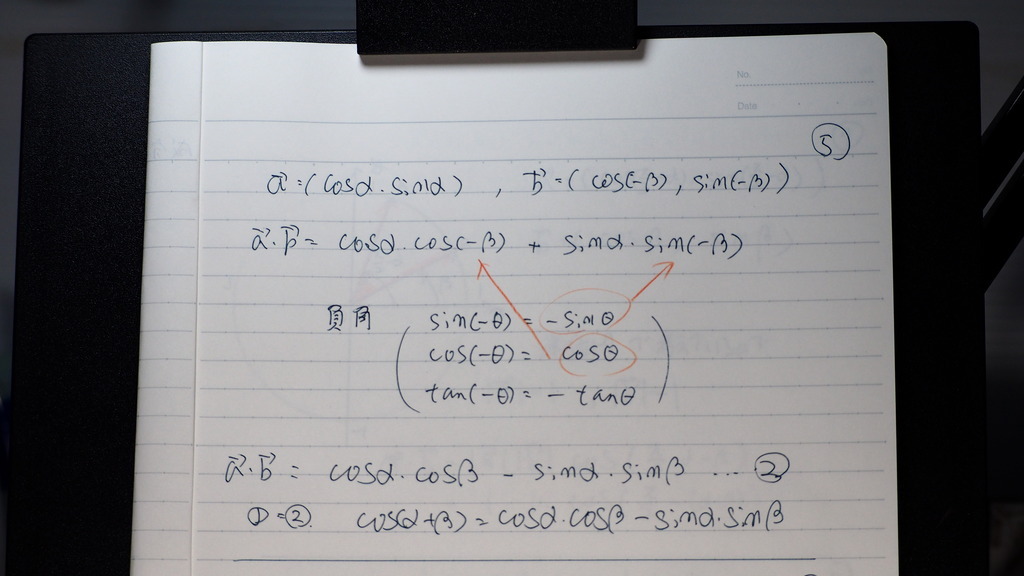
06
じゃーサインは どうするんだ
そこで

07
やっぱりね
矢線ベクトルの 内積と
成分の内積を 連立するんですが
パイ/2 - Θ
余角の 公式で
書換えが効いてじゃナイスカ
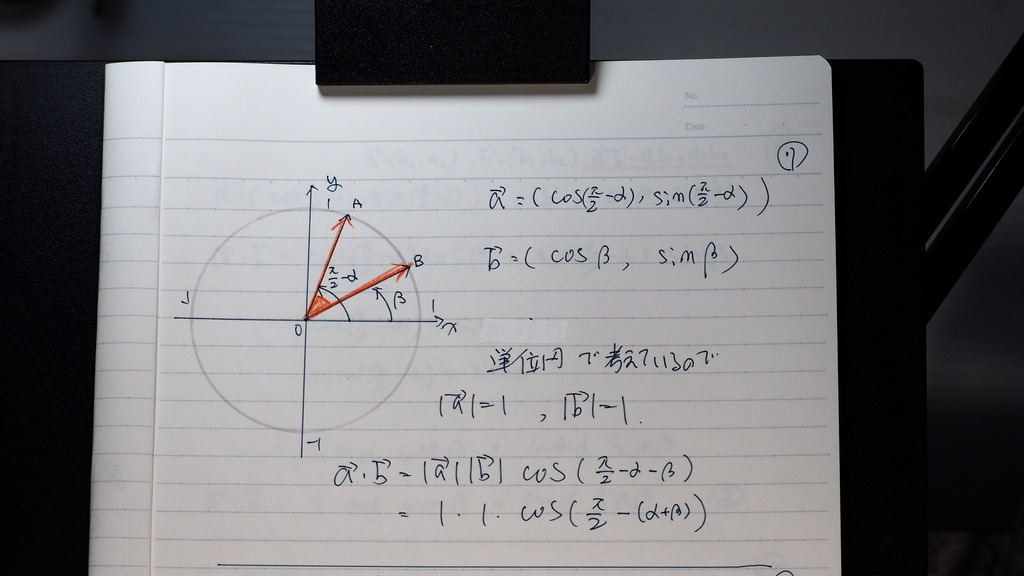
08
そうしたら
コサインが サインに代わるデショ
....➀
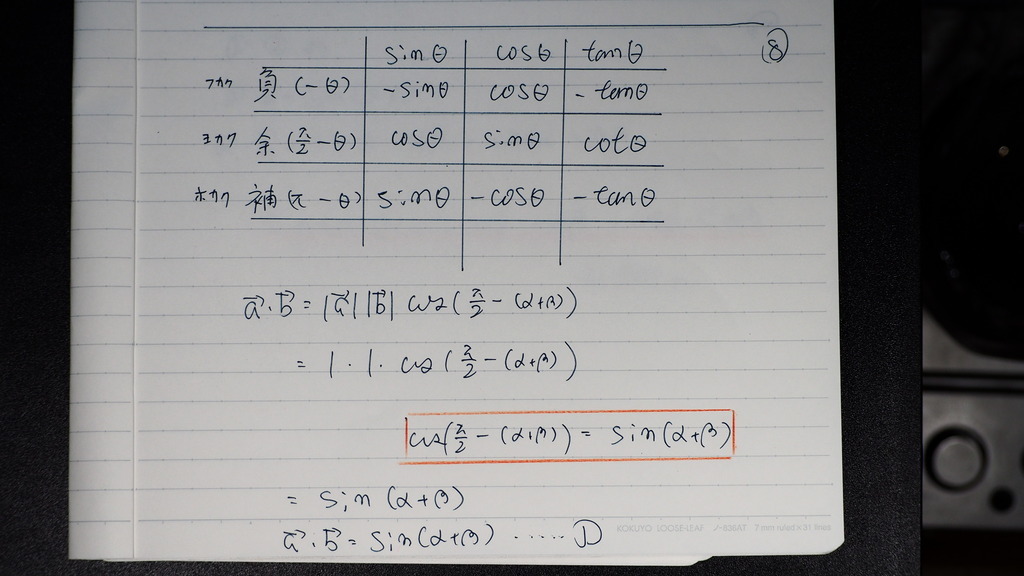
09
成分の方の内積も
余角が 書き換えができて
サインに 化けるので
...②
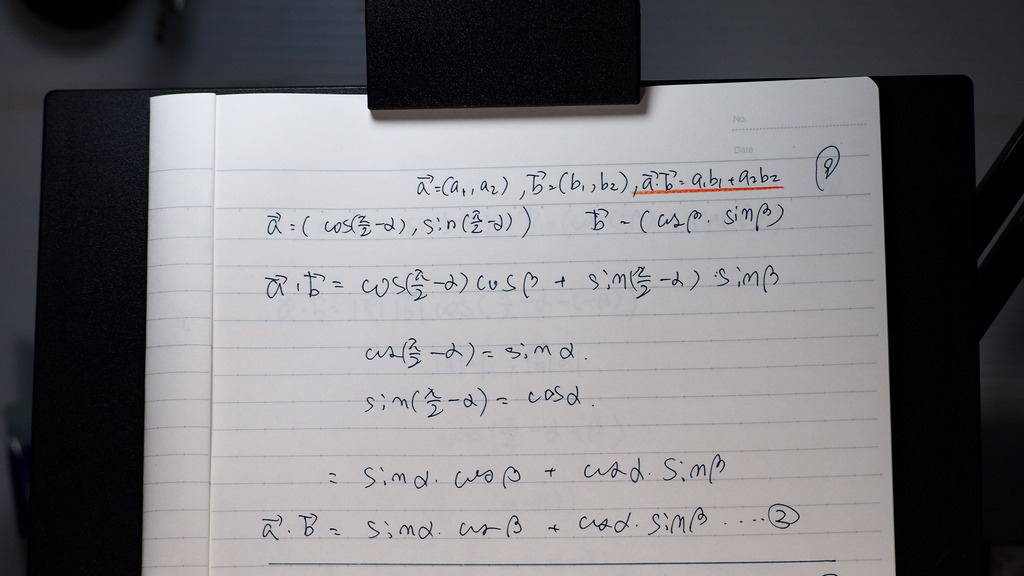
10
なったじゃナイスカ
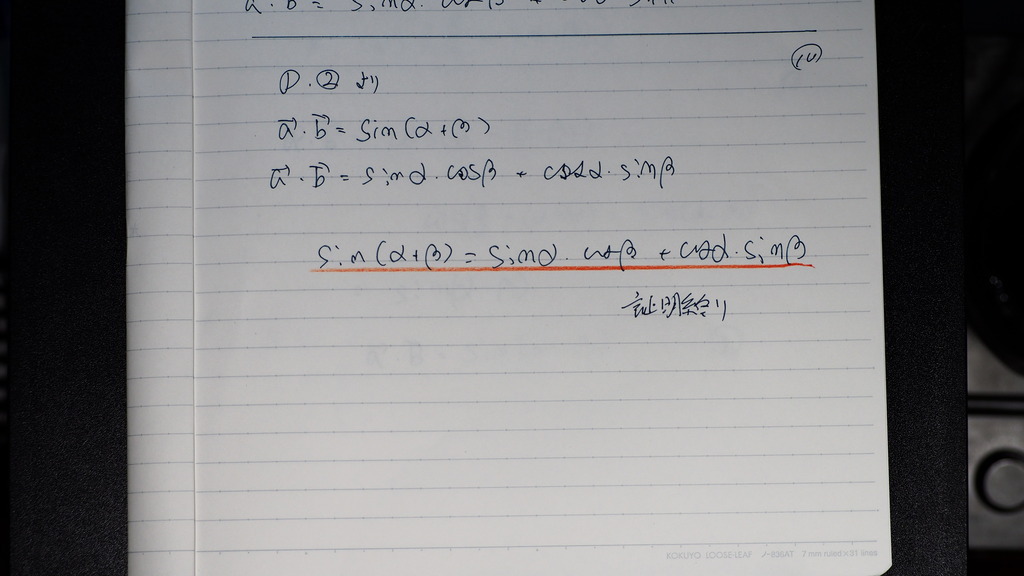
11
マイナス バージョンは
βを -βにすると
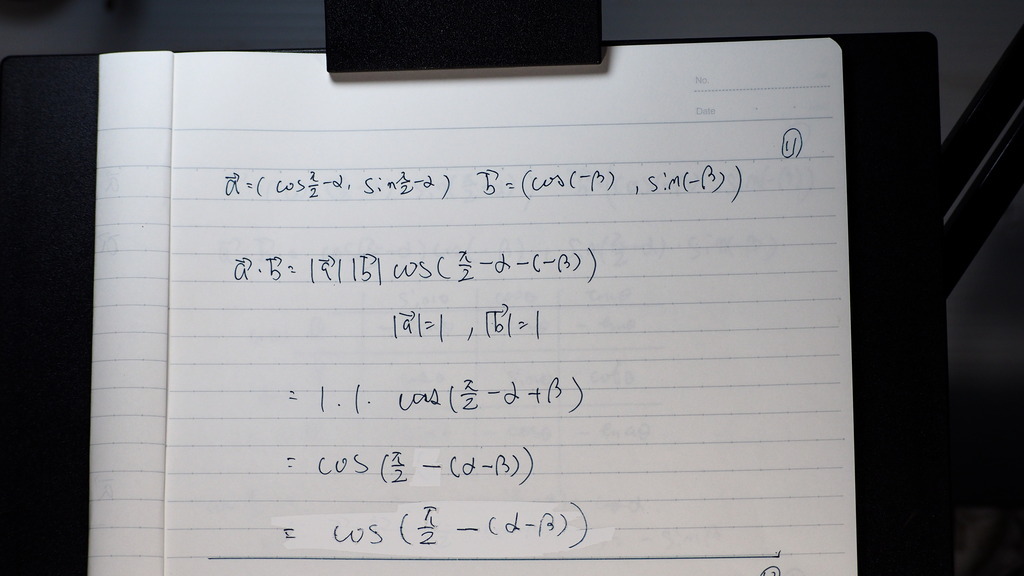
12
出てきたでしょ
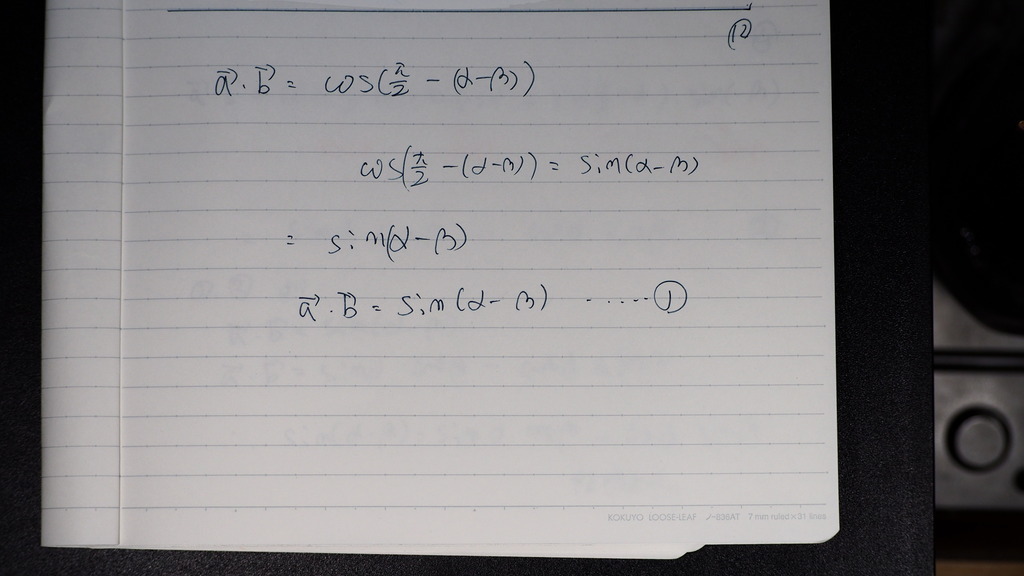
13
人を 恐れると 罠にかかる
しかし
人に 失礼なことは してはいけません
一番 覚えやすい方法で
グラフで できれば
それに こしたことはありませんが
人はね 年を 取るものなんですよ
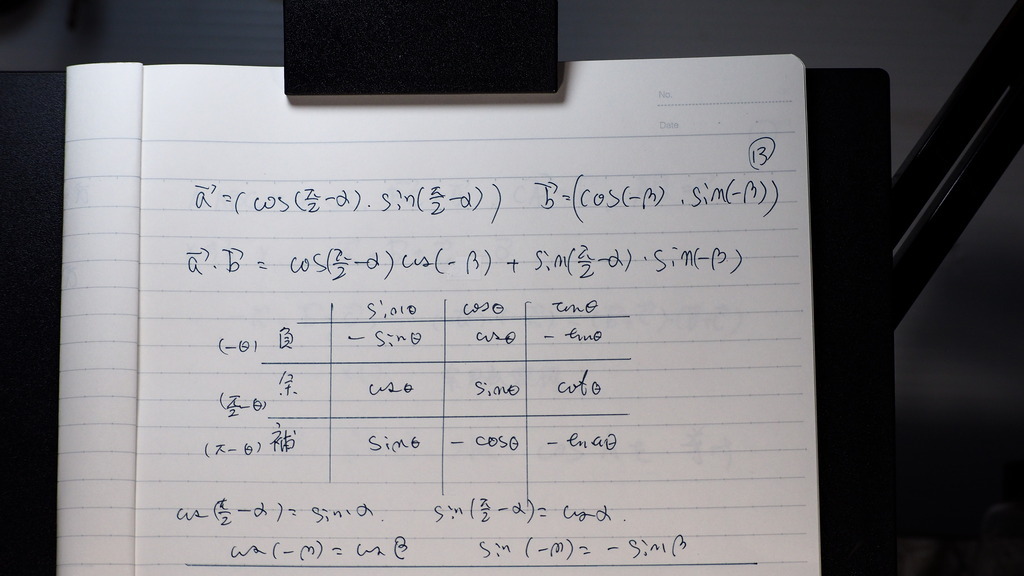
14
こんな感じに
変換で来て
なったデショ

15
今度は
余弦定理
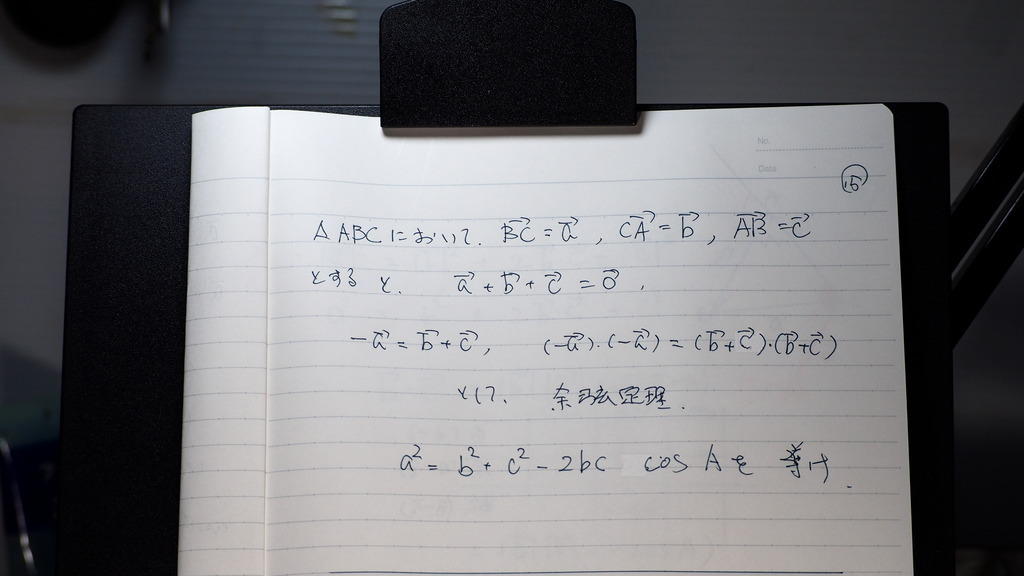
16
内積で
展開して
絶対値が 付くと ベクトルの
矢印は 残ってるけど
これは 大きさを 表してるので
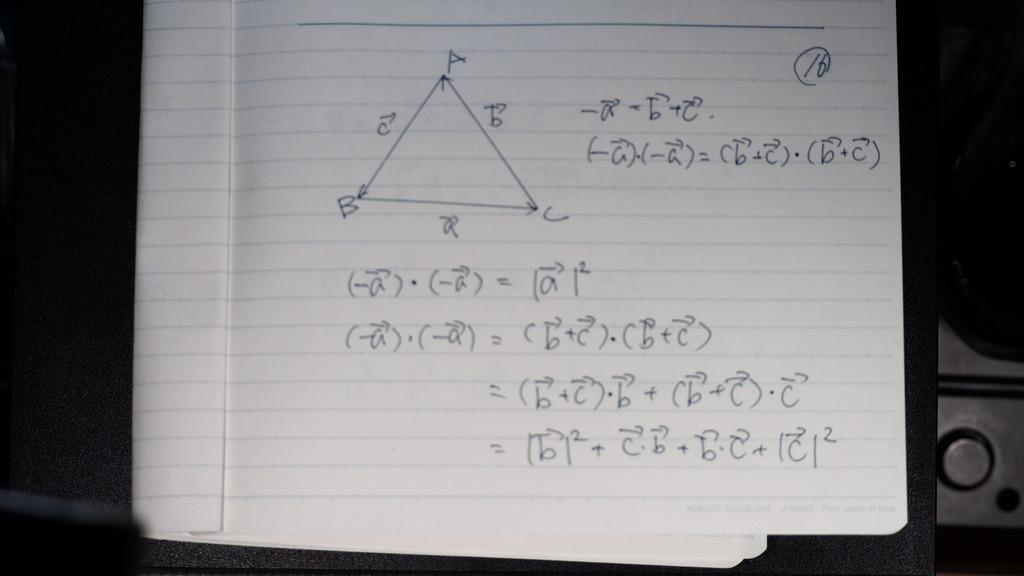
17
であるから
大きさにして
あとは
式の 合間にある
bドットc
この なす角は
ここだから
なす角は
始点をそろえたときの
角度
補角の 公式で
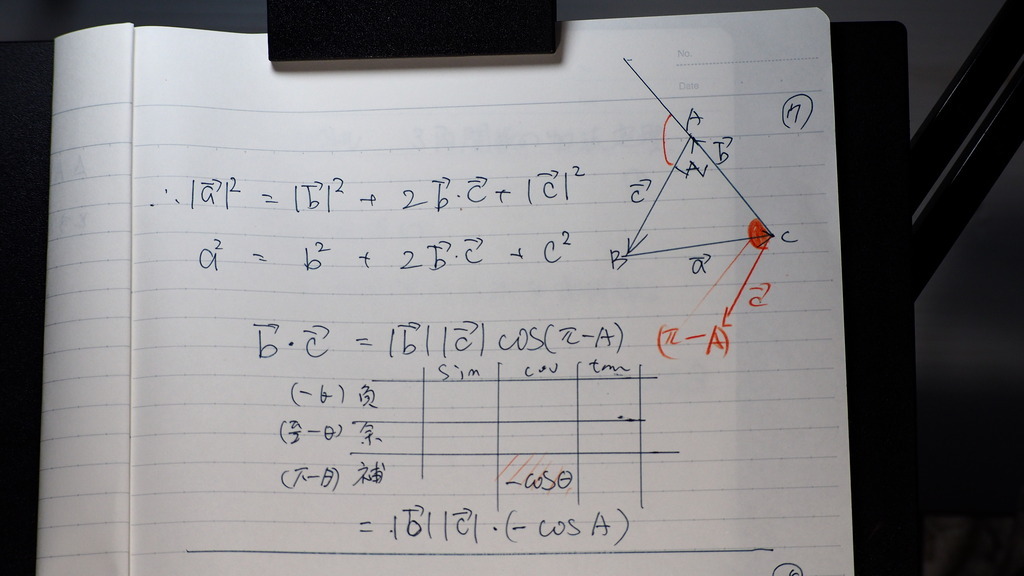
18
こんな感じで
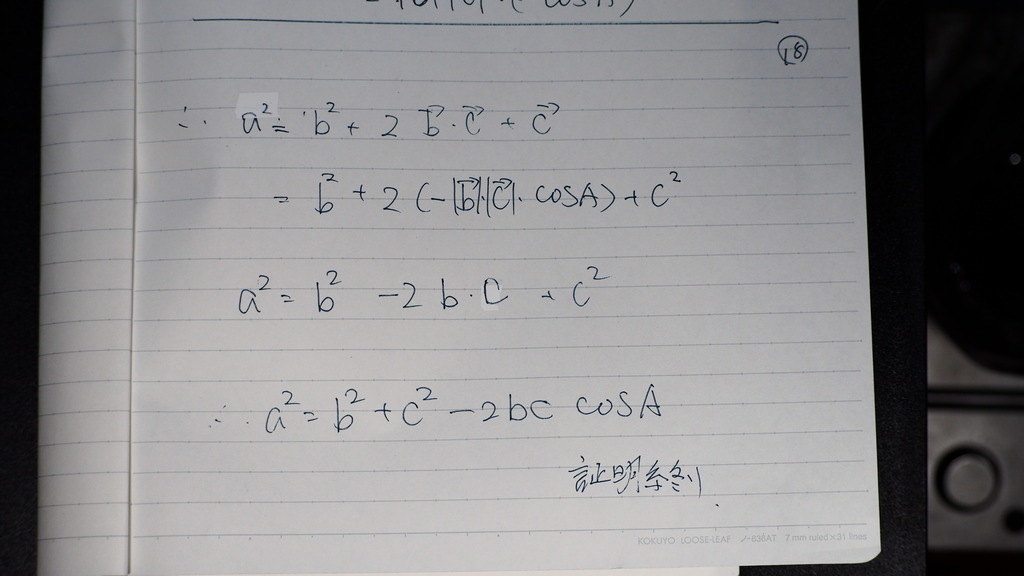
お疲れ様です。
空間座標と
01
三角関数で
加法定理と言うのがあるですが
それを
内積を使って
証明して
という問題
02
こんな
感じに
単位円を使って
Aベクトル Bベクトル
それぞれ
x軸となす角が
α 、 β
これを
座標を
使って 表せば
03
動径の 長さは 1だから
x成分は コサイン
y成分は サイン
矢線ベクトルの 内積の
定義式は
絶対値 A 、B は 共に1
コサインは Θがα-β...➀
成分の 内積は
コサインα コサインβ +
サインα サインβ.....②
➀②から
なったデショ
04
ここで
βを -βにすればさ
コサイン(α+β)
05
成分の方は
負角の公式から
書き換えられるので
なったデショ
06
じゃーサインは どうするんだ
そこで
07
やっぱりね
矢線ベクトルの 内積と
成分の内積を 連立するんですが
パイ/2 - Θ
余角の 公式で
書換えが効いてじゃナイスカ
08
そうしたら
コサインが サインに代わるデショ
....➀
09
成分の方の内積も
余角が 書き換えができて
サインに 化けるので
...②
10
なったじゃナイスカ
11
マイナス バージョンは
βを -βにすると
12
出てきたでしょ
13
人を 恐れると 罠にかかる
しかし
人に 失礼なことは してはいけません
一番 覚えやすい方法で
グラフで できれば
それに こしたことはありませんが
人はね 年を 取るものなんですよ
14
こんな感じに
変換で来て
なったデショ
15
今度は
余弦定理
16
内積で
展開して
絶対値が 付くと ベクトルの
矢印は 残ってるけど
これは 大きさを 表してるので
17
であるから
大きさにして
あとは
式の 合間にある
bドットc
この なす角は
ここだから
なす角は
始点をそろえたときの
角度
補角の 公式で
18
こんな感じで
お疲れ様です。