2022年12月04日
22025 大人のさび落とし 空間座標とベクトル 直線 円 の 方程式
大人のさび落とし
空間座標とベクトル 直線 円の 方程式
01
原点をO として
定点 A,B と 動点P
がある
次のベクトル方程式は
どんな図形を 表すか

02
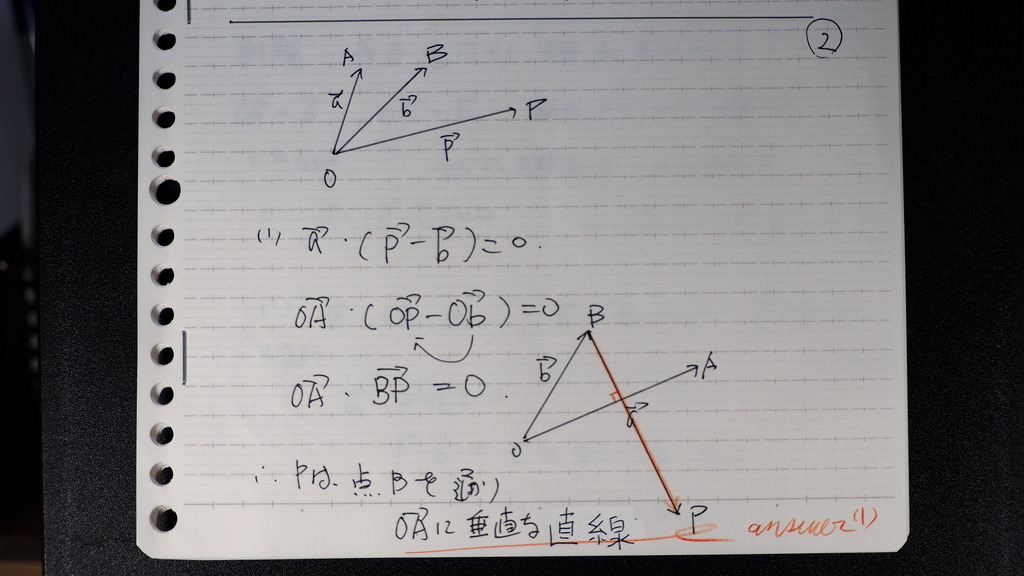
内積を 展開してくでしょ
動かないところ 黒矢線
動くところ 赤矢線
で
Pは Bを 通り
OAに 垂直な 直線
03
(2)
内積をベクトルで
表すと
APベクトル ⊥ BPベクトル
Pの位置だけが
∠APBが 90度を
保つように 変化する
これはさ
A,Bを 直径の
両端に持つ 円
直径ABであるから
中心角180度
その円周角は 90度
ゆえに
Pは ABを 直径の両端に持つ
円の周上
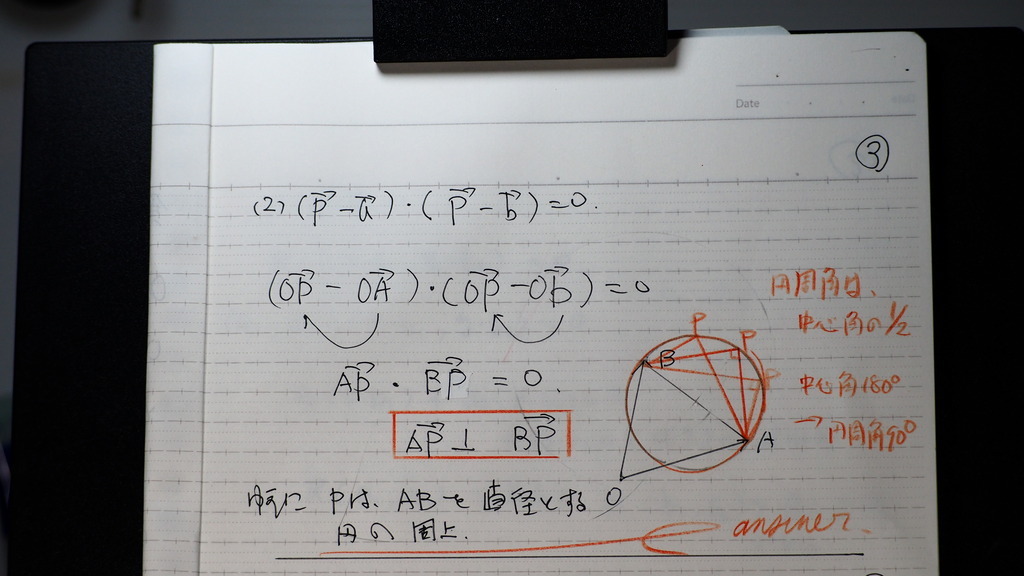
04
同じ問題ですが
ベクトルの
成分で 計算すると

05
(p-b)ベクトルは
直線BP
aベクトルと
内積の 形で
=0 何であるから
点Bを通り OAに垂直な
直線
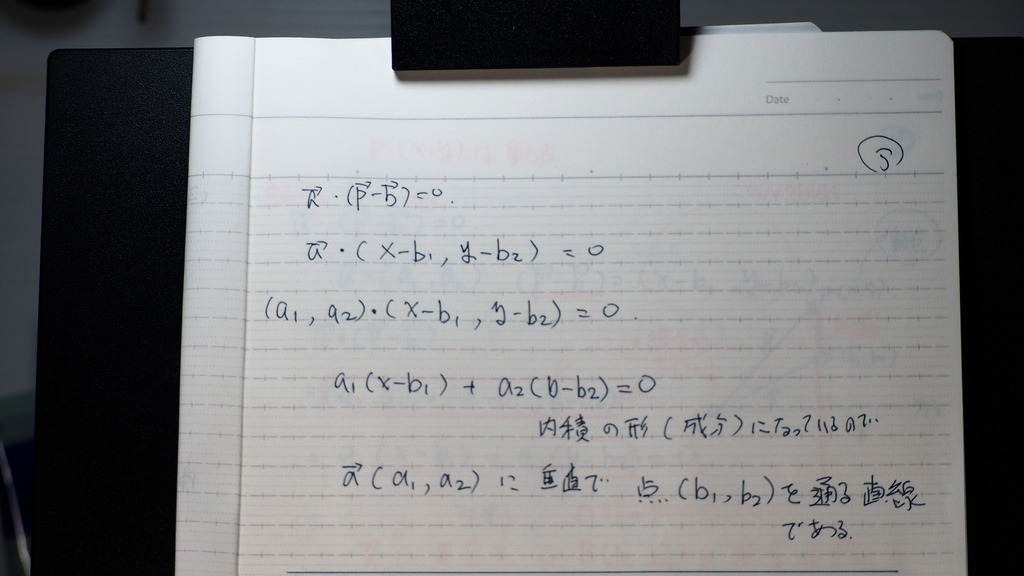
06
ずにすれば
一目りょうぜん

07
まとめた つもりだけど
わかるかな
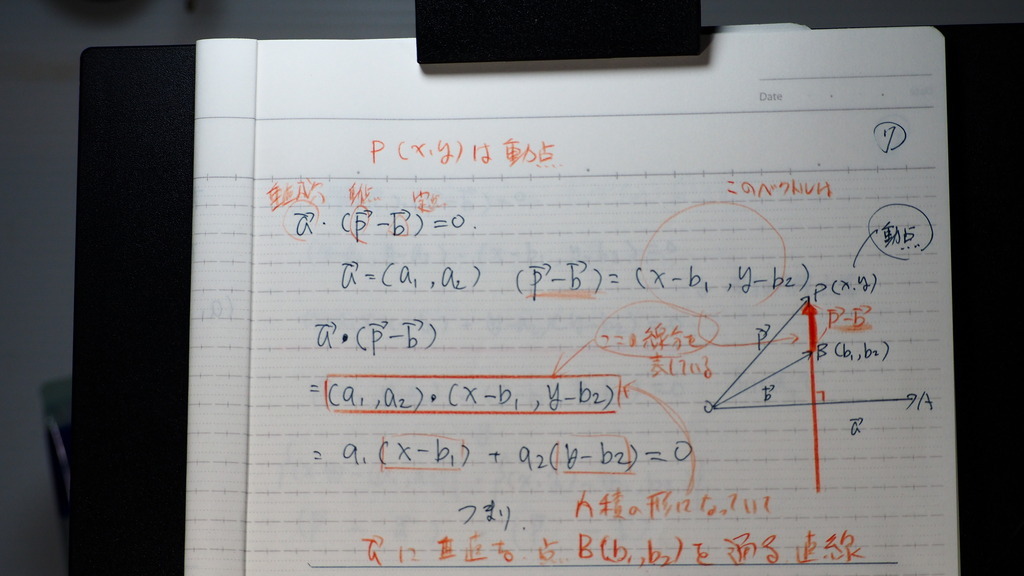
08
(2)
ベクトルで
表すと

09
成分の 計算は
コンななんですが
ただ いじってるだけか

10
兎も角
この式は
ABを 直径の両端とする
円

11
類題を
沢山持ってきました
行ってみましょう

12
動かないところ 黒
動くところ 赤
内積を
展開して

13
始点が 同じで
Aベクトルと 大きさが
同じように
動くのだから
始点を O として
半径aの円になる

14
次は
左辺を 展開して
まず Pベクトルの 大きさが
0の時

15
Pベクトルの 大きさが
ゼロでないときは
Oを 始点として
60度のなす角を 持つ 2つの
半直線

16
これは

17
(a-b)ベクトルは これだから
これに
垂直
こんなかんじで

18
これは
内積を
くくって
こんな感じだから

19
なんだこりゃ

20
内積を
左辺展開してって
じゃナイスカ
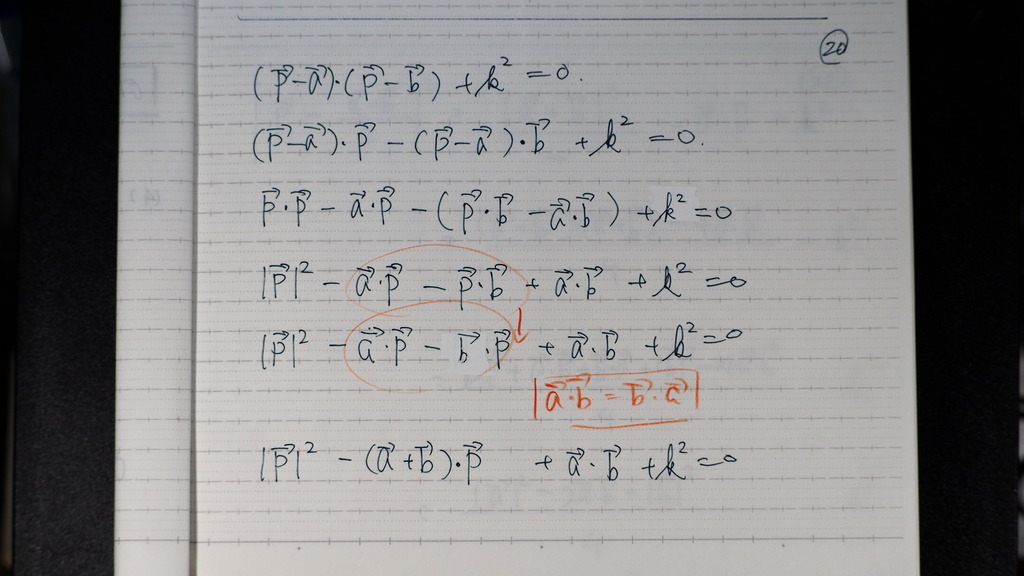
21
平方完成して
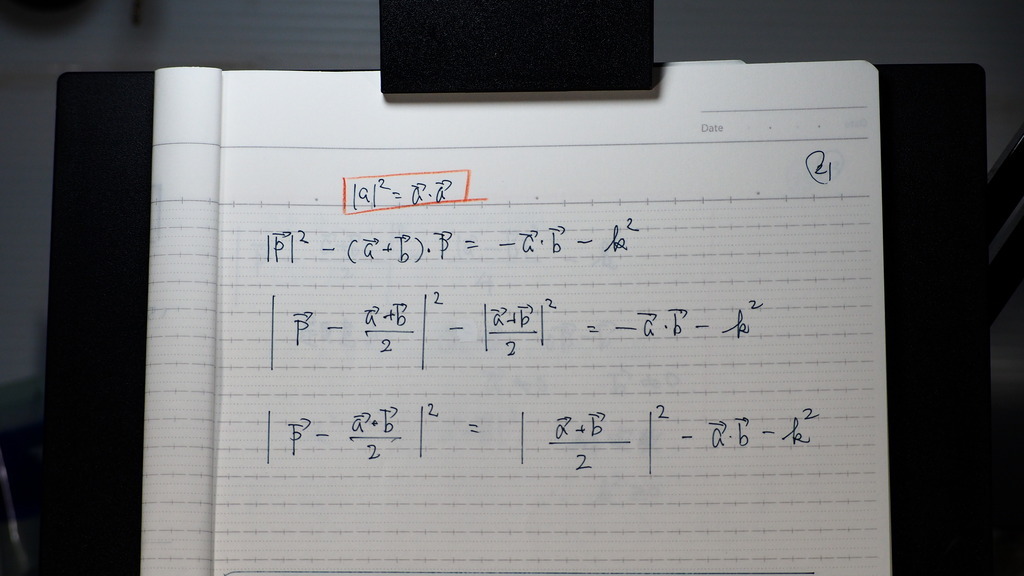
22
こんな感じで
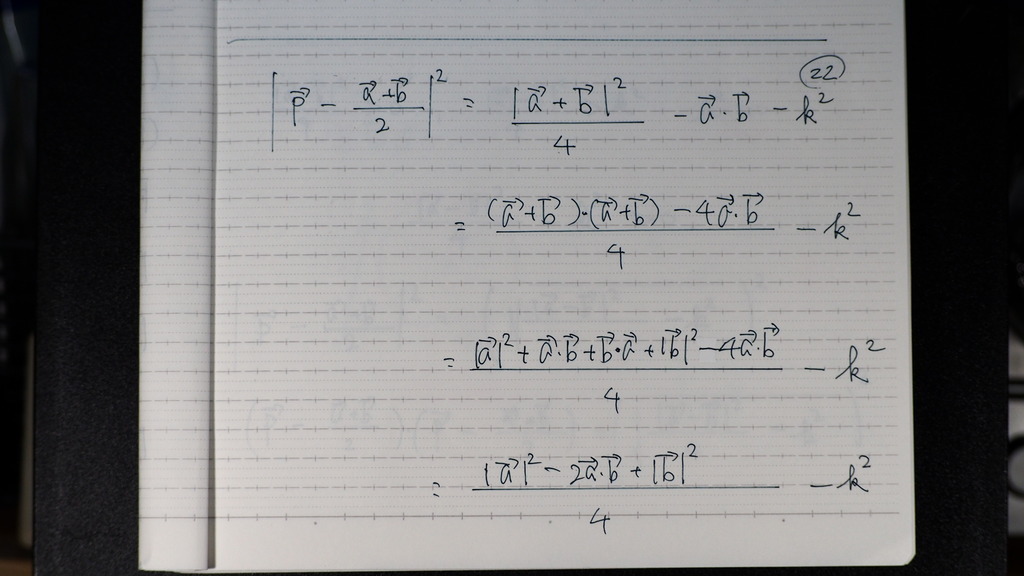
23
題意より

24
左辺は
円の 方程式に
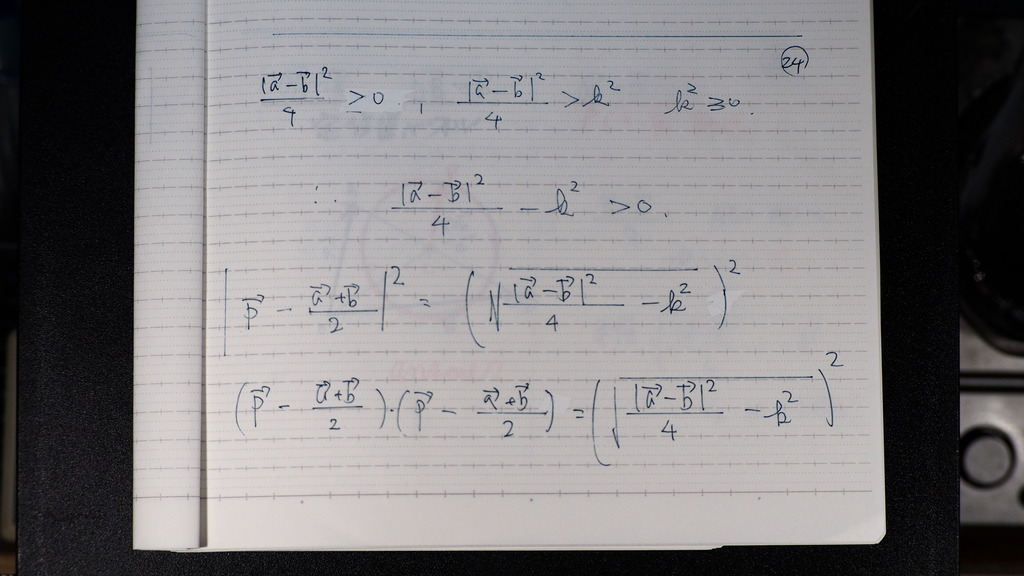
25
こんなだったじゃナイスカ
であるから

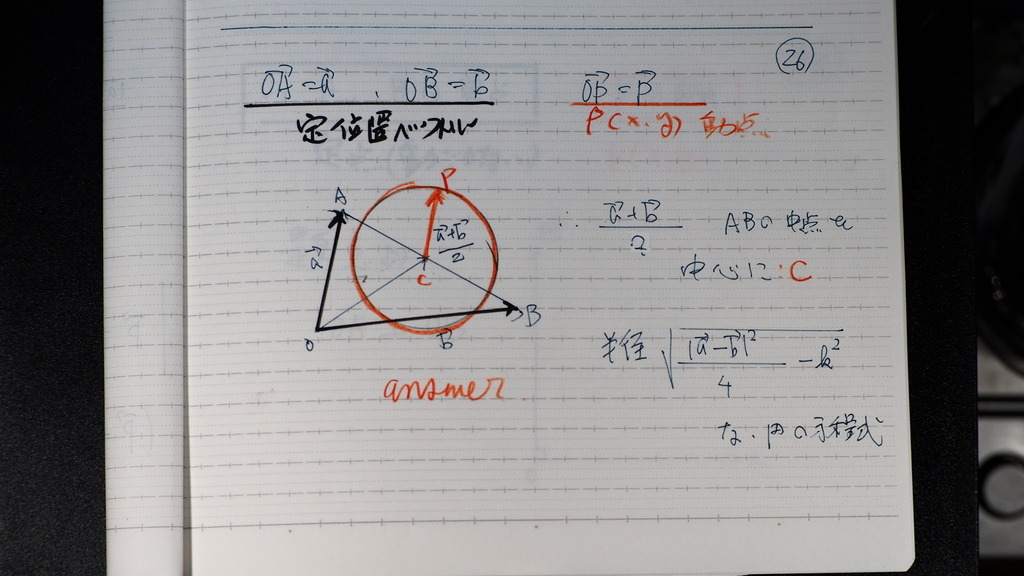
26
2分の a+bってのは
ABの 中点でしょ
そこが
円の中心
半径は
右辺に 2乗の形で
27
ラストは
これはさ
円の方程式が
3っ出て来て
ソレゾレ
領域があって
同時に 満たすところは

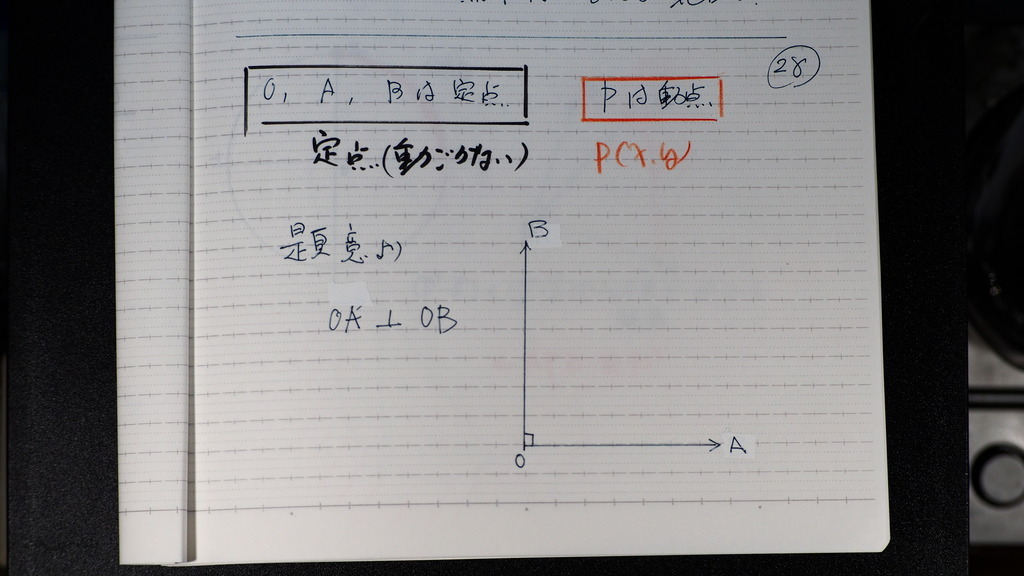
28
題意より
Aベクトルと Bベクトルは 垂直
始点は 同じO
29
初めの式は
ABを直径の両端に持つ
円 左辺=右辺ならば
左辺 大なりイコール
(グレイターイコール ザン)0であるから
内積が=0ならば 90度
内積が ゼロ以上であれば
内積の角度は コサインで
効いてくるので
0以上90以下 で 90度または鋭角

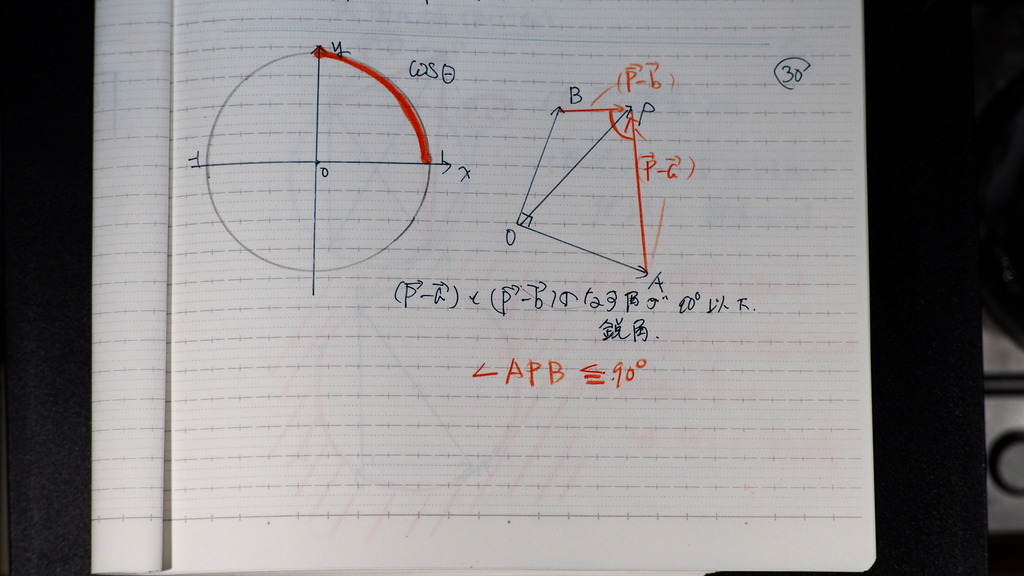
30
(p-b)と(p-a)の
ここのところが
90度以下
この角度は なす角と等しいので
31
Pの集合は
円周上を 含む
円の外側

32
こんな感じで
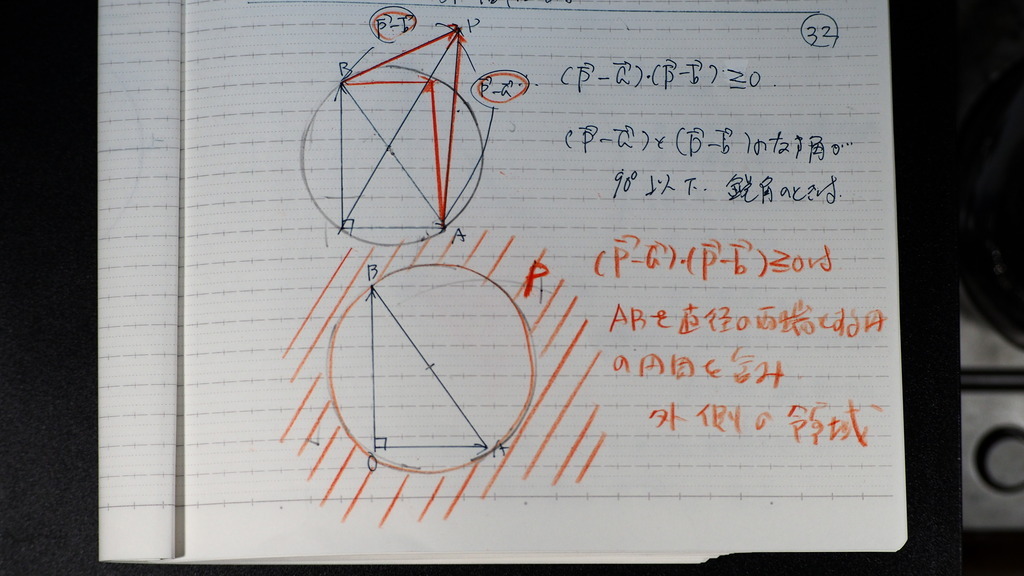
33
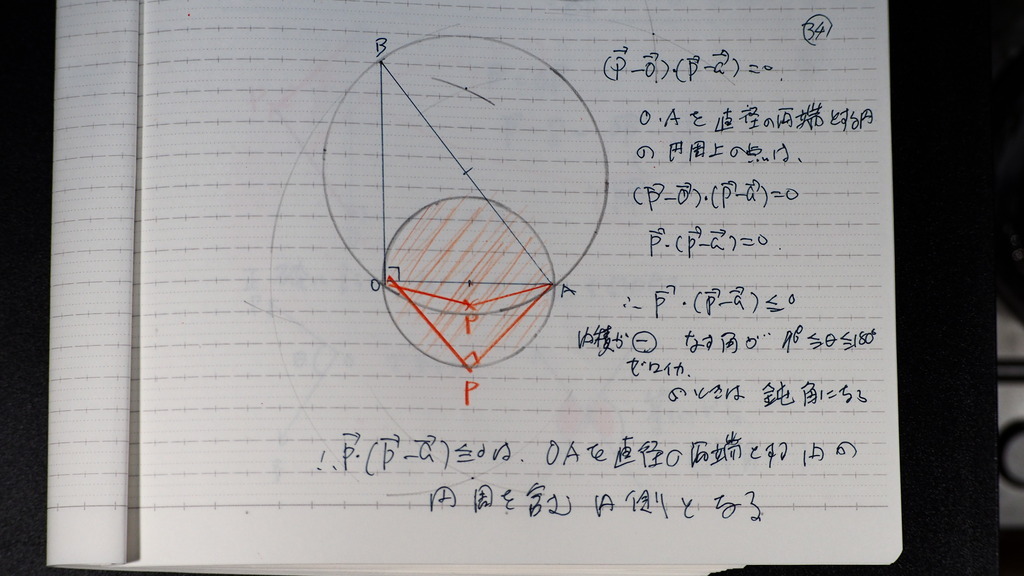
こっちの円は
OAを 直径の両端にする円
れすイコールザン 0
90度を含んで 鈍角

34
そのPの集合は
円周および その内部
35
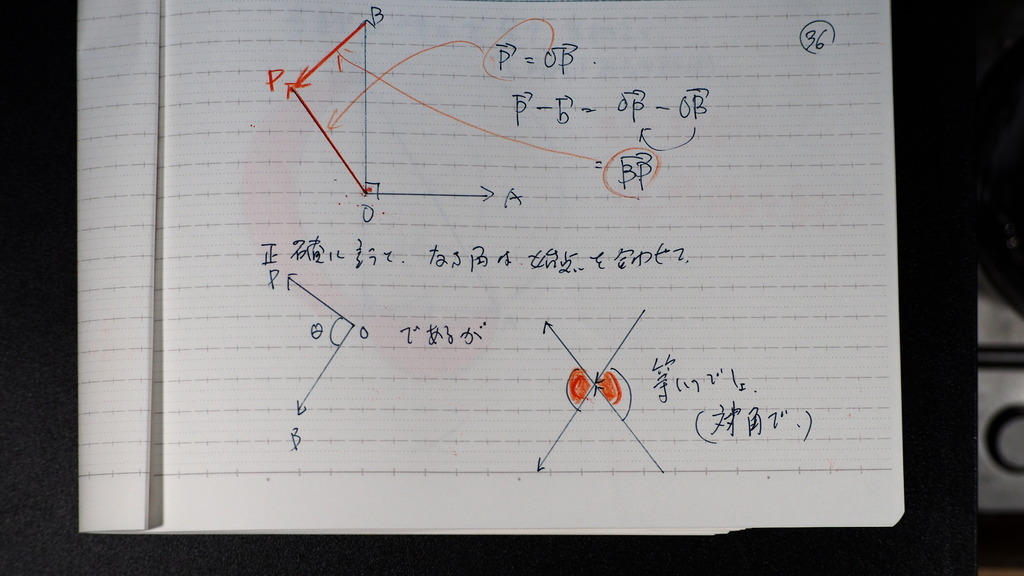
三つ目の円は
OBを 直径の
両端に持つ円で

36
なす角が
90度以上鈍角
37
こんな感じの
円周とその内部に 成るので

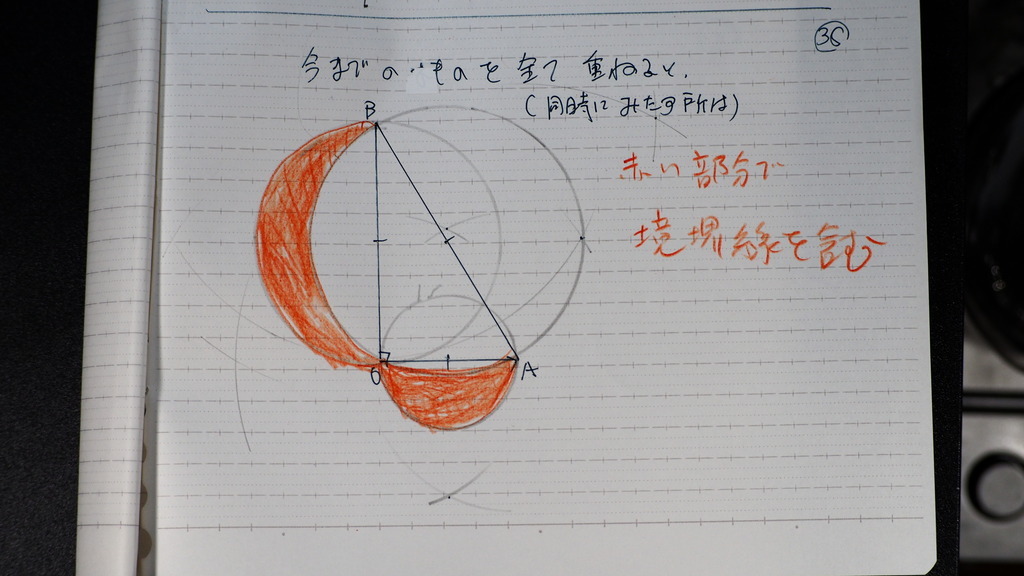
38
以上
3っの円を
重ねて
同時に 条件を
満たすのは
この範囲
境界線を含む
お疲れ様です。
空間座標とベクトル 直線 円の 方程式
01
原点をO として
定点 A,B と 動点P
がある
次のベクトル方程式は
どんな図形を 表すか
02
内積を 展開してくでしょ
動かないところ 黒矢線
動くところ 赤矢線
で
Pは Bを 通り
OAに 垂直な 直線
03
(2)
内積をベクトルで
表すと
APベクトル ⊥ BPベクトル
Pの位置だけが
∠APBが 90度を
保つように 変化する
これはさ
A,Bを 直径の
両端に持つ 円
直径ABであるから
中心角180度
その円周角は 90度
ゆえに
Pは ABを 直径の両端に持つ
円の周上
04
同じ問題ですが
ベクトルの
成分で 計算すると
05
(p-b)ベクトルは
直線BP
aベクトルと
内積の 形で
=0 何であるから
点Bを通り OAに垂直な
直線
06
ずにすれば
一目りょうぜん
07
まとめた つもりだけど
わかるかな
08
(2)
ベクトルで
表すと
09
成分の 計算は
コンななんですが
ただ いじってるだけか
10
兎も角
この式は
ABを 直径の両端とする
円
11
類題を
沢山持ってきました
行ってみましょう
12
動かないところ 黒
動くところ 赤
内積を
展開して
13
始点が 同じで
Aベクトルと 大きさが
同じように
動くのだから
始点を O として
半径aの円になる
14
次は
左辺を 展開して
まず Pベクトルの 大きさが
0の時
15
Pベクトルの 大きさが
ゼロでないときは
Oを 始点として
60度のなす角を 持つ 2つの
半直線
16
これは
17
(a-b)ベクトルは これだから
これに
垂直
こんなかんじで
18
これは
内積を
くくって
こんな感じだから
19
なんだこりゃ
20
内積を
左辺展開してって
じゃナイスカ
21
平方完成して
22
こんな感じで
23
題意より
24
左辺は
円の 方程式に
25
こんなだったじゃナイスカ
であるから
26
2分の a+bってのは
ABの 中点でしょ
そこが
円の中心
半径は
右辺に 2乗の形で
27
ラストは
これはさ
円の方程式が
3っ出て来て
ソレゾレ
領域があって
同時に 満たすところは
28
題意より
Aベクトルと Bベクトルは 垂直
始点は 同じO
29
初めの式は
ABを直径の両端に持つ
円 左辺=右辺ならば
左辺 大なりイコール
(グレイターイコール ザン)0であるから
内積が=0ならば 90度
内積が ゼロ以上であれば
内積の角度は コサインで
効いてくるので
0以上90以下 で 90度または鋭角
30
(p-b)と(p-a)の
ここのところが
90度以下
この角度は なす角と等しいので
31
Pの集合は
円周上を 含む
円の外側
32
こんな感じで
33
こっちの円は
OAを 直径の両端にする円
れすイコールザン 0
90度を含んで 鈍角
34
そのPの集合は
円周および その内部
35
三つ目の円は
OBを 直径の
両端に持つ円で
36
なす角が
90度以上鈍角
37
こんな感じの
円周とその内部に 成るので
38
以上
3っの円を
重ねて
同時に 条件を
満たすのは
この範囲
境界線を含む
お疲れ様です。