新規記事の投稿を行うことで、非表示にすることが可能です。
2017年03月16日
引き出し 01006 指数の計算
次の式を 簡単に せよですが
はじめは 指数の形で
行ってみます
括弧の中から
( )に まいなす 1/2 乗なので
( )の中の それぞれに マイナス1/2 乗がかかって
指数の 指数倍は 指数の掛け算
掛け算は 交換の法則が成り立つから
同じ 文字同士の 掛け算の順に 整理して
同じ文字の 指数の掛け算は
指数の部分の 足し算
整理して
これ
今度は
根号が 入ってる場合
平方根 立方根が 入ってますが
さっきのも
平方根 立方根 、 四乗根まで はいてたんですよね
なので
先ほどのような形に
外側から
指数化してくじゃナイスカ
平方根は 1/2 乗
( のなか身も )
平方根は 1/2乗
立方根分の 1は
立方根は 1/3 乗
立方根が 分母に来るので
-1/3 乗
これに
括弧の 外から 1/2乗が それぞれに
効いてくるので
括弧の 中身は
同じ文字だから
同じ文字の 指数の 掛け算は
指数部分の 足し算なので
指数部分を 通分して 足しておいて
指数の 指数倍は
指数の掛け算を やると
aの7/12乗
これを
根号の形に 変換すると
分母が 塁乗根
分子が 中身の指数
なので
12乗根 aの 7乗
類題じゃナイスカ
括弧の中からですよね
両方とも
3の指数だから
指数の足算
指数の 指数倍は
指数の掛け算
9だね
数字が 大きくとも
うろたえることなく
括弧の 中から
中括弧を 外すと
指数の指数倍は 指数の掛け算デショ
指数のマイナスは
分母だよ
分母に 持ってって
1/2は 平方根だよ
ここら辺は
間違いませぬように
で
次は
例に よって
指数の 形に そろえて
計算してから
もとに 戻す考えで
割るだから
分母でしょ
分母だよは ⊖乗
立方根だから
分母 分は -1/3
平方根は 1/2乗
括弧の 指数は 中身 一つ一つに 効いてくるから
それぞれに 指数の 指数倍は 指数の掛け算をして
整理して
掛け算は 交換の法則が できるので
文字を そろえて
同じ文字の 指数の掛け算は
指数部分の 足し算
全部 掛けるでしょ
累乗根の公式から
結合してくと
6乗根cの7乗は
c×c×c×c×c×c ×c
6乗は 6乗根の外に cで 出て来て
c 6乗根 c
結合して
整理すると
これ
ややこしく見えるけど
公式に したがって
外枠から 指数化してくじゃナイスカ
次は 内側を 指数化して
分母は ⊖乗 で
掛け合わせた形に
括弧の 中身は
同じ文字の 指数計算なので
指数部分の足算
整理して
指数の指数倍は 指数の掛け算
同じ文字の
指数計算は
指数の 掛け算
んん
これでよかったかな
0/30 だから 0じゃないですよね
指数の時は
0乗は 1
使った 公式は
指数は
普段 やらないから
さびが 速いです
0乗は ッテ 聞かれて
すぐ 正解できる人
以外に 少ないかもしれないよ。
表面仕上げも しなけりゃいけないのに
組んじゃって どーすんだ
はるなので
ごそごそしています
パスタ は チーズだけでなく
タバスコも
使う私です
未完成ですので
長い目で見てね
リターン
2017年03月07日
引き出し01005 展開の応用
式の 展開を 覚えたところで
応用なんだって
値のわかてる 式を使って
(1)(2) の式の 値を 求めなさいですが
行ってみましょう
使えそうな 公式を おもいだすでしょ
a,b,c,の 括弧 2乗なんか ど
展開してじゃナイスカ
うまいこと
行きそうなので
求める 式が 混じってるから
形が 見えてくるように
整理して
代入してみると
マイナス1/2
4乗は
二乗の時の 入れ子で
いけそうなので
展開して
分かってるとこを
代入すると
で
整理すると
まだ
違う式が 残ってるから
部分的に
また 括弧 二乗で 式を 作ると
展開して
せいりして
必要な式が 見えるように
変形してくと
で わかってるとこを
代入して
さっきの
部分的に 残ってた式の 値が出たので
一つ前の 式に 代入して
1/2
次は
簡単に いけそうなきがするー
コレダと
らくでいいなぁー
3乗 とか になると
急に うろたえだしますが
してる 公式を 書いてみて
下側を 使えばさ
展開式に
代入できるとこを
入れると
これです
次の問題は
式変形の 問題なんだけど
式を
書き換えるときに
ですね
書き換え後の 形 = yと置いて
書き換える とこを yの式で
表して
代入 展開 整理 後に
=y としたとこを
yを xに 戻すと
変形が 完了すると言うものです
実際に 行ってみます
実験かなにかに
出てくるのカナ?
xのとこに yの式で代入してくでしょ
展開して
整理して
yを もとに もどすと
さ
次は
類題なんですが
括弧の 二乗の 中身が 3っつってのは
よく出てくるんですね
(1) は まだいいけど
ここからは
計算を
頭でやらずに 手を動かして
分かってる とこを 代入しても
残りがあるときは
残りの 式も 作成して
整理して
代入して
先ほどの
値不明で 残ってたとこに 代入して
これでいいのだ
リターン
タグ:01005 展開の応用
2017年03月06日
引き出し01004 式の展開
私は 池上さんの ニュース番組が 好きです
もともと 社会科は 大の苦手なのに
あの番組に限っては
楽しみでしょうがありません
あれって何だろうね
池上さん の 本に ヒントあり
で
今日は 式の展開なんですが
公式が いろいろ あります
証明問題で出たのは
公式に 追加しました

5乗 マイナス 5乗 とか ですね
で
これらの 公式を 駆使して
展開して行くんでございますが

二乗 まいなす 二乗 は とにかく
よく出て来ます
先に
その組み合わせで
展開すると
連鎖的に
丁度 次に 必要なのがでてきて

指数の 計算を 間違わないように せねば
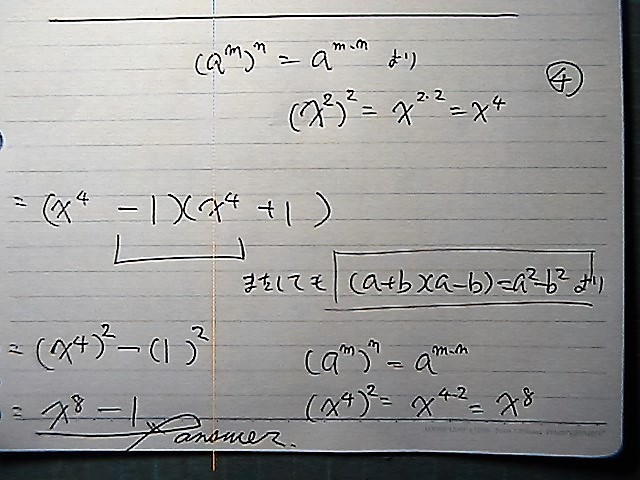
良く見ると
組み合わせられるのが
あるでしょ
で
展開しておいて

やむを得ないときは
直接に かけ合わせて

ここも 二乗 マイナス 二乗に
持ち込もうかと
思ったんですが
なんか 変だな
良く見ると

3乗 プラスマイナス 3乗 の公式が
見えてきたので
展開して
後は 指数の計算

これは
二乗 マイナす 二乗 か
んん
ちとまずい
そこで
指数の計算の 変形で

これで
二乗 - 二乗 が使えて
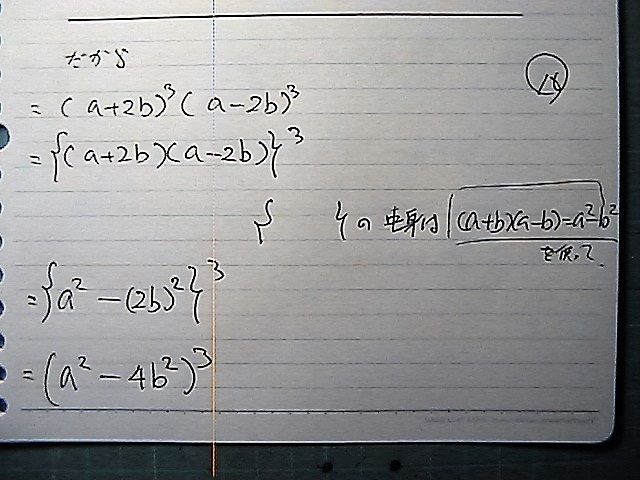
ケアレス ミスを せーへんよに
かっこ3乗の 展開
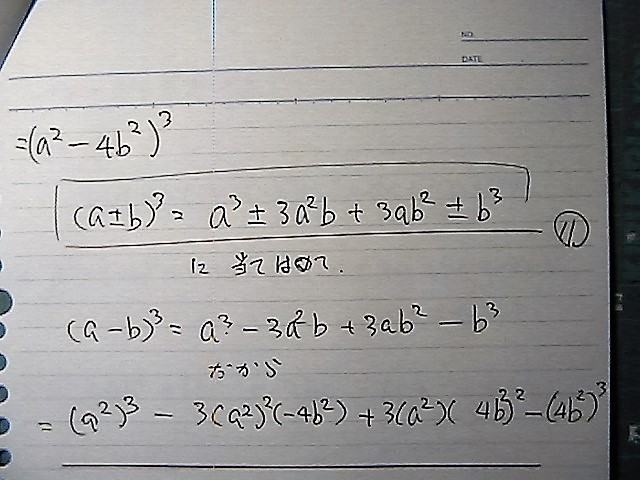
計算練習は
毎日やってないと
すぐ錆びてしまう
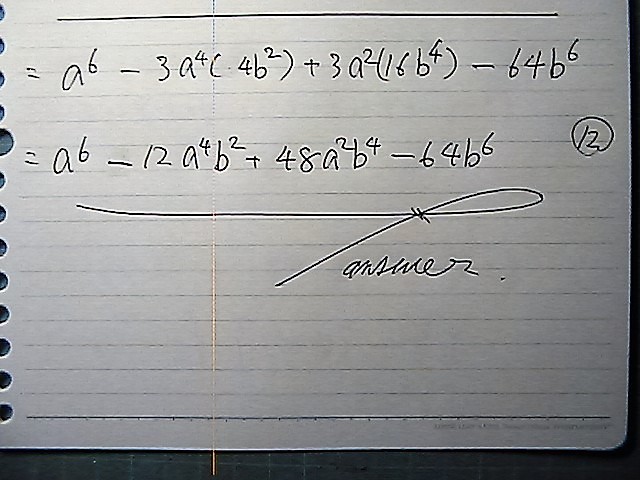
これは
a,b,c,の かっこ の 二乗公式に
あてはめて

ラストは
順をかんがえて
まず
こんなデショ

中身を
展開して
整理したらば
こんなデショ

計算を間違わなければ
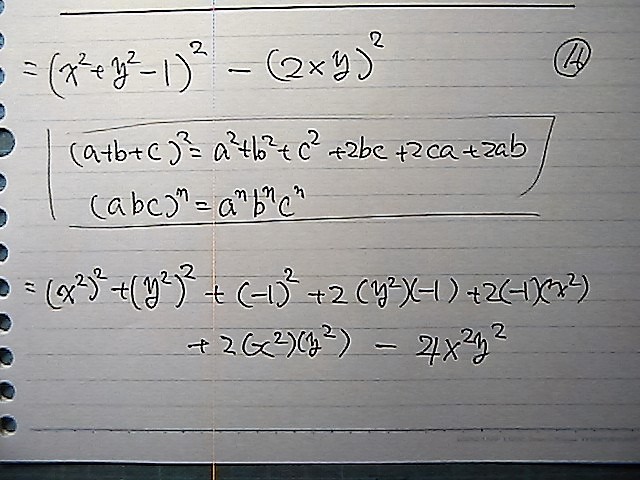
なんとなく
計算ミスの 痕跡が

最近
伸びてるんじゃなくですね
春だもんで
調子が悪い
きおつけましょうね
今日なんか
対向車線から
おー コッカコーラ
いいなぁー
と思ったら
救急車が
後ろから
ん
消防車 だった。
リターン
もともと 社会科は 大の苦手なのに
あの番組に限っては
楽しみでしょうがありません
あれって何だろうね
池上さん の 本に ヒントあり
で
今日は 式の展開なんですが
公式が いろいろ あります
証明問題で出たのは
公式に 追加しました
5乗 マイナス 5乗 とか ですね
で
これらの 公式を 駆使して
展開して行くんでございますが
二乗 まいなす 二乗 は とにかく
よく出て来ます
先に
その組み合わせで
展開すると
連鎖的に
丁度 次に 必要なのがでてきて
指数の 計算を 間違わないように せねば
良く見ると
組み合わせられるのが
あるでしょ
で
展開しておいて
やむを得ないときは
直接に かけ合わせて
ここも 二乗 マイナス 二乗に
持ち込もうかと
思ったんですが
なんか 変だな
良く見ると
3乗 プラスマイナス 3乗 の公式が
見えてきたので
展開して
後は 指数の計算
これは
二乗 マイナす 二乗 か
んん
ちとまずい
そこで
指数の計算の 変形で
これで
二乗 - 二乗 が使えて
ケアレス ミスを せーへんよに
かっこ3乗の 展開
計算練習は
毎日やってないと
すぐ錆びてしまう
これは
a,b,c,の かっこ の 二乗公式に
あてはめて
ラストは
順をかんがえて
まず
こんなデショ
中身を
展開して
整理したらば
こんなデショ
計算を間違わなければ
なんとなく
計算ミスの 痕跡が
最近
伸びてるんじゃなくですね
春だもんで
調子が悪い
きおつけましょうね
今日なんか
対向車線から
おー コッカコーラ
いいなぁー
と思ったら
救急車が
後ろから
ん
消防車 だった。
リターン
タグ:01004 式の展開
2017年03月05日
引き出し01003 組立除法
数Ⅰのひきだしの部屋です
なぜ こんな くどいことをするかというと
初めに 数Ⅰを やった当時は
ブログネタがなく
しょうがないから
自分のさび落としをして
お笑いで ごまかそうと
始めたのですが
楽しみに してくださる方から
もっと 丁寧に 書いてほしいを
要望されまして
できるだけ 丁寧なつもりなんですが
つい 計算してると
くしゃくしゃとなりがちで
日々 反省しながら
残りの 人生で
ほんの 少しの 方にでも
お役に 立てれば 幸いですで
ほんの 少し 丁寧バージョンです
行ってみます
組立除法
初めは
普通のやり方なんですが
各段階の
頭どうしの
割り算で

順次 やってくじゃナイスカ
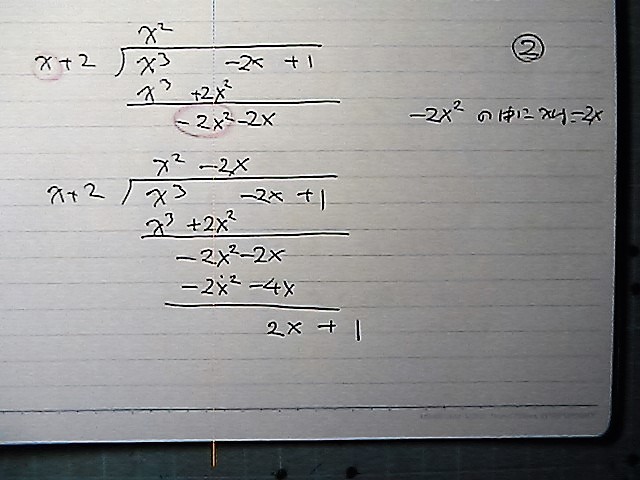
文字をそのまま使ってるので
何次 式 か 一目瞭然ですが
桁が 多かったり
割り算が たくさん あるときは
閉口してしまいます
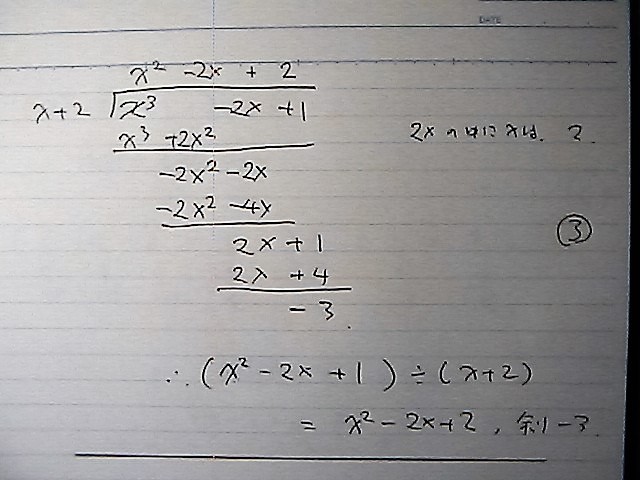
そこで
組立除法 があるんですが

今までは
係数を 分離して
その後 普通の 割り算
これでも
少しは
文字を省く分は 速いですが
割られる式じゃなくて
ですね
割る式の方を
=0になる xの 値にするんですよ

組立除法の 形は
こんな感じから スタート
初めは そのまま下に
次に 矢印の様に かけあわせて

矢印の様に 縦に
また
矢印の様に 掛けて
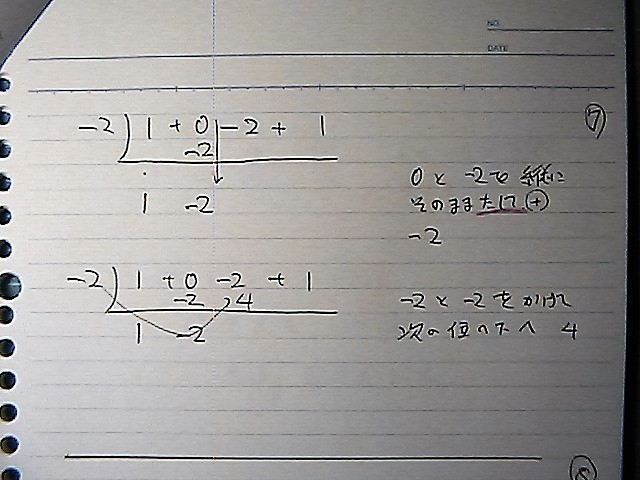
これを 繰り返しながら

最後まで来たらですね
3次式を 1次式で 割ったから
商は2次以下

2次 、1次 、 定数項 、余り
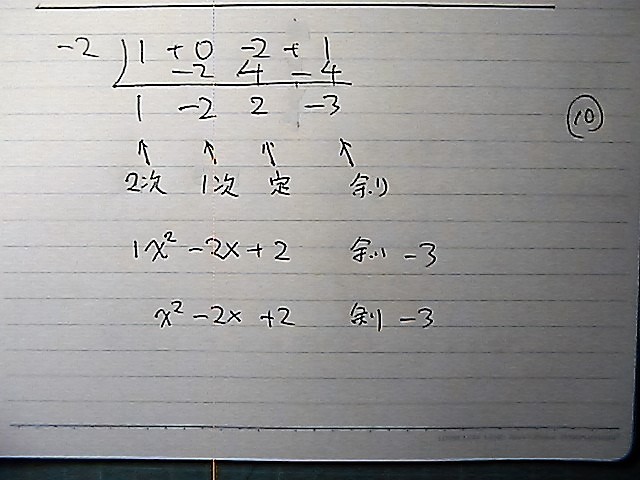
類題を
パラパラ漫画で

まずは
割られる式の 係数分離と
割る式の=0になる xの値
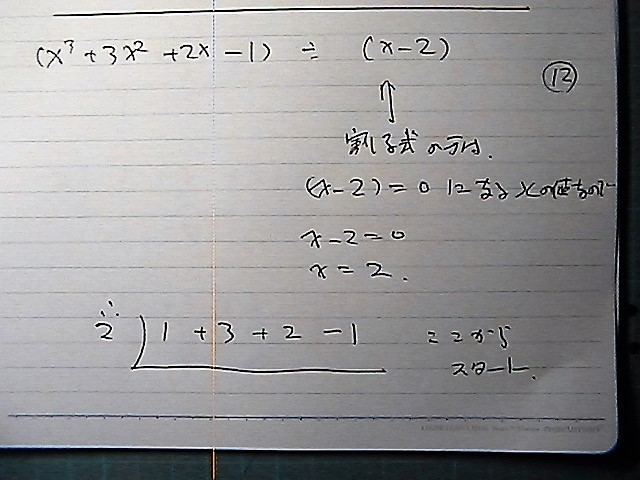
1,2,3
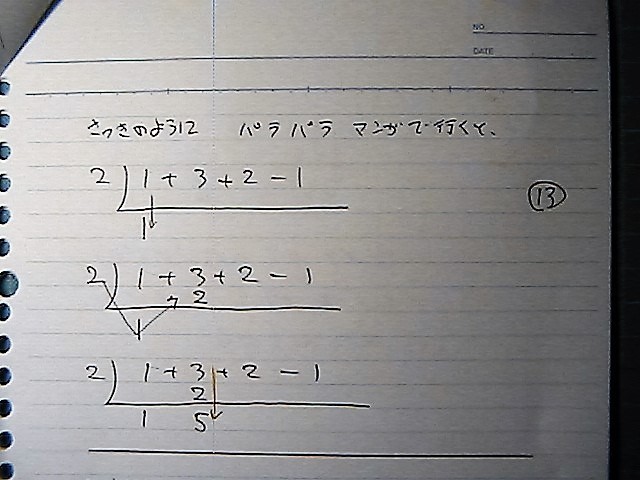
4.5.6
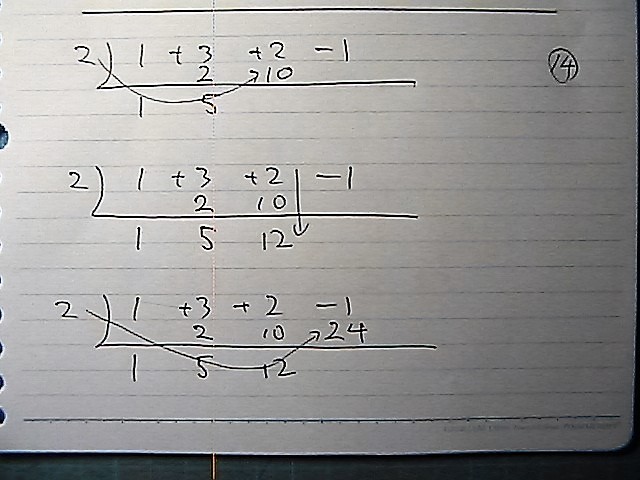
で
3次を1次で割ったから
商は2次以下
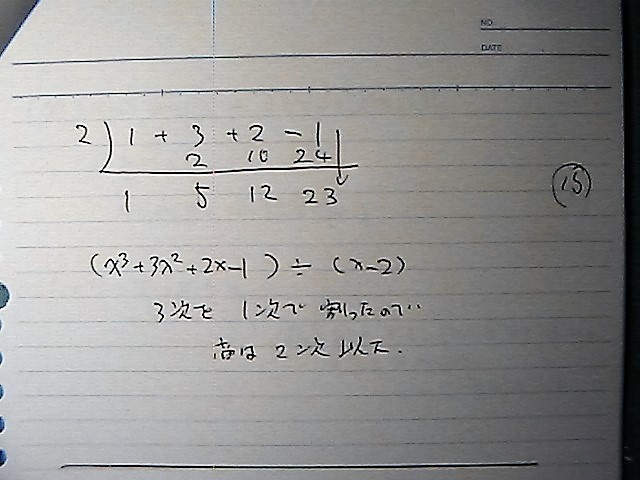
余りは 23
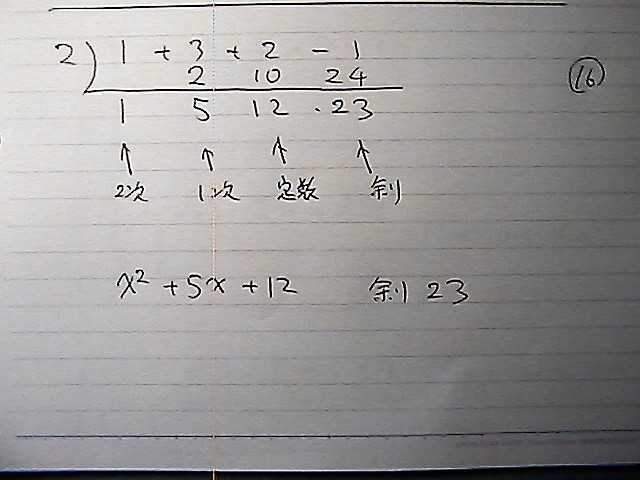
次はね
割り式が
因数分解できるんですよ
なので
二段構えで
いけます
今までと同じなんですが
1段目を
完成させてから
2段目へ

ぱらぱらと
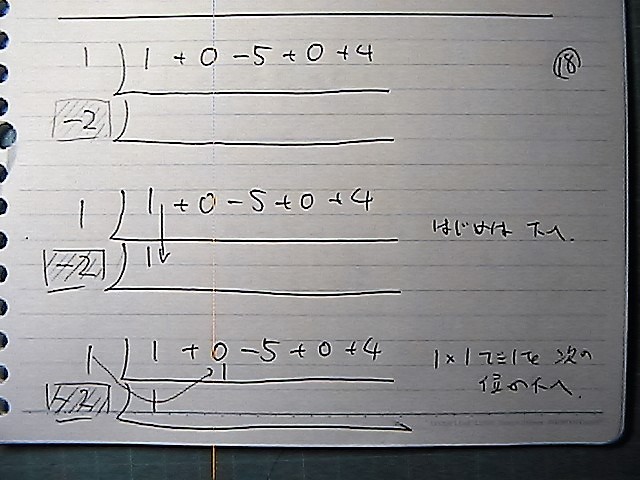
パラパラと

パらぱらと

一段目の次は
2段目へ

中略
こんな感じで

4次を 2回1次で割ってるので
商は 2次以下
余りは ゼロ

文字で 来てますが
割る式=0にする xの 値が でるので
そのまま
係数分離というよりも
そのまま
文字を
計算してくと

割る式=0になる
xを 求めて

組立除法で
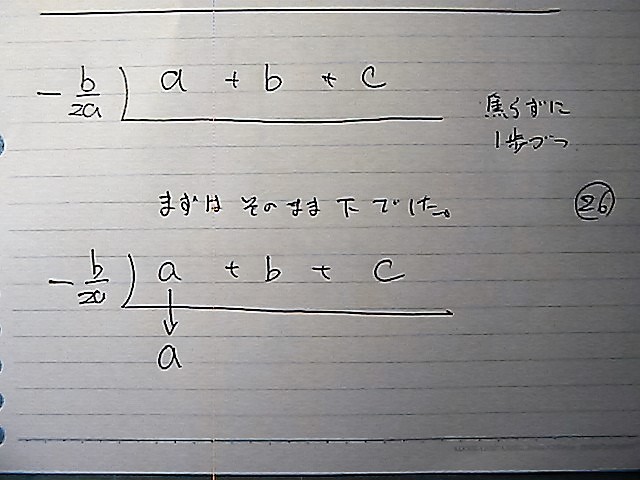
焦らずに 行ってみると
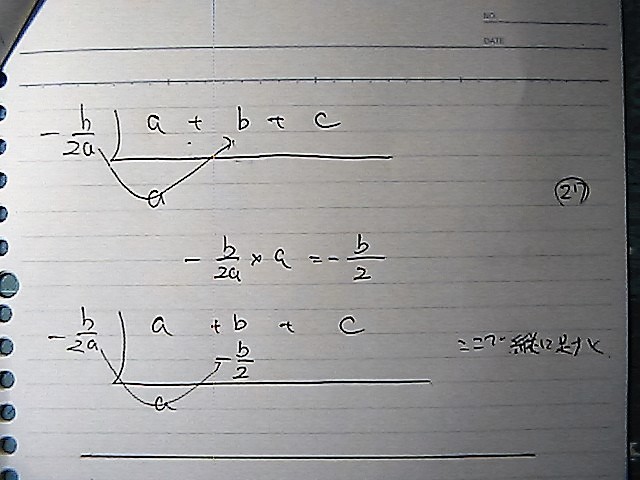
ダイジョカナ
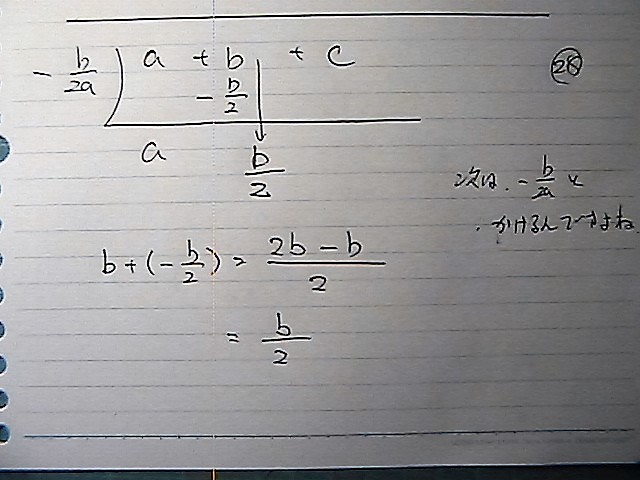
いいんかな
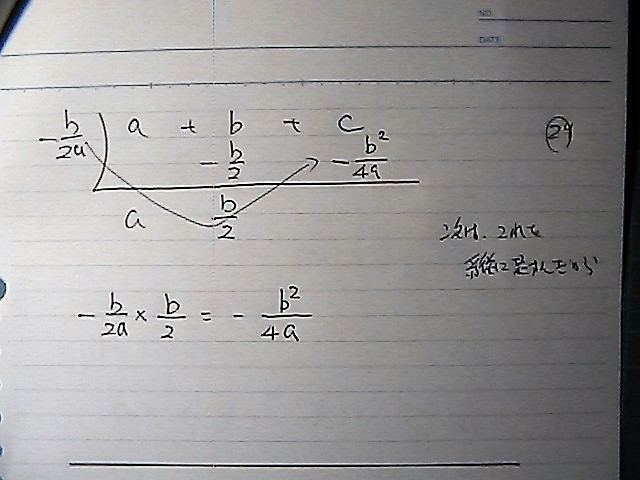
初めの頃は
分かってないので
ダイジョカナ なんですが
2回目ともなると
あー これは 何かの 形に にてるなぁー
ついいじってしまって
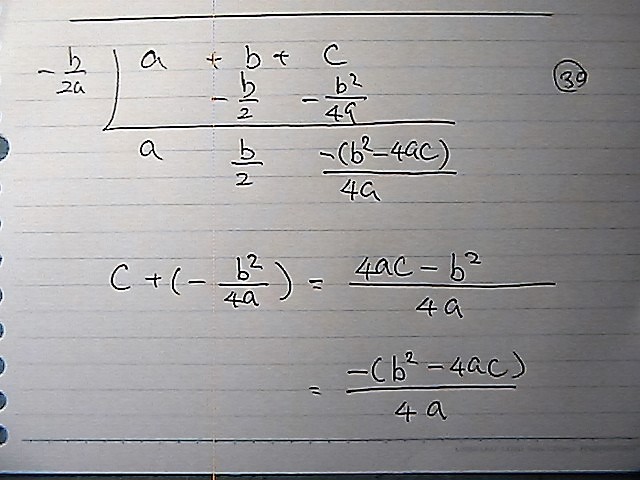
答えは これでいいんだって


リターン
なぜ こんな くどいことをするかというと
初めに 数Ⅰを やった当時は
ブログネタがなく
しょうがないから
自分のさび落としをして
お笑いで ごまかそうと
始めたのですが
楽しみに してくださる方から
もっと 丁寧に 書いてほしいを
要望されまして
できるだけ 丁寧なつもりなんですが
つい 計算してると
くしゃくしゃとなりがちで
日々 反省しながら
残りの 人生で
ほんの 少しの 方にでも
お役に 立てれば 幸いですで
ほんの 少し 丁寧バージョンです
行ってみます
組立除法
初めは
普通のやり方なんですが
各段階の
頭どうしの
割り算で
順次 やってくじゃナイスカ
文字をそのまま使ってるので
何次 式 か 一目瞭然ですが
桁が 多かったり
割り算が たくさん あるときは
閉口してしまいます
そこで
組立除法 があるんですが
今までは
係数を 分離して
その後 普通の 割り算
これでも
少しは
文字を省く分は 速いですが
割られる式じゃなくて
ですね
割る式の方を
=0になる xの 値にするんですよ
組立除法の 形は
こんな感じから スタート
初めは そのまま下に
次に 矢印の様に かけあわせて
矢印の様に 縦に
また
矢印の様に 掛けて
これを 繰り返しながら
最後まで来たらですね
3次式を 1次式で 割ったから
商は2次以下
2次 、1次 、 定数項 、余り
類題を
パラパラ漫画で
まずは
割られる式の 係数分離と
割る式の=0になる xの値
1,2,3
4.5.6
で
3次を1次で割ったから
商は2次以下
余りは 23
次はね
割り式が
因数分解できるんですよ
なので
二段構えで
いけます
今までと同じなんですが
1段目を
完成させてから
2段目へ
ぱらぱらと
パラパラと
パらぱらと
一段目の次は
2段目へ
中略
こんな感じで
4次を 2回1次で割ってるので
商は 2次以下
余りは ゼロ
文字で 来てますが
割る式=0にする xの 値が でるので
そのまま
係数分離というよりも
そのまま
文字を
計算してくと
割る式=0になる
xを 求めて
組立除法で
焦らずに 行ってみると
ダイジョカナ
いいんかな
初めの頃は
分かってないので
ダイジョカナ なんですが
2回目ともなると
あー これは 何かの 形に にてるなぁー
ついいじってしまって
答えは これでいいんだって
 |
リターン
タグ:01003 組立除法
2017年03月03日
引き出し01002 整式の割り算
整式の 割り算 行ってみましょう
そのまま
分数みたく できるときはですね
こんな公式があるので
部分的に
場合に分けてみると
m>n の時は
xが そんな感じで
m=n の時は
zが そんな感じで
同様に
m<n の時は
yが それですよね
( よく ローマ字 式に タイプするとき
間違ってさ
やいが とか )
なので
全部 まとめるとこんな感じ
今度は
掛け算の形のいなってませんもんで
分数みたくは できないじゃナイスカ
仕方ないからさ
普通に 割るでしょ
飛んでる次数は あけておくと やりやすく
各段階の 頭どうしの 割り算で
上から 下の 行を 引くでしょ
今度の 頭は -4 でいけますね
で
これ以上 いけないので
あまりがあると
こんな感じととこはさ
係数を分離すると
速いので
まず 降累乗順に 並べ替えて
係数を 拾い出し
飛んでる 次数のとこは ゼロ
3次式を 2次式で わるから
商は 1次以下
2-4は
2x-4
あまりは 11x+3
次も
係数を分離してじゃナイスカ
まず
降累乗 順に 並べ替えて
係数を分離して
4次を 2次で割ってるから
商は 2次以下
割られる数の しっぽは 3だから
ここまでで
商と 余り
次はさ
これは 係数を 分離できないので
ダイレクトに
しょうがないじゃナイスカ
あ
以外に 簡単だった
割り切れた模様です
なので
こんなで
係数を 分離しないで
やってみるでしょ
飛んでる 次数は アケテ おいて
間違わなければ
どっちでもいいんですけど
ラストは
整式に 文字が m、n 混ざってるんですが
割り切れるように
m、nを 定めよ
係数を 分離して
計算してくじゃナイスカ
ここで
割り切れなきゃいけないんです
整理してみてですね
このさ
下のところ
まる まる のとこが
ゼロじゃナイスカ
割り切れるんだもん
連立で
n=8
m=-64
なので
m、nは
こんな感じ
割り切れるでしょ
リターン
タグ:01002 整式の割り算
引き出し01001 整式の掛け算
構築中
先日 パソコンが 不調になってしまい
しばらくは
大人のさび落としが
アップできない状態 なのですが
( メンテナンス中 )
何せ よくわかりませんもんで
時間がかかるんでございます
それでですね
数Ⅰが 字が汚くて
疲れるという話で
気持ち 見やすく
初めのところから
やり直すかな
ともあれ
メンテナンス中です
あ 治った模様です
整式の 掛け算ですが
括弧の n乗とかのばやいは
中身の 掛け算 全部の 要素に 効いてくるので
で
掛け算は 順番を 入れ替えても
同じですが
( ) は 先に やらないといけないですので

後は 都合よく
順番を 整理して
同じ 文字の 指数の掛け算は
肩の数を足して
こんな感じに

括弧の
中身を 降順に 並べ替えると
計算がしやすく
長城式に並べて
肩の数の 計算をデショ

けせるとこを 消して
答え
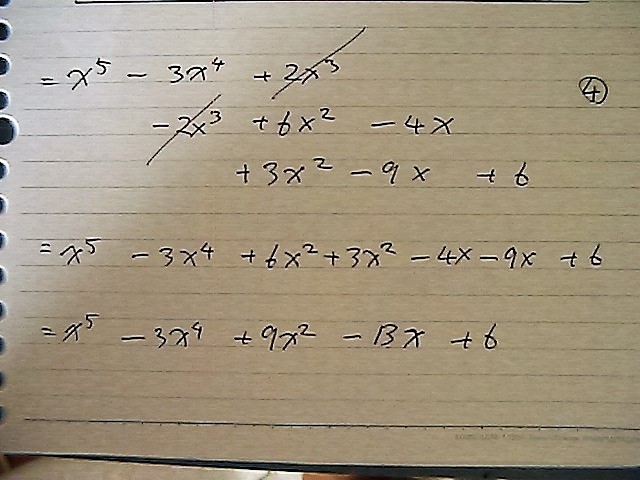
やっぱりさ
長城式に
かいて

指数の足算をして
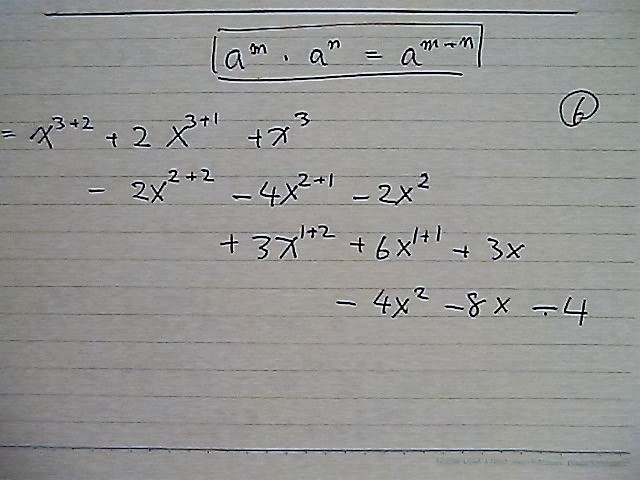
今度は 指数を そろえて
高楼式に して
縦で 計算すると
こんな感じで
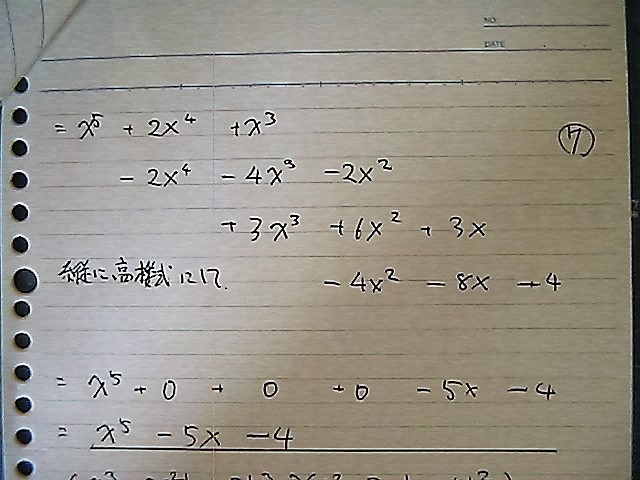
今度は どないでしょう
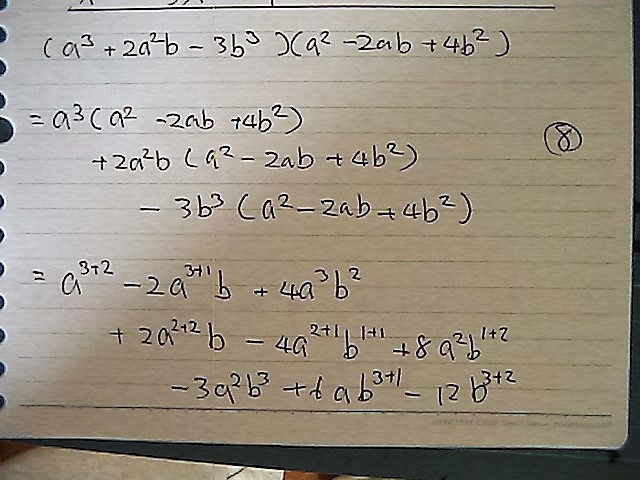
けせるとこを
けして
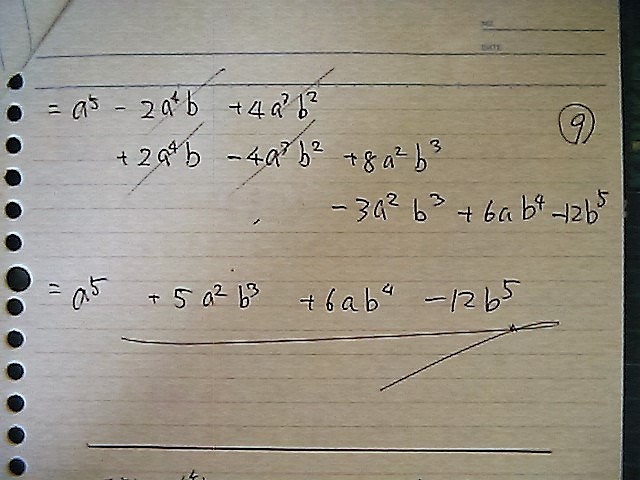
証明だから
左辺イコールで
計算して
右辺に なればさ

(1)は
横に 長城に展開して
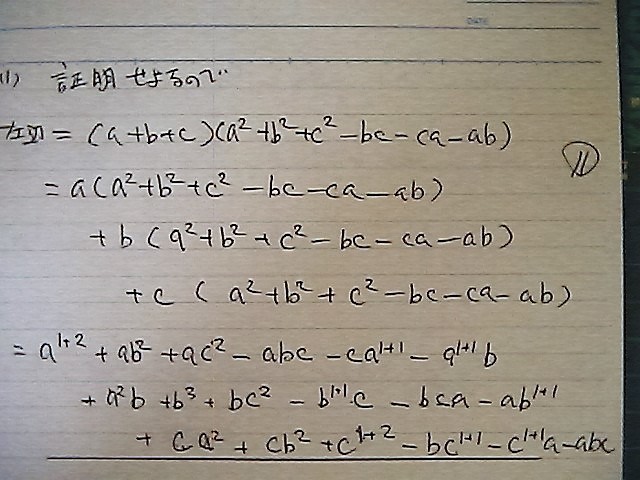
けせるとこけして

整理して
= 右辺
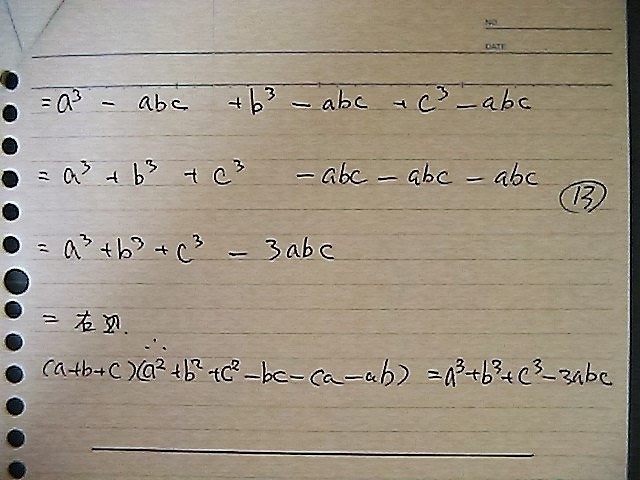
これも
これって
証明した後は
公式に 追加で
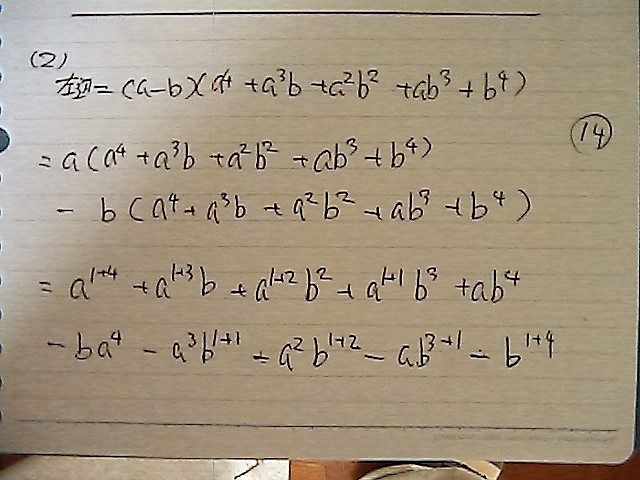
aマイナスbの対称形
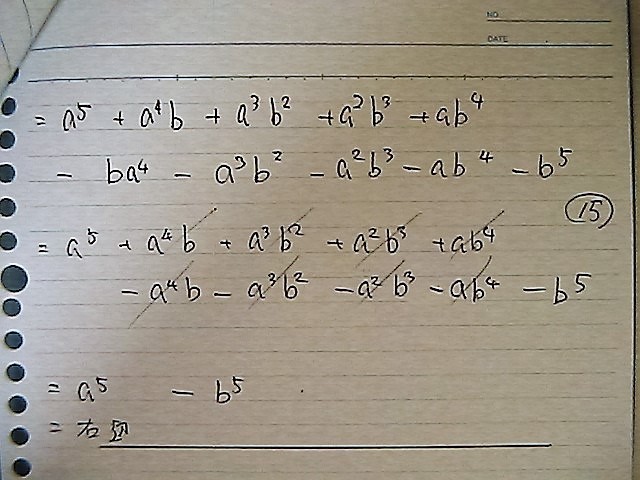
ジョジョニー
リターン
先日 パソコンが 不調になってしまい
しばらくは
大人のさび落としが
アップできない状態 なのですが
( メンテナンス中 )
何せ よくわかりませんもんで
時間がかかるんでございます
それでですね
数Ⅰが 字が汚くて
疲れるという話で
気持ち 見やすく
初めのところから
やり直すかな
ともあれ
メンテナンス中です
あ 治った模様です
整式の 掛け算ですが
括弧の n乗とかのばやいは
中身の 掛け算 全部の 要素に 効いてくるので
で
掛け算は 順番を 入れ替えても
同じですが
( ) は 先に やらないといけないですので
後は 都合よく
順番を 整理して
同じ 文字の 指数の掛け算は
肩の数を足して
こんな感じに
括弧の
中身を 降順に 並べ替えると
計算がしやすく
長城式に並べて
肩の数の 計算をデショ
けせるとこを 消して
答え
やっぱりさ
長城式に
かいて
指数の足算をして
今度は 指数を そろえて
高楼式に して
縦で 計算すると
こんな感じで
今度は どないでしょう
けせるとこを
けして
証明だから
左辺イコールで
計算して
右辺に なればさ
(1)は
横に 長城に展開して
けせるとこけして
整理して
= 右辺
これも
これって
証明した後は
公式に 追加で
aマイナスbの対称形
ジョジョニー
リターン
タグ:01001 整式の掛け算