2022年09月14日
22007 大人のさび落とし 空間座標とベクトル ベクトルの大きさ
大人のさび落とし
22007
ベクトルの大きさ
01
問題を 読んでね
この 条件式を 良く見ると

02
AB だけ 異物感があるでしょ
そこで
右辺の AB を 左辺の ベクトルで
表現したらば
これは
決まって使う手段ですが
AB= PB-PA

03
左辺に 集めて 整理すると

04
PC=2AP
ベクトルの 実数倍
方向が同じ
点Pを 共有している
つまり
A,P,Cは 一直線上にある
それで
AP:PC= 1:2
であるので

05
三角形ABCの 辺ACを 1:2に
内分する点が P
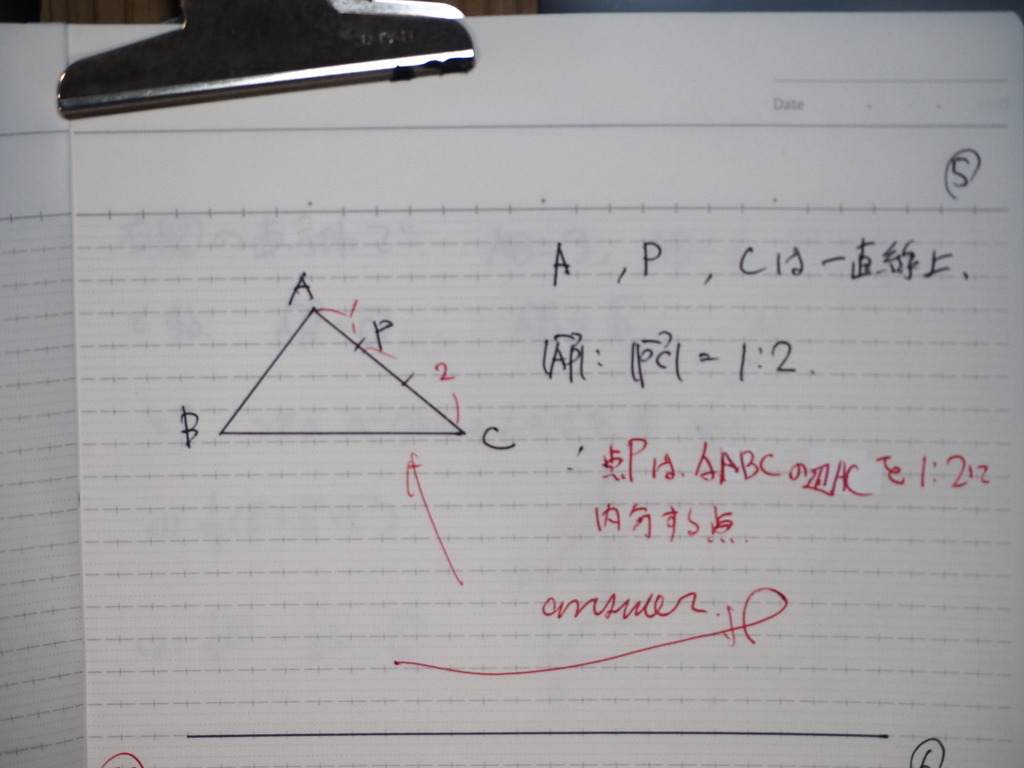
06
ここで
入れ知恵タイム
ベクトルの 大きさを 比較するとき
こんなカンじに 成るけど
右の 等号は a と bが 同じ向きの時
左の 等号は a と bが 反対向きの時

07
問題
右の図で
これこれの時
次の 値を 計算しなさい
良く見ると
a,b,c,は 互いに 垂直方向
そのまんま 足すわけには 行きません
立体的に
足し終えた後の
ベクトルの 大きさを 調べないと

08
こういう問題なんだね

09
AGが こんなだから

10
対角線AGの大きさを 調べて

11
(2)は
こんな感じに 成るから
この座表成分から
Aとの距離を 計算して

12
こんなですか

13
証明問題
まず
MN に関しては
こないだ も 同じものが出てたので
(22006の 1問目)

14
こんな感じで
ここまでは
出て来ますよ
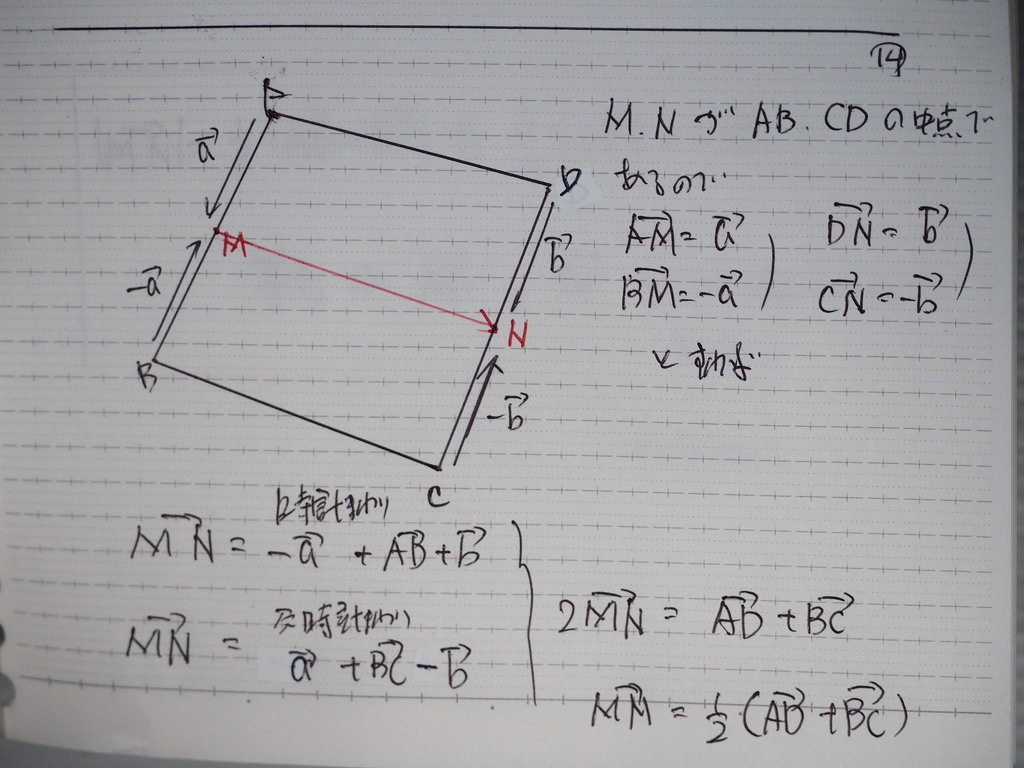
15
それで
これは 空間の ベクトルだから

16
左辺は 中辺に等しくて 右辺とは
こんな感じに 成る

17
問題
読んでいただいて
途中までは
一番 初めの問題と
ほぼ そっくり そのまま

18
こんな感じに

19
どがんな 位置に Pが あるか
見ると

20
こだからんな

21
題意より
求めるものは
三角形 ACP と BCP の
面積比
であるので
高さが おなじとかんがえて
底辺× 高さ 割る 2
違うとこは
底辺の 比だけ
なので
1:2
お疲れ様です。
メニュウ
22007
ベクトルの大きさ
01
問題を 読んでね
この 条件式を 良く見ると
02
AB だけ 異物感があるでしょ
そこで
右辺の AB を 左辺の ベクトルで
表現したらば
これは
決まって使う手段ですが
AB= PB-PA
03
左辺に 集めて 整理すると
04
PC=2AP
ベクトルの 実数倍
方向が同じ
点Pを 共有している
つまり
A,P,Cは 一直線上にある
それで
AP:PC= 1:2
であるので
05
三角形ABCの 辺ACを 1:2に
内分する点が P
06
ここで
入れ知恵タイム
ベクトルの 大きさを 比較するとき
こんなカンじに 成るけど
右の 等号は a と bが 同じ向きの時
左の 等号は a と bが 反対向きの時
07
問題
右の図で
これこれの時
次の 値を 計算しなさい
良く見ると
a,b,c,は 互いに 垂直方向
そのまんま 足すわけには 行きません
立体的に
足し終えた後の
ベクトルの 大きさを 調べないと
08
こういう問題なんだね
09
AGが こんなだから
10
対角線AGの大きさを 調べて
11
(2)は
こんな感じに 成るから
この座表成分から
Aとの距離を 計算して
12
こんなですか
13
証明問題
まず
MN に関しては
こないだ も 同じものが出てたので
(22006の 1問目)
14
こんな感じで
ここまでは
出て来ますよ
15
それで
これは 空間の ベクトルだから
16
左辺は 中辺に等しくて 右辺とは
こんな感じに 成る
17
問題
読んでいただいて
途中までは
一番 初めの問題と
ほぼ そっくり そのまま
18
こんな感じに
19
どがんな 位置に Pが あるか
見ると
20
こだからんな
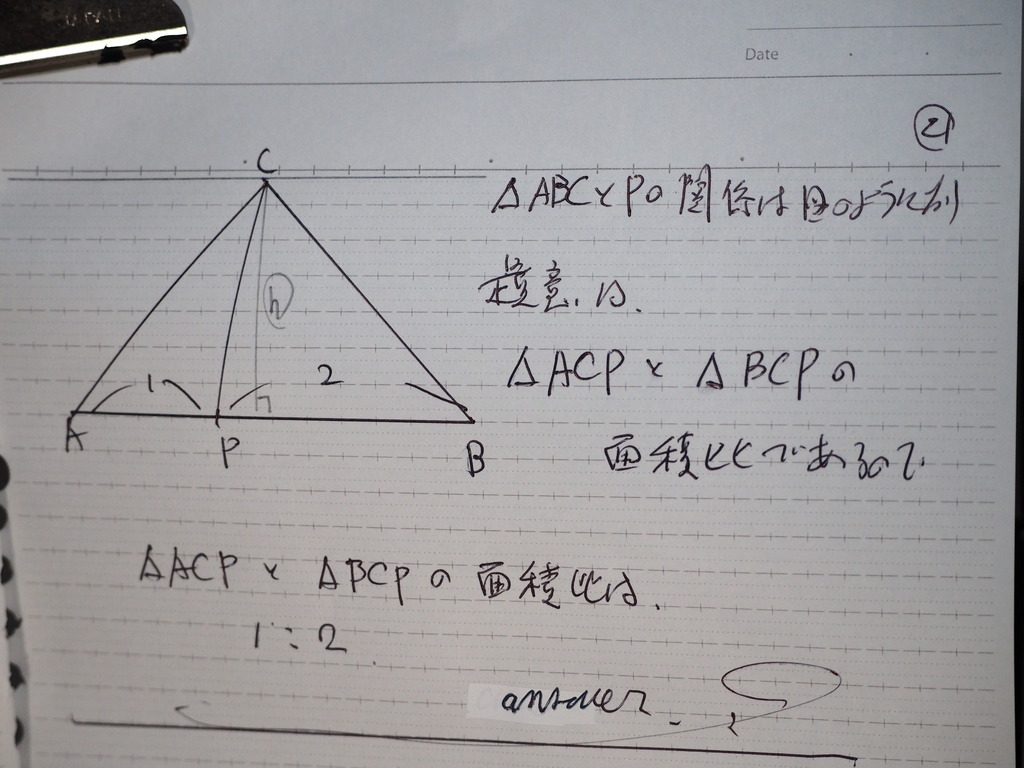
21
題意より
求めるものは
三角形 ACP と BCP の
面積比
であるので
高さが おなじとかんがえて
底辺× 高さ 割る 2
違うとこは
底辺の 比だけ
なので
1:2
お疲れ様です。
メニュウ