2022年08月10日
22002大人のさび落とし 空間座標とベクトルより 2点間の距離
大人のさび落とし
空間座標とベクトルから
二点間の距離
01
問題
正三角形であることの
証明と
この正三角形を
一つの面とする
正四面体の他の頂点をを求めなさい

02
三辺の 長さが 等しい
を 使ってみますと

03
個々に 計算して
成ってるよね
だからさ
正三角形
整理すれば 同じ だからさ
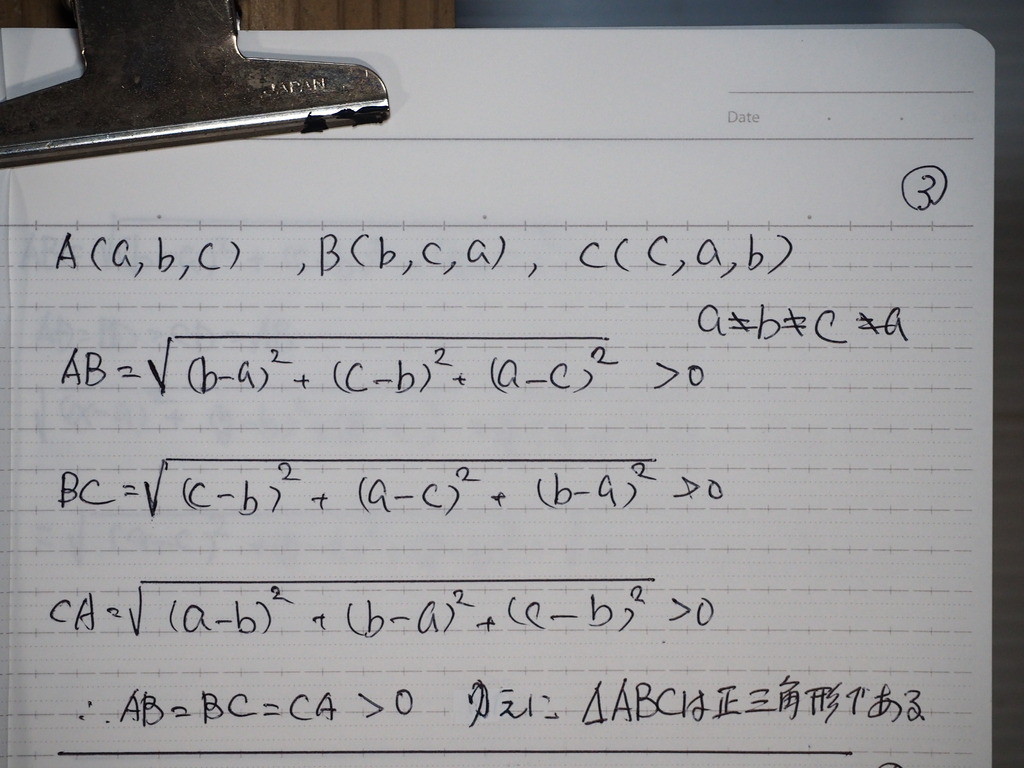
04
問題は
次だな
正四面体の 他の頂点
Dとすればさ
全て 正三角形の 面だから
AD=BD=CD=AB

05
これを 連立にしてくと
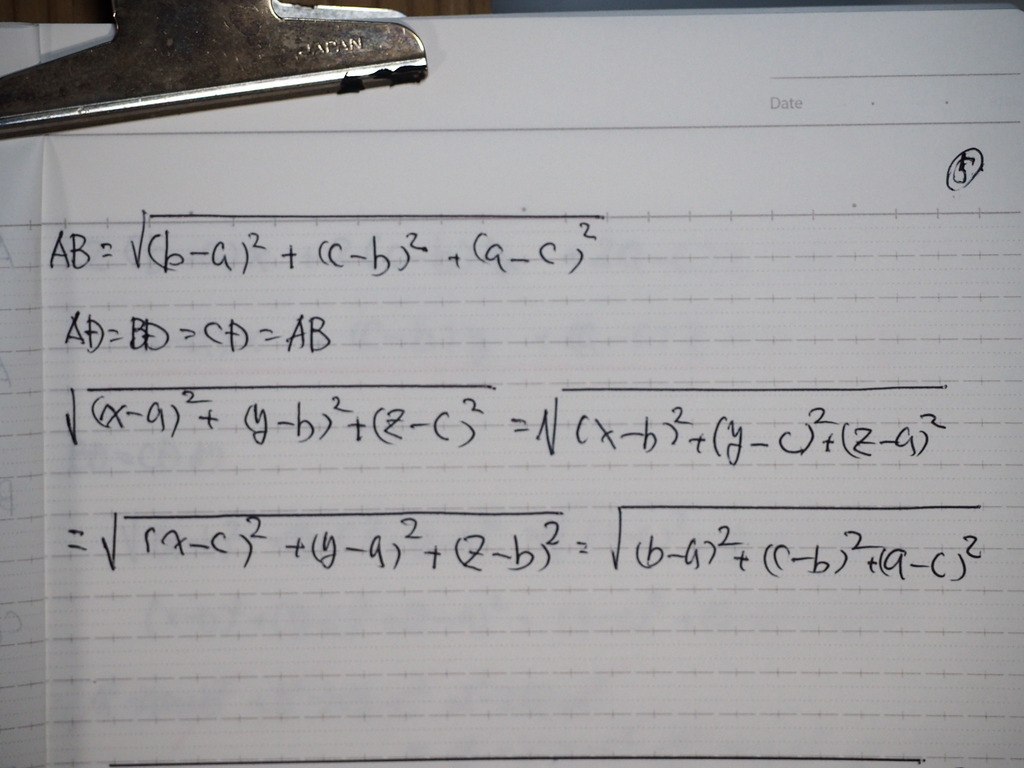
06
AD=BD より
計算してくと
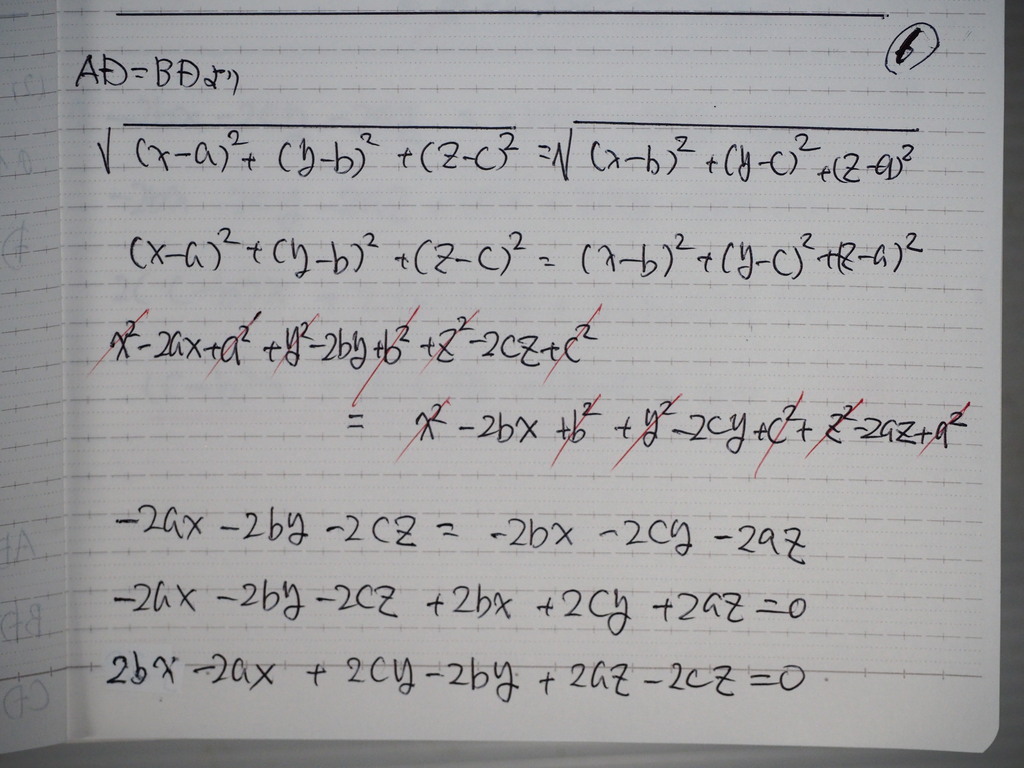
07
➀式
BD=CD より
計算してくと
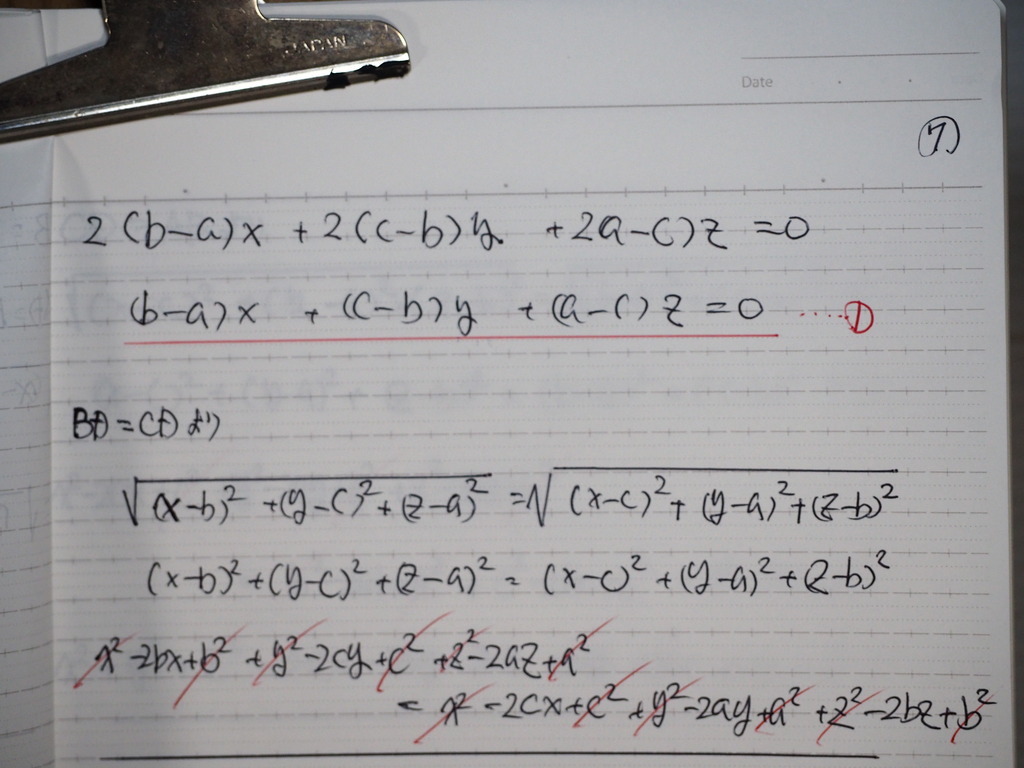
08
②式
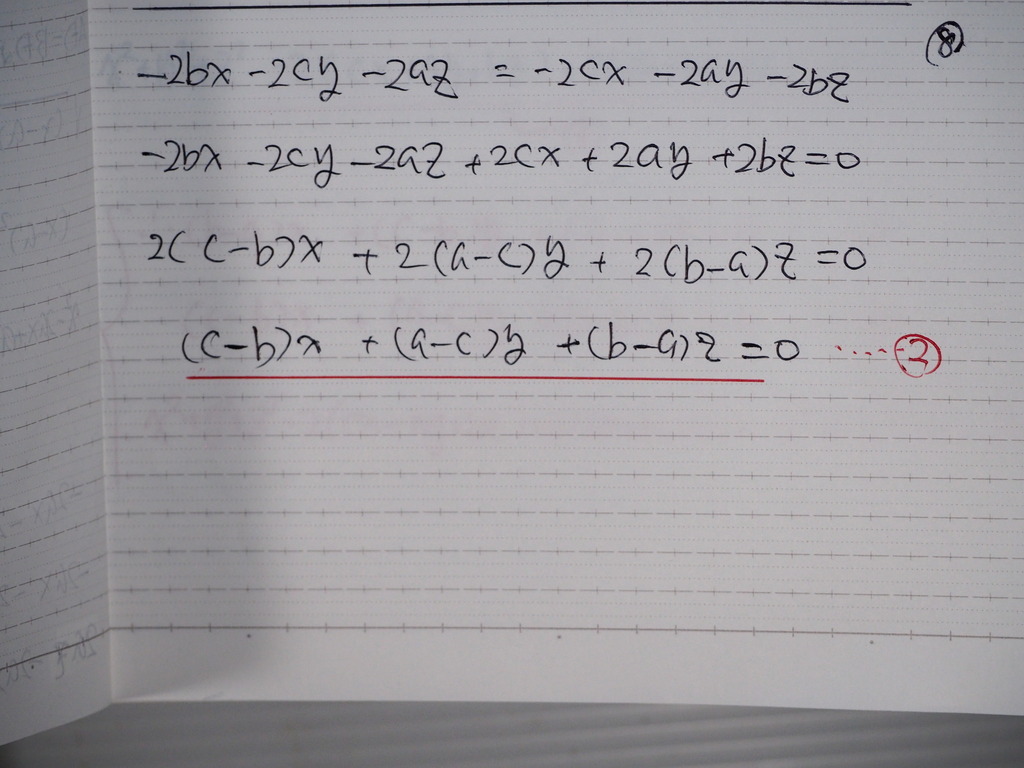
09
これも
コレは 種類が 違って見えるね
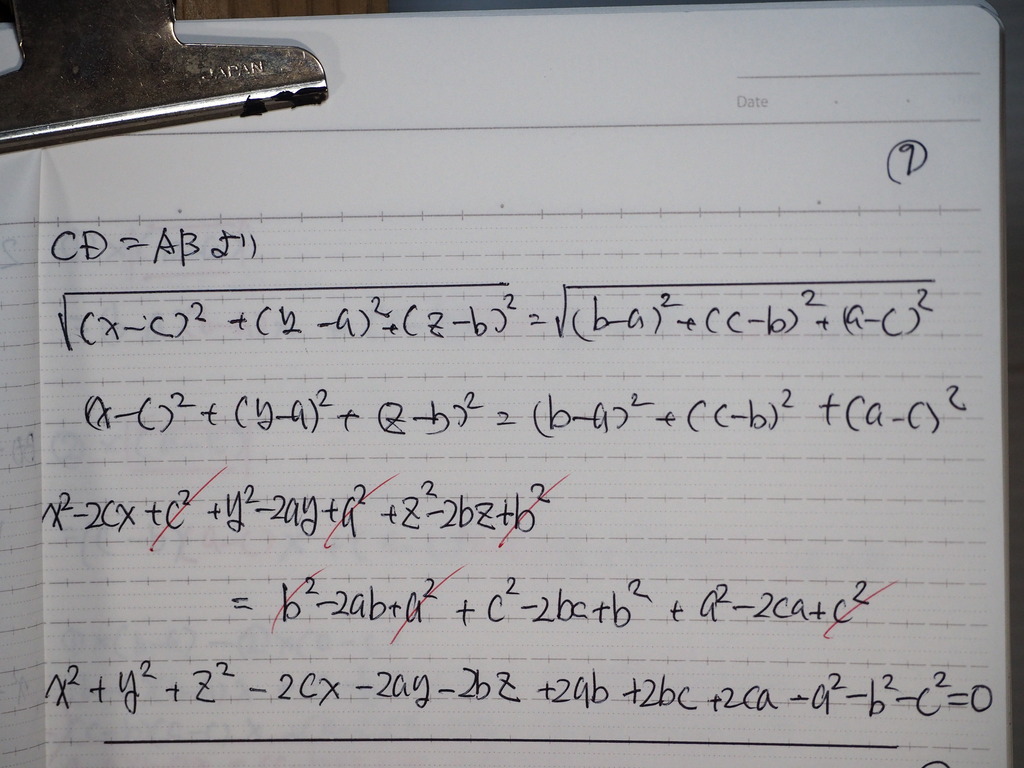
10
➀②③しきから
➀②をつかって
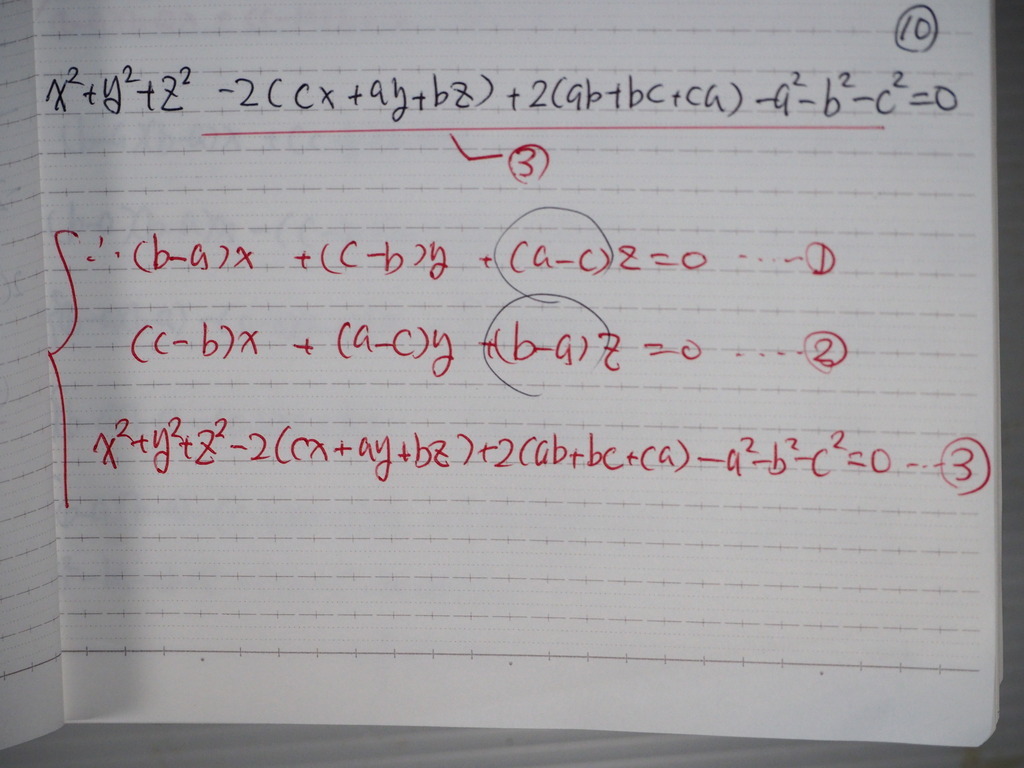
11
Zを 消去して
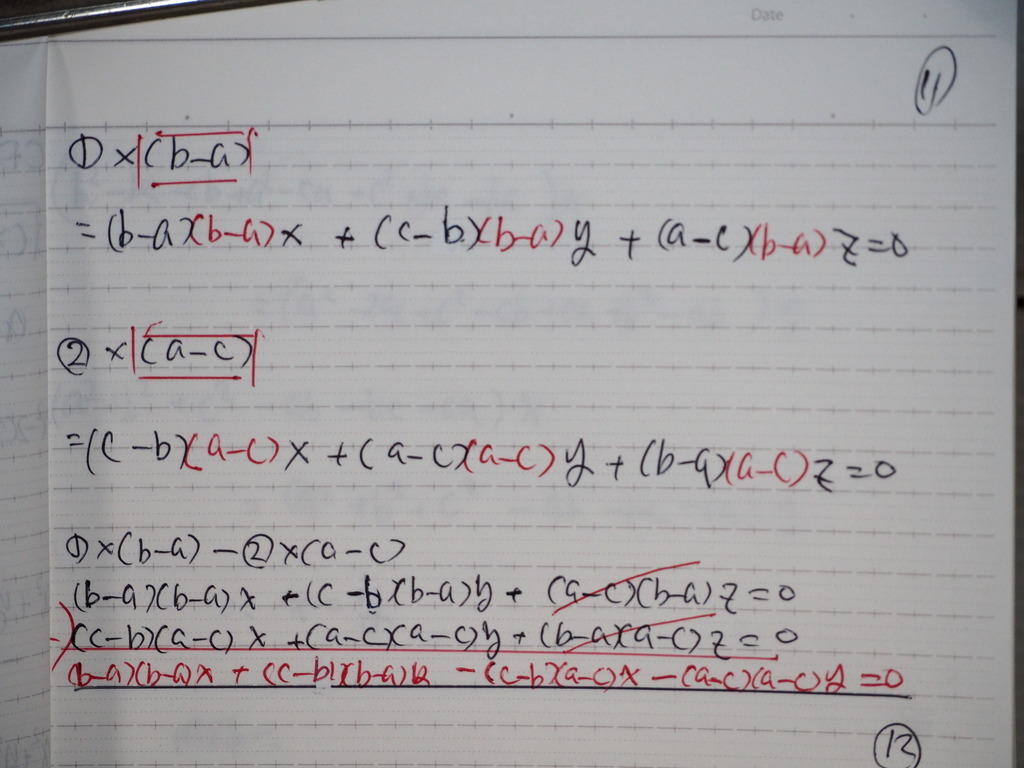
12
計算して
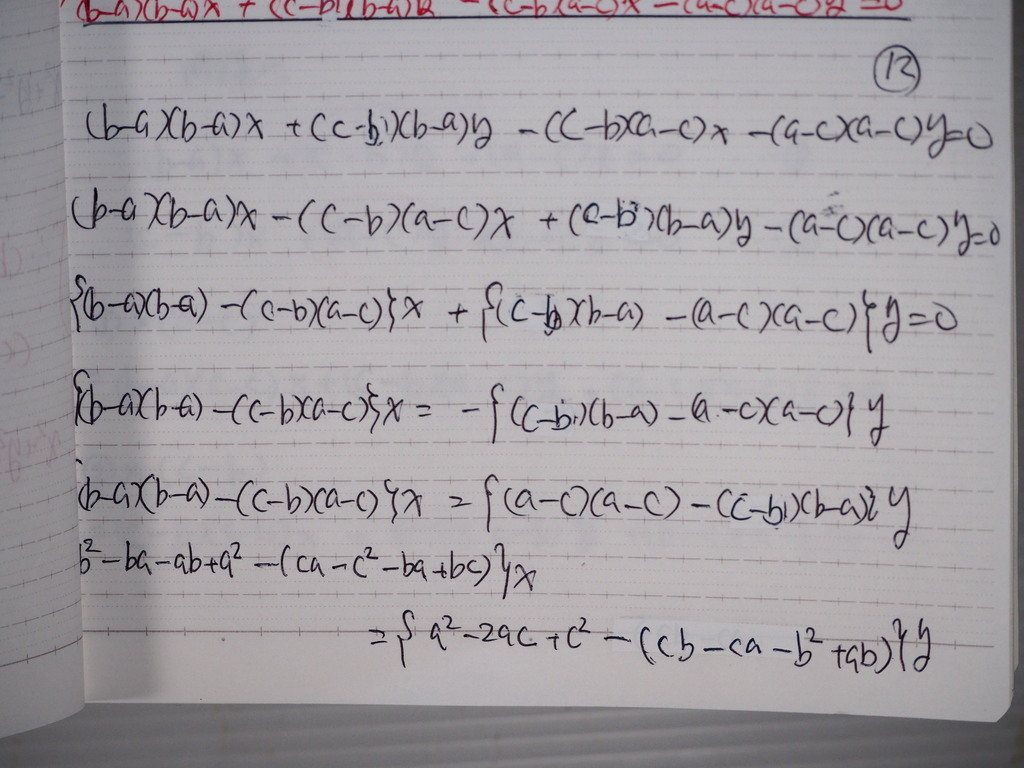
13
整理してくと
X=Y
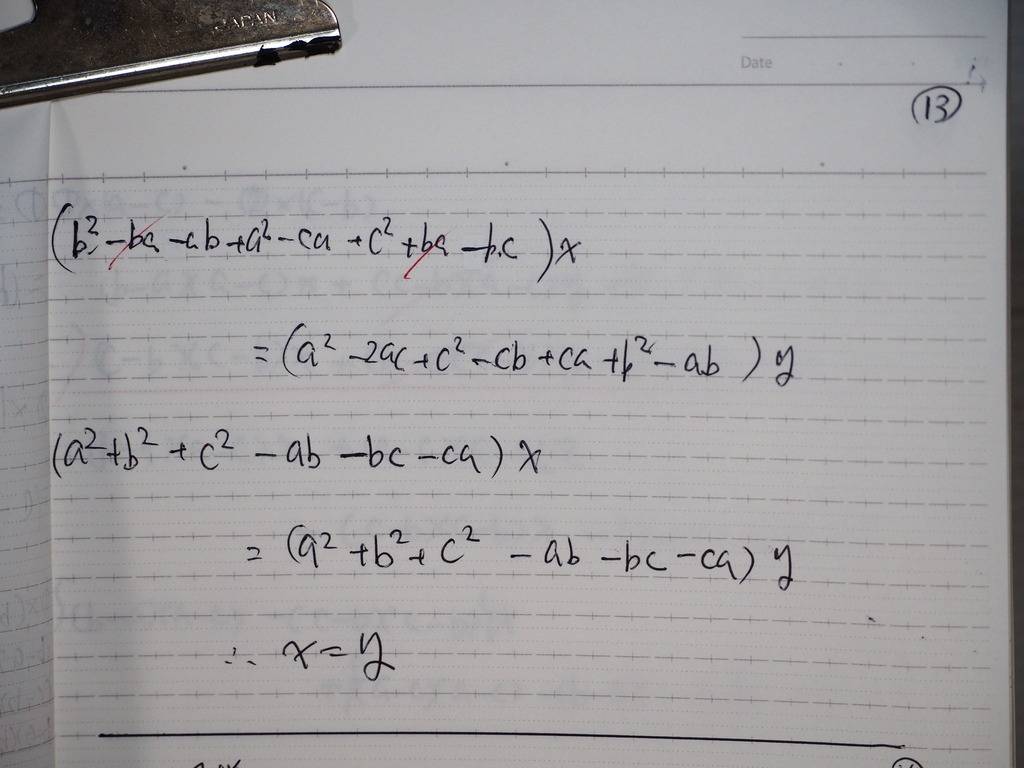
14
同様に
➀②を また少し変えて
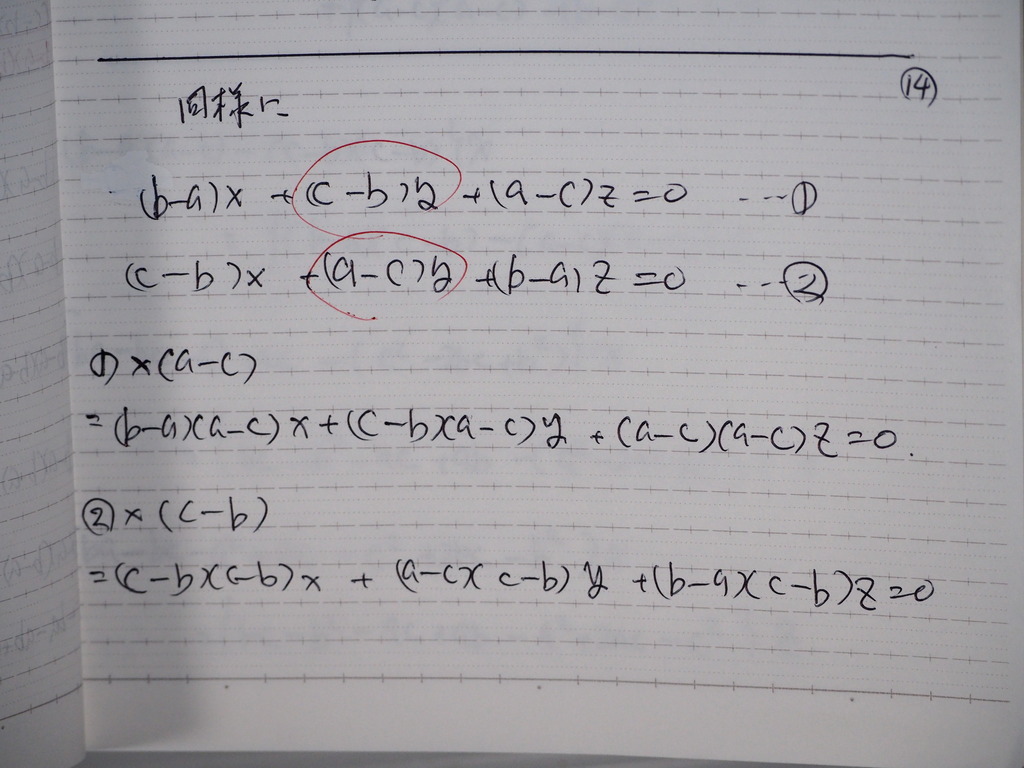
15
計算してくと
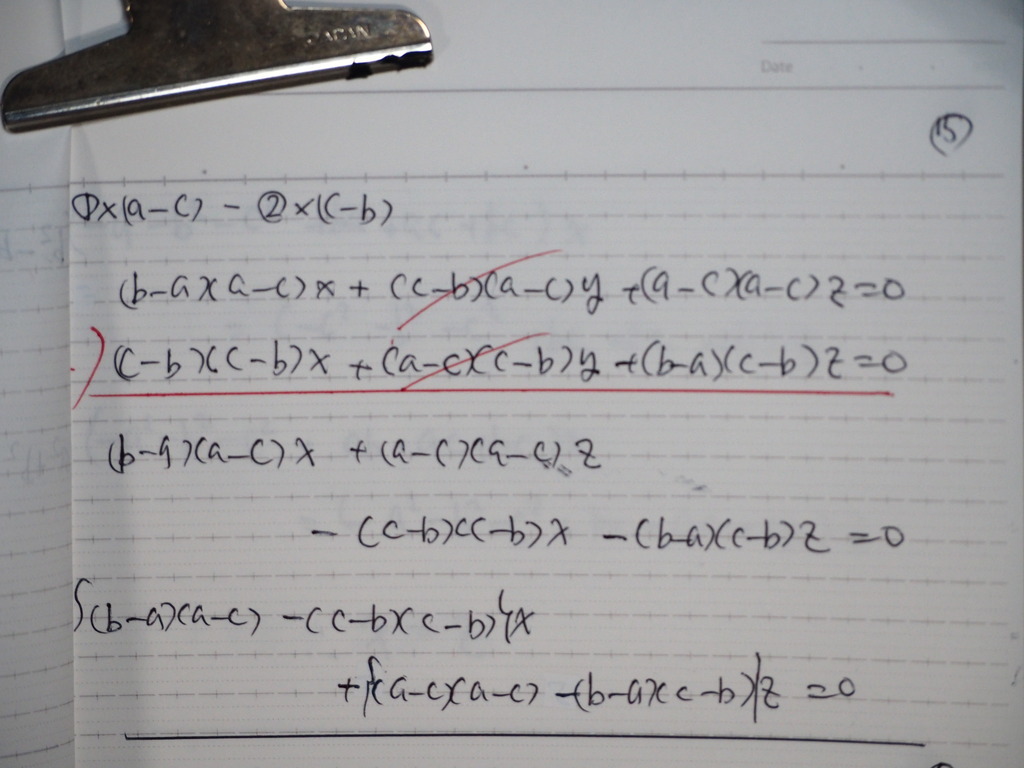
16
整理してくと
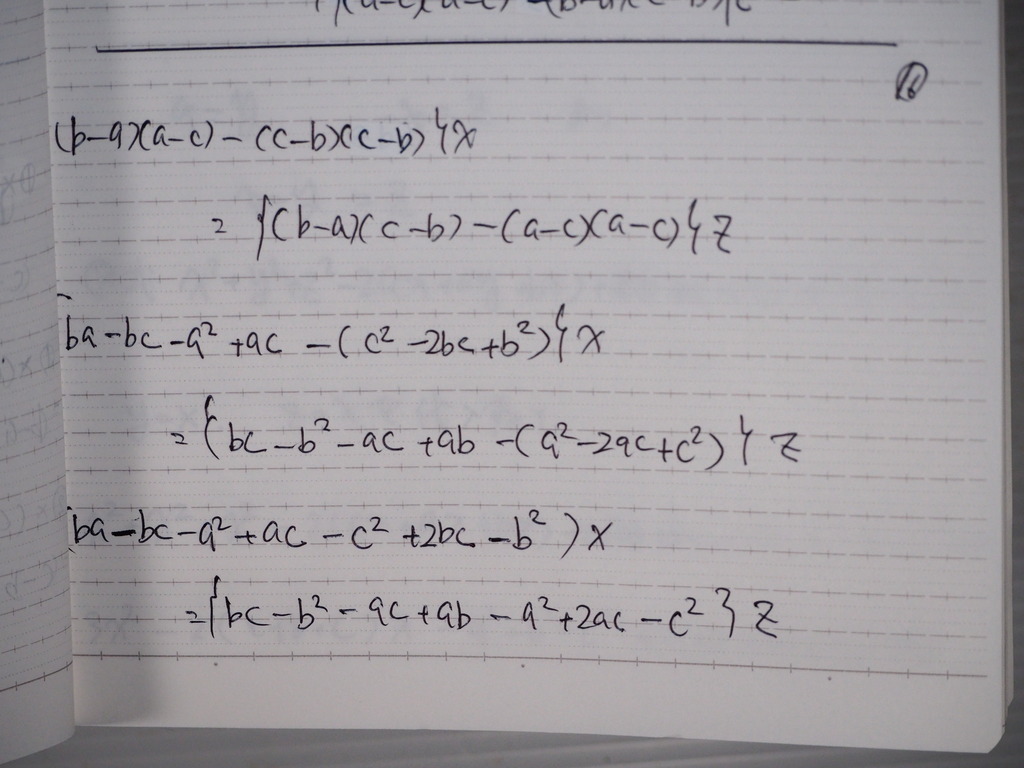
17
X=Z
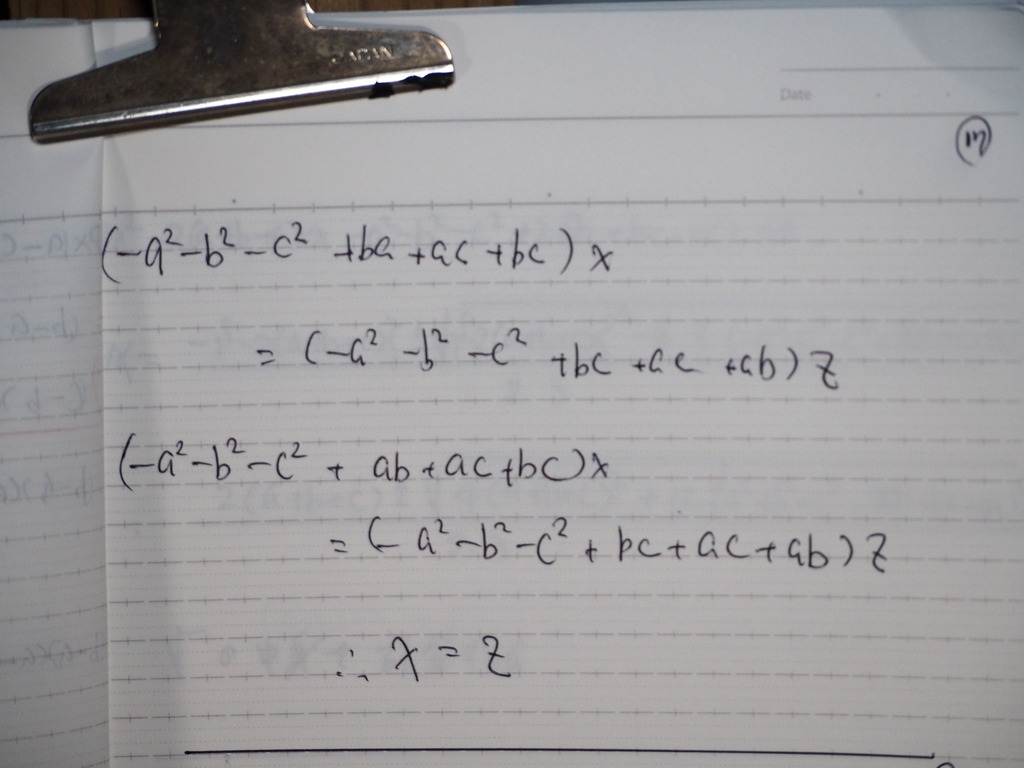
18
ナタメ X=Y=Z
これを ③式に
Y=X Z=X で
代入したらば

19
ここで
Xを 解の公式で 求めれば
X,Y,Z みんな 等しい値の
座標になるので
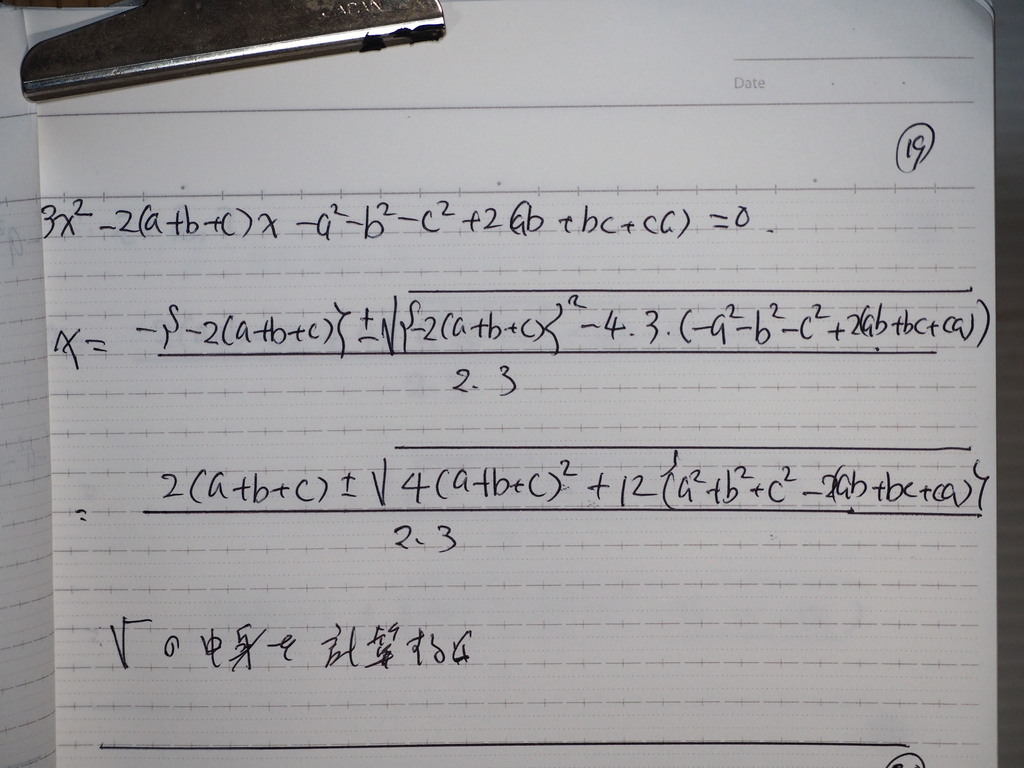
20
ルートの中身が出たから

21
整理してくと
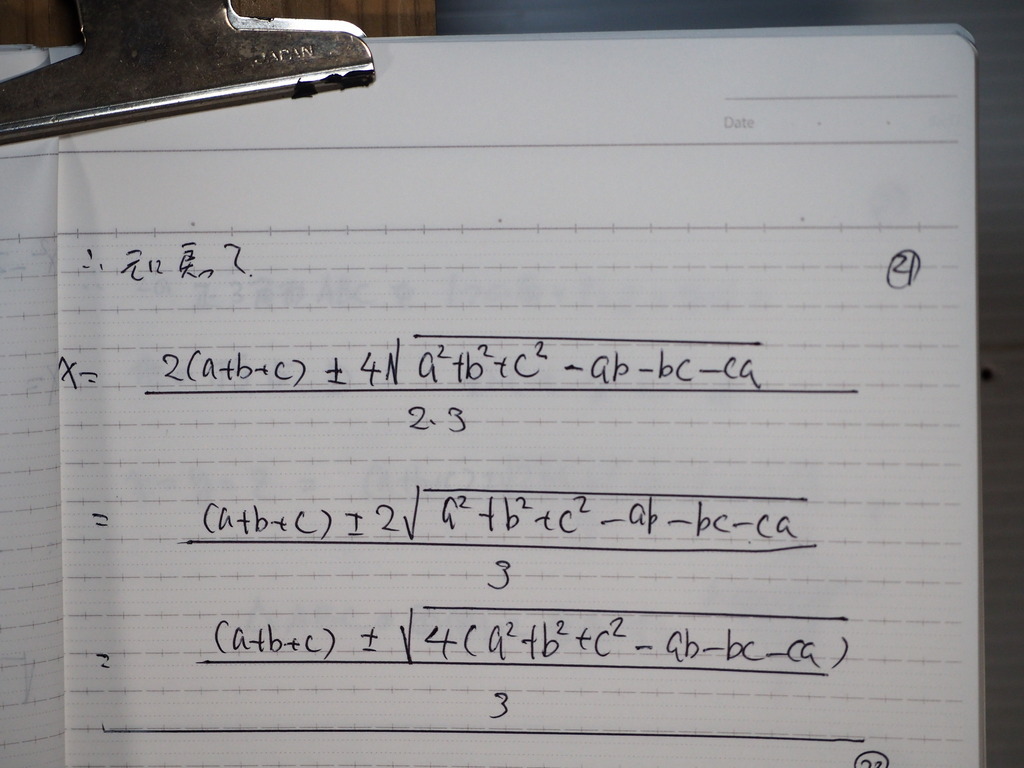
22
こんなカンじに
成ってじゃナイスカ
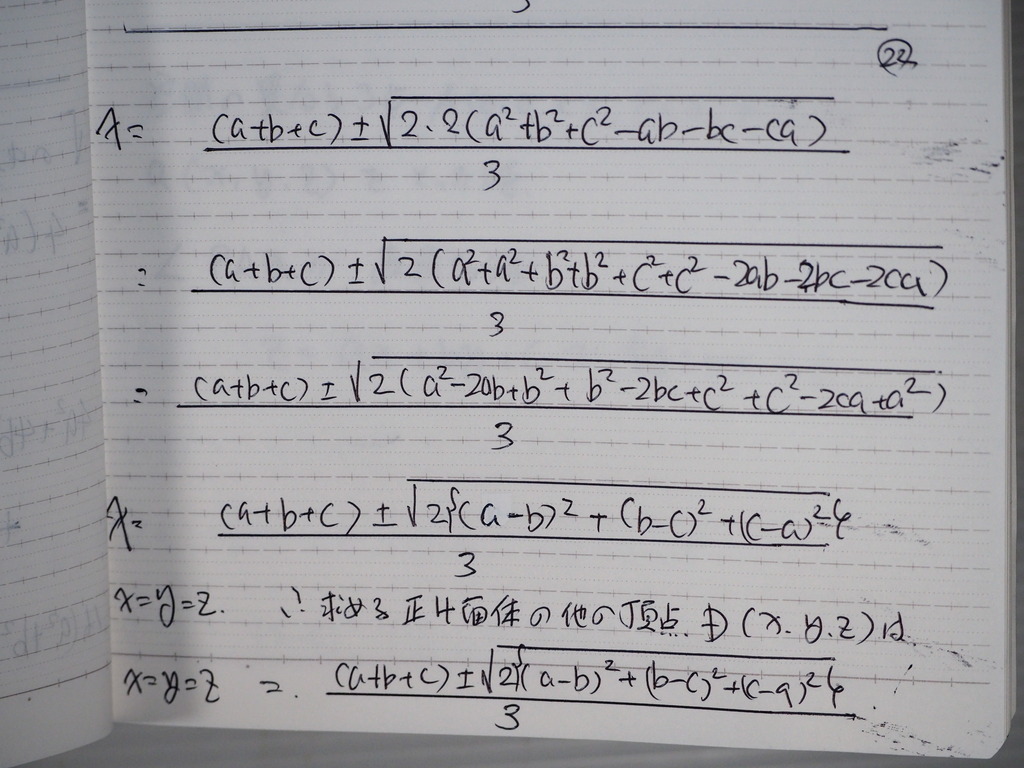
23
Dは 正三角形ABCの
両方の側に あるんだね

24
今度は なんか難しそうだけど
そんなことないですよ
行ってみましょう

25
この条件で 計算したらば
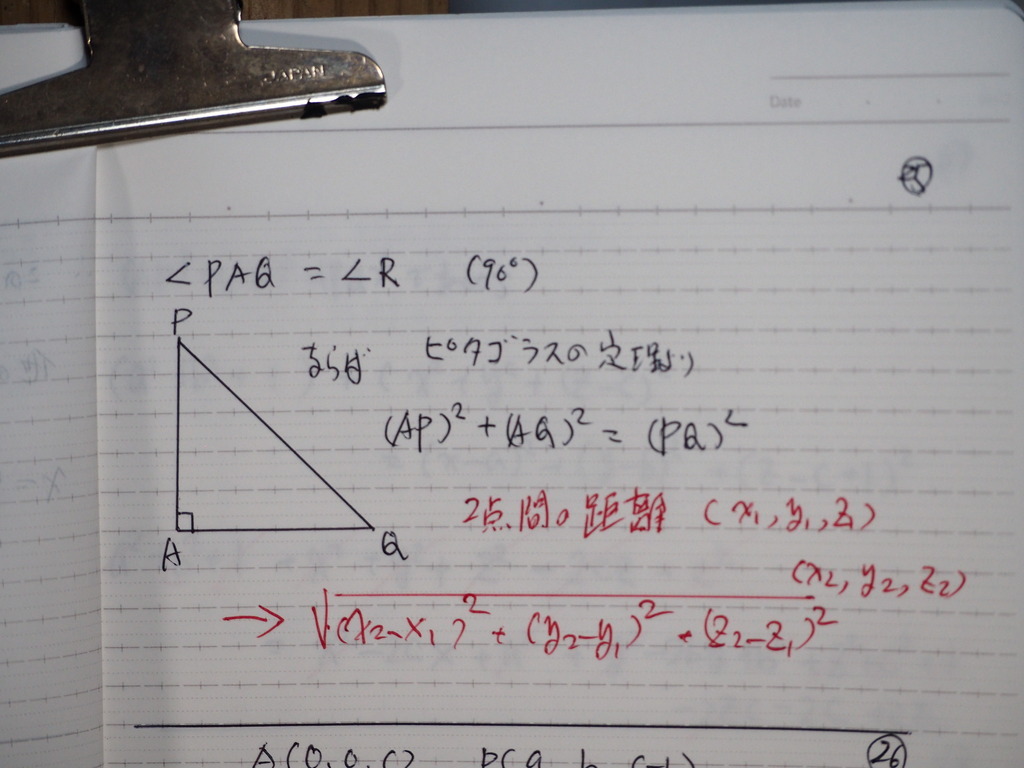
26
これを
ピタゴラスに入れて
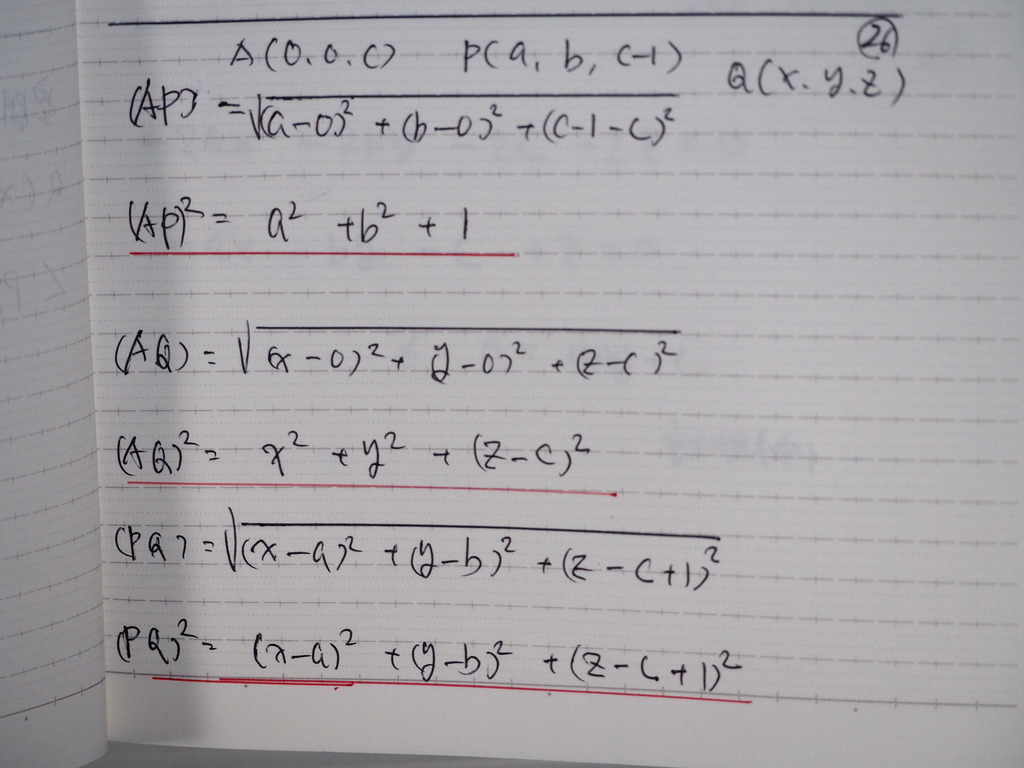
27
整理してくとだ
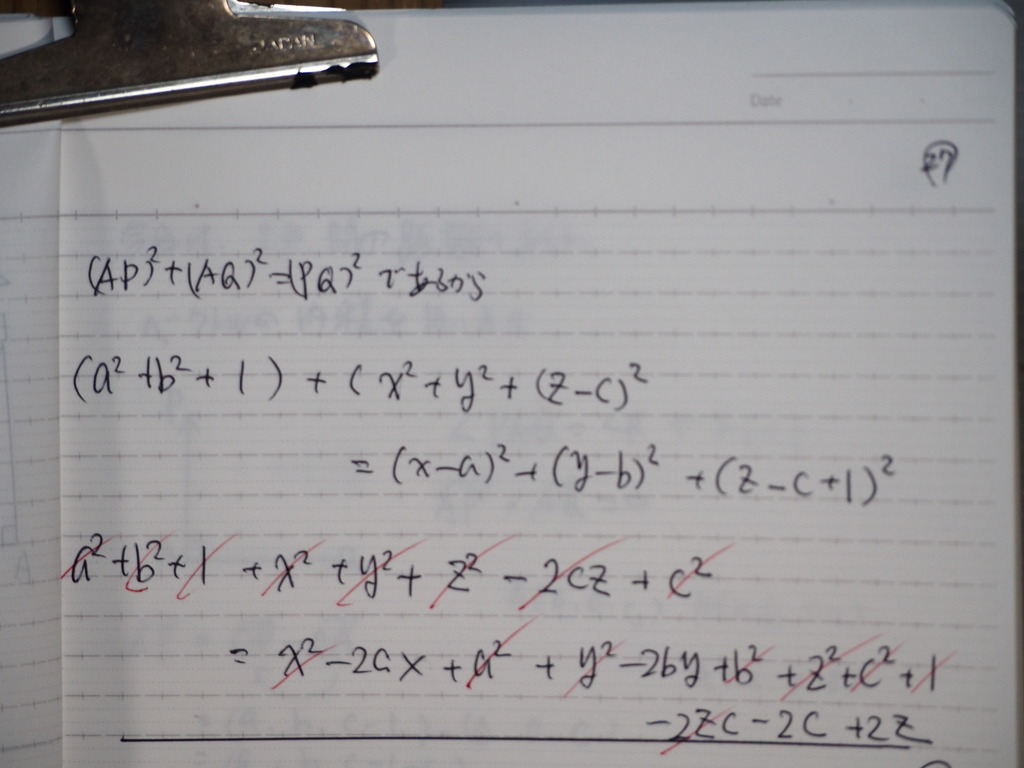
28
なったじゃナイスカ
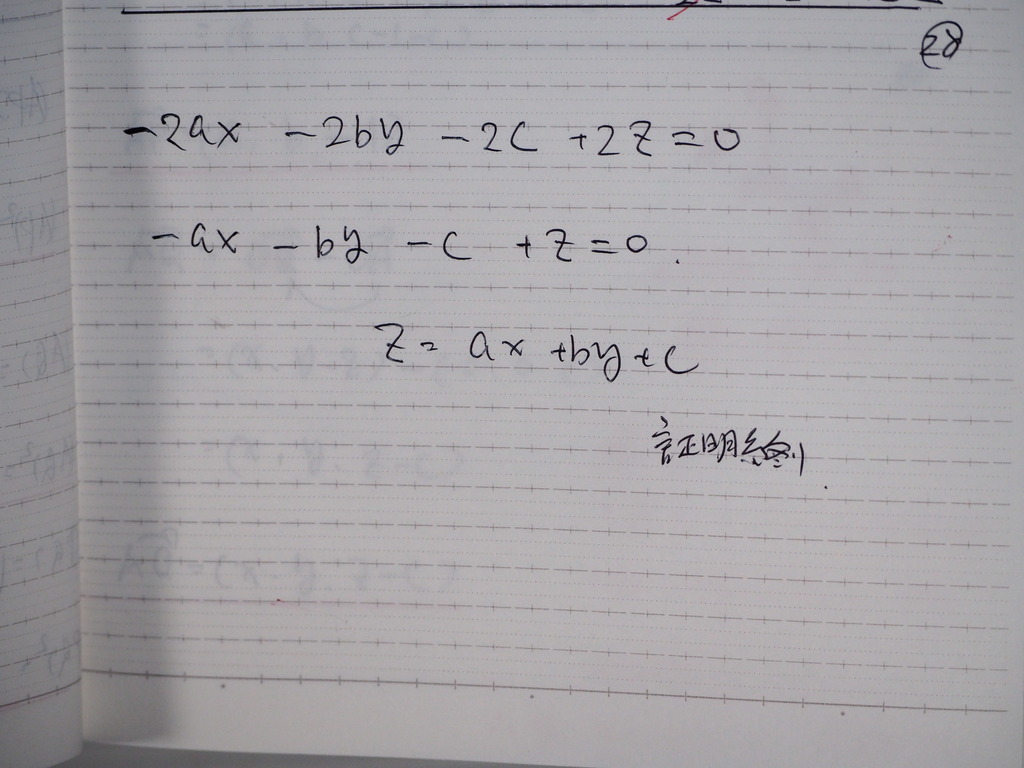
29
内積でも 解けるので
見ておくと

30
こっちの方が 早いね

31
今度 空間にある
正方形

32
条件を 見つけて

33
条件を 関係式に
してくと
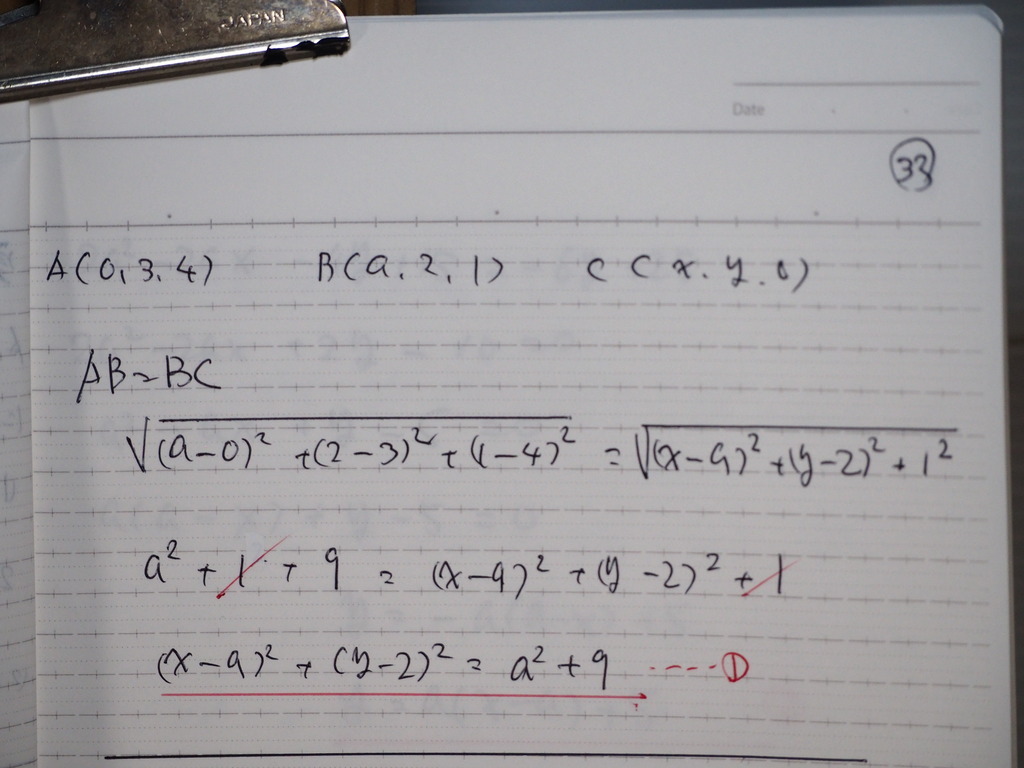
34
計算して
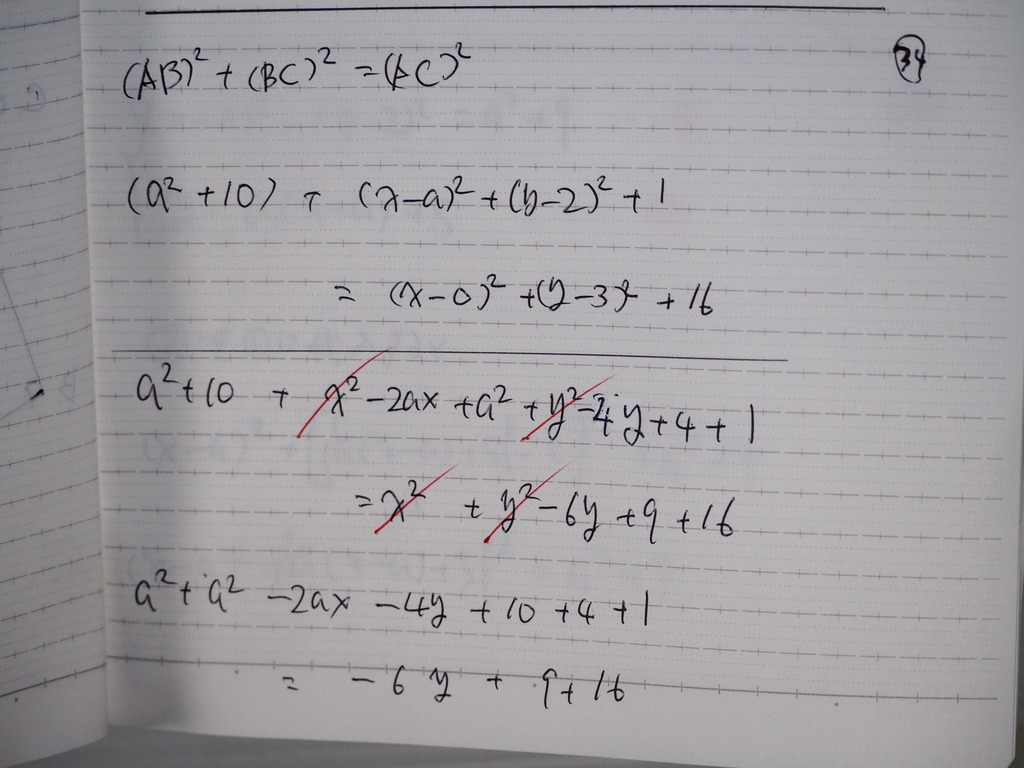
35
関係式 2本目
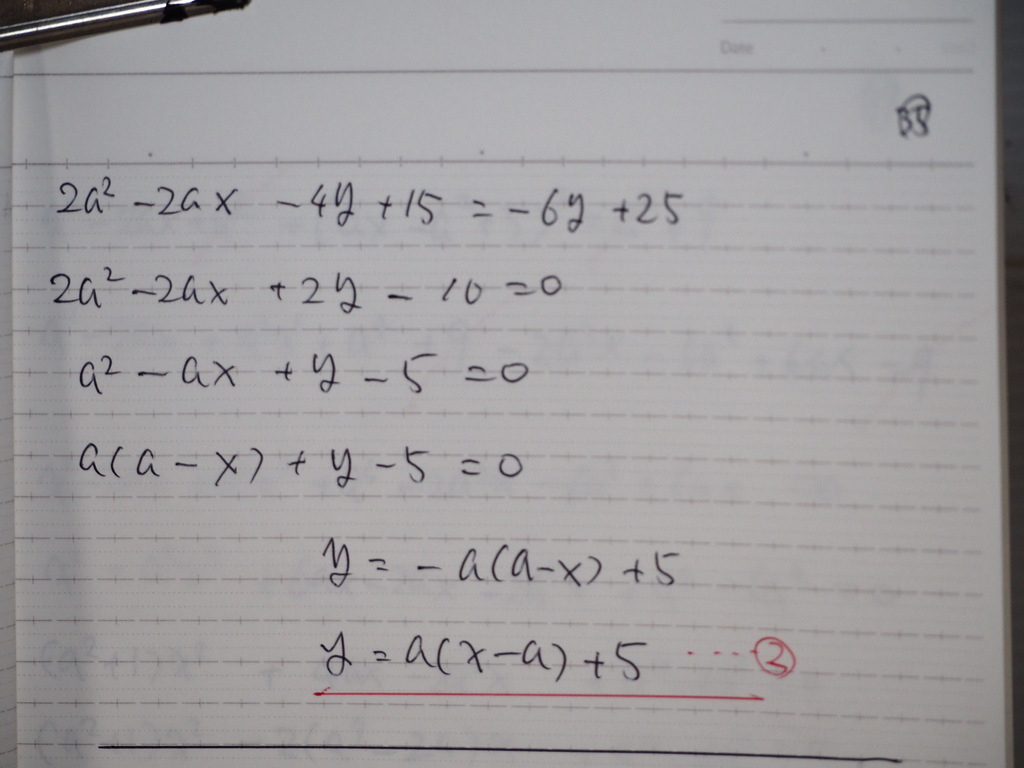
36
連立から
Xを解くと
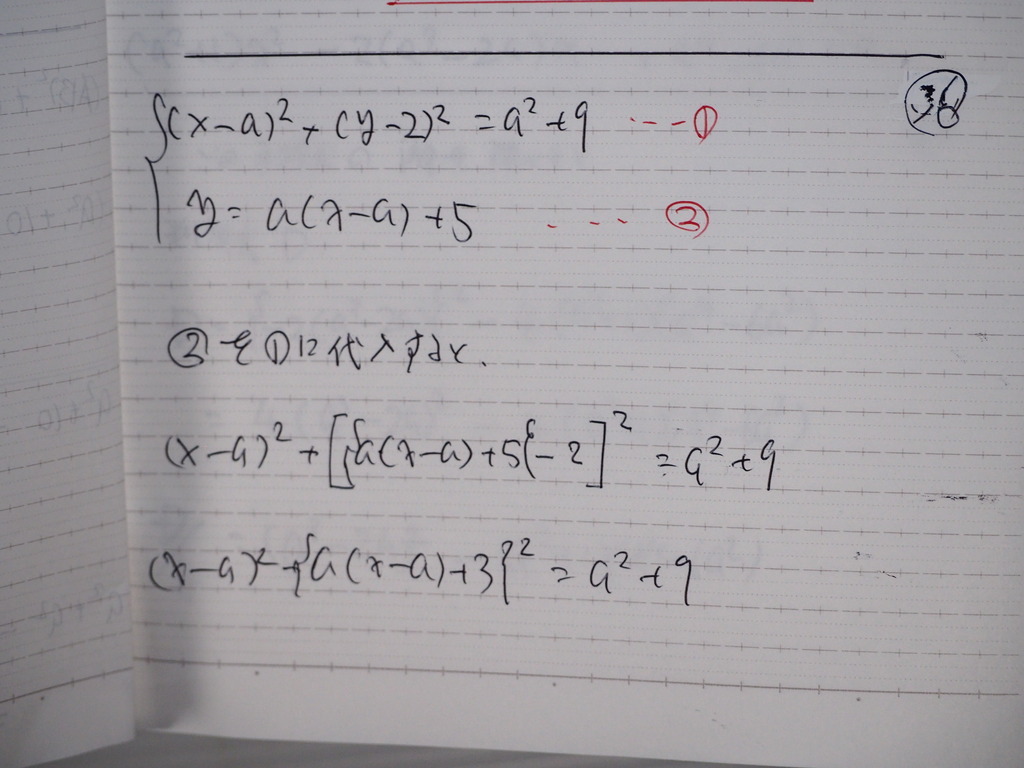
37
このXについての方程式は
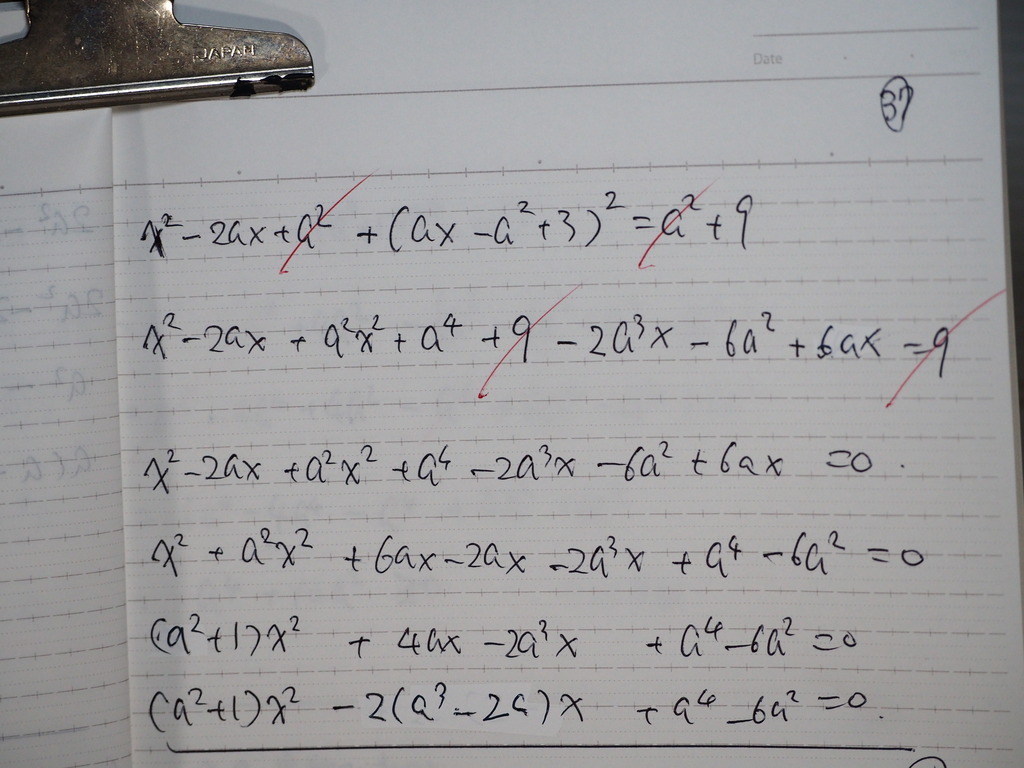
38
解を調べると
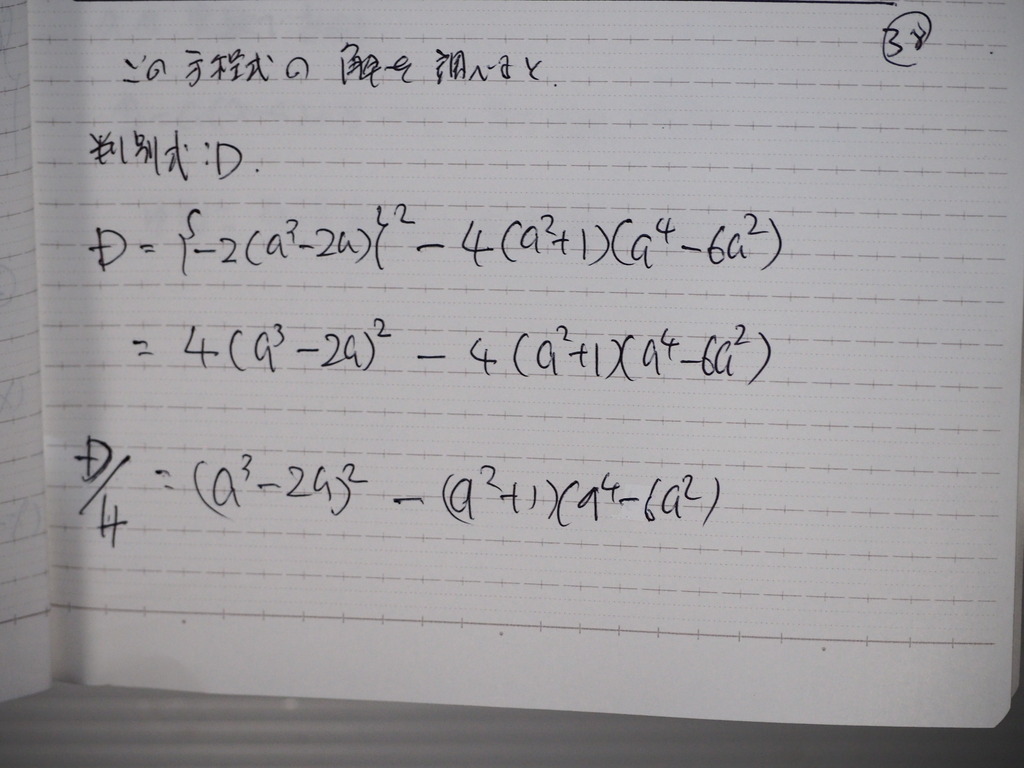
39
実数解を持つ
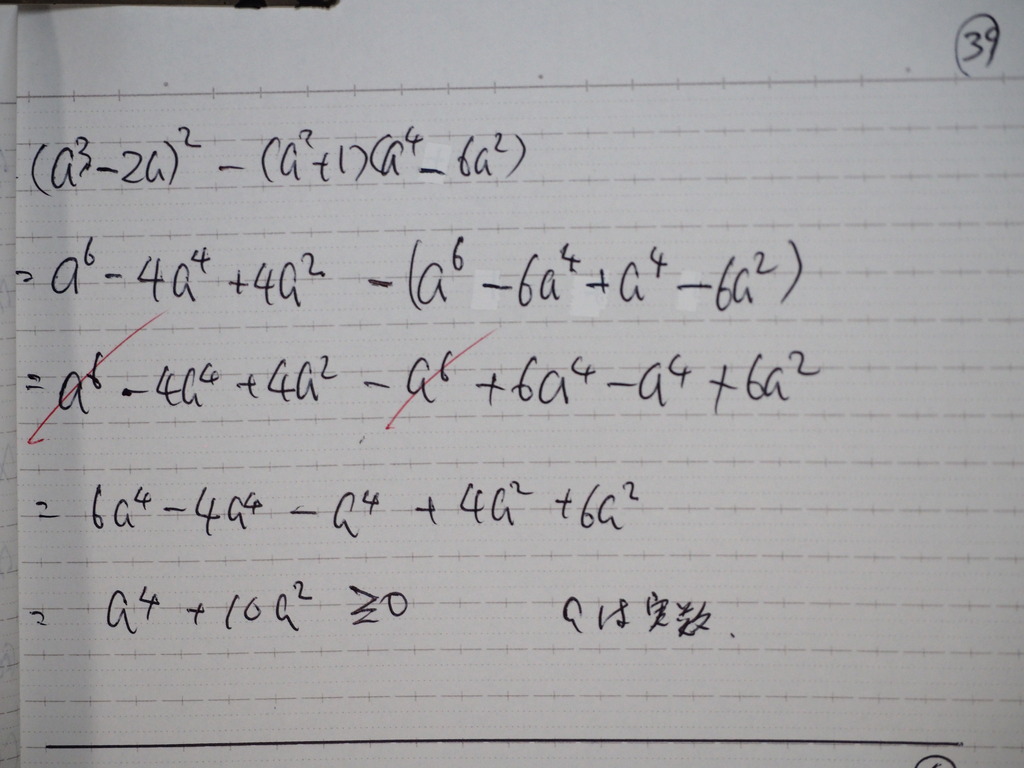
40
ナタメ
じゃナイスカ

おつかれさまです。
空間座標とベクトルから
二点間の距離
01
問題
正三角形であることの
証明と
この正三角形を
一つの面とする
正四面体の他の頂点をを求めなさい
02
三辺の 長さが 等しい
を 使ってみますと
03
個々に 計算して
成ってるよね
だからさ
正三角形
整理すれば 同じ だからさ
04
問題は
次だな
正四面体の 他の頂点
Dとすればさ
全て 正三角形の 面だから
AD=BD=CD=AB
05
これを 連立にしてくと
06
AD=BD より
計算してくと
07
➀式
BD=CD より
計算してくと
08
②式
09
これも
コレは 種類が 違って見えるね
10
➀②③しきから
➀②をつかって
11
Zを 消去して
12
計算して
13
整理してくと
X=Y
14
同様に
➀②を また少し変えて
15
計算してくと
16
整理してくと
17
X=Z
18
ナタメ X=Y=Z
これを ③式に
Y=X Z=X で
代入したらば
19
ここで
Xを 解の公式で 求めれば
X,Y,Z みんな 等しい値の
座標になるので
20
ルートの中身が出たから
21
整理してくと
22
こんなカンじに
成ってじゃナイスカ
23
Dは 正三角形ABCの
両方の側に あるんだね
24
今度は なんか難しそうだけど
そんなことないですよ
行ってみましょう
25
この条件で 計算したらば
26
これを
ピタゴラスに入れて
27
整理してくとだ
28
なったじゃナイスカ
29
内積でも 解けるので
見ておくと
30
こっちの方が 早いね
31
今度 空間にある
正方形
32
条件を 見つけて
33
条件を 関係式に
してくと
34
計算して
35
関係式 2本目
36
連立から
Xを解くと
37
このXについての方程式は
38
解を調べると
39
実数解を持つ
40
ナタメ
じゃナイスカ
おつかれさまです。