新規記事の投稿を行うことで、非表示にすることが可能です。
2022年12月09日
22028大人おさび落とし 空間座標とベクトル 2直線の垂直条件
心優しき圧力団体( PTA )の
方に捧ぐ大人のさび落とし
さいきんさ
色んな人が いろんなことを
見てるわけで
その中に 私もいたり
私もだったり
つまりね
世の中 不透明で
正直なことを いうと
ただでさえ 不安なのに
絶えられくなる
そんなわけで
余計なことを言わず
けっこう
みまもっててくださってまして
でもさ
お願いだ
受験生は もっと不安だし
親も同じだからさ
と
いうわけで
おもわず 頑張ってしまいました
16:39分
今日は仕上げるか
01
2直線の 垂直条件
まずさ
この辺を もう一回
おさえていただいて
こんな感じに 書けるときの
直線の方程式
分母は 方向係数
直線に 平行なベクトルになってる

02
Pの終点が
bの t倍で
動いていく

03
媒介変数を 使うと
直線上の 任意の点が
表現でき
t の 値によって
点の場所が決まる

04
で

05
問題

06
直線の 方程式を
辺々6で割って

07
こんな感じに
なったとこから
=t と置けば
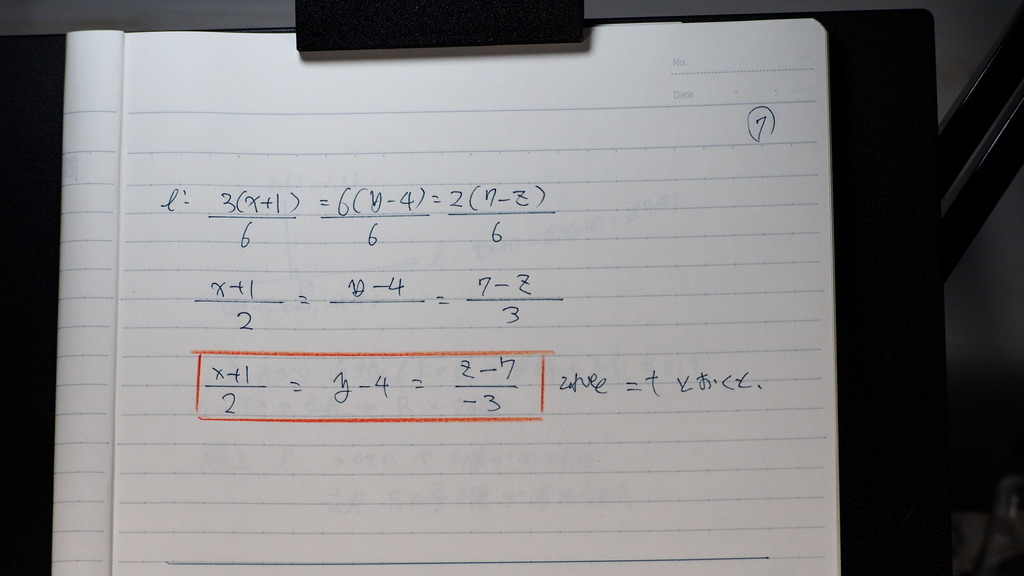
08
直線上の 任意の点は
媒介変数tを 使て
こうだから

09
Aから 直線上の 点に
おろした垂線の
交点を B とすれば
ベクトルの 内積を使って
ABベクトルと
直線の方向係数のベクトルが
垂直になるときの t を
求めればいいのだから

10
まず AB ベクトルは
で 直線の式から

11
方向係数のベクトル
直線に平行が (2,1、-3)である
ので
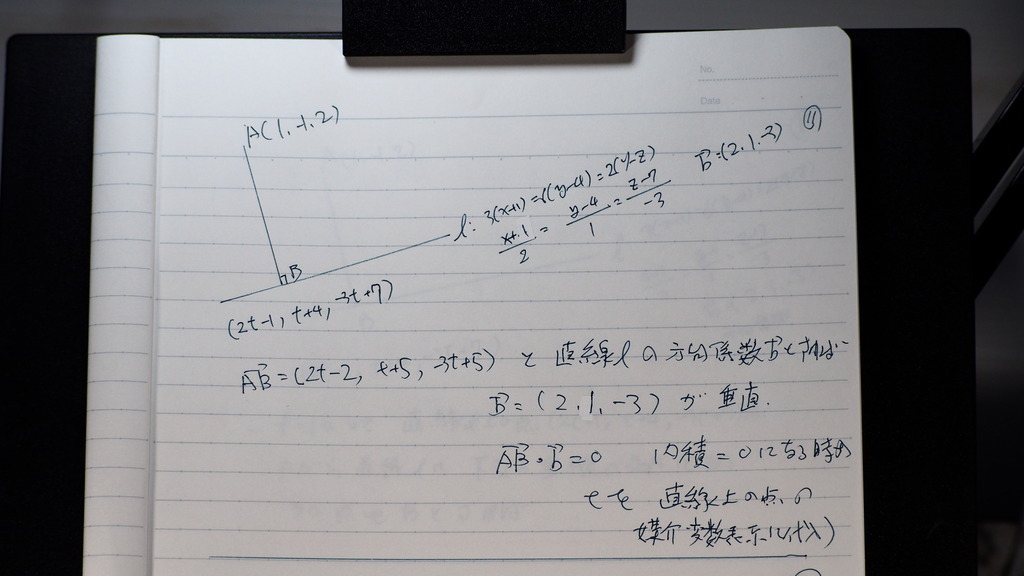
12
この 内積が =0になるとき
t=1

13
t=1を
直線上の
媒介変数表示に
代入すればさ
交点の 座標

14
こうだね

15
次に
この 直線の 方程式は
2点がわかるときの
公式から

16
答は これですが
たまたま
こんな感じのになってます
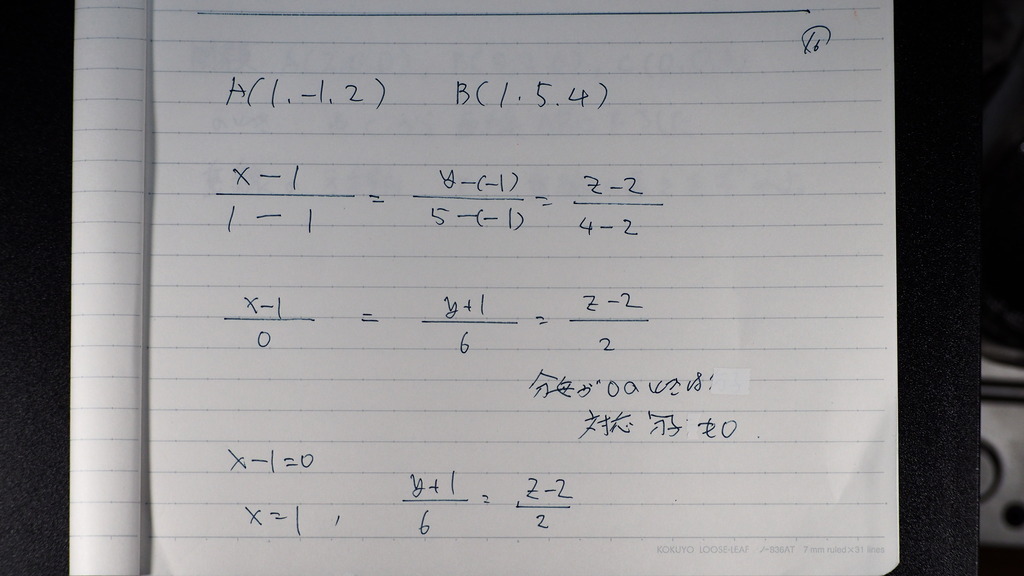
17
整理して
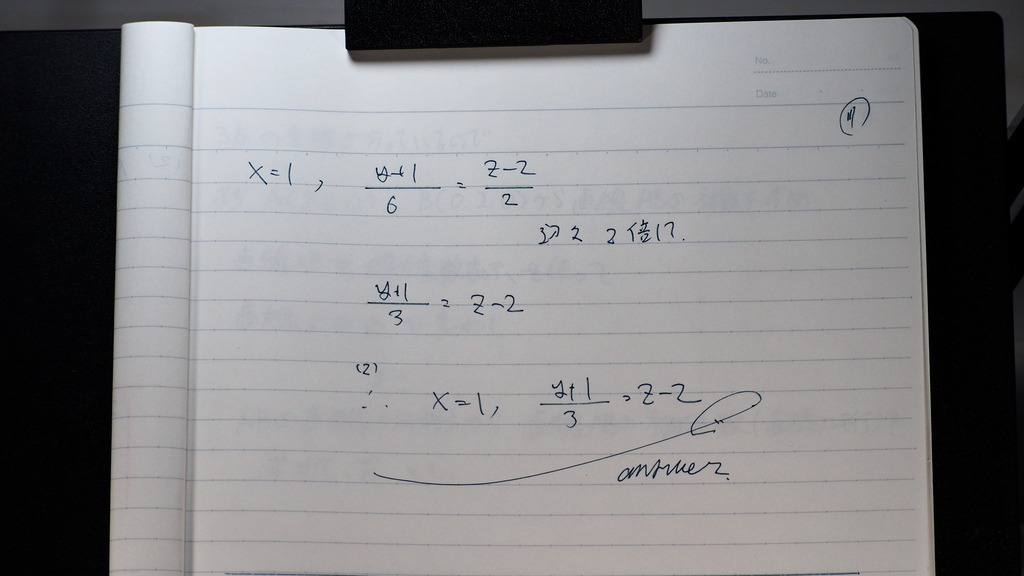
18
三点が 与えられていて
ややこしいんだけどさ

19
そこで
こんな手順で
行きたいと思います
ABの 方程式を求める
直線上の任意の点を
媒介表示にする
直線の方向係数を
方向ベクトル として
控えておく

20
直線上の 任意の点の中から
Cからの 垂線の交点のときを
Pとして
CP ベクトルをもとめ
CPベクトル と 方向ベクトル
の 内積から
t を 割り出し
P の 座標を決定して
C と P から
直線の方程式を
CPベクトルの 絶対値から
垂線の長さを

21
まず
直線の方てい式 AB

22
直線の方程式から
直線じょうの
任意の媒介変数表示
直線の 方向係数ベクトル

23
CP ベクトルは
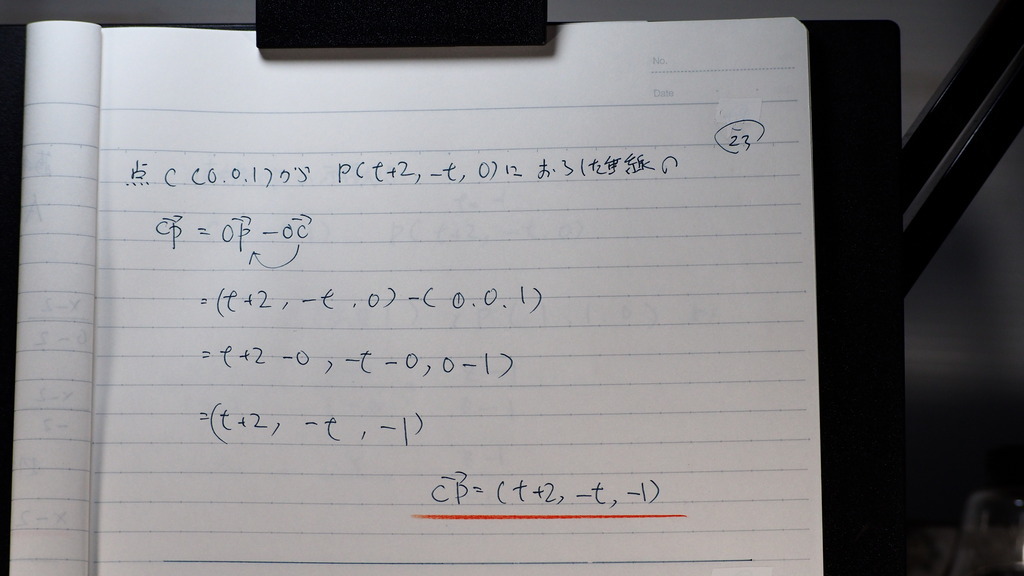
24
内積から tの値は
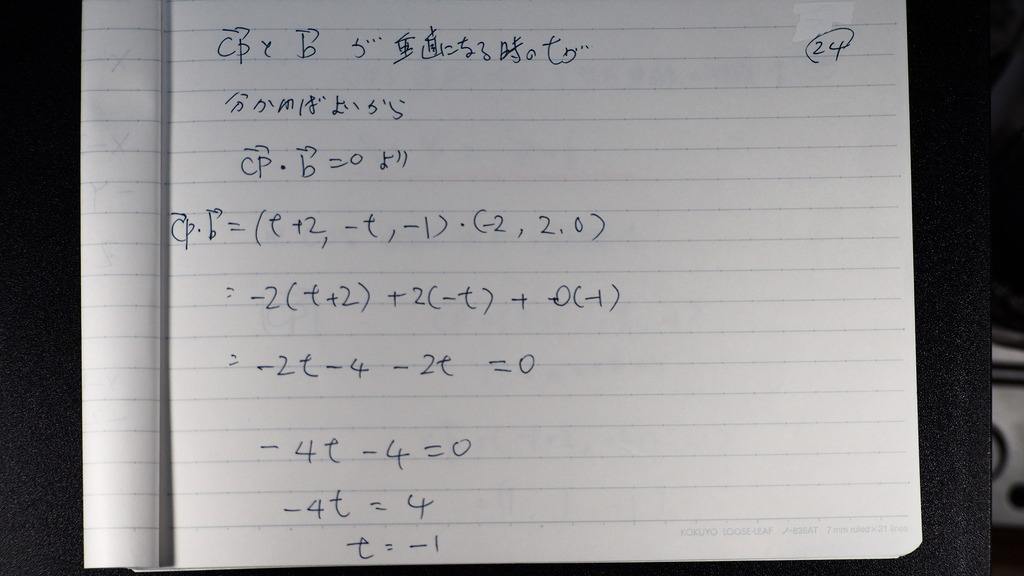
25
するって―ト
Pの座標は
コレダから
直線の方程式は こんなだね
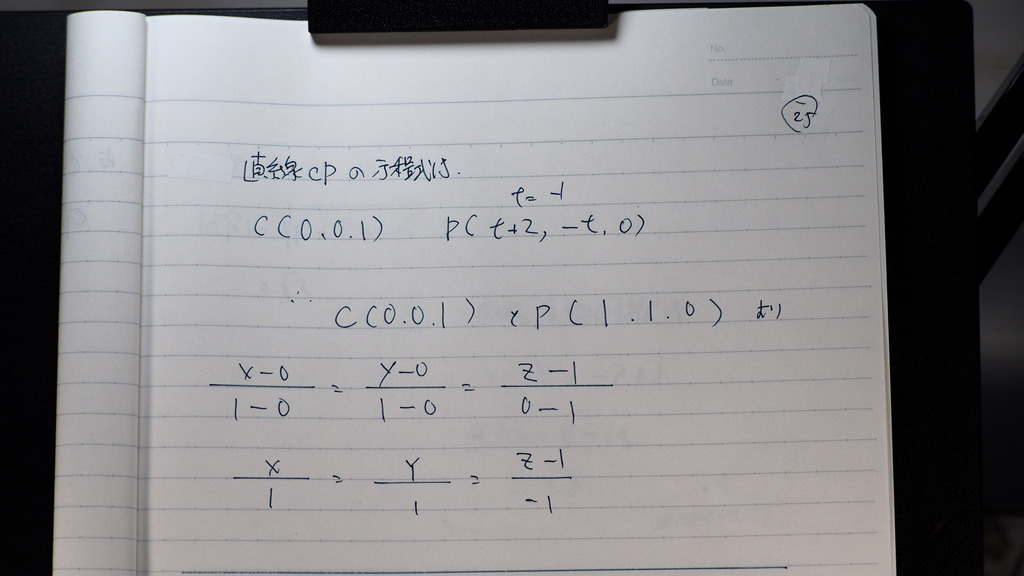
26
さっきの CPベクトルの
絶対値の値は
長さに 成るから

27
√3
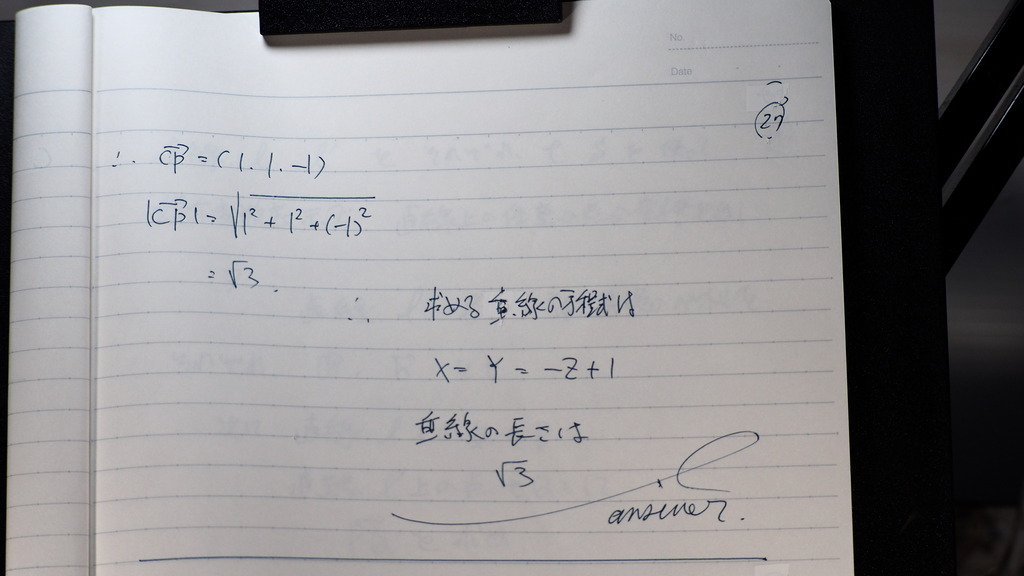
28
これはさ
ややっこしいんだ
問題

29
こんな手順で
ソレゾレ
2本の直線の方程式を
t、s と言う
媒介変数表示で
直線上の任意の点を
表し
また
それぞれの 方向係数を
a,b
で 表し
それぞれの 直線上の
点を P,Q とおいて
PQベクトルを 求めるでよ

30
両方の 直線の方向係数ベクトルに
PQベクトルが 垂直になるように
t s を 割り出すと
tから Pの座標
sから Qの座標
そうすれば 2点が出てるから
直線の方程式がわかると

31
直線L から
媒介変数表示
直線上の任意の点
と
方向係数ベクトル

32
直線L'も
媒介変数表示
直線上の任意の点の座標
と
方向係数ベクトル

33
PQ ベクトルは
こうでしょ
PQ・aは
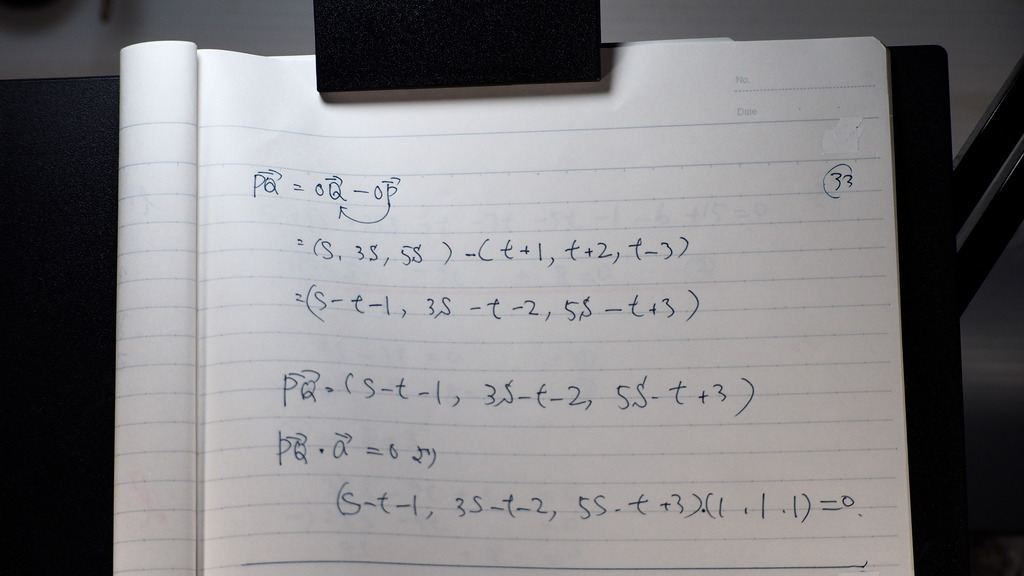
34
➀
PQ・bは
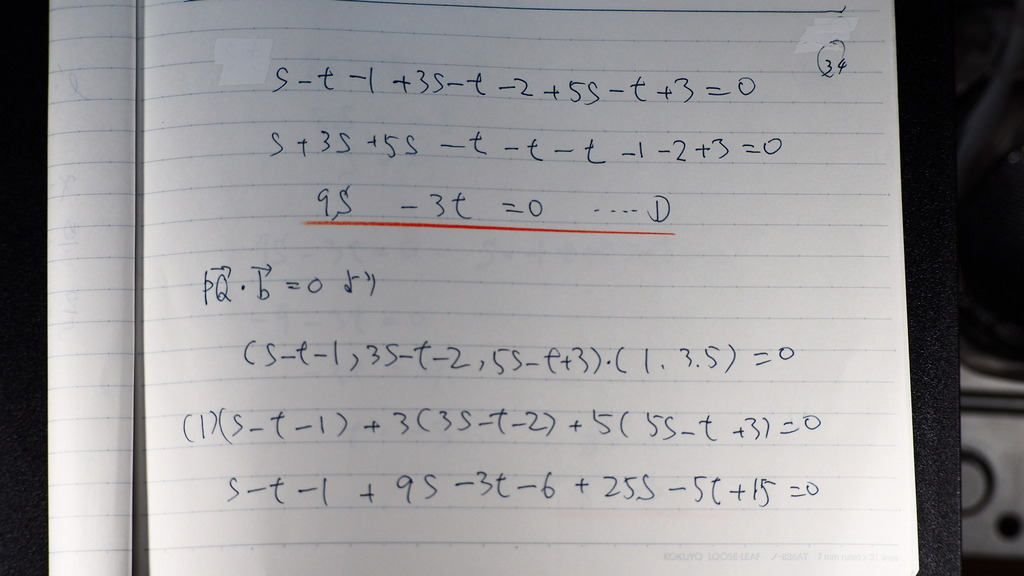
35
②
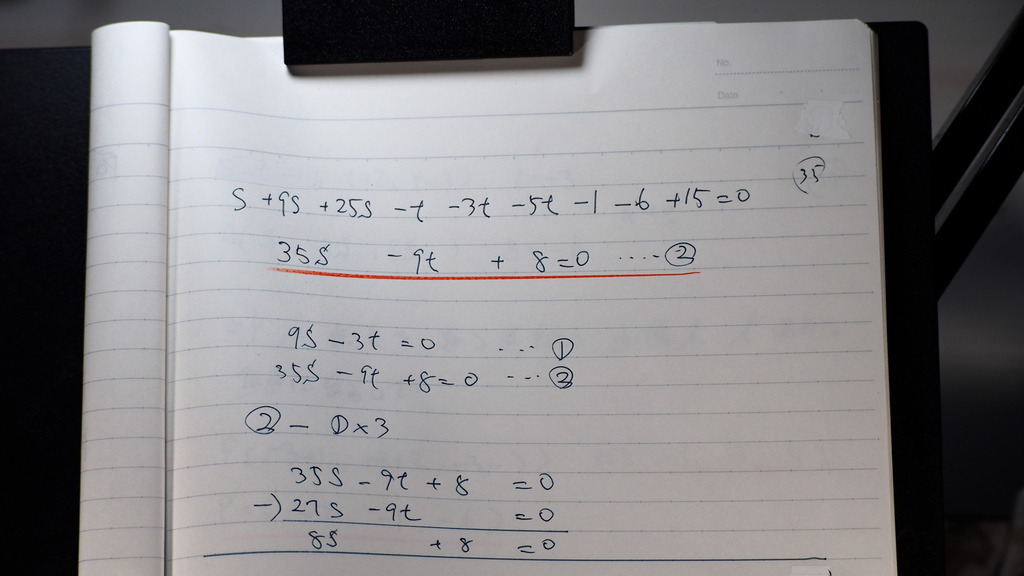
36
t、sが出てきたから
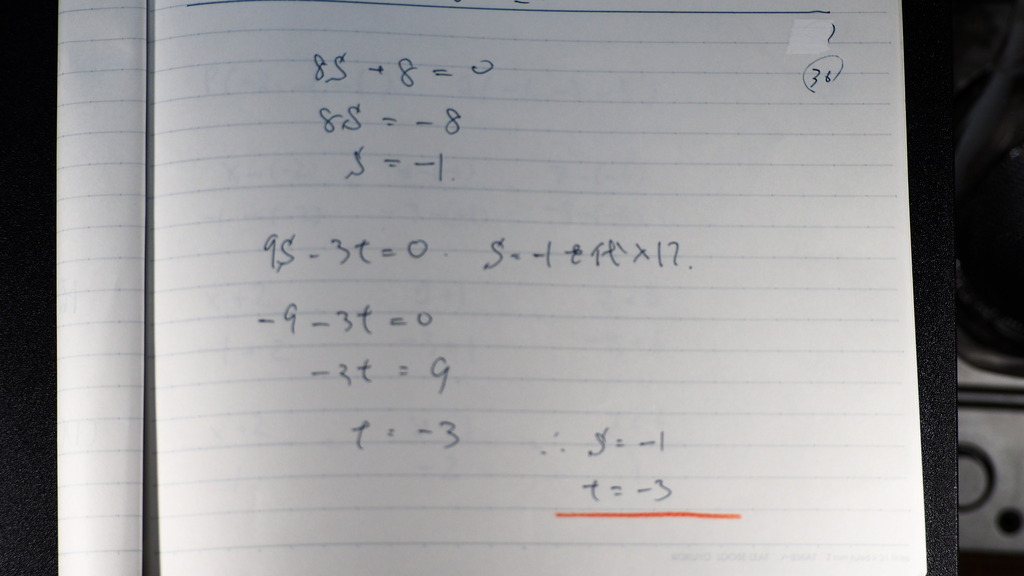
37
ソレゾレ
直線上の
垂直になるときの
座標
P と Q
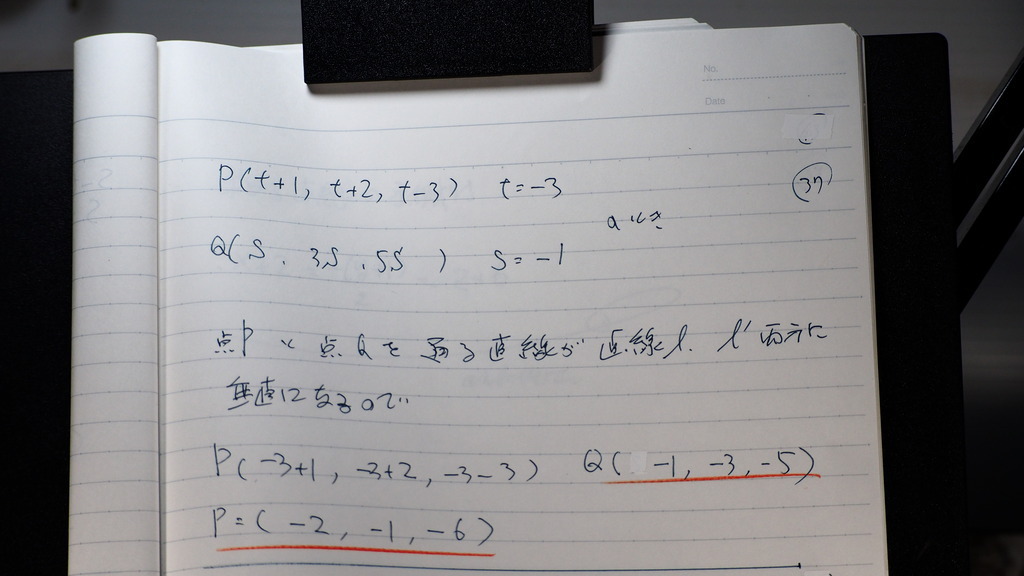
38
これがでれば
あとは 公式で
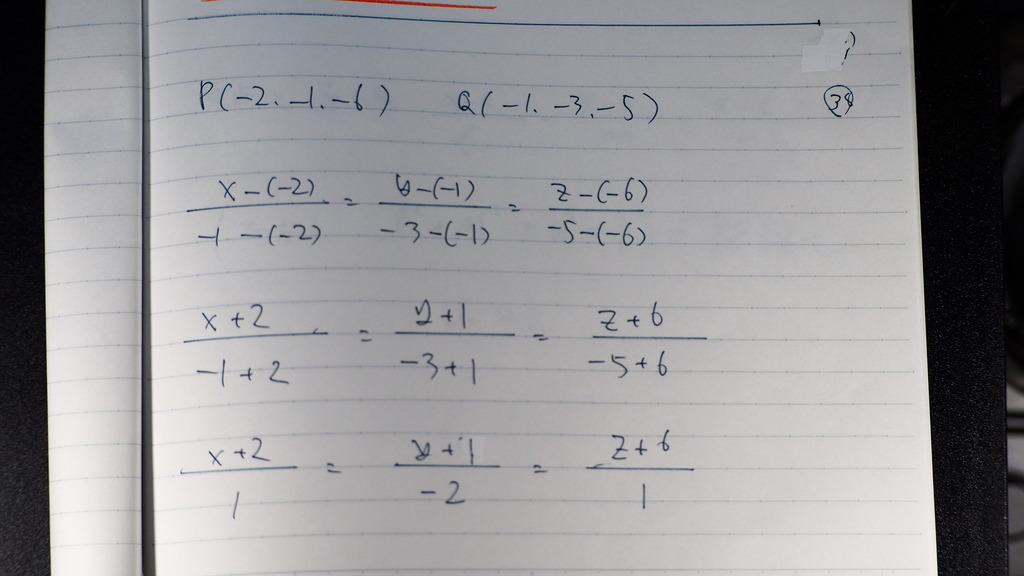
39
こんな感じですか
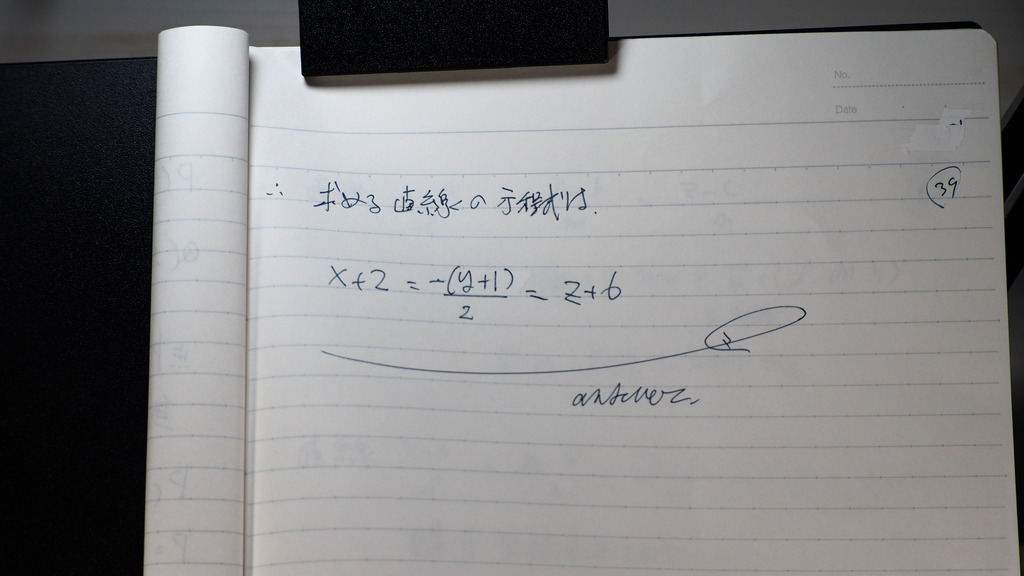
40
これはさ
計算がさ
対辺の様で そうでもなくて
どちなんだ
ま ともかく

41
直線の方向係数ベクトルは
分母から
つぎに
媒介変数表示にして
直線上の任意の点を
表現して

42
こんな感じに

43
原点と 直線上の点を
結ぶベクトルと
方向係数ベクトルが
垂直だから
この 内積の計算から
tの値を割り出し
OPベクトルの
絶対値で
距離を求めれば

44
ここがさ
文字の時は
全く同じだけれど
原点からのベクトルと
直線が 垂直になるとき
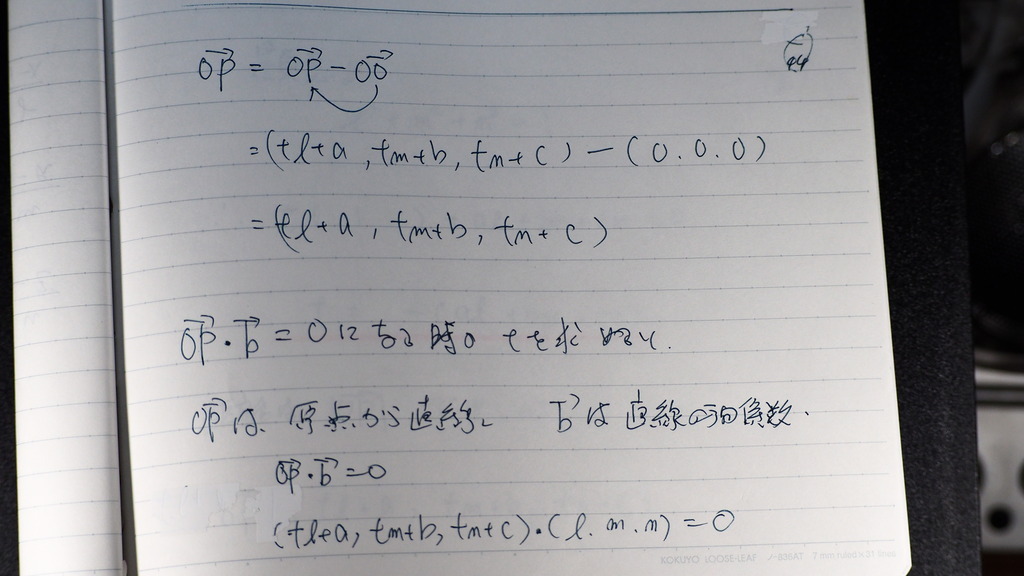
45
なんか 大変そうだな
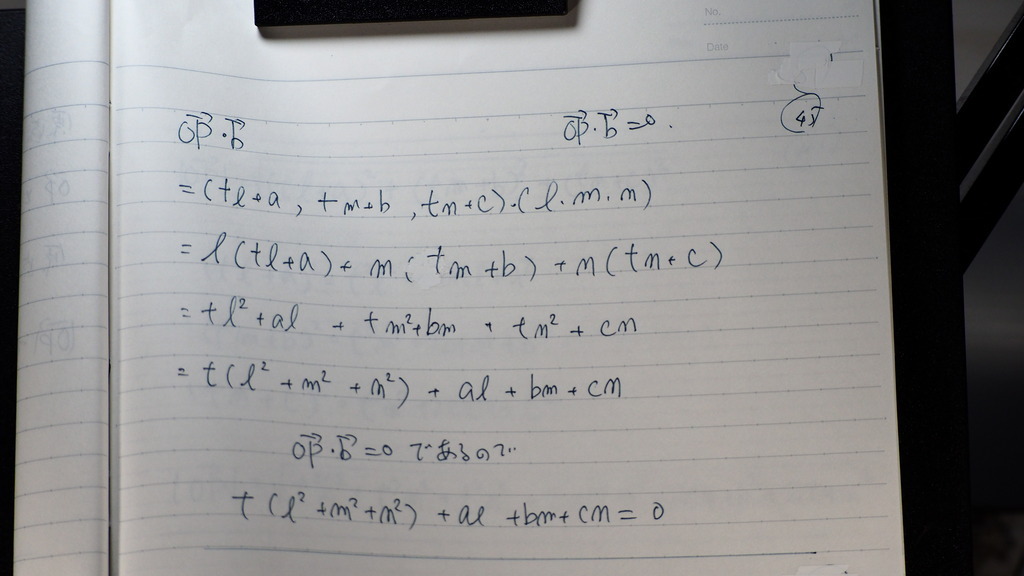
46
tはさ
こうだよ

47
で
いよいよ
距離を
ベクトルの おおきさから
求めると
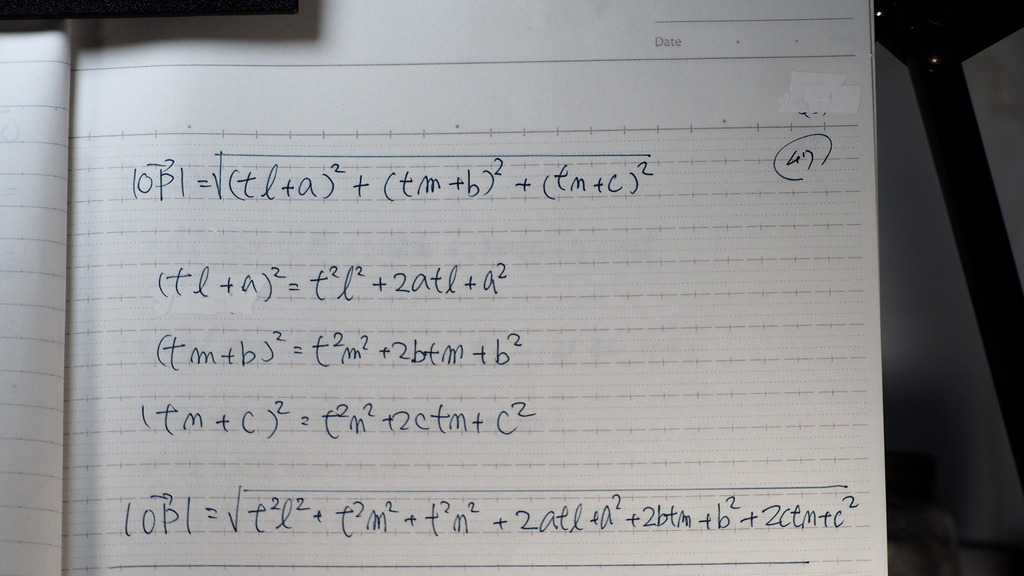
48
大丈夫そうな 感じで
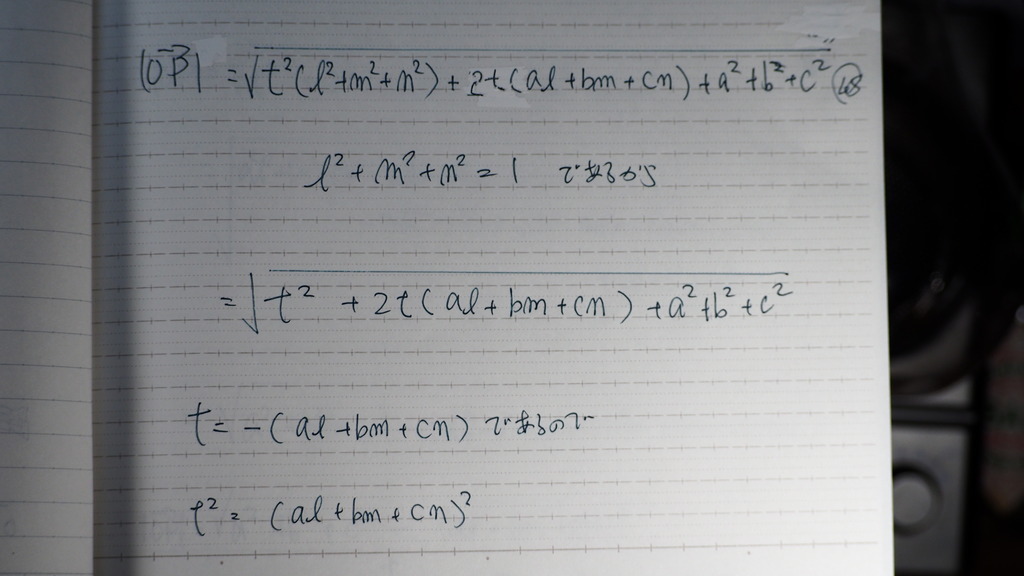
49
うまく できていて
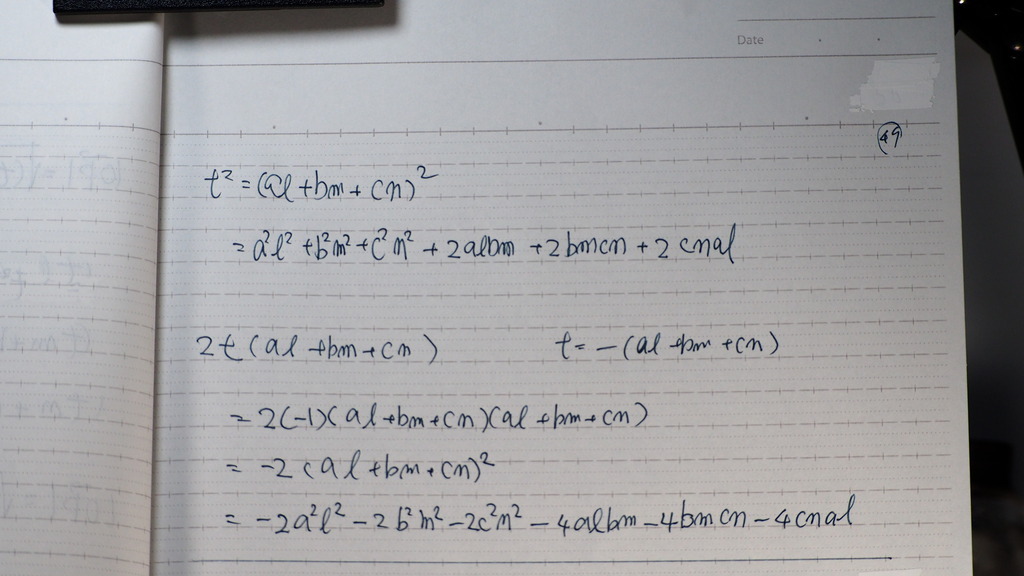
50
こんな感じです
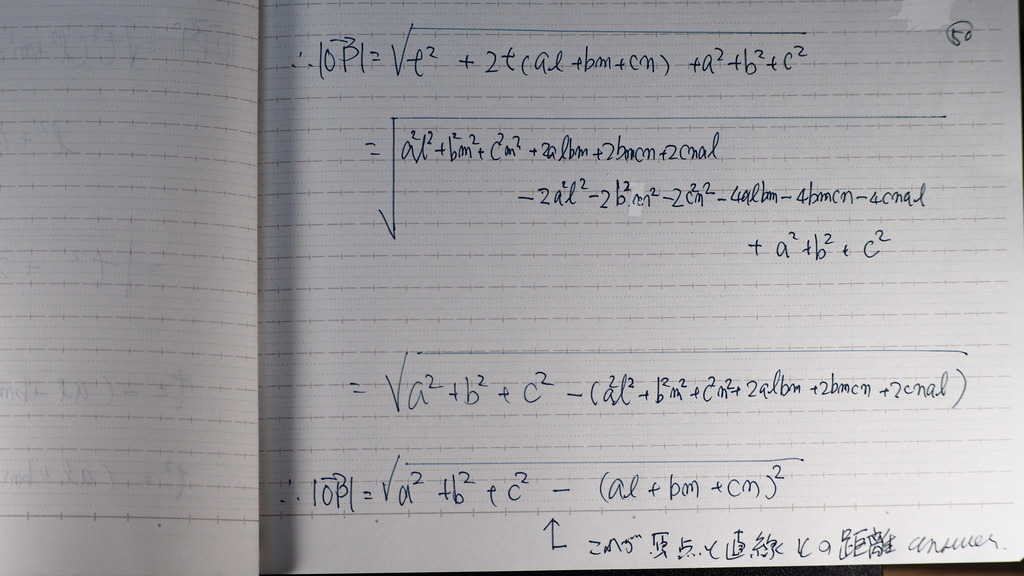
お疲れ様です。
方に捧ぐ大人のさび落とし
さいきんさ
色んな人が いろんなことを
見てるわけで
その中に 私もいたり
私もだったり
つまりね
世の中 不透明で
正直なことを いうと
ただでさえ 不安なのに
絶えられくなる
そんなわけで
余計なことを言わず
けっこう
みまもっててくださってまして
でもさ
お願いだ
受験生は もっと不安だし
親も同じだからさ
と
いうわけで
おもわず 頑張ってしまいました
16:39分
今日は仕上げるか
01
2直線の 垂直条件
まずさ
この辺を もう一回
おさえていただいて
こんな感じに 書けるときの
直線の方程式
分母は 方向係数
直線に 平行なベクトルになってる
02
Pの終点が
bの t倍で
動いていく
03
媒介変数を 使うと
直線上の 任意の点が
表現でき
t の 値によって
点の場所が決まる
04
で
05
問題
06
直線の 方程式を
辺々6で割って
07
こんな感じに
なったとこから
=t と置けば
08
直線上の 任意の点は
媒介変数tを 使て
こうだから
09
Aから 直線上の 点に
おろした垂線の
交点を B とすれば
ベクトルの 内積を使って
ABベクトルと
直線の方向係数のベクトルが
垂直になるときの t を
求めればいいのだから
10
まず AB ベクトルは
で 直線の式から
11
方向係数のベクトル
直線に平行が (2,1、-3)である
ので
12
この 内積が =0になるとき
t=1
13
t=1を
直線上の
媒介変数表示に
代入すればさ
交点の 座標
14
こうだね
15
次に
この 直線の 方程式は
2点がわかるときの
公式から
16
答は これですが
たまたま
こんな感じのになってます
17
整理して
18
三点が 与えられていて
ややこしいんだけどさ
19
そこで
こんな手順で
行きたいと思います
ABの 方程式を求める
直線上の任意の点を
媒介表示にする
直線の方向係数を
方向ベクトル として
控えておく
20
直線上の 任意の点の中から
Cからの 垂線の交点のときを
Pとして
CP ベクトルをもとめ
CPベクトル と 方向ベクトル
の 内積から
t を 割り出し
P の 座標を決定して
C と P から
直線の方程式を
CPベクトルの 絶対値から
垂線の長さを
21
まず
直線の方てい式 AB
22
直線の方程式から
直線じょうの
任意の媒介変数表示
直線の 方向係数ベクトル
23
CP ベクトルは
24
内積から tの値は
25
するって―ト
Pの座標は
コレダから
直線の方程式は こんなだね
26
さっきの CPベクトルの
絶対値の値は
長さに 成るから
27
√3
28
これはさ
ややっこしいんだ
問題
29
こんな手順で
ソレゾレ
2本の直線の方程式を
t、s と言う
媒介変数表示で
直線上の任意の点を
表し
また
それぞれの 方向係数を
a,b
で 表し
それぞれの 直線上の
点を P,Q とおいて
PQベクトルを 求めるでよ
30
両方の 直線の方向係数ベクトルに
PQベクトルが 垂直になるように
t s を 割り出すと
tから Pの座標
sから Qの座標
そうすれば 2点が出てるから
直線の方程式がわかると
31
直線L から
媒介変数表示
直線上の任意の点
と
方向係数ベクトル
32
直線L'も
媒介変数表示
直線上の任意の点の座標
と
方向係数ベクトル
33
PQ ベクトルは
こうでしょ
PQ・aは
34
➀
PQ・bは
35
②
36
t、sが出てきたから
37
ソレゾレ
直線上の
垂直になるときの
座標
P と Q
38
これがでれば
あとは 公式で
39
こんな感じですか
40
これはさ
計算がさ
対辺の様で そうでもなくて
どちなんだ
ま ともかく
41
直線の方向係数ベクトルは
分母から
つぎに
媒介変数表示にして
直線上の任意の点を
表現して
42
こんな感じに
43
原点と 直線上の点を
結ぶベクトルと
方向係数ベクトルが
垂直だから
この 内積の計算から
tの値を割り出し
OPベクトルの
絶対値で
距離を求めれば
44
ここがさ
文字の時は
全く同じだけれど
原点からのベクトルと
直線が 垂直になるとき
45
なんか 大変そうだな
46
tはさ
こうだよ
47
で
いよいよ
距離を
ベクトルの おおきさから
求めると
48
大丈夫そうな 感じで
49
うまく できていて
50
こんな感じです
お疲れ様です。
2022年12月07日
22027大人のさび落とし 空間座標とベクトル 空間の直線の方程式
大人のさび落とし
空間座標とベクトル 空間の直線の方程式
01
その前に
空間の 直線と 平面の
知識を 詰め込んで
行ってみましょう
空間の直線の 方程式は
通過点 の 位置ベクトルと
方向係数が わかれば

02
これと これ
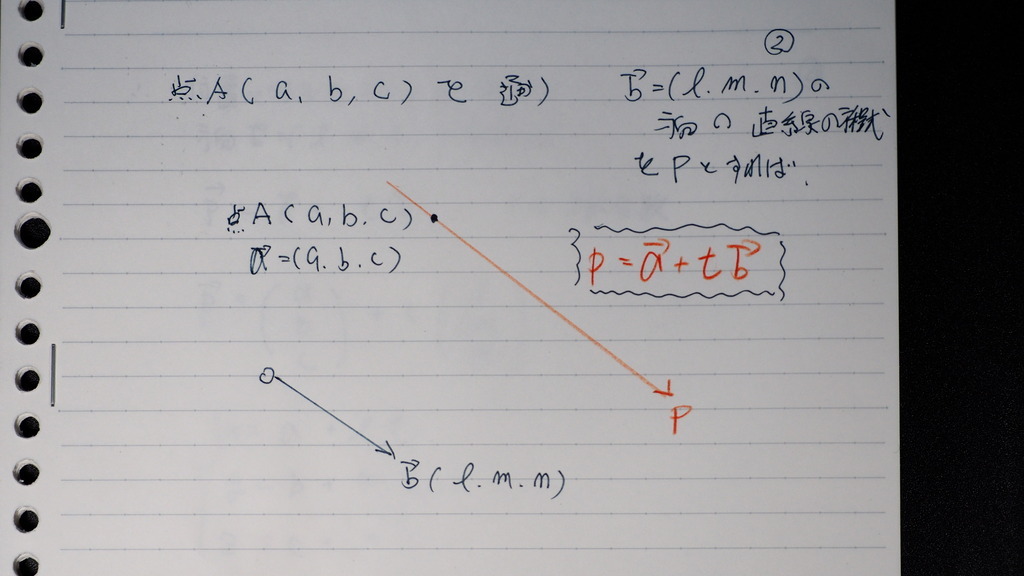
03
Pは aベクトルと
APベクトルの 和
APベクトルは
bベクトルの実数倍
その結果
OPの 終点Pの 軌跡は
赤い直線になると
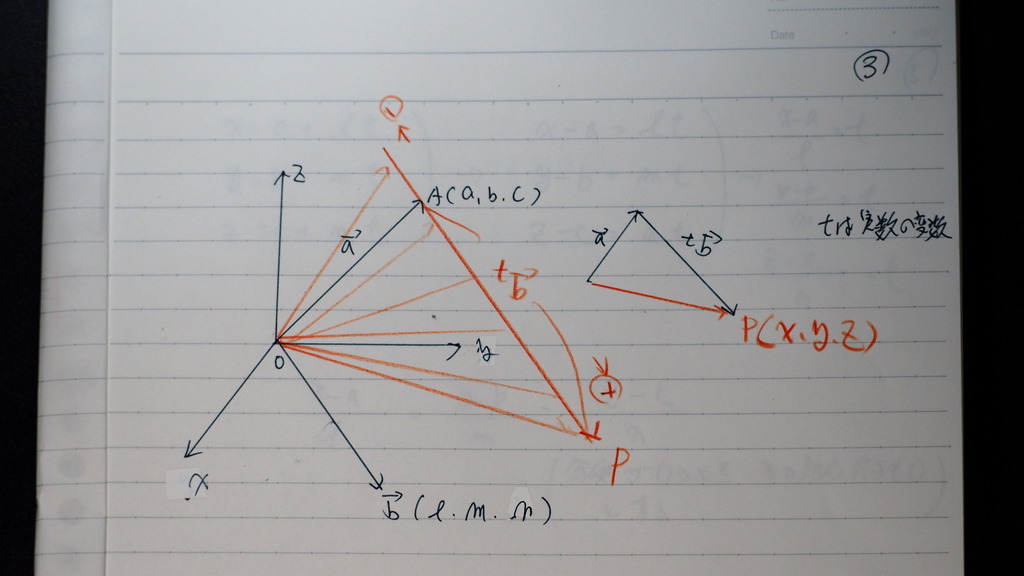
04
これを 媒介係数を使って
直交座標 (x、y、z)に分解すれば
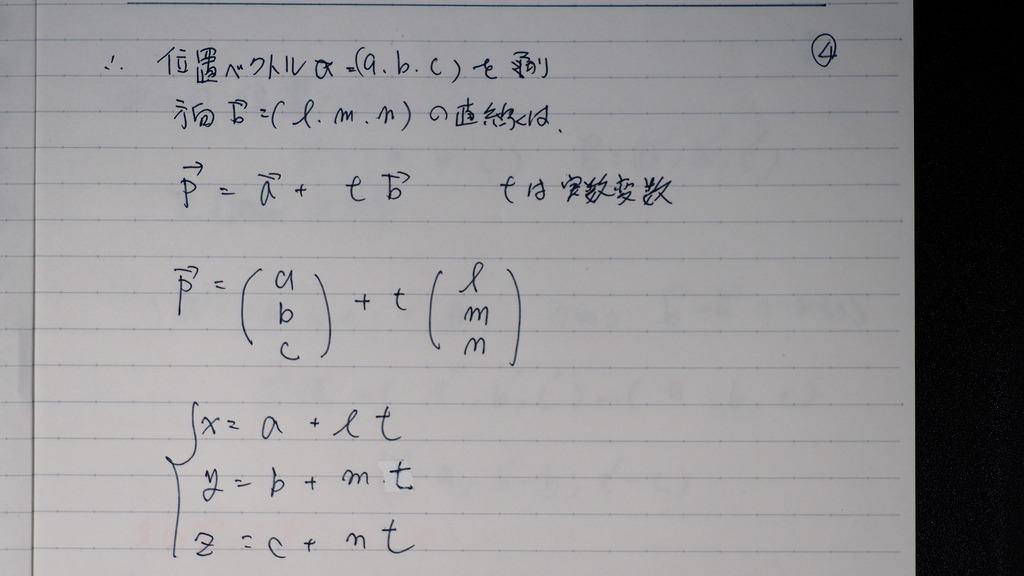
05
これらな
みな t=に形に
なるから
イコールで 結べて
こんな感じで 表せる
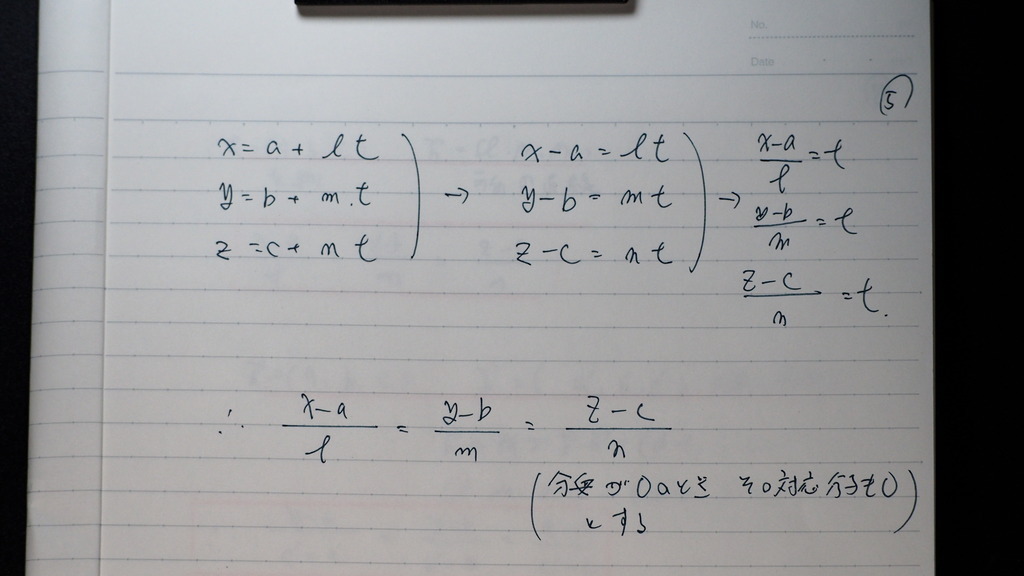
06
2点を 通るときは
一点は 通過点に考え
二点から
方向係数を 出せば
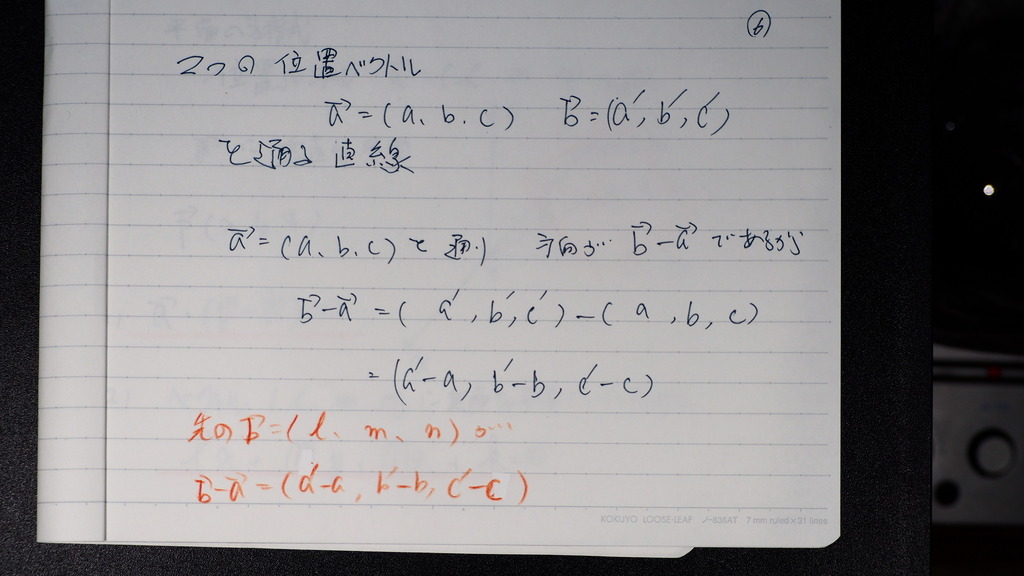
07
さっきと
おなじに
考えて
こんな感じでしょ
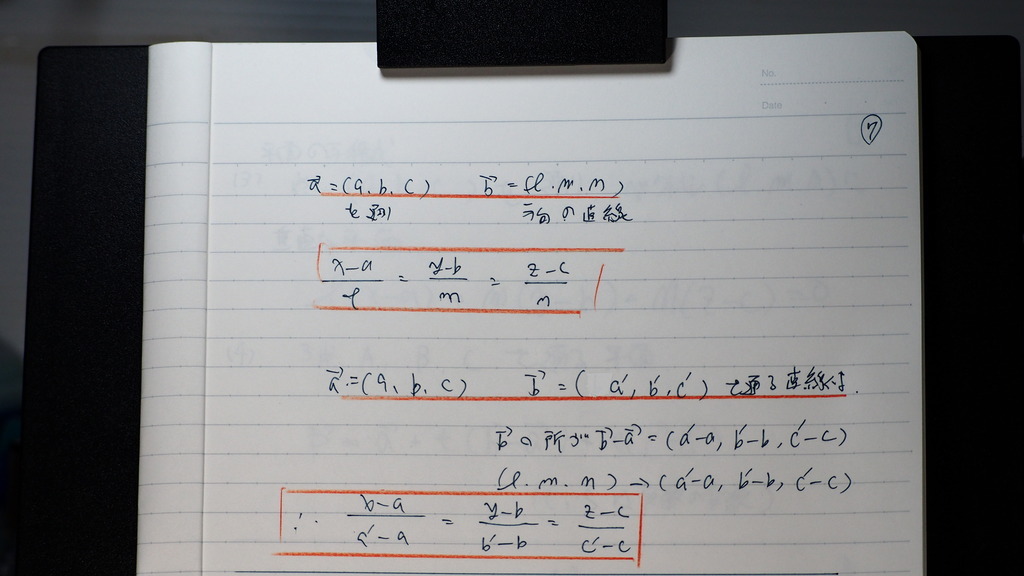
08
へてから
今度は
平面の方程式
パターン (1)
aベクトル を 通り
aベクトルに 垂直な平面
pベクトル マイナスbベクトルの
直線の中で
aベクトル 垂直なもの
の 集まり (平面)
(2)
ベクトル (L,M,N)に 垂直な
方程式
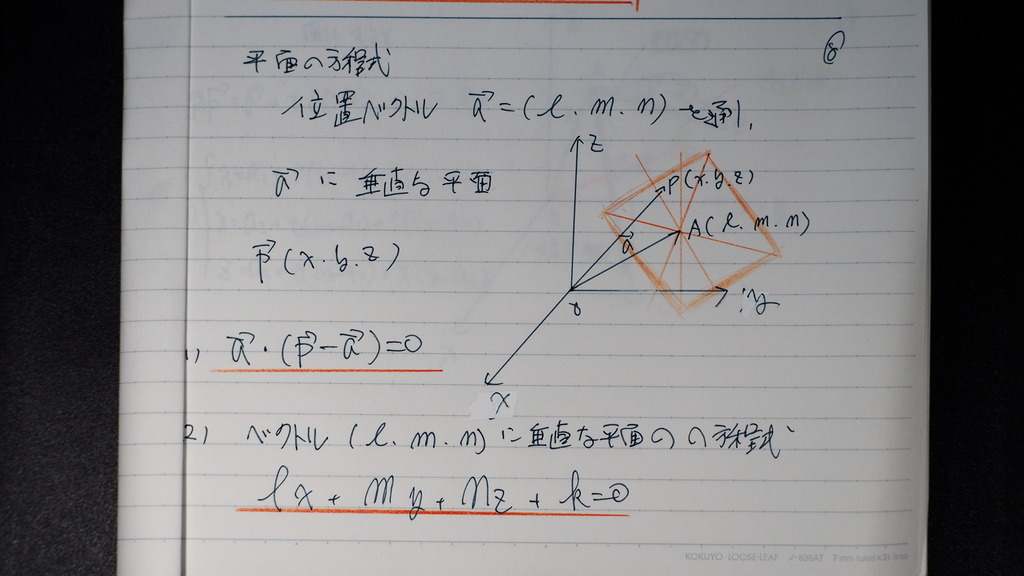
09
(3)
点Aを 通り
ベクトル(L,M,N)に垂直な 平面
(4)
3点 A,B,C を
通るときの 平面

10
図にすると
こんなだって
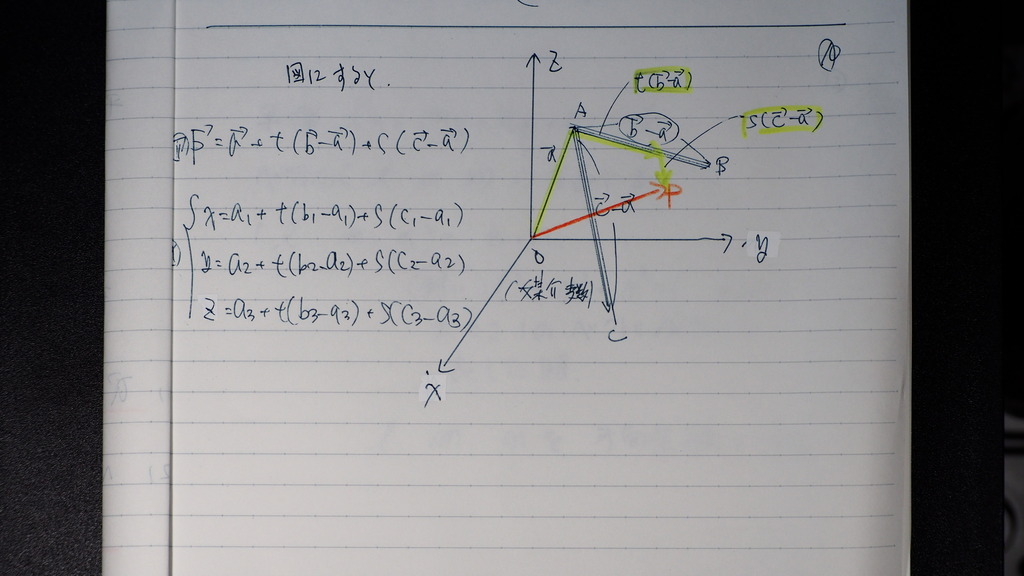
11
(5)
2平面が 交わるときは

12
捕捉

13
これらを 踏まえまして
今日は直線の方程式
問題行ってみましょう

14
(1)
ベクトルの 足し算で
OP 出てくるんですが
AP ベクトルのところは
bベクトルの実数倍
であるから

15
(2)
それぞれ
直交成分に すると
列で 書いた方が
分かりやすいカナと思って
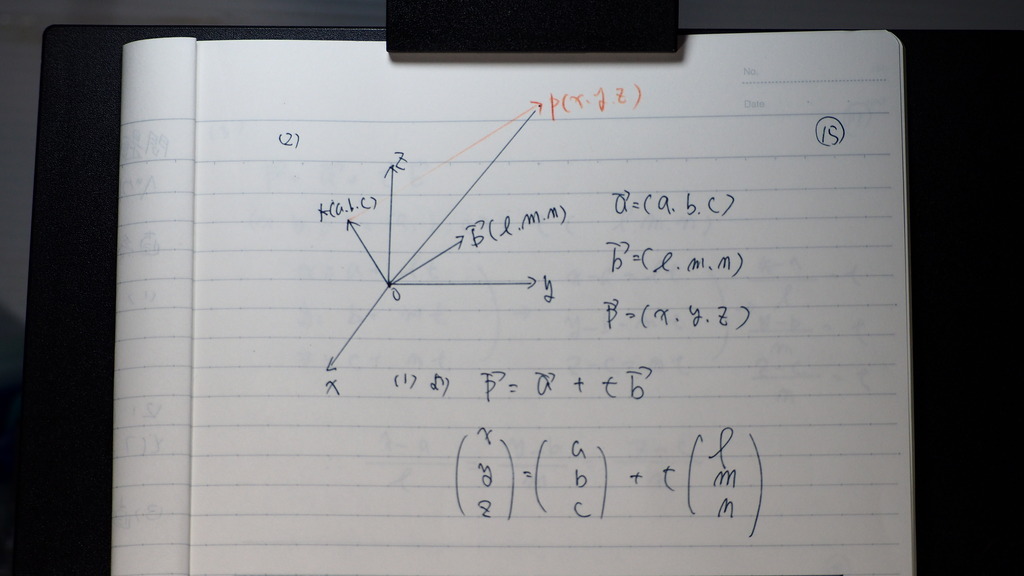
16
行で 書くと こんなだけど
同じことだからさ
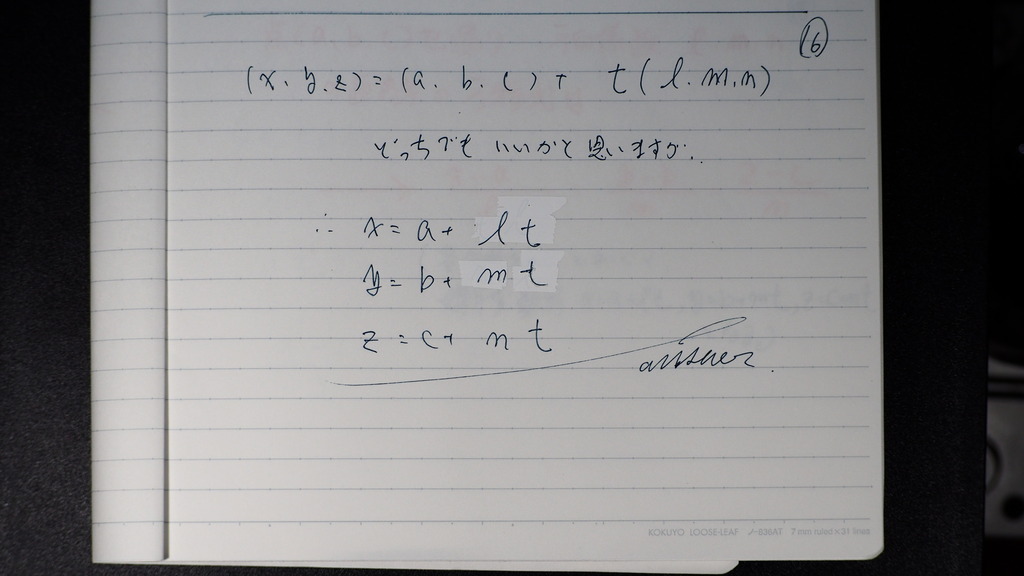
17
(3)
媒介変数付を
変形してくと
=t になるので
こんな 形に 書けますよ
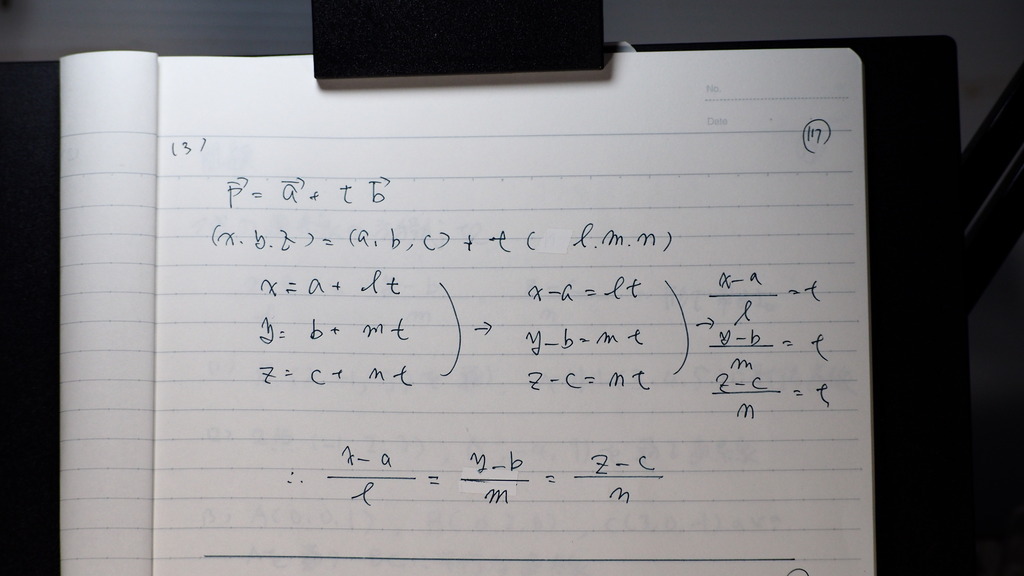
18
こんな 感じの 理論ですが

19
問題
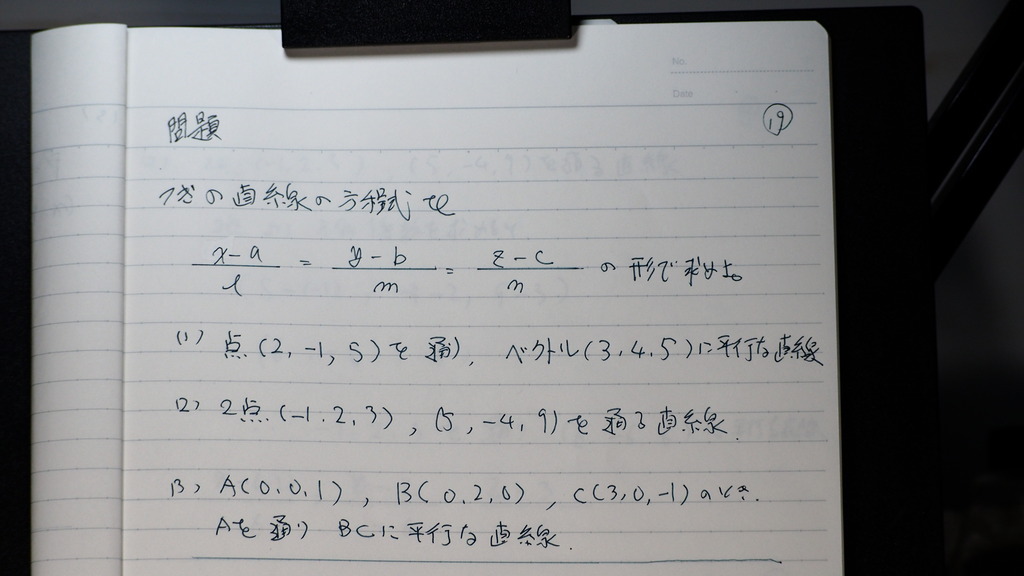
20
まず
(1) 理論に そのまま入れれば

21
片方を 通過点として
2点から 方向係数を 出せば
理論に入れて
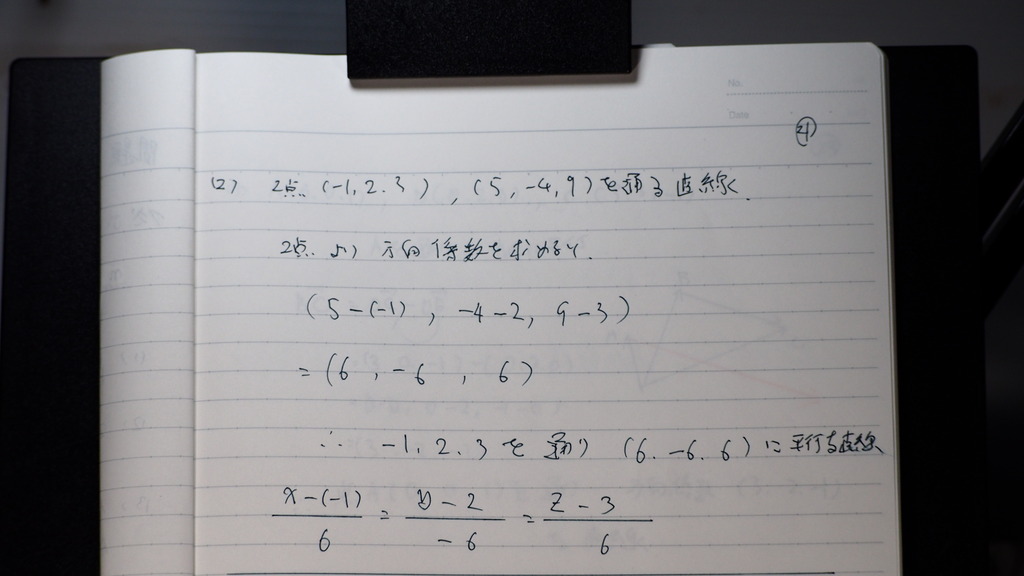
22
分母を はらうと
こんなですか
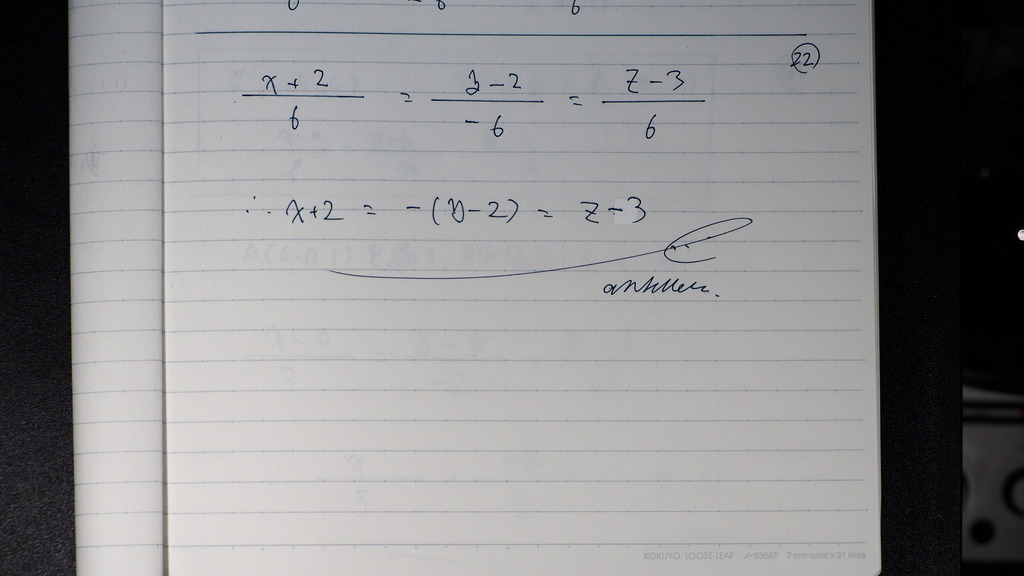
23
これもさ
似たようなもの
Aを とおって
方向係数は BC
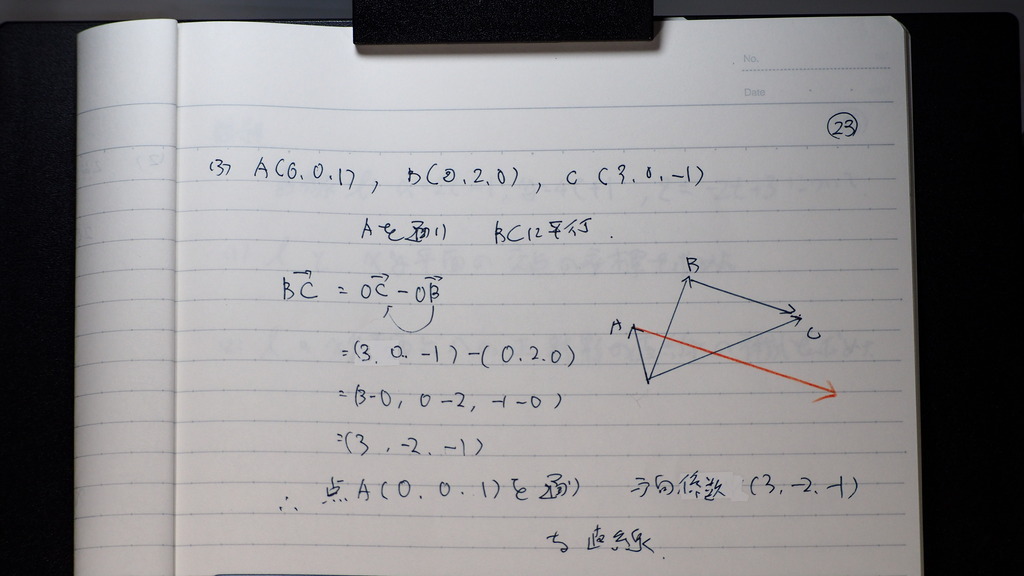
24
これを 理論に
入れれば

25
問題
今度は
媒介変数で
書いてあるけど

26
Z=0 ていうのが
XY 平面じゃナイスカ
だから
t を 先に 求めて
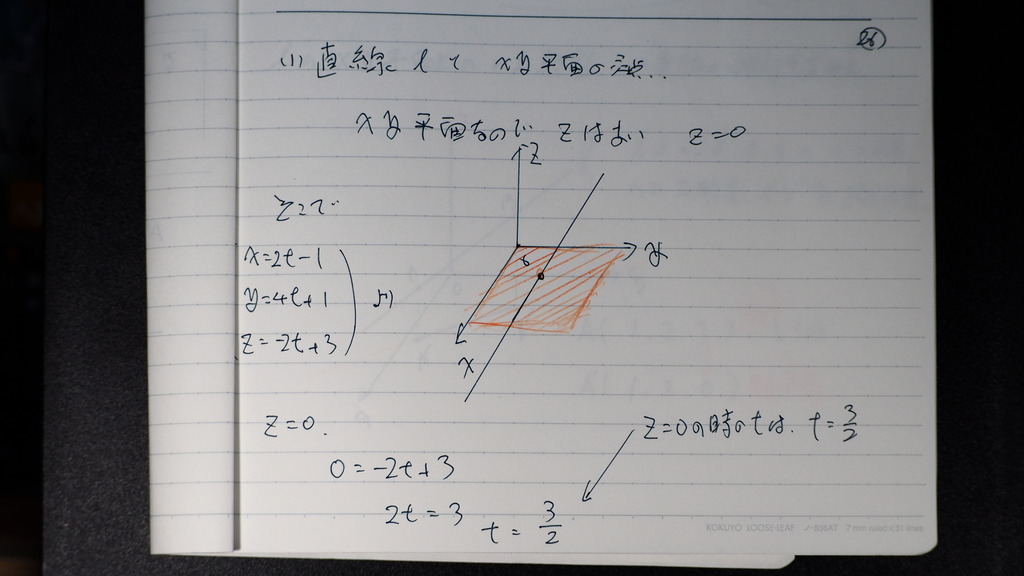
27
この時の 座標を
計算すると

28
直線Lの XY平面への正射影
影は XY 平面上なので
Z成分が 0
A A'
みたいに
z成分が 0
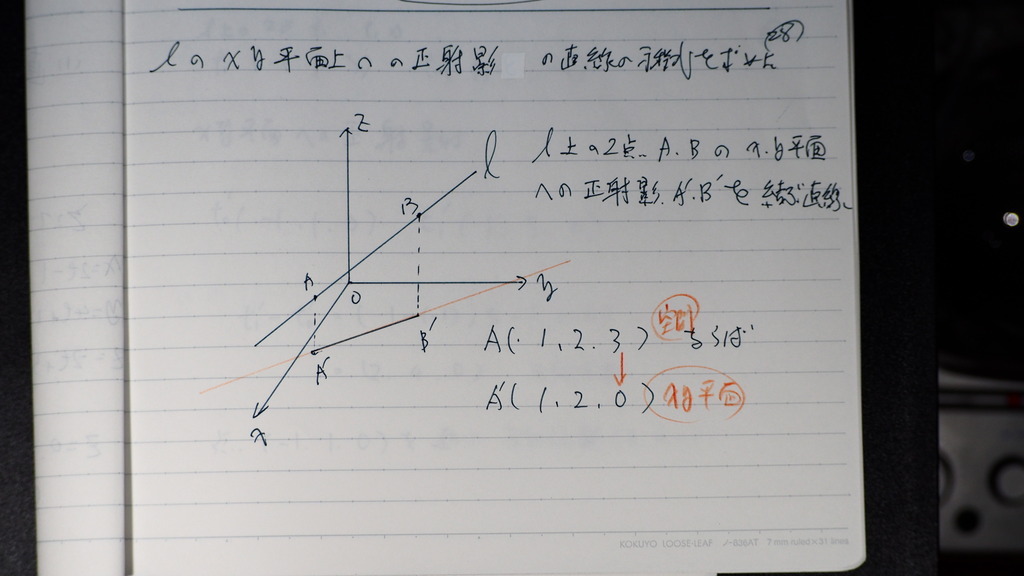
29
そこで
この 直線Lで
tに 何か 値を 2つ
代入して
その時の 座標を 求め
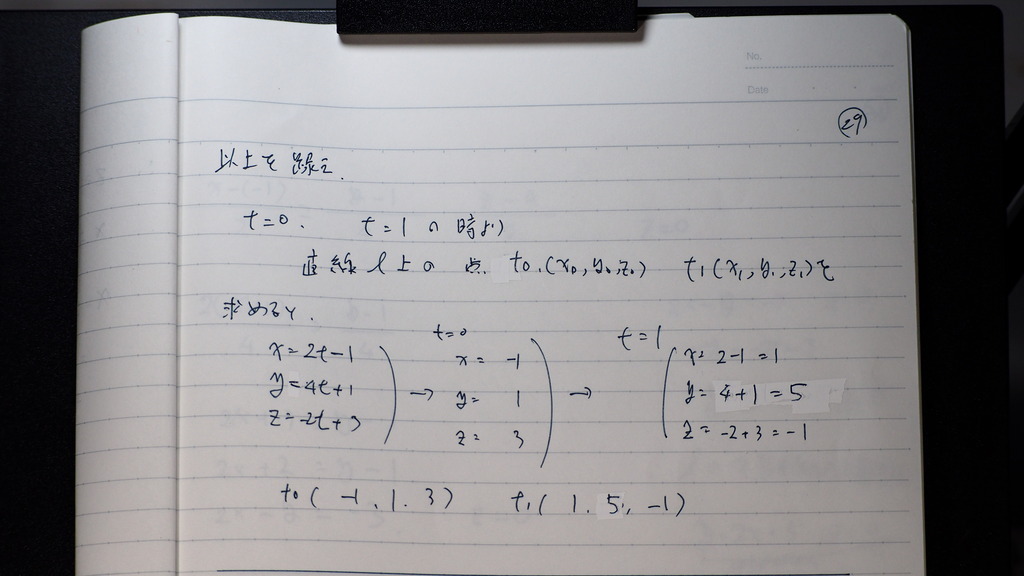
30
影は Z成分が 0であるので
あとは
方向係数 2,4,0
どちらか 点を 持ってきて
ここを 通るから

31
こんな感じで
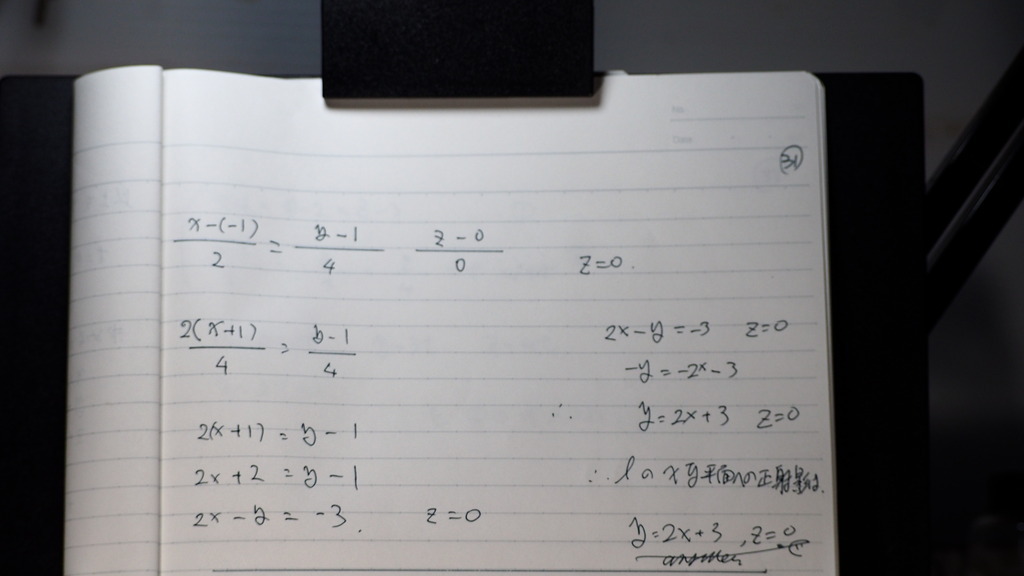
32
問題
2直線が 交わるとき
aの値と 交点の座標
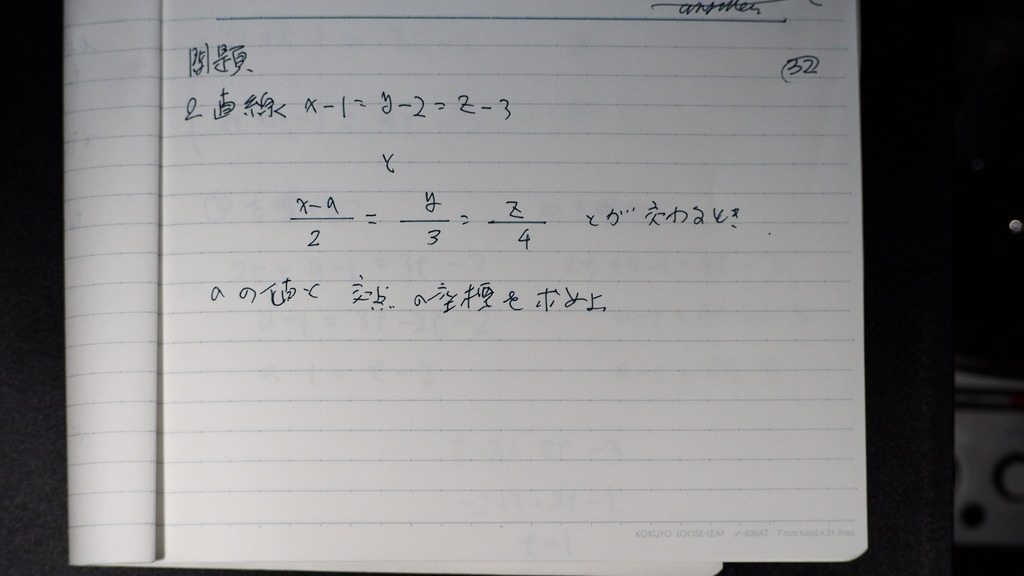
33
➀②から
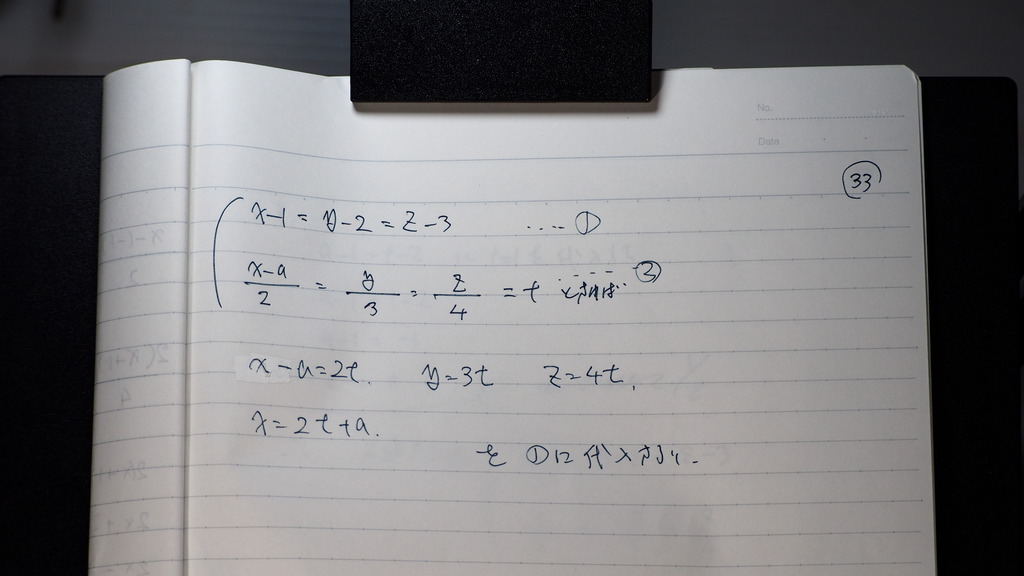
34
連立にして
2式 2変数であるから
出るわけで
tがでれば
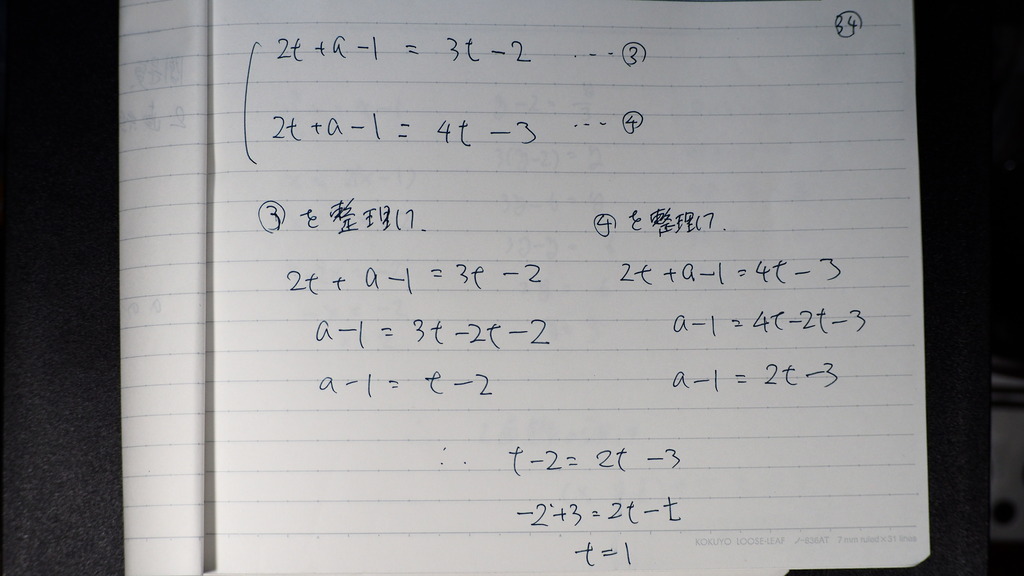
35
a=0
出てきた
二つの 直線の交点は
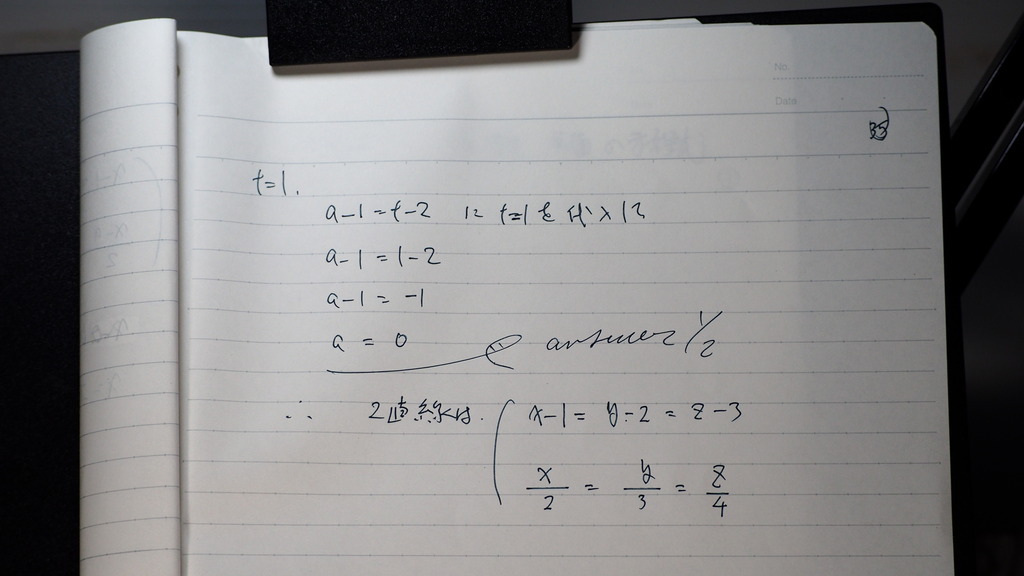
36
それぞれ x、y、z成分の
値が 同じくなるところなんだから
こんな感じで

おつかれさまです。
空間座標とベクトル 空間の直線の方程式
01
その前に
空間の 直線と 平面の
知識を 詰め込んで
行ってみましょう
空間の直線の 方程式は
通過点 の 位置ベクトルと
方向係数が わかれば
02
これと これ
03
Pは aベクトルと
APベクトルの 和
APベクトルは
bベクトルの実数倍
その結果
OPの 終点Pの 軌跡は
赤い直線になると
04
これを 媒介係数を使って
直交座標 (x、y、z)に分解すれば
05
これらな
みな t=に形に
なるから
イコールで 結べて
こんな感じで 表せる
06
2点を 通るときは
一点は 通過点に考え
二点から
方向係数を 出せば
07
さっきと
おなじに
考えて
こんな感じでしょ
08
へてから
今度は
平面の方程式
パターン (1)
aベクトル を 通り
aベクトルに 垂直な平面
pベクトル マイナスbベクトルの
直線の中で
aベクトル 垂直なもの
の 集まり (平面)
(2)
ベクトル (L,M,N)に 垂直な
方程式
09
(3)
点Aを 通り
ベクトル(L,M,N)に垂直な 平面
(4)
3点 A,B,C を
通るときの 平面
10
図にすると
こんなだって
11
(5)
2平面が 交わるときは
12
捕捉
13
これらを 踏まえまして
今日は直線の方程式
問題行ってみましょう
14
(1)
ベクトルの 足し算で
OP 出てくるんですが
AP ベクトルのところは
bベクトルの実数倍
であるから
15
(2)
それぞれ
直交成分に すると
列で 書いた方が
分かりやすいカナと思って
16
行で 書くと こんなだけど
同じことだからさ
17
(3)
媒介変数付を
変形してくと
=t になるので
こんな 形に 書けますよ
18
こんな 感じの 理論ですが
19
問題
20
まず
(1) 理論に そのまま入れれば
21
片方を 通過点として
2点から 方向係数を 出せば
理論に入れて
22
分母を はらうと
こんなですか
23
これもさ
似たようなもの
Aを とおって
方向係数は BC
24
これを 理論に
入れれば
25
問題
今度は
媒介変数で
書いてあるけど
26
Z=0 ていうのが
XY 平面じゃナイスカ
だから
t を 先に 求めて
27
この時の 座標を
計算すると
28
直線Lの XY平面への正射影
影は XY 平面上なので
Z成分が 0
A A'
みたいに
z成分が 0
29
そこで
この 直線Lで
tに 何か 値を 2つ
代入して
その時の 座標を 求め
30
影は Z成分が 0であるので
あとは
方向係数 2,4,0
どちらか 点を 持ってきて
ここを 通るから
31
こんな感じで
32
問題
2直線が 交わるとき
aの値と 交点の座標
33
➀②から
34
連立にして
2式 2変数であるから
出るわけで
tがでれば
35
a=0
出てきた
二つの 直線の交点は
36
それぞれ x、y、z成分の
値が 同じくなるところなんだから
こんな感じで
おつかれさまです。
2022年12月05日
22026 大人のさび落とし 空間座標とベクトル 三角関数の加法定理
大人のさび落とし
空間座標と
01
三角関数で
加法定理と言うのがあるですが
それを
内積を使って
証明して
という問題

02
こんな
感じに
単位円を使って
Aベクトル Bベクトル
それぞれ
x軸となす角が
α 、 β
これを
座標を
使って 表せば
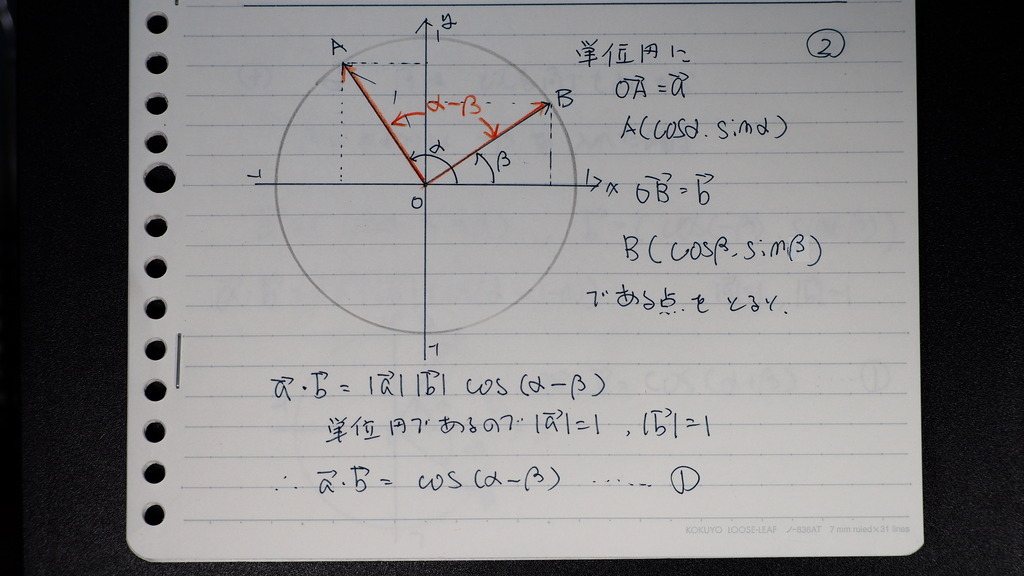
03
動径の 長さは 1だから
x成分は コサイン
y成分は サイン
矢線ベクトルの 内積の
定義式は
絶対値 A 、B は 共に1
コサインは Θがα-β...➀
成分の 内積は
コサインα コサインβ +
サインα サインβ.....②
➀②から
なったデショ
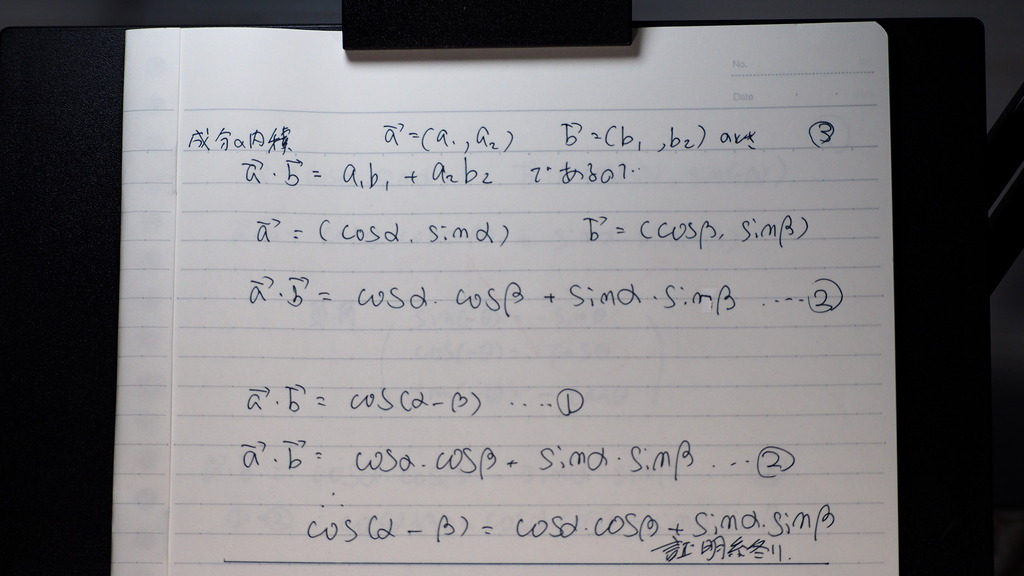
04
ここで
βを -βにすればさ
コサイン(α+β)

05
成分の方は
負角の公式から
書き換えられるので
なったデショ
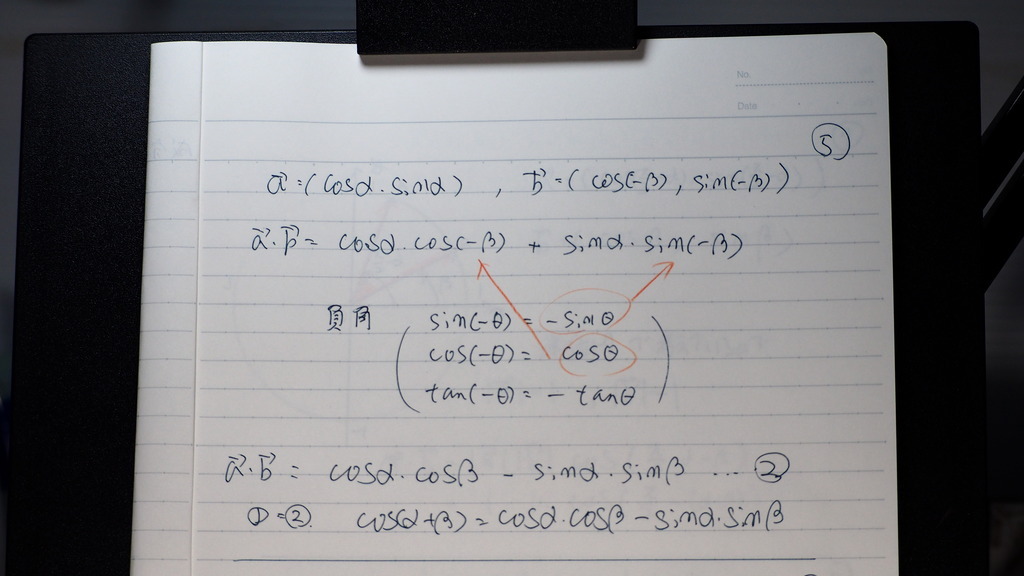
06
じゃーサインは どうするんだ
そこで

07
やっぱりね
矢線ベクトルの 内積と
成分の内積を 連立するんですが
パイ/2 - Θ
余角の 公式で
書換えが効いてじゃナイスカ
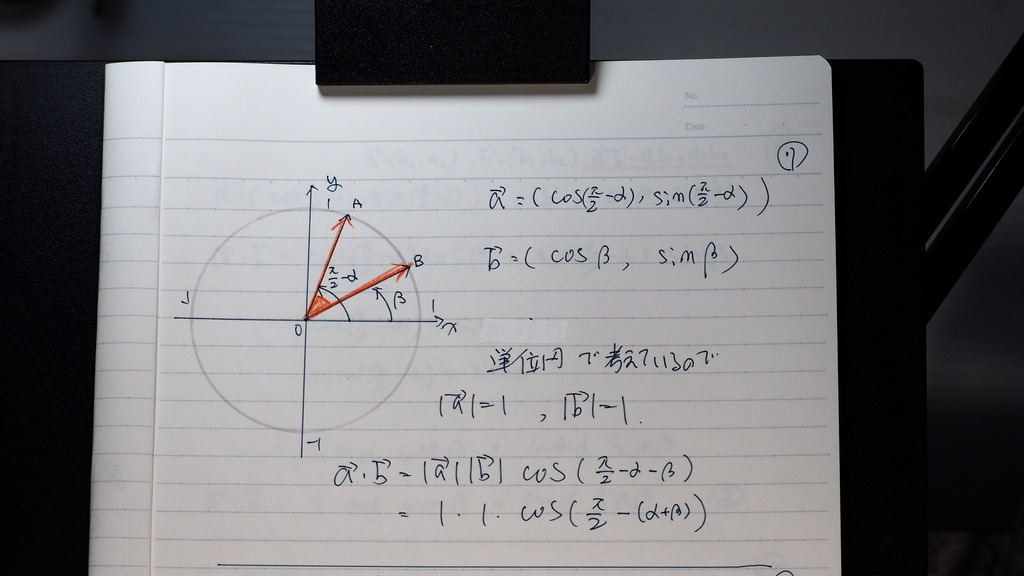
08
そうしたら
コサインが サインに代わるデショ
....➀
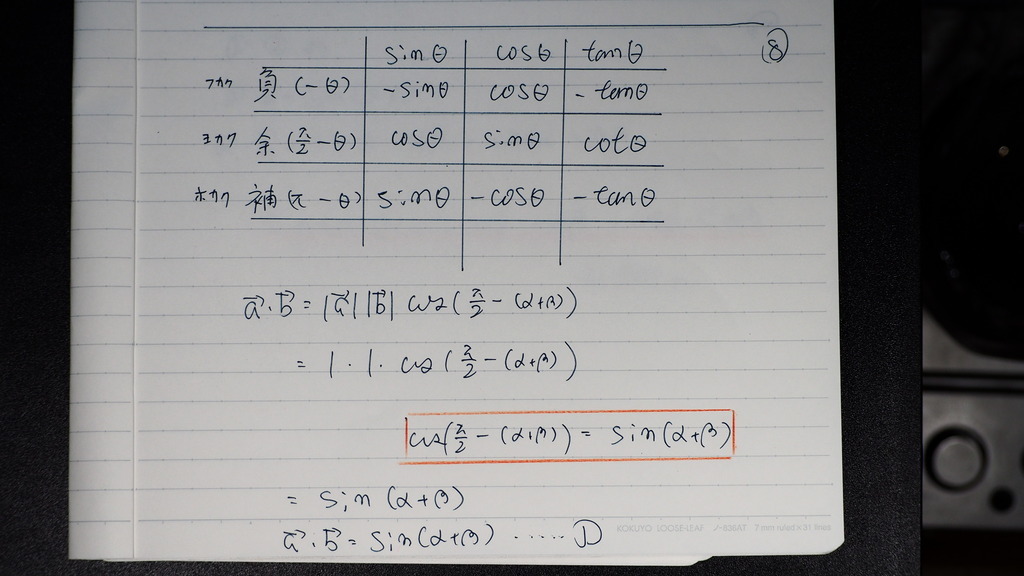
09
成分の方の内積も
余角が 書き換えができて
サインに 化けるので
...②
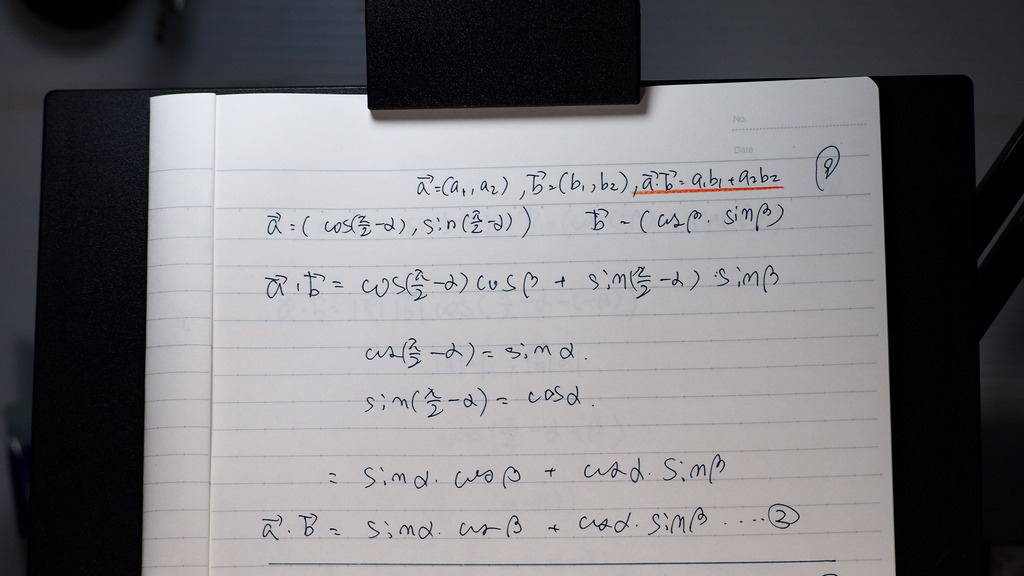
10
なったじゃナイスカ
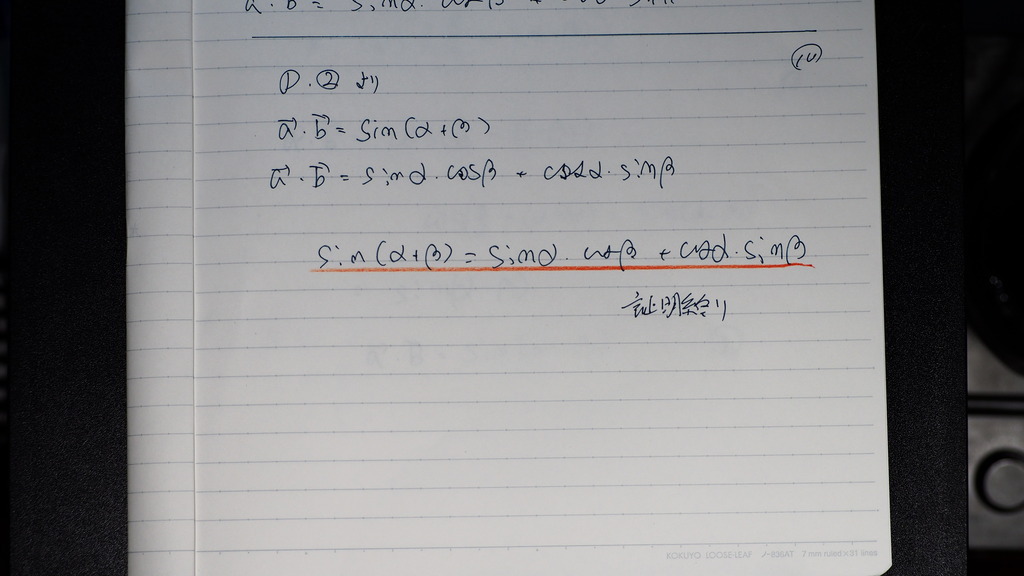
11
マイナス バージョンは
βを -βにすると
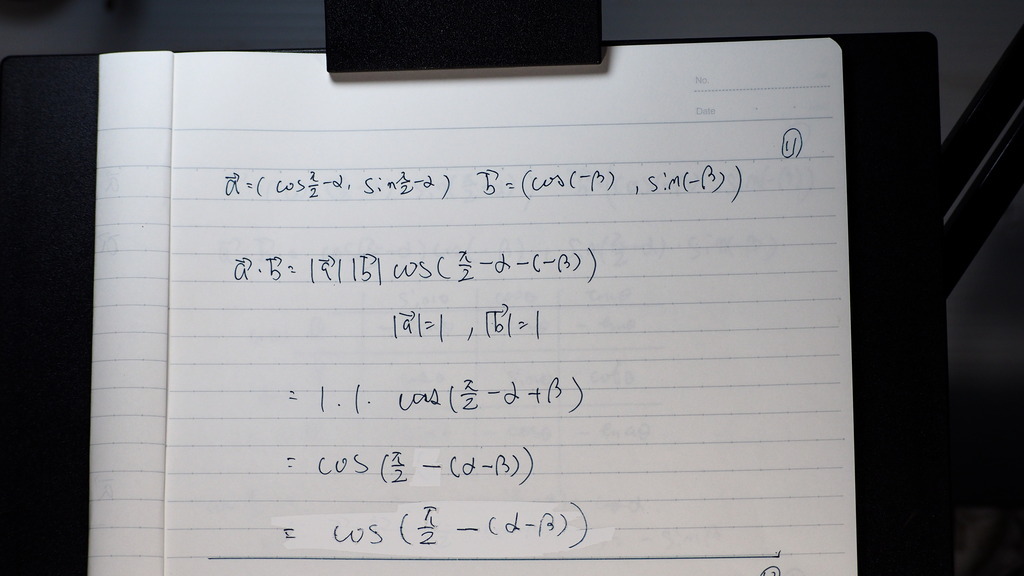
12
出てきたでしょ
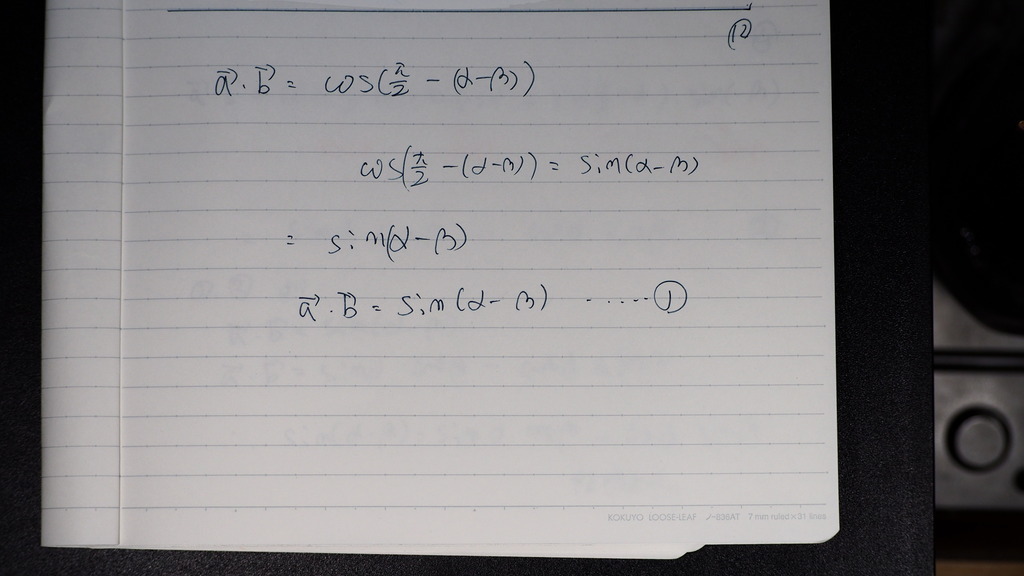
13
人を 恐れると 罠にかかる
しかし
人に 失礼なことは してはいけません
一番 覚えやすい方法で
グラフで できれば
それに こしたことはありませんが
人はね 年を 取るものなんですよ
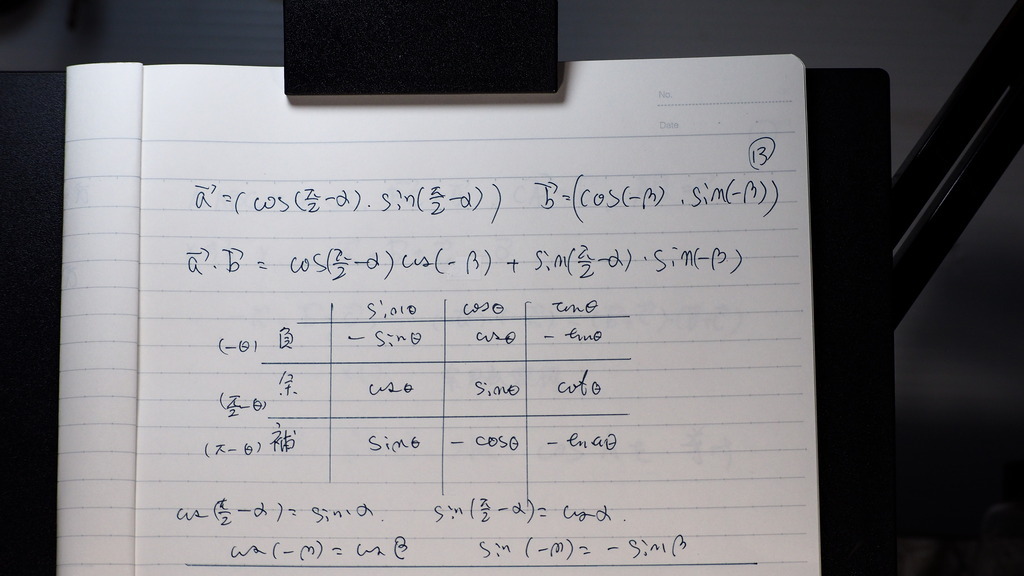
14
こんな感じに
変換で来て
なったデショ

15
今度は
余弦定理
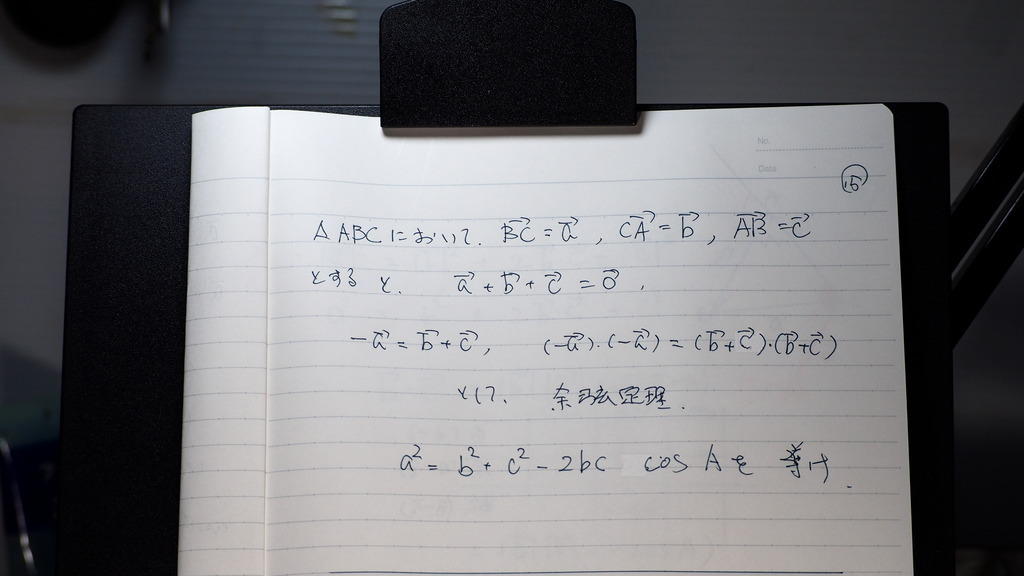
16
内積で
展開して
絶対値が 付くと ベクトルの
矢印は 残ってるけど
これは 大きさを 表してるので
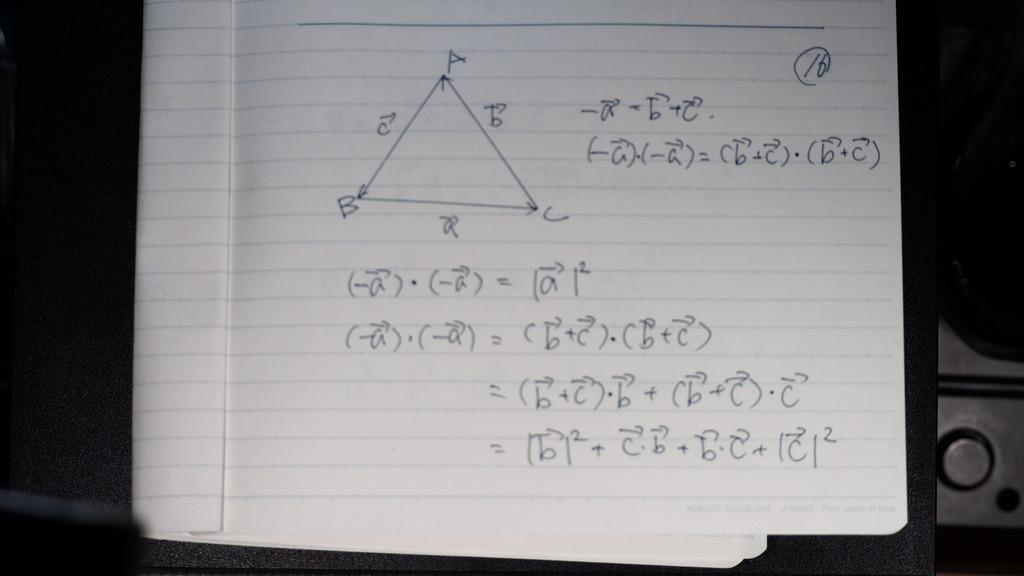
17
であるから
大きさにして
あとは
式の 合間にある
bドットc
この なす角は
ここだから
なす角は
始点をそろえたときの
角度
補角の 公式で
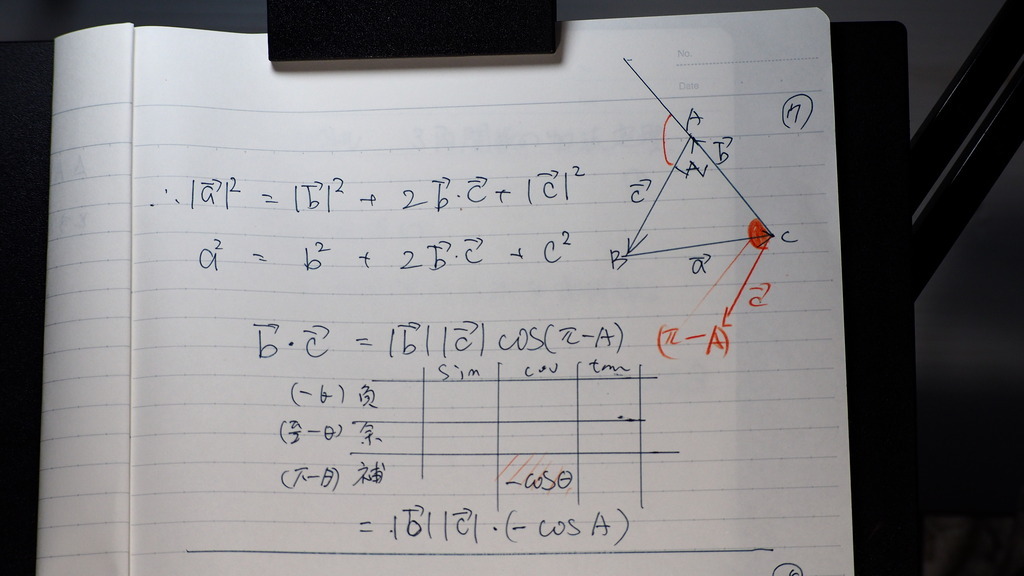
18
こんな感じで
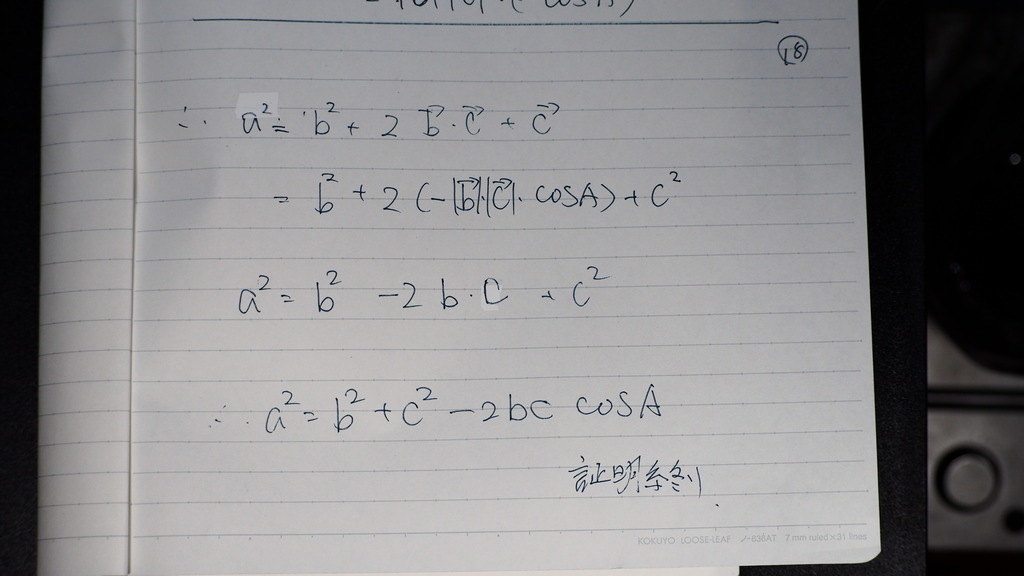
お疲れ様です。
空間座標と
01
三角関数で
加法定理と言うのがあるですが
それを
内積を使って
証明して
という問題
02
こんな
感じに
単位円を使って
Aベクトル Bベクトル
それぞれ
x軸となす角が
α 、 β
これを
座標を
使って 表せば
03
動径の 長さは 1だから
x成分は コサイン
y成分は サイン
矢線ベクトルの 内積の
定義式は
絶対値 A 、B は 共に1
コサインは Θがα-β...➀
成分の 内積は
コサインα コサインβ +
サインα サインβ.....②
➀②から
なったデショ
04
ここで
βを -βにすればさ
コサイン(α+β)
05
成分の方は
負角の公式から
書き換えられるので
なったデショ
06
じゃーサインは どうするんだ
そこで
07
やっぱりね
矢線ベクトルの 内積と
成分の内積を 連立するんですが
パイ/2 - Θ
余角の 公式で
書換えが効いてじゃナイスカ
08
そうしたら
コサインが サインに代わるデショ
....➀
09
成分の方の内積も
余角が 書き換えができて
サインに 化けるので
...②
10
なったじゃナイスカ
11
マイナス バージョンは
βを -βにすると
12
出てきたでしょ
13
人を 恐れると 罠にかかる
しかし
人に 失礼なことは してはいけません
一番 覚えやすい方法で
グラフで できれば
それに こしたことはありませんが
人はね 年を 取るものなんですよ
14
こんな感じに
変換で来て
なったデショ
15
今度は
余弦定理
16
内積で
展開して
絶対値が 付くと ベクトルの
矢印は 残ってるけど
これは 大きさを 表してるので
17
であるから
大きさにして
あとは
式の 合間にある
bドットc
この なす角は
ここだから
なす角は
始点をそろえたときの
角度
補角の 公式で
18
こんな感じで
お疲れ様です。
2022年12月04日
22025 大人のさび落とし 空間座標とベクトル 直線 円 の 方程式
大人のさび落とし
空間座標とベクトル 直線 円の 方程式
01
原点をO として
定点 A,B と 動点P
がある
次のベクトル方程式は
どんな図形を 表すか

02
内積を 展開してくでしょ
動かないところ 黒矢線
動くところ 赤矢線
で
Pは Bを 通り
OAに 垂直な 直線
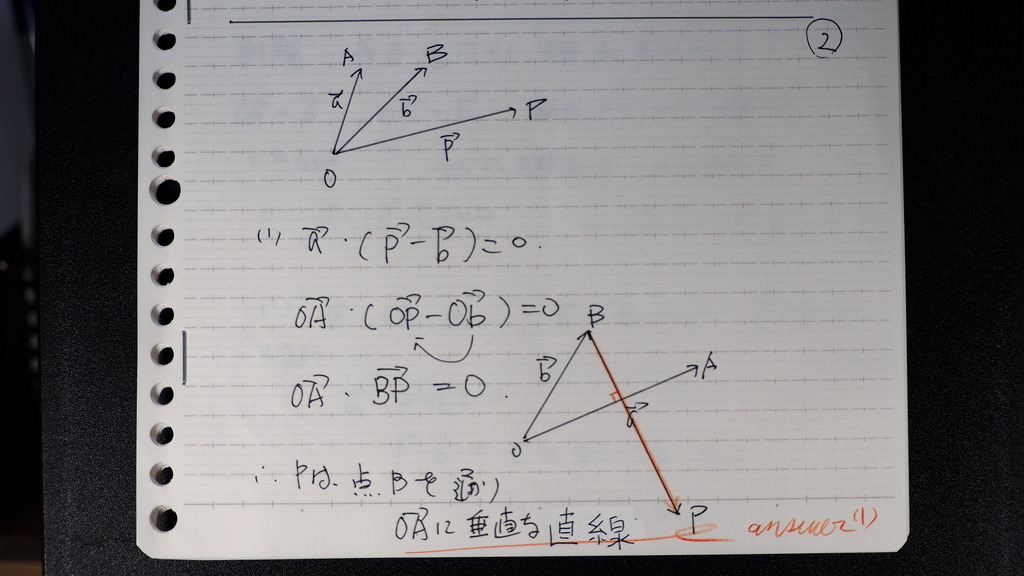
03
(2)
内積をベクトルで
表すと
APベクトル ⊥ BPベクトル
Pの位置だけが
∠APBが 90度を
保つように 変化する
これはさ
A,Bを 直径の
両端に持つ 円
直径ABであるから
中心角180度
その円周角は 90度
ゆえに
Pは ABを 直径の両端に持つ
円の周上
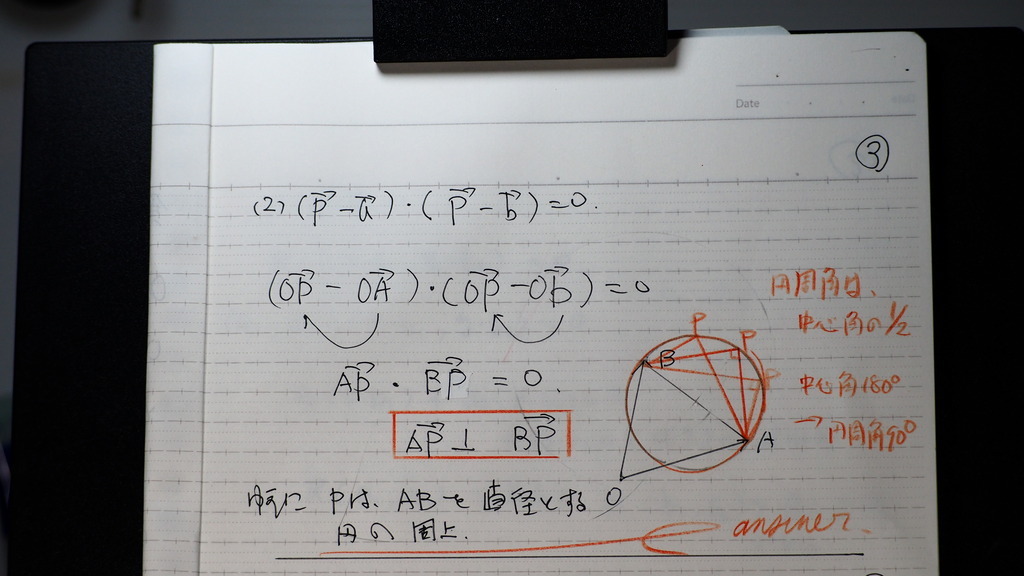
04
同じ問題ですが
ベクトルの
成分で 計算すると

05
(p-b)ベクトルは
直線BP
aベクトルと
内積の 形で
=0 何であるから
点Bを通り OAに垂直な
直線
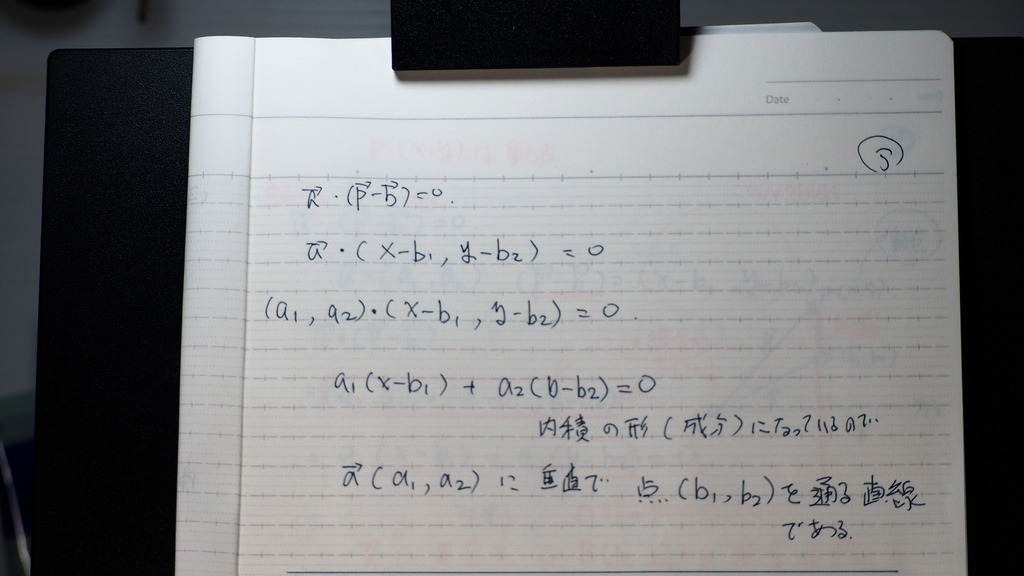
06
ずにすれば
一目りょうぜん

07
まとめた つもりだけど
わかるかな
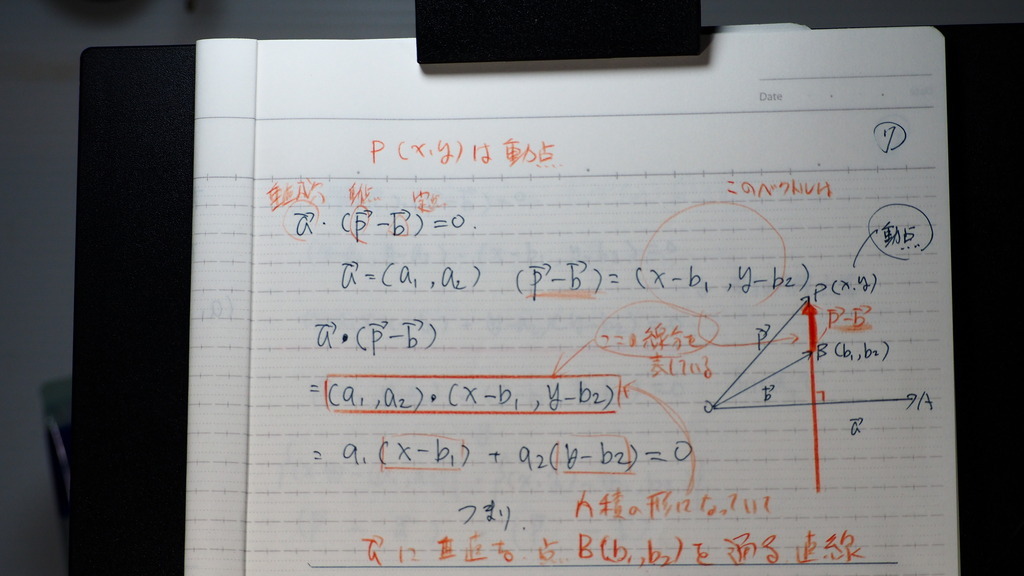
08
(2)
ベクトルで
表すと

09
成分の 計算は
コンななんですが
ただ いじってるだけか

10
兎も角
この式は
ABを 直径の両端とする
円

11
類題を
沢山持ってきました
行ってみましょう

12
動かないところ 黒
動くところ 赤
内積を
展開して

13
始点が 同じで
Aベクトルと 大きさが
同じように
動くのだから
始点を O として
半径aの円になる

14
次は
左辺を 展開して
まず Pベクトルの 大きさが
0の時

15
Pベクトルの 大きさが
ゼロでないときは
Oを 始点として
60度のなす角を 持つ 2つの
半直線

16
これは

17
(a-b)ベクトルは これだから
これに
垂直
こんなかんじで

18
これは
内積を
くくって
こんな感じだから

19
なんだこりゃ

20
内積を
左辺展開してって
じゃナイスカ
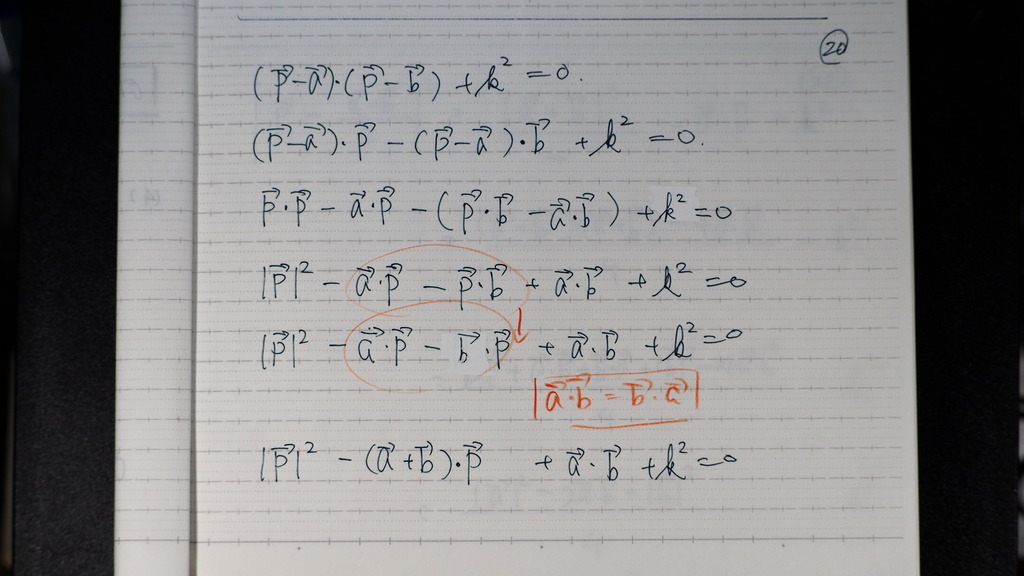
21
平方完成して
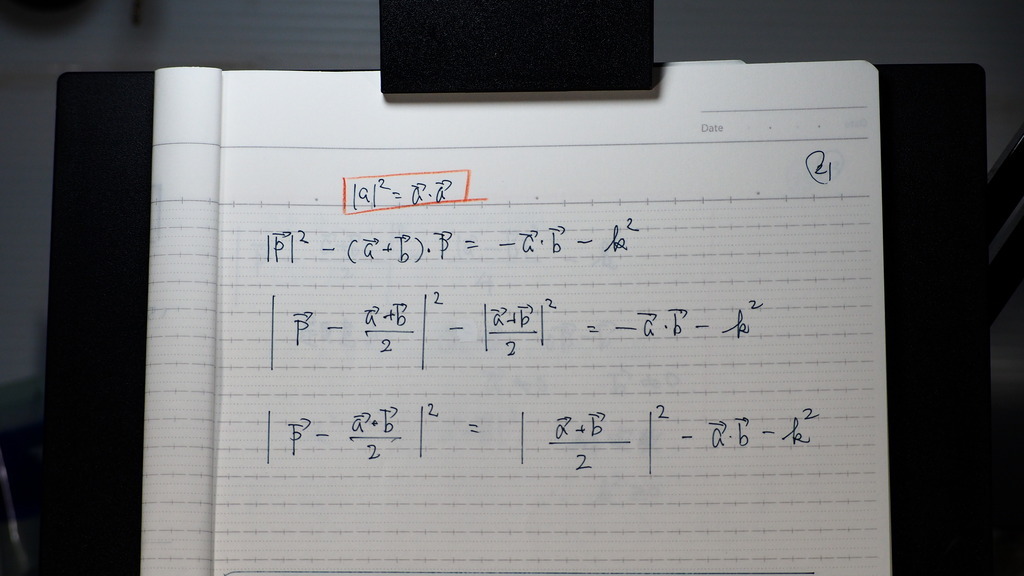
22
こんな感じで
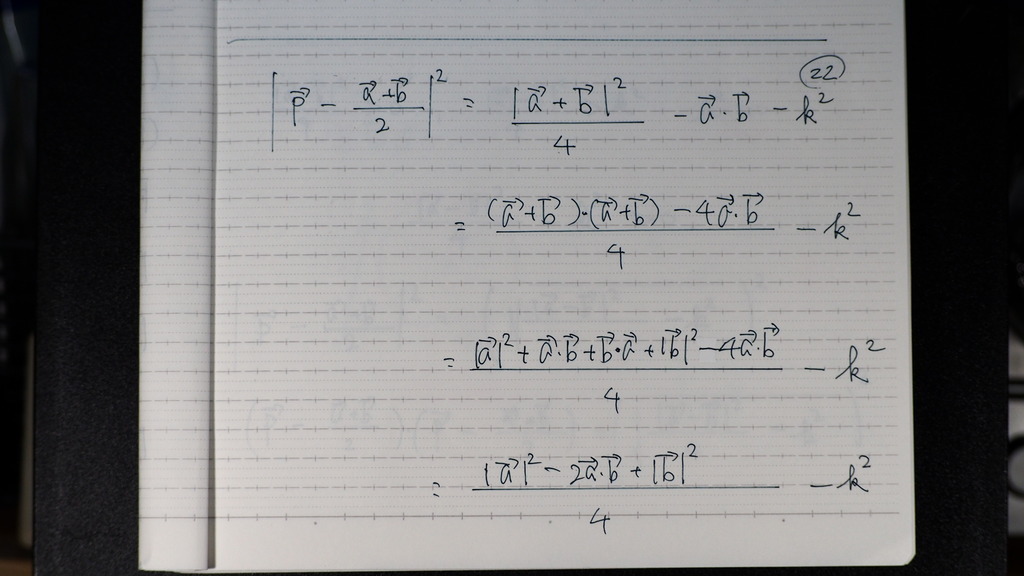
23
題意より

24
左辺は
円の 方程式に
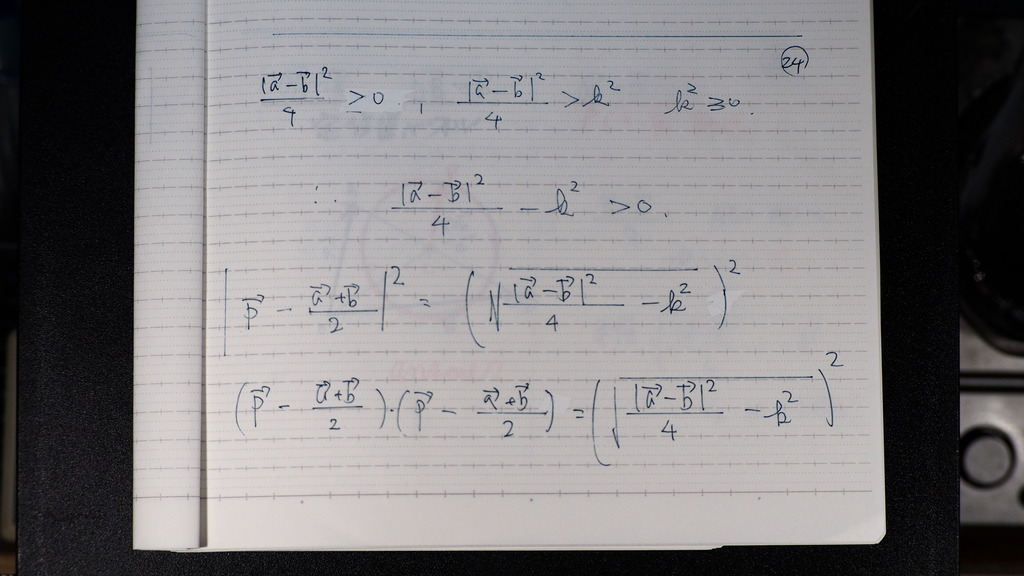
25
こんなだったじゃナイスカ
であるから

26
2分の a+bってのは
ABの 中点でしょ
そこが
円の中心
半径は
右辺に 2乗の形で
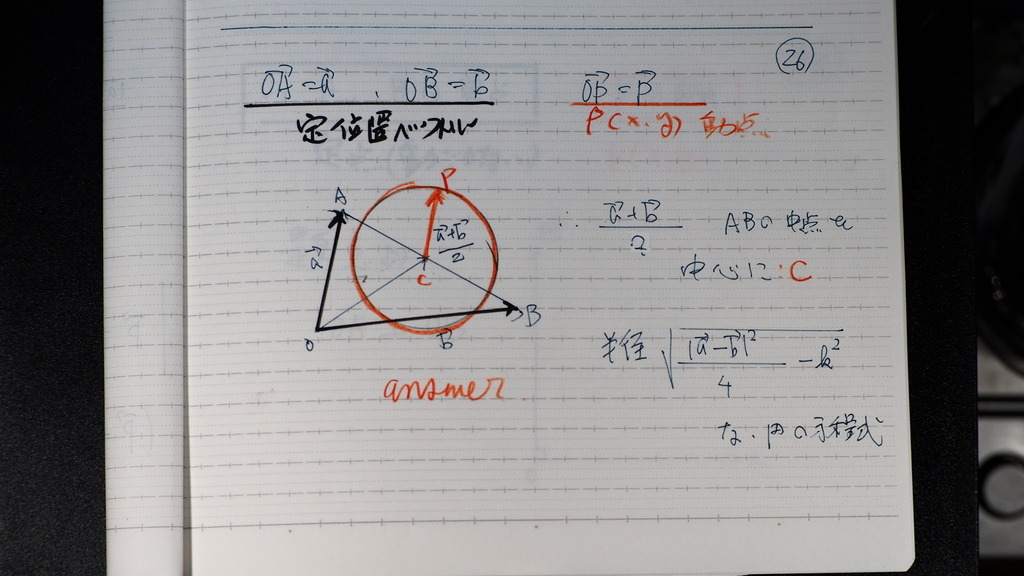
27
ラストは
これはさ
円の方程式が
3っ出て来て
ソレゾレ
領域があって
同時に 満たすところは

28
題意より
Aベクトルと Bベクトルは 垂直
始点は 同じO
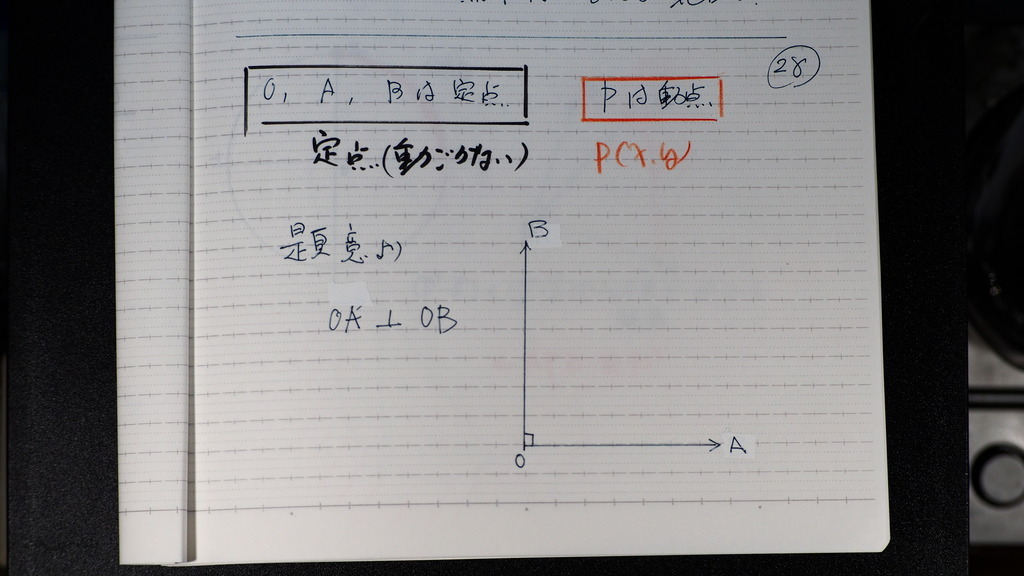
29
初めの式は
ABを直径の両端に持つ
円 左辺=右辺ならば
左辺 大なりイコール
(グレイターイコール ザン)0であるから
内積が=0ならば 90度
内積が ゼロ以上であれば
内積の角度は コサインで
効いてくるので
0以上90以下 で 90度または鋭角

30
(p-b)と(p-a)の
ここのところが
90度以下
この角度は なす角と等しいので
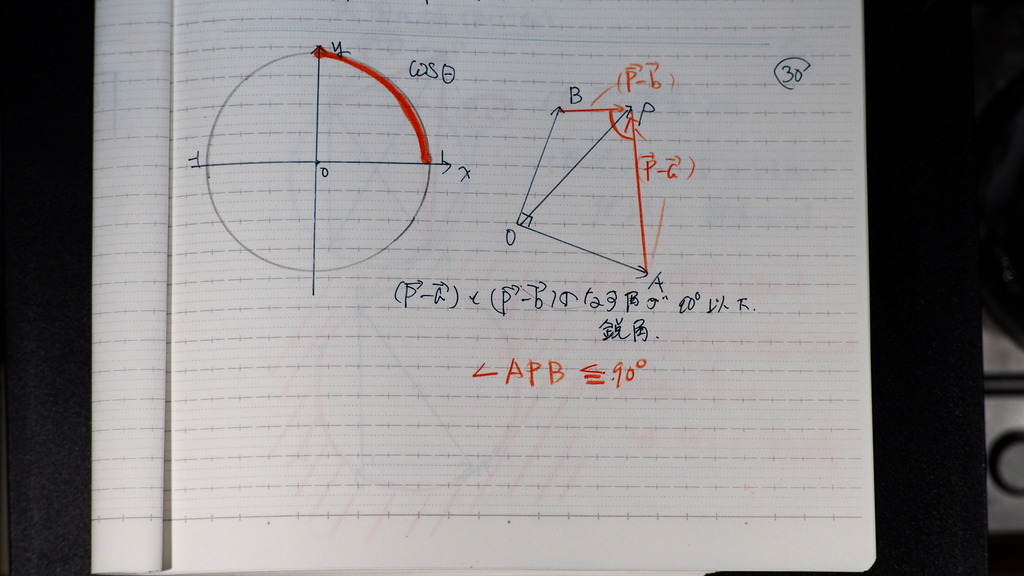
31
Pの集合は
円周上を 含む
円の外側

32
こんな感じで
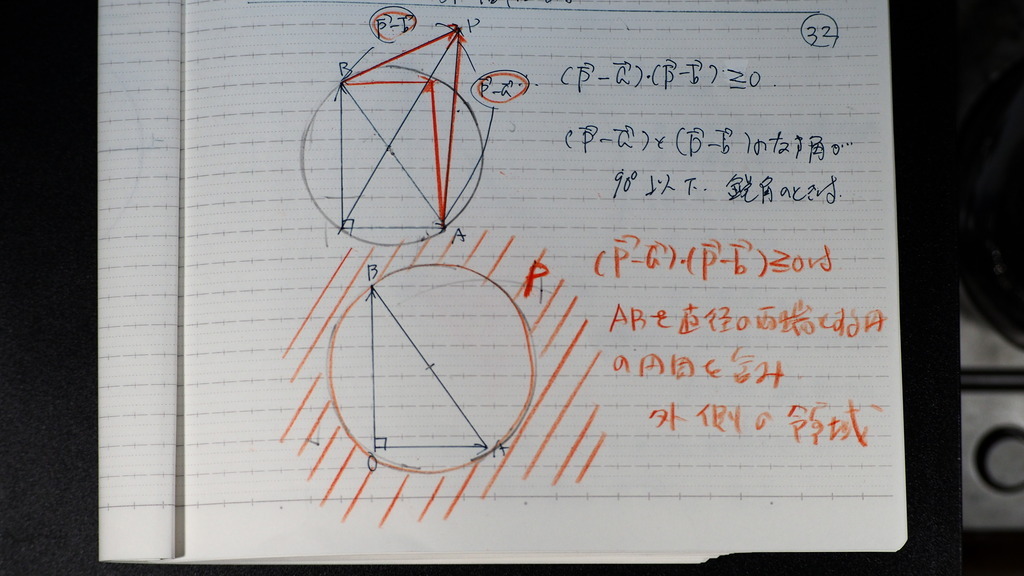
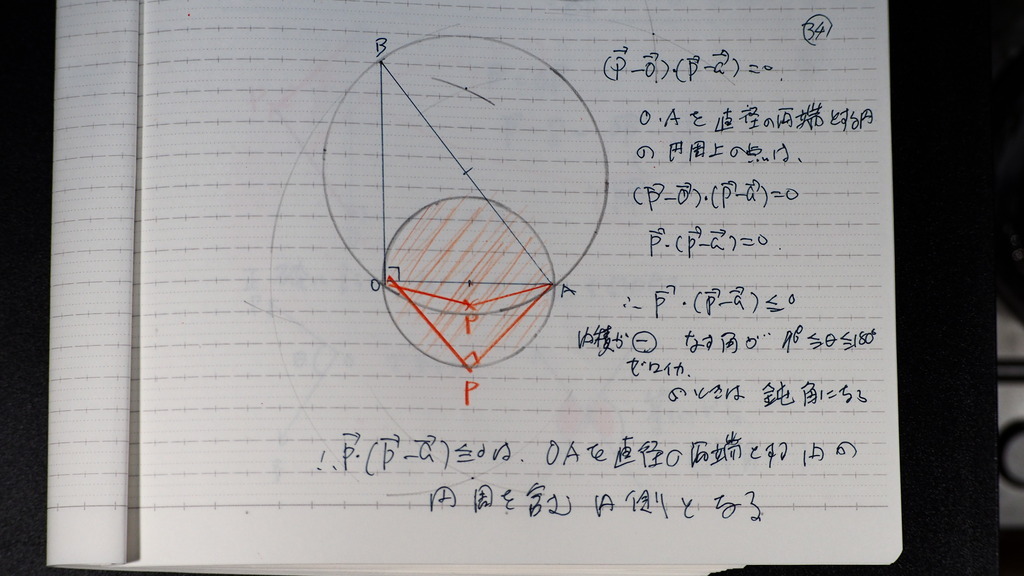
33
こっちの円は
OAを 直径の両端にする円
れすイコールザン 0
90度を含んで 鈍角

34
そのPの集合は
円周および その内部
35
三つ目の円は
OBを 直径の
両端に持つ円で

36
なす角が
90度以上鈍角
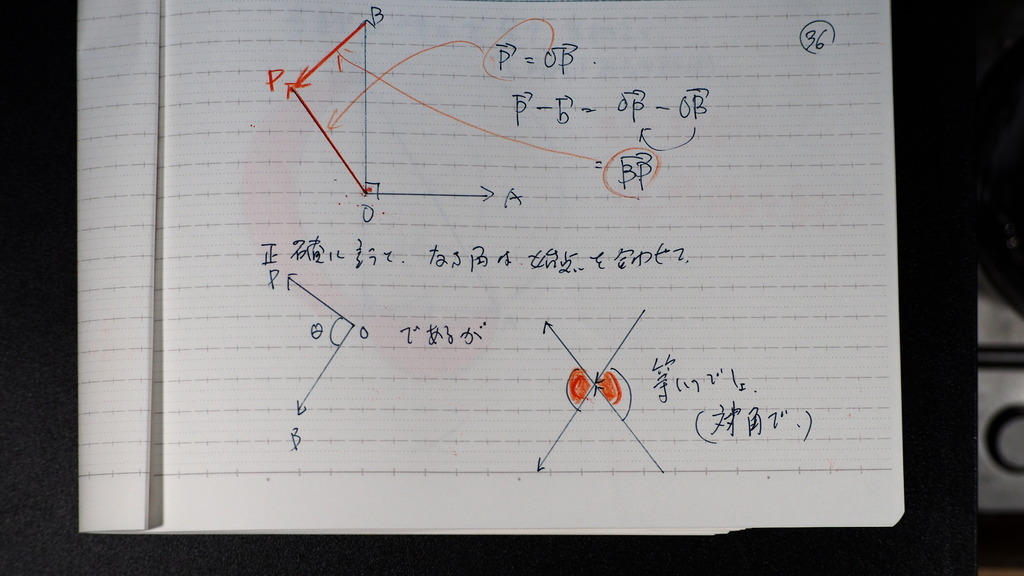
37
こんな感じの
円周とその内部に 成るので

38
以上
3っの円を
重ねて
同時に 条件を
満たすのは
この範囲
境界線を含む
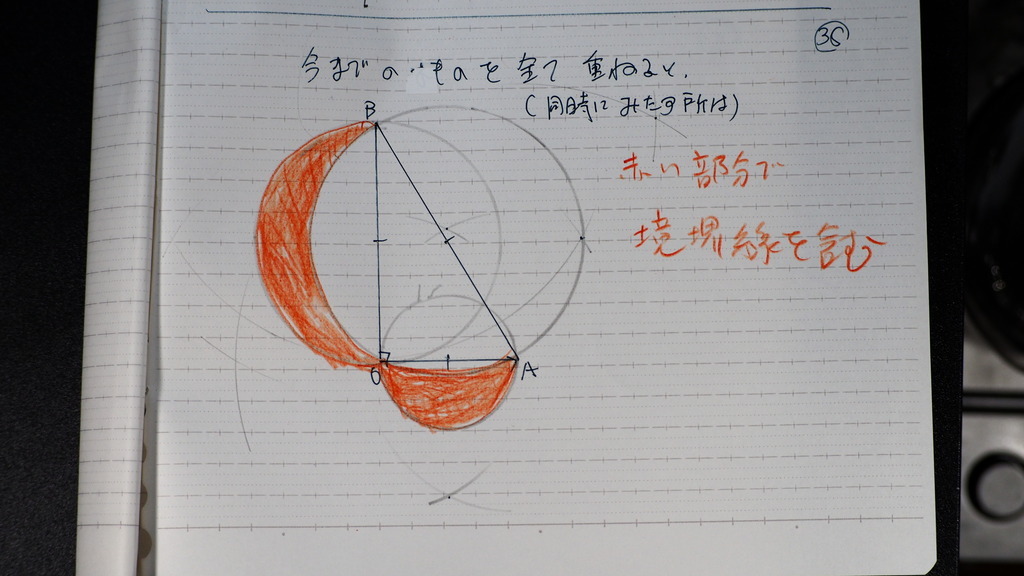
お疲れ様です。
空間座標とベクトル 直線 円の 方程式
01
原点をO として
定点 A,B と 動点P
がある
次のベクトル方程式は
どんな図形を 表すか
02
内積を 展開してくでしょ
動かないところ 黒矢線
動くところ 赤矢線
で
Pは Bを 通り
OAに 垂直な 直線
03
(2)
内積をベクトルで
表すと
APベクトル ⊥ BPベクトル
Pの位置だけが
∠APBが 90度を
保つように 変化する
これはさ
A,Bを 直径の
両端に持つ 円
直径ABであるから
中心角180度
その円周角は 90度
ゆえに
Pは ABを 直径の両端に持つ
円の周上
04
同じ問題ですが
ベクトルの
成分で 計算すると
05
(p-b)ベクトルは
直線BP
aベクトルと
内積の 形で
=0 何であるから
点Bを通り OAに垂直な
直線
06
ずにすれば
一目りょうぜん
07
まとめた つもりだけど
わかるかな
08
(2)
ベクトルで
表すと
09
成分の 計算は
コンななんですが
ただ いじってるだけか
10
兎も角
この式は
ABを 直径の両端とする
円
11
類題を
沢山持ってきました
行ってみましょう
12
動かないところ 黒
動くところ 赤
内積を
展開して
13
始点が 同じで
Aベクトルと 大きさが
同じように
動くのだから
始点を O として
半径aの円になる
14
次は
左辺を 展開して
まず Pベクトルの 大きさが
0の時
15
Pベクトルの 大きさが
ゼロでないときは
Oを 始点として
60度のなす角を 持つ 2つの
半直線
16
これは
17
(a-b)ベクトルは これだから
これに
垂直
こんなかんじで
18
これは
内積を
くくって
こんな感じだから
19
なんだこりゃ
20
内積を
左辺展開してって
じゃナイスカ
21
平方完成して
22
こんな感じで
23
題意より
24
左辺は
円の 方程式に
25
こんなだったじゃナイスカ
であるから
26
2分の a+bってのは
ABの 中点でしょ
そこが
円の中心
半径は
右辺に 2乗の形で
27
ラストは
これはさ
円の方程式が
3っ出て来て
ソレゾレ
領域があって
同時に 満たすところは
28
題意より
Aベクトルと Bベクトルは 垂直
始点は 同じO
29
初めの式は
ABを直径の両端に持つ
円 左辺=右辺ならば
左辺 大なりイコール
(グレイターイコール ザン)0であるから
内積が=0ならば 90度
内積が ゼロ以上であれば
内積の角度は コサインで
効いてくるので
0以上90以下 で 90度または鋭角
30
(p-b)と(p-a)の
ここのところが
90度以下
この角度は なす角と等しいので
31
Pの集合は
円周上を 含む
円の外側
32
こんな感じで
33
こっちの円は
OAを 直径の両端にする円
れすイコールザン 0
90度を含んで 鈍角
34
そのPの集合は
円周および その内部
35
三つ目の円は
OBを 直径の
両端に持つ円で
36
なす角が
90度以上鈍角
37
こんな感じの
円周とその内部に 成るので
38
以上
3っの円を
重ねて
同時に 条件を
満たすのは
この範囲
境界線を含む
お疲れ様です。
2022年11月30日
22024大人のさび落とし 空間座標とベクトル 軌跡と領域
軌跡と領域
01
ここは
過去問なので
微分 2次関数 解と係数の関係
内積 が 混在しています
行ってみましょう
こんな 問題ですが
02
内積の定義式は
矢線ベクトルと
成分と
あるじゃないですかね
そこで
点の座標が
表せれば ベクトルになるから
こんなイメージでさ
03
放物線上の
接点の x座標を
t とすれば
接点の 座標は ( t 、t二乗 )
x=t の時の
接線の 傾きは
一回微分で
f’(x) = 2x
tを代入すれば
2t
tにおける 接線の
方程式は
こんなデショ
04
で
この接線の 方程式の中から
点Pを 通るものだから
P(a、b) を
代入して
05
t は 放物線上の
x座標だから
06
2つの 異なる 点で
接してるから
2つの解を
α 、 β
とすれば
解と係数の関係から
こんなかんじになって
07
今の計算は なんだったかって
式の計算のとこで
よく出てくる
問題が
後で発生するので
ベクトルを
α、 β
a, b
で
表現して
08
内積を
計算するでしょ
これは 成分だから
単純に 掛け算で
ここから
α 、 β を a、bに
置き換えてくと
09
式の けいさんのとこで
やったじゃナイスカね
こんなのあったデショ
式の 値を 求めよ
10
で
こっちの方が
大変なんだけど
こんな感じで
よさそうなので
これが 内積
11
で
次は
内積が =0
直角になるとき
ここは
機転が必要ですが
左の かっこは
ゼロではない
( ここに出てくる 文字を
色々見てきますと )
12
つまり
右側の かっこが =0
であるから
y=-1/4
の 横線上に Pがある
13
こんな感じ
14
角APBが 鋭角の時
Pは どこの範囲にあるか
内積は
COSで 効いてくるので
15
ここが 鋭角の時
すると
16
ちょっと整理しとくね
接線の方程式のなかの
点Pを 通るもの
二つの
異なる接点と
Pでできる
角度が 鋭角の時
17
内積が 正
接線が 二つの異なる
解を持つため
判別式が
正
18
この連立から
b 点Pの y座標が
-1/4未満
19
つまり
y=-1/4を 含まず
それより マイナス側にいる
20
これは
一見難しそうなんですが
やり方を
一回おぼえると
21
内積の 成分計算
ゼロ と イチ の間
22
これらを
グラフに すれば
23
こんな感じ
境界線は 含まず
24
もう一つも
同じやり方で
そして
両方において
ゼロ と イチ の あいだになってる
とこを 見れば
25
こんな感じ
26
次はさ
何だこりゃ
27
OPをさ(x、y)とおく
28
成分計算
29
成分だから
xと yに
分けて
30
二乗してみよう
31
問題は
必ず 作った人がいるので
解けるようになっている
だからさ
これは 本当は
数学の 感じゃなくて
なんていやいいのかな
この公式使ってそうだなとか
32
足すでしょ
うまくできてるよね
33
なため
円ですか
こんな感じの円
お疲れ様です。
2022年11月29日
22023 大人のさび落とし 空間座標とベクトル 最大 最小
大人のさび落とし
空間座標とベクトル
最大 最小
01
ベクトルに
最小とか
最大とか あるのか?
2つの 大きさが 有 り
方向が 違う ベクトルを
足し合わせるとき
OA +t OB ( 今回は )
一番後ろに
図解付きで 書いておきますが
ベクトルの大きさが
最小になるときの tの値は
ベクトルの大きさが
最小になるとき
bベクトルと a+tb が
直交してることを 証明せよ

02
ベクトルの大きさを
2乗すると
内積で 展開できるので
出てきた 2次関数から
最小値を
割り出し
最小値は 頂点の座標の √をとれば
じゃナイスカ
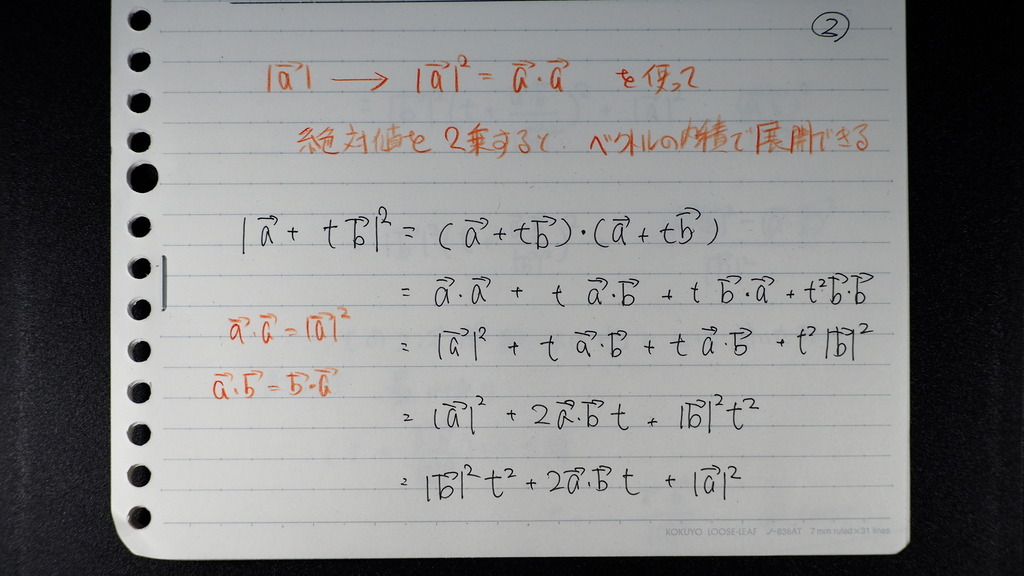
03
整理すると
二乗で 展開して
tの2次関数になるので
平方完成して
頂点が 下に凸 上に開いてるから
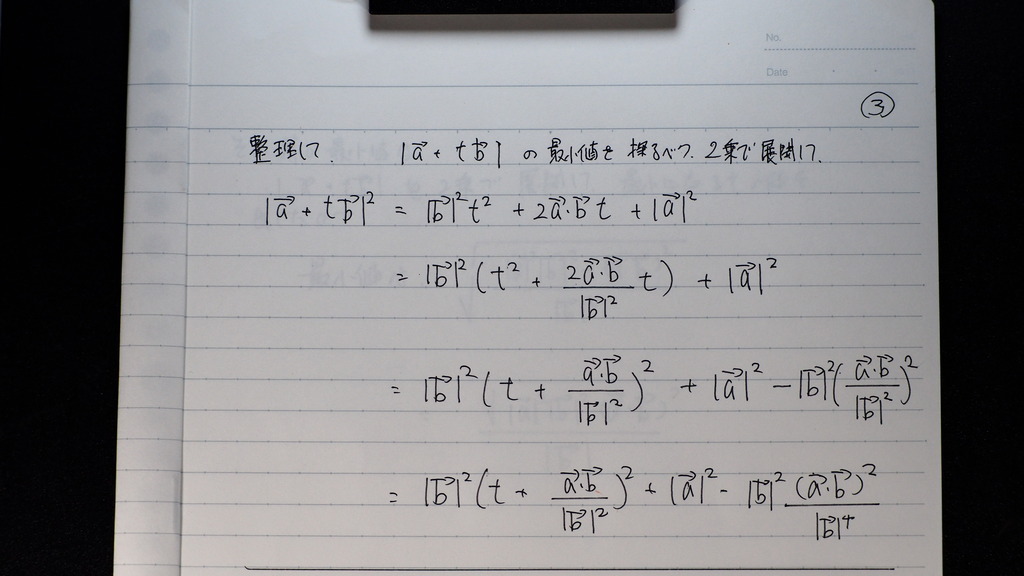
04
最小値は
t が この値の時
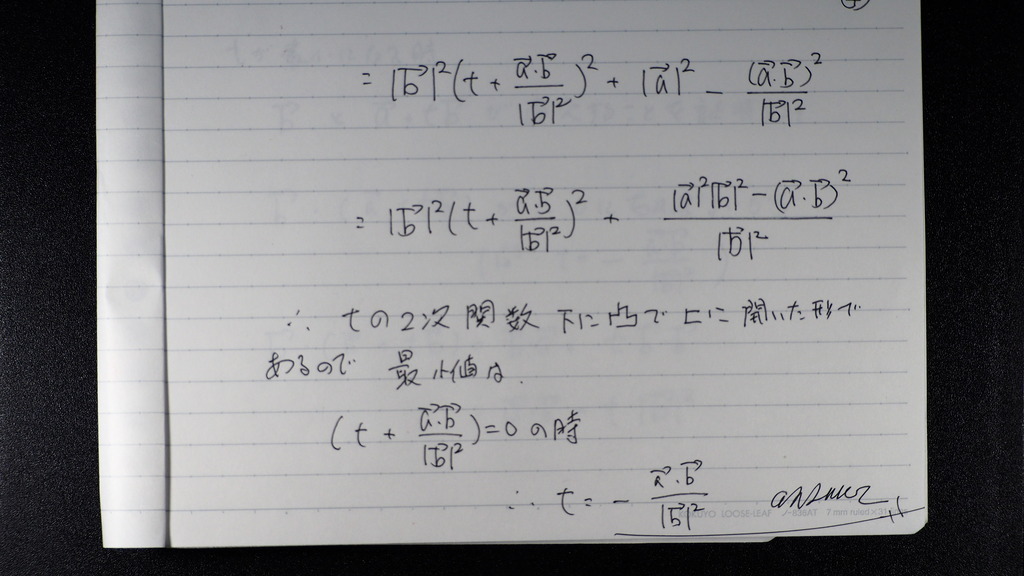
05
最小値は
ベクトルの大きさを
2乗で 展開したのだから
√を とれば
こんな感じに

06
t が 最小の時
直交するというのだけれど
内積を 計算するでしょ
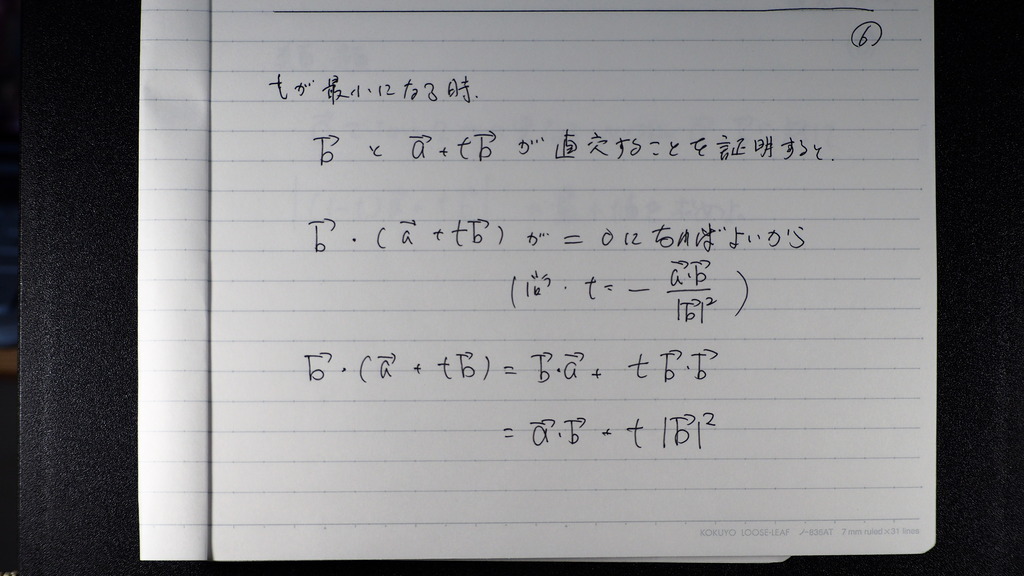
07
で ベクトルの
大きさが
最小になるときの
tのあたいを
代入したらば
内積が =0
つまり
直交している
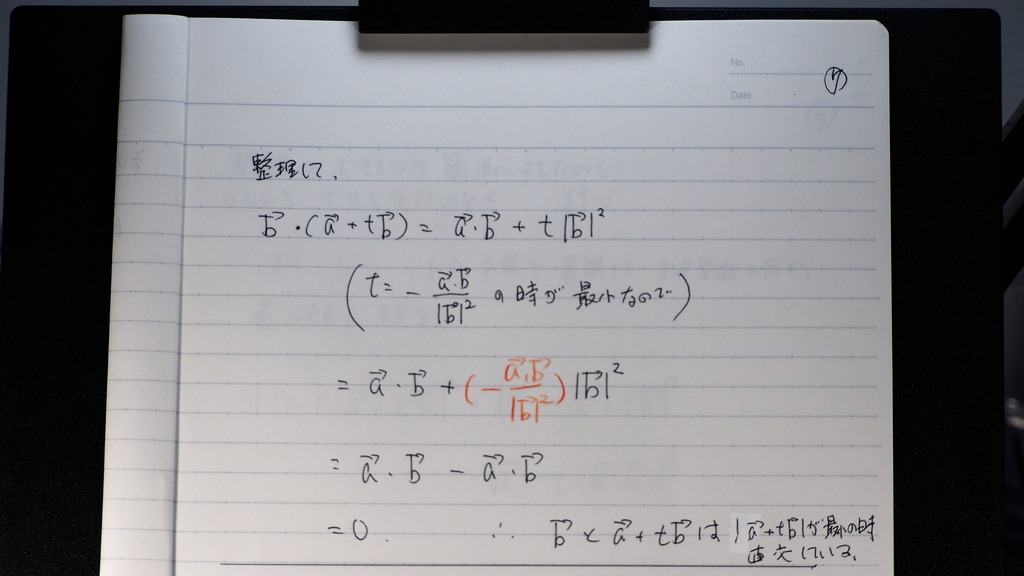
08
るいだい
ベクトルの
大きさの 最小値を
求めるんですが
2乗で
内積に展開して
後で
√を とれば
じゃナイスカ

09
できるだけ
簡単に したいので
置き換えとか
バンバン 使って

10
こうすればさ
少し簡単
さっきと
ほぼ同じ
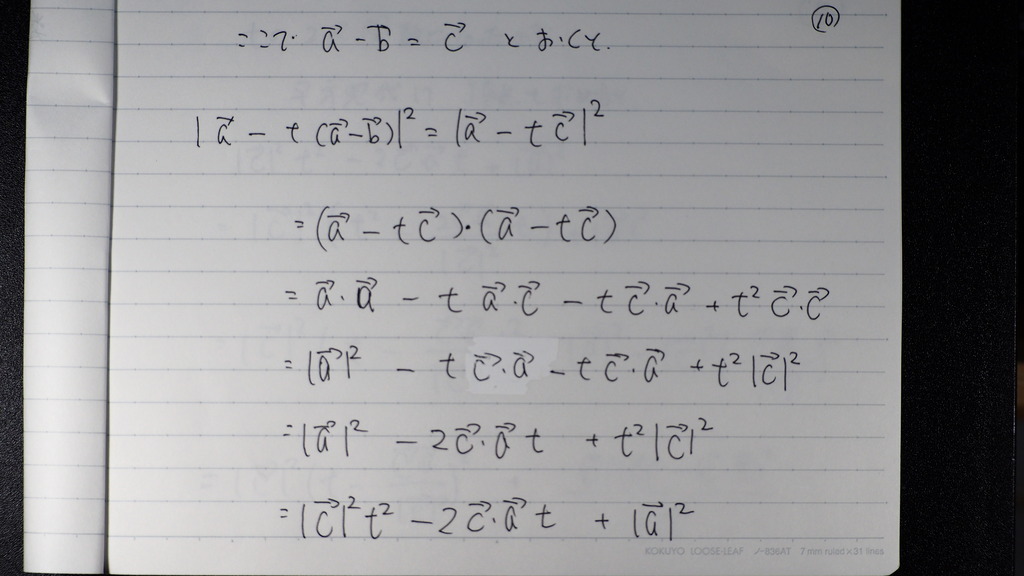
11
整理して
大きさを
2乗で 展開して
tの2次関数にして
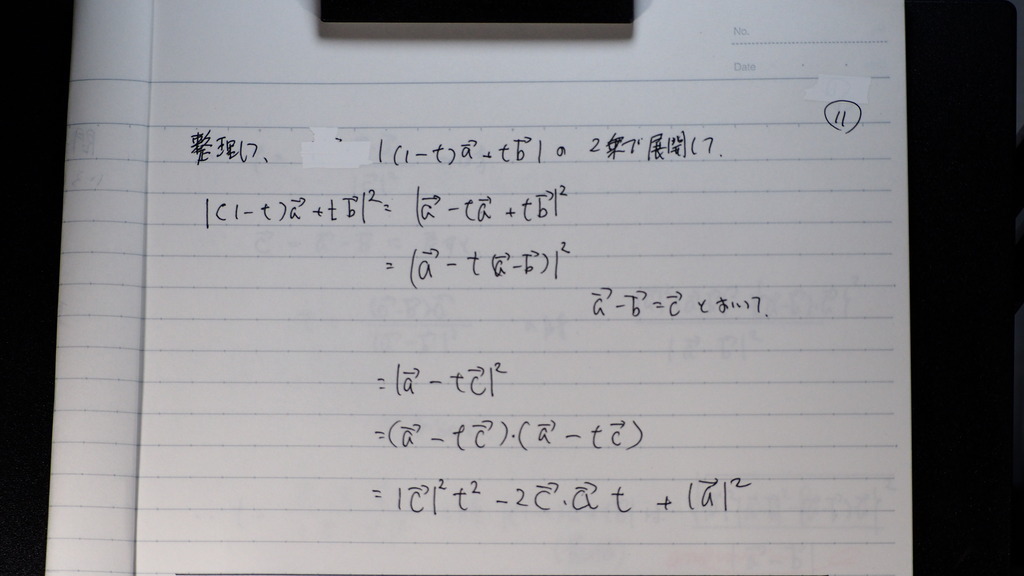
12
平方完成して
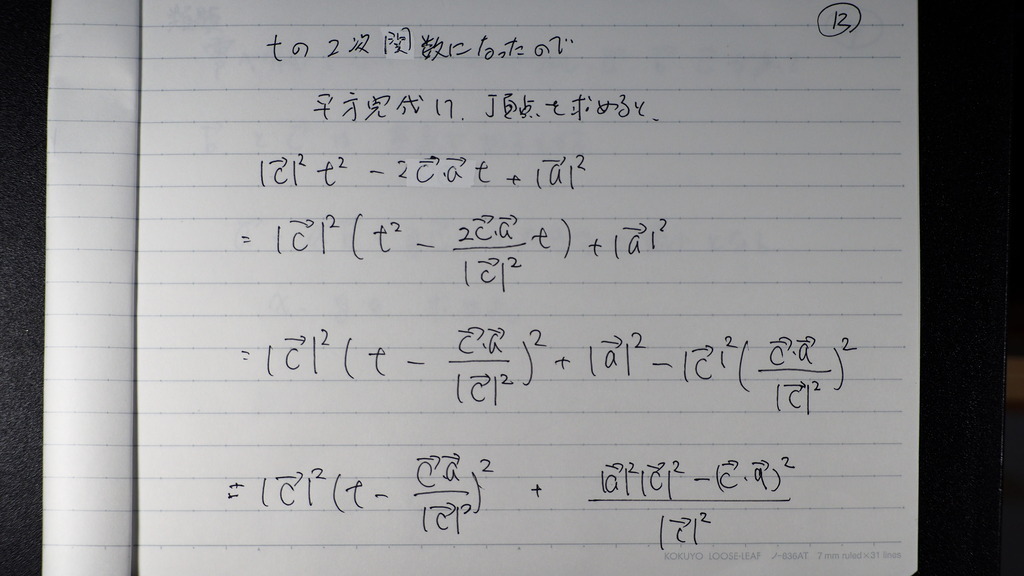
13
cベクトルを 元に戻せば
出てきた 頂点のt( 下に凸)
の時の 最小値を
√を取って
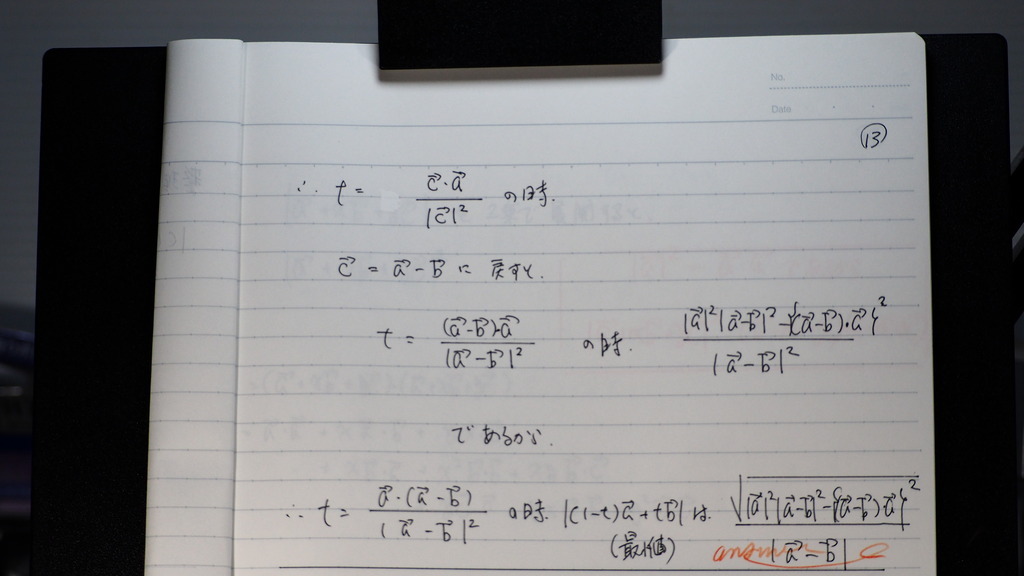
14
今度は
x、y とあるけど
行ってみましょう
ベクトルの 大きさを
2乗で 内積の形に
展開して行って

15
計算してくでしょ
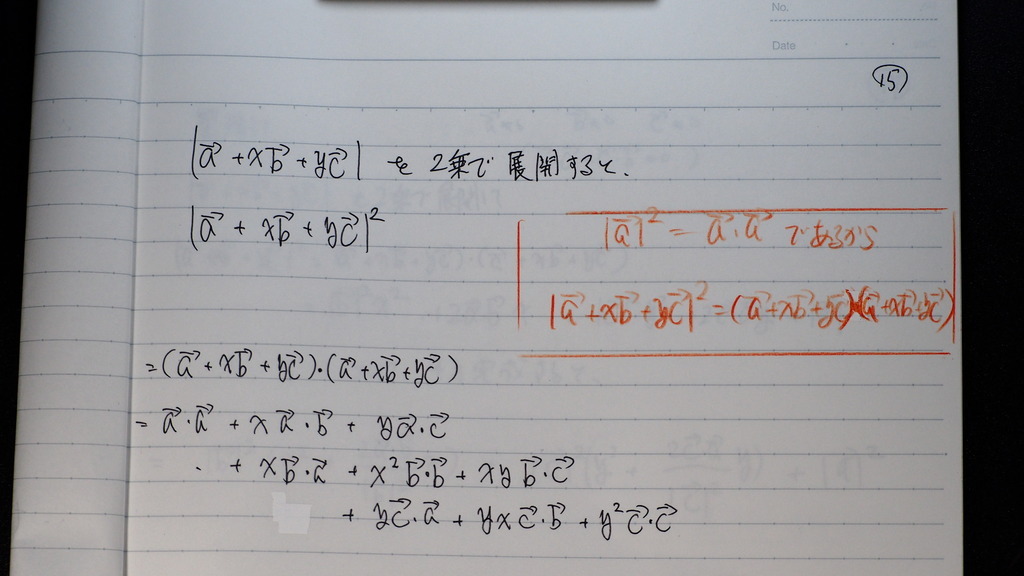
16
題意より bベクトルと
cベクトルは 垂直だから
b と c の 内積は =0
式が 少し簡単になって
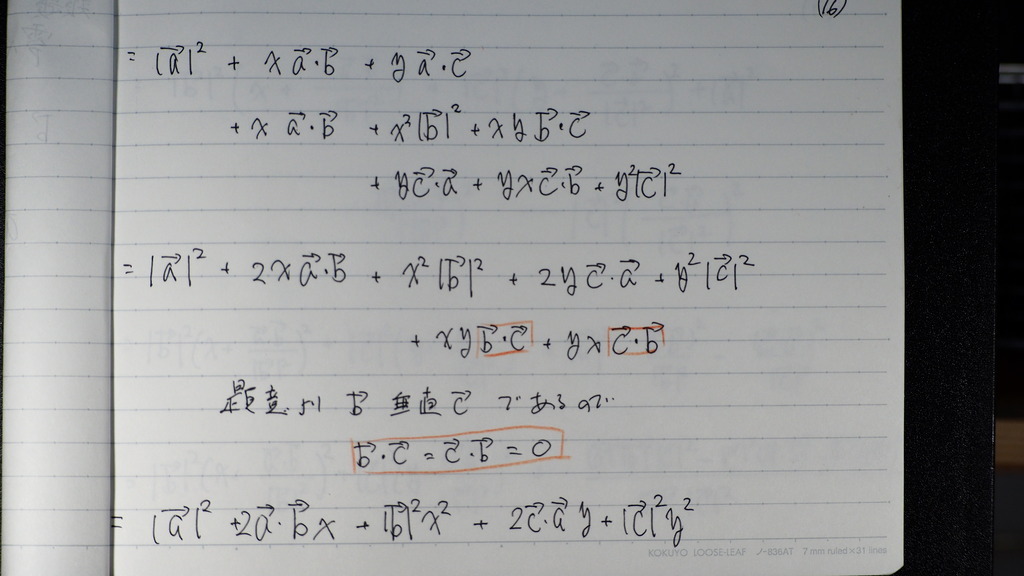
17
Xと yの 2次関数になってるので
ソレゾレ
平方完成して
最小値になるとき
円になるんだね
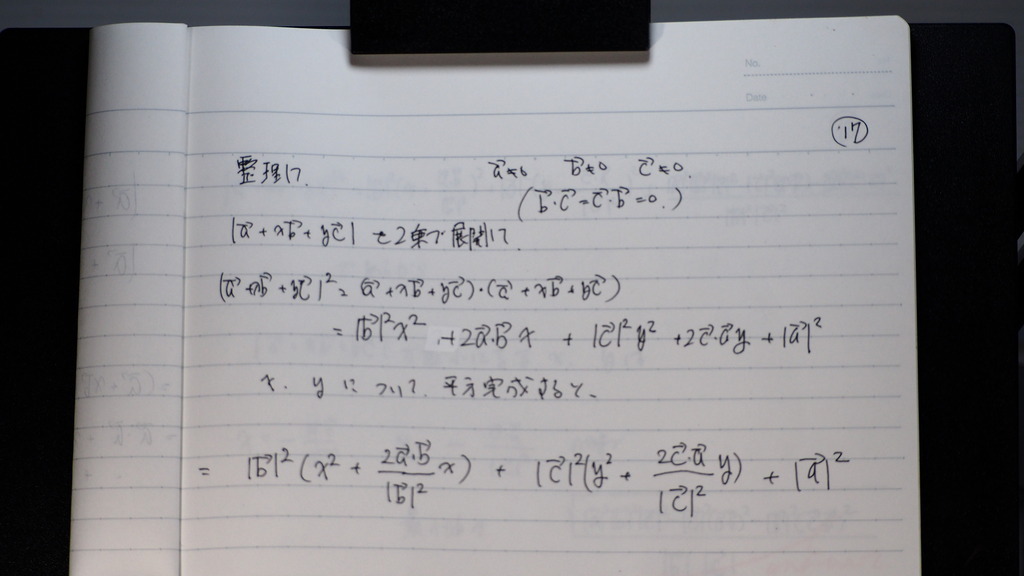
18
さいごまで 計算してですよ
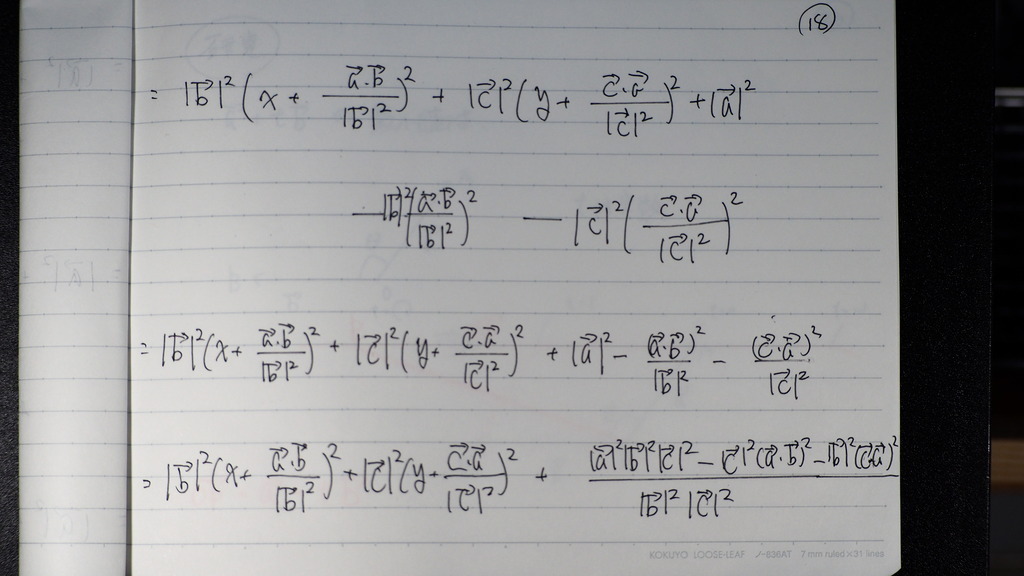
19
であるから
x、yが これこれの時
√を とった値が
最小値

20
で
お約束ですが
ベクトルの
最小値って
何なのというわけで
aと bと ベクトルがあって
a + tb は OPになるんだけど
bベクトルの t倍を aベクトルの
終点まで
平行移動して
足すと 成るでしょ
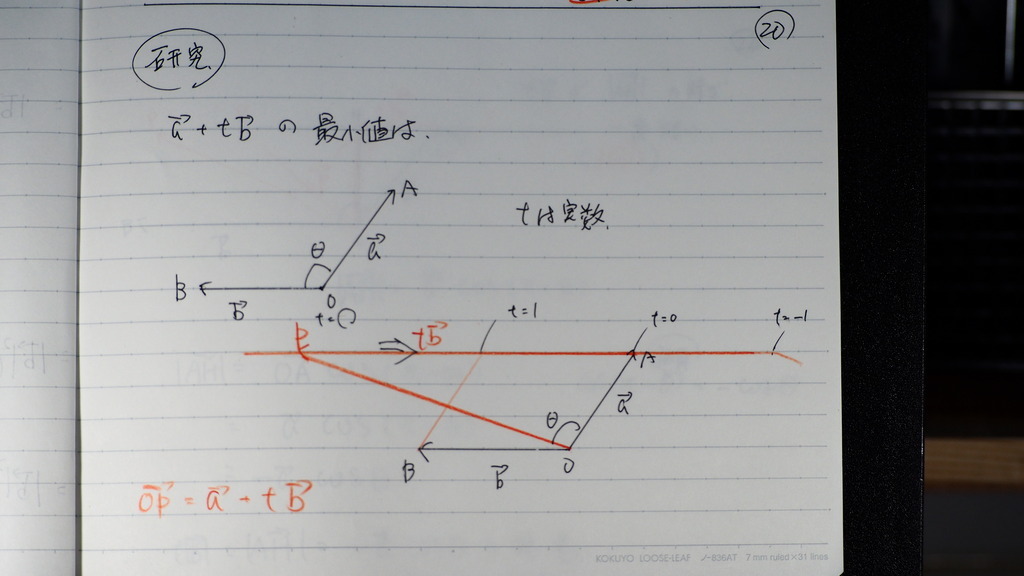
21
OP の 可能性は
無数にあるんだけれど
その中で
一番 短いもの
それが 最小値なんだから
大きさが 一番小さくなるとき
赤い矢印は (OP ベクトル)
どこでしょう
A を通って bベクトルに
平行な tbベクトル上で
Oから そこに おろした
垂線Hと 重なるときでしょ

22
AHベクトルの 大きさが
tbベクトル の大きさと
等しくなるとき
これを
計算すると

23
こんな感じで
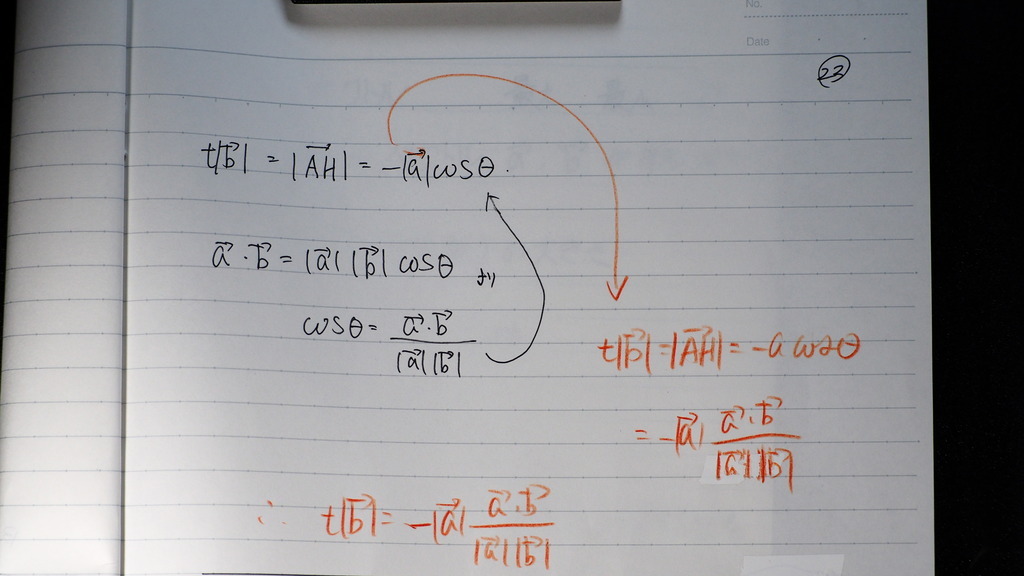
24
t=にしたら
図から 最小になるときの
tの値がでてきて
そのとき
bベクトルと a+tbベクトルは
直交しているでしょ
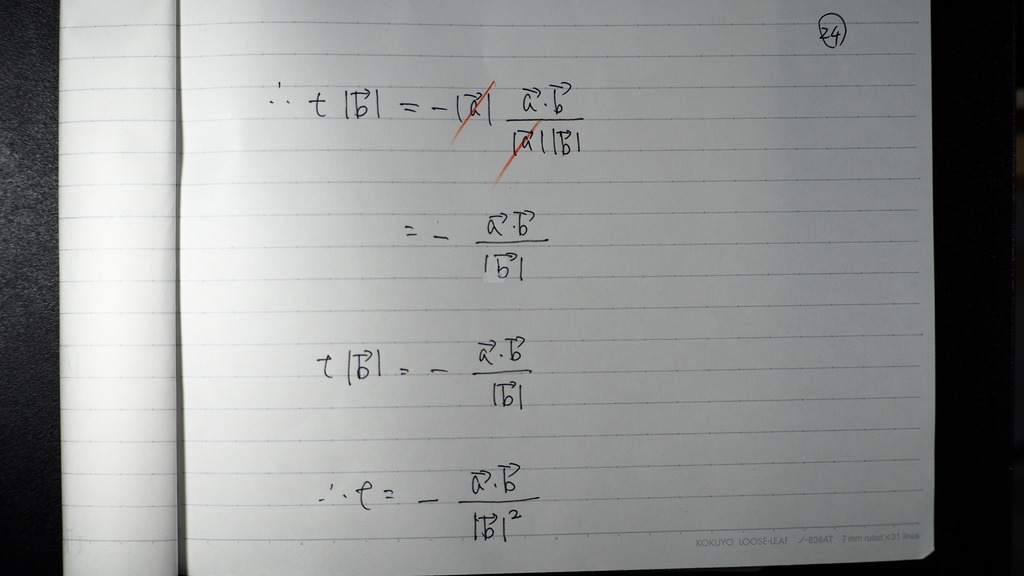
お疲れ様です。
空間座標とベクトル
最大 最小
01
ベクトルに
最小とか
最大とか あるのか?
2つの 大きさが 有 り
方向が 違う ベクトルを
足し合わせるとき
OA +t OB ( 今回は )
一番後ろに
図解付きで 書いておきますが
ベクトルの大きさが
最小になるときの tの値は
ベクトルの大きさが
最小になるとき
bベクトルと a+tb が
直交してることを 証明せよ
02
ベクトルの大きさを
2乗すると
内積で 展開できるので
出てきた 2次関数から
最小値を
割り出し
最小値は 頂点の座標の √をとれば
じゃナイスカ
03
整理すると
二乗で 展開して
tの2次関数になるので
平方完成して
頂点が 下に凸 上に開いてるから
04
最小値は
t が この値の時
05
最小値は
ベクトルの大きさを
2乗で 展開したのだから
√を とれば
こんな感じに
06
t が 最小の時
直交するというのだけれど
内積を 計算するでしょ
07
で ベクトルの
大きさが
最小になるときの
tのあたいを
代入したらば
内積が =0
つまり
直交している
08
るいだい
ベクトルの
大きさの 最小値を
求めるんですが
2乗で
内積に展開して
後で
√を とれば
じゃナイスカ
09
できるだけ
簡単に したいので
置き換えとか
バンバン 使って
10
こうすればさ
少し簡単
さっきと
ほぼ同じ
11
整理して
大きさを
2乗で 展開して
tの2次関数にして
12
平方完成して
13
cベクトルを 元に戻せば
出てきた 頂点のt( 下に凸)
の時の 最小値を
√を取って
14
今度は
x、y とあるけど
行ってみましょう
ベクトルの 大きさを
2乗で 内積の形に
展開して行って
15
計算してくでしょ
16
題意より bベクトルと
cベクトルは 垂直だから
b と c の 内積は =0
式が 少し簡単になって
17
Xと yの 2次関数になってるので
ソレゾレ
平方完成して
最小値になるとき
円になるんだね
18
さいごまで 計算してですよ
19
であるから
x、yが これこれの時
√を とった値が
最小値
20
で
お約束ですが
ベクトルの
最小値って
何なのというわけで
aと bと ベクトルがあって
a + tb は OPになるんだけど
bベクトルの t倍を aベクトルの
終点まで
平行移動して
足すと 成るでしょ
21
OP の 可能性は
無数にあるんだけれど
その中で
一番 短いもの
それが 最小値なんだから
大きさが 一番小さくなるとき
赤い矢印は (OP ベクトル)
どこでしょう
A を通って bベクトルに
平行な tbベクトル上で
Oから そこに おろした
垂線Hと 重なるときでしょ
22
AHベクトルの 大きさが
tbベクトル の大きさと
等しくなるとき
これを
計算すると
23
こんな感じで
24
t=にしたら
図から 最小になるときの
tの値がでてきて
そのとき
bベクトルと a+tbベクトルは
直交しているでしょ
お疲れ様です。
2022年11月20日
22022 大人のさび落とし 空間座標とベクトル 不等式の証明
ベクトルの 内積を 使った
不等式の証明問題
01
こんな感じなんですが

02
内積の 定義式を
使えるように
やってみるとじゃナイスカ
矢線ベクトルと
成分
の 二つがあるでしょ
題意にある式に 似たものが
出てくるじゃナイスカ

03
定義式の 二つは こうだから

04
イコールで結んで
題意よりの
値を 代入すると
コサインθ
こさいんの 値は
基本的に -1 から 1まで
それより 大きいのを
見たよっていうのは
振幅に
倍率が 掛かってるときですよね
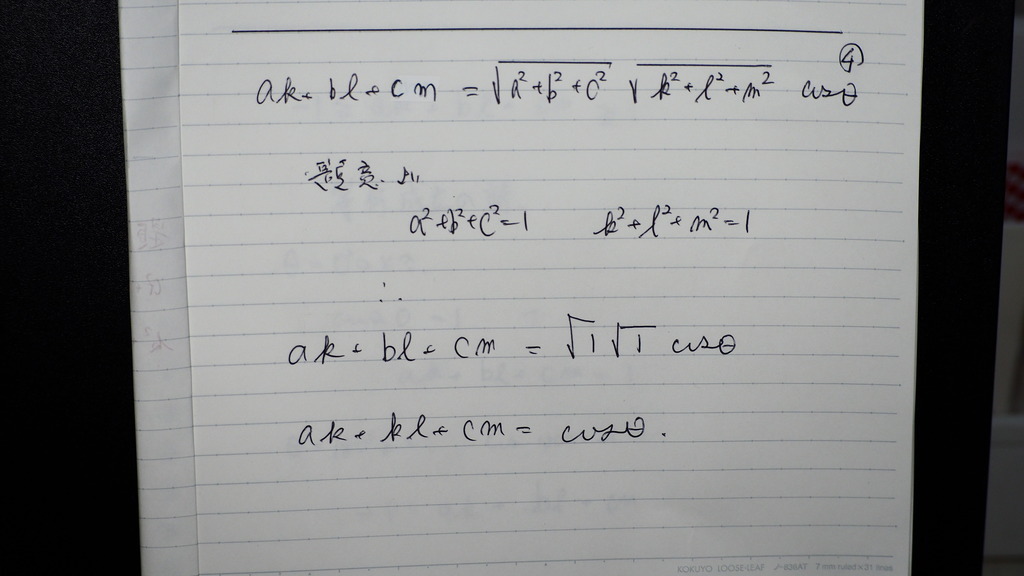
05
こさいんは
x軸への 動径の陰
06
だから
こんな感じに
で
等号成立は
Θが 0度か 180度の時

07
まとめると

08
次は
考え方は
殆ど 同じですが

09
こんな感じにしておいて
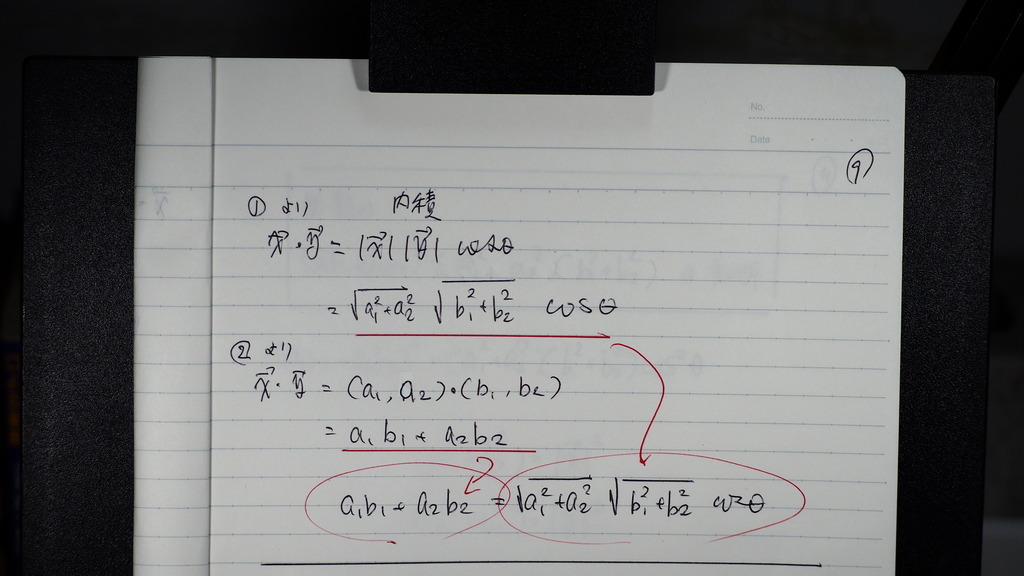
10
辺々二乗 したらば
証明式にちかくなったでしょ
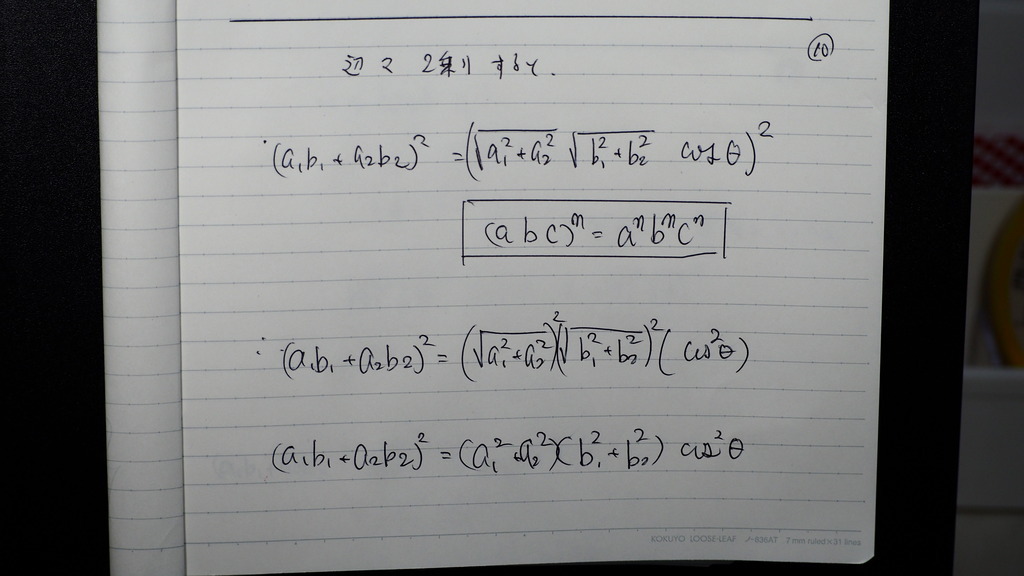
11
この証明なんだからさ
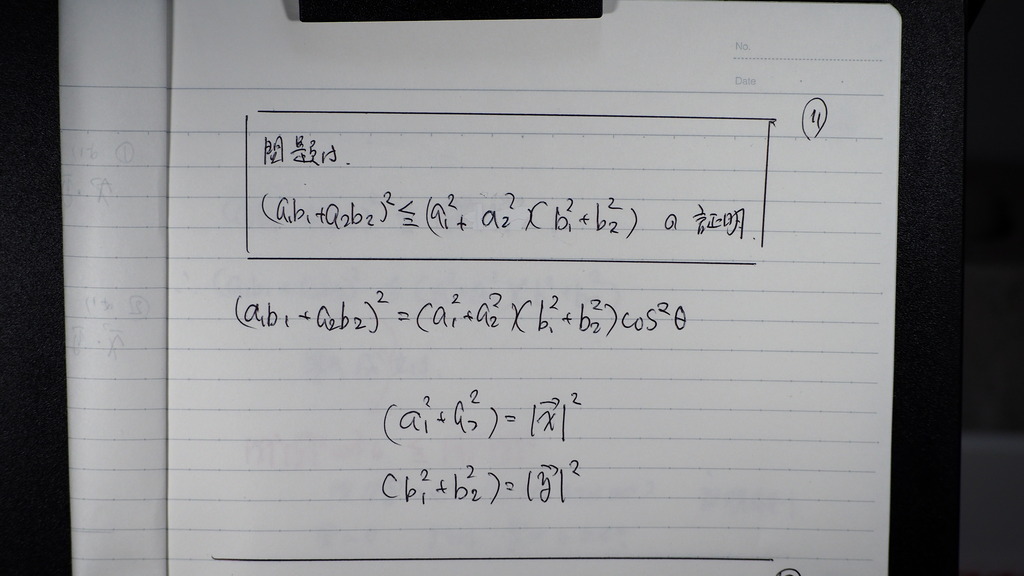
12
こさいんは
二乗したかから
0から1
同じ 大きさに 等倍なら変わらず
同じ大きさに 0.何倍 なら 小さくなる
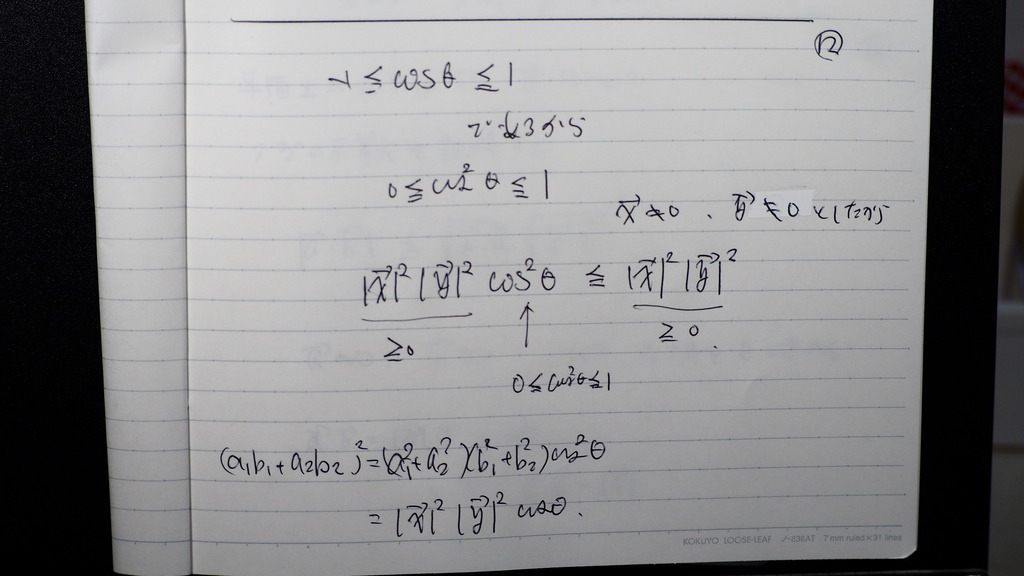
13
等号成立は
二つの ベクトルが 平行のとき
もしくは どちらかが ゼロの時

14
書き方が
少し違うだけなんだね

15
こんな感じでしょ

16
だから
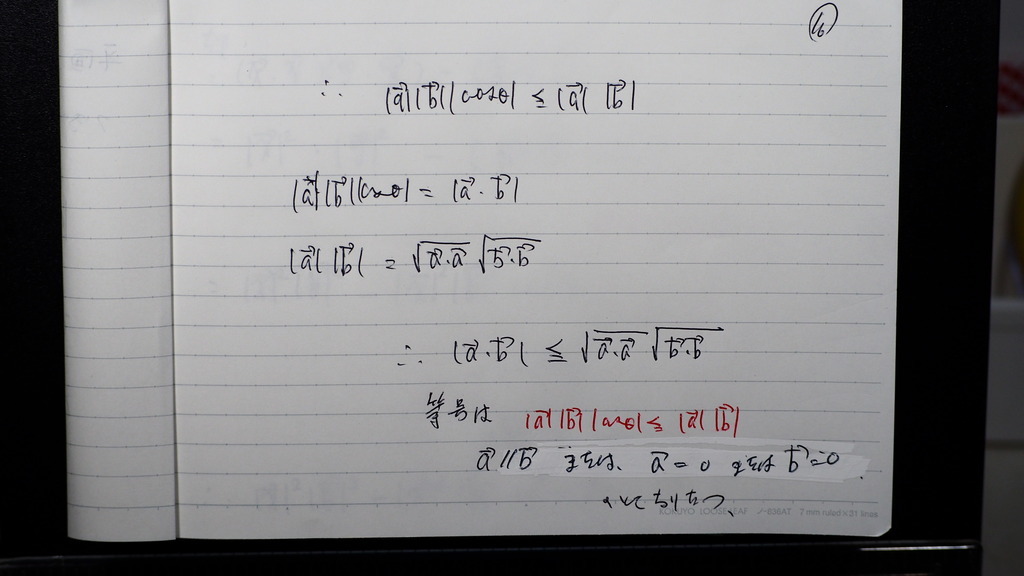
17
殆ど 同じですが
表現の仕方が
違うだけ
あとは
頭を 柔らかくして

18
落ち着いてやっていけば
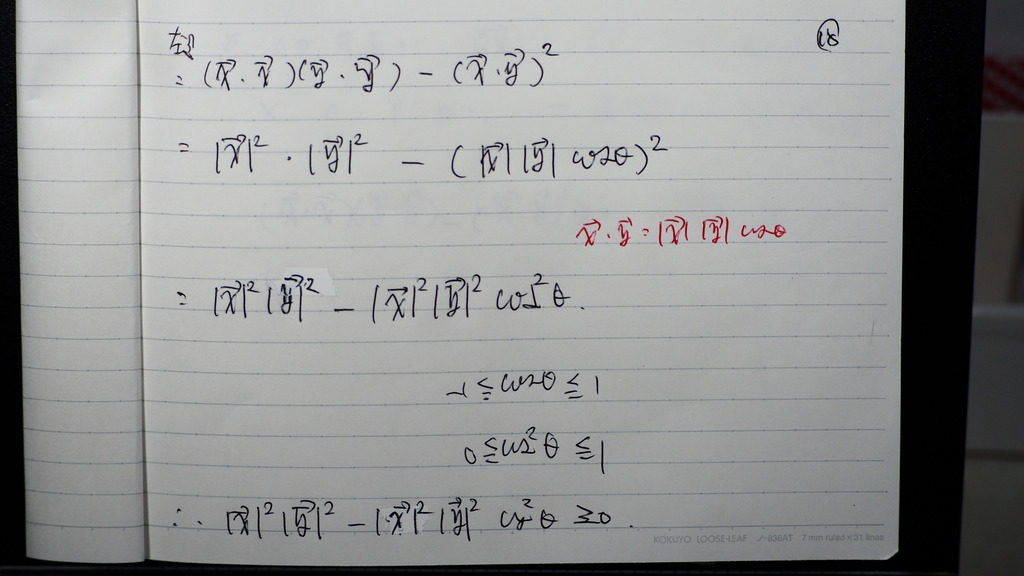
19
こんな感じになるので

20
特に 等号成立の時は
こんなです

お疲れ様です。
不等式の証明問題
01
こんな感じなんですが
02
内積の 定義式を
使えるように
やってみるとじゃナイスカ
矢線ベクトルと
成分
の 二つがあるでしょ
題意にある式に 似たものが
出てくるじゃナイスカ
03
定義式の 二つは こうだから
04
イコールで結んで
題意よりの
値を 代入すると
コサインθ
こさいんの 値は
基本的に -1 から 1まで
それより 大きいのを
見たよっていうのは
振幅に
倍率が 掛かってるときですよね
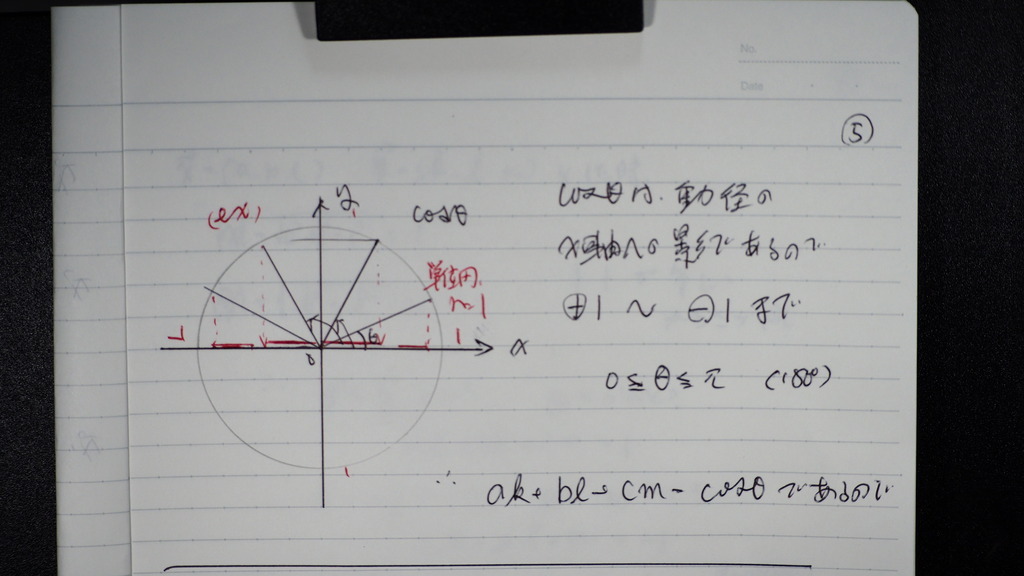
05
こさいんは
x軸への 動径の陰
06
だから
こんな感じに
で
等号成立は
Θが 0度か 180度の時
07
まとめると
08
次は
考え方は
殆ど 同じですが
09
こんな感じにしておいて
10
辺々二乗 したらば
証明式にちかくなったでしょ
11
この証明なんだからさ
12
こさいんは
二乗したかから
0から1
同じ 大きさに 等倍なら変わらず
同じ大きさに 0.何倍 なら 小さくなる
13
等号成立は
二つの ベクトルが 平行のとき
もしくは どちらかが ゼロの時
14
書き方が
少し違うだけなんだね
15
こんな感じでしょ
16
だから
17
殆ど 同じですが
表現の仕方が
違うだけ
あとは
頭を 柔らかくして
18
落ち着いてやっていけば
19
こんな感じになるので
20
特に 等号成立の時は
こんなです
お疲れ様です。
2022年11月16日
22021 大人のさび落とし 空間座標とベクトル ベクトルのなす角
ベクトルの なす角
なす角 と言うのは
二つの ベクトルがあるとき
ベクトルを 平行移動して
始点同士を 合わせたときに
できる 角度 のことです。
01
もんだい
座標が 与えられてます
空間だけど
角BAC と 三角形 ABC の
面積を 求めよ

02
まずは
余弦定理で
行ってみますが
三角形の 三辺の 長さが
分かってるときは
余弦定理で
座標が分かってるので
2点間の距離 空間 で
長さを 出しといて
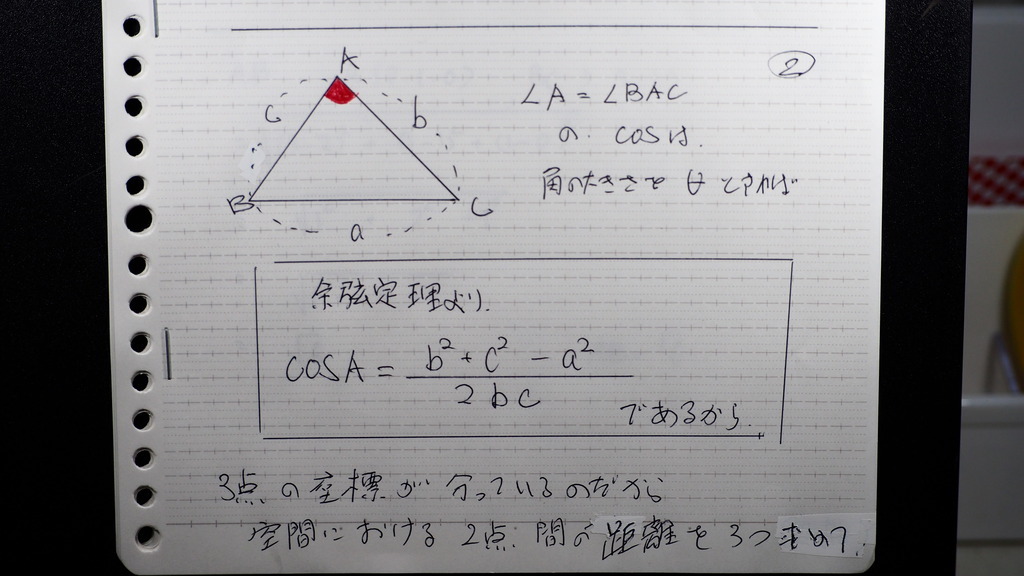
03
辺ABは

04
√6
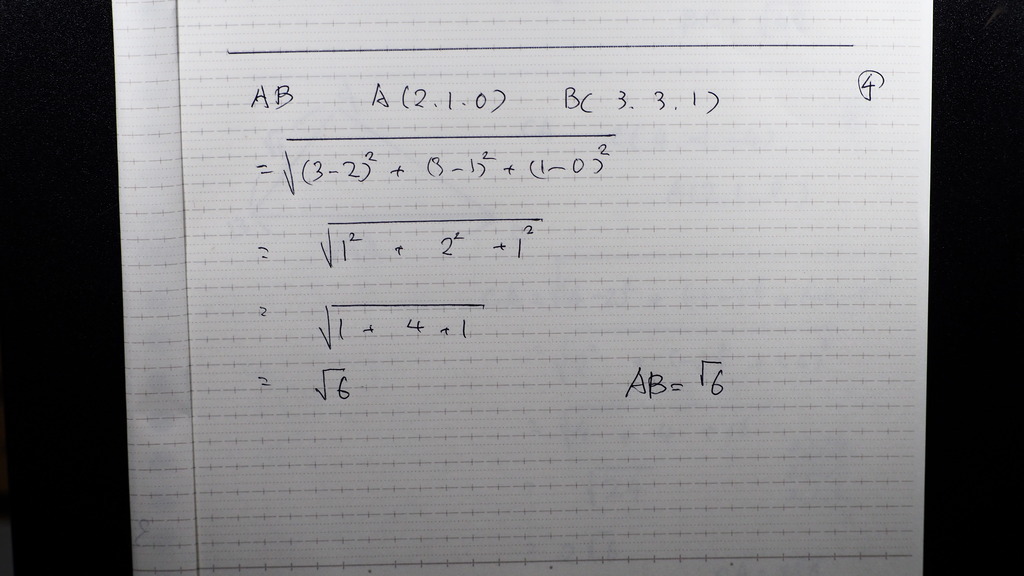
05
辺BCは √42
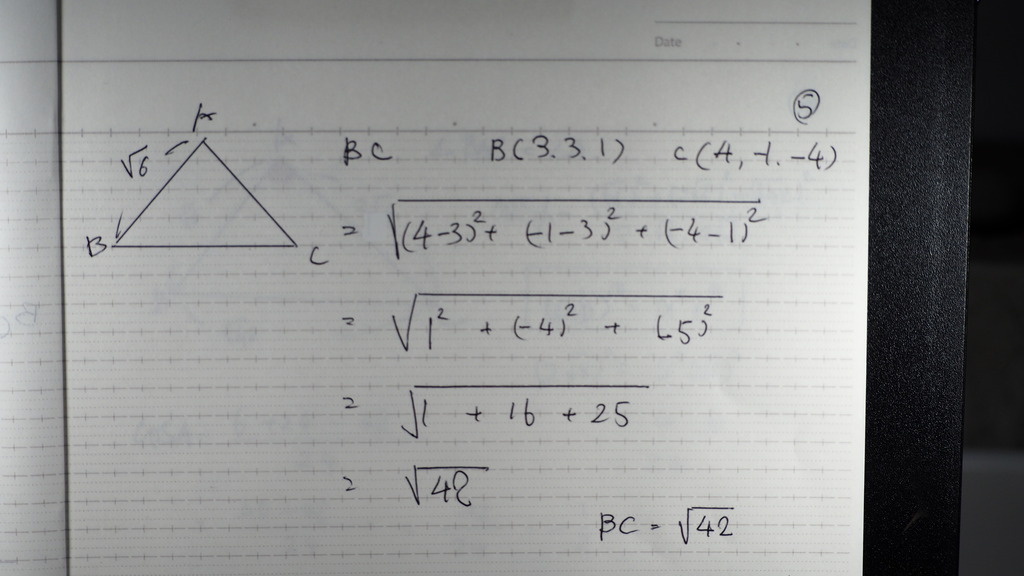
06
辺CAは
2√6

07
余弦定理に
代入して
COSの 値で
出て来ますが
-1/2
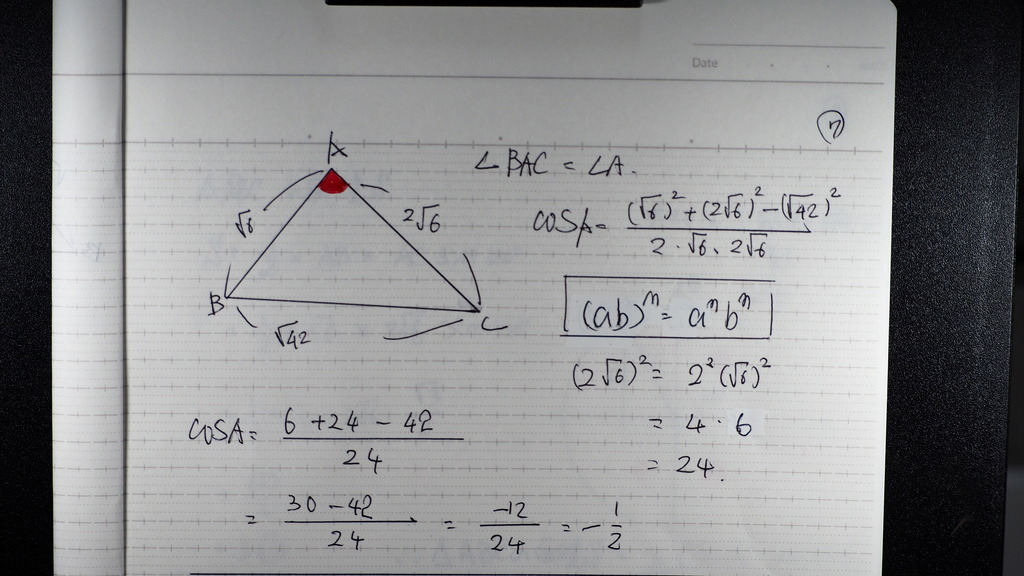
08
なす角はゼロ から 180 度 (パイ ラジアン)
コサインは 動径の
x軸への陰で
座標上
ゼロの時 ぜろ度
ゼロ から 90度 未満まで プラス
90度 の時 ぜろ
90度 から 180度 未満の時
マイナス
180度 の時 -1
なす角は 120度
三角形の 面積に時は
なす角の 斜辺のサイン 成分が
高さなので
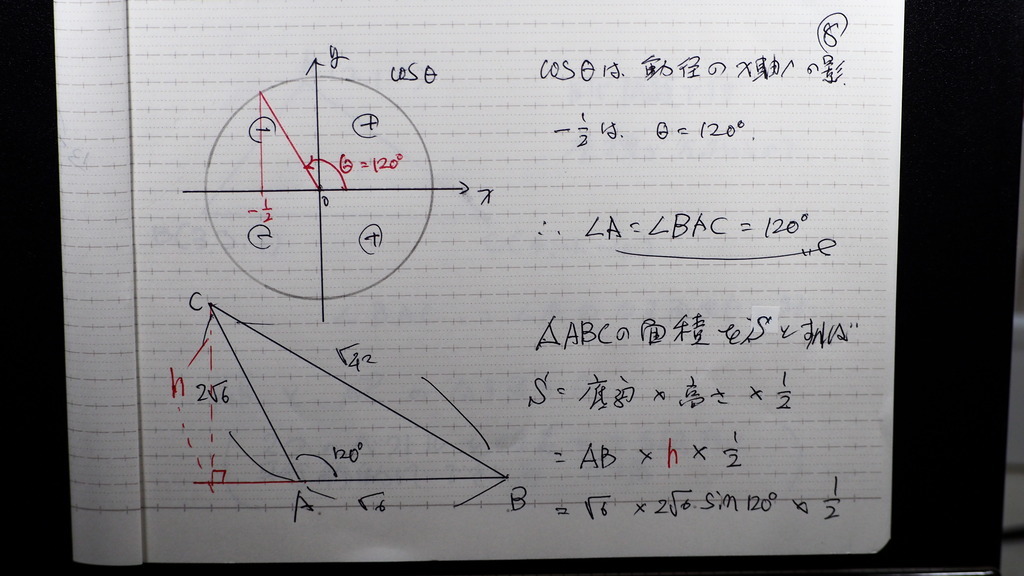
09
サイン120度は
√3/2
面積は
3√3

10
今の問題を
今度は
ベクトルの内積を使って
解くと
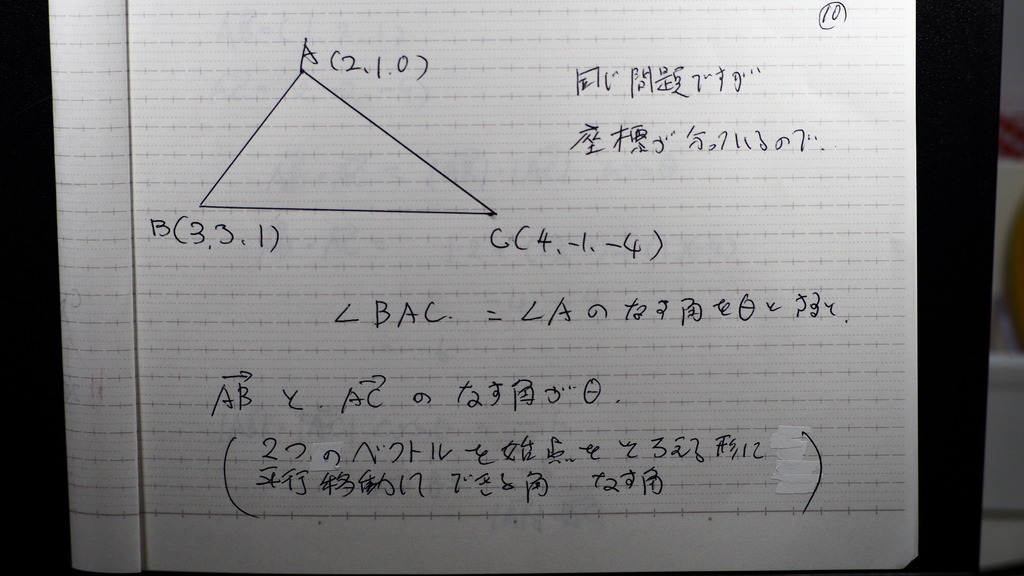
11
まず
なす角が
ここン所 であるから
2つのベクトル
AB AC を
成分で
計算して
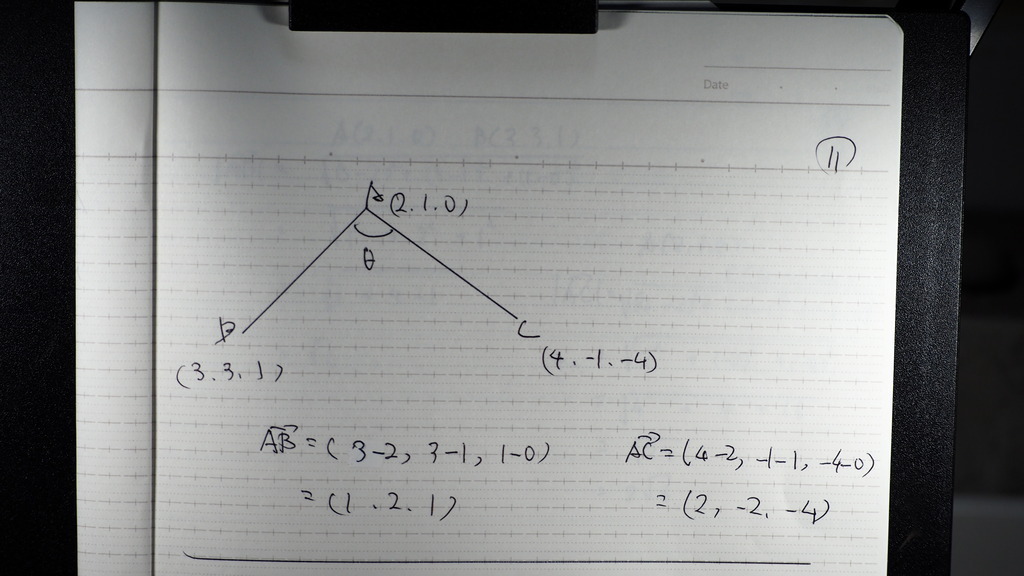
12
内積の定義式は
こんなだから
成分の方から
内積が -6
もう一つの 定義式から
COS Θ が こんなでしょ
分母の 絶対値は
2点間の 距離で求めて
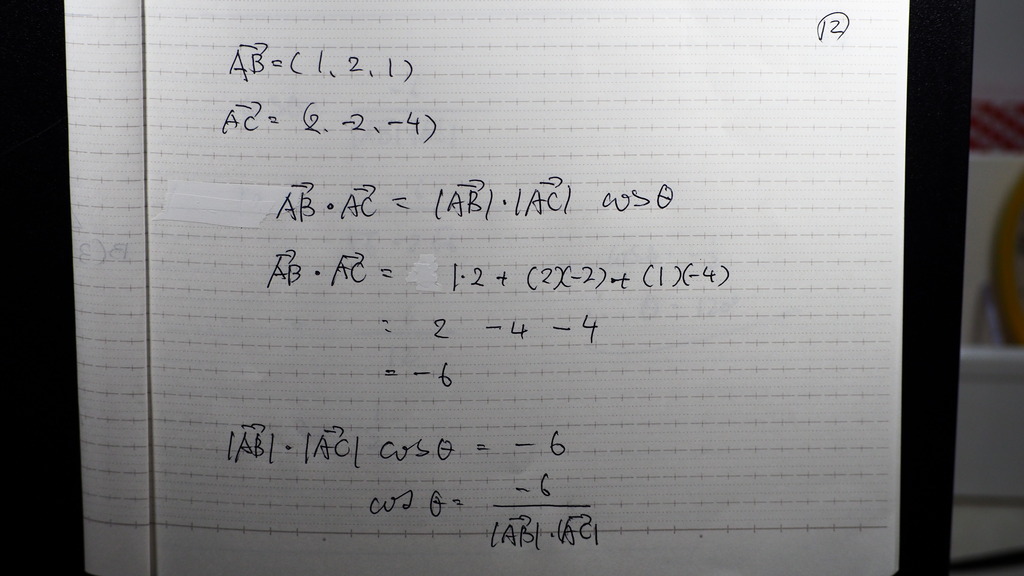
13
こんな感じになるので
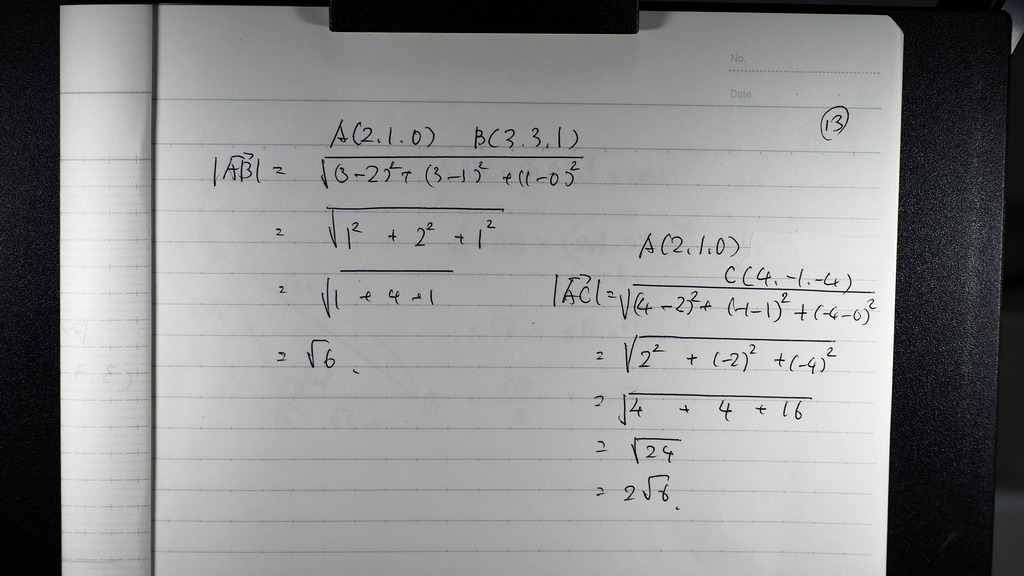
14
なす角が出て来て
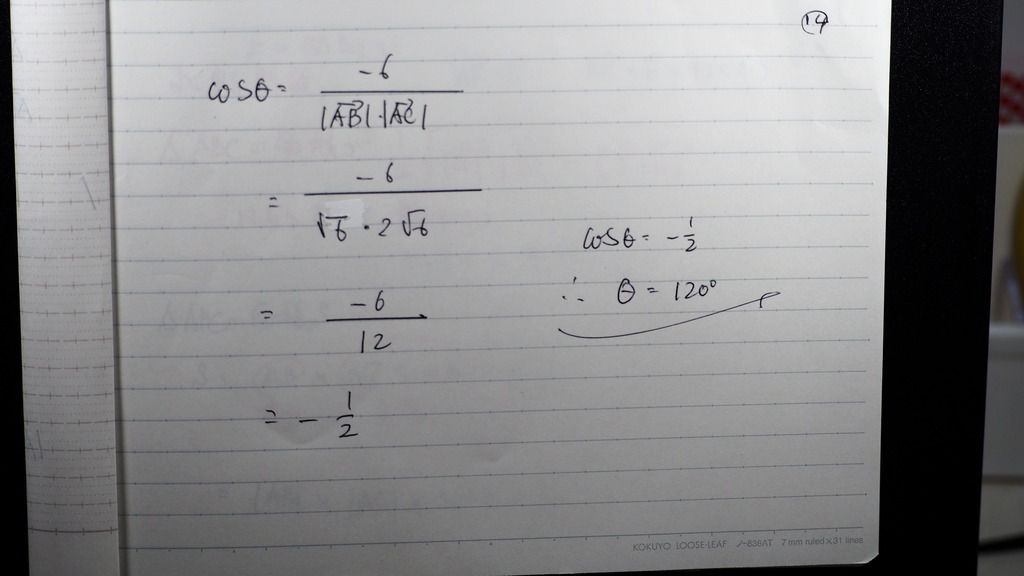
15
面積も
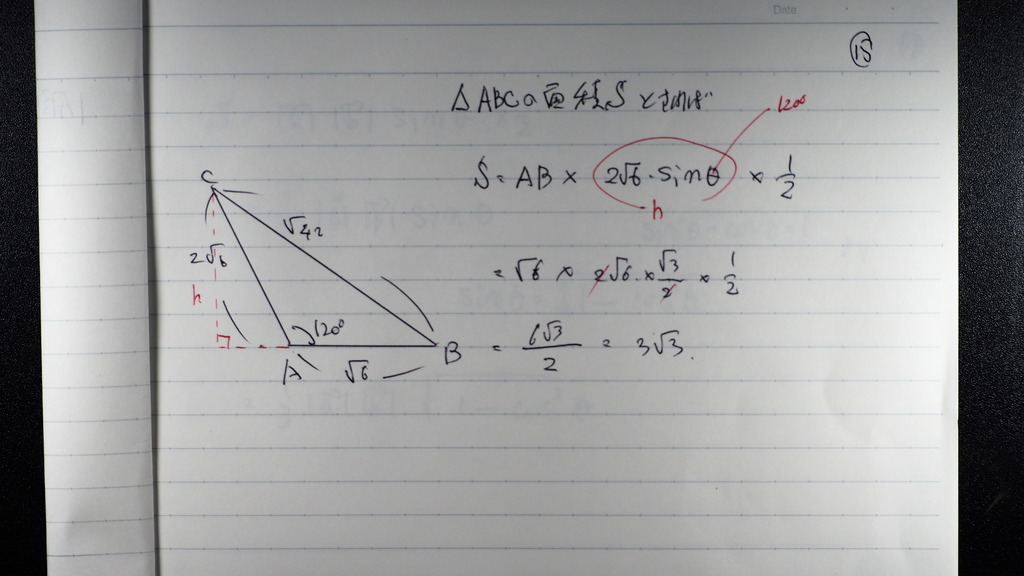
16
ところで
ここんとこの問題で
これが
非常に 良く 出題される
面積が
こんな感じで 書けることを
いえ
と言うんですが
さっきの
上の式から
少し いじってくと
なるですよ

17
底辺 AB で 書いてたけど
大きさと言う意味で
ベクトルに絶対値を付けて
ABを aベクトル
ACを bベクトルとすれば
こんな感じに なる
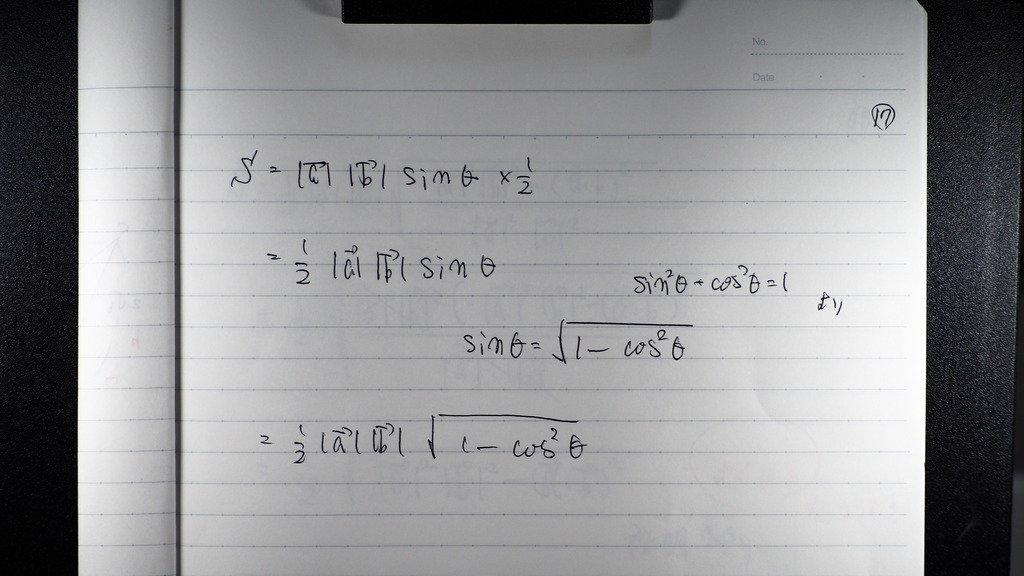
18
内積の 定義式の 変形で
COS θは
こんなだからさ
で
√の 外の 絶対値を
√の中に 入れれば
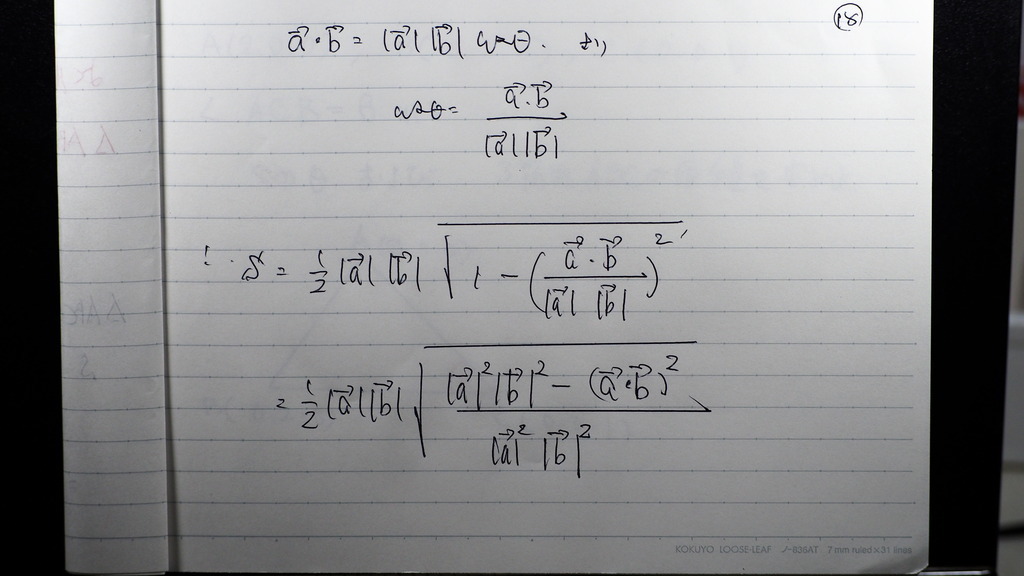
19
なったデショ

20
類題
内積を 使って
解いてきますか
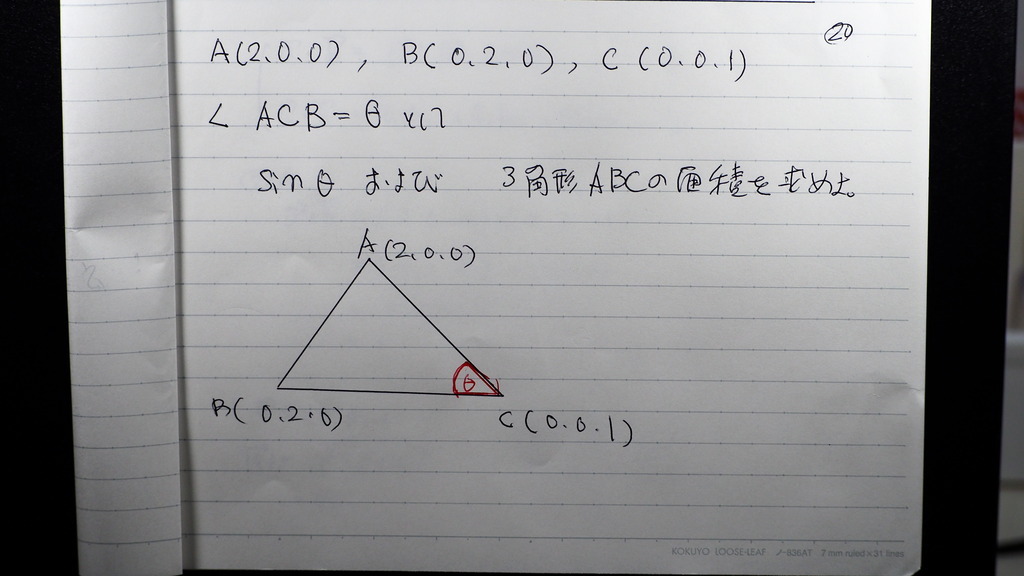
21
aベクトル bベクトル
を
こんな風に設定して
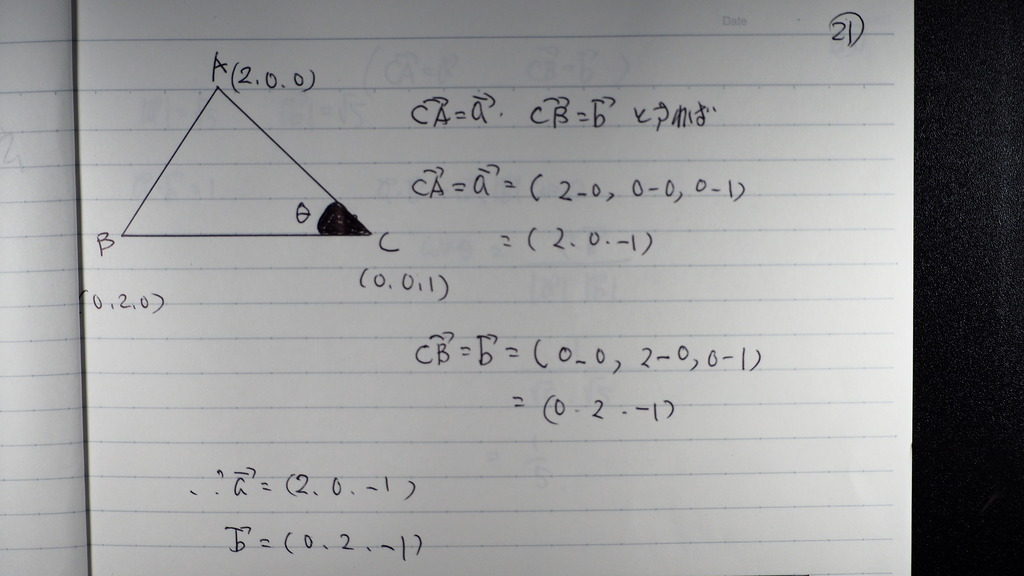
22
内積の定義式②
成分の方から
内積は 1
成分が分かってるので
ベクトルの
絶対値 ( 大きさ )を 求めて
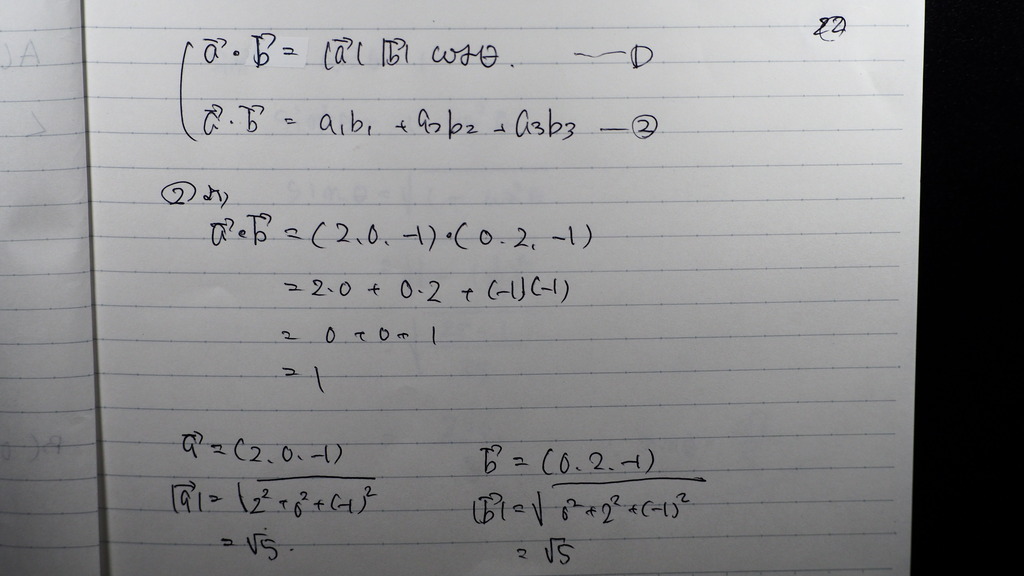
23
COS θは
1/5

24
題意では
サイン角で 求めよ なので
こんな感じに
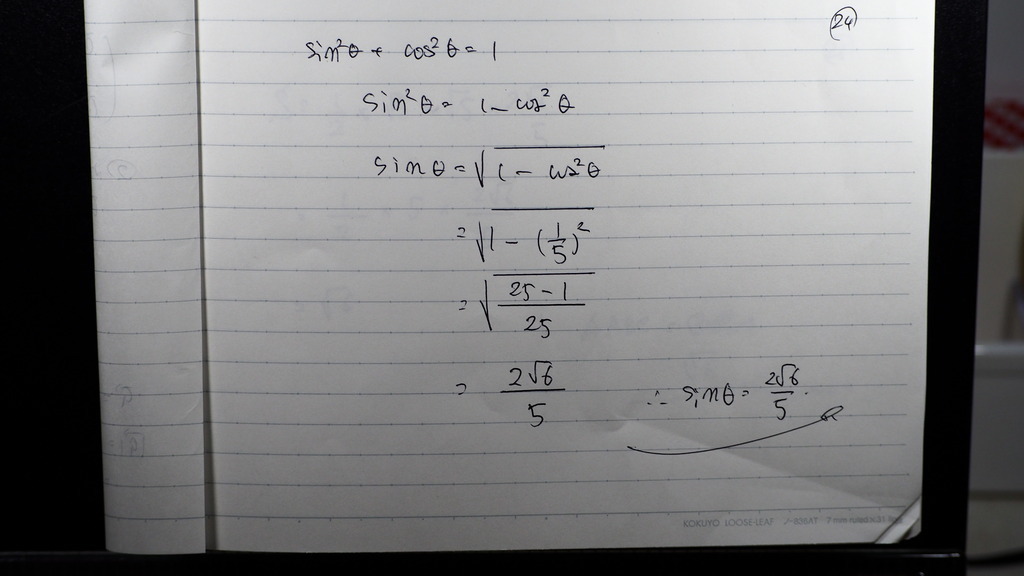
25
サイン角が出てれば
ベクトルの 絶対値の 積に
なす角のサイン角
それを 2で割れば
1/2 を 掛けるとも言いますが
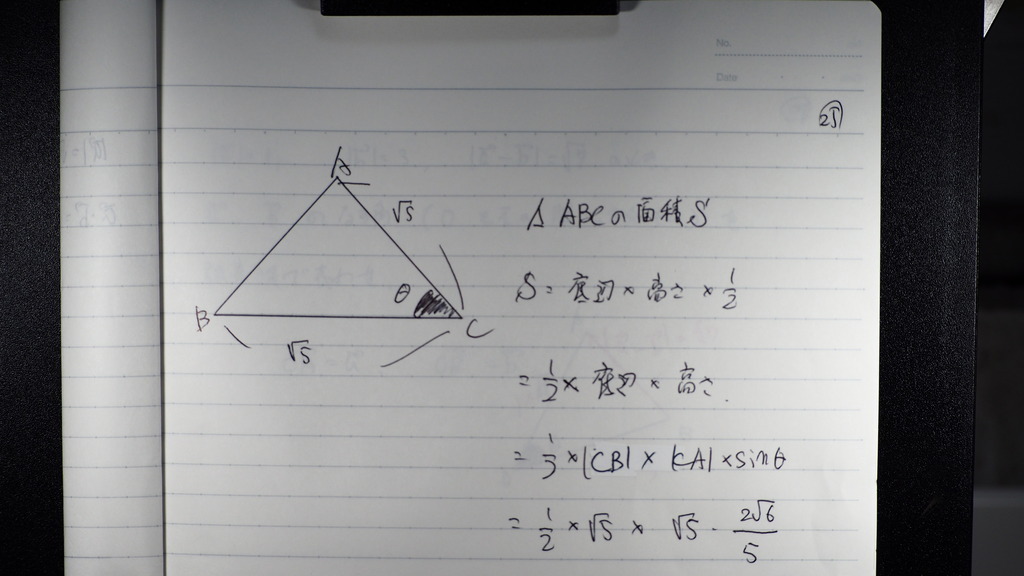
26
こんな感じで
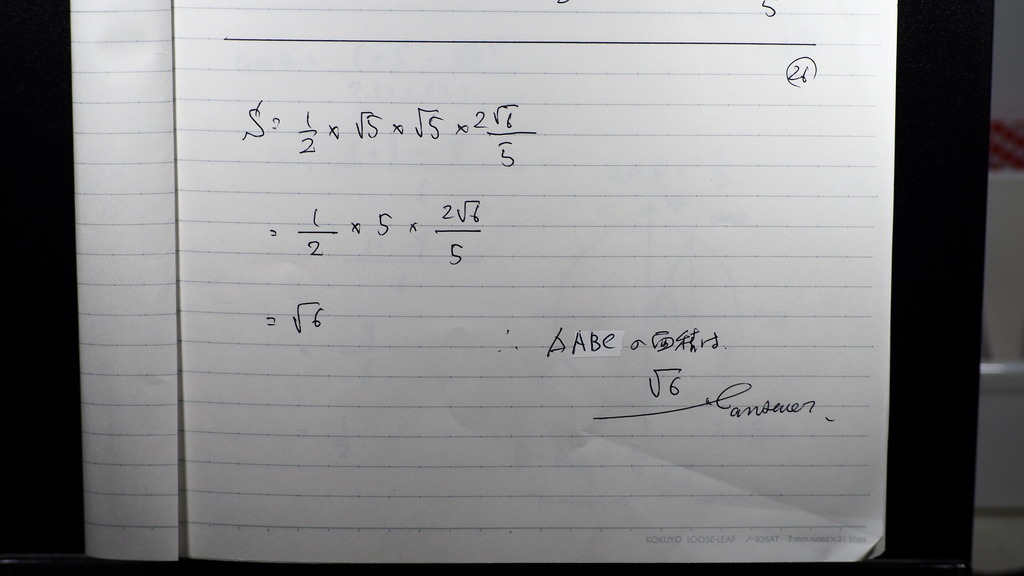
27
問題を 読んでね
図にしたら
コンななんですが
いいですか
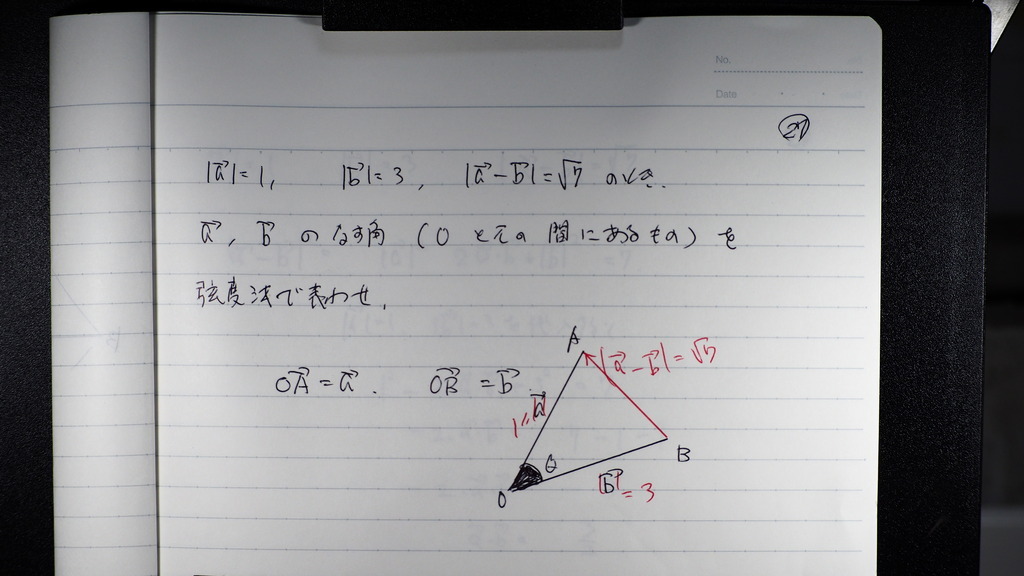
28
余弦定理で
弧度法で 表して
こんな感じで
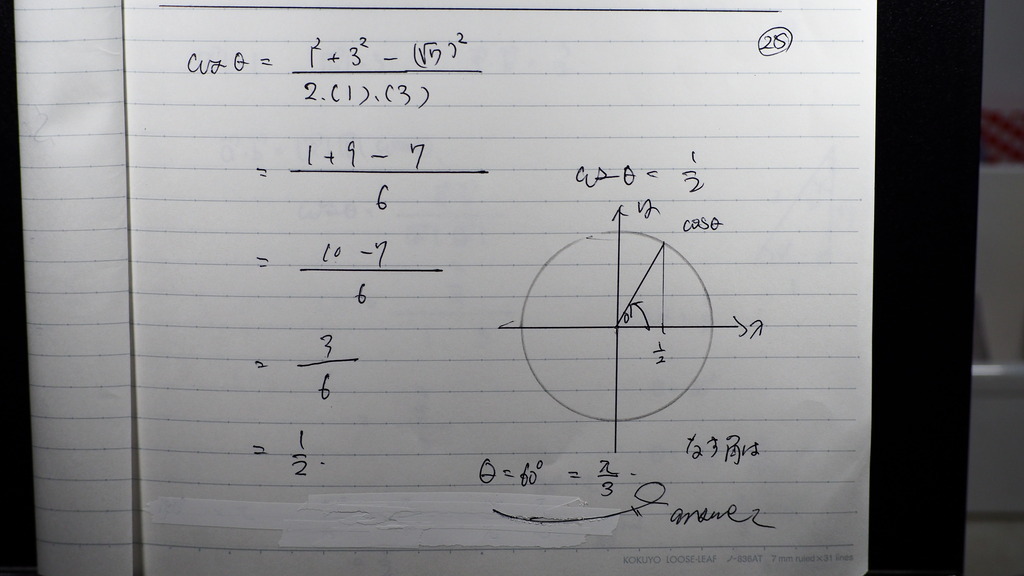
29
別の 解き方では
式変形してくとさ
内積が 出てきた
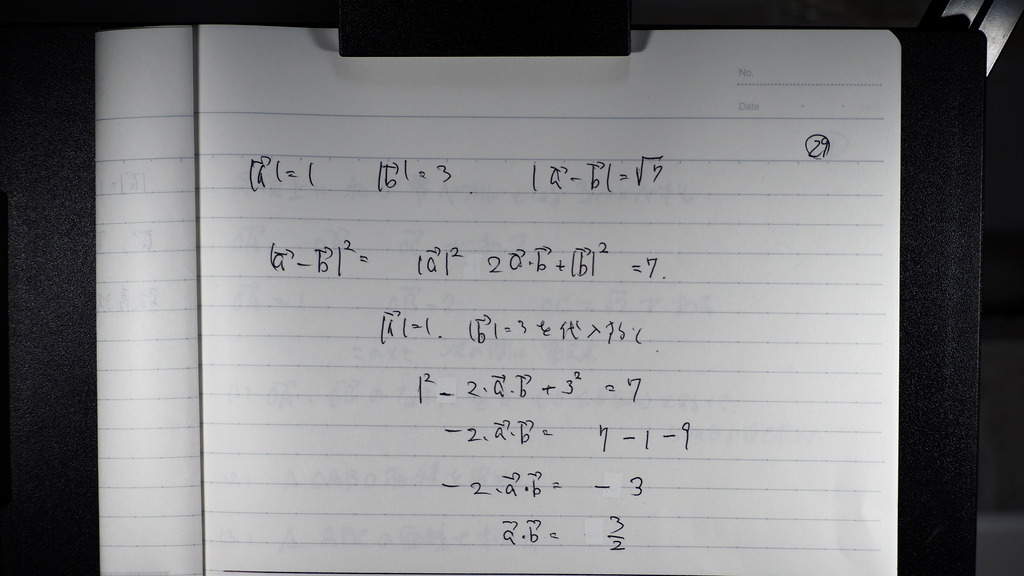
30
絶対値も わかってるので
COSΘは
1/2
であるので
180度は パイ
1度は パイ/180度(ラジアン)
60度は ?
(60×パイ)/ 180 単位ラジアン
パイ/3
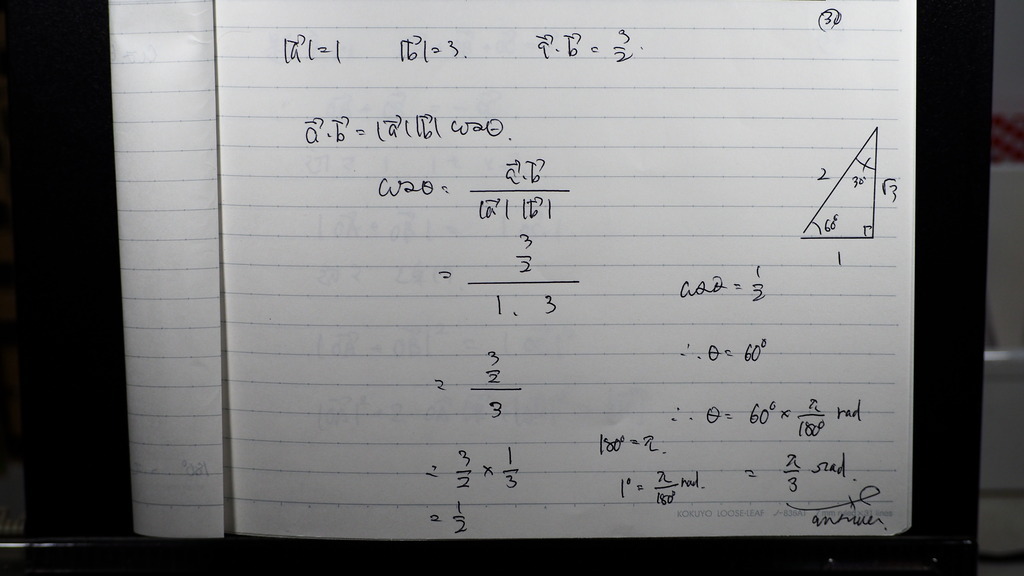
31
問題
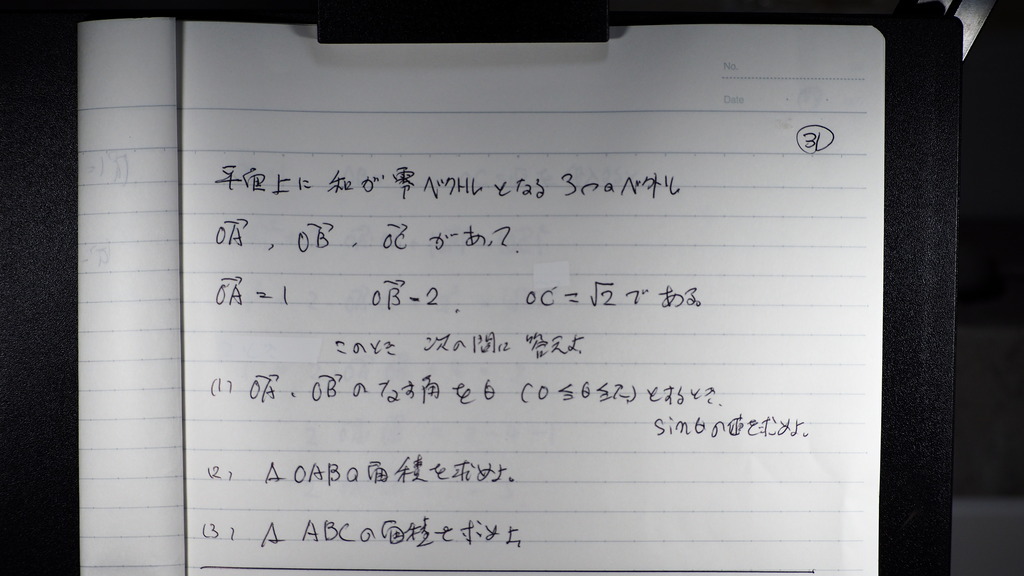
32
式変形してくとさ
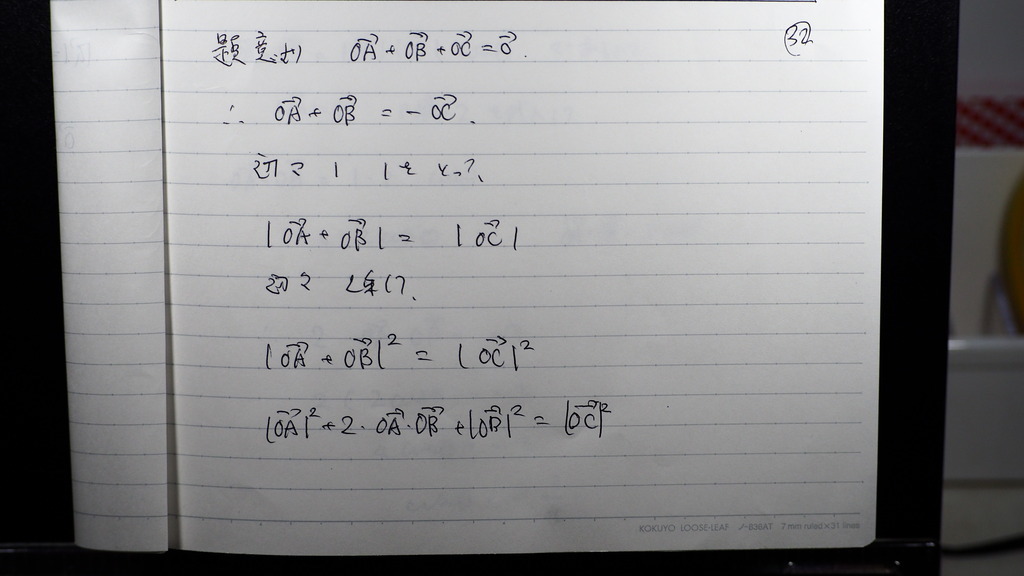
33
分かってるとこ 代入して

34
もうすこし
だいにゅうして
COSが出たので

35
サイン角は
で
なす角は 0から パイ(180度)
のものとするので
sigは 0から180度未満
までは プラス
180度から360未満が マイナス
であるので
なす角は 0から パイ(180度)
のものとするより
プラスの時だけ
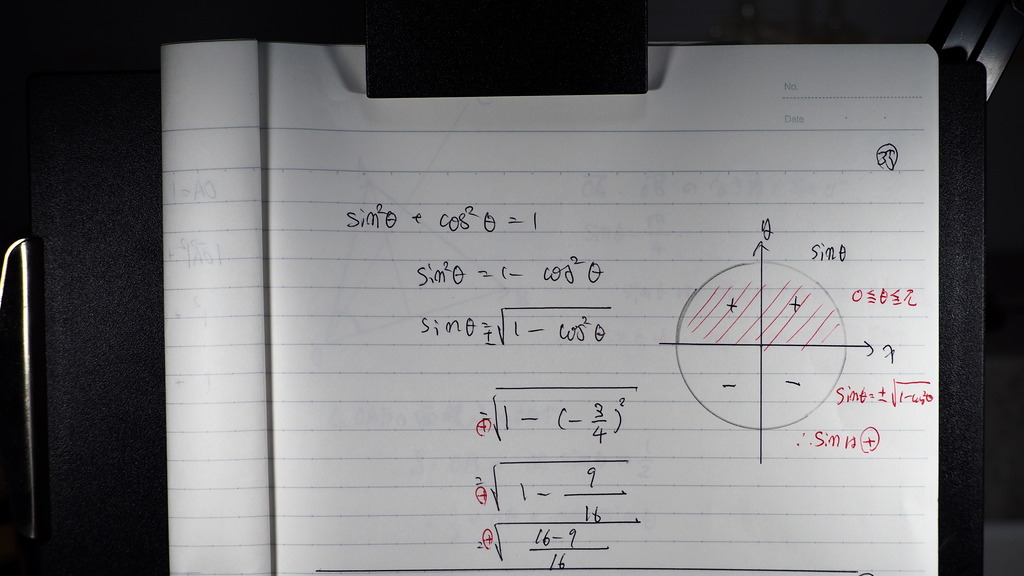
36
こんな感じで
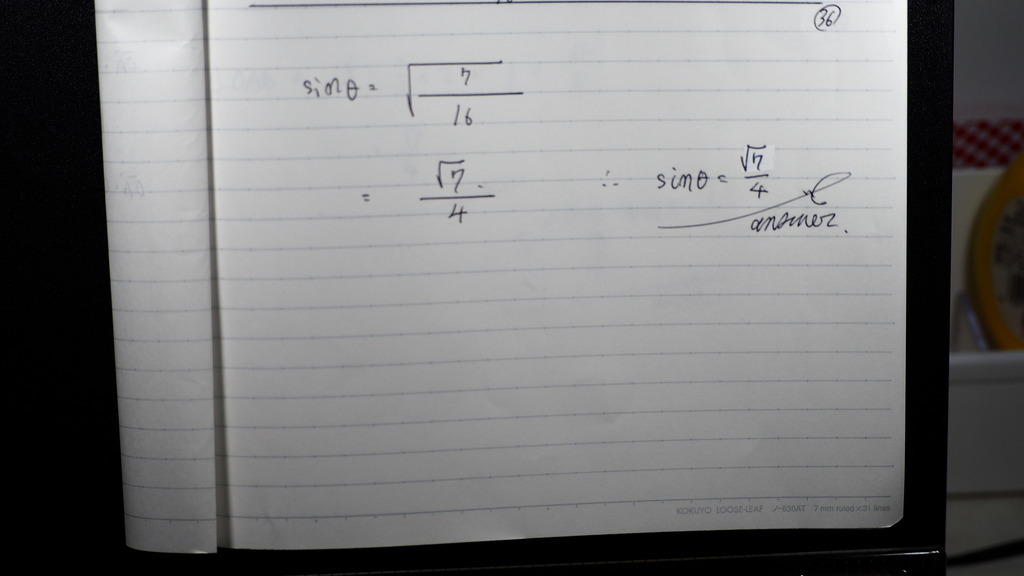
37
なす角の sin
と
なすベクトルのおおきさ
が
分かってるので
三角形OABの面積は
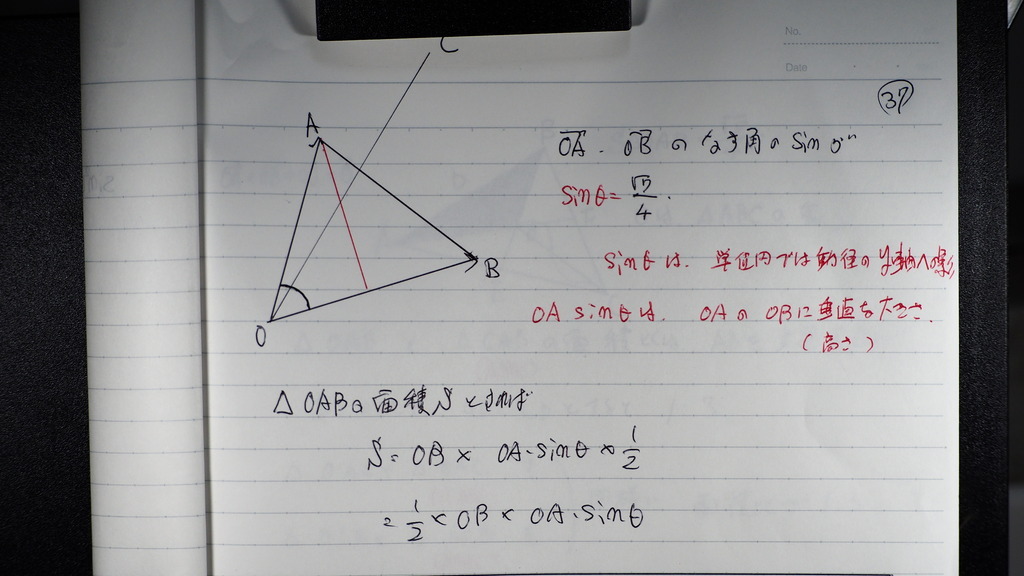
38
こんな感じで
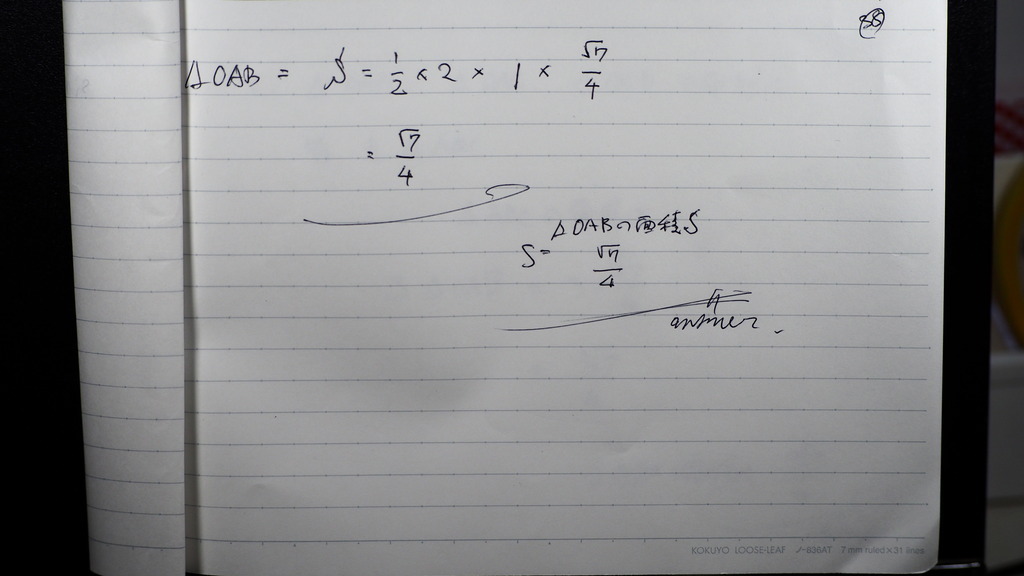
39
点Oは
題意より 重心
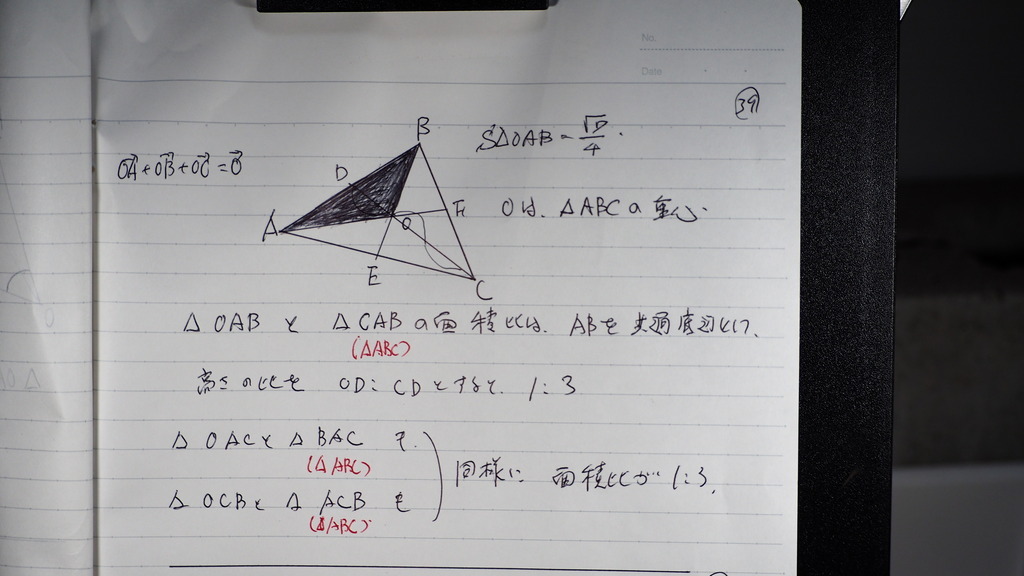
40
であるから
三角形ABCの面積は

お疲れ様です。
なす角 と言うのは
二つの ベクトルがあるとき
ベクトルを 平行移動して
始点同士を 合わせたときに
できる 角度 のことです。
01
もんだい
座標が 与えられてます
空間だけど
角BAC と 三角形 ABC の
面積を 求めよ
02
まずは
余弦定理で
行ってみますが
三角形の 三辺の 長さが
分かってるときは
余弦定理で
座標が分かってるので
2点間の距離 空間 で
長さを 出しといて
03
辺ABは
04
√6
05
辺BCは √42
06
辺CAは
2√6
07
余弦定理に
代入して
COSの 値で
出て来ますが
-1/2
08
なす角はゼロ から 180 度 (パイ ラジアン)
コサインは 動径の
x軸への陰で
座標上
ゼロの時 ぜろ度
ゼロ から 90度 未満まで プラス
90度 の時 ぜろ
90度 から 180度 未満の時
マイナス
180度 の時 -1
なす角は 120度
三角形の 面積に時は
なす角の 斜辺のサイン 成分が
高さなので
09
サイン120度は
√3/2
面積は
3√3
10
今の問題を
今度は
ベクトルの内積を使って
解くと
11
まず
なす角が
ここン所 であるから
2つのベクトル
AB AC を
成分で
計算して
12
内積の定義式は
こんなだから
成分の方から
内積が -6
もう一つの 定義式から
COS Θ が こんなでしょ
分母の 絶対値は
2点間の 距離で求めて
13
こんな感じになるので
14
なす角が出て来て
15
面積も
16
ところで
ここんとこの問題で
これが
非常に 良く 出題される
面積が
こんな感じで 書けることを
いえ
と言うんですが
さっきの
上の式から
少し いじってくと
なるですよ
17
底辺 AB で 書いてたけど
大きさと言う意味で
ベクトルに絶対値を付けて
ABを aベクトル
ACを bベクトルとすれば
こんな感じに なる
18
内積の 定義式の 変形で
COS θは
こんなだからさ
で
√の 外の 絶対値を
√の中に 入れれば
19
なったデショ
20
類題
内積を 使って
解いてきますか
21
aベクトル bベクトル
を
こんな風に設定して
22
内積の定義式②
成分の方から
内積は 1
成分が分かってるので
ベクトルの
絶対値 ( 大きさ )を 求めて
23
COS θは
1/5
24
題意では
サイン角で 求めよ なので
こんな感じに
25
サイン角が出てれば
ベクトルの 絶対値の 積に
なす角のサイン角
それを 2で割れば
1/2 を 掛けるとも言いますが
26
こんな感じで
27
問題を 読んでね
図にしたら
コンななんですが
いいですか
28
余弦定理で
弧度法で 表して
こんな感じで
29
別の 解き方では
式変形してくとさ
内積が 出てきた
30
絶対値も わかってるので
COSΘは
1/2
であるので
180度は パイ
1度は パイ/180度(ラジアン)
60度は ?
(60×パイ)/ 180 単位ラジアン
パイ/3
31
問題
32
式変形してくとさ
33
分かってるとこ 代入して
34
もうすこし
だいにゅうして
COSが出たので
35
サイン角は
で
なす角は 0から パイ(180度)
のものとするので
sigは 0から180度未満
までは プラス
180度から360未満が マイナス
であるので
なす角は 0から パイ(180度)
のものとするより
プラスの時だけ
36
こんな感じで
37
なす角の sin
と
なすベクトルのおおきさ
が
分かってるので
三角形OABの面積は
38
こんな感じで
39
点Oは
題意より 重心
40
であるから
三角形ABCの面積は
お疲れ様です。
2022年10月24日
22020大人のさび落とし ベクトルの垂直
ベクトルの垂直
01
ベクトルの 垂直を
証明する問題
内積を 使うんですが
=0
02
矢線ベクトルか
成分ベクトルか
03
まず 矢線ベクトルから
準備として
OA OB OC
を それぞれ a,b.c
ベクトル
題意を そのまま
条件式にしていくと
04
まず 一個目の 垂直条件から➀
05
二個目の 垂直条件から②
06
本題は
OC ⊥ AB
であるから
OCと AB の 内積を
計算すると
07
整理して
➀②を 代入して
=0
垂直だった
08
今のを
今度は 成分ベクトルで
やってみると
まず 準備として
空間座標
位置ベクトル
09
ベクトルの 成分計算
と
条件式➀の 成分の内積
10
展開して
輪環の順に
➀
11
条件式②を
成分 内積の計算
12
整理して
②
13
本題の
内積を
成分で
14
成分ベクトルの計算をしていって
ちょっとここで止めておいて
15
今度は
➀②指揮を足し合わせると
それを 整理すると
③式
16
③をさっき 止めといた所へ
代入したらば
=0
であるから
垂直だった
17
これは
期末試験で
ここが 範囲の時は
そのまんま
出ることが多い問題
18
こんな感じで
19
2つの ベクトルの 垂直で
大きさが 14のベクトル
を 求めよ
2つのベクトルは 成分で
与えられてると
20
題意から
式が
3本
わかんないとこも 3つ
題意を 計算式に
成分の 内積デショ
21
もう一個 成分の
内積デショ
それと
大きさ
22
連立が出て来て
➀から
②から
23
zが 出てきたので
24
求めるベクトルは
こんな感じで
25
今度はさ
ちょっと
勉強中の時は
ここで
せんべと かかじって
コーヒーなんかどう
せんべには
お茶のほうが
あ^^
26
座標はさ
こんなデショ
立方体だからさ
OD ABは こんなで
27
問題は ここ
PQができれば
もう 半分以上解けた
28
PはさXY 平面
直角2等辺三角形を つかって
xがt なら yは a-t
z=0
29
Qは OD上だから
x=sとすれば
y=s、z=s
Q(s,s,s)
30
PQベクトルは
こうだから
➀②を 計算すれば
31
➀より
Sが a/3
32
②より
tが a/2
33
PQの全貌が わかったらば
大きさを
計算して
34
こんな感じに
お疲れ様です。
2022年10月20日
22019 大人のさび落とし ベクトルのおおきさ
大人のさび落とし
ベクトルの大きさ
01
ベクトルの 和の 大きさが
こんな感じの
等式に 成ってることを
証明せよ
なので
左辺を 変形して
右辺に持って行こうと
02
図にすると
こんな感じで
03
大きさの 二乗は
同じ ベクトルの 内積
に成ってるので
分配の法則
交換の法則
04
整理してきますと
赤アンダーライン のとこの
計算を
具体的に
やってみると
05
こんな感じに
06
これも ほぼ 同じ
07
ここんとこは
直角だから
=0
08
これらを
一つ前の式に 代入して
ここまでは
大きさの 二乗で来てるから
09
√すると
左辺
これがさ
=右辺だから
オッケイ
10
問題
11
大きさは 絶対値
絶対値を2乗すれば
同じ ベクトルの 内積
また あとで
√ しましょう
12
こんな感じで
題意から わかってるとこ
具体的に 数値を 入れて
13
整理して
14
元に 戻すと
こうです
15
問題
これはさ
ベクトルの 設定の仕方で
半分 後は 計算
16
こんな感じに ベクトルを
設定できれば
あとは
計算
左辺
17
右辺
18
右辺は こんなだから
さっきの
左辺と同じ
証明終わり
19
昔むかし そのむかし
九州産業大学の入試問題
20
まずさ
条件式を 辺々二乗して
また
あとで √する方法で
左辺から
内積に 持ち込んで
展開してくと
21
左辺二乗は こんなだね
右辺二乗も
22
こんな感じに
23
ところで
与えられてる ベクトルの
絶対値2乗は
24
代入したらば
(1)
a,bの内積が
kで出て来て
25
まず かっこ1は いいと
26
k二乗だけど
分母にも
kがあるんで
2次関数の グラフが使えない
そこで
相加平均は 相乗平均に
等しいか それより 大きい
で
最小値を 求めると
27
最小になるときは k=1
最小値
1/2
その時の なす角は
28
Θ は ゼロ 以上 パイ 以下
60度
お疲れ様です。