新規記事の投稿を行うことで、非表示にすることが可能です。
2023年01月12日
22038 大人のさび落とし 平面図形(1)
大人のさび落とし
空間座標とベクトル
ベクトルの図形への応用
平面図形(1)
01
その前に
予備知識を
引算足し算
実数倍

02
同一 平面
垂直条件

03
分点 長さ なす角

04
三角形の面積
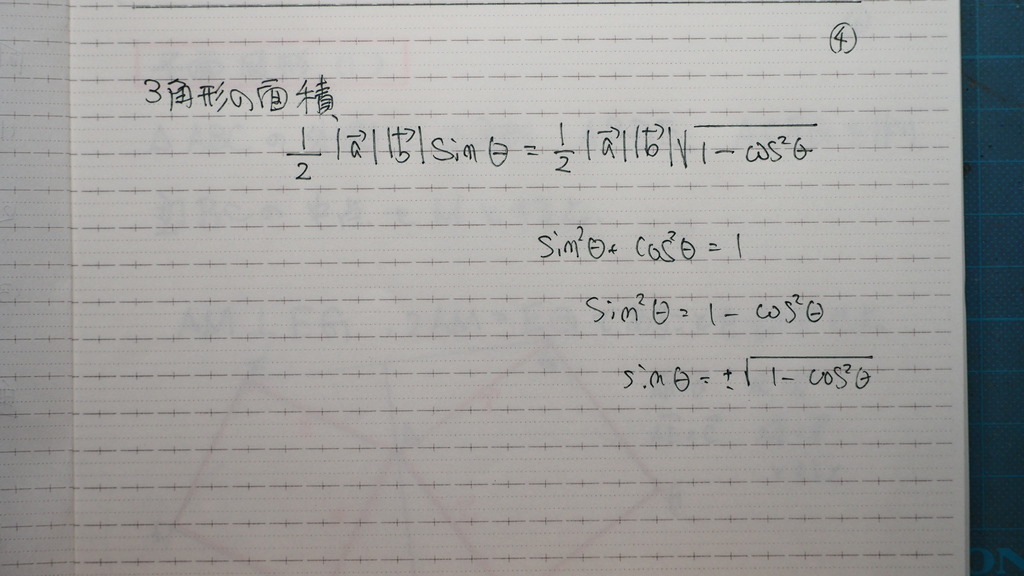
05
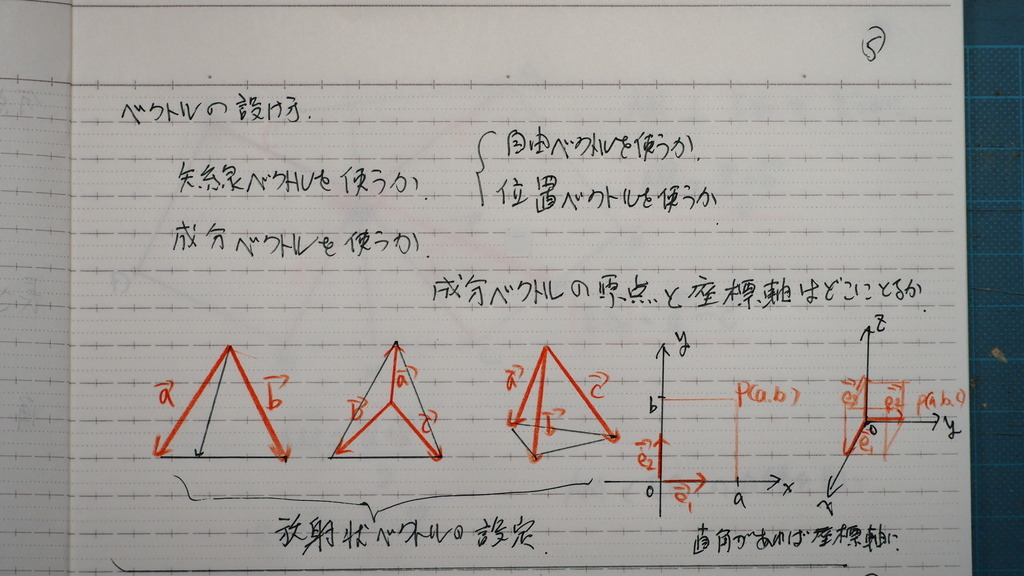
ベクトルの設け方た
これで
だいたい 決まってしまう
06
で
ここから 平面図形(1)
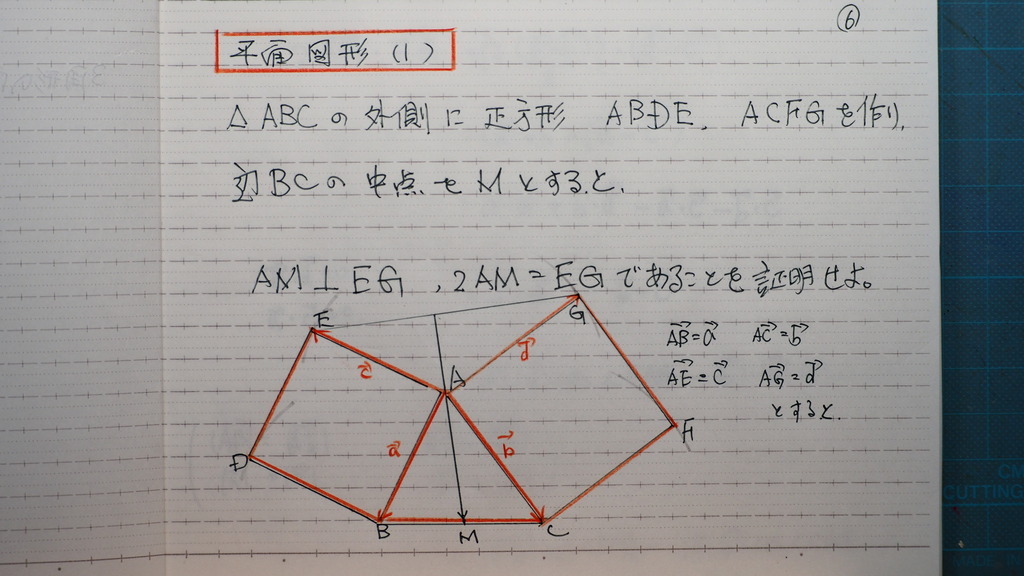
07
図のように
ベクトルを 設けて
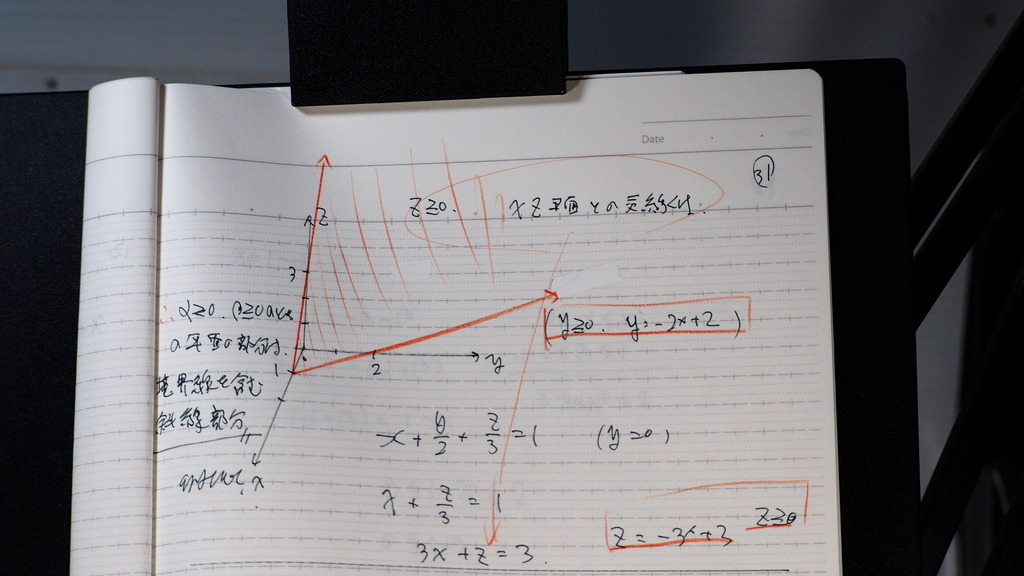
AM と EG の 内積を
計算すればさ
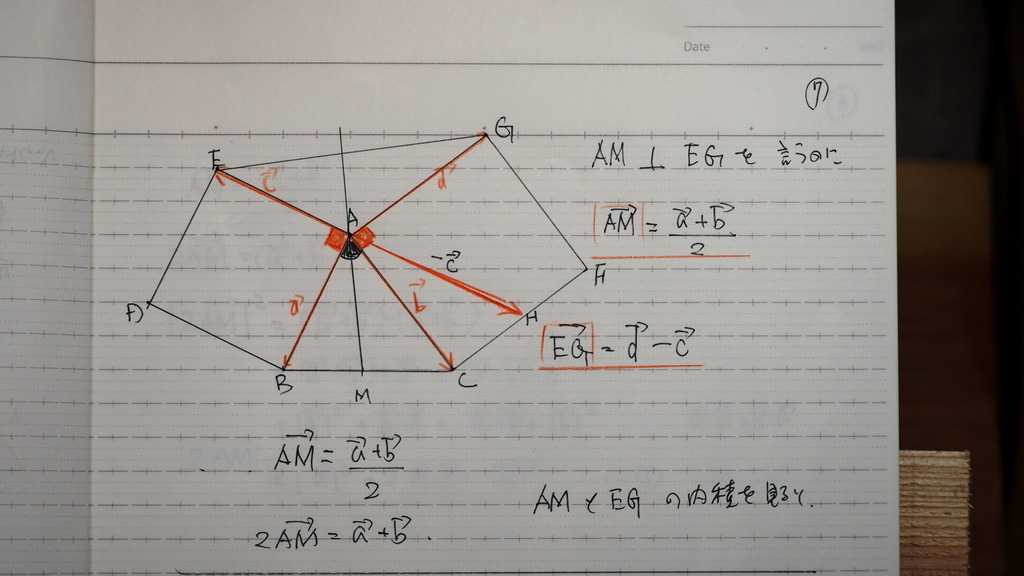
08
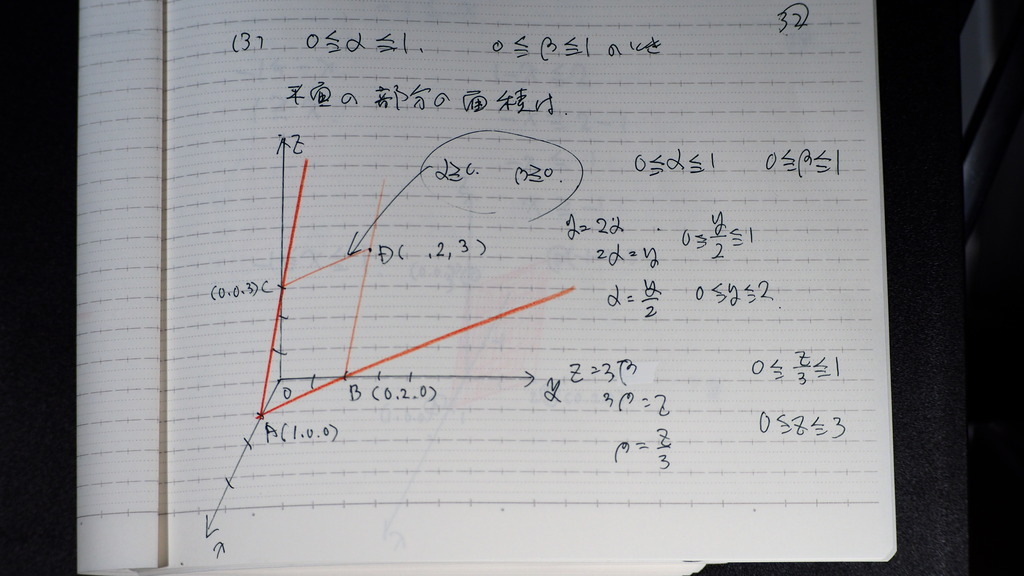
図形の 角度の問題で
=0になったので
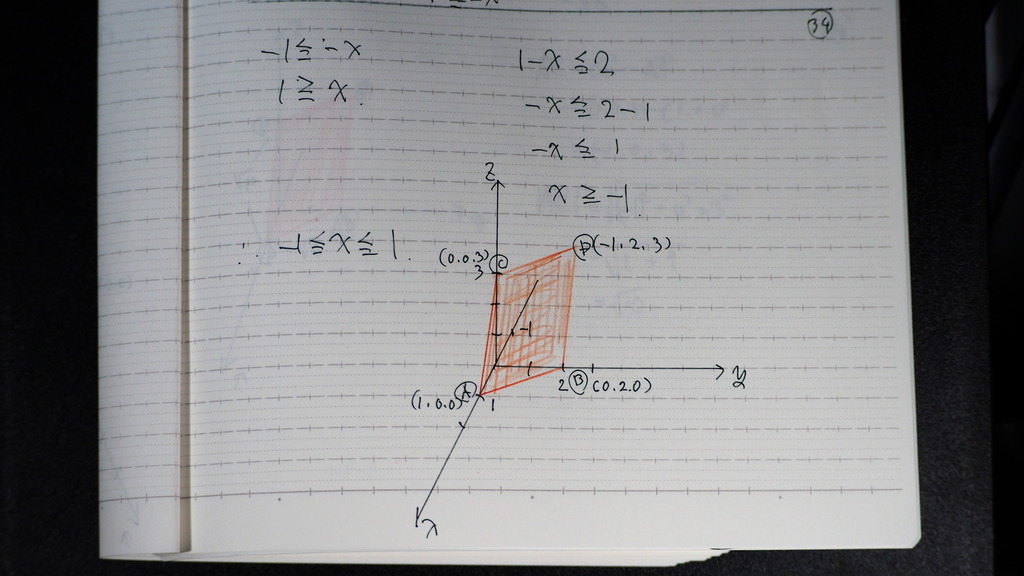
AM 垂直 EG

09
(2)は 2AM = EGを
いうんですが
2乗して
内積で
展開してくと
➀

10
EGは ②

11
➀②は 絶対値2乗のとこは
等しいと
ドット のところ
内積のとこは
絶対値の
等しいとこを置き換えて
ーc・dは
180-EAG
この ∠GAHとすれば
⑦ページの 図を
良く見ていただくと
等しいのが 見えてくる

12
これはですよ
ベクトルの 設定で
決まってしまいます
これができれが
もう オッケイ
あとは
内積の計算をすれば
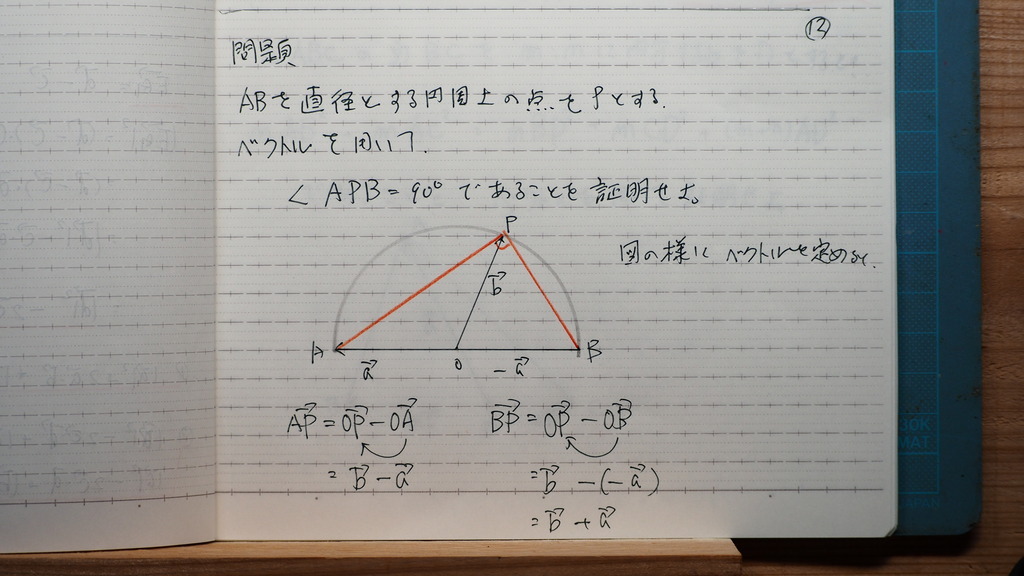
13
円周上なので
実は
a ベクトルも bベクトルも
半径で
長さが等しいので
=0
すなわち 垂直
∠APB=90度
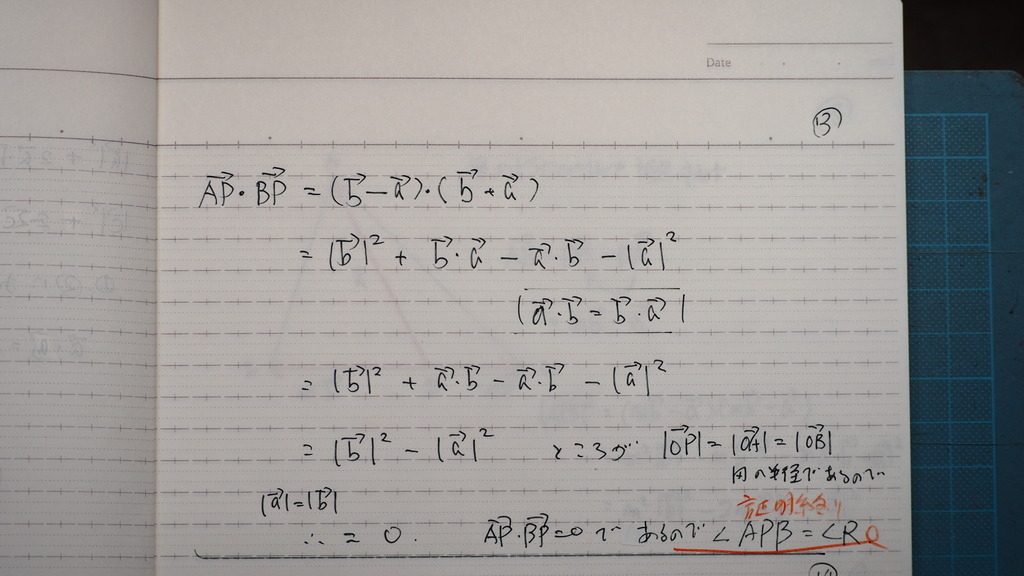
14
問題

15
図にように
ベクトルを
設定できさえすれば
もう
半分できた
あとは 計算あるのみ

16
計算は 自分の文字が
わかるように じゃナイスカ
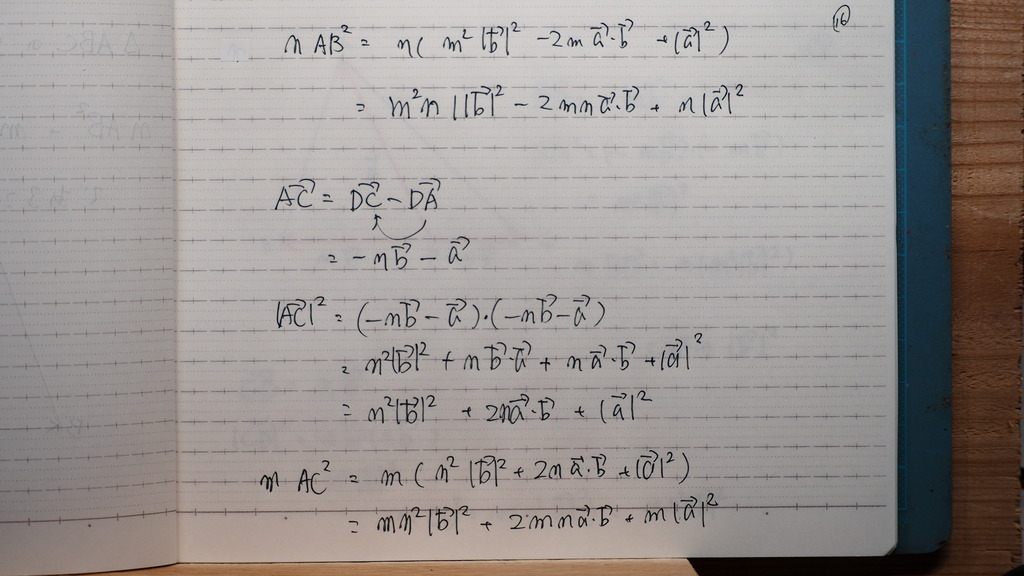
17
今日は 大丈夫だな
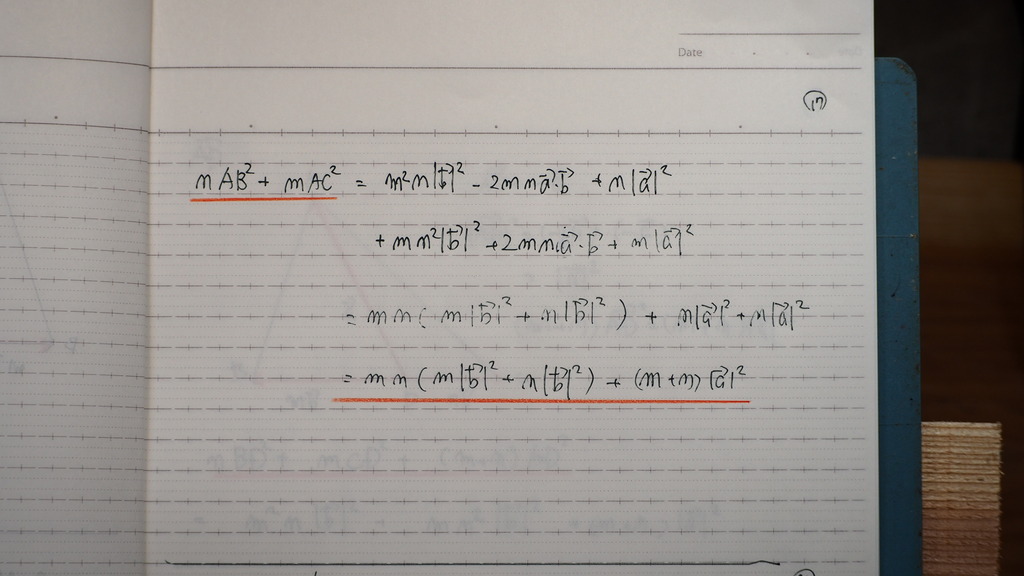
18
どこやってるか わかるかな
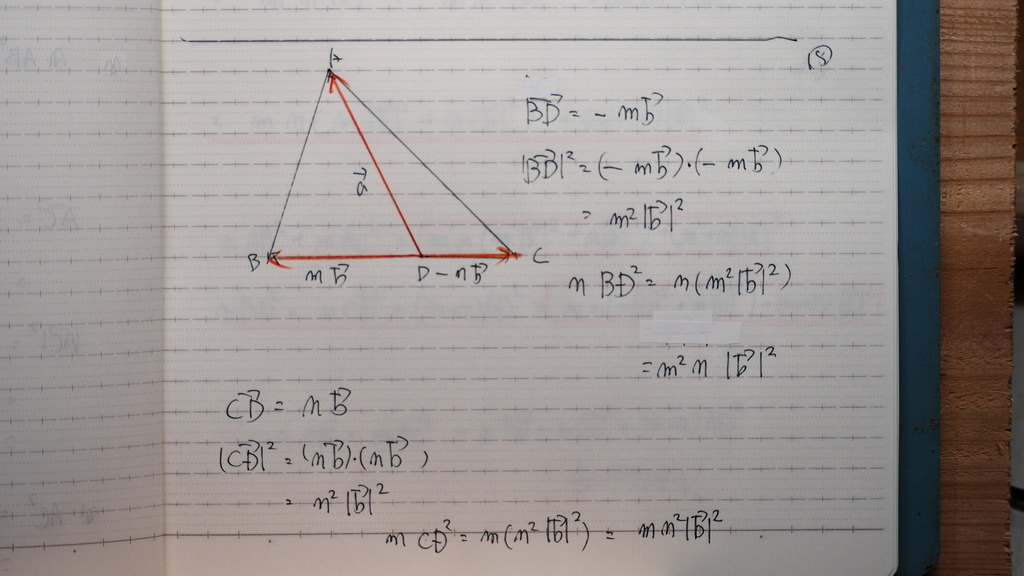
19
ソレゾレ
部品の 値を
計算してるんですが

20
で 全部 部品を 合計すると
左辺
右辺
おなじだったから
成り立つ

21
問題

22
図にすると
こんな感じで
ベクトルの設定を
こんな感じにしますと
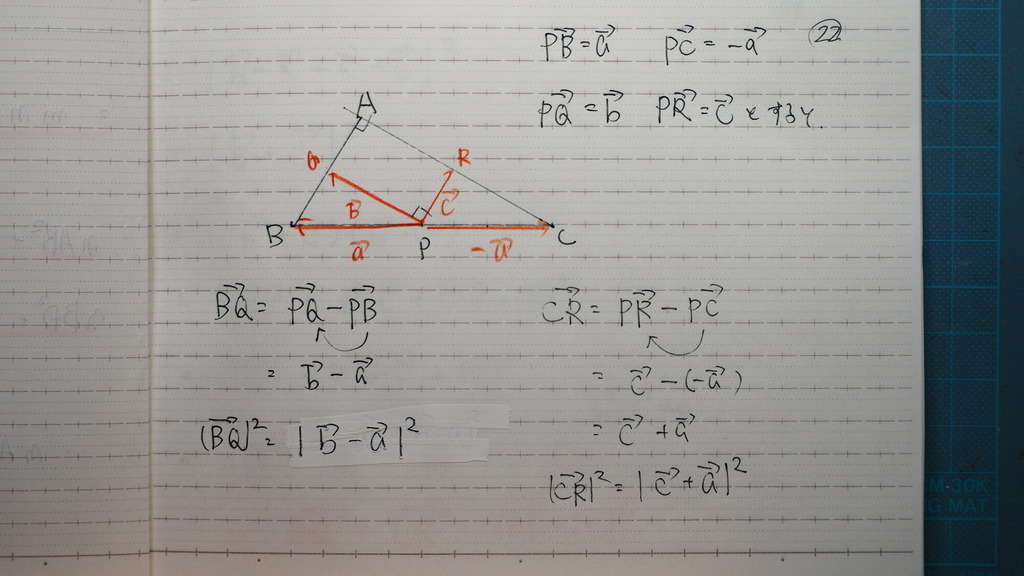
23
因数分解
みたいに 成ってるんですが
分かりますか
真ん中の項は =0

24
さらに 展開して
計算すると
こうでしょ
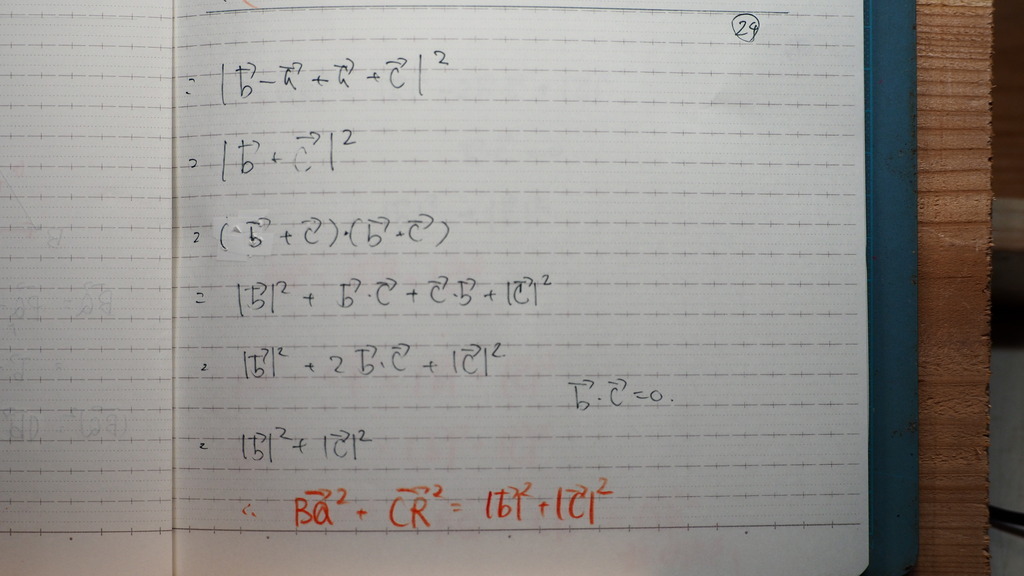
25
右辺は

26
で
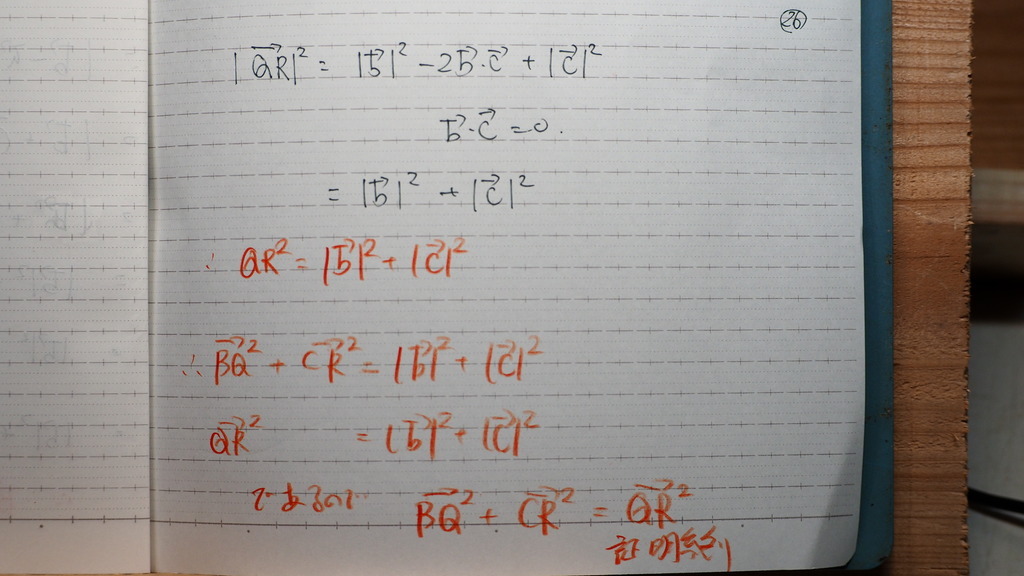
なったじゃナイスカ
お疲れ様です。
空間座標とベクトル
ベクトルの図形への応用
平面図形(1)
01
その前に
予備知識を
引算足し算
実数倍
02
同一 平面
垂直条件
03
分点 長さ なす角
04
三角形の面積
05
ベクトルの設け方た
これで
だいたい 決まってしまう
06
で
ここから 平面図形(1)
07
図のように
ベクトルを 設けて
AM と EG の 内積を
計算すればさ
08
図形の 角度の問題で
=0になったので
AM 垂直 EG
09
(2)は 2AM = EGを
いうんですが
2乗して
内積で
展開してくと
➀
10
EGは ②
11
➀②は 絶対値2乗のとこは
等しいと
ドット のところ
内積のとこは
絶対値の
等しいとこを置き換えて
ーc・dは
180-EAG
この ∠GAHとすれば
⑦ページの 図を
良く見ていただくと
等しいのが 見えてくる
12
これはですよ
ベクトルの 設定で
決まってしまいます
これができれが
もう オッケイ
あとは
内積の計算をすれば
13
円周上なので
実は
a ベクトルも bベクトルも
半径で
長さが等しいので
=0
すなわち 垂直
∠APB=90度
14
問題
15
図にように
ベクトルを
設定できさえすれば
もう
半分できた
あとは 計算あるのみ
16
計算は 自分の文字が
わかるように じゃナイスカ
17
今日は 大丈夫だな
18
どこやってるか わかるかな
19
ソレゾレ
部品の 値を
計算してるんですが
20
で 全部 部品を 合計すると
左辺
右辺
おなじだったから
成り立つ
21
問題
22
図にすると
こんな感じで
ベクトルの設定を
こんな感じにしますと
23
因数分解
みたいに 成ってるんですが
分かりますか
真ん中の項は =0
24
さらに 展開して
計算すると
こうでしょ
25
右辺は
26
で
なったじゃナイスカ
お疲れ様です。
2023年01月11日
22037 大人のさび落とし 空間座標とベクトル 列ベクトル
大人のさび落とし
空間座標とベクトル 列ベクトル
01
今は
行列は
習うんでしょうか?
私のときは
習いましたが
同世代で
習わない人もいましたし
我らの後
習わなくなり
その後
また 習うようになったりとか
今回は 列ベクトルだけだから
グリコの おまけ
みたいなもんですよ
書き方が
横から 縦
行から 列に 成っただけ

02
だからさ
同じなんだよ
ただ
横が 縦になっただけ
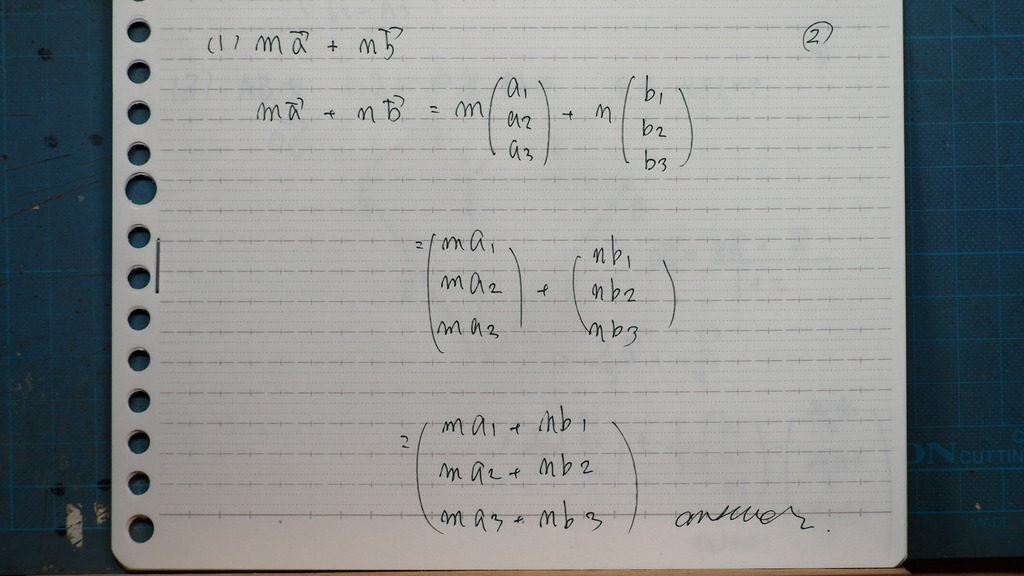
03
早い話が
こうやって 書いてもいいんだよ
とか
この方が
都合いい
ジャンか なぁー
見たいに
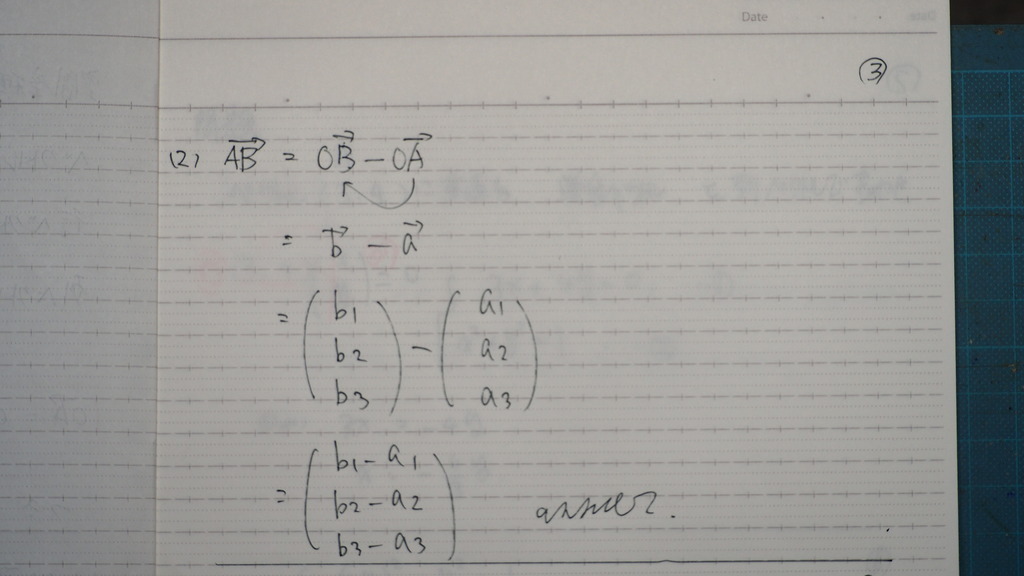
04
一回 見ておけば
さ
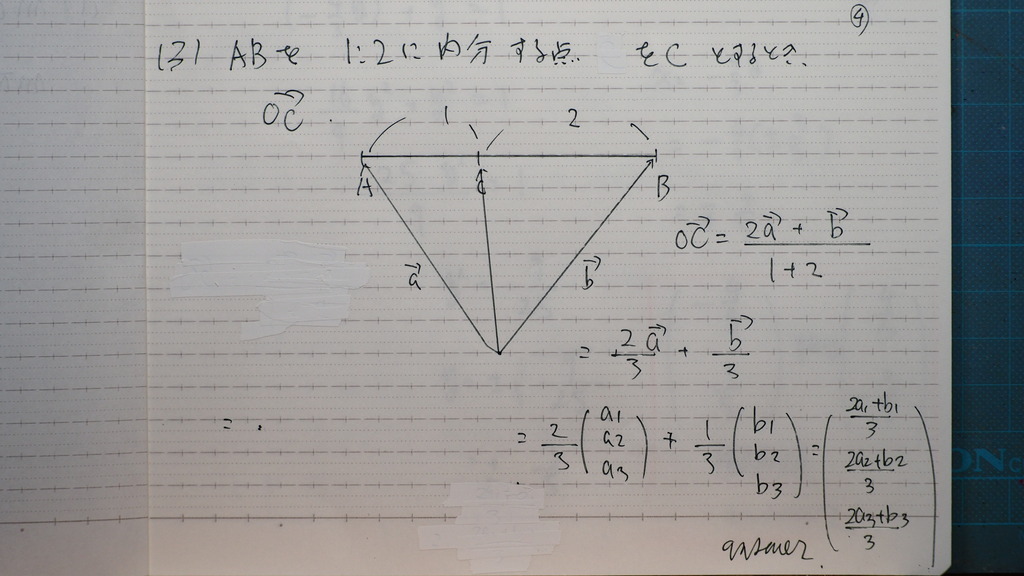
05
単位ベクトルだから
②が出てくる

06
ここは 計算

07
直線と 平面は
平行の時は
方向係数と 法線ベクトルが
垂直

08
二つの 成分を
行列で書くときは
必ず
行、 列 の 順番で
書く

09
これは
列行列を
使って 書いてあるけど
問題を 解くときは
この方が
やりやすいよね
解いてくと

10
t=の形にするでしょ
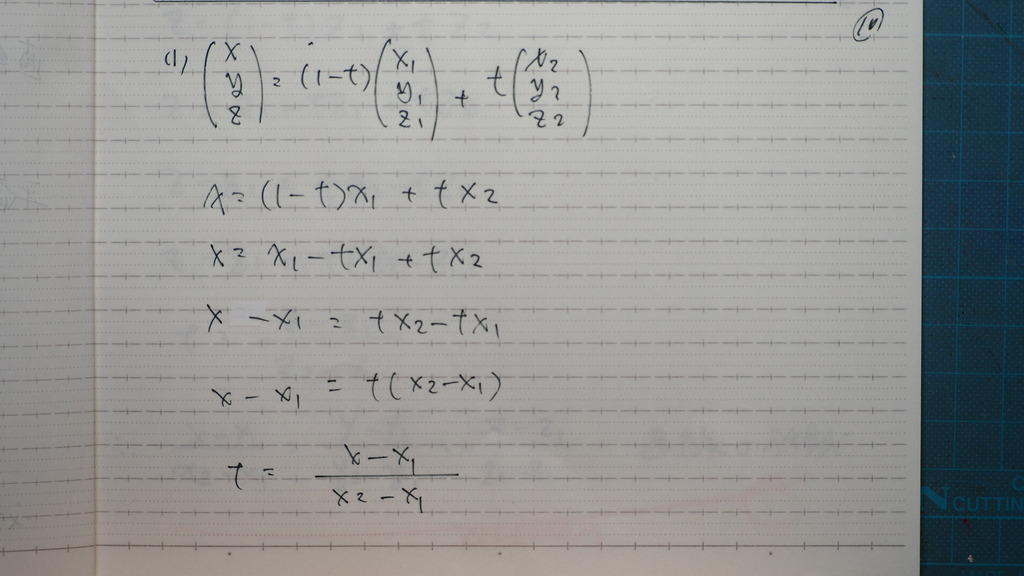
11
これも
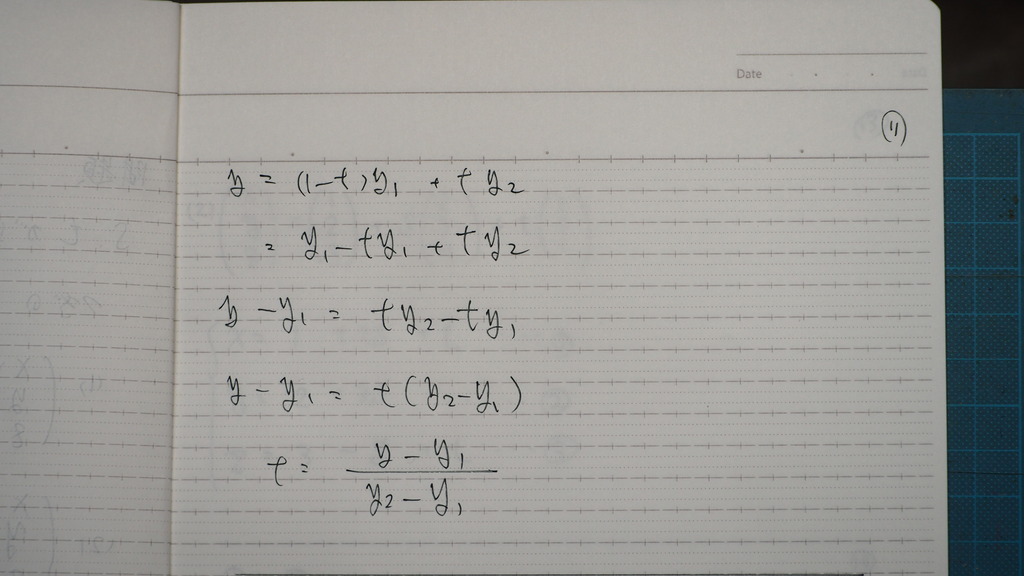
12
媒介変数表示の逆で
みんなつなげると
直線の方程式
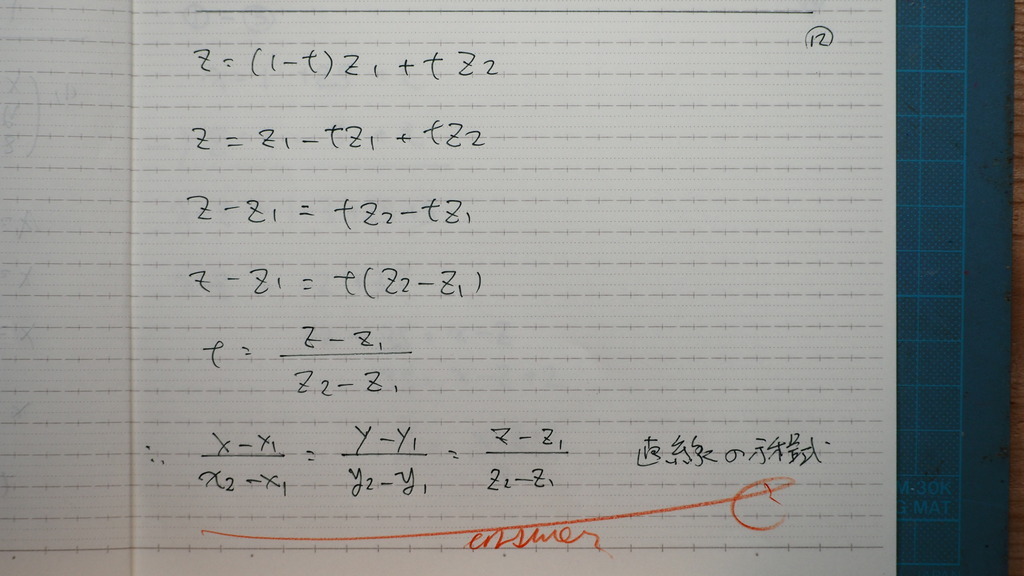
13
こっち方は

14
s=
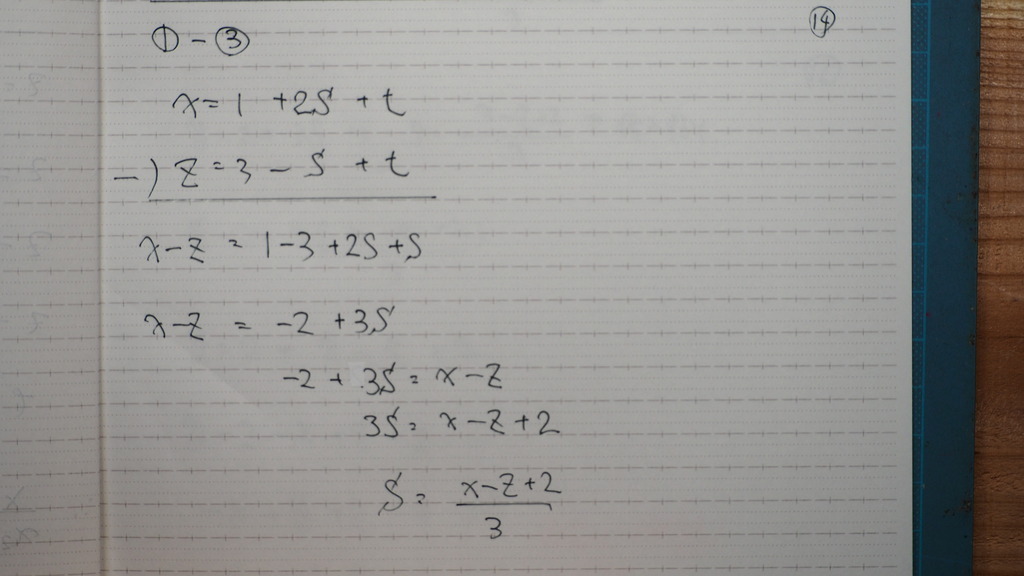
15
t=
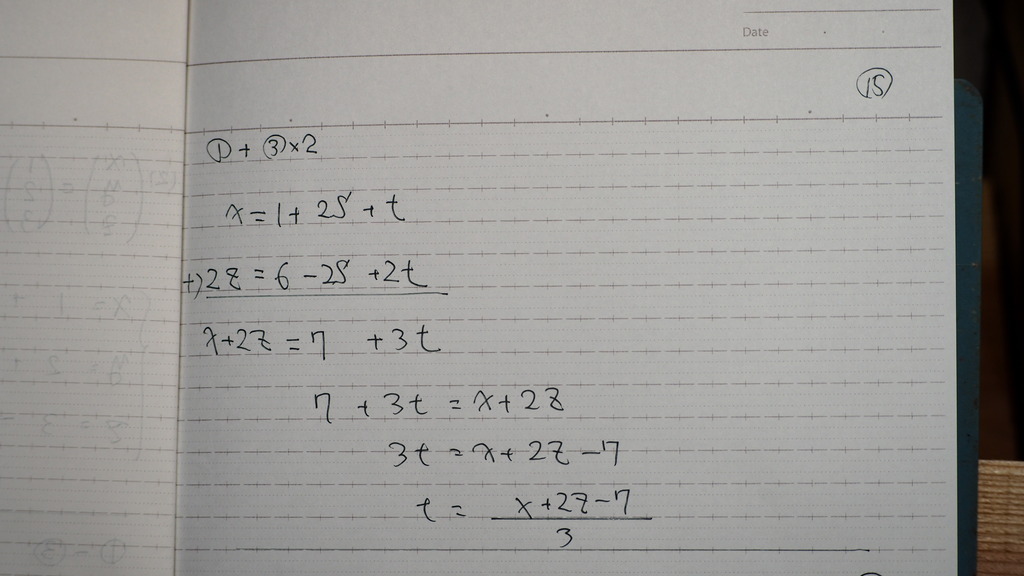
16
sだけで 出てしまったけれど
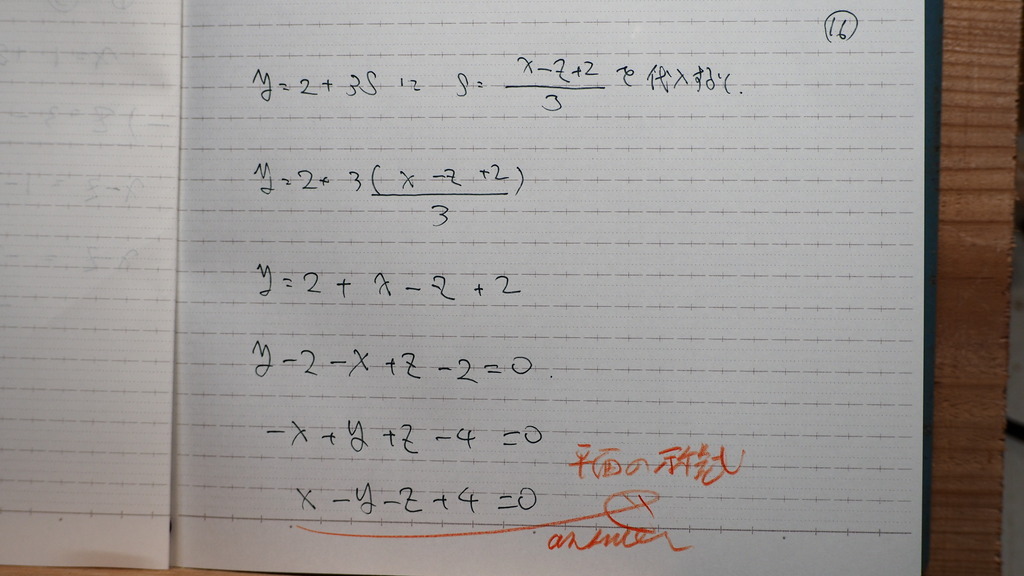
これでいいです
お疲れ様です。
空間座標とベクトル 列ベクトル
01
今は
行列は
習うんでしょうか?
私のときは
習いましたが
同世代で
習わない人もいましたし
我らの後
習わなくなり
その後
また 習うようになったりとか
今回は 列ベクトルだけだから
グリコの おまけ
みたいなもんですよ
書き方が
横から 縦
行から 列に 成っただけ
02
だからさ
同じなんだよ
ただ
横が 縦になっただけ
03
早い話が
こうやって 書いてもいいんだよ
とか
この方が
都合いい
ジャンか なぁー
見たいに
04
一回 見ておけば
さ
05
単位ベクトルだから
②が出てくる
06
ここは 計算
07
直線と 平面は
平行の時は
方向係数と 法線ベクトルが
垂直
08
二つの 成分を
行列で書くときは
必ず
行、 列 の 順番で
書く
09
これは
列行列を
使って 書いてあるけど
問題を 解くときは
この方が
やりやすいよね
解いてくと
10
t=の形にするでしょ
11
これも
12
媒介変数表示の逆で
みんなつなげると
直線の方程式
13
こっち方は
14
s=
15
t=
16
sだけで 出てしまったけれど
これでいいです
お疲れ様です。
22036 大人のさび落とし 空間座標とベクトル 回転体の方程式
空間座標と ベクトル
回転体の方程式
01
ななめの 空間直線を
z軸周りに
回転させてみたら
クビレ が できたよ
ッテいう
うれしい話ですが
この
方程式は
どんなモンジャラほいと

02
z軸周りに
回転させるので
断面は
xy平面に
原点中心の
半径が いくつかの円になる
しかしながら
zが したから 上に
上がっていくと
その断面の 半径が
k の関数で 変化していく
そこで
関数から
k を
消去して
z のかかわりを
出してくるんですが
やってみましょう
先ず 直線の
方程式を
求めてですよ

03
=k と置いて
媒介変数形表示

04
であるから
直線上の
任意の場所は
kを使って
こんな感じになるでしょ

05
Z軸上に
垂線を おろしてくると
半径
QPは
kの2次関数

06
Z=k の 交わり
は 円で
半径は kの関数

07
上から見たら
原点中心に
xy平面の 円
半径は
kの関数
Z=k を 代入して
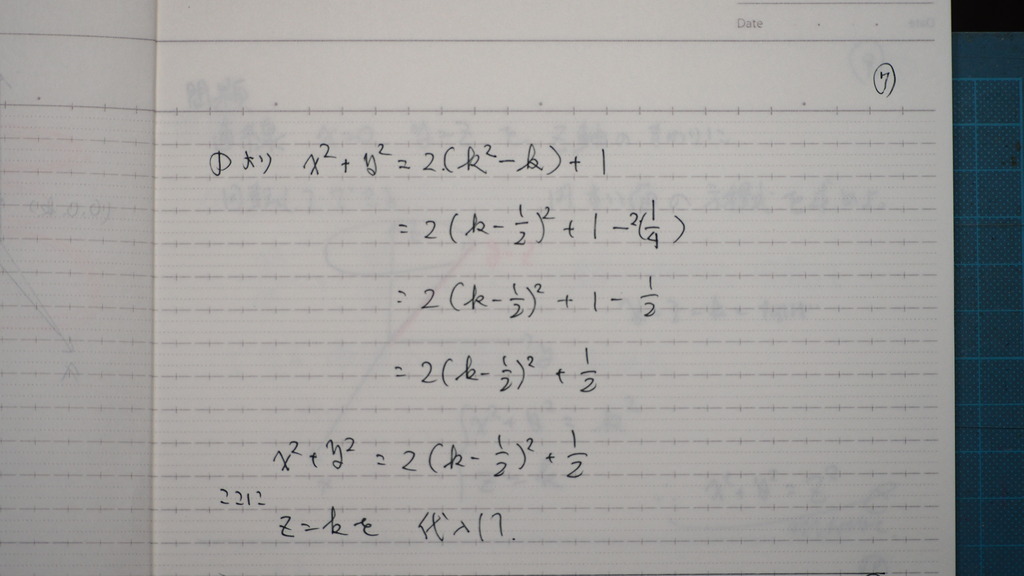
08
これが
今回の クビレ方程式
積分で
体積を だせば
こんな感じですが

09
問題
今度は
円すいの方程式
こんなんでいいカナ
簡単すぎる?

10
納得がいかない
じゃー
これは
難しいでしょ
説明が
しずらいですが
これです

11
今度はさ
いきなり
深いよ
今度は
xy 平面上の
楕円を
xじくまわりに
回すと
できる曲面の方程式は

12
楕円は
この 右辺が =1が
標準形で
a が b より大きいときは
aが 長軸の半径
bが 短軸の半径
b と aが
反対の時は
その逆
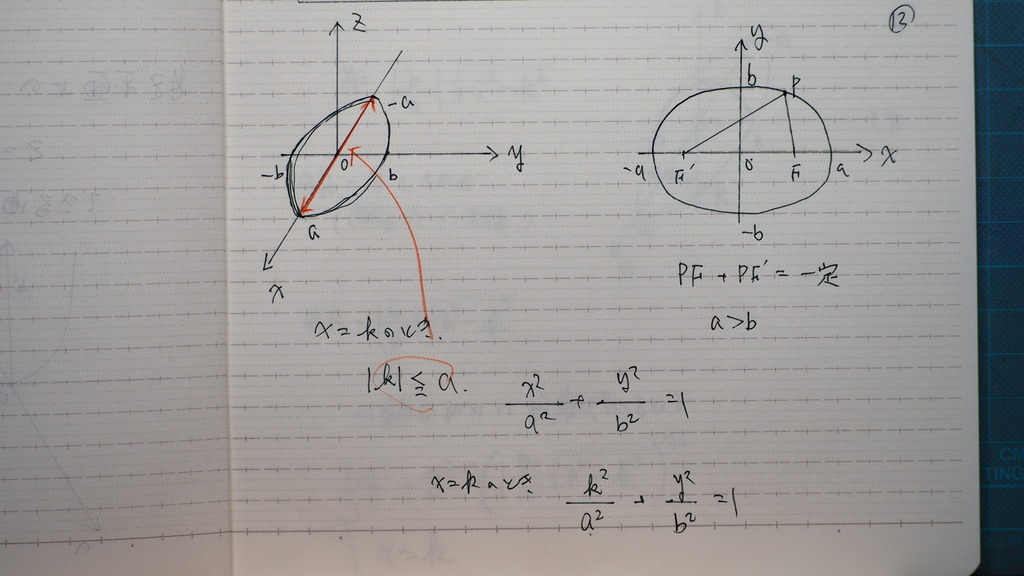
13
y=の式にするでしょ

14
図の QR が =y とすれば
断面の半径
x軸周りに
回転するので
xが 動くと
半径が 変わる
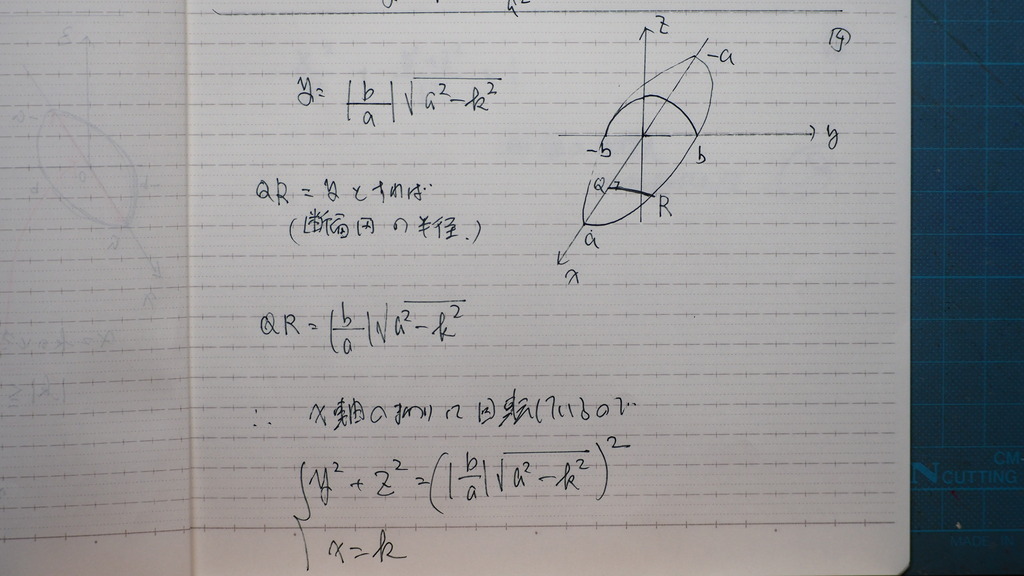
15
こんな感じになって

16
これが 曲面の方程式
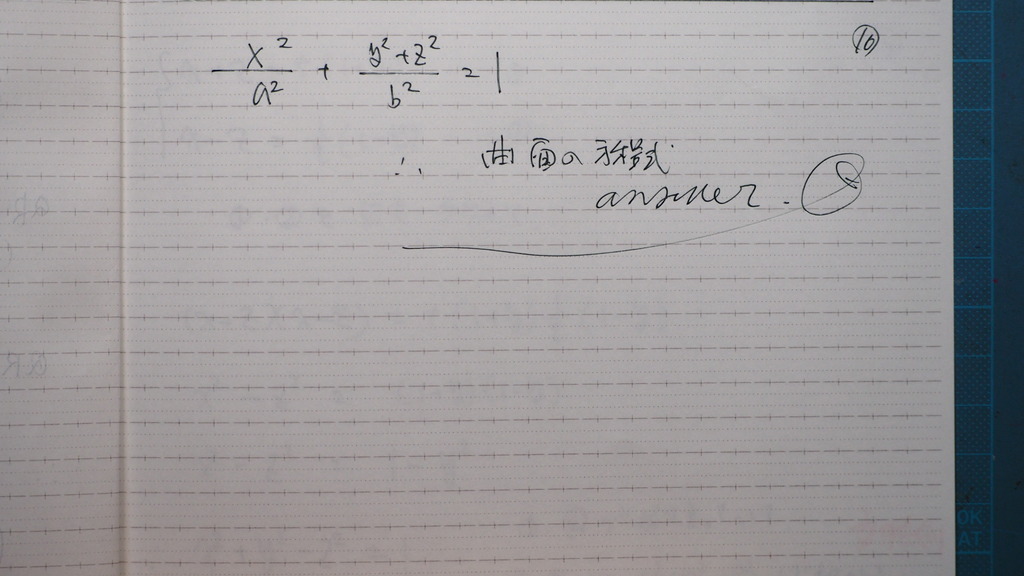
17
どうすりゃいいんだ

18
二つの 直線の
方程式を
掛け合わせるでしょ
そうしたら
題意の
曲面の方程式になったデショ
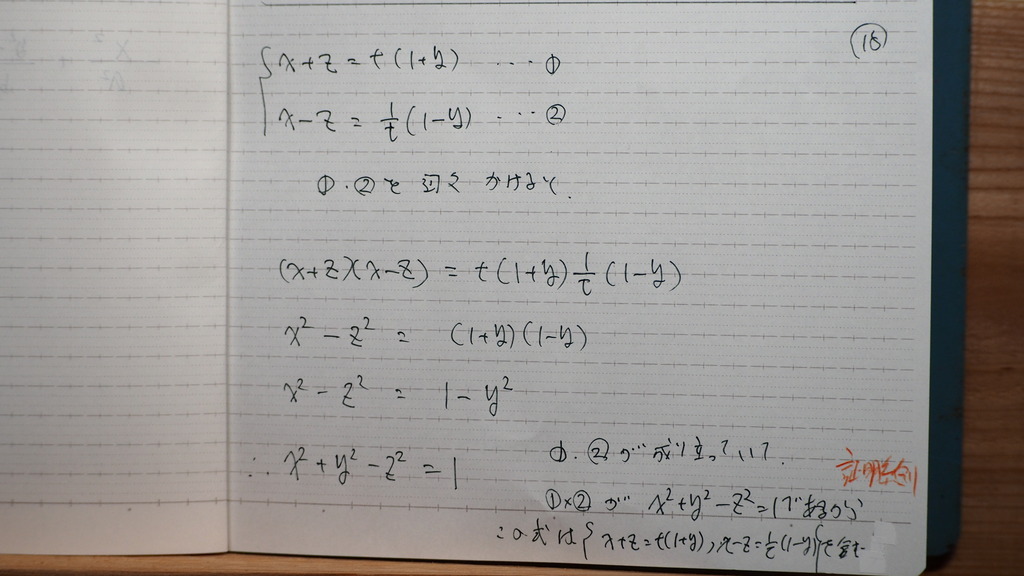
つまり
➀②が相方成り立っていて
掛け合わせたものが
曲面の式なので
曲面は 2直線を 含んでいる
お疲れ様です
回転体の方程式
01
ななめの 空間直線を
z軸周りに
回転させてみたら
クビレ が できたよ
ッテいう
うれしい話ですが
この
方程式は
どんなモンジャラほいと
02
z軸周りに
回転させるので
断面は
xy平面に
原点中心の
半径が いくつかの円になる
しかしながら
zが したから 上に
上がっていくと
その断面の 半径が
k の関数で 変化していく
そこで
関数から
k を
消去して
z のかかわりを
出してくるんですが
やってみましょう
先ず 直線の
方程式を
求めてですよ
03
=k と置いて
媒介変数形表示
04
であるから
直線上の
任意の場所は
kを使って
こんな感じになるでしょ
05
Z軸上に
垂線を おろしてくると
半径
QPは
kの2次関数
06
Z=k の 交わり
は 円で
半径は kの関数
07
上から見たら
原点中心に
xy平面の 円
半径は
kの関数
Z=k を 代入して
08
これが
今回の クビレ方程式
積分で
体積を だせば
こんな感じですが
09
問題
今度は
円すいの方程式
こんなんでいいカナ
簡単すぎる?
10
納得がいかない
じゃー
これは
難しいでしょ
説明が
しずらいですが
これです
11
今度はさ
いきなり
深いよ
今度は
xy 平面上の
楕円を
xじくまわりに
回すと
できる曲面の方程式は
12
楕円は
この 右辺が =1が
標準形で
a が b より大きいときは
aが 長軸の半径
bが 短軸の半径
b と aが
反対の時は
その逆
13
y=の式にするでしょ
14
図の QR が =y とすれば
断面の半径
x軸周りに
回転するので
xが 動くと
半径が 変わる
15
こんな感じになって
16
これが 曲面の方程式
17
どうすりゃいいんだ
18
二つの 直線の
方程式を
掛け合わせるでしょ
そうしたら
題意の
曲面の方程式になったデショ
つまり
➀②が相方成り立っていて
掛け合わせたものが
曲面の式なので
曲面は 2直線を 含んでいる
お疲れ様です
2023年01月09日
22035大人のさび落とし 空間座標とベクトル から 方べきの定理
大人のさび落とし
空間座標と ベクトル
方べきの定理
01
球に 点Aを通る 直線が
交わるとき
その 交点を P,Qとすれば
AP・AQは 常に 一定
であるということを
証明する問題

02
図に書くと こんなイメージで
直線の
方程式を
Aを 通る
方向係数
L,m,n の 直線
L,m,n は 方向余弦を 使うと
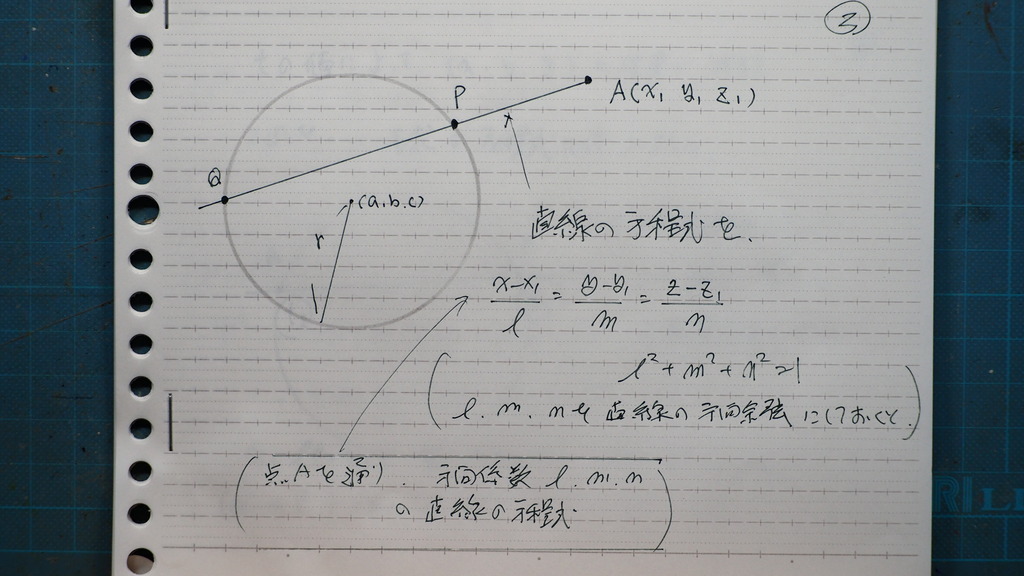
03
=t と置いて
直線の 媒介変数表示にして
tの値で
直線上の 場所が 出るように

04
直線の 媒介変数表示形を
球の方程式に 代入すると
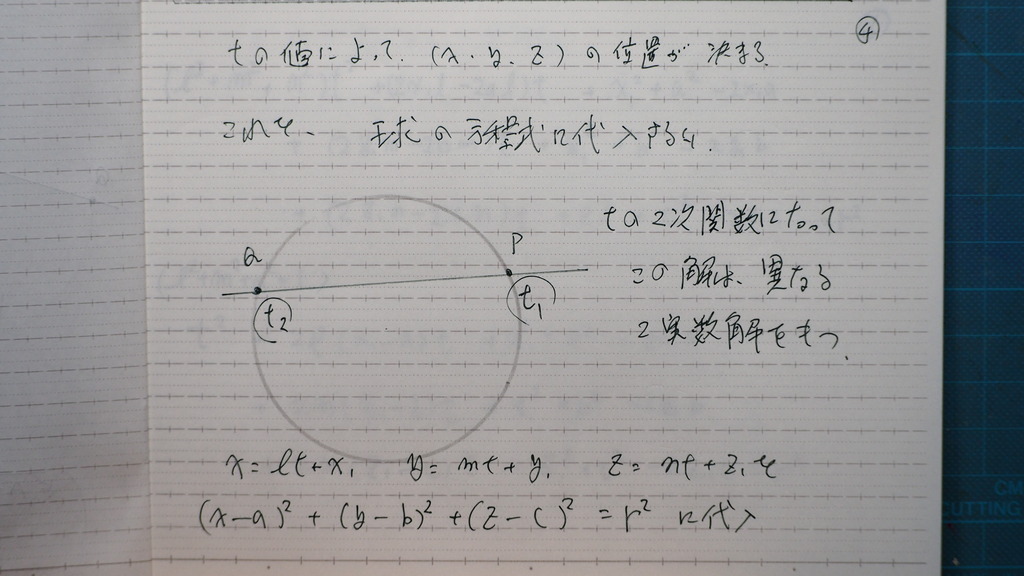
05
これを
tの2次関数に 整理して
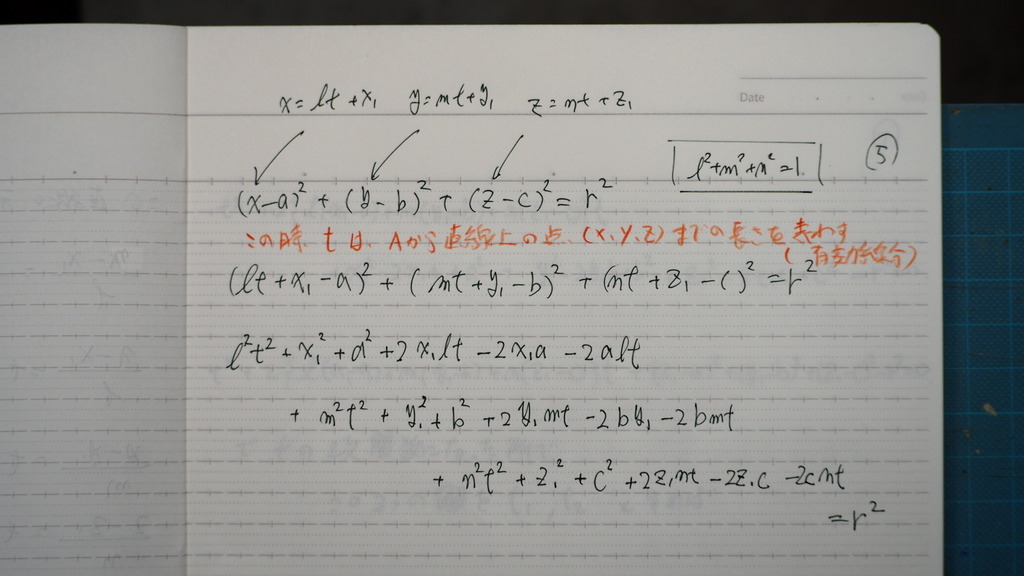
06
方向余弦を 使ってるので
=1を使って
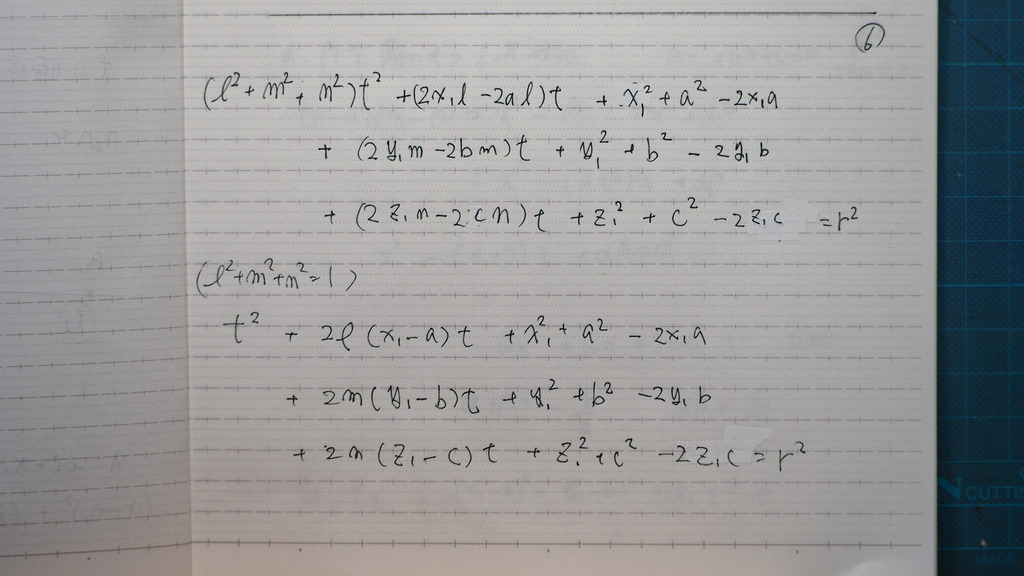
07
この2次関数の
2つの 解は
それぞれ
P 、Q を 表していて
今回は
点Aからの
線分とみなして

08
解と 係数の 関係から
α・β は t1・t2
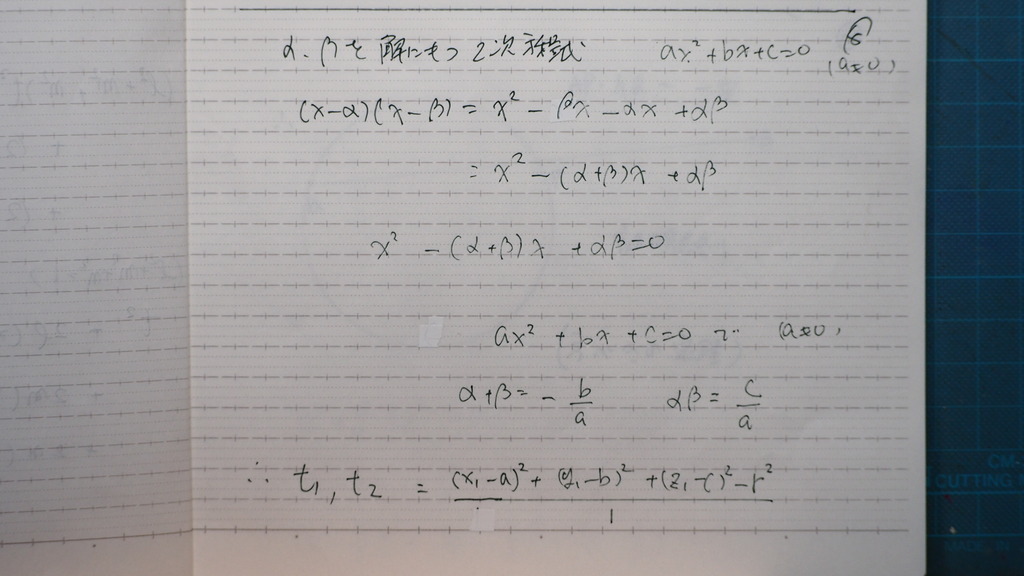
09
これが
AP・AQ の積と おなじであるから
一定である

10
方べきの定理
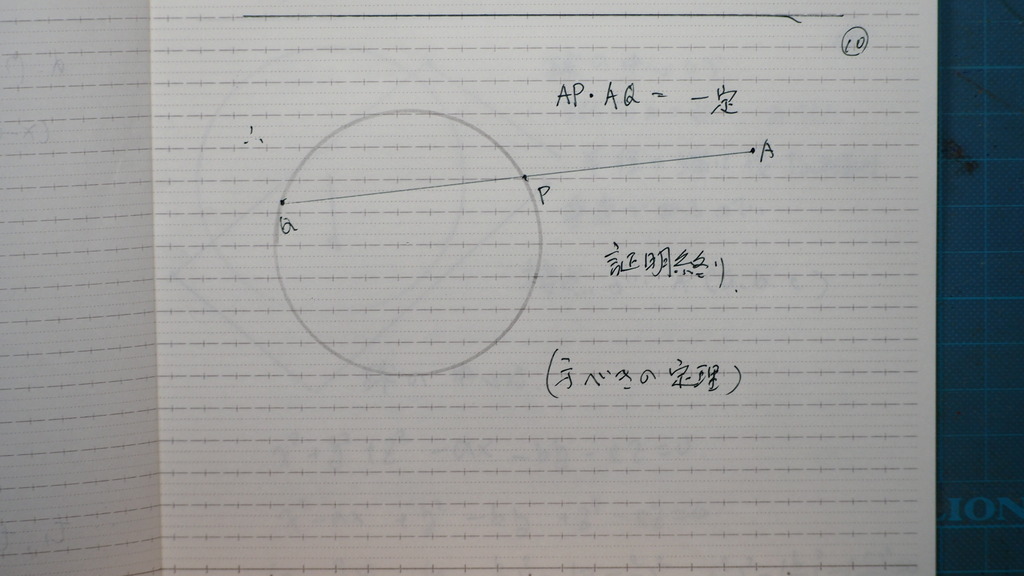
11
問題
先ず 球の接平面
次に
原点を 通る
直線と
球 、 接平面 の 交点を
P,Q
として
OP・OQ が 一定を
証明せよ

12
先ず 球の 接平面は
前回の とこでやってますが
球の 中心と そこからの
半径のはしに おける
平面との接点が 垂直であるから
まず
球の 中心を 知りたいから
変形して

13
球の 中心は これ
それと
接点Aとを 結ぶ
ベクトルが
平面の法線ベクトルだから
点A を 通り
法線ベクトルが分かれば

14
これを
展開した形に
しておくと
接平面の方程式
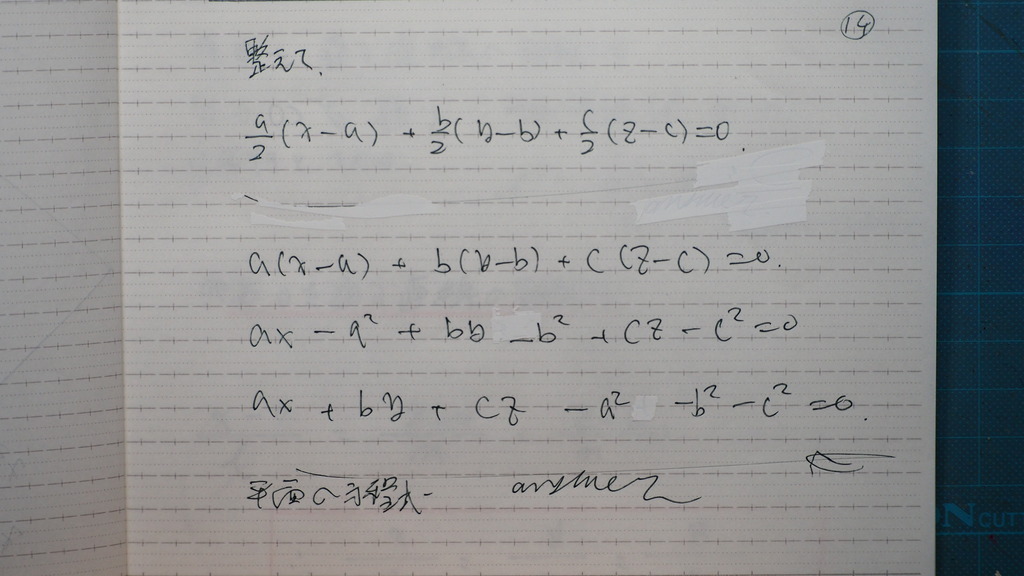
15
原点を
通る 直線が
球と この接平面に
交わるところを
P、Q としたとき
OP・OQの 積が
一定は

16
まず
原点(0,0,0)を 通る
直線であるので
方向係数を
L,m,n
方向余弦にして
それぞれの 2乗の 和が 1

17
使う方程式
3っ
直線の方程式
球の方程式
球の接平面の方程式

18
直線の 方程式を
媒介変数表示形にして
球の方程式に
代入していくと
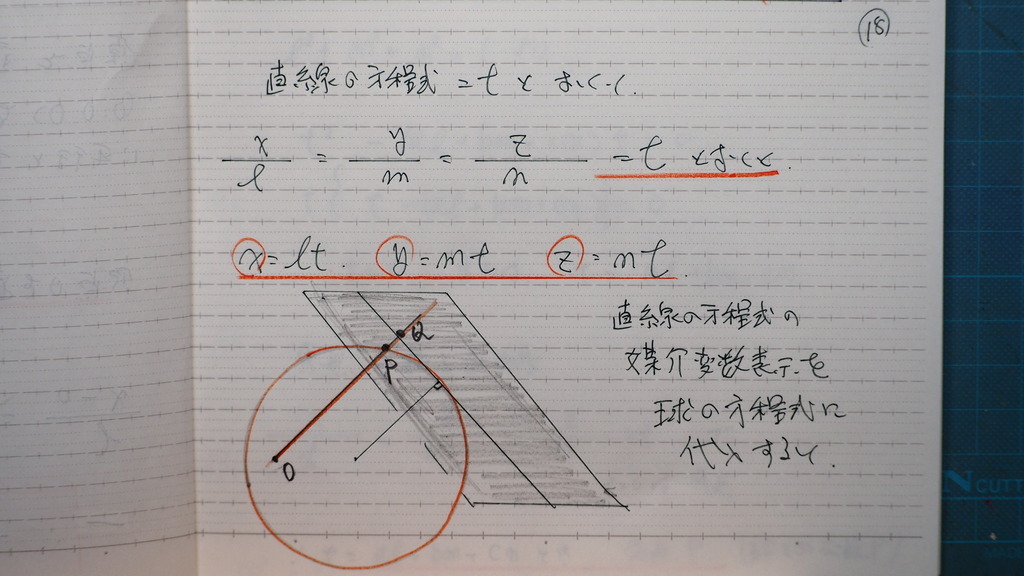
19
方向余弦を
使ってるので
=1になるを 使うんですよ
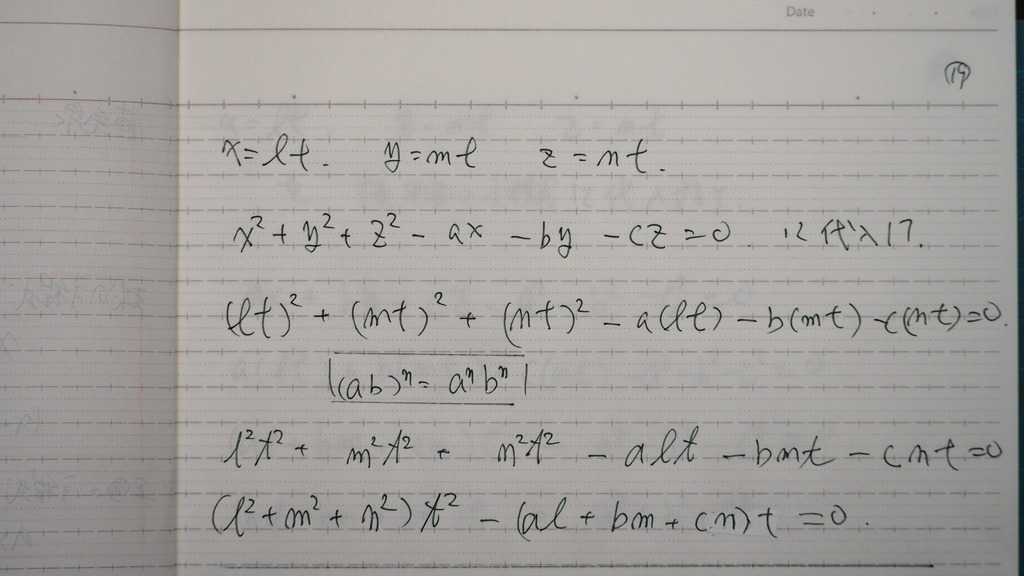
20
tは 0 または これこれ
t=0は
直線上で原点を 表してるので
もう一方が P
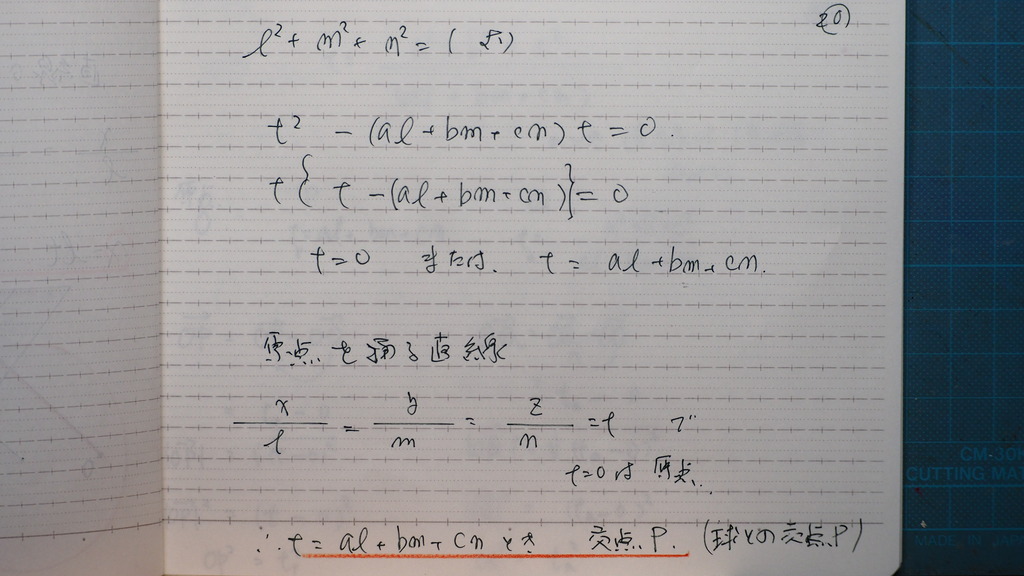
21
今度は
直線の媒介変数表示形を
球の接平面の方程式に
代入すると

22
tが
これは Qだから
OP OQ の二乗 を 計算して
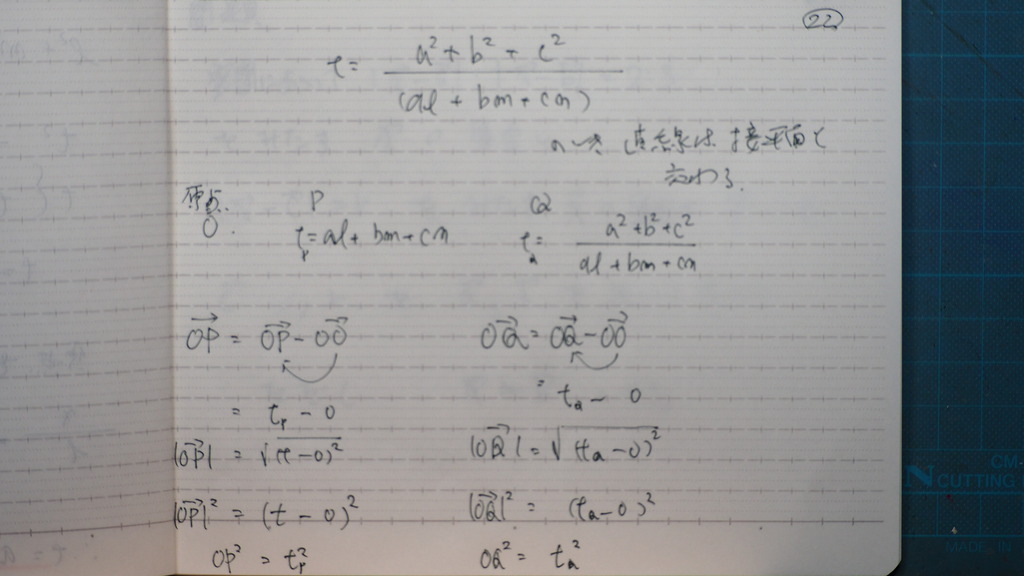
23
であるので
OP と OQの 積は
こんな感じで
これは
定点の値の 二乗の和の形
一定

24
問題
どういうことなのカナ

25
与式を
変形して
2乗して
展開して

26
ここから
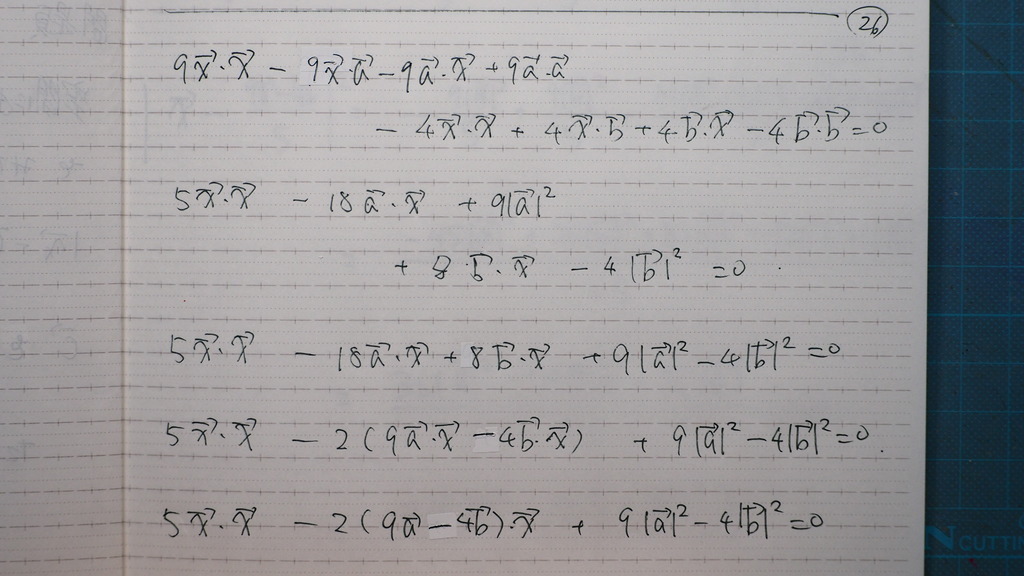
27
平方完成に 持ち込んで
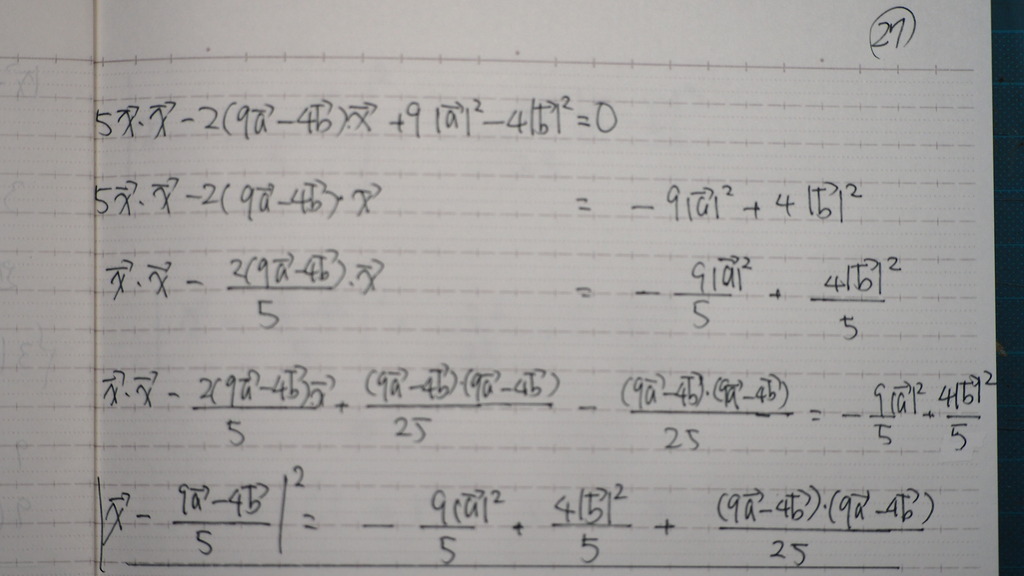
28
空気が 悪かったり
眠かったり
ブドウ糖が 減ってきたり
しますと
計算が
思うように 行きません
一回 寝て
起き
また ねて おき
3回目に
起きたときにですよ
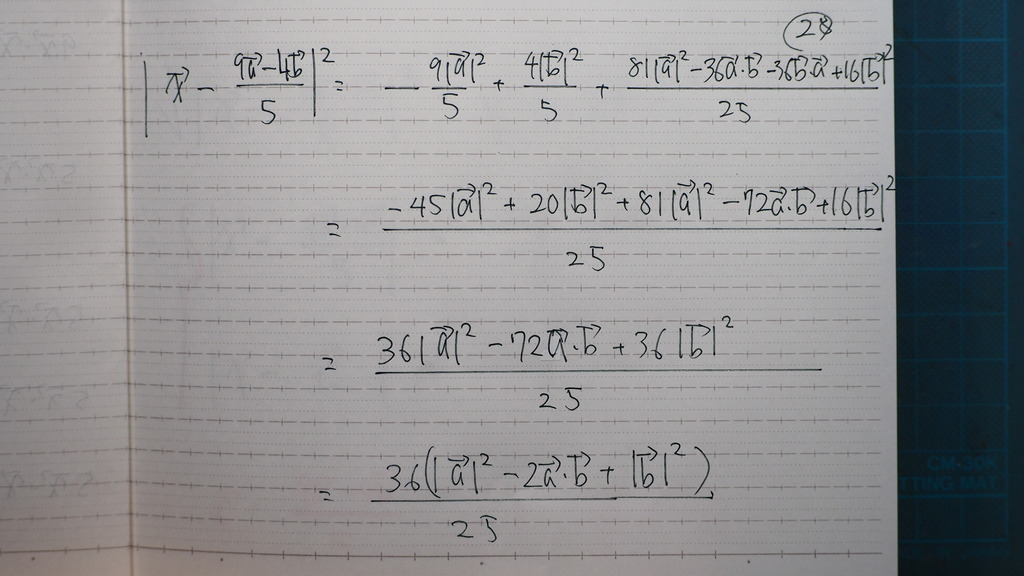
29
なんとか
たどり着きまして
出じゃナイスカ
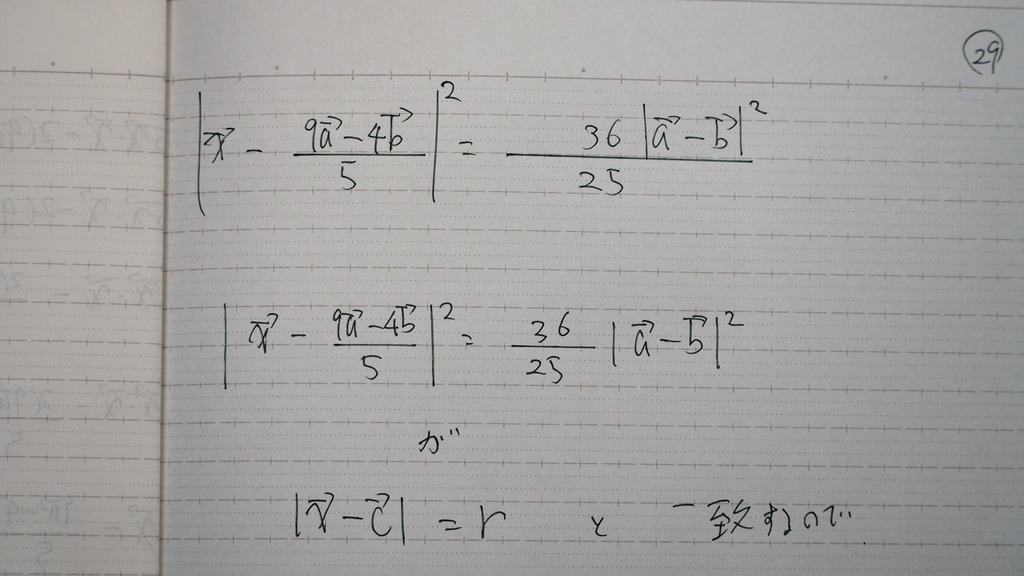
30
これがさ
なんだんだ
もう一つの 式に 等しいから
係数比較で
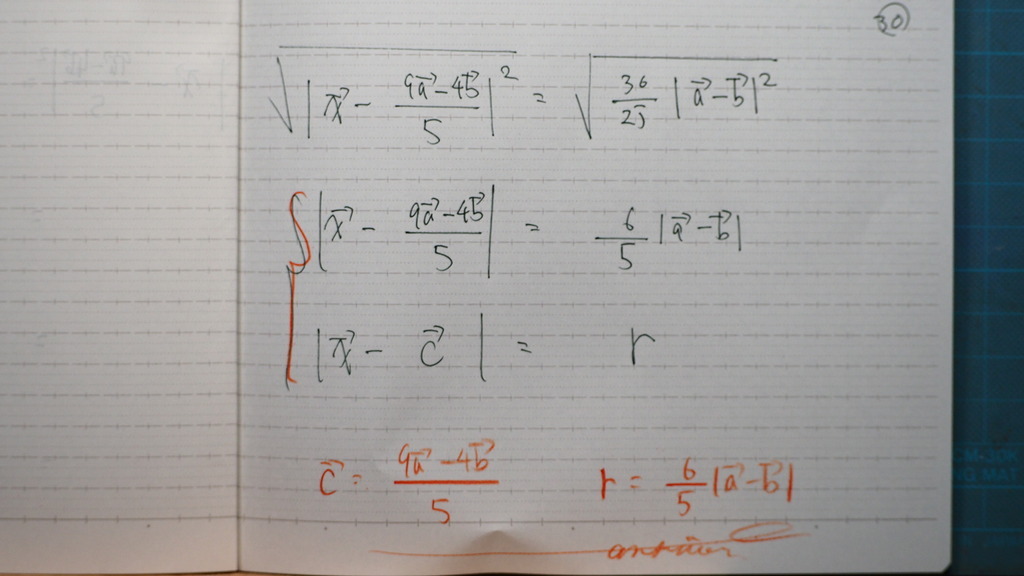
お疲れ様です。
空間座標と ベクトル
方べきの定理
01
球に 点Aを通る 直線が
交わるとき
その 交点を P,Qとすれば
AP・AQは 常に 一定
であるということを
証明する問題
02
図に書くと こんなイメージで
直線の
方程式を
Aを 通る
方向係数
L,m,n の 直線
L,m,n は 方向余弦を 使うと
03
=t と置いて
直線の 媒介変数表示にして
tの値で
直線上の 場所が 出るように
04
直線の 媒介変数表示形を
球の方程式に 代入すると
05
これを
tの2次関数に 整理して
06
方向余弦を 使ってるので
=1を使って
07
この2次関数の
2つの 解は
それぞれ
P 、Q を 表していて
今回は
点Aからの
線分とみなして
08
解と 係数の 関係から
α・β は t1・t2
09
これが
AP・AQ の積と おなじであるから
一定である
10
方べきの定理
11
問題
先ず 球の接平面
次に
原点を 通る
直線と
球 、 接平面 の 交点を
P,Q
として
OP・OQ が 一定を
証明せよ
12
先ず 球の 接平面は
前回の とこでやってますが
球の 中心と そこからの
半径のはしに おける
平面との接点が 垂直であるから
まず
球の 中心を 知りたいから
変形して
13
球の 中心は これ
それと
接点Aとを 結ぶ
ベクトルが
平面の法線ベクトルだから
点A を 通り
法線ベクトルが分かれば
14
これを
展開した形に
しておくと
接平面の方程式
15
原点を
通る 直線が
球と この接平面に
交わるところを
P、Q としたとき
OP・OQの 積が
一定は
16
まず
原点(0,0,0)を 通る
直線であるので
方向係数を
L,m,n
方向余弦にして
それぞれの 2乗の 和が 1
17
使う方程式
3っ
直線の方程式
球の方程式
球の接平面の方程式
18
直線の 方程式を
媒介変数表示形にして
球の方程式に
代入していくと
19
方向余弦を
使ってるので
=1になるを 使うんですよ
20
tは 0 または これこれ
t=0は
直線上で原点を 表してるので
もう一方が P
21
今度は
直線の媒介変数表示形を
球の接平面の方程式に
代入すると
22
tが
これは Qだから
OP OQ の二乗 を 計算して
23
であるので
OP と OQの 積は
こんな感じで
これは
定点の値の 二乗の和の形
一定
24
問題
どういうことなのカナ
25
与式を
変形して
2乗して
展開して
26
ここから
27
平方完成に 持ち込んで
28
空気が 悪かったり
眠かったり
ブドウ糖が 減ってきたり
しますと
計算が
思うように 行きません
一回 寝て
起き
また ねて おき
3回目に
起きたときにですよ
29
なんとか
たどり着きまして
出じゃナイスカ
30
これがさ
なんだんだ
もう一つの 式に 等しいから
係数比較で
お疲れ様です。
2023年01月07日
22034 大人のさび落とし 空間座標とベクトル 球と接平面
大人のさび落とし
球と 接平面
01
まず 問題
球の方程式を 導く

02
球面上の 一点での 接平面
と
2点を 通り
球接する平面

03
まず
ベクトルの 引き算で
出てきたものが
Pは 動点だから
動き回るんだけど
いも いつも 大きさが 同じ
ッテ式を
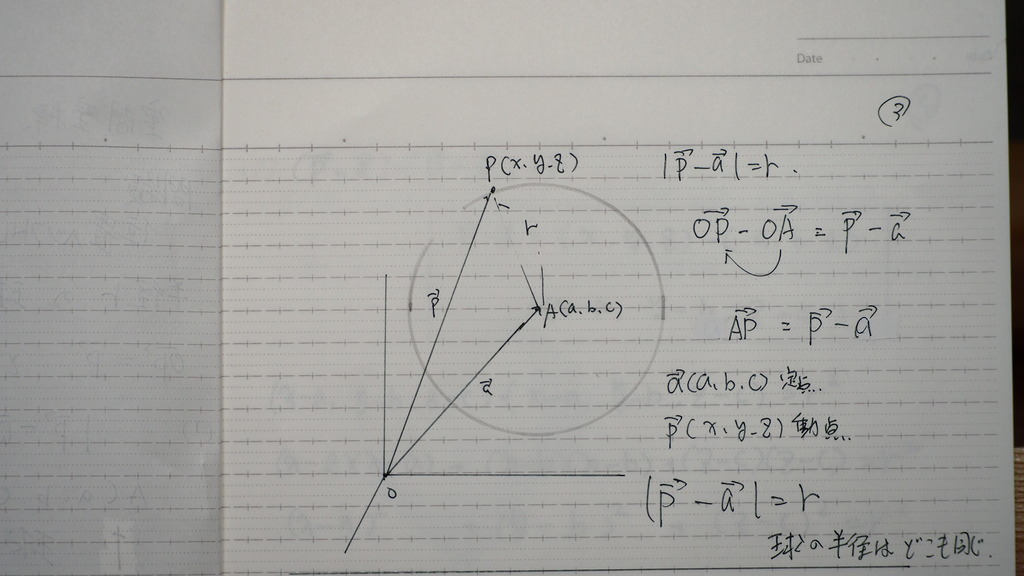
04
辺々2乗するでしょ
で
かっこの中身が
成分の引き算で

05
こんな感じに
成分の 引き算になるので
この 内積の 展開で
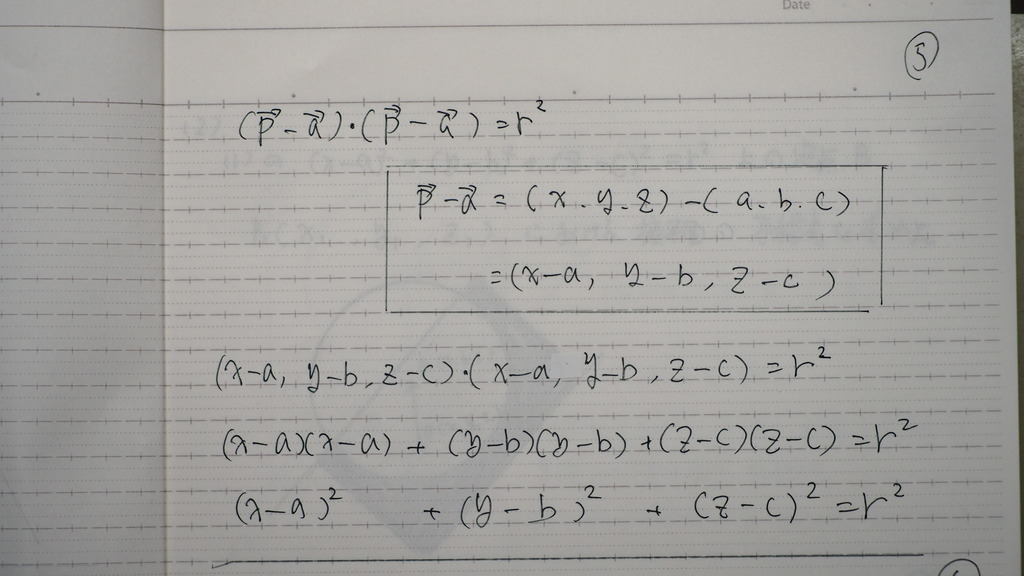
06
なりましたと
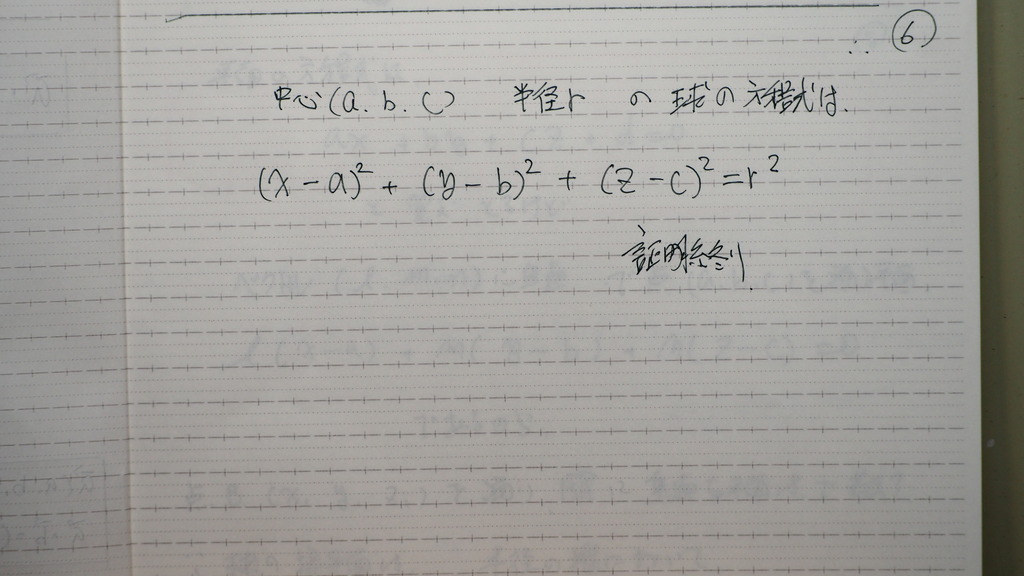
07
この 球面上の
点B における 接平面は
平面の 垂直成分は
球の中心から Bにおろした
垂線のベクトル
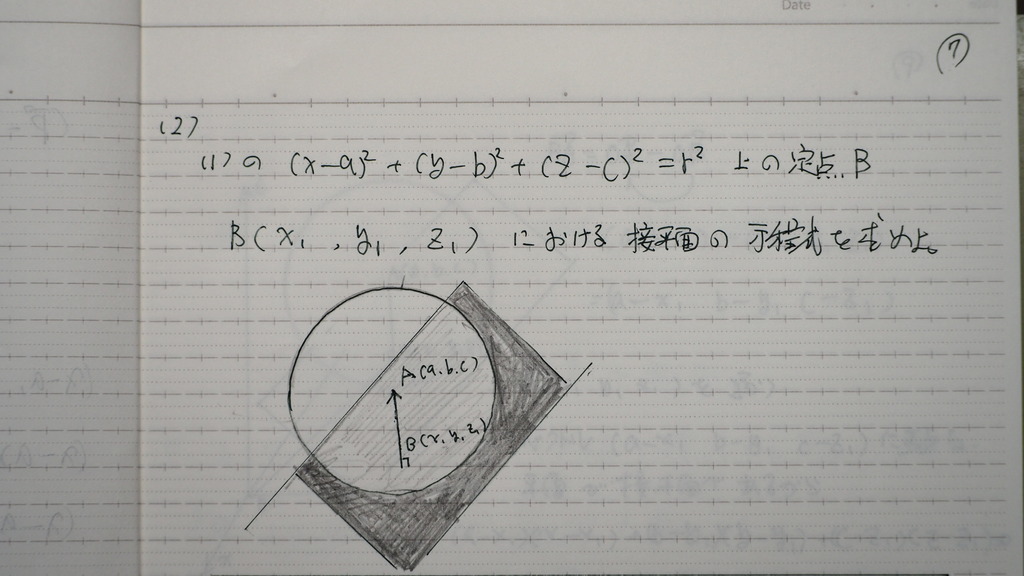
08
平面の 方程式は
垂直成分と
通過点がわかてるときの場合を
使って

09
BA ベクトル
平面に垂直な成分
と
通過点 B から
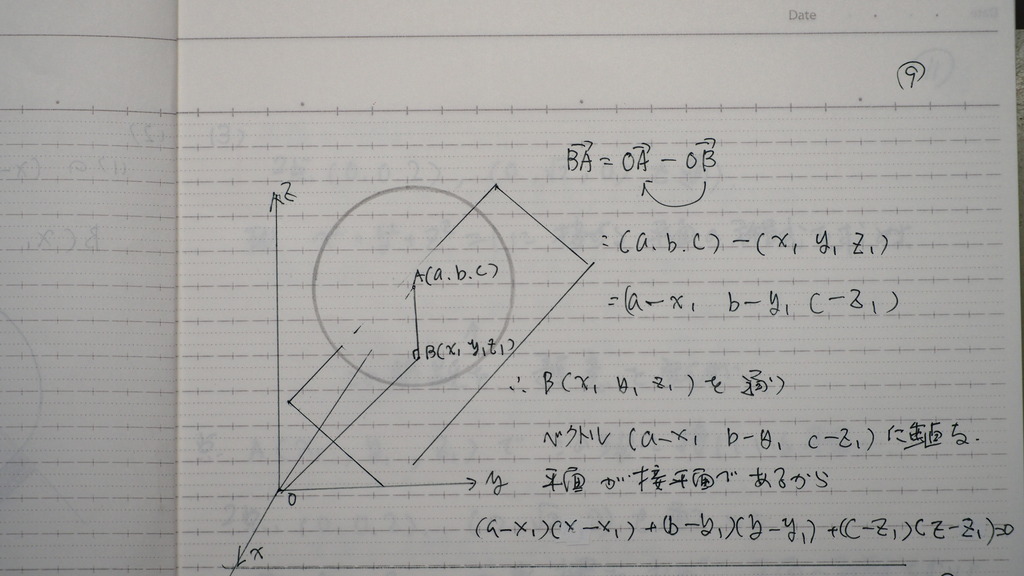
10
これに 代入してですよ

11
2点を 通り
球に接する平面は
今の (2) を
うまく使って
点B で
球に 接している
その平面が
2点も 通過するで
代入して
ここでは Aとすれば
Aの X1 Y1 Z1
を
特定すれば
平面の 方程式になるので

12
まず 球の方程式に
点Aで接する平面は

13
こんな形
それと
だいいから・・・

14
2点を
平面の 方程式に代入すると
②③
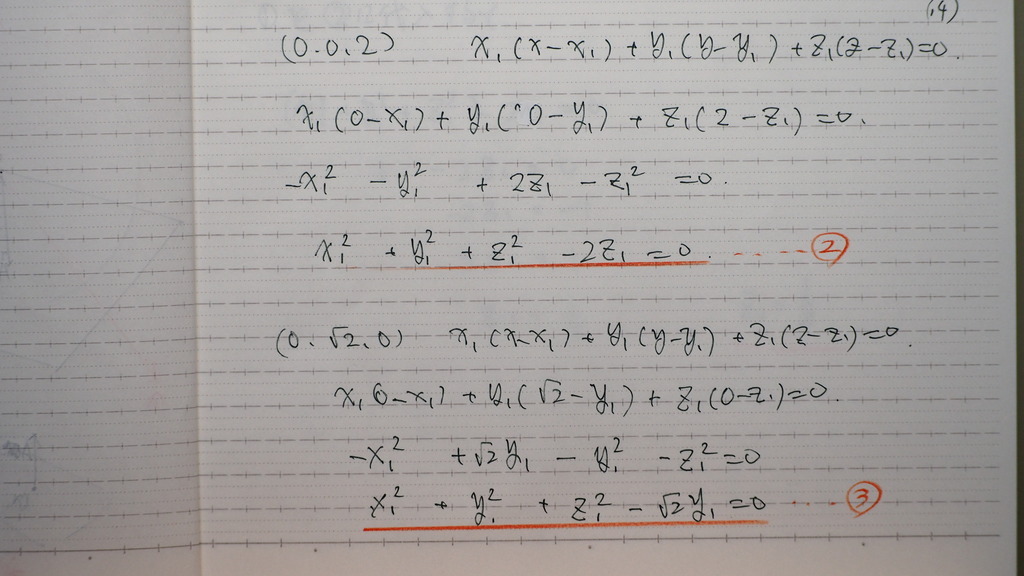
15
➀②③より
平面の方程式を
求めると

16
z1
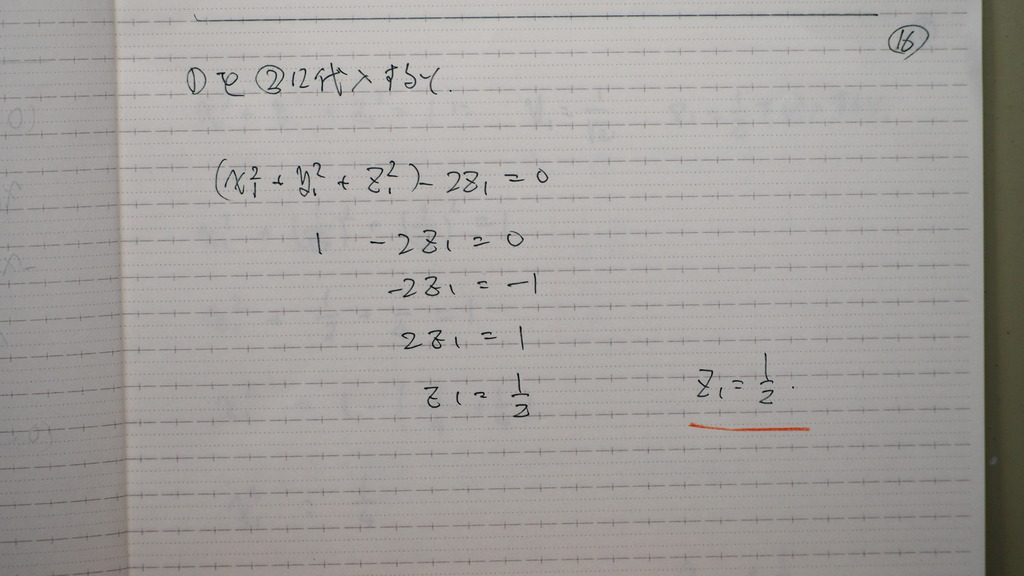
17
y1

18
x1
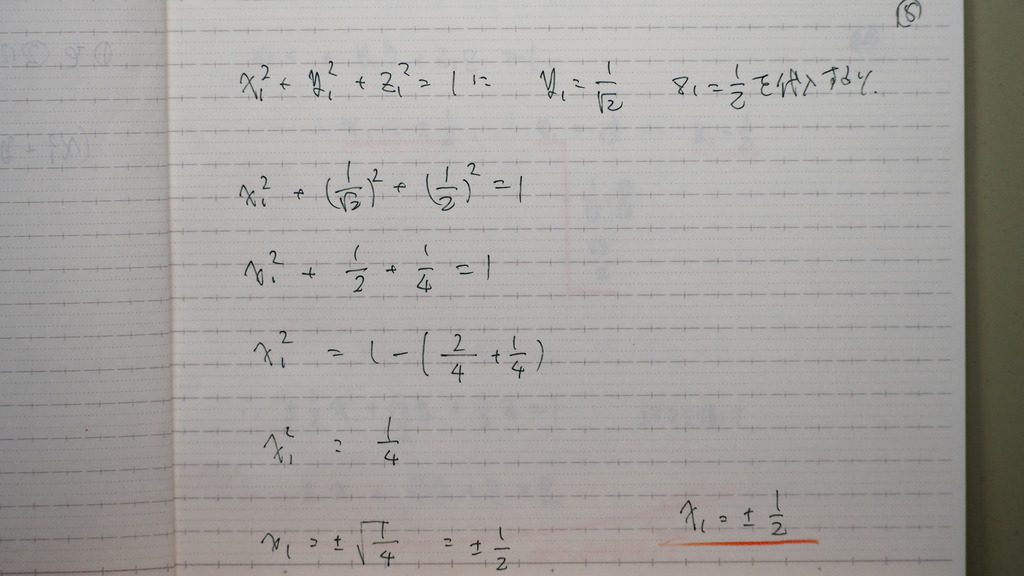
19
これを
整理した
平面の 方程式に 代入して
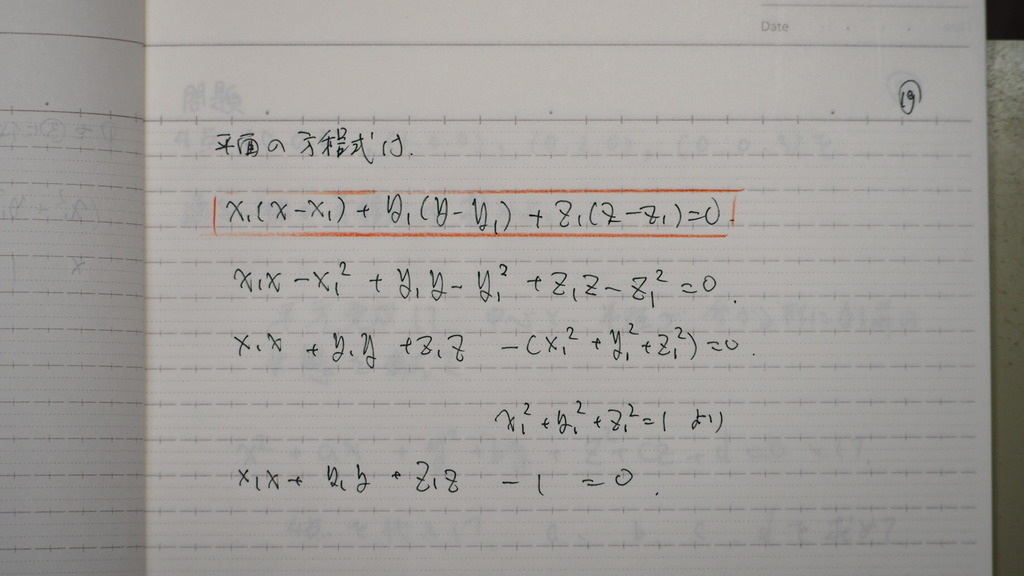
20
こんな感じに

21
4点を 通る
球の方程式
球の方程式の
平方完成する前の 形を
使って

22
4点を 逐次 代入してくと
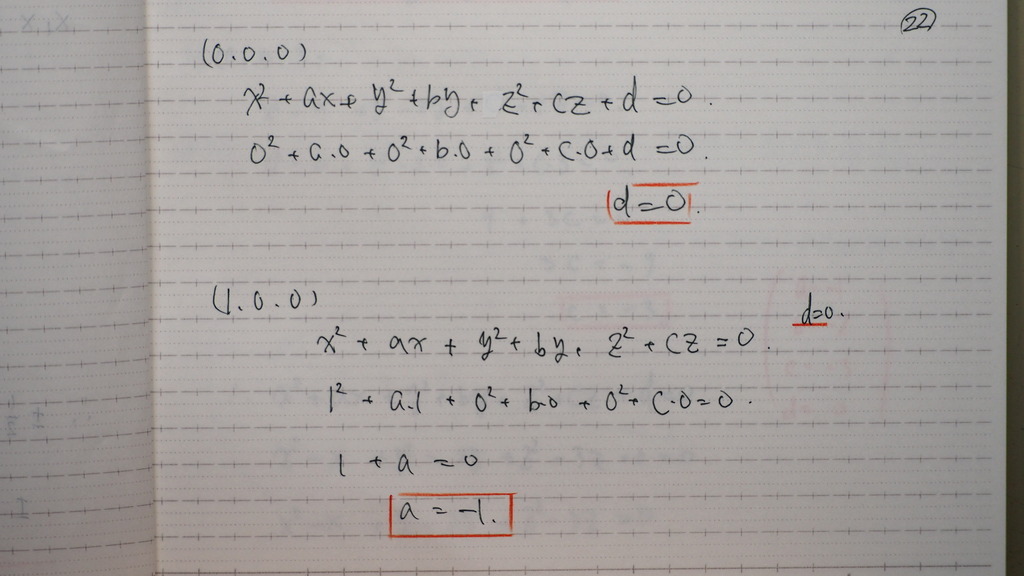
23
こんな感じに
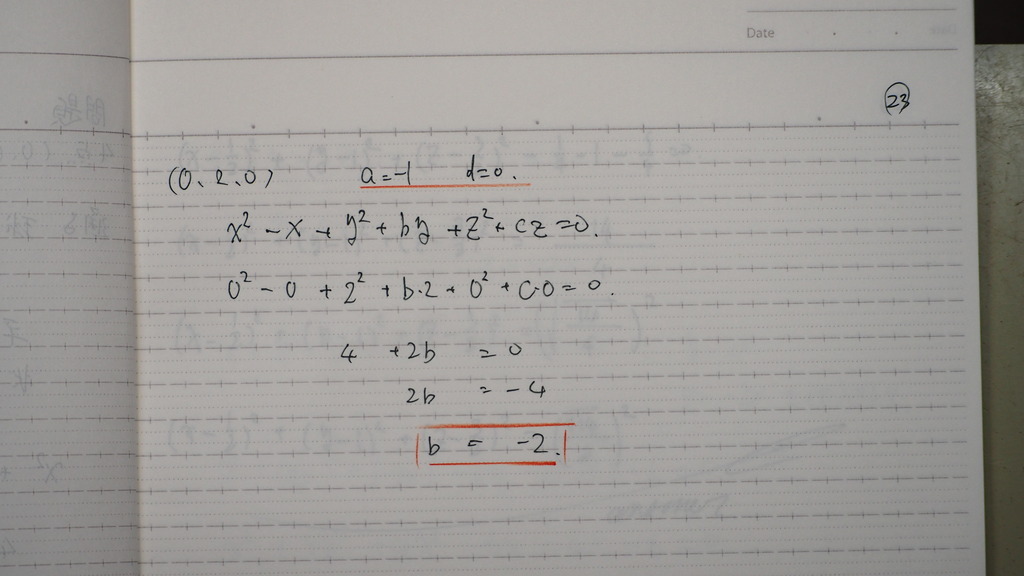
24
これらを
a,b,c,dに
代入したらば
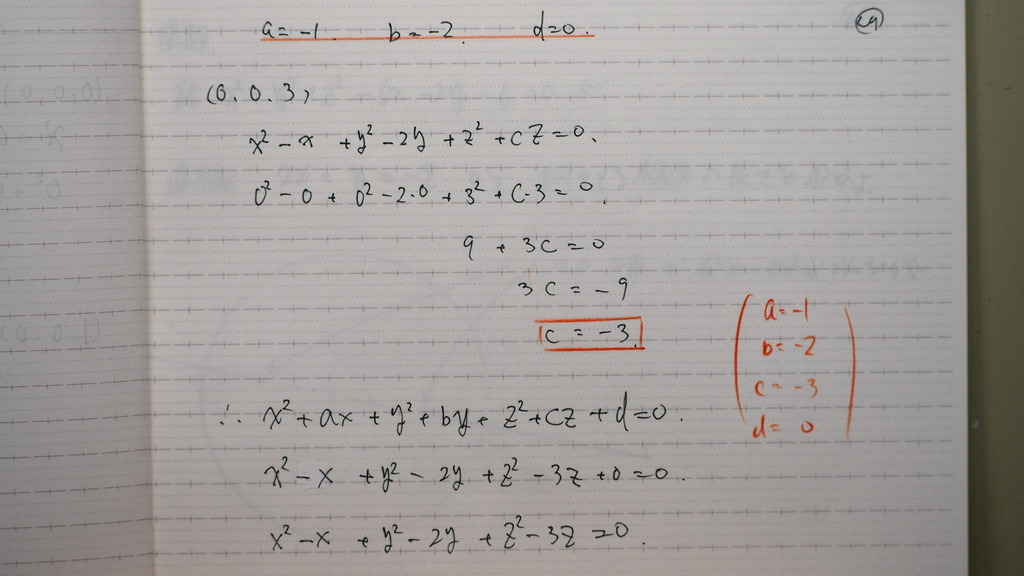
25
これです
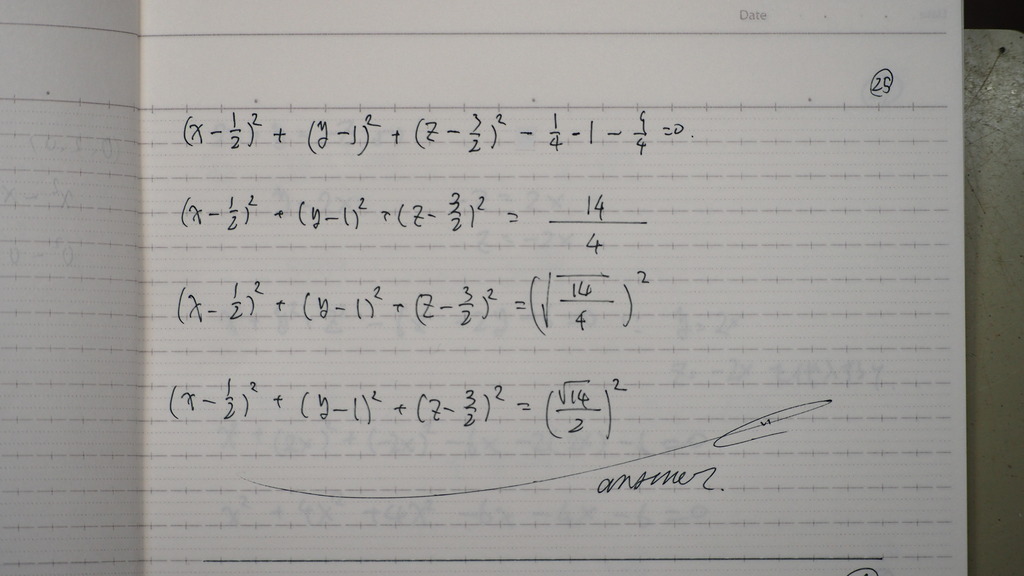
26
球の方程式が
切り取る
直線の 方程式の長さ

27
直線の 方程式の y、z を
xで 置き換えて
球の 方程式に
代入したらば
xの 2次方程式に
なるにおだけれど
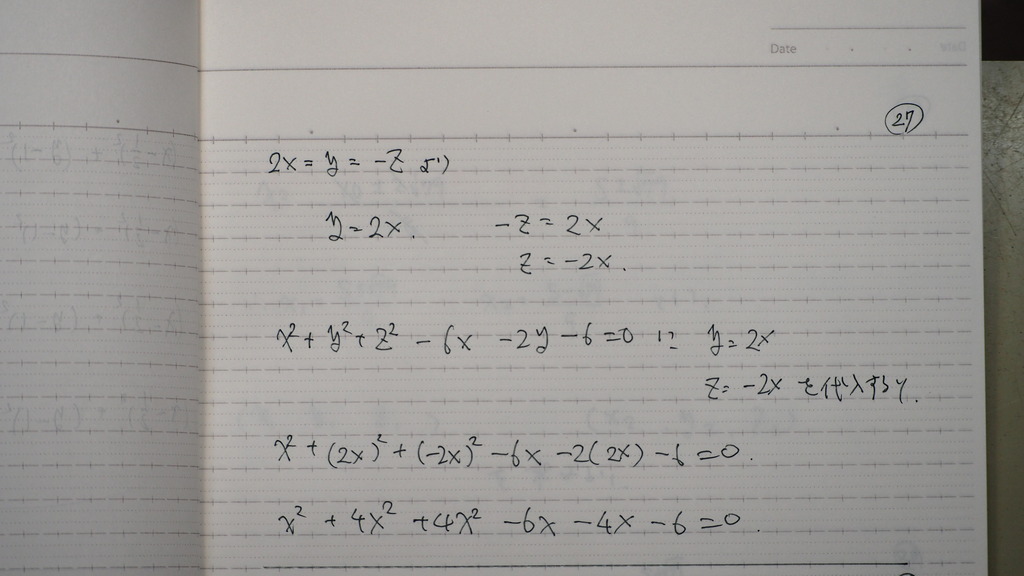
28
これは
異なる 2実数解を 持つので
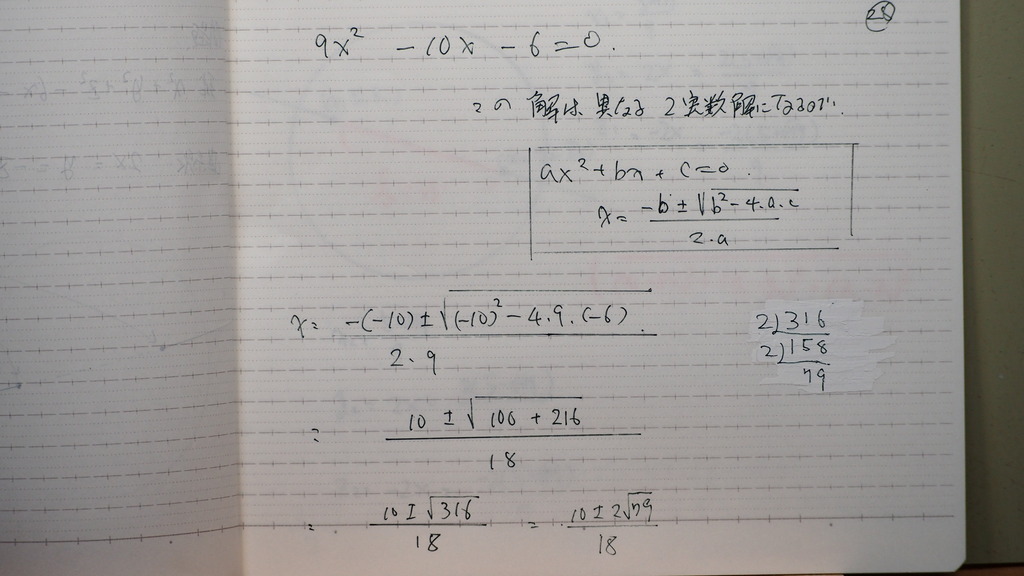
29
その一つを X1
もう一方を X2
として

30
2点間の 距離を
計算すると

31
こんなデショ
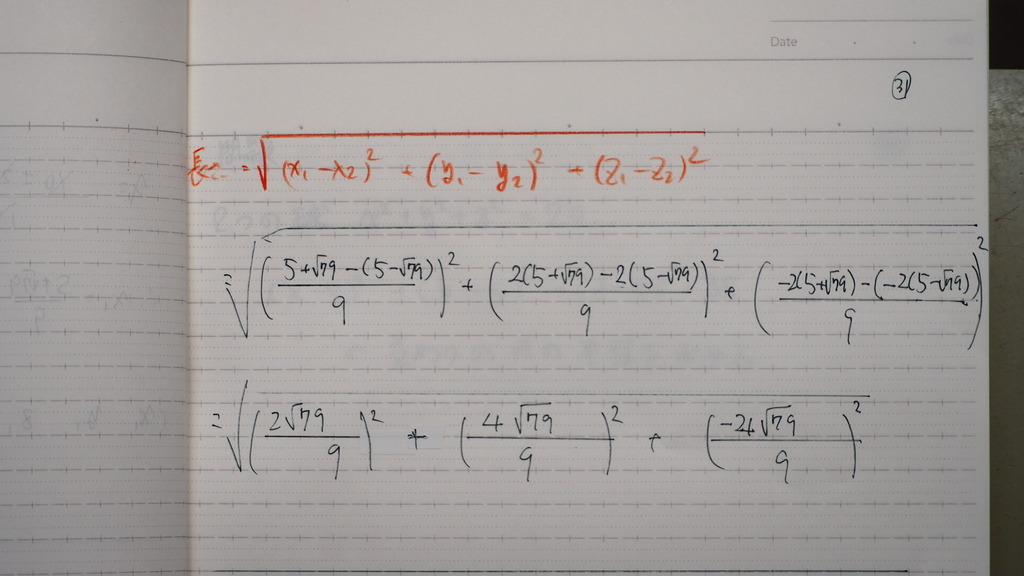
32
計算を
間違わないようにじゃナイスカ

33
2つの
球があってですよ
交わりの
円の 半径を 求めよ

34
平面のところで
こんなのを
やったんですが

35
球でも
おなじですよ

36
今回は
この式は
k=-1 とすれば
x2 y2 z2 が 消えて 平面を表す。
辺々引算して
出て来たのが
交円を含む 平面の方程式
のはずなので
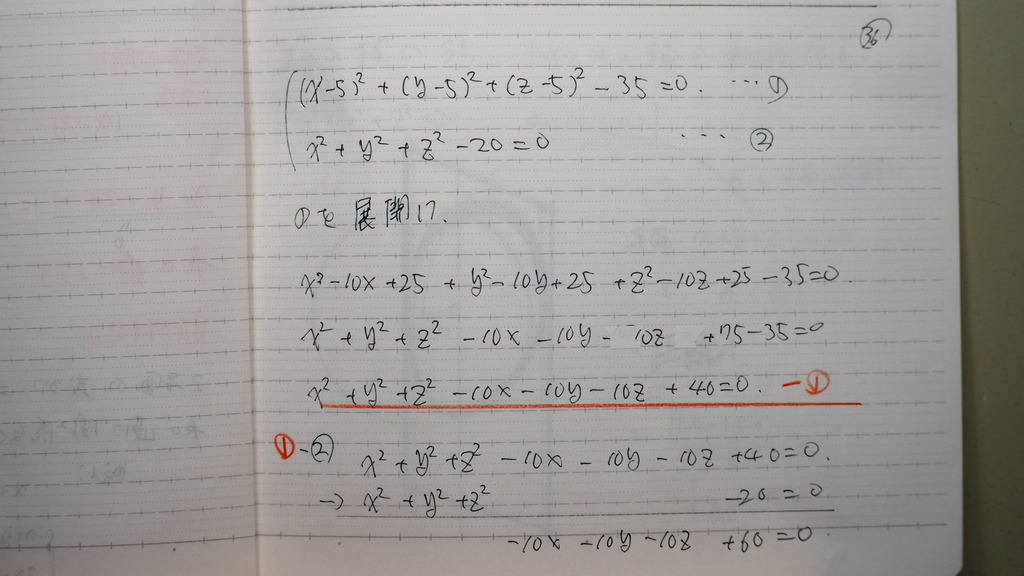
37
これを 使って

38
交円を 含む 平面までの
距離を 計算すると
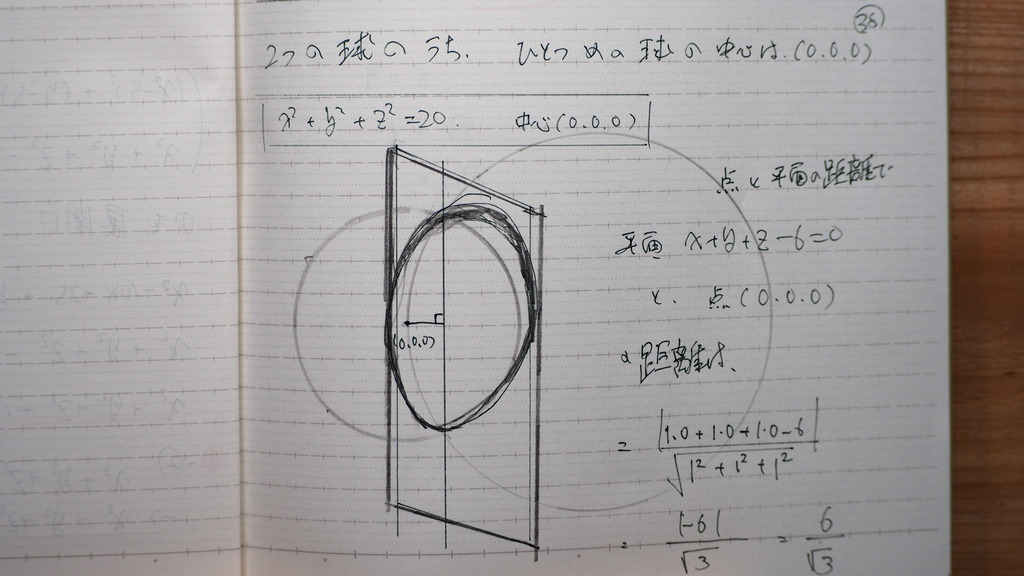
39
小さい球の
半径が分かってるので

お疲れ様です。
球と 接平面
01
まず 問題
球の方程式を 導く
02
球面上の 一点での 接平面
と
2点を 通り
球接する平面
03
まず
ベクトルの 引き算で
出てきたものが
Pは 動点だから
動き回るんだけど
ッテ式を
04
辺々2乗するでしょ
で
かっこの中身が
成分の引き算で
05
こんな感じに
成分の 引き算になるので
この 内積の 展開で
06
なりましたと
07
この 球面上の
点B における 接平面は
平面の 垂直成分は
球の中心から Bにおろした
垂線のベクトル
08
平面の 方程式は
垂直成分と
通過点がわかてるときの場合を
使って
09
BA ベクトル
平面に垂直な成分
と
通過点 B から
10
これに 代入してですよ
11
2点を 通り
球に接する平面は
今の (2) を
うまく使って
点B で
球に 接している
その平面が
2点も 通過するで
代入して
ここでは Aとすれば
Aの X1 Y1 Z1
を
特定すれば
平面の 方程式になるので
12
まず 球の方程式に
点Aで接する平面は
13
こんな形
それと
だいいから・・・
14
2点を
平面の 方程式に代入すると
②③
15
➀②③より
平面の方程式を
求めると
16
z1
17
y1
18
x1
19
これを
整理した
平面の 方程式に 代入して
20
こんな感じに
21
4点を 通る
球の方程式
球の方程式の
平方完成する前の 形を
使って
22
4点を 逐次 代入してくと
23
こんな感じに
24
これらを
a,b,c,dに
代入したらば
25
これです
26
球の方程式が
切り取る
直線の 方程式の長さ
27
直線の 方程式の y、z を
xで 置き換えて
球の 方程式に
代入したらば
xの 2次方程式に
なるにおだけれど
28
これは
異なる 2実数解を 持つので
29
その一つを X1
もう一方を X2
として
30
2点間の 距離を
計算すると
31
こんなデショ
32
計算を
間違わないようにじゃナイスカ
33
2つの
球があってですよ
交わりの
円の 半径を 求めよ
34
平面のところで
こんなのを
やったんですが
35
球でも
おなじですよ
36
今回は
この式は
k=-1 とすれば
x2 y2 z2 が 消えて 平面を表す。
辺々引算して
出て来たのが
交円を含む 平面の方程式
のはずなので
37
これを 使って
38
交円を 含む 平面までの
距離を 計算すると
39
小さい球の
半径が分かってるので
お疲れ様です。
2023年01月04日
22033大人のさび落とし 空缶座標とベクトル より 方向余弦
大人のさび落とし
空間座標 と ベクトル
より
方向余弦
01
空間直線が
x軸 y軸 z軸
と なす角を
ソレゾレ
α β γ とすれば
次の 等式が
成り立つことを 証明せよ

02
ベクトルは
平行移動していいので
原点まで
平行移動して
ソレゾレ
x軸 y軸 z軸
と なす角を
α β γ とすると
直線を P(x、y、z)
とする時
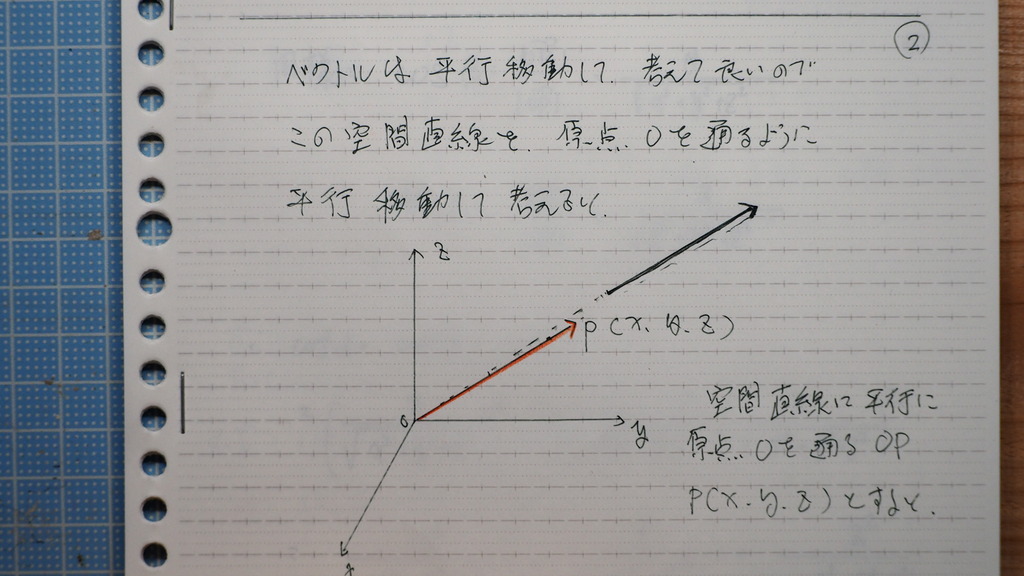
03
COSα
COSβ
COSγ
は
まず COSα から見てくと
OP 分の OA
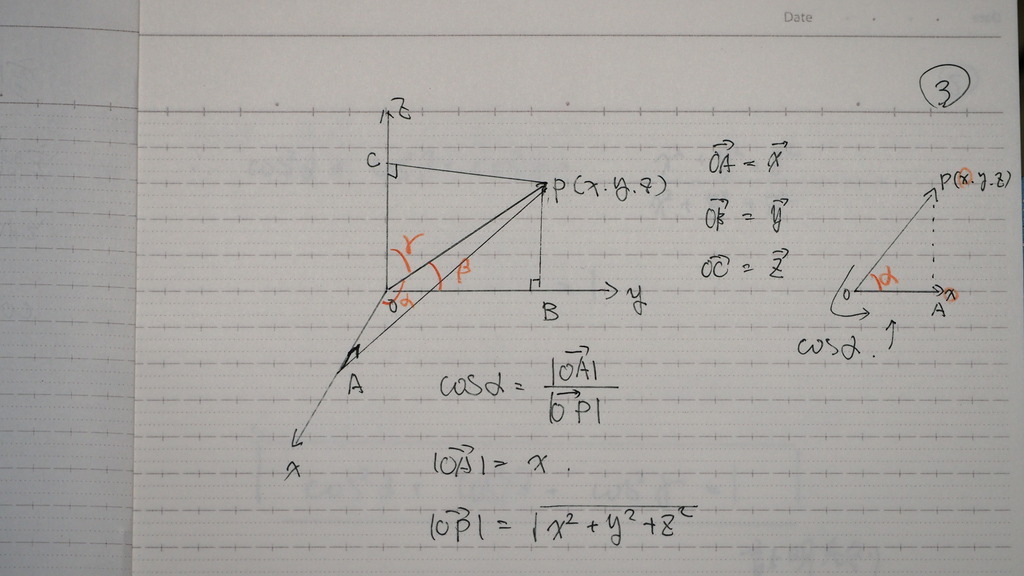
04
COSβ
COSγ
も 同様にして
出そろった
COSα
COSβ
COSγ
を それぞれ 2乗して
足してみますと
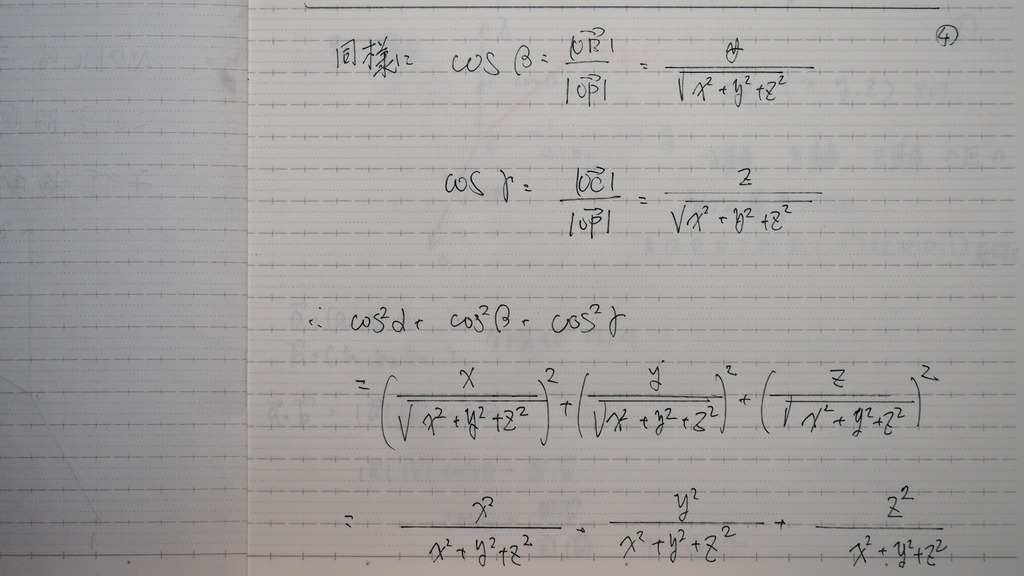
05
なったじゃナイスカ

06
ベクトルの
内積を 使った場合は
A,B,Cを
(1,0,0)(0,1,0)(0,0,1)
として
内積から
なす角 の COSを 求めると

07
こんな感じに

08
なるじゃ
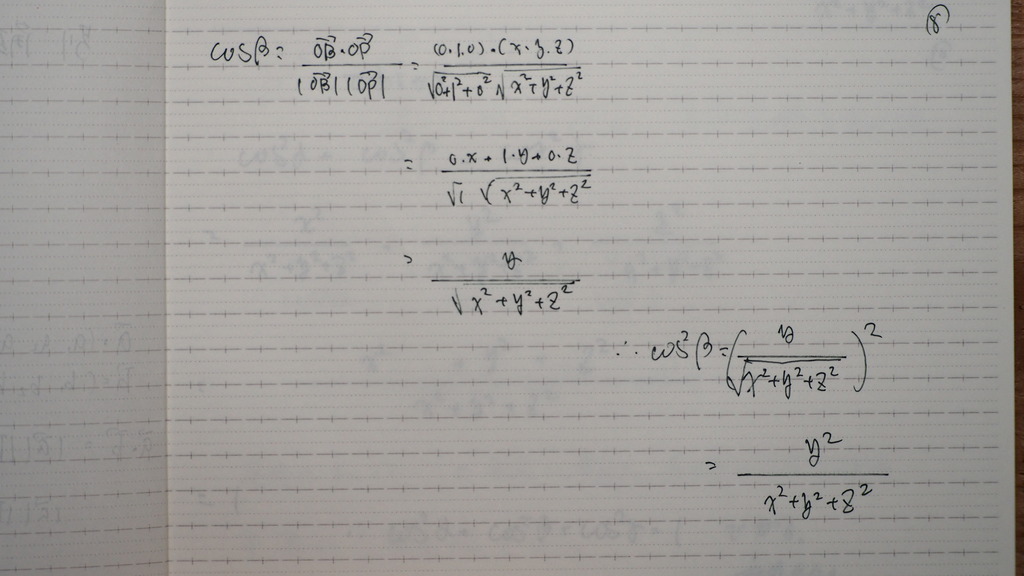
09
ナイスカ

10
であるから
ソレゾレ
2乗したものを
足すと
なったと
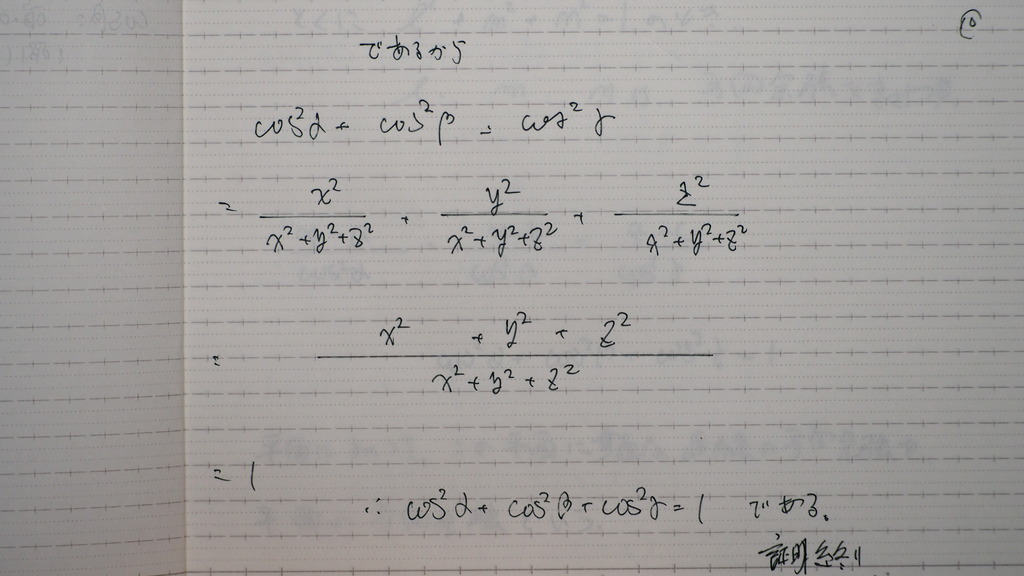
11
まとめ

12
こんな風にも
書けるてことカナ
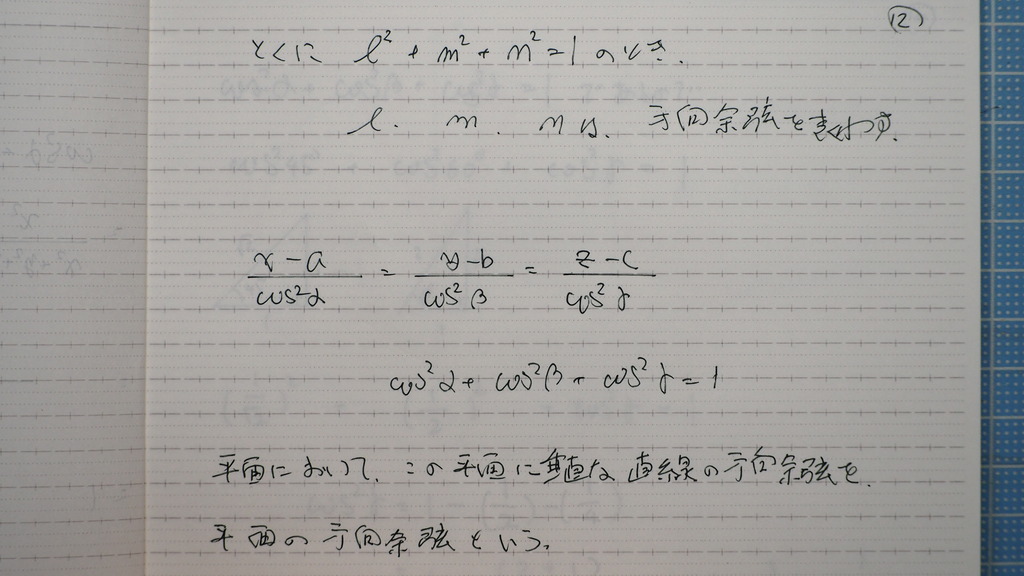
13
問題
空間直線が
x軸と 45度
y軸と 60度
の角度を
なすとき
z軸との なす角は
どれくらいか
群馬県では
懐かしい アニメを
夜中に
放送してましが
バルキリーが 放つ
ミサイルの横に
タコ酎ハイ に バドワイザー

14
で 今日は
z軸のなす角だから
さっき証明した式を
使って
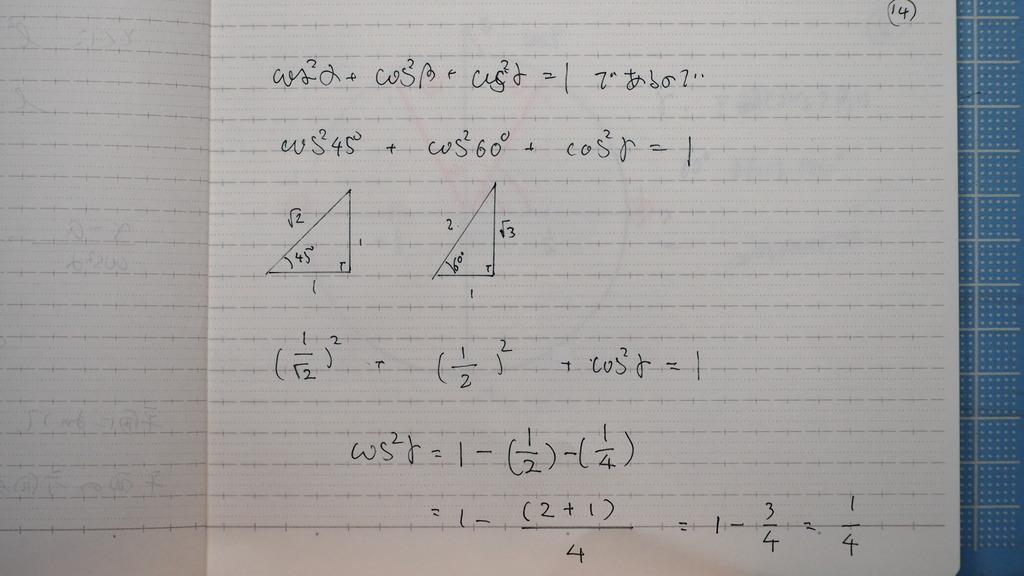
15
なす角は
0から180ど
その範囲で
プラスマイナスを
考えると
コサインなので
動径の x軸への影が
プラスマイナス 1/2
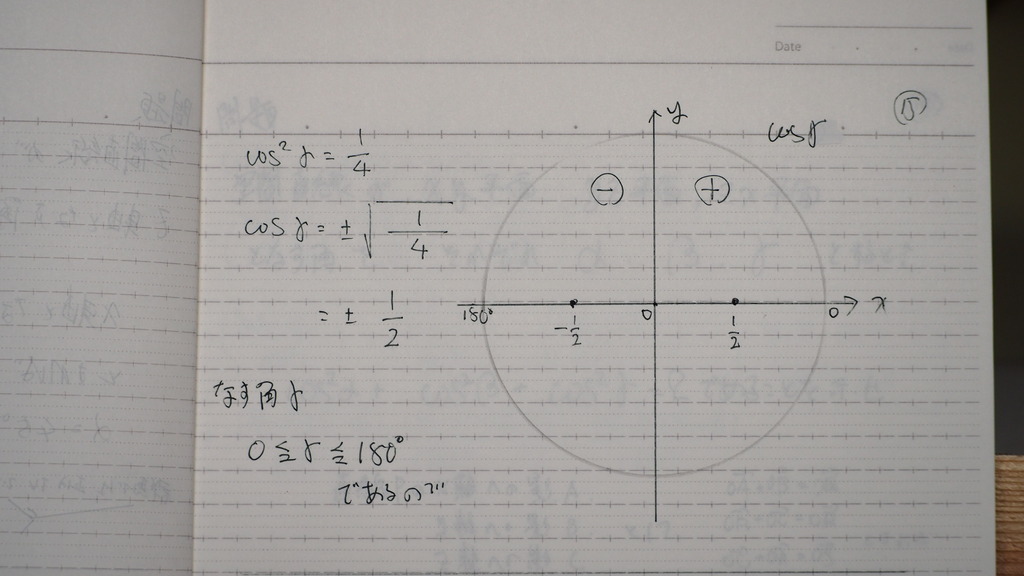
16
答は
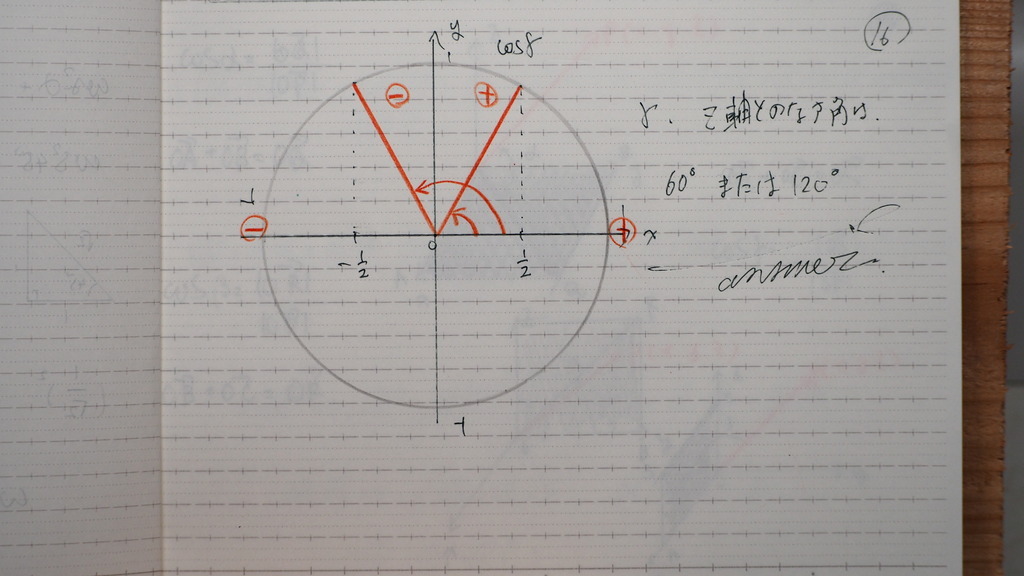
17
次は
ちょっと違うんですよ
直線が
平面と なす角
問題

18
xy yz zx
平面との
なす角であるから
こんな感じになるでよ
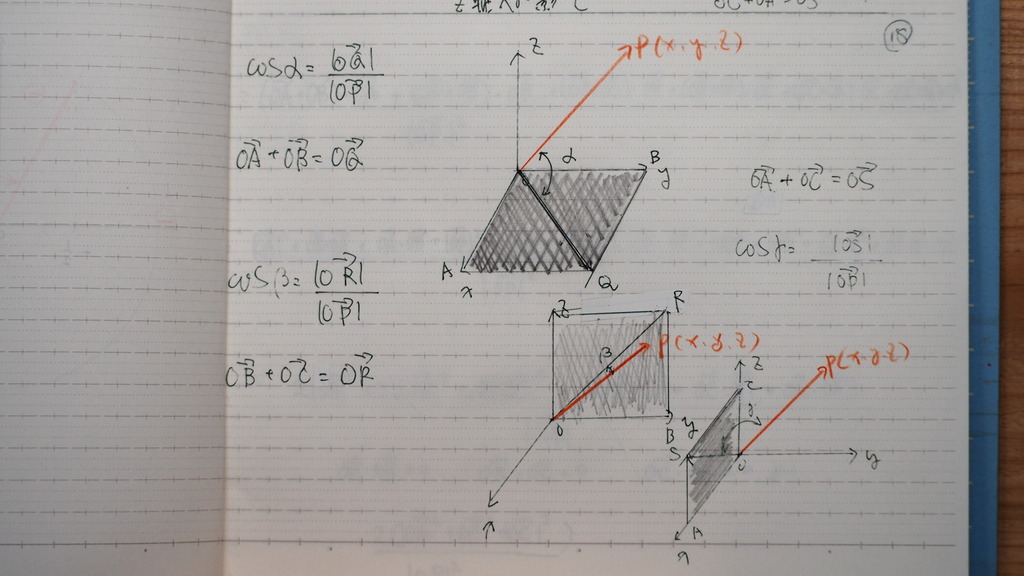
19
これを
計算してみると
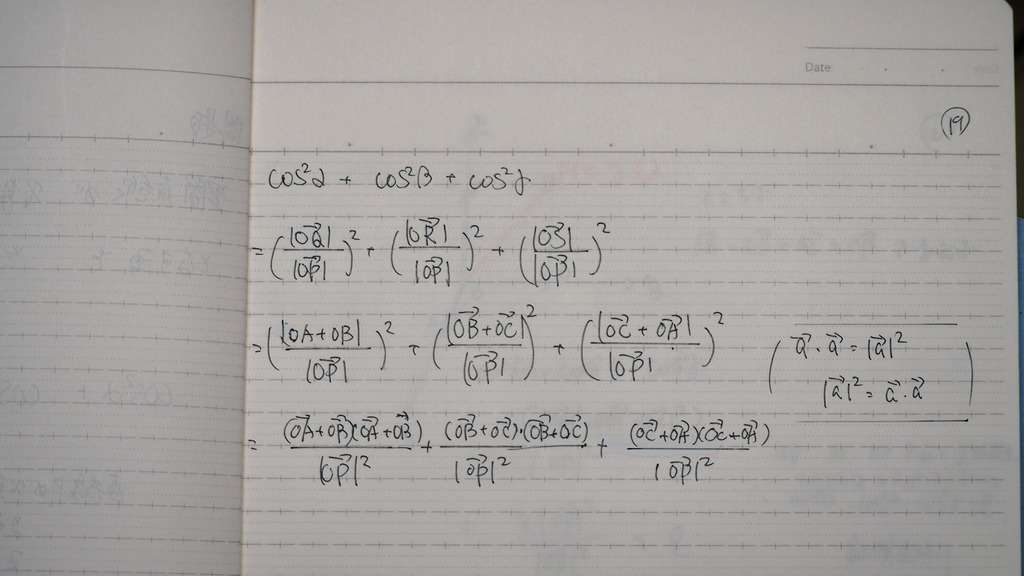
20
大丈夫かな
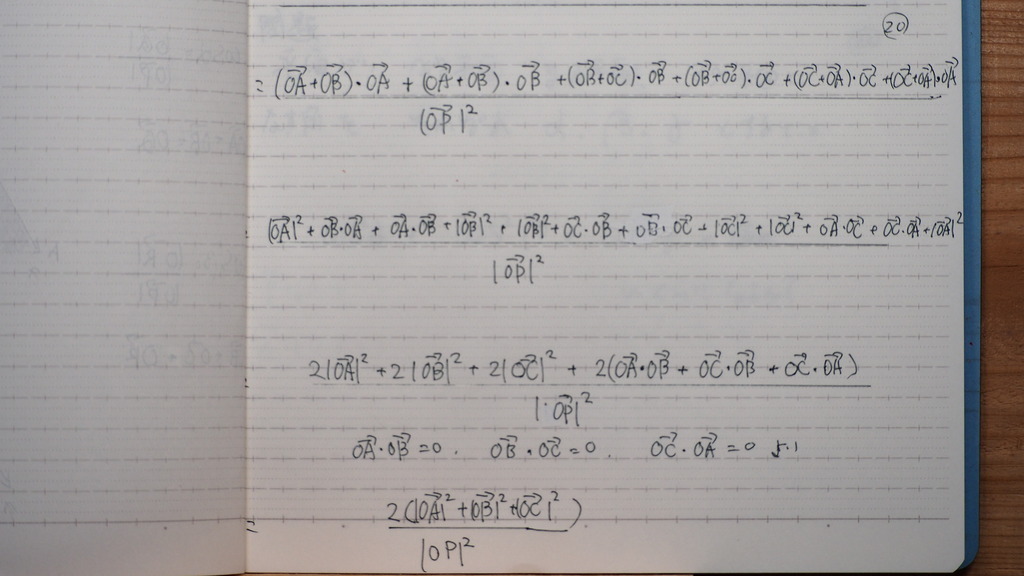
21
計算を
はぶいてますが
OA+OB+OC=OP
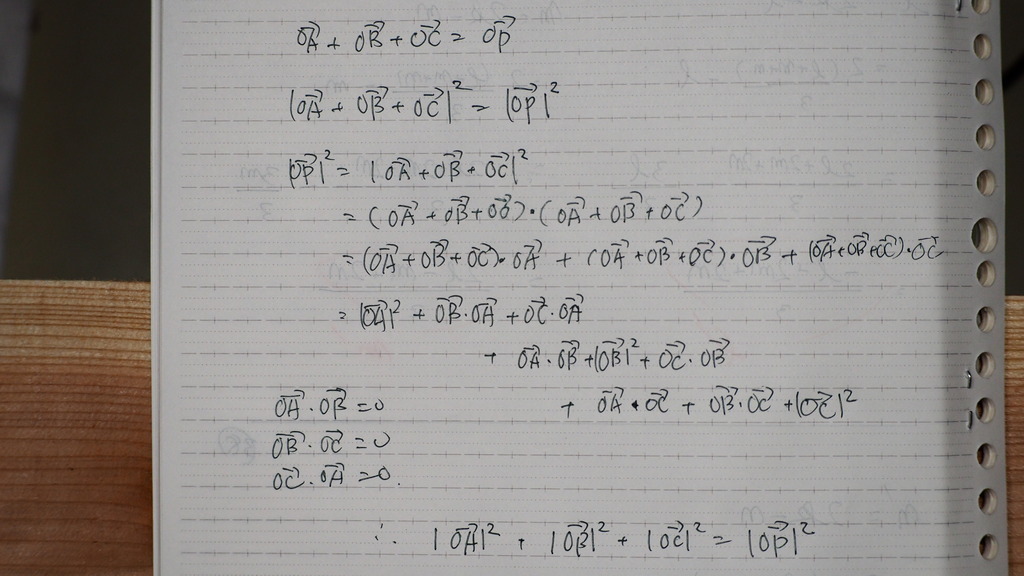
を
辺々 絶対値2乗すれば
直交座標系なので
OA OB OC の二乗以外の
項は =0 になってしまうので
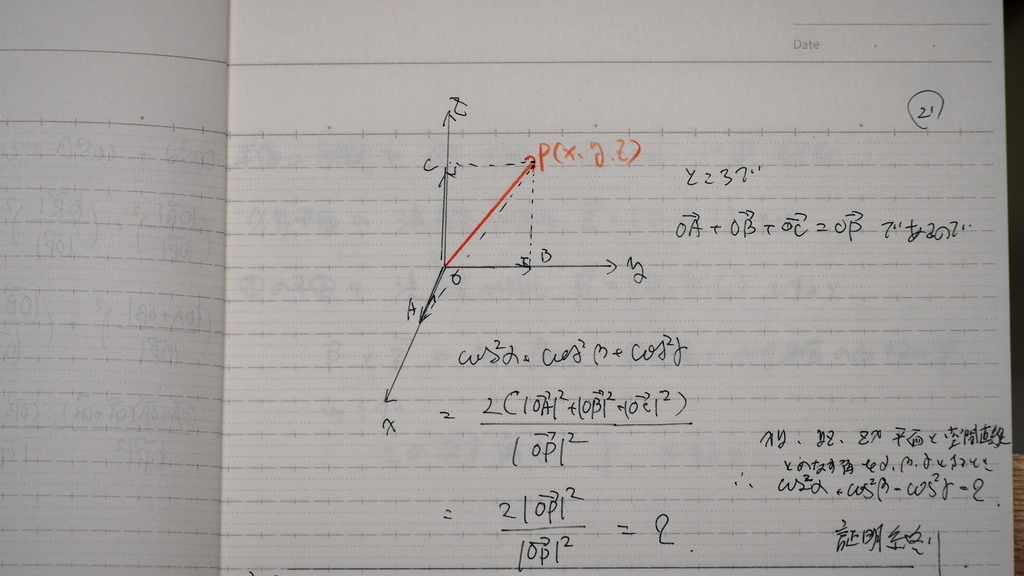
22
問題

23
平面の 方程式を ➀として
それぞれの 平面の法線ベクトル
と
平面の法線ベクトルで
なす角を 出してくると

24
xy平面は z方向が法線
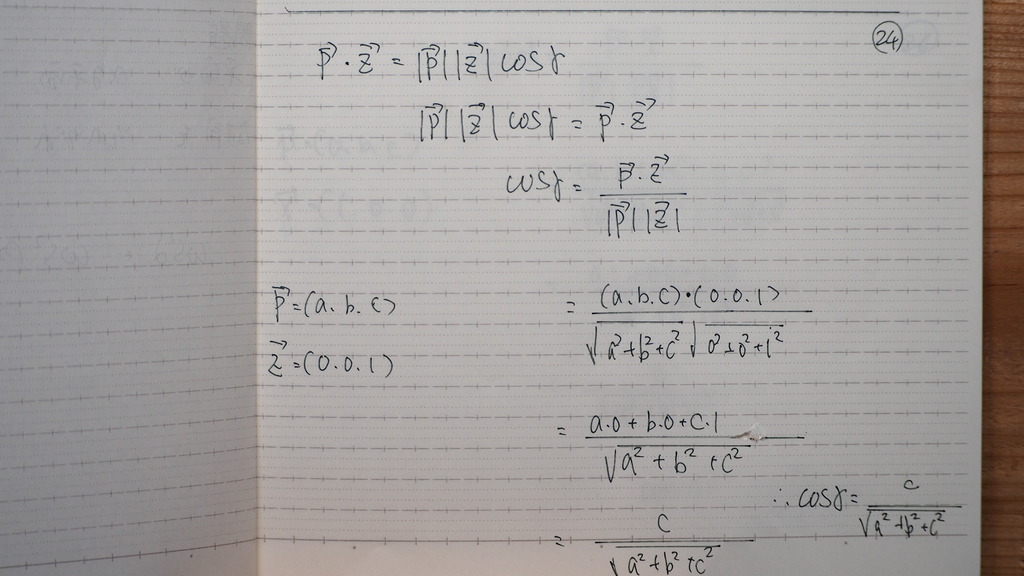
25
yz平面は x軸方向が 法線

26
こんな感じに
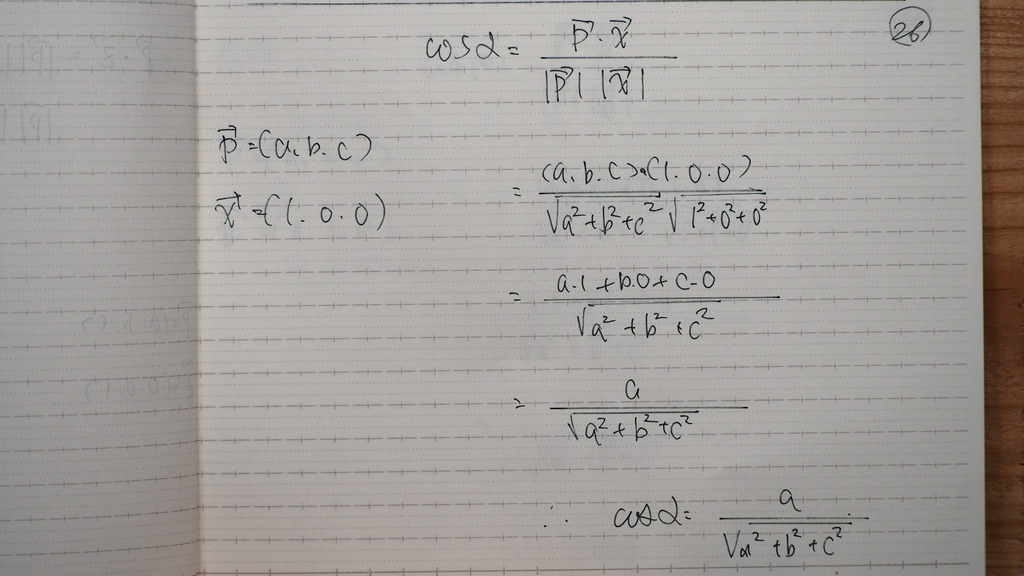
27
xz平面は y軸方向が 法線

28
出そろったので
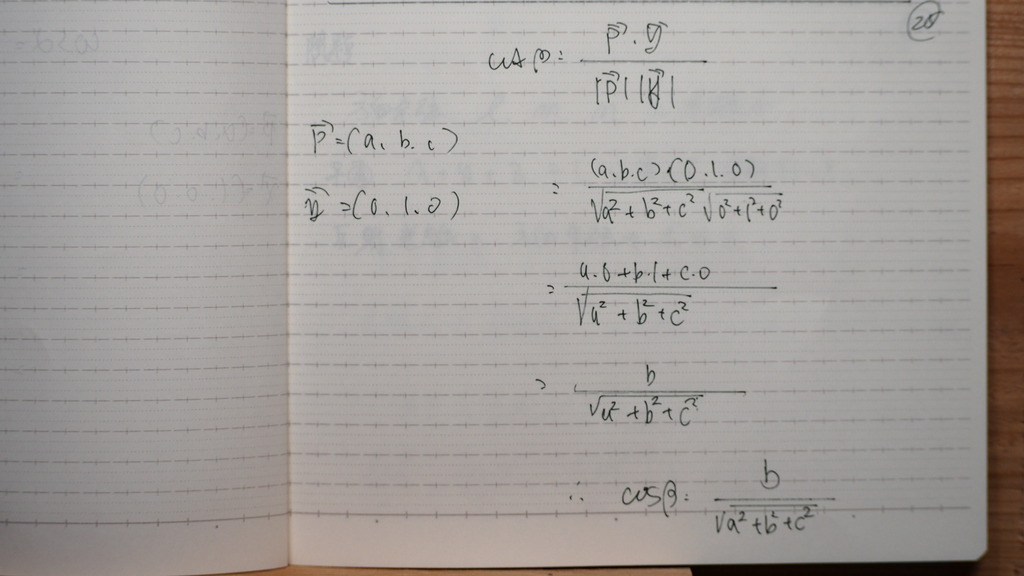
29
二乗して
計算してくと
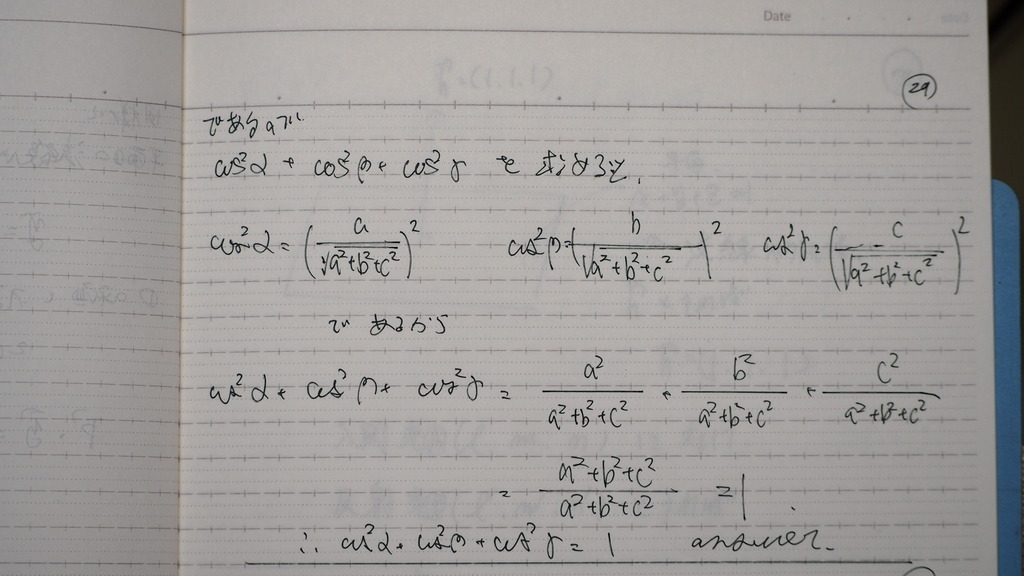
30
問題

31
こんな感じに
設定してですよ

32
入射光 反射光
対称になるから
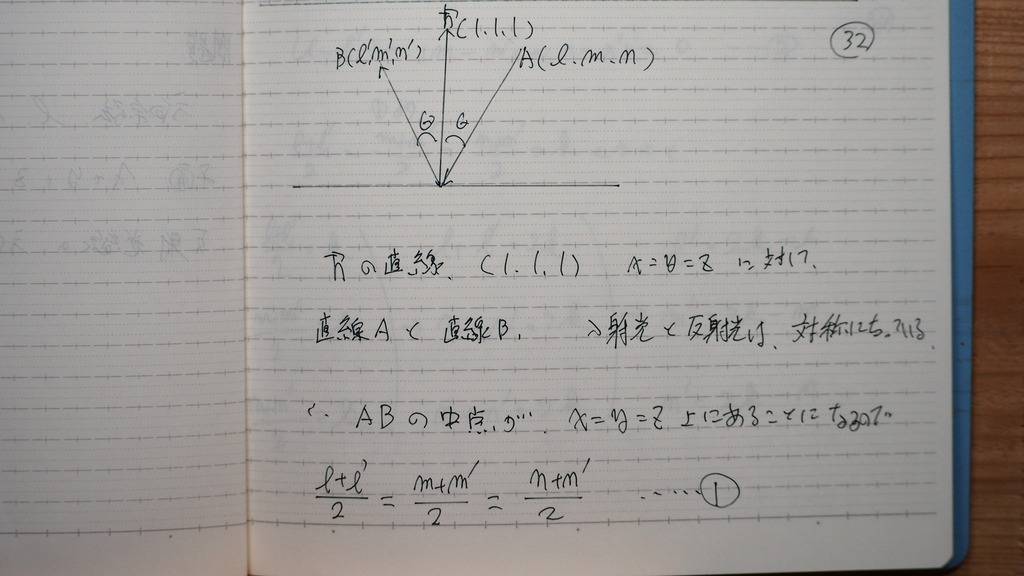
33
それと
AB と x=y=zは 垂直だから

34
中点が イコール を kと置いて
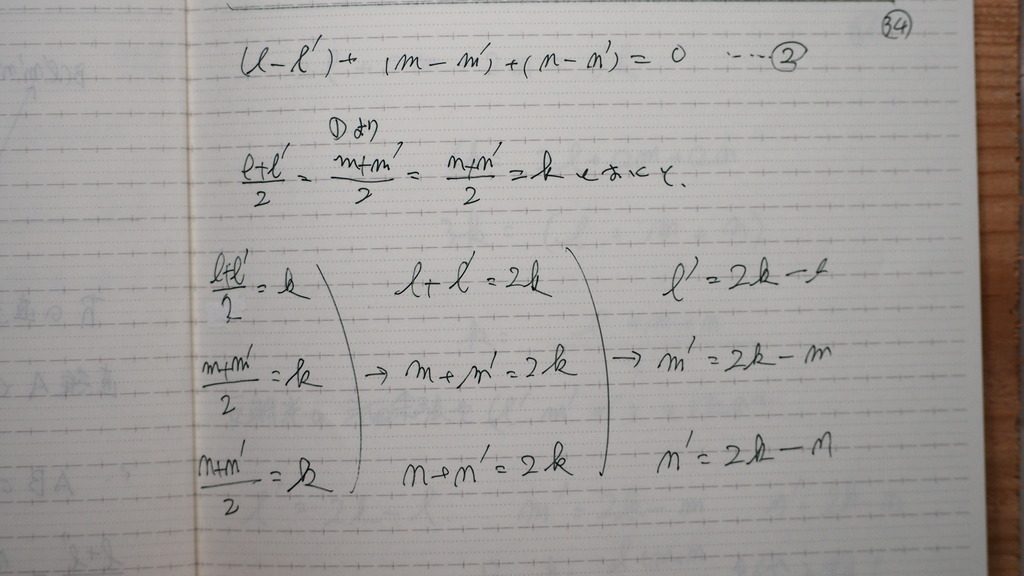
35
②式に 代入して
kを もとめて
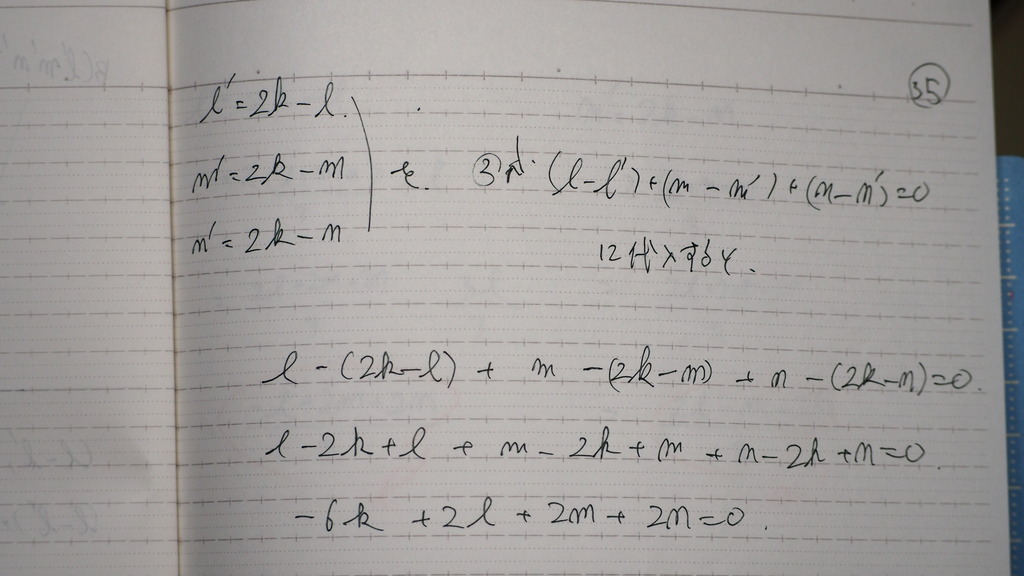
36
これで

37
反射光の 成分を
計算したらば
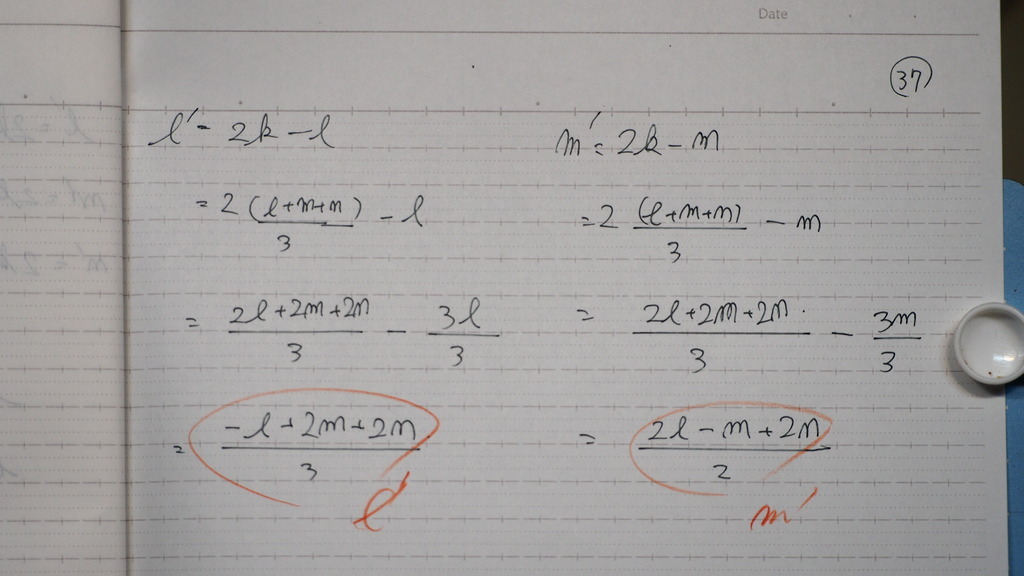
38
こんな感じ

空間座標 と ベクトル
より
方向余弦
01
空間直線が
x軸 y軸 z軸
と なす角を
ソレゾレ
α β γ とすれば
次の 等式が
成り立つことを 証明せよ
02
ベクトルは
平行移動していいので
原点まで
平行移動して
ソレゾレ
x軸 y軸 z軸
と なす角を
α β γ とすると
直線を P(x、y、z)
とする時
03
COSα
COSβ
COSγ
は
まず COSα から見てくと
OP 分の OA
04
COSβ
COSγ
も 同様にして
出そろった
COSα
COSβ
COSγ
を それぞれ 2乗して
足してみますと
05
なったじゃナイスカ
06
ベクトルの
内積を 使った場合は
A,B,Cを
(1,0,0)(0,1,0)(0,0,1)
として
内積から
なす角 の COSを 求めると
07
こんな感じに
08
なるじゃ
09
ナイスカ
10
であるから
ソレゾレ
2乗したものを
足すと
なったと
11
まとめ
12
こんな風にも
書けるてことカナ
13
問題
空間直線が
x軸と 45度
y軸と 60度
の角度を
なすとき
z軸との なす角は
どれくらいか
群馬県では
懐かしい アニメを
夜中に
放送してましが
バルキリーが 放つ
ミサイルの横に
タコ酎ハイ に バドワイザー
14
で 今日は
z軸のなす角だから
さっき証明した式を
使って
15
なす角は
0から180ど
その範囲で
プラスマイナスを
考えると
コサインなので
動径の x軸への影が
プラスマイナス 1/2
16
答は
17
次は
ちょっと違うんですよ
直線が
平面と なす角
問題
18
xy yz zx
平面との
なす角であるから
こんな感じになるでよ
19
これを
計算してみると
20
大丈夫かな
21
計算を
はぶいてますが
OA+OB+OC=OP
を
辺々 絶対値2乗すれば
直交座標系なので
OA OB OC の二乗以外の
項は =0 になってしまうので
22
問題
23
平面の 方程式を ➀として
それぞれの 平面の法線ベクトル
と
平面の法線ベクトルで
なす角を 出してくると
24
xy平面は z方向が法線
25
yz平面は x軸方向が 法線
26
こんな感じに
27
xz平面は y軸方向が 法線
28
出そろったので
29
二乗して
計算してくと
30
問題
31
こんな感じに
設定してですよ
32
入射光 反射光
対称になるから
33
それと
AB と x=y=zは 垂直だから
34
中点が イコール を kと置いて
35
②式に 代入して
kを もとめて
36
これで
37
反射光の 成分を
計算したらば
38
こんな感じ
2022年12月22日
22032大人のさび落とし 空間座標とベクトル 2平面のなす角
大人のさび落とし
空間座標とベクトル
2平面のなす角
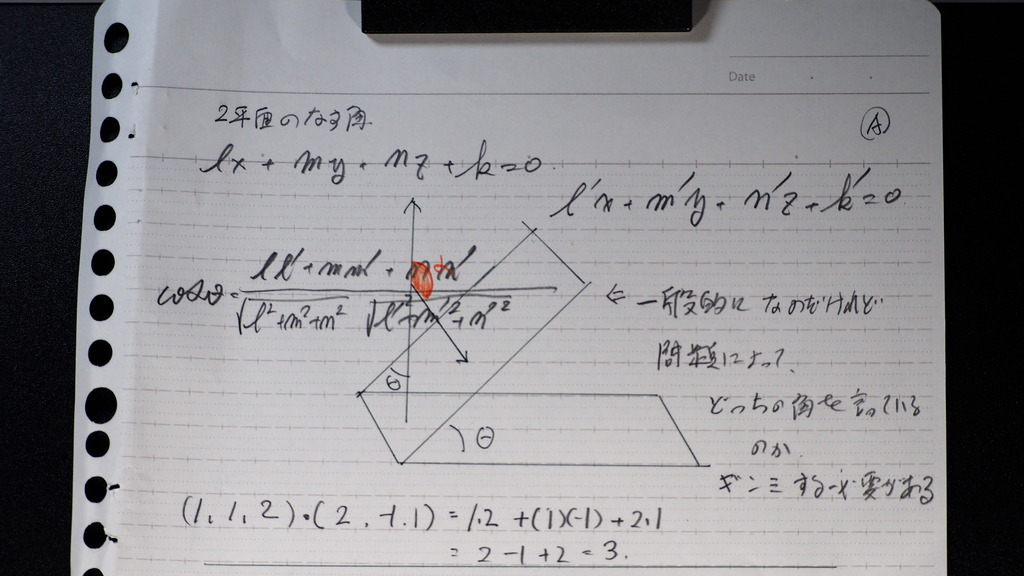
A
なす角の 計算は
平面同士の時は
法線ベクトル
の 内積で出るのだけれど
問題によって
どちらの 角度を
聞いているか
ぎんみ する必要がある
B
こちらの場合
隣接面の
側面の なす角
どっちかな
ッテ
吟味する必要がある
(机上の 数値計算の場合は)
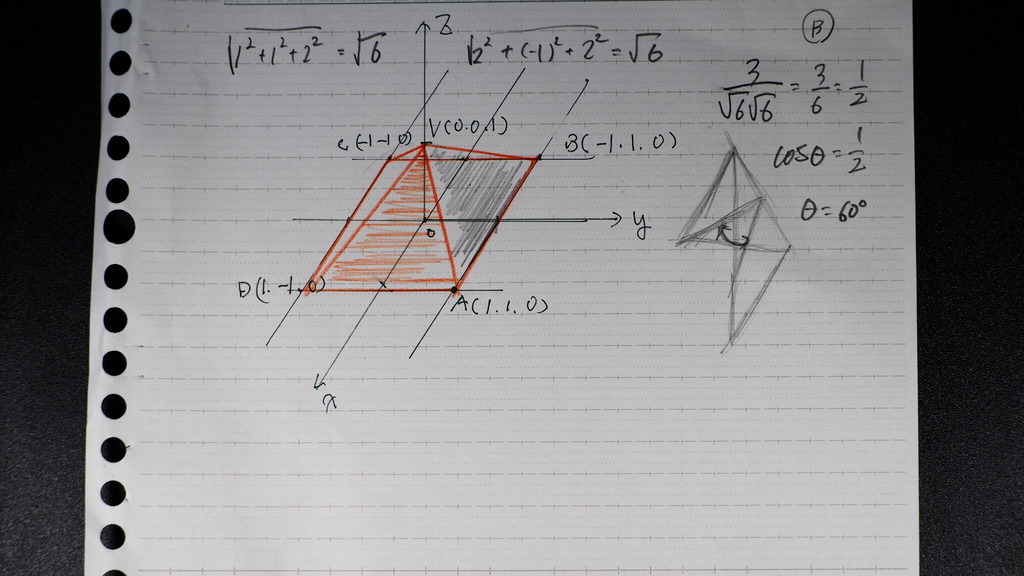
01
それらを
前置きしておいて
問題

02
xy 平面の
垂線ベクトルは
0,0,1
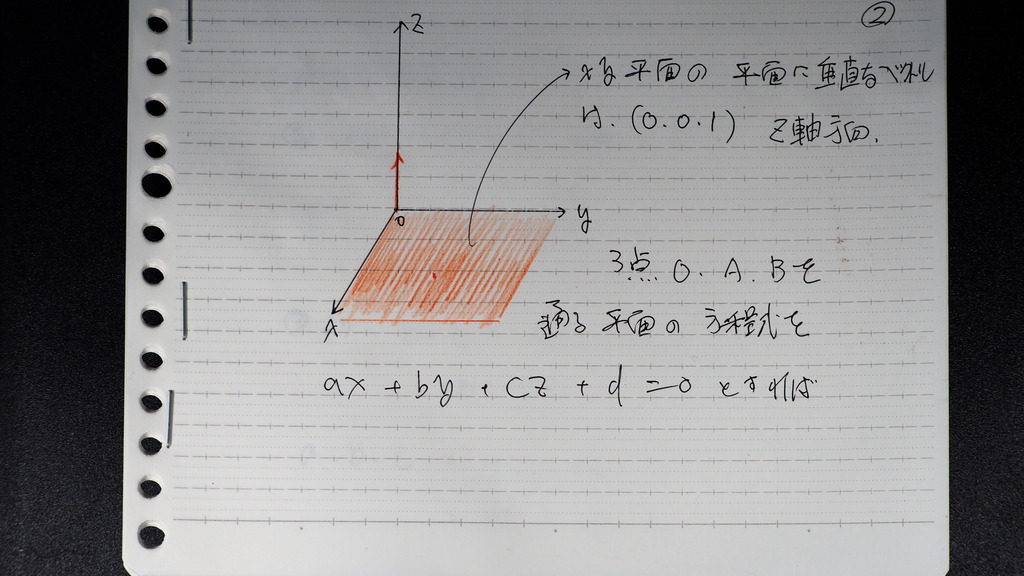
03
もう一つの 面は
計算しないと
わからないので
3点から
平面の式に
代入して
( 3点が わかるときは
ベクトルでも 出ますが )

04
全部 c で 表して
へてから -1、-1,1
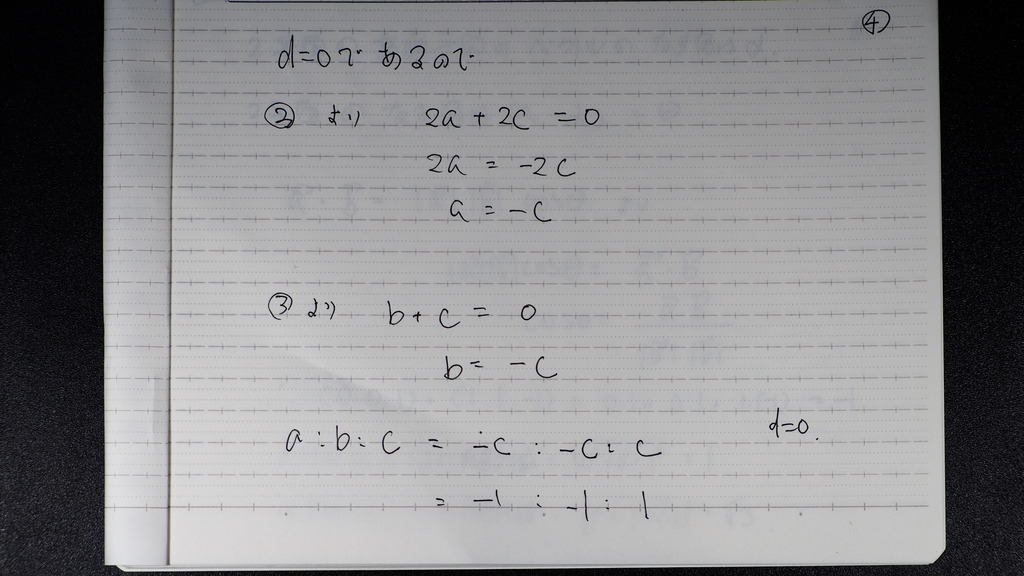
05
平面の式にして
符号を 整えて
1、1、-1
-1、-1,1 でもOK ですが
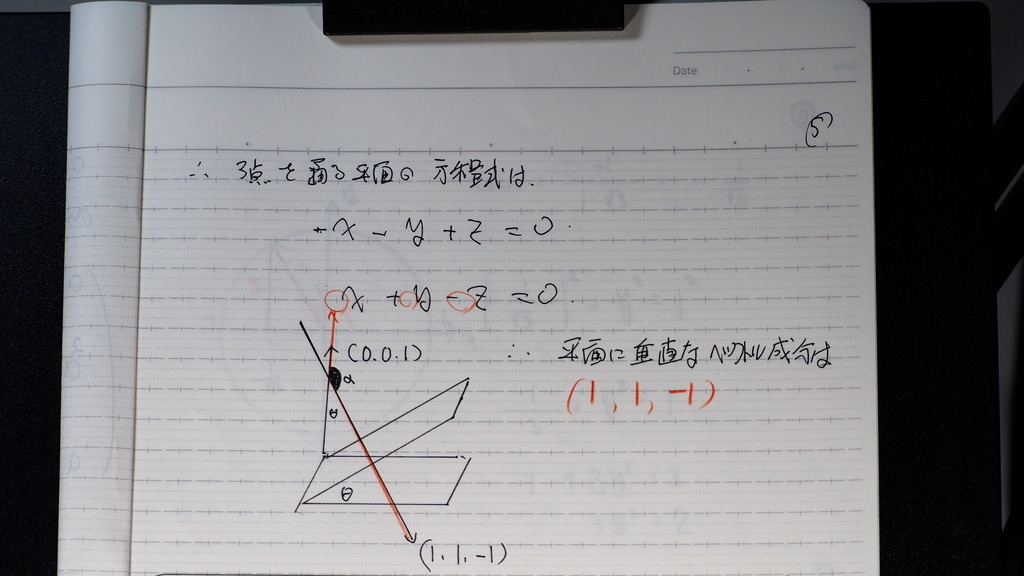
06
そうすれば
内積の計算から
コサインで
求めて

07
y を 求めると
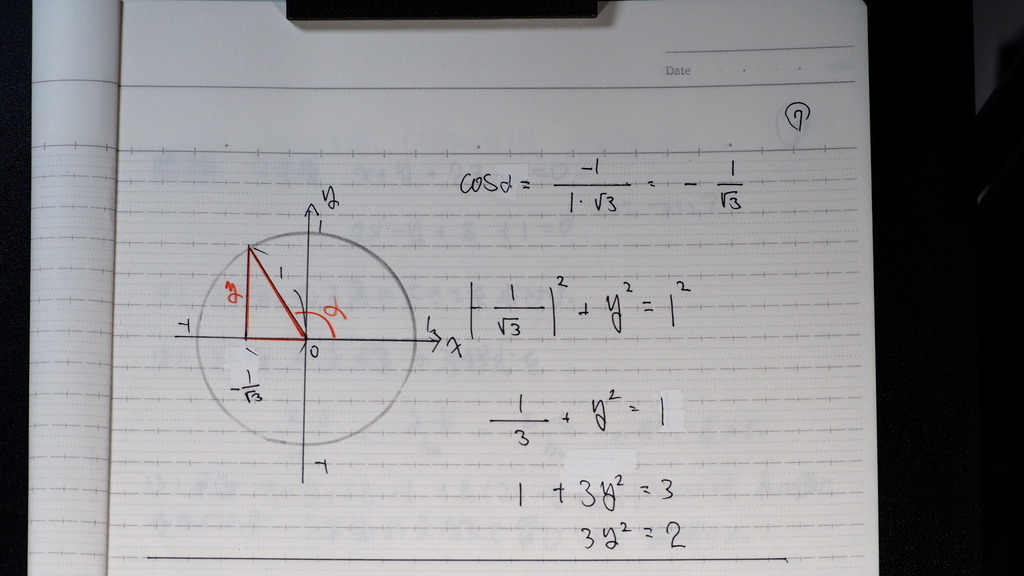
08
タンジェント αは -√2
図でいうところの
Θ が 今回 なす角 Θなので
補角を 使って
TanΘ は √2

09
今度は
そのまま 計算できるパターン
(1)なす角は
(2)2平面の 交線は
(3)この等式を 証明して
( 2平面の交線を 含む 平面の
方程式 )重要
(4)
を 落としてますが
原点と この2平面の 交線を
含む 平面の方程式を
求めよ
(3)の結果を 使うと早い

10
両平面の方程式から
垂線のベクトルを
内積で
計算して
なす角を 出すと

11
こんな感じに
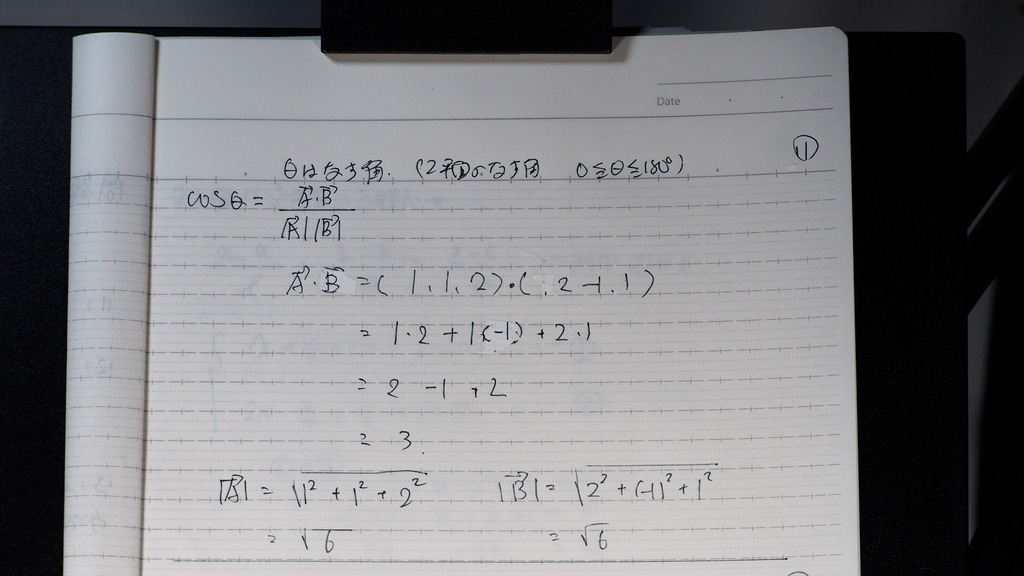
12
そのまま
60度
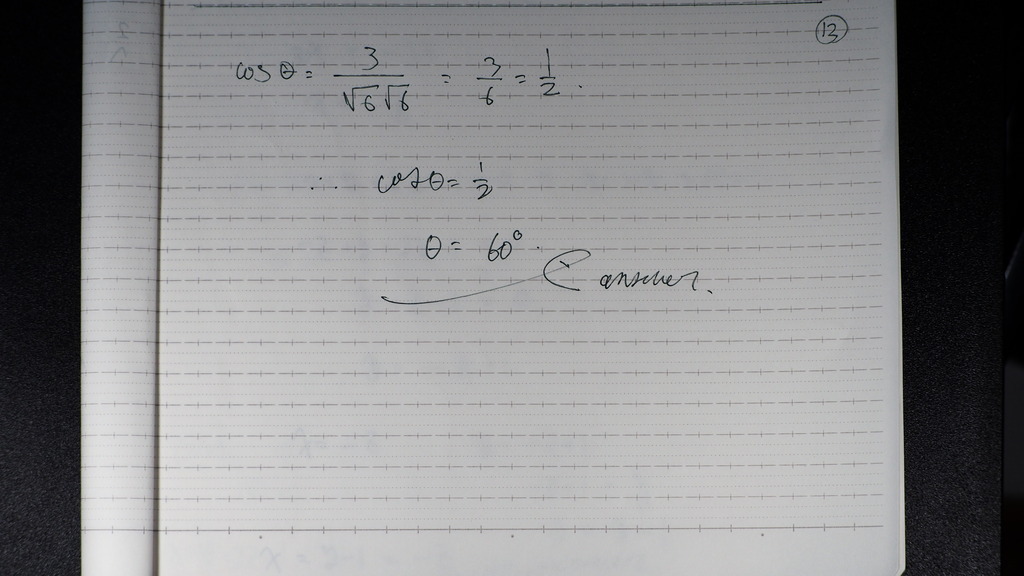
13
2平面の
交線は
そのまま 平面を
連立して解いて
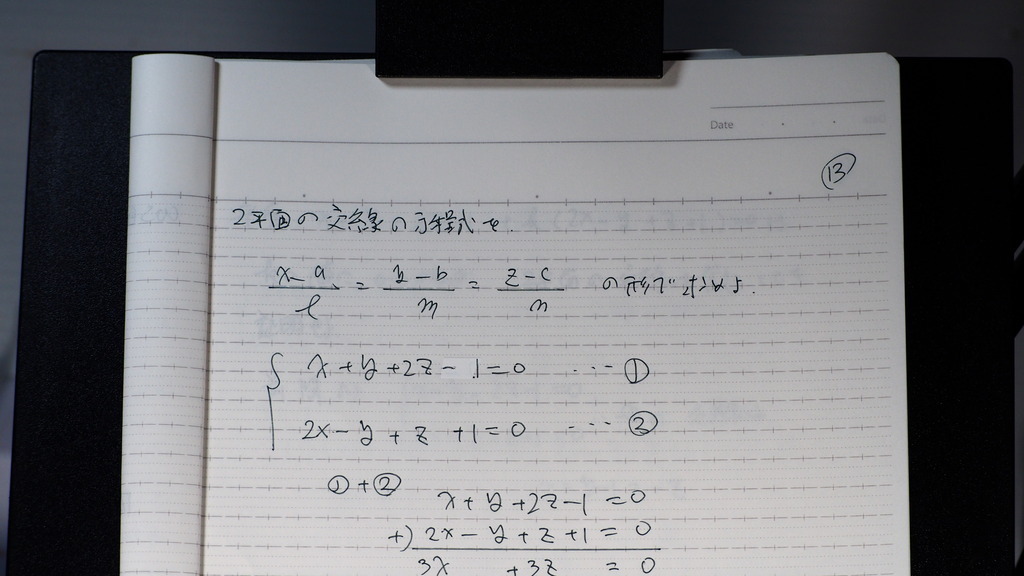
14
x=y-1=-z

15
この式を
証明して
まず
さっきの 2平面の連立
➀
これらの 二つの式は
すでに 成り立っている
しかも =0

16
0 + k(0) = 0
常に 成り立つデショ

17
今証明した
方程式を 使って
交線が 含まれているわけなんだから
さらに
指定された 点を 通るときの
kを 求めて
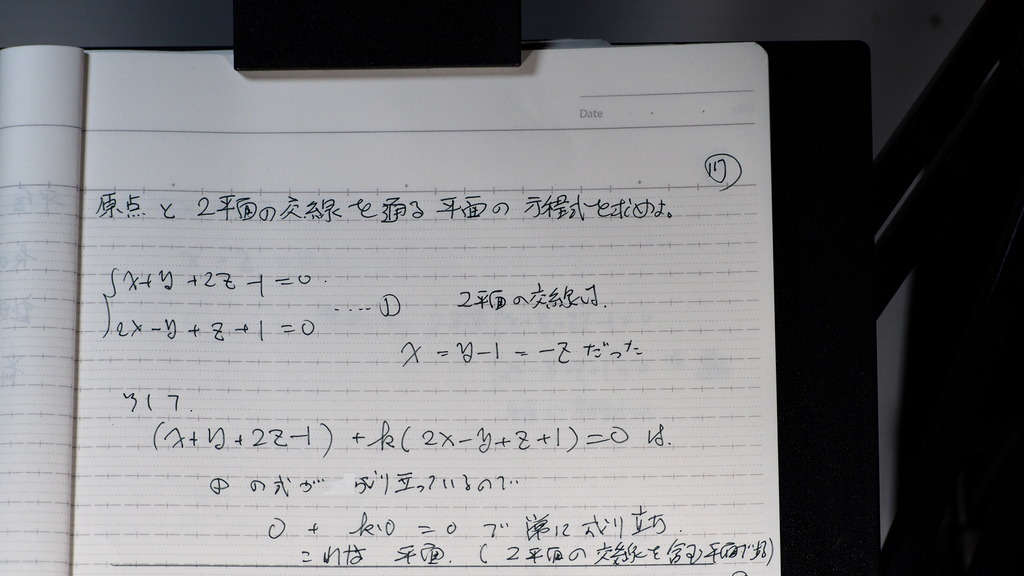
18
k=1
を 交線を 含む
平面の方程式の k に代入すれば
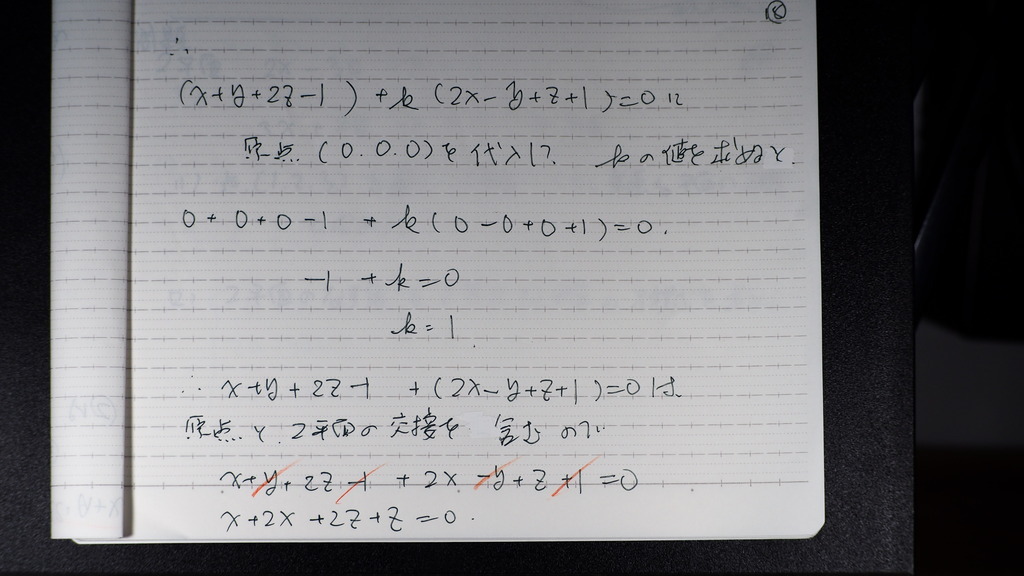
19
こんな感じに

20
問題

21
平面の 方程式を
ax + by + cz =d
と置いて
(1,2,3) を
代入
平面の方程式の 垂直成分
(a,b,c) と

22
それぞれの 平面の
垂直成分
(2、-3、4)
(3、 2、1)
の 内積が =0 を使って

23
計算してきますと
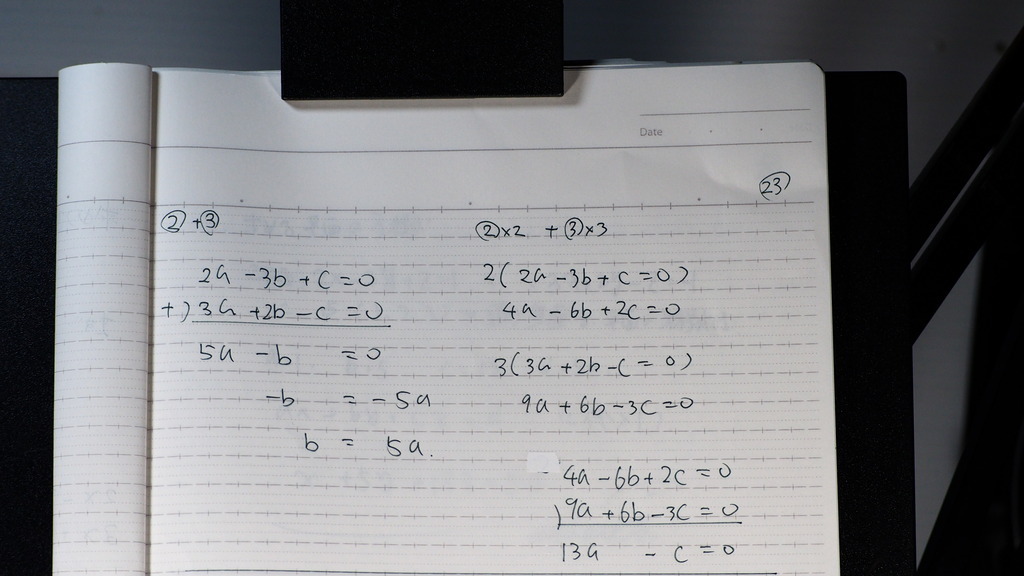
24
平面の方程式は
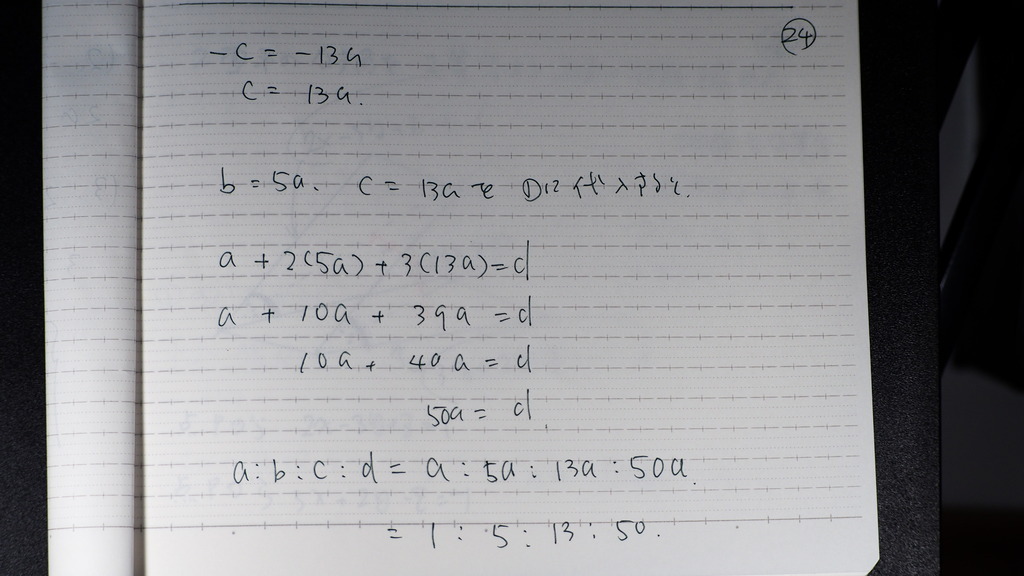
25
こんな感じで

26
2面の なす角を
2等分する
平面の 方程式は
なす角を
2等分する
平面上の 点をP (x、y、z)
とすれば
点と 平面との距離が
等しくなるよを
式で 表して

27
こんなかんじに 一つ目
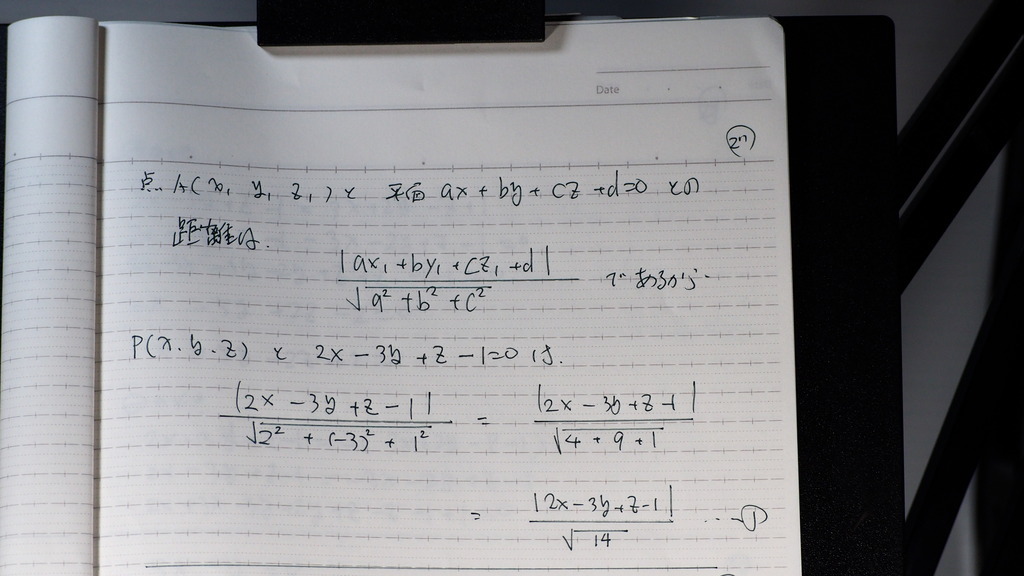
28
もう一方も
それを =で結んで
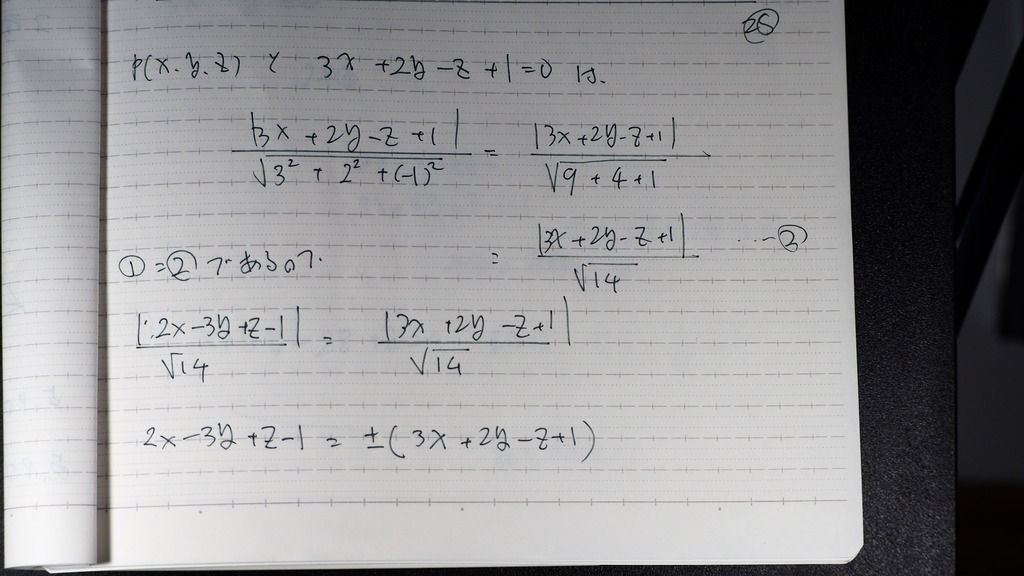
29
プラスの時
マイナスの時

30
であるので
こんな感じで

31
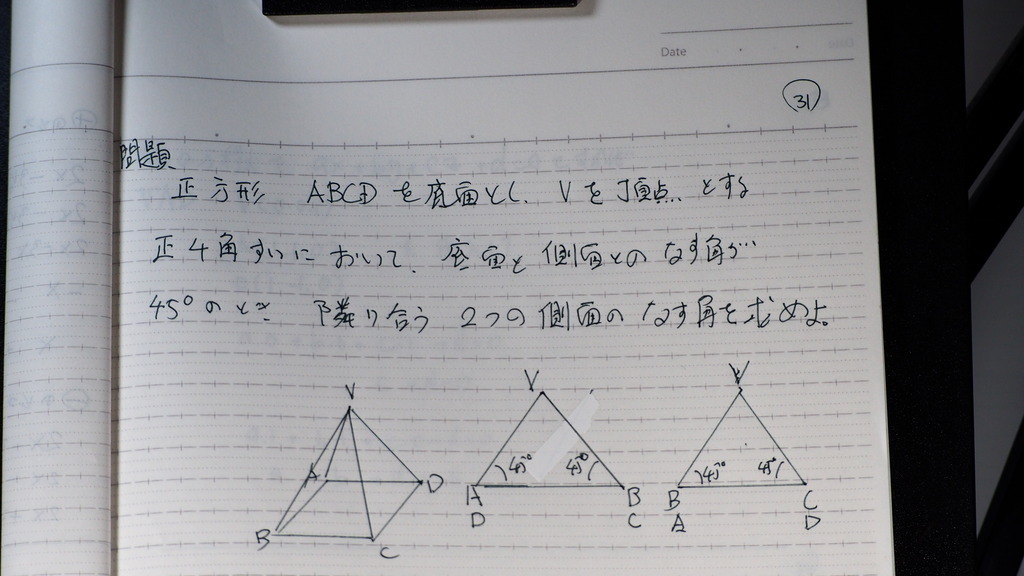
問題
32
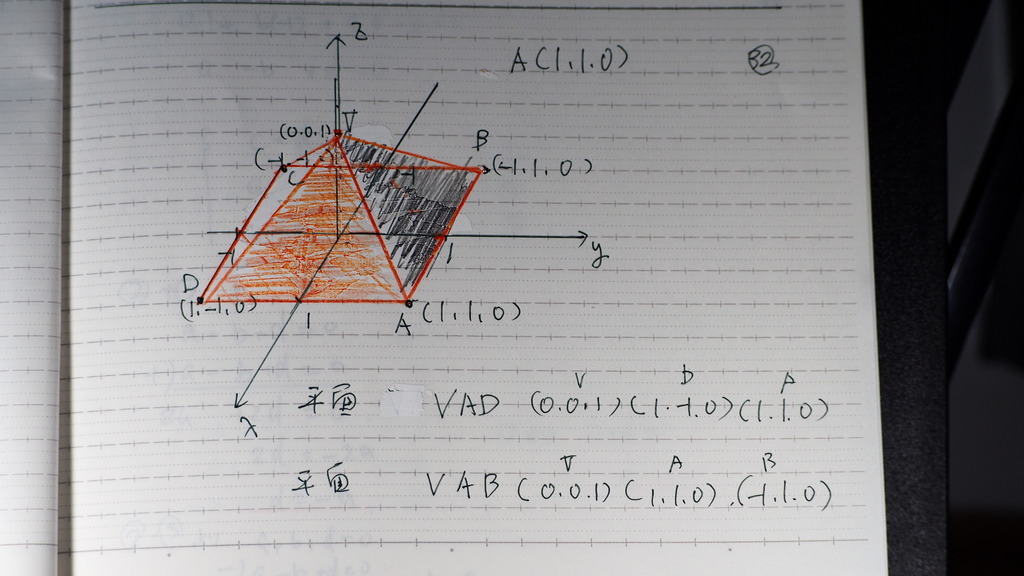
座標を 使ってみましょう
33
3点が わかれば
平面の 方程式が出るから
まず 平面VAD

34
計算ちゅうです

35
平面VADは x+z=1
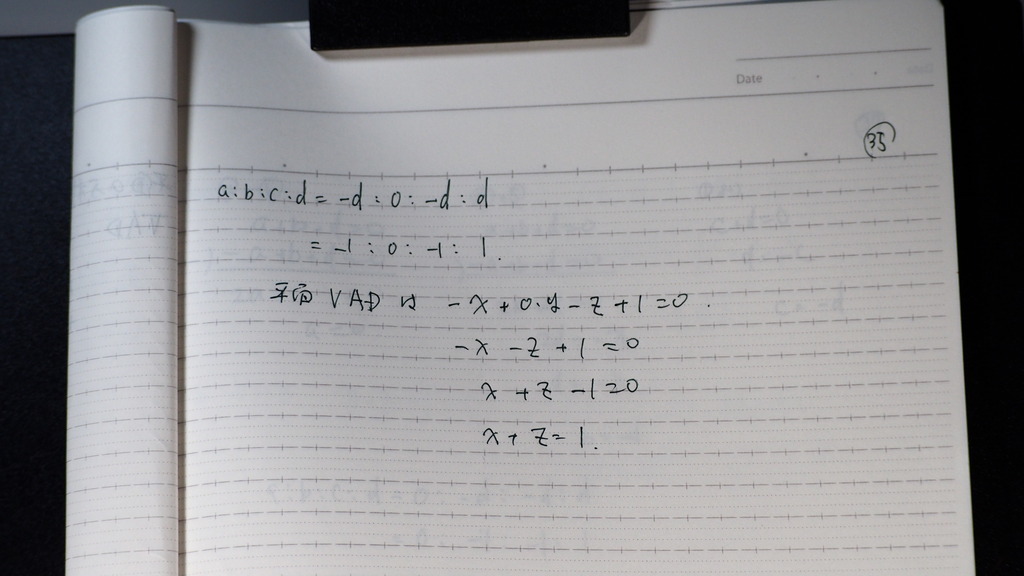
36
平面VABは

37
計算ちゅうです
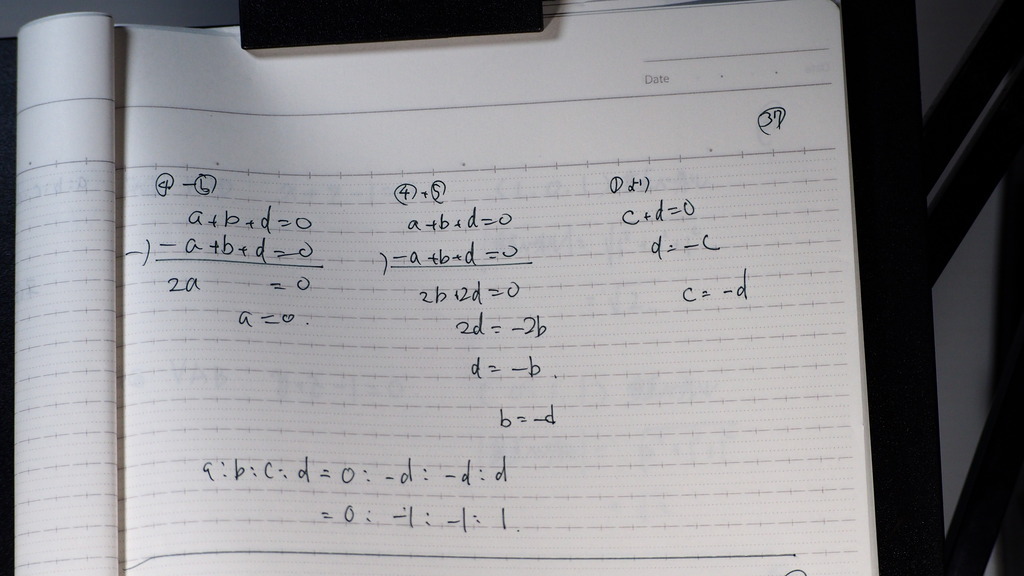
38
平面VABは y+z=1

39
で
なす角を 計算するんですが

40
側面のなす角は
120度
答は これです

考えてみましょう
お疲れ様です
空間座標とベクトル
2平面のなす角
A
なす角の 計算は
平面同士の時は
法線ベクトル
の 内積で出るのだけれど
問題によって
どちらの 角度を
聞いているか
ぎんみ する必要がある
B
こちらの場合
隣接面の
側面の なす角
どっちかな
ッテ
吟味する必要がある
(机上の 数値計算の場合は)
01
それらを
前置きしておいて
問題
02
xy 平面の
垂線ベクトルは
0,0,1
03
もう一つの 面は
計算しないと
わからないので
3点から
平面の式に
代入して
( 3点が わかるときは
ベクトルでも 出ますが )
04
全部 c で 表して
へてから -1、-1,1
05
平面の式にして
符号を 整えて
1、1、-1
-1、-1,1 でもOK ですが
06
そうすれば
内積の計算から
コサインで
求めて
07
y を 求めると
08
タンジェント αは -√2
図でいうところの
Θ が 今回 なす角 Θなので
補角を 使って
TanΘ は √2
09
今度は
そのまま 計算できるパターン
(1)なす角は
(2)2平面の 交線は
(3)この等式を 証明して
( 2平面の交線を 含む 平面の
方程式 )重要
(4)
を 落としてますが
原点と この2平面の 交線を
含む 平面の方程式を
求めよ
(3)の結果を 使うと早い
10
両平面の方程式から
垂線のベクトルを
内積で
計算して
なす角を 出すと
11
こんな感じに
12
そのまま
60度
13
2平面の
交線は
そのまま 平面を
連立して解いて
14
x=y-1=-z
15
この式を
証明して
まず
さっきの 2平面の連立
➀
これらの 二つの式は
すでに 成り立っている
しかも =0
16
0 + k(0) = 0
常に 成り立つデショ
17
今証明した
方程式を 使って
交線が 含まれているわけなんだから
さらに
指定された 点を 通るときの
kを 求めて
18
k=1
を 交線を 含む
平面の方程式の k に代入すれば
19
こんな感じに
20
問題
21
平面の 方程式を
ax + by + cz =d
と置いて
(1,2,3) を
代入
平面の方程式の 垂直成分
(a,b,c) と
22
それぞれの 平面の
垂直成分
(2、-3、4)
(3、 2、1)
の 内積が =0 を使って
23
計算してきますと
24
平面の方程式は
25
こんな感じで
26
2面の なす角を
2等分する
平面の 方程式は
なす角を
2等分する
平面上の 点をP (x、y、z)
とすれば
点と 平面との距離が
等しくなるよを
式で 表して
27
こんなかんじに 一つ目
28
もう一方も
それを =で結んで
29
プラスの時
マイナスの時
30
であるので
こんな感じで
31
問題
32
座標を 使ってみましょう
33
3点が わかれば
平面の 方程式が出るから
まず 平面VAD
34
計算ちゅうです
35
平面VADは x+z=1
36
平面VABは
37
計算ちゅうです
38
平面VABは y+z=1
39
で
なす角を 計算するんですが
40
側面のなす角は
120度
答は これです
考えてみましょう
お疲れ様です
2022年12月18日
22031 大人のさび落とし 空間座標とベクトル 直線と平面 ( 前置き 直線 平面 球)
大人のさび落とし
空間座標とベクトル
の 方程式
01
まず ざっと 方程式とか
理論とか
2直線の
平行

02
2直線の 垂直

03
2平面の 平行
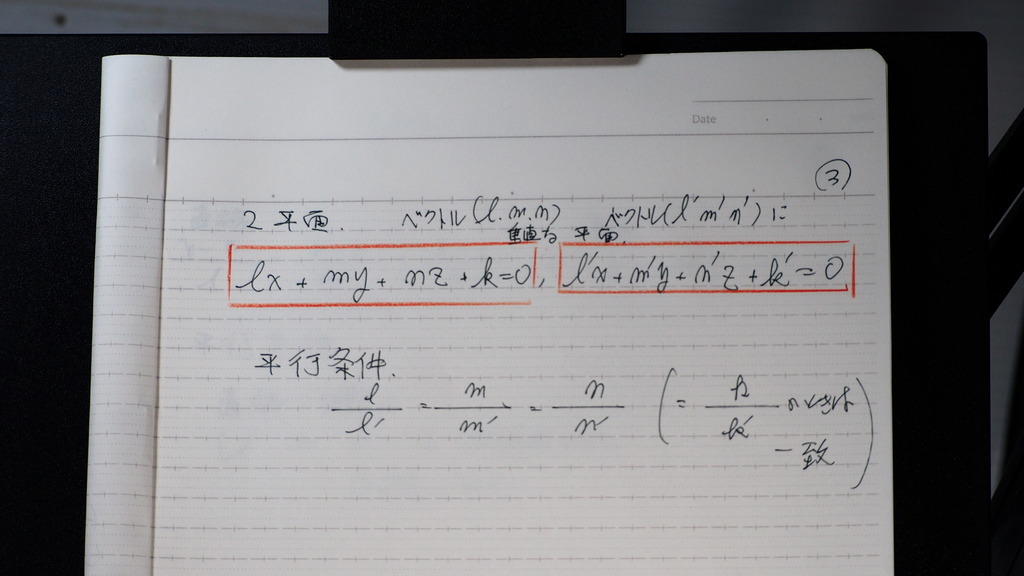
04
2平面の垂直

05
直線と 平面が 平行
直線の方向係数は
直線に平行

06
平面の方程式は
係数が 平面に垂直
であるので
内積が =0になる
逆に
直線が 平面に
垂直な時は
直線と 直線の 平行の時
のようになる

07
2平面のなす角
ここは 徐行して
確認してみてください
成ってるでしょ

08
であるから
2平面の垂直成分から
COSΘは こんな感じに

09
点と平面の距離は
こんな公式になるです

10
球の 方程式

11
A,Bが 直径の 両端に
あるときは

12
球面上の 接線の方程式は

13
以上踏まえまして
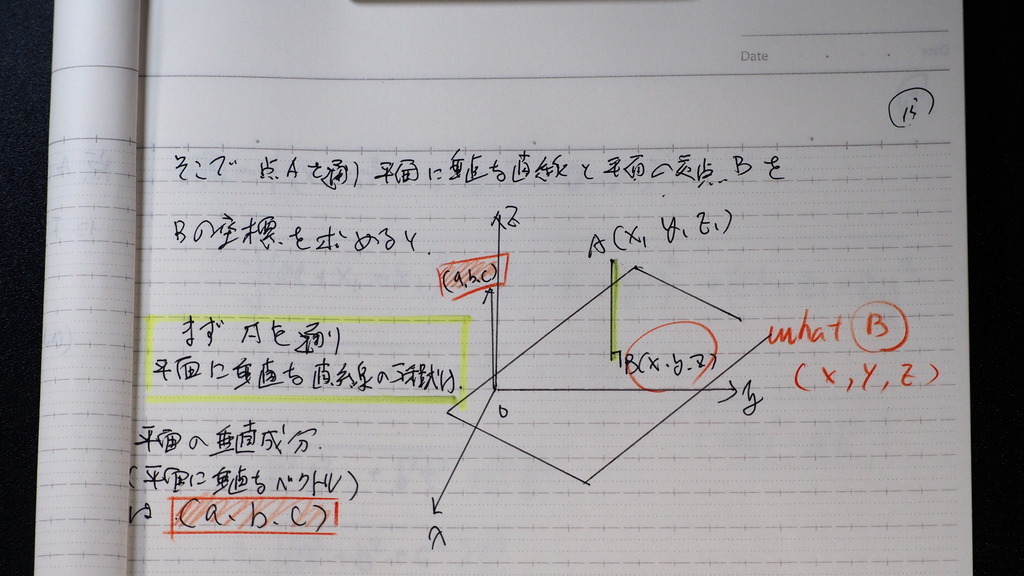
ここからは
問題を
今日は 平面と直線
空間の 点から
平面に おろした
垂線の長さ
つまり
点と平面の 距離
平面に 垂直な ベクトル
(a,b,c)
点Aを 通り
平面に 垂直な 直線と
平面の交点を
B とすれば

14
Bの 座標が分かっていれば
ABベクトルの 絶対値で
点A と 平面との
距離が出る

15
であるから
Bの座標を 求めたい
平面の 垂直成分が
そのまま
点Aを 通り
平面に 垂直な 直線の
方向係数ベクトル
であるので
16
直線の 方程式は
こんな感じ
これに =t と置いて
媒介変数形にするでしょ
だから
Bの x、y、z に
これを 代入すればさ

17
これが
点Aを 通り
平面に 垂直な 直線
と
平面との
距離なんだけど
ここで
tが分かればいいのだから
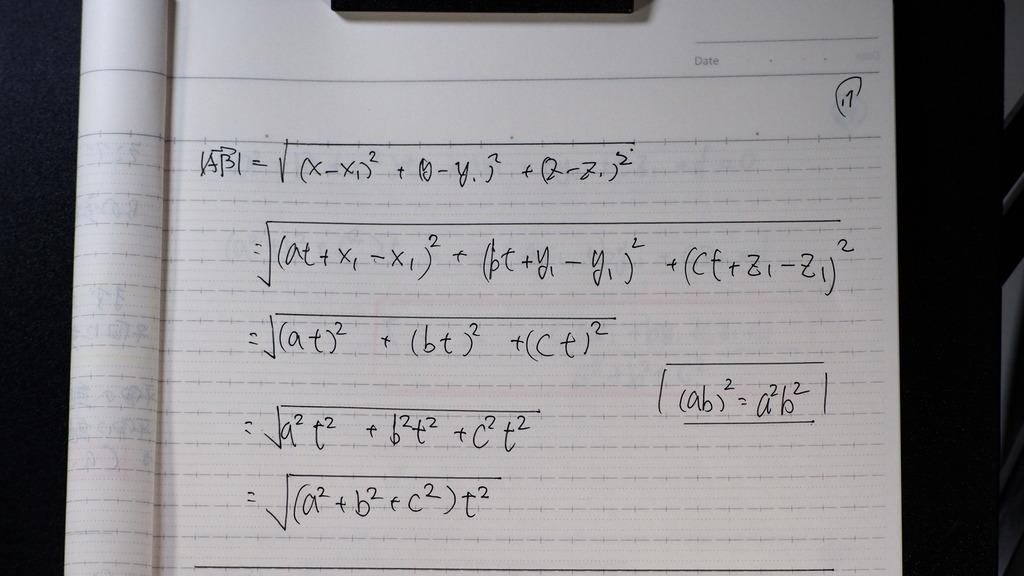
18
今度は
t を
求めるでしょ
X= Y= Z= の
媒介変数を
これは
直線上の点を
表してるので
平面の方程式に
代入すれば
共通なところ
交点になるので

19
すると
tは
こんなだから
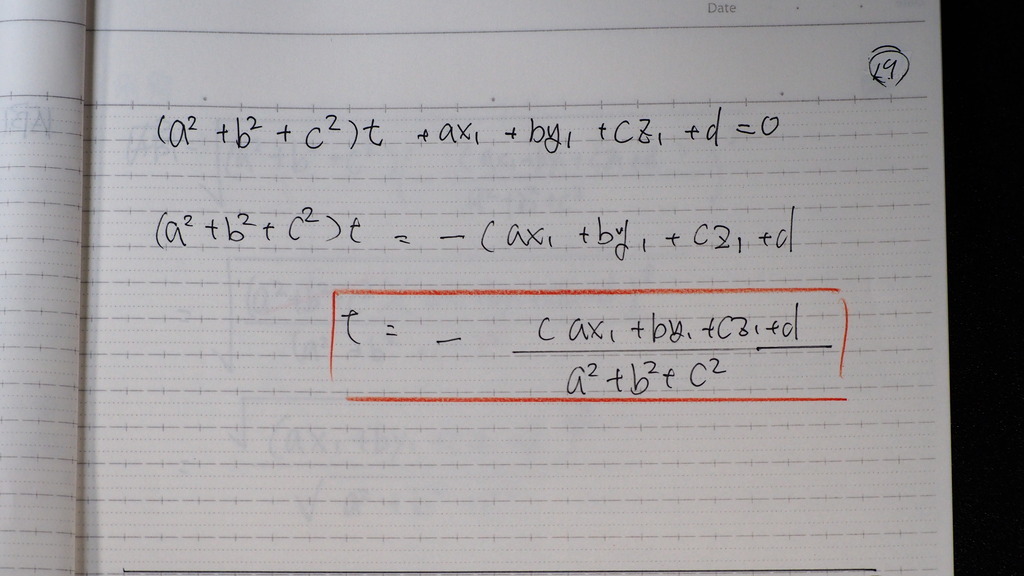
20
これを
さっきのに
代入したらば
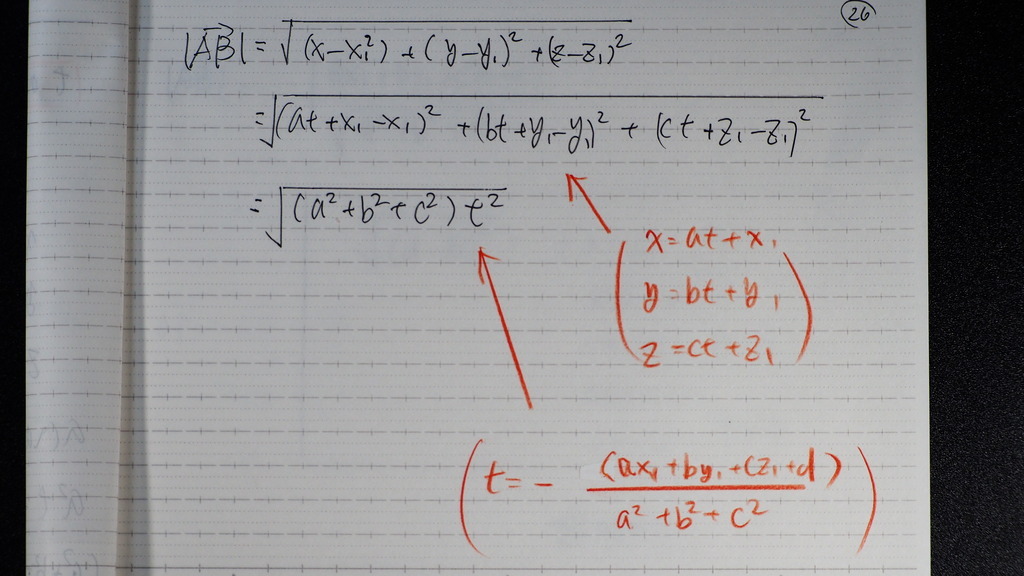
21
こんな感じで
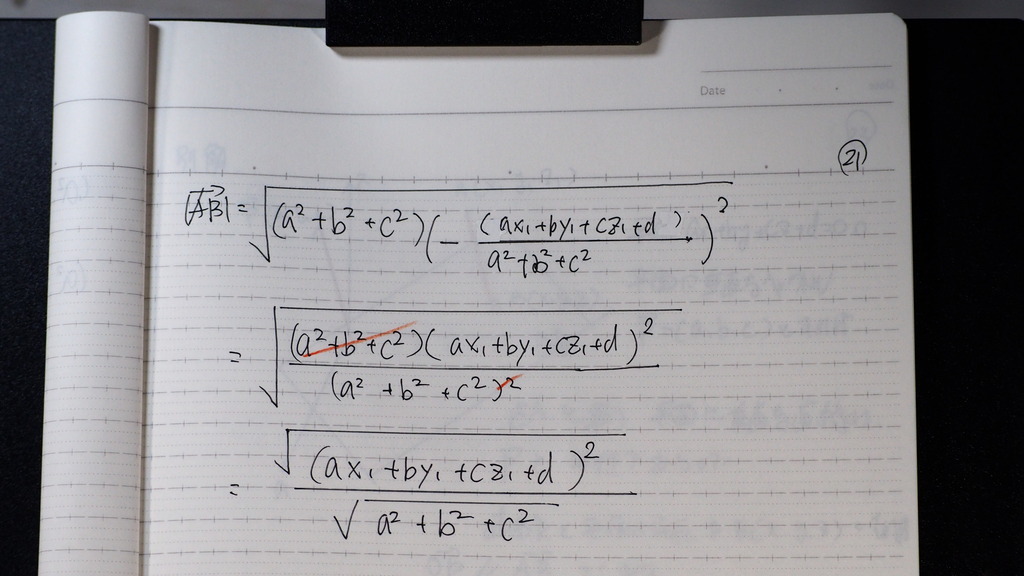
22
√を
外せば

23
別解は
平面の 垂直成分と
直線ABの方向係数が
等しいので
平行を使って
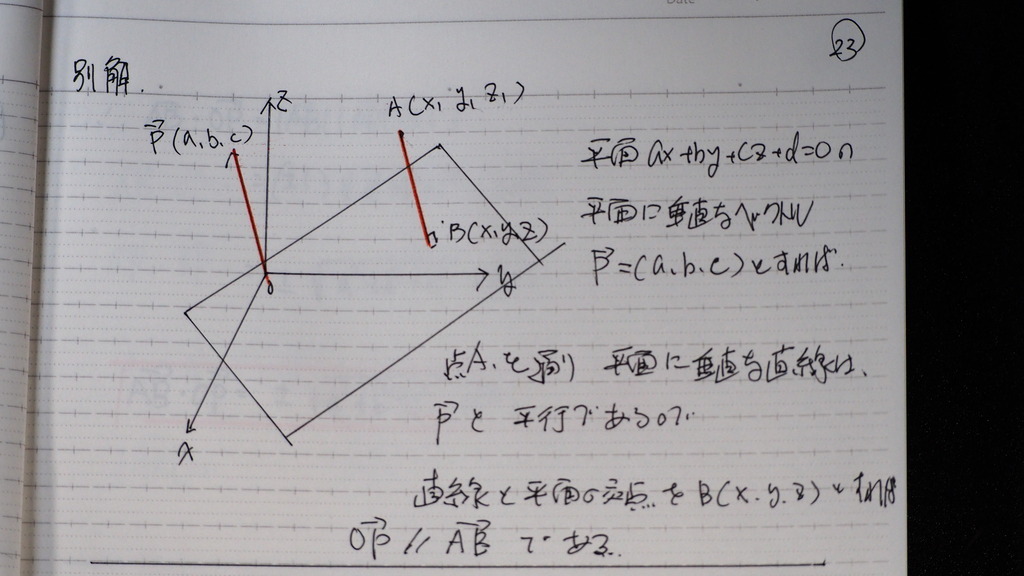
24
ABベクトル
OPベクトル
コサイン
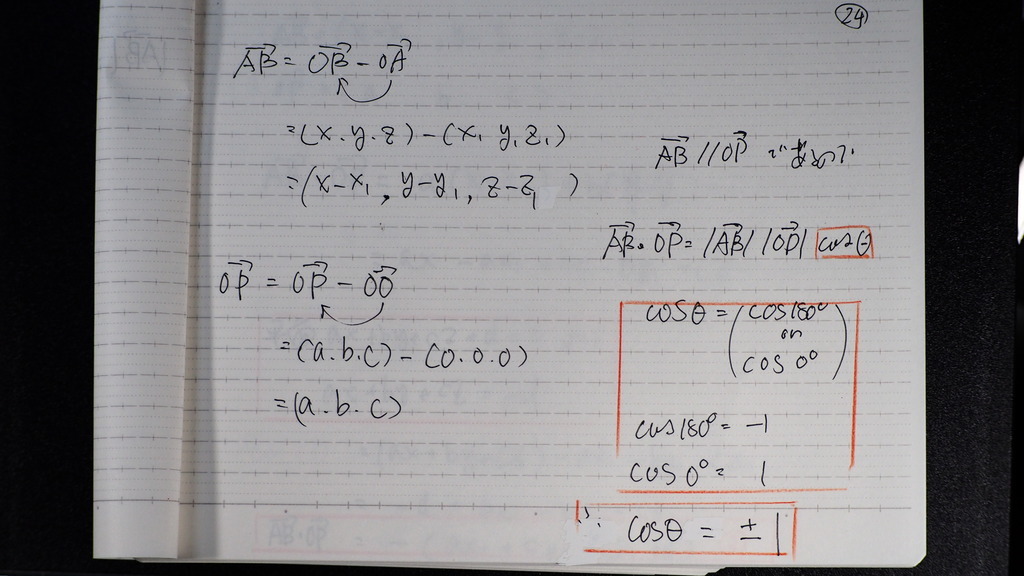
25
まず 矢線ベクトルから
➀

26
成分の内積から
②
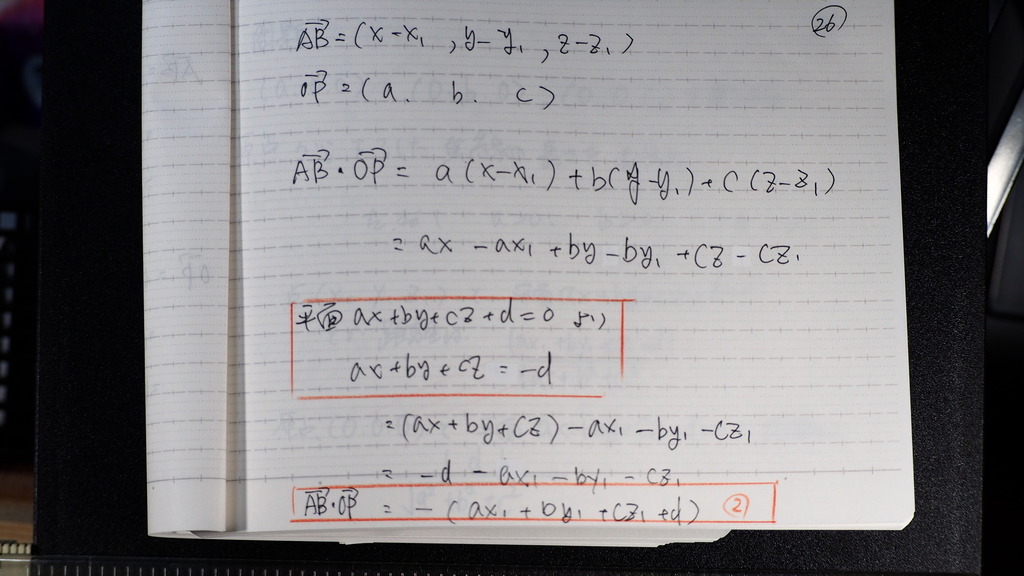
27
絶対値は
ゼロ以上だから

28
三点を 通る平面に
原点から
下した 垂線の長さ
原点と平面の距離だね

29
3点が
同一平面上にあれば
この式を
使って

30
平面の媒介変数形方程式
を 作っていくと

31
平面上の 全ての
ベクトルは
異なった 二つの
ベクトルの
和の形になる
じゃナイスカ
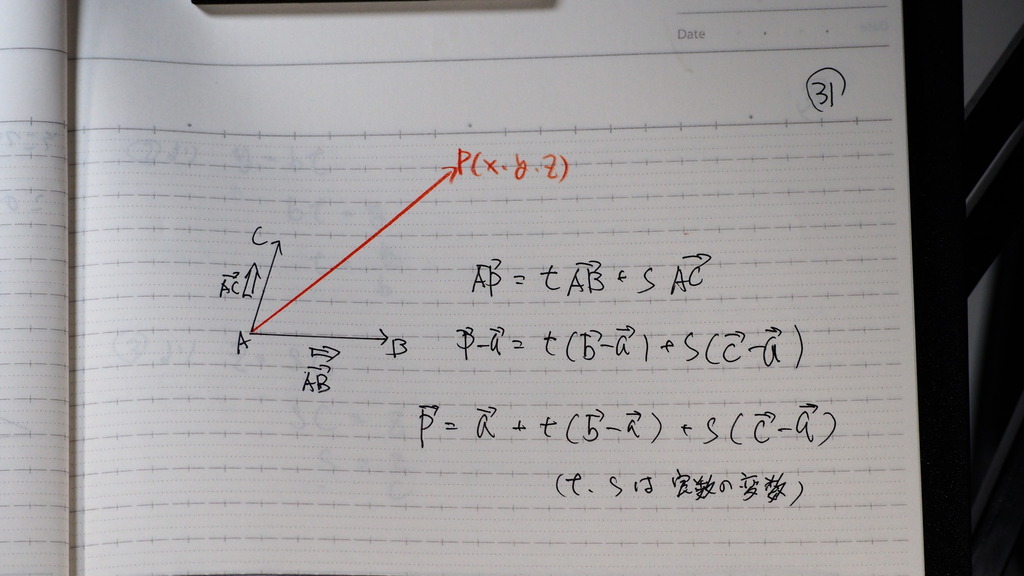
32
列で 書いた方が
分かりやすい
これを
連立に して
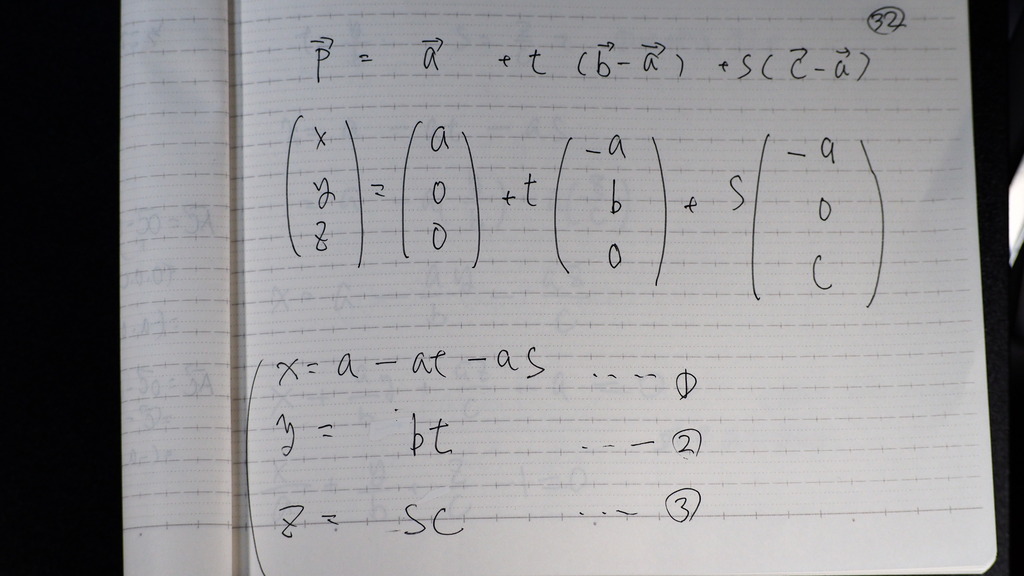
33
t は
s は
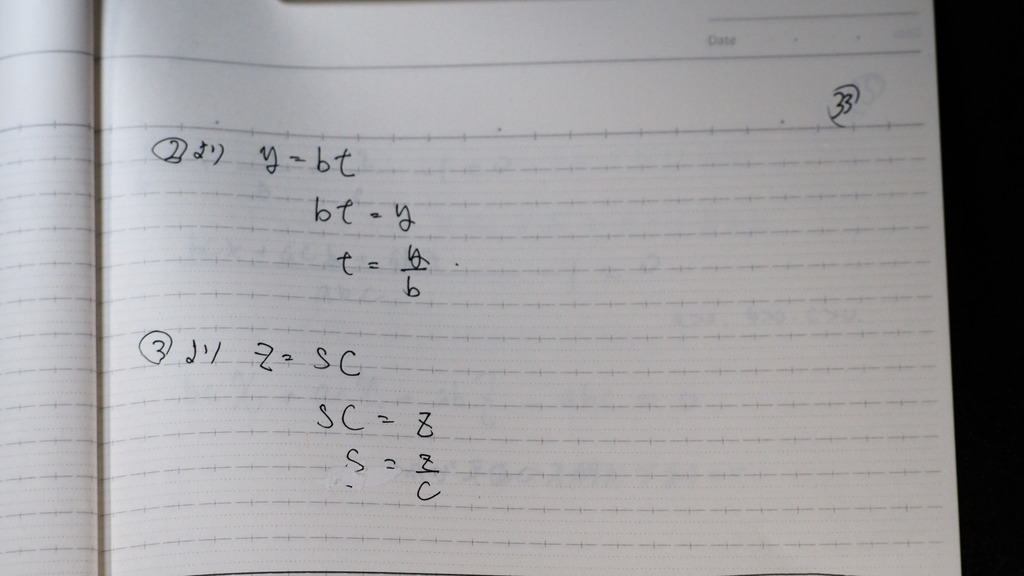
34
これを
➀に代入して
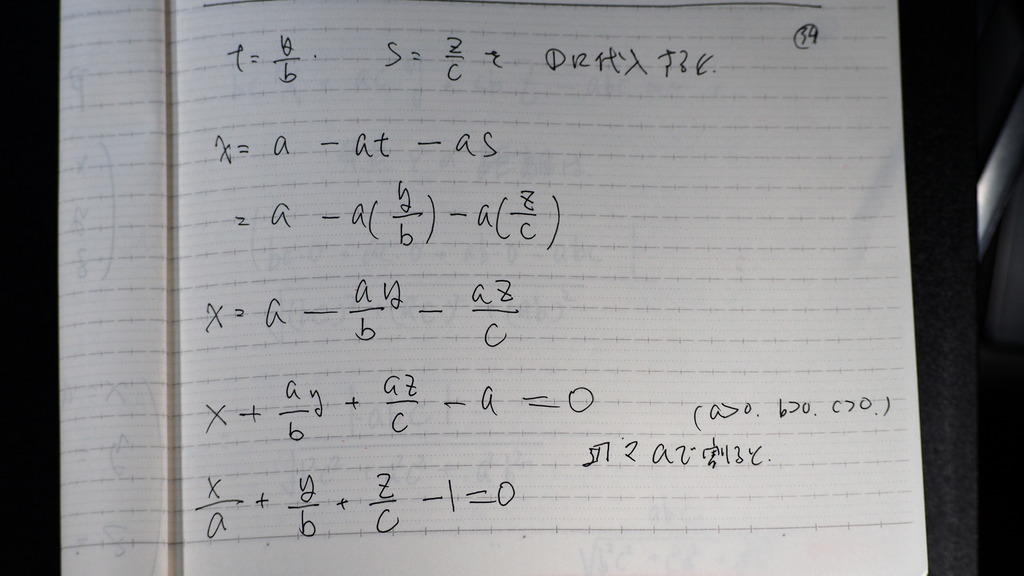
35
これが 平面の
方程式

36
原点との距離は
点と平面との
距離の公式を使って
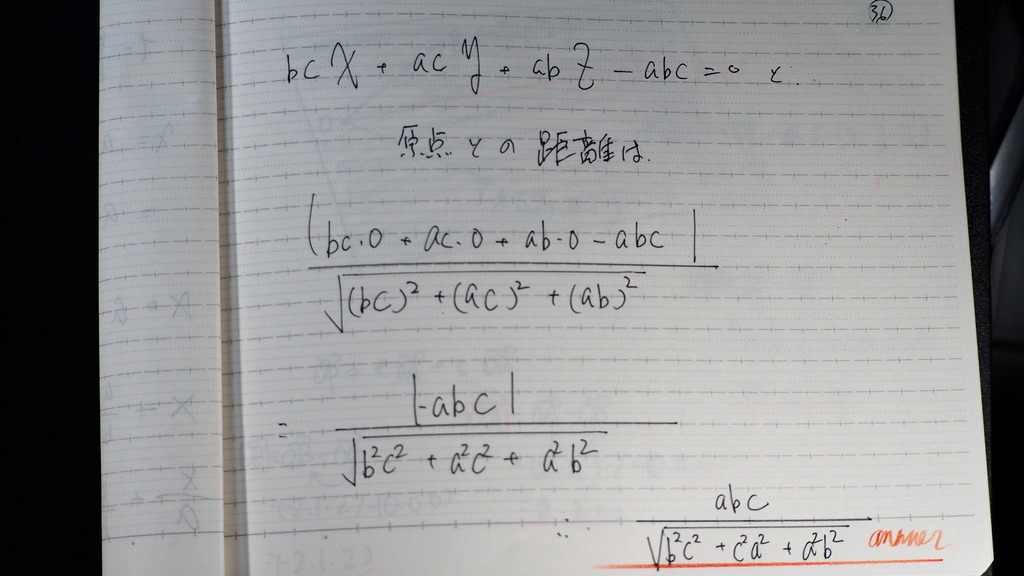
37
類題
今度は
原点でない 点と
平面との 距離
やり方は 同じ

38
AB ベクトル
と
ACベクトルの
和で
APベクトルを
出して

39
平面上に
原点が あるから
式が 少し簡単になる
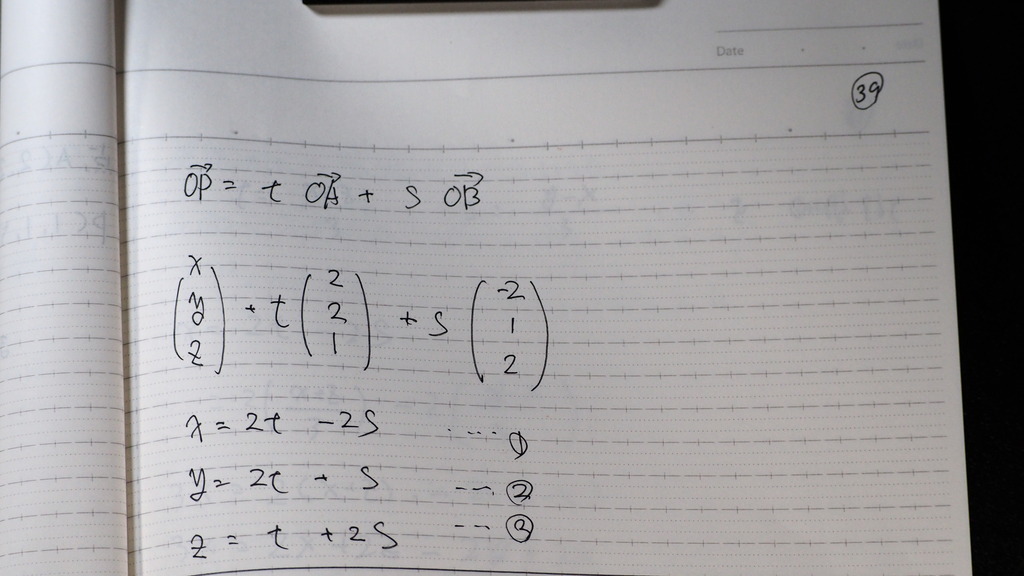
40
t s
を 求めて
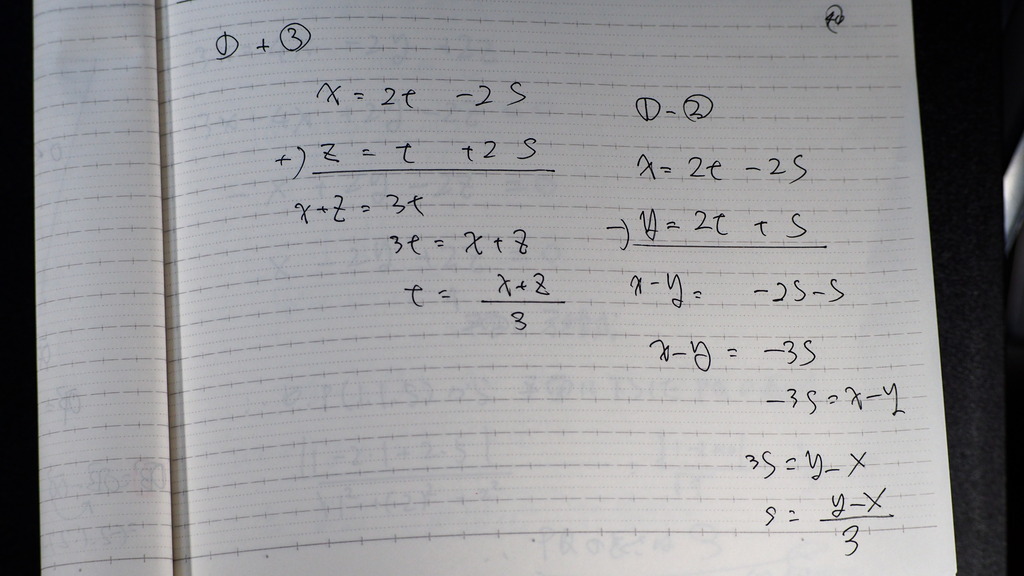
41
➀に 代入して
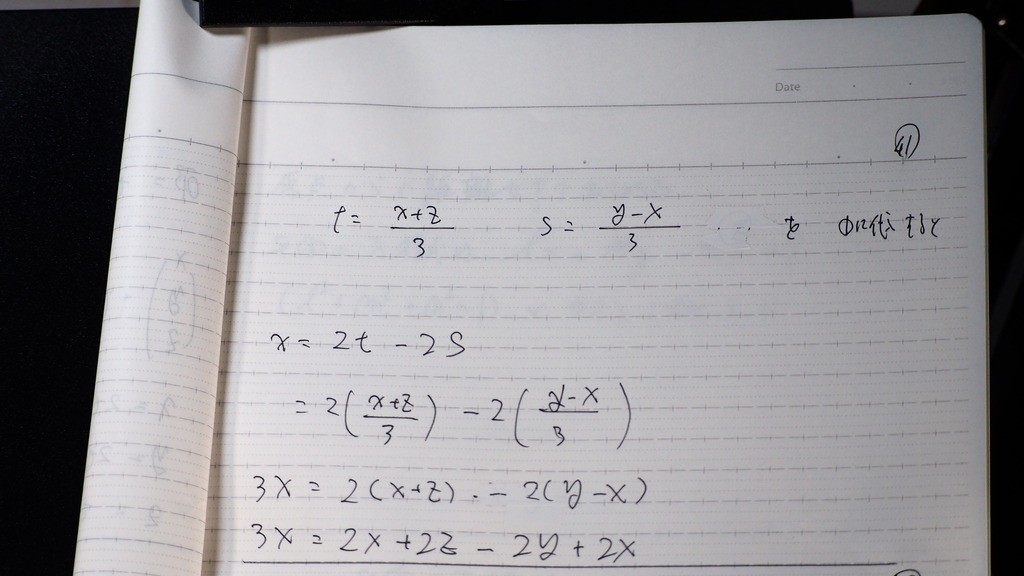
42
平面の
方程式が出たから
点と平面との距離
の公式で
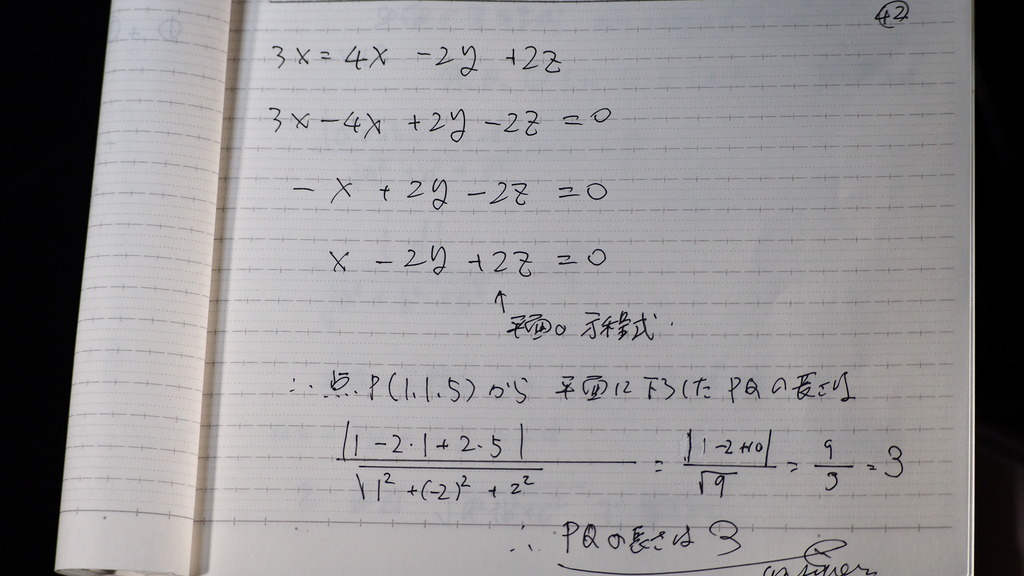
43
問題

44
まず 公式通りに
ここで
この 分母の
√を 使うんだって
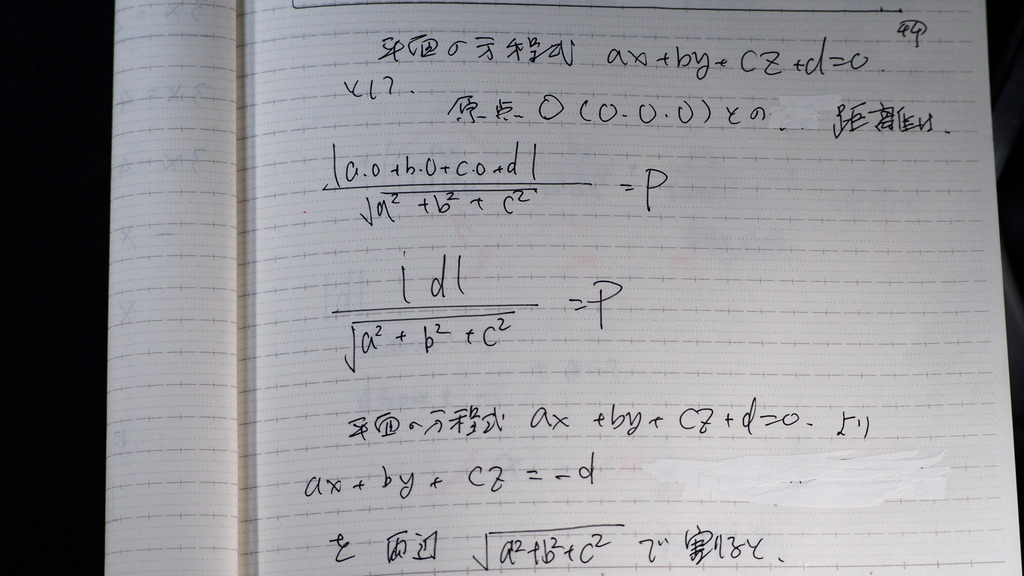
45
平面の式を
こんな感じに
考えれば

46
なるでしょ
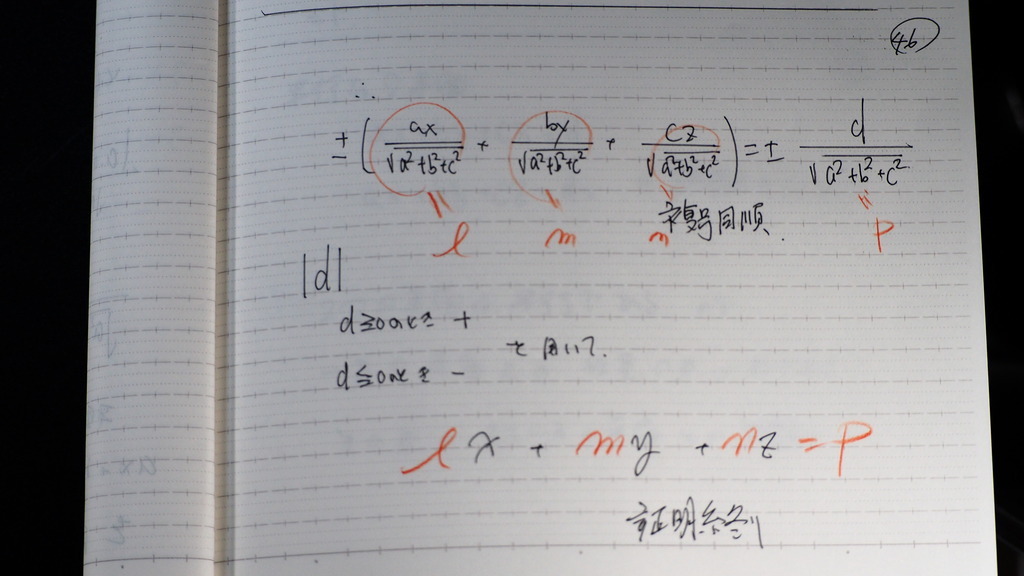
47
追記

48
平行な
2平面の距離は?

49
平面であれば
少なくとも
(a,b,c) の内
一つは ゼロではない
これを使って

50
こうなるんだって
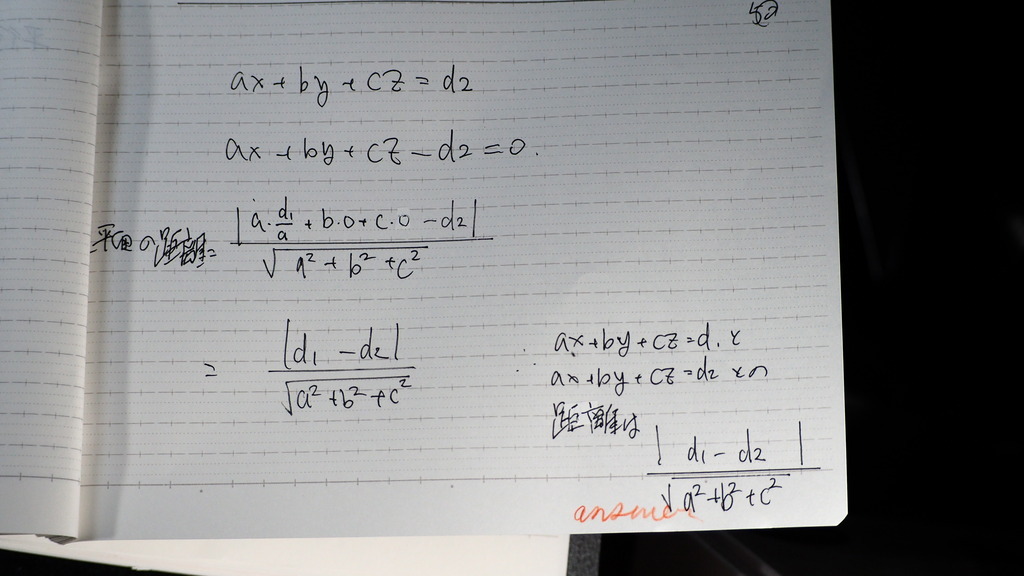
お疲れ様です。
空間座標とベクトル
の 方程式
01
まず ざっと 方程式とか
理論とか
2直線の
平行
02
2直線の 垂直
03
2平面の 平行
04
2平面の垂直
05
直線と 平面が 平行
直線の方向係数は
直線に平行
06
平面の方程式は
係数が 平面に垂直
であるので
内積が =0になる
逆に
直線が 平面に
垂直な時は
直線と 直線の 平行の時
のようになる
07
2平面のなす角
ここは 徐行して
確認してみてください
成ってるでしょ
08
であるから
2平面の垂直成分から
COSΘは こんな感じに
09
点と平面の距離は
こんな公式になるです
10
球の 方程式
11
A,Bが 直径の 両端に
あるときは
12
球面上の 接線の方程式は
13
以上踏まえまして
ここからは
問題を
今日は 平面と直線
空間の 点から
平面に おろした
垂線の長さ
つまり
点と平面の 距離
平面に 垂直な ベクトル
(a,b,c)
点Aを 通り
平面に 垂直な 直線と
平面の交点を
B とすれば
14
Bの 座標が分かっていれば
ABベクトルの 絶対値で
点A と 平面との
距離が出る
15
であるから
Bの座標を 求めたい
平面の 垂直成分が
そのまま
点Aを 通り
平面に 垂直な 直線の
方向係数ベクトル
であるので
16
直線の 方程式は
こんな感じ
これに =t と置いて
媒介変数形にするでしょ
だから
Bの x、y、z に
これを 代入すればさ
17
これが
点Aを 通り
平面に 垂直な 直線
と
平面との
距離なんだけど
ここで
tが分かればいいのだから
18
今度は
t を
求めるでしょ
X= Y= Z= の
媒介変数を
これは
直線上の点を
表してるので
平面の方程式に
代入すれば
共通なところ
交点になるので
19
すると
tは
こんなだから
20
これを
さっきのに
代入したらば
21
こんな感じで
22
√を
外せば
23
別解は
平面の 垂直成分と
直線ABの方向係数が
等しいので
平行を使って
24
ABベクトル
OPベクトル
コサイン
25
まず 矢線ベクトルから
➀
26
成分の内積から
②
27
絶対値は
ゼロ以上だから
28
三点を 通る平面に
原点から
下した 垂線の長さ
原点と平面の距離だね
29
3点が
同一平面上にあれば
この式を
使って
30
平面の媒介変数形方程式
を 作っていくと
31
平面上の 全ての
ベクトルは
異なった 二つの
ベクトルの
和の形になる
じゃナイスカ
32
列で 書いた方が
分かりやすい
これを
連立に して
33
t は
s は
34
これを
➀に代入して
35
これが 平面の
方程式
36
原点との距離は
点と平面との
距離の公式を使って
37
類題
今度は
原点でない 点と
平面との 距離
やり方は 同じ
38
AB ベクトル
と
ACベクトルの
和で
APベクトルを
出して
39
平面上に
原点が あるから
式が 少し簡単になる
40
t s
を 求めて
41
➀に 代入して
42
平面の
方程式が出たから
点と平面との距離
の公式で
43
問題
44
まず 公式通りに
ここで
この 分母の
√を 使うんだって
45
平面の式を
こんな感じに
考えれば
46
なるでしょ
47
追記
48
平行な
2平面の距離は?
49
平面であれば
少なくとも
(a,b,c) の内
一つは ゼロではない
これを使って
50
こうなるんだって
お疲れ様です。
2022年12月14日
22030 大人のさび落とし 空間座標とベクトル 平面の媒介変数形方程式
空間座標とベクトル
今日は
平面の方程式の
媒介変数形
01
問題

02
平面上の ベクトルは
異なる 二つのベクトルの
実数倍で
すべて 表せる

03
そこで
イメージとしては
対角線
APベクトルは
t倍のABベクトル
と
s倍のACベクトルの
和
(p-a)=t(b-a)+s(c-a)
この 左辺のaベクトルを
じゃナイスカ
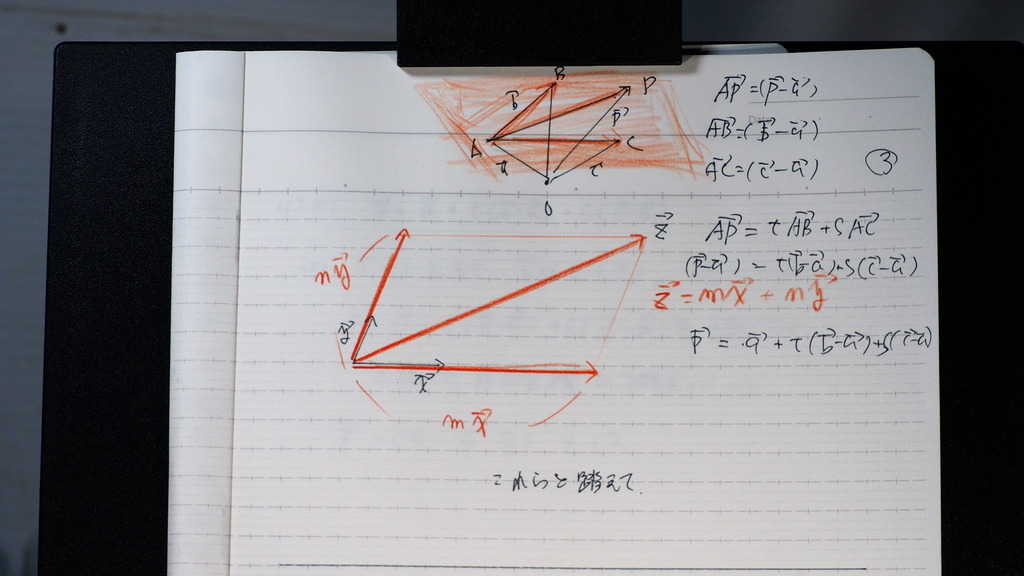
04
なったデショ

05
実際に
ベクトル方程式に
数値を 入れると

06
列で書いた方が
見やすいと思ってさ
ね
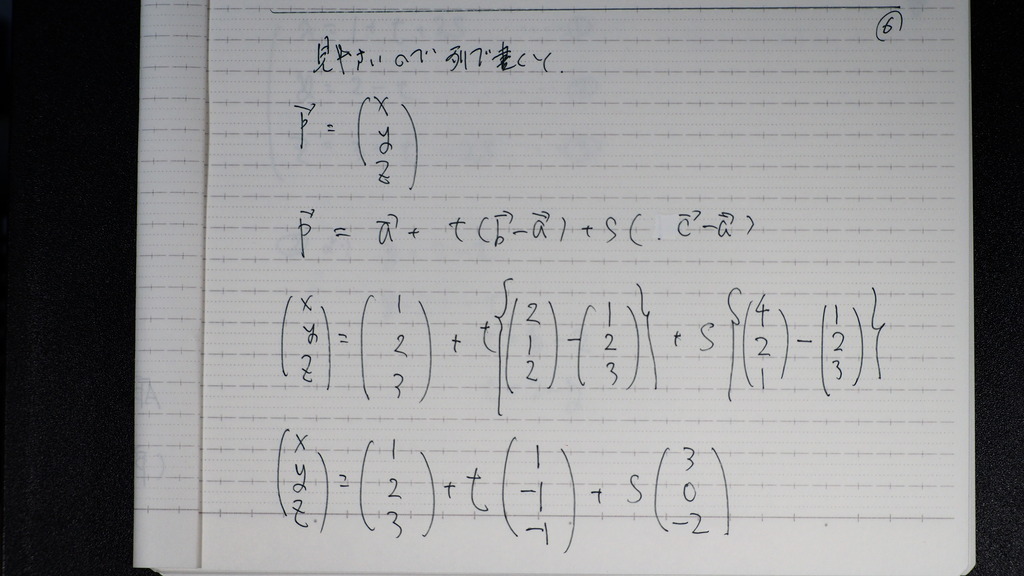
07
計算して
整理したらば

08
ここから
s、t を 消去して
x、y、z、定数の
式にすればいいので
まず t
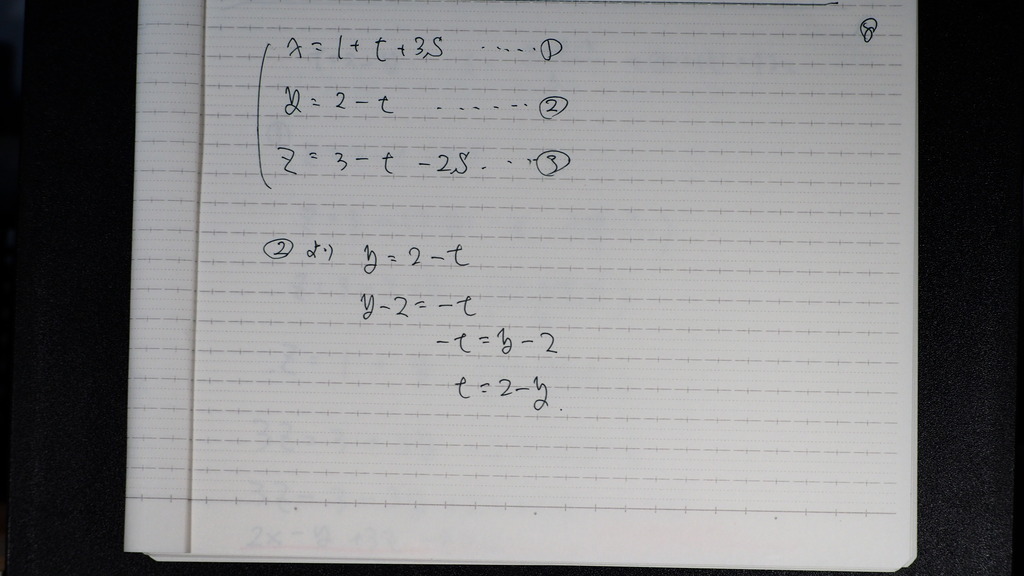
09
次に s

10
③式に t、sを 代入して
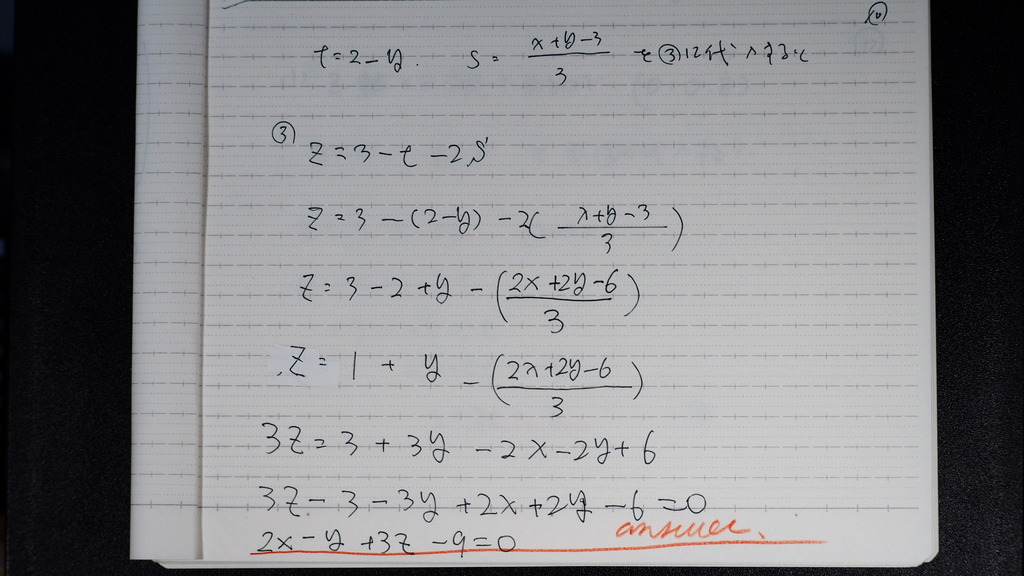
11
問題
まずですね
z軸との交点の座標は

12
x1=0、Y=0
を 代入したら
④

13
それと
⑤
④⑤より

14
tは 8/3

15
sは -7/3
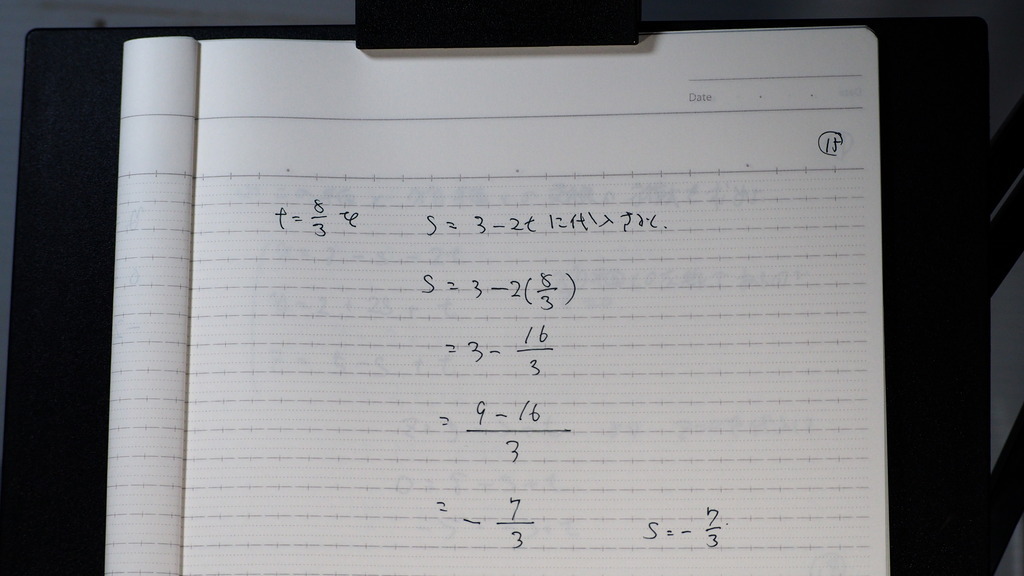
16
これら
t、sを
③式に 代入して
z=10
であるから
(0,0,10)

17
この平面と
xy平面の
交線は
Z=0を 代入して

18
xの式から
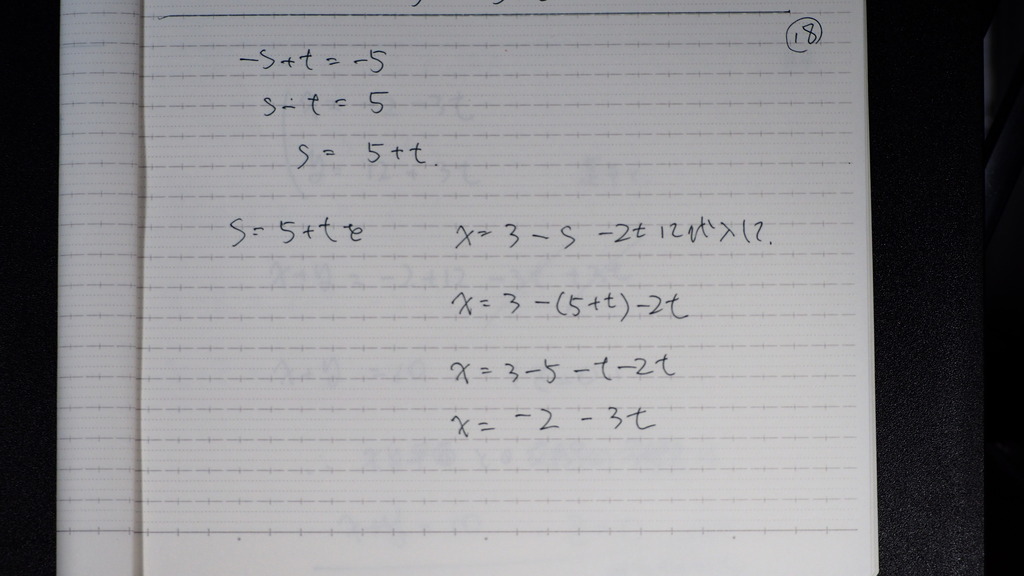
19
yの式から

20
これらを
足すでしょ
z=0の時に
x+y=10
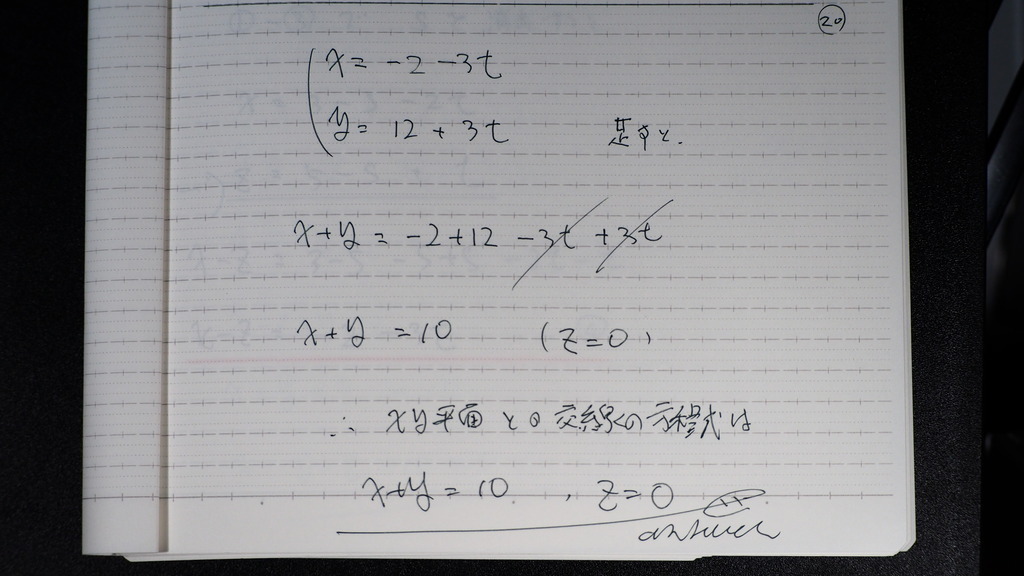
21
この さん式から
s、tを
消去すればいいのだから

22
色々やり方は
あるとおもいますが
➀-③から
④

23
②+③×2で
⑤

24
④⑤を 足すと
x+y+z-10=0
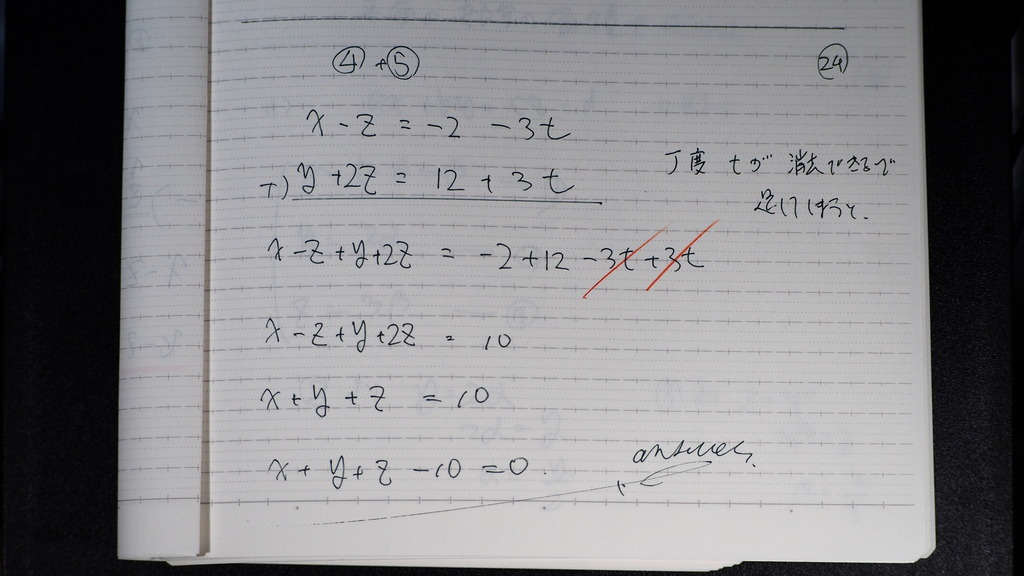
25
もんだい

26
(1)
y 、zから α 、β

27
平面の方程式は
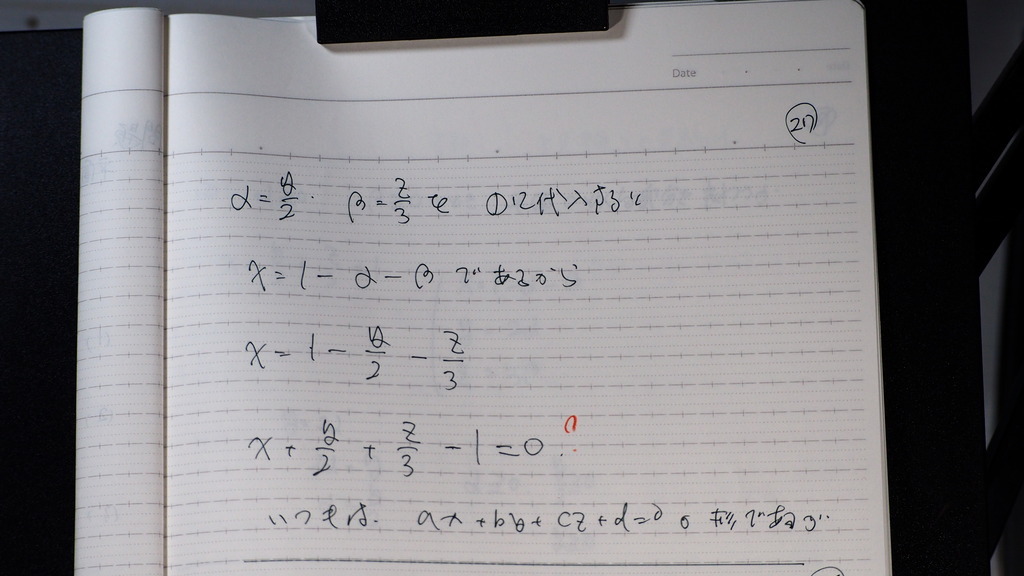
28
題意を 良く見ると
ax+by+cz+d=0
の形ではなく
ax+by+cz=d
であるので
ここで 指示違反で
原点は もったいない

29
(2)
α βの
範囲から
y、zは ゼロ以上

30
境界線を 求めると
y=-2x+2
xy平面は 平場ですが
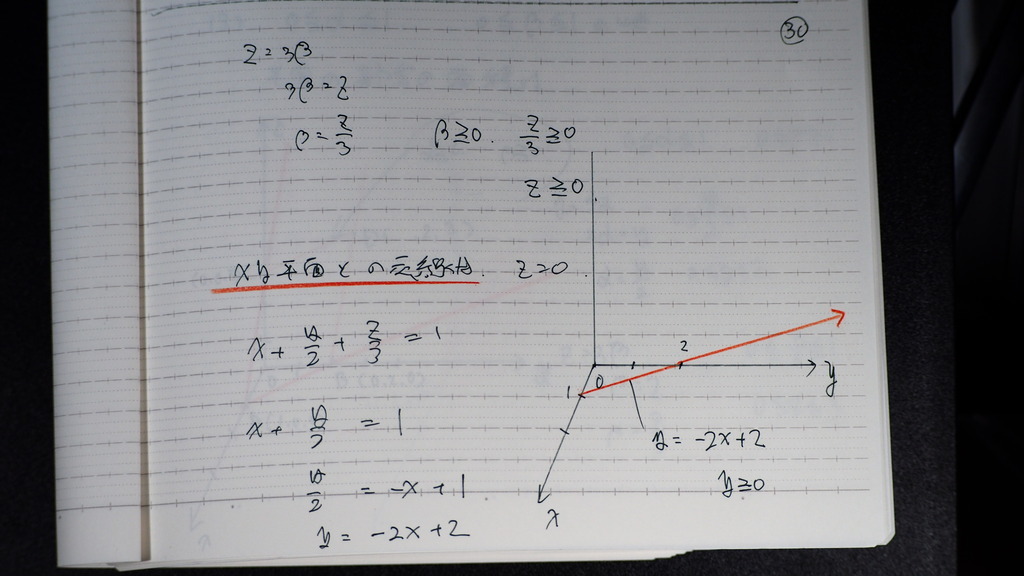
31
xz平面は
z=-3x+3
こんな感じで
赤斜線の部分
32
さらに
(3)
y z
の範囲が
33
xの範囲は

34
座標にすれば
35
辺の長さは
ベクトルの
絶対値で求まるので

36
底辺√5
ななめが √10

37
角度を 求めて
sinを 使いたいので
内積を いじりながら

38
COSがでれば
sinが出るというわけで

39
ね
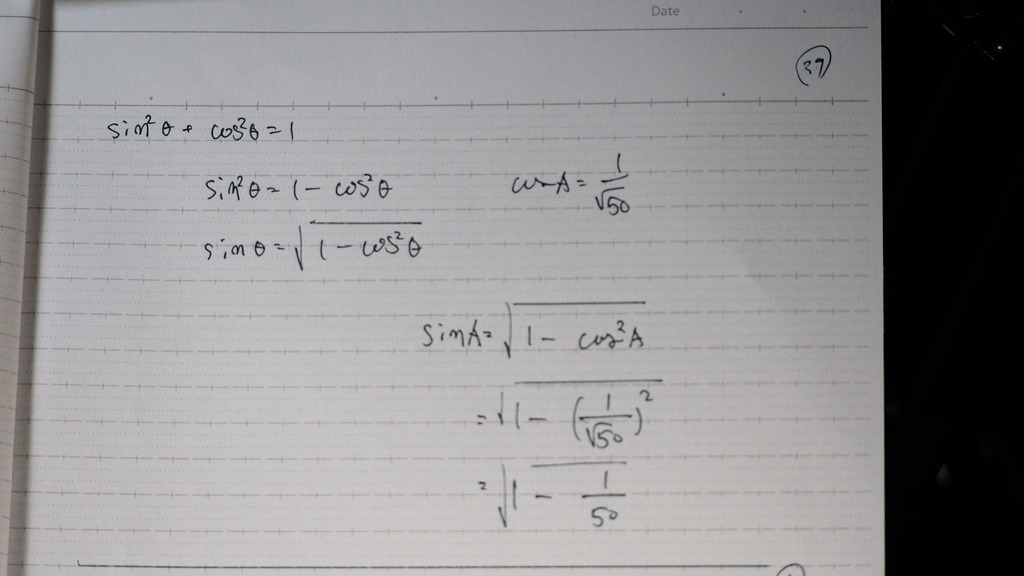
40
底辺 × 高さは
高さが 斜辺×sinA
であるので
7

お疲れ様です。
今日は
平面の方程式の
媒介変数形
01
問題
02
平面上の ベクトルは
異なる 二つのベクトルの
実数倍で
すべて 表せる
03
そこで
イメージとしては
対角線
APベクトルは
t倍のABベクトル
と
s倍のACベクトルの
和
(p-a)=t(b-a)+s(c-a)
この 左辺のaベクトルを
じゃナイスカ
04
なったデショ
05
実際に
ベクトル方程式に
数値を 入れると
06
列で書いた方が
見やすいと思ってさ
ね
07
計算して
整理したらば
08
ここから
s、t を 消去して
x、y、z、定数の
式にすればいいので
まず t
09
次に s
10
③式に t、sを 代入して
11
問題
まずですね
z軸との交点の座標は
12
x1=0、Y=0
を 代入したら
④
13
それと
⑤
④⑤より
14
tは 8/3
15
sは -7/3
16
これら
t、sを
③式に 代入して
z=10
であるから
(0,0,10)
17
この平面と
xy平面の
交線は
Z=0を 代入して
18
xの式から
19
yの式から
20
これらを
足すでしょ
z=0の時に
x+y=10
21
この さん式から
s、tを
消去すればいいのだから
22
色々やり方は
あるとおもいますが
➀-③から
④
23
②+③×2で
⑤
24
④⑤を 足すと
x+y+z-10=0
25
もんだい
26
(1)
y 、zから α 、β
27
平面の方程式は
28
題意を 良く見ると
ax+by+cz+d=0
の形ではなく
ax+by+cz=d
であるので
ここで 指示違反で
原点は もったいない
29
(2)
α βの
範囲から
y、zは ゼロ以上
30
境界線を 求めると
y=-2x+2
xy平面は 平場ですが
31
xz平面は
z=-3x+3
こんな感じで
赤斜線の部分
32
さらに
(3)
y z
の範囲が
33
xの範囲は
34
座標にすれば
35
辺の長さは
ベクトルの
絶対値で求まるので
36
底辺√5
ななめが √10
37
角度を 求めて
sinを 使いたいので
内積を いじりながら
38
COSがでれば
sinが出るというわけで
39
ね
40
底辺 × 高さは
高さが 斜辺×sinA
であるので
7
お疲れ様です。
2022年12月11日
22029 大人のさび落とし 空間座標とベクトル 平面の方程式
空間座標とベクトル 平面の方程式
01
平面の方程式
ある 空間ベクトルがあって
そのベクトルに 垂直な
平面
これが 平面の方程式なんですが
3次元空間で
ある方向に 矢印が向いてるでしょ
その
矢印に 垂直な
直線群を
考えると
無数にある 直線が
その
ベクトルに対して
平面を なしている

02
そこで
平面上の 任意の点を
どこにとっても
どんなにとっても
その 一つを P(x、y、z)
と しようか
PA ベクトルは
OA ベクトルに
垂直だよ
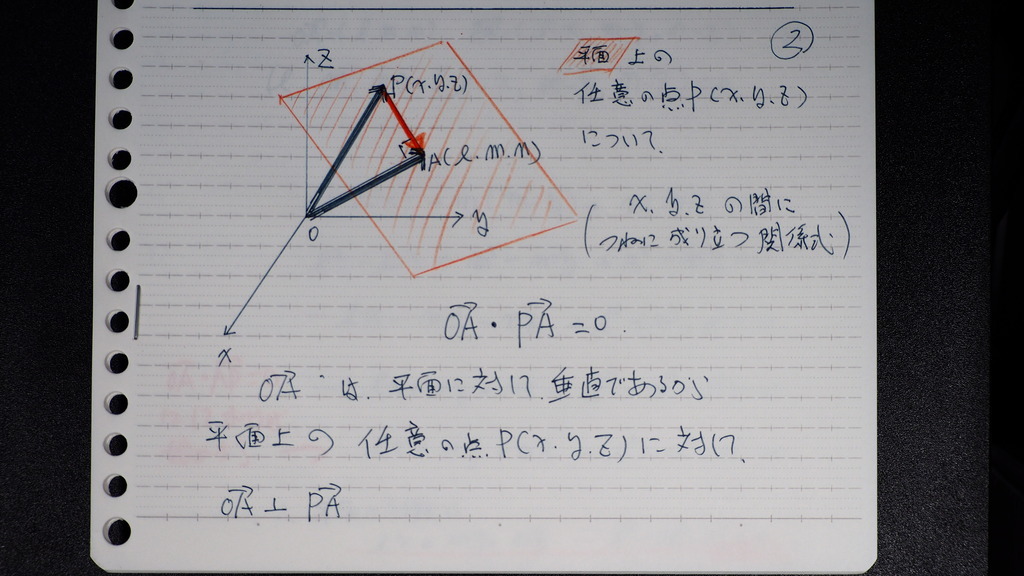
03
PA ベクトルを
けいさんして
成分でさ やったデショ
このベクトルと (l,m,n) が
垂直だから
内積=0

04
展開してくと
こんな感じで
途中で
マイナスを くくって
払ったんだけど
初めから
PA ベクトルじゃなくて
AP ベクトルで
計算すれば
同じこと
だから これが
平面の方程式

05
(a,b,c) は
平面に 垂直な ベクトルになるので
少なくとも
一つは 0 ではない
そうでないと
垂直な ベクトルにならず
点に なってしまう
(原点)
平面の
方程式に
平面上に ある 点を
代入して

06
➀②③④
として
➀-②
(②-➀) にした方がよかったかな
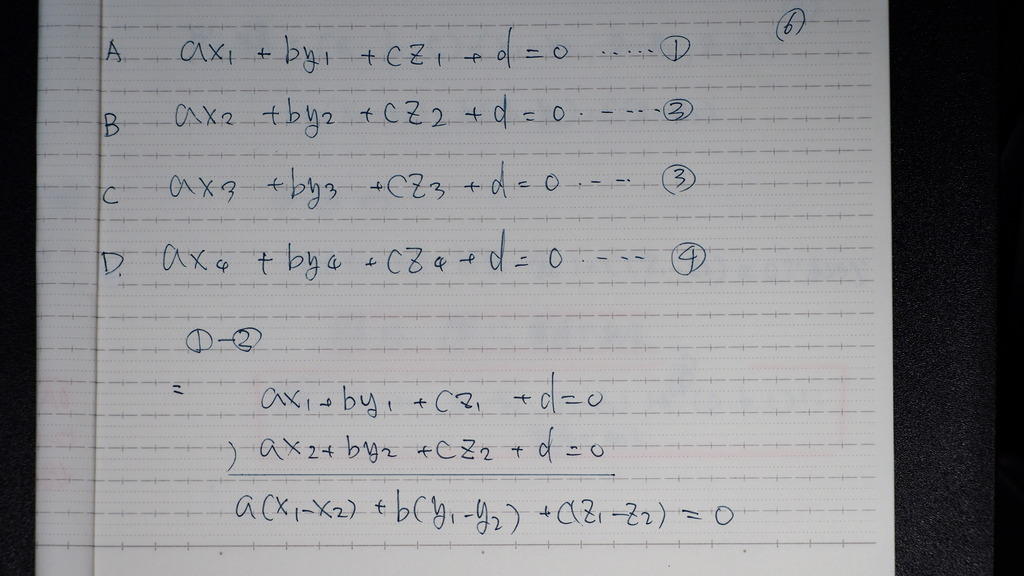
07
BA ベクトルと
P ベクトル と考えると
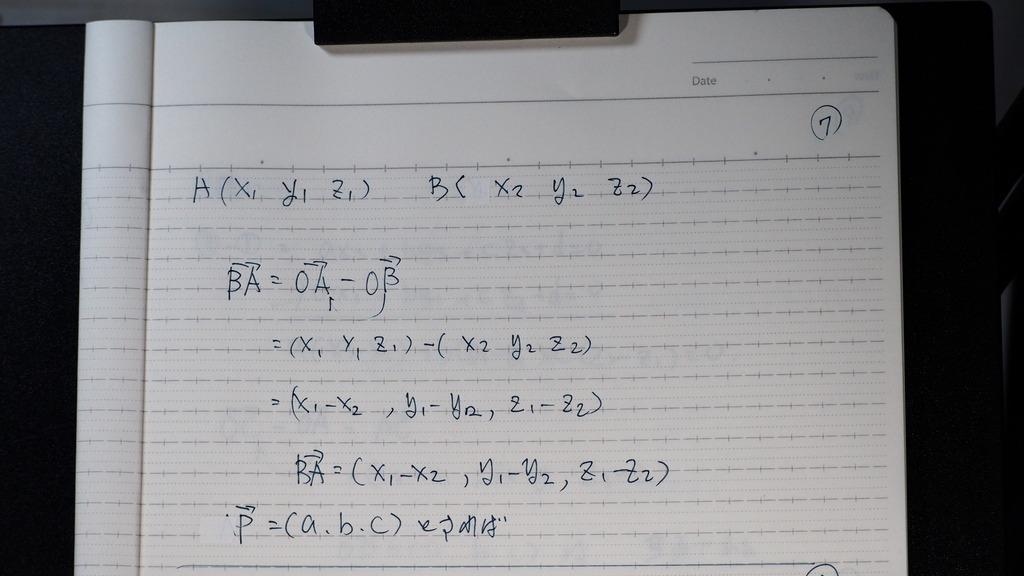
08
内積は こんな感じに 成るんだけど
このあたいは
➀-②より
=0
であるから
内積=0 で 垂直

09
同様に

10
同様に
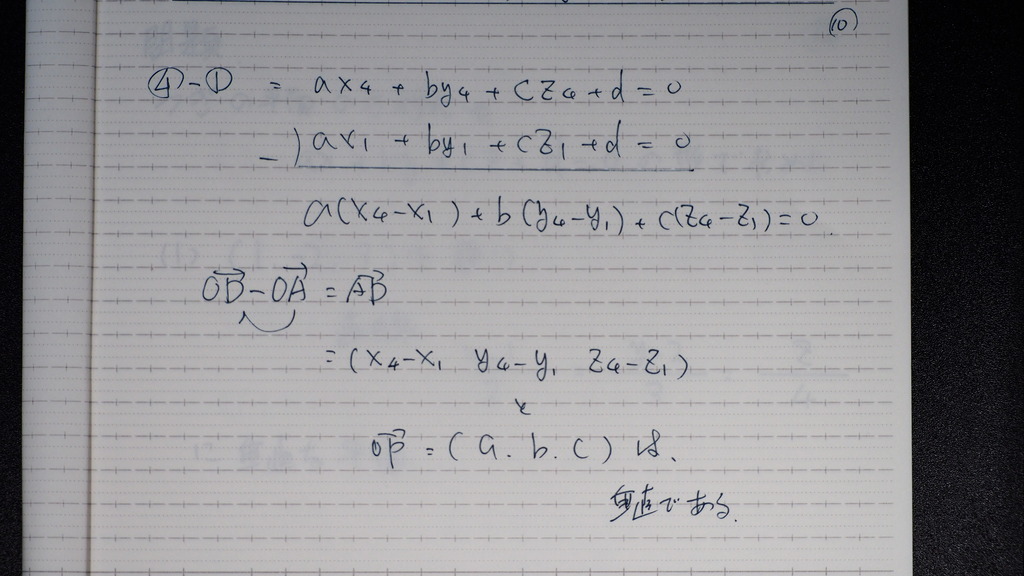
11
ゆえに

12
問題
これこれの点を とおり
これこれの 直線に 垂直な
平面の方程式
を
求めよ

13
平面の 方程式の 形は
こんなで
(a,b,c)は 平面に 垂直な
ベクトル
直線は こんな
で
直線の時の
分母は 方向係数
直線に平行な成分
題意では
直線に 垂直な平面とあるから
そのまま
直線の 方向係数が
今回は 平面の垂直方向を
向いている

14
であるので
平面の方程式に代入して
通過点を
(x,y,z)に 代入すれば
dは -8
求める
平面の方程式は
こんな

15
三点が
与えられてるときの
平面の
方程式

16
3点を 方程式に
代入して
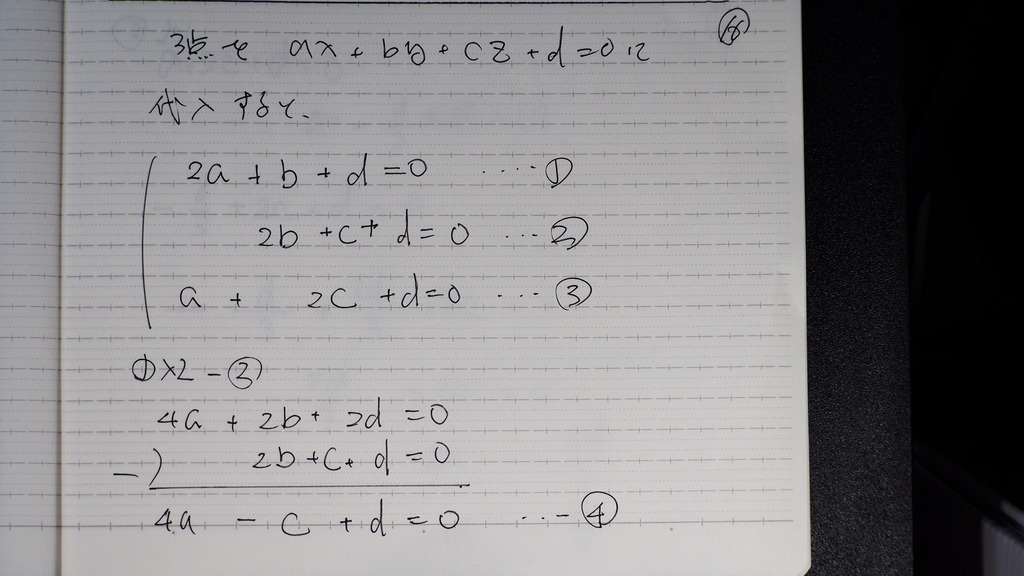
17
a=
-d/3
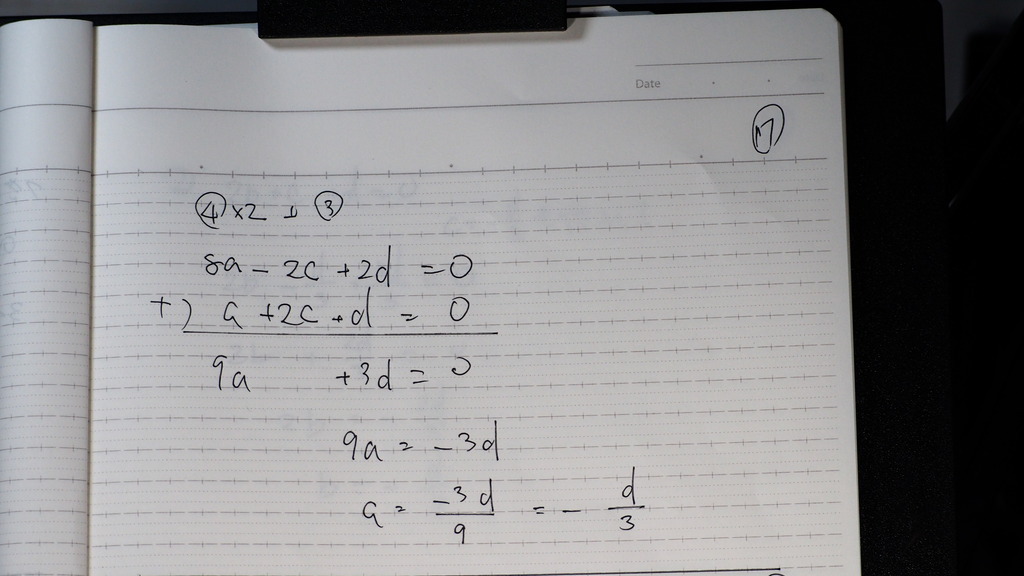
18
C=
-d/3
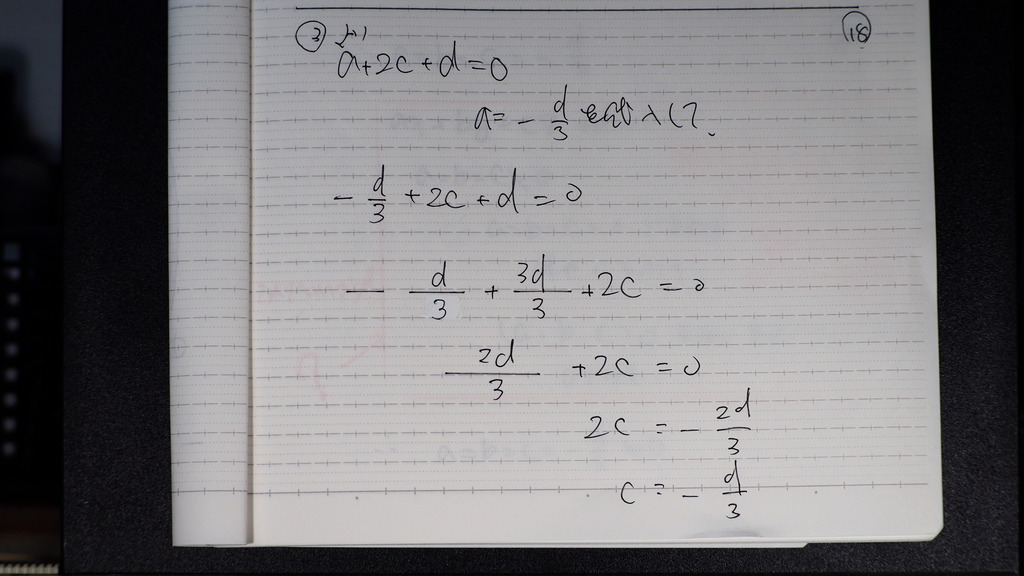
19
b=
-d/3
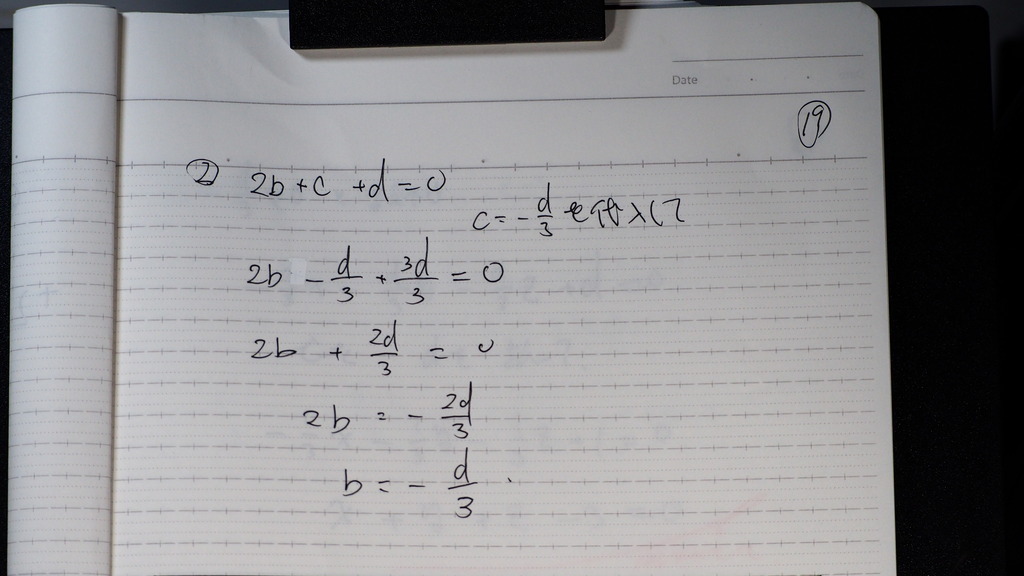
20
a=b=c=-d/3
a=b=cは 0ではないので
-d/3 も 0ではない
で
払って

21
整えると
平面の方程式は
こんな感じ
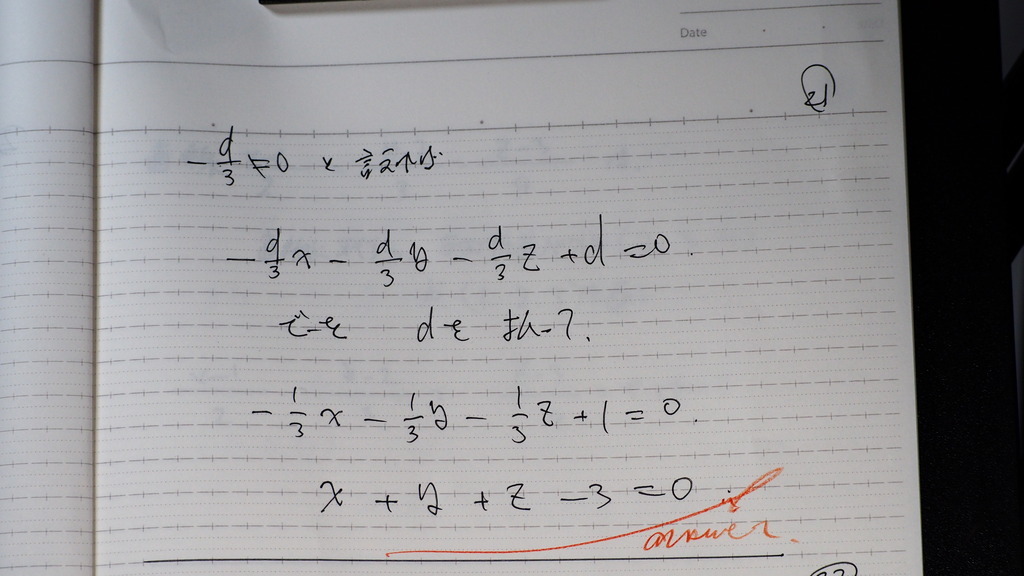
22
問題
平面の方程式を
求めよ

23
直線の
方程式から
これは (1,2,3)を 通る
方向ベクトルは
(2,3,4)

24
媒介変数表示にして
直線は
平面に 含まれてるから
tの値を
適当に 入れて
もう一点 求めて
t=1 とすれば

25
この 2点と
其の他 1点を
通るから

26
直線上の 2点と
(0,0,0) から
ベクトルを
2つ 出してベクトル
は 直線の方程式の
方向係数だから

27
直線の上の 2点の
ベクトルを
求めれば
一目瞭然

28
二点間の ベクトルは
直線の 方向係数に 成るでしょ
この3本と
平面に垂直なP(a,b,c)が 垂直だから

29
内積 =0 が3本
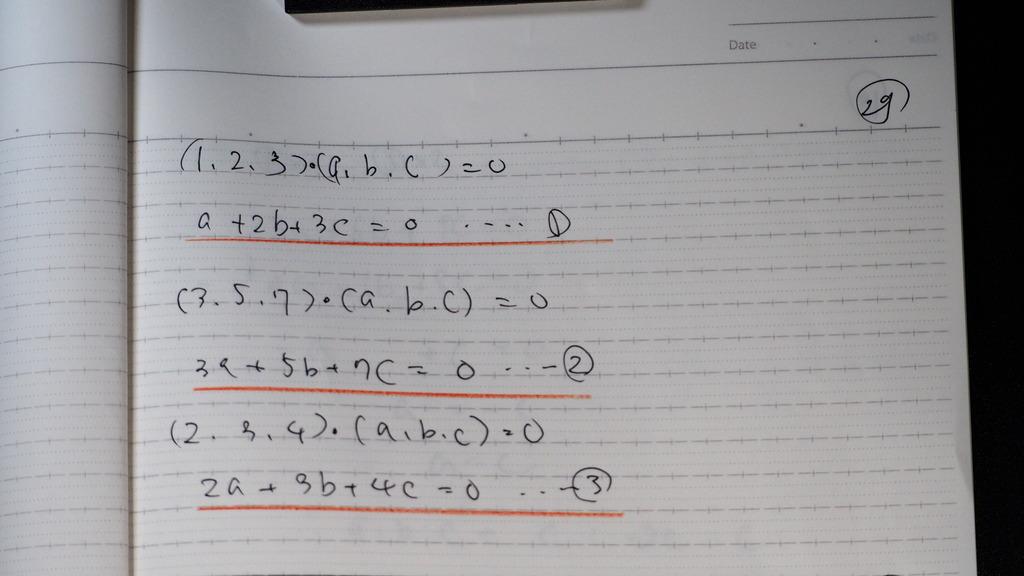
30
b=-2c
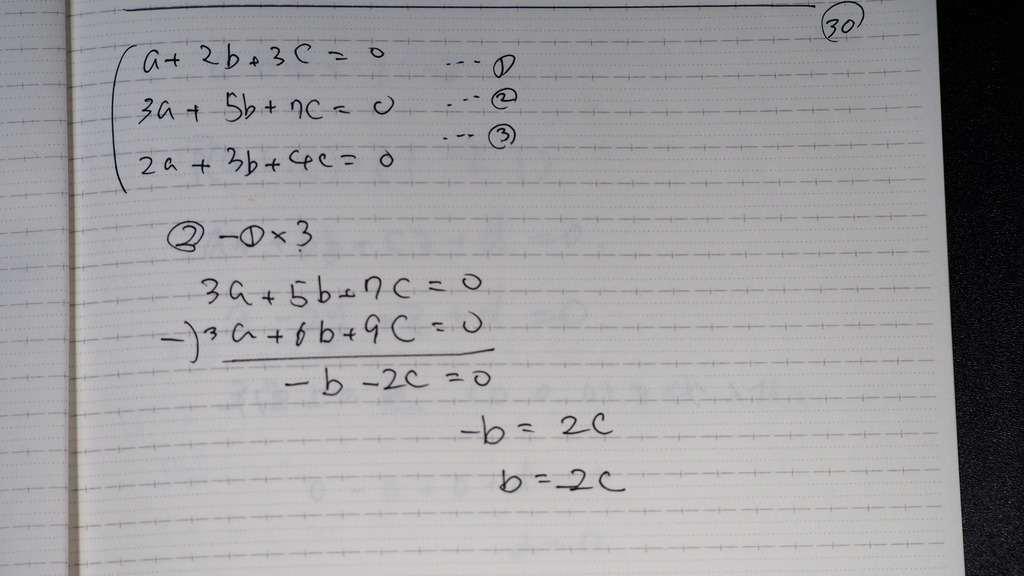
31
a=c
a:b:c=c:-2c:c
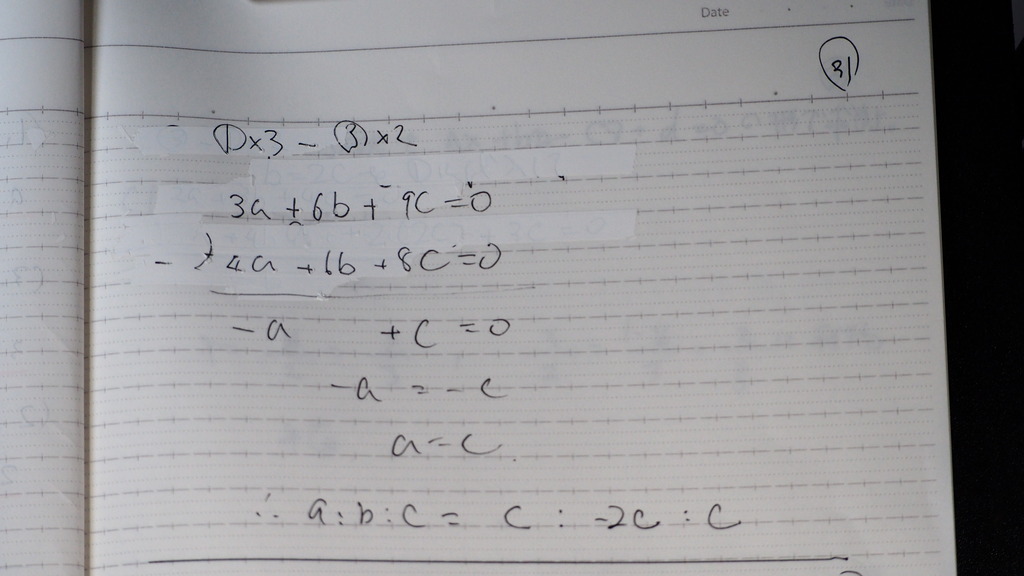
32
a:b:c= 1:-2:1
平面上の点と a,b,c
と 平面上の
点の座標から
d=0
であるので
平面の方程式は
こんな感じで

33
もんだい

34
2つの 直線の 方向係数ベクトル
と
平面の方程式の (a,b,c)は
垂直なので
内積の式が 2つ
文字が3つ

35
➀② と ③

36
➀②から
bは -c/7
aは -19c/7
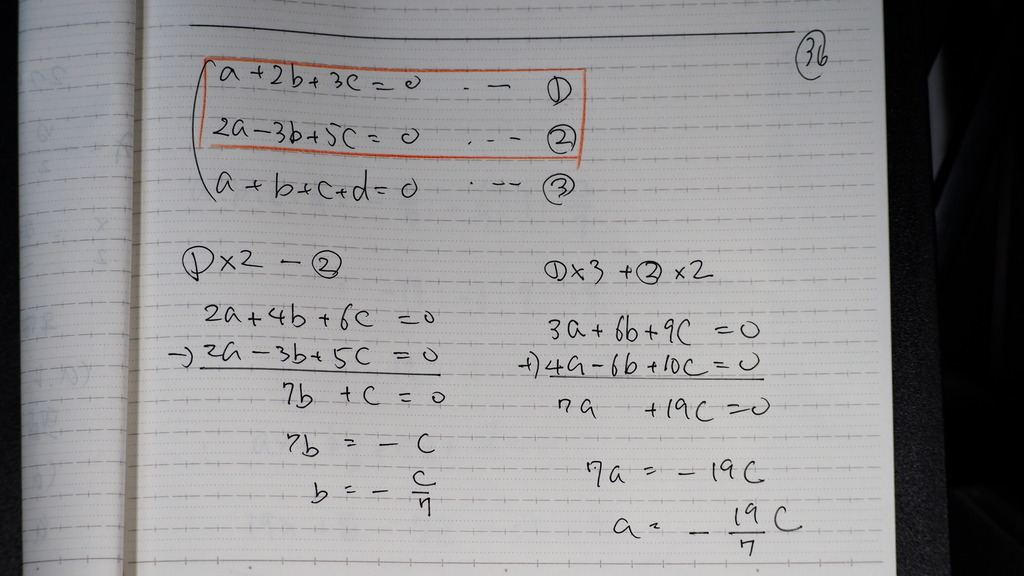
37
a:b:c は こんなデショ
で
③式より d=13c/7
でしょ
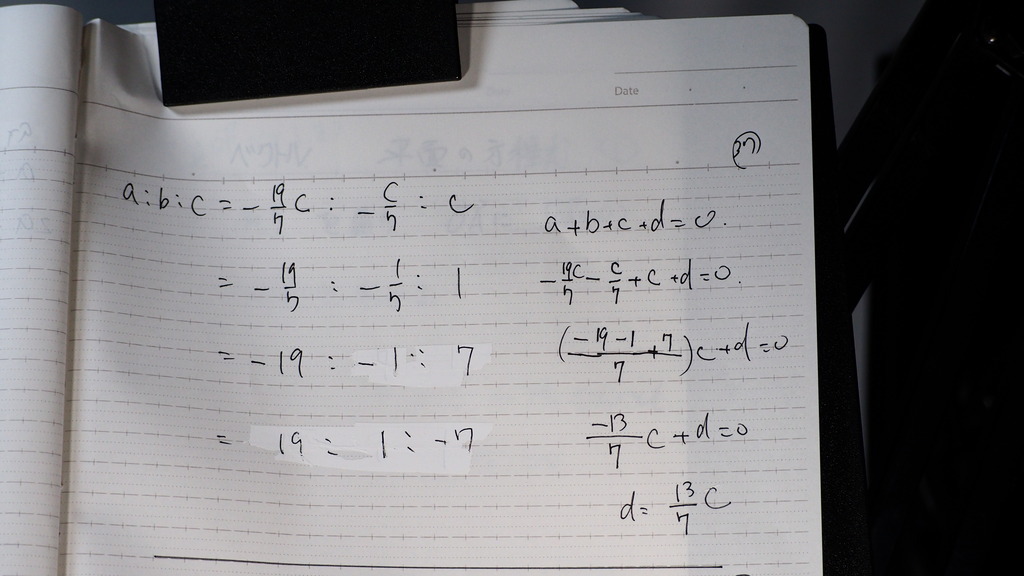
38
ナタメ
こうです

おつあれ様です。
01
平面の方程式
ある 空間ベクトルがあって
そのベクトルに 垂直な
平面
これが 平面の方程式なんですが
3次元空間で
ある方向に 矢印が向いてるでしょ
その
矢印に 垂直な
直線群を
考えると
無数にある 直線が
その
ベクトルに対して
平面を なしている
02
そこで
平面上の 任意の点を
どこにとっても
どんなにとっても
その 一つを P(x、y、z)
と しようか
PA ベクトルは
OA ベクトルに
垂直だよ
03
PA ベクトルを
けいさんして
成分でさ やったデショ
このベクトルと (l,m,n) が
垂直だから
内積=0
04
展開してくと
こんな感じで
途中で
マイナスを くくって
払ったんだけど
初めから
PA ベクトルじゃなくて
AP ベクトルで
計算すれば
同じこと
だから これが
平面の方程式
05
(a,b,c) は
平面に 垂直な ベクトルになるので
少なくとも
一つは 0 ではない
そうでないと
垂直な ベクトルにならず
点に なってしまう
(原点)
平面の
方程式に
平面上に ある 点を
代入して
06
➀②③④
として
➀-②
(②-➀) にした方がよかったかな
07
BA ベクトルと
P ベクトル と考えると
08
内積は こんな感じに 成るんだけど
このあたいは
➀-②より
=0
であるから
内積=0 で 垂直
09
同様に
10
同様に
11
ゆえに
12
問題
これこれの点を とおり
これこれの 直線に 垂直な
平面の方程式
を
求めよ
13
平面の 方程式の 形は
こんなで
(a,b,c)は 平面に 垂直な
ベクトル
直線は こんな
で
直線の時の
分母は 方向係数
直線に平行な成分
題意では
直線に 垂直な平面とあるから
そのまま
直線の 方向係数が
今回は 平面の垂直方向を
向いている
14
であるので
平面の方程式に代入して
通過点を
(x,y,z)に 代入すれば
dは -8
求める
平面の方程式は
こんな
15
三点が
与えられてるときの
平面の
方程式
16
3点を 方程式に
代入して
17
a=
-d/3
18
C=
-d/3
19
b=
-d/3
20
a=b=c=-d/3
a=b=cは 0ではないので
-d/3 も 0ではない
で
払って
21
整えると
平面の方程式は
こんな感じ
22
問題
平面の方程式を
求めよ
23
直線の
方程式から
これは (1,2,3)を 通る
方向ベクトルは
(2,3,4)
24
媒介変数表示にして
直線は
平面に 含まれてるから
tの値を
適当に 入れて
もう一点 求めて
t=1 とすれば
25
この 2点と
其の他 1点を
通るから
26
直線上の 2点と
(0,0,0) から
ベクトルを
2つ 出してベクトル
は 直線の方程式の
方向係数だから
27
直線の上の 2点の
ベクトルを
求めれば
一目瞭然
28
二点間の ベクトルは
直線の 方向係数に 成るでしょ
この3本と
平面に垂直なP(a,b,c)が 垂直だから
29
内積 =0 が3本
30
b=-2c
31
a=c
a:b:c=c:-2c:c
32
a:b:c= 1:-2:1
平面上の点と a,b,c
と 平面上の
点の座標から
d=0
であるので
平面の方程式は
こんな感じで
33
もんだい
34
2つの 直線の 方向係数ベクトル
と
平面の方程式の (a,b,c)は
垂直なので
内積の式が 2つ
文字が3つ
35
➀② と ③
36
➀②から
bは -c/7
aは -19c/7
37
a:b:c は こんなデショ
で
③式より d=13c/7
でしょ
38
ナタメ
こうです
おつあれ様です。