2022年11月16日
22021 大人のさび落とし 空間座標とベクトル ベクトルのなす角
ベクトルの なす角
なす角 と言うのは
二つの ベクトルがあるとき
ベクトルを 平行移動して
始点同士を 合わせたときに
できる 角度 のことです。
01
もんだい
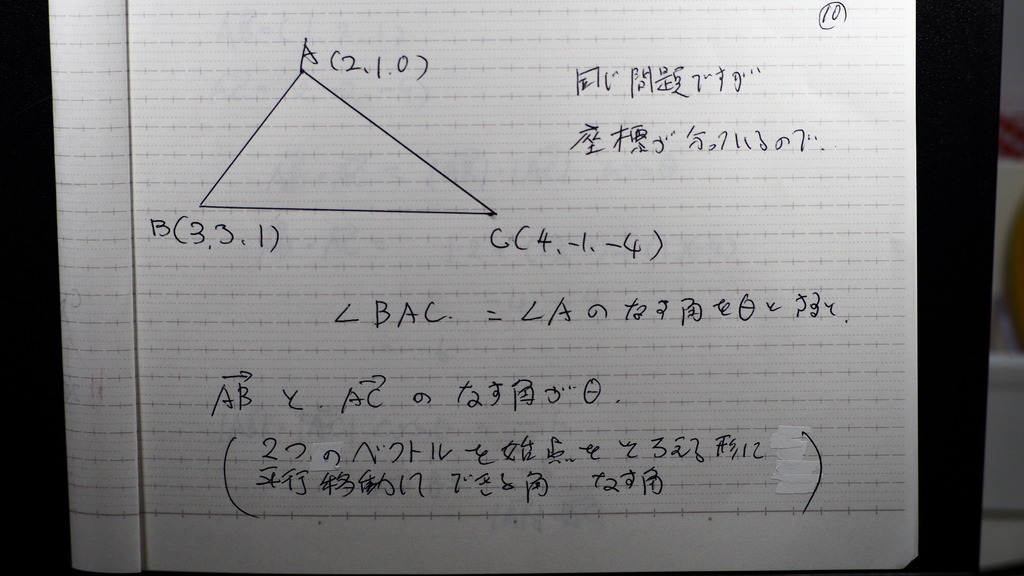
座標が 与えられてます
空間だけど
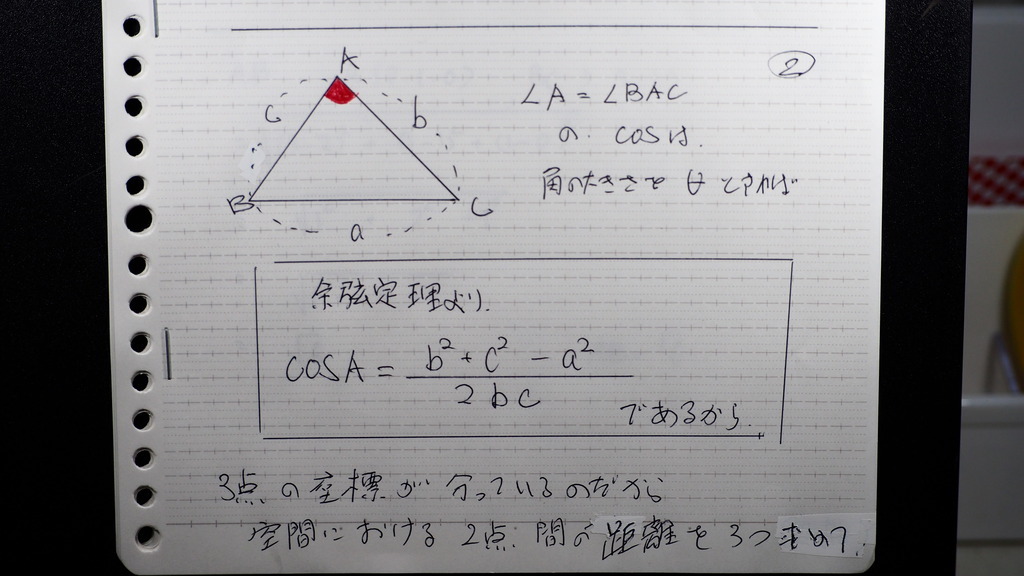
角BAC と 三角形 ABC の
面積を 求めよ

02
まずは
余弦定理で
行ってみますが
三角形の 三辺の 長さが
分かってるときは
余弦定理で
座標が分かってるので
2点間の距離 空間 で
長さを 出しといて
03
辺ABは

04
√6
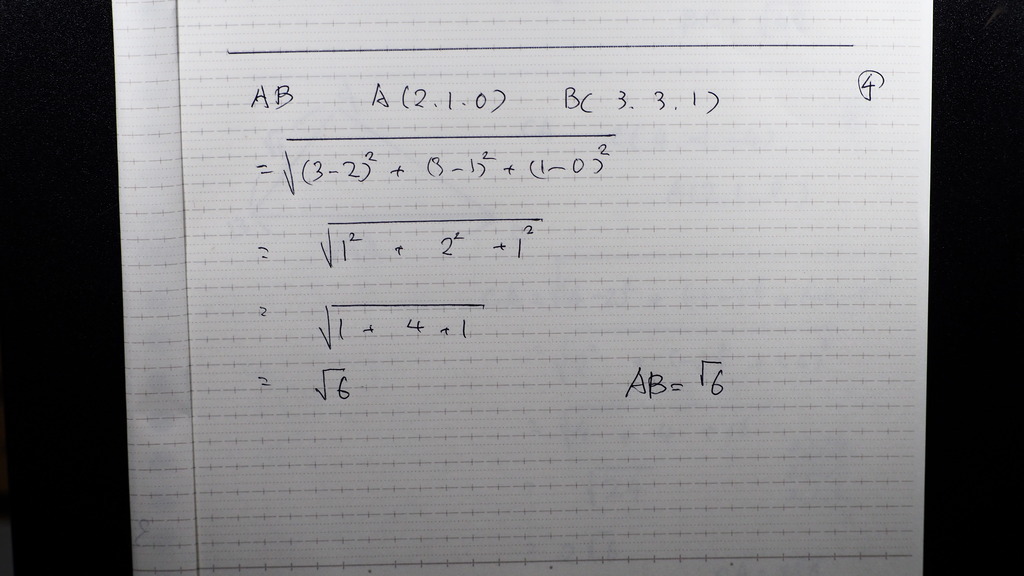
05
辺BCは √42
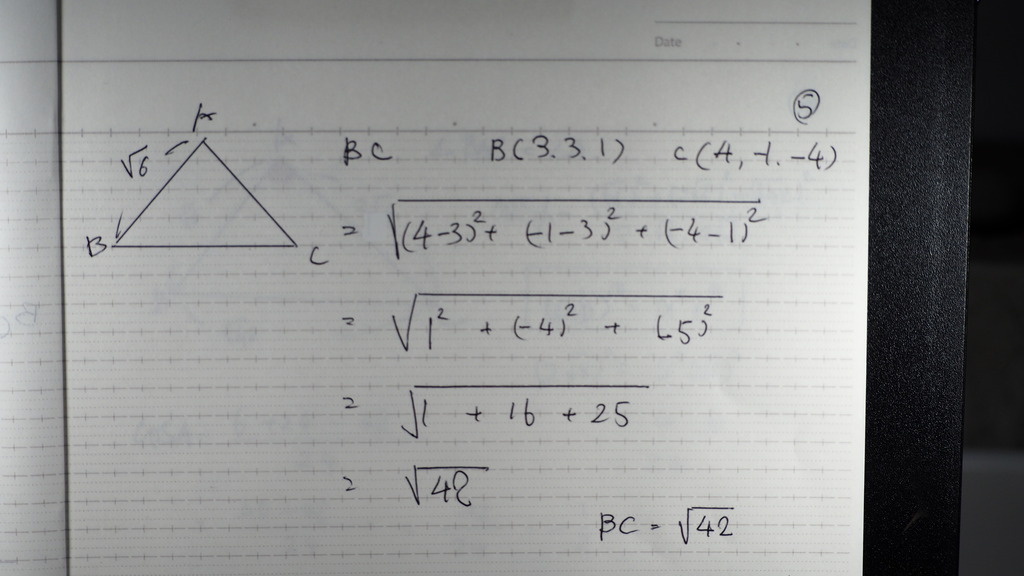
06
辺CAは
2√6

07
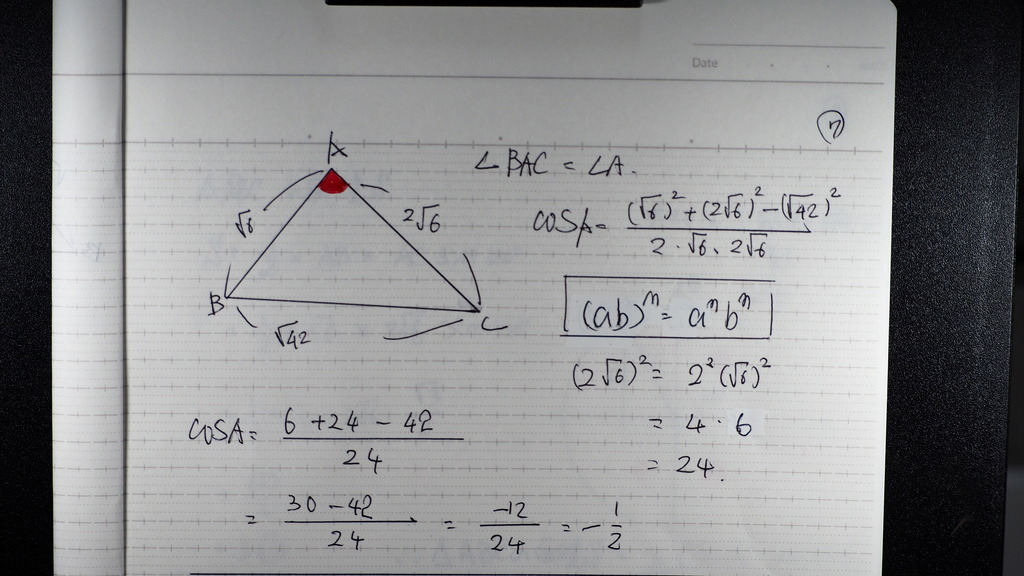
余弦定理に
代入して
COSの 値で
出て来ますが
-1/2
08
なす角はゼロ から 180 度 (パイ ラジアン)
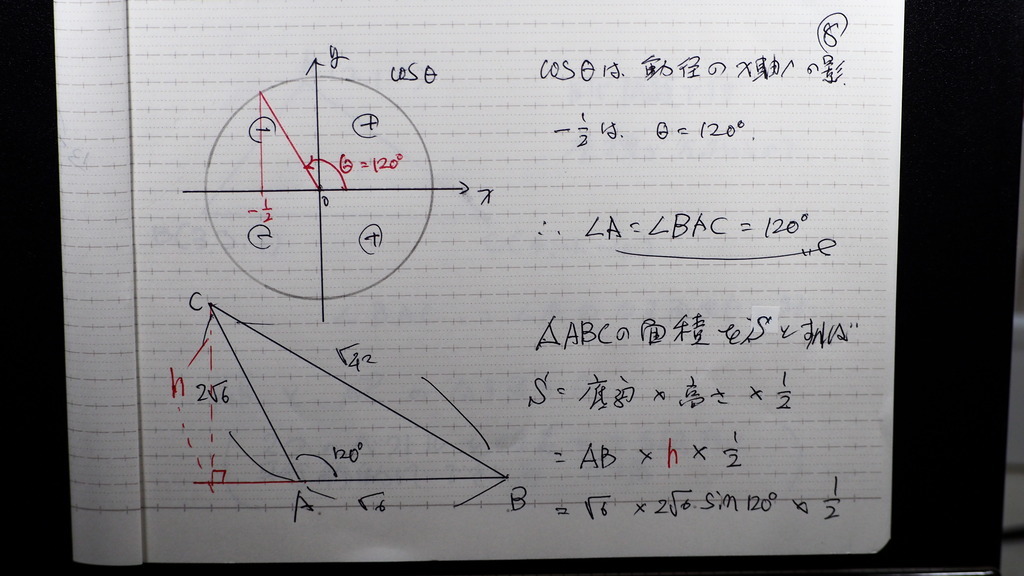
コサインは 動径の
x軸への陰で
座標上
ゼロの時 ぜろ度
ゼロ から 90度 未満まで プラス
90度 の時 ぜろ
90度 から 180度 未満の時
マイナス
180度 の時 -1
なす角は 120度
三角形の 面積に時は
なす角の 斜辺のサイン 成分が
高さなので
09
サイン120度は
√3/2
面積は
3√3

10
今の問題を
今度は
ベクトルの内積を使って
解くと
11
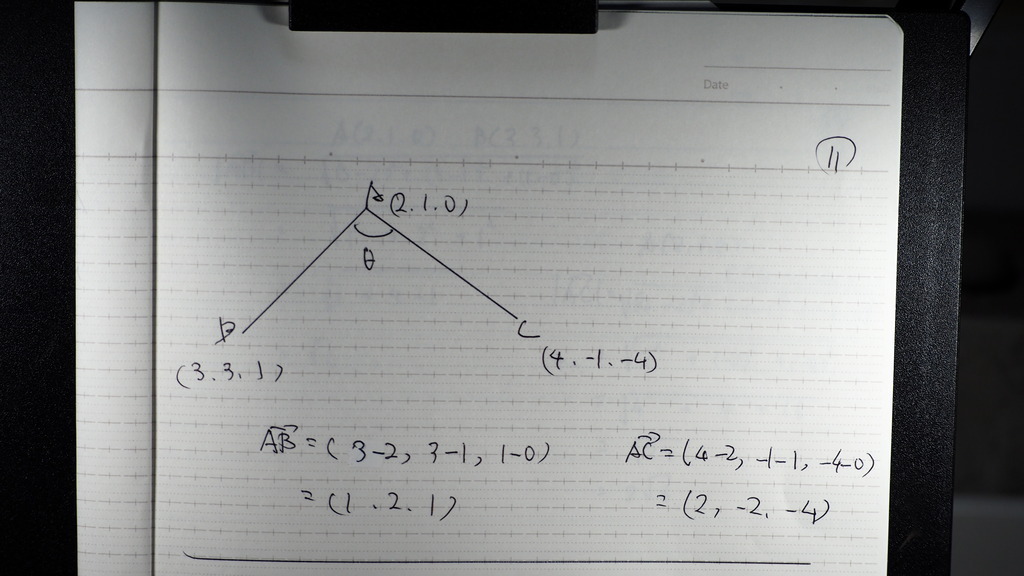
まず
なす角が
ここン所 であるから
2つのベクトル
AB AC を
成分で
計算して
12
内積の定義式は
こんなだから
成分の方から
内積が -6
もう一つの 定義式から
COS Θ が こんなでしょ
分母の 絶対値は
2点間の 距離で求めて
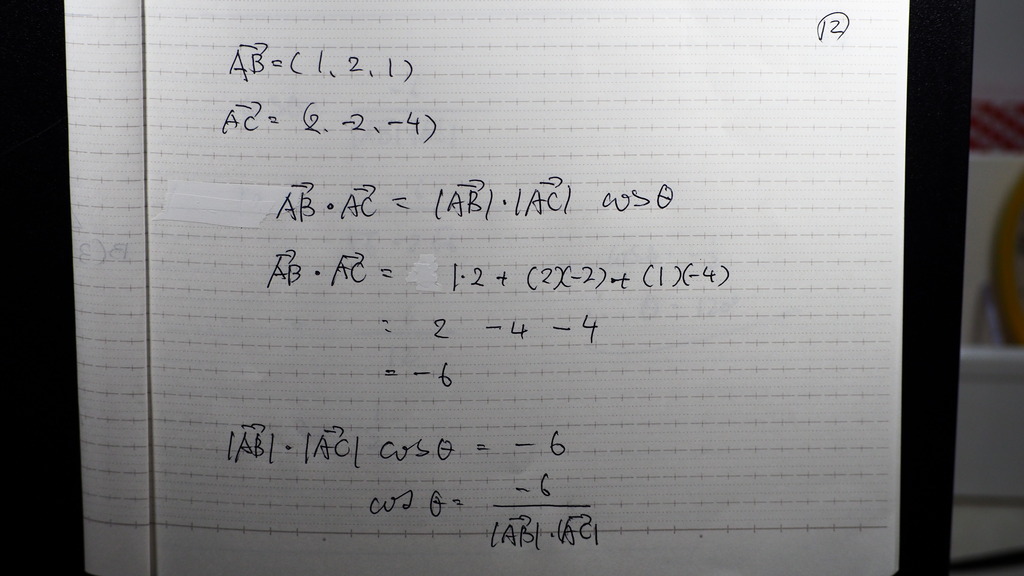
13
こんな感じになるので
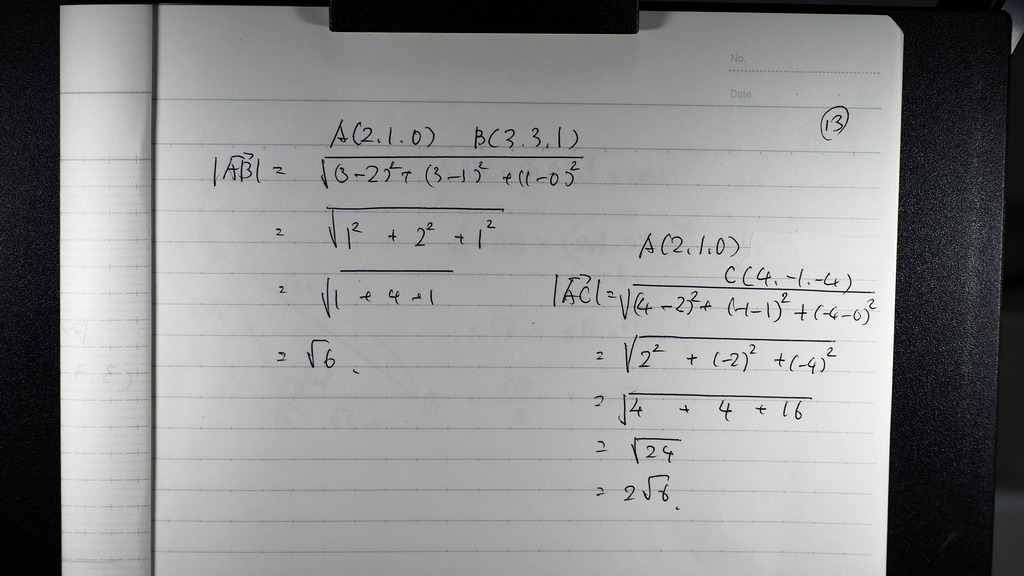
14
なす角が出て来て
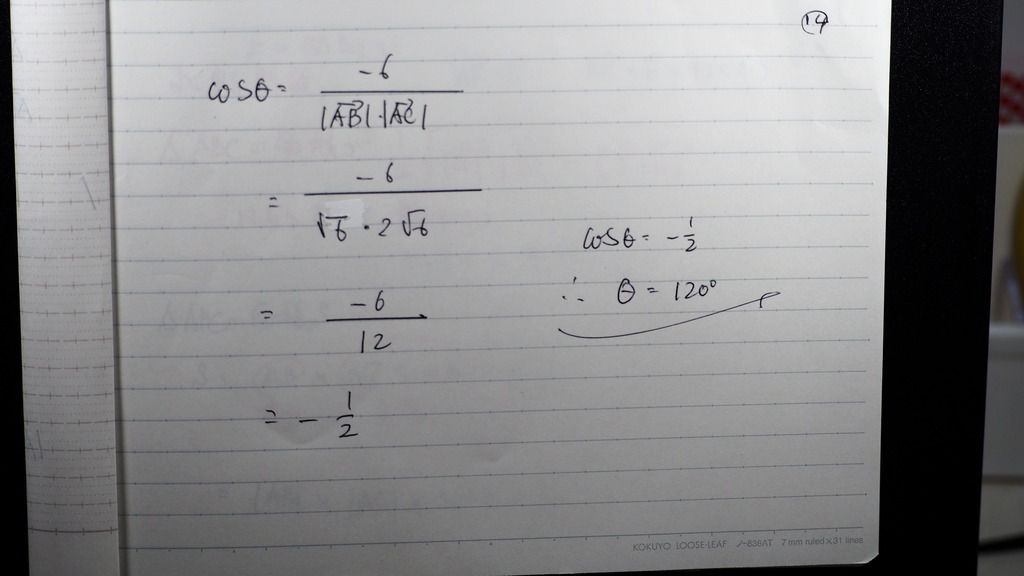
15
面積も
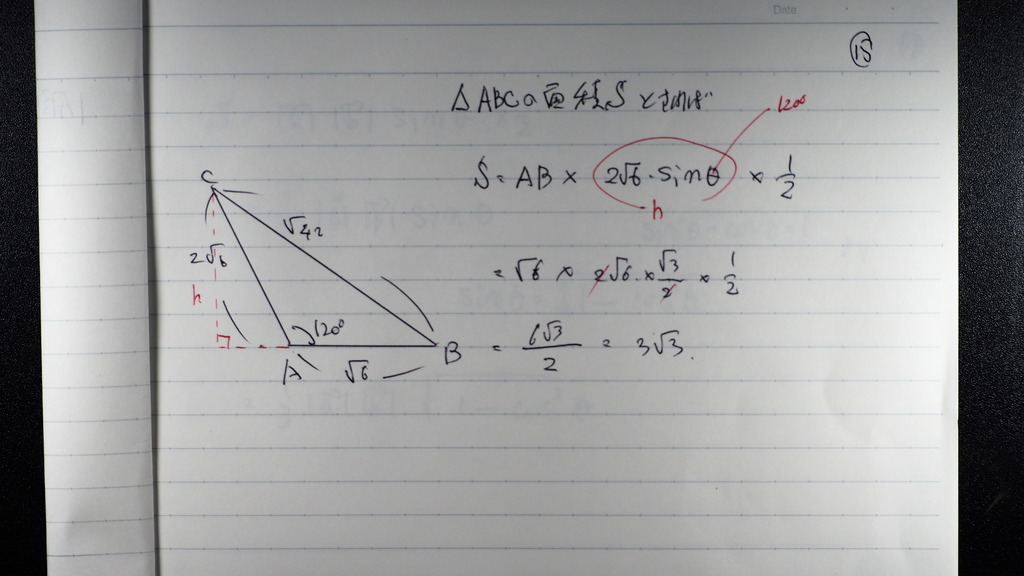
16
ところで
ここんとこの問題で
これが
非常に 良く 出題される
面積が
こんな感じで 書けることを
いえ
と言うんですが
さっきの
上の式から
少し いじってくと
なるですよ

17
底辺 AB で 書いてたけど
大きさと言う意味で
ベクトルに絶対値を付けて
ABを aベクトル
ACを bベクトルとすれば
こんな感じに なる
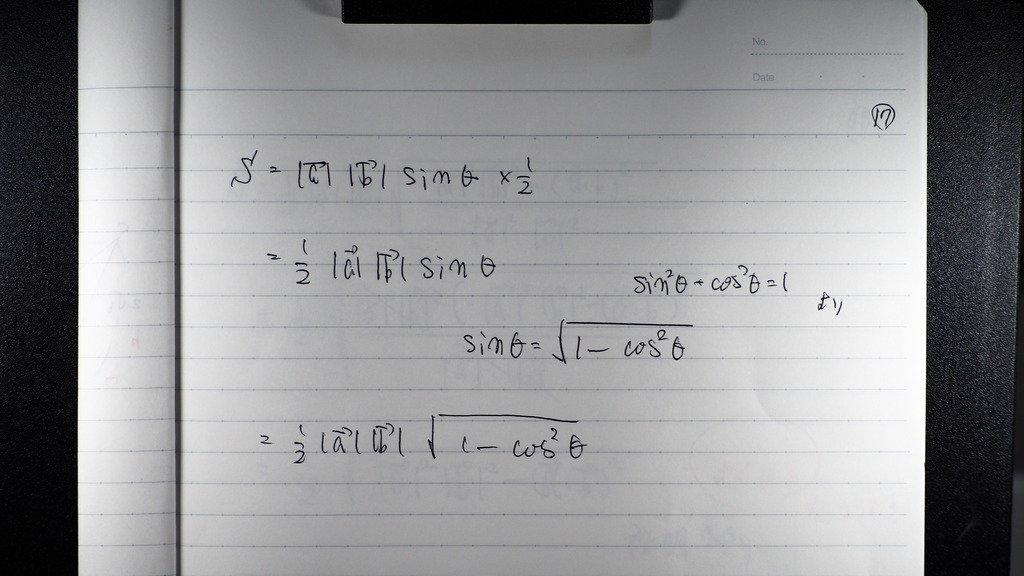
18
内積の 定義式の 変形で
COS θは
こんなだからさ
で
√の 外の 絶対値を
√の中に 入れれば
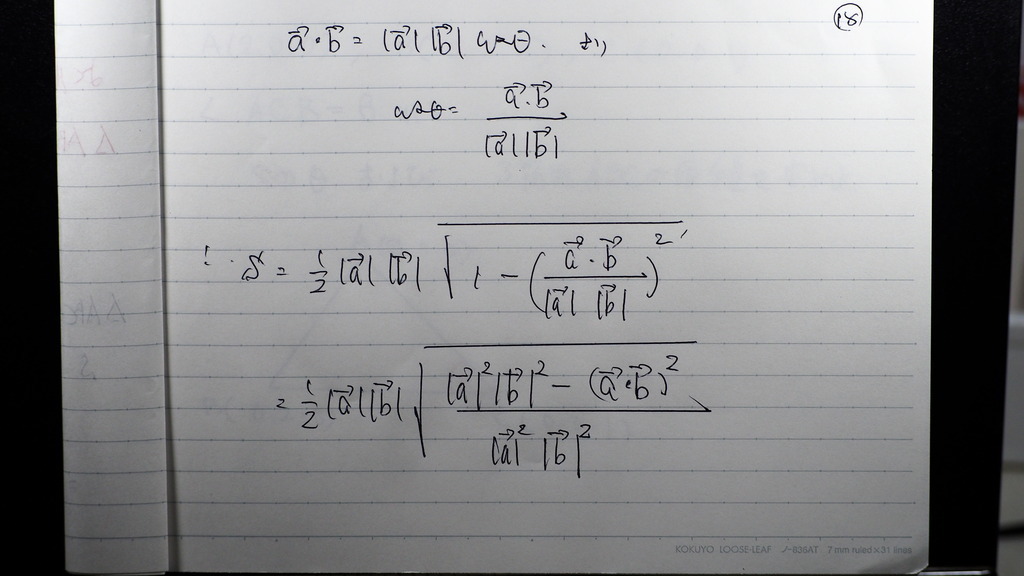
19
なったデショ

20
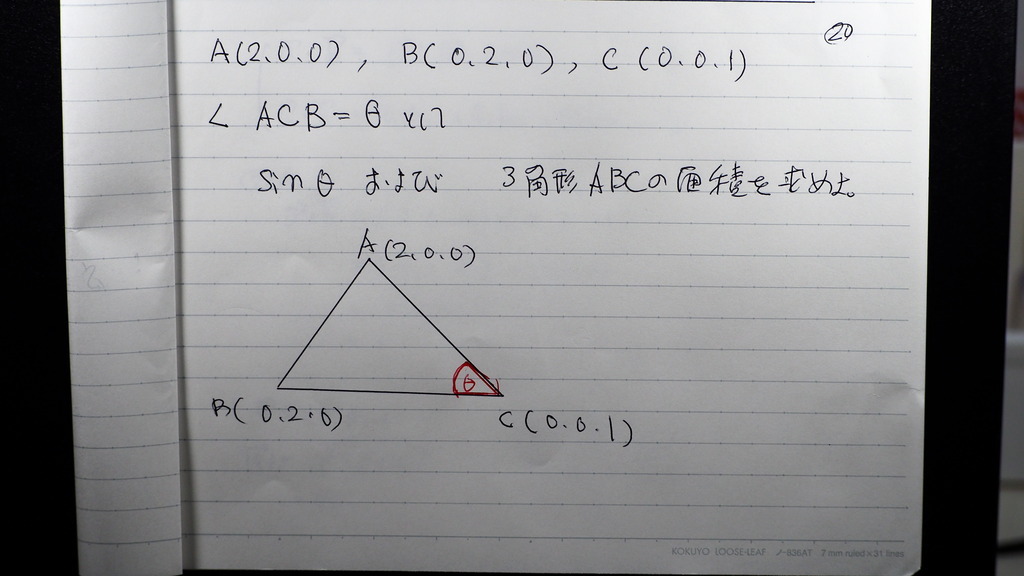
類題
内積を 使って
解いてきますか
21
aベクトル bベクトル
を
こんな風に設定して
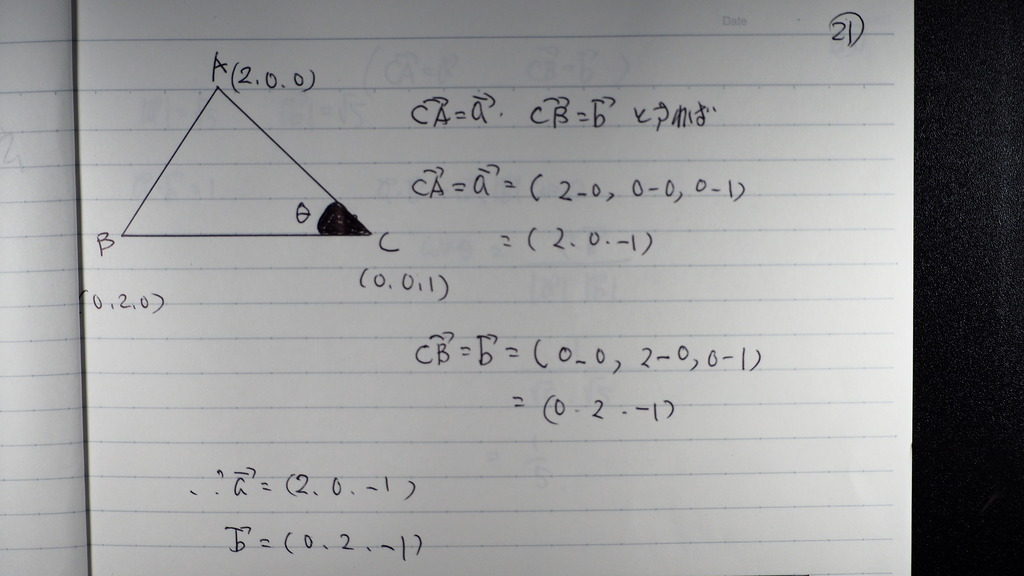
22
内積の定義式②
成分の方から
内積は 1
成分が分かってるので
ベクトルの
絶対値 ( 大きさ )を 求めて
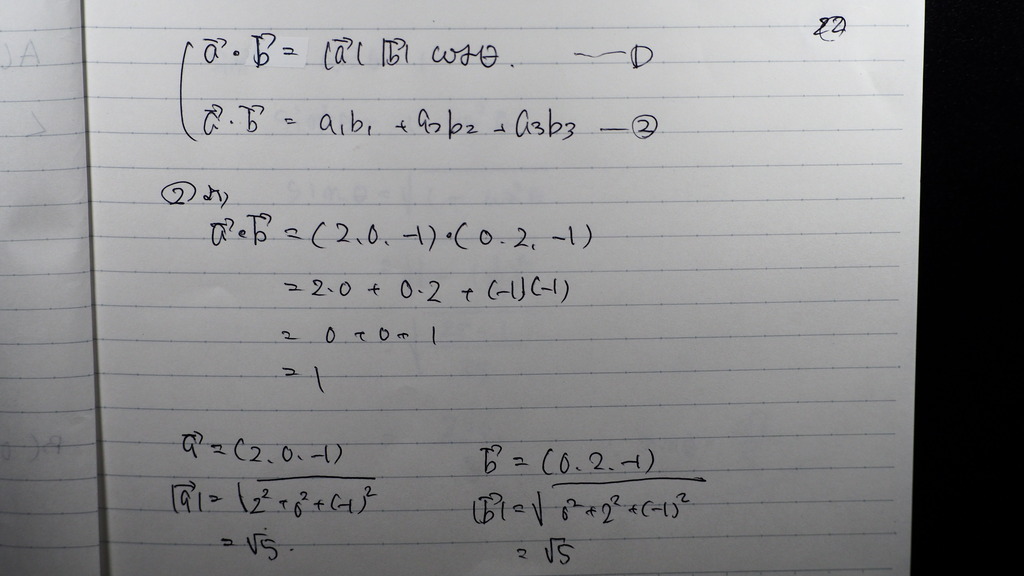
23
COS θは
1/5

24
題意では
サイン角で 求めよ なので
こんな感じに
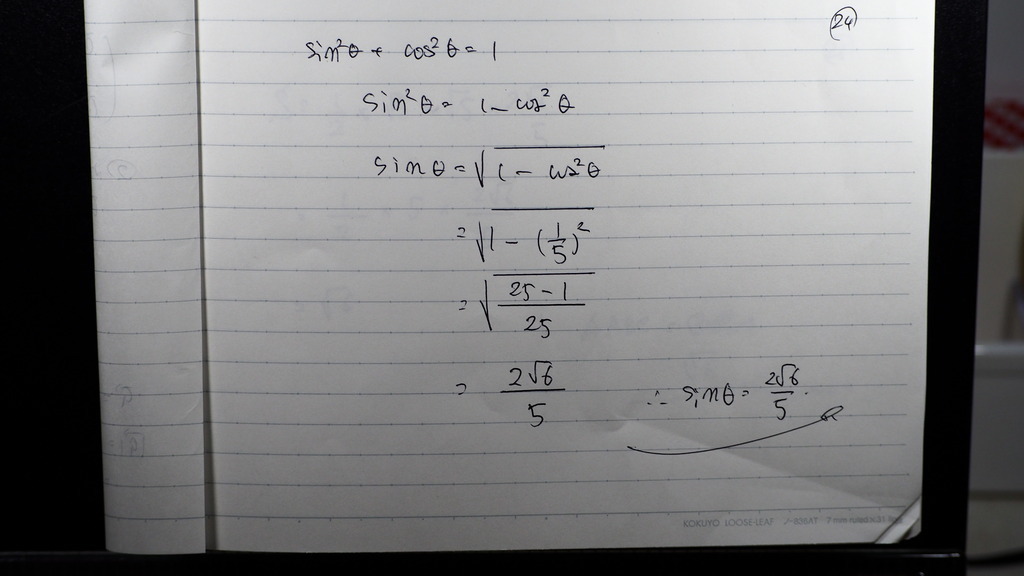
25
サイン角が出てれば
ベクトルの 絶対値の 積に
なす角のサイン角
それを 2で割れば
1/2 を 掛けるとも言いますが
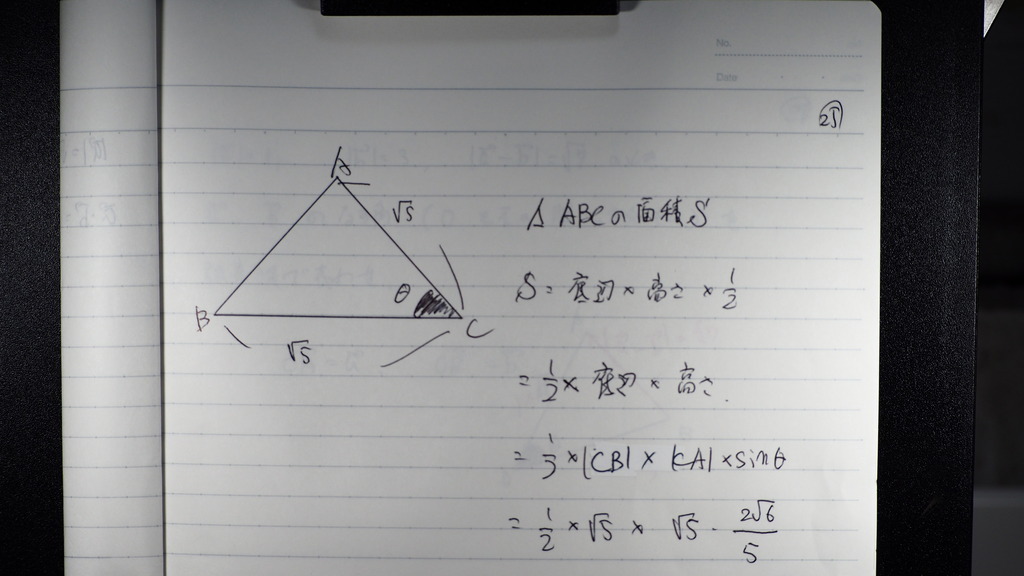
26
こんな感じで
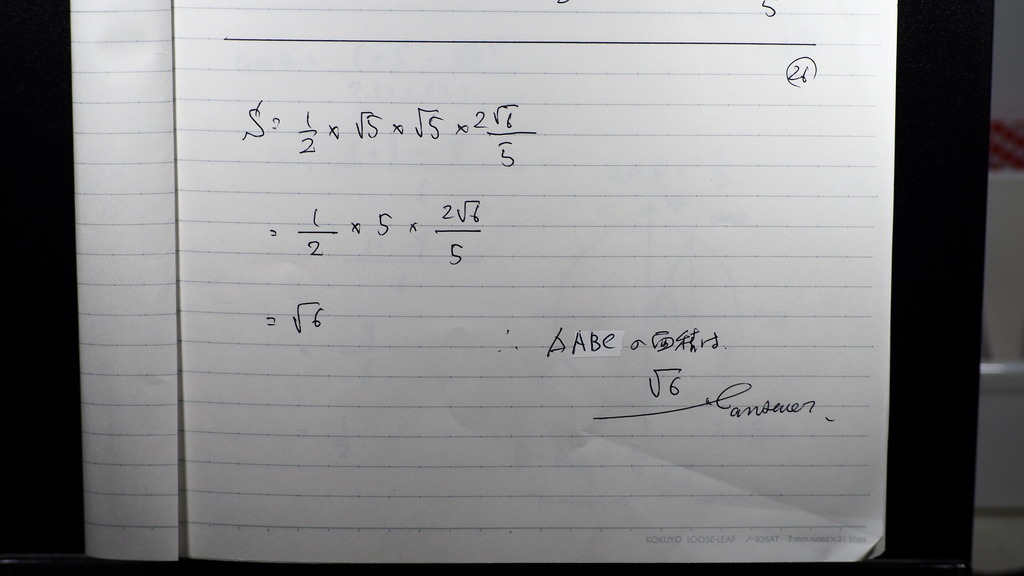
27
問題を 読んでね
図にしたら
コンななんですが
いいですか
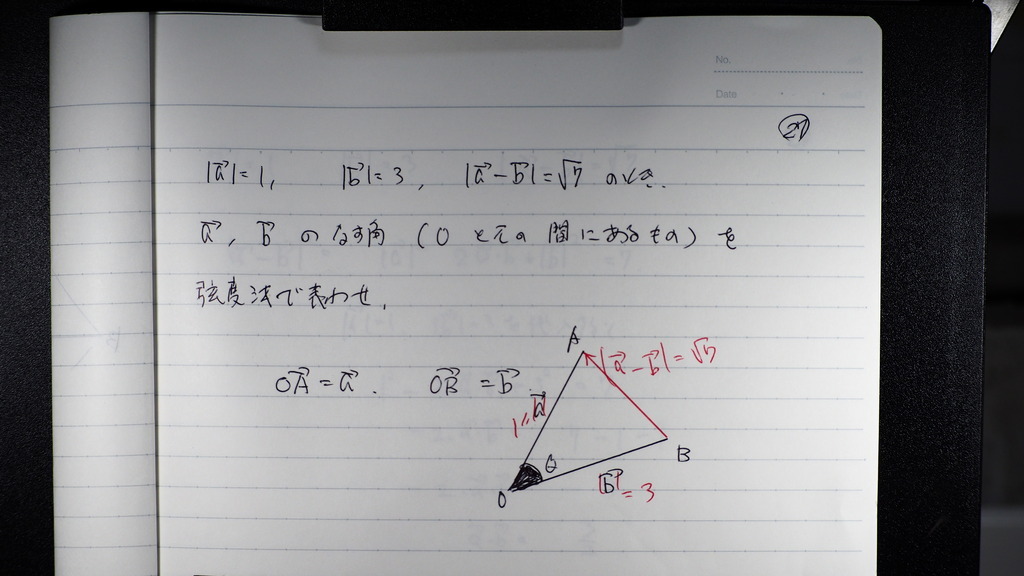
28
余弦定理で
弧度法で 表して
こんな感じで
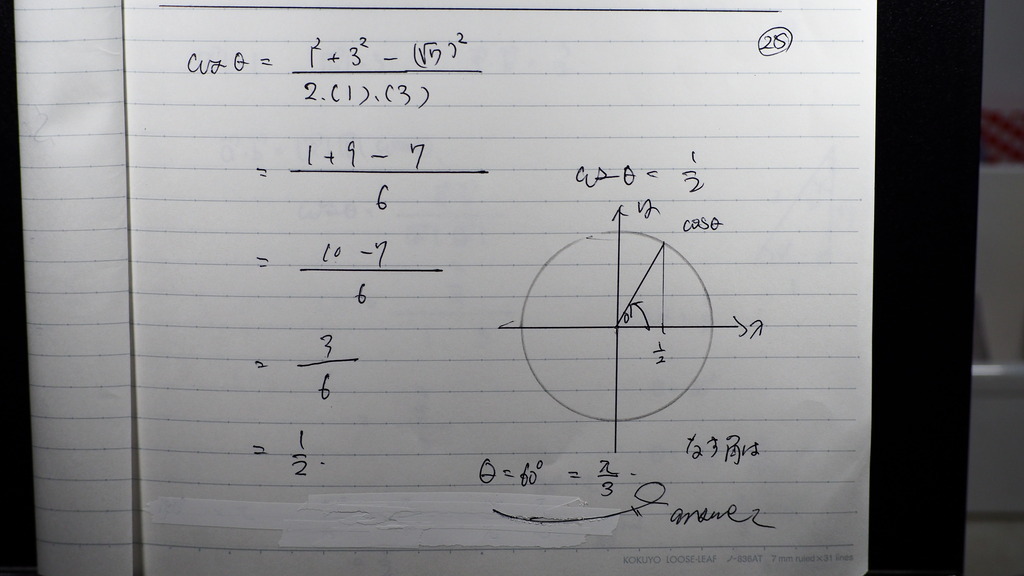
29
別の 解き方では
式変形してくとさ
内積が 出てきた
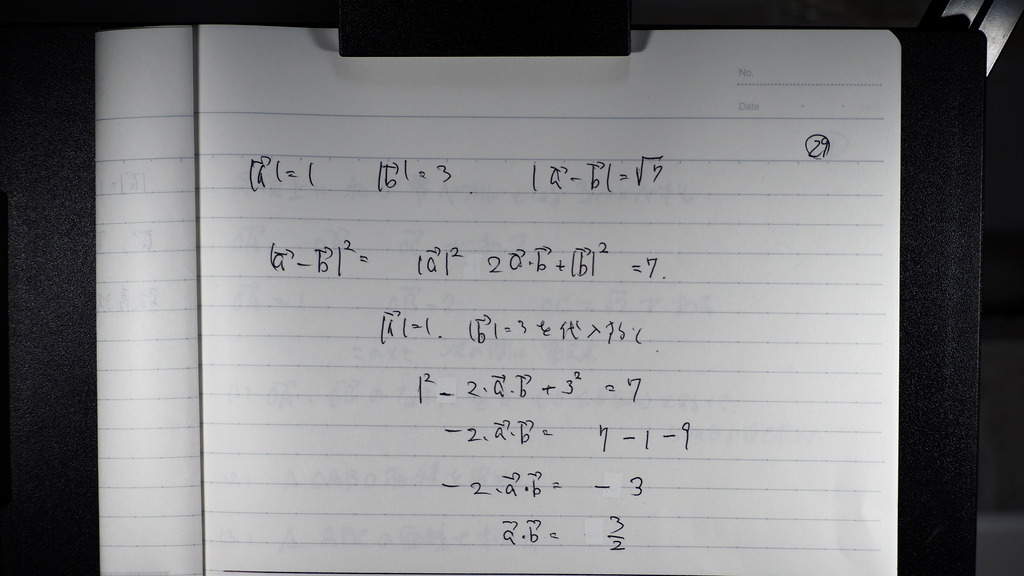
30
絶対値も わかってるので
COSΘは
1/2
であるので
180度は パイ
1度は パイ/180度(ラジアン)
60度は ?
(60×パイ)/ 180 単位ラジアン
パイ/3
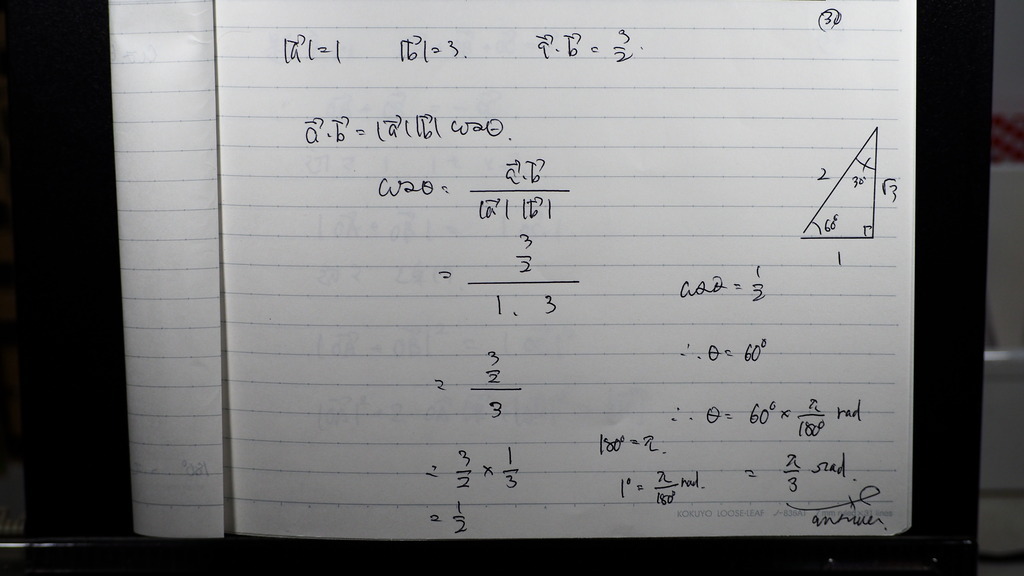
31
問題
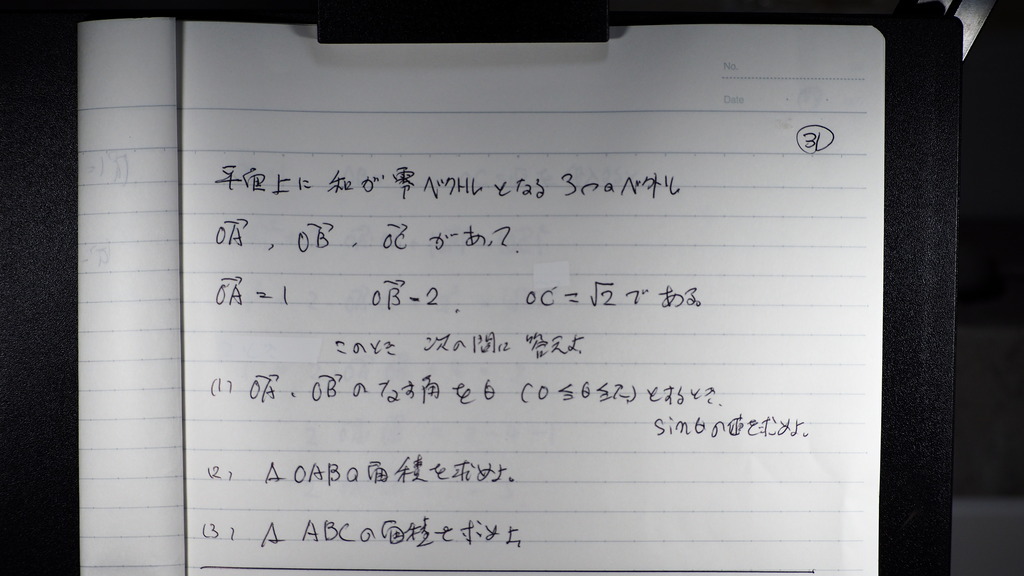
32
式変形してくとさ
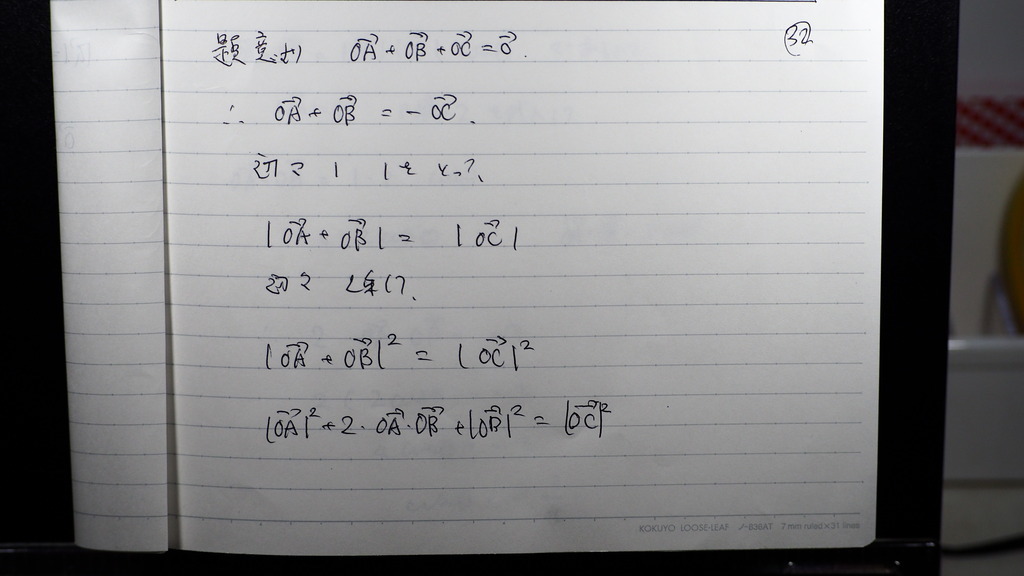
33
分かってるとこ 代入して

34
もうすこし
だいにゅうして
COSが出たので

35
サイン角は
で
なす角は 0から パイ(180度)
のものとするので
sigは 0から180度未満
までは プラス
180度から360未満が マイナス
であるので
なす角は 0から パイ(180度)
のものとするより
プラスの時だけ
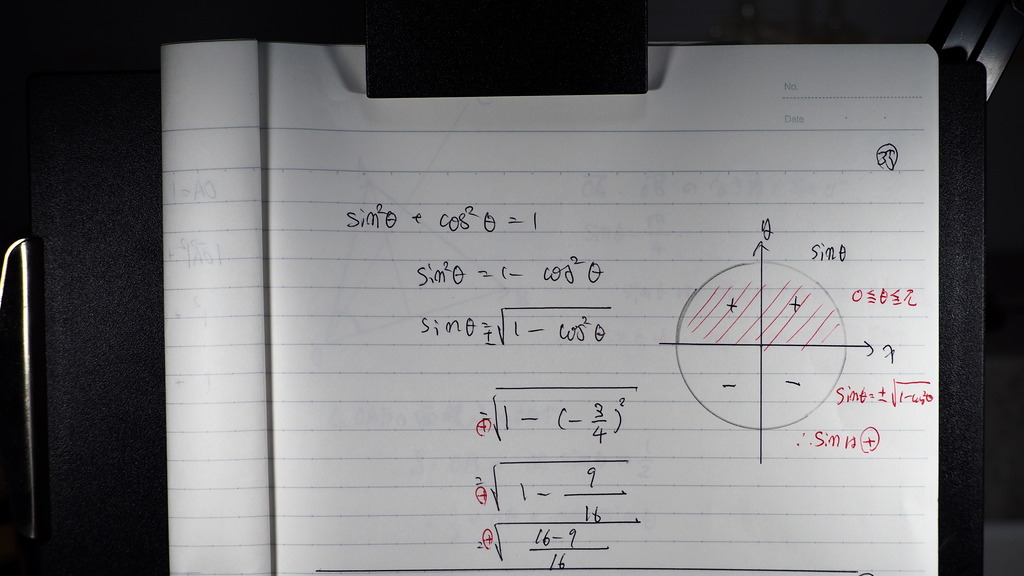
36
こんな感じで
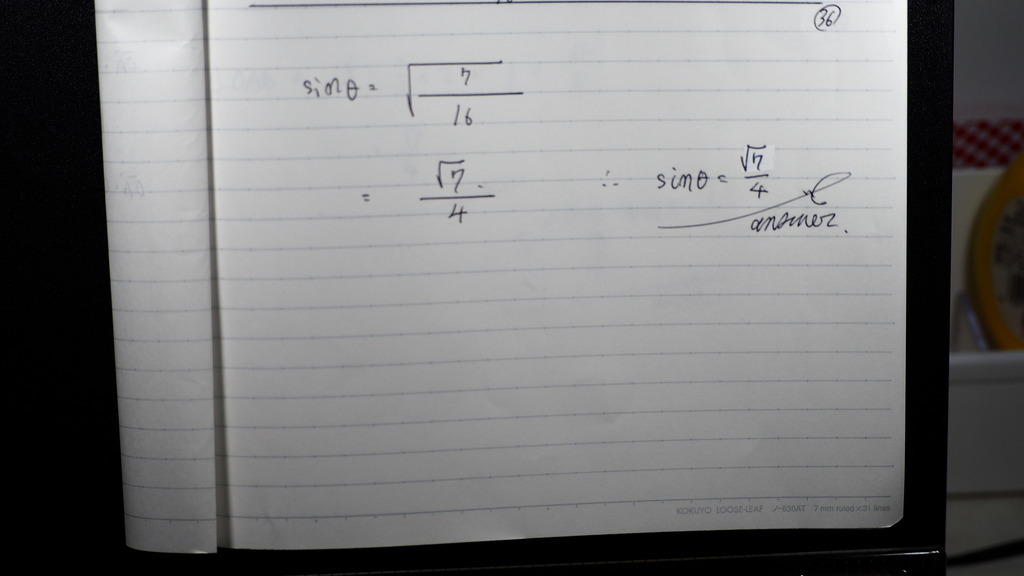
37
なす角の sin
と
なすベクトルのおおきさ
が
分かってるので
三角形OABの面積は
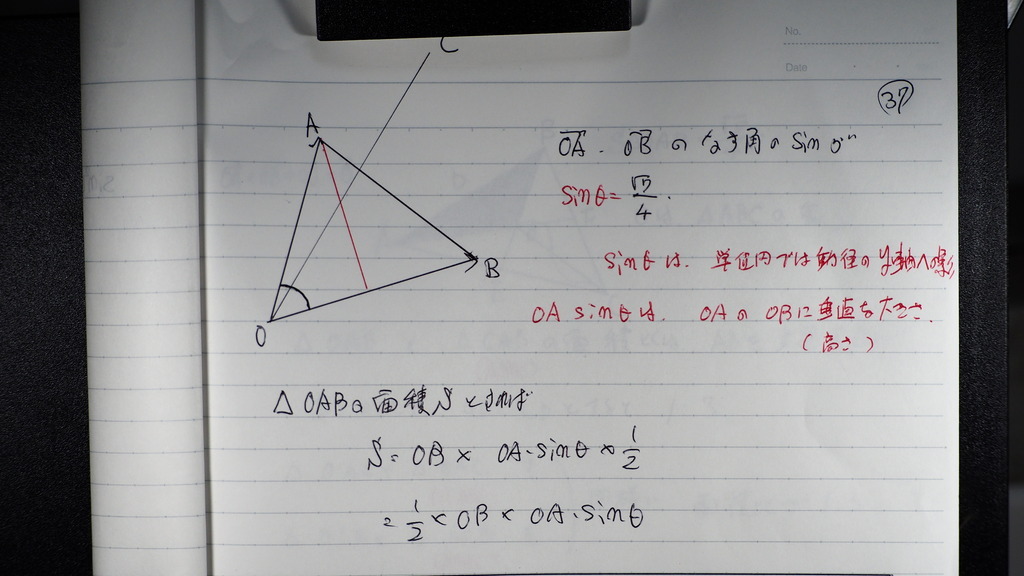
38
こんな感じで
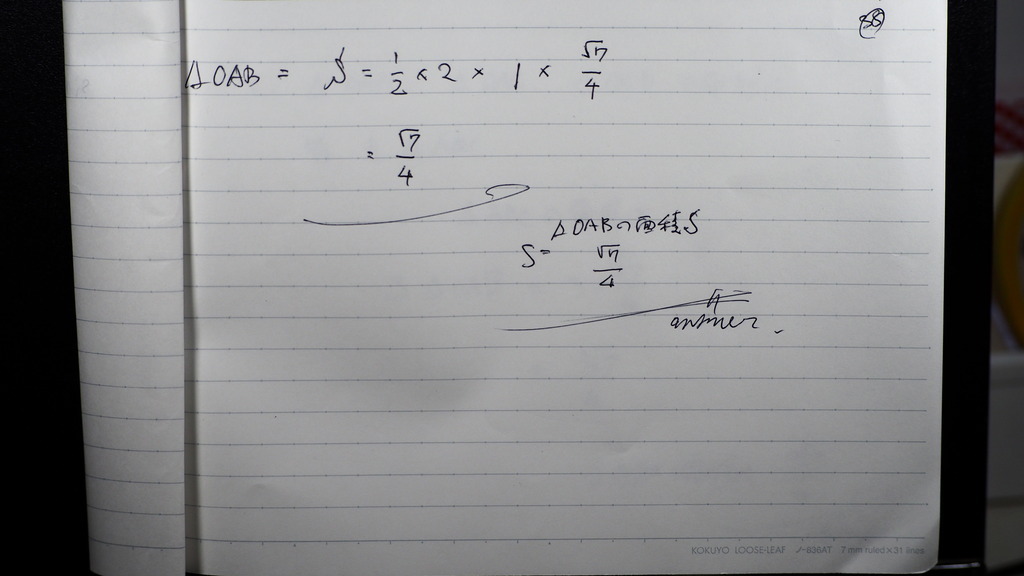
39
点Oは
題意より 重心
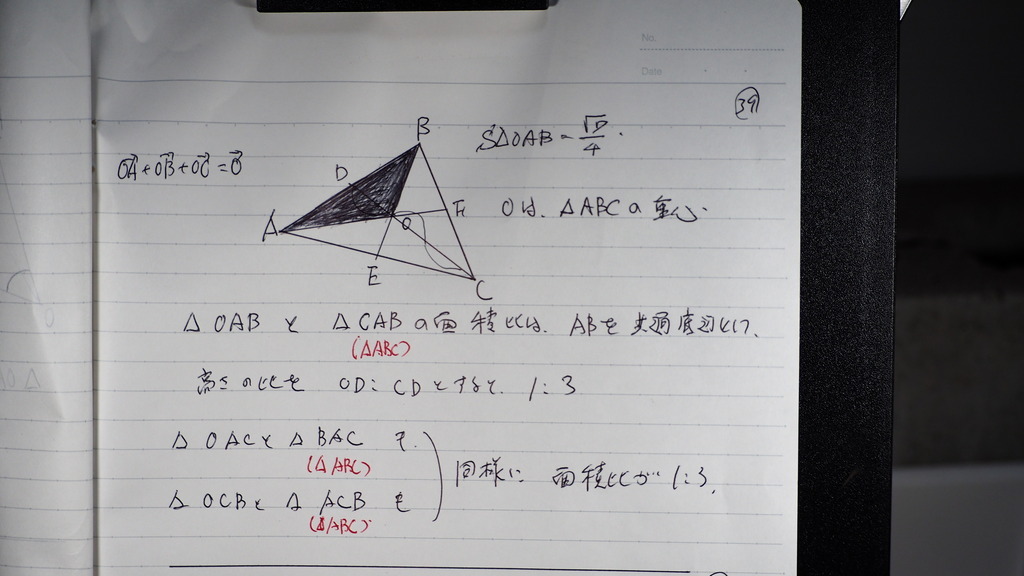
40
であるから
三角形ABCの面積は

お疲れ様です。
なす角 と言うのは
二つの ベクトルがあるとき
ベクトルを 平行移動して
始点同士を 合わせたときに
できる 角度 のことです。
01
もんだい
座標が 与えられてます
空間だけど
角BAC と 三角形 ABC の
面積を 求めよ
02
まずは
余弦定理で
行ってみますが
三角形の 三辺の 長さが
分かってるときは
余弦定理で
座標が分かってるので
2点間の距離 空間 で
長さを 出しといて
03
辺ABは
04
√6
05
辺BCは √42
06
辺CAは
2√6
07
余弦定理に
代入して
COSの 値で
出て来ますが
-1/2
08
なす角はゼロ から 180 度 (パイ ラジアン)
コサインは 動径の
x軸への陰で
座標上
ゼロの時 ぜろ度
ゼロ から 90度 未満まで プラス
90度 の時 ぜろ
90度 から 180度 未満の時
マイナス
180度 の時 -1
なす角は 120度
三角形の 面積に時は
なす角の 斜辺のサイン 成分が
高さなので
09
サイン120度は
√3/2
面積は
3√3
10
今の問題を
今度は
ベクトルの内積を使って
解くと
11
まず
なす角が
ここン所 であるから
2つのベクトル
AB AC を
成分で
計算して
12
内積の定義式は
こんなだから
成分の方から
内積が -6
もう一つの 定義式から
COS Θ が こんなでしょ
分母の 絶対値は
2点間の 距離で求めて
13
こんな感じになるので
14
なす角が出て来て
15
面積も
16
ところで
ここんとこの問題で
これが
非常に 良く 出題される
面積が
こんな感じで 書けることを
いえ
と言うんですが
さっきの
上の式から
少し いじってくと
なるですよ
17
底辺 AB で 書いてたけど
大きさと言う意味で
ベクトルに絶対値を付けて
ABを aベクトル
ACを bベクトルとすれば
こんな感じに なる
18
内積の 定義式の 変形で
COS θは
こんなだからさ
で
√の 外の 絶対値を
√の中に 入れれば
19
なったデショ
20
類題
内積を 使って
解いてきますか
21
aベクトル bベクトル
を
こんな風に設定して
22
内積の定義式②
成分の方から
内積は 1
成分が分かってるので
ベクトルの
絶対値 ( 大きさ )を 求めて
23
COS θは
1/5
24
題意では
サイン角で 求めよ なので
こんな感じに
25
サイン角が出てれば
ベクトルの 絶対値の 積に
なす角のサイン角
それを 2で割れば
1/2 を 掛けるとも言いますが
26
こんな感じで
27
問題を 読んでね
図にしたら
コンななんですが
いいですか
28
余弦定理で
弧度法で 表して
こんな感じで
29
別の 解き方では
式変形してくとさ
内積が 出てきた
30
絶対値も わかってるので
COSΘは
1/2
であるので
180度は パイ
1度は パイ/180度(ラジアン)
60度は ?
(60×パイ)/ 180 単位ラジアン
パイ/3
31
問題
32
式変形してくとさ
33
分かってるとこ 代入して
34
もうすこし
だいにゅうして
COSが出たので
35
サイン角は
で
なす角は 0から パイ(180度)
のものとするので
sigは 0から180度未満
までは プラス
180度から360未満が マイナス
であるので
なす角は 0から パイ(180度)
のものとするより
プラスの時だけ
36
こんな感じで
37
なす角の sin
と
なすベクトルのおおきさ
が
分かってるので
三角形OABの面積は
38
こんな感じで
39
点Oは
題意より 重心
40
であるから
三角形ABCの面積は
お疲れ様です。