2022年11月20日
22022 大人のさび落とし 空間座標とベクトル 不等式の証明
ベクトルの 内積を 使った
不等式の証明問題
01
こんな感じなんですが

02
内積の 定義式を
使えるように
やってみるとじゃナイスカ
矢線ベクトルと
成分
の 二つがあるでしょ
題意にある式に 似たものが
出てくるじゃナイスカ

03
定義式の 二つは こうだから

04
イコールで結んで
題意よりの
値を 代入すると
コサインθ
こさいんの 値は
基本的に -1 から 1まで
それより 大きいのを
見たよっていうのは
振幅に
倍率が 掛かってるときですよね
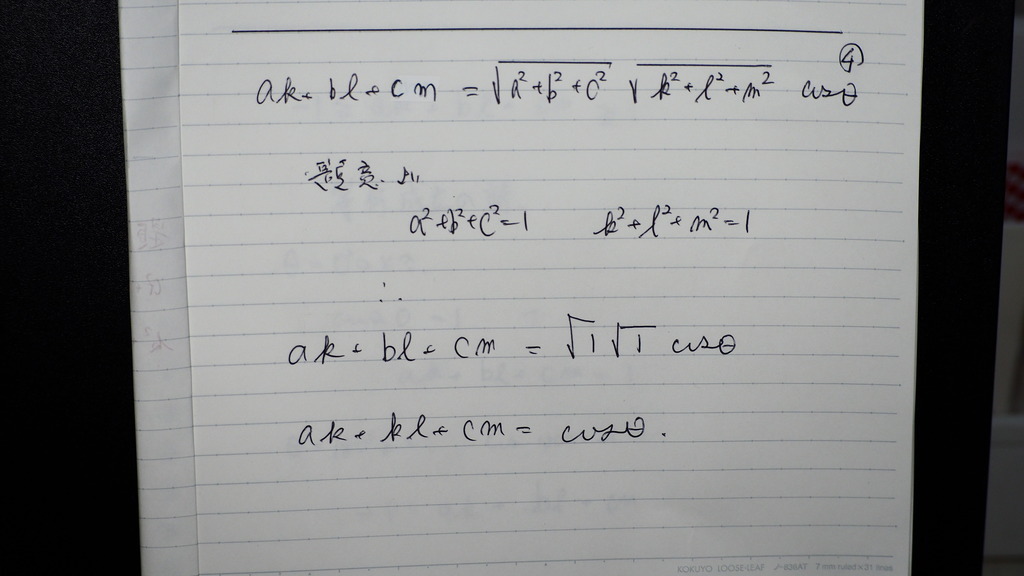
05
こさいんは
x軸への 動径の陰
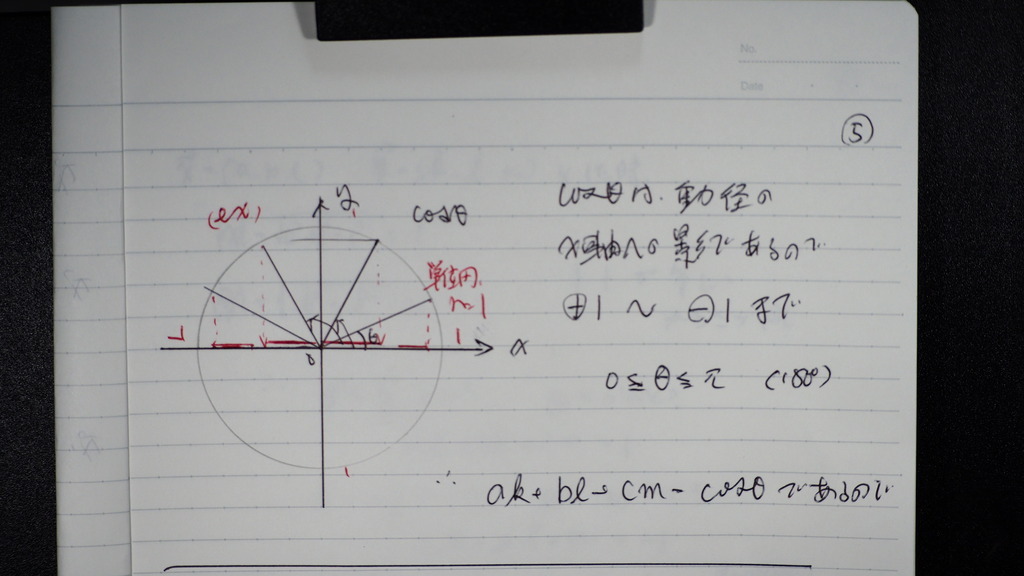
06
だから
こんな感じに
で
等号成立は
Θが 0度か 180度の時

07
まとめると

08
次は
考え方は
殆ど 同じですが

09
こんな感じにしておいて
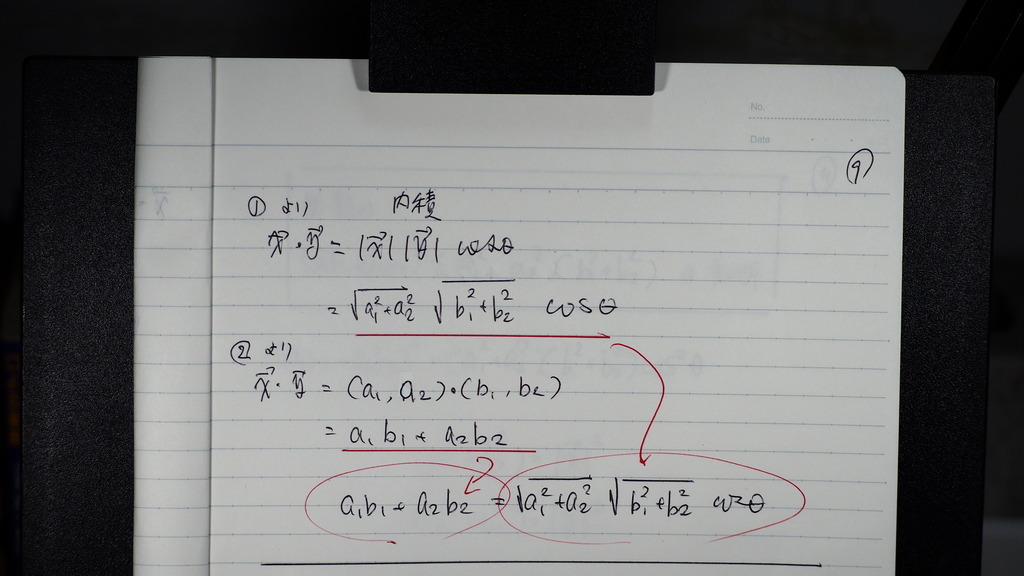
10
辺々二乗 したらば
証明式にちかくなったでしょ
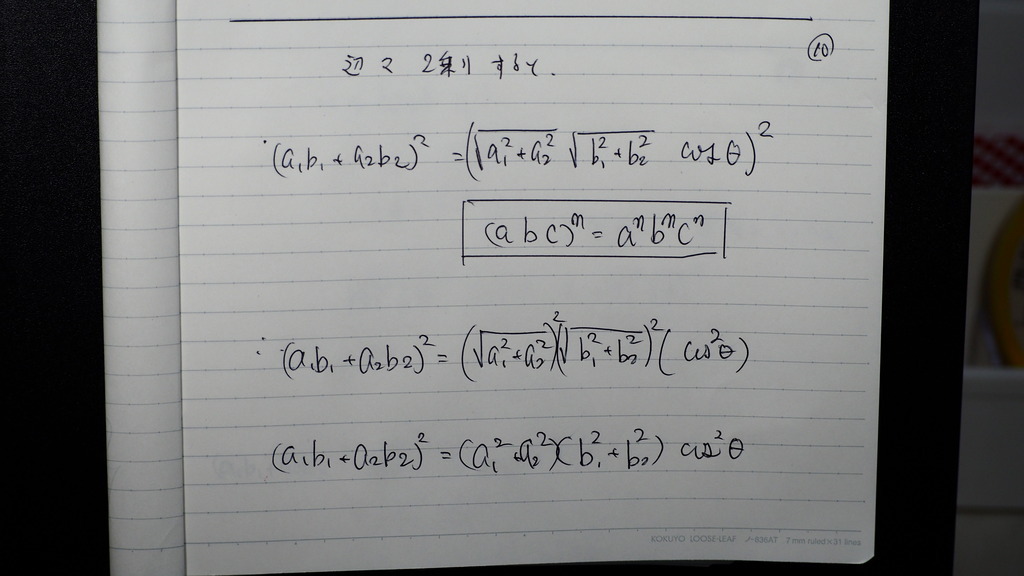
11
この証明なんだからさ
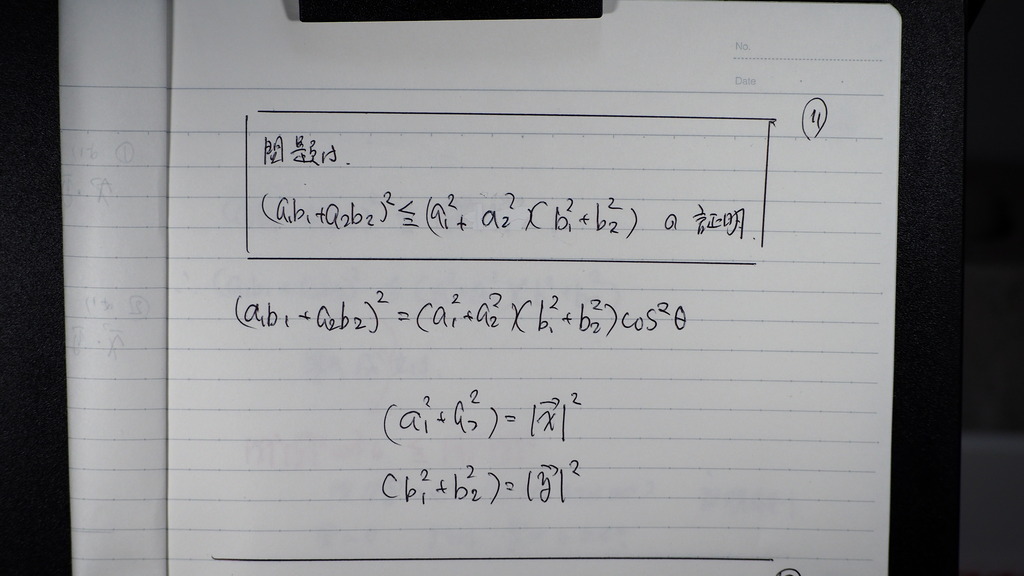
12
こさいんは
二乗したかから
0から1
同じ 大きさに 等倍なら変わらず
同じ大きさに 0.何倍 なら 小さくなる
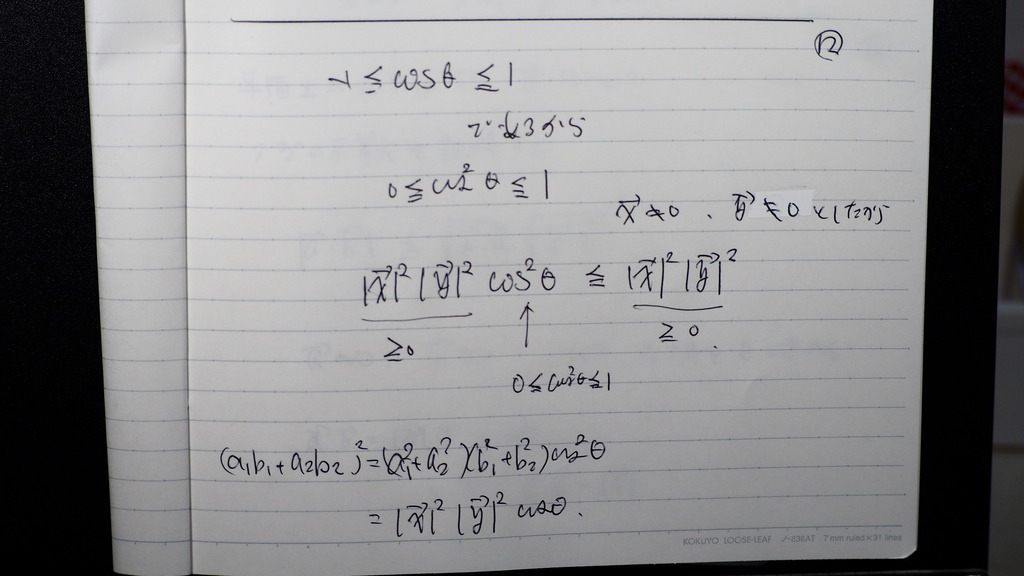
13
等号成立は
二つの ベクトルが 平行のとき
もしくは どちらかが ゼロの時

14
書き方が
少し違うだけなんだね

15
こんな感じでしょ

16
だから
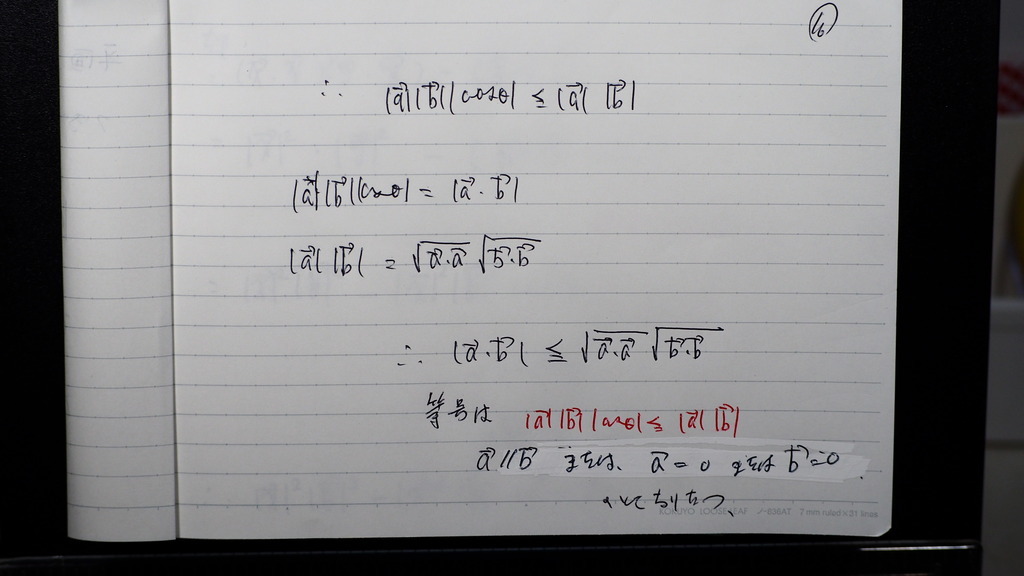
17
殆ど 同じですが
表現の仕方が
違うだけ
あとは
頭を 柔らかくして

18
落ち着いてやっていけば
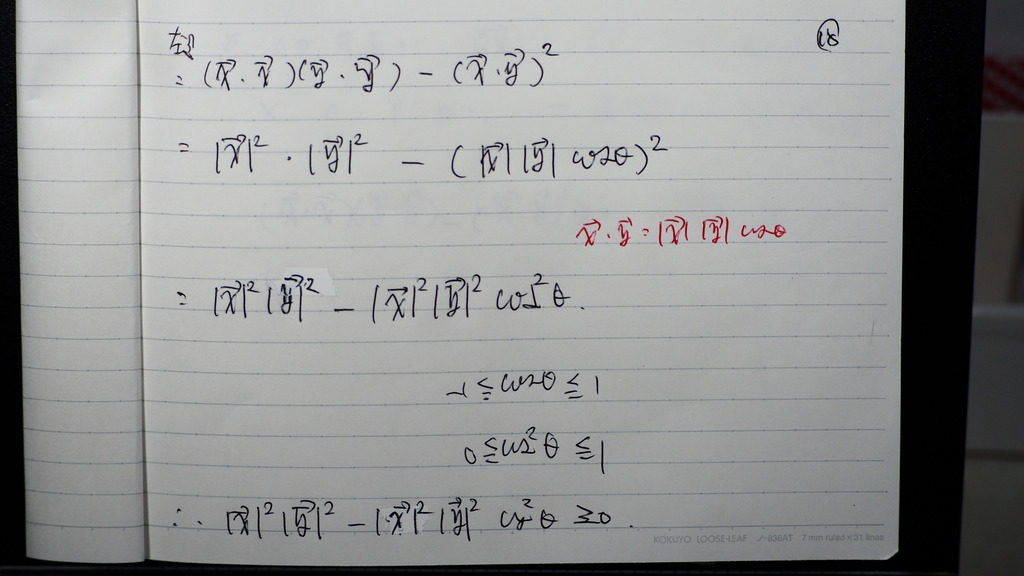
19
こんな感じになるので

20
特に 等号成立の時は
こんなです

お疲れ様です。
不等式の証明問題
01
こんな感じなんですが
02
内積の 定義式を
使えるように
やってみるとじゃナイスカ
矢線ベクトルと
成分
の 二つがあるでしょ
題意にある式に 似たものが
出てくるじゃナイスカ
03
定義式の 二つは こうだから
04
イコールで結んで
題意よりの
値を 代入すると
コサインθ
こさいんの 値は
基本的に -1 から 1まで
それより 大きいのを
見たよっていうのは
振幅に
倍率が 掛かってるときですよね
05
こさいんは
x軸への 動径の陰
06
だから
こんな感じに
で
等号成立は
Θが 0度か 180度の時
07
まとめると
08
次は
考え方は
殆ど 同じですが
09
こんな感じにしておいて
10
辺々二乗 したらば
証明式にちかくなったでしょ
11
この証明なんだからさ
12
こさいんは
二乗したかから
0から1
同じ 大きさに 等倍なら変わらず
同じ大きさに 0.何倍 なら 小さくなる
13
等号成立は
二つの ベクトルが 平行のとき
もしくは どちらかが ゼロの時
14
書き方が
少し違うだけなんだね
15
こんな感じでしょ
16
だから
17
殆ど 同じですが
表現の仕方が
違うだけ
あとは
頭を 柔らかくして
18
落ち着いてやっていけば
19
こんな感じになるので
20
特に 等号成立の時は
こんなです
お疲れ様です。