2022年11月29日
22023 大人のさび落とし 空間座標とベクトル 最大 最小
大人のさび落とし
空間座標とベクトル
最大 最小
01
ベクトルに
最小とか
最大とか あるのか?
2つの 大きさが 有 り
方向が 違う ベクトルを
足し合わせるとき
OA +t OB ( 今回は )
一番後ろに
図解付きで 書いておきますが
ベクトルの大きさが
最小になるときの tの値は
ベクトルの大きさが
最小になるとき
bベクトルと a+tb が
直交してることを 証明せよ

02
ベクトルの大きさを
2乗すると
内積で 展開できるので
出てきた 2次関数から
最小値を
割り出し
最小値は 頂点の座標の √をとれば
じゃナイスカ
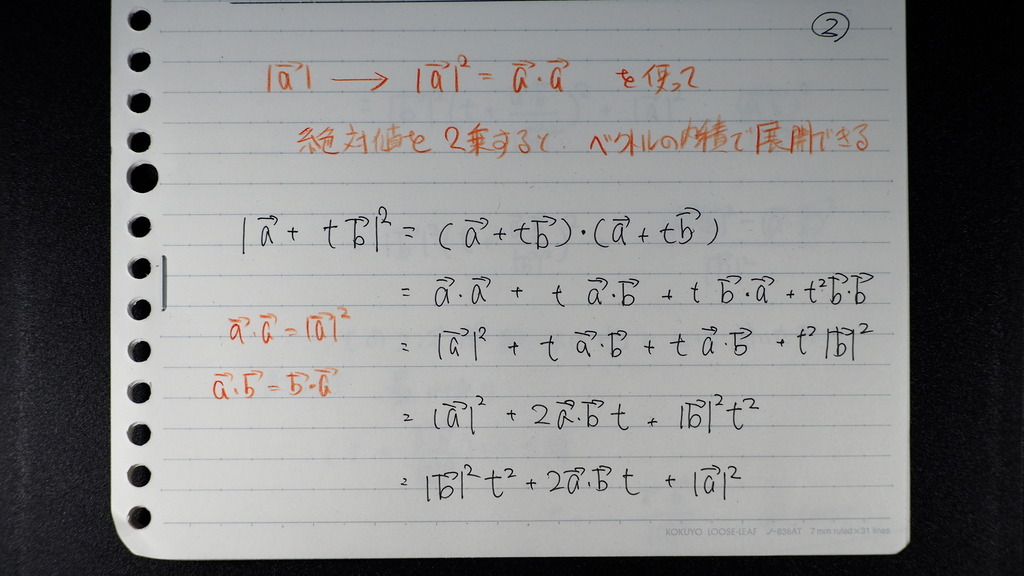
03
整理すると
二乗で 展開して
tの2次関数になるので
平方完成して
頂点が 下に凸 上に開いてるから
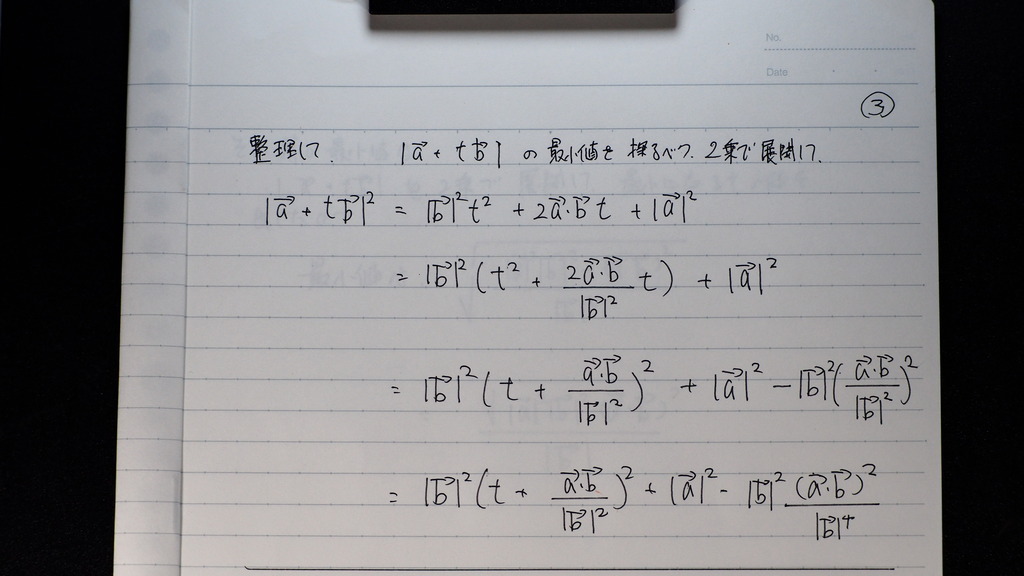
04
最小値は
t が この値の時
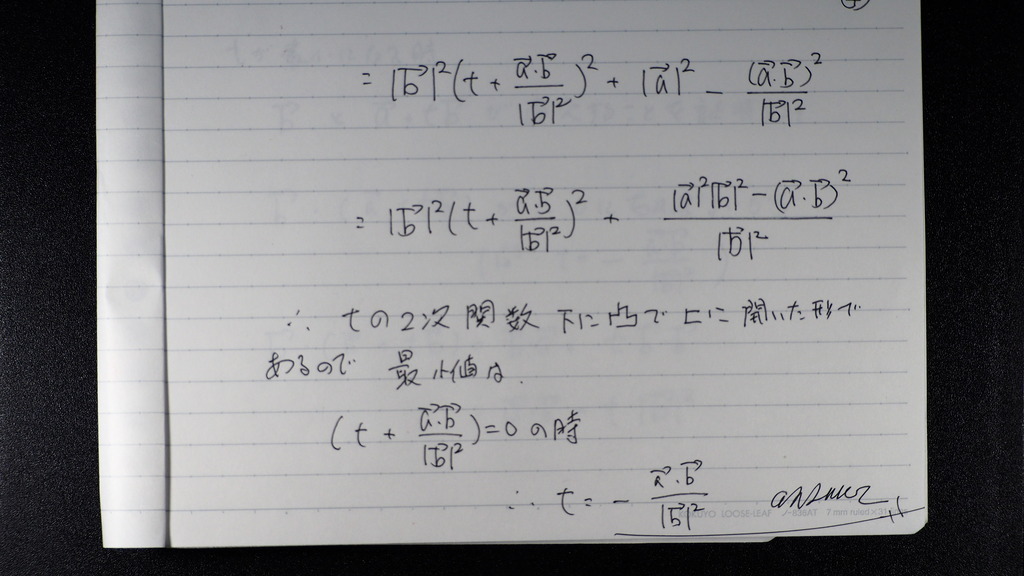
05
最小値は
ベクトルの大きさを
2乗で 展開したのだから
√を とれば
こんな感じに

06
t が 最小の時
直交するというのだけれど
内積を 計算するでしょ
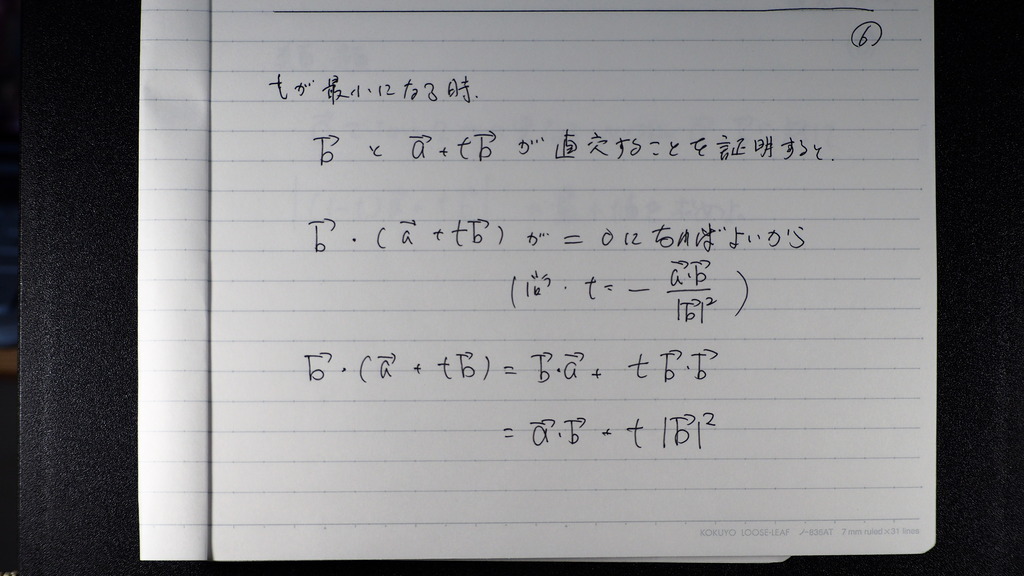
07
で ベクトルの
大きさが
最小になるときの
tのあたいを
代入したらば
内積が =0
つまり
直交している
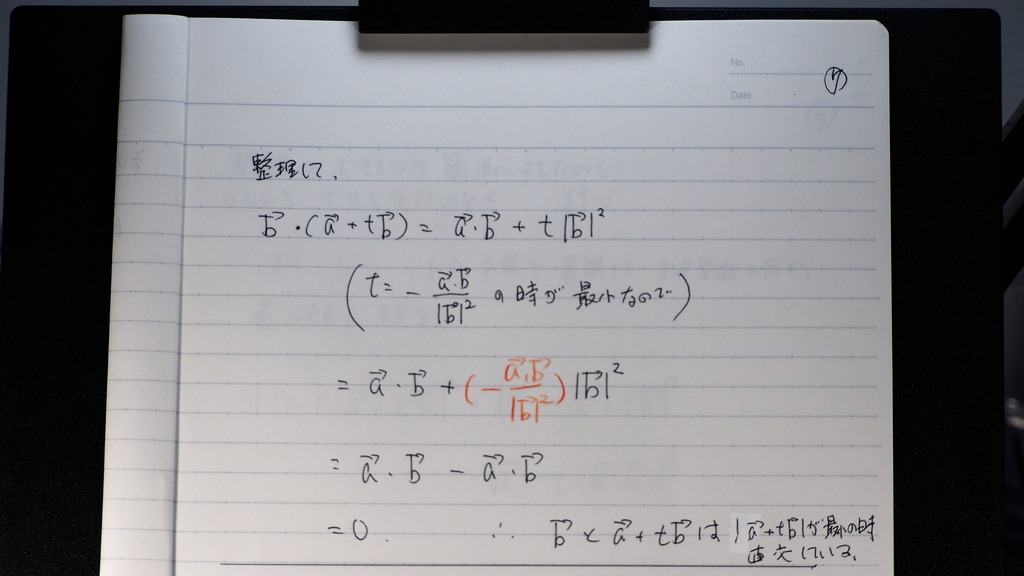
08
るいだい
ベクトルの
大きさの 最小値を
求めるんですが
2乗で
内積に展開して
後で
√を とれば
じゃナイスカ

09
できるだけ
簡単に したいので
置き換えとか
バンバン 使って

10
こうすればさ
少し簡単
さっきと
ほぼ同じ
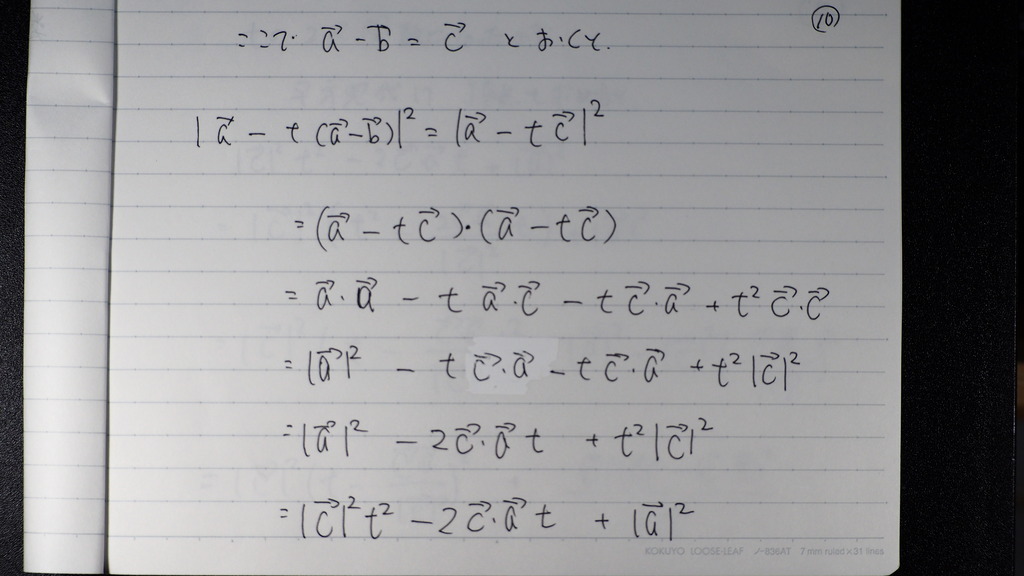
11
整理して
大きさを
2乗で 展開して
tの2次関数にして
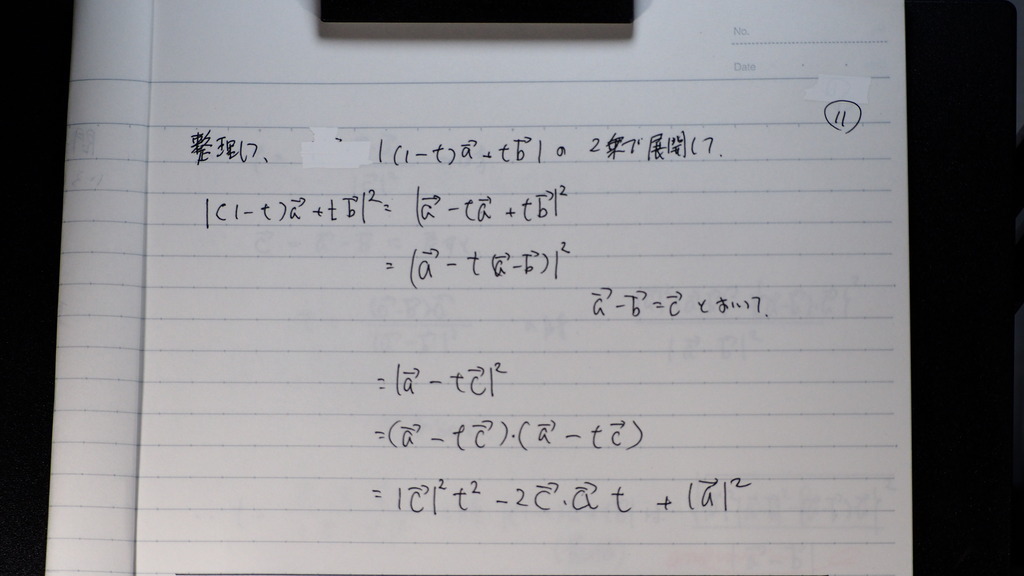
12
平方完成して
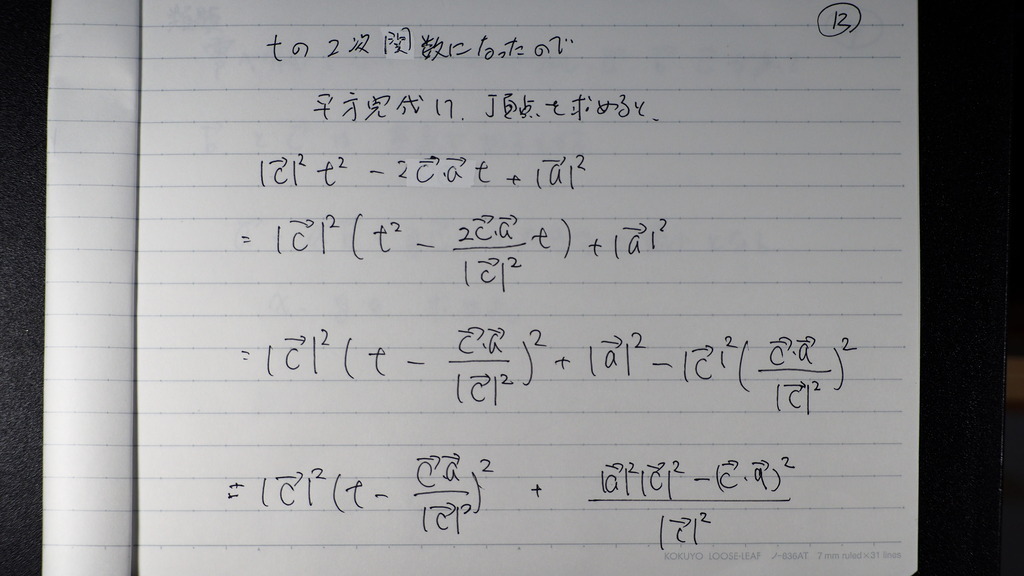
13
cベクトルを 元に戻せば
出てきた 頂点のt( 下に凸)
の時の 最小値を
√を取って
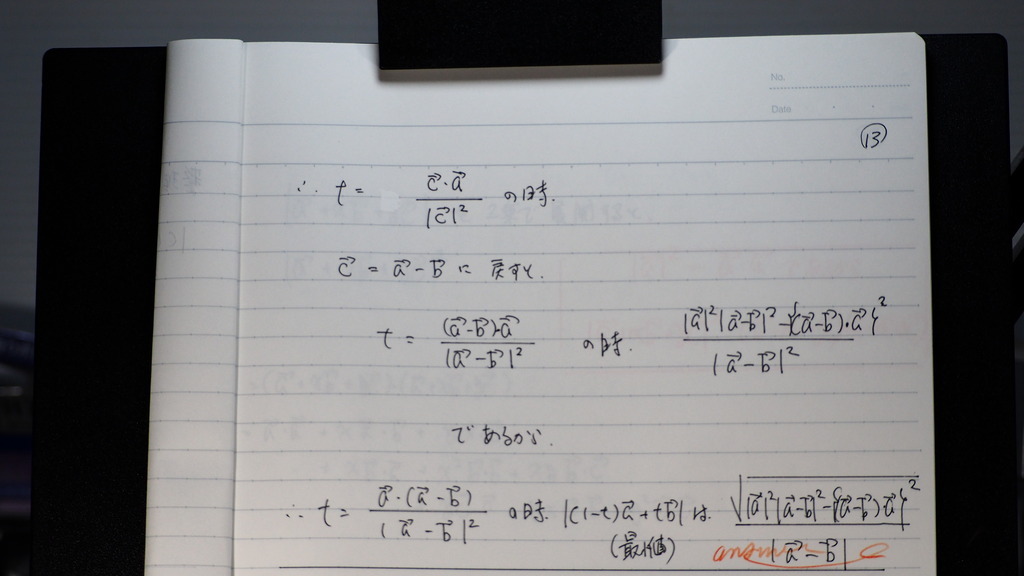
14
今度は
x、y とあるけど
行ってみましょう
ベクトルの 大きさを
2乗で 内積の形に
展開して行って

15
計算してくでしょ
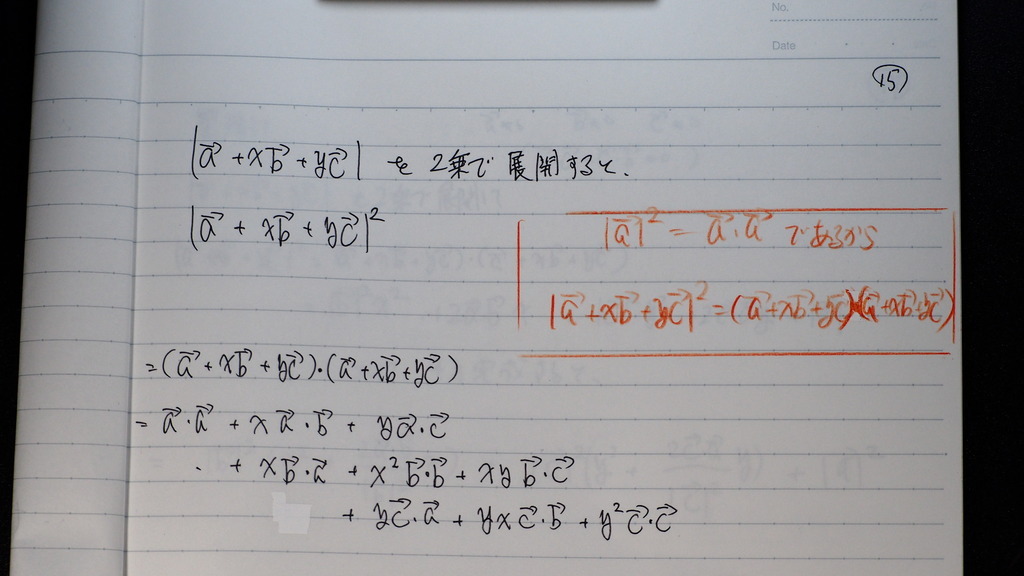
16
題意より bベクトルと
cベクトルは 垂直だから
b と c の 内積は =0
式が 少し簡単になって
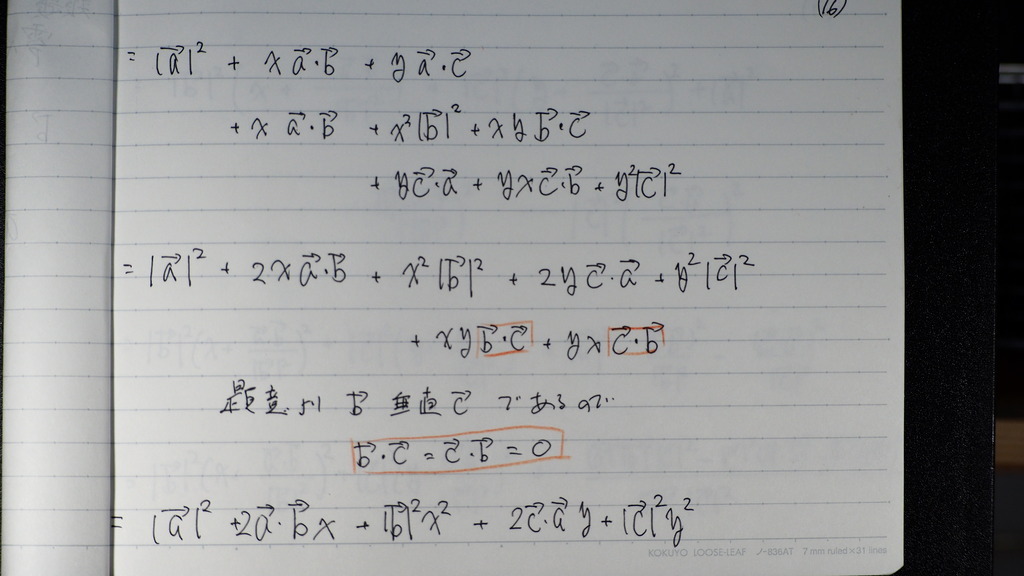
17
Xと yの 2次関数になってるので
ソレゾレ
平方完成して
最小値になるとき
円になるんだね
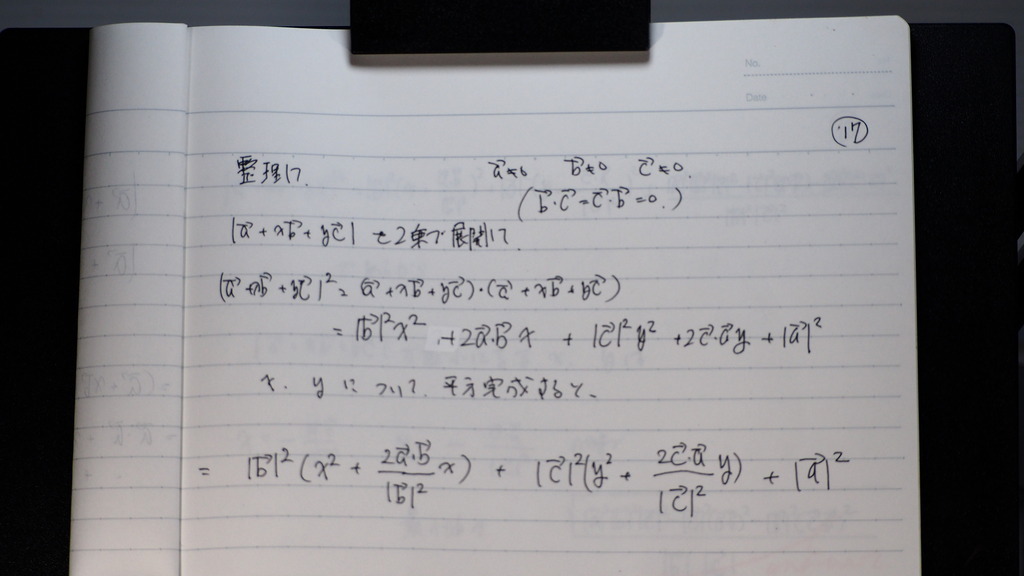
18
さいごまで 計算してですよ
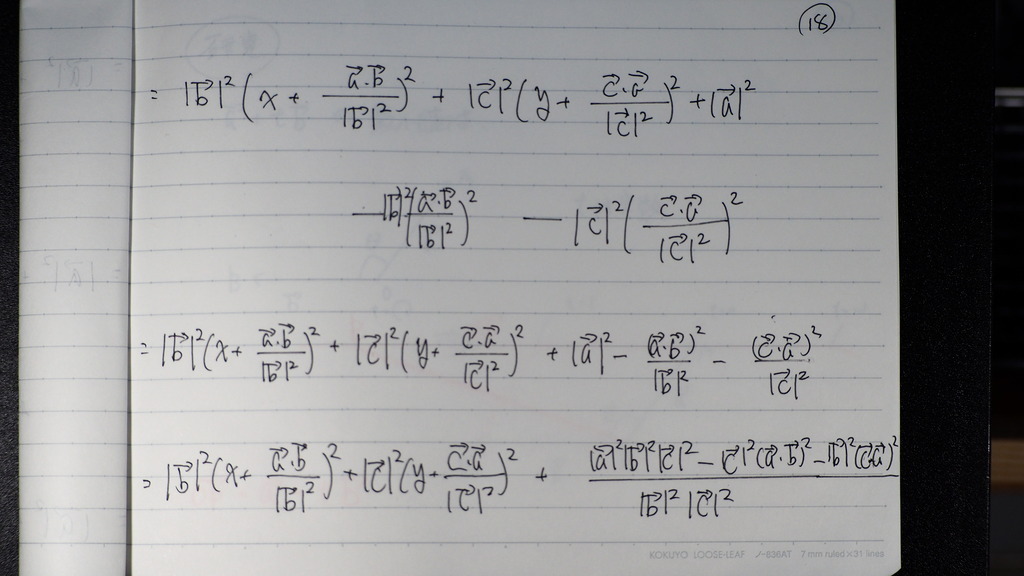
19
であるから
x、yが これこれの時
√を とった値が
最小値

20
で
お約束ですが
ベクトルの
最小値って
何なのというわけで
aと bと ベクトルがあって
a + tb は OPになるんだけど
bベクトルの t倍を aベクトルの
終点まで
平行移動して
足すと 成るでしょ
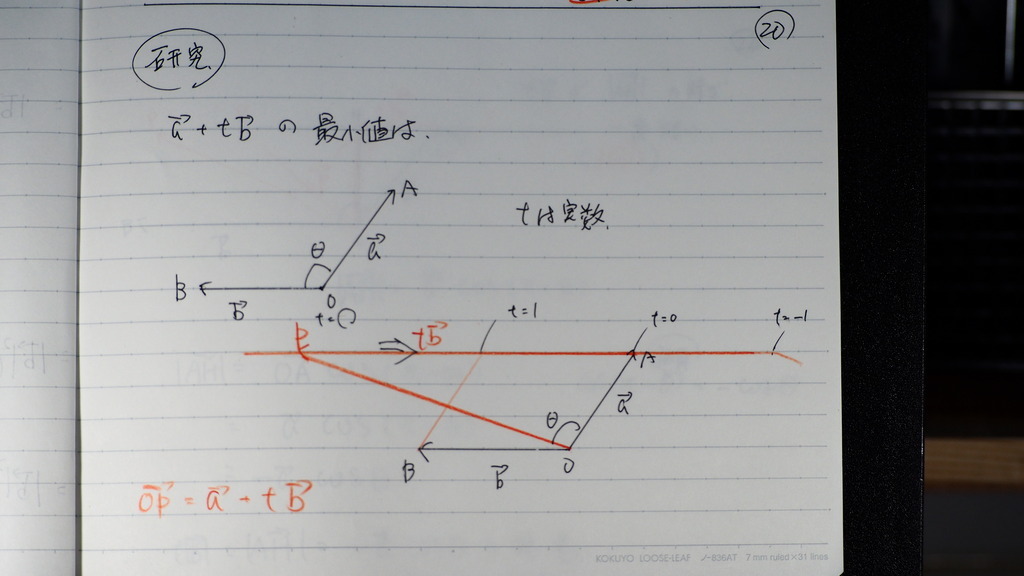
21
OP の 可能性は
無数にあるんだけれど
その中で
一番 短いもの
それが 最小値なんだから
大きさが 一番小さくなるとき
赤い矢印は (OP ベクトル)
どこでしょう
A を通って bベクトルに
平行な tbベクトル上で
Oから そこに おろした
垂線Hと 重なるときでしょ

22
AHベクトルの 大きさが
tbベクトル の大きさと
等しくなるとき
これを
計算すると

23
こんな感じで
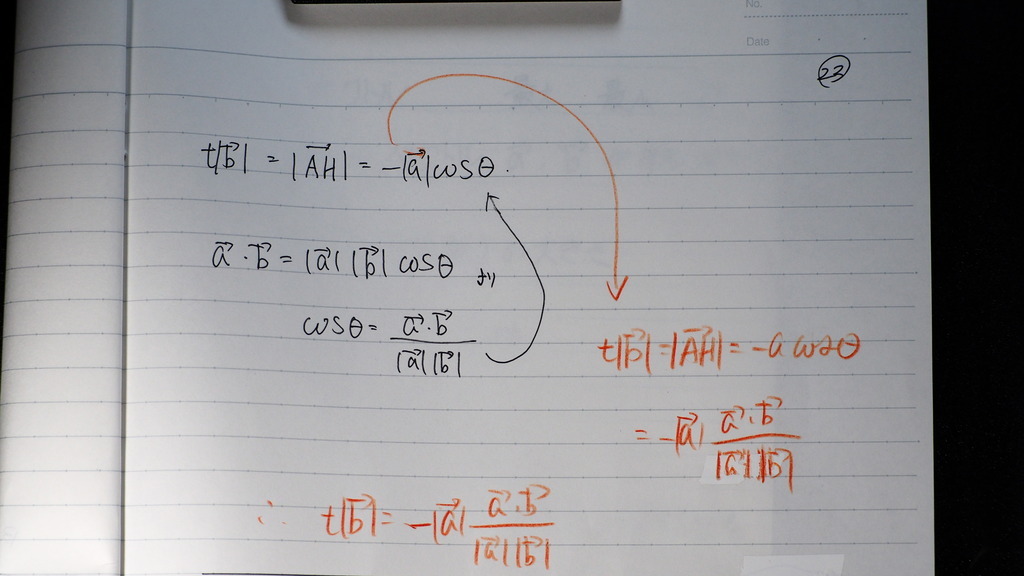
24
t=にしたら
図から 最小になるときの
tの値がでてきて
そのとき
bベクトルと a+tbベクトルは
直交しているでしょ
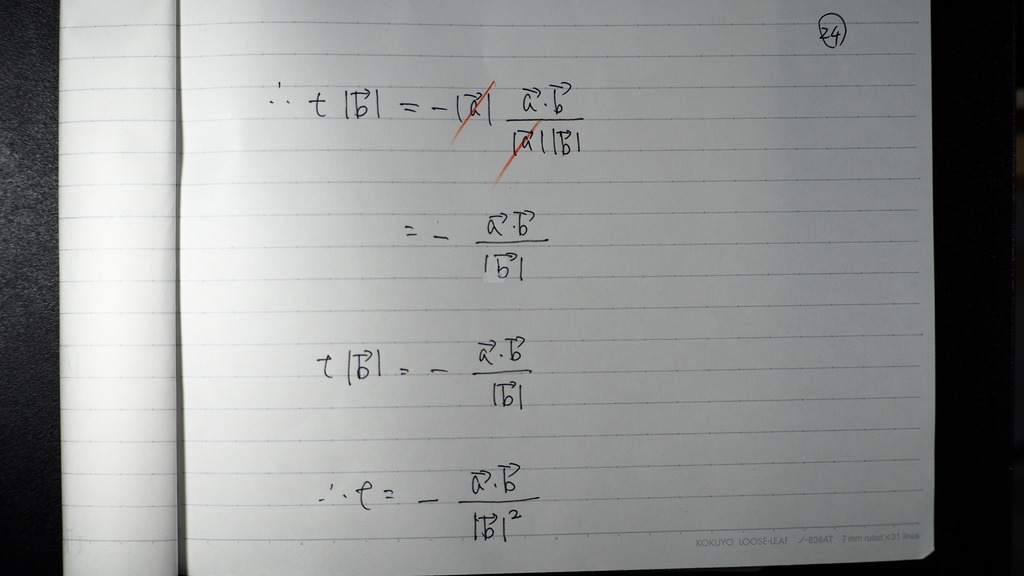
お疲れ様です。
空間座標とベクトル
最大 最小
01
ベクトルに
最小とか
最大とか あるのか?
2つの 大きさが 有 り
方向が 違う ベクトルを
足し合わせるとき
OA +t OB ( 今回は )
一番後ろに
図解付きで 書いておきますが
ベクトルの大きさが
最小になるときの tの値は
ベクトルの大きさが
最小になるとき
bベクトルと a+tb が
直交してることを 証明せよ
02
ベクトルの大きさを
2乗すると
内積で 展開できるので
出てきた 2次関数から
最小値を
割り出し
最小値は 頂点の座標の √をとれば
じゃナイスカ
03
整理すると
二乗で 展開して
tの2次関数になるので
平方完成して
頂点が 下に凸 上に開いてるから
04
最小値は
t が この値の時
05
最小値は
ベクトルの大きさを
2乗で 展開したのだから
√を とれば
こんな感じに
06
t が 最小の時
直交するというのだけれど
内積を 計算するでしょ
07
で ベクトルの
大きさが
最小になるときの
tのあたいを
代入したらば
内積が =0
つまり
直交している
08
るいだい
ベクトルの
大きさの 最小値を
求めるんですが
2乗で
内積に展開して
後で
√を とれば
じゃナイスカ
09
できるだけ
簡単に したいので
置き換えとか
バンバン 使って
10
こうすればさ
少し簡単
さっきと
ほぼ同じ
11
整理して
大きさを
2乗で 展開して
tの2次関数にして
12
平方完成して
13
cベクトルを 元に戻せば
出てきた 頂点のt( 下に凸)
の時の 最小値を
√を取って
14
今度は
x、y とあるけど
行ってみましょう
ベクトルの 大きさを
2乗で 内積の形に
展開して行って
15
計算してくでしょ
16
題意より bベクトルと
cベクトルは 垂直だから
b と c の 内積は =0
式が 少し簡単になって
17
Xと yの 2次関数になってるので
ソレゾレ
平方完成して
最小値になるとき
円になるんだね
18
さいごまで 計算してですよ
19
であるから
x、yが これこれの時
√を とった値が
最小値
20
で
お約束ですが
ベクトルの
最小値って
何なのというわけで
aと bと ベクトルがあって
a + tb は OPになるんだけど
bベクトルの t倍を aベクトルの
終点まで
平行移動して
足すと 成るでしょ
21
OP の 可能性は
無数にあるんだけれど
その中で
一番 短いもの
それが 最小値なんだから
大きさが 一番小さくなるとき
赤い矢印は (OP ベクトル)
どこでしょう
A を通って bベクトルに
平行な tbベクトル上で
Oから そこに おろした
垂線Hと 重なるときでしょ
22
AHベクトルの 大きさが
tbベクトル の大きさと
等しくなるとき
これを
計算すると
23
こんな感じで
24
t=にしたら
図から 最小になるときの
tの値がでてきて
そのとき
bベクトルと a+tbベクトルは
直交しているでしょ
お疲れ様です。