MSX追懐記

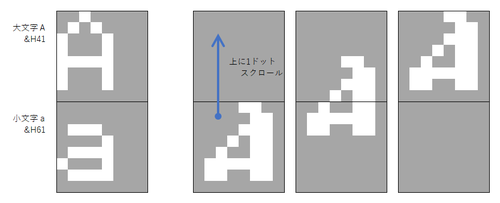
Laboratoryテーマ��6「自機に向かって飛んでくる敵弾」のマシン語サンプル作ってて思い出しました…。
「三平方の定理」使って弾道計算するなら、「割り算で計算結果が小数点にならないように、16ビット演算しなきゃいけない」のをすっかり忘れてました…。

なぜ16ビット計算が必要なのかを、「テーマ��6「自機に向かって飛んでくる敵弾」その�@」での数字を使って説明します。（2023年6月12日記事参照「テーマ��6「自機に向かって飛んでくる敵弾」その�@）

記事内のこの部分、これです。
マシン語は小数点を扱えませんので、小数点にならないよう事前に割られる数に「×100」若しくは「×10」しておく必要があります。
そのためには、8ビットだと0〜255までの値しか使用できないため、16ビットにする必要があるのです。

「テーマ��6「自機に向かって飛んでくる敵弾」その�A」のサンプルBASICプログラムでは何も考えずに普通に×100を組み込んでいました…。（2023年6月14日記事参照「テーマ��6「自機に向かって飛んでくる敵弾」その�A）


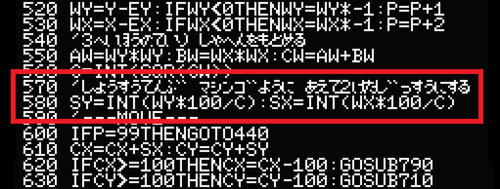
MSXプログラミングから離れて久しいので、8ビットの制約を忘れてました。
Windowsプログラミングだと、特に気にする必要ありませんからね…。
なんたって、マシン語で掛け算、割り算ができるし、マシン語使わなくても処理が早いので、ラジアン計算、三角関数（Sin、Cos、Tan）が普通言語で使えますからね…。

後日、16ビットの割り算サブルーチンLaboratryで公開します。

それと、実は私は自作シューティングゲームの弾道計算にこのロジックを使っていません。（おい。）
Laboratoryテーマ��9「32方向弾」の時に説明すると思いますが、処理速度と簡易性を重視した「なんちゃって弾道計算」ロジックを使っていました。
「なんちゃって」ですので、あまり人にお勧めできるものではないというのが正直なところですが。