�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2020�N09��06��
���ɂ���C�ɂ����͂�����H
����ɂ��́AYOSHIO�ł��B
�����u���O��q�ǒ������肪�Ƃ��������܂��I
����͗͂̂W��ځA���́E��C���ł��B
�c���ɁA�͂̃��X�g�ł��B
�ߋ��V��ڂ܂ł̗ʂ��������Ƃ�����A
����͊o���Ăق������Ƃ����ɍi�荞��ŁA
������₷���ł���ƍl���Ă��܂��B
����͑O�U��Ȃ��A�`������d�v���̐�������n�߂܂��傤�B
�����Ƃ́A�����ł����������̗��ł���A
�����Ƃ́A�����ł����鈳���ł���A
��C���Ƃ́A��C�i��C�j��鈳�����w���܂��B
�{���ł���A���������ׂ��Ȑ����������܂����A
���t�̋�ʂ����ɂ������̂���Ȃ̂ŁA
�C���[�W���t���₷���悤�}�ɂ��Ă݂܂����B
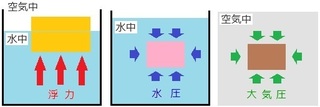
�� �C���[�W���₷���悤�ɂ����}���ł��B
�����ŁA���ӂ������_���R����܂��B
�P�ڂ́A�͂�����������ł��B
�����F�^������������������
�����E��C���F������������炩����
�Q�ڂ́A��C����\�����l�ƒP���ł��B
�P�C�� �� �P�O�P�RhPa�i�ǂݕ��F�w�N�g�p�X�J���j
�ŕ\����邱�Ƃ��o���Ă����܂��傤�B
�R�ڂ́A�������C���̑傫���ł��B
�����́A�[�����[������[���قǑ傫���Ȃ��A
��C���́A������������������قǑ傫���Ȃ�܂��B
���͂␅�����g�����v�Z��������܂����A
�܂��͂��ꂼ��̗͂̈Ⴂ�ɋ�ʂ�t����
�o���邱�Ƃ���n�߂Ă݂܂��傤�B
�ł́A�������C���̗͂̃|�C���g�͂R�B
�@ �����͐����Ő^�������������̗��ł���
�A �����������ł������������A�[���قǑ傫��
�B ��C���͍����قǑ傫���Ȃ�A�P�C�����P�O�P�RhPa�ŕ\�����
�Ȃ��Ȃ����̒��ŗ�������͓̂���ꍇ�́A
�}�Ȃǂ𗘗p���ăC���[�W�A�b�v���ł�����@������ƁA
�o���₷���ɂȂ����Ă��܂��ˁB
����ŁA�悤�₭�A�́E���͍͂���ŏI���ł��I
�ËL�E�v�Z�ȂǗl�X�������ŁA
�{���������肪�Ƃ��������܂��I
����͂��܂����A���K��o���Ȃ�����
�J��Ԃ����ƂŁA�͂��m���Ȃ��̂ɂȂ��Ă����܂�����ˁB
������ł������A�́E���́A�撣���Ă݂܂��H
�����u���O��q�ǒ������肪�Ƃ��������܂��I
����͗͂̂W��ځA���́E��C���ł��B
�c���ɁA�͂̃��X�g�ł��B
�ߋ��V��ڂ܂ł̗ʂ��������Ƃ�����A
����͊o���Ăق������Ƃ����ɍi�荞��ŁA
������₷���ł���ƍl���Ă��܂��B
����͑O�U��Ȃ��A�`������d�v���̐�������n�߂܂��傤�B
�����Ƃ́A�����ł����������̗��ł���A
�����Ƃ́A�����ł����鈳���ł���A
��C���Ƃ́A��C�i��C�j��鈳�����w���܂��B
�{���ł���A���������ׂ��Ȑ����������܂����A
���t�̋�ʂ����ɂ������̂���Ȃ̂ŁA
�C���[�W���t���₷���悤�}�ɂ��Ă݂܂����B

�� �C���[�W���₷���悤�ɂ����}���ł��B
�����ŁA���ӂ������_���R����܂��B
�P�ڂ́A�͂�����������ł��B
�����F�^������������������
�����E��C���F������������炩����
�Q�ڂ́A��C����\�����l�ƒP���ł��B
�P�C�� �� �P�O�P�RhPa�i�ǂݕ��F�w�N�g�p�X�J���j
�ŕ\����邱�Ƃ��o���Ă����܂��傤�B
�R�ڂ́A�������C���̑傫���ł��B
�����́A�[�����[������[���قǑ傫���Ȃ��A
��C���́A������������������قǑ傫���Ȃ�܂��B
���͂␅�����g�����v�Z��������܂����A
�܂��͂��ꂼ��̗͂̈Ⴂ�ɋ�ʂ�t����
�o���邱�Ƃ���n�߂Ă݂܂��傤�B
�ł́A�������C���̗͂̃|�C���g�͂R�B
�@ �����͐����Ő^�������������̗��ł���
�A �����������ł������������A�[���قǑ傫��
�B ��C���͍����قǑ傫���Ȃ�A�P�C�����P�O�P�RhPa�ŕ\�����
�Ȃ��Ȃ����̒��ŗ�������͓̂���ꍇ�́A
�}�Ȃǂ𗘗p���ăC���[�W�A�b�v���ł�����@������ƁA
�o���₷���ɂȂ����Ă��܂��ˁB
����ŁA�悤�₭�A�́E���͍͂���ŏI���ł��I
�ËL�E�v�Z�ȂǗl�X�������ŁA
�{���������肪�Ƃ��������܂��I
����͂��܂����A���K��o���Ȃ�����
�J��Ԃ����ƂŁA�͂��m���Ȃ��̂ɂȂ��Ă����܂�����ˁB
������ł������A�́E���́A�撣���Ă݂܂��H
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
2020�N09��05��
�͂��������A�˂͐L�т�I
����ɂ��́AYOSHIO�ł��B
����͗͂̂V��ځA�t�b�N�̖@���ł��B
�͂̑傫���ɂ˂��ւ��������̌v�Z�ł��B
�Ƃɂ����v�Z�͌��̗͂��āA�ǂݐi�߂Ă݂Ă��������ˁB
�c�ߋ��ɁA�m�����疭�Ȏ���������Ƃ����x������܂��B
�u�搶�A�ǂ����Ă˂̒������v�Z���悤�Ƃ����́H�v
�c�����A����Ȃ��ƕ�����Ȃ��ł��c�B
�������A�����������܂���c�B
����ǁA���̂悤�Ȏ���E�^��������Ă��邱�Ƃ��A��������ł���ˁB
�����ł����Ȃɋ����������Ă��炦�Ă���C������̂ŁB
����ł́A����̃e�[�}�ł����t�b�N�̖@���Ƃ́A
�˂̂̂т��A�������͂̑傫���ɔ�Ⴗ�鐫�����w���܂��B
���͂ɂ���ʂ�A�˂̂̂тƗ͂̑傫�����������OK�ł��B
���ۂ̊�{���́A���̂悤�ɏo�肳��܂��B
��j���̃O���t�̂悤�ɁA�˂P�Ƃ˂Q���ꂼ��ɗ͂�����������
�˂��L�т������������Ă���B
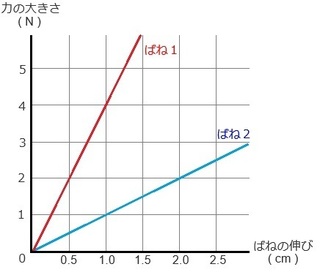
(1) �͂̑傫���Ƃ˂̐L�тɂ͂ǂ̂悤�ȊW�����邩�B
(2) (1)���番���鐫�������Ƃ������B
(3) �˂P�ɂU N �̗͂���������A�˂͉� cm �L�т邩�B
(4) �˂Q���P�O cm �L�т����A�� N �̗͂������������B
(1) �͂̑傫���Ƃ˂̐L�т̊W�́A
�@���W�ł��B
�@�����A�u���W��������Ȃ��c�v�Ƃ����ꍇ�́A
�@���₭�������đ��v�ł�����ˁB
�@���肪�������ƂɁA���̗͂̑傫���Ƃ˂̐L�т̊W�́A
�@���W�����o�Ă��܂���B
�@�ň��A���W�Ƃ������t��m���Ă��������ł�OK�ł��B
(2) �͂̑傫���Ƃ˂̐L�т̊W����킩�鐫���́A �t�b�N�̖@���ł��B
�@�]�k�ł����A���炭�O�܂ł��u�ǂ�Ȗ@�����H�v��
�@�o�肳��邱�Ƃ����������ł����A
�@�ŋ߂ł��u�ǂ�Ȑ������H�v�Ƃ����o��������Ă��܂��B
�@���t�ɘf�킳��Ȃ��悤�ɒ��ӂ��Ă݂Ă��������ˁB
�ł́A��������́A�v�Z�ł��ˁB������x�����m�F�ł��B
(3) �˂P�ɂU N �̗͂���������A�˂͉� cm �L�т邩�B
(4) �˂Q���P�O cm �L�т����A�� N �̗͂������������B
�c���肪�������ƂɁI
�O���t�ŏo�����ꂽ��A���ʂȌv�Z�����͕K�v����܂���I
���w�ŏK���܂����A��Ꭾ���g���ĉ����܂��B
(3) �˂P�̃O���t�����Ă݂܂��傤�B
�@�܂��́A�O���t�ŕ�����₷���_���P���������܂��B
�@�˂̐L�т��O�D�T cm �̎��A�͂̑傫�����QN �ł���ˁB
�@���̐��l���g���āA�O�D�Tcm�F�QN�@�Ŕ�̎������܂��B
�@���ɁA��肩���UN �̎��̂˂̐L�т����߂�̂ŁA
�@���߂���̂� X (cm) �Ƃ���ƁAX cm�F�UN�@�œ����悤�Ɏ������܂��B
�@�����āA��ꂽ�Q�̔�̎����u���v�łȂ��܂��B
�@�@�O�D�Tcm�F�QN �� X cm�F�UN
�@���̎��������A�����P�D�Tcm �Ƌ��߂��܂��B
���߂āA(3)�����ɃO���t���g�����t�b�N�̖@�����̉������́A
�@ �O���t���琔�l��������P�_���g���Ĕ�̎������
�A ��肩�狁�߂���̂��Œu���Ĕ�̎������
�B �@���A�̔�Ꭾ������ĉ���
�� ��̎��́A�P�ʂ̏��Ԃ����낦���悤�ɂ��܂��傤�B
���s���Ă��ǂ��̂ŁA�`�������W���邱�ƂŊ��o�����߂Ă��܂�����ˁB
�ł́A�Ō��(4)����L�̉������ʼn����܂��B
�@ �O���t���琔�l��������P�_���g���Ĕ�̎������
�@�˂̂̂т��P�D�Ocm �̎��ɁA�͂̑傫�����PN �Ȃ̂ŁA
�@�@�@�P�D�Ocm�F�PN�@�Ŕ�̎��ł��B
�A ��肩�狁�߂���̂��Œu���Ĕ�̎������
�@��肩��A�˂̐L�т��P�O cm�̎��̗͂̑傫���Ȃ̂ŁA
�@���߂���̂� Y (N) �Ƃ���ƁA�@
�@�@�@�P�Ocm�FY N�@�Ŕ�̎��ł��B
�@
�B �@���A�̔�Ꭾ������ĉ���
�@�@�@�P�D�Ocm�F�PN �� �P�Ocm�FY N
�@���̔�Ꭾ�������āA�����͂P�ON�@�ł��ˁB
�ł́A����̃t�b�N�̖@���ɂ��Ă͂R�̃|�C���g�B
�@ �t�b�N�̖@���́A�˂̐L�тƗ͂̑傫�������W
�A �v�Z������Ꭾ������čU��
�B ��̎�����鎞�́A�P�ʂ̏��Ԃ����낦��
���͖��ɃO���t�����邾���Őg�\���܂����A
�O���t���v�Z�������T�|�[�g�L����
�݂����Ȋ����Ŏv����悤�ɂȂ�ƁA�C�����y�ɂȂ��Ă��܂�����ˁB
����ŗ́E���͍͂Ō�Ȃ̂ŁA
�����ЂƓ���A���Ə����A�撣���Ă݂܂��H
�� �Ō�܂œǂ�Œ����Ă��肪�Ƃ��������܂����I
���̃u���O���ɂ�����܂������A
�u��Ꭾ�v���u�O���t�̌����v���A
������Ȃ����Ƃ�����A�R�����g�ŋL�����Ē����܂�����A
�u���O�ʼn��߂Đ�����������肽���Ǝv���܂��B
����͗͂̂V��ځA�t�b�N�̖@���ł��B
�͂̑傫���ɂ˂��ւ��������̌v�Z�ł��B
�Ƃɂ����v�Z�͌��̗͂��āA�ǂݐi�߂Ă݂Ă��������ˁB
�c�ߋ��ɁA�m�����疭�Ȏ���������Ƃ����x������܂��B
�u�搶�A�ǂ����Ă˂̒������v�Z���悤�Ƃ����́H�v
�c�����A����Ȃ��ƕ�����Ȃ��ł��c�B
�������A�����������܂���c�B
����ǁA���̂悤�Ȏ���E�^��������Ă��邱�Ƃ��A��������ł���ˁB
�����ł����Ȃɋ����������Ă��炦�Ă���C������̂ŁB
����ł́A����̃e�[�}�ł����t�b�N�̖@���Ƃ́A
�˂̂̂т��A�������͂̑傫���ɔ�Ⴗ�鐫�����w���܂��B
���͂ɂ���ʂ�A�˂̂̂тƗ͂̑傫�����������OK�ł��B
���ۂ̊�{���́A���̂悤�ɏo�肳��܂��B
��j���̃O���t�̂悤�ɁA�˂P�Ƃ˂Q���ꂼ��ɗ͂�����������
�˂��L�т������������Ă���B

(1) �͂̑傫���Ƃ˂̐L�тɂ͂ǂ̂悤�ȊW�����邩�B
(2) (1)���番���鐫�������Ƃ������B
(3) �˂P�ɂU N �̗͂���������A�˂͉� cm �L�т邩�B
(4) �˂Q���P�O cm �L�т����A�� N �̗͂������������B
(1) �͂̑傫���Ƃ˂̐L�т̊W�́A
�@���W�ł��B
�@�����A�u���W��������Ȃ��c�v�Ƃ����ꍇ�́A
�@���₭�������đ��v�ł�����ˁB
�@���肪�������ƂɁA���̗͂̑傫���Ƃ˂̐L�т̊W�́A
�@���W�����o�Ă��܂���B
�@�ň��A���W�Ƃ������t��m���Ă��������ł�OK�ł��B
(2) �͂̑傫���Ƃ˂̐L�т̊W����킩�鐫���́A �t�b�N�̖@���ł��B
�@�]�k�ł����A���炭�O�܂ł��u�ǂ�Ȗ@�����H�v��
�@�o�肳��邱�Ƃ����������ł����A
�@�ŋ߂ł��u�ǂ�Ȑ������H�v�Ƃ����o��������Ă��܂��B
�@���t�ɘf�킳��Ȃ��悤�ɒ��ӂ��Ă݂Ă��������ˁB
�ł́A��������́A�v�Z�ł��ˁB������x�����m�F�ł��B
(3) �˂P�ɂU N �̗͂���������A�˂͉� cm �L�т邩�B
(4) �˂Q���P�O cm �L�т����A�� N �̗͂������������B
�c���肪�������ƂɁI
�O���t�ŏo�����ꂽ��A���ʂȌv�Z�����͕K�v����܂���I
���w�ŏK���܂����A��Ꭾ���g���ĉ����܂��B
(3) �˂P�̃O���t�����Ă݂܂��傤�B
�@�܂��́A�O���t�ŕ�����₷���_���P���������܂��B
�@�˂̐L�т��O�D�T cm �̎��A�͂̑傫�����QN �ł���ˁB
�@���̐��l���g���āA�O�D�Tcm�F�QN�@�Ŕ�̎������܂��B
�@���ɁA��肩���UN �̎��̂˂̐L�т����߂�̂ŁA
�@���߂���̂� X (cm) �Ƃ���ƁAX cm�F�UN�@�œ����悤�Ɏ������܂��B
�@�����āA��ꂽ�Q�̔�̎����u���v�łȂ��܂��B
�@�@�O�D�Tcm�F�QN �� X cm�F�UN
�@���̎��������A�����P�D�Tcm �Ƌ��߂��܂��B
���߂āA(3)�����ɃO���t���g�����t�b�N�̖@�����̉������́A
�@ �O���t���琔�l��������P�_���g���Ĕ�̎������
�A ��肩�狁�߂���̂��Œu���Ĕ�̎������
�B �@���A�̔�Ꭾ������ĉ���
�� ��̎��́A�P�ʂ̏��Ԃ����낦���悤�ɂ��܂��傤�B
���s���Ă��ǂ��̂ŁA�`�������W���邱�ƂŊ��o�����߂Ă��܂�����ˁB
�ł́A�Ō��(4)����L�̉������ʼn����܂��B
�@ �O���t���琔�l��������P�_���g���Ĕ�̎������
�@�˂̂̂т��P�D�Ocm �̎��ɁA�͂̑傫�����PN �Ȃ̂ŁA
�@�@�@�P�D�Ocm�F�PN�@�Ŕ�̎��ł��B
�A ��肩�狁�߂���̂��Œu���Ĕ�̎������
�@��肩��A�˂̐L�т��P�O cm�̎��̗͂̑傫���Ȃ̂ŁA
�@���߂���̂� Y (N) �Ƃ���ƁA�@
�@�@�@�P�Ocm�FY N�@�Ŕ�̎��ł��B
�@
�B �@���A�̔�Ꭾ������ĉ���
�@�@�@�P�D�Ocm�F�PN �� �P�Ocm�FY N
�@���̔�Ꭾ�������āA�����͂P�ON�@�ł��ˁB
�ł́A����̃t�b�N�̖@���ɂ��Ă͂R�̃|�C���g�B
�@ �t�b�N�̖@���́A�˂̐L�тƗ͂̑傫�������W
�A �v�Z������Ꭾ������čU��
�B ��̎�����鎞�́A�P�ʂ̏��Ԃ����낦��
���͖��ɃO���t�����邾���Őg�\���܂����A
�O���t���v�Z�������T�|�[�g�L����
�݂����Ȋ����Ŏv����悤�ɂȂ�ƁA�C�����y�ɂȂ��Ă��܂�����ˁB
����ŗ́E���͍͂Ō�Ȃ̂ŁA
�����ЂƓ���A���Ə����A�撣���Ă݂܂��H
�� �Ō�܂œǂ�Œ����Ă��肪�Ƃ��������܂����I
���̃u���O���ɂ�����܂������A
�u��Ꭾ�v���u�O���t�̌����v���A
������Ȃ����Ƃ�����A�R�����g�ŋL�����Ē����܂�����A
�u���O�ʼn��߂Đ�����������肽���Ǝv���܂��B
2020�N09��04��
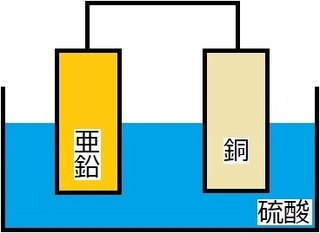
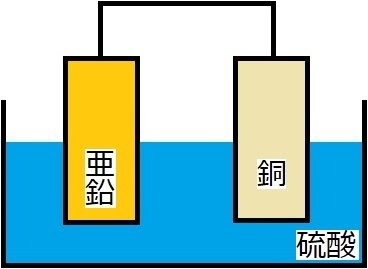
�u�d���v�Ɓu���ʁv�A�����Ⴄ�I�H
����ɂ��́AYOSHIO�ł��B
�ق��u���O�Ȃ���A�{���������肪�Ƃ��������܂��I
�́E���͍͂�����܂߂āA�c��R���\�肵�Ă��܂��B
�ł���������������₷���`������u���O��
�ł���Ǝv���Ă��܂��B
������Ȃ����Ƃ⍡����グ�Ăق������e������A
�R�����g���Ē����Ă�OK�ł��B
����͗͂̂U��ځA�d���Ǝ����ł��B
�c�H
�ǂ������������Ȃ����c�B
�u�����ו��̏d���A�ǂꂭ�炢����́H�v
�u�������̂̎�����ʂ��Ă݂܂��傤�B�v
�c���ʂɕς�����\���ł��Ȃ��c�B
�c�Ƃ��������A�����܂ōׂ�����������Đ������܂�����
�����A���ȂŊw�K����ꍇ�́A
������ƌ��t���g��������K�v������܂��B
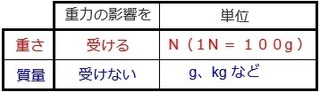
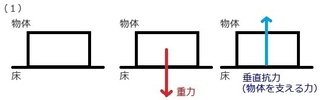
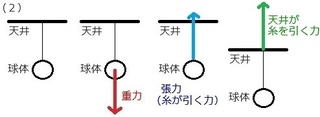
�ł́A�d���Ƃ́A���̂ɂ�����d�����w���܂��B
����A�����Ƃ́A���̂��̂��̂��������w���܂��B
���̂Q����������|�C���g�́A���Ȃ̖��ɕK�v�ɂȂ��Ă��܂��B
�Ⴆ�A���Ȃ̎����ȂǂŁA
�E�˂���
�E��M�V�т�
���g�������Ƃ�����Ǝv���܂��B
�m���Ă���������������|�C���g�͂P�B
�E�˂����́A���̂ɂ�����d�͂��e�����Ă��邱��
�E��M�V�т��́A���̂Ƃ̂荇�������d�͂̉e�����Ȃ�����
�Q��}�ɂ���ƁA�������������ł���ˁB
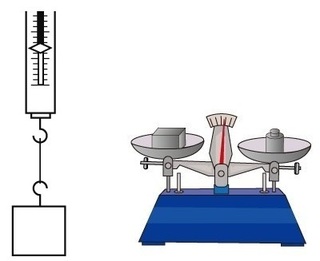
�i���F�˂���@�@�E�F��M�V�т�j
�˂����́A�t�b�N�ɕ��̂������|���ėʂ�̂ŁA
��ɉ������̏d�͂����������ƂɂȂ�܂��B
�������M�V�т��́A���̂ƕ����Ƃ̂荇���ŗʂ�̂ŁA
�d�͂��l���Ȃ��ėǂ����ƂɂȂ�܂��B
�ł́A�`���̏d���Ǝ��ʂł����A���̂悤�ɂ܂Ƃ߂Ă݂܂����B
�Ƃ�����ɁA�ׂ����g�������������܂��B
�����ŁA���̂悤�ȗ����l���Ă݂܂��B
��j�R�O�Og �̕��̂����̂悤�ɗʂ��������l����B
(1) �n���ł˂�����g�������̏d���͂����炩�H
(2) ���ł˂�����g�������̏d���͂����炩�H
(3) ���ŏ�M�V�т���g�������̎��ʂ͂����炩�H
(1) �n���̏ꍇ�́A���̂܂܂̕\�����g�p���āA
�@�@�R�O�Og �� �RN �������ł��B
(2) ���̏ꍇ�́A�n���̏d�͂�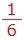 �ɂȂ�̂ŁA
�ɂȂ�̂ŁA
�@�@�R�O�O×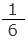 ���T�Og ���A
���T�Og ���A
�@�@�T�Og �� �O�D�TN �������ł��B
(3) ��M�V�т�́A�d�͂̉e�����Ȃ��̂ŁA
�@�@���̂܂��R�O�Og �������ł��B
���̂悤�ɁA�|�C���g�����܂��g�������邱�ƂŁA
�����U�����₷���Ȃ�܂��B
�����ŁA�d���Ǝ��ʂ̃|�C���g�͂R�B
�@ �d���͏d�͂̉e�����A�P�ʂ� N
�A ���ʂ͏d�͂Ƃ͊W�Ȃ��A�P�ʂ� g�Akg �Ȃ�
�B ���ŏd����ʂ�ꍇ�́A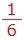 �{����
�{����
���ɁA�ʂ�ꏊ�Ƌ��߂�P���ɒ��ӂ��āA
�d���Ǝ��ʁA�撣���Ă݂܂��H
�ق��u���O�Ȃ���A�{���������肪�Ƃ��������܂��I
�́E���͍͂�����܂߂āA�c��R���\�肵�Ă��܂��B
�ł���������������₷���`������u���O��
�ł���Ǝv���Ă��܂��B
������Ȃ����Ƃ⍡����グ�Ăق������e������A
�R�����g���Ē����Ă�OK�ł��B
����͗͂̂U��ځA�d���Ǝ����ł��B
�c�H
�ǂ������������Ȃ����c�B
�u�����ו��̏d���A�ǂꂭ�炢����́H�v
�u�������̂̎�����ʂ��Ă݂܂��傤�B�v
�c���ʂɕς�����\���ł��Ȃ��c�B
�c�Ƃ��������A�����܂ōׂ�����������Đ������܂�����
�����A���ȂŊw�K����ꍇ�́A
������ƌ��t���g��������K�v������܂��B
�ł́A�d���Ƃ́A���̂ɂ�����d�����w���܂��B
����A�����Ƃ́A���̂��̂��̂��������w���܂��B
���̂Q����������|�C���g�́A���Ȃ̖��ɕK�v�ɂȂ��Ă��܂��B
�Ⴆ�A���Ȃ̎����ȂǂŁA
�E�˂���
�E��M�V�т�
���g�������Ƃ�����Ǝv���܂��B
�m���Ă���������������|�C���g�͂P�B
�E�˂����́A���̂ɂ�����d�͂��e�����Ă��邱��
�E��M�V�т��́A���̂Ƃ̂荇�������d�͂̉e�����Ȃ�����
�Q��}�ɂ���ƁA�������������ł���ˁB

�i���F�˂���@�@�E�F��M�V�т�j
�˂����́A�t�b�N�ɕ��̂������|���ėʂ�̂ŁA
��ɉ������̏d�͂����������ƂɂȂ�܂��B
�������M�V�т��́A���̂ƕ����Ƃ̂荇���ŗʂ�̂ŁA
�d�͂��l���Ȃ��ėǂ����ƂɂȂ�܂��B
�ł́A�`���̏d���Ǝ��ʂł����A���̂悤�ɂ܂Ƃ߂Ă݂܂����B
�Ƃ�����ɁA�ׂ����g�������������܂��B

�����ŁA���̂悤�ȗ����l���Ă݂܂��B
��j�R�O�Og �̕��̂����̂悤�ɗʂ��������l����B
(1) �n���ł˂�����g�������̏d���͂����炩�H
(2) ���ł˂�����g�������̏d���͂����炩�H
(3) ���ŏ�M�V�т���g�������̎��ʂ͂����炩�H
(1) �n���̏ꍇ�́A���̂܂܂̕\�����g�p���āA
�@�@�R�O�Og �� �RN �������ł��B
(2) ���̏ꍇ�́A�n���̏d�͂�
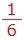 �ɂȂ�̂ŁA
�ɂȂ�̂ŁA�@�@�R�O�O×
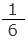 ���T�Og ���A
���T�Og ���A�@�@�T�Og �� �O�D�TN �������ł��B
(3) ��M�V�т�́A�d�͂̉e�����Ȃ��̂ŁA
�@�@���̂܂��R�O�Og �������ł��B
���̂悤�ɁA�|�C���g�����܂��g�������邱�ƂŁA
�����U�����₷���Ȃ�܂��B
�����ŁA�d���Ǝ��ʂ̃|�C���g�͂R�B
�@ �d���͏d�͂̉e�����A�P�ʂ� N
�A ���ʂ͏d�͂Ƃ͊W�Ȃ��A�P�ʂ� g�Akg �Ȃ�
�B ���ŏd����ʂ�ꍇ�́A
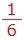 �{����
�{�������ɁA�ʂ�ꏊ�Ƌ��߂�P���ɒ��ӂ��āA
�d���Ǝ��ʁA�撣���Ă݂܂��H
2020�N09��03��
���͂͗͂Ɩʐς̊���Z�Ŏ菇�ǂ��I
����ɂ��́AYOSHIO�ł��B
����͗͂̂T��ځA���͂̌v�Z�ł��B
�O��S��ڂň������A
�͂̑傫���̕ϊ������͂̌����𗘗p�������������܂��B
��{���̉�������������Ă����܂��傤�B
�n�߂�O�ɁA���߂Ĉ��͂����߂�����ł��B
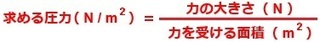
���̌������g������{���ł��B
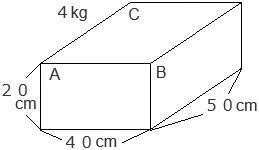
��j�}�̂悤�Ȏ��ʂSkg �̒����̂̕��̂����̏�ɒu�������̈��͂��l����B
�������A�PN �� �P�O�Og �Ƃ���B
(1) ��A���ɂ������̈��͂����߂�B
(2) ��B���ɂ������̈��͂����߂�B
���͂́A�K�v�Ȃ��̂����Ԃɋ��߂Ă������v�Z�ł��܂��B
�@ ���̂����ʂ� N �ɕϊ�����
�@�@�PN �� �P�O�Og�@�Ȃ̂ŁA�@�Skg �� �S�O�O�Og �� �S�ON
�@�ɕς��Ă����܂��B
�A ��ɂȂ�ʐ������߂�
(1) �̖�蕶�͂���A�u�ǂ̖ʂ���Ȃ邩�v��������悤�ɂȂ��Ă��܂��B
�@���̏ꍇ�́A��A�����Ȃ̂ŁAA�̖ʐ����������߂܂��B
�@�@�O�D�Q × �O�D�S �� �O�D�O�W
�@
�@�������A�K���P�ʂ� m �ɕς��Čv�Z���邱�Ƃ��������߂ł��B
�B �@���A�Ŋ���
�@���Ƃ͌����ɉ����Ċ���Z�����OK�ł��B
�@�@�S�ON ÷ �O�D�O�W �� �T�O�O
�� �T�O�O
���̂R�̎菇��ŁA���͂��v�Z���Ă����܂��B
�ł́A�����悤��(2)�������Ă݂܂��傤�B
(2) �@ ���ʂ� N ���ς��܂����A(1) �Ŏg�����S�ON ���g���܂��B
�@ �A ��B�����ɂȂ�̂ŁAB�̖ʐ������߂܂��B
�@�@�@�O�D�Q × �O�D�T ���O�D�P
�@�@ �K�� m �ɒ����Čv�Z���܂��傤�B
�@ �B �@���A�Ŋ������A���͂����߂܂��B
�@�@�@�S�O ÷ �O�D�P�� �S�O�O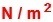
���͂̋��ߕ��̎菇�͂R�B
�@ ���ʂ� N �ɕϊ�����
�A ��ɂȂ�ʐ� �����߂�
�B �@���A�Ŋ���
�� �������A�ʐς͒����� m �ɒ����Čv�Z����
�������߂ɕK�v�Ȏ菇���������蓥�߂A
���͌v�Z�̊�{���N���A�ł���悤�ɂȂ�܂��B
�����v�Z�Ɋ���Ă�����A�悭�������Řr��������̂��I�X�X���ł��B
���Ɏ��Ԃ��������Ă������̂ŁA
���͌v�Z�̊�{�A�撣���Ă݂܂��H
����͗͂̂T��ځA���͂̌v�Z�ł��B
�O��S��ڂň������A
�͂̑傫���̕ϊ������͂̌����𗘗p�������������܂��B
��{���̉�������������Ă����܂��傤�B
�n�߂�O�ɁA���߂Ĉ��͂����߂�����ł��B
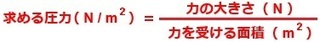
���̌������g������{���ł��B
��j�}�̂悤�Ȏ��ʂSkg �̒����̂̕��̂����̏�ɒu�������̈��͂��l����B
�������A�PN �� �P�O�Og �Ƃ���B
(1) ��A���ɂ������̈��͂����߂�B
(2) ��B���ɂ������̈��͂����߂�B

���͂́A�K�v�Ȃ��̂����Ԃɋ��߂Ă������v�Z�ł��܂��B
�@ ���̂����ʂ� N �ɕϊ�����
�@�@�PN �� �P�O�Og�@�Ȃ̂ŁA�@�Skg �� �S�O�O�Og �� �S�ON
�@�ɕς��Ă����܂��B
�A ��ɂȂ�ʐ������߂�
(1) �̖�蕶�͂���A�u�ǂ̖ʂ���Ȃ邩�v��������悤�ɂȂ��Ă��܂��B
�@���̏ꍇ�́A��A�����Ȃ̂ŁAA�̖ʐ����������߂܂��B
�@�@�O�D�Q × �O�D�S �� �O�D�O�W

�@
�@�������A�K���P�ʂ� m �ɕς��Čv�Z���邱�Ƃ��������߂ł��B
�B �@���A�Ŋ���
�@���Ƃ͌����ɉ����Ċ���Z�����OK�ł��B
�@�@�S�ON ÷ �O�D�O�W
 �� �T�O�O
�� �T�O�O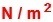
���̂R�̎菇��ŁA���͂��v�Z���Ă����܂��B
�ł́A�����悤��(2)�������Ă݂܂��傤�B
(2) �@ ���ʂ� N ���ς��܂����A(1) �Ŏg�����S�ON ���g���܂��B
�@ �A ��B�����ɂȂ�̂ŁAB�̖ʐ������߂܂��B
�@�@�@�O�D�Q × �O�D�T ���O�D�P
�@�@ �K�� m �ɒ����Čv�Z���܂��傤�B
�@ �B �@���A�Ŋ������A���͂����߂܂��B
�@�@�@�S�O ÷ �O�D�P�� �S�O�O
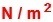
���͂̋��ߕ��̎菇�͂R�B
�@ ���ʂ� N �ɕϊ�����
�A ��ɂȂ�ʐ� �����߂�
�B �@���A�Ŋ���
�� �������A�ʐς͒����� m �ɒ����Čv�Z����
�������߂ɕK�v�Ȏ菇���������蓥�߂A
���͌v�Z�̊�{���N���A�ł���悤�ɂȂ�܂��B
�����v�Z�Ɋ���Ă�����A�悭�������Řr��������̂��I�X�X���ł��B
���Ɏ��Ԃ��������Ă������̂ŁA
���͌v�Z�̊�{�A�撣���Ă݂܂��H
�͂̑傫���͒P�ʂ�ς��ĕ\�����I
����ɂ��́AYOSHIO�ł��B
����͗͂̂S��ځA�͂̌v�Z�E���͂̕\�����ł��B
�c��͂�����Ă͒ʂ�Ȃ��A���Ȃ̌v�Z�ł����A
����͂����Ȃ�{�i�I�Ȍv�Z�ł͂Ȃ��A
�v�Z�ɏo�Ă��������P�ʂɂ��������܂��B
�������g�����v�Z�͎���A�b�v���܂��B
�c�{��ɓ���O�ɁA����̃e�[�}�̑O�U���
�������t��������������肪�����ł��c
�m���Ƃ���Șb���������Ƃ�����܂��B
�m���u�搶�A�����w�Z�ŗ͂∳�͂̌v�Z���K���܂����c�B�v
���u�����A���Ɍv�Z�ɐi�ˁB�v
�m���u�c�����������Ƃ����邯�ǁc�v
���u�c�H�v
�m���u�ǂ����āA�͂̑傫���𐔎��ŕ\�����Ƃ����́H
�@�@�@�����ł����v�Z������Ȃ̂Ɂc�B�v
���u�c�ǂ����Ă��낤�� �v
�v
�c�������Ƃ����Ǝv���܂����B�B�B
���Ȃ݂ɁA���܂��ԓ��ł��Ȃ������̂͌����܂ł�����܂���B�B�B
���������́A�u�����ē��R�v�̊��o�Ŏ��Ƃ��܂����A
��������́A��a�������������镔����������܂���B
�����Ȃ�A�͂���ȂǂŎ��ʁig���j���ڂŌ��ĕ�����܂����A
�͂̑傫���́A�ڂŌ����܂���B
�ڂŌ����Ȃ����Ƃ��A����������œ`����͓̂���ꍇ������܂��B
���ɁA�`����ꂽ���Ă��A
���Ȃ����Ȏq���炷��A�撣���ĕ����C���ɂ͂Ȃ�Ȃ����̂ł���ˁB
�c���݂܂���A�O�U�肪�����Ȃ�܂������A
����̗́E���͂̌v�Z�ɂ��ẮA
�o���Ăق������Ƃ��Q�_�����`���܂��B
���̗͂��Č��Ă��炦����������ł��B
�܂��A�P�ځB
��قǂ̂��Ƃ�ɂ��o�Ă��܂������A
�͂̑傫���́A�����ŕ\���K�v������܂��B
�o���邱�Ƃ́A
�PN �� �P�O�O��
�ŕ\�����[��������܂��B
���̎��A�͂̑傫���̒P�ʂ�N�i�j���[�g���j�ŕ\���܂��B
�c�ł́A�͂̑傫����P�ʂ��g���ĕ\����悤�ɂȂ�A
���̐��l�Ōv�Z���邱�ƂɂȂ��Ă��܂��B
�v�Z�͒��P���ȓ��e�̏ꍇ�́A��Ɉ��͌v�Z�ɂȂ�܂��B
�����łQ�ڂ́A���͂Ƃ��̕\�����ɂ��Ăł��B
���͂Ƃ������t�͎��X���ɂ��邱�Ƃ͂��邩������܂��A
���Ȃł��������Ƃ́A�P�ʖʐς�����ɂ�����͂̑傫�����w���܂��B
���͂�\���P�ʂ�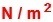 �i�j���[�g�����������[�g���j
�i�j���[�g�����������[�g���j
�ŕ\���܂��B
�܂��A�ꍇ�ɂ���ẮAPa�i�p�X�J���j�Ŋw�K����ꍇ������̂ŁA
�m���Ă����đ��͂Ȃ��ł��傤�B
�����āA���͌v�Z�ɕK�v�Ȍ������o���邱�ƂɂȂ����Ă����܂��B
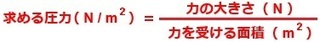
�����ł̒��ӓ_�́A�����ɂ��镪��̖ʐϒP���ł��B
�K�� �Ōv�Z�����悤�ɂ��܂��傤�B
�Ōv�Z�����悤�ɂ��܂��傤�B
�ł́A����̗́E���͂̃|�C���g�͂Q�B
�@ �͂̑傫���́A�PN �� �P�O�O�� �ɕϊ�����
�A ���͂����߂�������o���Ă�������
�⑫�Ƃ��ẮA����o�Ă����Q�̐V���ȒP�ʂƓǂݕ���
�������艟�����Ă������Ƃ��������߂��܂��B
����́A��ɒP�ʂƌ����ɏd�_��u���܂����B
����́A�P�ʂƌ����𗘗p�����v�Z��������グ�Ă����܂��B
�o���邱�Ƃ����ɃX�|�b�g���Ă�N���A���₷���Ȃ�̂ŁA
�́E���͂̒P�ʁA�撣���Ă݂܂��H
����͗͂̂S��ځA�͂̌v�Z�E���͂̕\�����ł��B
�c��͂�����Ă͒ʂ�Ȃ��A���Ȃ̌v�Z�ł����A
����͂����Ȃ�{�i�I�Ȍv�Z�ł͂Ȃ��A
�v�Z�ɏo�Ă��������P�ʂɂ��������܂��B
�������g�����v�Z�͎���A�b�v���܂��B
�c�{��ɓ���O�ɁA����̃e�[�}�̑O�U���
�������t��������������肪�����ł��c
�m���Ƃ���Șb���������Ƃ�����܂��B
�m���u�搶�A�����w�Z�ŗ͂∳�͂̌v�Z���K���܂����c�B�v
���u�����A���Ɍv�Z�ɐi�ˁB�v
�m���u�c�����������Ƃ����邯�ǁc�v
���u�c�H�v
�m���u�ǂ����āA�͂̑傫���𐔎��ŕ\�����Ƃ����́H
�@�@�@�����ł����v�Z������Ȃ̂Ɂc�B�v
���u�c�ǂ����Ă��낤��
�c�������Ƃ����Ǝv���܂����B�B�B
���Ȃ݂ɁA���܂��ԓ��ł��Ȃ������̂͌����܂ł�����܂���B�B�B
���������́A�u�����ē��R�v�̊��o�Ŏ��Ƃ��܂����A
��������́A��a�������������镔����������܂���B
�����Ȃ�A�͂���ȂǂŎ��ʁig���j���ڂŌ��ĕ�����܂����A
�͂̑傫���́A�ڂŌ����܂���B
�ڂŌ����Ȃ����Ƃ��A����������œ`����͓̂���ꍇ������܂��B
���ɁA�`����ꂽ���Ă��A
���Ȃ����Ȏq���炷��A�撣���ĕ����C���ɂ͂Ȃ�Ȃ����̂ł���ˁB
�c���݂܂���A�O�U�肪�����Ȃ�܂������A
����̗́E���͂̌v�Z�ɂ��ẮA
�o���Ăق������Ƃ��Q�_�����`���܂��B
���̗͂��Č��Ă��炦����������ł��B
�܂��A�P�ځB
��قǂ̂��Ƃ�ɂ��o�Ă��܂������A
�͂̑傫���́A�����ŕ\���K�v������܂��B
�o���邱�Ƃ́A
�PN �� �P�O�O��
�ŕ\�����[��������܂��B
���̎��A�͂̑傫���̒P�ʂ�N�i�j���[�g���j�ŕ\���܂��B
�c�ł́A�͂̑傫����P�ʂ��g���ĕ\����悤�ɂȂ�A
���̐��l�Ōv�Z���邱�ƂɂȂ��Ă��܂��B
�v�Z�͒��P���ȓ��e�̏ꍇ�́A��Ɉ��͌v�Z�ɂȂ�܂��B
�����łQ�ڂ́A���͂Ƃ��̕\�����ɂ��Ăł��B
���͂Ƃ������t�͎��X���ɂ��邱�Ƃ͂��邩������܂��A
���Ȃł��������Ƃ́A�P�ʖʐς�����ɂ�����͂̑傫�����w���܂��B
���͂�\���P�ʂ�
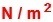 �i�j���[�g�����������[�g���j
�i�j���[�g�����������[�g���j�ŕ\���܂��B
�܂��A�ꍇ�ɂ���ẮAPa�i�p�X�J���j�Ŋw�K����ꍇ������̂ŁA
�m���Ă����đ��͂Ȃ��ł��傤�B
�����āA���͌v�Z�ɕK�v�Ȍ������o���邱�ƂɂȂ����Ă����܂��B
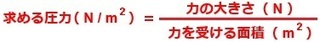
�����ł̒��ӓ_�́A�����ɂ��镪��̖ʐϒP���ł��B
�K��
 �Ōv�Z�����悤�ɂ��܂��傤�B
�Ōv�Z�����悤�ɂ��܂��傤�B�ł́A����̗́E���͂̃|�C���g�͂Q�B
�@ �͂̑傫���́A�PN �� �P�O�O�� �ɕϊ�����
�A ���͂����߂�������o���Ă�������
�⑫�Ƃ��ẮA����o�Ă����Q�̐V���ȒP�ʂƓǂݕ���
�������艟�����Ă������Ƃ��������߂��܂��B
����́A��ɒP�ʂƌ����ɏd�_��u���܂����B
����́A�P�ʂƌ����𗘗p�����v�Z��������グ�Ă����܂��B
�o���邱�Ƃ����ɃX�|�b�g���Ă�N���A���₷���Ȃ�̂ŁA
�́E���͂̒P�ʁA�撣���Ă݂܂��H
2020�N09��02��
�Q�l�ɁF�͂̍�}�̗�
����ɂ��́AYOSHIO�ł��B
����́A�O�`�������͂̍�}�̗�������Ă݂܂����B
�Ђ���Ƃ���ƁA�e�X�g�ɔ�������Œm���Ă����ƁA
�֗����ȁc�Ǝv����𒆐S�ɋ����Ă��܂��B
���ꂵ���_������Ǝv���܂����A
��낵����ΎQ�l�ɂ��Ă��炦��Ɗ������ł��B
�� ����͍�}�̗Ꭶ�����C���Ȃ̂ŁA���͂͏��Ȃ߂ł����A
�K�v�ȏ��ɂ͐��������Ă��܂��B
�@ ����ȏꏊ�ɕ���u��
��Ԋ�{�I�ȍ�}�̗�B
�ԁF���̂ɓ����d��
�F���̂������グ��i�x����j�����R��
�A �V�䂩�狅�̂��邷
�����āA��}�ɂ܂����₷���V�䂩��邵����B
�ԁF���̂ɓ����d��
�F�������̂������́�����
�F�V�䂪����������
����}�̃X�^�[�g�n�_�̌������́A
��蕶�̎��u�����v�����������ƁI
�B ���̂����Ă݂�
�ԁF���̂��E�ֈړ��������
�F���̂��������Ƃ���̂�W����́����C��
�����C�͂̃X�^�[�g�n�_�́A���̂Ƃ��イ����
�ڂ��������̐^���ɂ���A
���Ε����ɖ����������ƁI
�C �Q�̎���������i����A�̎��_�Łj
�ԁF���̂ɓ����d��
�F������������i�ނ������j��
���͂̍�}�̃X�^�[�g�n�_�́A���̒��S�ł��邱�ƁI
�l�X�ȗ���A���������Đ}�ɂ��Ă݂܂����B
���̂悤�ɁA�m�[�g�ɂ܂Ƃ߂鎞���}���Ă݂邱�ƂŁA
�E�����X�^�[�g�n�_
�E�����L������
���₷���Ȃ邾���łȂ��A�m�F���₷���Ȃ邩�ȂƎv���A
����Ă݂܂����B
�l�X�ȗ�Ƀ`�������W���āA�͂̍�}�A�撣���Ă݂܂��H
����́A�O�`�������͂̍�}�̗�������Ă݂܂����B
�Ђ���Ƃ���ƁA�e�X�g�ɔ�������Œm���Ă����ƁA
�֗����ȁc�Ǝv����𒆐S�ɋ����Ă��܂��B
���ꂵ���_������Ǝv���܂����A
��낵����ΎQ�l�ɂ��Ă��炦��Ɗ������ł��B
�� ����͍�}�̗Ꭶ�����C���Ȃ̂ŁA���͂͏��Ȃ߂ł����A
�K�v�ȏ��ɂ͐��������Ă��܂��B
�@ ����ȏꏊ�ɕ���u��

��Ԋ�{�I�ȍ�}�̗�B
�ԁF���̂ɓ����d��
�F���̂������グ��i�x����j�����R��
�A �V�䂩�狅�̂��邷

�����āA��}�ɂ܂����₷���V�䂩��邵����B
�ԁF���̂ɓ����d��
�F�������̂������́�����
�F�V�䂪����������
����}�̃X�^�[�g�n�_�̌������́A
��蕶�̎��u�����v�����������ƁI
�B ���̂����Ă݂�

�ԁF���̂��E�ֈړ��������
�F���̂��������Ƃ���̂�W����́����C��
�����C�͂̃X�^�[�g�n�_�́A���̂Ƃ��イ����
�ڂ��������̐^���ɂ���A
���Ε����ɖ����������ƁI
�C �Q�̎���������i����A�̎��_�Łj

�ԁF���̂ɓ����d��
�F������������i�ނ������j��
���͂̍�}�̃X�^�[�g�n�_�́A���̒��S�ł��邱�ƁI
�l�X�ȗ���A���������Đ}�ɂ��Ă݂܂����B
���̂悤�ɁA�m�[�g�ɂ܂Ƃ߂鎞���}���Ă݂邱�ƂŁA
�E�����X�^�[�g�n�_
�E�����L������
���₷���Ȃ邾���łȂ��A�m�F���₷���Ȃ邩�ȂƎv���A
����Ă݂܂����B
�l�X�ȗ�Ƀ`�������W���āA�͂̍�}�A�撣���Ă݂܂��H
2020�N09��01��
�͂̂荇���͂R��������������ׂ��I
����ɂ��́AYOSHIO�ł��B
����͗͂̂R��ځA�͂��荇�������ł��B
�O������}����@�𗘗p���Ă����̂ŁA
�܂������ɂȂ��Ă��Ȃ�����
�͂̂Q��ځu�͂̍�}�̓X�^�[�g�n�_�ɋC������I�v�i8/31�t�j
�������Ă���̕���������₷���ł��B
�iURL�����N�̓\����������炸�c�ʓ|�������܂��c�B�j
�O����e�Ƃ̈Ⴂ�́A
�O��F�͂̍�}�����邽�߂̊�{
����F�͂̍�}���s�����e�X�g�������
�ł��B
���炭�A���ԁE�����e�X�g�ň�x�͏o�肳���^�C�v�ł��B
�Ⴆ�A���̂悤�Ƀe�X�g�Ȃǂŏo�肳�ꂽ�Ƃ��܂��B
��j���̏�ɒu�������̂ɓ����d�͂Ɛ����R�͂���}���Ȃ����B
�c�����Ńp�j�b�N�ɂȂ��Ă��܂��āA
�܊p�����Ċ撣�����w�͂ʂɂ���������܂���B
�e�X�g�Ȃǂł̗͂̍�}�̃|�C���g�́A
���������Ė����悭�ǂނ����ł��B
�����ŁA�u���₢��A��}�Ȃ̂ɁA����ǂނ��āH�v
�Ǝv���̂͂����܂����B
�K����蕶�͂���A������}���������̂���������̂ŁA
�O��̃|�C���g�ł�������}�ɏd�v�ȃX�^�[�g�n�_���n�b�L�����܂��B
�ł́A��蕶�͂����}���������̂́A
�E���̂̓����d��
�E�����R��
�̂Q�ł��B
�����ŁA�O����e���m�F���Ă��炤�A
�d�́����̂̒��S����^���Ɍ������Ė���L������
�Ƃ���̂ŁA
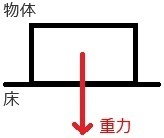
���ꂾ���ŁA�d�͂̍�}��OK�ł��B
���ɁA
�����R�́����̂Ɛڂ��Ă���ʂ���d�͂Ɣ��Ό����ɖ���L������
�Ƃ���̂ŁA
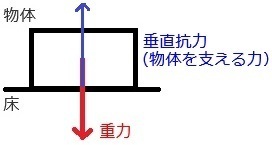
���ʂ���^��Ɍ������Ė���L�������ł��B
�ł́A���������ۂɐU��Ԃ��Ă��������|�C���g�͂R�B
�@ ��蕶�͂��悭�ǂ݁A��}���������͂��m�F����
�A �����͂���}����X�^�[�g�n�_�����߂�
�B ���߂�ꂽ�����ɖ���L��
������菇�悭�i�߂Ă������ƂƁA
�J��Ԃ����K���Ă������Ƃ��������߂ł��B
�c�������A���ꂾ���Ńe�X�g���Ȃǂ�������̂ł���A
��J���܂���B
���܂�ɗႪ���Ȃ�����̂ŁA���߂ĕʂ̃^�C�~���O��
�͂̍�}�̗Ⴞ�����A�b�v�������ƍl���Ă��܂��B
�i���R�́A���܂�ɗe�ʂ��傫���Ȃ��Ă��܂�����Ȃ̂ŁA������������K���ł��B�j
�����āA���̍�}���番���邱�Ƃ������P����܂��B
����́A����̃e�[�}�ł����͂��荇���R�����ł��B
������x��قǂ̐}�����Ă݂�ƁA

�@ �Q�̗͂����Ό����ł���@���@����������Ă��Ȃ�
�A �Q�̗͂��傫�����������@���@����������
�B �Q�̗͂��꒼�����ɂ���@���@�܂�Ȃ����Ă��Ȃ�
�Ԏ��͊o���Ă��������ł����A
���Ō��������ĕ�����₷�����Ă݂܂����B
���̂R�����́A���o�肳��Ă��������鏀����
�i�߂Ă����悤�ɂ��Ă��������ˁB
�ł́A����̗͂̂荇���̃|�C���g�́A
�@ ��}�������͂�ǂ�ō�}�̃X�^�[�g�n�_�����߂�
�A �͂��荇���R���������Ό����E�����傫���E�꒼��
�̂Q�ł��B
�c�ŏ��̐A���̍���U��Ԃ��Ă݂�ƁA
�������Ȃ��Ă��Ă��銴�������܂���ˁB
���̒��ł��A�K���ɂ����̃u���O��ǂ��������āA
���ȗ��Ȃ��撣���Ă��邱�Ƃ��A�{���ɂ��������Ƃł��I
�����Ȃ肷�ׂĂ�S�͂Ŋ撣�낤�Ƃ��Ȃ��Ă�������ł��B
���̓��e�̃|�C���g�͑�܂��ł����̂ŁA
�E���t�͈��ꓚ�`��
�E��}�͓������ł������̂Ŕ������K
�ŗ�����[�߂Ă�����悤�A
�������ł�������g���C���Ă݂Ă��������ˁB
�͂̂荇���A�撣���Ă݂܂��H
�i�Ō�ɕ��͒����Ȃ��Ă��߂�Ȃ����A��ǂ��肪�Ƃ��������܂��I�j
����͗͂̂R��ځA�͂��荇�������ł��B
�O������}����@�𗘗p���Ă����̂ŁA
�܂������ɂȂ��Ă��Ȃ�����
�͂̂Q��ځu�͂̍�}�̓X�^�[�g�n�_�ɋC������I�v�i8/31�t�j
�������Ă���̕���������₷���ł��B
�iURL�����N�̓\����������炸�c�ʓ|�������܂��c�B�j
�O����e�Ƃ̈Ⴂ�́A
�O��F�͂̍�}�����邽�߂̊�{
����F�͂̍�}���s�����e�X�g�������
�ł��B
���炭�A���ԁE�����e�X�g�ň�x�͏o�肳���^�C�v�ł��B
�Ⴆ�A���̂悤�Ƀe�X�g�Ȃǂŏo�肳�ꂽ�Ƃ��܂��B
��j���̏�ɒu�������̂ɓ����d�͂Ɛ����R�͂���}���Ȃ����B

�c�����Ńp�j�b�N�ɂȂ��Ă��܂��āA
�܊p�����Ċ撣�����w�͂ʂɂ���������܂���B
�e�X�g�Ȃǂł̗͂̍�}�̃|�C���g�́A
���������Ė����悭�ǂނ����ł��B
�����ŁA�u���₢��A��}�Ȃ̂ɁA����ǂނ��āH�v
�Ǝv���̂͂����܂����B
�K����蕶�͂���A������}���������̂���������̂ŁA
�O��̃|�C���g�ł�������}�ɏd�v�ȃX�^�[�g�n�_���n�b�L�����܂��B
�ł́A��蕶�͂����}���������̂́A
�E���̂̓����d��
�E�����R��
�̂Q�ł��B
�����ŁA�O����e���m�F���Ă��炤�A
�d�́����̂̒��S����^���Ɍ������Ė���L������
�Ƃ���̂ŁA

���ꂾ���ŁA�d�͂̍�}��OK�ł��B
���ɁA
�����R�́����̂Ɛڂ��Ă���ʂ���d�͂Ɣ��Ό����ɖ���L������
�Ƃ���̂ŁA

���ʂ���^��Ɍ������Ė���L�������ł��B
�ł́A���������ۂɐU��Ԃ��Ă��������|�C���g�͂R�B
�@ ��蕶�͂��悭�ǂ݁A��}���������͂��m�F����
�A �����͂���}����X�^�[�g�n�_�����߂�
�B ���߂�ꂽ�����ɖ���L��
������菇�悭�i�߂Ă������ƂƁA
�J��Ԃ����K���Ă������Ƃ��������߂ł��B
�c�������A���ꂾ���Ńe�X�g���Ȃǂ�������̂ł���A
��J���܂���B
���܂�ɗႪ���Ȃ�����̂ŁA���߂ĕʂ̃^�C�~���O��
�͂̍�}�̗Ⴞ�����A�b�v�������ƍl���Ă��܂��B
�i���R�́A���܂�ɗe�ʂ��傫���Ȃ��Ă��܂�����Ȃ̂ŁA������������K���ł��B�j
�����āA���̍�}���番���邱�Ƃ������P����܂��B
����́A����̃e�[�}�ł����͂��荇���R�����ł��B
������x��قǂ̐}�����Ă݂�ƁA

�@ �Q�̗͂����Ό����ł���@���@����������Ă��Ȃ�
�A �Q�̗͂��傫�����������@���@����������
�B �Q�̗͂��꒼�����ɂ���@���@�܂�Ȃ����Ă��Ȃ�
�Ԏ��͊o���Ă��������ł����A
���Ō��������ĕ�����₷�����Ă݂܂����B
���̂R�����́A���o�肳��Ă��������鏀����
�i�߂Ă����悤�ɂ��Ă��������ˁB
�ł́A����̗͂̂荇���̃|�C���g�́A
�@ ��}�������͂�ǂ�ō�}�̃X�^�[�g�n�_�����߂�
�A �͂��荇���R���������Ό����E�����傫���E�꒼��
�̂Q�ł��B
�c�ŏ��̐A���̍���U��Ԃ��Ă݂�ƁA
�������Ȃ��Ă��Ă��銴�������܂���ˁB
���̒��ł��A�K���ɂ����̃u���O��ǂ��������āA
���ȗ��Ȃ��撣���Ă��邱�Ƃ��A�{���ɂ��������Ƃł��I
�����Ȃ肷�ׂĂ�S�͂Ŋ撣�낤�Ƃ��Ȃ��Ă�������ł��B
���̓��e�̃|�C���g�͑�܂��ł����̂ŁA
�E���t�͈��ꓚ�`��
�E��}�͓������ł������̂Ŕ������K
�ŗ�����[�߂Ă�����悤�A
�������ł�������g���C���Ă݂Ă��������ˁB
�͂̂荇���A�撣���Ă݂܂��H
�i�Ō�ɕ��͒����Ȃ��Ă��߂�Ȃ����A��ǂ��肪�Ƃ��������܂��I�j
2020�N08��31��
�͂̍�}�̓X�^�[�g�n�_�ɋC������I
����ɂ��́AYOSHIO�ł��B
����͗́E���͂̂Q��ځA�͂̂荇���ł��B
�O��͗͂���ޕʂɐ������Ă��܂������A
��������̂ɓ����͂���}���Ă������ƂɂȂ�܂��B
�c�����A�������n�߂�O�ɁB
�m���ɋ����Ă��ċC�t�����Ƃ�����܂��B
����́A��}������Ƃ������Ƃł��B
��x�R�c�����߂�Ζ��Ȃ��̂ł����A
��������|�C���g��������A�������Ă���悤�ł��A
���̒����S�`���S�`�����܂���ˁc�B
�����ŁA��܂��A���|�C���g���������Ă����܂��傤�B
�͂̍�}�̃|�C���g�́A
��}�ɕK�v�Ȗ��̃X�^�[�g�n�_�̌��ߕ�
�ł��B
�X�^�[�g�n�_�����܂�A���̈������͂P�p�^�[���ł��B
�ł́A���߂ɁA�͂���ŕ\�����߂ɏd�v�ȃ|�C���g�ł��B
�͂�\�����̈Ӗ���m���Ă����܂��傤�B

�����v���ɁA��}�ň�ԑ厖�Ȃ��Ƃ́A
���̎n�_�̌��ߕ��ł��B
����������ƁA���������n�߂�X�^�[�g�n�_���������茈�߂���A
��}���U�����₷���Ȃ�܂��B
����ł́A�������}�̃|�C���g�����g���Ă����܂��B
�P�ڂ́A���}�̏ł��B
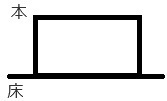
�F������o��������̂ł͂Ȃ��ł��傤���H
���Ȃǂ̏�ɁA�{�ς݂ɂ��Ă���c�B�i���͂�������イ�ł��j
�ł́A���̏ɗ͂�\�������������݂܂��B
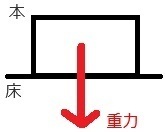
���d�͋�ԂłȂ���A��{�I�����̂ɂ͏d�͂�������܂��B
�d�͂̍�}�̃|�C���g�́A
���̂̒��S����^���Ɍ������Ė���L�������ł��B
���ꂾ���ő��v�B������Ƃ͍l���Ȃ��B
�������A���̐}�ɂ͂����P�������߂�����܂��B
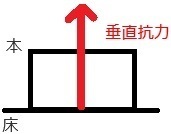
���̂��ڂ��Ă���ʂɓ���������ɕ��̂������Ԃ����Ƃ����������܂��B
���̗͂��A�����R���Ƃ����܂��B
�����R�͂̍�}�̃|�C���g�́A
���̂Ɛڂ��Ă���ʂ���d�͂Ɣ��Ό����ɖ���L�������ł��B
�ł́A�����P�̗�ł��B
�c���܂�V�䂩�狅�̂��邷���Ƃ����I�ɂ��܂��c
���Ȃ̖��ł͏o�肳��₷���ł��B
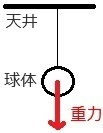
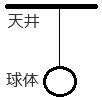
�P�ڂ̗�Ɠ������A���̂ɓ����d�͂����}���Ă����܂��傤�B
�d�͂̍�}�̃|�C���g�͑S�������ŁA
���̂̒��S����^���Ɍ������Ė���L�������ł��B
�������A���̐}�ɂ��A�����P�������߂�����܂��B
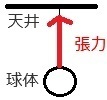
���̂�V�䂩��邹�闝�R�̂P�́A
���̂��������낤�Ƃ��鎅�̗͂����������ł��B
���̗͂��A���́i���傤��傭�j�Ƃ����܂��B
���͂���}����|�C���g�́A
���̂Ɏ���t������������d�͂Ɣ��Ό����ɖ���L�������ł��B
�ł́A����̗͂̍�}�̃|�C���g���R�B
�@ �̖͂��́A�����E�傫���E�n�_���ւ��
�A ���̂ɓ����d�͂́A���̂̒��S����^������������
�B �K���d�͂Ɣ��Ό����ɓ����͂���}�ł���i�����R�͂⒣�͂Ȃǁj
���t�E��}�E�����Ń`�F�b�N���邱�Ƃ���������̂ŁA
��}�|�C���g�J�Ɋm�F���Ĉ���N���A���Ă݂܂��傤�B
�ł炸�A��������ł��A�������B
����́A���̍�}���@�𗘗p���āA�͂̂荇�����܂Ƃ߂Ă����܂��B
���̃X�^�[�g�n�_�������������ŁA
�͂̍�}�A�撣���Ă݂܂��H
����͗́E���͂̂Q��ځA�͂̂荇���ł��B
�O��͗͂���ޕʂɐ������Ă��܂������A
��������̂ɓ����͂���}���Ă������ƂɂȂ�܂��B
�c�����A�������n�߂�O�ɁB
�m���ɋ����Ă��ċC�t�����Ƃ�����܂��B
����́A��}������Ƃ������Ƃł��B
��x�R�c�����߂�Ζ��Ȃ��̂ł����A
��������|�C���g��������A�������Ă���悤�ł��A
���̒����S�`���S�`�����܂���ˁc�B
�����ŁA��܂��A���|�C���g���������Ă����܂��傤�B
�͂̍�}�̃|�C���g�́A
��}�ɕK�v�Ȗ��̃X�^�[�g�n�_�̌��ߕ�
�ł��B
�X�^�[�g�n�_�����܂�A���̈������͂P�p�^�[���ł��B
�ł́A���߂ɁA�͂���ŕ\�����߂ɏd�v�ȃ|�C���g�ł��B
�͂�\�����̈Ӗ���m���Ă����܂��傤�B

�����v���ɁA��}�ň�ԑ厖�Ȃ��Ƃ́A
���̎n�_�̌��ߕ��ł��B
����������ƁA���������n�߂�X�^�[�g�n�_���������茈�߂���A
��}���U�����₷���Ȃ�܂��B
����ł́A�������}�̃|�C���g�����g���Ă����܂��B
�P�ڂ́A���}�̏ł��B

�F������o��������̂ł͂Ȃ��ł��傤���H
���Ȃǂ̏�ɁA�{�ς݂ɂ��Ă���c�B�i���͂�������イ�ł��j
�ł́A���̏ɗ͂�\�������������݂܂��B

���d�͋�ԂłȂ���A��{�I�����̂ɂ͏d�͂�������܂��B
�d�͂̍�}�̃|�C���g�́A
���̂̒��S����^���Ɍ������Ė���L�������ł��B
���ꂾ���ő��v�B������Ƃ͍l���Ȃ��B
�������A���̐}�ɂ͂����P�������߂�����܂��B

���̂��ڂ��Ă���ʂɓ���������ɕ��̂������Ԃ����Ƃ����������܂��B
���̗͂��A�����R���Ƃ����܂��B
�����R�͂̍�}�̃|�C���g�́A
���̂Ɛڂ��Ă���ʂ���d�͂Ɣ��Ό����ɖ���L�������ł��B
�ł́A�����P�̗�ł��B

�c���܂�V�䂩�狅�̂��邷���Ƃ����I�ɂ��܂��c
���Ȃ̖��ł͏o�肳��₷���ł��B

�P�ڂ̗�Ɠ������A���̂ɓ����d�͂����}���Ă����܂��傤�B
�d�͂̍�}�̃|�C���g�͑S�������ŁA
���̂̒��S����^���Ɍ������Ė���L�������ł��B
�������A���̐}�ɂ��A�����P�������߂�����܂��B

���̂�V�䂩��邹�闝�R�̂P�́A
���̂��������낤�Ƃ��鎅�̗͂����������ł��B
���̗͂��A���́i���傤��傭�j�Ƃ����܂��B
���͂���}����|�C���g�́A
���̂Ɏ���t������������d�͂Ɣ��Ό����ɖ���L�������ł��B
�ł́A����̗͂̍�}�̃|�C���g���R�B
�@ �̖͂��́A�����E�傫���E�n�_���ւ��
�A ���̂ɓ����d�͂́A���̂̒��S����^������������
�B �K���d�͂Ɣ��Ό����ɓ����͂���}�ł���i�����R�͂⒣�͂Ȃǁj
���t�E��}�E�����Ń`�F�b�N���邱�Ƃ���������̂ŁA
��}�|�C���g�J�Ɋm�F���Ĉ���N���A���Ă݂܂��傤�B
�ł炸�A��������ł��A�������B
����́A���̍�}���@�𗘗p���āA�͂̂荇�����܂Ƃ߂Ă����܂��B
���̃X�^�[�g�n�_�������������ŁA
�͂̍�}�A�撣���Ă݂܂��H
2020�N08��30��
�͂ɂ͂T�̎�ނ�����I
����ɂ��́AYOSHIO�ł��B
����́E���͂ł��B
���̒P���Ɣ�ׂāA�������߁i�Ƃ��������A���߁j�ł��B
���ȏ��Ȃǂ�ǂ�ł��c
�悭������Ȃ��E�S�`���S�`�����邱�Ƃ������Ă��܂��B
���܂ł������߂ɓ��e�����Ȃ���A
�d�v�|�C���g���܂Ƃ߂Ă����܂��ˁB
����́A�͂̂P��ځA���̂ɓ������ł��B
���w���Ȃň����͂Ƃ́c
�㍶�}�̂悤�ȁA���Ȃǂɒu���ꂽ���̂������牟���ē������ꍇ��A
��E�}�̂悤�ȁA�V�䂩�狅�̂��Ђ��Ȃǂł邵���ꍇ�ȂǁA
�l�X�ȏ�ʂ�����܂��B
�����ŁA���Ⴂ���Ă͂����Ȃ����Ƃ́A
�u�́��l�̎�ʼn��������́v�ł͂Ȃ����Ƃł��B
�l���܂߂����̂��A�ǂ̕����ɂǂꂾ���������Ƃ��Ă��邩��
�l��������ǂ���������܂���B
�ł́A���܂�s���Ɨ��Ȃ���E�}�̂悤�ȗ͂ɂ��āA
�ǂ̂悤�Ȏ�ނ����邩���܂Ƃ߂�ƁA
�@ �d�́@�@�@�A ���̗́@�@�@�B �d�C�̗�
�C �e���́@�@�@�D ���C��
�̎�ɂT����܂����A�ڂ������Ă݂܂��傤�B
�@ �d���́A���̂𗎂Ƃ����^���ɗ������Ă������ɓ������B
�@�i���L���͂ƃU�b�N���ƌ����l������悤�ł����c�B�j
�A ���̗��́AN�ɂ�N�ɂ������ɂȂ甽���������A
�@N�ɂ�S�ɂ��Ⴄ�ɂȂ炭���t���������B
�B �d�C�̗��́A�{�̓d�C�Ɓ[�̓d�C�������������蔽�����������肷����B
�@�Ⴆ�A�Ód�C��������₷����ɂȂ�܂��ˁB
�C �e�����́A�o�l�Ȃǂ�L������k�߂��肵�Ă����ɖ߂낤�Ƃ�����B
�@�փS�����A�s���ƒ����Ă��͂��ɂ߂�ƌ��ɖ߂�܂��ˁB
�D ���C�͂́c
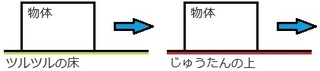
�Ⴆ�A�����̖͗l�ւ��ȂǂʼnƋ�Ȃǂ��ړ������鎞�A
�c���c���̏��Ȃ�X���[�Y�ɓ������Ă��A
�U���U���������イ����Ȃǂ͏�肭�^�ׂȂ��ł���ˁB
���̂悤�ɁA���C���́A���̂̓�����W����i�ז�����j�悤�ɓ������ł��B
�������Č��Ă݂�ƁA
�@�̏d�͂̂悤�ɁA���̂��������łȂ��A
�C�̒e���͂̂悤�ɁA���̂��ό`������A
�D�̖��C�͂̂悤�ɁA���̂��������Ȃǂ�ς���������
�Ƃ���������������܂��B
�ł́A���̂ɗ͂��������̃|�C���g���܂Ƃ߂�ƁA
�@ ���̂������グ����x�����肷����
�A ���̂��ό`������
�B ���̂��^�����ς������
���������Ă����悤�ɂ��܂��B
�Ō�ɁA����̗͂̓����ɂ͂Q�|�C���g������A
�@ �͂ɂ��d�́E���̗́E�d�C�̗́E�e���́E���C���̂T������
�A �͂̓����ɂ́A�����グ����x�����肾���łȂ��A
�@�ό`��^���̕ω��̖���������
�͂̃X�^�[�g���܂Ƃ߂邾���ł��A
�����̌��t���o�Ă��܂��B
�������A�O��܂ł̉��Ɠ������ڂɌ�������̂ł͂Ȃ��̂ŁA
�}�����p���Ȃ���C���[�W�A�b�v�ɂȂ��������̂ł��B
����́A����̂܂Ƃ߂����ɁA�e�X�g�Ȃǂɂ��Ή�������e��G��Ă����܂��B
�o���邱�ƂƂ܂Ƃ߂���ςł����A�͂̓����A�撣���Ă݂܂��H
���������Ƃ������A�ǂ݂Â炢�������X�������Ǝv���܂��B
����Ȓ��A�Ō�܂ň�ǂ��肪�Ƃ��������܂����I
����́E���͂ł��B
���̒P���Ɣ�ׂāA�������߁i�Ƃ��������A���߁j�ł��B
���ȏ��Ȃǂ�ǂ�ł��c
�悭������Ȃ��E�S�`���S�`�����邱�Ƃ������Ă��܂��B
���܂ł������߂ɓ��e�����Ȃ���A
�d�v�|�C���g���܂Ƃ߂Ă����܂��ˁB
����́A�͂̂P��ځA���̂ɓ������ł��B
���w���Ȃň����͂Ƃ́c

�㍶�}�̂悤�ȁA���Ȃǂɒu���ꂽ���̂������牟���ē������ꍇ��A
��E�}�̂悤�ȁA�V�䂩�狅�̂��Ђ��Ȃǂł邵���ꍇ�ȂǁA
�l�X�ȏ�ʂ�����܂��B
�����ŁA���Ⴂ���Ă͂����Ȃ����Ƃ́A
�u�́��l�̎�ʼn��������́v�ł͂Ȃ����Ƃł��B
�l���܂߂����̂��A�ǂ̕����ɂǂꂾ���������Ƃ��Ă��邩��
�l��������ǂ���������܂���B
�ł́A���܂�s���Ɨ��Ȃ���E�}�̂悤�ȗ͂ɂ��āA
�ǂ̂悤�Ȏ�ނ����邩���܂Ƃ߂�ƁA
�@ �d�́@�@�@�A ���̗́@�@�@�B �d�C�̗�
�C �e���́@�@�@�D ���C��
�̎�ɂT����܂����A�ڂ������Ă݂܂��傤�B
�@ �d���́A���̂𗎂Ƃ����^���ɗ������Ă������ɓ������B
�@�i���L���͂ƃU�b�N���ƌ����l������悤�ł����c�B�j
�A ���̗��́AN�ɂ�N�ɂ������ɂȂ甽���������A
�@N�ɂ�S�ɂ��Ⴄ�ɂȂ炭���t���������B
�B �d�C�̗��́A�{�̓d�C�Ɓ[�̓d�C�������������蔽�����������肷����B
�@�Ⴆ�A�Ód�C��������₷����ɂȂ�܂��ˁB
�C �e�����́A�o�l�Ȃǂ�L������k�߂��肵�Ă����ɖ߂낤�Ƃ�����B
�@�փS�����A�s���ƒ����Ă��͂��ɂ߂�ƌ��ɖ߂�܂��ˁB
�D ���C�͂́c

�Ⴆ�A�����̖͗l�ւ��ȂǂʼnƋ�Ȃǂ��ړ������鎞�A
�c���c���̏��Ȃ�X���[�Y�ɓ������Ă��A
�U���U���������イ����Ȃǂ͏�肭�^�ׂȂ��ł���ˁB
���̂悤�ɁA���C���́A���̂̓�����W����i�ז�����j�悤�ɓ������ł��B
�������Č��Ă݂�ƁA
�@�̏d�͂̂悤�ɁA���̂��������łȂ��A
�C�̒e���͂̂悤�ɁA���̂��ό`������A
�D�̖��C�͂̂悤�ɁA���̂��������Ȃǂ�ς���������
�Ƃ���������������܂��B
�ł́A���̂ɗ͂��������̃|�C���g���܂Ƃ߂�ƁA
�@ ���̂������グ����x�����肷����
�A ���̂��ό`������
�B ���̂��^�����ς������
���������Ă����悤�ɂ��܂��B
�Ō�ɁA����̗͂̓����ɂ͂Q�|�C���g������A
�@ �͂ɂ��d�́E���̗́E�d�C�̗́E�e���́E���C���̂T������
�A �͂̓����ɂ́A�����グ����x�����肾���łȂ��A
�@�ό`��^���̕ω��̖���������
�͂̃X�^�[�g���܂Ƃ߂邾���ł��A
�����̌��t���o�Ă��܂��B
�������A�O��܂ł̉��Ɠ������ڂɌ�������̂ł͂Ȃ��̂ŁA
�}�����p���Ȃ���C���[�W�A�b�v�ɂȂ��������̂ł��B
����́A����̂܂Ƃ߂����ɁA�e�X�g�Ȃǂɂ��Ή�������e��G��Ă����܂��B
�o���邱�ƂƂ܂Ƃ߂���ςł����A�͂̓����A�撣���Ă݂܂��H
���������Ƃ������A�ǂ݂Â炢�������X�������Ǝv���܂��B
����Ȓ��A�Ō�܂ň�ǂ��肪�Ƃ��������܂����I
2020�N08��29��
�u���C�N�F���ȂōD���ȕ���͉��ł����H
����ɂ��́AYOSHIO�ł��B
�O��u���O�ʼn��̊�{������ɂȂ����̂ŁA
�u���C�N�ŗ��Ȃ̕���ɂ��Ă��b���������ȂƎv���܂��B
�ȑO�̃u���O�ł��A���Ȃ͕��삪������邱�Ƃ��q�ׂ܂����B
�i�K���ɂ��j���̃u���O��ǂ�ł��������Ă���F�l�́A
���Ȃł͂ǂ̕��삪�D���ł����H
�A����l�̂̕s�v�c���������w�����x�A
�����̕ω��┽�����������w���w�x�A
���̂̓��������ŋN���錻�ۂɂ��ւ���w�����x�A
�V���w��n���w�Ȃǂ��������w�n�w�x�B
�����A���w��p��Ȃǂƈ���āA
���Ȃ��D���ɂȂ闝�R�͂P�ɍi��Ȃ��Ǝv���܂��B
�Ⴆ�A�A�A
�E�ËL������A�_�����₷������
�E�������y��������
���������߂�ӌ���������܂���ˁB
���w�������Z�i�w���A���[���m�����w��ł������ɁA
���Ȃ��炸������ǂ��w�i�w�Ɍ������i�H�x���Ǝv���܂��B
�ŏI�I�ɐi�w���邩�ǂ����͔����ɂ��āA
�u���̏����̖��͈�҂ɂȂ邱�Ƃ�����A���w������K�v�Ȃ̂��ȁv
�ȂǁA�i�H�ƌ����ė��Ȃ̕�����l�����ʂ������Ă��܂��B
�����_�ŗ��Ȃ��D���Ȑl�́A���͂�L���Ă������ƂɂȂ�܂��B
����ŁA���Ȃ�����������ǂ��ɂ��Ȃ�Ȃ��A�Ƃ�����ł͂���܂����B
�������Ȃ����A�����ł��ł���͈͂Ŋ撣���Ă݂邾���ŁA
���ʂ��ς�邱�Ƃ͑�������܂��B
�l���Ă��鏫���̕�������A�E���l���Ă���̂ł���A
�ǂ̂悤�Ȓm�����K�v���A
�ǂ̂悤�ȕ���̕����d�v���A
�ȂǂׂĂ݂邱�Ƃ��A����̕��̕ω��̂��������ɂȂ邩������܂���ˁB
���ɁA���Ȃ͕���̕���������傫���̂ŁA
�����ɕK�v�ȕ��������߂���A
�Ɍ����Ă��L���ɏ�����i�߂Ă����ޗ��ɂ��Ȃ�܂�����ˁB
�c�v���Ă���ȏ�ɁA�܂Ƃ܂肪���Ă��Ȃ���������܂���B�B�B
�v�����܂܂ɁA�v���̏���Â��Ă݂܂����B
����͗́E���͂��܂Ƃ߂Ă����܂��B
�O��u���O�ʼn��̊�{������ɂȂ����̂ŁA
�u���C�N�ŗ��Ȃ̕���ɂ��Ă��b���������ȂƎv���܂��B
�ȑO�̃u���O�ł��A���Ȃ͕��삪������邱�Ƃ��q�ׂ܂����B
�i�K���ɂ��j���̃u���O��ǂ�ł��������Ă���F�l�́A
���Ȃł͂ǂ̕��삪�D���ł����H
�A����l�̂̕s�v�c���������w�����x�A
�����̕ω��┽�����������w���w�x�A
���̂̓��������ŋN���錻�ۂɂ��ւ���w�����x�A
�V���w��n���w�Ȃǂ��������w�n�w�x�B
�����A���w��p��Ȃǂƈ���āA
���Ȃ��D���ɂȂ闝�R�͂P�ɍi��Ȃ��Ǝv���܂��B
�Ⴆ�A�A�A
�E�ËL������A�_�����₷������
�E�������y��������
���������߂�ӌ���������܂���ˁB
���w�������Z�i�w���A���[���m�����w��ł������ɁA
���Ȃ��炸������ǂ��w�i�w�Ɍ������i�H�x���Ǝv���܂��B
�ŏI�I�ɐi�w���邩�ǂ����͔����ɂ��āA
�u���̏����̖��͈�҂ɂȂ邱�Ƃ�����A���w������K�v�Ȃ̂��ȁv
�ȂǁA�i�H�ƌ����ė��Ȃ̕�����l�����ʂ������Ă��܂��B
�����_�ŗ��Ȃ��D���Ȑl�́A���͂�L���Ă������ƂɂȂ�܂��B
����ŁA���Ȃ�����������ǂ��ɂ��Ȃ�Ȃ��A�Ƃ�����ł͂���܂����B
�������Ȃ����A�����ł��ł���͈͂Ŋ撣���Ă݂邾���ŁA
���ʂ��ς�邱�Ƃ͑�������܂��B
�l���Ă��鏫���̕�������A�E���l���Ă���̂ł���A
�ǂ̂悤�Ȓm�����K�v���A
�ǂ̂悤�ȕ���̕����d�v���A
�ȂǂׂĂ݂邱�Ƃ��A����̕��̕ω��̂��������ɂȂ邩������܂���ˁB
���ɁA���Ȃ͕���̕���������傫���̂ŁA
�����ɕK�v�ȕ��������߂���A
�Ɍ����Ă��L���ɏ�����i�߂Ă����ޗ��ɂ��Ȃ�܂�����ˁB
�c�v���Ă���ȏ�ɁA�܂Ƃ܂肪���Ă��Ȃ���������܂���B�B�B
�v�����܂܂ɁA�v���̏���Â��Ă݂܂����B
����͗́E���͂��܂Ƃ߂Ă����܂��B