理科、頑張ってるね！

こんにちは、YOSHIOです。
今回は力の７回目、フックの法則です。
力の大きさにばねが関わった分野の計算です。
とにかく計算は肩の力を抜いて、読み進めてみてくださいね。


…過去に、塾生から妙な質問を受けたことが何度もあります。
「先生、どうしてばねの長さを計算しようとしたの？」
…正直、そんなこと分からないです…。
もちろん、答えられる訳がありません…。
けれど、このような質問・疑問を持っていることが、嬉しいんですよね。
少しでも理科に興味を持ってもらえている気がするので。



それでは、今回のテーマであるフックの法則とは、
ばねののびが、加えた力の大きさに比例する性質を指します。
文章にある通り、ばねののびと力の大きさだけ見ればOKです。


実際の基本問題は、下のように出題されます。
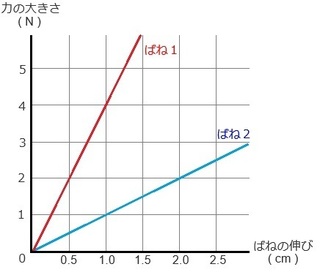
例）次のグラフのように、ばね１とばね２それぞれに力を加えた時の
ばねが伸びた長さを示している。

(1) 力の大きさとばねの伸びにはどのような関係があるか。
(2) (1)から分かる性質を何というか。
(3) ばね１に６ N の力を加えたら、ばねは何 cm 伸びるか。
(4) ばね２が１０ cm 伸びた時、何 N の力を加えた時か。


(1) 力の大きさとばねの伸びの関係は、
　比例関係です。
　もし、「比例関係が分からない…」という場合は、
　質問くださって大丈夫ですからね。
　ありがたいことに、この力の大きさとばねの伸びの関係は、
　比例関係しか出てきません。
　最悪、比例関係という言葉を知っておくだけでもOKです。

(2) 力の大きさとばねの伸びの関係からわかる性質は、 フックの法則です。
　余談ですが、しばらく前までは「どんな法則か？」と
　出題されることが多かったですが、
　最近では「どんな性質か？」という出題も増えています。
　言葉に惑わされないように注意してみてくださいね。



では、ここからは、計算ですね。もう一度問題を確認です。
(3) ばね１に６ N の力を加えたら、ばねは何 cm 伸びるか。
(4) ばね２が１０ cm 伸びた時、何 N の力を加えた時か。

…ありがたいことに！
グラフで出題されたら、特別な計算公式は必要ありません！
数学で習いますが、比例式を使って解きます。


(3) ばね１のグラフを見てみましょう。
　まずは、グラフで分かりやすい点を１つだけ見つけます。
　ばねの伸びが０．５ cm の時、力の大きさが２N ですよね。
　この数値を使って、０．５cm：２N　で比の式を作ります。

　次に、問題から６N の時のばねの伸びを求めるので、
　求めるものを X (cm) とすると、X cm：６N　で同じように式を作ります。

　そして、作れた２つの比の式を「＝」でつなげます。
　　０．５cm：２N ＝ X cm：６N
　この式を解けば、答え１．５cm と求められます。


改めて、(3)を元にグラフを使ったフックの法則問題の解き方は、
�@ グラフから数値が分かる１点を使って比の式を作る
�A 問題から求めるものを文字で置いて比の式を作る
�B �@＝�Aの比例式を作って解く
※ 比の式は、単位の順番をそろえるようにしましょう。

失敗しても良いので、チャレンジすることで感覚がつかめてきますからね。



では、最後に(4)を上記の解き方で解きます。
�@ グラフから数値が分かる１点を使って比の式を作る
　ばねののびが１．０cm の時に、力の大きさが１N なので、
　　　１．０cm：１N　で比の式です。

�A 問題から求めるものを文字で置いて比の式を作る
　問題から、ばねの伸びが１０ cmの時の力の大きさなので、
　求めるものを Y (N) とすると、　
　　　１０cm：Y N　で比の式です。
　
�B �@＝�Aの比例式を作って解く
　　　１．０cm：１N ＝ １０cm：Y N
　この比例式を解いて、答えは１０N　ですね。




では、今回のフックの法則については３つのポイント。
�@ フックの法則は、ばねの伸びと力の大きさが比例関係
�A 計算問題は比例式を作って攻略
�B 比の式を作る時は、単位の順番をそろえる
文章問題にグラフがあるだけで身構えますが、
グラフ＝計算を解くサポートキャラ
みたいな感じで思えるようになると、気分が楽になってきますからね。
次回で力・圧力は最後なので、
もうひと踏ん張り、あと少し、頑張ってみませんか？


※ 最後まで読んで頂いてありがとうございました！
このブログ中にもありましたが、
「比例式」やら「グラフの見方」やら、
分からないことがあれば、コメントで記入して頂けましたら、
ブログで改めて説明する場を作りたいと思います。